LAMPIRAN
A
(Data Teknis Sistem Tenaga)Keterangan:
VA Base = 258.8 MVA V Base = 275 kV
A.1 Data Generator Pangkalan Susu
Tabel A1 Data Generator PLTU Pangkalan Susu
Parameter Satuan Nilai
Produsen Beijing Beizhong Steam Turbine
Generator Co.,Ltd.
Kecepatan Nominal rpm 3000
Jumlah Kutub - 2
A.2 Saluran Transmisi
Tabel A.2 Reaktansi Saluran Transmisi Parameter X
Tabel A.3 Reaktansi Transformator Daya
Variabel Nilai Satuan
Daya nominal 260 MVA
V nominal 300 kV
R 0,003365 pu
j XL 0,16825 pu
A.4 Total Reaktansi Diluar Generator
Tabel A.4 Reaktansi Total
Sumber R j XL
Transformator 0,003365 0,16825 Saluran Transmisi 0,02439 0,21026
R total 0,027755
B
Penalaan PSSB.1 Hasil Penalaan PSS
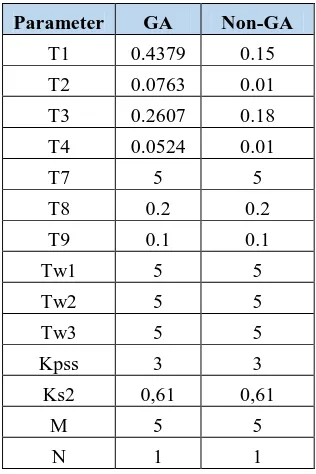
Tabel B.1 Hasil Penalaan Parameter PSS
Parameter GA Non-GA
T1 0.4379 0.15 T2 0.0763 0.01 T3 0.2607 0.18 T4 0.0524 0.01
T7 5 5
T8 0.2 0.2
T9 0.1 0.1
Tw1 5 5
Tw2 5 5
Tw3 5 5
Kpss 3 3
Ks2 0,61 0,61
M 5 5
47
DAFTAR PUSTAKA
[1] Kundur P., “Power System Stability and Control”, McGraw-Hill, New York,
1994
[2] Adi Soeprijanto, “Desain Kontroler Untuk Kestabilan Dinamik Sistem Tenaga
Listrik”, ITS Press, Surabaya, 2012
[3] Rashidi Mehran, Rashidi Farzan & Monavar Hamid, “Tuning of Power System
Stabilizer via Genetic Algorithm for Stabilization of Power Systems”, IEEE,
2003
[4] Michael J. Basler & Richard C. Schaefer, “Understanding Power System
Stability”, IEEE 2005
[5] Mondal Debasish, Chakrabarti Abhijit & Sengupta Aparajita, “Power System
Small Signal Stability Analisis and Control”, Academic Press, Oxforfd, 2014
[6] Robandi, Imam. “Modern Power System Control”, Penerbit Andi, Yogyakarta,
2009
[7] Santoso Ari, Pramonohadi Sasongko, Suharyanto. “Kombinasional AVR dan
PSS Generator Dengan Kendali Logika Fuzzy Dan Konvensional Pada
Peredaman Osilasi Frekuensi Rendah”, Seminar Nasional Komputer dan
Elektro Universitas Surakarta. 2012
[8] State Grid Hubei Electric Power System Institute. “Test Report for Power
System Stabilizer (PSS) of Indonesia Medan Power Plant (Unit 1)”, PLTU
48
[9] Beijing Jisi Electric Co., Ltd. “GEC-300 Excitation Control System Technical
Instruction”, Beijing, 2007
[10] The Institute of Electrical and Electronics Engineers. “IEEE Recommended
Practice for Excitation System Models for Power System Stability Studies”,
IEEE, New York, 1992
[11] Andrea Angel Zea.“Power System Stabilizers for The Synchronous Generator
(Tuning and Performance Evaluation)” Master Thesis, Chalmers Institute of
Technology, Gotheburg, Sweden. 2013
[12] Paul Malvino & David J. Bates. ”Electronics Principles”, McGraw-Hill Higher
Education. 2006
[13] A. Murdoch, S. Venkataraman, R.A. Lawson, and W.R. Pearson. “Integral of
Accelerating Power Type PSS : Part 1-Theory, Design, and Tuning
Methodology”, IEEE Transaction on Energy Conversion. 1999
[14] Norman S. Nise. “Control Systems Engineering”, John Wiley & Sons, Inc.
New Jersey. 2010
[15] G. Berube & L.M. Hajagos.”Accelerating-Power Based Power System
Stabilizers”, IEEE Tutorial Course-Power System Stabilization. 2007
[16] Katsuhiko Ogata. “Modern Control Engineering”, Fifth Edition. Pearson
Education, Inc. New Jersey, 2010
[17] T. Sutojo, Edy Mulyanto, and Vincent Suhartono. “ Kecerdasan Buatan”,
49
[18] Trujilo Hugo, Torres Cisneros & Chavez J.C., “Tuning of Power System
Stabilizer Using Genetic Algorithms”, IEEE, 2014
[19] Sri Kusumadewi & Hari Purnomo.,”Penyelesaian Masalah Optimasi dengan
Teknik-Teknik Heuristik”, Graha Ilmu, Yogyakarta, 2005
[20] Napitupulu, James. “Antarmuka Grafis Pengaturan Parameter PSS di PLTU 2
24
METODE PENELITIAN 3.1 Tempat dan Waktu
Penelitian telah dilakukan di PLTU 2 Sumut Pangkalan Susu yang memiliki
kapasitas sebesar 2 x 2x220 MW. PLTU tersebut terhubung ke Gardu Induk Binjai
melalui saluran transmisi 275 kVsepanjang ±70 km. Penelitian telah dilaksanakan
selama empat bulan dimulai dari bulan Juli hingga November 2015.
3.2 Data dan Peralatan
Data yang digunakan dalam penelitian ini adalah:
1. Data teknis generator PLTU 2 Sumut Pangkalan Susu pada Lampiran A.1
2. Data teknis PSS (Power System Stabilizer) dan AVR (Automatic Voltage
Regulator)
3. Data teknis transformator yang meliputi impedansi, daya nominal dan
tegangan nominal pada Lampiran A.3
4. Data teknis saluran transmisi yang meliputi panjang dan impedansi saluran
transmisi pada Lampiran A.2
5. Data beban harian generator untuk mencari data beban maksimum yang akan
digunakan untuk penalaan PSS
Sedangkan peralatan yang digunakan dalam penelitian ini adalah perangkat
lunak Matlab dan Simulink untuk melakukan pemrograman dan simulasi pengujian.
3.3 Variabel yang Diamati
25
1. Pe : Deviasi output daya elektrik generator selama gangguan. Variabel ini
menunjukkan keandalan sistem eksitasi sehingga secara tidak langsung
menunjukkan keandalan PSS.
2. ω : Kecepatan sudut rotor. Variabel ini juga menunjukkan keandalan PSS
dalam bekerja selama gangguan.
3. Settling time (waktu stabil) dan overshoot (amplitudo pada osilasi pertama)
dari ω dan Pe. Semakin kecil settling time dan overshoot maka menunjukkan
bahwa kinerja PSS yang ditala dengan Algoritma Genetika semakin baik.
3.4 Prosedur Penelitian
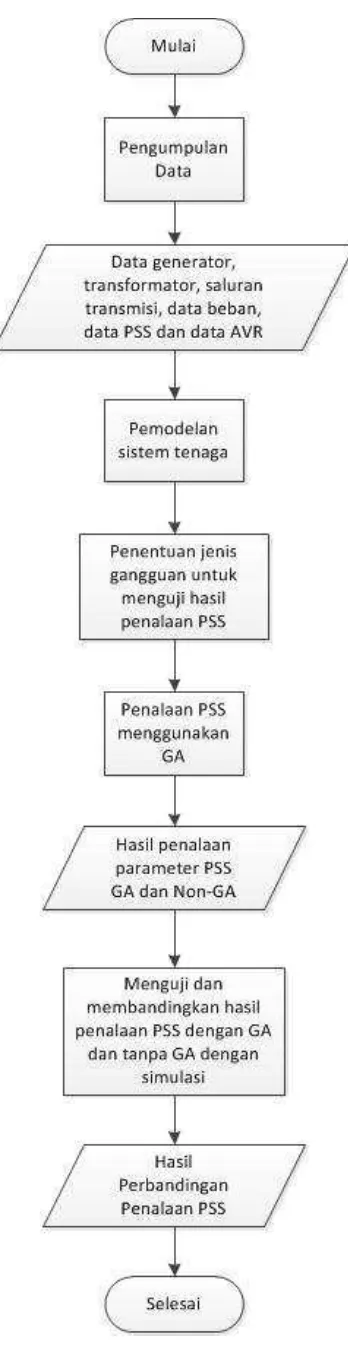
Penalaan PSS PLTU Pangkalan Susu meliputi serangkaian proses yang
panjang meliputi pengumpulan data, studi literatur, pemodelan matematis sistem,
penentuan jenis gangguan, pengujian hasil penalaan PSS, membandingkan penalaan
PSS bawaan dengan penalaan menggunakan Genetic Algorithm dan tahap terakhir
yaitu penarikan kesimpulan. Keseluruhan proses penelitian ditampilkan secara visual
26
27 3.4.1 Pelaksanaan Penelitian
Berdasarkan diagram alir pada Gambar 3.1 langkah-langkah yang dilakukan
selama penelitian adalah sebagai berikut:
1. Pengumpulan data
Data yang diperlukan pada penelitian ini terdiri dari:
-Data teknis pada Lampiran A1-A3 yang diperoleh dari PLTU Pangkalan
Susu
-Data setelan parameter PSS yang diperloleh secara real time dari unit sistem
eksitasi PLTU Pangkalan Susu yang terdapat pada Lampiran B.1
2. Pemodelan Sistem Tenaga
PLTU 2 Sumut Pangkalan Susu memiliki 2 generator dengan kapasitas
masing-masing sebesar 220 MW, namun penelitian ini hanya memasukkan
salah satu generator saja yaitu pembangkit unit 1 untuk dijadikan obyek
penelitian. Pemodelan yang dilakukan adalah sebagai berikut:
a. Pemodelan generator, transformator daya dan saluran transmisi
menjadi bentuk SMIB (Single Machine Infinite Bus), dengan kondisi
pembebanan yang sudah ditentukan maka konstanta K1-K6 dihitung
untuk membuat model SMIB yang dapat digunakan untuk penalaan
PSS.
b. Pemodelan PSS dan AVR, SMIB digabung dengan AVR dan PSS
untuk membuat model yang lengkap dari sistem tenaga
Model matematis yang diperoleh dari kedua langkah diatas kemudian
28
3. Menentukan jenis gangguan yang digunakan dalam pengujian hasil penalaan
PSS, yaitu:
a) Perubahan beban pada saat pembebanan maksimum:
- Penurunan beban 10%
- Kenaikan beban 10%
- Penurunan beban 20%
b) Pemutusan beban dalam jumlah yang besar
- Pemutusan beban 50%
4. Setelah membuat model sistem tenaga, dilakukan penalaan PSS
menggunakan GA dengan cara seperti pada Sub bab 3.4.2.
5. Melakukan pengujian hasil penalaan PSS dengan parameter bawaan terhadap
jenis gangguan yang sudah ditentukan, kemudian dilakukan juga pengujian
yang sama terhadap PSS yang telah ditala menggunakan GA. Variabel yang
diperhatikan adalah kecepatan sudut rotor ω dan daya elektrik Pe.
6. Saat terjadi gangguan, kecepatan sudut rotor ω dan daya elektrik Pe akan mengalami osilasi, hasil penalaan PSS dibandingkan dengan cara mengukur
nilai overshoot (amplitudo osilasi pertama) dan settling time (waktu menuju
stabil) kemudian diperoleh hasil perbandingan diantara keduanya.
7. Dari hasil perbandingan yang diperoleh, maka dapat ditarik beberapa
kesimpulan
8. Selesai
29
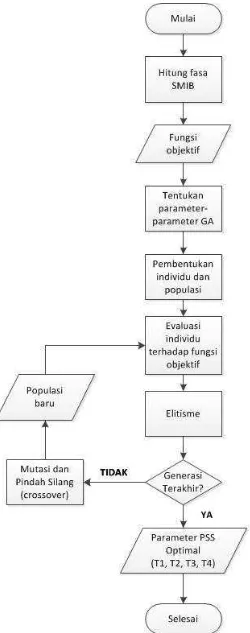
GA diterapkan untuk penalaan PSS menggunakan bahasa pemrograman
Matlab. Berdasarkan diagram alir pada Gambar 3.2, penalaan PSS menggunakan GA
dilakukan dengan langkah-langkah sebagai berikut:
1. Menghitung keterlambatan fasa SMIB dengan Persamaan (2.10) – (2.13)
2. Menyusun fungsi objektif berdasarkan keterlambatan fasa dari SMIB
3. Menentukan parameter-parameter GA
4. Pembentukan individu dan populasi
5. Elitisme
6. Pindah Silang
7. Mutasi
8. Mengulangi langkah 1-7 hingga generasi terakhir
9. Selesai
Parameter PSS yang dioptimalkan dengan GA adalah T1, T2, T3 dan T4
sedangkan parameter lainnya dibiarkan tetap sama seperti yang ditunjukkan pada
30
31
HASIL PENELITIAN DAN PEMBAHASAN 4.1 Pemodelan Sistem Tenaga
Berdasarkan data-data teknis yang diperoleh, PLTU 2 Sumut Pangkalan Susu
dimodelkan seperti pada gambar berikut ini:
Gambar 4.1 Pembangkit Tunggal-Bus Tak Hingga (SMIB)
Gambar 4.1 adalah model pembangkit tunggal yang terhubung dengan bus
tak-hingga yang dibuat secara manual untuk memberikan gambaran tentang obyek
penelitian. Rtotal dan XLtotal pada Gambar 4.1 berturut-turut adalah total resistansi dan
total reaktansi yang nilainya diberikan pada Lampiran A.4.
Setelah mendapatkan model skematik, maka Konstanta K1sampai K6 pada
Gambar 4.2 dihitung untuk mendapatkan model matematis dari sistem. Kondisi
pembebanan yang dipilih adalah sebagai berikut:
- Tanggal Pencatatan Beban : 20 Juli 2015 (Pukul 14.30 WIB)
- Beban P dan Q : 220 MW, 81 MVAR
Berdasarkan kondisi diatas, nilai K1-K6 dihitung menggunakan Matlab sesuai
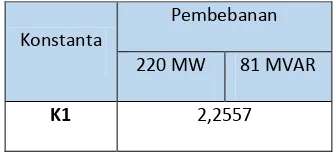
dengan Persamaan (2.21)-(2.27), hasilnya diberikan pada Tabel 4.1.
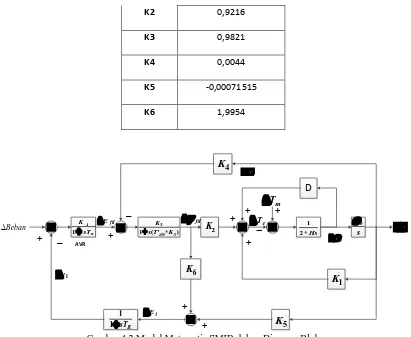
Tabel 4.1 Konstanta K1-K6
Konstanta
Pembebanan
220 MW 81 MVAR
32
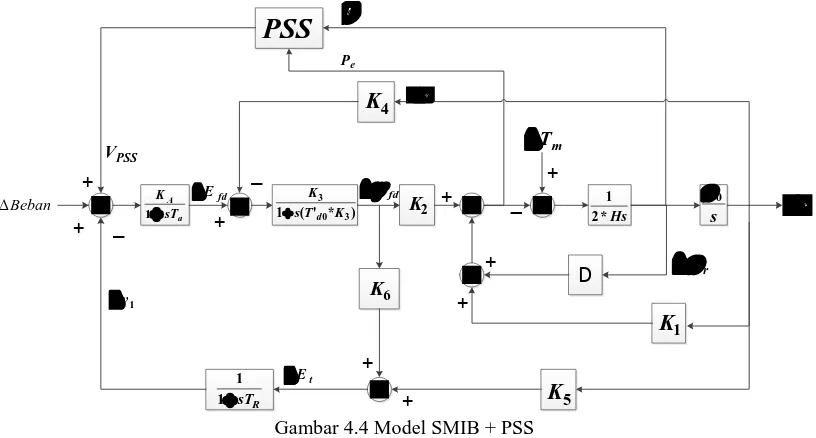
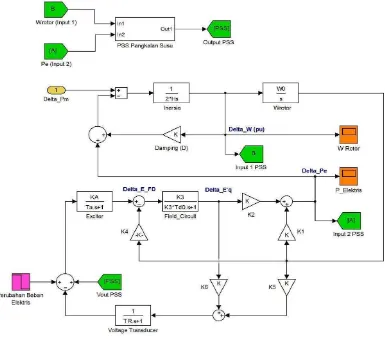
Gambar 4.2 Model Matematis SMIB dalam Diagram Blok 4.1.1 Power System Stabilizer (PSS)
PSS yang terpasang pada PLTU Pangkalan Susu ditunjukkan dalam diagram
blok pada Gambar 4.4.
Gambar 4.3 Power System Stabilizer pada GEC-300
33
Gabungan dari Gambar 4.2 dan 4.3 menghasilkan Gambar 4.4 yang merupakan
model matematis pembangkit yang dilengkapi dengan PSS, model tersebut sudah
dapat digunakan untuk melakukan simulasi di Simulink (Matlab).
2
Gambar 4.4 akan dibuat menggunakan Simulink untuk menguji hasil penalaan
PSS, baik yang menggunakan GA dan tanpa GA.
4.2 Penalaan PSS dengan Genetic Algorithm (GA)
Proses penalaan PSS dengan GA melalui beberapa langkah awal diantaranya
menghitung kompensasi fasa dan menyusun fungsi objektif, oleh karena itu harus
dilakukan beberapa proses perhitungan terlebih dahulu, kemudian dapat
menggunakan GA untuk mendapatkan parameter PSS yang optimal.
Penerapan GA dalam penalaan PSS dilakukan dengan bahasa pemrograman
Matlab, parameter yang didapatkan melalui GA diasumsikan sebagai hasil penalaan
optimal yang mampu membuat kinerja PSS menjadi lebih baik dari sebelumnya.
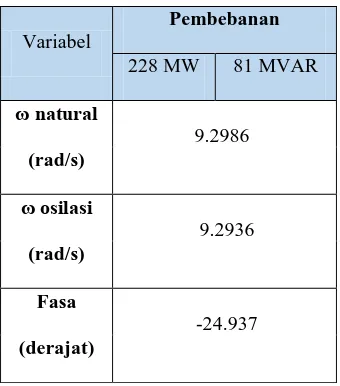
4.2.1 Penyusunan Fungsi Objektif GA
Frekuensi natural, frekuensi osilasi dan sudut fasa dari SMIB dihitung
34
dapat bekerja dengan baik.
(4.1)
Persamaan (4.1) adalah fungsi selisih antara sudut fasa yang dihasilkan SMIB
dan PSS. Fungsi tersebut disebut fungsi objektif yang digunakan untuk mengevaluasi
individu dalam GA. Setelah mendapatkan fungsi objektif, langkah selanjutnya
adalah menentukan parameter-parameter dalam GA.
4.2.2 Parameter GA
Untuk melakukan iterasi di dalam GA, parameter-parameter nya harus
ditentukan terlebih dahulu. Parameter GA yang digunakan dalam penalaan PSS
adalah sebagai berikut:
1. Individu
Parameter PSS yang dioptimalkan pada penelitian adalah T1-T4, sehingga
individu dalam GA memiliki 4 gen dengan bentuk seperti pada Tabel 4.3.
35
Gen 1 Gen 2 Gen 3 Gen 4
T1 T2 T3 T4
2. Populasi
Menurut Sri Kusumadewi [19], untuk sembarang masalah ukuran populasi
sebaiknya tidak lebih kecil dari 30, oleh karena itu pada penelitian ini
populasi berukuran 30 individu. Pembentukan populasi awal dilakukan
dengan memilih nilai T1-T4 secara acak (random) dengan batas-batas
sebagai berikut:
(4.2)
(4.3)
(4.4)
(4.5)
Berdasarkan batas atas dan batas bawah untuk T1, T2, T3 dan T4 pada
Persamaan (4.2) – (4.5), populasi awal dapat dibentuk sesuai dengan Persamaan (4.6) dan (4.7).
(4.6)
(4.7)
dimana:
i : individu ke-i dalam populasi, nilai i = 30
T1i, T2i, T3i, T4i : gen-gen dalam individu ke-i
rand : bilangan acak dalam interval 0-1
36
Tiap individu dalam populasi dievaluasi menggunakan fungsi objektif dan
dihitung nilai yang dihasilkannya. Berdasarkan yang dihasilkan, tiap
individu diurutkan dari yang paling baik hingga yang paling buruk.
4. Elitisme
Pada penelitian ini, dua individu terbaik dalam satu generasi disalin dan akan
digantikan jika terdapat dua individu yang lebih baik pada generasi
berikutnya.
5. Jumlah Generasi
Jumlah generasi adalah jumlah proses iterasi dalam GA, dalam penelitian ini
jumlah generasi adalah 100.
6. Pindah Silang (crossover)
Metode pindah silang yang digunakan dalam penalaan PSS adalah metode
pindah silang seragam, dengan cara sebagai berikut [2, 19]:
Individu 1 Individu 2
T1 T2 T3 T4
T1' T2' T3' T4'
Hasil pindah silang:
Individu baru 1 Individu baru 2
T1 T2' T3 T4'
T1' T2 T3' T4
Masing-masing individu secara berselang seling bertukar gen-gen sehingga
37 7. Mutasi
Proses mutasi yang digunakan dalam penalaan PSS adalah mutasi seragam
yang dilakukan dengan mengganti gen tertentu dari individu dengan nilai
random antara gen terbesar dan gen terkecil didalam individu tersebut.
Bila gen pertama didalam individu terpilih untuk
melakukan mutasi, maka individu baru dari hasil proses mutasi menjadi
, dimana TM adalah [2]:
TM = rand*(gen terbesar-gen terkecil) (4.8)
dimana :
gen terbesar : nilai terbesar antara T1 sampai T4
gen terkecil : nilai terkecil antara T1 sampai T4
rand : bilangan acak dalam interval 0-1
4.2.3 Hasil Penalaan PSS dengan GA
Setelah dilakukan optimumisasi dengan GA, didapatkan satu set parameter
PSS yang diasumsikan dapat bekerja dengan optimal yang diberikan pada Tabel 4.4.
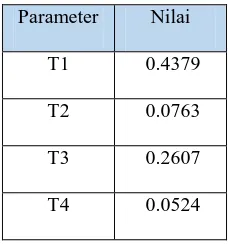
Tabel 4.4 Hasil Penalaan Parameter PSS dengan GA
Parameter Nilai T1 0.4379 T2 0.0763 T3 0.2607 T4 0.0524
Nilai T1, T2, T3 dan T4 pada Tabel 4.4 nantinya akan dimasukkan kedalam
rangkaian simulasi pada Gambar 4.5 untuk menguji keberhasilan GA dalam
38 4.3 Pengujian Hasil Penalaan PSS
Hasil penalaan PSS baik yang menggunakan GA dan tanpa menggunakan GA
harus diuji untuk mengetahui keandalannya. Pengujian dilakukan dengan simulasi
menggunakan Simulink dengan rangkaian simulasi ditunjukkan pada Gambar 4.5.
Karaktrerisitik hasil pengujian yang diperhatikan untuk melihat keandalan
penalaan PSS adalah nilai overshoot dan settling time dari osilasi kecepatan sudut
rotor dan daya elektrik generator.
Gambar 4.5 Rangkaian simulasi dalam Simulink
Rangkaian simulasi pada Gambar 4.5 memiliki setelan waktu simulasi selama
20 detik, output sistem yaitu P dan ω diamati dengan menggunakan scope.
39
Parameter PSS pada Lampiran B.1 diuji dengan kondisi gangguan yang sudah
ditentukan dengan hasil sebagai berikut:
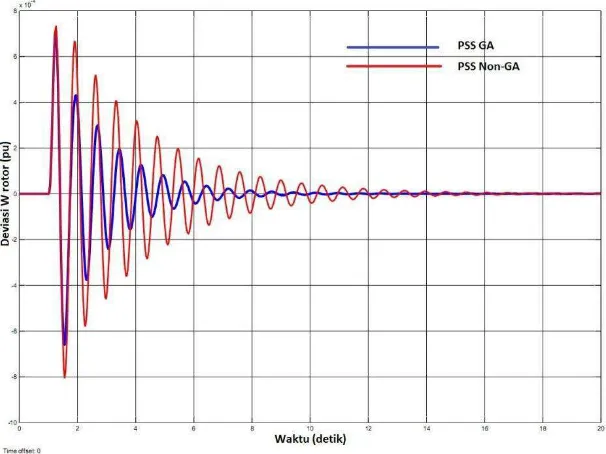
Gambar 4.6 Osilasi ω rotor pada saat beban turun 10%
Gambar 4.6 menunjukkan timbulnya osilasi kecepatan sudut rotor ketika beban
diturunkan 10% dari keadaan awal. Sama halnya dengan yang ditunjukkan pada
Gambar 4.7, gelombang osilasi daya elektrik Pe memiliki bentuk yang mirip namun
jauh berbeda magnitude-nya.
Gambar 4.6 dan 4.7 menunjukkan perbandingan hasil penalaan pada saat
penurunan beban sebesar 10 persen, terlihat peningkatan yang cukup signifikan
dalam settling time namun tidak ada peningkatan berarti pada nilai overshoot, terlihat
bahwa PSS yang ditala menggunakan GA menghasilkan settling time yang lebih
40
Gambar 4.7 Osilasi Pe pada saat beban turun 10%
Gambar 4.8 Osilasi ω rotor pada saat beban naik 10%
Ketika beban dinaikkan 10% dari keadaan awal, osilasi pada Gambar 4.8 dan
4.9 besarnya hampir sama namun dengan arah yang berlawanan dengan yang terjadi
pada saat beban diturunkan 10%.
Kinerja PSS pada kondisi ini menunjukkan bahwa PSS yang ditala
41
Gambar 4.9 Osilasi Pe pada saat beban naik 10%
Gambar 4.10 Osilasi ω rotor pada saat beban turun 20%
Respon ω dan Pe terhadap pengurangan beban sebesar 20% dari keadaan awal
ditunjukkan pada Gambar 4.10 dan 4.11. Overshoot yang terjadi lebih besar daripada
kondisi pengujian sebelumnya. PSS yang ditala menggunakan GA menghasilkan
42
Gambar 4.11 Osilasi Pe pada saat beban turun 20%
Setelah melakukan simulasi dengan variasi beban yang kecil, PSS diuji
kinerjanya dengan menerapkan gangguan pemutusan beban sebesar 50%. Hasilnya
diberikan pada Gambar 4.12 dan 4.13
43
Gambar 4.13 Osilasi Pe pada saat pemutusan beban 50%
Gambar 4.12 dan 4.13 menunjukkan bahwa osilasi yang timbul lebih besar lagi
daripada kondisi pengujian sebelumnya, tetapi masih dapat diredam oleh kedua hasil
penalaan PSS. Hal ini menunjukkan bahwa PSS di PLTU Pangkalan Susu dapat
bekerja pada gangguan yang cukup besar.
PSS yang ditala menggunakan GA memberikan kinerja yang lebih baik dari
pada PSS yang ditala tanpa menggunakan GA dalam semua kondisi pengujian yang
ditentukan, hal ini menunjukkan keberhasilan penerapan GA untuk penalaan PSS di
PLTU 2 Sumut Pangkalan Susu.
Perbandingan yang lebih detil dari kedua hasil penalaan PSS diberikan pada
Tabel 4.5, data tersebut menunjukkan bahwa untuk nilai overshoot, perbedaan
diantara keduanya tidak begitu jauh, sedangkan pada nilai settling time PSS yang
44
Tabel 4.5 Perbandingan Hasil Penalaan PSS
GA Non-GA GA Non-GA GA Non-GA GA Non-GA Beban Turun 10% 10,5 16,5 10,5 16,5 0,000710 0,0007315 -0,0425 -0,0425
Beban Naik 10% 10,5 16,5 12,5 16,5 -0,000705 -0,0007315 0,0425 0,0425
Beban Turun 20% 12,5 18 12,5 18 0,001410 0,0014500 -0,0850 -0,0850
Beban Turun 50% 13 18,5 13 18,5 0,003527 0,0036250 -0,2125 -0,2125
Settling Time (detik) Kecepatan Sudut Daya Listrik Jenis Gangguan
Overshoot (pu)
Kecepatan Sudut Daya Listrik
Hasil perbandingan penalaan PSS yang diberikan pada Gambar 4.6 – Gambar
4.13 dan Tabel 4.5 menunjukkan bahwa gangguan-gangguan yang terjadi pada
sistem menyebabkan osilasi pada ω dan Pe dengan amplitudo yang kecil (< 2 Hertz) , hal ini sesuai dengan lingkup penelitian tugas akhir ini yaitu small signal stability.
4.3.2 Penerapan Penalaan PSS dengan GA
Hasil penalaan PSS dengan GA dapat diterapkan dengan mengganti parameter
lama dengan parameter baru di kubikel PSS di PLTU Pangkalan Susu.
Gambar 4.14 Pengaturan Parameter PSS di Pangkalan Susu [20]
Gambar 4.14 menunjukkan tampilan perangkat lunak dari kubikel PSS yang
dapat digunakan untuk mengubah parameter PSS, dari gambar tersebut dapat dilihat
45
parameter PSS bawaan dari Pangkalan Susu (T1, T2, T3 dan T4). Nilai T1, T2, T3
dan T4 yang tersimpan diganti dengan menekan tombol-tombol yang dilingkari garis
kuning, setelah menekan tombol tersebut, nilainya diubah dengan menekan
tombol-tombol yang dilingkari garis biru sampai muncul angka yang sesuai dengan
parameter PSS yang baru.
Setelah mengubah nilai T1, T2, T3 dan T4, harus dilakukan konfirmasi dengan
menekan tombol ”Modification Confirm” yang dilingkari garis hijau pada Gambar
4.14, langkah terakhir adalah dengan menyimpan parameter PSS yang baru dengan
46 Bab 5
Kesimpulan dan Saran 5.1 Kesimpulan
Setelah memperoleh hasil penelitian dan pembahasan, penulis menarik
kesimpulan sebagai berikut:
1. PSS yang ditala menggunakan GA menunjukkan peningkatan yang
signifikan pada nilai settling time pada semua kondisi gangguan
2. Perbandingan nilai overshoot kecepatan rotor dan daya elektrik yang muncul
pada semua kondisi gangguan menunjukkan bahwa PSS yang ditala
menggunakan GA tidak menunjukkan peningkatan yang berarti pada
overshoot osilasi.
3. Secara keseluruhan PSS PLTU Pangkalan Susu yang ditala menggunakan
GA bekerja lebih baik dalam meredam osilasi dibandingkan dengan PSS
yang ditala tanpa menggunakan GA
5.2 Saran
Untuk tujuan pengembangan dari tugas akhir ini, kepada peneliti yang berniat
melanjutkan penelitian pada subjek yang sama, penulis memberikan saran sebagai
berikut:
1. Menggunakan metode algoritma lain untuk penalaan parameter PSS seperti
PSO (Particle Swarm Optimization) atau BFA (Bacterial Foraging
Algorithm)
2. Menggunakan sistem multimesin sehingga mampu mengoptimalkan sistem
4
Pada penelitian ini jenis kestabilan yang diteliti adalah small signal stability,
yaitu kestabilan sistem tenaga saat mengalami gangguan-gangguan yang kecil.
Berbeda dengan gangguan transien yang jarang terjadi, gangguan kecil pada sistem
tenaga sering muncul sebagai dampak dari dinamika sistem tenaga itu sendiri.
Gangguan kecil pada sistem tenaga contohnya adalah perubahan beban pada
pembangkit yang mengakibatkan osilasi pada kecepatan putar generator sehingga
mengganggu keserempakan dari sistem tenaga.
2.1.1 Sudut Rotor (δ)
Pada sistem dengan interkoneksi, rotor dari semua generator sinkron harus
berputar pada kecepatan yang sama (serempak). Selama operasi keadaan mantap,
daya listrik yang keluar dari generator harus seimbang dengan daya mekanis yang
masuk ke generator.
Daya input mekanis ke generator adalah hasil perkalian antara torsi dan
kecepatan rotor, PM = TMω. Hal ini diilustrasikan pada Gambar 2.1, torsi elektrik
akan muncul untuk melawan torsi mekanis karena ada beban yang disuplai oleh
generator, untuk mempertahankan operasi dalam kondisi tunak, setiap saat nilai torsi
mekanik Tm harus seimbang dengan torsi elektrik Te [4].
Gambar 2.1 Interaksi torsi mekanik dan elektrik pada generator [4]
Saat mengalami gangguan kecil, seperti variasi jumlah beban dan
5
dengan cepat, tetapi daya mekanik yang masuk ke generator berubah dengan lambat.
Karena adanya perbedaan respon kecepatan, muncul perbedaan temporer pada
keseimbangan daya (mekanik dan elektrik) pada rotor, menyebabkan rotor
mengalami percepatan atau perlambatan, tergantung pada perbedaan nilai Tm dan Te.
Karena kecepatan rotor berubah, maka sudut relatif rotor juga berubah. Gambar 2.2
menunjukkan hubungan antara sudut rotor, δ, GGM stator, F1, dan GGM rotor, F2.
Sudut rotor, δ, adalah sudut antara GGM rotor, F2, dan resultan vektor F1 dan F2,
yaitu R.
Gambar 2.2 GGM rotor, stator, resultan GGM dan sudut torsi [4] 2.1.2 Osilasi pada SMIB
Untuk menganalisis fenomena osilasi kecil pada generator sinkron, suatu
pembangkit dapat dimodelkan menjadi bentuk Single Machine Infinite Bus (SMIB)
yang merupakan sebuah pembangkit tunggal yang menyuplai daya ke suatu jaringan
listrik yang sangat besar sehingga diwakilkan oleh bus tak hingga. Pemodelan
generator menjadi SMIB diperkenalkan oleh Heffron dan Phillips pada 1952 dan
telah terbukti memberikan hasil yang baik dalam analisis small signal stability [5].
Dalam pemodelan SMIB yang digunakan untuk analisis small signal stability
dilakukan asumsi-asumsi sebagai berikut [5]:
6 b) Redaman dari stator diabaikan
c) Tahanan stator dianggap nol
d) Generator dianggap sebagai sumber tegangan konstan
e) Sudut rotor sama dengan sudut fasa tegangan output generator
Gambar 2.3 Pembangkit tunggal terhubung ke bus tak hingga [5]
Gambar 2.3 menunjukkan generator yang terhubung ke bus tak hingga, Vt
adalah tegangan terminal generator yang diasumsikan konstan saat sebelum
gangguan dan Vinf adalah tegangan pada bus tak hingga. Vt lead terhadap tegangan
bus tak hingga sejauh δ° yang terus berubah selama rotor berosilasi pada saat
gangguan [1, 5].
Arus yang mengalir pada sistem tenaga adalah [1] :
(2.1)
Daya kompleks generator diberikan dengan [1] :
(2.2)
Tahanan stator diabaikan agar torsi elektrik Te sama besarnya dengan daya listrik P,
sehingga [1] :
(2.3)
7
(2.4)
Menggunakan swing equation [1] :
(2.5)
(2.6)
dimana adalah deviasi kecepatan sudut rotor dalam satuan per unit, δ adalah
sudut rotor dalam radian, adalah base kecepatan sudut rotor dalam radian per
detik dan p adalah operator diferensial d/dt dengan t dalam detik.
Linearisasi Persamaan (2.5) menghasilkan dan substitusi Te dari Persamaan
(2.4) menghasilkan [1]:
(2.7)
dimana Ks adalah koefisien torsi sinkronisasi sebagai berikut [1]:
(2.8)
linearisasi Persamaan (2.7) menghasilkan [1]:
(2.9)
persamaan (2.7) dan (2.9) jika dituliskan dalam bentuk matriks menjadi [1]:
(2.10)
Persamaan (2.10) menunjukkan bahwa deviasi kecepatan sudut rotor
bergantung pada parameter sistem yaitu D, H, R, jXL dan kondisi operasi awal yang
diwakilkan dengan Vt dan . Matriks pada Persamaan (2.10) dapat dibentuk
8
Gambar 2.4 Diagram blok SMIB sederhana [5] Diagram blok pada Gambar 2.4 memberikan [1]:
(2.11)
Persamaan (2.11) disusun kembali menjadi [1]:
(2.12)
persamaan karakteristik dari Persamaan (2.14) adalah [5]:
(2.13)
Persamaan (2.13) sudah dalam bentuk umum seperti Persamaan (2.14) berikut [5]:
(2.14)
dengan akar-akar dari Persamaan (2.16) adalah [5]:
(2.15)
akar-akar pada Persamaan (2.15) adalah frekuensi natural dari rotor yaitu [5]:
(2.16)
dan rasio redaman adalah [1]:
9 maka frekuensi osilasi adalah [1]:
(2.18)
Persamaan (2.14) sampai (2.18) menunjukkan bahwa osilasi pada rotor
generator sinkron akan muncul jika ζ < 1, sedangkan osilasi pada SMIB tidak akan
muncul jika mengikuti Persamaan (2.19) [1] :
(2.19)
Persamaan (2.19) menunjukkan bahwa osilasi pada SMIB bergantung pada
nilai D, Ks, H dan ω0. Karena D, H dan ω0 nilainya tetap maka osilasi bergantung
pada nilai Ks. Ks adalah torsi sinkronisasi berupa torsi elektrik yang rumusnya
diberikan pada Persamaan (2.20) [1].
(2.20)
dimana:
K1 : Konstanta sinkronisasi torsi mekanik dan torsi elektronik
K2 : Konstanta efek perubahan tegangan internal generator terhadap Tm
: Perubahan sudut rotor
: Perubahan fluks rangkaian medan
Penjelasan mengenai Konstanta K1 dan K2 pada Persamaan (2.20) akan
diberikan pada subbab selanjutnya yaitu pembuatan model lengkap SMIB.
Berdasarkan frekuensi yang dihitung menggunakan Persamaan (2.18), osilasi
pada sistem tenaga terbagi atas beberapa jenis. Jenis – jenis osilasi pada sistem
tenaga dengan interkoneksi dan saluran transmisi yang banyak adalah sebagai
10
Gambar 2.5 Osilasi antar-unit (inter-unit oscillations) [4]
Inter-unit oscillations – Jenis osilasi ini secara umum melibatkan dua atau
lebih generator sinkron pada sebuah pembangkit tenaga listrik. Generator pada
Gambar 2.5 saling berayun satu sama lain, dengan frekuensi berkisar antara 1.5
sampai 3.0 Hertz.
Gambar 2.6 Osilasi mode lokal (local-mode oscillations) [4]
Local mode oscillations – Osilasi ini terjadi antara satu atau lebih generator
sinkron pada pembangkit relatif terhadap sistem tenaga atau pusat beban seperti yang
tampak pada Gambar 2.6. Rentang frekuensinya dari 0.7 - 2 Hertz. Jenis osilasi ini
akan semakin menjadi masalah saat pembangkit dalam kondisi beban dan sistem
transmisi dengan reaktansi yang tinggi.
Gambar 2.7 Osilasi antar-area (inter-area oscillations) [4]
Inter-area oscillations – Osilasi ini melibatkan kombinasi dari ayunan
beberapa mesin pada suatu bagian sistem tenaga terhadap bagian lain seperti yang
ditunjukkan pada Gambar 2.7. Frekuensinya berada pada rentang dibawah 0.5 Hertz.
11
Gambar 2.4 menunjukkan diagram blok SMIB yang paling sederhana, dalam
penelitian ini ditambahkan pengendali eksitasi berupa AVR (Automatic Voltage
Regulator) sehingga diagram blok SMIB menjadi seperti Gambar 2.5 berikut ini:
a
generator, fungsi transfer pada bagian ini adalah rumus dari Persamaan (2.7) [2]. K1
merupakan variabel sinkronisasi, yang berfungsi sebagai penyeimbang torsi mekanik
ataupun elektrik. Fungsi transfer dalam blok B menyatakan proses yang terjadi di
AVR. Perubahan beban menyebabkan penurunan tegangan baik tegangan output
generator maupun tegangan internal generator (diwakili oleh K5 dan K6).
Perubahan tegangan ini akan membuat AVR mengatur kembali tegangan
medan agar menstabilkan tegangan. Reduksi fluksi medan (reaksi jangkar) terjadi
akibat perubahan tegangan output generator (diwakili oleh K4). Fungsi transfer pada
blok C menyatakan hubungan tegangan internal generator dengan tegangan di
rangkaian medan. Ini merupakan model paling sederhana dari AVR. Variabel K2
12
K1-K6 adalah variabel transfer yang besarnya tergantung pada konfigurasi
jaringan dan pembebanan generator [2]. Nilai K1-K6 dapat dihitung menggunakan
persamaan-persamaan berikut ini [6]:
(2.21)
(2.22)
(2.23)
(2.24)
(2.25)
(2.26)
dimana :
(2.27)
Vinf : tegangan bus tak hingga
13
Re : jumlah resistansi antara generator dan bus tak hingga
Xe : jumlah reaktansi antara generator dan bus tak hingga
α : sudut antara tegangan dan arus generator
Xd : reaktansi stator sumbu d
X’d : reaktansi transien stator sumbu d
Model sistem tenaga pada Gambar 2.7 digunakan untuk mencari keterlambatan
fasa yang harus dikompensasi oleh PSS dengan cara sebagai berikut [2]:
(2.28)
(2.29)
(2.30)
Persamaan (2.28) digunakan untuk menghitung frekuensi natural sistem,
sedangkan Persamaan (2.29) digunakan untuk menghitung frekuensi osilasi pada
sistem tenaga yang teredam akibat adanya rasio yang dihitung menggunakan
Persamaan (2.30). Keterlambatan fasa yang dihasilkan oleh SMIB selanjutnya dapat
dihitung menggunakan persamaan berikut ini [2]:
(2.31)
θSMIB yang dihitung menggunakan Persamaan (2.31) adalah keterlambatan fasa
saat terjadi osilasi, keterlambatan fasa ini dikompensasi oleh PSS agar osilasi yang
timbul dapat diredam dengan baik.
14
Power System Stabilizer (PSS) adalah perangkat kendali pada sistem eksitasi
yang berfungsi untuk memberikan redaman terhadap osilasi elektromekanis yang
timbul pada generator. PSS meredam osilasi dengan membangkitkan komponen torsi
elektronik yang sefasa dengan deviasi kecepatan rotor, sehingga dapat
mengembalikan rotor ke putaran sinkronnya. Dalam menghasilkan torsi redaman,
PSS bekerja dengan mengolah satu atau lebih dari sinyal input berupa daya output
generator, kecepatan rotor dan sudut daya [1].
Gambar 2.9 Skematik generator PLTU dengan AVR dan PSS [7]
Gambar 2.9 menunjukkan bahwa PSS berfungsi sebagai pemberi sinyal
tambahan kepada AVR dalam mengontrol eksitasi generator, dengan sinyal input
berupa kecepatan sudut rotor ω yang diukur langsung dari putaran mekanik turbin
dan daya elektrik P [7]. Bagian-bagian penyusun PSS dan cara kerjanya akan
dijelaskan pada bagian berikutnya.
2.3.1 PSS PLTU Pangkalan Susu
Generator sinkron di PLTU Pangkalan Susu dilengkapi dengan sistem eksitasi
15
Pengaturan eksitasi generator dengan GEC-300 dilakukan melalui antarmuka grafis
seperti yang ditunjukkan pada Gambar 2.10 [9].
Gambar 2.10 Antarmuka Grafis GEC-300 Excitation System [9]
PSS yang terdapat pada GEC-300 direpresentasikan dalam model matematis
yang ditunjukkan dalam diagram blok pada Gambar 2.11.
Gambar 2.11 Power System Stabilizer di generator PLTU Pangkalan Susu [8]
Berdasarkan standar IEEE 421.5 tahun 1992, PSS pada GEC-300 adalah tipe
PSS 2A dengan 2 masukan sinyal AC yaitu daya listrik dan kecepatan sudut rotor
[10].
2.3.2 Bagian-Bagian PSS di PLTU Pangkalan Susu
PSS yang dipasang pada PLTU Pangkalan Susu memiliki bagian-bagian dan
cara kerja seperti berikut ini [4,11] :
1. L
16
Filter adalah perangkat elektronik yang digunakan untuk melewatkan sinyal
dengan rentang frekuensi tertentu [12]. PSS di PLTU Pangkalan Susu dilengkapi
dengan low-pass filter dengan frekuensi cut-off [13]:
(2.32)
Gambar 2.12 Low Pass Filter [14]
Fungsi alih rangkaian pada Gambar 2.12 adalah sebagai berikut [14]:
(2.33)
dengan: dan maka:
(2.34)
dari Persamaan (2.34) kita ketahui bahwa parameter T7 dalam Gambar 2.11 secara
fisik adalah nilai RC, dengan mengatur nilai T7, kita dapat mengatur frekuensi yang
masuk ke dalam PSS.
2. R
amp-track Filter
Ramp-track filter adalah low-pass filter bertingkat (multipole) yang berfungsi
untuk membatasi perubahan yang sangat cepat dari daya elektrik agar
karakteristiknya mirip dengan sinyal kecepatan rotor yang bergantung pada daya
17
Gambar 2.13 Blok ramp-track filter [13]
Gambar 2.13 menunjukkan blok ramp-track filter yang terdapat pada Gambar
2.13, filter memiliki parameter sesuai dengan Persamaan (2.35) berikut ini [15]:
(2.35)
Melalui ramp-track filter, sinyal yang keluar dari PSS dapat meniru sinyal
kecepatan putaran rotor sehingga bekerja dengan lebih akurat dibandingkan PSS
yang tidak memiliki filter tersebut [13].
3. W
ashout Filter
Washout filter adalah sebuah High-Pass Filter yang berfungsi untuk
melewatkan hanya sinyal perubahan input yang cukup besar yang akan diolah oleh
PSS. Filter ini memiliki frekuensi cut-off sebesar [13]:
(2.36)
Gambar 2.14 High Pass Filter [14]
Fungsi alih rangkaian pada Gambar 2.14 adalah sebagai berikut [14]:
18 dengan: dan maka:
(2.38)
dari Persamaan (2.38) kita ketahui bahwa parameter Tw1, Tw2 dan Tw3 dalam Gambar
2.11 secara fisik adalah nilai RC pada filter, dengan mengatur nilai Tw1, Tw2 dan Tw3
serta T7, maka PSS bekerja dalam wilayah kerja (bandwidth) yang bisa diatur sesuai
kebutuhan.
4. L
ead-Lag Phase Compensator
Untuk meredam osilasi pada rotor, PSS harus menghasilkan sinyal torsi
elektrik yang sefasa dengan perubahan deviasi kecepatan rotor. Hal tersebut
membutuhkan kompensator fasa untuk mengompensasi lag antara output PSS
dengan torsi elektrik yang dihasilkan [1].
Gambar 2.15 Lead-Lag Compensator [16]
Rangkaian pada Gambar 2.15 memiliki fungsi alih sebagai berikut [16]:
(2.39)
dari Persamaan (2.39) dapat diketahui kuantitas fisik parameter dalam Gambar 2.11 :
19
Besar fasa yang dihasilkan PSS untuk yang dihasilkan oleh lead-lag
compensator dihitung menggunakan Persamaan (2.40) berikut ini [2]:
(2.40)
dimana :
: Fasa yang dihasilkan PSS
ω : frekuensi osilasi pada sistem tenaga
Penalaan PSS dilakukan dengan menentukan parameter-parameter pada
tiap-tiap bagiannya sesuai dengan kondisi sistem tenaga tempatnya dipasang, oleh karena
itu pemilihan penalaan PSS dilakukan setelah terlebih dahulu menentukan kondisi
gangguan yang terjadi.
5. O
utput Voltage Limiter
Gambar 2.16 Pembatas Tegangan Ouput (Output Voltage Limiter) [12]
Pembatas tegangan pada PSS berfungsi untuk membatasi output PSS sehingga
tidak bekerja pada keadaan yang tidak diharapkan. Pembatasan tegangan output PSS
dilakukan dengan cara mengatur variabel-variabel pada Persamaan (2.41) dan (2.42)
sebagai berikut [1, 12]:
Tegangan output maksimum = (V1+0.7) Volt (2.41)
20 2.4 Genetic Algorithm (Algoritma Genetika)
Algoritma Genetika (GA) adalah teknik pencarian heuristik yang didasarkan
pada gagasan evolusi seleksi alam dan genetik. Algoritma ini memanfaatkan proses
seleksi alamiah yang dikenal dengan proses evolusi. Dalam proses evolusi, individu
secara terus menerus mengalami perubahan gen untuk menyesuaikan dengan
lingkungan hidupnya [17].
GA diperkenalkan oleh John Holland pada tahun 1975 di Universitas Michigan
untuk menyelesaikan permasalahan yang memiliki ciri sebagai berikut [17]:
1. Ruang pencarian sangat besar, kompleks, atau kurang dipahami
2. Tidak ada pengetahuan yang memadai untuk menyederhanakan ruang
pencarian yang sangat besar menjadi ruang pencarian yang lebih sempit
3. Tidak ada analisis matematis yang bisa menangani ketika metode
konvensional gagal menyelesaikan masalah yang dihadapi
4. Solusi yang dihasilkan tidak harus optimal, asal sudah memenuhi kriteria
sudah bisa diterima
5. Mempunyai kemungkinan solusi yang jumlahnya sangat banyak
Untuk memanfaatkan algoritma genetika, kita harus dapat menyandikan solusi
21
membandingkan nilai fitness-nya. Sebuah representasi algoritma genetika yang
efektif dan nilai fitness yang bermakna adalah kunci keberhasilan dalam aplikasi
algoritma genetika.
Untuk memahami cara kerja GA, berikut ini beberapa istilah yang harus
diketahui terlebih dahulu [17]:
a. Individu : representasi solusi dari permasalahan
b. Gen : variabel dalam solusi
c. Populasi : kumpulan dari individu dalam jumlah tertentu
d. Generasi : siklus proses evolusi
e. Fitness : nilai yang menyatakan keoptimalan solusi
Proses GA untuk mencari solusi adalah sebagai berikut [2, 17]:
1. Tahap penyandian (encoding), yaitu menyandikan gen dari individu. Gen
dapat dikodekan kedalam tiga bentuk, namun yang digunakan pada penelitian
ini adalah kode bilangan real :
a). kode biner (bilangan 0 dan 1)
contoh : 3 variabel (X1,X2,X3) dikodekan kedalam individu yang terdiri dari
3 gen yaitu X1(001), X2(010) dan X3(101).
b). kode bilangan real dimana nilai gen berada pada interval 0 sampai 1 contoh : 3 variabel (X1,X2,X3) dikodekan ke dalam individu yang terdiri dari
3 gen yaitu X1(0,5392), X2(0,6489) dan X3(0,1642).
22
contoh : 3 variabel (X1,X2,X3) dikodekan kedalam individu yang terdiri dari 9
gen, tiap-tiap variabel dikodekan kedalam 3 gen yaitu X1(212), X2(135) dan
X3 (439).
2. Membentuk populasi awal
Untuk membentuk populasi awal, kita harus menentukan jumlah individu
sebanyak N, kemudian membentuk populasi awal yang didalamnya terdapat
N individu yang dengan gen didalamnya dipilih secara acak (random).
3. Memformulasikan fungsi objektif
Dalam mencari individu terbaik (solusi), maka tiap individu di dalam
populasi akan dievaluasi melalui fungsi objektif. Setelah dievaluasi dengan
fungsi objektif, maka tiap individu akan memiliki nilai fitness yang
menyatakan kemampuan individu untuk bertahan hidup.
4. Elitisme
Elitisme adalah proses penyalinan individu yang memiliki nilai fitness terbaik
pada satu proses generasi untuk mencegah hilang atau rusaknya individu
tersebut pada saat proses mutasi dan kawin silang.
5. Pindah silang (crossover)
Pindah silang adalah proses memasangkan dua individu sebagai induk untuk
mendapatkan anak. pindah silang yang digunakan pada penelitian ini adalah
metode “pindah silang seragam”.
6. Mutasi
Mutasi adalah proses mengubah semua nilai gen yang terdapat di dalam
individu, dengan menggunakan indeks probabilitas mutasi. Pada penelitian
23
Langkah-langkah nomor 1-6 diulang sampai jumlah generasi tertentu dan hasil
yang terbaik sudah diperoleh. Gambar 2.17 menunjukkan diagram alir dari Genetic
Algorithm [18].
1 BAB 1 PENDAHULUAN 1.1 Latar Belakang
Power System Stabilizer (PSS) adalah alat kendali tambahan yang digunakan
pada sistem eksitasi generator sinkron untuk meredam osilasi elektromekanik pada
generator yang timbul akibat gangguan dan perubahan beban yang terjadi pada
sistem tenaga listrik.
PSS meredam osilasi pada rotor generator dengan memberikan sinyal
tambahan yang memproduksi torsi elektrik yang sefasa dengan deviasi kecepatan
rotor untuk mengembalikan rotor ke kecepatan sinkron. Dalam menghasilkan torsi
redaman, PSS bekerja dengan mengolah sinyal input berupa daya output generator,
frekuensi output dan sudut daya [1].
Dalam penggunaannya, parameter-parameter PSS harus di tala (tuning) agar
kinerjanya sesuai dengan kebutuhan serta cocok dengan karakter sistem tenaga yang
dikendalikannya, sehingga mampu menstabilkan generator saat terjadi perubahan
pembebanan [2].
Secara luas, penalaan PSS dilakukan dengan penentuan parameter yang
membuat PSS bekerja pada kondisi yang sudah diramalkan saja, hal ini membuat
PSS tidak bekerja dengan baik saat bekerja diluar kondisi yang sudah ditentukan.
Genetic Algorithm sebagai kecerdasan buatan cocok untuk menyelesaikan
permasalahan ini, karena dapat memperluas wilayah kerja PSS sekaligus
mempersingkat penghitungan, sehingga dapat menghasilkan satu set parameter
penalaan PSS yang efektif untuk segala kondisi pembebanan pada sistem tenaga [3].
Pada tugas akhir ini, penulis memilih PLTU 2 SUMUT Pangkalan Susu
2
generatornya sudah memakai PSS. Hasil penelitian ini diharapkan dapat menjadi
pertimbangan dalam penalaan PSS pada pembangkit lain yang akan dibangun,
khususnya Pembangkit Unit 3 dan 4 PLTU Pangkalan Susu yang akan segera
rampung pada beberapa tahun kedepan.
1.2 Perumusan Masalah
Dalam tugas akhir ini dirumuskan beberapa masalah, yaitu:
1. Bagaimana cara meningkatkan stabilitas sistem tenaga menggunakan PSS
serta cara penerapannya di PLTU 2 SUMUT Pangkalan Susu?
2. Bagaimana cara yang tepat untuk menerapkan Genetic Algorithm agar
dapat digunakan untuk penalaan PSS pada PLTU 2 Sumut Pangkalan
Susu?
1.3 Tujuan
Tujuan dari tugas akhir ini adalah:
1. Menerapkan metode Genetic Algorithm pada penalaan PSS dengan studi
kasus di PLTU 2 Sumut Pangkalan Susu
2. Membandingkan stabilitas sistem tenaga saat sebelum dan sesudah PSS
ditala menggunakan Genetic Algorithm
1.4 Batasan Masalah
Batasan masalah dalam tugas akhir ini adalah:
1. Kestabilan yang diteliti adalah small signal stability
2. Analisis dan percobaan disimulasikan menggunakan software Matlab
3
3. Sistem tenaga listrik yang menjadi obyek penelitian disederhanakan menjadi
bentuk Single Machine Infinite Bus (SM-IB)
1.5 Manfaat Tugas Akhir
Tugas akhir ini diharapkan dapat memberikan hasil penalaan PSS yang
mendekati optimal, sehingga dapat meningkatkan kestabilan unit pembangkitan
PLTU 2 SUMUT Pangkalan Susu. Hasil penelitian ini diharapkan dapat menjadi
bahan pertimbangan dalam penalaan PSS pada unit PLTU di wilayah lain.
1.6 Luaran Tugas Akhir
Dari tugas akhir ini, penulis mengharapkan luaran sebagai berikut:
1. Jurnal penelitian yang dipublikasikan secara nasional dan internasional
2. Seminar penelitan
BAB 2
TINJAUAN PUSTAKA 2.1 Small Signal Stability
Kestabilan sistem tenaga adalah kemampuan sistem tenaga untuk
mempertahankan keserempakannya pada kondisi normal serta mampu mencapai
kembali keserempakannya setelah mengalami gangguan [1]. Keserempakan dalam
sistem tenaga dicapai jika semua generator sinkron didalamnya bekerja dengan
i ABSTRAK
Gangguan berupa perubahan beban pada sistem tenaga dapat memicu osilasi
elektromekanis pada generator yang harus segera dihilangkan. PSS bekerja dengan
mengembalikan kesetaraan antara torsi mekanik dan torsi elektrik sehingga
kecepatan rotor kembali ke keadaan sinkron. Penggunaan PSS pada eksitasi
pembangkit harus diikuti dengan penalaan yang tepat agar memberikan hasil yang
terbaik. Obyek penelitian pada tugas akhir ini adalah PLTU 2 Sumut Pangkalan Susu
yang dimodelkan menjadi single machine infinite bus (SMIB), dengan metode
penalaan PSS menggunakan Genetic Algorithm (GA). PSS yang ditala menggunakan
GA dibandingkan dengan penalaan PSS bawaan dari PLTU Pangkalan Susu melalui
serangkaian kondisi pengujian yang sudah ditentukan. Hasil perbandingan
menunjukkan persentasi peningkatan settling time pada kondisi penurunan beban
10% dari 16,5 detik ke 10,5. Kondisi kenaikan beban 10% settling time meningkat
dari 16,5 detik ke 10,5 detik, pada kondisi penurunan beban 20% settling time naik
dari 18 detik ke 12,5 detik, sedangkan pada kondisi pemutusan beban 50% settling
time naik dari 18,5 detik ke 13 detik. Hasil dari keseluruhan perbandingan
menunjukkan bahwa PSS yang ditala menggunakan GA lebih baik dari PSS yang
ditala PSS dengan penalaan bawaan dari PLTU Pangkalan Susu.