A Generalisation of the Mean-Variance
Analysis
Valeri Zakamouline and Steen Koekebakker
University of Agder, Faculty of Economics, Service Box 422, 4604 Kristiansand, Norway E-mails: Valeri.Zakamouline@uia.no; Steen.Koekebakker@uia.no
Abstract
In this paper we consider a decision maker whose utility function has a kink at the reference point with different functions below and above this reference point. We also suppose that the decision maker generally distorts the objective probabilities. First we show that the expected utility function of this decision maker can be approximated by a function of mean and partial moments of distribution. This ‘mean-partial moments’ utility generalises not only mean-variance utility of Tobin and Markowitz, but also mean-semivariance utility of Markowitz. Then, in the spirit of Arrow and Pratt, we derive an expression for a risk premium when risk is small. Our analysis shows that a decision maker in this framework exhibits three types of aversions: aversion to loss, aversion to uncertainty in gains, and aversion to uncertainty in losses. Finally we present a solution to the optimal capital allocation problem and derive an expression for a portfolio performance measure which generalises the Sharpe and Sortino ratios. We demonstrate that in this framework the decision maker’s skewness preferences have first-order impact on risk measurement even when the risk is small.
Keywords: mean-variance utility, quadratic utility, mean-semivariance utility, risk aversion,loss aversion, risk measure,probability distortion,partial moments of distribution, risk premium, optimal capital allocation, portfolio performance evaluation,Sharpe ratio
JEL classification: D81,G11
1. Introduction
This paper presents a uniform framework that provides general insights into a broad class of models of choice under uncertainty where the utility function has a reference
point and/or the objective probabilities are distorted. We start with the justification of mean-partial moments utility which lays down a basis for this framework and generalises mean-variance utility. Then we proceed to the generalisation of some central results of the mean-variance analysis, namely, the Arrow-Pratt risk aversion and risk premium, the Arrow’s optimal capital allocation, and the Sharpe portfolio performance measure. The analysis presented in this paper also provides important new insights into the risk and reward measurement.
Expected Utility Theory (EUT) of von Neumann and Morgenstern (1944) has long been the main workhorse of modern financial theory. A von Neumann and Morgenstern’s utility function is defined over the decision maker’s wealth. The properties of a von Neumann and Morgenstern’s utility function have been studied in every detail. The concept of ‘risk aversion’ was analysed by Friedman and Savage (1948) and Markowitz (1952). They showed that the realistic assumption of diminishing marginal utility of wealth explains why people are risk averse. Measurement of risk aversion was developed by Pratt (1964) and Arrow (1971). These authors analysed the risk premium for small risks and introduced a measure which is now widely known as the ‘Arrow-Pratt measure of risk aversion’. The celebrated modern portfolio theory of Markowitz and the use of a mean-variance utility function can be justified by approximating a von Neumann and Morgenstern’s utility function by a function of mean and variance (see, for example, Samuelson (1970), Tsiang (1972) and Levy and Markowitz (1979)). In this sense, the use of the Sharpe ratio (Sharpe, 1966) as a measure of performance evaluation of risky portfolios is also well justified.
However, not very long after EUT was formulated by von Neumann and Morgenstern, questions were raised about its value as a descriptive model of choice under uncertainty. Allais (1953) and Ellsberg (1961) were among the first to challenge EUT. Influential experimental studies have shown the inability of EUT to explain many observed phenomena and reinforced the need to rethink much of the theory. An enormous amount of theoretical effort has been devoted towards developing alternatives1to EUT. In many of the alternative models of choice under uncertainty the decision maker’s utility has a reference point with different functions below and above the reference point (possibly with a kink at the reference point) and/or the decision maker distorts the objective probability distribution. One of the first examples of such type is the utility function of Markowitz (1952) with a concave segment below the reference point and a convex segment above the reference point. In the mean-lower partial moment model of Fishburn (1977) and Bawa (1978) the utility function is linear above the reference point and concave below the reference point.
The most influential among all alternative models of choice under uncertainty is Prospect Theory/Cumulative Prospect Theory (PT/CPT) of Kahneman and Tversky (1979) and Tversky and Kahneman (1992). PT/CPT can correctly predict individual choices even in cases in which EUT is violated.2 In PT/CPT the utility function is defined over gains and losses relative to some reference point, as opposed to wealth in EUT. The utility function has a kink at the reference point, with the slope of the loss function steeper than the gain function. This is called ‘loss aversion’ which is an
1For an excellent review of alternative theories, the interested reader can consult Starmer (2000). Besides, all financial phenomena based on nonrational behaviour among investors constitute now the main subject of Behavioural Finance. For a review and synthesis of Behavioural Finance, the interested reader can consult Subrahmanyam (2007).
important element of PT/CPT. The marginal value of both gains and losses decreases with their size. All these properties give rise to an asymmetric S-shaped utility function, concave for gains and convex for losses. Moreover, in PT/CPT the decision maker distorts the objective probability distribution by overweighting small probabilities.
Another prominent example of an alternative descriptive model of choice under uncertainty is Disappointment Theory (DT) of Bell (1985) and Loomes and Sugden (1986). In DT a decision maker is assumed to be ‘disappointment averse’. In particular, this model assumes that if the outcome of a decision is worse than expected, the sense of disappointment will be generated. On the other hand, an outcome better than expected will stimulate ‘elation’. The utility function in DT consists of two parts: the first part is a ‘basic’ utility similar to a utility function in EUT, whereas the second part accounts for the feelings of disappointment and elation. This second utility function is concave for outcomes worse than expected and convex for outcomes better than expected. Consequently, the total utility function is obviously concave below the reference point. However, it is difficult to say something definite about the shape of the total utility function above the reference point. If the sense of elation is very strong, the total utility function can be convex for outcomes better than expected.
Many researches have observed a tendency for individuals to mispercept objective probabilities, in particular, to subjectively weight objective probabilities. This effect can be captured by a model of choice under uncertainty that incorporates ‘decision weights’ instead of objective probabilities. Theories of this type were first discussed by Edwards (1955) and Edwards (1962). One of the best-known models of this type is Anticipated Utility Theory/Rank Dependent Expected Utility (AUT/RDEU) of Quiggin (1982). According to this theory, the decision maker’s utility function is defined in the same manner as in EUT, that is, over wealth. The main difference is the assumption that a decision maker distorts objective probabilities using some rule of distortion. Some examples of distortion are: overweighting/underweighting small probabilities; overweighting/underweighting probabilities of unfavourable outcomes; etc. A special case of the AUT/RDEU is the Dual Theory of Yaari (1987).
Even though the models where the utility function has a reference point and/or the objective probabilities are distorted have been known for quite a while, still there is only a few studies of some effects of loss aversion and probability distortion. Moreover, practically all of these studies consider the decision making in PT/CPT only. The study of the risk premium in a behavioural framework starts with the paper by Levy and Levy (2002) who considered a decision maker equipped with a von Neumann-Morgenstern utility function and a small gamble with two possible outcomes. They derived an expression for a risk premium which accounts for PT/CPT type of probability distortion and showed that this type of probability distortion systematically increases the risk premium. Davies and Satchell (2007) extended the model of Levy and Levy (2002) by introducing loss aversion in the decision maker’s utility.
optimal capital allocation problem and found that as the investment horizon decreases, the investor reduces the proportion of the risky asset in the complete portfolio and, thus, invests more in the risk-free asset.
Loss aversion and probability distortion may help explain the equity premium puzzle of Mehra and Prescott (1985). Bernartzi and Thaler (1995) and subsequently Barberis et al.(2001) found that loss aversion can explain why stock returns are too high relative to bond returns. Cecchetti et al.(2000) and Abel (2002) pointed out that pessimistic probability distortion may also cause the observed equity premium puzzle.
Despite some studies focusing on certain effects of loss aversion and probability distortion, still little is known about general implications from these alternative theories. The goal of this paper is to present a uniform framework that is able to provide general insights into this broad class of models of choice under uncertainty. In this paper we consider a decision maker with a generalised behavioural utility function that has a reference point. We assume that the decision maker regards the outcomes below the reference points as losses, and the outcomes above the reference point as gains. We suppose that the behavioural utility generally has a kink at the reference point and different functions below and above the reference point. We require only that the behavioural utility function is continuous and increasing in wealth and has at least the first and the second one-sided derivatives at the reference point. Moreover, we also suppose that the decision maker generally distorts the objective probability distribution. Note that our generalised framework encompasses EUT as well.
The first contribution of this paper is to provide an approximation analysis of the expected generalised behavioural utility function. Our analysis shows that the expected generalised behavioural utility function can be approximated by a function of mean and partial moments of distribution. This ‘mean-partial moments’ utility generalises not only mean-variance utility of Tobin and Markowitz, but also mean-semivariance utility mentioned by Markowitz (1959) and discussed further by many others. Mean-partial moments utility appears to have reasonable computational possibilities (in, for example, the optimal portfolio choice problem) as well as a great degree of flexibility in modelling different risk preferences of a decision maker.
The second contribution of this paper is, in the spirit of Pratt (1964) and Arrow (1971), to derive an expression for a risk premium when risk is small. We show that mean-partial moments utility allows for a much richer and detailed characterisation of a risk premium. It is well known that for a decision maker with mean-variance utility the only source of risk is variance. Moreover, the risk attitude of this decision maker is completely described by a single measure widely known as the Arrow-Pratt measure of risk aversion (which is, in fact, the aversion to uncertainty).3 In contrast, our analysis shows that a decision maker with a generalized behavioral utility distinguishes between three sources of risk: expected loss, uncertainty in losses, and uncertainty in gains. Consequently, a decision maker in our framework exhibits three types of aversions: aversion to loss, aversion to uncertainty in gains, and aversion to uncertainty in losses. Loss aversion leads to different weights of losses and gains in the expression for the risk premium. As compared to the analysis presented by Davies and Satchell (2007), our results are much more concise and explicit. We also provide comparative static analysis of the expression for the risk premium. Besides, our results are not limited to gambles with only two possible outcomes, but encompass continuous probability distributions as well.
3
The third contribution of this paper is to generalise Arrow’s famous solution to the optimal capital allocation problem for an investor. In this setting the investor’s objective is to optimally allocate his wealth between a risk-free and a risky asset. It is widely known that a mean-variance utility maximiser will always want to allocate some wealth to the risky asset if the risk premium is non-zero. In contrast, we show that an investor with the generalised behavioural utility function will want to allocate some wealth to the risky asset only when the perceived risk premium is sufficiently high (how high depends on the level of loss aversion and the degree of probability distortion). Otherwise, if the perceived risk premium is small, the investor avoids the risky asset altogether and invests all wealth in the risk-free asset. This result may help explain why many investors do not invest in equities.4 This result also illustrates that the equity premium puzzle discovered by Mehra and Prescott (1985) can be explained by either loss aversion or pessimistic probability distortion or a combination of these effects. As compared to the analysis presented by Gomes (2005), we derive not implicit, but explicit solutions to the optimal capital allocation problem and provide comparative static analyses of the solutions. Besides, in our setting we consider a general behaviour utility function, not only the piecewise-power utility motivated by PT/CPT. Moreover, our results are not limited to risky asset returns with only two possible outcomes, but encompass continuous probability distributions as well. Finally, in our analysis we generally consider the case where the investor distorts the probability distribution of the risky asset returns, in the analysis by Gomes the probability distribution is objective.
Our fourth contribution is to derive an expression for the portfolio performance measure of an investor with the generalised behavioural utility. This measure generalises the Sharpe and Sortino5ratios (see Sortino and Price (1994)). As compared to either the Sharpe or Sortino ratio where the investor’s risk preferences seemingly disappear, the computation of the generalised performance measure usually requires knowledge of the investor’s risk preferences. Hence, this performance measure is not unique for all investors, but rather it is anindividual performance measure. The explanation for this is that in our generalised framework an investor distinguishes between several sources of risk. Since each investor may exhibit different preferences to each source of risk, investors with different preferences might rank differently the same set of risky assets. The fifth contribution of this paper is to provide some new insights on risk mea-surement. In modern financial theory most often one uses variance as a risk measure. This is because in the EUT framework variance has the first-order impact on risk measurement, at least when the risk is small. We demonstrate that in many alternative theories variance is generally not a proper risk measure even if the risk is small. In these theories it is the decision maker’s skewness preferences that have first-order impact on risk measurement. This is the consequence of the presence of loss aversion and the fact that the decision maker’s degrees of risk aversions below and above the reference point might be substantially different. In the latter case if probability distributions are not symmetrical, then, depending on the signs and the values of skewness preferences, either the downside or the upside part of variance is a more adequate risk measure than variance.
4See, for example, Agnew et al. (2003) who report that about 48% of participants of retirement accounts do not invest in equities. This behavior clearly contradicts EUT. 5
The rest of the paper is organised as follows. In Section 2 we briefly review the justification of the mean-variance analysis and present the results we want to generalise. In Section 3 we present assumptions, definitions, and notation that we will use in our generalised framework. In Section 4 we perform the approximation analysis and generalise mean-variance utility. In Section 5 we generalise the Arrow-Pratt risk premium. In Section 6 we discuss briefly the impact of the decision maker’s skewness preferences on risk measurement in our generalised framework. In Section 7 we analyse the optimal capital allocation problem. In Section 8 we derive the expression for a portfolio performance measure. Section 9 concludes the paper.
2. Expected Utility Theory and the Mean-Variance Analysis
In this section we present a brief justification of the mean-variance analysis as well as some of its most important results. Throughout the paper we consider a decision maker with (random) wealthW. In this section we assume that the decision maker has a von Neumann-Morgenstern utility function which is defined over wealth as a single function U(W). The decision maker’s objective is to maximise the expected utility of wealth,E[U(W)], whereE[.] is the expectation operator.
We suppose that the utility functionU is increasing in wealth and is a differentiable function. Then, taking a Taylor series expansion around some (deterministic)W0, the
expected utility of the decision maker can be written as
E[U(W)]=
Our intension now is to keep the terms up to the second derivative ofU and disregard6
the terms with higher derivatives ofU. This gives us
E[U(W)]≈U(W0)+U(1)(W0)E[(W−W0)]+
Since a utility function is unique up to a positive linear transformation andU(1) >0,
then a convenient form of equivalent expected utility is
E[U(W)]= E
is the Arrow-Pratt measure of absolute risk aversion. The equivalent expected utility (1) can be interpreted as mean-variance utility since the termE[(W−W0)2] is proportional
to variance. Observe that we can arrive at the same expression for the expected utility as (1) if we assume that the utility function of the decision maker is quadratic
U(W)=(W −W0)−
1
2γ(W −W0)
2
. (3)
Consider now a risk averse decision maker with deterministic wealthW0. According to Arrow (1971, p. 90) ‘a risk averter is defined as one who, starting from a position of certainty, is unwilling to take a bet which is actuarially fair’. More formally, ifxis a fair gamble such thatE[x]=0, then
E[U(W0+x)]<U(W0). (4)
Beginning from the landmark papers of Arrow and Pratt, it became standard in economics to characterize the risk aversion in terms of either a certainty equivalent, C(x), or a risk premium,π(x), which are defined by the following indifference condition
E[U(W0+x)]=U(W0+C(x))=U(W0+E[x]−π(x)). (5)
This says that the decision maker is indifferent between receiving x and receiving a non-random amount ofC(x)= E[x]− π(x). Observe that for a fair gambleC(x) =
−π(x). If the risk of a fair gamble is small, then the decision maker’s preferences can be approximated by quadratic utility. The use of quadratic utility (3) in the indifference condition (5) forW =W0+xcombined with the assumption of risk aversion (4) gives the following expression7for the risk premium and certainty equivalent
π(x)= −C(x)= 1
2γVar[x]. (6)
This is the famous result of Pratt (1964).
Now consider the optimal capital allocation problem of an investor with the quadratic utility function. The investor wants to allocate his wealth between a risk-free and a risky asset. The return on the risky asset over a small time intervaltis
x =μt+σ√tε, (7)
where μ andσ are, respectively, the mean and standard deviation of the risky asset return per unit of time, andεis some (normalized) stochastic variable such thatE[ε]= 0 and Var[ε]=1. The return on the risk-free asset over the same time interval equals
r =ρt, (8)
whereρis the risk-free interest rate per unit of time. We assume that the risky asset can be either bought or sold short without any limitations and the risk-free rate of return is the same for both borrowing and lending. We further assume that the investor’s initial wealth isWIand he investsain the risky asset and, consequently,WI −ain the risk-free asset. Thus, the investor’s wealth aftertis
W =a(x−r)+WI(1+r). (9)
The investor’s objective is to chooseato maximise the expected utility
E[U∗(W)]=max
a E[U(W)]. (10)
Observe that there is some ambiguity in the choice of the level of wealthW0 around which we perform the Taylor series expansion. A reasonable choice isW0=WI(1+r).
7
We also need to disregard the term withC2
With this choiceW0 does not depend onaand the resulting risk measure (in this case, it isaE[(x−r)2]) exhibits the homogeneity property8 ina.
If, for example,tis rather small, then the risk is small and the use of quadratic utility is well justified. Consequently, using quadratic utility (3) in the investor’s objective function (10) we arrive to the following maximisation problem
E[U∗(W)]=max
a a E[x−r]− 1 2γa
2E[(x
−r)2].
The first-order condition of optimality ofagives
a= 1
γ
E[x−r]
E[(x−r)2], (11)
which is the famous Arrow’s solution (see Arrow (1971, p. 102)). Finally, using the expression for the optimal value ofa, we obtain that the maximum expected utility of the investor is given by
E[U∗(W)]= 1 2γ
(E[x−r])2 E[(x−r)2].
Note that for any investor the higher the value of (EE[([xx−r])2
−r)2], the higher the maximum
expected utility irrespective of the value ofγ. Thus, the value of
S R= E[x−r]
E[(x−r)2] , (12)
which is nothing else than the absolute value of the Sharpe ratio9 (see Sharpe (1966)), can be used as the ranking statistics in the performance measurement of risky assets. Observe that the Sharpe ratio is usually presented based on the assumption that either E[x − r] > 0 or short sales are restricted. Here we also allow for profitable short selling strategies. Therefore we compute the absolute value of the Sharpe ratio in order to properly measure the performance.
3. Assumptions, Definitions, and Notation
The purpose of this paper is to generalise the mean-variance analysis and some of its important results presented in the preceding section. Before proceeding to the analysis, in this section we would like to present the assumptions, definitions, and notation.
Assumption 1. We suppose that the decision maker’s utility function is continuous and increasing in wealth.
Assumption 2. We suppose that the decision maker’s utility function generally has a kink at the reference pointW0 and
U(W)=
U+(W) ifW ≥W0, U−(W) ifW <W0.
8In the landmark paper of Artzneret al.(1999), the authors argue that a sensible risk measure should satisfy several properties. One of these properties is the homogeneity property. This says that if one invests the amountain the risky asset, the measure that assesses the investment risk should be a homogeneous function ina. In other words, ‘twice the risk is twice as risky’. 9Observe thatE[(x
−r)2]
=Var[x]+(E[x]−r)2
This means that above the reference point the utility function is given byU+, whereas below the reference point the utility function is given byU−. The continuity assumption gives
U−(W0)=U+(W0)=U(W0). (13)
Assumption 3. The decision maker regards the outcomes below the reference points as losses, while the outcomes above the reference point as gains. Consequently, we will refer toU−as the utility function for losses, and toU+as the utility function for gains.
Assumption 4. We suppose that the left and right derivatives ofUat the reference point exist and finite. We denote the first-order left-sided derivative
U−(1)(W0)= lim
h→0−
U−(W0)−U−(W0+h)
h .
Similarly, we denote the first-order right-sided derivative10
U+(1)(W0)= lim
h→0+
U+(W0+h)−U+(W0)
h .
The higher-order one-sided derivatives ofU at the reference point are denoted in the similar manner byU(2)−(W0),U(2)+(W0), etc.
Assumption 5. We suppose that the decision maker generally distorts the objective probability distribution. More formally, suppose that the cumulativeobjectiveprobability distribution of a gambleX is given by FX. Then the expected payoff of the gamble in the objective world is
E[X]=
∞
−∞
xdFX(x).
Observe that the integral above is a Lebesgue-Stieltjes integral which is defined for both discrete and continuous distributions. We denote by QX the cumulativedistorted probability distribution function ofX. Under the distortion of probabilities, the expected payoff of the gamble for the decision maker is given by
E[X]=
∞
−∞
xdQX(x).
Note thatE[·] is generally not an expectation since there are some types of distortions for which∞
−∞d QX =1.
Since the probability distortion may depend either on the cumulative objective distribution function or on whether the outcomes of X are interpreted as losses or gains, we need to distinguish between the probability distortion ofX and−X. For this purpose we denote by QX¯the cumulative distorted probability distribution function of
the complementary11gamble ¯X = −X. Observe that generally
E[X] =E[X],
10To be more precise, we need to denote the left derivative as U(1)
−(W0−) and the right derivative asU(1)+(W0+), but this would enlarge the notation.
11
This says that the expected value of X under distortion of probabilities is generally different from the expected value ofXunder objective probabilities. This holds true for all moments of distribution ofX. Moreover,
E[−X] = −E[X].
This says that under the same rule of probability distortion the expected value of−X is generally not equal to the expected value ofX with the opposite sign. Illustrations are provided in Appendix A.
Assumption 6. If W =W0+ XwhereX is some gamble, then we suppose that
∞ −∞
U(W0)dQX =U(W0). (14)
This is true when either the sum of all distorted probabilities is equal to 1 (that is,
∞
−∞d QX =1) or the utility function is zero at the reference point (that is, as in PT/CPT U(W0)=0).
Definition 1 (Small risk distribution). As formalised by Samuelson (1970), a prob-ability distribution belongs to a family of ‘compact’ or ‘small risk’ distributions if as some specified parameter goes to zero, the distribution converges to a sure outcome. To demonstrate the construction of a small risk distribution, suppose that the decision maker’s wealthW =W0 +x andx =tεwhereεis some random variable. Astgoes to zero, the probability distribution ofW converges to the sure amountW0.
Definition 2 (The measure of loss aversion). The measure of loss aversion is given by
λ= U
(1) − (W0) U+(1)(W0)
. (15)
This mesasure of loss aversion was proposed by Bernartzi and Thaler (1995) and formalised by K¨obberling and Wakker (2005). Observe that if the decision maker does not exhibit loss aversion, then λ= 1. Loss aversion implies λ >1. Conversely, loss seeking behaviour impliesλ <1. Finally note that since the first-order derivatives of U are positive (follows from Assumption 1), the value of λ is also positive, that is,
λ >0.
Definition 3 (Two measures of risk aversion). Recall the measure of risk aversion (2) that was introduced by Arrow and Pratt. Since the utility function of the decision maker generally has different functions for losses and gains, we introduce:the measure of risk aversion in the domain of gains
γ+= −U
(2) + (W0) U+(1)(W0)
,
andthe measure of risk aversion in the domain of losses
γ−= −U
(2) − (W0) U−(1)(W0)
.
in the domain of gains. Finally, ifγ+=0, then the decision maker is risk neutral in the domain of gains.
Definition 4 (Lower and Upper Partial Moments). If the decision maker’s random wealth isW and the reference point isW0, a lower partial moment of (integer) ordern under the distortion of probability is given by
LP Mn(W,W0)=(−1)n
W0
−∞
(w −W0)ndQW(w).
The coefficient (−1)n is chosen to bring our definition of a lower partial moment in correspondence with the definition of Fishburn (1977). An upper partial moment of ordernunder the distortion of probability is given by
U P Mn(W,W0)=
∞
W0
(w −W0)ndQW(w).
The lower and upper partial moments of orderncomputed in the objective world are denoted byLPMn(W,W0) andUPMn(W,W0) respectively. Note here that ifXis some gamble, then without the distortion of probabilities
LPMn(X,0)=U PMn(−X,0).
This is generally not the case with probability distortion. That is, generally
LP Mn(X,0) =U P Mn(−X,0),
because in the computation ofLP Mn(X,0) we employQX, whereas in the computation ofU P Mn(−X,0) we useQX¯. The main reason for the introduction of a new definition of a lower partial moment is the necessity to distinguish between the computation of moments of distribution forXand−X. See Appendix A that illustrates the computation of partial moments with and without probability distortion.
Definition 5 (Optimistic probability distortion). We say that a decision maker is optimistic if he overweights the probabilities of favourable outcomes. For an optimistic decision makerE[X]>0 ifX is a fair gamble in the objective world, that is,E[X]=0.
Moreover, observe that for an optimistic decision makerE[−X]>0 as well. Illustrations are provided in Appendix A.
Definition 6 (Pessimistic probability distortion). We say that a decision maker is pessimistic if he overweights the probabilities of unfavourable outcomes. For a pes-simistic decision makerE[X]<0 ifXis a fair gamble in the objective world. Moreover, observe that for a pessimistic decision makerE[−X]<0 as well. For illustrations, see Appendix A.
Definition 7 (Performance Measure). By a performance measure we mean a score (number/value) attached to each financial asset. A performance measure is related to the level of expected utility provided by the asset. That is, the higher the performance measure of an asset, the higher level of expected utility the asset provides.
4. Mean-Partial Moments Utility and Piecewise-Quadratic Utility Function
decision maker generally distorts the objective probability distribution ofW such that the cumulative distorted probability distribution function isQW. The decision maker’s expected generalised behavioural utility is, therefore, given by
E[U(W)]=
supposing that the Taylor series converge and the integrals exist (also recall Assumption 6).
Theorem 1. If either utility functions U−and U+are at most quadratic in wealth or the probability distribution of W belongs to the family of small risk distributions, then the equivalent expected utility can be written as the following mean-partial moments utility
which means that we can assume the following piecewise-quadratic form for the utility function U distributions,12then we can assume that all the terms in (16) withLP M
n(W,W0) and
U P Mn(W,W0),n≥3, are of smaller order than the second partial moments. Hence, if we keep only the first and the second partial moments of distribution, the expected utility is
Since the utility function is unique up to a positive linear transformation and
U(1)+(W0)>0, an equivalent expected utility can be given by
Corollary 2. In the EUT framework, mean-partial moments utility (17) reduces to mean-variance utility (1), and piecewise-quadratic utility function (18) reduces to quadratic utility function (3).
Proof. For a von Neumann-Morgenstern utility function the left and right derivatives ofU at pointW0 are equal. Hence, for a von Neumann-Morgenstern utility function
λ=1 andγ−=γ+=γ. Finally note thatLPM2(W,W0)+UPM2(W,W0)=E[(W −
W0)2].
Corollary 3. If λ=1,γ+=0, and there is no probability distortion, then mean-partial moments utility (17) reduces to mean-semivariance utility of Markowitz
E[U(W)]= E[(W −W0)]−
1
2γ−LPM2(W,W0).
Remark 1. Observe that mean-semivariance utility is a particular case of mean-partial moments utility when the decision maker exhibits no loss aversion, risk aversion in the domain of losses, and risk neutrality in the domain of gains.
Remark2. Note that the result of Theorem 1 does not encompass the piecewise-power
utility function of PT/CPT. This utility is defined by U+(W) = (W − W0)α and U−(W) = −λ(W0 − W)β, with 0 < α <1 and 0 < β <1. Observe that one-sided
derivatives of this utility function at the reference point do not exist. However, the study of the financial decision making in the PT/CPT framework is rather straightforward since the value function of PT/CPT can be written in terms of partial moments without any approximation
reference point are determined by the values ofγ+andγ−, the decision maker’s attitudes towards risk in the PT/CPT utility are determined by the values ofαandβ.
It is worth noting that for a decision maker with mean-variance utility there is only one source of risk, namely, the variance which measures the total uncertainty (or dispersion). In contrast, a decision maker with mean-partial moments utility generally distinguishes between three sources of risk: the lower partial moment of order one which is related to the expected loss, the lower partial moment of order two which is related to the uncertainty in losses, and the upper partial moment of order two which is related to the uncertainty in gains. Note also that in mean-partial moments utility the measure of risk aversion in the domain of losses is scaled up by the measure of loss aversion. This suggests that a decision maker with loss aversion puts more weight on the uncertainty in losses than on the uncertainty in gains.
Observe that the piecewise-quadratic utility function (18) is very flexible with regard to the possibility of modelling different preferences of a decision maker. In this function
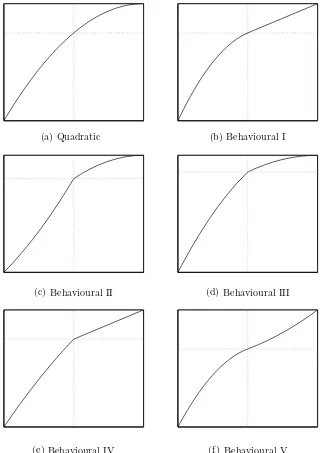
λcontrols the loss aversion, γ+ controls the concavity/convexity of utility for gains, whereasγ−controls the concavity/convexity of utility for losses. Some possible shapes of this utility function are presented in Figure 1.
In particular, Figure 1 presents the following six distinct shapes of the piecewise-quadratic utility function:
Quadratic: The shape of this utility function is given byλ=1 andγ−=γ+=γ >
0. This utility corresponds to quadratic utility in the EUT framework.
Behavioural I: The shape of this utility function is given by λ = 1, γ− > 0, and
γ+=0. This utility corresponds to mean-semivariance utility of Markowitz and the utility function of Fishburn (1977) where one uses the lower partial moment of the second order. The decision maker equipped with this utility exhibits no loss aversion, risk neutrality in the domain of gains, and risk aversion in the domain of losses.
Behavioural II: The shape of this utility function is given byλ >1,γ−<0, andγ+>
0. This corresponds largely to the utility function in PT/CPT. The decision maker equipped with this utility exhibits loss aversion, risk aversion in the domain of gains, and risk seeking in the domain of losses.
Behavioural III: The shape of this utility function is given by λ > 1,γ− > 0, and
γ+>0. The decision maker equipped with this utility exhibits loss aversion and risk aversions in the domains of losses and gains. This shape may represent a utility function in DT.
Behavioural IV: The shape of this utility function is given by λ > 1, γ− = γ+ =
0. The decision maker equipped with this utility exhibits loss aversion, but risk neutrality in the domains of losses and gains. This is a so-called ‘bilinear’ utility function.
Behavioural V: The shape of this utility function is given by λ ≥ 1, γ− > 0, and
Behavioural I
Behavioural II
Behavioural IV Behavioural V Behavioural III )
b ( c
i t a r d a u Q (a)
) d ( )
c (
) f ( )
e (
Fig. 1. Alternative shapes of the piecewise-quadratic utility function given by equation (18)
The decision maker’s wealth versus the utility scores.The intersection of the dotted lines shows the location of the reference point.Quadraticutility corresponds to quadratic utility in the EUT framework.
Behavioural I utility corresponds to mean-semivariance utility of Markowitz.Behavioural II utility corresponds largely to the utility function in PT/CPT.Behavioural IIIutility may represent a utility function in DT.Behavioural IVutility is a so-called ‘bilinear’ utility function. Finally,Behavioural V
5. Generalisation of the Arrow-Pratt Risk Premium
In this section we consider arisk aversedecision maker equipped with the generalised behavioural utility function and who generally distorts the objective probability distri-bution. Recall that we say that the decision maker is risk averse if a fair (in the objective world) gamble decreases the utility of the decision maker. More formally, for a fair gamblexsuch thatE[x]=0
E[U(W0+x)]<U(W0).
We want to derive the expressions for the certainty equivalent, C(x), and the risk premium,13π(x), which are now defined by the following indifference condition
E[U(W0+x)]=U(W0+C(x))=U(W0+E[x]−π(x)). (20)
Theorem 4. If either utility functions U−and U+are at most quadratic in wealth or the risk of a fair gamble is small, then for a risk averse decision maker the certainty equivalent and the risk premium of the fair gamble are given by
C(x)=1
Proof. If either utility functionsU−andU+are at most quadratic in wealth or the risk of a fair gamble is small (under the probability distortion), then, according to Theorem 1, the decision maker’s preferences can be represented by the piecewise-quadratic utility (18). Consequently, the expected utility ofW =W0 +x is given by
E[U(W0+x)]=U P M1(x,0)−
For a risk averse decision maker the certainty equivalent of a fair gamble is negative. Consequently, disregarded. Thus, the use of (23) and (24) in the indifference condition (20) gives the expression for the certainty equivalent (21). To derive the expression for the risk
premium, we useπ(x)=E[x]−C(x).
13
Corollary 5. In the EUT framework, the risk premium (22) reduces to the Arrow-Pratt
Observe that since a decision maker with a von Neumann-Morgenstern utility exhibits no loss aversion, both (infinitesimal) losses and gains are treated similarly (as clearly seen from equation (25)). Consequently, the Arrow-Pratt measure of risk aversion is really a measure of aversion to variance, or a measure of aversion to uncertainty (or dispersion) of the probability distribution. In other words, when risk is small, a decision maker with a von Neumann-Morgenstern utility exhibits only aversion to uncertainty. In addition, the risk premium is fully characterised by a measure of uncertainty aversion and the variance, which is a measure of uncertainty.
A utility function with loss aversion and different functions for losses and gains allows a much richer and detailed characterisation of risk aversion. According to equation (21) a decision maker exhibits three different types of aversions: aversion to loss, aversion to uncertainty in gains, and aversion to uncertainty in losses. The loss is measured by the expected loss, and the uncertainties in gains and losses are measured by the second upper partial moment ofxand the second lower partial moment ofxrespectively. Observe that losses and gains have different weights in the computation of the risk premium. In particular, for a loss averse decision maker, losses are λ times more important than gains. Finally, a brief comparative static analysis of the expressions for the certainty equivalent and the risk premium is presented by means of the following corollaries.
Corollary 6. The certainty equivalent decreases as the decision maker’s loss aversion increases. Conversely, the risk premium increases as the decision maker’s loss aversion increases.
Proof. The first-order derivatives of the certainty equivalent and risk premium with respect toλ ofBis positive. However, even if γ+ >0 the sign of Bis positive since in this case we need to impose the upper limit max(x)< γ1
+ to ensure that the utility function is
increasing14for all outcomes ofx. Therefore
B=
14To motivate for this, consider the piecewise-quadratic utility function (18). Ifγ
since y− 12γ+y2>0 for all y< 1
Corollary 7. The certainty equivalent decreases as the decision maker’s risk aversion in the domain of either gains or losses increases. Conversely, the risk premium increases as the decision maker’s risk aversion in the domain of either gains or losses increases.
Proof. The first-order derivatives of the certainty equivalent and risk premium with respect toγ+
sinceU P M2(x,0)>0. The first-order derivatives of the certainty equivalent and risk premium with respect toγ−
∂C(x)
6. Impact of the Decision Maker’s Skewness Preferences on Risk Measurement
In this section we discuss briefly the impact of the decision maker’s skewness preferences on risk measurement in our generalised behavioural framework. Recall that according to mean-partial moments utility (17) the decision maker distinguishes between three sources of risk. Suppose that W = W0 + x andx is a pure risk such that E[x] =0 and there is no probability distortion. Then the total risk ofx, as measured by the risk premium, is given by have equal weights in the computation of risk which means that the risk is proportional to variance, in particular,π(x)= 12γVar[x]. That is, within EUT variance has a first-order impact on risk measurement. By contrast, in many of the alternative theories we generally have γ− = γ+ and λ > 1 so that LPM2(x, 0) and UPM2(x, 0) have different weights in the computation of risk. However, if the probability distribution of x is symmetric, then LPM2(x,0)=U PM2(x,0)= 12Var[x] and the risk is again proportional to variance, at least when the value of λ is not markedly different from 1
If, on the other hand, the probability distribution of x is not symmetric, then LPM2(x, 0) = UPM2(x, 0). In particular, if the distribution of x is skewed to the left thenLPM2(x, 0)> UPM2(x, 0), whereas if the distribution ofxis skewed to the right thenLPM2(x, 0) <UPM2(x, 0). In this case skewness has a first-order impact on risk measurement when the value ofλis notably different from 1 and/or the values of γ− and γ+ are markedly different from each other. If, for example, γ− ≫ γ+
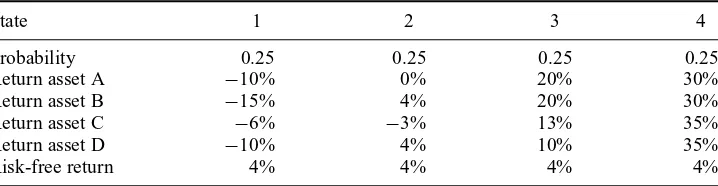
Table 1
Probability distributions of the three gambles: A, B, and C
Each gamble gives an uncertain outcome which depends on the future state of the world. The probabilities of the states are equal.
State 1 2 3 4
Objective probability 0.25 0.25 0.25 0.25
Payoff gamble A −10 −5 5 10
Payoff gamble B −12 −3 5 10
Payoff gamble C −9 −6 3 12
negative skewness. By contrast, ifγ−≪γ+ then the main source of risk is the term withUPM2(x, 0) which reflects the level of positive skewness. In other words, if the decision maker’s degrees of risk aversions below and above the reference point are substantially different, then, depending on the signs and the values of γ− and γ+, either the downside or the upside part of variance is a more proper risk measure than variance. Which part is actually a proper risk measure? The answer depends on the theory being used. Whereas in most models15the decision maker is more risk averse in the domain of losses than in the domain of gains and, therefore, the downside part of variance might be a proper risk measure, in PT/CPT the decision maker is risk seeking in the domain of losses and, thus, a proper risk measure might be the upside part of variance.
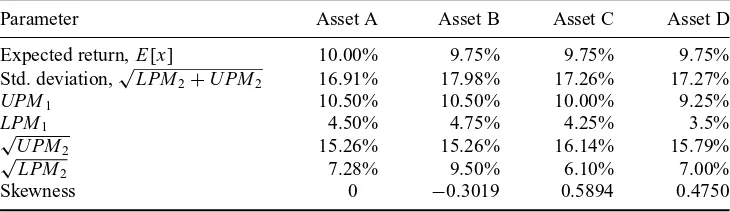
Next we provide an example constructed to demonstrate that a decision maker equipped with the generalised behaviour utility may exhibit strong preferences for skewness. The data for the example is provided in Table 1. In short, we would like to determine which gamble, A, B, or C, is considered to be the least risky. Each gamble gives an uncertain outcome which depends on the future state of the world. Observe that the probabilities of the states are equal so the presented results of comparison of the riskiness of the gambles do not depend on the probability distortion where a decision weight (distorted probability) of a state is computed using the objective probability of the state only (as, for example, in PT). Table 2 presents the descriptive parameters of the distributions of the three gambles. Note that all gambles have zero expected payoff. Gambles B and C have higher variance than gamble A. Gamble B has greater downside variance than gamble A, but lower upside variance. By contrast, gamble C has lower downside variance than gamble A, but greater upside variance. Note that the probability distribution of gamble A has zero skewness, whereas the probability distribution of gamble B is skewed to the left and the probability distribution of gamble C is skewed to the right.
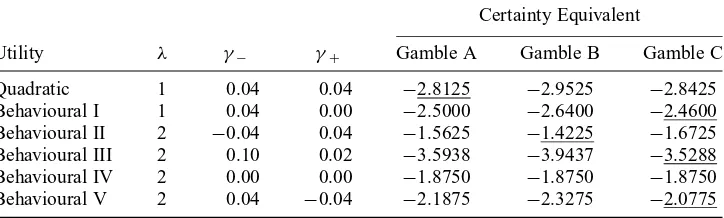
In this example we use the piecewise-quadratic utility function (18) which produces different preferences depending on the set of parameters (λ,γ−,γ+). We compute the certainty equivalents of the gambles for six different decision makers represented by the distinct shapes of the piecewise-quadratic utility presented in Section 4. We compute the certainty equivalent using equation (21). Observe that the higher the certainty
Table 2
Descriptive parameters of the distributions of the three gambles presented in Table 1
Observe that for each gamble the expected loss equals the expected gain so that all gambles have zero expected payoffs. Note that gambles B and C have higher variance than gamble A. However, gamble B has greater downside variance than gamble A, but lower upside variance. By contrast, gamble C has lower downside variance than gamble A, but greater upside variance. Note that the probability distribution of gamble A has zero skewness, whereas the probability distribution of gamble B is skewed to the left and the probability distribution of gamble C is skewed to the right.
Parameter Gamble A Gamble B Gamble C
LPM1 3.75 3.75 3.75
UPM1 3.75 3.75 3.75
Expected payoff,UPM1−LPM1 0 0 0
LPM2 31.25 38.25 29.25
UPM2 31.25 31.25 38.25
Variance,LPM2+UPM2 62.50 69.50 67.50
Skewness 0 −0.2718 0.3651
Table 3
The certainty equivalents of three gambles for decision makers with different shapes of the piecewise-quadratic utility function
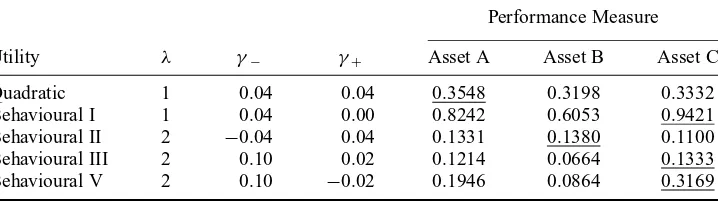
For each shape of the utility function the table reports the corresponding values ofλ,γ−, andγ+. Note that forBehavioural IandBehavioural IIIutilities the values ofγ−andγ+are distinctly different. The highest certainty equivalent for every decision maker is underlined. That is, the underlined certainty equivalent marks out the gamble which is considered to be the least risky for a distinct decision maker.
Certainty Equivalent
Utility λ γ− γ+ Gamble A Gamble B Gamble C
Quadratic 1 0.04 0.04 −2.8125 −2.9525 −2.8425
Behavioural I 1 0.04 0.00 −2.5000 −2.6400 −2.4600
Behavioural II 2 −0.04 0.04 −1.5625 −1.4225 −1.6725
Behavioural III 2 0.10 0.02 −3.5938 −3.9437 −3.5288
Behavioural IV 2 0.00 0.00 −1.8750 −1.8750 −1.8750
Behavioural V 2 0.04 −0.04 −2.1875 −2.3275 −2.0775
equivalent of a gamble for a particular decision maker, the less risky is the gamble for this decision maker (given that the gambles under question have the same expected payoff).
Behavioural I,Behavioural III, andBehavioural Vutilities in Table 3). We can say that the decision makers, for whom gamble C is the least risky, exhibit strong preference for positive skewness. Finally, the decision maker with convex loss function (Behavioural II) considers gamble B, which has highest downside variance (or negative skewness), to be the least risky.
7. Optimal Capital Allocation in the Generalized Framework
The set up of the problem is the same as that described in Section 2. That is, we consider an investor who wants to allocate the wealth between a risk-free and a risky asset. The returns on the risky and the risk-free assets over a small time intervalt are given by equations (7) and (8) respectively. The investor’s initial wealth isWI and the investor’s objective is to maximise the expected utility of his future wealth.
Since the resulting expression for the investor’s expected utility depends on whether the investor buys and holds or sells short the risky asset, we need to consider these two cases separately. In particular, if the investor uses the amount a≥ 0 to buy the risky asset, his future wealth is given by equation (9). If the investor sells short the risky asset such that the proceedings area≥0, his future wealth is given by
W =a(r−x)+WI(1+r).
Note that in both cases the value ofais non-negative. This is necessary to be able to distinguish between the probability distortion ofx −r andr −x.
Before attacking the optimal capital allocation problem, we need to choose a suitable reference pointW0 to which gains and losses are compared. One possible reference point is the ‘status quo’, that is, the investor’s initial wealth WI. Unfortunately, with this choice it is not possible to arrive at a closed-form solution for the optimal capital allocation problem unlessWI=0. However, according to Markowitz (1952), Kahneman and Tversky (1979), Loomes and Sugden (1986), and others, the investor’s initial wealth does not need to be the reference point. Following Barberiset al.(2001) we assume that the reference point isW0 = WI(1+r). This is the investor’s initial wealth scaled up by the risk-free rate. This choice of reference point is sensible for several reasons: (a) this level of wealth serves as a ‘benchmark’ wealth. The idea here is that the investor is likely to be disappointed if the risky asset provides a return below the risk-free rate of return; (b) with this reference point the performance measure does not depend on the investor’s wealth (see the subsequent section). That is, the investor’s utility of returns is independent of wealth; (c) this choice is also justified if we require that all partial moments should exhibit the homogeneity property ina(for explanation, see footnote 8). For example, if the investor is equipped with the Fisburn’s mean-lower partial moment of order two utility, then the risk of investing the amounta, as measured by downside deviation, equalsaLP M2(x−r,0), which seems reasonable.
Having decided on the investor’s reference wealth, we are ready to state and prove the following theorem.
Theorem 8. If either utility functions U−and U+are at most quadratic in wealth or the investment risk is small, then the investor’s optimal capital allocation problem has the following solution:
If
and
λγ−LP M2(x−r,0)+γ+U P M2(x−r,0)>0, (28)
then the optimal amountinvestedin the risky asset is given by
a= E[x−r]−(λ−1)LP M1(x−r,0)
λγ−LP M2(x−r,0)+γ+U P M2(x−r,0), (29)
and the investor’s maximum equivalent expected utility from the buy-and-hold (BH) strategy is given by
EB H[U∗(W)]= 1 2
(E[x−r]−(λ−1)LP M1(x−r,0))2
λγ−LP M2(x−r,0)+γ+U P M2(x−r,0). (30)
If
E[r−x]−(λ−1)LP M1(r−x,0)>0 (31)
and
λγ−LP M2(r−x,0)+γ+U P M2(r−x,0)>0, (32)
then the optimal amount of the risky asset that should besold shortis given by
a= E[r−x]−(λ−1)LP M1(r −x,0)
λγ−LP M2(r−x,0)+γ+U P M2(r−x,0), (33)
and the investor’s maximum equivalent expected utility from the short selling (SS) strategy is given by
ES S[U∗(W)]= 1 2
(E[r−x]−(λ−1)LP M1(r−x,0))2
λγ−LP M2(r −x,0)+γ+U P M2(r−x,0). (34)
If all the conditions (27), (28), (31), and (32) are satisfied, then the maximisation problem has two local maxima. In this case the optimal policy is the one which gives the highest expected utility (either buy-and-hold or sell short).
If neither (27) nor (31) is satisfied, then the investor’s optimal policy is to avoid the risky asset and invest all in the risk-free asset.
Proof. If either utility functionsU− and U+ are at most quadratic in wealth or the investment risk is small, then, according to Theorem 1, the investor’s preferences can be represented by the piecewise-quadratic utility (18).
First, we consider the buy-and-hold strategy. In this case the investor’s expected utility is given by
EB H[U(W)]=a(E[x−r]−(λ−1)LP M1(x−r,0))
−1
2a
2(λγ
−LP M2(x−r,0)+γ+U P M2(x−r,0)), (35)
inserting expression (29) for the optimal value ofainto (35), we obtain the solution for the investor’s maximum expected utility (30).
Second, we consider the short selling strategy. In this case the investor’s expected utility is given by
ES S[U(W)]=a(E[r−x]−(λ−1)LP M1(r−x,0))
−1
2a 2(
λγ−LP M2(r −x,0)+γ+U P M2(r−x,0)), (36)
where the expectation and the partial moments are computed using the cumulative distorted probability distribution function Qr−x. Observe again that the investor’s expected utility (36) is a quadratic function ina. To guarantee the existence of a local maximum, the investor’s expected utility should be concave in a, which means that condition (32) should be satisfied. The first-order condition of optimality of agives the solution (33). Since we assume thata≥0, the solution for the optimalais a valid solution only if condition (31) is satisfied. Otherwise, the solution isa = 0. Finally, inserting expression (33) for the optimal value ofainto (36), we obtain the solution for
the investor’s maximum expected utility (34).
Remark 3. Observe that if, for example, condition (27) is satisfied whereas condition (28) is not, then the higherathe higher the investor’s expected utility. In other words, in this case the investor is willing to borrow an infinite amount at the risk-free interest rate to invest in the risky asset. In this case the optimal capital allocation problem does not have a solution. For example, conditions (28) and (32) are violated if the investor appreciates uncertainty in losses,γ−<0, but is neutral to uncertainty in gains,γ+=
0. The other example when these conditions are violated occurs whenγ−=γ+=0, that is, the investor is neutral to both uncertainties. In the latter case the investor’s utility can be represented by so-called ‘bilinear’ utility. For bilinear utility the solution to the optimal capital allocation problem generally does not exist. This was noted by Sharpe (1998).
Corollary 9. In the EUT framework, the solution for the optimal amount that should be invested in the risky asset (or sold short) reduces to the Arrow’s solution given by (11).
Proof. This follows from the fact that for a von Neumann-Morgenstern utility function
λ=1 andγ−=γ+=γ.
Remark4. Observe from Arrow’s solution (11) that in the EUT framework it is always optimal to undertake a risky investment when E[x] =r. If E[x]>r, it is optimal for the investor to buy some amount of the risky asset, whereas ifE[x]<r, it is optimal for the investor to sell short some amount of the risky asset. By contrast, in our generalised framework the investor avoids the risky asset if
E[x−r]−(λ−1)LP M1(x−r,0)<0 and
E[r−x]−(λ−1)LP M1(r −x,0)<0.
probability distortion. For example, the higher the investor’s loss aversion, the higher the risk premium must be in order to motivate the investor to undertake a risky investment. It is easy to show that without any probability distortion aloss averse investor does not investif
1
λLPM1(x,r)<UPM1(x,r)< λLPM1(x,r).
However, some particular distortion of probabilities might cause the investor’s avoidance of the risky asset even with no loss aversion. In this case we must have
E[x−r]<0 and E[r−x]<0.
This may occur with a pessimistic probability distortion. In Appendix B we provide an example which demonstrates how a probability distortion might cause either avoidance of the risky asset or the existence of two local maxima in the optimal capital allocation problem. This result may help explain why many investors do not invest in equities. Furthermore, the equity premium puzzle may be explained by either loss aversion or pessimistic probability distortion or a combination of these effects. The explanation lies in the fact that to induce an investor with either loss aversion or pessimistic beliefs to buy equities, stock returns must be rather high relative to bond returns.
Remark5. Somewhat surprisingly, an investor with the original PT/CPT utility function will always invest in the risky asset. Given the expression for the investor’s value function in PT/CPT (19), it is rather straightforward to arrive at the following solution for the optimal capital allocation problem: If it is optimal for the investor to buy and hold the risky asset, then the optimal amount invested in the risky asset is given by
a=
αU P Mα(x−r,0)
λβLP Mβ(x−r,0)
1
β−α
. (37)
If, on the other hand, the short selling strategy is optimal, then the optimal amount that should be sold short is given by
a=
αU P Mα(r−x,0)
λβLP Mβ(r−x,0)
1
β−α
. (38)
The solution for the optimal capital allocation problem exists under condition thatβ > α. Observe that both values forain (37) and (38) are always non-negative which means that there are two local maxima (interior solutions) in the optimal capital allocation problem within the PT/CPT framework. The investor chooses the strategy that gives the highest utility, but he never avoids the risky investment even when E[x] = r or
E[x]=r.
Next we present a brief comparative static analysis of expressions (29) and (33) for the optimal amount invested in the risky asset.
Corollary 10. The optimal amount that should be invested in the risky asset (or sold short) decreases as the investor’s risk aversion in the domain of either gains or losses increases.
Proof. If it is optimal for the investor to buy-and-hold the risky asset, then the first-order derivative ofawith respect toγ+is
∂a
∂γ+ = −
(E[x−r]−(λ−1)LP M1(x−r,0))U P M2(r−x,0)
If it is optimal for the investor to sell short the risky asset, then the first-order derivative ofawith respect toγ+is
∂a
∂γ+ = −
(E[r−x]−(λ−1)LP M1(r−x,0))U P M2(r−x,0)
(λγ−LP M2(r−x,0)+γ+U P M2(r−x,0))2 <0.
Similarly, if it is optimal for the investor to buy-and-hold the risky asset, then the first-order derivative ofawith respect toγ−is
∂a
∂γ− = −
λ(E[x−r]−(λ−1)LP M1(x−r,0))LP M2(r−x,0) (λγ−LP M2(r−x,0)+γ+U P M2(r−x,0))2 <0.
If it is optimal for the investor to sell short the risky asset, then the first-order derivative ofawith respect toγ−is
∂a
∂γ− = −
λ(E[r−x]−(λ−1)LP M1(r−x,0))LP M2(r−x,0)
(λγ−LP M2(r−x,0)+γ+U P M2(r−x,0))2 <0.
Next consider the dependence of the optimal amount that should be invested in the risky asset (or sold short) on the loss aversion parameter λ. The computation of the first-order derivative ofa, given by (29), with respect toλgives
∂a
∂λ = −
A×LP M1(x−r,0)+γ−B×LP M2(r−x,0)
(λγ−LP M2(r −x,0)+γ+U P M2(r−x,0))2 ,
where
A=λγ−LP M2(r−x,0)+γ+U P M2(r−x,0),
B=E[x−r]−(λ−1)LP M1(x−r,0).
SinceA>0 (due to (28)) andB>0 (due to (27)), the sign of ∂∂λa is obviously negative if γ− ≥ 0. However, if γ− < 0, then the sign of ∂∂λa might be positive. The latter means that when the investor appreciates uncertainty in losses, then an increase in loss aversion might increase the optimal amount invested in the risky asset. This is obviously counter-intuitive. We believe that the explanation for this paradox lies in the fact that the piecewise-quadratic utility function (18) is not always increasing for all values ofW − W0. This might result in a number of paradoxes similar to those for the standard quadratic utility function. Note that ifγ−<0, then by condition (28) we must haveγ+>0. In this case the piecewise-quadratic utility is increasing only in the rangeγ1
− <W −W0<
1
γ+.
For example, if W − W0 decreases below γ1
−, then the investor’s utility begins to
increase which is not sensible. Generally, when the piecewise-quadratic utility function is not increasing for allW −W0, we can stumble upon some paradoxes. Some of these paradoxes will be due to the violation of the first-order stochastic dominance principle. For the standard quadratic utility function this type of paradoxes were first noted by Borch (1969) and Feldstein (1969).
8. Performance Measurement in the Generalized Framework