Determining Optimum Strata Boundary Points on Stratified Random Sampling using Dynamic Programming (Case: Expenditure per Capita of East Java Province Year 2008)

(1)

PENENTUAN TITIK-TITIK BATAS OPTIMUM STRATA

PADA PENARIKAN CONTOH ACAK BERLAPIS

DENGAN PEMROGRAMAN DINAMIK

(Kasus : Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008)

MAHYUDI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(2)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Penentuan Titik-titik Batas Optimum Strata pada Penarikan Contoh Acak Berlapis dengan Pemrograman Dinamik (Kasus: Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008) adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, September 2011

(3)

ABSTRACT

MAHYUDI. Determining Optimum Strata Boundary Points on Stratified Random Sampling using Dynamic Programming (Case: Expenditure per Capita of East Java Province Year 2008). Under direction of BUDI SUSETYO and UTAMI DYAH SYAFITRI.

Optimum stratification is the method of choosing the best boundaries that make strata internally homogeneous, given some sample allocation. In order to make the strata internally homogenous, the strata should be constructed in such a way that the strata variances for the characteristic under study be as small as possible. This could be achieved effectively by having the distribution of the main study variable known and create strata by cutting the range of the distribution at suitable points. The problem of finding Optimum Strata Boundaries (OSB) is considered as the problem of determining Optimum Strata Widths (OSW). The problem is formulated as a Mathematical Programming Problem (MPP), which minimizes the variance of the estimated population parameter under Neyman allocation subject to the restriction that sum of the widths of all the strata is equal to the total range of the distribution. The distributions of the study variable are considered as continuous with standard normal density functions. The formulated MPPs, which turn out to be multistage decision problems, can then be solved using dynamic programming technique proposed by Bühler and Deutler (1975). After the counting process using C++ program received the width of each stratum. From these results the optimal boundary point can be determined for each stratum. For the two strata to get the optimal point on the boundary x1 = 0.002. For the

formation of three strata obtained the optimal point on the boundary x1 = -0.546

and x2 = 0.552. For the formation of four strata obtained optimal boundary point is

x1 = -0.869, x2 = 0.003 and x3 = 0.878. In forming five strata obtained optimal

boundary point x1 = -1.096, x2 = -0.331, x3 = 0.339 and x4 = 1.107. The

establishment of a total of six strata obtained the optimal point on the boundary x1

= -1.267, x2 = -0.569, x3 = 0.005, x4 = 0.579 and x5 = 1.281.

(4)

RINGKASAN

MAHYUDI. Penentuan Titik-titik Batas Optimum Strata pada Penarikan Contoh Acak Berlapis dengan Pemrograman Dinamik (Kasus: Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008). Dibimbing oleh BUDI SUSETYO dan UTAMI DYAH SYAFITRI.

Penarikan contoh (sampling) dalam survei adalah suatu proses untuk memilih sebagian elemen dari suatu populasi dengan prosedur tertentu sehingga dapat digunakan untuk menduga parameter populasi. Untuk mencapai tujuan tersebut diperlukan metode penarikan contoh yang sesuai, salah satunya adalah penarikan contoh acak berlapis (stratified random sampling). Pada penarikan contoh acak berlapis, perlu diperhatikan peubah apa yang digunakan sebagai dasar pembentukan strata.

Apabila peubah kualitatif digunakan untuk stratifikasi, pada umumnya pembentukan strata tidak terlalu mengalami masalah, misalnya berdasarkan tingkat pendidikan, pekerjaan dan jenis kelamin. Sebaliknya jika peubah yang digunakan untuk stratifikasi adalah peubah kuantitatif maka diperlukan teknik tertentu untuk menentukan batas antar strata. Masalah penentuan batas optimum strata ekuivalen dengan masalah menentukan lebar optimum strata yang diformulasikan sebagai masalah pemrograman matematika. Salah satunya adalah pendekatan pemrograman dinamik Bühler dan Deutler yaitu dengan meminimumkan ragam dari parameter populasi yang diduga berdasarkan alokasi Neyman dengan batasan bahwa jumlah lebar dari semua strata sama dengan total jarak dari sebaran peubah yang diteliti.

Penelitian ini bertujuan untuk menerapkan pemrograman dinamik yang merupakan salah satu masalah pengoptimuman dalam pemrograman matematika untuk menentukan batas optimum strata dalam penarikan contoh acak berlapis. Penelitian ini menggunakan data sekunder yang diperoleh dari BPS yaitu data pengeluaran per kapita penduduk Jawa Timur Tahun 2008 dengan jumlah contoh sebanyak 8607 kepala rumah tangga.

Teknik pemrograman dinamik dimulai dengan pembentukan fungsi objektif. Dari fungsi objektif ini diperoleh persamaan rekursif yang menghubungkan tahapan yang berbeda dalam suatu metode yang menjamin bahwa tiap tahap solusi layak optimal, juga optimal dan layak untuk semua masalah. Dari persamaan rekursif ini akan diperoleh lebar dari masing-masing strata dan titik batas optimum pada tiap strata. Metode ini juga memberikan nilai optimum fungsi objektif untuk setiap strata L.

(5)

v Setelah dilakukan proses penghitungan dengan menggunakan program C++ diperoleh lebar tiap strata. Dari hasil ini dapat ditentukan titik-titik batas optimum untuk tiap strata. Untuk dua strata diperoleh titik batas optimum pada x1 = 0.002.

Untuk pembentukan tiga strata diperoleh titik batas optimum pada x1 = -0.546 dan

x2 = 0.552. Untuk pembentukan sebanyak empat strata diperoleh titik batas

optimum adalah x1 = -0.869, x2 = 0.003 dan x3 = 0.878. Pada pembentukan

sebanyak lima strata diperoleh titik batas optimum x1 = -1.096, x2 = -0.331, x3 =

0.339 dan x4 = 1.107. Sedangkan untuk pembentukan sebanyak enam strata

diperoleh titik batas optimum pada x1 = -1.267, x2 = -0.569, x3 = 0.005, x4 = 0.579

dan x5 = 1.281.

Metode pemrograman dinamik ini juga memberikan nilai optimum fungsi objektif untuk tiap jumlah strata. Hasilnya menunjukkan bahwa semakin banyak jumlah strata maka nilai optimum fungsi ini akan semakin kecil. Nilai optimum fungsi objektif untuk jumlah strata 2, 3, 4, 5, dan 6 berturut-turut adalah 0.599, 0.424, 0.328, 0.267 dan 0.225. Untuk melihat karakteristik keragaman dalam tiap jumlah strata dapat dilakukan uji khi-kuadrat yang dikenal dengan uji Bartlett. Hasil uji ini memperlihatkan bahwa adanya pebedaan yang nyata antara ragam-ragam pada setiap jumlah strata L. Artinya bahwa antar strata lebih bervariasi karakteristiknya (heterogen).

Penentuan strata dengan peubah kuantitatif dapat dilakukan dengan pendekatan pemrograman dinamik dan dapat menjadi salah satu alternatif pembentukan strata selain dengan menggunakan peubah kualitatif.

(6)

© Hak Cipta milik IPB, tahun 2011

Hak Cipta dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau meyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan yang wajar IPB.

(7)

PENENTUAN TITIK-TITIK BATAS OPTIMUM STRATA

PADA PENARIKAN CONTOH ACAK BERLAPIS

DENGAN PEMROGRAMAN DINAMIK

(Kasus : Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008)

MAHYUDI

Tesis

Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

(8)

(9)

ix Judul Tesis : Penentuan Titik-titik Batas Optimum Strata pada Penarikan Contoh Acak Berlapis dengan Pemrograman Dinamik (Kasus: Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008)

Nama : Mahyudi

NIM : G151080021

Disetujui Komisi Pembimbing

Dr. Ir. Budi Susetyo, MS

Ketua

Utami Dyah Syafitri, S.Si, M.Si

Anggota

Diketahui

Ketua Program Studi Statistika

Dr. Ir. Erfiani, M.Si

Dekan Sekolah Pascasarjana

Dr. Ir. Dahrul Syah, M.Sc. Agr

(10)

PRAKATA

Puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala karunia dan hidayah-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul

“Penentuan Titik-titik Batas Optimum Strata pada Penarikan contoh Acak Berlapis dengan Pemrograman Dinamik (Kasus: Pengeluaran per Kapita Propinsi Jawa Timur Tahun 2008”.

Terima kasih penulis ucapkan kepada Bapak Dr. Ir. Budi Susetyo, MS selaku ketua komisi pembimbing dan Ibu Utami Dyah Syafitri, S.Si, M.Si selaku anggota komisi pembimbing yang telah memberikan bimbingan, masukan dan saran yang sangat berarti dalam penyusunan tesis ini. Ungkapan terima kasih juga penulis sampaikan untuk istri tercinta yang tiada henti-hentinya memberikan doa dan motivasi untuk menyelesaikan tesis ini dan jagoan kecilku yang selalu menjadi penyemangat. Kedua orang tua dan seluruh keluarga atas segala doa dan kasih sayangnya. Teman-teman mahasiswa Pascasarjana Statistika yang telah membantu dan memberi dukungan selama penyusunan tesis ini. Serta semua pihak yang telah membantu penulis secara fisik, ilmu maupun dukungan moral dalam penyusunan tesis ini.

Penulis menyadari sepenuhnya bahwa tesis ini memiliki banyak kekurangan. Saran dan kritik yang sifatnya membangun sangat penulis harapkan demi perbaikan di masa yang akan datang. Semoga tesis ini dapat bermanfaat.

(11)

RIWAYAT HIDUP

Penulis dilahirkan di Tanjung Atap (Palembang) pada tanggal 20 Desember 1975 dari ayah Agussalim dan ibu Hadisah. Penulis merupakan putra kelima dari delapan bersaudara.

Pada tahun 1994 penulis lulus dari SMA Negeri 1 Tanjung Batu dan pada tahun yang sama diterima sebagai mahasiswa Jurusan Matematika FMIPA Universitas Sriwijaya Palembang melalui jalur UMPTN. Penulis memperoleh gelar Sarjana Sains pada tahun 1998 dan pada tahun 2008 penulis melanjutkan Program Magister Sains di Program Studi Statistika, Sekolah Pascasarjana, Institut Pertanian Bogor.

(12)

DAFTAR ISI

Halaman

DAFTAR TABEL ... xiiii

DAFTAR LAMPIRAN ... xiv

PENDAHULUAN ... 1

Latar Belakang ... 1

Tujuan Penelitian ... 2

TINJAUAN PUSTAKA ... 4

Penarikan Contoh Acak Berlapis ... Error! Bookmark not defined. Prinsip Pemrograman Dinamik ... Error! Bookmark not defined. Penentuan Batas Optimum Strata untuk Peubah Kuantitatif……… ... 7

Prosedur Solusi Menggunakan Teknik Pemrograman Dinamik ... Error! Bookmark not defined. Pemrograman Matematika Untuk Sebaran Normal………...………12

DATA DAN METODE ... 14

Data ... 14

Metode Penelitian... 14

HASIL DAN PEMBAHASAN ... 16

Data Pengeluaran Per Kapita propinsi Jawa Timur Tahun 2008 ... 16

Penentuan Titik-titik Batas Optimum Strata ... 18

Pengujian Kehomogenan Ragam………...23 Pembentukan Strata Pengeluaran Per Kapita Jawa Timur Tahun 2008………24

SIMPULAN DAN SARAN ... 27

Simpulan ... 27

Saran ... 27

DAFTAR PUSTAKA ... 28

(13)

DAFTAR TABEL

Halaman

Tabel 1 Titik-titik batas optimum strata dari sebaran normal baku ... Error! Bookmark not defined.20

Tabel 2 Hasil uji khi-kuadrat untuk setiap jumlah strataError! Bookmark not defined.23

(14)

DAFTAR GAMBAR

Halaman

(15)

xv

DAFTAR LAMPIRAN

Halaman

(16)

PENDAHULUAN

Latar Belakang

Penarikan contoh (sampling) dalam survei adalah suatu proses untuk memilih sebagian anggota dari suatu populasi dengan prosedur tertentu sehingga dapat digunakan untuk menduga parameter populasi secara sah. Untuk mencapai tujuan tersebut diperlukan metode penarikan contoh yang sesuai. Salah satu teknik penarikan contoh adalah penarikan contoh acak berlapis (stratified random sampling). Pada penarikan contoh acak berlapis, perlu diperhatikan peubah yang digunakan sebagai dasar pembentukan strata.

Apabila peubah kualitatif digunakan untuk stratifikasi, pada umumnya pembentukan strata tidak terlalu mengalami masalah, misalnya berdasarkan tingkat pendidikan, pekerjaan dan jenis kelamin. Sebaliknya, jika peubah yang digunakan untuk stratifikasi adalah peubah kuantitatif maka diperlukan teknik

tertentu untuk menentukan batas antar strata sesuai dengan kaidah teknik ini.

Pertimbangan dasar yang diperhatikan dalam penentuan batas-batas optimum strata adalah bahwa anggota populasi dalam strata harus sehomogen mungkin dan antar strata seheterogen mungkin, dengan perkataan lain ragam dalam strata harus sekecil mungkin dibandingkan ragam antar strata. Masalah yang timbul adalah penentuan titik optimum batas stratifikasi yang akan membagi populasi menjadi dua atau lebih strata sehingga memenuhi kriteria di atas.

Metode dalam penentuan titik batas optimum strata telah dikemukakan oleh beberapa peneliti. Lavallée dan Hidiroglou (1988) mengusulkan suatu algoritma untuk menentukan batas-batas strata suatu alokasi kuasa untuk contoh yang distrata dari unit-unit contoh yang tidak tentu. Hidiroglou dan Srinath (1993) dalam Khan (2008) menyajikan suatu algoritma yang lebih umum, yaitu dengan memberikan nilai-nilai yang berbeda untuk mengoperasikan parameter-parameter yang menghasilkan alokasi kuasa, alokasi Neyman, atau gabungan dari alokasi-alokasi ini.

(17)

2 modifikasi yang menggabungkan hubungan berbeda antara stratifikasi dan peubah-peubah yang diteliti. Nicolini (2001) mengusulkan suatu metode yang diberi nama Natural Class Method (NCM), untuk menentang metode Dalenius dan Hodges yang paling banyak digunakan, tetapi kedua metode tersebut tidak terbukti lebih efisien dari yang lain.

Lednicki dan Wieczorkowski (2003) dalam Khan (2008) mengajukan metode stratifikasi menggunakan metode simpleks dari Nelder dan Mead (1965) dalam Khan (2008). Kemudian Kozak (2004) menyajikan algoritma pencarian secara acak yang dimodifikasi sebagai metode stratifikasi optimum. Algoritma Kozak benar-benar lebih cepat dan efisien dibandingkan dengan algoritma Rivest, dan Lednicki dan Wieczorkowski dilihat dari kemampuan mengendalikan nilai yang lebih kecil pada fungsi objektif tetapi hal itu tidak dapat menjamin bahwa algoritma tersebut menunjukkan optimum global.

Mengingat bahwa masalah penentuan batas optimum strata ekuivalen dengan masalah menentukan lebar optimum strata Khan et al. (2002) dalam Khan (2008), mengatakan bahwa masalah lebar optimum strata sebagai masalah pemrograman matematika. Khan et al. (2002) menerapkan prosedurnya untuk menentukan batas optimum strata terhadap populasi yang memiliki sebaran uniform dan segitiga siku-siku. Kemudian Khan et al. (2005) memperluas

pendekatan pemrograman dinamik untuk menentukan batas optimum strata terhadap peubah eksponensial. Khan et al. (2008) juga melakukan pendekatan pemrograman dinamik terhadap peubah yang memiliki sebaran normal baku.

Salah satu pemrograman matematika yang dapat digunakan dalam menentukan lebar optimum strata adalah pendekatan pemrograman dinamik Bühler dan Deutler (1975). Formulasi masalah pemrograman matematika dengan meminimumkan ragam dari parameter populasi yang diduga berdasarkan alokasi Neyman dengan batasan bahwa jumlah lebar dari semua strata sama dengan total jarak dari sebaran peubah yang diamati.

Tujuan Penelitian

(18)

(19)

TINJAUAN PUSTAKA

Penarikan Contoh Acak Berlapis

Penarikan contoh acak berlapis adalah suatu rancangan penarikan contoh acak yang membagi N unit dari populasi ke dalam L strata yang tidak saling tumpang tindih, sehingga setiap strata memiliki Ni unit (i = 1, 2, ..., L). Seperti dinyatakan oleh Cochran (1977), salah satu alasan stratifikasi adalah dapat menghasilkan keuntungan tingkat keakuratan dalam pendugaan karakteristik total populasi.

Dalam pelaksanaannya, penarikan contoh acak berlapis diambil dengan cara yang sama seperti penarikan contoh acak sederhana, tetapi penarikan contoh dilakukan secara terpisah dan saling bebas dalam tiap strata. Jika N1, N2, ..., NL merupakan jumlah populasi dalam tiap strata dan n1, n2, ..., nL merupakan sampling unit yang terpilih secara acak dalam tiap strata, maka jumlah total contoh acak stratifikasi yang mungkin adalah sama dengan

( ) ( ) ( )

yang lebih kecil atau sama dengan , jumlah total contoh acak sederhana yang

mungkin.

Sebagai contoh, jika ada tiga strata dengan N1 = 3 , N2 = 5 dan N3 = 6 , jumlah total contoh yang mungkin dari n1 = 1 contoh dari strata pertama, n2 = 2 contoh dari strata kedua, dan n3 = 4 contoh dari strata ketiga adalah

Jumlah total contoh acak sederhana 7 contoh dari 14 contoh dalam populasi adalah

Peluang suatu contoh terpilih pada suatu strata tertentu dapat ditunjukkan

sama dengan (jika contoh dalam strata h). Seperti pada kasus di atas, peluang

(20)

5 Menurut Dalenius dalam Singh (1986), pada penerapan rancangan contoh berlapis perlu diperhatikan:

1. Pemilihan peubah stratifikasi; 2. Pemilihan jumlah L strata;

3. Penentuan cara populasi distratifikasi;

4. Pemilihan ukuran contoh nh yang diambil dari strata ke- h; 5. Pemilihan rancangan penarikan contoh di dalam strata.

Dalam pembentukan strata, diusahakan agar anggota-anggota yang hampir sama dimasukkan ke dalam satu strata sehingga ragam di dalam masing-masing strata menjadi homogen. Selain itu, akan lebih baik lagi jika perbedaan rata-rata karakteristik antar strata dibuat sebesar mungkin.

Prinsip-prinsip yang dapat digunakan dalam stratifikasi populasi adalah sebagai berikut:

1. Strata tidak boleh tumpang tindih (non-overlapping) dan harus melibatkan populasi secara keseluruhan;

2. Stratifikasi populasi harus dilakukan sehingga membuat strata homogen secara internal dengan mempertimbangkan karakteristik peubah penelitian;

3. Dalam beberapa situasi praktis ketika stratifikasi sulit untuk

mempertimbangkan karakteristik peubah penelitian, kesesuaian administrasi dapat dianggap sebagai dasar untuk stratifikasi.

Pebedaan mendasar untuk strata adalah nilai kuantitas y yang diukur dalam survei. Jika kita dapat membuat strata dengan nilai y, tidak akan terjadi tumpang tindih antar strata, dan ragam di dalam strata akan jauh lebih kecil daripada ragam keseluruhan terutama jika terdapat beberapa strata.

Keuntungan penerapan penarikan contoh berlapis:

1. Dapat diperoleh nilai dugaan dengan tingkat keakuratan lebih tinggi untuk setiap strata maupun untuk populasi secara keseluruhan;

(21)

6 3. Setiap strata dapat dianggap sebagai populasi tersendiri sehingga bisa saja menentukan presisi yang dikehendaki pada setiap strata dan disajikan tersendiri;

4. Secara administratif, pelaksanaannya menjadi lebih mudah.

5. Biaya pengumpulan dan analisis data seringkali dapat diperkecil dengan adanya pembagian populasi yang besar menjadi strata-strata yang lebih kecil.

Adapun kerugian penerapan penarikan contoh berlapis adalah:

1. Sering dijumpai kenyataan bahwa dasar yang tepat untuk mengelompokkan data sulit diperoleh. Akibatnya strata yang dibuat tidak sesuai dengan tujuan;

2. Diperlukan sebuah kerangka contoh yang terpisah dan berbeda untuk setiap kelompok.

Prinsip Pemrograman Dinamik

Pemrograman dinamik adalah prosedur matematika yang terutama dirancang untuk memperbaiki efisiensi perhitungan masalah pemrograman matematika tertentu dengan menguraikannya menjadi bagian-bagian masalah yang lebih kecil. Pemrograman dinamik pada umumnya menjawab masalah dalam

tahap-tahap, dengan setiap tahap meliputi tepat satu peubah optimisasi. Perhitungan di tahap yang berbeda-beda dihubungkan melalui perhitungan rekursif yang menghasilkan pemecahan optimal yang mungkin bagi seluruh masalah.

Pendekatan pemrograman dinamik didasarkan pada prinsip optimisasi Bellman dalam Siagian P ( 2006) yang mengatakan:

„suatu kebijakan optimal mempunyai sifat bahwa apa pun keadaan dan keputusan awal, keputusan berikutnya harus membentuk suatu kebijakan

optimal dengan memperhatikan keadaan dari hasil keputusan pertama.’

(22)

7 suatu keputusan didasarkan pada keadaan dari keputusan sebelumnya dan merupakan landasan bagi keputusan berikutnya.

Jika proses menghitung perolehan optimal sampai pada tahap ke- n, maka selesailah prosedur perhitungan berdasarkan pendekatan pemrograman dinamik. Langkah selanjutnya adalah menentukan keputusan optimal untuk seluruh persoalan. Dimulai dari keputusan optimal pada tahap ke- n dan kemudian menelusuri keputusan optimal pada tahap-tahap sebelumnya.

Diketahui pada tahap ke- n sehingga keputusan optimal untuk tahap ke- n dapat ditentukan, misalnya pada alternatif k. Tentu , yaitu biaya yang diperlukan untuk alternatif k sudah dapat diketahui. Karena itu

. Setelah melakukan perhitungan pada tahap (n-1), keputusan optimal pada tahap ini dapat ditentukan sesuai jumlah .

Misalkan keputusan diperoleh pada alternatif j sehingga pun dapat

diketahui, sehingga . Proses ini dilanjutkan terus, sampai diperoleh nilai sehingga dapat ditentukan keputusan

optimal pada tahap ke- 1. Keputusan optimal untuk seluruh persoalan adalah kumpulan dari semua keputusan optimal pada masing-masing tahap.

Penentuan Batas Optimum Strata Untuk Peubah Kuantitatif

Misalkan adalah batas-batas strata. Strata h mengandung semua unit dengan satu nilai X dalam interval [ untuk sehingga dan , dengan dan masing-masing adalah nilai minimum dan maksimum peubah stratifikasi (Baillargeon 2010).

Misalkan X adalah peubah acak, diskret atau kontinu dengan fungsi

kepadatan peluang . Untuk menduga rataan populasi µ dengan contoh acak distratifikasi, X dipartisi menjadi L strata [ ] ( ] ], sehingga

(1) Anggap bahwa dari strata h ( h = 1, 2, ..., L ) mengandung Nh unit, sebuah contoh

(23)

8 rataan stratifikasi ̅ ∑ ̅ adalah dugaan tak bias untuk µ dengan

ragam ̅ ∑ (2)

dengan ̅ ∑

∑ ( )

dan

∑

(Cochran 1977) .

Apabila fungsi frekuensi diketahui, nilai-nilai Wh dan pada persamaan (2) dapat diperoleh dengan

∫ (3)

∫ (4)

dengan ∫

(5)

adalah rataan dan adalah batas-batas dari strata ke- h. Kemudian persamaan (2) dibaca sebagai fungsi dari titik-titik batas strata dan ukuran contoh dengan ̅ ̅| .

Jika nh ditetapkan, tujuan stratifikasi optimum adalah untuk menentukan titik-titik batas optimum strata sehingga ̅ adalah minimum. Selain itu, jika rasio pengambilan contoh kecil atau pengambilan contoh

dengan pengembalian, maka masalah pengoptimuman berikut diperoleh,

tergantung pada tipe dari alokasi ukuran total contoh ∑ pada strata (Cochran 1977).

1. Alokasi proporsional Minimumkan ∑

dengan kendala (6) 2. Alokasi sama

Minimumkan ∑

dengan kendala (7) 3. Alokasi Neyman

(24)

9 Minimumkan ∑

dengan kendala (8) Masalah pada persamaan (6) dan (8) memiliki struktur sebagai berikut :

Minimumkan ∑

dengan kendala (9) Bühler dan Deutler (1975) telah menyarankan suatu metode pengoptimuman rekursif untuk menyelesaikan persamaan (9) menggunakan teknik pemrograman dinamik sebagai berikut.

Misalkan merupakan fungsi frekuensi dan dan adalah nilai x terkecil dan terbesar. Jika rataan populasi diduga berdasarkan alokasi Neyman, maka masalah penentuan batas-batas strata adalah untuk memotong jarak,

(10) pada titik-titik tengah sehingga ∑ pada persamaan (8) minimum.

Perhatikan bahwa memiliki n fungsi bagian linear atau non linear

sebagai berikut : {

(11)

Juga diasumsikan bahwa ada L strata, li jumlah strata yang dibentuk berdasarkan fungsi kepadatan dan ∑ .

Jika pada persamaan (11) dapat diintegralkan, menggunakan pernyataan persamaan (3), (4) dan (5), , dan diperoleh sebagai suatu fungsi dari titik-titik batas dan . Sehingga fungsi objektif pada persamaan

(25)

10 Dengan definisi dari di atas, jarak dari sebaran yang diberikan pada persamaan (10) dinyatakan sebagai fungsi dari lebar strata sebagai

∑ ∑ (12) Stratifikasi ke- k titik k = 1, 2, ..., L – 1 dinyatakan sebagai:

yang merupakan fungsi lebar strata ke- k dan batas strata ke (k – 1).

Perhatikan bahwa dengan menambahkan persamaan (12) sebagai batas/ kendala baru, masalah persamaan (9) dapat ditulis kembali sebagai masalah yang ekuivalen dengan penentuan lebar optimum strata sebagai berikut:

Minimumkan ∑ dengan kendala ∑ ,

dan (13) Nilai awal diketahui. Oleh karena itu, syarat pertama pada

fungsi objektif persamaan (13) adalah suatu fungsi dari itu sendiri. Jika diketahui, titik stratifikasi selanjutnya akan diketahui dan syarat kedua pada fungsi objektif akan menjadi fungsi dari itu sendiri.

Fungsi objektif merupakan fungsi itu sendiri, sehingga masalah pemrograman matematika persamaan (13) dinyatakan sebagai:

Minimumkan ∑ dengan kendala ∑ ,

dan (14) Prosedur Solusi Menggunakan Teknik Pemrograman Dinamik

(26)

11 Perhatikan submasalah berikut dari persamaan (14) untuk k strata pertama: Minimumkan ∑

dengan kendala ∑ ,

dan (15) dengan adalah lebar total yang tersedia untuk bagian dalam k strata atau

nilai tertentu pada k langkah. Catatan bahwa untuk . Fungsi transformasi diberikan oleh:

,

, ,

Ambil sebagai notasi nilai minimum fungsi objektif dari persamaan (15), yaitu: [ ∑ | ∑ dan ]. Dari definisi tersebut, masalah pemrograman matematika persamaan (14) ekuivalen untuk menentukan secara rekursif dengan menentukan untuk dan .

[ ∑

| ∑ dan ]

Untuk suatu nilai tetap dari ;

[ ∑ | ∑ dan ]

Menggunakan prinsip pengoptimalan Bellman, diperoleh hubungan berulang dari teknik pemrograman dinamik sebagai berikut:

(27)

12 Untuk langkah pertama, yaitu untuk k = 1:

⇒ (17) dengan adalah lebar optimum strata pertama. Hubungan persamaan (16) dan (17) diselesaikan secara rekursif untuk tiap dan dan diperoleh. Dari , lebar optimum strata ke- L, , diperoleh. Dari

lebar optimum strata ke- L-1, , diperoleh dan begitu seterusnya sampai diperoleh.

Pemrograman Matematika Untuk Sebaran Normal

Misalkan peubah penelitian x memiliki sebaran normal baku dengan fungsi kepadatan peluang diberikan oleh:

_√ ;

Menurut Bühler dan Deutler (1975), dengan menggunakan definisi persamaan (3), (4) dan (5), dapat dilihat bahwa:

√ √ ₍₁₈₎

√

_–( )

√ _√ _√ , dan

√ – _√

_√

– _√

_√

√

– _}

√

(28)

13 dengan

√ ∫

dan .

Dengan demikian, dengan menggunakan nilai pada persamaan (18) dan (19), masalah pemrograman matematika persamaan (14) dapat dinyatakan sebagai berikut:

Minimumkan ∑

√ –

_√

– _√

_√

√

– _}

dengan kendala ∑ ,

(29)

DATA DAN METODE

Data

Data yang digunakan dalam penelitian ini menggunakan data SUSENAS Propinsi Jawa Timur Tahun 2008 berupa data pengeluaran per kapita penduduk sebanyak 8607 Kepala Rumah Tangga.

Metode Penelitian

Pembentukan strata dengan menggunakan teknik pemrograman dinamik terbagi menjadi beberapa tahapan sebagai berikut.

Tahap 1. Penyusunan model/ fungsi objektif.

Langkah yang dilakukan pada tahap 1 adalah pembentukan fungsi objektif

seperti pada persamaan (20) di mana fungsi kendala ∑ , dengan . Kemudian tentukan fungsi lebar strata ke- , yaitu . Substitusikan nilai ini ke dalam fungsi objektif yang telah disusun. Gunakan persamaan (16) dan (17) untuk mendapatkan persamaan rekursifnya.

Tahap 2. Penyelesaian persamaan rekursif.

Langkah-langkah dalam penyelesaian persamaan rekursif adalah sebagai berikut.

1. Mulai dengan . Tetapkan .

2. Hitung , nilai minimum RHS (right hand side) dari persamaan rekursif yang diperoleh untuk , dan .

3. Simpan nilai dan .

4. Untuk , nyatakan peubah penjelas sebagai . 5. Tetapkan jika , di mana .

6. Hitung , nilai minimum RHS dari persamaan rekursif yang diperoleh untuk ; .

7. Simpan nilai dan .

(30)

15 9. Pada , diperoleh sehingga nilai optimum dari diperoleh. 10. Pada , gunakan penghitungan mundur untuk , baca

nilai dari , sehingga nilai optimum dari .

11. Ulangi langkah ke-10 sampai nilai optimum dari diperoleh dari .

Penyelesaian persamaan rekursif tersebut menggunakan Program C++.

Tahap 3. Penghitungan nilai optimum fungsi objektif.

Sebagai tahapan terakhir adalah menghitung nilai optimum fungsi objektif

untuk setiap strata L yaitu ∑ ∑ .

Untuk mengetahui karakteristik antar strata dilakukan pengujian kehomogenan ragam. Metode statistika untuk menguji kehomogenan ragam adalah uji khi-kuadrat yang dikenal dengan uji Bartlett. Hipotesis yang diuji pada uji Bartlett adalah:

H0 :

H1 : paling sedikit ada satu pasang , untuk setiap , di mana

Uji Bartlett dapat dilakukan untuk ulangan sama atau tidak sama. Uji khi-kuadarat untuk jumlah ulangan tidak sama adalah:

∑ ( ) ∑( )

_(∑ _∑)

dengan dbi adalah derajat bebas strata ke-i, si2 adalah ragam dari strata ke-i dan

s2gab adalah ragam gabungan untuk semua strata.

Dengan kaidah keputusan sebagai berikut:

Apabila , maka H0 ditolak artinya kehomogenan ragam tidak

dapat dipenuhi. Dan jika sebaliknya hipotesis kehomogenan ragam diterima.

(31)

HASIL DAN PEMBAHASAN

Data Pengeluaran Per Kapita Propinsi Jawa Timur Tahun 2008

Jawa Timur adalah provinsi yang terdiri dari 29 kabupaten dan 9 kota. Secara

umum wilayah provinsi Jawa Timur dapat dibagi menjadi dua bagian besar yaitu

Jawa Timur daratan dan Pulau Madura. Luas wilayah Jawa Timur daratan hampir

mencapai 90 persen dari luas keseluruhan, sedangkan wilayah Madura hanya sekitar

10 persen.

Peta wilayah kabupaten/ kota di Jawa Timur disajikan pada Gambar 1.

Gambar 1 Peta administratif Propinsi Jawa Timur

Data yang digunakan pada penelitian ini adalah data pengeluaran per kapita

penduduk Jawa Timur tahun 2008 dengan jumlah contoh n = 8607 Kepala Rumah

Tangga. Data ini diperoleh dari publikasi BPS dari hasil SUSENAS. Dari data tersebut dapat diperoleh informasi bahwa rata-rata pengeluaran per kapita

penduduk Jawa Timur adalah Rp337.105,93 dan ragam Rp8.49 x 1010. Pengeluaran minimum adalah sebesar Rp41.349,94 dan pengeluaran maksimum sebesar Rp5.442.241,45.

(32)

17 menunjukkan bahwa adanya penyimpangan asumsi kenormalan sepeti terlihat pada Gambar 2.

Gambar 2 Probability plot dari pengeluaran per kapita

Untuk dapat memenuhi asumsi kenormalan telah dilakukan beberapa metode transformasi antara lain tansformasi akar dan transfomasi hubungan antara rataan dan simapangan baku. Akan tetapi hasilnya belum dapat memenuhi asumsi

kenormalan. Transfomasi Box-Cox memberikan nilai lambda -0.11. Hasil dari transformasi ini belum dapat menunjukkan bahwa asumsi kenormalan dapat

terpenuhi.

Setelah dilakukan beberapa jenis tansformasi, hasil yang paling mendekati asumsi kenormalan adalah transformasi log seperti disajikan pada Gambar 3 sebagaimana terlihat bahwa titik-titik cenderung mengumpul di sekitar garis lurus.

Log_Kapita

(33)

18 Penentuan Titik-titik Batas Optimum Strata

Untuk data contoh pengeluaran per kapita (nilai setelah diubah menjadi normal baku) dengan n = 8607 diperoleh nilai terkecil dan nilai terbesar masing-masing adalah -3.302 dan 5.169. Ini menunjukkan bahwa jarak dari distribusi adalah

5.169 – (-3.302) = 8.471

Sehingga fungsi objektif persamaan (20) dapat dinyatakan sebagai:

Minimumkan ∑

√ –

_√

– _√

_√

√

– _}

dengan kendala ∑

dan (22) Stratifikasi ke- (k-1) diberikan oleh

(34)

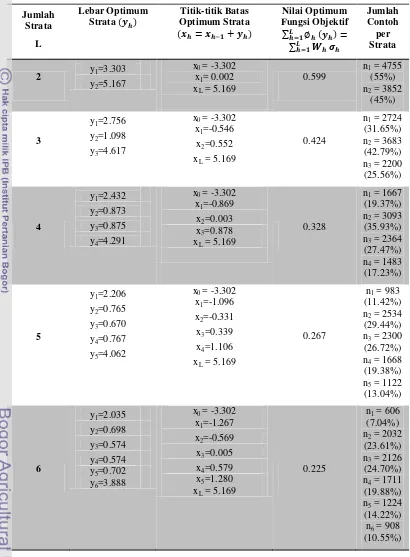
19 Penyelesaian persamaan rekursif (22) dan (23) menggunakan pemrograman C++ (Lampiran 1) untuk menentukan lebar strata optimum . Tabel 1 menunjukkan hasil dari penyelesaian ini disertai dengan nilai optimum

(35)

20 Tabel 1 Titik-titik batas optimum strata dari sebaran normal baku

Jumlah

Untuk dua strata diperoleh titik batas optimum pada x1 = 0.002. Ini berarti

(36)

21 adalah y1 = 3.303. Ragam strata pertama adalah sebesar . Sedangkan

lebar strata kedua adalah y2 = 5.167 dengan jumlah contoh n2 = 3852 dan ragam

sebesar . Pada pembentukan dua strata diperoleh nilai optimum fungsi objektifnya adalah 0.599.

Pembentukan sebanyak tiga strata diperoleh titik batas optimum pada x1 =

-0.546. Ini berarti bahwa semua data yang nilainya lebih kecil dari titik batas x1

akan masuk pada strata pertama di mana jumlah contoh sebanyak n1 = 2724 dan

lebar strata pertama adalah y1 = 2.756. Ragam strata pertama adalah sebesar

. Titik batas optimum antara strata kedua dan ketiga adalah pada x2 = 0.552. Untuk strata kedua lebarnya adalah y2 = 1.098 dengan jumlah contoh n2 =

3683 dan ragam sebesar . Lebar strata ketiga adalah y3 = 4.617 dengan

jumlah contoh sebesar n3 = 2200 dan ragam . Untuk tiga strata

diperoleh nilai optimum fungsi objektifnya adalah sebesar 0.424.

Untuk pembentukan sebanyak empat strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = -0.869. Ini berarti bahwa semua data yang

nilainya lebih kecil dari titik batas x1 akan masuk pada strata pertama dengan

jumlah contoh sebanyak n1 = 1667 dan lebar strata pertama adalah y1 = 2.432.

Ragam strata pertama adalah sebesar . Titik batas optimum antara strata kedua dan ketiga adalah pada x2 = 0.003. Untuk strata kedua lebarnya adalah

y2 = 0.873 dengan jumlah contoh n2 = 3093 dan ragam sebesar . Titik

batas optimum antara strata ketiga dan keempat adalah x3 = 0.878. Lebar strata

ketiga adalah y3 = 0.875 dengan jumlah contoh sebesar n3 = 2364 dan ragam

. Sedangkan untuk strata keempat dengan lebar sebesar y4 = 4.291

memiliki jumlah contoh sebanyak n4 = 1483 dan ragam . Nilai

optimum fungsi objektif untuk empat strata adalah sebesar 0.328.

Pada pembentukan sebanyak lima strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = -1.096. Ini berarti bahwa semua data yang

nilainya lebih kecil dari titik batas x1 akan masuk pada strata pertama dengan

(37)

22 y2 = 0.765 dengan jumlah contoh n2 = 2534 dan ragam sebesar . Titik

. Untuk strata keempat dan kelima, titik batasnya adalah pada x4 = 1.106. Strata keempat memiliki lebar y4 = 0.767 dengan jumlah contoh sebesar n4 =

1668 dan ragam . Sedangkan untuk strata kelima dengan lebar sebesar y5 = 4.062 memiliki jumlah contoh sebanyak n5 = 1122 dan ragam .

Nilai optimum fungsi objektif untuk lima strata adalah sebesar 0.267.

Untuk pembentukan sebanyak enam strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = -1.267. Ini berarti bahwa semua data

yang nilainya lebih kecil dari titik batas x1 akan masuk pada strata pertama dengan

Ragam strata pertama adalah sebesar . Titik batas optimum antara strata kedua dan ketiga adalah pada x2 = -0.569. Untuk strata kedua lebarnya adalah

y2 = 0.698 dengan jumlah contoh n2 = 2032 dan ragam sebesar Titik

. Untuk strata keempat dan kelima, titik batasnya adalah pada x4 = 0.579. Strata keempat memiliki lebar y4 = 0.574 dengan jumlah contoh sebesar n4 =

1711 dan ragam . Titik batas optimum antara strata kelima dan keenam adalah pada x5 = 1.281. Untuk strata kelima dengan lebar strata y5 = 0.702

memiliki jumlah contoh sebanyak n5 = 1224 dan ragam sebesar .

Sedangkan .untuk strata keenam dengan lebar sebesar y6 = 3.888 memiliki jumlah

contoh sebanyak n6 = 908 dan ragam . Nilai optimum fungsi

objektif untuk enam strata adalah sebesar 0.225.

(38)

23 Pengujian Kehomogenan Ragam

Hasil uji khi-kuadrat untuk setiap strata disajikan pada Tabel 2.

Tabel 2 Hasil uji khi-kuadrat untuk setiap jumlah strata

(39)

24 Pembentukan Strata Pengeluaran Per Kapita Jawa Timur Tahun 2008

Lebar strata dan titik-titik batas optimum strata pada Tabel 1 merupakan hasil yang didapatkan dari data yang sudah ditransformasi. Untuk data pengeluaran per kapita Propinsi Jawa Timur Tahun 2008 disajikan pada Tabel 3.

Tabel 3 Titik-titik batas optimum strata pengeluaran per kapita Jawa Timur 2008

Jumlah Strata

Untuk dua strata diperoleh titik batas optimum pada x1 = 277325.345. Ini

(40)

25 strata pertama adalah y1 = 235933.33. Ragam strata pertama adalah sebesar

. Sedangkan lebar strata kedua adalah y2 = 5164855.22 dengan

jumlah contoh n2 = 3852 dan ragam sebesar .

Pembentukan sebanyak tiga strata diperoleh titik batas optimum pada x1 =

202272.809. Ini berarti bahwa semua data yang nilainya lebih kecil dari titik batas

x1 akan masuk pada strata pertama di mana jumlah contoh sebanyak n1 = 2724 dan

lebar strata pertama adalah y1 = 160922.869. Ragam strata pertama adalah sebesar

. Titik batas optimum antara strata kedua dan ketiga adalah pada

x2 = 380751.914. Untuk strata kedua lebarnya adalah y2 = 178461.96 dengan

jumlah contoh n2 = 3683 dan ragam sebesar . Lebar strata ketiga

adalah y3 = 5061394.43 dengan jumlah contoh sebesar n3 = 2200 dan ragam

.

Untuk pembentukan sebanyak empat strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = 167875.686. Ini berarti bahwa semua data

yang nilainya lebih kecil dari titik batas x1 akan masuk pada strata pertama di

mana jumlah contoh sebanyak n1 = 1667 dan lebar strata pertama adalah y1 =

126525.06. Ragam strata pertama adalah sebesar . Titik batas optimum antara strata kedua dan ketiga adalah pada x2 = 277605.081. Untuk strata

kedua lebarnya adalah y2 = 109712.00 dengan jumlah contoh n2 = 3093 dan ragam

sebesar . Titik batas optimum antara strata ketiga dan keempat adalah x3 = 459449.009. Lebar strata ketiga adalah y3 = 181764.55 dengan jumlah

contoh sebesar n3 = 2364 dan ragam . Sedangkan untuk strata

keempat dengan lebar sebesar y4 = 4982767.37 memiliki jumlah contoh sebanyak

n4 = 1483 dan ragam .

Pada pembentukan sebanyak lima strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = 147398.356. Ini berarti bahwa semua data

(41)

26 sebesar 567979981. Titik batas optimum antara strata ketiga dan keempat

adalah x3 = 336869.805. Lebar strata ketiga adalah y3 = 107872.16 dengan jumlah

contoh sebesar n3 = 2300 dan ragam . Untuk strata keempat dan

kelima, titik batasnya adalah pada x4 = 524125.804. Strata keempat memiliki lebar y4

= 187136.51 dengan jumlah contoh sebesar n4 = 1668 dan ragam

. Sedangkan untuk strata kelima dengan lebar sebesar y5 =

4918068.71 memiliki jumlah contoh sebanyak n5 = 1122 dan ragam

.

Pada pembentukan sebanyak enam strata diperoleh titik batas optimum strata pertama dan kedua adalah x1 = 133543.689. Ini berarti bahwa semua data

kedua lebarnya adalah y2 = 66063.52 dengan jumlah contoh n2 = 2534 dan ragam

sebesar . Titik batas optimum antara strata ketiga dan keempat adalah x3 = 277805.066. Lebar strata ketiga adalah y3 = 78167.16 dengan jumlah

contoh sebesar n3 = 2300 dan ragam . Untuk strata keempat dan

kelima, titik batasnya adalah pada x4 = 386780.9265. Strata keempat memiliki lebar

y4 = 108808.63 dengan jumlah contoh sebesar n4 = 1668 dan ragam

. Titik batas optimum antara strata kelima dan keenam adalah pada x5 =

579495.950. Untuk strata kelima dengan lebar sebesar y5 = 191543.53 memiliki

jumlah contoh sebanyak n5 = 1122 dan ragam . Sedangkan

.untuk strata keenam dengan lebar sebesar y6 = 4862690.16 memiliki jumlah

contoh sebanyak n6 = 908 dan ragam sebesar .

(42)

27

SIMPULAN DAN SARAN

Simpulan

Penentuan titik-titik batas optimum strata dapat dianggap sebagai masalah pemrograman matematika dan dapat diselesaikan dengan teknik pemrograman dinamik. Metode ini dapat diterapkan pada data dengan sebaran yang berbeda karena memiliki fungsi objektif yang berbeda pula sesuai dengan sebaran datanya.

Metode ini memberikan hasil berupa lebar masing-masing strata. Oleh karena itu dapat ditentukan titik-titik batas optimum strata dan juga jumlah contoh pada masing-masing strata. Titik-titik batas yang diperoleh menghasilkan ragam di dalam strata sehomogen mungkin dan ragam antar strata seheterogen mungkin. Untuk dua strata diperoleh titik batas optimum pada x1 = 0.002. Untuk

pembentukan tiga strata diperoleh titik batas optimum pada x1 = -0.546 dan x2 =

0.552. Untuk pembentukan sebanyak empat strata diperoleh titik batas optimum adalah x1 = -0.869, x2 = 0.003 dan x3 = 0.878. Pada pembentukan sebanyak lima

strata diperoleh titik batas optimum x1 = -1.096, x2 = -0.331, x3 = 0.339 dan x4 =

1.107. Sedangkan untuk pembentukan sebanyak enam strata diperoleh titik batas optimum pada x1 = -1.267, x2 = -0.569, x3 = 0.005, x4 = 0.579 dan x5 = 1.281.

Metode pemrograman dinamik ini juga memberikan nilai optimum fungsi objektif untuk tiap jumlah strata. Hasilnya menunjukkan bahwa semakin banyak jumlah strata maka nilai optimum fungsi ini akan semakin kecil. Nilai optimum fungsi objektif untuk jumlah strata 2, 3, 4, 5, dan 6 berturut-turut adalah 0.599, 0.424, 0.328, 0.267 dan 0.225.

Saran

(43)

DAFTAR PUSTAKA

Aoyama H. 1954. A Study of Stratified Random Sampling. Annals of The Institute of Statistical Mathematics 6:1-36.

Bühler W and Deutler T. 1975. Optimal Stratification and Grouping by Dynamic Programming. Metrika 22:161-175.

BPS [Badan Pusat Statistik] Provinsi Jawa Timur. 2008. Pendataan Potensi Desa 2008 Propinsi Jawa Timur . Jawa timur: Badan pusat Statistik.

Baillargeon S and Rivest LP. 2010. Univariate Stratification of Survey Populations with The Package Stratification. Paper in Progress.

Cochran WG. 1977. Sampling Techniques, 3rd Edition. New York: John Willey & Sons.

Khan EA, Khan MGM, Ahsan MJ. 2002. Optimum Stratification: A Mathematical Programming Approach. Culcutta Statistical Association Bulletin 52 (special):205-208.

Khan MGM, Najmussehar, Ahsan MJ. 2005. Optimum Stratification for Exponential Study Variable Under Neyman Allocation. Journal of Indian Society of Agriculture Statistics 59(2):146-150.

Khan MGM, Niraj Nand, Nesar Ahmad. 2008. Determining The Optimum Strata Boundary Points Using Dynamic Programming. Survey Methodology 34: 205-214.

Kish L. 1965. Survey Sampling. New York: John Willey & Sons.

Kozak M. 2004. Optimal Stratification Using Random Search Method in Agricultural Surveys. Statistics in Transition 6(5):797-806.

Lavallée P. 1988. Two-way Optimal Stratification using Dynamic Programming. Procedings of The Section on Survey Research Methods; Virginia:646-651.

Lavallée P, Hidiroglou M. 1988. On The stratification of Skewed populations. Survey Methodology 14:33-43.

Levy, Paul S, Stanley L. 1995. Sampling of Populations Methods and Applications Third Edition. New York: John Willey & Sons.

Nicolini G. 2001. A Method to Define Strata Boundaries. Departmental Working Papers 2001-01. Department of Economics, University of Milan, Italy.

Rivest LP. 2002. A Generalization of Lavallée and Hidiroglou Algorithm for Stratification in Business Survey. Survey Methodology 28:191-198.

(44)

(45)

Lampiran 1 Program C++ untuk analisis penentuan titik-titik batas optimum strata dan nilai optimum fungsi objektif

/*This program finds the optimum strata boundaries and Optimum strata widths of Normal distribution*/

#include <iostream>

#include <math.h>

#include <assert.h>

#include <conio.h>

#include <stdio.h>

//#include "erfunc.h"

using namespace std;

typedef double Number;

//#include <math.h>

//#include<iostream.h>

Number erff(Number x);

double geterf(double x){

// Number erff(Number );

// Number erffc(Number );

// Number x;

// cout << "\n\n Enter x.\n";

// cout << "\n Wanna check? Note that erf(0) = 0, and

erf(infnity) = 1, \n";

// cout << "\n erf(-x) = - erf(x), erfc(x) = 1 - erf(x),

erfc(-x) = 2 - erfc(erfc(-x) \n";

// cin >> x;

return erff(x);

}

/*****************************************************************

Returns the error function

erf(x) = 2*(int_0^x e^{-t^2} dt)/sqrt(pi) .

C.A. Bertulani May/15/2000

*****************************************************************/

Number erff(Number x)

(46)

31 Lampiran 1 (lanjutan)

Number gammp(Number a, Number x);

return x < 0.0 ? -gammp(0.5,x*x) : gammp(0.5,x*x);

}

/*****************************************************************

Returns the complementary error function

erfc(x) = 1- erf(x)

= 2*(int_x^infinity e^{-t^2} dt)/sqrt(pi) .

******************************************************************

Number erffc(Number x)

{

Number gammp(Number a, Number x);

Number gammq(Number a, Number x);

return x < 0.0 ? 1.0+gammp(0.5,x*x) : gammq(0.5,x*x);

}

/*****************************************************************

Returns the imcomplete gamma function

P(a,x) = (int_0^x e^{-t} t^{a-1} dt)/Gamma(a) , (a > 0).

*****************************************************************/

Number gammp(Number a, Number x)

{

void gcf(Number *gammcf, Number a, Number x, Number *gln);

void gser(Number *gamser, Number a, Number x, Number *gln);

Number gamser,gammcf,gln;

if (x < 0.0 || a <= 0.0) cerr<< "Invalid arguments in routine gammp";

if (x < (a+1.0)) {

gser(&gamser,a,x,&gln);

return gamser;

} else { /*Use the continued fraction representation */

gcf(&gammcf,a,x,&gln); /* and take its complement.*/

return 1.0-gammcf;

}

(47)

/*****************************************************************

Returns the imcomplete gamma function

Q(a,x) = 1-P(a,x)

= (int_x^infinity e^{-t} t^{a-1} dt)/Gamma(a) , (a > 0).

*****************************************************************/

Number gammq(Number a, Number x)

{

void gcf(Number *gammcf, Number a, Number x, Number *gln);

void gser(Number *gamser, Number a, Number x, Number *gln);

Number gamser,gammcf,gln;

if(x<0.0||a<=0.0)cerr<<"Invalid arguments in routine gammq";

if (x < (a+1.0)) {/* Use the series representation */

gser(&gamser,a,x,&gln);

return 1.0-gamser;/* and take its complement. */

} else { /* Use the continued fraction representation. */

gcf(&gammcf,a,x,&gln);

return gammcf;

}

/*****************************************************************

Returns the imcomplete gamma function P(a,x) evaluated by its series

representation as gamser.

Also returns ln(Gamma(a)) as gln.

*****************************************************************/

#define ITMAX 100

#define EPS 3.0e-7

void gser(Number *gamser, Number a, Number x, Number *gln)

{

Number gamma_ln(Number xx);

int n;

Number sum,del,ap;

(48)

if (x <= 0.0) {

if (x < 0.0) cerr << "x less than 0 in routine gser";

*gamser=0.0;

cerr <<"a too large, ITMAX too small in routine gser";

return;

Returns the imcomplete gamma function Q(a,x) evaluated by its

continued fraction representation as gammcf.

Also returns ln(Gamma(a)) as gln.

*****************************************************************/

#define ITMAX 100 /* Maximum allowed number of iterations. */

#define EPS 3.0e- /* Relative accuracy */

#define FPMIN 1.0e-30 /*Number near the smallest representable */

/* floating point number. */

void gcf(Number *gammcf, Number a, Number x, Number *gln)

{

Number gamma_ln(Number xx);

int i;

(49)

*gln=gamma_ln(a);

b=x+1.0-a;/*etup fr evaluating continued fracion by modified Lent'z */

c=1.0/FPMIN; /* method with b_0 = 0. */

d=1.0/b;

h=d;

for (i=1;i<=ITMAX;i++) {/* Iterate to convergence. */

an = -i*(i-a);

if (i > ITMAX)cerr << "a too large, ITMAX too small in gcf";

(50)

35

# define v 0.19947114020071633897 //1/(2sqrt(2*PI))

# define w 0.25 // 1/4

# define x 0.15915494309189533577 // 1/(2*PI)

# define z 100 //(refine to 5 dp )

/*

Recursive

function receives the parameter k and dk,yk to calculate f.

*/

double RootVal(int k, double d, double y); // calculates the value of the minimal elements

(51)

const double inc = 0.001; //PRECISION AMMOUNT

const double inc2 = 0.00001; //PRECISION AMMOUNT

const double prec = 1/inc;

const int stages = 8;

const int points = 1000 ; //Keep this to be 1/inc

const int factor =4;

//When passing parameter to function. n = your value divid by inc to make it precise.

// eg. function(3,1) will be passed as function(3,1000)

int ylimits[10];//stores the 3dp values for refining

const int e = (int)(g*points*z+1);

const int p=(int)(g*points);

double minkf2[stages][e];//stores minimum f to 6dp

double dk2[stages][e];//stores minimum d for the 6dp calculations

main()

{

//initialize minkf

cout<<"Initializing points ...."<<endl;

for (int i=0; i < stages;i++)

for(int j=0;j<(p+1);j++)

minkf2[i][j]= -9999;

for (int k=0; k < stages;k++)

for(int l=0;l<e;l++)

minkf2[k][l]= -9999;

cout<<"Initialiationcomplete"<<endl<<endl<<"Calculating...."<<endl <<endl;

cout<<"enter h = Number of Stage " << endl;

cin >> h;

cout<<"enter s = Initial value " << endl;

cin >> s;

(52)

float d6,d5,d4,d3,d2,d1, y6,y5,y4,y3,y2,y1;

int temp;

//backward calculation for the 3dp results

d6 = g;

y6 = dk2[6][p];

d5=d6-y6;

temp = (int)(d5*points);

y5=dk2[5][temp];

d4=d5-y5;

y4=dk2[4][temp];

d3=d4-y4;

y3=dk2[3][temp];

d2=d3-y3;

y2=dk2[2][temp];

d1=d2-y2;

y1=d1;

//printf("\nd6: %f y6: %f",d6,y6);

//printf("\nd5: %f y5: %f",d5,y5);

//printf("\nd4: %f y4: %f",d4,y4);

// printf("\nd3: %f y3: %f",d3,y3);

//printf("\nd2: %f y2: %f",d2,y2);

//printf("\nd1: %f y1: %f",d1,y1);

//setup the limits for the 6dp calculations

temp = (int)(y6*points*z);

ylimits[6] = temp;

ylimits[5] = temp;

ylimits[4] = temp;

(53)

ylimits[3] = temp;

ylimits[2] = temp;

ylimits[1] = temp;

//printf("\n\nRefining...\n");

f=fun(h,e-1,inc2,ylimits[h]-factor*z,ylimits[h]+factor*z false);//

cout <<"stage: h = " << h << " distance: g = " << g<< endl;

// printf("\n\nAccurate values derved after refining\n");

printf("\nf(h,g): %.10f \n" ,f);

//Backward calucation for the 6 dp

d6=g;

y6 = dk2[6][(e-1)];

d5=d6-y6;

temp = (int)(d5*points*z);

y5=dk2[5][temp];

d4=d5-y5;

y4=dk2[4][temp];

d3=d4-y4;

y3=dk2[3][temp];

d2=d3-y3;

y2=dk2[2][temp];

d1=d2-y2;

y1=d1;

printf("\nd6: %f y6: %f",d6,y6);

(54)

getch();

} //end main

double RootVal(int k, double d, double y)//calculate the root value of the current distribution

{

double rtval;

double calc;

calc=v*(d-y+s)*exp(-1*pow((d-y+s),2)/2)*geterf((d+s)/sqrt(2))

-v*(d+s)*exp(-1*pow((d+s),2)/2)*geterf((d+s)/sqrt(2))

-v*(d-y+s)*exp(-1*pow((d-y+s),2)/2)*geterf((d-y+s)/sqrt(2))

+v*(d+s)*exp(-1*pow((d+s),2)/2)*geterf((d-y+s)/sqrt(2))

+ w * pow((geterf((d+s)/sqrt(2))- geterf((d-y+s)/sqrt(2))),2)

- x * pow((exp(-1*pow((d-y+s),2)/2) -exp(-1*pow((d+s),2)/2)),2);

if(calc<0)

{

// cout<<"\nError: Negative Root\n";

// rtval = -1;

}

else

{

calc = sqrt(calc);

}

rtval = calc;

return rtval;

}

//

double fun(int k,int n,double incf,int minYk,int maxYk,bool

isFirstRun)//this functions performs the same actions as

"function".

//it only defers in terms of the iterations of the for loop.

{

assert (k>=1); //Abort if k is negative

double dblRetVal;

double d =n*incf; //d value for the function

(55)

40

for(int i=minYk;i<=maxYk;i++)//iterate over the interval allowed to calculate the 6dp results.

{

if(minkf2[k-1][col]==-9999) {//check if the result has been previously calculated

if(isFirstRun){

val=root+fun((k-1), col, incf, 0, col, true); //if not, calculate the result

}

else{

val = root+ fun((k-1),col,incf,ylimits[k-1]- factor*z,ylimits[k-1]+ factor*z,false);//if not, calculate the result

}

else

val = root+ minkf2[k-1][col];//if result exists, use it for calculations

}

(56)

{

min =val;//base case

}

else

{

min = Minimum(min,val);//get the minimum if the result and the current mininmum

}

if(min == val){miny=y;}//get the position of the current minimum

}//end for

dblRetVal = min;

}//end else

//store the f and the d value of the minimum calculated.

col = n;

minkf2[k][col] = dblRetVal;

dk2[k][col]=miny;

return dblRetVal;

(57)

42 Lampiran 2 Program macro SAS untuk uji Bartlett

%MACRO BARTLET(DATASET,FACTOR,RESP);

%*---; %* name: bartlet.sas ; %* title: Bartletts test for homogeneity of variances ; %* ; %* The test allows for unequal number of observations per ; %* group. ; proc sort data=&DATASET; /* SORT BY THE CLASSIFICATION VAR. */ by &FACTOR;

proc means noprint; /* STORE THE VARIANCE & NUMBER OF */ by &FACTOR; /* OBSERVATIONS FOR EACH LEVEL. */ var &RESP;

output out=sumry var=variance n=num;

m = totn*log(snvar/totn)-slogvar; c = 1 + (1/(3*(a-1)))*(sfract-1/totn);

(58)