ABSTRACT
NURUL AIN. The Application of Homotopy Perturbation Method to Solve Nutrition Recycle
Problems. Under supervision of Jaharuddin and Ali Kusnanto.
Ecosystem is an ecological system that is formed by a mutual inseparable relationship between living organism and environment. The interaction among the components within an ecosystem, especially the nutrition recycle, can be modeled by using mathematical equation. The nutrition recycle model can be classified as a nonlinear problem. This phenomenon can be best represented by homotopy perturbation method. Homotopy perturbation method is defined as an analytical approach to solve a nonlinear problem. Based on this method, it can be concluded that the solution of nutrition recycle problem has a form of power series. By using MATHEMATICA software, it has been shown that the higher order of series used, the better model can be obtained. The model is expected to resemble the real solution. If the growth rate of autotroph is higher than its mortality rate, then the amount of abiotic nutrition and detritus organism will be declining, but the number of autotroph will increase. In the case rate of equal growth and mortality rate of autotroph, it will result into a decrease in abiotic nutrition, detritus organism, and autotroph number.
ABSTRAK
NURUL AIN. Penyelesaian Masalah Daur Ulang Nutrisi dengan Menggunakan Metode Perturbasi
Homotopi. Dibimbing oleh Jaharuddin dan Ali Kusnanto.
Ekosistem adalah suatu sistem ekologi yang terbentuk karena hubungan timbal balik tidak terpisahkan antara makhluk hidup dengan lingkungannya. Interaksi berbagai komponen pada suatu ekosistem, khususnya proses daur ulang nutrisi dimodelkan secara matematika. Model proses daur ulang nutrisi yang diperoleh merupakan masalah taklinear. Model ini diselesaikan dengan metode perturbasi homotopi. Metode perturbasi homotopi merupakan suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Berdasarkan metode ini diperoleh bahwa penyelesaian model daur ulang nutrisi berbentuk deret pangkat. Dengan menggunakan bantuan software MATHEMATICA diperoleh bahwa semakin tinggi orde deret yang digunakan, semakin mendekati penyelesaian sesungguhnya. Jika tingkat pertumbuhan autotrof lebih besar dari laju kematiannya, maka banyaknya nutrisi abiotik dan organisme detritus mengalami penurunan sedangkan organisme autotrof mengalami peningkatan. Jika tingkat pertumbuhan dan laju kematian autotrof sama, maka banyaknya nutrisi abiotik, organisme autotrof, dan organisme detritus mengalami penurunan.
I PENDAHULUAN
1.1 Latar Belakang
Model matematika dapat digunakan sebagai penjelasan terhadap suatu fenomena (alami atau buatan) dan sering muncul dalam permasalahan di bidang biologi, fisika, ekonomi, teknik, dan lainnya. Salah satu model matematika yang akan dibahas dalam karya ilmiah ini didasarkan pada interaksi berbagai komponen pada suatu ekosistem, khususnya ekosistem kolam air tawar.
Ekosistem adalah suatu sistem ekologi yang terbentuk karena hubungan timbal balik tidak terpisahkan antara makhluk hidup dengan lingkungannya. Komponen penyusun ekosistem terdiri dari faktor abiotik dan faktor biotik. Faktor abiotik adalah komponen yang bukan berasal dari makhluk hidup, seperti air, udara, sinar matahari, mineral-mineral, dan lainnya. Sebagian nutrisi abiotik dapat berupa bahan organik dan senyawa anorganik yang kemudian diubah menjadi senyawa organik oleh organisme detritus (pengurai) untuk dimanfaatkan oleh organisme autotrof (organisme yang dapat membuat makanannya sendiri). Sedangkan, komponen biotik adalah komponen yang berasal dari makhluk hidup, seperti tumbuhan, hewan, organisme tingkat rendah, dan organisme autotrof.
Penelitian mengenai proses daur ulang nutrisi pada suatu ekosistem telah banyak dilakukan, antara lain penelitian pada penyelesaian analisis kestabilan dari model proses daur ulang nutrisi dalam suatu kolam nutrisi (Yusfridawati 2005) tetapi, tidak mencari penyelesaian hampiran dan penyelesaian numerik dari model tersebut. Penelitian lain, yang ditulis oleh Blachet (2008) difokuskan pada hubungan antara mangsa dan pemangsa dengan melibatkan komponen biotik, abiotik, dan organisme detritus.
Dalam banyak kasus, masalah taklinear sulit untuk diselesaikan, khususnya penyelesaian secara analitik. Model proses daur ulang nutrisi yang dibahas dalam karya ilmiah ini merupakan masalah taklinear yang akan diselesaikan dengan metode perturbasi homotopi. Metode homotopi merupakan bentuk umum dari metode perturbasi dan metode dekomposisi adomian (Jaharuddin 2008). Terdapat beberapa keunggulan dari metode homotopi diantaranya tetap valid sekalipun masalah taklinear tersebut memuat sembarang parameter. Selain itu, dapat melakukan penyesuaian dan pembatasan daerah kekonvergenan serta tingkat hampiran
deret sesuai keperluan, kemudian dapat mengefisienkan penyelesaian hampiran dari masalah taklinear (Liao 2004). Metode perturbasi homotopi diperkenalkan oleh He (1999). Metode perturbasi homotopi merupakan suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Metode ini berhasil diterapkan untuk menyelesaikan berbagai masalah taklinear seperti pada ilmu fisika, ilmu komputer, ilmu biologi, dan lainnya (He 2008). Dalam bidang biologi, khususnya diterapkan pada interaksi berbagai komponen di suatu kolam nutrisi. Dalam karya ilmiah ini akan dibahas proses daur ulang nutrisi yang terjadi pada suatu kolam yang didalamnya terdapat tiga komponen. Komponen pertama adalah nutrisi abiotik. Komponen kedua adalah organisme autotrof. Sedangkan, komponen ketiga adalah organisme detritus. Model proses daur ulang nutrisi ini akan diselesaikan dengan metode perturbasi homotopi (Odibat 2009). Berdasarkan metode ini pula akan dibandingkan penyelesaian hampiran metode perturbasi homotopi dengan penyelesaian numerik dari model ekosistem.
1.2 Tujuan
Berdasarkan latar belakang di atas, maka tujuan karya ilmiah ini adalah:
1. Menggunakan metode perturbasi homotopi untuk menyelesaikan model proses daur ulang nutrisi dalam suatu kolam.
2. Menggambarkan grafik penyelesaian model proses daur ulang nutrisi dalam kolam dan memberikan tafsiran fisisnya.
1.3 Sistematika Penulisan
II LANDASAN TEORI
Pada bagian ini akan dibahas teori-teoriyang digunakan dalam menyusun karya ilmiah ini. Teori-teori tersebut meliputi asumsi dan model ekosistem serta metode perturbasi homotopi.
2.1 Asumsi dan Model
Dalam suatu ekosistem dapat terjadi proses daur ulang nutrisi. Komponen penyusun daur ulang nutrisi ini terdiri dari tiga komponen. Komponen pertama adalah nutrisi abiotik berupa kalium (K), fosfor (P), oksigen (O2), karbon dioksida (CO2), dan mineral-mineral lainnya. Komponen kedua adalah organisme autotrof, seperti algae plankton. Kemudian, komponen ketiga adalah organisme detritus yang berupa bakteri dan fungi (jamur). Komponen penyusun daur ulang nutrisi ini dinamakan kolam nutrisi. Nutrisi abiotik yang berada pada kolam nutrisi berperan sebagai bahan mentah yang digunakan oleh autotrof (produsen) untuk membuat makanannya sendiri. Kemudian nutrisi biotik yang berupa organisme autotrof dimakan oleh organisme yang berperan sebagai konsumen tingkat pertama. Dinamakan konsumen tingkat pertama, karena organisme tersebut pertama kali mengambil makanan dari produsen. Setelah itu, proses berlanjut pada tingkat konsumen yang lebih tinggi sampai akhirnya konsumen tingkat akhir mati dan berakhir pada organisme detritus.
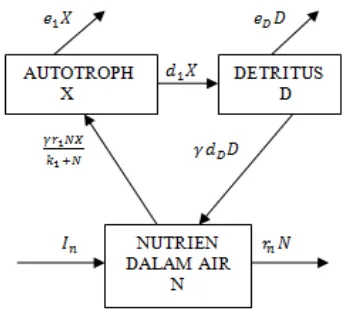
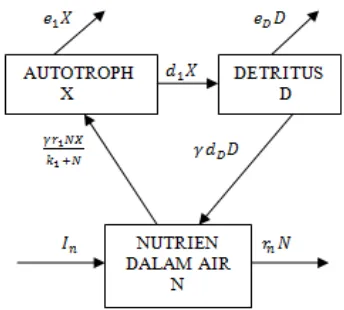
Detritus merupakan organisme yang menguraikan bahan organik yang berasal dari organisme mati, seperti feses, daun yang gugur, dan bangkai organisme mati dari semua tingkat trofik (Campbell et al. 2004). Pengurai disebut juga komponen makro (sapotrof) karena makanan yang dimakan berukuran lebih besar. Detritus menguraikan kembali konsumen dan produsen tingkat akhir menjadi nutrisi abiotik. Organisme pengurai menyerap sebagian hasil penguraian tersebut melepaskan bahan-bahan sederhana sehingga dapat digunakan kembali oleh produsen. Model proses daur ulang nutrisi yang ditinjau adalah model yang disusun oleh (Deangelis et al. 1986). Pada proses permodelan, sistem yang ditinjau dibagi atas tiga komponen, yaitu: nutrisi abiotik, organisme autotrof, dan organisme detritus seperti dalam Gambar 1. Misalkan banyaknya nutrisi abiotik dalam kolam nutrisi adalah , banyaknya autotrof dalam kolam nutrisi adalah , dan banyaknya detritus dalam kolam nutrisi adalah .
Gambar 1 Model tiga komponen dari kolam nutrisi abiotik, autotrof, dan detritus.
Berdasarkan Gambar 1 laju perubahan banyaknya nutrisi yang berada dalam kolam nutrisi dipengaruhi oleh:
1. Banyaknya nutrisi yang masuk ke dalam kolam nutrisi per satuan waktu, dinotasikan .
2. Banyaknya nutrisi yang hilang per satuan waktu, karena keluarnya air dari dalam kolam. Keluarnya air dari dalam kolam nutrisi dapat disebabkan oleh kebocoran atau hal lainnya. Banyaknya nutrisi yang hilang dinotasikan . Dengan suatu konstanta yang disebut tingkat kehilangan nutrisi.
3. Banyaknya nutrisi dalam kolam nutrisi yang dimakan oleh organisme autotrof per satuan waktu adalah , dengan bergantung pada banyaknya nutrisi pada kolam nutrisi dinotasikan , dengan suatu konstanta yang menyatakan perbandingan banyaknya nutrisi dengan banyaknya organisme autotrof dan detritus. Untuk masing-masing dan menyatakan tingkat pertumbuhan autotrof dan tingkat jenuh nutrisi.
4. Banyaknya nutrisi yang diperoleh dari hasil urai yang dilakukan oleh organisme detritus per satuan waktu, dinotasikan
3
Oleh karena itu, laju perubahan banyaknya nutrisi yang berada dalam kolam, secara matematis dinyatakan dengan:
.
Laju perubahan banyaknya organisme autotrof yang berupa nutrisi dipengaruhi oleh:
1. Banyaknya organisme autotrof yang keluar dan diuraikan oleh organisme pengurai per satuan waktu, dinotasikan
dengan suatu konstanta yang disebut laju kematian autotrof yang memengaruhi detritus.
2. Banyaknya organisme autotrof yang keluar dan tidak diuraikan oleh organisme pengurai per satuan waktu, tetapi meninggalkan sistem, dinotasikan dengan suatu konstanta yang disebut laju kematian autotrof yang tidak dapat diuraikan.
3. Banyaknya organisme autotrof yang terbentuk per satuan waktu karena tersedianya nutrisi yang ada pada kolam nutrisi, yaitu .
Oleh karena itu, laju perubahan banyaknya autotrof yang berada dalam kolam, secara matematis dinyatakan oleh :
.
Selanjutnya, laju perubahan banyaknya organisme detritus dipengaruhi oleh :
1. Banyaknya organisme autotrof yang diuraikan oleh organisme detritus per satuan waktu yang dinotasikan oleh . 2. Banyaknya hasil urai dari organisme
detritus yang menjadi nutrisi dalam kolam nutrisi per satuan waktu yang dinotasikan
.
3. Banyaknya organisme detritus yang meninggalkan sistem per satuan waktu dengan laju .
Oleh karena itu, laju perubahan banyaknya detritus yang berada dalam kolam, secara matematis diperoleh :
.
Dengan demikian, proses daur ulang nutrisi dalam kasus ini dimodelkan oleh sistem persamaan sebagai berikut:
. .
Model bagi masalah daur ulang nutrisi pada kolam sederhana yang diberikan oleh sistem persamaan (2.1) akan diselesaikan dengan menggunakan metode perturbasi homotopi. Metode ini akan dijelaskan sebagai berikut:
2.2 Metode Perturbasi Homotopi
Berikut ini diberikan ilustrasi konsep dasar metode homotopi berdasarkan alur pada pustaka (Jaharuddin 2008). Misalkan diberikan persamaan diferensial berikut:
, Ω (2.2)
dengan suatu operator turunan yang taklinear dan fungsi yang akan ditentukan dan bergantung pada peubah bebas
. Selanjutnya didefnisikan pula suatu operator linear yang memenuhi
, bila . (2.3)
Sehingga operator dapat dibagi menjadi dua bagian, yaitu dan yang masing-masing merupakan operator linear dan taklinear. Jadi, persamaan diferensial (2.2) dapat ditulis:
. (2.4)
Misalkan pendekatan awal dari penyelesaian persam (2.2) dan , suat am sikan fungsi real
aan u par eter. Didefini
, :Ω , , dan suatu fungsi H sebagai ber kut: i
,
atau
, .
Berdasarkan persamaan (2.5), maka untuk dan masing-masing memberikan persamaan berikut:
4
, , ,
dan
, , , .
Sehingga menurut persamaan (2.2) dan persamaan (2.3) diperoleh bahwa fungsi
,
dan
, ,
masing-masing merupakan penyelesaian dari persamaan
, ,
dan
, , .
Dengan demikian peningkatan nilai dari 0 ke 1 menyatakan perubahan nilai , dari ke . Dalam topologi, proses ini disebut deformasi. Proses deformasi yang ditinjau meliputi deformasi orde nol dan orde tinggi. Pada deformasi orde nol memberikan penyelesaian awal , sedangkan deformasi orde tinggi memberikan penyelesaian
, , … , . Untuk menentukan
, , , . . . dilakukan sebagai berikut. Jika
persamaan (2.5) diturunkan terhadap hingga kali dan dihitung pada kemudian dibagi oleh !, maka diperoleh persamaan berikut:
; , , |
dan dinotasikan
!
Dalam metode perturbasi homotopi, fungsi , yang dinyatakan pada persamaan (2.6) merupakan penyelesaian dari persamaan
, .
Berdasarkan persamaan (2.5), maka diperoleh .
Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (2.2) dengan pendekatan awal dan ,
, , … yang akan ditentukan. Persamaan
untuk menentukan , , , … diperoleh dengan menggunakan metode perturbasi, dimana persamaan (2.6) disubstitusikan ke dalam persamaan (2.5) dan diperoleh . Secara umum diperoleh dengan menyamakan koefisien kepangkatan
, dan merupakan pendekatan awal dari penyelesaian . Selanjutnya, misalkan diberikan suatu masalah yang dinyatakan oleh sistem ersamaan diferensial berikut : p
, .
Penyelesaian eksak masalah nilai awal (2.8) adalah
5
e e . .
Berikut ini akan dicari penyelesaian dari masalah nilai awal persamaan (2.8) dengan menggunakan metode perturbasi homotopi. Berdasarkan persamaan (2.5) dan persamaan (2.7) diperoleh persamaan berikut:
. (2.10)
Misalkan penyelesaian persamaan (2.10) dinyatakan dalam persamaan beriku : t
, , , ,
, , , ,
(2.11) Jika persamaan (2.11) disubstitusikan ke dalam persamaan (2.10), kemudian dipisahkan berda kan derajat kepangkatan , maka koefisi e ikan
sar
en m mber ,
, . .
Jika persamaan (2.12) diintegralkan terhadap , maka diperoleh
,
, .
Bentuk lain dari , dan , dengan , , , , (dibuktikan dalam lampiran 1).
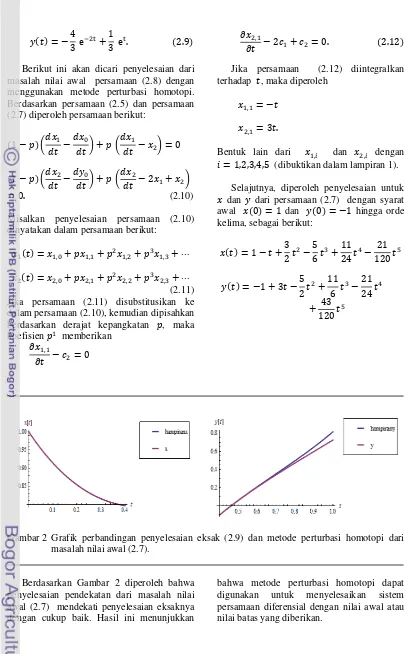
Selajutnya, diperoleh penyelesaian untuk dan dari persamaan (2.7) dengan syarat awal dan hingga orde kelima, sebagai berikut:
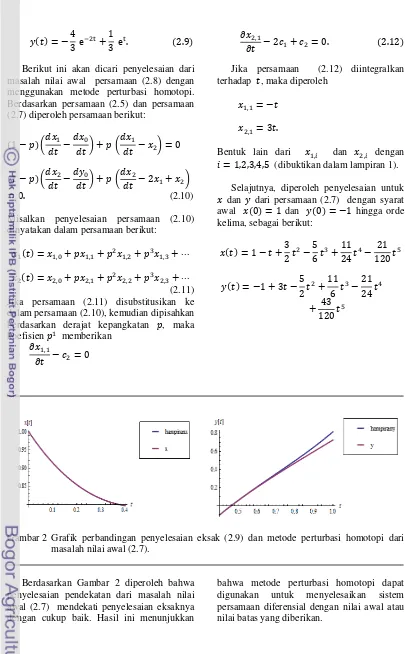
Gambar 2 Grafik perbandingan penyelesaian eksak (2.9) dan metode perturbasi homotopi dari masalah nilai awal (2.7).
Berdasarkan Gambar 2 diperoleh bahwa penyelesaian pendekatan dari masalah nilai awal (2.7) mendekati penyelesaian eksaknya dengan cukup baik. Hasil ini menunjukkan
III PEMBAHASAN
; , , Pada bagian ini akan dibahas penggunaan
metode perturbasi homotopi untuk menyelesaikan suatu masalah taklinear. Metode ini digunakan untuk menyelesaikan model matematika bagi proses daur ulang nutrisi dalam suatu kolam.
3.1Analisis Metode
Dalam karya ilmiah ini akan dibahas suatu masalah taklinear, khususnya pada masalah ekosistem, digunakan metode perturbasi homotopi untuk menentukan penyelesaian pendekatannya.
Berikut ini akan dibahas perluasan dari konsep dasar metode homotopi seperti yang diuraikan pada landasan teori. Untuk itu diperlukan fungsi , , , yang tidak hanya bergantung pada dan , tetapi juga bergantung pada parameter bantu dan fungsi bantu . Misalkan fungsi H dinyatakan sebagai berikut
; , ,
; , ,
; , , . (3.1)
Selanjutnya, misalkan fungsi , , , merupakan penyelesaian dari persamaan berikut:
Berdasarkan persamaan (3.1), maka untuk dan masing-masing memberikan persamaan berikut:
; , , ; , ,
dan
; , , ; , , .
Berdasarkan persamaan (2.2) dan persamaan (2.3), maka penyelesaian dari
persamaan ; , , dan
; , , masing-masing adalah
dan
; , , .
Kedua penyelesaian di atas bergantung pada parameter bantu h dan fungsi bantu
yang dipilih sembarang, pemilihan parameter bantu h, fungsi bantu T (x), pendekatan awal , dan operator linear perlu memperhatikan validitas dari metode homotopi. Dengan pemilihan ini terjamin adanya fungsi ; , , dan turunan-kekonvergenan dari deret (3.3) di . Jadi untuk , dari persamaan (3.3) diperoleh
; , , .
∞
7
Karena ; , , , maka diperoleh ∞
.
(3.5)
Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (2.2) dengan pendekatan awal dan ,
, , … yang akan ditentukan. Persamaan
untuk menentukan , , , … diperoleh dengan menggunakan metode perturbasi, dimana persamaan (3.3) disubstitusikan ke dalam persamaan (3.2), dengan menyamakan koefisien dari derajat kepangkatan , maka diperoleh penyelesaian dari persamaan (3.5).
3.2Aplikasi Metode
Untuk lebih memahami metode yang telah dijelaskan pada bagian sebelumnya. Tinjau sistem persamaan diferensial berikut:
.
Secara umum sistem persamaan diferensial (3.6) dapat dinyatakan dalam persamaan berikut:
. ,
dengan nilai awal
, , … ,
Berdasarkan persamaan (2.4) dan persamaan (3.6), diperoleh
.
(3.8) Secara umum persamaan (3.8) dapat dinyatakan dalam persamaan berikut:
,
(3.9) dengan suatu operator linear dan operator taklinear. Berdasarkan persamaan (3.1) dan persamaan (3.6) diperoleh
.
(3.10) Secara umum persamaan (3.10) dapat dinyatakan dalam persamaan berikut:
,
8
dengan , dan merupakan penyelesaian pendekatan awal. Parameter mengalami peningkatan dari 0 sampai 1. Misalkan penyelesaian dari persamaan (3.7) dinyatakan alam deret ku d asa be i ut r k :
Sebagai ilustarasi, misalkan . Dimisalkan penyelesaian pendekatan awal
, merupakan suatu konstanta. Jika persaman (3.12) disubstitusikan ke dalam persamaan (3.11), kemudian dipisahkan berdasarkan derajat kepangkatan , maka ko sien mem ikan persamaan berikut:
efi ber
, , , , , ,
(3.13) dengan syarat awal
, , , dan , .
(3.14) Penyelesaian masalah nilai awal persamaan (3.13) adalah
, , , dan , . Koefisien , memberikan persamaan berikut: Secara umum untuk sembarang koefisien memberikan persamaan berikut:
, , .
dengan syarat awal , .
Koefisien , memberikan persamaan berikut:
,
, ,
dengan syarat batas , .
Koefisien , memberikan persamaan berikut: dapat dinyatakan dalam persaman berikut:
,
, ,
dengan syarat batas , .
(3.17) (Bukti dapat dilihat pada lampiran 2)
Berdasarkan ilustrasi yang telah djelaskan di atas diperoleh bahwa, jika diberikan masalah taklinear dengan persamaan diferensial pada sistem persamaan (3.6), maka dengan metode perturbasi homotopi diperoleh penyelesaian pendekatan berbentuk
, . .
dengan , diperoleh dari persamaan (3.17)
3.3Contoh Kasus pada Masalah Daur
Ulang Nutrisi
9
organisme detritus dalam kolam nutrisi, maka persamaan (2.1) menja id persamaan berikut:
, merupakan parameter-parameter pada persamaan (2.1). Dalam proses ini, dimisalkan:
Berikut ini akan ditentukan penyelesaian dari masalah nilai awal persamaan (3.19) dengan metode perturbasi homotopi yang telah diuraikan pada bagian sebelumnya. Sehingga, penyelesaian masalah nilai awal persamaan (3.19) hingga orde kelima berbentuk:
Nilai , ditentukan berdasarkan persamaan (3.16) dan persamaan (3.17). Berdasarkan persamaan (3.16) dan persamaan (3.19 di) peroleh penyelesaian berikut:
, ,
, . ,
, . .
Berdasarkan persamaan (3.17) dan persamaan 19) dipero er maan berikut:
(3. leh p sa Berikut ini akan dilakukan kajian tentang masalah daur ulang nutrisi untuk . ,
, . , . , . ,
. , . . Ditinjau dua kasus
berdasarkan tingkat pertumbuhan dan laju kematian autotrof. Kasus pertama bilamana tingkat pertumbuhan dan laju kematian autotrof berbeda. Sedangkan kasus kedua bilamana tingkat pertumbuhan dan laju kematian autotrof sama.
Kasus 1. Misal an k
. , . .
10
Berdasarkan persamaan (3.22) dan persamaan (3.20) diperoleh penyelesaian masalah nilai awal persamaan (3.19) berbentuk
Dengan demikian penyelesaian masalah daur ulang nutrisi pada persamaan (2.1), untuk komponen N, X, D yang masing‐masing
menyatakan banyaknya nutrisi abiotik dalam
kolam nutrisi, banyaknya autotrof dalam kolam nutrisi, dan banyaknya detritus dalam olam nutrisi. Untuk kasus dan kasus
rde kelima adalah k
hingga o
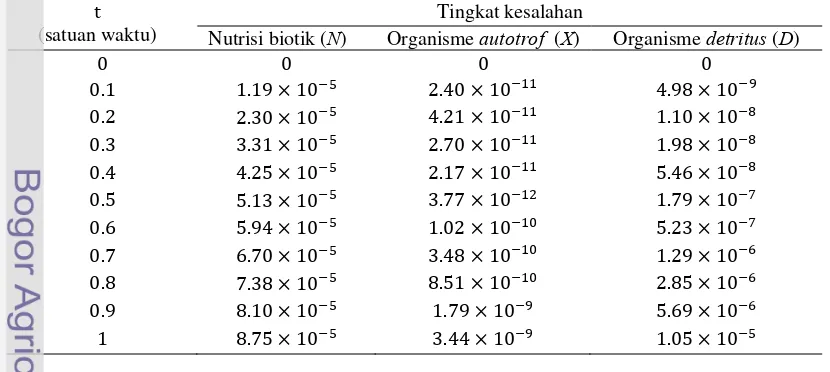
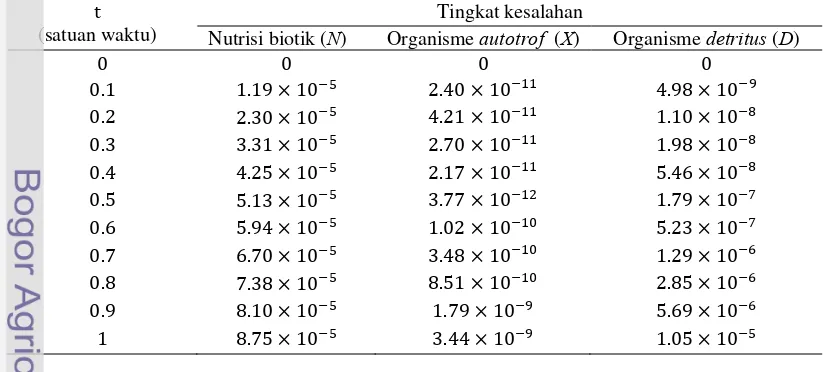
Tabel T ngkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian numerik
pada kasu 1
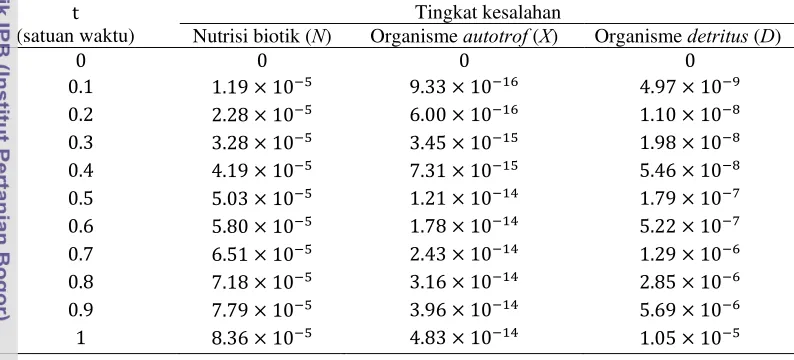
Tabel 1 berikut ini menunjukkan bahwa tingkat kesalahan untuk penyelesaian nutrisi biotik (N), organisme autotrof (X), dan organisme detritus (D) pada kasus 1 hingga orde kelima dengan penyelesaian numeriknya sangat kecil.
i s t (satuan waktu)
Tingkat kesalahan
Nutrisi biotik (N) Organism eautotrof (X) Organisme detritus (D)
Berdasarkan Tabel dapat disimpulkan bahwa semakin tinggi orde yang digunakan, maka semakin mendekati penyelesaian sebenarnya.
11
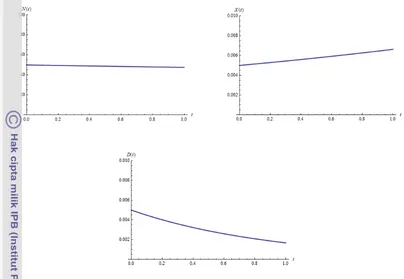
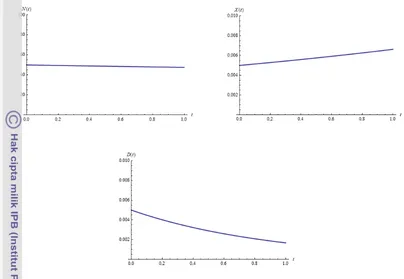
Gambar 3 Grafik penyelesaian dengan metode perturbasi homotopi dari masalah nilai awal (2.1) orde kelima untuk kasus 1.
12
Gambar 3 dan Gambar 4 memperlihatkan perilaku nutrisi abiotik, organisme autotrof, dan organisme detritus selama proses daur ulang nutrisi berlangsung. Pada kasus pertama perilaku nutrisi abiotik menunjukkan bahwa banyaknya nutrisi abiotik pada saat terjadi proses daur ulang nutrisi menurun dengan sangat lambat. Hal ini dikarenakan oleh beberapa hal, diantaranya banyaknya nutrisi yang hilang dari kolam karena keluarnya air dari kolam nutrisi yang disebabkan oleh kebocoran pada kolam. Penyebab lainnya adalah banyaknya nutrisi yang digunakan leh organisme autotrof untuk membuat
nya sendiri. Selain itu, tingginya
tingkat pertumbuhan autotrof mengakibatkan tingginya jumlah organisme autotrof. Seiring dengan penurunan nutrisi abiotik organisme autotrof mengalami peningkatan dengan lebih cepat. Sedangkan, untuk organisme detritus mengalami penurunan dengan lebih cepat, hal ini terjadi karena banyaknya organisme
autotrof yang telah mati tidak dapat
diuraikan oleh detritus. Detritus yang tidak dapat menguraikan autotrof disebabkan oleh adanya kebocoran pada kolam.
o makanan
Tabel T gkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian numerik
pada kasu
Tabel 2 berikut ini menunjukkan bahwa galat untuk penyelesaian N, X, D pada kasus 2 hingga orde kelima dengan penyelesaian numeriknya sangat kecil.
in
Berdasarkan Tabel dapat disimpulkan bahwa semakin tinggi orde yang digunakan, maka semakin mendekati
enyelesaian sebenarnya. p
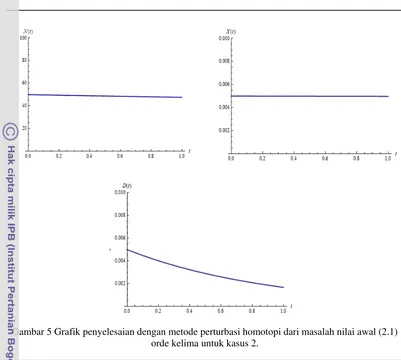
Gambar 5 dan Gambar 6 berikut ini menunjukkan grafik penyelesaian untuk nutrisi biotik (N), organisme autotrof (X), dan
rganisme detritus (D) yang didekati hingga rde kelima.
13
Gambar 5
Gam
Grafik penyel
mbar 6 Grafik
lesaian dengan ord
penyelesaian
n metode pert de kelima untu
numerik dari
turbasi homoto uk kasus 2.
masalah nilai
opi dari masal
awal (2.1) un
lah nilai awal
14
Gambar 5 dan Gambar 6 memperlihatkan perilaku nutrisi abiotik, organisme autotrof, dan organisme detritus selama proses daur ulang nutrisi berlangsung. Untuk kasus kedua perilaku nutrisi abiotik menunjukkan bahwa banyaknya nutrisi abiotik pada saat terjadi proses daur ulang nutrisi mengalami penurunan dengan sangat lambat. Untuk organisme autotrof pun mengalami penurunan dengan sangat lambat, hal ini dikarenakan oleh beberapa hal, diantaranya nutrisi yang digunakan untuk membuat
IV SIMPULAN
Metode perturbasi homotopi yangdigunakan untuk menyelesaikan model proses daur ulang nutrisi dalam suatu kolam nutrisi sangat sederhana karena hanya melibatkan pengintegralan biasa. Model proses daur ulang nutrisi yang ditinjau berupa kolam air tawar yang didalamnya terdapat tiga komponen, yaitu nutrisi biotik, organisme autotrof, organisme detritus. Dalam metode perturbasi homotopi diperoleh bahwa semakin tinggi orde yang digunakan semakin mendekati penyelesaian sesungguhnya. Hal ini terlihat pada galat (tingkat kesalahan) dari orde kelima dengan penyelesaian numeriknya lebih kecil dibandingkan penyelesaian numerik dari orde keempat.
Dalam karya ilmiah ini, disimulasikan dua kasus model proses daur ulang nutrisi. Kedua kasus tersebut berdasarkan tingkat
pertumbuhan dan laju kematian autotrof. Pada kasus pertama, jika tingkat pertumbuhan autotrof lebih tinggi dibandingkan dengan laju kematian autotrof, diperoleh hasil bahwa: 1. Banyaknya nutrisi abiotik mengalami
penurunan.
2. Banyaknya organisme autotrof mengalami peningkatan.
3. Banyaknya organisme detritus mengalami penurunan.
Pada kasus kedua, jika tingkat pertumbuhan dan laju kematian autotrof sama, diperoleh hasil bahwa:
1. Banyaknya nutrisi abiotik mengalami penurunan.
2. Banyaknya organisme autotrof mengalami penurunan.
PENYELESAIAN MASALAH DAUR ULANG NUTRISI
DENGAN MENGGUNAKAN METODE PERTURBASI HOMOTOPI
NURUL AIN
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
DAFTAR PUSTAKA
Blanchet S, Loot G, Dodson JJ. 2008.
Competition, predation and flow rate as mediators of direct and indirect effects in a stream food chain. Springer-Verlag.
Campbell NA, Reece JB, Mitchell LH. 2004.
Biologi Jilid 3. Jakarta: Erlangga. Lestari R, penerjemah. Terjemahan dari: Biology.
Deangelis DL. 1986. Nutrient Recycling and
System Resillence in a Model of an Experimental Aquatic System. Mathematical Ecology, 189-215.
He JH. 1999. Homotopy Perturbation Tehcnique.
Computer Methods in Applied Mechanics and Engineering 178:257-262.
He JH. 2008. Topological Methods in Nonlinear
Analysis. Recent Development of the Homotopy Perturbation Method 31:205-209.
Jaharuddin. 2008. Analisis Homotopi dalam
Penyelesaian suatu Masalah Taklinear. Jurnal Matematika dan Aplikasinya, 7:6-16.
Liao S. 2004. Beyond Perturbation: Introduction to
the Homotopi Analysis Method. Boca Raton, London, New York Washington, D.C.
Odibat Z, Bertelle C. 2009. Application of
Homotopy Perturbation Method for Ecosystem Modelling. http://wwwlih.univ-lehavre.fr/~bertelle/cossombook/odibat4cosso m06.pdf [8 Desember 2010].
Yusfridawati. 2005. Analisi Kestabilan Model
PENYELESAIAN MASALAH DAUR ULANG NUTRISI
DENGAN MENGGUNAKAN METODE PERTURBASI HOMOTOPI
NURUL AIN
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRACT
NURUL AIN. The Application of Homotopy Perturbation Method to Solve Nutrition Recycle
Problems. Under supervision of Jaharuddin and Ali Kusnanto.
Ecosystem is an ecological system that is formed by a mutual inseparable relationship between living organism and environment. The interaction among the components within an ecosystem, especially the nutrition recycle, can be modeled by using mathematical equation. The nutrition recycle model can be classified as a nonlinear problem. This phenomenon can be best represented by homotopy perturbation method. Homotopy perturbation method is defined as an analytical approach to solve a nonlinear problem. Based on this method, it can be concluded that the solution of nutrition recycle problem has a form of power series. By using MATHEMATICA software, it has been shown that the higher order of series used, the better model can be obtained. The model is expected to resemble the real solution. If the growth rate of autotroph is higher than its mortality rate, then the amount of abiotic nutrition and detritus organism will be declining, but the number of autotroph will increase. In the case rate of equal growth and mortality rate of autotroph, it will result into a decrease in abiotic nutrition, detritus organism, and autotroph number.
ABSTRAK
NURUL AIN. Penyelesaian Masalah Daur Ulang Nutrisi dengan Menggunakan Metode Perturbasi
Homotopi. Dibimbing oleh Jaharuddin dan Ali Kusnanto.
Ekosistem adalah suatu sistem ekologi yang terbentuk karena hubungan timbal balik tidak terpisahkan antara makhluk hidup dengan lingkungannya. Interaksi berbagai komponen pada suatu ekosistem, khususnya proses daur ulang nutrisi dimodelkan secara matematika. Model proses daur ulang nutrisi yang diperoleh merupakan masalah taklinear. Model ini diselesaikan dengan metode perturbasi homotopi. Metode perturbasi homotopi merupakan suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Berdasarkan metode ini diperoleh bahwa penyelesaian model daur ulang nutrisi berbentuk deret pangkat. Dengan menggunakan bantuan software MATHEMATICA diperoleh bahwa semakin tinggi orde deret yang digunakan, semakin mendekati penyelesaian sesungguhnya. Jika tingkat pertumbuhan autotrof lebih besar dari laju kematiannya, maka banyaknya nutrisi abiotik dan organisme detritus mengalami penurunan sedangkan organisme autotrof mengalami peningkatan. Jika tingkat pertumbuhan dan laju kematian autotrof sama, maka banyaknya nutrisi abiotik, organisme autotrof, dan organisme detritus mengalami penurunan.
PENYELESAIAN MASALAH DAUR ULANG NUTRISI
DENGAN MENGGUNAKAN METODE PERTURBASI HOMOTOPI
NURUL AIN
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul : Penyelesaian Masalah Daur Ulang Nutrisi dengan Menggunakan
Metode Perturbasi Homotopi
Nama : Nurul Ain
NRP : G54070025
Menyetujui,
Pembimbing I
Pembimbing II
Dr. Jaharuddin, M.S.
Drs. Ali Kusnanto, M.Si.
NIP. 19651102 199302 1001
NIP. 19650820 199003 1001
Mengetahui
Ketua Departemen Matematika
Dr. Berlian Setiawaty, M.S.
NIP. 19650505 198903 2 004
KATA PENGANTAR
Assalamu’alaikum Warahmatullahi Wabarakatuh.Puji dan syukur penulis panjatkan kepada Allah SWT karena atas segala rahmat dan karunia-Nya penulis dapat menyelesaikan skripsi ini dengan baik. Penyusunan karya ilmiah ini tidak lepas dari peranan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Keluargaku tercinta: Ayah dan Ibu (terima kasih atas doa, dukungan, kesabaran, kepercayaan, dan kasih sayangnya), adik-adikku (terima kasih atas doa, dukungan, kasih sayang, dan dukungannya), serta keluarga besar baik dari Ayah maupun dari Ibu (terima kasih atas doanya). 2. Dr. Jaharuddin, M.S. selaku dosen pembimbing I (terima kasih atas semua ilmu, masukan,
arahan, kesabaran, dukungan, dan bantuannya selama penulisan skripsi ini).
3. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing II (terima kasih atas semua ilmu, saran, dan dukungannya).
4. Drs. Siswandi, M.Si. selaku dosen penguji (terima kasih atas semua ilmu dan sarannya). 5. Segenap dosen Departemen Matematika: Bu Anggi, Bu Ida, Pak Donny, Pak Hadi, Pak Wayan,
Pak Prapto, dan lainnya (terima kasih atas semua ilmu yang telah diberikan).
6. Staf Departemen Matematika: Pak Yono, Bu Susi, Mas Heri, Pak Bono, Bu Ade, Mas Deni, dan lainnya (terima kasih atas bantuan dan dukungannya).
7. Sahabat-sahabatku:Finny, ririh, yuli (terima kasih atas motivasi dan bantuannya). 8. Tutor-tutor: Wahyu, Ririh, Mba ana (terima kasih atas saran, motivasi dan bantuannya). 9. Kakak-kakak Matematika S2, 41, 42, dan 43: Mbak Ana, Pak Hadi, Kak Erni, Kak Andrew,
Kak Aini, Kak Apri, Kak Agung, Kak Vera, Kak Cici, Kak Iput, Kak Nanu, Ka Narsih, dan lainnya (terima kasih atas ilmu, bantuan, dan semuanya).
10.Teman-teman Matematika angkatan 44:Ririh, Yuli, Wahyu, Yuyun, Lingga, Masay, Diana, Yogie, Lugina, Ayum, Iam, Yanti, Selvie, Nurul, Pepi, Devi, Istiti, Iresa, Sari, Anis, Fikri, Wenti, Sri, Fajar, Mutia, Rachma, Ayung, Iful, Cita, Tanty, Arina, Deva, Aqil, Lilis, Imam, Aswin, Eka, Aze, Ali, Vianey, Nadiroh, Nurus, Na’im, Dhika, Ima, Dora, Atik, Fani, Phunny, Dian, Rofi, Della, Tyas, Denda, Pandi, Rizqy, Indin, Sholih, Siska, Lili, Tita, Lina, Endro, Ruhi, Lukman, Puying, Tendhy, Ikhsan, Chopa, dan Zae (terima kasih atas doa, semangat, dukungan, bantuan, dan kebersamaannya).
11.Adik-adik Matematika angkatan 45 dan 46: Aci, Vivi, Ade, Santi, Rahma, Prama, Irma, Heru, Putri, Isna, Rischa, Regita, Tya, Mega, Bram, Heryanto, Hardono, Fenny, Anggun, Ali Vikri, Kunedi, andri, windy, ivon, dan lainnya (terima kasih atas dukungan dan bantuannya).
12.Teman-teman BEM FMIPA Kabinet Totalitas kebangkitan: Yakub, Aci, Asep, Debie, Ayu, Arina, Ary, Tiara, Lida, Ade, Ayu, Cipta, Kirana, Panji, James, Teguh, dan lainnya (terima kasih atas motivasi dan kebersamaannya).
13.Teman-teman kosan tanjung atas:Finny, Ria, Cli, Kak Ana, Teh Uli, Teh Tri, dan Aya (terima kasih atas motivasi dan dukungannya).
14.Teman-teman lainnya yang telah mendukung secara moril selama ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
Bogor, Agustus 2011
RIWAYAT HIDUP
Penulis merupakan anak pertama dari enam bersaudara, puteri pasangan Safrin dan Ida Asyidda. Penulis lahir di Jakrta pada tanggal 27 mei 1989. Pendidikan SD ditempuh pada tahun 1995-2001 di SD Negeri Cikampek Utara 1, penulis melanjutkan sekolah di SLTP Negeri 2 Cikampek pada tahun 2001-2004. Pendidikan menengah atas ditempuh oleh penulis pada tahun 2004- 2007 di SMA Negeri 1 Cikampek.
Penulis diterima sebagai mahasiswi di Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI) pada tahun 2007. Penulis memilih mayor Matematika minor Kewirausahaan Agribisnis. Selama menjadi mahasiswa penulis tercatat sebagai staf divisi kewirausahaan Gugus Mahasiswa Matematika periode 2008-2009 dan staf internal Badan Eksekutif Mahasiswa Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor (Kabinet Totalitas Kebangkitan) periode 2009-2010. Selain itu, penulis juga aktif dalam berbagai kegiatan kepanitiaan dan pelatihan yang diselenggarakan oleh GUMATIKA dan BEM Fakultas Matematika dan Ilmu Pengetahuan Alam.
DAFTAR ISI
Halaman
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... ix
I PENDAHULUAN ... 1
II LANDASAN TEORI
2.1 Asumsi dan Model ... 2 2.2 Metode Perturbasi Homotopi ... 3
III PEMBAHASAN
3.1 Analisis Metode ... 6 3.2 Aplikasi Metode ... 7 3.3 Contoh Kasus Pada Masalah Daur Ulang Nutrisi ... 8
IV KESIMPULAN ... 15
DAFTAR PUSTAKA ... 16
DAFTAR TABEL
Halaman 1Tingkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian
numerik pada kasus 1 ... 10 2 Tingkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian
numerik pada kasus 2 ... 12 3Tingkat kesalahan metode perturbasi homotopi orde keempat dengan penyelesaian
numerik pada kasus 1 ... 29 4 Tingkat kesalahan metode perturbasi homotopi orde keempat dengan penyelesaian
numerik pada kasus 2 ... 29
DAFTAR GAMBAR
Halaman
1 Model tiga komponen dari kolam nutrisi abiotik, autotrof, dan detritus ... 2 2 Grafik perbandingan penyelesaian eksak dan metode homotopi masalah nilai awal (2.7) .... 5 3 Grafik penyelesaian dengan metode perturbasi homotopi dari masalah nilai awal (2.1)
orde kelima untuk kasus 1 ... 11 4 Grafik penyelesaian numerik dari masalah nilai awal (2.1) untuk kasus 1 ... 11 5 Grafik penyelesaian dengan metode perturbasi homotopi dari masalah nilai awal (2.1)
orde kelima untuk kasus 2 ... 13 6 Grafik penyelesaian numerik dari masalah nilai awal (2.1) untuk kasus 2 ... 13
DAFTAR LAMPIRAN
Halaman
1 Metode perturbasi homotopi untuk masalah nilai awal (2.7) ... 18 2 Penurunan persamaan (3.17) ... 20 3 Penyelesaian sistem persamaan (3.19) ... 23 4 Program penyelesaian numerik Gambar 4 ... 28 5 Program penyelesaian numerik Gambar 6 ... 28 6 Tingkat kesalahan metode perturbasi homotopi orde keempat dengan
penyelesaian numeriknya pada kasus 1 ... 29 7 Tingkat kesalahan metode perturbasi homotopi orde keempat dengan
I PENDAHULUAN
1.1 Latar Belakang
Model matematika dapat digunakan sebagai penjelasan terhadap suatu fenomena (alami atau buatan) dan sering muncul dalam permasalahan di bidang biologi, fisika, ekonomi, teknik, dan lainnya. Salah satu model matematika yang akan dibahas dalam karya ilmiah ini didasarkan pada interaksi berbagai komponen pada suatu ekosistem, khususnya ekosistem kolam air tawar.
Ekosistem adalah suatu sistem ekologi yang terbentuk karena hubungan timbal balik tidak terpisahkan antara makhluk hidup dengan lingkungannya. Komponen penyusun ekosistem terdiri dari faktor abiotik dan faktor biotik. Faktor abiotik adalah komponen yang bukan berasal dari makhluk hidup, seperti air, udara, sinar matahari, mineral-mineral, dan lainnya. Sebagian nutrisi abiotik dapat berupa bahan organik dan senyawa anorganik yang kemudian diubah menjadi senyawa organik oleh organisme detritus (pengurai) untuk dimanfaatkan oleh organisme autotrof (organisme yang dapat membuat makanannya sendiri). Sedangkan, komponen biotik adalah komponen yang berasal dari makhluk hidup, seperti tumbuhan, hewan, organisme tingkat rendah, dan organisme autotrof.
Penelitian mengenai proses daur ulang nutrisi pada suatu ekosistem telah banyak dilakukan, antara lain penelitian pada penyelesaian analisis kestabilan dari model proses daur ulang nutrisi dalam suatu kolam nutrisi (Yusfridawati 2005) tetapi, tidak mencari penyelesaian hampiran dan penyelesaian numerik dari model tersebut. Penelitian lain, yang ditulis oleh Blachet (2008) difokuskan pada hubungan antara mangsa dan pemangsa dengan melibatkan komponen biotik, abiotik, dan organisme detritus.
Dalam banyak kasus, masalah taklinear sulit untuk diselesaikan, khususnya penyelesaian secara analitik. Model proses daur ulang nutrisi yang dibahas dalam karya ilmiah ini merupakan masalah taklinear yang akan diselesaikan dengan metode perturbasi homotopi. Metode homotopi merupakan bentuk umum dari metode perturbasi dan metode dekomposisi adomian (Jaharuddin 2008). Terdapat beberapa keunggulan dari metode homotopi diantaranya tetap valid sekalipun masalah taklinear tersebut memuat sembarang parameter. Selain itu, dapat melakukan penyesuaian dan pembatasan daerah kekonvergenan serta tingkat hampiran
deret sesuai keperluan, kemudian dapat mengefisienkan penyelesaian hampiran dari masalah taklinear (Liao 2004). Metode perturbasi homotopi diperkenalkan oleh He (1999). Metode perturbasi homotopi merupakan suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Metode ini berhasil diterapkan untuk menyelesaikan berbagai masalah taklinear seperti pada ilmu fisika, ilmu komputer, ilmu biologi, dan lainnya (He 2008). Dalam bidang biologi, khususnya diterapkan pada interaksi berbagai komponen di suatu kolam nutrisi. Dalam karya ilmiah ini akan dibahas proses daur ulang nutrisi yang terjadi pada suatu kolam yang didalamnya terdapat tiga komponen. Komponen pertama adalah nutrisi abiotik. Komponen kedua adalah organisme autotrof. Sedangkan, komponen ketiga adalah organisme detritus. Model proses daur ulang nutrisi ini akan diselesaikan dengan metode perturbasi homotopi (Odibat 2009). Berdasarkan metode ini pula akan dibandingkan penyelesaian hampiran metode perturbasi homotopi dengan penyelesaian numerik dari model ekosistem.
1.2 Tujuan
Berdasarkan latar belakang di atas, maka tujuan karya ilmiah ini adalah:
1. Menggunakan metode perturbasi homotopi untuk menyelesaikan model proses daur ulang nutrisi dalam suatu kolam.
2. Menggambarkan grafik penyelesaian model proses daur ulang nutrisi dalam kolam dan memberikan tafsiran fisisnya.
1.3 Sistematika Penulisan
II LANDASAN TEORI
Pada bagian ini akan dibahas teori-teoriyang digunakan dalam menyusun karya ilmiah ini. Teori-teori tersebut meliputi asumsi dan model ekosistem serta metode perturbasi homotopi.
2.1 Asumsi dan Model
Dalam suatu ekosistem dapat terjadi proses daur ulang nutrisi. Komponen penyusun daur ulang nutrisi ini terdiri dari tiga komponen. Komponen pertama adalah nutrisi abiotik berupa kalium (K), fosfor (P), oksigen (O2), karbon dioksida (CO2), dan mineral-mineral lainnya. Komponen kedua adalah organisme autotrof, seperti algae plankton. Kemudian, komponen ketiga adalah organisme detritus yang berupa bakteri dan fungi (jamur). Komponen penyusun daur ulang nutrisi ini dinamakan kolam nutrisi. Nutrisi abiotik yang berada pada kolam nutrisi berperan sebagai bahan mentah yang digunakan oleh autotrof (produsen) untuk membuat makanannya sendiri. Kemudian nutrisi biotik yang berupa organisme autotrof dimakan oleh organisme yang berperan sebagai konsumen tingkat pertama. Dinamakan konsumen tingkat pertama, karena organisme tersebut pertama kali mengambil makanan dari produsen. Setelah itu, proses berlanjut pada tingkat konsumen yang lebih tinggi sampai akhirnya konsumen tingkat akhir mati dan berakhir pada organisme detritus.
Detritus merupakan organisme yang menguraikan bahan organik yang berasal dari organisme mati, seperti feses, daun yang gugur, dan bangkai organisme mati dari semua tingkat trofik (Campbell et al. 2004). Pengurai disebut juga komponen makro (sapotrof) karena makanan yang dimakan berukuran lebih besar. Detritus menguraikan kembali konsumen dan produsen tingkat akhir menjadi nutrisi abiotik. Organisme pengurai menyerap sebagian hasil penguraian tersebut melepaskan bahan-bahan sederhana sehingga dapat digunakan kembali oleh produsen. Model proses daur ulang nutrisi yang ditinjau adalah model yang disusun oleh (Deangelis et al. 1986). Pada proses permodelan, sistem yang ditinjau dibagi atas tiga komponen, yaitu: nutrisi abiotik, organisme autotrof, dan organisme detritus seperti dalam Gambar 1. Misalkan banyaknya nutrisi abiotik dalam kolam nutrisi adalah , banyaknya autotrof dalam kolam nutrisi adalah , dan banyaknya detritus dalam kolam nutrisi adalah .
Gambar 1 Model tiga komponen dari kolam nutrisi abiotik, autotrof, dan detritus.
Berdasarkan Gambar 1 laju perubahan banyaknya nutrisi yang berada dalam kolam nutrisi dipengaruhi oleh:
1. Banyaknya nutrisi yang masuk ke dalam kolam nutrisi per satuan waktu, dinotasikan .
2. Banyaknya nutrisi yang hilang per satuan waktu, karena keluarnya air dari dalam kolam. Keluarnya air dari dalam kolam nutrisi dapat disebabkan oleh kebocoran atau hal lainnya. Banyaknya nutrisi yang hilang dinotasikan . Dengan suatu konstanta yang disebut tingkat kehilangan nutrisi.
3. Banyaknya nutrisi dalam kolam nutrisi yang dimakan oleh organisme autotrof per satuan waktu adalah , dengan bergantung pada banyaknya nutrisi pada kolam nutrisi dinotasikan , dengan suatu konstanta yang menyatakan perbandingan banyaknya nutrisi dengan banyaknya organisme autotrof dan detritus. Untuk masing-masing dan menyatakan tingkat pertumbuhan autotrof dan tingkat jenuh nutrisi.
4. Banyaknya nutrisi yang diperoleh dari hasil urai yang dilakukan oleh organisme detritus per satuan waktu, dinotasikan
3
Oleh karena itu, laju perubahan banyaknya nutrisi yang berada dalam kolam, secara matematis dinyatakan dengan:
.
Laju perubahan banyaknya organisme autotrof yang berupa nutrisi dipengaruhi oleh:
1. Banyaknya organisme autotrof yang keluar dan diuraikan oleh organisme pengurai per satuan waktu, dinotasikan
dengan suatu konstanta yang disebut laju kematian autotrof yang memengaruhi detritus.
2. Banyaknya organisme autotrof yang keluar dan tidak diuraikan oleh organisme pengurai per satuan waktu, tetapi meninggalkan sistem, dinotasikan dengan suatu konstanta yang disebut laju kematian autotrof yang tidak dapat diuraikan.
3. Banyaknya organisme autotrof yang terbentuk per satuan waktu karena tersedianya nutrisi yang ada pada kolam nutrisi, yaitu .
Oleh karena itu, laju perubahan banyaknya autotrof yang berada dalam kolam, secara matematis dinyatakan oleh :
.
Selanjutnya, laju perubahan banyaknya organisme detritus dipengaruhi oleh :
1. Banyaknya organisme autotrof yang diuraikan oleh organisme detritus per satuan waktu yang dinotasikan oleh . 2. Banyaknya hasil urai dari organisme
detritus yang menjadi nutrisi dalam kolam nutrisi per satuan waktu yang dinotasikan
.
3. Banyaknya organisme detritus yang meninggalkan sistem per satuan waktu dengan laju .
Oleh karena itu, laju perubahan banyaknya detritus yang berada dalam kolam, secara matematis diperoleh :
.
Dengan demikian, proses daur ulang nutrisi dalam kasus ini dimodelkan oleh sistem persamaan sebagai berikut:
. .
Model bagi masalah daur ulang nutrisi pada kolam sederhana yang diberikan oleh sistem persamaan (2.1) akan diselesaikan dengan menggunakan metode perturbasi homotopi. Metode ini akan dijelaskan sebagai berikut:
2.2 Metode Perturbasi Homotopi
Berikut ini diberikan ilustrasi konsep dasar metode homotopi berdasarkan alur pada pustaka (Jaharuddin 2008). Misalkan diberikan persamaan diferensial berikut:
, Ω (2.2)
dengan suatu operator turunan yang taklinear dan fungsi yang akan ditentukan dan bergantung pada peubah bebas
. Selanjutnya didefnisikan pula suatu operator linear yang memenuhi
, bila . (2.3)
Sehingga operator dapat dibagi menjadi dua bagian, yaitu dan yang masing-masing merupakan operator linear dan taklinear. Jadi, persamaan diferensial (2.2) dapat ditulis:
. (2.4)
Misalkan pendekatan awal dari penyelesaian persam (2.2) dan , suat am sikan fungsi real
aan u par eter. Didefini
, :Ω , , dan suatu fungsi H sebagai ber kut: i
,
atau
, .
Berdasarkan persamaan (2.5), maka untuk dan masing-masing memberikan persamaan berikut:
4
, , ,
dan
, , , .
Sehingga menurut persamaan (2.2) dan persamaan (2.3) diperoleh bahwa fungsi
,
dan
, ,
masing-masing merupakan penyelesaian dari persamaan
, ,
dan
, , .
Dengan demikian peningkatan nilai dari 0 ke 1 menyatakan perubahan nilai , dari ke . Dalam topologi, proses ini disebut deformasi. Proses deformasi yang ditinjau meliputi deformasi orde nol dan orde tinggi. Pada deformasi orde nol memberikan penyelesaian awal , sedangkan deformasi orde tinggi memberikan penyelesaian
, , … , . Untuk menentukan
, , , . . . dilakukan sebagai berikut. Jika
persamaan (2.5) diturunkan terhadap hingga kali dan dihitung pada kemudian dibagi oleh !, maka diperoleh persamaan berikut:
; , , |
dan dinotasikan
!
Dalam metode perturbasi homotopi, fungsi , yang dinyatakan pada persamaan (2.6) merupakan penyelesaian dari persamaan
, .
Berdasarkan persamaan (2.5), maka diperoleh .
Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (2.2) dengan pendekatan awal dan ,
, , … yang akan ditentukan. Persamaan
untuk menentukan , , , … diperoleh dengan menggunakan metode perturbasi, dimana persamaan (2.6) disubstitusikan ke dalam persamaan (2.5) dan diperoleh . Secara umum diperoleh dengan menyamakan koefisien kepangkatan
, dan merupakan pendekatan awal dari penyelesaian . Selanjutnya, misalkan diberikan suatu masalah yang dinyatakan oleh sistem ersamaan diferensial berikut : p
, .
Penyelesaian eksak masalah nilai awal (2.8) adalah
5
e e . .
Berikut ini akan dicari penyelesaian dari masalah nilai awal persamaan (2.8) dengan menggunakan metode perturbasi homotopi. Berdasarkan persamaan (2.5) dan persamaan (2.7) diperoleh persamaan berikut:
. (2.10)
Misalkan penyelesaian persamaan (2.10) dinyatakan dalam persamaan beriku : t
, , , ,
, , , ,
(2.11) Jika persamaan (2.11) disubstitusikan ke dalam persamaan (2.10), kemudian dipisahkan berda kan derajat kepangkatan , maka koefisi e ikan
sar
en m mber ,
, . .
Jika persamaan (2.12) diintegralkan terhadap , maka diperoleh
,
, .
Bentuk lain dari , dan , dengan , , , , (dibuktikan dalam lampiran 1).
Selajutnya, diperoleh penyelesaian untuk dan dari persamaan (2.7) dengan syarat awal dan hingga orde kelima, sebagai berikut:
Gambar 2 Grafik perbandingan penyelesaian eksak (2.9) dan metode perturbasi homotopi dari masalah nilai awal (2.7).
Berdasarkan Gambar 2 diperoleh bahwa penyelesaian pendekatan dari masalah nilai awal (2.7) mendekati penyelesaian eksaknya dengan cukup baik. Hasil ini menunjukkan
III PEMBAHASAN
; , , Pada bagian ini akan dibahas penggunaan
metode perturbasi homotopi untuk menyelesaikan suatu masalah taklinear. Metode ini digunakan untuk menyelesaikan model matematika bagi proses daur ulang nutrisi dalam suatu kolam.
3.1Analisis Metode
Dalam karya ilmiah ini akan dibahas suatu masalah taklinear, khususnya pada masalah ekosistem, digunakan metode perturbasi homotopi untuk menentukan penyelesaian pendekatannya.
Berikut ini akan dibahas perluasan dari konsep dasar metode homotopi seperti yang diuraikan pada landasan teori. Untuk itu diperlukan fungsi , , , yang tidak hanya bergantung pada dan , tetapi juga bergantung pada parameter bantu dan fungsi bantu . Misalkan fungsi H dinyatakan sebagai berikut
; , ,
; , ,
; , , . (3.1)
Selanjutnya, misalkan fungsi , , , merupakan penyelesaian dari persamaan berikut:
Berdasarkan persamaan (3.1), maka untuk dan masing-masing memberikan persamaan berikut:
; , , ; , ,
dan
; , , ; , , .
Berdasarkan persamaan (2.2) dan persamaan (2.3), maka penyelesaian dari
persamaan ; , , dan
; , , masing-masing adalah
dan
; , , .
Kedua penyelesaian di atas bergantung pada parameter bantu h dan fungsi bantu
yang dipilih sembarang, pemilihan parameter bantu h, fungsi bantu T (x), pendekatan awal , dan operator linear perlu memperhatikan validitas dari metode homotopi. Dengan pemilihan ini terjamin adanya fungsi ; , , dan turunan-kekonvergenan dari deret (3.3) di . Jadi untuk , dari persamaan (3.3) diperoleh
; , , .
∞
7
Karena ; , , , maka diperoleh ∞
.
(3.5)
Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (2.2) dengan pendekatan awal dan ,
, , … yang akan ditentukan. Persamaan
untuk menentukan , , , … diperoleh dengan menggunakan metode perturbasi, dimana persamaan (3.3) disubstitusikan ke dalam persamaan (3.2), dengan menyamakan koefisien dari derajat kepangkatan , maka diperoleh penyelesaian dari persamaan (3.5).
3.2Aplikasi Metode
Untuk lebih memahami metode yang telah dijelaskan pada bagian sebelumnya. Tinjau sistem persamaan diferensial berikut:
.
Secara umum sistem persamaan diferensial (3.6) dapat dinyatakan dalam persamaan berikut:
. ,
dengan nilai awal
, , … ,
Berdasarkan persamaan (2.4) dan persamaan (3.6), diperoleh
.
(3.8) Secara umum persamaan (3.8) dapat dinyatakan dalam persamaan berikut:
,
(3.9) dengan suatu operator linear dan operator taklinear. Berdasarkan persamaan (3.1) dan persamaan (3.6) diperoleh
.
(3.10) Secara umum persamaan (3.10) dapat dinyatakan dalam persamaan berikut:
,
8
dengan , dan merupakan penyelesaian pendekatan awal. Parameter mengalami peningkatan dari 0 sampai 1. Misalkan penyelesaian dari persamaan (3.7) dinyatakan alam deret ku d asa be i ut r k :
Sebagai ilustarasi, misalkan . Dimisalkan penyelesaian pendekatan awal
, merupakan suatu konstanta. Jika persaman (3.12) disubstitusikan ke dalam persamaan (3.11), kemudian dipisahkan berdasarkan derajat kepangkatan , maka ko sien mem ikan persamaan berikut:
efi ber
, , , , , ,
(3.13) dengan syarat awal
, , , dan , .
(3.14) Penyelesaian masalah nilai awal persamaan (3.13) adalah
, , , dan , . Koefisien , memberikan persamaan berikut: Secara umum untuk sembarang koefisien memberikan persamaan berikut:
, , .
dengan syarat awal , .
Koefisien , memberikan persamaan berikut:
,
, ,
dengan syarat batas , .
Koefisien , memberikan persamaan berikut: dapat dinyatakan dalam persaman berikut:
,
, ,
dengan syarat batas , .
(3.17) (Bukti dapat dilihat pada lampiran 2)
Berdasarkan ilustrasi yang telah djelaskan di atas diperoleh bahwa, jika diberikan masalah taklinear dengan persamaan diferensial pada sistem persamaan (3.6), maka dengan metode perturbasi homotopi diperoleh penyelesaian pendekatan berbentuk
, . .
dengan , diperoleh dari persamaan (3.17)
3.3Contoh Kasus pada Masalah Daur
Ulang Nutrisi
9
organisme detritus dalam kolam nutrisi, maka persamaan (2.1) menja id persamaan berikut:
, merupakan parameter-parameter pada persamaan (2.1). Dalam proses ini, dimisalkan:
Berikut ini akan ditentukan penyelesaian dari masalah nilai awal persamaan (3.19) dengan metode perturbasi homotopi yang telah diuraikan pada bagian sebelumnya. Sehingga, penyelesaian masalah nilai awal persamaan (3.19) hingga orde kelima berbentuk:
Nilai , ditentukan berdasarkan persamaan (3.16) dan persamaan (3.17). Berdasarkan persamaan (3.16) dan persamaan (3.19 di) peroleh penyelesaian berikut:
, ,
, . ,
, . .
Berdasarkan persamaan (3.17) dan persamaan 19) dipero er maan berikut:
(3. leh p sa Berikut ini akan dilakukan kajian tentang masalah daur ulang nutrisi untuk . ,
, . , . , . ,
. , . . Ditinjau dua kasus
berdasarkan tingkat pertumbuhan dan laju kematian autotrof. Kasus pertama bilamana tingkat pertumbuhan dan laju kematian autotrof berbeda. Sedangkan kasus kedua bilamana tingkat pertumbuhan dan laju kematian autotrof sama.
Kasus 1. Misal an k
. , . .
10
Berdasarkan persamaan (3.22) dan persamaan (3.20) diperoleh penyelesaian masalah nilai awal persamaan (3.19) berbentuk
Dengan demikian penyelesaian masalah daur ulang nutrisi pada persamaan (2.1), untuk komponen N, X, D yang masing‐masing
menyatakan banyaknya nutrisi abiotik dalam
kolam nutrisi, banyaknya autotrof dalam kolam nutrisi, dan banyaknya detritus dalam olam nutrisi. Untuk kasus dan kasus
rde kelima adalah k
hingga o
Tabel T ngkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian numerik
pada kasu 1
Tabel 1 berikut ini menunjukkan bahwa tingkat kesalahan untuk penyelesaian nutrisi biotik (N), organisme autotrof (X), dan organisme detritus (D) pada kasus 1 hingga orde kelima dengan penyelesaian numeriknya sangat kecil.
i s t (satuan waktu)
Tingkat kesalahan
Nutrisi biotik (N) Organism eautotrof (X) Organisme detritus (D)
Berdasarkan Tabel dapat disimpulkan bahwa semakin tinggi orde yang digunakan, maka semakin mendekati penyelesaian sebenarnya.
11
Gambar 3 Grafik penyelesaian dengan metode perturbasi homotopi dari masalah nilai awal (2.1) orde kelima untuk kasus 1.
12
Gambar 3 dan Gambar 4 memperlihatkan perilaku nutrisi abiotik, organisme autotrof, dan organisme detritus selama proses daur ulang nutrisi berlangsung. Pada kasus pertama perilaku nutrisi abiotik menunjukkan bahwa banyaknya nutrisi abiotik pada saat terjadi proses daur ulang nutrisi menurun dengan sangat lambat. Hal ini dikarenakan oleh beberapa hal, diantaranya banyaknya nutrisi yang hilang dari kolam karena keluarnya air dari kolam nutrisi yang disebabkan oleh kebocoran pada kolam. Penyebab lainnya adalah banyaknya nutrisi yang digunakan leh organisme autotrof untuk membuat
nya sendiri. Selain itu, tingginya
tingkat pertumbuhan autotrof mengakibatkan tingginya jumlah organisme autotrof. Seiring dengan penurunan nutrisi abiotik organisme autotrof mengalami peningkatan dengan lebih cepat. Sedangkan, untuk organisme detritus mengalami penurunan dengan lebih cepat, hal ini terjadi karena banyaknya organisme
autotrof yang telah mati tidak dapat
diuraikan oleh detritus. Detritus yang tidak dapat menguraikan autotrof disebabkan oleh adanya kebocoran pada kolam.
o makanan
Tabel T gkat kesalahan metode perturbasi homotopi orde kelima dengan penyelesaian numerik
pada kasu
Tabel 2 berikut ini menunjukkan bahwa galat untuk penyelesaian N, X, D pada kasus 2 hingga orde kelima dengan penyelesaian numeriknya sangat kecil.
in
Berdasarkan Tabel dapat disimpulkan bahwa semakin tinggi orde yang digunakan, maka semakin mendekati
enyelesaian sebenarnya. p
Gambar 5 dan Gambar 6 berikut ini menunjukkan grafik penyelesaian untuk nutrisi biotik (N), organisme autotrof (X), dan
rganisme detritus (D) yang didekati hingga rde kelima.
13
Gambar 5
Gam
Grafik penyel
mbar 6 Grafik
lesaian dengan ord
penyelesaian
n metode pert de kelima untu
numerik dari
turbasi homoto uk kasus 2.
masalah nilai
opi dari masal
awal (2.1) un
lah nilai awal
14
Gambar 5 dan Gambar 6 memperlihatkan perilaku nutrisi abiotik, organisme autotrof, dan organisme detritus selama proses daur ulang nutrisi berlangsung. Untuk kasus kedua perilaku nutrisi abiotik menunjukkan bahwa banyaknya nutrisi abiotik pada saat terjadi proses daur ulang nutrisi mengalami penurunan dengan sangat lambat. Untuk organisme autotrof pun mengalami penurunan dengan sangat lambat, hal ini dikarenakan oleh beberapa hal, diantaranya nutrisi yang digunakan untuk membuat
IV SIMPULAN
Metode perturbasi homotopi yangdigunakan untuk menyelesaikan model proses daur ulang nutrisi dalam suatu kolam nutrisi sangat sederhana karena hanya melibatkan pengintegralan biasa. Model proses daur ulang nutrisi yang ditinjau berupa kolam air tawar yang didalamnya terdapat tiga komponen, yaitu nutrisi biotik, organisme autotrof, organisme detritus. Dalam metode perturbasi homotopi diperoleh bahwa semakin tinggi orde yang digunakan semakin mendekati penyelesaian sesungguhnya. Hal ini terlihat pada galat (tingkat kesalahan) dari orde kelima dengan penyelesaian numeriknya lebih kecil dibandingkan penyelesaian numerik dari orde keempat.
Dalam karya ilmiah ini, disimulasikan dua kasus model proses daur ulang nutrisi. Kedua kasus tersebut berdasarkan tingkat
pertumbuhan dan laju kematian autotrof. Pada kasus pertama, jika tingkat pertumbuhan autotrof lebih tinggi dibandingkan dengan laju kematian autotrof, diperoleh hasil bahwa: 1. Banyaknya nutrisi abiotik mengalami
penurunan.
2. Banyaknya organisme autotrof mengalami peningkatan.
3. Banyaknya organisme detritus mengalami penurunan.
Pada kasus kedua, jika tingkat pertumbuhan dan laju kematian autotrof sama, diperoleh hasil bahwa:
1. Banyaknya nutrisi abiotik mengalami penurunan.
2. Banyaknya organisme autotrof mengalami penurunan.
DAFTAR PUSTAKA
Blanchet S, Loot G, Dodson JJ. 2008.
Competition, predation and flow rate as mediators of direct and indirect effects in a stream food chain. Springer-Verlag.
Campbell NA, Reece JB, Mitchell LH. 2004.
Biologi Jilid 3. Jakarta: Erlangga. Lestari R, penerjemah. Terjemahan dari: Biology.
Deangelis DL. 1986. Nutrient Recycling and
System Resillence in a Model of an Experimental Aquatic System. Mathematical Ecology, 189-215.
He JH. 1999. Homotopy Perturbation Tehcnique.
Computer Methods in Applied Mechanics and Engineering 178:257-262.
He JH. 2008. Topological Methods in Nonlinear
Analysis. Recent Development of the Homotopy Perturbation Method 31:205-209.
Jaharuddin. 2008. Analisis Homotopi dalam
Penyelesaian suatu Masalah Taklinear. Jurnal Matematika dan Aplikasinya, 7:6-16.
Liao S. 2004. Beyond Perturbation: Introduction to
the Homotopi Analysis Method. Boca Raton, London, New York Washington, D.C.
Odibat Z, Bertelle C. 2009. Application of
Homotopy Perturbation Method for Ecosystem Modelling. http://wwwlih.univ-lehavre.fr/~bertelle/cossombook/odibat4cosso m06.pdf [8 Desember 2010].
Yusfridawati. 2005. Analisi Kestabilan Model
18
Lampiran 1 Metode perturbasi homotopi untuk masalah nilai awal
persamaan (2.7)
Perhatikan persamaan (2.7) berikut:
dengan syarat awal , .
Substitusikan persam n (2.11) ke dalamaa persamaan (2.10), maka diperoleh
, ,
, , , , , , ,
, ,
, , , , ,
,
, , , , ,
dengan nilai awal , ; , , , , … , .
Setelah dipisahkan berdasarkan derajat kepangkatan dari , untuk koefisien , , , , , diberikan oleh persamaan berikut :
, ,
,
, , , ,
,
, , , ,
,
, , , ,
,
, ,
Jika persamaan di atas diintegralkan terhadap , untuk koefisien , , … , , diperoleh , , , , sebaga ber u
, ,
i ik t:
, ,
, ,
19
, ,
, , ,
Jadi, penye esaial n dan ada h la
, , , , ,
, , , , , .
Dengan demikian penyelesaian masalah nilai awal (2.7) dengan syarat awal dan el a ad ah
hingga orde k im al :
20
Lampiran 2 penurunan persamaan (3.17)
Jika persamaan (3.12) disubstitusikan ke dalam persamaan (3.11), untuk , , , dan , , maka diperoleh
, ,
, ,
, , , , , , , ,
, , , , , , ,
, ,
, ,
, , , , , , , ,
, , , , , , ,
, ,
, ,
, , , , , , , ,
, , , , , , ,
dengan syarat awal , , , dan , .
Pisahkan ruas kiri berdasarkan derajat kepangkatan , maka diperoleh
, ,
, , , ,
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , ,
,
21
, ,
, , , ,
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , ,
, ,
, , , ,
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , , .
Dimisalkan penyelesaian pendekatan awal , merupakan suatu konstanta. Koefisien memberikan persamaan berikut :
, , , , , ,
dengan syarat awal
, , , , , .
Penyelesaian nilai a alw tersebut adalah:
, , , , , .
Koefisien memberikan persamaan berikut :
,
, , , ,
,
, , , ,
,
, , , , ,
dengan syarat batas
22
Koefisien memberikan persamaan berikut:
,
, , , , , , ,
,
, , , , , , ,
,
, , , , , , , ,
dengan syarat batas
, , , , , .
Secara umum diperoleh koefisien berikut:
,
, ,
dengan syarat awal , .
Koefisien dapat dinyatakan dalam persaman berikut:
,
, , ,
23
Lampiran 3 penyelesaian sistem persamaan (3.19)
Perhatikan sistem persamaan (3.19) berikut:
dengan syarat awal
, , , . , , . ,
Dimisalkan,
• , , , , , ,
• , , , , , ,
• , , , , , ,
• , ,
Be asar an persama
, , ,
rd k an (3.19) diperoleh
,
, , , , , , ,
,
,
, , , , , , , , , , , , ,
, , ,
, , ,
,
, , , , , , , , , , , ,
, , , , , , , , , , , , ,
, , , , , , , , , , ,
, , , , , , , , , ,
,
,
, ,
,
, ,
,
, ,
25
Berdasarkan persamaan (3.16) diperoleh
, , , , , ,
mak koa efisien , mem erikan penyeb lesaian ebagai beriku s t:
, , , . , , .
Berdasarkan persamaa (3n .17) dan persamaan (3.19), koefisien memberikan persamaan berikut:
, , ,
Koefisien , membe ikan persamaan berikut:
, , ,
r
,
, , , , , , , , , ,
26
Koefisien , memberikan persamaan berikut:
27
Denga i le ah daur u nutrisi pada persamaan (2.1), untuk komponen
N, X, D ngga orde kelima berbentuk:
n demik an penye saian masal lang masing-masing untuk kasus 1 dan kasus 2 hi
, , , , , ,
, , , , ,
,
, , , , , ,
Kasus 1. Misalkan
. , . , . ,
. ,
, . ,
. , . , .