BILANGAN KROMATIK LOKASI GRAF AMALGAMASI BINTANG TERTENTU

(1)

LOCATING-CHROMATIC NUMBER OF CERTAIN

AMALGAMATION OF STAR GRAPHS

Abstract

Let c be a proper k-coloring of connected graph G and is the set consisting of the color classes of V(G). The color code of v is ordered k-tuple ( ) which is = min | for . If every G has different color code, then c is called the locating coloring of G. The minimum numbers of colors needed in a locating coloring of is called the locating chromatic number of G, denoted by

Amalgamation of star graphs, obtained from copies of amalgamation star by connecting a leaf from each through a track. The result of the research are: If , and then ( ) to

, then ( ) another . If ,

, and then ( ) to , then ( ) for another .

(2)

BINTANG TERTENTU

ABSTRAK

Misalkan c adalah suatu pewarnaan-k sejati dari graf terhubung G dan adalah himpunan yang terdiri dari kelas – kelas warna

dari V(G). Kode warna dari v adalah k-pasang terurut ( ) dengan = min | untuk . Jika setiap G mempunyai kode warna yang berbeda, maka c disebut pewarnaan lokasi G. Banyaknya warna minimum yang diperlukan dalam pewarnaan lokasi dari G disebut bilangan kromatik lokasi graf G, dinotasikan

Graf amalgamasi bintang, diperoleh dari buah graf bintang amalgamasi

dengan cara menghubungkan sebuah daun dari setiap melalui sebuah

lintasan. Hasil dari penelitian adalah : Jika , , dan maka ( ) untuk , selanjutnya ( ) untuk

lainnya. Jika dan maka ( ) untuk , selanjutnya ( ) untuk lainnya. .

(3)

BILANGAN KROMATIK LOKASI GRAF AMALGAMASI

BINTANG TERTENTU

Oleh

C. Ike Tri Widyastuti

Tesis

Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Magister Sains

Pada

Jurusan Matematika Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(4)

Tesis

Oleh

C. Ike Tri Widyastuti

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(5)

DAFTAR GAMBAR

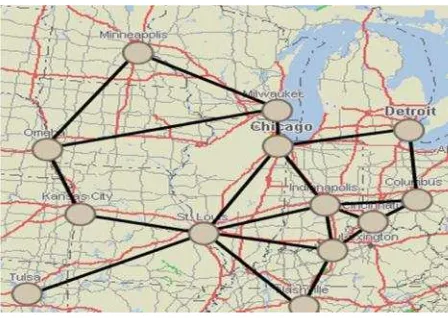
Halaman Gambar 1. Jalur penerbangan bandara Chicago dan bandara - bandara

tujuannya ... 2

Gambar 2. buah graf bintang ... 5

Gambar 3. Graf ... 6

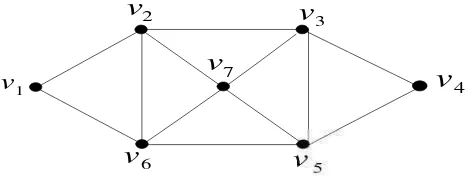
Gambar 4. Contoh graf G dengan 7 titik dan 8 sisi ... 9

Gambar 5. Graf dan graf , ... 12

Gambar 6. Contoh graf Eulerian ... 12

Gambar 7. Contoh graf Halmitonian ... 13

Gambar 8. Contoh pohon dan hutan ... 14

Gambar 9. Graf bintang ... 14

Gambar 10. Graf bintang ganda ... 15

Gambar 11. Graf ulat... 15

Gambar 12. Graf pohon pisang ... 16

Gambar 13. Graf kembang api ... 16

Gambar 14. Graf almagamasi bintang ... 17

(6)

Gambar 18. Pewarnaan lokasi minimum pada Graf ... 24

Gambar 19. Pohon T dari berorde dengan ... 24

Gambar 20. Pewarnaan lokasi minimum pada graf ... 28

Gambar 21. Pewarnaan lokasi minimum pada graf ... 29

Gambar 22. Konstruksi graf ... 34

Gambar 23. Pewarnaan lokasi minimum pada graf untuk 2 39

Gambar 24. Pewarnaan lokasi minimum pada graf untuk ... 44

Gambar 25. Pewarnaan lokasi minimum pada graf untuk dan ... 50

(7)

DAFTAR ISI

Halaman

DAFTAR ISI ... i

DAFTAR GAMBAR ... ii

BAB I PENDAHULUAN 1.1 Latar Belakang Masalah ... 1

1.2 Perumusan Masalah ... 5

1.3 Tujuan Penelitian ... 6

1.4 Manfaat Penelitian ... 7

BAB II KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf ... 8

2.2 Graf Pohon dan Beberapa Kelas dari Graf Pohon ... 13

BAB III METODOLOGI PENELITIAN BAB IV BILANGAN KROMATIK LOKASI GRAF BAB V HASIL DAN PEMBAHASAN 5.1 Bilangan Kromatik Lokasi untuk dengan Bilangan Asli ... 35

(8)

6.2 Saran ... 54

(9)

(10)

(11)

MOTO

Yang harus diwaspadai dalam sebuah perjalanan bukanlah waktu, tetapi langkah kaki. Waktu akan terus melaju, sementara langkah kaki kapan saja bisa berhenti.

(12)

(13)

PERSEMBAHAN

Karya ini kupersembahkan untuk yang terkasih:

Ayahanda dan Ibunda, Alm. Bapak D. Saridjo Dwiatmoko dan Ibu Christina Kamtini.

Kakak dan Adikku, Mas Ahen, Mbak Henny, Elis, dan Tata.

(14)

RIWAYAT HIDUP

Penulis dilahirkan di Tanjung Karang pada tanggal 23 Januari 1976 merupakan anak ketiga dari lima bersaudara pasangan Bapak Dominicus Saridjo Dwiatmoko dan Ibu Christina Kamtini.

Pendidikan formal yang pernah ditempuh :

1. Sekolah Dasar (SD) di SD Xaverius Rawa Laut, Bandar Lampung pada tahun 1983 – 1989.

2. Sekolah Menengah Pertama (SMP) di SMP Xaverius Pasir Gintung, Bandar Lampung pada tahun 1989 – 1992.

3. Sekolah Menengah Atas (SMA) di SMA Pangudi Luhur Van Lith Muntilan, Jawa Tengah tahun 1992 – 1995.

4. S1 Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sanata Dharma Yogyakarta pada tahun 1995 – 2002.

5. Akta Mengajar Universitas Negeri Yogyakarta pada tahun 2004-2005

(15)

SANWACANA

Puji syukur penulis panjatkan kepada Allah Bapa sumber kehidupan dan pengharapan yang telah melimpahkan berkat-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul “Bilangan Kromatik Lokasi Graf Amalgamasi Bintang Tertentu“.

Tesis ini merupakan salah satu syarat yang harus dipenuhi guna memperoleh gelar Magister Sains di Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Lampung. Penulis menyadari bahwa penulisan tesis ini tidak terlepas dari bantuan dan dorongan dari berbagai pihak, baik secara moril maupun materil. Pada kesempatan ini penulis ingin mengucapkan terima kasih kepada :

1. Ibu Dr. Asmiati, S.Si., M.Si, selaku pembimbing I sekaligus pembimbing akademik yang telah memberikan bimbingan, arahan, dan sumbangan pemikiran dalam penulisan tesis ini.

(16)

membangun pada penulis dalam menyelesaikan tesis ini.

4. Bapak Drs. Mustofa Usman, M.A, Ph.D, selaku Ketua Program Studi Magister Matematika yang telah membimbing dan memberikan arahan kepada penulis.

5. Seluruh dosen yang telah mendidik dan membimbing penulis selama menyelesaikan masa studi.

6. Orang tua penulis khususnya Ibu dan Alm. Bapak serta keluarga yang selalu mendoakan, memberikan semangat, dan dukungan kepada penulis dari awal masa studi sampai penulisan tesis ini selesai.

7. Sahabat kehidupanku, Joseph Emmanuel yang selalu menemani dan memberi energi semangat selama penulis berjuang menyelesaikan studi. 8. Sr. M. Pauli, FSGM selaku kepala sekolah dan segenap rekan kerja penulis

di SMA Fransiskus Bandar Lampung untuk semangat dan perhatiannya selama penulis berjuang menyelesaikan studi.

9. Teman-teman angkatan 2013 atas diskusi, kebersamaan, dan suasana kuliah yang indah dan tak terlupakan.

Harapan penulis semoga Tuhan Yang Maha Esa berkenan membalas segala kebaikan semua pihak yang telah membantu. Semoga tulisan ini dapat bermanfaat bagi perkembangan ilmu pengetahuan.

(17)

I. PENDAHULUAN

1.1 Latar Belakang

Konsep teori graf diperkenalkan pertama kali oleh seorang matematikawan Swiss, Leonard Euler pada tahun 1736, dalam permasalahan jembatan Konigsberg. Teori graf merupakan salah satu bagian ilmu dari matematika yang semakin lama semakin berkembang. Banyak permasalahan yang dapat dinyatakan dan diselesaikan dengan menggunakan teori graf. Salah satunya adalah menyelesaikan masalah jalur penerbangan untuk menentukan jalur tercepat .

(18)

Gambar 1. Jalur penerbangan bandara Chicago dan bandara-bandara tujuannya

Alternatif yang digunakan dalam menyelesaikan masalah jalur penerbangan tersebut adalah dengan menggunakan graf. Graf merupakan alat bantu untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Pengambilan jalur terpendek dari bandara asal ke bandara tujuan dapat dilakukan dengan membuat grafik garis. Dengan demikian, permasalahan jalur terpendek tersebut dapat direprensentasikan dalam graf, dimisalkan bandara Chicago dan bandara-bandara tujuan sebagai titik (vertex) dan jalur penerbangannya dinyatakan sebagai sisi (edge).

(19)

3

memiliki kontribusi besar bagi perkembangan ilmu pengetahuan adalah teori pewarnaan lokasi.

Kajian tentang pewarnaan lokasi adalah kajian yang cukup baru dalam teori graf. Misalkan c suatu pewarnaan titik pada graf G dengan ( ) ( ) untuk u dan v yang bertetangga di G. Misalkan himpunan titik–titik yang diberi warna i, yang selanjutnya disebut kelas warna, maka Π= { , , , } adalah himpunan yang terdiri dari kelas– kelas warna dari V(G). Kode warna ( ) dariv adalah k-pasang terurut ( , ), ( , ), , ( , ) dengan ( , ) = min{ ( , )| }

untuk1 . Jika setiapGmempunyai kode warna yang berbeda, makacdisebut pewarnaan lokasiG. Bilangan kromatik lokasi dariG, dan dinotasikan dengan ( )

adalah bilangan terkecil sehingga mempunyai pewarnaaan- lokasi (Chartrand, dkk, 2002).

Teori pewarnaan lokasi pertama kali dikaji oleh Chartrand dkk. (2002) dengan menentukan lokasi dari beberapa kelas graf sebagai berikut. Untuk lintasan dengan

3 diperoleh ( ) = 3. Untuk graf siklus diperoleh dua hasil yaitu ganjil

berlaku ( ) = 3 dan untuk genap berlaku ( ) = 4. Selanjutnya juga diperoleh ( ) untuk graf multipartit lengkap dan graf bintang ganda. Pada tahun 2003 Chartrand dkk. membuktikan bahwa bilangan kromatik lokasi graf dengan orde yang memuat graf multipartit lengkap berorde ( 1) sebagai subgraf

(20)

bilangan kromatik lokasi dengan batas atasnya ( 2). Selain itu, Chartrand dkk. (2003) menunjukkan bahwa terdapat pohon berorde 5dengan bilangan kromatik lokasi jika dan hanya jika {3, 4, , 2, }.

Selanjutnya beberapa penelitian Asmiati dkk. (2011-2014) juga memberikan pemikiran untuk melatarbelakangi kajian penelitian ini. Pada tahun 2011-2012, Asmiati dkk. berhasil meneliti bilangan kromatik lokasi graf amalgamasi bintang, bilangan kromatik lokasi kembang api (firecracker graph), karakterisasi graf memuat siklus dengan bilangan kromatik lokasi tiga, dan dimensi partisi graf amalgamasi bintang. Sedangkan pada tahun 2013-2014, Asmiati dkk. berhasil meneliti karakterisasi graf pohon dengan bilangan kromatik lokasi tiga, graf amalgamasi pohon berbilangan kromatik lokasi empat dan bilangan kromatik lokasi graf amalgamasi bintang non homogen. Masalah penentuan bilangan kromatik lokasi pada suatu graf, masih terbuka untuk dikaji karena belum adanya teorema yang digunakan untuk menentukan bilangan kromatik lokasi pada sembarang graf.

Graf amalgamasi bintang _, adalah gabungan (amalgamasi) dari graf-graf bintang

yang diperoleh dengan mengidentifikasi sebuah daun dari setiap bintang dengan titik hasil identifikasinya disebut pusat amalgamasi. Kajian graf amalgamasi bintang _,

ini cukup menarik untuk dikaji lebih dalam, maka penulis ingin menentukan bilangan kromatik lokasi grafamalgamasi bintang _, . Penelitian ini juga merupakan

(21)

5

1.2 Perumusan Masalah

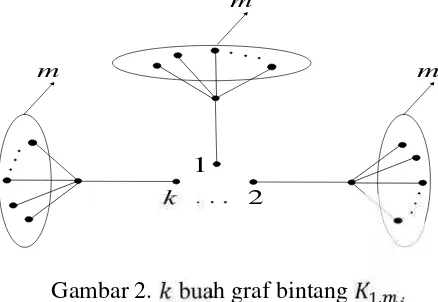
Misalkan terdapat buah graf bintang _, , 1, = 1,2,3, , dengan ,

adalah bilangan bulat. Graf amalgamasi titik bintang _,( _, _{, ,} ₎, dari 2,

adalah graf yang diperoleh dengan mengidentifikasi sebuah daun dari setiap bintang. Titik hasil identifikasi disebut pusat amalgamasi, dinotasikan . Titik yang berjarak satu dari pusat amalgamasi disebut titik tengah, dinotasikan , = 1,2,3, , 1

dan titik daun ke- dari titik tengah adalah , = 1,2,3, , . Jika 1 untuk

semua , graf amalgamasi bintang dinotasikan sebagai _, (Asmiati dkk. (2012)).

2

k

1

m m

m

Gambar 2. buah graf bintang _,

(22)

l

12

l

22

l23

l

k

2 1 

l112

l

122

l

132

l

m

2 1

l

221

l

222

l

223

l

m

2 2

l

312

l

322

l

233

l

k 2 1 ) 1 (

l

m 2 3

l

k 2 2 ) 1 (

l

k 2 3 ) 1 (

l

k m

2 ) 1 (

l

1n

l

n2

l

3n

l

nk1

l

11n

l

12n

l

13n

l

1nm

l

n21

l

n22

l

n23

l

n2m

l

n31

l

n32

l

n33

l

n(k1)1

l

n3m

l

(nk1)2

l

n(k1)m

l

11

l12

l

13

l

k

1 1 

l

111

l

112

l

113

l

m

1 1

l

121

l

122

l

123

l

m

1 2

l

131

l

132

l

133

l

k 1 1 ) 1 (

l

m 1 3

l

k 1 2 ) 1 (

l

k 1 3 ) 1 (

l

k m

1 ) 1 (

x

1

x

2 xn

y₁ y2 yn

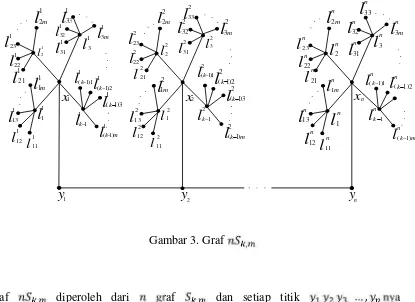
Gambar 3. Graf _,

Graf , diperoleh dari graf , dan setiap titik , , _,, , nya

dihubungkan oleh suatu lintasan. Pada penelitian ini akan ditentukan bilangan kromatik lokasi untuk graf _, untuk , , bilangan asli.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah menentukan bilangan kromatik lokasi dari graf

(23)

7

1.4 Manfaat Penelitian

Manfaat yang didapat dari penelitian ini adalah sebagai berikut:

1. Mengembangkan wawasan tentang teori graf terutama tentang bilangan kromatik lokasi dari graf amalgamasi bintang _, .

2. Memberikan sumbangan pemikiran untuk memperluas dan memperdalam ilmu matematika dalam bidang teori graf terutama tentang bilangan kromatik lokasi dari graf amalgamasi bintang _, .

(24)

Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini.

2.1 Konsep Dasar Graf

Pada bagian ini akan dijelaskan beberapa konsep dasar dari graf yang diambil dari Deo, 1989. Sebuah graf G adalah himpunan terurut (V(G), E(G)), dengan ( )

menyatakan himpunan titik (vertex) { , , } dari dengan ( ) 0, dan ( )

menyatakan himpunan sisi (edge) { , , } yakni pasangan tak terurut dari ( ). Banyaknya himpunan titik ( ) disebut orde dari graf . Jika dan dihubungkan oleh sisi maka dan dikatakan bertetangga (adjacent), sedangkan titik dan dikatakan menempel (incident) dengan sisi , demikian juga sisi dikatakan

(25)

9

Loop adalah sisi yang memiliki titik awal dan titik akhir yang sama. Sisi paralel adalah sisi yang memiliki dua titik ujung yang sama. Graf yang tidak mempunyai sisi ganda atauloop disebut graf sederhana (simple graph). Pada graf terhubung G, jarak diantara dua titik dan y adalah panjang lintasan terpendek diantara kedua titik tersebut, dinotasikan dengan ( , ).

Istilah lain yang sering muncul pada pembahasan graf adalah jalan (walk), lintasan (path) dan sirkuit (circuit). Jalan (walk) adalah barisan berhingga dari titik dan sisi dimulai dan diakhiri dengan titik sedemikian sehingga setiap sisi menempel dengan titik sebelum dan sesudahnya. Lintasan (path) adalah jalan yang memiliki dan melewati titik yang berbeda. Graf G dikatakan graf terhubung jika terdapat lintasan yang menghubungkan setiap dua titik yang berbeda. Sirkuit adalah lintasan tertutup (closed path), yaitu lintasan yang memiliki titik awal dan titik akhir yang sama. Sirkuit dibedakan menjadi dua macam, yaitu sirkuit genap dan sirkuit ganjil. Sirkuit genap adalah sirkuit dengan banyaknya titik genap, dan sirkuit ganjil adalah sirkuit dengan banyaknya titik ganjil.

6 v 4 v 1 v 2

v v3

5 v 1 e 2 e 3 e 4 e 5 e 6 e 8 e 10 e 11 e 7 v 9 e 7 e

(26)

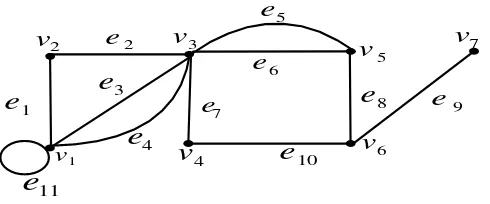
Berdasarkan uraian di atas, pada Gambar 4. terlihat ( ) = { , , , , , , }

dan ( ) = , , , , , , , , , , . Dapat.dilihat bahwa sisi

menempel (incident) dengan titik dan dan titik menempel pada sisi dan . Titik bertetangga (adjacent) dengan titik karena terdapat sisi-sisi yang menghubungkan dan . Demikian pula dengan titik bertetangga dengan titik

, dan titik bertetangga dengan titik , maka dapat ditulis ( ) = { , }.

Derajat graf pada Gambar 4. adalah ( ) = 5, ( ) = 2, ( ) = 6 ( ) = 2,

( ) = 3, ( ) = 3, dan ( ) = 1adalah daun karena berderajat satu. Loop

pada titik yaitu , sedangkan , , dan disebut sisi-sisi paralel pada graf yang mempunyai 2 titik ujung yang sama. Secara jelas dapat disimpulkan bahwa graf pada Gambar 4. bukan merupakan graf sederhana karena pada graf tersebut memiliki loop dan sisi paralel. Contoh jalan pada Gambar 4. dapat dipilih

, contoh lintasan adalah dan contoh sirkuit adalah

.

(27)

11

Lemma 2.1(Narsing Deo dkk. 1989)Jumlah derajat semua titik pada graf G adalah genap, yaitu dua kali jumlah sisi pada graf tersebut. Dengan kata lain jika ( , )

maka:

( ) = 2 (2.1.1)

Contoh dari jumlah derajat seluruh titik pada graf Gambar 4. adalah ( ) + ( ) + ( ) + ( ) + ( ) + ( ) + ( ) = 5 + 2 + 6 + 2 + 3 + 3 + 1 =

22 = dua kali jumlah sisi.

Teorema 2.1(Narsing Deo dkk. 1989)Untuk sembarang graf G, banyaknya titik yang berderajat ganjil, selalu genap.

Bukti : Jika titik-titik berderajat ganjil dan genap dipandang secara terpisah, jumlah ruas kiri persamaan (2.1.1) dapat dinyatakan sebagai jumlah dari dua bilangan. Pertama diperoleh dari titik-titik berderajat ganjil dan kedua dari titik-titik berderajat genap. Jadi,

( ) = + ( ) (2.1.2)

dengan dari titik-titik genap dan ( ) dari titik-titik ganjil. Karena ruas

kiri persamaan (2.1.2) genap, dan suku pertama dari ruas kanan adalah genap, maka suku kedua ruas kanan juga pasti genap.

(28)

Karena dalam persamaan (2.1.3) tiap ( ) adalah bilangan ganjil, maka jumlah

keseluruhannya pastilah genap. ■

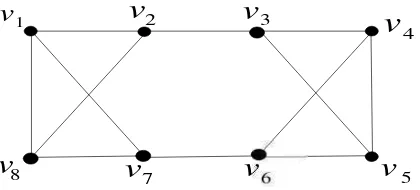
Berikut ini akan dijelaskan juga mengenai subgraf, graf Eurelian dan graf Hamiltonian. Sebuah subgraf dari graf (V(G), E(G))adalah sebuah graf (V(H), E(H)) sedemikian hingga ( ) ( ), dan ( ) ( ). Sebagai contoh pada Gambar 5. graf adalah salah satu subgraf dari graf .

1 v 4 v 2 v 3 v 5 v 1 e 2 e 3 e 4 e 6 e G 5 e 1 v 4 v 3 v 5 v 3 e 6 e H

Gambar 5. Graf dan graf ,

Graf dikatakan Eulerian jika terdapat lintasan tertutup yang memuat semua sisi

pada graf .Lintasan yang demikian disebut lintasan Eulerian (Eulerian path).

4 v 1 v 2 v 3 v 5 v 6 v 7 v

(29)

13

Dari Gambar 6., dapat ditentukan lintasan tertutup

.Jadi merupakan graf Eulerian.

Sirkuit dalam graf yang memuat semua titik dari , disebut sirkuit Hamiltonian. Graf yang memiliki sirkuit Hamiltonian disebut graf Hamiltonian.

4

v

1

v

2

v

3

8

v

₇

v

₆

v

₅

Gambar 7. Contoh graf Halmitonian

Contoh sirkuit Hamiltonian pada Gambar 7. adalah

.

2.2 Graf Pohon dan Beberapa Kelas dari Graf Pohon

(30)

[image:30.612.155.495.84.224.2]

Gambar 8. Contoh pohon dan hutan

Beberapa kelas graf pohon yang berkaitan dengan penelitian ini, sebagai berikut

1. Graf Bintang (Star Graph)

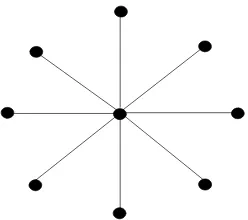
Graf bintangK1,n(star) adalah suatu graf terhubung yang mempunyai satu titik

berderajatnyang disebut pusat dan titik lainnya berderajat satu .

Gambar 9. Graf bintang _,

[image:30.612.259.383.469.579.2]

(31)

15

2. Graf Bintang Ganda (Double Star Graph)

[image:31.612.219.437.226.327.2]

Suatu graf pohon disebut graf bintang ganda jika graf pohon tersebut mempunyai tepat dua titik dan berderajat lebih dari satu. Jika dan berturut-turut berderajat + 1dan + 1, dinotasikan dengan _, (Chartrand dkk.,2002).

Gambar 10. Graf bintang ganda _,

3. Graf Ulat (Caterpillar Graph)

Graf ulat adalah graf pohon yang memiliki sifat apabila dihapus semua daunnya akan menghasilkan lintasan (Gallian.,2012).

[image:31.612.184.464.510.570.2]

(32)

4. Graf Pohon Pisang (Banana Tree)

[image:32.612.201.458.221.322.2]

Graf Pohon pisang _, adalah graf yang diperoleh dari buah ke graf bintang dengan cara menghubungkan sebuah daun dari setiap graf bintang suatu titik baru. Titik baru itu disebut titik root. (Chen dkk.,1997).

Gambar 12. Graf pohon pisang _,

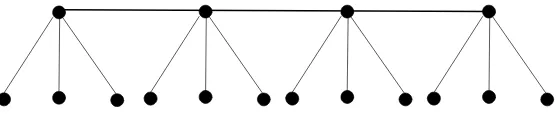
5. Graf Kembang Api

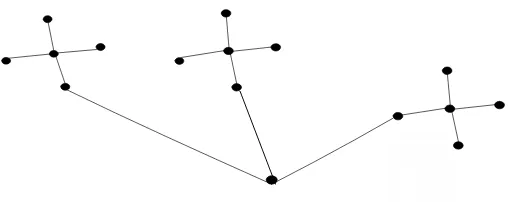
Graf kembang api seragam, _, adalah graf yang diperoleh dari nbuah buah graf bintang dengan cara menghubungkan sebuah daun dari setiap melalui sebuah lintasan (Chen dkk.(1997)).

[image:32.612.175.483.536.624.2]

(33)

17

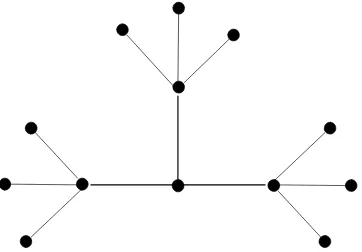
6. Graf Almagamasi Bintang

[image:33.612.233.414.197.323.2]

Graf almagamasi bintang seragam, _, adalah amalgamasi dari k buah graf bintangK1,m.(Asmiati dkk.(2012))

Gambar 14. Graf almagamasi bintang ,

Selanjutnya diberikan beberapa lemma dan teorema yang berkaitan dengan graf pohon sebagai berikut:

Teorema 2.2(Harsfield, N. dan G. Ringel, 1994)Jika adalah pohon dengan titik (vertex ) dan sisi (edge), maka = + 1.

Bukti: Jika adalah pohon dengan satu sisi maka teorema benar untuk . Asumsikan teorema benar untuk semua pohon dengan sisi kurang dari , artinya

(34)

akibatnya sisi terhubung titik terbuang. Sehingga pohon terbentuk dengan ( 1)

dan ( 1) sisi dengan asumsi 1 = ( 1) + 1 diperoleh 1 = atau

= + 1. ■

Teorema 2.2 (Harsfield, N. dan G. Ringel, 1994) Graf adalah pohon jika dan hanya jika ada terdapat tepat satu lintasan diantara kedua titik tersebut.

Bukti:

(1) Akan ditunjukkan graf adalah pohon maka ada terdapat tepat satu lintasan di antara kedua titik. Misalkan pohon , dan titik-titik di maka pohon

dihubungkan lintasan ke . Anggaplah dua lintasan dari ke ,

= dan = . Jika berbeda dengan

, selanjutnya sampai ditemukan suatu titik yang memuat yang juga dalam sehinggmempunyai siklus . Jika = , maka kita lihat pada .

Untuk beberapa , , karena ada dua lintasan sebagai asumsi.

Selanjutnya dari sampai ditemukan suatu titik yang memuat dalam yang juga dalam dan selanjutnya ambil kembali ke , dan kita mendapatkan siklus lagi. Tetapi adalah pohon, sehingga tidak ada siklus. Jadi asumsi bahwa ada dua lintasan salah.

(35)

19

. Jelas bahwa ada dua lintasan dari ke . Ini kontradiksi, karena mempunyai tepat satu lintasan diantara dua titik. Jadi graf tidak memuat

(36)

Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk. (2002). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf.

Pewarnaan titik pada graf adalah : ( ) {1,2,3, , }dengan syarat untuk setiap dua titik yang bertetangga harus memiliki warna yang berbeda. Minimum banyaknya warna yang digunakan untuk pewarnaan titik pada graf disebut bilangan kromatik, yang dinotasikan ( ).

1 1

1

2 2

2

1

v

2

v

3

v

4

v

5

v

6

v

7

[image:36.612.234.418.472.536.2]

v

Gambar 15. Contoh bilangan kromatik dengan ( ) = 2

Berikut ini diberikan definisi bilangan kromatik lokasi graf yang diambil dari (Chartrand, dkk, 2002). Misalkan c suatu pewarnaan titik pada graf G dengan

(37)

✁

adalah himpunan yang terdiri dari kelas –kelas warna dari V(G). Kode warna ( )

dari v adalah k-pasang terurut ( , ), ( , ), , ( , ) dengan ( , ) =

min{ ( , )| } untuk 1 . Jika setiap G mempunyai kode warna yang

berbeda, maka c disebut pewarnaan lokasi G. Banyaknya warna minimum yang digunakan untuk pewarnaan lokasi disebut bilangan kromatik lokasi dari G, dan dinotasikan dengan ( ). Karena setiap pewarnaan lokasi juga merupakan pewarnaan, maka ( ) ( ).

Teorema 3.1 (Chartrand dkk, 2002) Misal adalah suatu pewarnaan lokasi pada graf terhubung . Jika dan adalah dua titik pada graf sedemikian sehingga

( , ) = ( , ) untuk setiap ( ) { , }, maka ( ) ( ). Dalam hal

khusus, jika dan adalah titik-titik yang tidak bertetangga di sedemikian sehingga ( ) ( ), maka ( ) ( ).

Bukti: Misalkan adalah suatu pewarnaan lokasi pada graf terhubung dan misalkan = { , , , }adalah partisi dari titik-titik ke dalam kelas warna . Untuk titik , ( ), andaikan ( ) = ( ) sedemikian sehingga titik dan berada dalam kelas warna yang sama, misal dari . Akibatnya,

( , ) = ( , )= 0. Karena ( , ) = ( , ) untuk setiap ( ) { , }

maka ( , ) = ( , ) untuk setiap , 1 . Akibatnya, ( ) = ( )

(38)

Akibat 3.1(Chartrand dkk, 2002)Jika adalah suatu graf terhubung yang memuat suatu titik yang bertetangga dengan daun di , maka ( ) + 1.

Bukti:Misalkan adalah suatu titik yang bertetangga dengan daun , , , di . Berdasarkan Teorema 3.1, setiap pewarnaan lokasi dari mempunyai pewarnaan yang berbeda untuk setiap , = 1,2, , . Karena bertetangga dengan semua , maka harus mempunyai warna yang berbeda dengan semua daun . Akibatnya

( ) + 1. ■

[image:38.612.225.407.311.391.2]

3 2 2 1 4 1 v 3 v 4 v 7 v 2 v 2 1 5 v 8 v 9 v 6 v 1 3

Gambar 16. Contoh pewarnaan lokasi minimum pada Graf

Teorema 3.2(Chartrand dkk, 2003) Misalkan adalah derajat maksimum di graf maka ( ) + 1.

Beberapa teorema penelitian sebelumnya yang mendukung penelitian ini adalah sebagai berikut.

Teorema 3.3 (Chartrand dkk, 2002) Bilangan kromatik lokasi graf lintasan

(39)

✄ ☎

Bukti: Perhatikan bahwa ( ) = 1 dan ( ) = 2 . Jelaslah bahwa ( ) 3

untuk 3 . Berdasarkan Teorema 3.2. ( ) + 1, dengan derajat titik maksimum. Karena pada , = 2 maka ( ) 2 + 1. Akibatnya ( ) 3.

Jadi, ( ) 3. ■

1 2 3 1 2 1 2 1

1

[image:39.612.169.474.224.262.2]

v v₂ v3 v4 v5 v6 vn1 vn

Gambar 17. Pewarnaan lokasi minimum pada graf lintasan

Teorema 3.4 (Chartrand dkk, 2002) Untuk bilangan bulat dan dengan

1 dan 2, _, = + 1.

Bukti: Berdasarkan Akibat 3.1, diperoleh batas bawah yaitu , + 1.

Selanjutnya, akan ditentukan batas atasnya, yaitu _, + 1. Misalkan

adalah pewarnaan titik menggunakan ( + 1) warna sebagaimana terlihat pada Gambar 18. Perhatikan bahwa kode warna dari setiap titik _, berbeda, akibatnya

(40)

[image:40.612.210.451.87.167.2]

1  b u v 1  a 1 1 a b 2 2 3

Gambar 18. Pewarnaan lokasi minimum pada Graf _,

Teorema 3.5 (Chartrand dkk, 2002) Terdapat pohon berorde 5 yang mempunyai bilangan kromatik jika dan hanya jika {3, 4, , 2, }.

1 1  k u 2

k 2 1 2

2

v v3 v4

1

v v_n__k_₁

1

2

u u1

1



[image:40.612.150.496.335.407.2]

k

Gambar 19. PohonT dari berorde dengan ( ) =

Bukti: Pertama misalkan {3, 4, , 2, }. Untuk = 3, misalkan = , untuk = , misalkan = , . Sehingga diasumsikan bahwa 4 2.

Misalkan didapat dari lintasan : , , , dengan menambahkan

( 1) titik baru , , , dan hubungkan setiap , untuk1 1

dengan . Berikanlah warna pada , warna 1 pada jika genap , warna 2

pada jika 3 dan ganjil, dan warna pada , untuk 1 1 lihat

(41)

✞ ✟

berdasarkan akibat 3.1 ( ) maka ( ) = . ■

Lemma 3.2 (Asmiati dkk, 2011) Misalkan adalah pewarnaan lokasi dari _, menggunakan paling sedikit warna dengan , 2. Pewarnaan adalah pewarnaan lokasi jika dan hanya ( ) = ( ), mengakibatkan

( ) = 1,2,3,…, − 1 dan ( ) = 1,2,3,…, − 1 adalah dua himpunan yang berbeda.

Bukti: Misalkan = ( ) = 1,2,3,…, − 1 dan = { ( ( ) =

1,2,3,…, − 1}. Misalkan adalah pewarnaan lokasi dari _, , ≥ 2, ≥ 2 dan

( ) = ( ), untuk suatu ≠ . Andaikan = . Karena ( , ) = ( , ) untuk

setiap ∈ ( ) = 1,2,3,…, − 1 ∪ = ( ) = 1,2,3,…, − 1 ,

maka kode warna dari dan sama. Jadi bukan pewarnaan lokasi, suatu kontradiksi. Akibatnya ≠ . Misalkan Π suatu partisi dari ( ) dari terhadap kelas-kelas warna|Π| ≥ . Pandang ( ) = ( ), ≠ . Karena ≠ , maka terdapat warna dan sedemikian sehingga ( ∈ , ∉ ) atau ( ∈ , ∉ ).

Selanjutnya akan ditunjukkan bahwa kode warna untuk setiap ∈ , .

 Jelas bahwa ( ) ≠ ( ), karena kedua kode warna tersebut berbeda pada ordinat ke- atau ke- .

(42)

Kasus 1: Jika ( ) = ( ), maka berdasarkan premis dari teorema ini, ≠ . Jadi

( ) ≠ ( ).

Kasus 2: Misalkan ( ) = dan ( ) = , dengan ≠ . Maka ( ) ≠ ( ) karena kedua kode warna tersebut berbeda sekurang-kurangnya

pada ordinat yang ke- dan .

 Jika ( ) = ( ), maka kode warna dari ( ) memuat sedikitnya dua komponen yang bernilai 1. Akibatnya ( ) = ( ).

Berdasarkan semua kasus di atas, dapat dilihat bahwa kode warna untuk semua titik di _, berbeda, maka merupakan pewarnaaan lokasi. ■

Lemma 3.3 (Asmiati dkk, 2011) Misalkan adalah pewarnaan lokasi dari ,

menggunakan + warna dan ( ) = ( + − 1) + − 1

− 1 , ≥ 0, maka ≤ ( ).

Bukti:Misal adalah pewarnaan lokasi dari , menggunakan + warna, Untuk

suatu titik tetap , misal ( ) warna dari titik tengah . maka banyak kombinasi warna yang digunakan oleh = 1,2,3,…, − 1 adalah + − 1

− 1 .

Karena satu warna digunakan untuk titik pusat amalgamasi , maka terdapat

( + − 1) untuk , untuk setiap = 1,2,3,…, . Dari Lemma 3.2, diperoleh nilai maksimum dari adalah ( ) = ( + − 1) + − 1

− 1 , ≥ 0,

(43)

27

Teorema 3.6 (Asmiati dkk, 2011) Jika ( ) = ( + − 1) + − 1

− 1 untuk ≥ 0, ≥ 2, dan ≥ 3, maka

, =

; 2 ≤ ≤ (0), ≥ 3 + ; ( − 1) < < ( ), ≥ 1

Bukti: Pertama-tama akan dicari batas bawah dan batas atas dari _, untuk

2 ≤ ≤ (0) = − 1.

(1) Batas bawah dari _, .

Berdasarkan Akibat 3.1, setiap titik bertetangga dengan ( − 1)daun, untuk

titik = 1,2,3,…, . Dengan demikian _, ≥ .

(2) Batas atas dari _,

Misalkan adalah pewarnaan dari _, menggunakan warna. Tanpa

mengurangi keumuman , misal ( ) = 1dan ( ) = + 1untuk = 1,2,3,…, . Karena daun-daun harus mempunyai kode warna yang berbeda, maka daun-daun

= 1,2,…, − 1 diberi warna oleh {1,2,…, }\ { + 1} untuk sebarang .

Maka, berdasarkan Lemma 3.1, adalah pewarnaan lokasi. Dengan demikian

, ≤ .

Selanjutnya, akan dicari batas bawah dan batas atas untuk

(44)

(1) Batas bawah dari ,

Karena > ( − 1), maka berdasarkan Lemma 2.3, _, ≥ + . Pada

sisi lain, jika > ( ) maka berdasarkan Lemma 3.3, ( _, ) ≥ + + 1.

Dengan demikian, _, ≥ + jika ( − 1) < < ( ).

(2) Batas atas dari ,

Karena ( ) = 1 dan warna dari titik tengah adalah 2,3,…, + . Karena

( − 1) < < ( ), ≥ 1 maka banyak titik tengah yang mempunyai warna

yang sama tidak lebih dari + + 1

− 1 , untuk sebarang . Akibatnya

jika ( ) = 1,2,3,…, − 1 ≠ ( ) = 1,2,3,…, − 1 . Berdasarkan

Lemma 3.3, adalah pewarnaan lokasi. Jadi, , ≤ + untuk

( − 1) < < ( ). ■

[image:44.612.213.423.457.604.2]

3 1 2 4 5 1 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 6

(45)

29

3

2

4

1

1 2

2

2 1

1 1

1

2

3

3 3

4

2

3 3

4

4 4

[image:45.612.213.422.88.244.2]

4 3

(46)

Pada bagian ini akan dikaji dan didiskusikan hasil-hasil penelitian untuk bilangan

kromatik lokasi pada graf amalgamasi bintang tertentu ✡ untuk

☛ ☛ . Berikut

ini diberikan konstruksi graf ✡ .

l

12

l

22

l

23

l

k

2 1



l

112

l

122

l

132

l

m

2

1

l

221

l

222

l

223

l

m

2

l

231

l

232

l

332

l

k 2 1 ) 1 (

l

m 2 3

l

k 2 2 ) 1 (

l

k 2 3 ) 1 (

l

k m

2

) 1 (

l

1n

l

n2

l

n3

l

nk1

l

11n

l

12n

l

13n

l

1nm

l

n21

l

n22

l

n23

l

n2m

l

n31

l

n32

l

n33

l

n(k1)1

l

n3m

l

n(k1)2

l

n(k1)m

l

11

l12

l

13

l

k

1 1



l

111

l

112

l

113

l

m

1

l

121

l

122

l

123

l

m

1 2

l

131

l

132

l

133

l

k 1 1 ) 1 (

l

m 1 3

l

k 1 2 ) 1 (

l

k 1 3 ) 1 (

l

k m

1 ) 1 (

x

1

x

2

x

n [image:46.612.131.566.383.632.2]

y

₁

y

₂

y

_n

(47)

35

Misalkan graf amalgamasi bintang tertentu adalah graf yang diperoleh dari graf

☞ dengan cara menghubungkan sebuah daun dari setiap ☞ melalui sebuah

lintasan. Graf amalgamasi bintang tertentu dinotasikan ☞ . Misalkan ☞ ✌

✍ ✍ ✍ = 1,2,3,…, ; = 1,2,3,…, − 1, = 1,2,3,…, dan

, = { | = 1,2,3,…, − 1} ∪ , , | = 1,2,3,…, ; =

1,2,3,…, − 1, = 1,2,3,…, .

5.1 Bilangan Kromatik Lokasi , untuk ≤ dengan , , Bilangan Asli

Pada bagian ini akan didiskusikan bilangan kromatik lokasi , untuk ≤

dengan , , bilangan asli.

Teorema 5.1

Misalkan _, adalah graf amalgamasi bintang tertentu untuk ≤ , ≥ 2 dan

≥ 2

, =

+ 1 ; 1 ≤ ≤

− 1

+ 2 ;

Bukti: Pertama-tama akan dicari batas bawah dan batas atas dari , untuk

(48)

Berdasarkan Akibat 3.1, setiap titik untuk = 1,2,3,…, dan

= 1,2,3,…, − 1 bertetangga dengan daun. Dengan demikian

, ≥ + 1. (5.1.1)

Misalkan adalah suatu pewarnaan lokasi dari , menggunakan( + 1)

warna.

Misal beri warna:

 ( ) = 1, untuk = 1,2,3,…,

 ( ) = 2, untuk ganjil dan ( ) = 3, untuk genap, = 1,2,3,…,

 = {2,3,…, + 1}, untuk = 1,2,3,…, dan = 1,2,3,…, − 1

 = {1,2,3,…, + 1}✧ , untuk = 1,2,3,…, dan = 1,2,3,…,

− 1dan = 1,2,3,…,

Akibatnya pewarnaan akan membangun suatu partisi Π = { , , ,…, }

pada _, , dengan adalah himpunan dari semua titik yang bewarna

untuk = 1,2,3,…, + 1. Selanjutnya akan ditunjukkan bahwa kode warna

untuk setiap , berbeda. Misalkan , ∈ , dan ( ) = ( )

maka pandang kasus-kasus berikut ini:

 Jika = , = untuk suatu , dan ≠ , maka ( ) ≠ ( ) karena

(49)

37

 Jika = , = untuk suatu , , , maka ( ) ≠ ( ), karena pada

( ) , titik yang diberi warna ( + 1) terdapat sekurang-kurangnya dua

komponen bernilai satu, sedangkan pada ( ) , titik yang diberi warna

( + 1) memuat tepat tepat satu komponen yang bernilai 1.

 Jika = , = untuk suatu , , , dan ≠ , maka ( ) ≠ ( ),

karena pada ( ) , titik yang diberi warna ( + 1) terdapat

sekurang-kurangnya dua komponen bernilai satu, sedangkan pada ( ) , titik yang diberi warna( + 1) memuat tepat tepat satu komponen yang bernilai 1.

 Jika = , = , untuk suatu , maka ( ) ≠ ( ). karena pada

( ) , titik yang diberi warna ( + 1) terdapat tepat dua komponen yang

bernilai 1, sedangkan pada ( ), titik yang diberi warna ( + 1) terdapat sekurang-kurangnya dua komponen bernilai satu.

 Jika = , = , untuk suatu , , dan ≠ maka ( ) ≠ ( )

karena pada ( ) , titik yang diberi warna ( + 1) terdapat tepat dua

komponen yang bernilai 1, sedangkan pada ( ), titik yang diberi warna

( + 1) terdapat sekurang-kurangnya dua komponen bernilai satu.

 Jika = , = untuk suatu , , maka ( ) ≠ ( ). karena pada

( ), titik yang diberi warna ( + 1) terdapat tepat dua komponen yang

bernilai 1, sedangkan pada ( ), titik yang diberi warna ( + 1) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = untuk suatu , , , dan ≠ maka ( ) ≠ ( )

(50)

komponen yang bernilai 1, sedangkan pada ( ), titik yang diberi warna

( + 1) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = maka untuk suatu , , maka ( ) ≠ ( ) karena pada

( ), titik yang diberi warna ( + 1) terdapat sekurang-kurangnya dua

komponen bernilai satu, sedangkan pada ( ), titik yang diberi warna

( + 1) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = , maka untuk suatu , , , , dan ≠ , ≠ maka

( ) ≠ ( ) karena pada ( ), titik yang diberi warna ( + 1) terdapat

sekurang-kurangnya dua komponen bernilai satu, sedangkan pada ( ), titik yang diberi warna( + 1) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = , maka untuk suatu , , , , ≠ maka ( ) ≠ ( )

karena titik ≠ sehingga ( , ) ≠ ( , ).

Dengan demikian dapat disimpulkan bahwa kode warna dari semua ,

untuk ≤ adalah berbeda. Jadi _, ≤ + 1. (5.1.2)

Berdasarkan (5.1.1) dan (5.1.2) dapat disimpulkan bahwa kode warna dari semua

, untuk ≤ , ≥ 2 dan ≥ 2, untuk1 ≤ ≤ adalah berbeda.

(51)

39

Sebagai ilustrasi, diberikan pewarnaan lokasi _, untuk 1 ≤ ≤ 2 yang dapat

dilihat pada gambar berikut:

[image:51.612.164.481.164.302.2]

1 3 2 1 2 2 3 1 4 4 5 5 1 5 3 1 4 2 2 1 3 3 4 5

Gambar 23. Pewarnaan lokasi minimum pada graf _, untuk 1 ≤ ≤ 2

Selanjutnya akan dicari batas bawah dan batas atas untuk > .

Berdasarkan akibat 3.1 diperoleh _, ≥ + 1 untuk> , tetapi akan

ditunjukkan bahwa ( + 1) tidaklah cukup untuk mewarnai. Untuk suatu kontradiksi, andaikan terdapat pewarnaan ( + 1) lokasi pada _, untuk

≤ , ≥ 2 dan ≥ 2dan > . Karena > , maka terdapat suatu

, , , dengan ≠ sedemikian hingga , = , =

{1,2,3,…, + 1}. Sangat jelas = akibatnya = untuk

suatu = 1,2,3,…, − 1, = 1,2,3,…, adalah sama, suatu kontradiksi. Jadi

(52)

Misalkan adalah pewarnaan dari _, menggunakan( + 2) warna.

 ( ) = 1, untuk = 1,2,3,…,

 = {2,3,…, + 2}, untuk = 1,2,3,…, dan = 1,2,3,…, − 1

 = {1,2,3,…, + 2}✎ , untuk = 1,2,3,…, dan = 1,2,3,…,

− 1dan = 1,2,3,…, .

 Jika = {1,2,3,…, + 2}, didefinisikan

= 1,2,3,…, = ✎{1,2} , jika = 1, = 1

✎{ + 2} , lainnya.

Pewarnaan akan membangun suatu partisi Π = _, . Akan ditunjukkan

bahwa kode warna dari semua titik di _, berbeda.

( ) =

0 ; komponen ke − 1

2 ; komponen − ( + 1)

2 ; lainnya

Untuk ≥ 2ganjil

( ) =

1 ; komponen ke − 2 dan ke −

2 ; komponen ke – + 1

(53)

41

Untuk ≥ 2genap

( ) =

1 ; komponen ke − ( + 1)

+ 3 ; lainnya

( ) =

1 ; komponen ke −

3 ; lainnya

Untuk ≥ 2ganjil

( ) =

+ 2 ; lainnya

Untuk ≥ 2genap

( ) =

+ 2 ; lainnya

( ) =

(54)

( ) =

0 ; komponen ke − ( − 1)

3 ; lainnya

Untuk = 2,3,…, − 1

=

3 ; lainnya

Untuk ≥ 2 = 1,2,3,…, − 1

=

+ 4 ; lainnya

( ) =

0 ; lainnya

Untuk = 2,3,…,

( ) =

2 ; lainnya

( ) =

(55)

43

( ) =

1 ; komponen ke − ( − 1)

4 ; lainnya

Untuk ≥ 2 , = 1,2,3,…, − 1, = 1,2,3,…,

=

0 ; komponen ke −

+ 5 ; lainnya

Karena kode warna dari semua titik berbeda, akibatnya adalah

Pewarnaan lokasi pada , . Jadi , ≤ + 2 untuk

> . (5.1.4)

Berdasarkan persamaan (5.1.3) dan (5.1.4), dapat disimpulkan bahwa kode warna

dari semua _, untuk ≤ , ≥ 2 dan ≥ 2, untuk > adalah

berbeda. Jadi _, = + 2. ■

Sebagai ilustrasi, diberikan pewarnaan lokasi _, untuk > 2 yang dapat

(56)

[image:56.612.120.562.90.209.2]

1 3 2 2 2 3 1 4 4 5 5 1 5 3 1 4 2 2 1 3 3 4 5 1 1 3 2 1 2 2 3 1 4 4 5 5 1 5 3 1 4 2 2 1 3 3 4 5 1 1 5 1 4 2 2 1 3 3 4 5 6 3

Gambar 24. Pewarnaan lokasi minimum pada graf _, untuk > 2

5.2 Bilangan Kromatik Lokasi , untuk > dengan , , Bilangan Asli

Pada bagian ini akan didiskusikan bilangan kromatik lokasi _, untuk >

dengan , , bilangan asli.

Lemma 5.1

Misalkan adalah pewarnaan lokasi dari _, menggunakan paling sedikit

( − ) warna dengan > , ≥ 2, ≥ 2 , ≥ 0, = − − 2. Pewarnaan adalah pewarnaan lokasi jika dan hanya = ( ), ≠ dan ≠

mengakibatkan ( ) = 1,2,3,…, dan { ( )| = 1,2,3,…, } adalah dua himpunan yang berbeda.

Bukti: Misalkan = ( ) = 1,2,3,…, dan = { ( )| = 1,2,3,…, }.

(57)

45

= ( ) , untuk suatu ≠ , dan ≠ . Andaikan = . Karena

( , ) = ( , ) untuk setiap ∈ ✏ ( ) = 1,2,3,…, ∪

{ ( )| = 1,2,3,…, } , maka kode warna dari dan sama. Jadi bukan

pewarnaan lokasi, suatu kontradiksi . Akibatnya ≠ .

Misalkan Π suatu partisi dari ( ) dari terhadap kelas-kelas warna |Π| ≥ . Pandang = ( ) , ≠ , dan ≠ . Karena ≠ , maka terdapat warna dan sedemikian sehingga ( ∈ , ∉ ) atau ( ∈ , ∉ ). Selanjutnya akan

ditunjukkan bahwa kode warna untuk setiap ∈ _, berbeda.

 Jelas bahwa ≠ ( ), karena kedua kode warna tersebut berbeda pada

ordinat ke- atau ke- .

 Jika ≠ ( ), untuk setiap ≠ , dibagi menjadi dua kasus.

Kasus 1: Jika = ( ) , maka berdasarkan premis dari teorema ini, ≠ . Jadi

≠ ( ).

Kasus 2: Misalkan = dan ( ) = , dengan ≠ . Maka ≠

( ) karena kedua kode warna tersebut berbeda sekurang-kurangnya

pada ordinat yang ke- dan .

 Jika ( ) = ( ), maka kode warna dari ( ) memuat sedikitnya 1 komponen

yang bernilai 1. Akibatnya ( ) = ( ).

 Jika ( ) = ( ), maka kode warna dari ( )memuat sedikitnya 2 komponen

(58)

Berdasarkan semua kasus di atas, dapat dilihat bahwa kode warna untuk semua titik di _, berbeda, maka merupakan pewarnaaan lokasi. ■

Lemma 5.2

Misalkan ≥ 1, ≥ 0 , = − − 2 jika adalah pewarnaan − lokasi

dari _, dan ( ) = ( ) , maka ≥ ( ).

Bukti: Misalkan adalah pewarnaan( − ) lokasi dari , . Untuk suatu ,

misalkan ( ) adalah warna dari titik antara , maka banyaknya kombinasi warna

dari = 1,2,3,…, adalah − − 1 . Karena satu warna sudah digunakan

untuk mewarnai titik pusat , maka terdapat ( − − 1)warna untuk mewarnai

untuk setiap = 1,2,…, dan = 1,2,3,…, − 1. Dari Lemma 4.2, diperoleh nilai

maksimum untuk adalah ( ) = ( ), ≥ 0. ■

Teorema 5.2

Misalkan , adalah graf amalgamasi bintang tertentu untuk≥ 0, > ,

≥ 3, ≥ 2, = − − 2

, =

− ; 1 ≤ ≤ ( ) ,

(59)

47

Bukti: Pertama-tama akan dicari batas bawah dan batas atas dari , untuk

1 ≤ ≤ ( ) = ( ) .

Berdasarkan Akibat 3.1, setiap titik untuk = 1,2,3,…, dan

= 1,2,3,…, − 1bertetangga dengan = − − 1 daun. Dengan demikian

, ≥ − . (5.1.5)

Misalkan adalah suatu pewarnaan lokasi dari _, menggunakan

( − ) warna. Misal beri warna:

 ( ) = 1, untuk = 1,2,3,…, .

 ( ) = 2, untuk ganjil dan ( ) = 3, untuk genap, = 1,2,3,…, .

 = {2,3,…, − }, untuk = 1,2,3,…, dan = 1,2,3,…, − 1.

 = {1,2,3,…, − }✑ , untuk = 1,2,3,…, dan

= 1,2,3,…, − 1dan = 1,2,3,…, .

Akibatnya pewarnaan akan membangun suatu partisi Π = { , , ,…, }

pada _, , dengan adalah himpunan dari semua titik yang bewarna

untuk = 1,2,3,…, − . Selanjutnya akan ditunjukkan bahwa kode warna untuk

setiap , berbeda. Misalkan , ∈ , dan ( ) = ( ) maka

(60)

 Jika = , = untuk suatu , dan ≠ , maka ( ) ≠ ( ) karena

( , ) ≠ ( , ).

 Jika = , = untuk suatu , , , maka ( ) ≠ ( ), karena pada

( ), titik yang diberi warna ( − ) terdapat sekurang-kurangnya 1

komponen bernilai satu, sedangkan pada ( ) , titik yang diberi warna

( − )memuat tepat tepat satu komponen yang bernilai 1.

 Jika = , = untuk suatu , , , dan ≠ , maka ( ) ≠ ( ),

karena pada ( ) , titik yang diberi warna ( − ) terdapat sekurang-kurangnya 1 komponen bernilai satu, sedangkan pada ( ), titik yang diberi warna ( − ) memuat tepat satu komponen yang bernilai 1.

 Jika = , = , untuk suatu , maka ( ) ≠ ( ), karena pada

( ) , titik yang diberi warna ( − ) terdapat tepat dua komponen yang

bernilai 1, sedangkan pada ( ), titik yang diberi warna ( − ) terdapat sekurang-kurangnya dua komponen bernilai satu.

 Jika = , = , untuk suatu , , dan ≠ maka ( ) ≠ ( )

karena pada ( ) , titik yang diberi warna ( − ) terdapat tepat dua komponen yang bernilai 1, sedangkan pada ( ), titik yang diberi warna

− terdapat sekurang-kurangnya dua komponen bernilai satu.

 Jika = , = untuk suatu , , maka ( ) ≠ ( ). karena pada

( ), titik yang diberi warna ( − ) terdapat tepat dua komponen yang

(61)

49

 Jika = , = untuk suatu , , , dan ≠ maka ( ) ≠ ( )

karena pada ( ) , titik yang diberi warna ( − ) terdapat tepat dua komponen yang bernilai 1, sedangkan pada ( ), titik yang diberi warna

( − ) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = maka untuk suatu , , maka ( ) ≠ ( ) karena

pada ( ), titik yang diberi warna ( − ) terdapat sekurang-kurangnya

dua komponen bernilai satu, sedangkan pada ( ), titik yang diberi warna

( − ) terdapat tepat satu komponen yang bernilai satu.

 Jika = , = , maka untuk suatu , , , , dan ≠ , ≠ maka

( ) ≠ ( ) karena pada ( ), titik yang diberi warna ( − ) terdapat

sekurang-kurangnya dua komponen bernilai satu, sedangkan pada ( ), titik yang diberi warna( − ) terdapat tepat satu komponen yang bernilai satu.

Karena kode warna dari semua titik berbeda, akibatnya adalah pewarnaan

(62)

Berdasarkan (5.1.5) dan (5.1.6) dapat disimpulkan bawa kode warna dari semua

, untuk > , ≥ 2 dan ≥ 2, ≤ ( ) adalah berbeda. Jadi

, = − untuk1 ≤ ≤ ( ). ■

Sebagai ilustrasi, diberikan pewarnaan lokasi _, untuk 1 ≤ ≤ 4 yang dapat

[image:62.612.163.513.284.445.2]

2 1 2 3 2 4 4 1 3 5 5 2 2 3 4 1 5 1 3 4 5 2 1 2 3 2 4 4 1 3 5 5 1 1 3 4 5 2 1 2 3 4 4 1 3 5 5 2 2 1 1 3 4 5 2 1 2 3 2 4 4 1 3 5 5 1 1 3 4 5 3 3

Gambar 25. Pewarnaan lokasi minimum pada graf _,

untuk 1 ≤ ≤ 4dan = 0

Selanjutnya akan dicari batas bawah dan batas atas untuk > ( ).

(1) Batas bawah dari _,

Berdasarkan akibat 3.1 diperoleh _, ≥ − untuk > ( ) , tetapi akan

ditunjukkan bahwa ( − ) tidaklah cukup untuk mewarnai. Untuk suatu

kontradiksi, andaikan terdapat pewarnaan ( − ) lokasi pada _, untuk

(63)

51

, , , dengan ≠ sedemikian hingga , = , =

{1,2,3,…, − }. Sangat jelas = akibatnya = untuk

suatu = 1,2,3,…, − 1, = 1,2,3,…, adalah sama, suatu kontradiksi. Jadi

, ≥ − + 1untuk > ( ). (5.1.7)

Misalkan adalah pewarnaan dari _, menggunakan( − + 1) warna.

 ( ) = 1, untuk = 1,2,3,…,

 = {2,3,…, ( − + 1)}, untuk = 1,2,3,…, dan = 1,2,3,…, − 1

 = {1,2,3,…,( − + 1)}✒ , untuk = 1,2,3,…, dan

= 1,2,3,…, − 1dan = 1,2,3,…,

 Jika = {1,2,3,…, − + 1}, didefinisikan

= 1,2,3,…, = ✒{1,2} , jika = 1, = 1

✒{ − + 1} , lainnya.

Dengan demikian banyaknya titik antara yang diberi warna tidak lebih dari

− − 1

, untuk sebarang . Hal ini dapat dilakukan karena > ( ). Akibatnya

= ( ), ≠ , dan ≠ , maka dapat disusun ( ) = 1,2,3,…, ≠

{ ( )| = 1,2,3,…, }. Berdasarkan Lemma 5.2, adalah pewarnaan lokasi. Jadi

(64)

Berdasarkan persamaan (5.1.7) dan (5.1.8), dapat disimpulkan bahwa kode warna

dari semua _, untuk > , ≥ 3 dan ≥ 2, untuk > ( )adalah

berbeda. Jadi , = − + 1. ■

Sebagai ilustrasi, diberikan pewarnaan lokasi _, untuk > 4 yang dapat

[image:64.612.120.554.281.436.2]

2 1 2 3 2 4 4 1 3 5 5 2 2 3 4 6 5 1 3 4 5 2 1 2 3 2 4 4 1 3 5 5 1 1 3 4 5 2 1 2 3 4 4 1 3 5 5 2 2 1 1 3 4 5 2 1 2 3 2 4 4 1 3 5 5 1 1 3 4 5 3 3 5 2 1 2 3 2 4 4 1 3 5 5 1 1 3 4 5 3

Gambar 26. Pewarnaan lokasi minimum pada graf ,

(65)

VI. KESIMPULAN

6.1 Kesimpulan

Penelitian ini mendiskusikan tentang penentuan bilangan kromatik lokasi graf

amalgamasi bintang _, , untuk , , bilangan asli. Graf _, adalah graf yang

diperoleh dari buah bintang _, dengan cara menghubungkan sebuah daun dari

setiap _, melalui sebuah lintasan. Berdasarkan hasil observasi diperoleh bahwa

bilangan kromatik lokasi graf amalgamasi bintang _, untuk ✓ , ✔ ✕ dan

✔ ✕adalah

, ✖

+✗ ;✗

✗

✘✕ ;

sedangkan graf amalgamasi bintang , untuk ✙, > ,

3,dan ✕

, = ;✗ ( ) ,

✚ +✗ ; .

Pada penelitian ini, terlihat bahwa perluasan dari graf amalgamasi bintang _, yaitu

(66)

6.2 Saran

Penelitian ini memberikan masalah terbuka untuk penelitian selanjutnya, yaitu menentukan bilangan kromatik lokasi graf _, dengan mensubdivisi titik di sisi-sisi

(67)

DAFTAR PUSTAKA

Asmiati, The Locating-Chromatic Number of Non-Homogeneous Almagamation of Stars,Far East Journal of Mathematical Science (FJMS),93(1), 89-96, 2014.

Asmiati, Baskoro, E.T, Characterizing of Graphs Containing Cycle with Locating-Chromatic Number Three,AIP Conf.Proc.,1450, 351-357, 2012.

Asmiati, Assiyatun, H, Baskoro, E.T, Suprijanto, D, Simanjuntak, R, Uttunggadewa, S, Locating-Chromatic Number of Firecracker Graph,Far East Journal of Mathematical Sciences,63(1),11-23, 2012.

Asmiati, Assiatun, H, Baskoro, E.T, Locating-Chromatic Number of Almagamation of Stars,ITB J.Sci.,43A, 1-8, 2011.

Chartrand, G, Erwin, D, Henning, M.A, Slater, P.J, dan Zhang, P.2002. The locating-Chromatic Number of a Graph,Bull.inst. combin. Apll., 36,89-101.

Chartrand, G, Erwin, D, Henning, M.A, Slater, P.J, dan Zhang, P.2003. Graf of Order nwith Locating-Chromatic Numbern-1,Discrate Math.,269,65-79. Chartrand, G.Zhang, P,Chromatic Graph Teory.2009.CRC Press.

Chen,W., Lü, H., and Yeh, Y., (1997): Operation of Interlaced Tree and Graceful Tree,Shoutheast Asian Bull. Math.,21, 337-348.

Deo, Narsingh. 1989.Grap Theory with Applications to Engineering and Competer Science. Prentice Hall of India Private Lomited, New Delhi.

(68)