Teorema Integral Cauchy

TEOREMA INTEGRAL CAUCHY

Drs. GIM TARIGAN

Fakultas Matematika dan Ilmu Pengetahuan Alam Jurusan Matematika

Universitas Sumatera Utara

PENDAHULUAN

Dalam tulisan ini dapat kita lihat bahwa teorema Green dapat membuktikan perbedaan pembuktian teorema integral Cauchy yang menggunakan teorema Green dan menggunakan beberapa teorema riil variabel seperti teorema Weiestrass-Bolzano, teorema Nested, teorema Heine-Borel dan lain-lain. Oleh karena itu tujuan dalam tulisan ini menunjukkan suatu studi pembuktian teorema integral Cauchy dengan tujuan memperlihatkan persamaan dan perbedaan pengidentifikasian masalah.

Persamaannya: Didalam pembuktian sama-sama menggunakan integral garis.

Perbedaannya: Didalam pembuktian dengan menggunakan teorema Green lebih menekankan integral garis, sedang didalam pembuktian dengan menggunakan beberapa teorema riil variabel, lebih menekankan pengertian-pengertian seperti teorema Weiestrass-Bolzano, teorema Nested, teorema Heine-Borel.

Adapun kegunaan pembahasan skripsi ini adalah untuk dapat lebih mudah mempelajari rumus integral Cauchy dan rumus umum integral Cauchy dimana hal ini, sebagai alat/penunjang dalam mempelajari teorema residu.

METODA

2.1. Beberapa teorema riil variabel

Dalam bagian ini akan dibicarakan beberapa teorema yakni teorema Weiestrass-Bolzano, teorema kumpulan Nested, teorema Heine-Borel yang menyangkut pengertian-pengertian titik limit, titik sekutu, kumpulan tertutup dan terbatas. Selanjutnya dibicarakan mengenai kontinu seragam (uniform Continue).

Teorema 2.1.1.:

Andaikan S suatu kumpulan dalam bidang sedemikian sehingga S kumpulan tak berhingga dan terbatas. Maka S mempunyai paling sedikit satu titik limit.

Bukti : Teorema ini akan dibuktikan untuk S = R2_{. Dengan [a,b; c,d] dimaksud}

kumpulan Q dari semua titik z = (x,y), dimana a ≤ x ≤ b, c ≤ y ≤ d.

Karena S terbatas maka terdapatlah bilangan M sehingga z< M untuk semua z ∈ S.

Ambil a = c = -M; b = d = M, Qo = [a,b; c,d]

Jadi S ⊂ Qo.

Pandang empat himpunan.

[a, ½ (a+b); c, ½ (c+d)] , [a, ½(a+b); ½(c+d), d] [½ (a+b), b; c, ½(c+d)] , [½(a+b), b; ½(c+d), d] yang unionnya adalah Qo.

Salah satu dari keempat himpunan ini dinyatakan dengan Q1 = [a1, b1 ;

Q1 dibagi sampai n diperoleh suatu barisan {Qn} n = 1,2,3, …

sehingga Qn = [an, bn ; cn, dn]

an ≤ an+1 < b n+1≤ bn

cn ≤ c n+1 < dn+1 ≤ dn

2

c

d

a

b

n n n n n

a

b

−

=

−

=

−

Qn memuat tak berhingga bagian dari S, mempunyai batas atas terkecil

dan batas bawah terbesar sehingga, A = sup an , B = inf bn

C = sup cn , D = inf dn

Karena untuk semua n dan m berlaku :

an ≤ an+m < bn+m ≤ bn, dan A ≤ bm untuk semua m maka A ≤ B.

A

B

a

b

2

n

≤

−

−

Jika B > A akan berlaku;

,...

2

,

1

n

,

2

a

b

a

b

A

B

bahwa

jelas

n n n

=

−

=

−

≤

−

untuk semua n yang tidak mungkin. Jadi A = B.

Dengan cara yang sama dapat dibuktikan bahwa C = D.

Akan diperlihatkan bahwa titik z = (A,C) adalah titik limit dari S.

Misalkan N suatu lingkungan dari z dengan jari-jari r, z ∈ Qn untuk semua

n.

,

r

a

b

2 1 n

2

p

−

Jika n dipilih sedemikian sehingga

Maka Qn ⊂ N(z,r).

Karena Qn memuat tak berhingga banyaknya titik-titik dari S, demikian

juga N(z,r) , maka terbukti bahwa z titik limit dari S.

Teorema 2.1.2. (kumpulan Nested).

Misalkan S1, S2, …, Sn sekumpulan barisan pada suatu bidang yang memenuhi

sifat-sifat sebagai berikut :

1. ∀Sn, tertutup, Sn≠ φ

2. Sn+1 ⊆ Sn , ∀n

3. limn→∞ diam Sn = 0

sekutu

titik

satu

hanya

dan

satu

atas

terdiri

S

Maka

1 n

n

I

∞

=

Bukti :

Misalkan p1, p2 ∈ Sn

Jika p1≠ p2 maka p1-p2  = d > 0.

d

p

p

S

diam

S

S

s

0

S

diam

lim

2 1 no no

n 1 n

n

n

⇒

∃

∋

−

=









⊆

=

+ ∞

→

p

Akibat p1, p2∉ Sno→ Kontradiksi dengan Sn ⊆ Sno

Jadi harus p1 = p2 atau Sn memuat satu dan hanya satu titik persekutuan ∀n.

Jadi :

sekutu

titik

satu

hanya

dan

satu

atas

terdiri

S

1 n

n

I

∞

=

Cara lain :

Sn :kumpulan tak berhingga

Sn : kumpulan terbatas

∞

n

.

sekutu

titik

satu

hanya

dan

satu

atas

terdiri

S

Claim

1

n

I

=

Dengan teorema 2.1.1 maka Sn mempunyai sekurang-kurangnya satu titik

limit.

Ambil zn∈ Sn ; ditinjau 2 kasus :

Kasus 1. Zn terdiri dari titik-titik yang sama.

Jika zn terdiri dari titik-titik yang sama, maka jelas terdiri atas satu

dan hanya satu titik sekutu.

I

∞

=1 n

n

S

Kasus 2. Jika zn terdiri dari titik-titik yang berlainan maka zn terbatas, dan

tak berhingga, menurut teorema 2.1 maka zn mempunyai

sekurang-kurangnya satu titik limit. Misalkan titik limitnya p.

P

∈

S

n

Z

n+1

, z

n+2

, …

∈

S

n

Dimana

S

= kumpulan titik-titik limit

' n n

n n

n 1 n

S

S

S

tertutup

S

n

;

S

S

∪

=

⇒







∀

⊆

+

' n

p

Akibat terdiri atas satu dan hanya satu titik persekutuan.

.

n

,

S

p

S

'_n

⇒

∈

_n

∀

∈

_∞

I

=1 n

Teorema 2.1.3. (Heine-Borel).

Andaikan S kumpulan tertutup, terbatas pada suatu bidang dan Φ koleksi disk yang menutup S.

Maka ada suatu bagian koleksi yang terbatas banyaknya menutup S.

Bukti : Dibuktikan secara kontradiksi. Dianggap bahwa tak terhingga banyaknya disk yang diperlukan menutup S.

Pandang R seperti pada gambar.

R

R

1

RRRR

Gbr.:1 (Disk yang menutupi bidang s) S terbatas, S ⊂ R.

R dibagi menjadi 4 (empat) empat persegi panjang maka S ⊂ R telah terbagi menjadi empat kumpulan bagian yang masing-masing menjadi bagian dari empat persegi panjang tersebut, dan masing-masing bagian S ditutupi tak terhingga banyaknya disk.

Pandang R1 memuat bagian S.

R1 dibagi seperti pada R diperoleh R2 ⊂ R1 yang memuat kumpulan bagian

S juga memerlukan tak terhingga banyaknya disk menutup S. Proses dilanjutkan sampai tak terhingga sehingga diperoleh : R1, R2, R3, …,Rn,…

atau R1 ⊃ R2 ⊃ R3 ⊃ … ⊃ Rn …, ………..(1)

yang memuat kumpulan bagian S, dimana masing-masing bagian S ditutupi tak berhingga banyaknya disk.

Barisan ini memenuhi sifat :

1. Setiap Rk tertutup (paling sedikit memuat satu titik)

2. Rk⊂ Rk-1 untuk k = 2,3,…

3. diam Rk→ 0 bila k →∞

Menurut teorema 2.2, p merupakan titik sekutu dari Rk. Karena diam Rk→

0 maka N(p,r) memuat beberapa Rk. Rk memuat tak berhingga banyaknya

titik-titik S, karena itu jelas N(p,r) memuat tak berhingga banyaknya

titik-titik S. Jadi p merupakan titik-titik limit dari S. S tertutup maka p ∈ S.

Kumpulan bagian dari S ⊂ N(p,r) ditutupi beberapa disk. Jadi ada paling

sedikit satu disk D yang memuat p. Ambil diam Rm cukup kecil sedemikian

sehingga Rm berada dalam disk.

Jadi satu disk D menutup bagian S ⊂ Rm

Kontradiksi dengan pernyataan 1. Teorema : 2.1.4.

z - w> λ Bukti :

Z ∈ C ⊂ R (seperti pada gambar)

C

W

Gbr.:2 (lingkungan Nq yang memuat didalam path C)

Karena R kumpulan terbuka (tidak memuat batas R) maka ada lingkungan NZ ⊂ R. Dicari suatu NZ sedemikian sehingga untuk setiap z

pada path C dan ambil lingkungan MZ yang lain dari z dengan jari-jari ½

NZ. Koleksi MZ jelas menutup C.

C kumpulan tertutup dan terbatas maka menurut teorema 2.1.3; MZ

jumlahnya berhingga dan cukup menutup C namakan : M1, M2, … , Mk.

Jari- jari disk dari koleksi MZ adalah k bilangan riil positif dan selanjutnya

dapat dicari jari-jari MZ yang terkecil namakan λ.

Selanjutnya dibuktikan bahwa bilangan λ memenuhi kesimpulan teorema diatas.

Andaikan z suatu titik pada C dan w suatu titik dalam R, z harus berada pada satu dari setiap Mn yang pusatnya q, maka :

| q – z | < λ dan

| q – w | > 2λ akan dibuktikan : | z – w | > λ.

dari | q – w | > 2λ

2λ < | q – w | = | q – z + z + w |

2λ < | q – w | ≤| q – z | + | z - w | 2λ < λ + | z – w |

2λ - λ < | z – w |

Teorema 2.1.5.

Misalkan f(z) kontinu pada setiap titik dari kumpulan B B : kumpulan tertutup dan terbatas.

Maka f kontinu seragam pada B. Bukti :

Untuk membuktikan kontinu seragam dari f(z),pada B diberikan

ε>0 ∃ δ>0 ∋| f(z) – f(p) | < ε bila : | z – p | < δ……….. (1) Ambil q∈B, karena f kontinu pada B maka f kontinu pada q, ini berarti :

∀ε>0 ∃λq>0 ∋| f(q) – f(w) | < ε/2 bila | q – w | < λq .

Dengan mengulangi proses yang sama untuk setiap q∈B,diperoleh koleksi dari Nq (satu untuk setiap q∈B)dengan pusat q dan jari-jari λq.

Untuk setiap Nq, perhatikan suatu disk Mq yang bukan sepusat denagn Nq

dan berjari-jari λq/2, maka menurut teorema 2.3 koleksi Mq menutup B

terbatas banyaknya.

Jari-jari Mq dinyatakan dengan :

2

,

,

2

,

2

,

2

3 2

1

λ

λ

λ

k

λ

K

adalah k bilangan positif, dan dipilih jari-jari Mq terkecil disebut δ.

Dibuktikan bahwa δ memenuhi (1). Untuk titik z dan titik p dalam B maka berlaku | z – p | < δ.

Karena z berada pada salah satu dari k disk (dinamakan Mv dan pusatnya

v) menutup B, diperoleh :

|

z – v

|

λ

v

/2 <

λ

v

dan

|

f(z) – f(v)

|

<

ε

/2

karena

|

z – p

|

<

δ

<

λ

v

/2 maka diperoleh

|

p – v

|

≤

|

z – p

|

+

|

z – v

|

<

λ

v

/2 +

λ

v

/2 =

λ

v

karena

|

f(p) – f(v)

|

<

ε

/2

maka



f(z) – f(p)

≤



f(z) – f(v)



+



F(p) – f(v)

<

2

2

ε

+

ε

jadi



f(z) – f(p)

<

ε

.

2.2. Integral Garis Dari Fungsi Kompleks

Misalkan f(z) fungsi yang kontinu pada setiap titik pada path C yang berhingga. Path C dibagi menjadi n bagian dengan memilih titik-titik zo, z1, z2, ... ,z n-1 sembarang titik pada path C. Selanjutnya pada setiap bagian zk-1 dan zk

Y

a=z

o

X

Gbr.: 3 Path C yang dibagi atas n bagian sembarang Dinyatakan bahwa : ∆z1 = z1 - zo

∆z2 = z2 – z1 ∆z3 = z3 – z2

M

∆

z

n

= z

n

– z

n-1

Definisikan :

S

n

= f(t

1

)

∆

z

1

+ f(t)

∆

z

2

+ ... + f(t

n

)

∆

z

n

Dengan menyebut :

∆

z

k

= z

k

– z

k-1

∀

k=1,2, ... , n diperoleh :

S

n

=

k

n

k

k

z

t

f

∆

∑

=

1

)

(

Untuk n →∞ maka ∆zk → 0, maka :

( )

k

n

k

k n

c

n b

a

t

f

S

dz

z

f

dz

z

f

∆Ζ

=

=

=

∑

∫

∫

= ∞ →

→ ∆Ζ

1 0

lim

lim

)

(

)

(

Dimana : ∆z = max {∆z1, ∆z2, ... , ∆zn} disebut : integral garis dari f(z), fungsi

kompleks.

(

)(

)

∫

∫

∫

∫

∫

+

+

−

=

+

+

=

c c c

c c

udy

vdx

i

vdy

udx

dz

z

f

idy

dz

iv

u

dz

z

f

)

(

)

(

Teorema : 2.2.1.

Misalkan p konstanta sembarang.

C+K suatu path yang mengandung dua path C dan K. f(z) dan g(z) dapat diintegalkan sepanjang C dan K, maka :

1.

∫

=

∫

c

c

dz

z

f

p

dz

z

f

p

(

)

(

)

2.

∫

+

=

∫

+

c c c

dz

z

g

dz

z

f

z

g

z

f

(

)

(

)}

(

)

(

)

{

∫

k

3.

∫

∫

∫

+k

=

+

c c

dz

z

f

dz

z

f

dz

z

f

(

)

(

)

(

)

4.

∫

∫

−c

=

−

c

dz

z

f

dz

z

f

(

)

(

)

5. Andaikan bahwa f(z) dapat diintegralkan sepanjang C, untuk semua M>0, fungsi f memenuhi f(z) ≤ M∀z pada C dan andaikan sepanjang C adalah L maka berlaku :

ML dz z f c ≤

∫

( )

Bukti : Menurut definisi berlaku :

∫

∑

= ∞ → ∆Ζ = c n k k n dz z f 1 lim ) (

karena berlaku :

(

)

ML

M

t

f

t

f

n k k k n k k n k k k

≤

∆Ζ

≤

∆Ζ

≤

∆Ζ

∑

∑

∑

= = = 1 1 1

)

(

)

(

Maka :

( )

t ML

f dz z f k n k k

n ∆Ζ ≤

=

∑

∫

→ ∞ 1

lim )

2.3. Teorema Green

Teorema : 2.3.1 . (Teorema Green pada Bidang).

Misalkan : P(x,y) dan Q(x,y) dua fungsi yang kontinu dan mempunyai turunan parrsial yang kontinu pada suatu daerah D, dan pada batas daerah D. Maka teorema Green menyatakan bahwa :

∫

∫

∫













∂

∂

−

∂

∂

=

+

c D

y

P

x

Q

dy

Q

dx

P

Teorema ini berlaku untuk daerah terhubung sederhana (simply connegted region) dan daerah terhubung tak sederhana (multiple connected region).

Bukti:

Y

H

F

g

e

f

X

Gbr.: 4 Path C yang tertutup sederhana

Misalkan C path tertutup sedrhana yang memenuhi bahwa setiap garis sejajar dengan sumbu koordinat pada bidang akan memotong path C paling banyak di dua titik (seperti pada gambar diatas).

Akan dibuktikan :

1.

∫ ∫ dx dy

y P dx

P

c D∫

     

∂ ∂ −

=

2.

∫ ∫ dx dy

x Q dx

Q

c D∫ 

 

 

∂ ∂ =

Bukti 1 : Misalkan persamaan path dari E,G,F adalah ; y = y1(x), dan persamaan path dari E,H,F adalah

( )

( )

( )

( )

(

)

(

)

∫

∫

∫

∫

∫

∫

∫

∫∫

−

=

−

−

=

−

=

=





























∂

∂

=













∂

∂

= = = c f e e f f e x y x y f e x y y x y y f e x D

dx

P

dx

y

x

P

dx

y

x

P

dx

y

x

P

y

x

P

dx

y

x

P

dx

dy

y

P

dxdy

y

P

2 1 1 2

,

)

,

(

,

)

,

(

)

,

(

2 1 2 1

dy

dx

y

P

dx

P

∫

∫∫













∂

∂

−

=

c

Jadi :

Bukti 2 : Misalkan persamaan path dari G, E, H adalah x = x1(y)

Persamaan path dari G, F, H adalah x = x2(y).

( ) ( )

dy

dx

x

Q

dxdy

x

Q

h g y y x x y x x

D

∫ ∫

∫∫

₌ =₌





























∂

∂

=













∂

∂

2 1

( )

x

y

( )( )

dy

Q

h g y x y x

∫

=

2 1

,

(

x

y

) ( )

Q

x

y

dy

Q

h

g

∫

−

=

[

₂

,

₁

,

]

(

)

∫

( )

∫

+

=

g h h g

dy

y

x

Q

dy

y

x

Q

₂

,

₁

,

Akibatnya

:

dy

dx

y

P

x

Q

Qdy

Pdx

D

c

∫∫

∫





−

∂

∂





∂

∂

=

+

Misalkan path C tertutup, untuk path C memenuhi bahwa garis-garis yang sejajar sumbu-sumbu koordinat memotong path C lebih dari dua titik (seperti pada gambar dibawah ini).

Y

U

S

T

T

V

X

Gbr.:5. Path C tertutup tak sederhana

Buat garis S T sedemikian sehingga daerah D (daerah yang dibatasi oleh path C) menjadi dua daerah D1 dan daerah D2 dengan batas kedua daerah tersebut

merupakan path tertutp sederhana.

Path pertama adalah S T U S dan kedua S V T S, sehingga menurut teorema Green berlaku

:

dy

dx

y

P

x

Q

Qdy

Pdx

D

STUS

∫

∫∫









∂

∂

−

∂

∂

=

+

1

dy

dx

y

P

x

Q

Qdy

Pdx

D

SVTS

∫

∫∫









∂

∂

−

∂

∂

=

+

2

Karena :

=

∫ ∫ ∫ ∫ ∫ ∫ ∫

∫

+

=

+

=

−

ST TUS SVTS SVT TS TS ST

STUS

dan

,

Maka berlaku :

∫ ∫ ∫ ∫ ∫

∫

+

=

+

+

+

SVTS ST TUS SVT TS

STUS

∫ ∫

+

=

TUS SVT

∫

=

Dari

∫∫ ∫∫ ∫∫

+

=

1 2

D D D

Jadi :

dy

dx

y

P

x

Q

Qdy

Pdx

D

c

∫∫

∫





−

∂

∂





∂

∂

=

+

Dibuktikan teorema Green pada bidang juga berlaku untuk daerah tersambung tak sederhana D seperti pada gambar dibawah ini :

Y

H

A

L

X

Gbr.:6.Daerah tersambung D

Pilih titik untuk A L K J H I G F E sedemikian sehingga path A I E F G I A L K J H A adalah suatu path tertutup sederhana, dan daerah yang dibatasi oleh path ini adalah tersambung sederhana, sehingga teorema Green berlaku :

Karena

c

maka berlaku :

D

dy

dx

y

P

x

Q

Qdy

Pdx

∫∫

∫





−

∂

∂





∂

∂

=

+

−

=

∫ ∫

AI IA

∫ ∫

∫ ∫

∫

=

+

+

+

IA ALKJHA

AI IEFGI

HA AIEFGIALKJ

∫

+

∫

=

IEFGI ALKJHA

Jadi bila C1 adalah path ALKJHA dan C2 path IEFGI adalah path yang memuat C1 dan

C2 maka:

∫

+

∫

=

∫

1 2

c c c

dy

dx

y

P

x

Q

Qdy

Pdx

D

c

∫∫

∫





−

∂

∂





∂

∂

=

+

Teorema 2.3.2 (Teorema Green dalam bentuk kompleks)

Andaikan

B( )

fungsi kontinu dan mempunyai turunan-turunan parsial yang kontinu pada daerah D dan batasnya

(path C),

dengan

z = x + iy, = x – iy

maka

:

z

z

z

,

dA

z

B

i

dz

z

z

B

D

c

∫∫

∫

(

,

)

=

2

∂

∂

dimana

dA = dx dy.

Bukti : Misalkan B

( ) = P(x,y) + iQ(x,y)

z z

,

maka menurut teorema Green berlaku

:

(

P

iQ

)(

dx

idy

dz

z

z

B

c c

+

+

=

∫

∫

(

,

)

)

)

(

)

∫

(

∫

−

+

+

=

c c

Pdy

Qdx

i

Qdy

Pdx

dy

dx

y

Q

x

P

i

dxdy

y

P

x

Q

D

D

∫∫

∫∫





−

∂

∂





∂

∂

+









∂

∂

−

∂

∂

−

=

+

[

]

dx

dy

x

Q

y

P

i

y

Q

x

P

i

D









∂

∂

+

∂

∂









∂

∂

−

∂

∂

=

∫∫

dy

dx

z

B

i

D

∫∫

∂

∂

=

2

PEMBUKTIAN TEOREMA INTEGRAL CAUCHY

Dalam bab ini dibicarakan mengenai pembuktian teorema integral cauchy, yang mana pembuktiannya dapat digolongkan atas dua cara:

Pertama dibuktikan dengan menggunakan teorema Green. Dan kedua dibuktikan dengan menggunakan beberapa teorema riil variabel.

Teorema:

Misalkan f(z) analitik pada daerah terhubung.

C adalah path tertutup dalam daerah terhubung maka :

∫

=

c

dz

z

f

(

)

0

Pada mulanya Cauchy membuktikan teorema tersebut dengan memakai pembatasan bahwa f(z) mmemenuhi f′(z) juga kontinu di D (daerah).

Selanjutnya Goursat membuktikan teorema tersebut dengan menghilangkan syarat tambahan (pembatasan tadi) untuk f(z). Sejak itu teorema tersebut dinamakan sebagai teorema Cauchy-Goursat.

3

.1. Pembuktian Teorema Integral Cauchy Dengan Menggunakan Teorema Green. Teorema : Misalkan f(z) analitik pada daerah terhubung R. C adalah path tertutup

dalam daerah terhubung, maka:

∫

=

c

dz

z

f

(

)

0

Bukti : Karena f(z) = u + iv diketahui analitik dan mempunyai yurunan kontinu maka :

y

u

i

y

v

x

v

i

x

u

z

f

∂

∂

−

∂

∂

=

∂

∂

+

∂

∂

=

)

(

'

Sehingga :

v

∂

( )

( )

2

1

L

L

L

L

L

L

L

L

L

L

L

L

y

u

x

y

v

x

u

∂

∂

−

=

∂

∂

∂

=

∂

∂

Kontinu di dalam dan pada path C.

Jadi teorema Green dapat digunakan, sehingga diperoleh :

(

u

iv

)(

dx

idy

dz

z

f

c c

+

+

=

∫

(

)

∫

)

)

Dengan menggunakan persamaan 1 dan 2 diperoleh :

(

)

∫

(

∫

=

∫

−

+

+

c

c c

udy

vdx

i

vdy

udx

dz

z

f

(

)

dxdy

y

v

x

u

i

dxdy

y

u

x

v

dz

z

f

d

d

d













∂

∂

−

∂

∂

+













∂

∂

−

∂

∂

−

=

∫∫

∫

(

)

∫∫

0

)

(

=

∫

f

z

dz

c

Cara lain :

Dengan menuliskan

f(z) = B ( ),

dan karena

f(z)

bebas dari

maka

z

z

z

=

0

∂

∂

z

B

,

∫

∫∫

=

∂

∂

=

c

D

dy

dx

z

B

dz

z

f

(

)

0

sehingga

:

Selanjutnya teorema integral Cauchy dibuktikan dengan menggunakan beberapa teorema dari riil variabel.

3.2. Pembuktian Teorema Integral Cauchy Dengan Menggunakan Beberapa Teorema Riil Variabel.

Misalkan f(z) analitik pada daerah tersambung sederhana R dan C suatu path tertutup termuat dalam R.

Maka :

∫

=

c

dz

z

f

(

)

0

Bukti :

Kasus 1. Path C suatu segitiga.

[image:15.612.112.499.546.720.2]

Path C dibagi menjadi beberapa segitiga yakni C1, C2, C3 dan C4 (seperti dalam

gambar berikut).

A D B

Gbr. : 7. Path C dalam bentuk segitiga

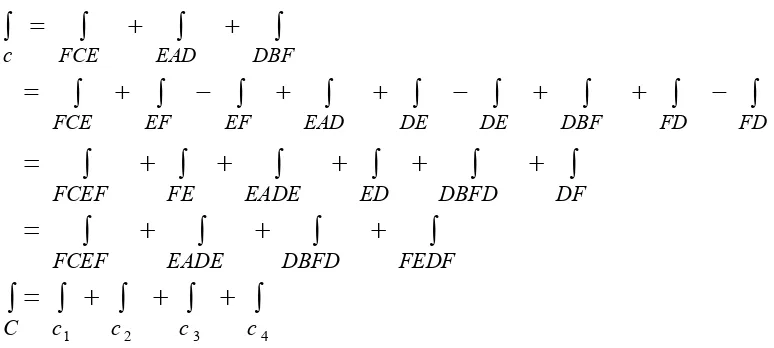
Perhatikan bahwa sisi C3 dijalani dua kali dengan arah yang berlainan, maka:

∫

=

∫

+

∫

+

c FCE EAD DBF

∫

∫

∫

∫ ∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

+

+

+

=

+

+

+

=

+

+

+

+

+

=

C c c c c

FCEF EADE DBFD FEDF

FCEF FE EADE ED DBFD DF

1 2 3 4

∫

∫

∫

∫

∫

∫

∫

∫

+

−

+

+

−

+

+

−

=

EF EF EAD DE DE DBF FD FD

Dengan menggunakan hubungan ini, selanjutnya bahwa paling sedikit satu C1 adalah

benar bahwa:

)

1

(

4

1

4

1 1

4 3 2 1

4 3 2 1

1 2 3 4

K

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫ ∫ ∫ ∫ ∫

≥

⇒

≤

+

+

+

≤

+

+

+

=

+

+

+

=

C C

C C

C C C C C

C C C C C

C C C C C

Dengan menggunakan k1 sebagai salah satu dari segitiga, dimana ketidaksamaan

adalah benar maka diperoleh:

Selanjutnya perhatikan k1; k1 dibagi seperti pada C diperoleh suatu segitiga

k2⊂k1 sedemikian sehingga :

) 2 ( 4

1

K

∫

∫

≤

K C

Dari bentuk (2) dan (3) diperoleh : 1 2

) 3 (

4

∫

K

∫

≤

K K

∫

∫

∫

∫

∫

≤

        ≤ ≤

2

2 1

2

4

4 4 4

K C

K K

C

Jika proses dilakukan sampai n kali diperoleh :

)3(

4∫2 K

∫ ≤ K

K

) 4 (

4

∫

K

∫

≤

n

K n

C

Perhatikan bahwa bagian-bagian segitiga k1, k2, k3, … , kn adalah kumpulan tertutup

dan terbatas yang limn→∞diam kn = 0, jika n → ∞. Maka k1, k2, … , kn … adalah

Nested. Menurut teorema 2.1.2 :

I

∞

=1

n n

k

k

nterdiri atas satu dan hanya satu titik sekutu.

p

∈

I

∞ maka p ∈ C atau p titik dalam C.

n=1

n

k

∀

∈

>

0

∃

δ

>

0

sedemikian sehingga :

δ

ε

−

<

≤

′

−

−

−

f

p

bila

z

p

p

z

p

f

z

f

,

)

(

)

(

)

(

ε

≤

−

′

−

−

−

p

z

p

z

p

f

p

f

z

f

(

)

(

)

(

)

(

)

(

z

p

)

p

z

p

f

p

f

z

f

(

)

−

(

)

′

(

)

(

−

)

≤

ε

−

Maka ada suatu bilangan kompleks q (tergantung pada harga z) dengan sifat q< ∈ sedemikian sehingga :



f(z) – f(p) - f

′

(p) (z-p)



≤

q



(z-p)



f(z) – f(p) - f

′

(p) (z-p) = q (z-p)

f(z) = f(p) + f

′

(p) (z-p) + q(z-p) ………(5)

atau :

)

(

)

(

)

(

p

f

p

z

p

f

z

f

q

−

′

−

−

=

Karena limn_→∞ diam kn = 0 dan p

∈

∞

I

=1

n n

k

kn ; kumpulan terbatas dan tak terhingga, maka menurut teorema 2.1.1 ⇒ p

merupakan titik limit.

Akibatnya ada N(p,δ) atau lingkungan N dengan p titik pusat, δ jari-jari.

N

(p , δ)

Gbr.: 8. Lengkungan N(p , _δ)

Akibatnya untuk setiap z dalam kn atau z pada kn mempunyai sifat z-p < δ dan

karena itu … (5) dipenuhi untuk setiap z, maka :

[

]

∫

∫

=

+

′

−

+

−

n

n k

k

dz

p

z

q

p

z

p

f

p

f

dz

z

f

(

)

(

)

(

)

(

)

(

)

∫

∫

∫

+

′

−

+

−

=

n n

n k k

k

dz

p

z

q

dz

p

z

p

f

dz

p

f

(

)

(

)

(

)

(

)

∫

∫

∫

∫

+

′

−

′

+

−

=

n

n n

n k k k

k

dz

p

z

q

dz

p

f

p

dz

z

p

f

dz

p

f

(

)

(

)

(

)

(

)

(

f

)

∫

=

0

n k

dz

p

)

(

=

′

p

zdz

f

∫

0

n k

0

)

(

=

′

∫

n k

dz

p

f

p

Jadi

:

)

6

(

;

)

(

)

(

=

∫

−

ε

<

ε

K

∫

f

z

dz

q

z

p

dz

q

C

q

n

n k

k

Selanjutnya disebutkan dua fakta yang akan diperlukan sebagai berikut :

1.

mengenai keliling lingkaran-lingkaran ; k1, k2, … , kn. Nyatakan keliling lingkaran

C=C dan k1 = k1, diperoleh :

n n

C

k

C

k

k

C

k

2

,

,

2

2

,

2

2 1 2

1

=

=

=

K

=

2. Jarak antara dua titik pada segitiga ≤ ½ keliling segitiga atau z-p≤ ½ kn.

Selanjutnya gunakan teorema 2.2.1 dan dua fakta diatas pada persamaan (6) diperoleh:

∫

∫

=

−

n n k k

p

z

q

dz

z

f

(

)

(

)

n n n k n n k k k

C

C

k

k

k

dz

p

z

q

q

dz

p

z

q

dz

p

z

q

dz

z

f

n n n n

4

2

2

2

2

2

,

)

(

)

(

)

(

2 2 2

ε

ε

ε

ε

ε

=













=

≤

•

•

≤

−

≤

≤

−

≤

−

=

∫

∫

∫

∫

Jadi : kn n

C

dz

z

f

4

2

)

(

2

ε

≤

∫

Telah dibuktikan :

∫

∫

≤

n k n C

4

ε

ε

2

)

(

4

2

4

)

(

4

)

(

2

2

C

dz

z

f

C

dz

z

f

dz

z

f

C C

n n

k n

n

=

•

≤

≤

∫

∫

∫

Karena

ε

>

0, dan

C

terbatas maka

:

2

2

0

)

(

=

∫

C

dz

z

f

Kasus 2 : path C adalah polygon tertutup.

Dalam hal ini dinyatakan bahwa polygon C dapat dibagi menjadi segitiga-segitiga yang terbatas jumlahnya yakni : C1, C2, … , Cn sedemikian

sehingga setiap sisi dari setiap segitiga yang tidak berimpit dengan beberapa sisi dari C (sebahagian dari padanya) akan terletak dalam C. Dengan menjalani setiap segitiga ini (seperti pada Gbr.9) dengan arah

yang ditentukan pada path C dan menggunakan hasil kasus 1, diperoleh

:

0

2 1

=

+

+

+

∫

∫

∫

N C C

C

L

Gbr.: 9. Path C dalam bentuk polygon

Tetapi setiap sisi dari segitiga ini menjadi interior poligon tersebut dijalani dua kali dalam arah yang berlainan, maka nilai integral sepanjang sisi dalam interior ini tidak menambah perjumlahan dari integral tersebut, dan hanya sisi-sisi yang asli dari poligon tersebut yang berperan dalam integral tersebut maka :

0

)

(

=

∫

C

dz

z

f

Kasus 3 : C sembarang path tertutup.

Misalkan path C terletak pada daerah R, dimana f(z) analitik. Pilih n buah titik pada path C : z1, z2, … , zn sebut zo = zn, dengan menghubungkan

[image:19.612.91.299.62.208.2]

Gbr.: 10. Path C sembarangan

Maka membuktikan kasus ini diperlukan empat hal yang menjadi landasan sebagai berikut :

1. Menurut definisi : 2.2

C

)

(

)

(

lim

)

(

₁

0 −

→

Σ

−

=

∫

f

z

dz

_µ

f

t

k

z

k

z

k

Sebut S

n

=

Σ

f(t

k

) (z

k

– z

k-1

)

∫

s

n

dz

z

f

0

lim

)

(

→

=

_µ

C

2. Menurut teorema 2.1.4. C

N

n

dz

z

f

N

n

s

≤

∀

>

−

∋

∃

>

∀

ε

0

∫

(

)

ε

,

C sembarang path dalam R ⇒ ∃ λ > 0, λ ∈ R ∋ ∀ z ∈ C dan ∀w pada batas R, maka berlaku z-w> λ.

Perhatikan Q adalah kumpulan yang terdiri dari semua titik-titik dalam R yang jaraknya dari batas R ≥ λ/2 atau ditulis : Q = {z ; z-w≥λ/2.

Jelas Q ; tertutup dan terbatas.

f(z) analitik ⇒ f(z) kontinu pada Q. Menurut teorema 2.1.5 maka f(z) kontinu seragam pada Q, akibatnya : ∀ε> 0, ∃δ > 0 ∋ : ∀z, p ∈Q berlaku :

f(z) – f(p) <ε, bila z-p< δ. 3. Berikan ε> 0, sembarang, ambil partisi P;

zo, z1, z2, … , zn dari C memenuhi :

a.  f – Sn< ε

b. Bagian path [zk-1, zk] dengan ; zk-1, zk≤ λ/2.

c. Panjang setiap bagian path juga < δ, dimana δ ditentukan kontinu seragam (dijamin oleh 2).

Kondisi a s/d c berlaku pada partisi P. Suatu tali dapat digambarkan sebagai panjang zk-1 ke zk untuk k=1,2,3, … yang semuanya terletak dalam Q ⊂ R.

Karena panjang dari tiap bagian path [zk-1, zk] lebih kecil dari < δ maka zk –

zk-1< δ. Oleh karena itu tiap kali (chord) zk-1 ke zk lebih kecil dari δ, karena itu

jika z adalah tiap titik pada tali (chord) ke k maka : z – zk< δ, karena itu f(z) – f(zk)< ε.

Akibatnya ; ∀k=1,2,… dan tiap titik < pada chord ke k ∃ εk(z) ∈ C ∋εk(z)< ε

yang bebas dari z dan : f(z) = f(zk) + εk(z) .

0

→

−

∫

∫

_Π

C

Berdasarkan 1 s/d 4 diatas, maka cukup dibuktikan ; Dari kasus 2

=

₀

∫

Π

Jika partisi P menuju garis lengkung, misalnya : µ → 0 akkhirnya diperoleh (untuk mudahnya misalkan zn = zo);

∫

∑ ∫

Π

=

= ₋ n k z z k k

dz

z

f

dz

z

f

1 ₁

)

(

)

(

n zk

[

]

∑ ∫

∑

∑ ∫

∑ ∫

∑ ∫

∑ ∫

= = − = = = = − − − − −

+

=

+

−

=

+

=

+

=

n k z z k n n k n k z z k k k k n k z z n k z z k k k z k k k k k k k k k k k

dz

z

S

dz

z

z

z

z

f

dz

z

dz

z

f

dz

z

z

f

1 1 1 1 1 1 1 1 1 1 1 1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

ε

ε

ε

ε

∫

∑ ∫

Π = −

=

−

n k z z k n k k

dz

z

S

dz

z

f

1 ₁

)

(

)

(

ε

=

−

∑ ∫

∫

ε

(

)

n z k

n

z

dz

Dimana ∏ menyatakan panjang keliling poligon yang terbatas, dengan mengunakan relasi 3(a) diperoleh :

C

Π

+

<

−

+

−

≤









−

+









−

=

−

−

+

−

≤

−

∫

∫

∫

∫

∫

∫

∫

∫

∫

∫

Π

Π Π

Π Π

ε

ε

n n

C

n n

C

n n C C

S

S

S

S

S

S

Jadi

:

∫ ∫ (

−

=

Π

+

)

Π

C

ε

1

Karena ε> 0 sembarang, dan ∏ + 1 besaran yang terbatas:

∫ ∫

−

=

Π

C

0

sehingga :

∫

=

∫

=

Π

C

dz

z

f

dz

z

DAFTAR PUSTAKA

Konrad Knopp, DR., Theory of Functions, Part One, Elements of the General Theory of Analytic functions, New York, Dover Publication, Inc, 1945.

Margha M, Drs., Fungsi dengan Peubah Kompleks, Armico, Bandung, Edisi Pertama, 1982.

Paliouras, John D., Complex Variable for Scientists And Engineers, Mac Millan Publishing, Co., 1975.

Spiegel, Murray, Ph.D., Theory and Problema of Complex Variable, Schaum’s, Out Line Series, Mc Graw-Hill Book Company, New York, London, Sydney, Toronto.

Spiegel, Murray, Ph.D., Theory and Problema of Riel Variable, Schaum’s, Mc Graw-Hill Book Company, New York, London, Sydney, Toronto.