Metode Pencarian Langsung Untuk Menyelesaikan Problema Knapsack

Oleh:

SKRIPSI

SRI WAHYUNI

050803028

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : METODE PENCARIAN LANGSUNG UNTUK MENYELESAIKAN PROBLEMA KNAPSACK

Kategori : SKRIPSI

Nama : SRI WAHYUNI

Nomor Induk Mahasiswa : 050803028

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA

UTARA

Medan, Oktober 2009 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Elly Rosmaini, M. Si Prof. Dr. Herman Mawengkang NIP 196005201985032002 NIP : 194611281974031001

Diketahui/Disetujui oleh

Departeman Matematika FMIPA USU Ketua.

PERNYATAAN

METODE PENCARIAN LANGSUNG UNTUK MENYELESAIKAN PROBLEMA KNAPSACK

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Oktober 2009

PENGHARGAAN

Segala puji dan syukur penulis haturkan atas kehadirat Allah Subhanna Wa Ta’ala

yang telah melimpahkan Nikmat dan karunia-Nya, sehingga penulis berhasil menyelesaikan skripsi ini dalam waktu yang telah ditetapkan. Dan tak lupa pula shalawat dan salam senantiasa tercurah kepada Nabi Allah, Muhammad Shalallahu

‘Alaihi Wassalam yang diutus sebagai rahmat untuk sekalian alam serta keluarga dan

sahabat beliau serta orang-orang yang berpegang teguh dengan petunjuk Sunnah beliau hingga hari kiamat.

Dalam kesempatan ini, penulis ingin mengucapkan jazakumullahu khairan

katsiran kepada semua pihak yang telah membantu dan membimbing penulis dalam

penyusunan skripsi ini, ucapan terima kasih saya sampaikan kepada :

1. Bapak Prof. Dr. Herman Mawengkang selaku pembimbing I dan Dra. Elly Rosmaini M. Si selaku pembimbing II yang telah memberikan bimbingan dan pengarahan kepada saya sehingga skripsi ini dapat saya selesaikan.

2. Bapak Drs. Suwarno Ariswoyo, M.Si. dan Drs. H. Haluddin Panjaitan selaku dosen penguji saya.

3. Bapak Dr. Saib Suwilo, M.Sc. dan Drs. Henry Rani Sitepu, M.Sc. selaku Ketua dan Sekretaris Departemen Matematika

4. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumetera Utara.

5. Semua Dosen pada Departemen Matematika FMIPA USU, pegawai di FMIPA USU

6. Terkhusus kedua orangtua tercinta, Bapak Suharno dan Ibu Sari Armaini, dan kedua Adik saya serta semua keluarga besar Alm. Sopan yang selama ini memberikan bantuan dan dorongan yang diperlukan.

7. Seluruh teman-teman kuliah dan junior Matematika khususnya stambuk 2005 dan juga teman terdekat saya Rima, Nenna, Sundari, Febby, Chinta, Lia, Radhi, Santri dan Dika serta sahabat-sahabat saya di Pelajar Islam Indonesia (PII) yang telah memberikan semangat, dorongan dan saran dalam pengerjaan skripsi ini.

ABSTRAK

EXHAUSTIVE SEARCH METODH TO SOLVE KNAPSACK PROBLEMS

ABSTRACT

DAFTAR ISI

Halaman

PERSETUJUAN ii

PERNYATAAN iii

PENGHARGAAN iv

ABSTRAK v

ABSTRACT vi

DAFTAR ISI vii

DAFTAR TABEL viii

DAFTAR GAMBAR ix

Bab 1 PENDAHULUAN 1

1.1Latar Belakang 1

1.2Identifikasi Masalah 2

1.3Tujuan Penelitian 2

1.4Tinjauan Pustaka 3

1.5Kontribusi Penelitian 4

1.6Metode Penelitian 4

Bab 2 LANDASAN TEORI 5

2.1 Problema Knapsack dengan Algoritma Branch and Bound 5

2.1.1 Algoritma Branch and Bound 5

2.1.2 Pohon 6

2.1.3 Metode 6

2.2 Problema Knapsack dengan Algoritma Greedy 11

2.2.1 Greedy by Profit 12 2.2.2 Greedy by Weight 13

2.2.3 Greedy by Density 14

2.3 Problema Knapsack dengan Exhautives Search 16

2.4 Problema Knapsack dengan Algoritma Genetika 18

2.4.1 Algoritma Genetika 18

2.4.2 Penerapan Algoritma Genetika pada Problema Knapsack 19

2.4.3 Flowchart 22 Bab 3 PEMBAHASAN 23 3.1 Pendekatan Basis 23

3.2 Metode Derivatif 24

3.3 Hasil 26

3.4 Algoritma 29

Bab 4 KESIMPULAN DAN SARAN 32 4.1 Kesimpulan 32

4.2 Saran 32

DAFTAR TABEL

Halaman Tabel 2.1 Keterangan berat, Keuntungan dan P/W tiap Jenis Barang 7

Tabel 2.2 Greedy by Profit 13

Tabel 2.3 Greedy by Weight 14

Tabel 2.4 Greedy by Density 15

Tabel 2.5 Greedy by Density 16

DAFTAR GAMBAR

Halaman Gambar 2.1 Akar Pohon Problema Knapsack dengan n-4 7 Gambar 2.2 Pohon Status Problema Knapsack Tahap Awal 9 Gambar 2.3 Pohon Status Problema Knapsack Tahap Kedua 9 Gambar 2.4 Pohon Status Problema Knapsack Tahap Ketiga 10

Gambar 2.5 Pohon Status Problema Knapsack 10

ABSTRAK

EXHAUSTIVE SEARCH METODH TO SOLVE KNAPSACK PROBLEMS

ABSTRACT

PENDAHULUAN

1.1. Latar Belakang

Problema Knapsack merupakan sebuah persoalan yang menarik. Problema Knapsack adalah masalah dimana kita dihadapkan dengan persoalan optimasi pemilihan benda untuk dimasukkan ke dalam sebuah wadah yang memiliki keterbatasan ruang dan daya tampung tetapi benda yang akan dimasukkan ke dalam wadah tersebut haruslah tetap dalam keadaan utuh bukan merupakan fraksi dari benda tersebut. Masing-masing benda yang ada memiliki sebuah nilai yang berupa berat, volume, harga, atau nilai lainnya yang dapat dipakai sebagai penentu dalam proses pemilihannya. Sedangkan wadah memiliki sebuah nilai konstanta yang dimilikinya dan merupakan sebuah pembatas dalam proses pemilihan benda untuk dimasukkan ke dalam wadah tersebut. Pada akhir proses diinginkan hasil yang optimum di mana memiliki nilai keuntungan yang paling besar yang dapat dicapai dengan benda yang berada pada wadah tersebut. Sehingga harus diambil sebuah cara memasukkan benda-benda ke dalam wadah sehingga dapat menghasilkan hasil yang optimum. Dalam dunia nyata problema Knapsack ini sering sekali digunakan terutama pada bidang (jasa) pengangkutan barang (seperti pengangkutan peti kemas dalam sebuah kapal). Dalam penelitian ini akan dibahas penerapan salah satu cara untuk menyelesaikan problema Knapsack yang ada yaitu dengan menggunakan metode pencarian langsung sehingga didapatkan penyelesaian optimal.

Dari metode pencarian langsung, ide dasar adalah pandang problema program integer (PI)

Min P=CT x Kendala Ax≤b

x≥0

x_j cacah untuk berbagaij∈J

( )

xB k = βk −αki

( )

xN i−...−αkj∗

( )

xN j_∗ −...−αk,n−m

( )

xN n₋m

andaikan

( )

x_{B k} peubah bernilai cacah dan β_k tidak bernilai cacah, β_k dipartisi menjadi komponen bulat dan pecahan β_k =

[ ]

β_k + f_k. Jika ingin dinaikan

( )

x_{B k} ke cacah terdekat

(

[ ]

β +1

)

, dapat dinaikan peubah tak basis, misalnya

( )

x_{N j∗} diatas batasannya asalkan α_kj∗ yaitu salah satu elemen vektor α_j∗ negatif. Ambil ∆_j∗ dapat dinyatakan sebagai :

∗ ∗ = ₋− ∆

kj k j

f α

1

peubah nonbasis lainnya tetap di nol. Jadi setelah disubstitusi ∆_j∗ untuk

( )

x_{N j∗}

diperoleh

( )

x_{B k} =

[ ]

β +1. Sekarang

( )

x_{B k} suatu bilangan cacah. Terlihat jelas peubah tak basis sangat berperan dalam membulatkan nilai peubah basis terkait.

Dengan latar belakang inilah maka penulis memilih judul “Metode Pencarian Langsung Untuk Menyelesaikan Problema Knapsack”

1.2 Identifikasi Masalah

Beberapa penelitian sebelumnya telah mampu menyelesaikan Problema Knapsack diantaranya dengan menggunakan metode Branch and Bound, Algoritma Greedy, Algoritma Genetika dan lainnya. Namun hasil yang didapat masih banyak kekurangan dan membuka peluang untuk menyelesaikan metode lain untuk menghasilkan penyelesaian yang optimal.

1.3 Tujuan Penelitian

1.4 Tinjauan Pustaka

Sebagai sumber pendukung teori dalam penulisan ini, maka penulis mengggunakan beberapa pustaka antara lain :

1. Silvano Martello dan Paolo Toth, 1989. Knapsack Problems,

Algorithms an Computer Implementations menyatakan bahwa

seandainya seseorang yang membawa wadah harus mengisi wadahnya dengan memilih diantara berbagai jenis barang yang mungkin akan memberikan keuntungan yang maksimum. Inilah problema knapsack dapat diformulasikan dalam bentuk matematika dengan bilangan pada barang tersebut dari 1 sampai n dan memperkenalkan sebuah vekor biner dengan variable x_j

(

j=1,...,n

)

dinyatakan sebagai :

1 jika objek dipilih; 0 lainnya

j

j x = 



Kemudian, jika p_j adalah keuntungan maksimum yang diperoleh dari barang j,w_j adalah berat benda dan c adalah ukuran wadah, masalahnya akan dipilih dari diantara seluruh vekor biner x dengan

constraint :

c x

p _j

n

j

j ≤

∑

₌₁

Maksimasi dari fungsi objektif :

∑

n₌ j

j x p

1 1

2. H. Kellerer, U. Pferschy dan D. Pisinger, 2004. Knapsack Problems

menyatakan bahwa Problema Knapsack didefinisikan sebagai : Kita memberika sebuah perumpamaan dari Problema Knapsack dengan himpunan objek N, berada pada objek j dengan profit pj dan bobot wj dan harga c.

Sebagai alternatif, sebuah Problema Knapsack dapat diformulasikan sebagai sebuah solusi dari berbagai formulasi Linier Integer Programming :

Maksimumkan

∑

=

n

j j jx p

1

(1)

Kendala w x c

n

j j j ≤

∑

₌₁ (2)

1.5 Kontribusi Penelitian

Adapun kontribusi yang dapat diberikan melalui hasil penelitian ini nantinya adalah : 1. Penelitian ini diharapkan sebagai acuan/ pedoman dalam

mengembangkan model penyelesaian Problema Knapsack.

2. Dapat membantu menyelesaikan problema di dunia nyata yang berkaitan dengan Problema Knapsack.

1.6 Metodologi Penelitian

Dalam penyusunan tulisan ini, penulis menggunakan studi literature dengan menerapkan teori-teori yang behubungan dengan masalah yang dibahas. Penelitian ini dilakukan sebagai berikut :

Langkah-1 : Menjelaskan bentuk umum problema Knapsack dan memaparkan beberapa penyelesaian yang telah ada sebelumnya untuk menyelesaikan problema Knapsack.

Langkah-2 : Menjelaskan bentuk umum problema Knapsack, metode pencarian langsung dan asumsinya.

Langkah-3 : Menganalisis dan merumuskan model penyelesaian problema Knapsack dengan menggunakan metode pencarian langsung.

BAB 2

LANDASAN TEORI

Pada bab ini akan dibicarakan beberapa model penyelesaian problema Knapsack dengan memakai beberapa metode yang telah ada yang akan digunakan pada bab pembahasan.

2.1 Problema Knapsack dengan Algoritma Branch and Bound.

2.1.1. Algoritma Branch and bound

Sebagaimana pada algortima runut-balik, algoritma Branch & Bound juga merupakan metode pencarian didalam ruang solusi secara sistematis. Ruang Solusi diorganisasikan ke dalam pohon ruang status. Pembentukan pohon ruang status. Pembentukan pohon ruang status pada algoritma Branch & Bound berbeda dengan pembentukan pohon pada algoritma runut balik. Bila pada algoritma runut-balik ruang solusi dibangun secara Depth-First Search (DFS), maka pada algoritma Branch & Bound ruang solusi dibangun dengan skema Breadth-First Search (BFS). Pada algoritma Branch & Bound, pencarian ke simpul solusi dapat dipercepat dengan memilih simpul hidup berdasarkan nilai ongkos (cost). Setiap simpul hidup diasosiasikan dengan sebuah ongkos yang menyatakan nilai batas (bound). Pada prakteknya, nilai batas untuk setiap simpul umumnya berupa taksiran atau perkiraan. Fungsi heuristik untuk menghitung taksiran nilai tersebut dinyatakan secara umum sebagai :

( ) ( ) ( )

i f i g i

cˆ = + ˆ

yang dalam hal ini,

( )

( )

( )

ongkosmencapaisimpul tujuan darisimpulakar (diperkirakan) ˆ

akar dari simpul mencapai untuk

ongkos

simpul untuk ongkos ˆ

i i

g

i i

f

i i

c

= = =

Nilai cˆ digunakan untuk mengurutkan pencarian. Simpul berikutnya yang dipilih untuk diekspansi adalah simpul yang memiliki cˆ minimum (Simpul-E). Strategi memilih simpul-E seperti ini dinamakan strategi pencarian berdasarkan biaya terkecil (least cost search).

Prinsip dari algoritma branch and bound ini adalah :

1. Masukkan simpul akar ke dalam antrian Q. Jika simpul akar adalah simpul solusi (goal node), maka solusi telah ditemukan. Stop.

2. Jika Q kosong, tidak ada solusi . Stop.

3. Jika Q tidak kosong, pilih dari antrian Q simpul i yang mempunyai cˆ

( )

i

paling kecil. Jika terdapat beberapa simpul i yang memenuhi, pilih satu secara sembarang.

4. Jika simpul i adalah simpul solusi, berarti solusi sudah ditemukan, stop. Jika simpul i bukan simpul solusi, maka bangkitkan semua anak-anaknya. Jika i tidak mempunyai anak, kembali ke langkah 2.

5. Untuk setiap anak j dari simpul i, cˆ

( )

j hitung , dan masukkan semua anak-anak tersebut ke dalam antrian Q.

6. Kembali ke langkah 2.

2.1.2. Pohon

Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit. Dengan setiap kemungkinan solusi dianggap sebagai sebuah simpul dan akar dari pohon, banyak algoritma yang menggunakan ruang solusi berupa pohon ini karena akan lebih memudahkan dalam penelusuran solusi yang ada berupa simpul-simpul pohon.

2.1.3. Metode

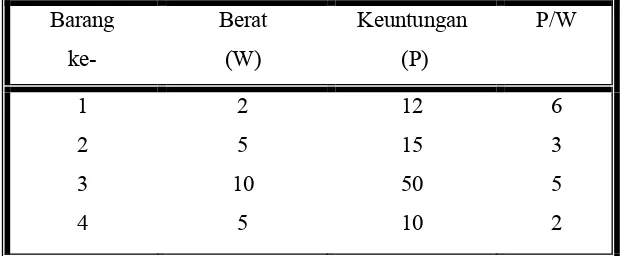
tangga keliling harus memilih barang-barang yang akan dijual setiap harinya dengan batas daya angkut gerobak yang dimilikinya. Untuk mempermudah, kita misalkan pedagang keliling tersebut hanya memiliki 4 jenis barang untuk dijual dengan berat dan keuntungan penjualan yang berbeda-beda untuk tiap jenisnya. Gerobak yang akan dipakai untuk mengangkut barang-barang tersebut hanya mampu menampuk beban seberat 16kg. Berikut merupakan tabel penggambaran berat dan keuntungan yang akan diperoleh untuk tiap penjualan barang tersebut.

Barang ke-

Berat (W)

Keuntungan (P)

P/W

1 2 3 4

2 5 10

5

12 15 50 10

6 3 5 2 Tabel 2.1 Keterangan berat, keuntungan dan P/W

tiap jenis barang

Dalam algoritma ini , kita akan menentukan cost dari tiap tiap simpul anak untuk dapat menentukan simpul mana yang kelak akan dibangkitkan yaitu simpul dengan cost tertinggi dalam penelusuran pohon untuk mencapai solusi dari permasalahan ini. Dalam permasalahan ini, kita akan mencari simpul-simpul yang akan membawa kita pada keuntungan terbesar oleh karena itu urutan pembangkitan simpul akan ditentukan oleh simpul mana yang memiliki cost tertinggi.

Cost dari tiap simpul akan ditentukan dengan perhitungan :

( ) ( ) ( )

i f i g i

cˆ = + ˆ

yang dalam hal ini,

( )

i =

cˆ cost untuk simpul i

( )

i =

f cost untuk sampai ke simpul i dalam hal ini merupakan keuntungan dari simpul akar ke simpul i.

( )

i =

gˆ cost dari simpul i untuk sampai ke simpul tujuan, dalam hal ini dapat diperoleh dengan menggunakan rumus :

Pada tahap awal kita akan melakukan perhitungan dengan menggunakan rumus diatas untuk memperoleh batas awal atau akar dari pohon yang juga merupakan simpul pertama. Pada keadaan ini, batas dihitung dengan pemikiran bahwa belum ada satupun barang yang dimasukan kedalam alat pengangkut maka kita dapat memilih 6 sebagai (P/W) terbesar karena belum ada satu barangpun yang dimasukan kedalam alat pengangkut dan kapasitas daya angkutpun masih utuh yaitu seberat 16 kg.

( ) ( ) ( )

i f i g i

cˆ = + ˆ

( )

i =

cˆ keuntungan yang diperoleh sampai disimpul awal + (P/W0max*daya angkut yang tersisa

= 0 + 6 * = 96

Maka kita memperoleh 96 batas awal atau cost dari simpul awal.

96

Gambar 2.1 Akar Pohon Problema Knapsack dengan n-4

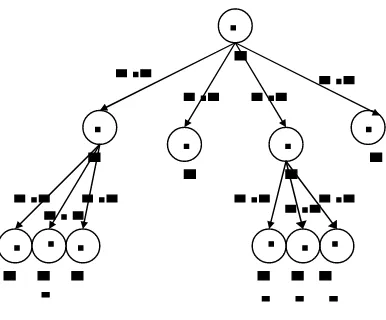
Selanjutnya kita akan membangkitkan simpul-simpul anak dari akar pohon yaitu dengan membangkitkan simpul 1, simpul 2, simpul 3 dan simpul 4 sebagai gambaran dari 4 pilihan barang yang akan dimasukan pertama kali pada alat pengangkut dengan x1 merupakan keuntungan yang akan diperoleh pada penjualan

tiap barang tersebut. Kemudian kita akan menghitung cost dari tiap simpul anak yang hidup dan juga kelayakannya untuk tetap hidup atau harus dibunuh. Dalam hal ini, simpul yang jumlah dari lintasannya tidak bisa lagi dibangkitkan (jika ditambah barang lagi kedalam alat pengangkut maka beratnya akan melebihi daya angkut) akan dibunuh.

( )

(

)

( )

(

)

( )

(

)

( )

4 10 6*

(

16 5

)

76

1

2 3 4 5

12 1 =

x

1

3 4 5

2 8 7 12 1 = x 96 x₁ =10 x₁ =15 x₁ =50

82 81 86 76

Gambar 2.2 Pohon status problema Knapsack tahap awal

Dari simpul-simpul yang telah dibangkitkan dan dihitung cost nya, maka diperoleh bahwa simpul 4 lah yang memiliki cost tertinggi oleh karena itu maka simpul 4 akan di perluas lagi. Simpul 6 ,7,8 akan dibangkitkan sebagai perluasan dari simpul 4 dengan barang yang mungkin dimasukan kedalam alat pengangkut adalah barang ke 1,2 dan 4. kemudian kita akan mengkitung cost dari simpul 6,7dan 8.

( ) (

) (

)

( ) (

)

(

)

( ) (

8 50 10

)

6*

(

16 10 5

)

66

ˆ 71 5 10 16 * 6 15 50 7 ˆ 74 2 10 16 3 12 50 6 ˆ = − − + + = = − − + + = = − − + + = c c c

Setelah melakukan perhitungan, kita dapat melihat bahwa ketiga simpul yaitu simpul 6,7 dan 8 tidak bias lagi diperluas oleh karena itu ketiga simpul ini akan dibunuh dengan menambahkan keterangan huruf B pada bagian bawah simpulnya. Simpul

96 x₁=10 x₁ =15 x₁ =50

80 81 86 76

x₂ =12 x₂ =15 x₂ =10

74 71 66

B B B

Gambar 2.4 Pohon status problema Knapsack tahap ketiga

Sekarang kita hanya memiliki simpul 2,3 dan 5 sebagai simpul hidup. Diantara simpul-simpul tersebut, simpul 2 lah yang memiliki cost terbesar sehingga selanjutnya akan dilakukan perluasan pada simpul 2 dengan metode yang serupa dan diperoleh simpul 9,10, dan 11 dengan cost 72,74, dan 67. pada simpul 2, dapat dilihat bahwa simpul tersebut tidak dapat lagi diperluas oleh karena itu makan simpul ini akan dibunuh.

Gambar 2.5 Pohon status knapsack problem

kapan kita harus berhenti karena telah sampai kepada solusi tetapi penyelesaian masalah akan dilakukan dengan membandingkan solusi pada tiap daun. Dalam persoalan ini, akan dibandingkan jumlah keuntungan yang diperoleh pada tiap daun dan solusi permasalah merupakan lintasan yang menuju daun yang memiliki keuntungan terbesar.

Dari gambar diatas dapat disimpulkan bahwa solusi permasalahan dibentuk oleh lintasan yang menuju simpul 13 dan 7 dimana keduanya merupakan solusi yang serupa yaitu memilih barang 2 dengan berat 5 kg , keuntungan 15 dan barang 3 dengan berat 10 kg, keuntungan 50 sebagai solusi permasalahan dan akan menghasilkan keuntungan yang maksimal pada penjualan yaitu sebesar 65.

2.2 Problema Knapsack dengan Algoritma Greedy

Problema knapsack 0/1 pada bab ini akan dibahas dengan menggunakan strategy greedy. Pendekatan yang digunakan di dalam algoritma greedy adalah membuat pilihan yang “tampaknya” memberikan perolehan terbaik, yaitu dengan membuat pilihan optimum local (local optimum) pada setiap langkah dengan harapan bahwa sisanya mengarah ke solusi optimum global (global optimum)

Algoritma greedy adalah algoritma yang memecahkan masalah langkah per langkah, pada setiap langkah :

1. Mengambil pilihan yang terbaik yang dapat diperoleh pada saat itu tanpa memperhatikan konsekuensi ke depan (prinsip “take what you can get now!”) 2. Berharap bahwa dengan memilih optimum lokal pada setiap langkah akan berakhir dengan optimum global.

Dengan algoritma greedy, persoalan knapsack dapat dipecahkan dengan memasukkan objek satu per satu ke dalam knapsack. Sekali objek dimasukkan ke dalam knapsack, objek tersebut tidak bias dikeluarkan lagi.

2.2.1. Greedy by profit

Pada setiap langkah , knapsack diisi dengan objek yang mempunyai keuntungan terbesar. Strategi ini mencoba memaksimumkan keuntungan dengan memilih objek yang paling menguntungkan terlebih dahulu.

Pertama kali yang dilakukan adalah secara menurun objek – objek berdasarkan profitnya. Kemudian baru diambil satu – persatu objek yang dapat ditampung oleh knapsack sampai knapsack penuh atau sudah tidak ada objek lagi yang bias dimasukkan. Algoritmanya yaitu :

Berdasarkan algoritma diatas maka dapat dihitung komplesitas waktu asimptotik-nya adalah O(n)

Sebagai data pengujian diberikan data-data untuk w (Weight) dan P (Profit) :

Dengan kapasitas knapsack W = 16

procedure Giby Profit (var dt3 : arrayData;W : real); Var i,j: integer temp: data cW: real tukar:boolean program UrutkanDataBerdasarkanProfit(dt3) While((cW<W)and(i<=length(dt3))do if(dt3[i].w<=W-cW)then

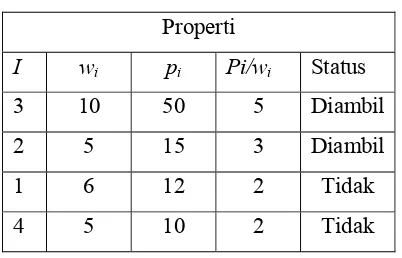
Tabel 2.2 Greedy by profit

Properti

I wi pi Pi/wi Status

3 10 50 5 Diambil

2 5 15 3 Diambil

1 6 12 2 Tidak 4 5 10 2 Tidak

2.2.2. Greedy by weight.

Pada setiap langkah, knapsack diisi dengan objek yang mempunyai berat paling ringan. Strategi ini mencoba memaksimumkan keuntungan dengan memasukkan sebanyak mungkin objek ke dalam knapsack.

Pertama kali yag dilakukan adalah mengurutkan secara menaik objek-objek berdasarkan weightnya. Kemudian baru diambil satu persatu objek yang dapat ditampung oleh knapsack sampai knapsack penuh atau sudah tidak ada objek lagi yang bias dimasukkan. Algoritma greedy by profit sebagai berikut :

Berdasarkan algoritma di atas maka dapat dihitung komplesitas waktu asimptotik-nya adalah O(n)

procedure Giby Weight (var dt3 : arrayData;W : real); Var

i,j: integer temp: data cW: real tukar:boolean program

UrutkanDataBerdasarkanWeight(dt3) While((cW<W)and(i<=length(dt3))do if(dt3[i].w<=W-cW)then

Sebagai data pengujian diberikan data-data untuk w (Weight) dan P (Profit) :

Dengan kapasitas knapsack W = 16

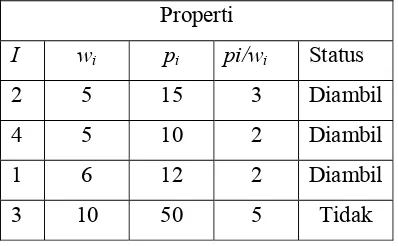
Tabel 2.3 Greedy by weight

Properti

I wi pi pi/wi Status

2 5 15 3 Diambil

4 5 10 2 Diambil

1 6 12 2 Diambil

3 10 50 5 Tidak

2.2.3. Greedy by density

Pada setiap langkah, knapsack diisi dengan objek yang mempunyai densitas terbesar. Strategi ini mencoba memaksimumkan keuntungan dengan memilih objek yang mempunyai keuntungan per unit berat terbesar.

Pertama kali yang dilakukan adalah mencari nilai profit per unit (density) dari tiap-tiap objek. Kemudian objek-objek tersebut diurutkan berdasarkan densitynya. Kemudian baru diambil satu-persatu objek yang dapat ditampung oleh knapsack sampai knapsack penuh atau sudah tidak ada objek lagi yang bisa dimasukkan.

Pemilihan objek berdasarkan salah satu dari ketika strategi di atas tidak menjamin akan memberikan solusi optimal. Berbeda dengan strategi brute force yang selalu dapat memberikan hasil yang optimal. Tetapi greedy mengurangi jumlah langkah (kompleksitas) pencarian.

Berdasarkan algoritma diat maka dapat dihitung komplesitas waktu asimptotik-nya adalah O(n)

Sebagai data pengujian diberikan data-data untuk w (Weight) dan P (Profit) :

Dengan kapasitas knapsack W = 16

Tabel 2.4 Greedy by density

Properti

I wi pi pi/wi Status

3 10 50 5 Diambil

2 5 15 3 Diambil

4 5 10 2 Tidak 1 6 12 5 Tidak procedure GbyPW (var dt3 : arrayData;W : real);

Var i,j: integer temp: data cW: real tukar:boolean program UrutkanDataBerdasarkanWeight(dt3) →//Mengurutkan data berdasarkan

while((cW<W)and(i<=length(dt3))do //nilai density yang terbesar if(dt3[i].w<=W-cW)then //ke nilai yang terkecil cW←cW+dt3[i].w

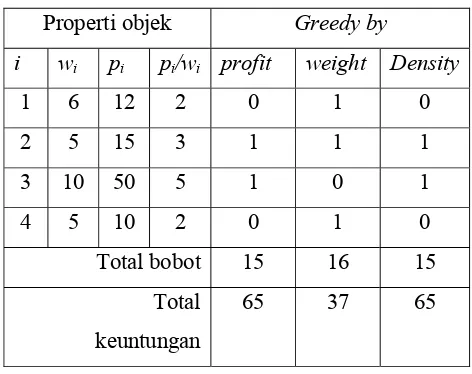
Maka, hasil akhirnya kita mendapatkan dta seperti di bawah ini:

Tabel 2.5 Greedy by density

Properti objek Greedy by

i wi pi pi/wi profit weight Density

1 6 12 2 0 1 0

2 5 15 3 1 1 1

3 10 50 5 1 0 1

4 5 10 2 0 1 0

Total bobot 15 16 15 Total

keuntungan

65 37 65

2.3 Problema Knapsack dengan Exhaustive Search

Exhaustive Search merupakan salah satu strategi dalam Brute Force atau pendekatan secara langsung pada permasalahannya. Langkah-langkah pencarian solusi 0/1 Knapsack secara exhaustive search dirangkum dalam table di bawah ini dengan sebagai data pengujian diberikan data-data untuk w (Weight) dan P (Profit) :

Dengan kapasitas knapsack W = 16 10

5

50 ;

10

15 ;

5

12 ;

2

1 4

1 3

1 2

1 1

= =

= =

= =

= =

p w

p w

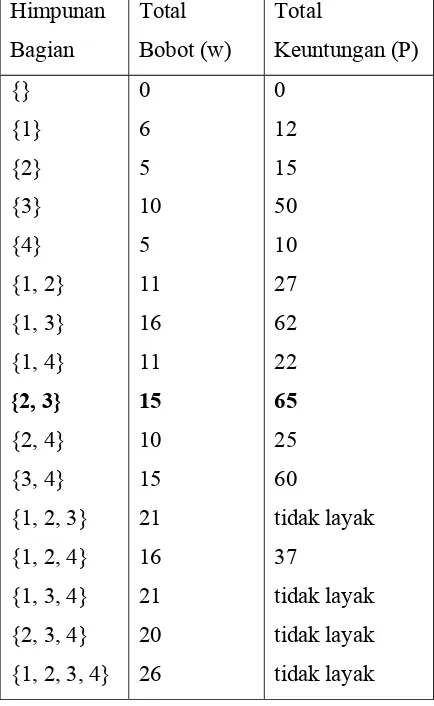
p w

Tabel 2.6 Exhaustive search Himpunan Bagian Total Bobot (w) Total Keuntungan (P) {} {1} {2} {3} {4} {1, 2} {1, 3} {1, 4} {2, 3} {2, 4} {3, 4} {1, 2, 3} {1, 2, 4} {1, 3, 4} {2, 3, 4} {1, 2, 3, 4}

0 6 5 10 5 11 16 11 15 10 15 21 16 21 20 26 0 12 15 50 10 27 62 22 65 25 60 tidak layak 37 tidak layak tidak layak tidak layak

Himpunan bagian objek yang memberikan keuntungan maksimum adalah {2, 3} dengan total keuntungan adalah 65.

2.4 Problema Knapsack dengan Algoritma Genetika

2.4.1. Algoritma Genetika

Algoritma genetika adalah algoritma komputasi yang diinspirasi oleh teori evolusi yang kemudian diadopsi menjadi algoritma komputasi untuk mencari solusi suatu permasalahan dengan cara yang alamiah. Algoritma ini dikembangkan oleh Goldberg yang terinspirasi dari teori evolusi Darwin yang menyatakan bahwa kelangsungan hidup suatu makhluk dipengaruhi oleh aturan “yang kuat adalah yang menang”. Darwin juga menyatakan bahwa kelangsungan hidup suatu makhluk dapat dipertahankan melalui proses reduksi, crossover, dan mutasi.

Sebuah solusi yang dibangkitkan dalam Algoritma Genetika disebut sebagai kromosom, sedangkan kumpulan kromosom-kromosom tersebut disebut sebagai populasi. Sebuah kromosom dibentuk dari komponen – komponen penyusun yang disebut sebagai gen dan nilainya dapat berupa bilangan numeric, biner, symbol atau pun karakter tergantung dari permasalahan yang ingin diselesaikan. Kromosom-kromosom tersebut akan berevolusi secara berkelanjutan yang disebut dengan generasi. Dlam tiap generasi, kromosom-kromosom tersebut dievaluasi tingkat keberhasilan solusinya terhadap masalah yang ingin diselesaikan (fungsi_objektif) menggunakan ukuran yang disebut fitness.

Untuk memilih kromosom yang tetap dipertahankan untuk generasi selanjutnya, dilakukanlah proses seleksi. Kromosom dengan nilai fitness tinggi akan memiliki peluang lebih besar untuk terpilih lagi pada generasi selanjutnya.

terbaik yang dihasilkan oleh Algoritma Genetika terhadap permasalahan yang ingin diselesaikan.

Algoritma Genetika sangat cocok untuk menyelesaikan masalah optimasi dengan ruang lingkup yang besar, karena Algoritma Genetika selalu bergerak dengan mencari sejumlah solusi sekaligus, selama solusi tersebut masih bersifat feasible (tidak melanggar constraint). Dengan setting parameter yang tepat, diharapkan salah satu dari sekian banyak solusi yang dibangkitkan oleh Algoritma Genetika merupakan solusi optimum global.

Akan tetapi, Algoritma Genetika ini juga masih memiliki kelemahan yaitu ketidakpastian untuk menghasilkan solusi optimum global, karena sebagian besar dari algoritma ini berhubungan dengan bilangan random yang bersifat probabilistik. Peranan programer disini adalah memaksimalkan probabilitas dalam menghasilkan solusi optimum global dengan cara membuat suatu skema pengolahan input argumen (fungsi fitness) dan setting parameter yang tepat.

2.4.2. Penerapan Algoritma Genetika dalam Problema Knapsack

Berikut adalah pengolahan fitness dan setting parameter yang kami terapkan : • Representasi Barang

Kami merepresentasikan barang dalam dua array, dimana array pertama berisi weight (berat) barang, dan array kedua berisi profit (keuntungan) barang.

Weight :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

180 170 100 150 270 120 190 140 180 100 140 70 150 120 190 140 80 150 200 130

Profit :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

200 150 90 220 250 80 170 120 190 70 160 110 120 160 220 140 120 110 160 180

Adapun constraint yang digunakan dalam aplikasi ini adalah weight. Jadi, total berat dari sekumpulan barang yang dipilih tidak boleh melebihi kapasitas Knapsack.

• Enconding Kromosom

Untuk mempresentasikan kromoso, kami menggunakan array 1 dimensi yang berisi 1 atau 0.

Misal:

Kromosom : 1 0 0 1 0 0 0 1 1 1 0 1 0 1 0 1 0 1 0 0 Art : Barang 1, 4, 8, 9, 10, 12, 14, 16, 18 diambil

Barang 2, 3, 5, 6, 7, 11, 13, 15, 17, 19, 20 tidak diambil.

• Termination Conditions

Pencarian solusi berhenti jika terdapat > 60% kromosom yang mempunyai nilai fitness maksimum ATAU jumlah lebih besar limit evolusi yang telah ditentukan (jika jumlah evolusi > 1000).

• Fitness Function

Pada evolusi di dunia nyata, individu bernilai fitness tinggi akan bertahan hidup. Sedangkan individu bernilai fitnesss rendah akan mati. Pada AG, suatu individu dievaluasi berdasarkan suatu fungsi tertentu sebagai ukuran niali fitness nya. Pada aplikasi ini, fitness dihitung dengan menjumlahkan profit tiap barang yang masuk ke dalam knapsack. Jika berat total dalam satu kromosom lebih besar daripada kapasitas maksimum knapsack, maka nilai fitnessnya diassign 0.

Selain dihitung nilai fitnessnya, dihitung pula berat total dari tiap kromosom untuk kemudian dilakukan pengecekan, dimana apabila ada kromosom yang berat totalnya melebihi kapasitas dari knapsack, maka akan dilakukan pencarian gen dalam kromosom tersebut yang bernilai 1 untuk diganti dengan nilai 0. Hal ini dilakukan terus menerus sampai dipastikan bahwa semua kromosom tidak ada yang melanggar constraint.

Dengan begitu setiap kromosom memiliki kemungkinan untuk terpilih menjadi parent secara lebih merata (lebih adil).

• Selection Function

Aplikasi ini menggunakan metode seleksi Roulette Wheel yang dikombinasikan dengan Elitism. Roulette Wheel merupakan suatu metode pemilihan kromosom untuk dijadikan parent, dimana komosom dengan fitness tinggi mempunyai peluang lebih besar untuk dijadikan parent. Sedangkan Elitism adalah suatu metode yang berguna untuk mempertahankan nilai best fitness suatu generasi agar tidak turun di generasi berikutnya.Dalam AG caranya adalah dengan mengcopykan individu terbaik (maxfitness) sebanyak yang dibutuhkan

• Crossover

Crossover merupakan proses mengkombinasikan bit bit dalam satu kromosom dengan kromosom lain yang terpilih sebagai parent. Jumlah kromosom yang mengalami crossover ditentukan oleh parameter Pcrossover. Dimana Pcrossover ini kami assign sebesar 80%, karena kami mengharapkan 80% dari populasi mengalami crossover agar populasi individu menjadi lebih variatif.

• Mutation

Mutation diperlukan untuk mengembalikan informasi bit yang hilang akibat crossover. Mutasi ini dilakukan pada tingkat gen, dan jumlah gen yang dimutasi kami batasi dalam suatu variable Permutasi sebesar 5%. Nilai ini kami rasa cukup karena semakin banyak gen yang dimutasi maka kualitas dari suatu individu bisa mengalami penurunan.

[image:33.612.214.565.90.647.2]

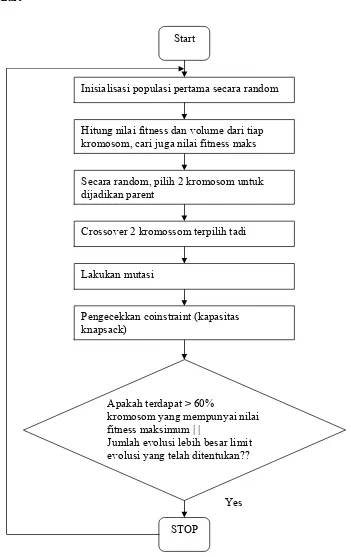
2.4.3. Flowchart

Gambar 2.6 Flowchart Algoritma Genetika Start

Inisialisasi populasi pertama secara random

Hitung nilai fitness dan volume dari tiap kromosom, cari juga nilai fitness maks

Secara random, pilih 2 kromosom untuk dijadikan parent

Crossover 2 kromossom terpilih tadi

Lakukan mutasi

Pengecekkan coinstraint (kapasitas knapsack)

Apakah terdapat > 60%

kromosom yang mempunyai nilai fitness maksimum | |

Jumlah evolusi lebih besar limit evolusi yang telah ditentukan??

STOP No

BAB 3

PEMBAHASAN

3.1. Pendekatan Basis

Sebelum kita memproses kasus Problema Knapsack, terlebih dahulu kita membahas ide dasarnya adalah pandang Problema Program Integer (PI) :

Minimum P=cT x (1)

Kendala Ax≤b (2)

x≥0 (3)

J j berbagai untuk

cacah ∈

j

x (4)

Komponen vektor

( )

x_{B k} layak basis terhadap PI yang diselesaikan sebagai problema kontinu dapat ditulis sebagai :

( )

xB k =βk −αki

( )

xN i −...−αkj∗

( )

xN j∗−...−αk,n−m

( )

xN n−m (5)

Catatan bahwa, pernyataan ini dapat ditemukan pada Tabel Akhir Simpleks. Andaikan

( )

x_{B k} adalah sebuah variabel integer dan kita asumsikan bahwa β_k dipartisi menjadi komponen integer dan sebagian kecil komponen telah diberikan yaitu:

[ ]

+ ,0≤ ≤1

= k k k

k β f f

β (6)

andaikan kita ingin menaikkan

( )

x_{B k} ke integer terdekat,

(

[ ]

β +1

)

. Ide dasar dari solusi yang baik kita boleh menaikkan variabel non basis, misalnya

( )

x_{N j∗} diatas batasannya dari Nol, asalkan α_kj∗yaitu salah satu elemen vektor α_kj∗ adalah negatif.

Ambil ∆_j∗ dijumlahkan dari bukan variabel

( )

x_{N j∗}. Sedemikian hingga nilai numerik dari skalar

( )

x_{B k} adalah integer.

∗

∗ ∗ = ₋− ∆

kj k j

f α

1

(7)

ketika hasil bukan basis tetap Nol. Dapat dilihat setelah mensubstistusikan ke persamaan (7) untuk

( )

x_{N j∗} dan dimasukkan ke perhitungan partisi dari β_k diberikan pada persamaan (6), kita tunjukkan :

( )

xB k =

[ ]

β +1

Maka,

( )

x_{B k} sekarang adalah integer.

Sekarang jelas bahwa bermain dengan varibel non basis adalah tugas yang sangat penting untuk integer yang cocok dengan variabel non-basis. Maka, hasilnya adalah untuk menjelaskan bahwa harus menjadi variabel non-integer untuk pembulatan,

Theorema 1. Tunjukkan bahwa IP (1)-(4) mempunyai solusi optimal, kemudian beberapa dari variabel non basis

( )

x_{N j∗} = 1, … ,n harus menjadi variabel non integer.

Bukti.

Menyelesaikan masalah slack variabel kontinu (bukan integer, kecuali pada kasus persamaan kendala). Jika kita mengesumsikan bahwa vektor variabel basis x_B terdiri dari seluruh slack variabel kemudian seluruh variabel integer akan menjadi vektor non-basis x_N dan karena itu bernilai integer.

3.2. Metode derivative

dibutuhkan agar dapat melihat bagaimana pergerakan maksimum dari bukan basis

( )

xN j∗ dinyatakan bahwa seluruh komponen dari x solusi layak.

Rasio ini akan diuji pada 2 kasus :

1. Variabel basis

( )

x_{B i≠k} dikurangi ke nol (batasan rendah) pertama. 2. Variabel basis

( )

x_{B k} dinaikkan ke integer.

Khususnya, cocok untuk tiap-tiap kasus diatas. Persamaan akan dihitung :

        = >

≠ * 0 *

1 min j i k i k α β ϑ α (8) * 2 =∆j

θ (9)

Sejauh akan dikeluarkan bukan basis

( )

x_{N j∗} batasan dari Nol, maka vector x adalah solusi layak akan bergantung pada uji rasio θ* diberikan sebagai berikut :

*

θ = min

(

θ₁,θ₂

)

(10)

Nyatanya, jika θ* =θ₁, persamaan dari variabel basis

( )

x_{B i≠k} akan tepat pada batasan rendah sebelum

( )

x_{B k} menjadi integer. Jika θ* =θ₂, nilai numerik dari variabel basis

( )

xB k akan menjadi integer dan layak untuk masih dipertahankan. Sama halnya, kita

mampu untuk mendapatkan hasil numerik dari variabel basis

( )

x_{B k} untuk integer tertutup

[ ]

β_k . Pada kasus ini bergerak penuh dari variabel non-basis khusus,

( )

x_{N j∗}, cocok untuk beberapa elemen vektor α_j, diberikan oleh :

kj k f f α =

∆ ' (11)

Urutan untuk mempertahankan uji layak untuk uji rasio θ* masih dibutuhkan. Mengingat bergerak dari variabel non-basis khusus, ∆, dinyatakan pada persamaan (7) dan (11). Hanya faktor persamaan tersebut membutuhkan perhitungan elemen yang cocok dari vektor α_j dapat dinyatakan sebagai :

, 1 ,

1 =

=_B− _j

j

j α

Oleh karena itu, untuk mendapatkan elemen utama dari vektor α_j kita akan

mampu membedakan kolom yang cocok untuk matriks [B]-1. Andaikan kita membutuhkan nilai dari elemen α_kj∗, misalkan vT_k untuk kolom ke – k vektor [B]-1,

kemudian kita mempunyai : 1

−

=e B

v T

k T

k (13)

berikutnya adalah nilai numerik dari α_kj∗ dihasilkan dari :

*

aj vT_k kj∗ =

α (14)

pada istilah Linier Programming (LP) operasi dilakukan pada persamaan (12) dan (13) dikatakan nilai operasi. Vektor mengurangi harga d_j digunakan untuk ukuran

kelemaan dari fungsi objektif dikarenakan oleh melepaskan variabel non-basis dari batasannya. Akibatnya, memutuskan non basis akan dilepaskan pada proses pembulatan, vektor d_j harus dimasukkan ke dalam perhitungan, maka

meminimumkan kelemahannya. Anggap bahwa solusi kontinu minimum diberikan batasan terendah pada beberapa solusi layak-integer. Namun, jumlah dari variabel khusus non-basis diberikan pada persamaan (7) atau (11), bergantung pada beberapa cara dari elemen yang cocok dari vektor α_j. Oleh karena itu, dapat diamati dengan

kelemahan dari nilai fungsi objektif antara melepaskan variabel non-basis

( )

x_{N j∗} agar

pembulatan variabel basis

( )

x_{B k} dapat diukur oleh rasio :

*

kj k d

α (15)

Urutan untuk meminimumkan kelemahan dari solusi optimal kontinu kita menggunakan strategi selanjutnya untuk menentukan yang mana variabel non basis bias dinaikkan ke batasan nol, maka,

m n j d kj k

j = −

        ,..., 1 , min * α (16)

Dari strategi “kendala aktif” dan partisi dari kendala yang cocok untuk basis (B), superbasis (S) dan non-basis (N) variabel dapat dituliskan :













=





























N S N

b

b

x

x

x

I

N

S

B

(18) atau b Nx Sx

Bx_b + _S + _N = (18)

x_N = b_N (19)

Basis matriks B di asumsikan bujursangkar dan non-singular, kita dapatkan:

N S

B Wx x

x =β − −α (20)

dimana

b B−1 =

β (22)

S B

W = 1 ₍₂₃₎

N B−1

=

α (24)

digeneralkan. Selanjutnya, theorema (1) diatas akan dijelaskan untuk Problema Knapsack.

Theorema 2. Andaikan Problema Knapsack mempunyai batasan solusi kontinu yang

optimal, kemudian kita dapat selalu mendapatkan non-integer y_j pada vektor variabel

basis optimum.

Bukti.

1. Jika variabel ini adalah non-basis, maka akan dibatasi. Oleh karena itu harus bernilai integer.

2. Jika y_jsuperbasis, mungkin untuk membuat basis y_j dan membawanya

kedalam non-basis pada batasannya diletakkan pada superbasis.

Bagaimanapun, uji rasio untuk persamaan (10) tidak dapat digunakan sebagai alat untuk jaminan bahwa menemukan hasil solusi integer optimal pada wilayah yang layak. Malahan, dapat digunakan uji kelayakan dari Minos pada urutan untuk cek apakah solusi integer layak atau tidak layak.

3.3. Hasil

Theorema 3. solusi optimal berlaku untuk Problema Knapsack yang mana seluruh integer variabel adalah superbasis.

Bukti.

1. Jika seluruh variabel integer di N, maka akan dibatasi.

2. Jika sebuah variabel adalah basis maka mungkin untuk yang lainnya. • Simpangan dengan variabel superbasis kontinu, atau

• Membuat variabel integer superbasis ini dan membawanya ke non-basis pada pada batasannya untuk mengganti basis yang memberikan solusi umum.

Pada kasus yang lainnya akan terjadi berbeda dan variabel basis

( )

x_{B i≠k} boleh batasannya sebelum

( )

x_{B k} menjadi integer. Atau dengan kata lain, berada pada situasi dimana :

1 * =∆

θ

Pada kasus ini kita mengerjakan variabel basis

( )

x_{B i}ke N dan posisinya pada basis variabel vektor akan digantikan oleh non-basis

( )

x_{N j∗}. Catatan

( )

x_{B k} masih variabel bais non-integer dengan nilai baru.

3.4. Algoritma

Setelah menyelesaikan masalah tersebut, langkah untuk mencari suboptimal tetapi solusi layak integer dari sebuah solusi optimal kontinu dapat dinyatakan sebagai berikut :

Misalkan,

[ ]

+ , 0≤ ≤1

= x f f

x (25)

menjadi solusi bagi permasalahan tersebut,

[ ]

x adalah komponen integer dari variabel non-integer x dan f sebagain kecil komponen.

Langkah 1. Dapatkan baris *i integer tak layak terkecil, seperti

{

i i

}

i* =min f ,1− f

Langkah 2. Hitung 1 * *

− =e B vT_{i i}T

adalah operasi utama. Langkah 3. Hitung σ_ij =vT_i*a_j

Dengan j tepat untuk meminimumkan

        ij j d j σ

I. Untuk nonbasis j pada batas terendah

Jika 0σ_ij < dan δ_i* = f_i hitung

(

)

ij i σδ

−− = ∆ 1 *

Jika 0σ_ij > dan δ_i* =1− f_i hitung

(

)

ij i σδ* 1− = ∆

Jika 0σ_ij < danδ_i* =1− f_i hitung

ij i σ δ − = ∆ *

Jika 0σ_ij > dan δ_i* = f_ihitung

ij i σδ*

= ∆

II. Untuk nonbasis j pada batas teratas

Jika 0σ_ij < dan δ_i* =1− f_i hitung

(

)

ij i σδ

−− = ∆ 1 *

Jika 0σ_ij > dan δ_i* = f_i hitung

(

)

ij i σδ* 1− = ∆

Jika 0σ_ij > dan δ_i* =1− f_i hitung

ij i σδ*

= ∆

Jika 0σ_ij < dan δ_i* = f_i hitung

ij i σ δ − = ∆ *

Sebaliknya unuk menuju non-basis non-integer selanjutnya atau superbasis j

(jika tersedia).

Akhirnya kolom j* dinaikkan dari batas terendah atau dikurangi dari batas teratas. Jika tak satupun berhasil lanjut ke i*.

Langkah 4. Hitung * 1

* j

j B α

α ₌ −

Langkah 5. Uji rasio; akan ada tiga kemungkinan untuk variabel basis pada urutan tetap layak dengan melepaskan non basis j* dari batasannya.

Jika j* batas terendah

Andaikan         − = >

≠ * 0 _*

min ij i B k i l x A i k α α         − − = >

≠ * 0 _*

min ij B i k i i k x u B α α ∆ = C

Pengerjaan maksimum dari j* bergantung pada :

(

A, B, C

)

min =

ϑ

Jika j* batas teratas

Andaikan         − = >

≠ * 0 _*

min ' ij i B k i l x A i k α α         − − = >

≠ * 0 _*

min ' ij B i k i i k x u B α α ∆ = ' C

Pengerjaan maksimum dari j* bergantung pada :

(

', ', '

)

min A B C

=

ϑ

Langkah 6. Pertukaran basis untuk 3 kemungkinan. 1. Jika A atau A’

• xBi'menjadi nonbasis pada batas terendah li'

• xj* menjadi bais (diganti xBi')

• xi* tetap basis (non-integer) 2. Jika B atau B’

• xBi'menjadi nonbasis pada batas teratas ui'

• xj* menjadi basis (diganti xBi')

3. Jika C atau C’

• xj* menjadi basis (diganti xi*)

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Kesimpulan yang dapat diproleh dari hasil penelitian yang telah dilakukan dalam tulisan ini adalah sebagai berikut :

1. Strategi melepaskan variabel non-basis dari batasannya, dikombinasikan dengan Metode “kendala aktif”, dan ide dari superbasis telah dihasilkan dari Problema Knapsack dan Integer Programming.

2. Setelah diselesaikan sebuah masalah dengan mengabaikan syarat-syarat pengintegralan, strategi ini digunakan untuk kekuatan variabel basis non-integer yang cocok untuk mengerjakan lingkungan point integernya.

3. Uji komputasi untuk tahap pengerjaan pada penelitian ini telah diuji coba pada pendekatan masalah yang lebih besar dapat dijalankan.

4.2. Saran

2. Problema Knapsack ini sering sekali terjadi di dunia nyata. Telah banyak penelitian dengan berbagai algoritma untuk menyelesaikannya diharapkan dapat menemukan algoritma lainnya yang dapat menghasilkan hasil yang lebih optimal.

DAFTAR PUSTAKA

Hapsoro, Bayu Kusumo. Diakses 10 Maret 2009. Knapsack Problem dengan

Algoritma Genetika. http: //stttelkom.ac.id

Kellerer, Hans, dkk. 2004. Knapsack Problems. Austria : University of Graz

Martello, Silvano dan Paolo Toth. 1989. Knapsack Problems: Algorithms and

computer Implementations. DEIS : University of Bologna.

Mawengkang, Herman. An Improved Direct Feasible Search Approach For Solving

Mixed-Integer Non Linier programming Problems : University of sumatera

Utara.

Muthohar, Muhammad Fiqri. Diakses 10 Maret 2009. Penerapan Algoritma Branch and Bound Pada Masalah Integer Knapsack. http : //www.informatika.org

Perdana, Naufal, dkk. Diakses 10 Maret 2009. Berbagai Macam Strategi Dalam

Mengatasi Permasalahan knapsack 0/1. http: //stttelkom.ac.id

Permata, Anggi Shena. Diakses 10 Maret 2009. Pemecahan Masalah Knapsack

Dengan Menggunakan Algoritma Branch and Bound. http:

//www.informatika.org

Susmito. Rendro, dkk. Diakses 10 Maret 2009 Knapsack Problem with Greedy Strategy. http: //stttelkom.ac.id