SIMULASI DINAMIKA ALIRAN SUNGAI CILIWUNG HULU
BERDASARKAN PRINSIP
ACTIVE - WALKER
DYO DWI PRAYUDA
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul “Simulasi Dinamika Aliran Sungai Ciliwung Hulu berdasarkan Prinsip Active-Walker” adalah benar karya saya dengan arahan dari Komisi Pembimbing dan belum pernah diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir Skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
DYO DWI PRAYUDA. Simulasi Dinamika Aliran Sungai Ciliwung Hulu Berdasarkan Prinsip Active-Walker. Dibimbing oleh HUSIN ALATAS dan HIDAYAT PAWITAN.
Active Walker (AW) merupakan salah satu pemodelan berbasis agen di mana walker sebagai agen dapat mengubah lingkungannya ketika ia berjalan, dan langkah selanjutnya dipengaruhi oleh lingkungan yang berubah tersebut. Pada penelitian ini dimodelkan dinamika aliran sungai Ciliwung Hulu berdasarkan prinsip active walker tersebut. Pemodelan ini menggunakan data DEM SRTM yang memiliki resolusi spasial 90 m x 90 m dan 15 m x 15 m. Data tersebut diolah dengan menggunakan software ArcGIS 9.3 untuk melihat data elevasi dari setiap titik-titik sungai. Data elevasi ini digunakan sebagai lanskap dalam pemodelan hulu sungai Ciliwung berdasarkan prinsip active walker. Pemodelan ini juga menggunakan data aliran, lebar dan kedalaman sungai yang didapat dari hasil survei lapang. Dari penelitian ini, didapat kesimpulan bahwa sungai Gunung Mas memiliki pengaruh terhadap kelajuan akhir di Bendungan Katulampa dibandingkan sungai Katulampa. Simulasi ini memiliki karakteristik aliran sungai yang hampir sama dengan keadaan DAS Ciliwung Hulu sehingga prinsip AW dapat digunakan untuk pemodelan sungai Ciliwung Hulu.
Kata Kunci : Active Walker, DAS Ciliwung Hulu, Aliran sungai
ABSTRACT
DYO DWI PRAYUDA. Dynamics Simulation of Ciliwung River Upstream Based on Active-Walker Principle. Supervised by HUSIN ALATAS dan HIDAYAT PAWITAN.
Active Walker ( AW ) is agent based modeling where walker as an agent change its environment when it runs , and the next step is influenced by the changing environment. In this study, modeled the dynamics of the Ciliwung River upstream based on active walker principle. This model use DEM SRTM data that has a spatial resolution of 90 m x 90 m and 15 m x 15 m. The data were processed using ArcGIS 9.3 software to view elevation data points of each river. The elevation data are used as landscape in Ciliwung river upstream model based on active walker principle. This model also uses a data of flow, width and depth of the river were obtained from field survey. From this research, we concluded that river of Gunung Mas has influence on the end speed of Katulampa’s dam than river of Katulampa. This simulation has similar characteristics of river flow with state of Upper Ciliwung so the AW principle can be used for modeling the Ciliwung river upstream .
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Fisika
SIMULASI DINAMIKA ALIRAN SUNGAI CILIWUNG HULU
BERDASARKAN PRINSIP
ACTIVE - WALKER
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2014
Judul Skripsi : Simulasi Dinamika Aliran Sungai Ciliwung Hulu Berdasarkan Prinsip Active-Walker
Nama : Dyo Dwi Prayuda NIM : G74100001
Disetujui oleh
Dr. Husin Alatas Pembimbing I
Prof. Dr. Ir. Hidayat Pawitan Pembimbing II
Diketahui oleh
Dr. Akhiruddin Maddu, M.Si Ketua Departemen Fisika
PRAKATA
Puji dan syukur penulis sampaikan ke hadirat Allah SWT yang telah melimpahkan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini. Dan tak lupa pula shalawat beriring salam kepada junjungan alam Muhammad SAW yang telah membawa kita dari zaman jahiliah ke zaman yang penuh ilmu seperti saat ini.
Skripsi ini penulis buat sebagai syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor. Skripsi ini membahas tentang “Simulasi Dinamika Aliran Sungai Ciliwung Hulu Berdasarkan Prinsip Active-Walker.”
Ucapan terima kasih penulis ucapkan kepada orang tua penulis dan teman-teman yang telah mendukung penulis dalam menyelesaikan tugas ini. Dan kepada pembimbing yang telah memberikan kepercayaan dan menyempatkan waktu kepada penulis untuk dapat menyelesaikan skripsi ini.
Semoga dengan dibuatnya skripsi ini pembaca dapat mengambil manfaatnya. Akhir kata penulis mengucapkan terima kasih.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 2
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
Prinsip Active-Walker 2
Jaringan Sungai DAS Ciliwung Hulu 3
METODE 3
Waktu dan Tempat Penelitian 3
Alat dan Bahan 3
Prosedur Analisis Data 4
HASIL DAN PEMBAHASAN 7
Simulasi dinamika aliran sungai Ciliwung Hulu 7
Perbandingan data survei dengan simulasi 11
SIMPULAN DAN SARAN 11
Simpulan 11
Saran 12
DAFTAR PUSTAKA 12
LAMPIRAN 13
DAFTAR TABEL
1 Data survei lapang masing-masing sungai di Ciliwung Hulu 8
2 Variasi kelajuan aliran pada tiap sungai 8
3 Variasi kelajuan aliran pada tiap sungai (asumsi terjadinya hujan pada
sungai Katulampa) 9
4 Variasi kelajuan aliran dengan pertambahan pada sungai Citeko 10
DAFTAR GAMBAR
1 Aliran air pada sungai 4
2 Aliran air pada percabangan sungai 5
3 Pola Aliran Sungai Ciliwung Hulu 7
4 Pembagian daerah stasiun cuaca di DAS Ciliwung Hulu 7 5 Hasil simulasi dengan variasi kelajuan tiap sungai 8 6 Hasil simulasi dengan variasi kelajuan tiap sungai (asumsi terjadinya
hujan pada sungai Katulampa) 9
7 Hasil simulasi dengan pertambahan kelajuan awal pada tiap sungai 10 8 Penggalan-area daerah aliran sungai Ciliwung Hulu 11
DAFTAR LAMPIRAN
PENDAHULUAN
Latar Belakang
Bagi masyarakat dan sebagian besar dari ilmuwan, sains biasanya dilihat sebagai sebuah algoritma untuk memprediksi dengan presisi tak terbatas secara teoritis. Misalnya memprediksi masa depan suatu obyek alami berdasarkan keadaannya pada saat ini. Isaac Newton (1643-1727), peletak dasar-dasar ilmu fisika, menunjukkan lebih dari tiga abad yang lalu bahwa dengan menggunakan beberapa konsep teoritis, seperti hukum gravitasi universal, seseorang dapat menghasilkan penjelasan untuk menafsirkan esensi dari gerak benda-benda luar angkasa. Hal ini dapat memprediksi secara akurat seperti terjadinya gerhana matahari atau bulan di masa yang akan datang. Sejak saat itu, pemikiran ilmiah didominasi oleh paradigma Newtonian. Alam semesta dapat dikualifikasikan sebagai persoalan yang sederhana4.
Selama tiga abad, paradigma Newtonian ini mencapai keberhasilan dalam mengeksplorasi hal kecil seperti komposisi atom, nuklir dan subnuklir sampai hal yang besar contohnya kosmologi. Di sisi yang lain, peristiwa sehari-hari pada dasarnya berkaitan antara fenomena yang melibatkan benda-benda yang dibentuk oleh interaksi subunit dan berlangsung pada skala makroskopik, ruang dan waktu. Dalam hal ini sangat mungkin memprediksi gerhana matahari atau bulan di masa datang, tetapi tidak mampu memprediksi cuaca di kawasan tersebut. Ini merupakan sesuatu yang menjadi daya tarik bahwa paradigma Newtonian memberikan pemikiran ilmiah yang menimbulkan gagasan mengenai kompleksitas atau dapat disebut sebagai sistem kompleks. Kompleksitas bukan sebuah metafora belaka atau cara yang baik untuk menempatkan hal-hal menarik tertentu, Hal ini merupakan fenomena yang berakar ke dalam hukum alam, di mana sistem yang melibatkan sejumlah besar berinteraksi subsistem di mana-mana4.
2
Tujuan Penelitian
Penelitian ini bertujuan membuat suatu model dinamika aliran dari hulu sungai Ciliwung berdasarkan prinsip Active-Walker. Dari simulasi dapat mengetahui besarnya kelajuan aliran sungai pada bendungan Katulampa.
TINJAUAN PUSTAKA
Prinsip Active Walker
Active Walker (AW) adalah salah satu pemodelan berbasis agen di mana walker sebagai agen dapat mengubah lingkungannya ketika ia berjalan, dan langkah selanjutnya dipengaruhi oleh lingkungan yang berubah tersebut. Dalam bentuk yang paling sederhana, perubahan lanskap oleh walker tetap sama pada setiap langkah. Secara umum, perubahan lansekap oleh walker dan/atau lingkungan itu sendiri mungkin tergantung waktu. Kemunculan “Active Walker” dapat dilihat dari tiga perspektif yang berbeda:5
1. AW sebagai prinsip mengorganisasi diri
Berbagai macam struktur dan pola diamati di alam dapat diklasifikasikan ke dalam sejumlah kecil kategori, banyak dalam kategori yang sama mirip satu sama lain. Untuk menghasilkan secara efisien, adalah wajar untuk mengasumsikan bahwa alam akan mengadopsi beberapa prinsip pengorganisasian sederhana. Dua kasus yang ekstrim adalah "Prinsip Keteraturan" dan "Prinsip Ketakteraturan," misalnya pada kristal dan gas. Sebuah skema yang lebih menarik adalah "Prinsip Self-Similarity," sehingga menimbulkan fraktal. Namun, tidak setiap struktur dalam alam adalah fraktal, harus ada setidaknya satu lagi skema, dan itu adalah "Prinsip Active Walker". Dengan meninggalkan aturan perubahan lansekap dan aturan melangkah dari walker (yang akan ditentukan sesuai dengan fenomena tertentu dalam pemodelan), skema AW sangat sederhana dan fleksibel, dan oleh karena itu sangat kuat. Tergantung pada aturan yang diadopsi, AW bisa menimbulkan struktur fraktal maupun non-fraktal.5
2. AW membuat kondisi yang baru pada setiap langkahnya
3 3. AW digunakan sebagai agen simulasi
Baru-baru ini, simulasi berbasis agen merupakan pendekatan yang banyak digunakan dalam pemodelan sistem yang kompleks, khususnya dalam sistem biologi, ekologi dan sosial. Para agen mungkin atau tidak menjadi sangat cerdas, tetapi mereka selalu harus melakukan beberapa tugas seperti penginderaan dan pengukuran lingkungan, melakukan beberapa perhitungan, dan mengubah lokasi mereka dan keadaan internal. Dengan definisi ini, partikel-partikel yang digunakan dalam simulasi cairan Monte Carlo juga agen, partikel tersebut harus menjaga momentum dan energinya sendiri, menghitung hukum kekekalan momentum dan energi, dan mengubah arah pergerakan yang sesuai. Dalam hal ini, semua simulasi (mulai dari satu tingkat ke bawah) adalah berbasis agen5.
Jaringan Sungai pada DAS Ciliwung Hulu
Jaringan sungai dapat mempengaruhi besarnya debit aliran sungai yang dialirkan oleh anak-anak sungainya. Parameter ini dapat diukur secara kuantitatif dari nisbah percabangan yaitu perbandingan antara jumlah alur sungai orde tertentu dengan orde sungai satu tingkat di atasnya. Nilai ini menunjukkan bahwa semakin tinggi nisbah percabangan berarti sungai tersebut memiliki banyak anak-anak sungai dan fluktuasi debit yang terjadi juga semakin besar9.
Orde sungai adalah posisi percabangan alur sungai di dalam urutannya terhadap induk sungai pada suatu DAS. Semakin banyak jumlah orde sungai, semakin luas dan semakin panjang pula alur sungainya. Orde sungai dapat ditetapkan dengan metode Strahler. Berdasarkan metode Strahler, alur sungai paling hulu yang tidak mempunyai cabang disebut dengan orde pertama (orde 1), pertemuan antara orde pertama disebut orde kedua (orde 2), demikian seterusnya sampai pada sungai utama9.
METODE
Waktu dan Tempat Penelitian
Penelitian ini dilaksanakan pada bulan Juni 2013 sampai bulan Desember 2013. Tempat penelitian dilakukan di laboratorium Fisika Teori dan Komputasi, Departemen Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor (IPB) dan DAS hulu sungai Ciliwung.
Alat dan Bahan
4
Prosedur Analisis Data
Prinsip Active-Walker
Active walker (AW) adalah salah satu pemodelan berbasis agen di mana walker sebagai agen dapat mengubah lingkungannya ketika ia berjalan, dan langkah selanjutnya dipengaruhi oleh lingkungan yang berubah tersebut. Dinamika aliran sungai berdasarkan prinsip AW ditentukan oleh tiga aturan:
1. Aliran air didefinisikan sebagai agen dengan kecepatan aliran, lebar dan kedalaman sungai sebagai komponen-komponennya
2. Air mengalir menuju tempat yang lebih rendah
3. Pertemuan dua agen dari cabang sungai yang berbeda ditentukan dengan hukum kekekalan massa-momentum
Hukum kekekalan Energi Mekanik
Air sungai mengalir dari daerah yang tinggi menuju daerah yang lebih rendah berdasarkan hukum kekekalan energi dengan kelajuan aliran sebagai berikut:
Hukum kekekalan energi mekanik
(1.1)
(1.2)
g (1.3)
g (1.4)
dengan:
= kelajuan aliran sungai pada waktu ke t (m/s) = kelajuan aliran sungai awal (m/s)
g = konstanta gravitasi terkoreksi (m/s2)
Δh = perbedaan ketinggian sungai (m)
5 Hukum Kekekalan Massa-Momentum
Pada percabangan sungai terjadi tumbukan antara aliran air. Diasumsikan tumbukan ini terjadi secara inelastis. Aliran air pada percabangan sungai memenuhi hukum kekekalan massa-momentum sebagai berikut :
Hukum kekekalan momentum
(2)
Hukum kekekalan massa
(3)
dengan , persamaan (5) menjadi:
(4)
masing-masing suku dibagi dengan perubahan waktu
(5.1)
(5.2)
Dari persamaan (4) dan (7b)
(6.1)
(6.2)
(6.3)
Dengan dan persamaan (8c) menjadi :
g g
g (7)
dengan :
= kedalaman sungai (m) = lebar sungai (m)
= kelajuan aliran sungai (m/s)
g = konstanta gravitasi terkoreksi (m/s2)
g = 9 x 10-5 m/s2
= perbedaan ketinggian sungai (m) = sudut antara dan
6
Perubahan Bentuk Sungai
Pada percabangan sungai, energi total sungai yang bertumbukan lebih besar daripada energi pada sungai hasil tumbukan. Selisih dari energi ini digunakan untuk menggerus sungai. Penggerusan sungai menyebabkan perubahan bentuk pada sungai. Penggerusan ini terjadi pada lebar dan kedalaman sungai. Penggerusan pada lebar dan kedalaman sungai diasumsikan terjadi secara eksponensial.
Penggerusan pada lebar sungai:
; (8.1) ; > (8.2)
dengan:
= lebar sungai pada waktu ke t (m) = lebar sungai awal (m)
α = konstanta penggerusan lebar sungai
α = 0.62821 x 10-2
Penggerusan pada kedalaman sungai:
; (9.1) ; > (9.2)
dengan:
= kedalaman sungai pada waktu ke t (m) = kedalaman sungai awal (m)
β = konstanta penggerusan kedalaman sungai
β = 0.55 x 10-2
Pengolahan Data DEM SRTM
7
HASIL DAN PEMBAHASAN
Simulasi dinamika aliran sungai Ciliwung Hulu
Bagian hulu DAS (Daerah Aliran Sungai) Ciliwung meliputi sebagian besar wilayah Kabupaten Bogor dan Kota Bogor. DAS Ciliwung Hulu seluas 14.860 ha secara geografis terletak pada 106º 49º 40” – 07º 00’ 5” BT dan 6 º 38’ 5“ LS
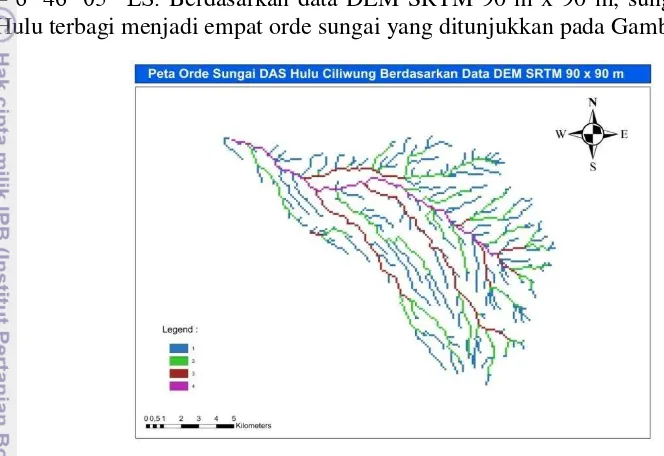
– 6º 46’ 05” LS. Berdasarkan data DEM SRTM 90 m x 90 m, sungai Ciliwung Hulu terbagi menjadi empat orde sungai yang ditunjukkan pada Gambar 3.
Gambar 3 Pola Aliran Sungai Ciliwung Hulu
Pada simulasi dinamika aliran sungai Ciliwung Hulu ini didefinisikan sebanyak 126 sumber air (titik awal air mengalir) yang terdapat pada DAS Ciliwung Hulu. Sumber-sumber air ini dikelompokkan menjadi lima bagian berdasarkan stasiun cuaca di DAS Ciliwung Hulu yaitu Katulampa, Ciliwung Hulu, Citeko, Gunung Mas, dan Pasir Muncang. Pembagian daerah aliran sungai dapat dilihat pada Gambar 4.
8
Dari penelitian ini akan dilihat besarnya kelajuan aliran sungai pada keluaran DAS yang merupakan bendungan Katulampa. Kedalaman, lebar dan kelajuan aliran sungai masing-masing daerah berdasarkan survei lapang dapat dilihat pada tabel berikut:
Tabel 1 Data survei lapang masing-masing sungai di Ciliwung Hulu
Stasiun cuaca Kelajuan aliran (m/s) Lebar sungai (m) Kedalaman sungai (m)
Katulampa 0.527 1.55 0.3
Ciliwung Hulu 0.429 3.12 0.1
Citeko 0.342 4.85 0.2
Gunung Mas 0.94 2.77 0.4
Pasir Muncang 0.437 1.81 0.3
Berdasarkan data tersebut, pada bendungan Katulampa dalam simulasi ini menghasilkan kelajuan aliran sebesar 0.94 m/s, kedalaman sungai 0.4248 m dan lebar sungai sebesar 70 m. Untuk mempelajari dinamika aliran sungai Ciliwung Hulu divariasikan kelajuan aliran pada masing-masing sungai seperti yang tertera pada tabel berikut:
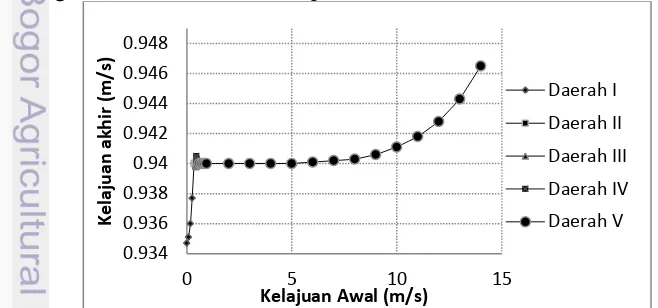
Tabel 2 Variasi kelajuan aliran sungai pada tiap sungai Kelajuan sungai pertama dapat dilihat dengan perubahan kelajuan yang konstan maka kelajuan di bendungan Katulampa mengalami perubahan secara eksponensial. Sedangkan pada sungai kedua sampai keempat, perubahan kelajuan aliran sungai pada keluaran DAS terlihat konstan. Pada sungai kelima kelajuan awal ditambah hingga mencapai 14 m/s untuk melihat perubahan kelajuan yang terjadi di bendungan Katulampa. Semakin besar kelajuan awal pada sungai kelima maka kelajuan aliran di bendungan Katulampa semakin besar. Perubahan yang terjadi pada sungai kelima ialah secara eksponensial.
9 Pada simulasi ini juga diasumsikan terjadinya hujan pada sungai tertentu sehingga kelajuan aliran sungai tersebut meningkat. Sungai yang dijadikan sampel ialah sungai Katulampa. Pada sungai ini diasumsikan kelajuan aliran sungai meningkat menjadi 1.527 m/s. Kelajuan aliran pada setiap sungai dapat dilihat pada tabel berikut:
Tabel 3 Variasi kelajuan aliran sungai pada tiap sungai (asumsi terjadinya hujan pada sungai Katulampa)
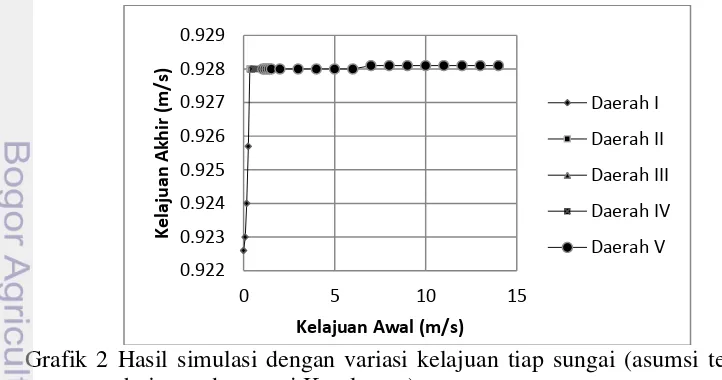
Hasil dari simulasi tersebut dapat dilihat pada Grafik 2. Dari Grafik 2, dapat dilihat perubahan kelajuan aliran pada keluaran DAS menunjukkan hasil yang hampir sama dengan grafik 1. Perubahan secara eksponensial terjadi pada sungai pertama. Sedangkan perubahan konstan terjadi pada sungai kedua sampai keempat. Selain itu, kelajuan awal pada sungai kelima juga ditambah hingga 14 m/s. Kelajuan akhir di bendungan Katulampa terlihat konstan dengan penambahan tersebut. Dari kedua sungai tersebut dapat diketahui bahwa penambahan kelajuan awal pada sungai Katulampa tidak mempunyai pengaruh besar terhadap kelajuan di bendungan Katulampa. Sedangkan pada sungai Gunung Mas perubahan kelajuan awal akan mempengaruhi kelajuan pada bendungan Katulampa. Berdasarkan simulasi ini dilihat bahwa kelajuan aliran air di bendungan Katulampa menghasilkan respon yang berbeda dengan pertambahan kelajuan aliran air pada tiap aliran sungai.
Grafik 2 Hasil simulasi dengan variasi kelajuan tiap sungai (asumsi terjadinya hujan pada sungai Katulampa)
Dalam simulasi juga dilihat perubahan kelajuan aliran pada bendungan Katulampa dengan pertambahan kelajuan aliran pada setiap sungai. Pertambahan
10
kelajuan aliran sebesar 0.1, 0.2, dan 0.3 m/s. Dari pertambahan ini, divariasikan kelajuan pada sungai pertama (Citeko). Kelajuan aliran yang telah ditambah, kemudian divariasikan menjadi lima kelajuan awal. Variasi kelajuan awal tersebut dapat dilihat pada Tabel 4.
Tabel 4 Variasi kelajuan aliran dengan pertambahan pada sungai Citeko
Kelajuan awal (m/s) v0 (m/s) v0 + 0.1 (m/s) v0 + 0.2 (m/s) v0 + 0.3 (m/s)
Hasil simulasi merupakan kelajuan akhir pada bendungan Katulampa berdasarkan variasi kelajuan awal. Kelajuan akhir tiap pertambahan diselisihkan dengan kelajuan akhir tanpa pertambahan kelajuan. Pembagian variasi kelajuan awal pada grafik dapat dijelaskan menurut rumus berikut :
dengan :
= variasi kelajuan awal
Hasil simulasi ini dapat dilihat pada Grafik 3. Dengan pertambahan kelajuan awal secara konstan pada setiap sungai dihasilkan kelajuan aliran di Bendungan Katulampa yang berbeda tiap pertambahan.
11 Perbandingan data survei dengan simulasi
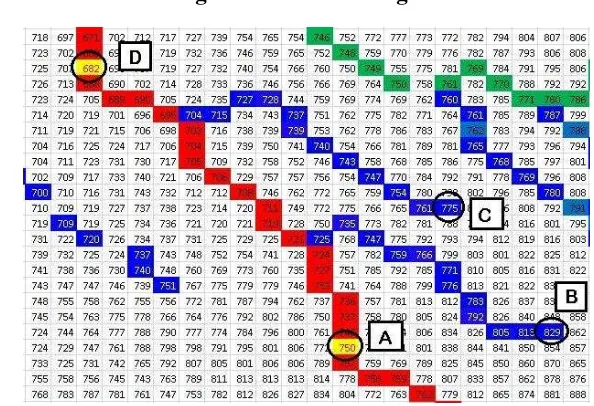
Untuk membandingkan hasil simulasi kelajuan aliran pada DAS Ciliwung Hulu dengan data survei lapang, diambil salah satu penggalan-area pada DAS Ciliwung. Titik A, B dan C merupakan kelajuan awal pada simulasi, sedangkan titik D merupakan titik yang akan dilihat besar kelajuan alirannya dari simulasi. Dari data survei lapang, kelajuan aliran air pada titik A sebesar 0.342 m/s dan pada titik D sebesar 0.9 m/s. Untuk titik B dan C, diasumsikan memiliki kelajuan aliran yang sama dengan titik A. Asumsi ini berdasarkan persamaan karakteristik lansekap pada daerah tersebut. Dari hasil simulasi didapatkan kelajuan aliran pada titik D sebesar 0.7311 m/s. Hasil ini mendekati kelajuan aliran pada data survei lapang. Dari hasil tersebut dapat dilihat bahwa karakteristik dari simulasi ini hampir sama dengan keadaan DAS Ciliwung Hulu.
SIMPULAN DAN SARAN
Simpulan
DAS Ciliwung Hulu memiliki karakteristik sungai yang terbagi menjadi empat orde berdasarkan metode strahler. Prinsip AW dapat digunakan dalam simulasi dinamika aliran dari sungai Ciliwung Hulu. Berdasarkan variasi kelajuan aliran tiap sungai, dapat disimpulkan bahwa sungai yang mempengaruhi kelajuan di Bendungan Katulampa ialah sungai Gunung Mas. Sungai ini dapat dijadikan sebagai fokus utama dalam pengurangan kelajuan di Bendungan Katulampa seperti pembuatan waduk. Berdasarkan perbandingan data survei dan simulasi dari penggalan-area Ciliwung Hulu, disimpulkan bahwa simulasi ini memiliki karakteristik aliran sungai yang hampir sama dengan keadaan DAS Ciliwung Hulu sebenarnya.
12
Saran
Perlu data survei yang lebih baik dan akurat untuk melihat karakteristik dari simulasi. Untuk simulasi, perlu pengkajian lagi untuk mengkoreksi kesalahan dalam pemograman. Hal ini agar kelajuan aliran dapat divariasikan pada setiap daerah dan dapat disimpulkan sungai yang mempunyai pengaruh terbesar terhadap kelajuan aliran akhir di Bendungan Katulampa.
DAFTAR PUSTAKA
[1] Giancoli, Douglas C. 2008. Fisika Jilid I (Terjemahan). Jakarta : Erlangga. [2] Jalali, Mohammad Reza, Abbas Afshar, Miguel A. Marino. 2005. “Ant
Colony Optimization Algorithm (ACO); A new heuristic approach for
engineering optimization”. Proceedings of the 6th WSEAS Int. Conf. on Evolutionary Computing, Lisbon, Portugal, June 16-18, 2005 (pp188-192). 7 September 2013.
[3] Lam, Lui. 1998. Nonlinear Physic for Beginners. Singapore : World Scientific Publishing Co. Pte. Ltd.
[4] Lam, Lui. 2003. Introduction to Nonlinear Physics. USA : Springer-Verlag New York, Inc.
[5] Lam, Lui. Desember 2004, "Active Walks: The First Twelve Years (Part I)". International Journal of Bifurcation and Chaos, Vol. 15, No. 8 (2005) 2317-2348, http://www.worldscientific.com/doi/abs/10.1142/ S02181274 05013344.
[6] Lam, Lui. Mei 2005, "Active Walks: The First Twelve Years (Part II)". International Journal of Bifurcation and Chaos, Vol. 16, No. 2 (2006) 239-268, http://www.worldscientific.com/doi/abs/10.1142/S0211274060 14782. [7] Nicolis, Gregoire, Catherine Nicolis. 2007. Foundations of Complex
Systems. Singapore : World Scientific Publishing Co. Pte. Ltd.
[8] Rabanal, Pablo, Ismael Rodr´ıguez, and Fernando Rubio. 007. Using River Formation Dynamics to Design Heuristic Algorithms. S.G. Akl et al.(Eds.):
UC 2007, LNCS 4618, pp. 163–177, 2007.
http://www.researchgate.net/publication/221302036_Using_River_Form ation_Dynamics_to_Design_Heuristic_Algorithms. 4 September 2013. [9] Rahayu S, Widodo RH, van Noordwijk M, Suryadi I dan Verbist B. 2009.
Monitoring Air di Daerah Aliran Sungai. Bogor, Indonesia. World Agroforestry Centre - Southeast Asia Regional Office. http://www.worldagroforestry.org/downloads/publications/PDFs/B16396.P DF (Diakses 22 September 2013).
13
LAMPIRAN
Lampiran 1 : Program untuk simulasi formasi dan dinamika sungai Ciliwung Hulu.
v0 = [0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 0.342045455 0.342045455 ... 0.342045455 0.342045455 ...
14
0.428977273 0.428977273 0.428977273 0.428977273 ... 0.428977273 0.428977273 0.428977273 0.428977273 ... 0.428977273 0.428977273 0.428977273 0.428977273 ... 0.428977273 0.436538462 0.436538462 0.436538462 ... 0.436538462 0.436538462 0.436538462 0.436538462 ... 0.436538462 ...
0.527419355 0.527419355 0.527419355 0.527419355 ... 0.527419355 0.527419355 ...
15
alpha1 = 0.62821e-2; %konstanta penggerusan lebar sungai beta1 = 0.55e-2; %konstanta penggerusan kedalaman sungai alpha2 = 0.62821e-2;
cf = 0.9e-4*(1+dh./h0); %konstanta gravitasi terkoreksi k0 = 0;
l0 = 0;
% Initial Condition
while p <=length(A) % && p~=0
16
if (v(i-1,j) ~= 0) && (i~=a+1) && (j~=b) if R1 == 0
17
18
elseif (v(i,j+1) ~= 0) && (j~=b-1) && (i~=a) if R4 == 0
19 exp(alpha1*width(i+1,j+1)/width(i,j));
elseif width(i+1,j+1) < width(i,j) width(i,j) = width(i+1,j+1)*...
elseif (v(i-1,j-1) ~= 0) && (i~=a+1) && (j~=b+1) if R6 == 0 elseif width(i-1,j-1) < width(i,j)
width(i,j) = width(i-1,j-1)*...
elseif (v(i+1,j-1) ~= 0) && (i~=a-1) && (j~=b+1) if R7 == 0
v(i,j) = sqrt(h(i,j)^2*width(i,j)^2*(v(a,b)^2+...
20 elseif width(i+1,j-1) < width(i,j)
width(i,j) = width(i+1,j-1)*...
21 exp(alpha1*width(i-1,j+1)/width(i,j));
22
if s > 8 k = 0; else
k = k + 1; end
s = 0; end
p = p + 1; k = 1; T = 1;
R1 = 0;R2 = 0;R3 = 0;R4 = 0; R5 = 0;R6 = 0;R7 = 0;R8 = 0; end
figure(1) surf(v);
shading flat;
view(0,270);
title('Speed Lanscape');colorbar;
figure(2) surf(width);
shading flat;
view(0,270);
title('Width Lanscape');colorbar;
figure(3) surf(h);
shading flat;
view(0,270);
title('Depth Lanscape');colorbar;
figure(4) surf(Debit);
shading flat;
view(0,270);
23