PERHITUNGAN PENAMPANG HAMBURAN ELASTIK
ELEKTRON SIGMA
��
+→ ��
+,
��
�→ ��
�, DAN
��
−→ ��
−AHMAD YASIN
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN SUMBER
INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi yang berjudul perhitungan penampang hamburan elastik elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ− adalah benar karya saya dengan arahan pembimbing bapak
Sidikrubadi Pramudito, M.Si dan belum diajukan kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun yang tidak diterbitkan dari penulis lain telah dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis ini kepada Institut Pertanian Bogor.
Bogor, Maret 2013
Ahmad Yasin
ABSTRAK
AHMAD YASIN, perhitungan penampang hamburan elastik elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan Σ−→ Σ−. Dibimbing oleh SIDIKRUBADI PRAMUDITO, M.Si.
Perhitungan penampang hamburan elastik dari interaksi Σ+→
Σ+, Σ0 → Σ0, dan Σ−→ Σ− dilakukan melalui studi pustaka untuk mempelajari ulang teori yang telah dikemukakan sebelumnya, kemudian dicocokkan dengan data yang telah dilakukan dalam eksperimen. Nilai yang didapat dari perhitungan tersebut bergantung pada energi elektron datang dan sudut hamburnya. Pada variasi sudut antara 50 sampai 1350 nilai penampang hamburan semakin kecil dengan pertambahan sudut. Serupa dengan itu pada selang energi elektron datang antara 0.3 GeV sampai 3.5 GeV terjadi penurunan nilai penampang hamburan dengan pertambahan energi. Perbedaan nilai penampang hamburan yang signifikan dari ketiga interksi tersebut terjadi pada sudut 50 terdapat perubahan kemiringan kurva setiap perubahan sudut.
Kata kunci : penampang hamburan, negatif, nol, sigma-positif.
ABSTRACT
AHMAD YASIN, calculation of the elastic scattering cross section electron sigma
Σ+→ Σ+, Σ0 → Σ0, and Σ−→ Σ−. Supervised by SIDIKRUBADI PRAMUDITO, M.Si.
Elastic scattering cross-section calculation of Σ+→ Σ+, Σ0 → Σ0, and
Σ−→ Σ−interaction research by literature study to review the theories that
have been proposed, then the result matched with experiment data. Values obtained from these calculations depend on incoming electrons energy and scattering angle. On angular variation between 50 to 1350 the scattering cross section values was decreasing by increasing angle. Similarly, there was decreasing value of scattering cross section in energy range between 0.3 GeV to 3.5 GeV as well as increasing energy electron. Scattering cross section difference value of the three interactions perform in the 50 angle. There was a slope change in curve with every angle changes.
PERHITUNGAN PENAMPANG HAMBURAN ELASTIK
ELEKTRON SIGMA
��
+→ ��
+,
��
�→ ��
�, DAN
��
−→ ��
−AHMAD YASIN
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Departemen Fisika
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul : Perhitungan Penampang Hamburan Elastik Elektron Sigma
Σ+→ Σ+, Σ0 → Σ0, dan Σ−→ Σ− Nama : Ahmad Yasin
NIM : G74080065
Disetujui oleh
Drs. Sidikrubadi Premudito, M.Si.
Pembimbing
Diketahui oleh
Dr. Akhiruddin Maddu, M.Si
Kepala Departemen Fisika
PRAKATA
Segala puji hanya untuk Allah SWT yang menciptakan segala sesuatunya dengan keteraturan. Tak lupa shalawat dan salam kepada utusannya Muhammad SAW sebagai pembawa risalah kenabian dan ilmu pengetahuan.
Alhamdulillah, Penelitian tugas akhir dengan judul perhitungan penampang hamburan elastik elektron sigma Σ+ → Σ+, Σ0 → Σ0, dan Σ−→ Σ−, akhirnya dapat diselesaikan dengan baik. Ucapan terimakasih juga penulis sampaikan kepada :
1. Abi dan Umi, Abdurrahman Tamin dan Suharni Sutono (alm.) atas dukungan serta doa tulusnya yang telah diberikan selama proses belajar di IPB. Juga Bunda yang sempat memberikan dorongan di akhir perjuangan. Adik-adikku Salsabila Khatibatunnisa, Ainun Mardhiah, Muhammad Kholil, Shoffa Adillah, Fathi Mubarak, Rif’at Basya yang selalu memberikan inspirasi, semangat, dukungan, canda dan kebersamaan.
2. Bapak Drs. Sidikrubadi Pramudito, M.Si. atas kesabarannya sebagai dosen pembimbing dengan terus memberikan bimbingan, saran, bahkan kritik dan motivasi. Bapak Jajang Juansah, M.Si selaku pembimbing akasemik. Bapak Dr.Muhammad Nur Indro M.Si dan Bapak Dr.Akhiruddin Maddu M.Si atas masukan dan sarannya sebagai dosen penguji. Bapak Dr. Husin Alatas, M.Si. sebagai kepala bagian teori. Juga bapak kepala departemen fisika yang juga sudah disebutkan namanya serta segenap dosen fisika yang telah banyak memberikan ilmunya.
3. Kak Didik, Kak Gema Buana Putra, Kak Hari Bowo, Kak Erik Wahyu, Kak Maulana Syawal yang sempat memberi banyak Inspirasi tentang kehidupan dan pembelajaran.
4. Beasiswa Karya Salemba Empat (KSE), Beasiswa Peningkatan Prestasi Akademik (PPA), Beasiswa Mandiri DPU-DT, serta semua pihak yang sempat membantu penulis untuk biaya perkuliahan.
5. Seluruh civitas Departemen Fisika IPB, Fakultas MIPA, Fisika 45, KMF, HIMAFI, Kader KAMMI Daerah Bogor juga Komisariat IPB, santri PPM Al-Inayah, pejuang Serum-G IPB, rekan-rekan DPM MIPA 2009-2010, Penghuni Badut, finalis nasional OSN Pertamina 2011, SAS’11, sahabat 198-199, keluarga El-Imtyaz, Designer salamART, BeM-dt, dan Laskar Mahameru, atas kenangan dan kebersamaan kita selama ini.
6. Semua pihak yang telah menemani, menginspirasi, menyemangati, memberikan masukan mengkritik penulis sepanjang perjalanan menuntut ilmu hingga terselesaikannya skripsi ini.
Semoga Allah membalas semuanya dengan yang lebih baik, agar silaturahmi kita tetap terjaga tanpa batas waktu. Dan semoga tulisan ini dapat member manfaat yang seluas-luasnya.
Bogor, Maret 2013
vi
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... vi
DAFTAR LAMPIRAN ... vi
PENDAHULUAN ... 1
Latar Belakang ... 1
Rumusan Masalah ... 1
Tujuan Penelitian ... 1
Hipotesa ... 1
TINJAUAN PUSTAKA ... 2
Penampang Hamburan ... 2
Penampang Hamburan Elektron Sigma ... 2
Kinematika Hamburan Elektron Sigma ... 3
METODE ... 4
Tempat dan Waktu Penelitian ... 4
Alat dan Bahan ... 4
Prosedur Penelitian ... 4
HASIL DAN PEMBAHASAN ... 6
Karakteristik Σ+, Σ0, Dan Σ sebagai Partikel Sasaran ... 6
Penampang Hamburan Elektron Sigma ... 6
Model Penampang Hamburan Pada Sudut Kecil ... 7
Model Penampang Hamburan Pada Sudut Besar ... 9
KESIMPULAN DAN SARAN ... 11
DAFTAR PUSTAKA ... 12
LAMPIRAN ... 13
DAFTAR GAMBAR
Halaman 1 Proses hamburan elastik elektron sigma ... 4 2 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 50
... 8 3 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 150
... 9 4 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 900
... 10 5 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi sudut hamburan pada energi elektron
datang 0,3 GeV ... 10
DAFTAR LAMPIRAN
Halaman 1 Program Komputer ... 12 2 Grafik Penampang Hamburan Pada Berbagai Sudut Hambur ... 14 3 Data Hasil Perhitungan Penampang Hamburan
PENDAHULUAN
Latar Belakang
Jauh pada masa lalu manusia telah menduga bahwa materi walaupun kelihatannya kontinyu, memiliki struktur tertentu pada tingkat mikroskopis di luar jangkauan indra. Dugaan ini mengambil bentuk yang nyata hingga kira-kita satu setengah abad yang lalu, ketika itu keberadaan atom dan molekul, partikel dasar dalam bentuk yang lazim telah dapat ditunjukkan.1
Selanjutnya upaya pencarian partikel yang elementer terus berkembang, menghasilkan penemuan-penemuan sejumlah partikel yang dianggap sebagai penyusun alam semesta. Partikel tersebut dikelompokkan menjadi empat family,
boson, lepton, meson, dan barion. Meson dan barion dikenal sdebagai hadron. Klasifikasi tersebut umumnya muncul dari spin, masa, dan jenis interaksi partikel.2
Hadron kemudian diyakini merupakan partikel berstruktur yang tersusun atas kuark. Kuark dibayangkan sebagai partikel elementer seperti juga lepton, pada hakikatnya merupakan partikel titik yang tidak memiliki struktur internal, tetapi berbeda dengan lepton, kuar memiliki muatan listrik pecahan.1
Sigma merupakan salah satu kelompok hadron dari kelas barion. Seperti hadron lainnya, ia tersusun dari kuark. Sigma-positif (Σ+), sigma-nol (Σ0), dan sigma-negatif (Σ−), ketiganya tersusun dari tiga buah kuark. Σ+memiliki dua buah kuark up(u) dan sebuah kuark strange(s). Σ0 terdiri dari satu kuark u, satu kuark s dan satu kuark down(d). Dua buah kuark d dan sebuah kuark s juga terdapat pada pada Σ−.3
Perumusan Masalah
1. Bagaimana perumusan penampang hamburan elastik dari interaksi Σ+→
Σ+, Σ0 → Σ0, dan Σ−→ Σ−?
2. Bagaimana nilai masing-masing penampang hamburan elastik dari Σ+→
Σ+, Σ0 → Σ0, dan Σ−→ Σ−?
Tujuan Penelitian
Tujuan dari dilaksanakannya penelitian ini adalah untuk melakukan perhitungan penampang hamburan elastik Σ+ → Σ+, Σ0 → Σ0, dan Σ−→
Σ−.
Hipotesa
2
TINJAUAN PUSTAKA
Penampang Hamburan
Pada fisika partikel, interaksi dan sifat-sifat partikel dapat diketahui dari eksperimen melalui hamburan dan peluruhan partikel. Pada proses hamburan, dilakukan pengukuran terhadap penampang hamburan dari interaksi pertikel tertentu. Hal tersebut berbeda dengan proses peluruhan yang melakukan pengukuran pada waktu hidup dari suatu partikel untuk meluruh menjadi dua, tiga, atau lebih.2
Penampang hamburan didefinisikan sebagai peluang partikel penembak berinteraksi dengan partikel target. Partikel target dimisalkan memiliki suatu bidang dengan luas tertentu yang disebut sebagai penampang terhadap partikel datang. Setiap partikel datang yang masuk akan berinteraksi dengan partikel target. Besarnya peluang interaksinya ditentukan oleh luas penampang.1, 2
Penampang Hamburan Elastik Elektron-Sigma
Hamburan elektron merupakan salah satu teknik yang digunakan untuk menghitung penampang hamburan suatu partikel. Interaksi elektromagnetik antara elektron dengan hadron, dalam hal ini Sigma-positif (Σ+), sigma-nol (Σ0), dan sigma-negatif (Σ−) merupakan interaksi antara partikel-partikel bermuatan. Besar muatan untuk elektron, Σ+, Σ0, dan Σ−masing-masing secara berurutan adalah – , + , 0, dan − . Pada interaksi ini medan elektromagnetik �� dihasilkan dari arus transisi sigma.2
Interaksi elektromagnetik terjadi tidak hanya oleh muatan total sigma, tetapi juga melibatkan struktur internal sigma. Sigma merupakan salah satu hadron dari kelas barion yang memiliki tiga buah kuark. Dimana Σ+memiliki dua buah kuark up(u) dan sebuah kuark strange(s). Σ0 terdiri dari satu kuark u, satu kuark s dan satu kuark down(d). Dua buah kuark d dan sebuah kuark s juga terdapat pada pada
Σ−. Sehingga bentuk formulasi arus transisi sigma dituliskan sebagai berikut.2, 3
�
� =
1 2 �� +2M� 2 2 ��� � �− . �. (1)
Dengan F1 dan F2 merupakan faktor bentuk, � merupakan momen magnetik anomalus, dan M adalah massa sigma.2, 4
Pada 2 → 0, yaitu dalam pertukaran foton pada panjang gelomang yang besar sigma akan terlihat memiliki moment magnetik 1+�
2 . Sehingga pada limit ini dapat dipilih 1(0) = 0, dan 2(0) = 1.2, 5
Interaksi elektromagnetik penampang hamburan diferensial dapat dihitung denga menggunakan formula Rosenbluth pada persamaan berikut.4, 5
3
Persaman tersebut dapat disederhanakan dengan memperkenalkan sepasang faktor bentuk lain yang merupakan kombinasi linear dari F1 dan F2 pada Persamaan (3) dan Persamaan (4). 4, 5
= 1− �� 2 (3)
= 1+� 2 (4)
Sehingga Persamaan (2) dituliskan kembali
�
GE dan GM berturut-turut memiliki hubungan distribusi muatan dan momen
magnetik sigma. Nilai numerik GE dan GM ditentukan dari berbagai eksperimen yang dinyatakan dalam parametrasi.2, 5
=−�� 1
Mv merupakan masa dipole vektor yang bernilai 0.84 GeV dari hasil hamburan elektron proton.5
Kinematika Hamburan Elektron-Sigma
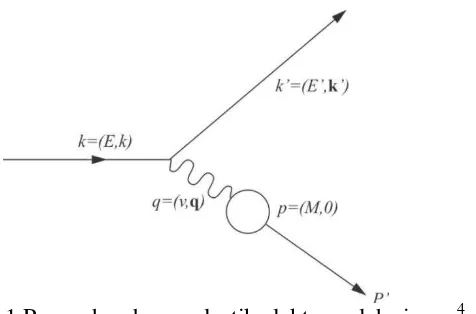
Dalam bentuk vektor-empat persamaan energi hamburan elektron sigma secara lengkap dapat dituliskan mengikuti Gambar 1. Dengan p dan p’ berturut-turut merupakan energi sigma awal dan energi sigma setelah terhambur oleh elektron. Mengikuti kekekalan energy dapat diperlihatkan bahwa = � − �′, dan
′ = + . Dalam bentuk vektor-empat di definisikan bahwa 4
���
� ≡ �.�= �2 = 2− ��. (9)
Dari persamaan energi relativistik 2 =�2+ 2, untuk nilai ≫ sehingga 2 ≅ �2sehingga �2 ≅0. Karena =� − �′ maka dapat diperoleh 2 ≅ −2� ∙
�′ kemudian melalui perkalian vektor-empat sebagai mana didefinisikan sebelumnya didapat 4
4
Gambar 1 Proses hamburan elastik elektron oleh sigma 4
Untuk ′ = + dengan cara yang sama akan didapatkan 2 ≅ −2 ∙
sehingga
2 ≅ −2 . (11)
Gambar 1 menunjukkan proses terjadinya hamburan elektron oleh sigma. Seperti ditunjukkan pada gambar tersebut dan dengan memasukkan Persamaan
(11) didapatkan persamaan ≅ − ′ = − 2
2 . Sehingga ′/ dapat dituliskan sebagai
′
= 1
(1 +2 sin�2) .
(12)
METODE
Waktu dan Tempat
Penelitian dilaksanakan pada sejak bulan Maret 2012 hingga bulan Maret 2013. Bertempat di Departemen Fisika, Fakultas Matematika dan Ilmu Pengetahuian Alam, Institut Pertanian Bogor.
Alat
Peralatan yang akan digunakan dalam penelitian ini adalah perangkat lunak Microsoft Ofice 2007 dan MATLAB R2009a.
Prosedur Penelitian
Perhitungan penampang hamburan elastik Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−dengan beberapa macam factor bentuk dilakukan dengan metode
5
1. Persiapan
Pada tahapan ini dilakukan upaya untuk memahami secara lebih mendalam konsep perhitungan penampang hamburan partikel. Persiapan penelitian dimulai dengan mempelajari teori-teori dasar tentang pertikel, lepton dan kuark.
Perhitungan penampang hamburan elektron sigma diawali dengan proses analitik melalui melakukan kajian terhadap elektrodinamika partikel. Notasi vektor-empat digunakan untuk menyederhanakan perumusan pada relativitas khusus. Satuan alamiah disederhanakan dengan c = ℏ= 1. Akibat dari penyederhanaan nilai c dan ℏ tersebut satuan masa dan energi, juga satuan panjang dan waktu dapat disetarakan. Untuk mempermudah selanjutnya akan digunakan satuan GeV untuk masa dan energi, dan satuan GeV-1 untuk satuan panjang dan waktu. Persamaan elektromagnetik Maxwell digunakan untuk menganalisis interaksi elektromagnetik pada partikel-partikel bermuatan tersebut. Selain itu Persamaan Dirac memiliki peranan yang cukup penting dalam mengidentifikasikan keadaan partikel sesuai teori kuantum maupun relatifistik.2,5,6,7
Tahapan ini penting untuk membangun landasan pemikiran dan pemahaman yang matang untuk proses selanjutnya.
2. Pengambilan data
Pengambilan data tidak dilakukan secara langsung, melainkan mencari data yang sudah di publikasikan sebelumnya untuk dilakukan perhitungan ulang. Sumber yang diambil harus baik dan dapat dipercaya.
3. Pengolahan data
Tahapan ini dimulai setelah dilakukan kajian pustaka tentang penurunan persamaan hamburan, dan didapat sejumlah data dari hasil eksperimen yang tidak dilakukan sendiri. Pada tahapan ini dilakukan perumusan ulang kinematika hamburan elastik elekton-sigma dengan mengikiti teori yang telah diajukan sebelumnya. Perhitungan penampang hamburan elastik Σ+→ Σ+, Σ0 → Σ0, dan Σ−→ Σ−.
Penampang hamburan diferensial elektron-sigma sebagaimana yang telah di definisikan pada Persamaan (5) merupakan pendekatan dari asumsi (− 2)→0.4 Akibatnya perlu diperhatikan nilai-nilai energi datang dan sudut � agar memenuhi asumsi tersebut. Nilai (− 2) pada Persamaan (11) harus bernilai positif. Dengan demikian energi datang bernilai minimum 0.287 GeV. selanjutnya nilainya divariasikan hingga energi 3.5 GeV. Pengambilan batas akhir 3.5 GeV untuk menjaga keadaan elastik dari hamburan elektron sigma. Variasi nilai pada energy datang yang lebih kecil dibuat lebih banyak untuk memperhalus bentuk kurva yang dihasilkan.2
Besarnya sudut (�) berubah-ubah antara 00 samapi 1800. Karena pada sudut
6
4. Penarikan kesimpulan
Pada tahapan ini dilakukan penarikan kesimpulan secara menyeluruh terkait metode, proses, serta hasil perhitungan yang telah dilakukan, sehingga dapat memberikan pandangan yang manyeluruh terkait kekurangan dan kelabihan dari panelitian yang telah dilakukan. pada akhirnya dilakukan pembandingan antara hasil penelitian dengan hipotesis.
HASIL DAN PEMBAHASAN
Karakteristik �+, ��, Dan �− Sebagai Partikel Sasaran
Hiperon merupakan kelompok dari barion dengan masa yang lebih berat dari neutron. Karenanya keadaan hiperon tidak mantap, dan akan meluruh menjadi partikel yang lain yang lebih setabil. Umur rata-rata hiperon kurang dari 10-9 detik. Sehingga dengan karakteristik yang demikian, akan sulit dilakukan pengukuran secara langsung terhadap penampang hamburan dari hadron dalam eksperimen nyata. Namun upaya untuk melakukan hal tersebut tetap ada. Karena keterbatasan ini juga penulis hanya melakukan perhitungan secara teoritis terhadap penampang hamburan sigma.1
Hiperon Sigma memiliki dari tiga kuark. Dua kuark diantaranya merupakan kuark up(u) atau kuark down(d) atau keduanya dan satu sisanya merupakan kuark
strange(s). Dengan komposisi, Σ+memiliki dua buah kuark u dan sebuah kuark s.
Σ0terdiri dari satu kuark u, satu kuark s dan satu kuark d. Sedangkan pada
Σ−terdapat dua buah kuark d dan sebuah kuark s.3
Struktur internal sigma yang terdiri dari beberapa kuark tersebut mempengaruhi bentuk penampang hamburan diferensial yang dihasilkan pada perhitungan selanjutnya. Keberadaan struktur internal tersebut diwakili oleh faktor bentuk GE maupun GM sebagaimana yang dituliskan pada Persamaan (6) dan (7). Dari Partikel Data Group diperoleh data karakteristik sigma-positif, sigma-nol, Dan sigma-negatif.6
Sigma-positif memiliki nilai masa sebesar 1.18937GeV. Partikel ini memiliki waktu hidup 0.8018 × 10−9. Besar momen magnetiknya 2.458 � . Sigma-nol memiliki nilai masa sebesar 1.192642 GeV. Partikel ini memiliki waktu hidup 7.4 × 10−20. Besar momen magnetiknya 1.61 � . Sedangkan sigma-negatif memiliki nilai masa sebesar 1.197449GeV. Partikel ini memiliki waktu hidup 1.479 × 10−20. Besar momen magnetiknya −1.160 � .6
Penampang Hamburan Elektron Sigma
7
Dengan perbandingan nilai E’/E sebagaimana seperti yang telah dituliskan pada Persamaan (12).
Perhitungan penampang hamburan diferensial selanjutnya dilakukan secara numerik dengan memasukkan data tentang karakteristik Σ+, Σ0, Dan Σ− ke dalam Persamaan (5) dengan memvariasikan sudut dan energi datang elektron pada batasan yang telah ditentukan sebelumnya. Nilai 2 dan 2 diperoleh dari Persamaan (6) dan Persamaan (7) dengan memasukkan hasil dari Persamaan (8). Program komputer untuk menghitung nilai penampang hamburan menggunakan MATLAB R2009a diperlihatkan pada Lampiran 1.
Nilai penampang hamburan diferensial untuk interaksi Σ+→ Σ+, Σ0 →
Σ0, dan Σ−→ Σ− akan berbeda satu dengan yang lainnya karena perbedaan masa dan momen magnetik dari masing-masing partikel yang terlibat. Lampiran 2 menunjukkan grafik hubungan antara energi datang elektron dengan penampang hamburan elastik untuk untuk Σ+→ Σ+, Σ0 → Σ0, dan Σ−→ Σ−. Untuk sudut dibawah 300, nilai penampang hamburan terdapat pada Lampiran 3.
Nilai penampang hamburan yang ditunjukkan pada Lampiran 2 menunjukkan angka yang semakin kecil dengan kenaikan energi elektron datang. Hal yang sama juga terjadi pada setiap kenaikan sudut. Hal ini menunjukkan interaksi elektromagnetik antara elektron dengan sigma-positif, elektron dengan sigma-nol, dan elektron dengan sigma-negatif lebih efektif pada sudut-sudut yang kecil. Kondisi yang sama ternyata juga terjadi pada hamburan elektron neutron pada perhitungan yang lain.2
Perbedaan penampang hamburan dari interaksi antara elektron dengan sigma-positif, elektron dengan sigma-nol, dan elektron dengan sigma-negatif tidak hanya terjadi karena faktor perbedaan nilai momen magnetiknya tetapi juga karena perbedaan nilai masa. Ketiga interaksi tersebut pada dasarnya memberikan bentuk kurva penampang hamburan yang serupa pada setiap sudutnya, namun memiliki perbedaan pada nilai-nilai yang dihasilkannya.
Model Penampang Hamburan Pada Sudut Kecil
Hubungan antara penampang hamburan elektron sigma ( Σ+ → Σ+,
Σ0 → Σ0, dan Σ−→ Σ−) dan energi elektron datang untuik sudut 50
8
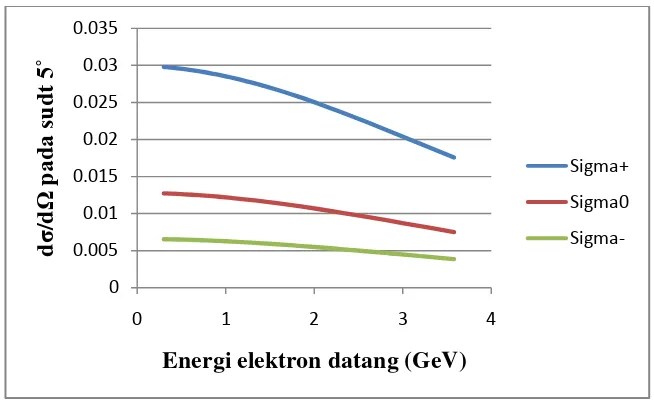
Gambar 2 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 50 .
Gambar 2 menunjukkan perbandingan nilai penampang hamburan (dσ/dΩ) pada sudut 50. Sekilas dapat diperlihatkan bahwa penampang hamburan dari elektron oleh sigma-positif memiliki nilai yang lebih besar dibandingkan dengan penampang hamburan elektron oleh sigma-nol. Sedangkan penampang hamburan dari elektron oleh sigma-negatif menunjukkan nilai yang paling kecil diantara ketiganya. Pada energi dibawah 1 GeV nilai penampang hamburannya lebih besar, kemudian menurun bersamaan dengan peningkatan nilai energi datang.
Nilai penampang hamburan terbesar pada sudut hamburan 50 dihasilkan dari hamburan Σ+→ Σ+, pada energi datang elektron sebesar 0.3 GeV dengan nilai penampang hamburan sebesar 0.0297. Nilai penampang hamburan Σ0 →
Σ0 adalah 0.0127 pada energi datang elektron 0.3 GeV. Masih pada energi datang elektron 0.3 GeV nilai penampang hamburan Σ−→ Σ− sebesar 0.00645. Sedangkan secara keseluruhan nilai terkecil terjadi pada Σ−→ Σ− pada energi datang elektron 3.5 GeV dengan nilai penampang hamburan sebesar 0.0038.
Selisih terbesar terjadi pada energi elektron datang yang terkecil yaitu pada energi 0.3 GeV. Selisih penampang hamburan antara Σ+→ Σ+ dengan Σ0 →
Σ0 adalah 0,01708. Selisih penampang hamburan antara Σ+→ Σ+ dengan
Σ−→ Σ− adalah 0.02324, dan Selisih penampang hamburan antara Σ0 → Σ0 dengan Σ−→ Σ− adalah 0.00616. Pada setiap penambahan energi, selisih penampang antara ketiga partikel sasaran menjadi semakin kecil.
Dari grafik yang pada lampiran 2 dapat dilihat selisih nilai penampang hamburan yang lebih besar terjadi pada sudut-sudut kecil dibandingkan dengan selisih yang terjadi pada sudut yang besar. Keadaan tersebut tampak pada kurva-kurva yang berjauhan pada grafik-grafik yang menunjukkan nilai penampang hamburan pada sudut di bawah 300.
Pada Gambar 2 maupun Gambar 3 diperlihatkan penurunan nilai penampang hamburan pada sudut dibawah 300 seiring dengan bertambahnya energi elektron datang. Penurunan yang paling dominan terjadi pada selang energi datang antara 1 GeV sampai 3 GeV. Hal ini dapat dilihat dari tingginya nilai gradien kurva pada selang tersebut dibandingkan dengan selang energi yang lain.
9
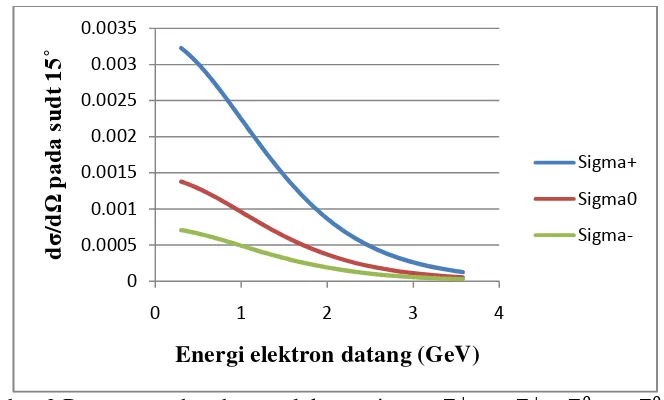
Gambar 3 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 150 .
Model Penampang Hamburan Pada Sudut Besar
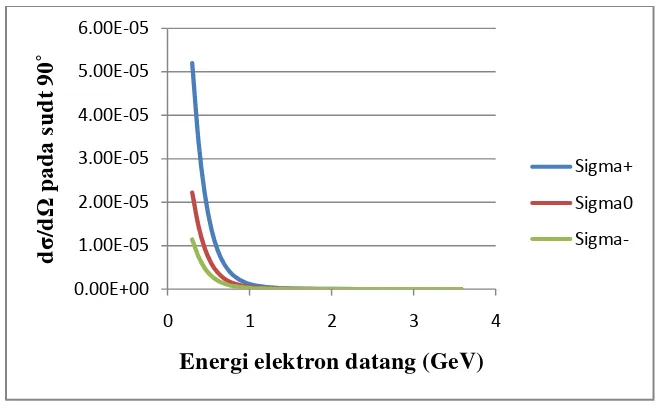
Gambar 4 menunjukkan perbandingan nilai penampang hamburan (dσ/dΩ) pada sudut 900. Pada sudut-sudut yang besar nilai penampang hamburan jauh lebih kecil dibanding dengan nilai penampang hamburan pada sudut-sudut yang kecil atau dibawah 300. Pada sudut 900 seperti diperlihatkan pada Gambar 3nilai penampang hamburan tertingi terjadi pada energi elektron datang yang terendah yakni 0.3 GeV.
Penampang hamburan elastik Σ+→ Σ+ pada sudut 900 untuk energi elektron datang 0.3 GeV bernilai 5.19 × 10−5. Nilai tersebut merupakan nilai penampang hamburan tertinggi untuk semua hasil perhitungan penampang hamburan pada sudut 900. Selanjutnya nilai penampang hamburan Σ0 → Σ0
Selisih antara ketiganya terlihat lebih besar pada energi elektron datang yang kecil. Pada energi-energi yang lebih besar selisih nilai panampang hamburan antara ketiga interaksi partikel tersebut cenderung lebih kecil, bahkan hampir sama. Hal ini dapat ditunjukkan dari kurva yang berhimpit untuk nilai energi elektron datang yang tinggi pada Gambar 4.
10
Gambar 4 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi energi elektron datang pada sudut 900 .
Terlihat perubahan nilai kelengkungan kurva antara energi datang dengan penampang hamburan. Perubahan kelengkungan ini terlihat cukup jelas pada selang antara 50 hingga 300. Nilai penampang hamburan sendiri semakin kecil setiap pertambahan nilai sudut hamburnya. pada setiap nilai energi elektron datang yang sama, nilai penampang hamburan pada sudut-sudut yang kecil lebih bersar dibanding nilai penampang hambran pada sudut-sudut besar. Gambar 5 menunjukkan nilai penampang hamburan terhadap variasi sudut pada energi electron datang tertentu.
Gambar 5 Penampang hamburan elektron sigma Σ+→ Σ+, Σ0 → Σ0, dan
Σ−→ Σ−terhadap variasi sudut hamburan pada energi elektron
11
SIMPULAN DAN SARAN
Simpulan
Penampang hamburan didefinisikan sebagai peluang partikel penembak berinteraksi dengan partikel target. Setiap partikel datang yang masuk akan berinteraksi dengan partikel target. Besarnya peluang interaksinya ditentukan oleh luas penampang.
Perhitungan penampang hamburan elektron sigma diawali dengan proses analitik berupa kajian terhadap elektrodinamika partikel. Notasi vektor-empat digunakan untuk menyederhanakan perumusan pada relativitas khusus. Satuan alamiah disederhanakan dengan c = ℏ= 1. Persamaan elektromagnetik Maxwell digunakan untuk menganalisis interaksi elektromagnetik pada partikel-partikel bermuatan tersebut. Selain itu persamaan Dirac memiliki peranan yang cukup penting dalam mengidentifikasikan keadaan partikel sesuai teori kuantum maupun relatifistik. Pada penelitian ini dilakukan perhitungan nilai penampang hamburan elektron sigma pada berbagai sudut datang dan energi datang untuk interaksi elektron dengan sigma positif, elektron dengan sigma nol dan elektron dengan sigma negatif.
Hasil perumusan penampang hamburan elektron sigma ditunjukkan pada Persamaan (5). Nilai hasil perhitungan penampang hamburan untuk sudut hambur dibawah 300 diperlihatkan pada Lampiran 3. Untuk sudut-sudut hambur yang lain diperlihatkan dalam bentuk grafik hubungan antara penampang hamburan dengan energi elektron datang pada Lampiran 2. Perbedaan nilai penampang hamburan dari ketiga interaksi tersebut terjadi karena perbedaan besar masa dan momen magnetik dari tiap-tiap partikel sasaran.
Nilai penampang hamburan pada sudut yang besar, yakni antara 600 hingga 1350 hampir memiliki nilai yang sama pada energi elektron datang diatas 1 GeV. Pada kondisi itu nilai penampang hamburan mendekati nol. Pada sudut-sudut dibawah 300 nilai penampang hamburan dari masing - masing tadi memiliki perbedaan yang cukup terlihat. Pada energi datang yang tinggi, untuk sudut datang dibawah 300 tidak menunjukkan nilai penampang hamburan yang mendekati nol.
Pada setiap pertambahan sudut sebagaimana digambarkan pada lampiran 2 terlihat perubahan nilai kelengkungan kurva antara energi datang dengan penampang hamburan. Perubahan kelengkungan ini terlihat cukup jelas pada selang antara 50 hingga 300. Sedangkan untuk bentuk kurva di bawah 50 tidak tercantum pada lampiran penelitian ini. Hasil perhitungan penampang hamburan juga menujukkan perubahan kelengkungan kurva energi elektron datang dengan penampang hamburan pada setiap perubahan sudut.
Saran
12
yang kecil. Perlu juga dilakukan perhitungan untuk sudut hambur yang lebih kecil dari 50.
DAFTAR PUSTAKA
1. Beiser A. Konsep Fisika Modern Edisi Keempat. Terjemahan Liong. Jakarta: Erlangga. 2005, 479-481
2. Pohan AS. Perhitungan Penampang Hamburan Elastik dengan Dua Macam Faktor Bentuk: Glaster dan Miler. Skripsi. Jurusan Fisika. Bogor: Institut Pertanian Bogor. 2011
3. Wikipedia. Sigma Barion [internet]. 2012. http://en.wikipedia.org/wiki/ Sigma_baryon [Februari 2013]
4. Helzen F, Martin AD. Quark and Lepton: an Introduction Course in Modern Particle Physics. John Wiley and Son. 1984, 172-179
5. Geis E, Kohl M, Ziskin V. The Charge Form Factor of the Neutron at Low Momentum Transfer from the 2H(e ,e’n)p Reaction. arXiv: 0803.3827v2. 2008
6. Beringer J, et al. Σ Barion (�=−1/ = 1). Partikel Data Group. PR D86. 1010001 [internet]. 2012. http://pdg.lbl.gov/2012/tables/rpp2012-tab-baryons-Sigma.pdf [Februari 2013].
13
MSnol = 1.192642; % masa sigma0 dalam GeV
MSn = 1.197449; % masa sigma- dalam GeV
MuSp = 2.458; % momen magnetik sigma+ dalam GeV
MuSnol = 1.61; % momen magnetik sigma0 dalam GeV
MuSn = -1.160 ;% momen magnetik sigma0 dalam GeV
Emin_el = 0.287; % energi datang elektron minimum dalam GeV
14
GmSp(j,i) = MuSp*GdSp(j,i);
GmSnol(j,i) = MuSnol*GdSnol(j,i); GmSn(j,i) = MuSn*GdSn(j,i);
dSOSp(j,i) =
alpha^2/(4*E(j)^2*sin(th(i)/2)^4)*(E2Sp(j,i)/E(j))*(((GeSp(j,i) ^2+tauSp(j,i)*GmSp(j,i)^2)/(1+tauSp(j,i))*cos(th(i)/2)^2)+2*tau Sp(j,i)*GmSp(j,i)^2*sin(th(i)/2)^2);
dSOSnol(j,i) =
alpha^2/(4*E(j)^2*sin(th(i)/2)^4)*(E2Snol(j,i)/E(j))*(((GeSnol( j,i)^2+tauSnol(j,i)*GmSnol(j,i)^2)/(1+tauSnol(j,i))*cos(th(i)/2 )^2)+2*tauSnol(j,i)*GmSnol(j,i)^2*sin(th(i)/2)^2);
dSOSn(j,i) =
alpha^2/(4*E(j)^2*sin(th(i)/2)^4)*(E2Sn(j,i)/E(j))*(((GeSn(j,i) ^2+tauSn(j,i)*GmSn(j,i)^2)/(1+tauSn(j,i))*cos(th(i)/2)^2)+2*tau Sn(j,i)*GmSn(j,i)^2*sin(th(i)/2)^2);
end
15
Lampiran 2 Grafik Penampang Hamburan Pada Berbagai Sudut
Lampiran 3 Data Hasil Perhitungan Penampang Hamburan pada Sudut di Bawah 300
sigma-plus sigma-nol sigma-minus
E datang 5 10 15 30 5 10 15 30 5 10 15 30
0.3 0.029784 0.007375 0.003226 0.000745 0.012708 0.003147 0.001377 0.000318 0.006544 0.00162 7.09E-04 1.64E-04
0.377778 0.029703 0.007295 0.003149 0.000681 0.012674 0.003113 0.001344 0.000291 0.006526 0.001603 0.000692 0.00015
0.455556 0.029606 0.007201 0.003061 0.000615 0.012632 0.003073 0.001306 2.62E-04 0.006505 0.001582 0.000673 0.000135
0.533333 0.029494 0.007095 0.002962 0.000547 0.012585 0.003027 0.001264 2.34E-04 0.006481 0.001559 0.000651 0.00012
0.611111 0.029368 0.006976 0.002855 4.82E-04 0.012531 0.002977 0.001218 2.06E-04 0.006453 0.001533 0.000628 0.000106
0.688889 0.029227 0.006846 0.002741 4.20E-04 0.012471 0.002921 0.00117 1.79E-04 0.006422 0.001504 0.000602 9.24E-05
0.766667 0.029072 0.006706 0.002621 3.63E-04 0.012405 0.002862 0.001119 1.55E-04 0.006388 0.001474 0.000576 7.99E-05
0.844444 0.028904 0.006556 0.002498 3.11E-04 0.012333 0.002798 0.001066 1.33E-04 0.006351 0.001441 0.000549 6.85E-05
0.922222 0.028722 0.006398 0.002371 2.65E-04 0.012255 0.00273 1.01E-03 1.13E-04 0.006311 0.001406 0.000521 5.84E-05
1 0.028527 0.006233 0.002243 2.25E-04 0.012172 0.00266 9.57E-04 9.59E-05 0.006268 0.00137 0.000493 4.94E-05
1.077778 0.028318 0.006061 0.002115 1.89E-04 0.012083 0.002586 9.03E-04 8.09E-05 0.006222 0.001332 0.000465 4.17E-05
1.327778 0.027568 0.005475 0.001716 0.000107 0.011763 0.002336 0.000732 4.57E-05 0.006058 0.001203 0.000377 2.36E-05
1.577778 0.026702 0.004865 0.001355 5.96E-05 0.011394 0.002076 0.000578 2.54E-05 0.005867 0.001069 2.98E-04 1.31E-05
1.827778 0.025737 0.004258 0.001046 3.32E-05 0.010982 0.001817 0.000446 1.42E-05 0.005656 0.000936 2.30E-04 7.30E-06
2.077778 0.024689 0.003677 0.000794 1.87E-05 0.010535 0.001569 0.000339 7.97E-06 0.005425 0.000808 1.75E-04 4.11E-06
2.327778 0.023574 0.003137 0.000594 1.07E-05 0.010059 0.001339 0.000254 4.56E-06 0.00518 0.000689 0.000131 2.35E-06
2.577778 0.022409 0.002648 0.000441 6.23E-06 0.009562 0.00113 0.000188 2.66E-06 0.004924 0.000582 9.70E-05 1.37E-06
2.827778 0.02121 0.002215 0.000325 3.71E-06 0.00905 0.000945 0.000139 1.59E-06 0.004661 0.000487 7.15E-05 8.17E-07
3.077778 0.019992 0.001838 0.000239 2.26E-06 0.008531 0.000784 0.000102 9.66E-07 0.004393 0.000404 5.25E-05 4.98E-07
3.327778 0.01877 0.001516 0.000175 1.41E-06 0.008009 0.000647 7.47E-05 6.02E-07 0.004125 0.000333 3.85E-05 3.10E-07
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 21 Desember 1989. Anak pertama dari tujuh bersaudara dari pasangan Bapak RahmanTamin dan Ibu Suharni (alm.). Penulis menyelesaikan pendidikan dasar di Sekolah Dasar Islam Terpadu (SDIT) Iqro’ Bekasi pada tahun 2002. Setelah itu penulis melanjutkan pendidikan menengah di SMPIT YAPIDH Bekasi (lulus 2005) dan SMA Negeri 21 Jakarta (lulus 2008).
Tahun 2008 penulis diterima sebagai mahasiswa di Institut Pertanian Bogor (IPB) melalui jalur Seleksi Nasional Perguruan Tinggi Negeri (SNMPTN) di Departemen Fisika Fakultas Matematika dan Ilmu Pengtahuan Alam.