Masalah Pengoptimuman Multikriteria dalam Penjadwalan Tenaga Sukarelawan di Daerah Bencana

(1)

Masalah Pengoptimuman Multikriteria dalam Penjadwalan Tenaga Sukarelawan di Daerah Bencana. Dibimbing oleh dan

.

(2)

Volunteer Scheduling at Disaster Area. Supervised by and .

(3)

# $ % & "'

Sukarelawan adalah seseorang atau sekelompok orang yang secara ikhlas karena panggilan nuraninya memberikan apa yang dimilikinya tanpa mengharapkan imbalan. Sukarelawan memiliki peran yang sangat penting dalam kehidupan masyarakat. Mereka sangat dibutuhkan ketika ada suatu masalah yang sedang terjadi di suatu tempat, seperti saat terjadi bencana alam gunung meletus yang terjadi di Jawa Tengah dan Yogyakarta, serta bencana gempa bumi dan tsunami di Jepang baru!baru ini.

Organisasi kemanusiaan yang bertugas menangani masalah sukarelawan masih mengalami kesulitan dalam mengelola para sukarelawan tersebut. Mereka kesulitan dalam masalah pengiriman dan penugasan para sukarelawan ke daerah!daerah yang membutuhkan. Oleh sebab itu, perlu dibuat sebuah model penjadwalan sukarelawan sebaik mungkin. Model penjadwalan sukarelawan ini akan mempertimbangkan keinginan dari setiap sukarelawan untuk menentukan pilihan blok waktu dan tugas yang diinginkannya. Masalah penjadwalan

sukarelawan ini dapat dimodelkan dalam bentuk pengoptimuman multikriteria. Pengoptimuman multikriteria merupakan masalah pengoptimuman yang memiliki lebih dari satu fungsi objektif. Masalah penjadwalan sukarelawan dapat diselesaikan dengan beberapa metode, di antaranya metode kendala!ε dan metode pembobotan.

Karya ilmiah ini merupakan rekonstruksi dari tulisan Falasca et al. (2009) yang berjudul “An optimization model for humanitarian relief volunteer management”. Dalam karya ilmiah ini akan diperlihatkan formulasi dan penyelesaian masalah penjadwalan sukarelawan kemanusiaan dengan menggunakan bantuan software LINGO 8.0.

()( "

Karya tulis ini bertujuan:

1. memformulasikan masalah penjadwalan tenaga sukarelawan dalam bentuk pengoptimuman multikriteria,

2. menyelesaikan masalah pengoptimuman multikriteria tersebut dengan metode kendala!ε dan metode pembobotan.

%!$*'$ ! " +"% $ %,+"+-+ . ("'-+ +"% $/

Misalkan , , … , menyatakan suatu fungsi dalam variabel!variabel , , … , . , , … , adalah suatu persamaan linear, apabila f fungsi linear.

%,+"+-+ . %$#+0 &- ! " +"% $/

Untuk sembarang fungsi linear , , … , dan sembarang bilangan b, pertidaksamaan , , … , dan , , … , disebut dengan pertidaksamaan linear.

(Winston 1995)

Menurut Winston (1995), pemrograman linear (PL) adalah suatu masalah pengoptimuman yang memenuhi ketentuan! ketentuan sebagai berikut:

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi linear yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel!variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear. c) Variabel keputusan harus taknegatif atau

tidak dibatasi tandanya.

Suatu PL dikatakan memiliki bentuk standar jika berbentuk seperti yang didefinisikan di bawah ini.

%,+"+-+ 1 . %"#(& # "0 $ /

Suatu pemrograman linear didefinisikan mempunyai bentuk standar sebagai berikut:

(4)

# $ % & "'

bentuk pengoptimuman multikriteria. Pengoptimuman multikriteria merupakan masalah pengoptimuman yang memiliki lebih dari satu fungsi objektif. Masalah penjadwalan sukarelawan dapat diselesaikan dengan beberapa metode, di antaranya metode kendala!ε dan metode pembobotan.

()( "

%!$*'$ ! " +"% $ %,+"+-+ . ("'-+ +"% $/

%,+"+-+ . %$#+0 &- ! " +"% $/

(Winston 1995)

%,+"+-+ 1 . %"#(& # "0 $ /

(5)

2 A disebut matriks kendala.

(Nash & Sofer 1996)

%,+"+-+ . %$ 2 +-+3% /

Solusi optimum terbaik adalah suatu titik dalam daerah fisibel yang menyebabkan nilai fungsi objektif terkecil (masalah minimisasi). Sedangkan, solusi optimum suatu PL maksimisasi adalah suatu titik dalam daerah fisibel yang menyebabkan nilai fungsi objektif terbesar.

(Winston 1995)

* (-+

Untuk menyelesaikan suatu masalah PL, metode simpleks merupakan salah satu metode yang dapat menghasilkan solusi optimum. Metode ini mulai dikembangkan oleh Dantzig pada tahun 1947. Metode ini adalah metode yang umum digunakan untuk menyelesaikan masalah PL. Metode simpleks ini berupa metode iteratif (proses mencari solusi yang dilakukan secara berulang!ulang hingga didapatkan solusi yang diinginkan) untuk menyelesaikan masalah PL berbentuk standar.

Pada PL (1), vektor x yang memenuhi kendala disebut sebagai solusi dari PL (1). Misalkan matriks A dapat dinyatakan

sebagai , sedangkan B

merupakan matriks berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Matriks B disebut matriks basis untuk PL (1).

Misalkan x dapat dinyatakan sebagai

vektor dengan adalah vektor variabel basis dan adalah vektor variabel nonbasis, maka

(2)

Karena B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2) dapat

i. Solusi tersebut memenuhi kendala PL. ii. Kolom!kolom dari matriks koefisien yang

berpadanan dengan komponen taknol adalah bebas linear.

(Nash & Sofer 1996)

%,+"+-+ 5 . * (-+ +-+3% -+-/

Vektor x disebut solusi fisibel basis jika x merupakan solusi basis dan 0.

(Nash & Sofer 1996)

*"#*2

Misalkan diberikan pemrograman linear berikut:

minimumkan 2 3 ,

dengan kendala 2 4

2 _! 11

_# 5. (4)

Dari PL tersebut didapatkan

% 2 1 11 2 0

Maka matriks basisnya adalah

%1 0 00 1 0 0 0 1'.

Dengan menggunakan matriks basis tersebut diperoleh

0 0 (_,

4 11 5 (_{. (5)}

(6)

%,+"+-+ 6 . #$+&- -+-/

Suatu matriks disebut matriks basis untuk PL jika matriks tersebut adalah matriks taksingular, yaitu matriks yang determinannya tidak sama dengan nol.

(Garfinkel & Nemhauser 1972)

%!$*'$ ! " +"% $ + "' " ( # Model pemrograman linear bilangan bulat (PLBB) atau integer linear programming (ILP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat. Model PLBB yang semua variabelnya bernilai bilangan bulat disebut pemrograman bilangan bulat murni. Sedangkan, model PLBB yang hanya sebagian variabelnya bernilai bilangan bulat disebut pemrograman bilangan bulat campuran. Model PLBB yang hanya mengharuskan nilai nol atau satu untuk variabelnya dinamakan pemrograman bilangan bulat 0!1.

%,+"+-+ 7 . %!$*'$ ! " +"% $ % &- -+/ PL!relaksasi merupakan pemrograman linear yang diperoleh dari suatu PLBB dengan menghilangkan kendala bilangan bulat atau kendala 0!1 pada setiap variabelnya.

Untuk masalah meminimumkan, nilai fungsi objektif yang optimum di PL!relaksasi lebih kecil atau sama dengan nilai fungsi objektif yang optimum di PLBB, sedangkan untuk masalah memaksimumkan nilai fungsi objektif yang optimum di PL!relaksasi lebih besar atau sama dengan nilai fungsi objektif yang optimum di PLBB.

(Winston 1995)

%,+"+-+ . *0% #%! #+& %"(' - "/ Bentuk umum dari model matematika masalah penugasan adalah sebagai berikut:

min , , -. -. meminimumkan biaya penjadwalan. Asumsikan xijsebagai penugasan dari sumber

i ke tujuan j. Nilai xij sama dengan satu jika

sumber i ditugaskan pada tujuan j, sedangkan bernilai nol jika selainnya. Parameter bij

adalah biaya penugasan untuk sumber i ke tujuan j. Parameter 1_- adalah jumlah penugasan setiap sumber i pada tujuan j. Parameter 7_. adalah jumlah sumber i yang ditugaskan pada setiap tujuan j.

(Siswanto 2006)

1 %!$*'$ ! " ( #+*3)%&#+,

Masalah pengoptimuman yang telah didiskusikan sebelumnya adalah masalah pengoptimuman yang hanya memiliki satu fungsi objektif. Sedangkan, masalah pengoptimuman yang akan dibahas sekarang adalah masalah pengoptimuman yang memiliki lebih dari satu fungsi objektif. Masalah pengoptimuman yang dimaksud adalah masalah pengoptimuman multikriteria. Pada masalah pengoptimuman multikriteria ini, ada beberapa istilah yang harus diketahui seperti pengambilan keputusan multikriteria atau multiple criteria decision making (MCDM). Sebuah masalah pengoptimuman multikriteria dapat dikatakan sebagai MCDM jika terdapat lebih dari satu hal yang harus diperhatikan dalam model tersebut sebagai tujuan atau kriterianya.

(Eiselt & Sandblom 2007)

%,+"+-+ . *$!( -+ /

Masalah pengoptimuman multikriteria biasanya diformulasikan sebagai berikut.

min [f1(x), f2(x), …, fk(x)],

(7)

4

%#*0% %!3*3*# "

Metode pembobotan merupakan salah satu metode penyelesaian yang tertua dan metode yang paling sederhana dari MCDM. Metode ini pertama kali direkomendasikan oleh Zadeh. Metode ini menggabungkan semua fungsi objektif yang ada dalam model, dan setiap fungsi objektif tersebut diberikan bobot (w) yang berbeda. Misalkan diberikan permasalahan MCDM seperti pada model (6). Setelah dilakukan metode pembobotan, fungsi objektif gabungannya akan seperti persamaan berikut

min z = w1 f1(x)+ …+ wk fk(x). (7)

Fungsi objektif tersebut selanjutnya dioptimumkan dengan menggunakan variasi bobot yang berbeda. Nilai total dari bobot! bobot tersebut harus satu, yaitu:

w1 + w2 + …. + wk = 1.

%#*0% %"0 9ε

Ide dasar metode ini adalah mengubah hampir semua fungsi objektifnya menjadi kendala. Metode ini hanya menyisakan satu fungsi objektif saja, misalkan fungsi objektifnya adalah f1(x). Fungsi objektif

lainnya akan diubah menjadi kendala. Fungsi objektif yang akan diubah menjadi kendala pertama!tama harus dicari solusi optimalnya. Solusi optimal tersebut setelah dikalikan dengan parameter ε akan menjadi nilai dari sisi kanan kendala baru. Setelah itu, optimumkan fungsi objektif f1(x) dengan

menambahkan kendala!kendala baru tersebut. Fungsi objektif tersebut dicari solusi optimalnya dengan mencoba beberapa nilaiε berbeda. Misalkan formulasi model (6) akan dicoba diselesaikan dengan menggunakan metode kendala!ε. Tahapan pengoptimuman model (6), yaitu:

merupakan solusi dari fungsi objektif ke!i. "'& 2

max f1(x)

dengan kendala

gj (x) ≤ 0 ; j = 1, 2, …, m

fi (x) ≥ ε fi* (x) ; 0 ≤ ε ≤ 1, i = 2, 3, …, k

Langkah 2 dilakukan berulang kali dengan menggunakan nilai ε yang berbeda sehingga

(Falasca et al. 2009) *"#*2

Misalkan diberikan model seperti di bawah ini: dengan menggunakan metode kendala!ε. Misalkan fungsi objektif 1 ditetapkan sebagai fungsi objektif, maka fungsi objektif 2 harus diubah menjadi kendala. Tahapan pengoptimuman model (8), yaitu:

"'& 2

(8)

Sekarang nilai z1 bergantung pada nilai ε.

Nilai ε yang diperbolehkan adalah yang kurang dari satu karena jika nilai ε lebih besar dari satu maka nilai sisi kanan dari kendala baru 3x1 – x2 ≥ 12ε akan lebih besar dari dua

belas. Sedangkan pada Langkah 1 diketahui bahwa solusi maksimum kendala baru tersebut adalah dua belas (z1*= 12). Karena itu tidak

akan ditemukan solusi jika nilai dari sisi kanan kendala baru tersebut lebih besar dari dua belas. Model (10) harus diselesaikan berulang!ulang untuk nilai ε yang berbeda. Solusi yang didapatkan dari pengoptimuman Langkah 2 disajikan pada Tabel 1.

Tabel 1 Solusi pengoptimuman Langkah 2

Ε x1 x2 z1 semakin besar. Untuk lebih jelas, disajikan grafik perubahan nilai z1* dan z2* pada

Gambar 1 (lihat Lampiran 1).

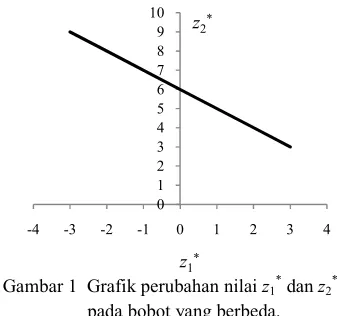
Gambar 1 Grafik perubahan nilai z1 *

dan z2 *

pada bobot yang berbeda.

1 %-&$+4-+ - 2

Model penjadwalan tenaga sukarelawan berbeda dengan model penjadwalan tenaga kerja biasa. Kunci utama perbedaan kedua model tersebut adalah tujuannya. Tujuan model penjadwalan tenaga sukarelawan lebih mementingkan misi kemanusiaan daripada memaksimumkan keuntungan. Perbedaan penting lainnya adalah terkait dengan keahlian yang dimiliki sumberdaya manusianya. Model

penjadwalan tenaga kerja yang biasa mengasumsikan bahwa semua tenaga kerja memiliki keahlian yang dibutuhkan untuk menyelesaikan tugas. Namun, pada masalah penjadwalan tenaga sukarelawan harus dipertimbangkan bahwa adanya beberapa sukarelawan mungkin tidak memiliki tingkat keterampilan yang diperlukan untuk menyelesaikan tugas!tugas tertentu.

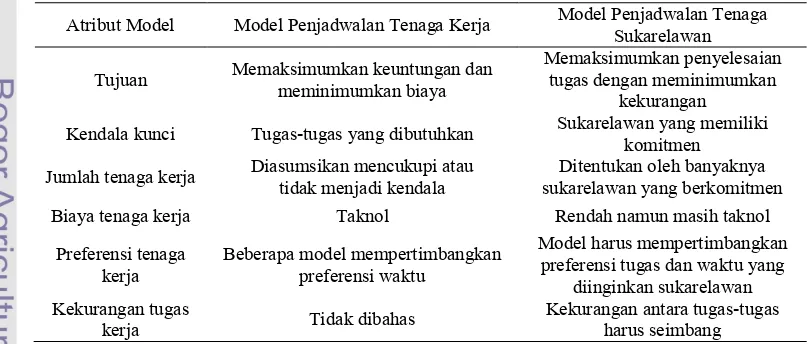
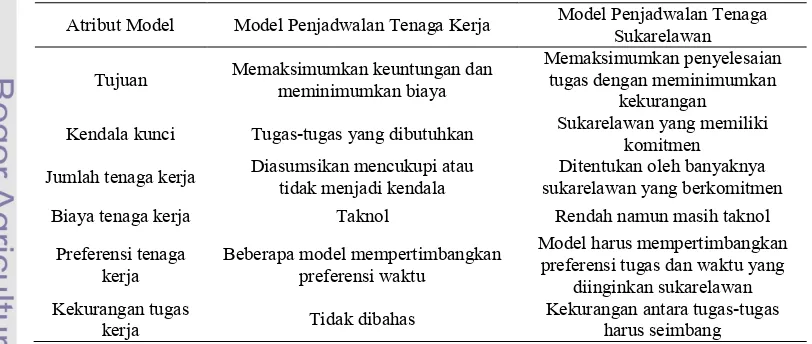
Tabel 2 Perbedaan antara model tenaga kerja dan model sukarelawan

Model manajemen sukarelawan tersebut juga harus mempertimbangkan hipotesis!hipotesis

lain yang sebelumnya telah diuji oleh

Atribut Model Model Penjadwalan Tenaga Kerja Model Penjadwalan Tenaga Sukarelawan

Tujuan Memaksimumkan keuntungan dan meminimumkan biaya

Memaksimumkan penyelesaian tugas dengan meminimumkan

kekurangan

Kendala kunci Tugas!tugas yang dibutuhkan Sukarelawan yang memiliki komitmen

Jumlah tenaga kerja Diasumsikan mencukupi atau tidak menjadi kendala

Ditentukan oleh banyaknya sukarelawan yang berkomitmen

Biaya tenaga kerja Taknol Rendah namun masih taknol

Preferensi tenaga kerja

Beberapa model mempertimbangkan preferensi waktu

Model harus mempertimbangkan preferensi tugas dan waktu yang

diinginkan sukarelawan Kekurangan tugas

kerja Tidak dibahas

(9)

5

dan z2 *

1 %-&$+4-+ - 2

kekurangan

kerja Tidak dibahas

(10)

7

1. Tingkat komitmen (TK) tenaga kerja atau sukarelawan dipengaruhi secara langsung oleh penempatan tugasnya.

2. Pemanfaatan tenaga kerja sukarelawan melebihi TK akan meningkatkan TK di masa depan. Sebaliknya, pemanfaatan sukarelawan di bawah TK akan mengurangi TK di masa depan. Dalam hal ini, model manajemen sukarelawan harus menghindari pemanfaatan sukarelawan secara berlebihan.

3. Model harus memberikan solusi untuk menghindari adanya sukarelawan yang tidak digunakan.

4. Tuntutan tugas melebihi TK yang ada akan mengakibatkan adanya biaya kekurangan. Itu menunjukkan bahwa model manajemen sukarelawan harus memaksimumkan penyelesaian tugas dengan cara menggunakan sukarelawan sebanyak mungkin untuk menghindari kekurangan tersebut.

Karakteristik!karakteristik yang dibahas di atas dibutuhkan untuk menunjukkan bahwa formulasi model matematika dalam manajemen sukarelawan pada hakikatnya berbeda dengan model yang biasa.

1 *$!( -+ - 2

Langkah awal membangun model penjadwalan sukarelawan ini adalah mendeskripsikan masalah tersebut dengan jelas dan lengkap. Selanjutnya, masalah tersebut diformulasikan dengan bentuk pemrograman multiobjektif yang siap diselesaikan dengan metode yang sudah ditentukan.

Pemodelan masalah ini dibuat berdasarkan adanya keterbatasan dana dan juga mempertimbangkan preferensi tugas dan waktu yang diinginkan sukarelawan.

Variabel keputusan dalam masalah penjadwalan ini ialah dapat mengerjakan tugas k.

Ki = himpunan tugas yang dapat dikerjakan ditugaskan pada sukarelawan i. <- = jumlah maksimum blok waktu yang

ditugaskan pada sukarelawan i. =- = jumlah maksimum penugasan maksimum untuk mengerjakan tugas k.

Fungsi objektif yang pertama ialah meminimumkan total biaya kekurangan yaitu biaya yang disebabkan karena tuntutan tugas yang melebihi sukarelawan yang ada. Formulasi fungsi objektif pertama ialah:

min E , , F.:;.: :GH .G

("'-+ 3)%&#+,

Fungsi objektif yang kedua ingin meminimumkan jumlah penugasan pada blok waktu dan tugas yang tidak diinginkan

(11)

7

yang dibutuhkan pada blok waktu j dengan penugasan k, yaitu:

, -.: ;.: D.:, -GIJK

8 G 7, L G M.

2. Total biaya penugasan sukarelawan tidak boleh melebihi anggaran yang tersedia, yaitu:

3. Sukarelawan i bertugas selama paling sedikit <_- blok waktu dan paling banyak <- blok waktu dalam satu periode, yaitu: <- , , -.:

:GH .G

<-, 5 G O.

4. Sukarelawan i tidak diperbolehkan mengerjakan lebih dari satu tugas pada blok waktu yang sama, yaitu:

, -.: 1, :GH

5 G O, 8 G 7.

5. Sukarelawan i sebanyak!banyaknya dapat bertugas pada =_- blok waktu yang tidak

6. Sukarelawan i sebanyak!banyaknya dapat bertugas pada >_- tugas yang tidak setiap blok waktu j sebanyak!banyaknya sebesar ?_:, yaitu:

, ;.: ?:, L G M .G

.

8. Variabel keputusanxijk bernilai 0 atau 1.

-.:G Q0,1R; i∈V, j∈T, k∈K.

9. Variabel yjk bernilai bilangan bulat

taknegatif.

yjk ≥ 0, yjk ∈ Z, i∈V, j∈T, k∈K

:

Masalah penjadwalan sukarelawan ini akan diselesaikan dengan menggunakan metode kendala!ε dan metode pembobotan.

%#*0% %"0 9ε

Pada metode ini, sekumpulan solusi optimal harus dibangkitkan. Langkah pertama minimumkan fungsi objektif 1 dengan kendala!kendala yang ada. Pada saat itu, fungsi objektif 2 diasumsikan tidak ada dalam model. Setelah didapatkan nilai dari fungsi objektif 1 (z1

*

), tambahkan sebuah parameter baru (ε > 1) ke dalam model. Nilai parameter ε tersebut dikalikan dengan solusi z1* dan

dijadikan sebagai nilai dari sisi kanan fungsi objektif 1. Selanjutnya fungsi objektif 1 diubah menjadi kendala baru dalam model ini.

, , F.:;.: S T. :GH

.G

Langkah selanjutnya selesaikan fungsi objektif 2 dengan memperhatikan kendala! kendala yang ada dan kendala baru di atas. Solusi akhir (z2

*

) sekarang bergantung pada nilai dari ε. Setelah itu, harus dilakukan penyelesaian model berulang!ulang untuk nilai ε yang berbeda sehingga didapatkan nilai z1

*

dan z2 *

. Selanjutnya, gambarkan kurva trade off dari kombinasi nilai z1* dan z2*

tersebut. Pembuat keputusan akan:

a. memeriksa kurva trade off.

b. memilih titik pada kurva tersebut yang paling tepat dalam menyeimbangkan kedua solusi yang saling bertentangan itu. c. menerapkan jadwal yang sesuai.

%#*0% %!3*3*# "

Pada metode ini, kedua fungsi objektif yang ada pada model penjadwalan akan digabungkan menjadi satu fungsi objektif saja. Fungsi objektifnya akan berubah menjadi seperti di bawah ini:

min E > U, , F.:;.:

dengan w adalah bobot yang bernilai antara nol sampai dengan satu (0 ≤ w ≤ 1).

(12)

, -.: ;.: D.:, -GIJK

8 G 7, L G M.

:GH .G

<-, 5 G O.

, -.: 1, :GH

5 G O, 8 G 7.

, ;.: ?:, L G M .G

.

-.:G Q0,1R; i∈V, j∈T, k∈K.

taknegatif.

yjk ≥ 0, yjk ∈ Z, i∈V, j∈T, k∈K

:

%#*0% %"0 9ε

*

, , F.:;.: S T. :GH

.G

*

dan z2 *

%#*0% %!3*3*# "

min E > U, , F.:;.:

(13)

8

:

#(0+

-(-Pada studi kasus ini, tersedia 40 orang sukarelawan yaitu R1, R2, …, R40 yang harus ditugaskan pada serangkaian tugas selama satu minggu. Daftar tugas!tugas sukarelawan selama seminggu di daerah bencana diberikan seperti di bawah ini:

1. Tugas 1 (K1): menyediakan tempat pengungsian dan mengawasi proses pengungsian.

2. Tugas 2 (K2): mencari dan menyelamatkan korban ke daerah yang aman.

3. Tugas 3 (K3): menyediakan perlengkapan dan makanan yang dibutuhkan korban bencana.

4. Tugas 4 (K4): mengamankan akses daerah bencana dan menjamin keamanan. 5. Tugas 5 (K5): mengobati dan merawat

korban!korban yang terluka.

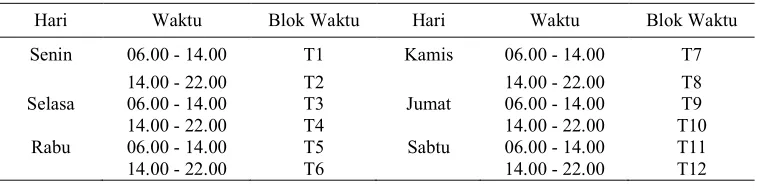
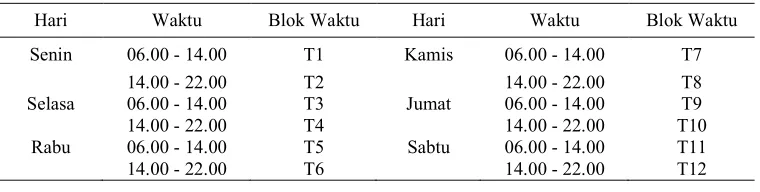
Waktu bertugas yang diberikan untuk para sukarelawan ini adalah enam hari (Senin–Sabtu). Per harinya dibagi lagi menjadi dua blok waktu yaitu shift pagi (pukul 06.00–14.00) dan shift sore (pukul 14.00– 22.00), sehingga dalam seminggu tersebut ada dua belas blok waktu. Untuk lebih lengkapnya, daftar blok waktu disajikan pada Tabel 3.

Tabel 3 Daftar blok waktu

Setiap sukarelawan diperbolehkan memilih tugas dan blok waktu yang diinginkannya. Permintaan tugas dan blok

waktu yang diinginkan oleh masing!masing sukarelawan secara lengkap disajikan pada Tabel 4.

Tabel 4 Daftar permintaan blok waktu dan tugas yang diinginkan setiap sukarelawan

Sukarelawan Tugas Shift Sukarelawan Tugas Shift

R1 K2 pagi R21 K4 Pagi

R3 K5 pagi R23 K2 Sore

R4 K5 sore R24 K1 Sore

R5 K3 sore R25 K5 Pagi

R8 K1 pagi R28 K2 pagi

R9 K2 sore R29 K5 sore

R11 K3 sore R31 K3 pagi

R15 K3 pagi R35 K3 sore

Hari Waktu Blok Waktu Hari Waktu Blok Waktu

Senin 06.00 ! 14.00 T1 Kamis 06.00 ! 14.00 T7

14.00 ! 22.00 T2 14.00 ! 22.00 T8

Selasa 06.00 ! 14.00 T3 Jumat 06.00 ! 14.00 T9

14.00 ! 22.00 T4 14.00 ! 22.00 T10

Rabu 06.00 ! 14.00 T5 Sabtu 06.00 ! 14.00 T11

(14)

Jika sukarelawan i memilih untuk ditugaskan pada shift pagi maka artinya sukarelawan tersebut bersedia ditempatkan pada blok waktu T1, T3, T5, T7, T9, T11. Jika sukarelawan i memilih untuk ditugaskan pada shift sore maka artinya sukarelawan tersebut bersedia ditempatkan pada blok waktu T2, T4, T6, T8, T10, T12.

Selain data!data yang ditampilkan di atas, ada beberapa lagi parameter yang harus ditentukan nilainya, yaitu:

1. Biaya akibat kekurangan sukarelawan dalam mengerjakan tugas ke!k dan waktu ke!j (djk) disajikan pada Tabel 5.

Tabel 5 Biaya kekurangan djk (juta rupiah)

Blok Waktu K1 K2 K3 K4 K5 diasumsikan sebesar 600 (juta) rupiah. 3. Biaya yang dikeluarkan untuk

menugaskan sukarelawan i pada blok waktu j dengan tugas k (cijk) dicantumkan

pada Lampiran 2.

4. Maksimum jumlah blok waktu yang ditugaskan pada sukarelawan i < -adalah 7.

5. Minimum jumlah blok waktu yang ditugaskan pada sukarelawan i (<_-) adalah 6.

6. Jumlah maksimum penugasan sukarelawan i pada blok waktu yang tidak diinginkannya (=_-) adalah 2.

7. Jumlah maksimum penugasan sukarelawan i pada tugas yang tidak diinginkannya (>_-) adalah 2.

8. Kekurangan maksimum sukarelawan (jumlah orang) untuk tugas k selama seminggu (?_:) adalah 4.

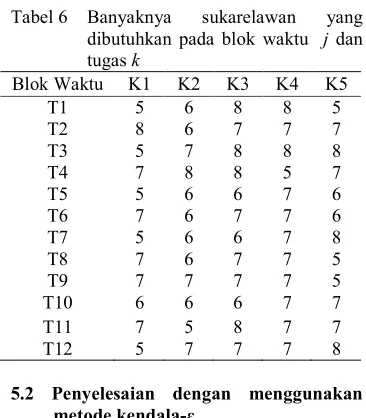
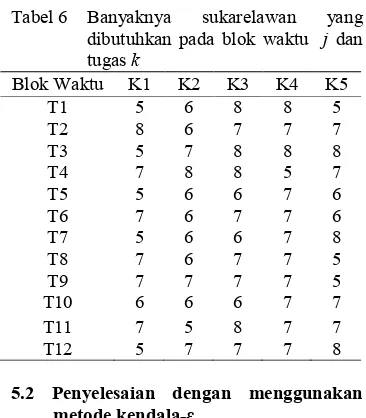
9. Jumlah sukarelawan yang dibutuhkan pada blok waktu j dan tugas k (D_.:) ditampilkan pada Tabel 6.

Tabel 6 Banyaknya sukarelawan yang dibutuhkan pada blok waktu j dan

Minimumkan fungsi objektif 1 dengan kendala!kendala yang ada. Asumsikan fungsi objektif kedua tidak ada dalam model.

(15)

10

"'& 2

Selanjutnya, minimumkan fungsi objektif 2 dengan kendala!kendala yang ada dan kendala baru dari fungsi objektif 1, yaitu:

min E , , , @-.: -.:

Langkah 2 diulang untuk beberapa nilai ε yang berbeda. Setiap nilai ε yang digunakan akan diperoleh nilai z2 dan ;.: yang berbeda.

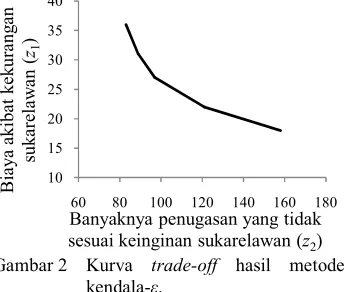
Nilai ;_.: yang diperoleh tadi digunakan untuk mencari nilai yang baru. Nilai z1 baru dan fungsi objektif 2 dapat ditampilkan seperti yang disajikan pada Gambar 2.

Gambar 2 Kurva trade off hasil metode Skenario ini sangat cocok digunakan untuk penanganan bencana yang harus dilakukan secara cepat atau untuk memulihkan keadaan setelah bencana. Saat itu, penanganan korban yang selamat lebih dutamakan daripada hal lainnya. Oleh karena itu, sukarelawan yang ada diharuskan bekerja lebih keras dan secepat mungkin meskipun jadwal yang diperoleh nanti tidak sesuai dengan keinginan para sukarelawan. Skenario kedua (ε = 2) lebih cocok untuk memulihkan keadaan setelah bencana dengan jangka waktu yang lebih panjang. Oleh karena itu, penentuan jadwal sukarelawan dapat dibuat sesuai dengan keinginan dari para sukarelawan.

Kedua skenario di atas mempunyai kelebihan dan kekurangannya msing!masing. Skenario pertama lebih mengutamakan untuk meminimumkan fungsi objektif 1 daripada fungsi objektif 2. Skenario kedua adalah kebalikan dari skenario pertama. Selanjutnya pilih sembarang titik pada kurva trade off. Misalkan dipilih skenario kedua yaitu saat nilai ε = 2. Hasil dari skenario ini ditampilkan dalam bentuk tabel penjadwalan sukarelawan seperti yang disajikan pada Tabel 8.

10

(16)

Tabel 8 Jadwal sukarelawan (ε = 2)

Jadwal sukarelawan yang disajikan pada Tabel 8 merupakan solusi perhitungan Langkah 2 pada saat ε = 2 dengan menggunakan LINGO 8.0 (lihat Lampiran 4). Jadwal sukarelawan yang diberikan garis bawah pada Tabel 8 menunjukkan jadwal sukarelawan yang tidak sesuai dengan keinginan dari sukarelawan tersebut.

1 %"8% %- + " 0%"' " !%"''(" & " !%#*0% 4%!3*3*# "

Pada metode pembobotan, cara menyelesaikan model penjadwalan sukarelawan tersebut adalah dengan menggabungkan kedua fungsi objektifnya menjadi satu fungsi objektif saja. Setiap fungsi objektif diberikan bobot yang bernilai positif. Fungsi objektif 1 diberikan bobot sebesar w sedangkan fungsi objektif 2 diberikan bobot sebesar (1 w). Formulasi model setelah menggunakan metode pembobotan diberikan seperti di bawah ini.

(17)

12

Pengoptimuman model di atas dilakukan beberapa kali dengan menggunakan bobot yang berbeda. Bobot yang diperbolehkan adalah bobot yang bernilai antara nol sampai dengan satu (0 ≤ w ≤ 1), sehingga akan didapatkan nilai z1, z2, dan z gabungan yang

berbeda pada setiap nilai bobot seperti yang disajikan pada Tabel 9. Perhitungannya dapat dilihat pada Lampiran 5.

Tabel 9 Solusi yang diperoleh dari metode

Untuk memudahkan dalam membaca Tabel 9, dibuat grafik seperti yang disajikan pada Gambar 3.

Gambar 3 Grafik solusi dengan metode pembobotan.

Pada Gambar 3, garis yang diberikan warna hijau menunjukkan garis nilai z* terhadap bobot (w), semakin besar bobot yang digunakan semakin besar juga nilai z*. Garis yang berwarna biru menunjukkan garis nilai z1 yang terakhir berwarna merah menunjukkan garis nilai z2* terhadap w. Garis nilai z2*

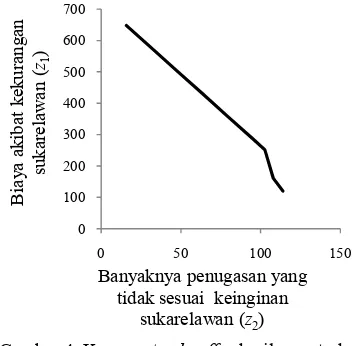
terhadap w berbeda dari garis!garis yang lain karena semakin besar bobot yang digunakan semakin kecil nilai z2*. Gambar 4

menunjukkan kurva trade off antara nilai z1 *

dan z2 *

dengan menggunakan metode pembobotan. dapat diambil kesimpulan bahwa semakin besar bobot (w) yang digunakan menyebabkan semakin besar biaya yang diakibatkan oleh kekurangan sukarelawan (z1), sementara

banyaknya penugasan yang tidak sesuai dengan keinginan sukarelawan (z2) semakin

mengecil. Gambar 4 juga menunjukkan bahwa perubahan nilai z1 dan z2 berbanding terbalik tidak sesuai keinginan

(18)

:

+!4( "

Dalam penulisan karya ilmiah ini telah diperlihatkan karakteristik model penjadwalan sukarelawan. Model penjadwalan sukarelawan ini memiliki dua fungsi objektif. Tujuannya adalah meminimumkan biaya yang diakibatkan kekurangan sukarelawan dan meminimumkan penugasan sukarelawan yang tidak sesuai dengan keinginan dari setiap sukarelawan. Penyelesaian masalah dicari dengan metode kendala!ε dan metode pembobotan.

Model penjadwalan sukarelawan ini dapat diselesaikan dengan bantuan software LINGO 8.0. Setelah dilakukan pengoptimuman pada model menggunakan software LINGO 8.0, dapat dibuat sebuah kurva trade off antara kedua fungsi objektifnya. Kurva trade off yang diperoleh kedua metode tersebut ternyata sama. Dari kurva trade off tersebut dapat disimpulkan bahwa perubahan nilai fungsi

objektif pertama dan kedua berbanding terbalik. Hal itu menunjukkan semakin besar biaya yang dikeluarkan akibat adanya kekurangan sukarelawan menyebabkan penugasan sukarelawan yang tidak sesuai dengan keinginannya semakin sedikit.

$ "

Pada karya ilmiah ini data yang digunakan adalah data hipotetik. Saran untuk penulisan karya ilmiah selanjutnya adalah menggunakan data sebenarnya di lapangan misalnya kasus bencana Gunung Merapi di Yogyakarta dan Jawa Tengah. Dengan begitu, model ini membantu instansi, dalam hal ini organisasi kemanusiaan, dalam membuat penjadwalan sukarelawan yang baik. Selain itu, untuk menyelesaikan masalah ini bisa dicoba menggunakan metode lain.

Eiselt HA, Sandblom CL. 2007. Linear Programming and Its Applications. Berlin: Springer.

Falasca M, Zobel CW, Fetter GM. 2009. An optimization model for humanitarian relief volunteer management. Di dalam: Landgren J, Jul S, editors. Proceedings

of the 6th ISCRAM Conference;

Gothenburg, Mei 2009. Virginia Tech: Pamplin College of Business.

Garfinkel RS & GL Nemhauser. 1972. Integer Programming. New York: John Wiley & Sons.

Nash SG & A Sofer. 1996. Linear and Nonlinear Programming. New York: McGraw!Hill.

Ravindran RA. 2009. Operations Research Methodologies. New York: CRC Press.

Siswanto. 2006. Operations Research Jilid 1. Bogor: Erlangga.

Winston WL. 1995. Introduction to Mathematical Programming 2nd ed. New York: Duxbury.

(19)

(20)

(21)

Masalah Pengoptimuman Multikriteria dalam Penjadwalan Tenaga Sukarelawan di Daerah Bencana. Dibimbing oleh dan

.

(22)

Volunteer Scheduling at Disaster Area. Supervised by and .

(23)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains

pada

(24)

Judul

: Masalah Pengoptimuman Multikriteria dalam Penjadwalan Tenaga

Sukarelawan di Daerah Bencana

Nama

: Albrian Wedhaswara Murtanto

NIM

: G54061446

Menyetujui,

Pembimbing I

Pembimbing II

Dr. Toni Bakhtiar, M.Sc.

Dra. Farida Hanum, M.Si.

NIP 19720627 199702 1 002

NIP 19651019 199103 2 002

Mengetahui,

Ketua Departemen Matematika

Dr. Berlian Setiawaty, M.S.

NIP 19650505 198903 2 004

(25)

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala limpahan rahmat dan nikmat sehat sehingga penulis mampu menyelesaikan karya ilmiah ini. Penyusunan karya ilmiah ini tidak terlepas dari dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis ingin mengucapkan terima kasih kepada:

1. Bapak dan Ibu tersayang, terima kasih atas didikan, kasih sayang, nasihat, semangat, serta doa yang tiada henti!hentinya; doa selalu menjadi penerang jalan penulis,

2. Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing I, Dra. Farida Hanum, M.Si. selaku pembimbing II; terima kasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis,

3. Dr. Ir. Amril Aman, M.Sc. selaku dosen penguji, terima kasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis,

4. Kakakku tersayang (Astri Ireka Murtanti), adikku tercinta (Aldhi Tanca Muriantono dan Arwin Mursaptono), terima kasih atas semangat dan dukungannya,

5. Dosen!dosen Departemen Matematika, terima kasih atas ilmu yang telah diberikan,

6. Pak Yono, Bu Ade, Bu Susi, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terima kasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di Departemen Matematika,

7. Guru!guru SMA Negeri 80 Jakarta, SLTP Negeri 30 Jakarta, dan SD Negeri Kebon Bawang 05 Pagi; tanpamu, penulis takkan berdiri di sini,

8. Kakak kelas angkatan 41 dan 42 yang tidak bisa penulis sebutkan satu per satu,

9. Teman!teman angkatan 43: Ria, Margi, Suci, Aini, Nene, Putri, Lina, Lia, Erni, Rias, Arum, Nia, Destya, Resti, Nidya, Tami, Maria Herlina, Narsih, Desy, Ratna Agung, Cici, Vera, Rizki SN, Rizki NS, Kiki, Apri, Ace, Mamet, Supri, Irsyad, Copi, Wira, Peli, Arif, Mubarok, Ryan, Fardan, Nanu, Dwi, Adi, Ecka, Sendy, Dandi, Izul, Adam, Kunto, Syahrul, Faisol, Elly, Hendra, Razon, Kabil, Sabar, Gandi, Andrew, Ucok, dan Nobo; terima kasih atas doa, dukungan dan semangatnya, terima kasih atas kebersamaannya selama 3 tahun di Math’43, 10. Adik kelas angkatan 44, 45 dan 46 yang tidak bisa penulis sebutkan satu per satu,

11. Teman!teman di rumah indekos: Risal, Peli, Tito, Dwi, Tedy, Wahyu, Ridho, Onta, Dono, Ipank dan lainnya yang tidak bisa ditulis satu per satu, terima kasih atas doa, dukungan, dan persahabatannya.

Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca. Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.

Bogor, September 2011

(26)

Penulis lahir di Jakarta pada tanggal 4 Oktober 1988 sebagai anak kedua dari empat bersaudara, anak dari pasangan Sartono dan Sri Murni. Tahun 2000 penulis lulus dari SDN Kebon Bawang 05 Pagi Jakarta. Tahun 2003 penulis lulus dari SLTPN 30 Jakarta. Tahun 2006 penulis lulus dari SMAN 80 Jakarta dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Seleksi Penerimaan Mahasiswa Baru (SPMB). Pada tahun 2007, penulis memilih mayor Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

(27)

! "

DAFTAR GAMBAR ... vii DAFTAR TABEL ... vii DAFTAR LAMPIRAN ... vii

I PENDAHULUAN

1.1 Latar Belakang ... 1 1.2 Tujuan ... 1

II LANDASAN TEORI

2.1 Pemrograman Linear ... 1 2.2 Pemrograman Linear Bilangan Bulat ... 3 2.3 Pemrograman Multiobjektif ... 3 2.4 Metode Penyelesaian ... 3

III DESKRIPSI DAN FORMULASI MASALAH

3.1 Deskripsi Masalah ... 5 3.2 Formulasi Masalah ... 6

IV METODE PENYELESAIAN

4.1 Metode Kendala!ε ... 7 4.2 Metode Pembobotan ... 7

V STUDI KASUS DAN PENYELESAIANNYA

5.1 Studi Kasus ... 8 5.2 Penyelesaian dengan Menggunakan Metode Kendala!ε... 9 5.3 Penyelesaian dengan Menggunakan Metode Pembobotan ... 11

VI SIMPULAN DAN SARAN ... 13

DAFTAR PUSTAKA ... 13

LAMPIRAN ... 14

(28)

1 Grafik perubahan nilai z1* dan z2* pada bobot yang berbeda ... 5

2 Kurva trade off hasil metode kendala!ε ... 10 3 Grafik solusi dengan metode pembobotan.. ... 12 4 Kurva trade off hasil metode pembobotan ... 12

! " 1 Solusi pengoptimuman Langkah 2 ... 5 2 Perbedaan antara model tenaga kerja dan model sukarelawan ... 5 3 Daftar blok waktu ... 8 4 Daftar permintaan blok waktu dan tugas yang diinginkan setiap sukarelawan ... 8 5 Biaya kekurangan djk (juta rupiah) ... 9

6 Banyaknya sukarelawan yang dibutuhkan pada blok waktu j dan tugas k ... 9 7 Solusi yang diperoleh dari metode kendala!ε ... 10 8 Jadwal sukarelawan (ε = 2) ... 11 9 Solusi yang diperoleh dari metode pembobotan... 12

! "

1 Syntax Program LINGO 8.0 untuk Menyelesaikan Masalah Pemrograman Linear pada

Contoh (2) dengan Metode Kendala!ε beserta Hasil yang Diperoleh ... 15 2 Data Input Program LINGO 8.0 untuk Masalah Penjadwalan Sukarelawan dengan Metode

Kendala!ε dan Metode Pembobotan ... 17

3 Syntax Program LINGO 8.0 untuk Masalah Penjadwalan Sukarelawan dengan Metode

Kendala!ε ... 31 4 Hasil Komputasi LINGO 8.0 Langkah 5 setelah dilakukan running ... 37

5 Syntax Program LINGO 8.0 untuk Masalah Penjadwalan Sukarelawan dengan Metode

Pembobotan ... 42

(29)

# $ % & "'

sukarelawan ini dapat dimodelkan dalam bentuk pengoptimuman multikriteria. Pengoptimuman multikriteria merupakan masalah pengoptimuman yang memiliki lebih dari satu fungsi objektif. Masalah penjadwalan sukarelawan dapat diselesaikan dengan beberapa metode, di antaranya metode kendala!ε dan metode pembobotan.

()( "

%!$*'$ ! " +"% $ %,+"+-+ . ("'-+ +"% $/

%,+"+-+ . %$#+0 &- ! " +"% $/

(Winston 1995)

%,+"+-+ 1 . %"#(& # "0 $ /

(30)

terhadap

0 (1)

Dengan c dan x merupakan vektor berukuran n, vektor b berukuran m, sedangkan A merupakan matriks berukuran m × n. Matriks A disebut matriks kendala.

(Nash & Sofer 1996)

%,+"+-+ . %$ 2 +-+3% /

Solusi optimum terbaik adalah suatu titik dalam daerah fisibel yang menyebabkan nilai fungsi objektif terkecil (masalah minimisasi). Sedangkan, solusi optimum suatu PL maksimisasi adalah suatu titik dalam daerah fisibel yang menyebabkan nilai fungsi objektif terbesar.

(Winston 1995)

* (-+

Untuk menyelesaikan suatu masalah PL, metode simpleks merupakan salah satu metode yang dapat menghasilkan solusi optimum. Metode ini mulai dikembangkan oleh Dantzig pada tahun 1947. Metode ini adalah metode yang umum digunakan untuk menyelesaikan masalah PL. Metode simpleks ini berupa metode iteratif (proses mencari solusi yang dilakukan secara berulang!ulang hingga didapatkan solusi yang diinginkan) untuk menyelesaikan masalah PL berbentuk standar.

Pada PL (1), vektor x yang memenuhi kendala disebut sebagai solusi dari PL (1). Misalkan matriks A dapat dinyatakan

sebagai , sedangkan B

merupakan matriks berukuran m × m yang elemennya berupa koefisien variabel basis dan N merupakan matriks yang elemennya berupa koefisien variabel nonbasis pada matriks kendala. Matriks B disebut matriks basis untuk PL (1).

Misalkan x dapat dinyatakan sebagai

vektor dengan adalah vektor variabel basis dan adalah vektor variabel nonbasis, maka

(2)

Karena B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2) dapat

i. Solusi tersebut memenuhi kendala PL. ii. Kolom!kolom dari matriks koefisien yang

berpadanan dengan komponen taknol adalah bebas linear.

(Nash & Sofer 1996)

%,+"+-+ 5 . * (-+ +-+3% -+-/

Vektor x disebut solusi fisibel basis jika x merupakan solusi basis dan 0.

(Nash & Sofer 1996)

*"#*2

Misalkan diberikan pemrograman linear berikut:

minimumkan 2 3 ,

dengan kendala 2 4

2 _! 11

_# 5. (4)

Dari PL tersebut didapatkan

% 2 1 11 2 0

Maka matriks basisnya adalah

%1 0 00 1 0 0 0 1'.

Dengan menggunakan matriks basis tersebut diperoleh

0 0 (_,

4 11 5 (_{. (5)}

(31)

3

%,+"+-+ 6 . #$+&- -+-/

Suatu matriks disebut matriks basis untuk PL jika matriks tersebut adalah matriks taksingular, yaitu matriks yang determinannya tidak sama dengan nol.

%!$*'$ ! " +"% $ + "' " ( # Model pemrograman linear bilangan bulat (PLBB) atau integer linear programming (ILP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat. Model PLBB yang semua variabelnya bernilai bilangan bulat disebut pemrograman bilangan bulat murni. Sedangkan, model PLBB yang hanya sebagian variabelnya bernilai bilangan bulat disebut pemrograman bilangan bulat campuran. Model PLBB yang hanya mengharuskan nilai nol atau satu untuk variabelnya dinamakan pemrograman bilangan bulat 0!1.

%,+"+-+ 7 . %!$*'$ ! " +"% $ % &- -+/ PL!relaksasi merupakan pemrograman linear yang diperoleh dari suatu PLBB dengan menghilangkan kendala bilangan bulat atau kendala 0!1 pada setiap variabelnya.

Untuk masalah meminimumkan, nilai fungsi objektif yang optimum di PL!relaksasi lebih kecil atau sama dengan nilai fungsi objektif yang optimum di PLBB, sedangkan untuk masalah memaksimumkan nilai fungsi objektif yang optimum di PL!relaksasi lebih besar atau sama dengan nilai fungsi objektif yang optimum di PLBB.

(Winston 1995)

%,+"+-+ . *0% #%! #+& %"(' - "/ Bentuk umum dari model matematika masalah penugasan adalah sebagai berikut:

min , , -. -. meminimumkan biaya penjadwalan. Asumsikan xijsebagai penugasan dari sumber

i ke tujuan j. Nilai xij sama dengan satu jika

sumber i ditugaskan pada tujuan j, sedangkan bernilai nol jika selainnya. Parameter bij

adalah biaya penugasan untuk sumber i ke tujuan j. Parameter 1_- adalah jumlah penugasan setiap sumber i pada tujuan j. Parameter 7_. adalah jumlah sumber i yang ditugaskan pada setiap tujuan j.

(Siswanto 2006)

1 %!$*'$ ! " ( #+*3)%&#+,

Masalah pengoptimuman yang telah didiskusikan sebelumnya adalah masalah pengoptimuman yang hanya memiliki satu fungsi objektif. Sedangkan, masalah pengoptimuman yang akan dibahas sekarang adalah masalah pengoptimuman yang memiliki lebih dari satu fungsi objektif. Masalah pengoptimuman yang dimaksud adalah masalah pengoptimuman multikriteria. Pada masalah pengoptimuman multikriteria ini, ada beberapa istilah yang harus diketahui seperti pengambilan keputusan multikriteria atau multiple criteria decision making (MCDM). Sebuah masalah pengoptimuman multikriteria dapat dikatakan sebagai MCDM jika terdapat lebih dari satu hal yang harus diperhatikan dalam model tersebut sebagai tujuan atau kriterianya.

%,+"+-+ . *$!( -+ /

Masalah pengoptimuman multikriteria biasanya diformulasikan sebagai berikut.

min [f1(x), f2(x), …, fk(x)],

(32)

%#*0% %!3*3*# "

Metode pembobotan merupakan salah satu metode penyelesaian yang tertua dan metode yang paling sederhana dari MCDM. Metode ini pertama kali direkomendasikan oleh Zadeh. Metode ini menggabungkan semua fungsi objektif yang ada dalam model, dan setiap fungsi objektif tersebut diberikan bobot (w) yang berbeda. Misalkan diberikan permasalahan MCDM seperti pada model (6). Setelah dilakukan metode pembobotan, fungsi objektif gabungannya akan seperti persamaan berikut

min z = w1 f1(x)+ …+ wk fk(x). (7)

Fungsi objektif tersebut selanjutnya dioptimumkan dengan menggunakan variasi bobot yang berbeda. Nilai total dari bobot! bobot tersebut harus satu, yaitu:

w1 + w2 + …. + wk = 1.

%#*0% %"0 9ε

Ide dasar metode ini adalah mengubah hampir semua fungsi objektifnya menjadi kendala. Metode ini hanya menyisakan satu fungsi objektif saja, misalkan fungsi objektifnya adalah f1(x). Fungsi objektif

lainnya akan diubah menjadi kendala. Fungsi objektif yang akan diubah menjadi kendala pertama!tama harus dicari solusi optimalnya. Solusi optimal tersebut setelah dikalikan dengan parameter ε akan menjadi nilai dari sisi kanan kendala baru. Setelah itu, optimumkan fungsi objektif f1(x) dengan

menambahkan kendala!kendala baru tersebut. Fungsi objektif tersebut dicari solusi optimalnya dengan mencoba beberapa nilaiε berbeda. Misalkan formulasi model (6) akan dicoba diselesaikan dengan menggunakan metode kendala!ε. Tahapan pengoptimuman model (6), yaitu:

merupakan solusi dari fungsi objektif ke!i. "'& 2

max f1(x)

dengan kendala

gj (x) ≤ 0 ; j = 1, 2, …, m

fi (x) ≥ ε fi* (x) ; 0 ≤ ε ≤ 1, i = 2, 3, …, k

Langkah 2 dilakukan berulang kali dengan menggunakan nilai ε yang berbeda sehingga

(Falasca et al. 2009) *"#*2

Misalkan diberikan model seperti di bawah ini: dengan menggunakan metode kendala!ε. Misalkan fungsi objektif 1 ditetapkan sebagai fungsi objektif, maka fungsi objektif 2 harus diubah menjadi kendala. Tahapan pengoptimuman model (8), yaitu:

"'& 2

(33)

5

dan z2 *

1 %-&$+4-+ - 2

kekurangan

kerja Tidak dibahas

(34)

7

1. Tingkat komitmen (TK) tenaga kerja atau sukarelawan dipengaruhi secara langsung oleh penempatan tugasnya.

2. Pemanfaatan tenaga kerja sukarelawan melebihi TK akan meningkatkan TK di masa depan. Sebaliknya, pemanfaatan sukarelawan di bawah TK akan mengurangi TK di masa depan. Dalam hal ini, model manajemen sukarelawan harus menghindari pemanfaatan sukarelawan secara berlebihan.

3. Model harus memberikan solusi untuk menghindari adanya sukarelawan yang tidak digunakan.

4. Tuntutan tugas melebihi TK yang ada akan mengakibatkan adanya biaya kekurangan. Itu menunjukkan bahwa model manajemen sukarelawan harus memaksimumkan penyelesaian tugas dengan cara menggunakan sukarelawan sebanyak mungkin untuk menghindari kekurangan tersebut.

Karakteristik!karakteristik yang dibahas di atas dibutuhkan untuk menunjukkan bahwa formulasi model matematika dalam manajemen sukarelawan pada hakikatnya berbeda dengan model yang biasa.

1 *$!( -+ - 2

Langkah awal membangun model penjadwalan sukarelawan ini adalah mendeskripsikan masalah tersebut dengan jelas dan lengkap. Selanjutnya, masalah tersebut diformulasikan dengan bentuk pemrograman multiobjektif yang siap diselesaikan dengan metode yang sudah ditentukan.

Pemodelan masalah ini dibuat berdasarkan adanya keterbatasan dana dan juga mempertimbangkan preferensi tugas dan waktu yang diinginkan sukarelawan.

Variabel keputusan dalam masalah penjadwalan ini ialah dapat mengerjakan tugas k.

Ki = himpunan tugas yang dapat dikerjakan ditugaskan pada sukarelawan i. <- = jumlah maksimum blok waktu yang

ditugaskan pada sukarelawan i. =- = jumlah maksimum penugasan maksimum untuk mengerjakan tugas k.

Fungsi objektif yang pertama ialah meminimumkan total biaya kekurangan yaitu biaya yang disebabkan karena tuntutan tugas yang melebihi sukarelawan yang ada. Formulasi fungsi objektif pertama ialah:

min E , , F.:;.: :GH .G

("'-+ 3)%&#+,

Fungsi objektif yang kedua ingin meminimumkan jumlah penugasan pada blok waktu dan tugas yang tidak diinginkan

(35)

7

, -.: ;.: D.:, -GIJK

8 G 7, L G M.

:GH .G

<-, 5 G O.

, -.: 1, :GH

5 G O, 8 G 7.

, ;.: ?:, L G M .G

.

-.:G Q0,1R; i∈V, j∈T, k∈K.

taknegatif.

yjk ≥ 0, yjk ∈ Z, i∈V, j∈T, k∈K

:

%#*0% %"0 9ε

*

, , F.:;.: S T. :GH

.G

*

dan z2 *

%#*0% %!3*3*# "

min E > U, , F.:;.:

(36)

:

#(0+

-(-Pada studi kasus ini, tersedia 40 orang sukarelawan yaitu R1, R2, …, R40 yang harus ditugaskan pada serangkaian tugas selama satu minggu. Daftar tugas!tugas sukarelawan selama seminggu di daerah bencana diberikan seperti di bawah ini:

1. Tugas 1 (K1): menyediakan tempat pengungsian dan mengawasi proses pengungsian.

2. Tugas 2 (K2): mencari dan menyelamatkan korban ke daerah yang aman.

3. Tugas 3 (K3): menyediakan perlengkapan dan makanan yang dibutuhkan korban bencana.

4. Tugas 4 (K4): mengamankan akses daerah bencana dan menjamin keamanan. 5. Tugas 5 (K5): mengobati dan merawat

korban!korban yang terluka.

Waktu bertugas yang diberikan untuk para sukarelawan ini adalah enam hari (Senin–Sabtu). Per harinya dibagi lagi menjadi dua blok waktu yaitu shift pagi (pukul 06.00–14.00) dan shift sore (pukul 14.00– 22.00), sehingga dalam seminggu tersebut ada dua belas blok waktu. Untuk lebih lengkapnya, daftar blok waktu disajikan pada Tabel 3.

Tabel 3 Daftar blok waktu

Setiap sukarelawan diperbolehkan memilih tugas dan blok waktu yang diinginkannya. Permintaan tugas dan blok

waktu yang diinginkan oleh masing!masing sukarelawan secara lengkap disajikan pada Tabel 4.

Tabel 4 Daftar permintaan blok waktu dan tugas yang diinginkan setiap sukarelawan

Sukarelawan Tugas Shift Sukarelawan Tugas Shift

R4 K5 sore R24 K1 Sore

Hari Waktu Blok Waktu Hari Waktu Blok Waktu

Senin 06.00 ! 14.00 T1 Kamis 06.00 ! 14.00 T7

14.00 ! 22.00 T2 14.00 ! 22.00 T8

Selasa 06.00 ! 14.00 T3 Jumat 06.00 ! 14.00 T9

14.00 ! 22.00 T4 14.00 ! 22.00 T10

Rabu 06.00 ! 14.00 T5 Sabtu 06.00 ! 14.00 T11

(37)

9