Metode Branch and Bound (AND/OR) pada Load Balancing

METODE BRANCH AND BOUND (AND/OR) PADA LOAD

BALANCING

SKRIPSI

ANGELINE LOUIS

110803033

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : Metode Branch and Bound (AND/OR) pada

Load Balancing

Kategori : Skripsi

Nama : Angeline Louis

Nomor Induk Mahasiswa : 110803033

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Disetujui di Medan, Februari 2015

Komisi Pembimbing

Pembimbing 2, Pembimbing 1,

Dr. Faigiziduhu Bu’ulolo, M.Si. Dr. Elly Rosmaini, M.Si.

NIP. 19531218 198003 1 003 NIP. 19600520 198503 2 002

Disetujui oleh:

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

METODE BRANCH AND BOUND (AND/OR) PADA LOAD BALANCING

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Februari 2015

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan yang Maha Penyayang, atas

kemurahan dan berkat yang telah diberikan sehingga penulis dapat menyelesaikan

skripsi dengan judul Metode Branch and Bound (AND/OR) pada Load Balancing

guna melengkapi syarat memperoleh gelar sarjana Matematika pada Fakultas

Matematika dan Ilmu Pengetahuan Alam di Universitas Sumatera Utara.

Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang

kepada semua pihak yang telah membantu dan membimbing penulis dalam

penyusunan skripsi ini, ucapan terima kasih penulis sampaikan kepada Ibu Dr.

Elly Rosmaini, M.Si selaku pembimbing I dan Bapak Dr. Faigiziduhu Bu’ulolo,

M.Si selaku pembimbing II yang telah memberikan bimbingan dan pengarahan

sehingga skripsi ini dapat penulis selesaikan. Bapak Drs. Marihat Situmorang,

M.Kom dan Ibu Dra. Normalina Napitupulu, M.Sc selaku dosen pembanding.

Bapak Prof. Dr. Tulus, Vor.Dipl.Math, M.Si dan Ibu Dr. Mardiningsih, M.Si

selaku Ketua dan Sekretaris Departemen Matematika FMIPA-USU Medan. Dekan

dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara. Seluruh Staff dan Dosen pada Departemen

Matematika FMIPA-USU dan pegawai di FMIPA-USU. Seluruh teman jurusan

Matematika khususnya stambuk 2011, adik-adik junior stambuk 2012, stambuk

2013, stambuk 2014 serta Abang dan Kakak alumni. Akhirnya tidak terlupakan

Ayahanda Lo Kok Kiang, Ibunda Muraina, serta keluarga yang selama ini

memberikan bantuan dan dorongan yang diperlukan. Semoga Tuhan Yang Maha

METODE BRANCH AND BOUND (AND/OR) PADA LOAD BALANCING

ABSTRAK

Load balancing merupakan suatu teknik untuk menyeimbangkan muatan pada

server untuk menghindari terjadinya kelebihan muatan. Muatan yang akan

dibahas adalah muatan di dalam server pada komputer dibagian CPU (perangkat

keras). Biasanya di dalam sebuah komputer terdapat beberapa server yang sudah

terbagi. Namun terdapat faktor lain yang menyebabkan server tidak dapat

menampung muatan secara optimal. Metode branch and bound mempunyai

metode lanjutan yaitu AND/OR. Meskipun AND/OR dinilai tidak dapat

membantu banyak, namun AND/OR dapat mengatasi celah-celah yang sudah

diabaikan bahkan memperkuat nilai optimal terbesar yang sudah didapatkan pada

metode branch and bound.

Kata kunci: Program Integer, Keseimbangan Muatan, Metode Branch and

BRANCH AND BOUND METHOD (AND/OR) IN LOAD BALANCING

ABSTRACT

Load Balancing is a technique to balance the load on the server to prevent

overloading. The load is a load that will be discussed in a server on the computer

at the CPU (Hardware). Usually in a computer, there are several servers that have

been divided. But there are other factors that cause the server can’t hold the load

optimally. Branch and bound methods have advanced method that is AND/OR.

Although AND/OR assessed can’t help much, but AND/OR overcome the gaps that have been ignored even reinforce the largest optimal value has been

established at the branch and bound method.

Keyword: Integer Programming, Load Balancing, Branch and Bound Method,

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

Bab 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Tujuan Penelitian 2

1.4 Manfaat Penelitian 3

1.5 Metodologi Penelitian 3

Bab 2 TINJAUAN PUSTAKA 4

2.1 Pengertian Load Balancing 4

2.2 Program Integer 5

2.3 Program Integer (Metode Branch and Bound) 6

Bab 3 PEMBAHASAN 7

3.1 Metode Simpleks 7

3.2 Metode Branch and Bound 11

3.3 Contoh kasus 17

Bab 4 KESIMPULAN DAN SARAN

4.1 Kesimpulan 38

4.2 Saran 39

METODE BRANCH AND BOUND (AND/OR) PADA LOAD BALANCING

ABSTRAK

Load balancing merupakan suatu teknik untuk menyeimbangkan muatan pada

server untuk menghindari terjadinya kelebihan muatan. Muatan yang akan

dibahas adalah muatan di dalam server pada komputer dibagian CPU (perangkat

keras). Biasanya di dalam sebuah komputer terdapat beberapa server yang sudah

terbagi. Namun terdapat faktor lain yang menyebabkan server tidak dapat

menampung muatan secara optimal. Metode branch and bound mempunyai

metode lanjutan yaitu AND/OR. Meskipun AND/OR dinilai tidak dapat

membantu banyak, namun AND/OR dapat mengatasi celah-celah yang sudah

diabaikan bahkan memperkuat nilai optimal terbesar yang sudah didapatkan pada

metode branch and bound.

Kata kunci: Program Integer, Keseimbangan Muatan, Metode Branch and

BRANCH AND BOUND METHOD (AND/OR) IN LOAD BALANCING

ABSTRACT

Load Balancing is a technique to balance the load on the server to prevent

overloading. The load is a load that will be discussed in a server on the computer

at the CPU (Hardware). Usually in a computer, there are several servers that have

been divided. But there are other factors that cause the server can’t hold the load

optimally. Branch and bound methods have advanced method that is AND/OR.

Although AND/OR assessed can’t help much, but AND/OR overcome the gaps that have been ignored even reinforce the largest optimal value has been

established at the branch and bound method.

Keyword: Integer Programming, Load Balancing, Branch and Bound Method,

BAB 1

PENDAHULUAN

1.1Latar Belakang

Load balancing merupakan suatu teknik yang digunakan untuk mendistribusikan

dua atau lebih jalur koneksi agar dapat berjalan optimal, memaksimalkan

throughput (kecepatan transfer antara pengguna layanan ke penyedia layanan, dan

penyedia layanan ke pengguna layanan) dan menghindari overload (kelebihan

muatan pada server) pada salah satu koneksi (Sirajuddin dkk, 2012). Untuk itu

selanjutnya hanya disebut load balancing.

Load balancing digunakan apabila sebuah server (sistim komputer yang

menyediakan jenis layanan tertentu) memiliki jumlah user (pengguna server) yang

melebihi kapasitas dan juga digunakan untuk mendistribusikan beban kerja secara

merata pada dua atau lebih computer, CPU (Central Processing Unit) yang

merupakan perangkat keras pada komputer yang berfungsi untuk menerima data

dan melaksanakan perintah dari perangkat lunak atau sumber daya lainnya untuk

mendapat pemanfaatan sumber daya yang optimal.

Branch and bound adalah salah satu teknik yang digunakan untuk

mendapatkan hasil yang optimal pada persoalan mencari nilai maksimum atau

minimum. Dalam metode branch and bound, hasil yang disebut optimal adalah

hasil yang berupa integer (bilangan cacah) bukan nol (0) dan berada di wilayah

feasible (layak). Pada metode branch and bound terdapat beberapa metode lain

yang merupakan bagian dari branch and bound di mana metode-metode tersebut

dapat memberikan hasil yang lebih optimal. Salah satunya adalah metode

Pada dasarnya penggunaan algoritma AND/OR sama seperti algoritma

branch and bound. Perbedaannya terdapat pada pemilihan cabangnya. Algoritma

branch and bound hanya memilih cabang-cabang yang dapat menghasilkan nilai

yang feasible (layak) dan mengeliminasi cabang yang menghasilkan nilai tidak

feasible. Selanjutnya metode AND/OR tidak mengeliminasi cabang yang

menghasilkan nilai tidak feasible. Semua cabang pada metode AND/OR akan

diselesaikan untuk mendapatkan hasil yang optimal dengan menggunakan metode

simpleks.

Dalam pencarian persamaan untuk load balancing, digunakan algoritma

branch and bound yang membagi beberapa bagian dari permasalahan pada CPUs

yang berbeda-beda. Hal ini beresiko tinggi karena jika terdapat perbedaan dengan

interval yang cukup besar, maka dapat terjadi kerusakkan pada persamaan. Untuk

menghindari kerusakkan, maka digunakan metode AND/OR karena dapat

memberi hasil yang cukup signifikan. Dari uraian di atas maka penulis

mengajukan judul tugas akhir yaitu “Metode Branch and Bound (AND/OR)

pada Load Balancing”.

1.2Rumusan Masalah

Berdasarkan latar belakang di atas, maka rumusan masalah yang akan dibahas

adalah bagaimana caranya menyeimbangkan muatan-muatan pada server supaya

tidak terjadi overload.

1.3Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk menyelesaikan masalah load balancing

1.4Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai berikut.

1. Dapat mencari solusi alternatif untuk menyelesaikan persoalan load balancing

dengan cara yang lebih sederhana.

2. Dapat digunakan sebagai tambahan informasi dan referensi bacaan bagi yang

hendak melakukan penelitian serupa.

1.5Metodologi Penelitian

Penelitian ini adalah penelitian literatur yang disusun dengan langkah-langkah

sebagai berikut:

1. Menganalisis metode branch and bound.

2. Menjelaskan pengertian dari load balancing dan AND/OR branch and bound.

3. Menyelesaikan persoalan load balancing dengan metode AND/OR branch

and bound.

BAB 2

TINJAUAN PUSTAKA

Penggambaran suatu versi dari kelanjutan algoritma branch and bound pada

model grafik digunakan untuk menyeimbangkan muatan dengan memperkirakan

bagian-bagian dari permasalahan. Melalui pembelajaran kelanjutan algoritma

branch and bound, maka hasil yang optimal didapatkan dengan mudah pada

berbagai masalah yang rumit dengan menggunakan ratusan persamaan yang

terdapat pada CPUs (Otten dan Dechter, 2012).

2.1 Pengertian Load Balancing

Load balancing berasal dari kata load yang berarti muatan dan balancing yang

berarti keseimbangan maka secara sederhana pengertian dari load balancing

adalah menyeimbangkan muatan. Keunggulan dari penggunaan teknik load

balancing:

1. Waktu Respon. Salah satu manfaat terbesar adalah untuk meningkatkan

kecepatan akses file saat dibuka. Dengan dua atau lebih server yang saling

berbagi beban, masing-masing akan berjalan lebih cepat karena beban

tidak berada pada satu server saja. Ini berarti ada lebih banyak sumber

daya untuk memenuhi penggunaan user.

2. Redundansi. Dengan load balancing, akan mewarisi sedikit redundansi.

Sebagai contoh, jika akses berjalan seimbang di tiga server dan salah satu

Load balancer (perangkat load balancing) menggunakan beberapa

peralatan yang sama untuk menjalankan tugas yang sama. Hal ini memungkinkan

pekerjaan dilakukan dengan lebih cepat dibandingkan apabila dikerjakan oleh

hanya satu peralatan saja dan dapat meringankan beban kerja peralatan, serta

mempercepat waktu respons. Load balancer bertindak sebagai penengah di antara

layanan utama dan pengguna, di mana layanan utama merupakan sekumpulan

server yang siap melayani banyak pengguna.

Pada waktu load balancer menerima permintaan layanan dari user, maka

permintaan tersebut akan diteruskan ke server utama. Biasanya load balancer

dengan pintar dapat menentukan server mana yang memiliki load yang lebih

rendah dan respons yang lebih cepat. Bahkan bisa menghentikan akses ke server

yang sedang mengalami masalah dan hanya meneruskannya ke server yang dapat

memberikan layanan (Lukitasari dan Oklilas, 2010). Hal ini salah satu kelebihan

yang umumnya dimiliki load balancer, sehingga layanan seolah-olah tidak ada

gangguan di mata pengguna.

2.2 Program Integer

P. Siagian (1987) dalam bukunya “Penelitian Operasional: Teori dan Praktek”, mengemukakan bahwa bentuk umum program integer adalah:

Max/Min: 



n_

j cjxj

Z ₁ , j1,2,...n

kendala: m _i

i 1aijxj(  )b



 , i1,2,...,m



 _j

j x

x 0, integer

di mana: a_ij,b_i,c_jdiketahui sebagai konstanta. Jika:

1. x_j semua bilangan cacah, maka problema disebut problema

2. x_j sebagian bilangan cacah dan yang lainnya boleh tidak, maka

disebut problem integer campuran

3. x_j salah satu nol atau satu, problema disebut problema program

integer nol-satu (0-1).

Setiap pertidaksamaan menjadi kendala tambahan untuk sebagian

permasalahan baru dan mempunyai efek mempersempit daerah layak sehingga

pemecahan tak bulat bagi x_jdari bilangan cacah yang mungkin terhadap

persoalan semula diabaikan. Demikian dilakukan seterusnya sampai peubah yang

di harapkan sudah bernilai cacah karena hal ini menjamin solusi yang feasible

(Hamdy A. Taha, 1987).

2.3. Program Integer (Metode Branch and Bound)

Branch and bound adalah algoritma umum untuk mencari solusi optimal dari

berbagai masalah optimasi. Branch and bound bukan sebuah teknik solusi khusus

terbatas untuk masalah program integer (bilangan cacah). Branch and bound

adalah pendekatan solusi yang dapat diterapkan pada beberapa jenis masalah.

Pendekatan branch and bound didasarkan pada prinsip bahwa himpunan total

solusi feasible dapat dipartisi menjadi bagian yang lebih kecil yang kemudian

dapat dievaluasi secara sistematis sampai penyelesaian optimal yang terbaik

ditemukan (Fien Zulkarijah, 2004).

Prinsip dasar metode ini adalah memecah daerah feasible suatu masalah

program linier dengan membuat beberapa bagian permasalahan. Ada dua konsep

dasar dalam algoritma branch and bound, yaitu:

1. Branching adalah proses membagi-bagi permasalahan menjadi

beberapa bagian permasalahan yang mungkin mengarah ke

2. Bounding adalah proses mencari/menghitung batas atas dan batas

bawah untuk solusi optimal pada bagian permasalahan yang

mengarah ke penyelesaian.

BAB 3

PEMBAHASAN

Pada bab ini, akan dijelaskan metode-metode yang penulis gunakan dalam

pembahasan. Adapun metode yang akan digunakan adalah metode simpleks dan

metode branch and bound.

3.1 Metode Simpleks

Metode simpleks adalah prosedur pemecahan program linier yang lebih efisien

daripada metode grafik. Meskipun problem program linier dapat diselesaikan

secara grafik, akan tetapi hampir seluruh problem program linier sesungguhnya

tidak dapat diselesaikan dengan cara ini, karena pada umumnya program linier

mempunyai lebih dari 3 variabel.

Secara umum, bentuk umum dari program linier dapat dimodelkan sebagai

Prosedur (tahap proses) untuk menyelesaikan program linier dengan

menggunakan metode simpleks adalah sebagai berikut:

Tahap 1. Merumuskan problema ke dalam model simpleks.

Tahap 2. Menyusun tabel simpleks iterasi awal dengan penambahan slack variabel

Tahap 3. Mengecek nilai optimal tabel simpleks dengan cara sebagai berikut:

a. Kalau sudah optimal, tafsirkan hasil penyelesaian.

b. Kalau belum optimal, teruskan penyelesaian pada tahap berikutnya.

Tahap 4. Mengidentifikasi variabel yang akan masuk dalam tabel.

Tahap 5. Mengidentifikasi variabel yang akan dikeluarkan dalam tabel.

Tahap 6. Menyusun tabel simpleks baru.

Tahap 7. Mengecek nilai optimal tabel simpleks baru tersebut:

a. Kalau sudah optimal, tafsirkan hasil penyelesaian. b. Kalau belum optimal, kembali kepada prosedur tahap 4.

Tahap 1. Perumusan Model Simpleks

Untuk menyusun rumusan program linier ke dalam model matematika simpleks,

perlu mengubah bentuk tanda ketidaksamaan kendala ke dalam bentuk tanda sama

dengan (=) agar persamaan kendala dalam keadaan seimbang. Bentuk ini biasanya

dikatakan sebagai bentuk standar, sehingga bentuk standarnya dapat dirumuskan

sebagai berikut: (Asumsikan untuk permasalahannya menggunakan tanda ≤).

m

s s

s₁, ₂,, _adalah

slack variabel

Pada permasalahan dalam penelitian ini, tanda ketidaksamaan kendala

adalah lebih kecil atau sama dengan (≤), diubah menjadi tanda sama dengan (=)

dengan syarat menambah variabel slack (s_i) pada sisi bagian kiri persamaan

kendala. Slack variabel perlu ditambahkan agar persamaan garis kendala

memenuhi persyaratan penyelesaian pada daerah kelayakan (feasible).

Tahap 2. Menyusun Tabel Simpleks

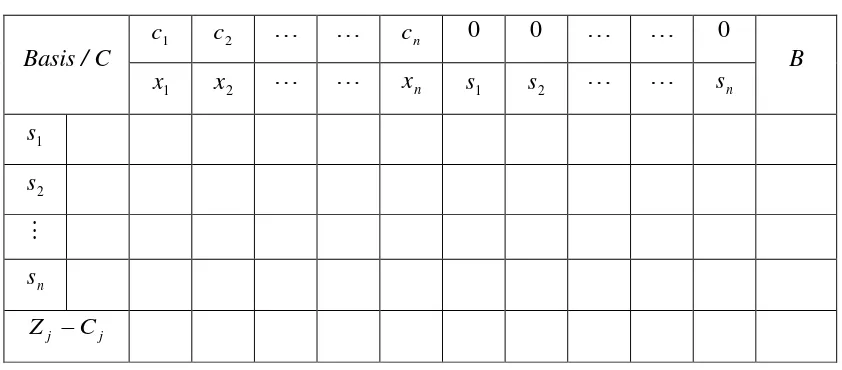
Ada beberapa macam format tabel simpleks. Salah satu format yang akan penulis

gunakan dapat dilihat pada Tabel 3.1.

Tabel 3.1. Format Tabel Simpleks

Basis / C 1

c c₂   c_n 0 0   0

B

1

x x₂   xn s1 s2   sn

1

s

2

s



n

s

j

j C

Z 

Penjelasan tabel simpleks di atas:

1. C = Nilai kontribusi setiap variabel basis dalam proses iterasi.

2. Basis = Variabel basis dalam proses iterasi (nilainya tidak sama dengan

nol).

3. B = Nilai variabel basis dalam proses iterasi.

4. Zj Cj = Nilai kontribusi dalam problema meminimalkan dari setiap

Tahap 3. Pengecekan Optimalisasi Tabel Simpleks Iterasi Awal

Pengecekan apakah tabel simplek pada iterasi awal telah atau belum optimal

dilakukan dengan cara melihat nilai Z_j C_j masing-masing variabel fungsi

tujuan. Apabila Zj Cj untuk semua variabel bernilai nol atau positif, maka

penyelesaian problema tersebut telah optimal. Apabila tidak, maka dilakukan

tahap proses selanjutnya.

Tahap 4. Identifikasi Variabel yang Akan Masuk

Untuk menentukan variabel yang mana akan masuk dalam pertimbangan untuk

diproses pada iterasi berikutnya adalah variabel keputusan (variabel non-basis)

yang mempunyai nilai Z_j C_j terbesar. Variabel non-basis dimasukkan untuk

proses iterasi berikutnya karena variabel s₁,s₂,,s_ntelah masuk dalam proses

iterasi awal. Nilai Zj Cj terbesar yang memiliki nilai terbesar diyakini dapat

meningkatkan hasil yang diperoleh dalam proses iterasi selanjutnya.

Tahap 5. Identifikasi Variabel yang Akan Keluar

Dengan adanya variabel yang masuk ke dalam tabel simpleks, maka salah satu

dari variabel basis harus keluar dari tabel simpleks tersebut agar diperoleh

peningkatan nilai tujuan maksimum. Cara mengidentifikasi variabel yang akan ke

luar adalah dengan mencari hasil bagi antara nilai solusi dan nilai substitusi

marjinal yang terkecil dan bilangan tersebut bernilai non-negatif.

Tahap 6. Penyusunan Tabel Simpleks Iterasi Pertama

Untuk menyusun tabel simpleks iterasi pertama, harus mencari koefisien elemen

pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari dengan

titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen pivot.

Koefisien-koefisien baris pivot yang baru dicari dengan menggunakan rumus

sebagai berikut:

Nilai Baris Pivot Baru = Nilai Baris Pivot Lama : Elemen Pivot

Untuk menghitung nilai baris baru lainnya, dilakukan dengan menggunakan

rumus sebagai berikut:

Nilai Baris Baru = Nilai Baris Lama – (Elemen Baris x Nilai Baris

Pivot Baru)

Tahap 7. Pengecekan Optimalisasi Tabel Simpleks Iterasi Pertama

Pengecekan apakah tabel simpleks pada iterasi pertama telah atau belum optimal.

Apabila Z_j C_j untuk semua variabel bernilai nol atau positif, maka

penyelesaian problema tersebut telah optimal. Apabila tidak, maka kembali pada

prosedur Tahap 4.

3.2 Metode Branch and Bound

Proses dari metode branch and bound dimulai dengan menyelesaikan program

linier dengan mengabaikan persyaratan cacahnya. Misalnya diketahui problema

program bilangan cacah yang disebut dengan problema 0, yaitu:

Problema 0 Maks: f₀ 10x₁ 7x₂

10 3

4x1  x2 



 _{1 2}

2

1,x 0,x ,x

Sekarang problema 0 dipandang sebagai problema program linier dan

disebut problema 1:

Problema 1 Maks: f₁ 10x₁ 7x₂

setelah syarat cacahnya dihilangkan.

Ada 2 hubungan antara problema 0 dan problema 1 yaitu:

1. Hubungan batas

Misalkan f0*dan * 1

f sebagai nilai fungsi tujuan untuk solusi feasible

optimum problema 0 dan problema 1, maka:

* 1 *

0 f

f 

Ini berarti bahwa nilai solusi optimum dari fungsi tujuan untuk problema

program integer (problema 0) tidak boleh melebihi nilai solusi optimum

dari fungsi tujuan problema program linier (problema 1). Hubungan ini

disebut bounding.

2. Hubungan optimalitas

Jika solusi telah optimal untuk problema 1 dan feasible untuk problema 0,

maka solusi juga optimal untuk problema 0.

Jika solusi optimal untuk problema 1 adalah juga feasible untuk problema

0 dengan syarat dimana *

f , maka hasil harus optimal untuk problema 0.

Akan tetapi, misalkan hasil optimum untuk problema 1 tidak feasible

untuk problema 0 maka problema 1 diubah menjadi m problema baru yang

memenuhi syarat sebagai berikut:

a) Solusi optimal untuk problema 1 tidak feasible untuk setiap

b) Sekurang-kurangnya terdapat satu nilai optimal untuk

problema 0 adalah feasible untuk salah satu solusi dari m

problema baru.

Rumusan dari m problema baru disebut branching. Terdapat banyak cara

untuk merumuskan m problema baru tersebut. Salah satu di antaranya yang paling

baik adalah cara dari R.J. Dakin dengan memisalkan salah satu dari x_jadalah

solusi problema 1 yang mempunyai nilai bukan integer pada penyelesaian optimal

program linier maka [x_j]x_j [x_j]1, di mana [x_j] dan [x_j]1 adalah dua bilangan cacah yang berurutan. Dari syarat tersebut kemudian dibentuk dua

program integer yang baru yang dikatakan problema 2 dan problema 3 sedemikian

sehingga:

Problema 2 = problema 1 ditambah kendala x_j [x_j]

Problema 3 = problema 1 ditambah kendala x_j [x_j]1

Dengan demikian syarat pertama (a) telah terpenuhi yaitu solusi optimum

untuk problema 1 pasti tidak feasible untuk problema 2 maupun untuk problema

3. Pada saat yang sama, solusi optimum untuk problema 0 masih tetap dalam

ruang solusi dari problema 2 dan problema 3, karena tidak ada solusi integer layak

yang terbuang dari ruang penyelesaian. Ini berarti bahwa syarat kedua (b) juga

terpenuhi di mana solusi optimal untuk problema 0 masih tetap feasible untuk

salah satu dari problema 2 atau problema 3.

Secara umum, bentuk umum dari program integer adalah sebagai berikut:

Dengan demikian, diasumsikan penjabaran bentuk umum dari fungsi

tujuan dan fungsi kendala program integer adalah sebagai berikut.

Maksimumkan:

Selanjutnya, asumsikan fungsi kendala program integer adalah sebagai berikut.

Langkah-langkah Metode Branch and Bound

Prosedur atau langkah-langkah metode branch and bound adalah sebagai berikut.

1. Selesaikan masalah program linier dengan metode simpleks.

2. Teliti solusi optimumnya. Apabila variabel keputusan yang diharapkan

merupakan bilangan integer, maka solusi optimum integer telah tercapai.

Apabila satu atau lebih variabel keputusan yang diharapkan ternyata bukan

bilangan integer, lanjutkan ke langkah 3.

3. Jadikan solusi pada penyelesaian langkah 1 menjadi batas atas dan untuk batas

bawahnya merupakan solusi yang variabel keputusannya telah diintegerkan

(rounded – down).

4. Pilih variabel yang mempunyai nilai pecahan terbesar (artinya bilangan

desimal terbesar dari masing-masing variabel untuk dijadikan pencabangan ke

dalam sub-sub masalah). Tujuannya adalah untuk menghilangkan solusi yang

tidak memenuhi persyaratan integer dalam masalah itu. Pencabangan itu

dilakukan secara mutually exclusive untuk memenuhi persyaratan integer

dengan jaminan tidak ada solusi feasible (layak) yang diikutsertakan.

5. Untuk setiap sub-masalah, nilai optimum fungsi tujuan ditetapkan sebagai

batas atas. Solusi optimum yang diintegerkan menjadi batas bawah (solusi

yang sebelumnya memiliki nilai tidak bulat kemudian bulatkan). Sub-sub

masalah yang memiliki batas atas kurang dari batas bawah yang ada, tidak

diikutsertakan pada analisa selanjutnya. Suatu solusi integer feasible (layak)

adalah sama baik atau lebih baik dari batas atas untuk setiap sub masalah yang

dicari. Jika solusi yang demikian terjadi, suatu sub masalah dengan batas atas

Langkah-langkah Metode Branch and Bound (AND/OR)

Prosedur atau langkah-langkah metode branch and bound (AND/OR) adalah

sebagai berikut.

1. Selesaikan masalah program linier dengan metode simpleks.

2. Teliti solusi optimumnya. Apabila variabel keputusan yang diharapkan

merupakan bilangan integer, maka solusi optimum telah tercapai. Apabila

satu atau lebih variabel keputusan yang diharapkan ternyata bukan

bilangan integer, lanjutkan ke langkah 3.

3. Jadikan solusi pada penyelesaian langkah 1 yang belum integer menjadi

batas atas dan batas bawah dengan solusi yang telah diintegerkan

(rounded-down).

4. Setelah melakukan langkah ketiga dan solusi optimum dengan nilai integer

telah tercapai, maka hentikan pencarian. Apabila variabel keputusan belum

integer, maka dilakukan pencabangan seperti langkah tiga dengan

menambahkan kendala pada masing-masing batas atas dan batas bawah.

5. Apabila solusi optimum telah tercapai, lakukan pencabangan pada langkah

1 dengan menambahkan kendala pada langkah 4. (Ini yang membedakan

branch and bound dengan AND/OR, branch and bound menganggap

solusi yang dilakukan pada langkah 1 ditambahkan dengan langkah 3

kemudian langkah 4 lebih memenuhi syarat sehingga tidak lagi dilakukan

penyelesaian langkah 1 dengan kendala 4. Sedangkan pada AND/OR

langkah 1 dengan kendala 4 juga diperhitungkan karena dianggap dapat

mengatasi celah-celah yang diabaikan dan juga memperkuat solusi

optimumnya).

6. Jika terdapat kendala pada pencabangan branch and bound berikutnya,

Berlanjut untuk seterusnya sampai hasil dari AND/OR dapat lebih

optimum atau dapat memperkuat hasil yang didapatkan pada branch and

bound.

Contoh penyelesaian soal dengan metode AND/OR (diambil dari buku

Hamdy A Taha, Operations Research edisi 8):

Lima item diletakkan pada sebuah kapal dengan berat wi, volume vi, dan harga

i

r untuk setiap item i pada table berikut.

Item i Berat unit,wi(tons) Volume unit,vi(

3

yd ) Harga unit,ri(100$)

1 5 1 4

2 8 8 7

3 3 6 6

4 2 5 5

5 7 4 4

Berat dan volume kargo yang maksimum adalah 112 tons dan 109yd3 masing-masing. Rumuskan dengan model persamaan linier yang integer dan tentukan harga kargo yang paling maksimal.

Penyelesaian:

a. Ubah ke bentuk model persamaan program linier.

Misalkan:

Item 1: x₁

Item 2: x₂

Item 3: x₃

Item 4: x₄

Bentuk persamaan linier menjadi:

standar dengan menambahkan variabel slack (s_i)

Maks: Z 4x₁7x₂6x₃5x₄ 4x₅

c. Selesaikan masalah program linier dengan metode simpleks.

Iterasi 3

d. Teliti solusi optimumnya. Apabila variabel keputusan yang diharapkan

merupakan bilangan integer, maka solusi optimum integer telah tercapai.

Apabila satu atau lebih variabel keputusan yang diharapkan ternyata bukan

bilangan integer, lanjutkan ke langkah 3 dengan menambahkan kendala

] yang berurutan. Namun terlebih dahulu pada persamaan program linier di

Penghitungan persamaan dan kendala awal dilakukan kembali dengan

menambahkan kendala x₁ 14 dan x₁ 15.

Iterasi 00

Iterasi 002 Iterasi 003

Iterasi 001

Iterasi 004 Iterasi 005

Iterasi 006 Iterasi 007

Iterasi 008 Iterasi 009

Iterasi 00

Iterasi 012 Iterasi 013

Iterasi 011

Iterasi 014 Iterasi 015

Iterasi 016 Iterasi 017

Iterasi 018 Iterasi 019

Iterasi 020 No Feasible Solution

Iterasi 00

Iterasi 023 No Feasible Solution

Iterasi 022

Iterasi 024 No Feasible Solution

Iterasi 025 No Feasible Solution

Iterasi 026 Iterasi 027

Iterasi 028 No Feasible Solution

Iterasi 031 No Feasible Solution

Iterasi 030

Iterasi 032 No Feasible Solution

Iterasi 033 Iterasi 034

Iterasi 035 Iterasi 036

Iterasi 013

Iterasi 037 Iterasi 038

Iterasi 041 No Feasible Solution

Iterasi 040

Iterasi 042 No Feasible Solution

Iterasi 043 No Feasible Solution

Iterasi 044 No Feasible Solution

Iterasi 015

Iterasi 051 Iterasi 052 Iterasi 009

Iterasi 053 Iterasi 054

Iterasi 055 Iterasi 056

Iterasi 057 Iterasi 058

Iterasi 047 Iterasi 048

Iterasi 019

Dari hasil penghitungan diatas, didapatkan beberapa solusi optimal yaitu:

Iterasi 010: x₁ 13;x₃ 6;x₄ 11;x₅ 1;Z 147

Iterasi 016: x₁ 12;x₂ 2;x₃ 6;x₄ 9;Z143

Iterasi 021: x₁ 12;x₂ 2;x₃ 5;x₄ 10;Z 142

Iterasi 026: x₁ 9;x₂ 3;x₃ 3;x₄ 10;x₅ 2;Z 133

Iterasi 029: x₁ 10;x₂ 3;x₃ 3;x₄ 10;x₅ 1;Z133

Iterasi 032: x₁ 10;x₂ 3;x₃ 1;x₄ 10;x₅ 2;Z 125

Iterasi 034: x₁ 10;x₂ 1;x₃ 6;x₄ 11;Z 138

Iterasi 059 No Feasible Solution

Iterasi 003

Iterasi 060 Iterasi 061

Iterasi 062 Iterasi 063

Iterasi 064 Iterasi 065

Iterasi 035: x₁ 12;x₂ 1;x₃ 5;x₄ 11;x₅ 1;Z 144

Iterasi 038: x₁ 13;x₂ 2;x₃ 3;x₄ 11;Z139

Iterasi 039: x₁ 13;x₂ 2;x₃ 3;x₄ 11;Z139

Iterasi 043: x1 13;x2 2;x4 11;x5 1;Z 125

Iterasi 045: x₁ 13;x₂ 1;x₃ 6;x₄ 10;Z 145

Iterasi 046: x₁ 13;x₂ 1;x₃ 4;x₄ 10;x₅ 1;Z 137

Iterasi 048: x₁ 11;x₂ 1;x₃ 6;x₄ 10;x₅ 1;Z141

Iterasi 049: x₁ 12;x₂ 1;x₃ 6;x₄ 10;Z 141

Iterasi 050: x₁ 7;x₂ 2;x₃ 6;x₄ 10;Z 128

Iterasi 052: x₁ 14;x₂ 1;x₃ 4;x₄ 11;Z 142

Iterasi 053: x₁ 14;x₃ 6;x₄ 11;Z 147

Iterasi 056: x₁ 14;x₃ 5;x₄ 10;x₅ 1;Z 140

Iterasi 057: x₁ 14;x₃ 4;x₄ 11;x₅ 1;Z 139

Iterasi 058: x₁ 14;x₃ 2;x₄ 11;x₅ 2;Z131

Iterasi 061: x1 15;x3 1;x4 17;Z 151

Iterasi 065: x₁ 16;x₄ 16;Z144 Iterasi 066: x₁ 15;x₄ 18;Z 150 Iterasi 067: x1 15;x4 15;x5 1;Z 139

Maka hasil optimal yang paling maksimum adalah hasil dari iterasi (061):

151 ;

17 ;

1 ;

15 _{3 4}

1  x  x  Z 

Langkah-langkah AND/OR

Iterasi (001) dicabangkan dengan kendala-kendala yang terdapat pada

penghitungan branch and bound yaitu: x₁ 9, x₁ 10, x₁ 11, x₁ 12, x₁ 13,

Dari kendala diatas, di dapatkan beberapa hasil yang optimal yaitu:

6

Maka hasil optimal yang paling maksimal adalah pada penghitungan iterasi awal

Hasil Z maksimal dari penghitungan branch and bound sama dengan AND/OR

Branch and Bound yaitu 151. Tetapi nilai variabel xn yang didapatkan berbeda.

Hal ini dapat terjadi pada beberapa kasus tertentu dan hasil yang akan digunakan

tergantung manfaat dan kegunaan. Variabel yang bernilai nol bukan berarti mati

atau tidak berguna lagi tetapi jika variabel tersebut terisi tidak memberikan

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

1. Metode branch and bound merupakan metode efektif dalam penyelesaian

suatu permasalahan maksimasi. Akan tetapi dalam kasus tertentu, branch and

bound mengalami kesulitan untuk memilih apabila pada Z maksimal yang

sama mempunyai nilai variabel x₁,x₂,,x_n yang berbeda seperti pada

contoh kasus diatas.

2. Branch and bound (AND/OR) menghasilkan penyelesaian optimum yang

dihasilkan oleh branch and bound. Hal ini dapat menjadi alasan menggunakan

AND/OR sebagai metode tambahan karena terdapat banyak kemungkinan

penyelesaian manakah yang akan dipilih jika Z dari setiap penyelesaian

tersebut adalah sama.

4.2. Saran

Perlu diadakan penelitian lebih lanjut supaya AND/OR lebih banyak digunakan

sebagai alternatif utama bukan alternatif tambahan untuk mendapatkan hasil yang

DAFTAR PUSTAKA

Bangun, E. 2004. Kajian Strategis untuk Menyelesaikan Integer Program dengan Metode Branch and Bound. [Tesis]. Medan: Universitas Sumatera Utara, Program Pascasarjana.

Lukitasari, Desy dan Oklilas, Ahmad Fali. 2010. Analisis Perbandingan Load Balancing Web Server Cluster Menggunakan Linux Virtual Server. Universitas Sriwijaya: Jurnal Generic Fakultas Ilmu Komputer, 1: 31.

Otten, Lars dan Dechter, Rina. 2012. Advances in Distributed Branch and Bound.

European Conference on Artificial Intelligence, 242: 917-918.

Shieny, Aprilia. 2003. Aplikasi Branch and Bound untuk menyelesaikan integer programming. Jurnal Teknik Informatika, 23: 68-78.

Siagian, P. 1987. Penelitian Operasional: Teori dan Praktek, Jakarta. Indonesia: UI-Pres.

Sitorus, P. 1997. Program Linier. Universitas Trisakti. Jakarta.

Sirajuddin, Affandi, Ahmad dan Setijadi, Eko. 2012. Rancangan Bangun Server Learning Management System Menggunakan Load Balancer dan Reverse Proxy, Surabaya: Jurnal Teknik Pomits, 1: 1.

Taha, Hamdy A. 1987. Operation Research: An Introduction, New York: Macmillan Publishing Company.

Winston, W.L. 2004. Operation Research Applications and Algorthms. 4th edition. Duxbury, New York.