PENENTUAN BATAS BAWAH PADA
METODE
BRANCH AND PRICE
SKRIPSI
MEILIANA
080803036
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PENENTUAN BATAS BAWAH PADA METODE BRANCH AND PRICE
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat untuk mencapai gelar sarjana sains
MEILIANA 080803036
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : PENENTUAN BATAS BAWAH PADA METODE BRANCH AND PRICE
Kategori : SKRIPSI
Nama : MEILIANA
Nomor Induk Mahasiswa : 080803036
Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA
UTARA
Medan, April 2012 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Prof. Dr. Herman Mawengkang Prof. Dr. Drs. Iryanto, M.Si NIP 19461128 1974031 001 NIP. 19460404 1971071 001
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua.
PERNYATAAN
PENENTUAN BATAS BAWAH PADA METODE
BRANCH AND
PRICE
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2012
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan yang Maha Penyayang, atas kemurahan dan berkat yang telah diberikan sehingga penulis dapat menyelesaikan
skripsi dengan judul ”Penentuan Batas Bawah pada Metode Branch and Price” guna melengkapi syarat memperoleh gelar sarjana Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam di Universitas Sumatera Utara.
Dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada semua pihak yang telah membantu dan membimbing penulis dalam penyusunan skripsi ini, ucapan terima kasih saya sampaikan kepada :
1. Bapak Prof. Dr. Drs. Iryanto, M.Si selaku pembimbing I dan Bapak Prof. Dr. Herman Mawengkang selaku pembimbing II yang telah memberikan bimbingan dan pengarahan kepada saya sehingga skripsi ini dapat saya selesaikan.
2. Bapak Drs. Sawaluddin, M.IT dan Bapak Syahril Efendi, S.Si, MIT selaku dosen penguji saya.
3. Bapak Prof. Drs. Tulus, Vordipl.Math, M.Si, Ph.D. dan Ibu Dra.Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika.
4. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
5. Semua Dosen pada Departemen Matematika FMIPA USU dan pegawai di FMIPA USU.
Penulis menyadari masih banyak kekurangan dan kelemahan dalam penulisan skripsi ini. Untuk itu penulis minta maaf kepada seluruh pembaca bila ada kesalahan serta penulis mengharapkan saran dan kritikan demi kesempurnaan skripsi ini. Akhir kata, semoga skripsi ini dapat bermanfaat bagi kita semua.
Medan, Juli 2012 Penulis,
ABSTRAK
Program bilangan bulat (Integer Programming) merupakan sutau program linear khusus dimana variabel-variabel keputusannya harus merupakan bilangan bulat. Ada banyak cara untuk menyelesaikan program bilangan bulat ini, diantaranya metode
branch and price. Seperti halnya metode branch and bound, dalam penyelesaianya menggunakan metode branch and price akan memerlukan iterasi-iterasi yang panjang. Untuk memperpendek iterasi itu maka ditentukan batas bawahnya.
DETERMINE THE LOWER BOUND OF BRANCH AND PRICE METHOD
ABSTRACT
Integer Programming is a specific linear programming where the variables of decision are integer. There are so many kind of way to finish this integer programming; one of them is Branch and Price method. Like Branch and Bound method, in the step to finish the integer programming in Branch and Price method need the iterations that are too long. To make the iteration to be short then should be given the lower bound.
DAFTAR TABEL
Halaman
Tabel 2.1 Tabel Simpleks 16
Tabel 3.1 Tabel Simpleks awal 22
Tabel 3.2 Tabel Simpleks untuk bagian 1 23
Tabel 3.3 Tabel Simpleks untuk bagian 2 23
Tabel 3.4 Tabel Simpleks untuk bagian 3 25
Tabel 3.5 Tabel Simpleks untuk bagian 5 26
Tabel 3.6 Tabel Simpleks untuk bagian 6 27
Tabel 3.7 Tabel Simpleks awal 28
Tabel 3.8 Tabel Simpleks untuk bagian 1 29
Tabel 3.9 Tabel Simpleks untuk bagian 2 29
Tabel 3.10 Tabel Simpleks untuk bagian 3 31
Tabel 3.11 Tabel Simpleks untuk bagian 4 31
Tabel 3.12 Tabel Simpleks awal 34
Tabel 3.13 Tabel Simpleks untuk bagian 1 35
Tabel 3.14 Tabel Simpleks untuk bagian 2 36
Tabel 3.15 Tabel Simpleks untuk bagian 4 37
Tabel 3.16 Tabel Simpleks awal 39
Tabel 3.17 Tabel Simpleks untuk bagian 1 40
Tabel 3.18 Tabel Simpleks untuk bagian 3 42
DAFTAR GAMBAR
Halaman Gambar 3.1 Percabangan untuk iterasi awal 22
Gambar 3.2 Percabangan untuk iterasi 1 24
Gambar 3.3 Percabangan untuk iterasi 2 25
Gambar 3.4 Percabangan untuk iterasi 3 27
Gambar 3.5 Percabangan untuk iterasi awal 28
Gambar 3.6 Percabangan untuk iterasi 1 30
Gambar 3.7 Percabangan untuk iterasi 2 32
Gambar 3.8 Percabangan awal 34
Gambar 3.9 Percabangan untuk iterasi 1 36
Gambar 3.10 Percabangan untuk iterasi 2 38
Gambar 3.11 Percabangan awal 39
Gambar 3.12 Percabangan untuk iterasi 1 42
ABSTRAK
Program bilangan bulat (Integer Programming) merupakan sutau program linear khusus dimana variabel-variabel keputusannya harus merupakan bilangan bulat. Ada banyak cara untuk menyelesaikan program bilangan bulat ini, diantaranya metode
branch and price. Seperti halnya metode branch and bound, dalam penyelesaianya menggunakan metode branch and price akan memerlukan iterasi-iterasi yang panjang. Untuk memperpendek iterasi itu maka ditentukan batas bawahnya.
DETERMINE THE LOWER BOUND OF BRANCH AND PRICE METHOD
ABSTRACT
Integer Programming is a specific linear programming where the variables of decision are integer. There are so many kind of way to finish this integer programming; one of them is Branch and Price method. Like Branch and Bound method, in the step to finish the integer programming in Branch and Price method need the iterations that are too long. To make the iteration to be short then should be given the lower bound.
Bab 1
PENDAHULUAN
1.1 Latar Belakang
Program linear bilangan bulat (Integer Linear Programming) merupakan suatu model program linear khusus yang digunakan untuk menyesuaikan suatu masalah program linear Dimana nilai-nilai variabel keputusannya haruslah merupakan bilangan bulat. Persyaratan ini dilakukan mengingat ada variabel-variabel yang tidak mungkin dalam bilangan pecahan, seperti pabrik, rumah, karyawan, dan lain-lain.
Metode Branch and Bound merupakan salah satu metode dalam penyelesaian program bilangan bulat yang menggunakan percabangan dan pembatasan. Metode ini didasarkan pada penambahan baris pada saat percabangan. Penambahan baris ini tentu tidak efektif karena akan membuat proses penyelesaiannya menjadi panjang. Oleh karena itu, maka digunakanlah metode branch and price.
Pada metode branch and price penentuan batas bawah dilakukan agar proses penyelesaian program linear bilangan bulat menjadi lebih efisien. Oleh karena itu, pada metode branch and price batas bawah perlu diperoleh agar jumlah iterasi dapat diperpendek.
Berdasarkan hal-hal di atas maka penulis memilih judul tugas akhir sebagai berikut : “Penentuan Batas Bawah pada MetodeBranch and Price”.
1.2 PERUMUSAN MASALAH
Masalah yang akan dibahas dalam tulisan ini adalah bagaimana menentukan batas bawah pada metode branch and price.
1.3 TINJAUAN PUSTAKA
Alvelos Filipe (2005) mengemukakan bahwa ketika menyelesaikan sebuah simpul dari pohon Branch and Price, batas bawah didapatkan pada setiap iterasi dari kolom generasi. Jika batas bawah lebih besar dari nilai wajib, maka simpul dapat dipotong, karena solusi bilangan bulat terbaik yang ditemukan pada batas bawah ini dan turunannya (jika ada) akan memiliki sebuah nilai yang lebih besar dari nilai calon.
Adam N. Letchford (2011) mengemukakan bahwa untuk mengerti kenapa master problem adalah sebuah formulasi yang lebih kuat dari original problem dapat dilihat pada batas bawah yang didapatkan ketika menyelesaikan Program linear relaksasi dari dua masalah.
Program linear relaksasi dari masalah asli diberikan sebagai berikut:
Dimana:
= Fungsi tujuan.
= Kendala kedua pada program linear yang telah direlaksasi.
Adam N. Letchford menunjukkan bahwa menyelesaikan Program linear relaksasi dari master problem sama dengan menyelesaikan:
Dimana:
= Fungsi tujuan.
= Convex kombinasi dari kendala pertama.
= Kendala kedua pada program linear yang telah direlaksasi.
Jadi, jika , Program linear relaksasi dari master problem akan memberikan sebuah batas yang lebih baik dari masalah aslinya.
Geoffrion (1974) juga menunjukkan bahwa menyelesaikan Program linear relaksasi dari master problem memberikan batas bawah terbaik yang mungkin didapat dengan Langrangian relaksasi. Oleh karena itu, jika menggunakan pengali yang terbaik pada langrangian relaksasi, maka akan mendapatkan batas yang sama.
Matin W.P Savelsbergh (2002) dalam jurnal yang berjudul “Branch-and-price:
Integer programming with Column Genertion, BP” mengemukakan setelah beberapa
iterasi pada kolom generasi, maka harus diputuskan untuk mengakhiri proses kolom generasi (Branch and Price) jika nilai solusi program linear pada batasan master problem saat ini telah memberikan sebuah nilai batas bawah, dan nilai batas atas yang cukup dekat pada program linear.
1.4 TUJUAN PENELITIAN
1.5KONTRIBUSI PENELITIAN
Mamfaat dari penelitian ini adalah:
1. Menambah wawasan penulis mengenai penentuan batas bawah pada Metode
Branch and Price.
2. Dapat menjadi referensi pada mahasiswa agar dapat mengerti mengenai penggunaan Metode Branch and Price dan mampu menentukan batas bawahnya pada integer programming agar dalam proses pencarian solusi menjadi lebih efisien.
1.6 METODE PENELITIAN
Penelitian ini adalah penelitian literatur dan metode yang dilakukan adalah
1. Mengadakan studi literatur dari buku dan jurnal-jurnal mengenai penentuan batas metode branch and price .
2. Mempelajari permasalahan yang melibatkan batas bawah pada Metode Branch and Price dan menyelesaikannya menggunakan langkah-langkah yang telah dipelajari dari buku ataupun jurnal.
3. Menganalisa masalah mengenai penentuan batas bawah pada Metode Branch and Price dan kemudian dianalisa lebih lanjut untuk dikembangkan.
Bab 2
LANDASAN TEORI
2.1 Program Linear
Menurut Sitorus, Parlin (1997), Program Linier merupakan suatu teknik penyelesaian optimal atas suatu problema keputusan dengan cara menentukan terlebih dahulu suatu fungsi tujuan (memaksimalkan atau meminimalkan) dan kendala-kendala yang ada ke dalam model matematik persamaan linear. Program Linear berkaitan dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi tujuan linier dengan beberapa kendala linier yang dapat diselesaikan untuk mencapai suatu nilai optimum. Nilai optimum itu bisa meupakan nilai maksimum ataupun nilai minimum.
Metode ini paling banyak digunakan dalam bisnis dan ekonomi, namun juga dapat dimanfaatkan dalam sejumlah perhitungan ilmu teknik. Misalnya, dalam ekonomi, fungsi tujuan dapat berkaitan dengan pengaturan secara optimal sumber-sumber daya untuk memperoleh keuntungan maksimal atau biaya minimal, sedangkan fungsi batasan menggambarkan batasan-batasan kapasitas yang tersedia yang dialokasikan secara optimal ke berbagai kegiatan. Industri yang memanfaatkan pemrograman linear di antaranya ialah industri transportasi, energi, telekomunikasi, dan manufaktur. Pemrograman linear juga terbukti berguna dalam membuat model berbagai jenis masalah dalam perencanaan, perancangan rute, penjadwalan, pemberian tugas, dan desain.
yang dikehendaki adalah kondisi yang menyebabkan maksimum atau minimum. Fungsi kendala merupakan fungsi matematika yang mengendalikan nilai variabel keputusan. Fungsi kendala terdiri dari fungsi kendala berupa pembatas yang disimbolkan , fungsi kendala berupa syarat yang disimbolkan , dan fungsi kendala berupa keharusan yang disimbolkan .
Dalam program linear terdapat beberapa karakteristik dalam menyelesaikan suaru persoalan yaitu
1. Sifat linearitas, sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa cara. Secara statistik, kita dapat memeriksa kelinearan menggunakan grafik (diagram pencar).
2. Sifat proporsional, sifat proporsional dipenuhi jika kontribusi setiap variabel pada fungsi tujuan atau penggunaan sumber daya yang membatasi proporsional terhadap level nilai variabel. Misalnya jika harga per unit produk adalah sama berapapun jumlah yang dibeli, maka sifat proporsional dipenuhi. Atau dengan kata lain, jika pembelian dalam jumlah besar mendapatkan diskon, maka sifat proporsional tidak dipenuhi.
3. Sifat additivitas, sifat ini mengasumsikan bahwa tidak ada bentuk perkalian silang diantara berbagai aktivitas, sehingga tidak akan ditemukan bentuk perkalian silang pada model. Sifat additivitas berlaku baik bagi fungsi tujuan maupun pembatas (kendala). Sifat additivitas dipenuhi jika fungsi tujuan merupakan penambahan langsung kontribusi masing-masing variabel keputusan. Untuk fungsi kendala, sifat additivitas dipenuhi jika nilai kanan merupakan total penggunaaan masing-masing variabel keputusan.
4. Sifat divisibilitas, sifat ini berarti unit aktivitas dapat dibagi ke dalam sembarang level fraksional, sehingga nilai variabel keputusan non integer dimungkinkan.
Ada beberapa syarat yang harus dipenuhi dalam merumuskan suatu problema keputusan ke dalam suatu model matematika program linearn yakni sebagai berikut: 1. Memiliki kriteria tujuan.
2. Sumber daya yang tersedia sifatnya terbatas.
3. Semua variabel dalam model memiliki hubungan matematis bersifat linear. 4. Koefisien model diketahui dengan pasti.
5. Bilangan yang digunakan dapat bernilai bulat atau pecahan. 6. Semua variabel harus bernilai nonnegatif.
Urutan pertama dalam penyelesaian program linear adalah mempelajari sistem relevan dan mengembangkan pernyataan permasalahan yang dipertimbangakan dengan jelas. Penggambaran sistem dalam pernyataan ini termasuk pernyataan tujuan, sumber daya yang membatasi, alternatif keputusan yang mungkin (kegiatan atau aktivitas), batasan waktu pengambilan keputusan, hubungan antara bagian yang dipelajari dan bagian lain dalam perusahaan, dan lain-lain.
Penetapan tujuan yang tepat merupakan aspek yang sangat penting dalam formulasi masalah. Untuk membentuk tujuan optimalisasi, diperlukan identifikasi anggota manajemen yang benar-benar akan melakukan pengambilan keputusan dan mendiskusikan pemikiran mereka tentang tujuan yang ingin dicapai.
satu. Tetapi pada bagian ini kita hanya akan tertarik dengan permasalahan optimal dengan satu tujuan.
Bagian kedua merupakan model matematik yang merepresentasikan sumber daya yang membatasi. Fungsi kendala bisa berbentuk persamaan (=) atau
pertidaksamaan (≤ atau ≥). Fungsi kendala disebut juga sebagai konstrain. Konstanta
(baik sebagai koefisien maupun nilai kanan) dalam fungsi kendala maupun pada tujuan dikatakan sebagai parameter model. Model matematika mempunyai beberapa keuntungan dibandingakan pendeskripsian permasalahan secara verbal. Salah satu keuntungan yang paling jelas adala model matematik menggambarkan permasalahan secara lebih ringkas. Hal ini cenderung membuat struktur keseluruhan permasalahan lebih mudah dipahami, dan membantu mengungkapkan relasi sebab akibat penting. Model matematik juga memfasilitasi yang berhubungan dengan permasalahan dan keseluruhannya dan mempertimbangkan semua keterhubungannya secara simultan. Terakhir, model matematik membentuk jembatan ke penggunaan teknik matematik dan komputer kemampuan tinggi untuk menganalisis permasalahan.
= koefisien dari variabel keputusan
= Koefisien dari variabel keputusan dalam kendala = sumber daya yang tersedia dalam kendala
ke-Ada berbagai cara dalam menyelesaikan program linear diantaranya menggunakan metode grafik, metode simpleks, metode dual simpleks, metode Teknik M. Metode grafik digunakan untuk menyelesaikan program linear dengan dua variabel. Metode simpleks, metode dual simpleks dan teknik M banyak digunakan untuk menyelesaikan program linear dengan banyak variabel.
Kasus program linier sangat beragam. Dalam setiap kasus, hal yang penting adalah memahami setiap kasus dan memahami konsep permodelannya. Meskipun fungsi tujuan misalnya hanya mempunyai kemungkinan bentuk maksimisasi atau minimisasi, keputusan untuk memilih salah satunya bukan pekerjaan mudah. Tujuan pada suatu kasus bisa menjadi batasan pada kasus yang lain. Harus hati-hati dalam menentukan tujuan, koefisien fungsi tujuan, batasan dan koefisien pada fungsi pembatas agar dapat menyelesaikan program linear secara tepat.
2.2 Program Bilangan Bulat (Integer Programming)
Model Linear programming yang telah didiskusikan sejauh ini masih tetap berlanjut, dalam pengertian bahwa variabel keputusan diperbolehkan dalam bentuk pecahan. Sering ini sebagai asumsi realistik. Sebagai contoh sebuah perusahaan dapat
memproduksi dari bahan yang dapat dibagi seperti wine dan juga masih
beralasan untuk menerima sebuah solusi yang memberikan nilai perjam produksi
automobile sebesar jika modelnya berdasarkan pada rata-rata waktu produksi.
Maks atau Min : ∑
Kendala:
∑
bulat untuk semua
Keterangan:
= Fungsi tujuan = Variabel keputusan
= koefisien dari variabel keputusan
= Koefisien dari variabel keputusan dalam kendala = sumber daya yang tersedia dalam kendala
ke-Masalah ini dikatakan sebagai ke-Masalah Linear Integer Programming. Sitorus, Parlin (1997), Integer Programming merupakan suatu model program linear yang khusus Dimana nilai variabel-variabel keputusan dalam penyelesaian optimal harus merupakan bilangan integer (bulat). Persyaratan bahwa nilai variabel keputusan harus integer mengingat nilai (banyaknya/jumlah) tidak mungkin dalam bilangan pecahan, seperti kertas, barang produksi, tentara, dan lain sebagainya.
Terdapat 3 macam permasalahan dalam pemrograman bulat, yaitu:
1. Pemrograman bulat murni, yaitu kasus dimana semua variabel keputusan harus berupa bilangan bulat.
2. Pemrograman bulat campuran, yaitu kasus dimana beberapa, tapi tidak semua, variabel keputusan harus berupa bilangan bulat
2.2.1 Beberapa Model Integer Programming
Thie, Paul. R. (1979) dalam bukunya memberikan beberapa persoalan yang dapat diformulasikan sebagai model integer programming. Ada dua hal yang akan dibahas yakni: modal penganggaran belanja, penjadwalan.
a. Modal Penganggaran Belanja
Pada model masalah modal penganggaran belanja, keputusan menyangkut seleksi dari sejumlah nilai dari investasi potensial. Keputusan berinvestasi mungkin untuk memilih diantara lokaso penanaman yanng mungkin, untuk memilih sebuah bentuk dari perlengkapan modal, atau untuk menyelesaikan ketika sebuah himpunan dari proyek penelitian dan pengembangan. Hal itu selalu membuat tidak mengerti untuk mempertimbangkan memilih investasi dari aktivitas ini, dan akhirnya masalahnya akan menjadi program bilangan bulat ya atau tidak, Dimana variabel keputusan yang diambil menjadi = 0 atau 1, menandakan bahwa investasi ke- diterima atau ditolak.
Asumsikan bahwa adalah hasil konstribusi dari investasi ke- dan adalah jumlah
sumber daya ke- , seperti uang atau tenaga kerja yang digunakan dalam investasi ke- , masalah ini dapat di formulasikan sebagai berikut:
Maksimalkan ∑
Kendala
∑
Tujuannya adala untuk memaksimalkan total kontribusi dari semua investasi tanpa melebihi ketersediaan yang terbatas dari sumber daya.
Pada umumnya, masalah ini juga disebut Knapsack problem, karena dapat disamakan pada sebuah situasi dimana pejalan kaki harus memutuskan barang-barang apa saja yang dimasukkan dalam perjalanannya. Di sini adalah nilai atau kegunaan
dari barang yang di masukkan Dimana , tujuannya adalah memaksimalkan
dengan mengganti variabel pembatas 0-1. Knapsack problem penting karena sejumlah program bilangan bulat dapat ditunjukkan sama dengan masalahnya, dan lebih jauh, karena langkah penyelesaian pada model knapsack telah memotivasi langkah-langkah untuk menyelesaikan program bilangan bulat umum.
b. Penjadwalan
Segala tingkat pada masalah yang menunjuk seperti antrian, penjadwalan, dan rute adalah tidak terpisahkan dengan program bilangan bulat. Sebagai contoh, menjadwalkan siswa, fakultas, dan ruang kelas sedemikian hingga jumlah dari siswa yang tidak mengambil pilihan pertama dari kelas di minimalkan. Ada batasan pada jumlah dan ukuran dari ruangan kelas yang tersedia pada suatu waktu, ketersediaan dari jumlah fakultas pada waktu tertentu, dan pilihan dari siswa untuk waktu tertentu. Lebih jelasnya, siswa ke- dijadwalkan pada kelas ke- selam periode ke- atau tidak. Oleh karena itu, variabelnya harus nol atau satu.
2.2.2 Metode penyelesaian Integer Programming
Beberapa metode penyelesaian masalah program bilangan bulat adalah metode pembulatan (rounding method), metode grafik (graphic method), metode cabang dan batas (branch and bound method), dan metode branch and price.
Metode grafik hanya dapat dilakukan apabila jumlah variabel keputusan adalah dua. Metode ini menggunakan pendekatan pencarian. Untuk mencari penyelesaian optimal, dilakukan dengan cara mencari titik penyelesaian optimal yang terdapat di dalam daerah kelayakandengan koordinatnya harus bilangan integer yang mendekati titik optimal yang diperoleh dengan menggunakan metode grafik biasa. Metode branch and bound dan metode branch and price lebih sering digunakan karena hasil yang diperoleh lebih baik dan lebih teliti dari kedua metode lainnya.
2.3 Metode Simpleks
Dalam penyelesaian program linear metode grafik mempunyai kelemahan yaitu variabel keputusannya harus dua. Pelu diketahui bahwa hanya sedikit masalah dalam kehidupan nyata yang mengandung dua variabel. Pada kenyataanya beberapa situasi melibatkan banyak variabel keputusan dan banyak kendala. Oleh karena itu haruslah ada metode yang dapat menyelesaikan program linear dengan banyak variabel. Metode ini dinamakan metode simpleks.
Metode simpleks sebenarnya sama saja dengan metode grafik di dalam mencari titik penyelesaian optimal di daerah kelayakan (mencari nilai titik-titik ekstrim di daerah kelayakan). Dalam pengoperasiannya, metode simpleks dimulai dari titik awal (titik 0) dan bergerak ke titik ekstrim lain yang memiliki nilai penyelesaian yang optimal.
Ada beberapa istilah yang sangat sering digunakan dalam metode simpleks, diantaranya :
1. Iterasi adalah tahapan perhitungan dimana nilai dalam perhitungan itu tergantung dari nilai tabel sebelumnya.
2. Variabel non basis adalah variabel yang nilainya diatur menjadi nol pada sembarang iterasi. Dalam terminologi umum, jumlah variabel non basis selalu sama dengan derajat bebas dalam sistem persamaan.
kendala merupakan pertidaksamaan ≤ ) atau variabel buatan (jika fungsi kendala menggunakan pertidaksamaan ≥ atau =). Secara umum, jumlah
variabel basis selalu sama dengan jumlah fungsi pembatas (tanpa fungsi non negatif).
4. Solusi atau nilai kanan merupakan nilai sumber daya pembatas yang masih tersedia. Pada solusi awal, nilai kanan atau solusi sama dengan jumlah sumber daya pembatas awal yang ada, karena aktivitas belum dilaksanakan.
5. Variabel slack adalah variabel yang ditambahkan ke model matematik
kendala untuk mengkonversikan pertidaksamaan ≤ menjadi persamaan (=).
Penambahan variabel ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel slack akan berfungsi sebagai variabel basis.
6. Variabel surplus adalah variabel yang dikurangkan dari model matematik
kendala untuk mengkonversikan pertidaksamaan ≥ menjadi persamaan (=).
Penambahan ini terjadi pada tahap inisialisasi. Pada solusi awal, variabel surplus tidak dapat berfungsi sebagai variabel basis.
7. Variabel buatan adalah variabel yang ditambahkan ke model matematik
kendala dengan bentuk ≥ atau = untuk difungsikan sebagai variabel basis awal.
Penambahan variabel ini terjadi pada tahap inisialisasi. Variabel ini harus bernilai 0 pada solusi optimal, karena kenyataannya variabel ini tidak ada. Variabel hanya ada di atas kertas.
8. Kolom pivot (kolom kerja) adalah kolom yang memuat variabel masuk. Koefisien pada kolom ini akn menjadi pembagi nilai kanan untuk menentukan baris pivot (baris kerja).
9. Baris pivot (baris kerja) adalah salah satu baris dari antara variabel basis yang memuat variabel keluar.
10.Elemen pivot (elemen kerja) adalah elemen yang terletak pada perpotongan kolom dan baris pivot. Elemen pivot akan menjadi dasar perhitungan untuk tabel simpleks berikutnya.
12.Variabel keluar adalah variabel yang keluar dari variabel basis pada iterasi berikutnya dan digantikan oleh variabel masuk. Variabel keluar dipilih satu dari antara variabel basis pada setiap iiterasi. Variabel ini pada iterasi berikutnya akan bernilai nol.
Prosedur (tahap proses) untuk menyelesaikan program linear dengan menggunakan metode simpleks sebagai berikut:
Tahap 1 : Merumuskan problema ke dalam bentuk standar (model simpleks). Bentuk kanonik merupakan suatu bentuk Dimana bagian kanan pembatas ( ) adalah non negatif. Dengan demikian, jika salah satu dari negatif, maka diperlukan untuk mengalikannya dengan -1. Sebagai penambahan bahwa penting juga semua pembatas haruslah dalam bentuk persamaan. Agar mencapai bentuk itu maka diperlukan untuk menambah nilai non negatif yang dinamakan slack variabel . Variabel slack ini menyeimbangkan kegunaan sebenarnya dari bagian kiri pada pertidaksamaan dengan adanya bagian kanan. Dengan demikian bentuk umum persamaan linear sekarang dapat ditulis sebgai berikut:
Maksimalkan akan mempengaruhi nilai fungsi tujuan. Dengan demikian, adalah nol pada fungsi tujuan.
Tahap 2 : Menyusun tabel simpleks
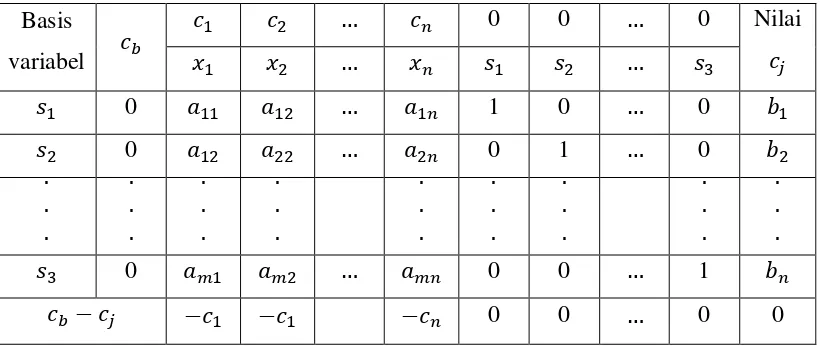
Tabel 2.1 : Tabel simpleks
Tahap 3 : Tentukan kolom pivot.
Penentuan kolom pivot dilihat dari koefisien fungsi tujuan (nilai di sebelah kanan baris z) dan tergantung dari bentuk tujuan. Jika tujuan maksimisasi, maka kolom pivot adalah kolom dengan koefisien paling negatif. Jika tujuan minimisasi , maka kolom pivot adalah kolom dengan koefisien positif terbesar. Jika kolom pivot ditandai dan ditarik ke atas, maka kita akan mendapatkan variabel keluar. Jika nilai paling negatif (untuk tujuan maksimisasi) atau positif terbesar (untuk tujuan minimisasi) lebih dari satu, pilih salah satu secara sembarang.
Tahap 4: Tentukan baris pivot.
Baris pivot ditentukan setelah membagi nilai solusi dengan nilai kolom pivot yang bersesuaian (nilai yang terletak dalam satu baris). Dalam hal ini, nilai negatif dan 0 pada kolom pivot tidak diperhatikan, artinya tidak ikut menjadi pembagi. Baris pivot adalah baris dengan rasio pembagian terkecil. Jika baris pivot ditandai dan ditarik ke kiri, maka kita akan mendapatkan variabl keluar. Jika rasio pembagian terkecil lebih dari satu, pilih salah sau secara sembarang.
Tahap 5 : Tentukan elemen pivot.
Tahap 6 : Bentuk tabel simpleks baru.
Tabel simpleks baru dibentuk dengan pertama sekali menghitung nilai baris pivot baru. Baris pivot baru adalah baris pivot lama dibagi dengan elemen pivot. Baris baru lainnya merupakan pengurangan nilai kolom pivot baris yang bersangkutan dikali baris pivot baru dalam satu kolom terhadap baris lamanya yang terletak pada kolom tersebut.
Tahap 7 : Periksa apakah tabel sudah optimal.
Keoptimalan tabel dilihat dari koefisien fungsi tujuan (nilai pada baris z) dan tergantung dari bentuk tujuan. Untuk tujuan maksimisasi, tabel sudah optimal jika semua nilai pada baris z sudah positif atau 0. Pada tujuan minimisasi, tabel sudah optimal jika semua nilai pada baris z sudah negatif atau 0. Jika belum, kembali ke tahap 3 , jika sudah optimal baca solusi optimalnya.
2.4 Metode Branch and Bound
Lev, Benjamin dan Weiss, Howard J. (1982), metode Branch and Bound (cabang dan batas) adalah suatu metode umum untuk mencari solusi optimal dari berbagai permasalahan optimasi, terutama untuk optimasi diskrit dan kombinatorial. Konsep dari metode branch and bound pertama sekali ditemukan oleh Land and Doig (1960). Ide dasarnya adalah membagi daerah fisible menjadi daerah yang lebih kecil. Metode branch and bound menggunakan sebuah langkah yang menempatkan batas atas dan batas bawah sebagai solusi ketika secara sistematis menyelesaikan subproblem.
Prosedur penyelesaiaan problema program linear integer dengan metode ini adalah sebagai berikut:
1. Penyelesaian optimal dengan metode program linear biasa.
Problema yang dihadapi diselesaikan terlebih dahulu dengan menggunakan metode program linear biasa (metode grafik atau metode simpleks) sampai diperoleh hasil optimal.
2. Pemeriksaan Penyelesaian Optimal
Hasil optimal pada langkah pertama diperiksa apakah variabel keputusan yang diperoleh bernilai integer atau pecahan. Apabila ternyata nilai semua variabel keputusan tersebut merupakan bilangan bulat positif (non negative integer), maka penyelesaian optimal telah tercapai. Apabila tidak, maka proses iterasi dilanjutkan.
3. Branching
Apabila penyelesaian optimal belum tercapai, maka peroblema tersebut dimodifikasi ke dalam dua sub problema (branching) dengan memasukkan kendala baru ke masing-masing subproblema tersebut. Variabel kendala baru tersebut harus bersifat saling pengecualian (mutually exclusive constraints) sehingga memenuhi persyaratan penyelesaian integer.
4. Bounding
nilai batas bawah dari setiap problema, maka penyelesaian optimal integer telah tercapai. Apabila tidak, maka subproblema yang memiliki nilai batas atas dan nilai batas bawah yang terbaik dipilih selanjutnya menjadi subproblema yang baru. Proses iterasi kembali pada langkah 2, sehingga demikian terus.
Penggunaan metode branch and bound banyak sekali diantaranya knapsack problem, integer programming, travelling sales problem, cutting stock problem dan banyak lagi kegunaanya. Penggunaan metode ini tentulah untuk mencari nilai pembulatan terbaik pada masing-masing masalah.
2.5 Metode Branch and Price
Metode branch and price adalah ssuatu teknik dalam menyelesaikan program integer yang berskala besar. Dantzig dan Wolfe (1960) mengusulkan teknik column generasi sebagai sebuah skema untuk menyelesaikan masalah linear programming berskala besar yang mempunyai banyak variabel. Algoritma umum dari metode branch and price ini diperkenalkan oleh Barnhart (1998) dan Vanderbeck dan Wolsey (1996).
Berikut ini merupakan ringkasan pengertian mengenai algoritma branch and price: 1. Branch and price merupakan teknik column generation untuk menyelesaikan
program integer berskala besar.
2. Pada tiap node dari tree branch and price, kolom dapat dibangkitkan untuk memperkuat linear programming relaksasi.
3. Pada branch and price, kumpulan kolom dibuang dari linear programming relaxation sebuah program integer berskala besar karena terdapat terlalu banyak kolom yang harus ditangani secara efisien dan kebanyakan dari kolom itu menghasilkan variabel yang bernilai nol padaa solusi optimal.
4. Kemudian cek keoptimalan, sebuah subproblem yang disebut juga dengan
„pricing problem‟ diselesaikan untuk mengidentifikasi adanya kolom yang
memasuki basis. Pricing problem dilakukan untuk mengetahui adanya variabel keputusan yang memiliki reduced cost negatif.
6. Percabangan terjadi ketika tidak terdapat kolom yang melalui proses pricing dan solusi program integer tidak memenuhi batasan kondisi integral.
Column Generation menyediakan penguraian dari sebuah masalah menjadi master dan subproblem. Penguraian ini memungkinkan adanya penafsiran dan pengaturan kontektual untuk penambahan beberapa batasan penting. Dalam branch and price, kolom disisihkan dari relaksasi linear programming karena terdapat terlalu banyak kolom yang ditangani secara efisien. Kemudian untuk memeriksa keoptimalan dari sebuah solusi linear programming, subproblem yang disebut pricing problem, yang merupakan bagian permasalahan untuk dual linear programming diselesaikan untuk mencoba mengidentifikasi kolom yang akan memasuki basis. Jika terdapat kolom yang di maksud tersebut, maka solusi linear programming dioptimasi kembali. Percabangan terjadi ketika tidak terdapat kolom yang dinilai dapat memasuki basis dan solusi linear programming tidak memenuhi batasan integral.
Terdapat beberapa kesulitan dalam penggunaan teknik column generation untuk linear programming dalam solusi integer programming, yaitu:
1. Integer programming konvensional bercabang pada variabel yang mungkin tidak efektif karena memperbaiki variabel yang dapat merusak struktur pricing problem. Menyelesaikan linear programming dan subproblem menjadi optimal mungkin menjadi tidak efisien, dimana beberapa aturan berbeda akan digunakan untuk menangani pohon branch and price.
2. Linear programming relaksasi dari master problem diselesaikan yang dengan column generation integral dan menggunakan prosedur standard branch and bound untuk master problem pada kolom yang ada tidak seperti halnya mencari solusi optimal, atau yang baik atau yang mungkin fisibel terhadap permasalahan yang sebenarnya.
Bab 3
PEMBAHASAN
3.1 Penentuan Batas Bawah pada Metode Branch and Bound
Batas bawah akan ditentukan setelah menyelesaikan bentuk umum program linear. Bentuk umum program linear diberikan sebagai berikut:
Maks atau Min : ∑ , untuk
Kendala:
∑ atau atau , untuk
Setelah menyelesaikan bentuk umum di atas maka akan didapatkan nilai dari variabel dan jika nilai tersebut dimasukkan ke dalam fungsi tujuan maka akan
didapatkan fungsi tujuan awal. Pada kasus minimasi fungsi tujuan awal tersebut akan menjadi batas bawah awal. Pada kasus maksimasi nilai variabel tersebut harus di bulatkan ke bawah menggunakan metode pembulatan biasa dan kemudian dimasukkan ke dalam fungsi tujuan maka akan menghasilkan fungsi tujuan baru yang akan menjadi batas bawah awal.
Contoh persoalan kasus maksimasi: Maks
s.t dan integer
Penyelesaian:
Selesaikan persoalan di atas menggunakan metode simpleks sehingga diperoleh tabel simpleks sebagai berikut:
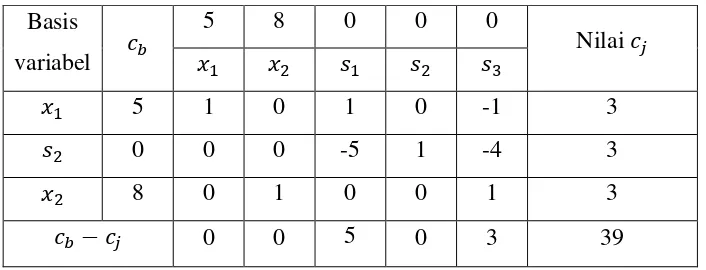
Tabel 3.1 : Tabel simpleks awal
Basis variabel
5 8 0 0
Nilai
5 1 0 2,25 0,25 2,25 8 0 1 -1,25 -0,25 3,75
0 0 1,25 -0,75 41,25
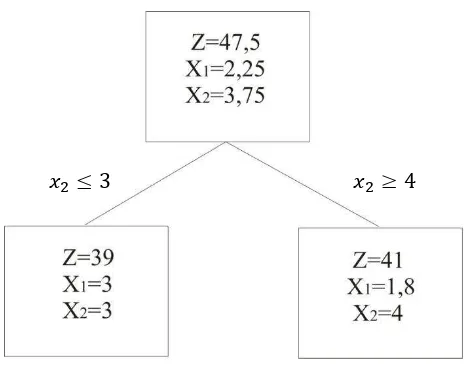
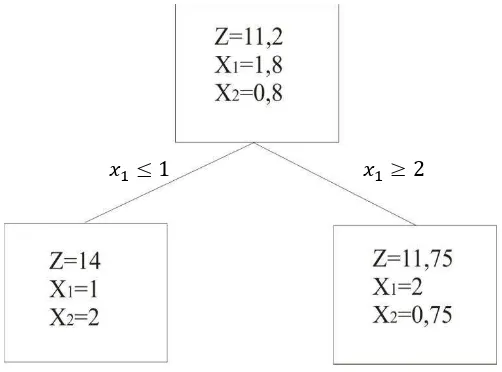
Dari tabel simpleks di atas didapatkan nilai , dan
Gambar 3.1 : Percabangan untuk iterasi awal
Dapat dilihat solusi menghasilkan nilai yang merupakan batas atas. Nilai batas bawah diperoleh dengan melakukan pembulatan ke bawah pada kedua variable keputusan sehingga didapatkan nilai . Karena solusi belum bulat optimal, maka perlu dilakukan percabangan untuk menemukan solusi optimum bulat. Untuk melakukan percabangan perhatikan nilai variable keputusan yang terbesar, dalam hal ini akan menjadi suatu kendala baru yakni dan .
Iterasi 1
Selesaikan bagian 1 dengan menggunakan metode simpleks sehingga diperoleh tabel simpleks
sebagai berikut:
Tabel 3.2 : Tabel simpleks untuk bagian 1
Basis
Selesaikan bagian 2 dengan menggunakan metode simpleks sehingga diperoleh tabel simpleks
sebagai beikut :
Tabel 3.3 : Tabel simpleks untuk bagian 2
Gambar 3.2 : Percabangan untuk iterasi 1
Karena pada bagian 1 sudah memiliki solusi bulat dan nilai dijadikan batas bawah baru dan juga dijadikan nilai calon. Selanjutnya perhatikan bagian 2, pada bagian ini masih terdapat variable keputusan yang tidak bulat dan nilai dijadikan batas atas baru. Oleh karena itu, dilakukan percabangan lagi dengan nilai
dan .
Iterasi 2 Bagian 3
Maks s.t
Bagian 4
Maks s.t
Bagian 3:
Selesaikan bagian 3 dengan menggunakan metode simpleks sehingga diperoleh tabel
Tabel 3.4 : Tabel simpleks untuk bagian 3
Basis variabel
5 8 0 0 0 0 0
Nilai
0 0 0 1 -0,11 0 0 0 0.56
0 0 0 0 0,11 -1 1 1 0,44
8 0 1 0 0,11 0 0 0 4,44
5 1 0 0 0 0 0 0 1
0 0 0 0,88 0 0 0 40,56
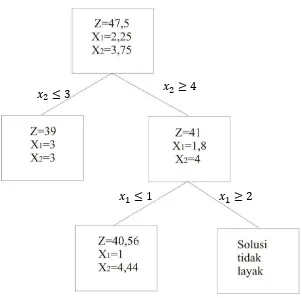
Dari tabel di atas diperoleh dan dan
Bagian 4:
Pada bagian ini tidak mempunyai solusi layak.
Gambar 3.3 : Percabangan untuk iterasi 2
Perhatikan pada bagian 3 masih terdapat variable keputusan yang tidak bulat dan nilai masih memenuhi batas yang telah ditentukan yang kemudian
dijadikan batas atas. Oleh karena itu, dilakukan percabangan lagi dengan nilai dan . Pada bagian 4 solusi tidak layak dikarenakan terdapat kendala yang tidak dipenuhi.
Selesaikan bagian 5 dengan menggunakan metode simpleks sehingga diperoleh tabel simpleks
sebagai berikut:
Tabel 3.5 : Tabel simpleks untuk bagian 5
Bagian 6:
Selesaikan bagian 6 dengan menggunakan metode simpleks sehingga diperoleh tabel simpleks
sebagai berikut :
Tabel 3.6 : Tabel simpleks untuk bagian 6
Basis variabel
5 8 0 0 0 0 0 0 0
Nilai
0 0 0 1 -0,2 0 0 0,8 0 -0,8 1
0 0 0 0 0 -1 0 1 1 -1 1
8 0 1 0 0 0 0 1 0 -1 5
0 0 0 0 -0,2 0 1 1,8 0 -1,8 1
5 0 0 0,2 0 0 -1,8 0 1,8 0
0 0 0 1 0 0 -1 0 1 40
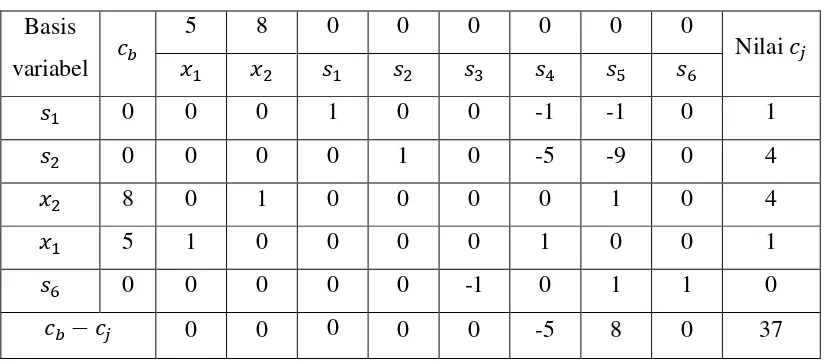
Dari tabel di atas diperoleh dan dan
Perhatikan pada bagian 5 nilai sudah merupakan solusi bulat. Karena nilai lebih kecil dari nilai calon maka solusi pada bagian ini bukan merupakan solusi bulat optimum. Perhatikan bagian 6 nilai juga sudah merupakan solusi bulat dan karena lebih besar dari nilai calon maka merupakan solusi
Untuk melakukan percabangan perhatikan nilai variable keputusan yang terbesar,
Selesaikan bagian 1 dengan menggunakan metode simpleks sehingga diperoleh tabel simpleks
sebagai berikut :
Tabel 3.8 : Tabel simpleks untuk bagian 1
Basis
Selesaikan bagian 2 ini dengan menggunakan metode simpleks sehingga diperoleh tabel
simpleks sebagai berikut :
Tabel 3.9 : Tabel simpleks untuk bagian 2
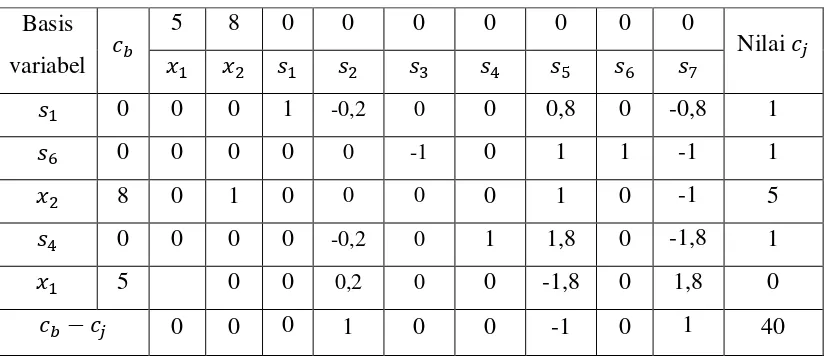
Dari tabel di atas diperoleh dan dan
Gambar 3.6 : Percabangan untuk iterasi 1
Karena pada bagian 1 memiliki nilai yang lebih besar dari batas yang telah ditentukan maka dikatakan inferior. Selanjutnya perhatikan bagian 2, pada bagian ini masih terdapat variable keputusan dan nilai fungsi tujuan yang tidak bulat. Nilai
ini akan dijadikan batas bawah baru. Oleh karena itu, dilakukan percabangan lagi dengan nilai dan .
Iterasi 2 Bagian 3
Min Z : s.t
Bagian 4
Bagian 3:
Selesaikan bagian 3 ini dengan menggunakan metode simpleks sehingga diperoleh tabel
simpleks sebagai berikut :
Tabel 3.10 : Tabel simpleks untuk bagian 3
Basis
Selesaikan bagian 4 ini dengan menggunakan metode simpleks sehingga diperoleh tabel
simpleks sebagai berikut :
Tabel 3.11 : Tabel simpleks untuk bagian 4
Gambar 3.7 : Percabangan untuk iterasi 2
Perhatikan pada bagian 3 nilai melebihi batas yang telah ditentukan maka dikatakan inferior. Pada bagian 4 nilai batas atas sudah sama dengan batas bawah maka nilai sudah optimum dan karena tidak ada percabangan lagi maka nilai
sudah merupakan nilai optimum.
3.1 Penentuan Batas Bawah pada Metode Branch and Price
Penyelesaian program integer dengan metode Branch and Price adalah dengan cara mendualkan bentuk primal program linear. Bentuk umum program linear sebagai berikut:
Maks atau Min : ∑ , untuk
Kendala:
∑ atau atau , untuk
ruas kanan bagi dual, tanda ketidaksamaan pada pembatas akan bergantung pada fungsi tujuannya, fungsi tujuan berubah bentuk (maksimasi menjadi minimasi dan sebaliknya), setiap kolom pada primal berubah menjadi baris (pembatas) pada dual. Bentuk umum di atas akan didualkan menjadi:
Min atau Maks : ∑ , untuk Kendala:
∑ atau atau , untuk
Selanjutnya untuk menentukan batas bawah dimulai dari menyelesaikan bentuk dual di atas. Setelah menyelesaikan bentuk dual tersebut akan didapatkan nilai dan nilai tersebut akan dimasukkan ke dalam fungsi tujuan untuk menghasilkan nilai fungsi tujuan. Pada kasus minimasi dalam bentuk dual tersebut nilai fungsi tujuan tersebut akan menjadi batas bawah awal. Untuk kasus maksimasi maka nilai akan dibulatkan ke bawah terlebih dahulu dengan metode pembulatan yang untuk selanjutnya nilai tersebut dimasukkan ke dalam fungsi tujuannya, maka fungsi tujuan tersebut akan menjadi batas bawah awal.
Penyelesaian :
Bagian 1:
Kemudian diselesaikan dengan menggunakan metode simpleks diperoleh:
Tabel 3.13 : Tabel simpleks untuk bagian 1
Basis
Tabel 3.14 : Tabel simpleks untuk bagiann 2
Basis variabel
2 3 2 0 0 Nilai
2 0 1,33 1 1 -0,33 6
2 1 0,67 0 0 0,33 10
0 1 0 2 0 32
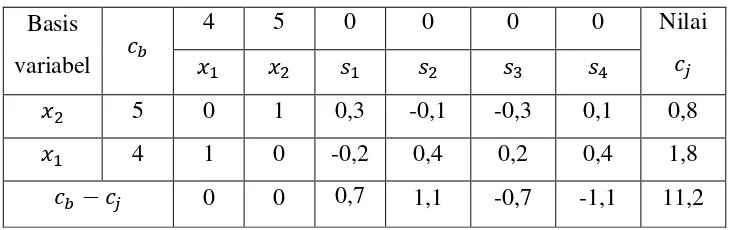
Dari tabel di atas diperoleh nilai untuk primal adalah , , dan
dan nilai untuk dual adalah , , dan
Gambar 3.9 : Percabangan untuk iterasi 1
Iterasi 2
pada bagian ini tidak mempunyai solusi layak.
Bagian 4:
Kemudian diselesaikan dengan menggunakan metode simpleks diperoleh : Tabel 3.15 : Tabel simpleks untuk bagian 4
Gambar 3.10 : Percabangan untuk iterasi 2
Pada bagian 3 percabangan dihentikan karena tidak memiliki solusi layak. Perhatikan pada bagian 4 nilai sudah melewati batas yang telah ditentukan. Oleh karena itu, pada bagian 4 dikatakan inferior. Karena tidak bisa melakukan percabangan lagi maka nilai dikatakan optimal dengan , .
Contoh kasus minimasi
Min
s.t
dan integer
Penyelesaian :
Bagian 1:
Bentuk dual dari bagian 1 ini akan diubah kembali menjadi bentuk primal sebagai berikut :
Min
s.t
Kemudian diselesaikan dengan menggunakan metode simpleks diperoleh :
Tabel 3.17 : Tabel simpleks untuk bagian 1
Basis variabel
2 3 -1 0 0 0 0 Nilai
1 0 2,67 1 1 -0,67 -1 0,67 0,67
3 1 0,67 0 0 0,33 0 -0,33 1,67
0 0,33 0 0 0,33 -1 -0,33 5,67
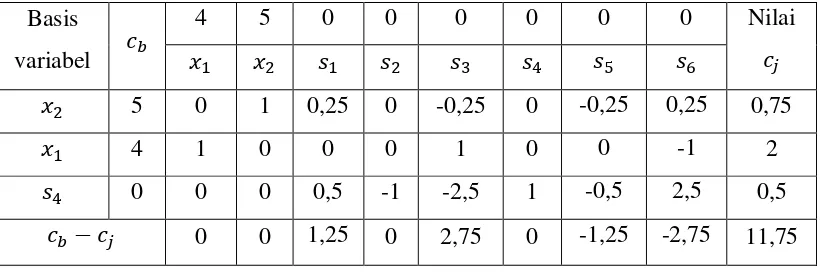
Dari tabel di atas diperoleh nilai untuk primal adalah sebagai berikut dan
, dan dan nilai untuk dual adalah , dan
.
Bagian 2:
Gambar 3.12 : Percabangan untuk iterasi 1
Pada bagian 1 pada bagian dual masih terdapat nilai variabel keputusan yang belum bulat. Oleh karena itu, akan dilanjutkan dengan melakukan percabangan yakni untuk
dan dan nilai dijadikan batas atas baru. Selanjutnya perhatikan bagian 2, pada bagian ini tidak memiliki solusi yang layak.
Iterasi 2
Bagian 3
Maks s.t
Bagian 4
Maks s.t
Bagian 3:
Min
s.t
Kemudian diselesaikan dengan menggunakan metode simpleks diperoleh :
Tabel 3.18 : Tabel simpleks untuk bagian 3
Basis variabel
2 3 -1 0 0 0 0 0 Nilai
1 2 4 1 0 1 0 -1 0 4
0 3 2 0 1 0 1 0 -1 5
1 1 0 0 1 0 -1 0 4
Dari tabel di atas diperoleh nilai untuk primal adalah sebagai berikut dan
, , dan dan nilai untuk dual adalah , dan
Bagian 4:
Bentuk dual dari bagian 4 ini akan diubah kembali menjadi bentuk primal sebagai berikut :
Min
s.t
Tabel 3.19 : Tabel simpleks untuk bagian 4
Basis variabel
2 3 -1 -1 0 0 0 0 Nilai
-1 0 4 1,5 1 1,5 -1 -1,5 1 1
3 1 2 0,5 0 0,5 0 -0,5 0 2
0 -1 1 0 0 1 0 -1 5
Dari tabel di atas diperoleh nilai untuk primal adalah , , , dan dan nilai untuk dual adalah , , dan
Gambar 3.13 : Percabangan untuk iterasi 2
Bab 4
KESIMPULAN DAN SARAN
4.1Kesimpulan
Dari hasil uraian dan pembahasan yang telah dikemukakan sebelumnya, maka dapat disimpulkan bahwa :
1. Seperti halnya pada metode Branch and Bound, penentuan batas bawah perlu dilakukan agar iterasi-iterasi pada metode branch and price dapat diperpendek.
2. Nilai batas bawah pada setiap percabangan semakin lama akan semakin mendekati batas atas yang pada akhirnya mungkin akan menjadi solusi optimum.
4.2Saran
DAFTAR PUSTAKA
Alvelos, Filipe.P.P. 2005. Branch-and-Price and Multicommodity Flows. Thesis. Portugal:University of Minho
Barnhart, C., Johnson, E.L., Nemhauser, G.L., Savelsbergh, M.W.P., and Vance, P.H. 1998.
Branch-and-Price: Column Generation for SolvingInteger Programs. Operations Research ,hal:316–329.
Geoffrion, A.M. 1974. Lagrangean Relaxation for Integer Programming. Dalam Geoffrion.
Mathematical Programming Study. Vol 2: hal:82-114.
Letchford, Adam N. 2011. An introduction to Branch-and-price. Department of Management Science Lancaster University, UK
Lev, Benjamin dan Weiss, Howard J. 1982. Introduction to Mathematical Programming.
New York : Elsevier North Holland.
Savelsbergh, Martin W.P. 2002. Branch-and-price: Integer programming with Column Generation, BP”. Encyclopedia of Optimization. Vol : 2 : hal : 218-221
Siswanto. 2007. Operation Research. Jilid 1. Yogyakarta : Erlangga
Sitorus, Parlin. 1997. Program Linear. Jakarta : Universitas Trisakti