EFEKTIVITAS PENDEKATAN MATEMATIKA REALISTIK (PMR) DITINJAU DARI KEMAMPUAN PEMAHAMAN KONSEP MATEMATIS SISWA (Studi pada Siswa Kelas VIII Semester Genap SMP Negeri 20 BandarLampung Tahun Pelajaran 2012/2013)
Teks penuh
Gambar

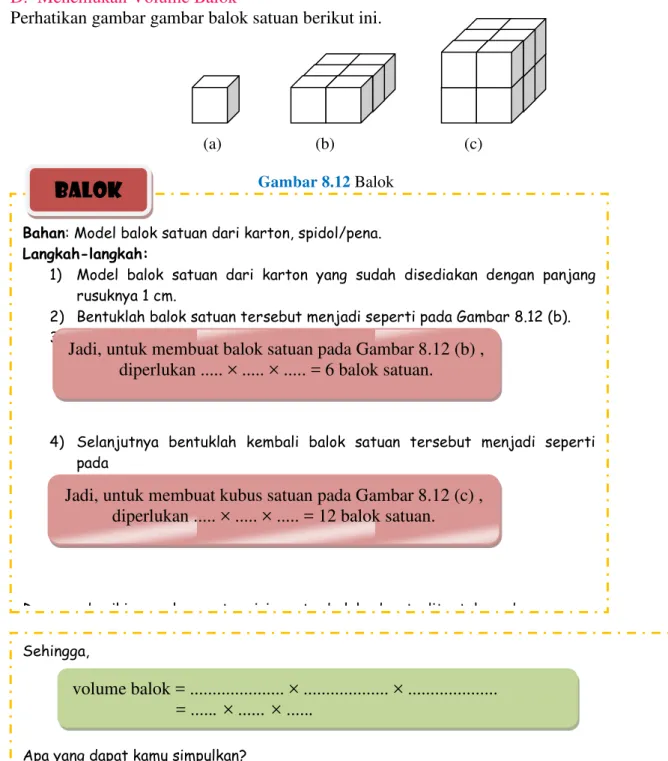
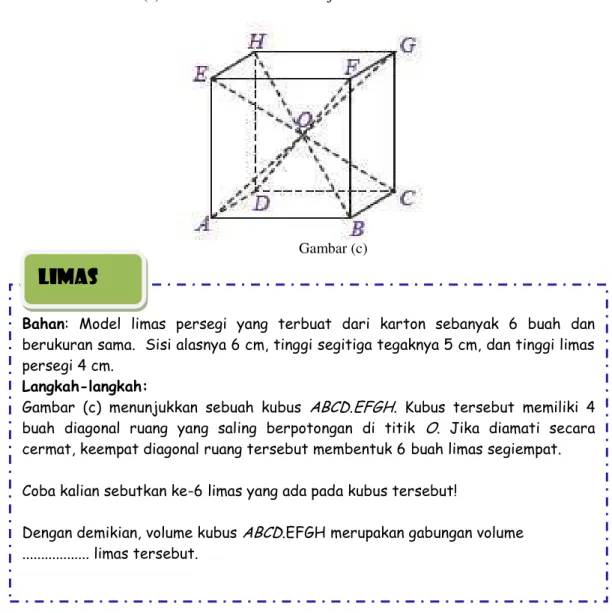
Dokumen terkait
Teori evolusi sosio-kultural Sanderson dalam buku berjudul Makro Sosiologi (2003) digunakan untuk menjelaskan penyebab terjadinya reaktualisasi fungsi bale banjar di Kota Denpasar
Pengaruh Konsentrasi Pelarut (n-Heksana) terhadap Rendemen Hasil Ekstraksi Minyak Biji Alpukat untuk Pembuatan Krim Pelembab Kulit (Suratmin Utomo).. PENGARUH KONSENTRASI
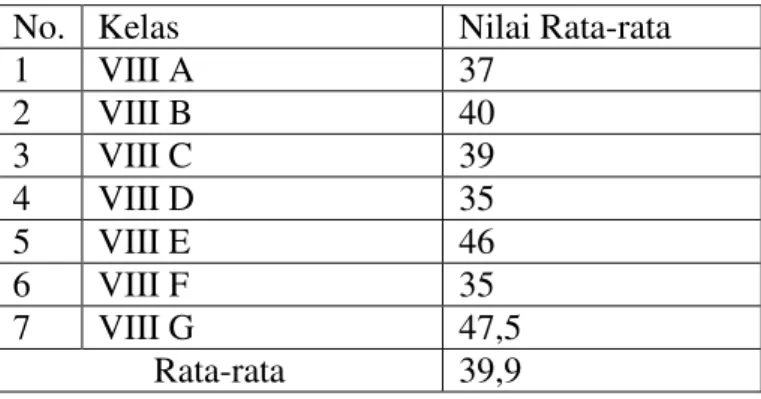
Judul Proyek Tugas Akhir : Medan Traditional Handicraft Center Tema : Arsitektur Metafora.. Rekapitulasi Nilai
tidak mengetahui bahwa Salmah adalah Mas Merah yang disebut Salam
Bencana erosi tanah yang terjadi di desa Watuagung ada beberapa faktor mulai dari tingginya intensitas curah hujan dan lokasi yang sangat berpotensi erosi tanah atau
Penelitian ini bertujuan untuk mengetahui apakah: (1) ada hubungan antara persepsi siswa tentang variasi gaya mengajar guru dengan prestasi belajar siswa; (2) ada hubungan
Berdasarkan data statistik di PPN Kejawanan tahun 2011, hampir setengahnya 47% hasil volume produksi jenis ikan yang didaratkan di PPN Kejawanan yaitu Cumi-cumi
Manfaat laporan tersebut sangat tergantung dari nilai ketepatwaktuan pelaporan tersebut, sebaliknya laporan yang tidak tersaji tepat pada waktunya akan mengurangi nilai manfaat dari