APLIKASI
MOBILE
PENENTUAN RUTE TERPENDEK
DI KEBUN RAYA BOGOR MENGGUNAKAN
ALGORITME DIJKSTRA
DANY PAMBUDI
DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Aplikasi Mobile Penentuan Rute Terpendek di Kebun Raya Bogor Menggunakan Algoritme Dijkstra adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
DANY PAMBUDI. Aplikasi Mobile Penentuan Rute Terpendek di Kebun Raya Bogor Menggunakan Algoritme Dijkstra. Dibimbing oleh FIRMAN ARDIANSYAH.
Kebun Raya Bogor (KRB) mempunyai banyak pohon, koleksi tanaman, dan tempat menarik yang berada dalam daerah yang luas sekitar 87 Ha. Selain itu, KRB juga memiliki gedung museum, laboratorium, dan tempat penting yang cukup banyak sehingga menyulitkan seseorang untuk mencapai lokasi tersebut. Karena jarak masing-masing lokasi yang jauh ini, navigasi atau pemandu menjadi hal penting untuk wisatawan yang ingin mengelilingi KRB dengan waktu seoptimal mungkin. Masalah tersebut dapat diselesaikan dengan pemodelan graf untuk menentukan rute terpendek dari masing-masing lokasi menggunakan algoritme Dijkstra. Berdasarkan hasil uji coba perbandingan jarak pada aplikasi dengan jarak pedometer didapatkan rata-rata selisih jarak kesalahan adalah 65.3 meter, hal ini dikarenakan data koordinat lokasi yang didapatkan dari Google Maps berbeda dengan koordinat lokasi yang diterima sinyal GPS saat di KRB pada aplikasi pedometer.
Kata kunci: navigasi, graf, rute terpendek, algoritme Dijkstra
ABSTRACT
DANY PAMBUDI. Mobile Application Determination Shortest Route in Bogor Botanical Gardens using Dijkstra’s Algorithm. Supervised by FIRMAN ARDIANSYAH.
Bogor Botanical Gardens (BBG) has many trees, plant collections, and points of interest which located in a wide area around 87 hectares. In addition, BBG also has a museum building, laboratory, and many important places which give difficulty for a person to reach those location. Because of the distance of each location, navigation or guide becomes essential for travelers who want to looking around BBG with optimum time. These problems can be solved by graph modelling to determine the shortest route from each location using Dijkstra algorithm. Based on the results of comparative testing in applications with spacing distance pedometer difference obtained an average error distance is 65.3 meters, this is because the location coordinate data obtained from different Google Maps with location coordinates of the received GPS signal while in KRB on pedometer application.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Ilmu Komputer
pada
Departemen Ilmu Komputer
APLIKASI
MOBILE
PENENTUAN RUTE TERPDENDEK
DI KEBUN RAYA BOGOR MENGGUNAKAN
ALGORITME DIJKSTRA
DANY PAMBUDI
DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN INSTITUT PERTANIAN BOGOR
Penguji:
Judul Skripsi : Aplikasi Mobile Penentuan Rute Terpendek di Kebun Raya Bogor Menggunakan Algoritme Dijkstra
Nama : Dany Pambudi NIM : G64114033
Disetujui oleh
Firman Ardiansyah, SKom MSi Pembimbing
Diketahui oleh
Dr Ir Agus Buono, MSi MKom Ketua Departemen
PRAKATA
Puji dan syukur penulis ke hadirat Allah subhanahu wata’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat berserta salam juga penulis sampaikan kepada Nabi Muhammad shalallahu ’alaihi wa sallam, berserta para keluarga, shahabat dan umatnya hingga akhir zaman.
Penulis menyadari bahwa tanpa bimbingan dan dorongan dari semua pihak, penulisan skripsi ini tidak akan berjalan lancar. Banyak pihak yang telah membantu penulis hingga terselesaikannya tugas akhir ini. Oleh sebab itu, penulis ingin mengucapkan rasa terima kasih kepada:
1. Ayahanda Sukarni dan Ibunda Sujinah serta kakak penulis Anton Sapto Aji yang senantiasa mendoakan, memotivasi, dan memberikan kasih sayangnya kepada penulis.
2. Bapak Firman Ardiansyah, SKom MSi selaku dosen pembimbing yang telah membimbing dan mengarahkan penulis selama penelitian tugas akhir ini. 3. Bapak Auzi Asfarian, SKomp MKom dan Ibu Karlisa Priandana, ST MEng
selaku dosen penguji.
4. Seluruh pihak pegawai Kebun Raya Bogor yang telah sedikit membantu dalam memberikan booklet untuk melengkapi data penelitian.
5. Adinda Rahma Tiara Safesmi yang juga senantiasa mendoakan, memberikan semangat dan motivasi kepada penulis.
6. Seluruh teman-teman Ilkomerz atas ilmu, semangat, dan dukungannya, khususnya : Reisa Prasaptaraya, Nurul Arifin Subandi, dan Endrik Sugiyanto. 7. Seluruh pegawai di Badan Pengkajian dan Penerapan Teknologi yang telah
memotivasi dan memberikan waktu kepada penulis untuk menyelesaikan skripsi ini.
Penulis menyadari bahwa masih terdapat kekurangan dalam penulisan skripsi ini. Namun, penulis berharap dengan segala kekurangan yang ada semoga tulisan ini bisa memberikan manfaat kelak di kemudian hari. Amin.
Bogor, Oktober 2014
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 1
Ruang Lingkup Penelitian 2
Manfaat Penelitian 2
METODE 2
Analisis Kebutuhan 3
Pengambilan Data 3
Implementasi 3
Pengujian 4
HASIL DAN PEMBAHASAN 4
Analisis Kebutuhan 4
Pengambilan Data 4
Implementasi 5
Pengujian 9
SIMPULAN DAN SARAN 11
Simpulan 11
Saran 11
DAFTAR PUSTAKA 11
LAMPIRAN 12
DAFTAR TABEL
1 Parameter data lokasi 4
2 Parameter data rute 4
3 Contoh data lokasi pada SQLite 5
4 Perbandingan jarak terpendek pada aplikasi dengan jarak pedometer 10
DAFTAR GAMBAR
1 Diagram metode penelitian (Raymond 2004) 2
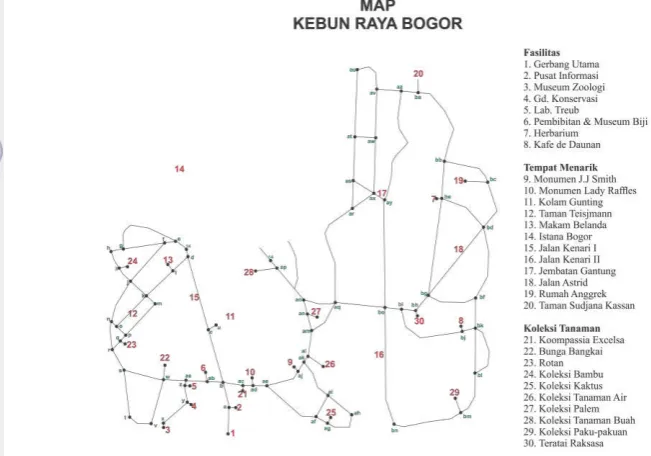
2 Node-node map Kebun Raya Bogor 5
3 Contoh proses Dijkstra 7
4 Antarmuka halaman utama 8
5 Fasilitas 8
6 Tempat menarik 8
7 Koleksi tanaman 8
8 Simulasi rute menuju bunga bangkai 9
9 Simulasi rute menuju tanaman air 9
DAFTAR LAMPIRAN
1 Data lokasi pada SQLite lengkap 12
2 Diagram alir Dijkstra 13
3 Simulasi rute menggunakan aplikasi bonav 14
PENDAHULUAN
Latar Belakang
Aktivitas wisata di Indonesia telah memberikan kontribusi yang cukup besar dalam perekonomian nasional karena mampu menggerakkan sektor ekonomi suatu wilayah. Kegiatan perjalanan yang dilakukan oleh seseorang atau sekelompok orang dengan mengunjungi tempat atau lingkungan tertentu untuk tujuan rekreasi dan mempelajari keunikan daya tarik wisata yang dikunjungi dalam jangka waktu sementara (Williams 1998). Salah satu kebutuhan informasi yang menarik dalam perangkat mobile adalah kemudahan untuk pencarian suatu lokasi. Dengan kemampuan Global Positioning System (GPS) sekarang ini, jarak menuju suatu tempat juga dapat ditampilkan beserta rutenya. Namun rute yang disajikan belum optimal dan belum tentu merupakan rute terpendek. Jarak untuk menuju daerah wisata menjadi pertimbangan tersendiri dari sekian banyak jalan yang tersedia dan dapat dilintasi. Wisatawan membutuhkan rute terpendek untuk mencapai tempat wisata yang dituju guna mempersingkat waktu perjalanan sehingga wisatawan dapat mengunjungi beberapa daerah wisata sekaligus dengan waktu yang seoptimal mungkin dalam 1 hari (Wijaya 2012).
Salah satu pilihan informasi menarik untuk pencarian suatu lokasi dalam perangkat mobile adalah Google Maps. Dengan Google Maps, pengguna dapat melakukan penelusuran peta guna mencari lokasi yang diinginkan. Kekurangan dari Google Maps diantaranya adalah harus terhubung langsung dengan koneksi internet dan penyajian data rute terpendek hanya terdapat pada jalan-jalan utama. Tersedianya peta yang berbasis offline seperti OpenStreetMap (OSM) dan ilmu matematika yang membahas mengenai graf cocok digunakan untuk mengatasi kekurangan yang telah diuraikan sebelumnya.
Konsep rute terpendek sering kali digunakan untuk menyelesaikan rute suatu tempat ke tempat yang lain. Pada pencarian rute terpendek, hal yang menjadi perhatian utama adalah menentukan jalur-jalur yang dapat dilalui sehingga dapat diperoleh rute tependek dari suatu tempat tertentu ke tempat lain.
Kebun Raya Bogor (KRB) terdiri atas banyak pohon, dan koleksi tanaman yang berada dalam daerah yang luas sekitar 87 Ha. Selain itu, KRB juga memiliki gedung museum, laboratorium dan tempat penting yang cukup banyak sehingga menyulitkan seseorang untuk mencapai lokasi tersebut. Kondisi saat ini seseorang hanya diberikan petunjuk arah berupa peta berbentuk leaflet. Informasi yang ada dalam peta tersebut belum disertai dengan posisi seseorang saat itu dan jarak tiap-tiap lokasi yang akan dituju. Melalui masalah tersebut, perlu dikembangkan sebuah aplikasi untuk mendapatkan rute terpendek yang dapat digunakan untuk memandu perjalanan di KRB.
Tujuan Penelitian
2
Ruang Lingkup Penelitian
Penelitian ini dilakukan untuk wilayah KRB. Lokasi yang akan digunakan dalam pengembangan sistem adalah lokasi-lokasi penting di KRB yang terletak di ruang terbuka dan ruang tertutup. Pengenalan lokasi dilakukan berdasarkan posisi yang ditampilkan pada GPS yaitu lintang dan bujur pada permukaan bumi. Aplikasi ini untuk mengetahui rute terpendek menggunakan algoritme Dijkstra dan pada penelitian ini, AR hanya menampilkan titik objek dan tidak diimplementasikan untuk mencari rute terpendek. Aplikasi yang akan dibuat dikhususkan untuk sistem operasi Android.
Manfaat Penelitian
Aplikasi yang dihasilkan diharapkan dapat membantu proses navigasi di wilayah KRB dan menjadi pemandu dalam menentukan rute terpendek dari
Gambar 1 Diagram metode penelitian (Raymond 2004)
Analisis Kebutuhan
Pada tahap ini akan dianalisis spesifikasi yang dibutuhkan baik dari perangkat lunak maupun perangkat keras serta data yang dibutuhkan untuk pengembangan sistem. Adapun data yang diperoleh adalah buku panduan dari KRB, denah lokasi, serta beberapa foto yang diambil di KRB.
3
a. Perangkat Keras
Perangkat keras yang digunakan untuk membuat program dan simulasi pada emulator menggunakan komputer dengan spesifikasi sebagai berikut:
1. Processor Intel Core i5-3230M 2.6GHz 2. RAM DDR3 6 GB
3. Harddisk 500 GB
4. Sistem operasi Windows 8 yang sudah terintegrasi dengan Java Enviroment serta dilengkapi dengan Android SDK dan AVD manager.
Sedangkan untuk implementasi digunakan perangkat smartphone Samsung Galaxy Grand dengan spesifikasi sebagai berikut:
1. Processor 1.2 GHz Cortex-A9 processor, Mali 400MP GPU 2. RAM 1 GB
3. OS Android 4.1.2 (Jelly Bean) 4. Memori internal 8 GB
5. Layar 480 x 800 pixels, 5.0 inch
6. Wi-Fi 802.11 a/b/g/n, dual-band, DLNA, Wi-Fi Direct, Wi-Fi hotspot b. Perangkat lunak
Pembuatan pemodelan sistem, penggambaran denah, pembuatan program, dan simulasi membutuhkan perangkat lunak sebagai berikut:
1. Eclipse Kepler 2. Notepad ++ v6.4.4
3. Android Development Tools 16.0.1
4. Android SDK rl6 (dilengkapi dengan plug in dan add ons Google API)
Pengambilan Data
Tahap ini akan dilakukan pengambilan data berupa koordinat masing-masing lokasi di KRB. Data koordinat lokasi yang dikumpulkan berjumlah 30 lokasi. Pengambilan data koordinat latitude dan longitude dilakukan menggunakan Google Maps.
Implementasi
4
Pengujian
Tahap ini digunakan untuk mengevaluasi dan memperbaiki program yang telah dibuat serta menguji akurasi jarak tiap lokasi. Pengujian ini dilakukan menggunakan smartphone Android di lokasi KRB. Aplikasi ini membutuhkan GPS dalam kondisi aktif untuk mendapatkan posisi koordinat awal dari pengguna. Setelah itu, pengguna memilih lokasi yang ingin dituju berdasarkan kategori seperti fasilitas, tempat menarik, dan koleksi tanaman. Uji coba ini dilakukan untuk menguji perbandingan jarak terpendek pada aplikasi yang telah dibuat dengan jarak pedometer atau penghitung langkah saat berjalan kaki.
HASIL DAN PEMBAHASAN
Analisis Kebutuhan
Data Lokasi dan Data Rute
Data lokasi dan data rute yang digunakan adalah data contoh. Lokasi yang digunakan adalah lokasi penting yang terdapat di Kebun Raya Bogor. Setiap lokasi dan rute memiliki empat buah parameter yang dapat dilihat pada Tabel 1 dan Tabel 2. Pada penelitian ini, data lokasi dan data rute disimpan dalam database SQLite.
Tabel 1 Parameter data lokasi
Nama Parameter Tipe
ID Integer
Lokasi Text
Latitude Text
Longitude Text
Tabel 2 Parameter data rute
Nama Parameter Tipe
5
dipakai adalah yang sesuai dengan pengambilan koordinat di Google Maps dengan memperhitungkan jalan balik arah sebagai bobot jarak. Node-node yang diperoleh dari peta tersebut ditunjukkan pada Gambar 2.
Gambar 2 Node-node map Kebun Raya Bogor
Implementasi
Data koordinat yang telah diperoleh dari Google Maps kemudian disimpan pada database SQLite. Adapun contoh isi data lokasi yang disimpan pada database SQLite dapat dilihat pada Tabel 3. Isi data lokasi pada SQLite selengkapnya dapat dilihat pada Lampiran 1.
Tabel 3 Contoh data lokasi pada SQLite
ID Lokasi Latitude Longitude
1 Gerbang Utama -6.602784 106.798546 2 Pusat Informasi -6.602525 106.798701 3 Museum Zoologi -6.602999 106.797545 4 Monumen J.J Smith -6.602565 106.797975 5 Monumen Lady Raffles -6.602125 106.797591 6 Kolam Gunting -6.601912 106.797998 7 Koompassia Excelsa -6.595773 106.802116 8 Bunga Bangkai -6.598875 106.803609
9 Rotan -6.601374 106.799828
Algoritme Dijkstra
6
jarak antar kota, waktu pengiriman, ongkos pembangunan, dan sebagainya (Dijkstra 1959).
Algoritme Dijkstra merupakan sebuah graph search algorithm yang menyelesaikan single source shortest path problem dengan cara mencari jalur terpendek dari satu start vertex lalu memeriksa dan membandingkan setiap jalur. Walaupun demikian, Dijkstra dapat dimodifikasi sehingga dapat digunakan untuk mencari jalur terpendek dari setiap vertex. Untuk sparse graph, yaitu graph dengan jumlah edge yang lebih kecil dari V2, Dijkstra dapat memiliki time complexity yang lebih kecil (Cormen et al 2009).
Input dari algoritme Dijktra adalah sebuah graf berarah yang berbobot (weigthed directed graph) G dan sebuah vertex s dalam G serta V adalah himpunan semua vertex dalam graf G.
G = (V,E) Keterangan:
G : Graph V : Vertex (titik) E : Edge (jarak)
Ada empat langkah yang perlu dilakukan Dijkstra sebelum melakukan pencarian jarak terpendek:
S : menentukan kumpulan vertex pada graph dengan lokasi awal dan lokasi akhir ditentukan.
V-S : kumpulan dari vertex pada graph dengan shortest path dari satu start ke vertex belum diketahui.
D : array berisi perkiraan jarak terpendek dari start ke setiap vertex. T : nilai total dari jarak yang ditempuh.
sp : shortest path
Cara kerja algoritme Dijkstra adalah: 1. Isi S sebagai start (lokasi awal).
2. Jika lokasi awal ≠ lokasi akhir maka isi V-S dengan lokasi yang terhubung dengan lokasi awal.
3. Isi D dengan urutan lokasi yang terhubung dengan lokasi awal yang berdasarkan jarak terpendek dari lokasi awal.
4. Isi T dengan jarak yang ditempuh dan selalu bertambah bila ada jarak yang baru.
5. Apabila lokasi awal = lokasi akhir berarti proses pencarian akan selesai,
tetapi apabila lokasi awal ≠ lokasi akhir lanjutkan langkah ke-2.
7
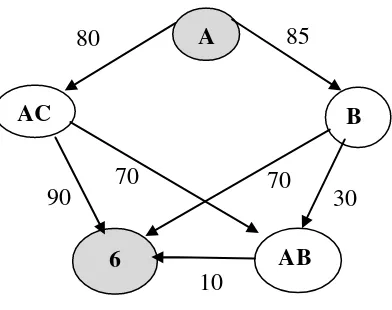
Gambar 3 Contoh proses Dijkstra
Langkah yang dilakukan dalam penyelesaian proses pencarian rute terpendek dari titik A sebagai lokasi Pintu Gerbang ke titik 6 sebagai lokasi Pembibitan dan Museum Biji dengan Dijkstra adalah:
1. S = {A}, V-S = {B, AB, AC, 6,},
D = {sp (A, A) = 0, sp (A, AC) = 80, sp (A, B) = 85}, T = 0
Tentukan titik dan jarak antar titik yang berhubungan dengan titik awal. 2. S = {A, AC}, V-S = {B, AB, 6},
D = {sp (A, B) = 85, sp (A, 6) = 170, sp (A, AB) = 115}, T = 80
Ambil titik AC, karena titik AC memiliki jarak yang paling pendek dari titik B dan jadikan Titik AC sebagai titik awal.
3. S = {A, B}, V-S = {AB, 6},
D = {sp (A, 6) = 170, sp (A, AB) = 115}, T = 85
Karena titik AC yang terhubung dengan titik 6 memiliki nilai jarak lebih besar dibandingkan dengan titik AB maka titik AB yang diambil.
4. S = {A, B, AB}, V-S = {6}, D = {sp (A, AB) = 115}, T = 115
Ambil titik D karena memiliki jarak lebih pendek dari pada titik C. 5. S = {A, B, AB, 6}, V-S = { },
D = { }, T = 125
Jadi dapat diperoleh jarak terpendek dari titik A sebagai lokasi Pintu Gerbang ke titik 6 sebagai lokasi Pembibitan dan Museum Biji akan melewati A – B – AB – 6 dengan total jarak yang di tempuh = 125.
Pembacaan Masukan Pengguna
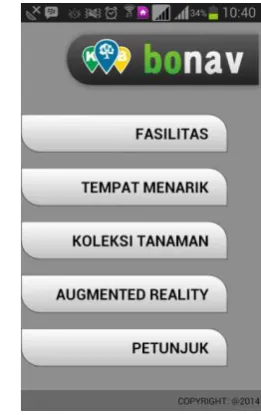
Pada tahap ini, sistem akan menerima masukan dari pengguna. Aplikasi ini diberi nama Botanical Navigation (Bonav). Sistem akan menampilkan daftar kategori menu yang dapat dipilih oleh pengguna. Gambar 4 memperlihatkan antarmuka yang digunakan untuk memilih menu. Pada halaman utama terdapat 5
8
menu dengan button berupa fasilitas, tempat menarik, koleksi tanaman, augmented reality, dan petunjuk.
Gambar 4 Antarmuka halaman utama
Pemilihan Lokasi
Pada tahap ini, sistem akan menampilkan lokasi-lokasi yang sesuai dengan kategori yang dipilih oleh pengguna. Pada menu, terdapat 3 lokasi utama yaitu fasilitas, tempat menarik, dan koleksi tanaman. Setelah pengguna memilih menu pada halaman utama, sistem akan menampilkan list button sesuai kategori. Adapun rincian dari masing-masing lokasi utama dapat dilihat pada Gambar 5, 6, dan 7.
Gambar 5 Fasilitas Gambar 6 Tempat menarik
9
Akses Layanan GPS
Pada tahap ini, sistem akan meminta layanan GPS yang tersedia. Setelah permintaan layanan dikirimkan, sistem akan menunggu data lokasi terbaru yang dikirimkan oleh satelit GPS. Terdapat jeda waktu antara permintaan layanan sampai diterimanya data lokasi terbaru. Selama data lokasi terbaru belum diterima, aplikasi tidak akan menampilkan data lokasi awal dan rute terpendek tidak dapat diproses.
Pengujian
Simulasi Rute
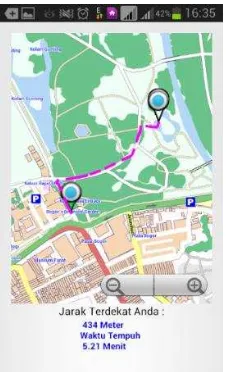
Tahap ini, sistem akan menampilkan jarak terdekat dari lokasi pengguna menuju lokasi yang yang telah dipilih pada menu utama. Informasi yang ditampilkan pada simulasi rute ini adalah detail peta, jarak dalam meter dan waktu tempuh dalam menit. Tampilan simulasi rute dapat dilihat pada Gambar 8 dan Gambar 9. Gambar 8 menggambarkan simulasi rute menuju Bunga Bangkai dan Gambar 9 menggambarkan simulasi rute menuju Tanaman Air. Hasil simulasi rute selengkapnya dapat dilihat pada Lampiran 3.
Gambar 8 Simulasi rute menuju
10
Tabel 4 Perbandingan jarak terpendek pada aplikasi dengan jarak pedometer No
.
Lokasi Awal Lokasi Tujuan Jarak aplikasi
11
SIMPULAN DAN SARAN
Simpulan
Penelitian ini menghasilkan aplikasi mobile menggunakan algoritme Dijkstra di KRB yang dapat digunakan untuk mencari jarak terpendek dari masing-masing lokasi yang ada di KRB. Hasil uji coba rata-rata selisih jarak kesalahan pada aplikasi dibandingkan jarak pada pedometer adalah 65.3 Meter, hal ini dikarenakan data koordinat lokasi yang didapatkan dari Google Maps berbeda dengan koordinat lokasi yang diterima sinyal GPS saat di KRB pada aplikasi pedometer.
Saran
Untuk penelitian selanjutnya, dapat dibangun sebuah web server yang menyediakan data yang besar bagi sistem untuk menampung deskripsi masing-masing lokasi, detail jalan, serta kompleksitas data sesuai keinginan pengguna. Dengan menggunakan web server, diharapkan proses manajemen data menjadi lebih mudah dan kapasitas data yang dapat disimpan menjadi lebih besar. Selain itu, pada penelitian selanjutnya penentuan rute terpendek pada algoritme Dijkstra dapat dibandingkan dengan algoritme lain yang serupa untuk mengetahui jarak dan running time yang paling optimal.
DAFTAR PUSTAKA
Ahuja, Ravinda K, Thomas LM, James BO. 1993.Network Flows. Prentice Hall. Alexander, McNeill R. 2002. Energetics and optimization of human walking and
running: The 2000 Raymond Pearl memorial lecture. American Journal of Human Biology. 14 (5):641–648. doi:10.1002/ajhb.10067
Cormen TH, Leiserson CE, Rivest RL, Stein C. 2009. Introduction to Algorithms Third Edition. Cambridge: The MIT Press.
Dijkstra EW.1959.A Note on Two Problems in Connection with Graphs, Numer. Math, 1: 269-271.
Feiner BS, MacIntyre B, Seligmann D. 1993. Communications of the ACM - Special issue on computer augmented environments: back to the real world. New York: ACM. 36(7):52–62.
McLeod R, Schell JG. 2004. Sistem Informasi Manajemen. Jakarta: PT. Indeks. Wijaya IWGS, Susanto EH. 2012. Penerapan Algoritma Djikstra untuk
Menemukan Rute Terpendek Daerah Wisata di Kabupaten Banyuwangi Pada Location Based Service di Platform Android. Di dalam: Adhyarini E, Prasetyo W, Mulya MKH, Yanuarsa D, editor. Prosiding Seminar Nasional Manajemen Teknologi XV; 2012 Feb 4; Surabaya, Indonesia. Surabaya (ID): Institut Teknologi Surabaya. C-30-1
12
Lampiran 1 Data lokasi pada SQLite lengkap
ID Lokasi Latitude Longitude
1 Gerbang Utama -6.602784 106.798546 2 Pusat Informasi -6.602525 106.798701 3 Museum Zoologi -6.602999 106.797545 4 Gd. Konservasi -6.602565 106.797975
5 Lab. Treub -6.602125 106.797591
6 Pembibitan & Museum Biji -6.601912 106.797998
7 Herbarium -6.595773 106.802116
8 Kafe de Daunan -6.598875 106.803609 9 Monumen J.J Smith -6.601374 106.799828 10 Monumen Lady Raffles -6.601819 106.798903 11 Kolam Gunting -6.600143 106.797728 12 Taman Teisjmann -6.600857 106.795815 13 Makam Belanda -6.599536 106.796357 14 Istana Bogor -6.598001 106.797365 15 Jalan Kenari I -6.59961 106.796925 16 Jalan Kenari II -6.599818 106.80192 17 Jembatan Gantung -6.596285 106.800871 18 Jalan Astrid -6.597138 106.803245 19 Rumah Anggrek -6.595395 106.802655 20 Taman Sudjana Kassan -6.592981 106.801142 21 Koompassia Excelsa -6.60204 106.798728 22 Bunga Bangkai -6.601673 106.796813
23 Rotan -6.601502 106.795895
13
Lampiran 2 Diagram alir Dijkstra
Mulai
Input lokasi awal dan lokasi tujuan
Lokasi awal terhubung
dengan lokasi akhir
Ambil jarak terpendek ke lokasi berikutnya
Ubah lokasi terpendek menjadi lokasi awal
Lokasi awal = lokasi akhir?
Selesai
ya
ya tidak
14
Lampiran 3 Simulasi rute menggunakan aplikasi bonav
Pembibitan ke Museum Zoologi
Makam Belanda ke Kolam Gunting
Kolam Gunting ke Monument Lady Raffles
Monumen Lady Raffles ke Jembatan Gantung
Taman Teisjmann ke Makam Belanda
15
Lampiran 4 Simulasi rute menggunakan aplikasi pedometer
Pintu Gerbang menuju Bunga Bangkai
Pembibitan menuju Museum Zoologi
Jembatan Gantung menuju Taman Sudjana Kassan
16
RIWAYAT HIDUP
Penulis dilahirkan di kota Cilegon pada tanggal 27 Desember 1989. Penulis merupakan anak kedua atau bungsu dari pasangan Bapak Sukarni dan Ibu Sujinah.
Penulis menyelesaikan pendidikan sekolah dasar di SD YPWKS V Cilegon, SMP Negeri 2 Cilegon, Sekolah Menengah Atas di SMA Negeri 1 Cilegon, Program Diploma Institut Pertanian Bogor, dan lulus pada tahun 2011. Pada tahun yang sama tahun 2011 penulis diterima di Fakultas Matematika dan Ilmu Pengetahuan Alam program studi Ilmu Komputer Institut Pertanian Bogor melalui tes seleksi masuk alih jenis ILKOM IPB.
Selama masa perkuliahan di IPB penulis aktif dalam berbagai kegiatan kampus. Penulis menjadi staf Departemen Pemberdayaan Sumber Daya Masyarakat Badan Eksekutif Mahasiswa Kabinet Persatuan Perjuangan periode 2009/2010. Pada periode 2010/2011 penulis menjadi Koordinator Badan Informasi Mahasiswa Departemen Komunikasi dan Informasi Badan Eksekutif Mahasiswa kabinet Gema Diploma. Pada periode yang sama Penulis juga mengikuti kegiatan MIPRO sebagai staf MICRO. Pada tahun 2014, kegiatan penulis diluar akademik yang menunjang pendidikan adalah bekerja di salah satu Lembaga Pemerintah Non Kementerian Badan Pengkajian dan Penerapan Teknologi sebagai Engineer staf pada unit Pusat Data, Informasi, dan Standardisasi. Pada periode tersebut penulis aktif mengikuti kegiatan training dan seminar, diantaranya adalah training Instalasi, Konfigurasi, dan Administrasi Zimbra Mail Server & Collaboration Suite serta seminar sosialisasi GOV-CSIRT