APLIKASI MULTI OBJECTIVE FUZZY LINEAR PROGRAMMING
DALAM MASALAH PERENCANAAN PERSEDIAAN PRODUKSI
SKRIPSI
EVI THERESIA SIPAYUNG
060803046
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
EVI THERESIA SIPAYUNG 060803046
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
ii
PERSETUJUAN
Judul : APLIKASI MULTI OBJECTIVE FUZZY LINEAR
PROGRAMMING DALAM MASALAH
PERENCANAAN PERSEDIAAN PRODUKSI
Kategori : SKRIPSI
Nama : EVI THERESIA SIPAYUNG
Nomor Induk Mahasiswa : 060803046
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2011 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Djakaria Sebayang, M.Si Drs. Faigiziduhu Bu’ulolo, M.Si NIP. 19511227 198503 1 002 NIP. 19531218 1980031 003
Diketahui/ Disetujui oleh:
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
APLIKASI MULTI OBJECTIVE FUZZY LINEAR PROGRAMMING DALAM MASALAH PERENCANAAN PERSEDIAAN PRODUKSI
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juni 2011
iv
PENGHARGAAN
Puji syukur dan terima kasih kepada Yesus Kristus atas kasih, anugrah serta perlindunganNya kepada penulis sehingga dapat mengerjakan dan menyelesaikan skripsi ini.
Ucapan terima kasih juga penulis ucapkan kepada Drs. Faigiziduhu Bu’ulolo, M.Si dan Drs. Djakaria Sebayang, M.Si selaku Dosen pembimbing penulis dalam penyelesaian skripsi ini, atas setiap bimbingan dan motivasi yang telah diberikan. Penulis juga mengucapkakan terima kasih kepada Drs. Suwarno Ariswoyo, M.Si dan Drs. H. Haludin Panjaitan selaku Dosen penguji, atas setiap saran dan masukannya selama pengerjaan skripsi ini. Ucapan terima kasih juga penulis tujukan kepada Ketua dan Sekretaris Departemen Prof. Dr. Tulus, M.Si dan Dra. Mardiningsi, M.Si dan kepada Bapak dan Ibu dosen pada Departemen Matematika FMIPA USU beserta semua Staf Administrasi di FMIPA USU. Terima kasih yang sebanyak-banyaknya juga penulis tujukan kepada kedua orang tua yang sangat saya cintai dan saya banggakan Bapak JM. Sipayung dan Ibu T. br. Purba atas semua dukungan dalam doa, motivasi, kasih sayang, serta semua dukungan materil dan moril yang membantu penulis dalam menyelesaikan skripsi ini. Juga kepada abang saya Fernando dan adik-adik saya, Lia, Riska dan Kristiani, terima kasih atas dukungan dan doa kalian. Penulis juga mengucapkan terima kasih kepada semuanya teman-teman seperjuangan jurusan Matematika USU stambuk 2006 atas kebersamaan kita selama ini, atas persahabatan dan saling mendukung di antara kita. Terkhusus buat persahabatan penulis dengan Lusi, Marlina dan Nova buat semangat, doa, motivasi dan teguran pada penulis dalam menyelesaikan skripsi ini. Terima kasih juga penulis ucapkan kepada semua teman dan sahabat yang lain yang membantu penyelesaian skripsi ini. Terima kasih atas semua doa dan dukungannya. Kiranya kasih karunia dan kemurahan Tuhan yang menyertai kita semua. Amin.
Penulis,
ABSTRAK
Skripsi ini bertujuan untuk memperlihatkan kegunaan dari modifikasi fungsi keanggotaan kurva-s dalam permasalahan perencanaan persediaan produksi yang terbatas dengan variabel kontinu. Dalam hal ini, parameter-parameter fuzzy dari pemrograman linier dimodelkan dengan fungsi keanggotaan non-linier seperti fungsi kurva-s. Tulisan ini dimulai dengan memperkenalkan dan membangun modifikasi fungsi keanggotaan kurva-s dan menyajikan pembahasan numerik dalam kehidupan nyata dari permasalahan persediaan produksi. Hasil komputasi menunjukkan keunggulan dari funggsi keanggotaan kurva-s dengan teknik program linier fuzzy
vi
APPLICATION OF MULTI OBJECTIVE FUZZY LINEAR PROGRAMMING IN SUPPLY PRODUCTION PLANNING PROBLEM
ABSTRACT
DAFTAR ISI
Daftar Tabel viii
Daftar Gambar ix
Bab 1 Pendahuluan
1.1 Latar Belakang 1
1.2 Identifikasi Masalah 3
1.3 Tinjauan Pustaka 3
1.4 Tujuan Penelitian 4
1.5 Manfaat Penelitian 4
1.6 Metode Penelitian 4
Bab 2 Landasan Teori
2.1 Program Linier (Linear Programming) 5
2.1.1 Karakteristik Pemrograman Linier 5
2.1.2 Formulasi Permasalahan 6
2.1.3 Metode Simpleks 9
2.2 Teori Himpunan Fuzzy 18
2.2.1 Fungsi Keanggotaan Fuzzy 19
2.2.2 Bilangan Fuzzy Triangular 19
2.2.3 Bilangan Fuzzy Trapezoidal 21
2.2.4 Bilangan Fuzzy Kurva-S 22
2.3 Multi Objective Fuzzy Linear Programming 25
Bab 3 Pembahasan
3.1 Fungsi Keanggotaan Logistik 27
3.2 Modifikasi Fungsi Keanggotaan Kurva-S 28
3.3 Parameter Sumber Daya Fuzzy 31
3.4 Pembahasan Numerik 32
Bab 4 Kesimpulan dan Saran
4.1 Kesimpulan 44
4.2 Saran 44
Daftar Pustaka 45
viii
DAFTAR TABEL
Halaman
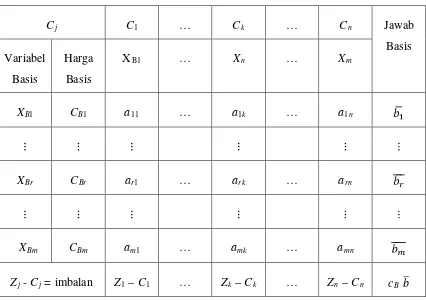
Tabel 2.1 Bentuk Tabel Simpleks 9
Tabel 2.2 Bentuk Awal Tabel Simpleks Sebelum Pivoting 11 Tabel 2.3 Bentuk Awal Tabel Simpleks Sesudah Pivoting 14 Tabel 2.4 Tabel Simpleks untuk Solusi Awal (Iterasi 0) 15 Tabel 2.5 Tabel Simpleks untuk Solusi yang Baru (Iterasi 1) 16 Tabel 2.6 Tabel Simpleks untuk Solusi Akhir (Iterasi 2) 17 Tabel 3.1 Tabel Simpleks untuk Solusi Awal (Kasus 1) 34 Tabel 3.2 Tabel Simpleks untuk Solusi yang Baru (Kasus 1) 34 Tabel 3.3 Tabel Simpleks untuk Solusi Akhir (Kasus 1) 35 Tabel 3.4 Tabel Simpleks untuk Solusi Awal (Kasus 2) 36
Tabel 3.5 Input Data untuk Pendapatan 38
Tabel 3.6 Input Data untuk Polusi 40
Tabel 3.7 Fuzzy Band untuk Total Pendapatan 41
Tabel 3.8 Fuzzy Band untuk Total Polusi 42
DAFTAR GAMBAR
Halaman
Gambar 2.1 Bilangan Fuzzy Triangular 20
Gambar 2.2 Himpunan Fuzzy : Berat (Kurva Triangular) 20
Gambar 2.3 Bilangan Fuzzy Trapezodial 21
Gambar 2.4 Himpunan Fuzzy : Berat (Kurva Trapezodial) 22 Gambar 2.5 Bilangan Fuzzy Kurva-S : PERTUMBUHAN 22 Gambar 2.6 Bilangan Fuzzy Kurva-S : PENYUSUTAN 23
Gambar 2.7 Karakteristik Fungsi Kurva-S 23
Gambar 2.8 Bilangan Fuzzy Kurva-S : TUA 24
Gambar 2.9 Bilangan Fuzzy Kurva-S : MUDA 25
Gambar 3.1 Fungsi Keanggotaan Logistik 27
v
ABSTRAK
Skripsi ini bertujuan untuk memperlihatkan kegunaan dari modifikasi fungsi keanggotaan kurva-s dalam permasalahan perencanaan persediaan produksi yang terbatas dengan variabel kontinu. Dalam hal ini, parameter-parameter fuzzy dari pemrograman linier dimodelkan dengan fungsi keanggotaan non-linier seperti fungsi kurva-s. Tulisan ini dimulai dengan memperkenalkan dan membangun modifikasi fungsi keanggotaan kurva-s dan menyajikan pembahasan numerik dalam kehidupan nyata dari permasalahan persediaan produksi. Hasil komputasi menunjukkan keunggulan dari funggsi keanggotaan kurva-s dengan teknik program linier fuzzy
APPLICATION OF MULTI OBJECTIVE FUZZY LINEAR PROGRAMMING IN SUPPLY PRODUCTION PLANNING PROBLEM
ABSTRACT
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dunia usaha dan pembangunan dalam segala bidang dewasa ini berkembang dengan
sangat pesat. Hal ini merupakan akibat dari berbagai kemajuan yang dicapai umat
manusia dalam berbagai bidang teknologi dan ilmu pengetahuan. Dunia usaha atau
lingkungan pembangunan tidak lain merupakan suatu sistem yang dinamis yang
unsur-unsurnya satu sama lain saling mempengaruhi, saling menunjang dan
terdapatnya hubungan ketergantungan.
Dalam pemrograman matematika, permasalahan dinyatakan sebagai optimasi
beberapa fungsi tujuan yang diberikan kendala tertentu. Sehingga metode
penyelesaian diarahkan pada pemrograman matematika dengan tujuan tunggal seperti
metode simpleks dalam program linier. Dalam menerapkan pemrograman matematika,
pengambil keputusan menyadari bahwa ada permasalahan dalam kehidupan nyata
yang mempertimbangkan multiple objective. Untuk mendatangkan permasalahan yang
multiple objective dengan sebuah model yang dapat diselesaikan oleh metode
penyelesaian program matematika tujuan tunggal, multiple objective harus
dikombinasikan dalam beberapa cara untuk menjadikan satu tujuan tunggal.
Banyak permasalahan dalam operasi riset, ilmu keputusan, teknik dan
managemen sebagian besar telah dipelajari dari sudut pandang optimisasi. Karena
pengambilan keputusan banyak dipengaruhi oleh gangguan-gangguan dari keadaan
sosial dan ekonomi, sehingga pendekatan optimisasi tidak selalu menjadi yang terbaik
(Vasant, 2004). Karena berada di bawah pengaruh yang demikian, banyak masalah
mungkin lebih baik digunakan daripada optimisasi. Dalam hal ini, dapat diterima
bahwa tingkat aspirasi pada masalah yang dibicarakan diselesaikan berdasarkan
pengalaman masa lalu dan pengetahuan yang dimiliki oleh pengambil keputusan,
dalam kasus ini di mana tingkat aspirasi dari seorang pengambil keputusan seharusnya
dipertimbangkan untuk memecahkan masalah dari segi strategi kepuasan. Oleh karena
itu, lebih natural bahwa ketidakjelasan dalam sistem fuzzy dinyatakan sebagai
bilangan fuzzy oleh pengambil keputusan.
Dalam dunia nyata proses pembuatan keputusan dalam teknik dan bisnis, teori
pengambilan keputusan menjadi salah satu bidang yang paling penting. Teori tersebut
tidak hanya yang berhubungan pada kriteria tunggal (single criteria), tapi juga konsep
yang memuaskan dari beberapa kriteria. Proses keputusan dengan beberapa kriteria
berhubungan dengan penilaian manusia. Proses tersebut sulit untuk dimodelkan.
Unsur penilaian manusia berada dalam area preferensi yang didefinisikan pengambil
keputusan. Pertama mencoba memodelkan proses keputusan dengan beberapa kriteria
dalam bisnis dan teknik yang mengarah pada konsep multi obejective linear
programming. Dalam pendekatan ini pengambil keputusan menyokong
masing-masing tujuan dengan sejumlah goal yang harus dipenuhi. Istilah memuaskan
membutuhkan pencarian solusi untuk masalah multi kriteria, yang dipilih, dipahami
dan dilaksanakan dengan percaya diri. Keyakinan bahwa solusi terbaik telah
ditemukan diperkirakan melalui solusi ideal, yakni solusi yang mengoptimalkan
semua kriteria secara simultan. Karena secara praktek tidak tercapai, pengambil
keputusan mempertimbangkan solusi layak terdekat dengan solusi ideal.
Jenis fungsi keanggotaan yang beraneka ragam digunakan dalam program
linier fuzzy dan aplikasinya seperti pada fungsi keanggotaan linier, fungsi keanggotaan
tipe tangent, fungsi keanggotaan interval linier, fungsi keanggotaan logistic, fungsi
keanggotaan linier konkaf. Karena jenis tangent, dari fungsi keanggotaan, fungsi
keanggotaan eksponensial, dan fungsi keanggotaan hiperbolik merupakan fungsi non
linier. Program matematik fuzzy didefinisikan dengan hasil fungsi keanggotaan
non-linier dalam program non-non-linier. Biasanya fungsi keanggotaan non-linier ditugaskan untuk
menghindari ke non-linieran. Namun, ada beberapa kesulitan dalam menyeleksi solusi
masalah yang ditulis dalam fungsi keanggotaan linier. Dengan demikian, dalam
3
kesulitan tersebut. Lebih lanjut, fungsi keanggotaan kurva-S cukup fleksibel
manggambarkan ketidakjelasan dalam parameter fuzzy untuk masalah perencanaan
persediaan produksi.
Dalam tulisan ini, metodologi baru fungsi keanggotaan kurva-S yang
dimodifikasi menggunakan program linier fuzzy dalam perencanaan persediaan
produksi dan aplikasinya pada pengambilan keputusan dilakukan. Terutama program
linier fuzzy didasarkan pada ketidakjelasan dalam parameter fuzzy seperti variabel
sumber daya yang diberikan pembuat keputusan dianalisis.
1.2 Identifikasi Masalah
Permasalahan yang akan dibahas adalah mengenai fungsi keanggotaan kurva-S yang
dimodifikasi menggunakan program linier fuzzy yang diterapkan dalam masalah
perencanaan persediaan produksi.
1.3 Tinjauan Pustaka
Sutapa, Nyoman (2000) dalam jurnalnya menuliskan bahwa dalam pengambilan
keputusan yang dimodelkan dalam program linier, dalam prakteknya sering sulit
dipenuhi karena ada ketidakpastian yang muncul diakibatkan oleh suatu kebijakan.
Untuk memecahkan dan mengakomodasi ketidakpastian, didekati dengan teori
himpunan fuzzy dengan menggunakan fungsi keanggotaan linier.
Vasant (2004) mengatakan bahwa biasanya fungsi keanggotaan linier
digunakan untuk menghindari non-linieritas. Namun demikian, ada beberapa kesulitan
dalam memilih solusi masalah yang ditulis dalam fungsi keanggotaan linier.
Perhatian perencanaan dan pengendalian produksi telah banyak dilakukan.
Vasant (2003, 2006) program linier fuzzy yang diaplikasikan pada perencanaan
produksi menggunakan fungsi keanggotaan non-linier bentuk kurva-S yang
Hadiguna (2008) dalam jurnalnya menuliskan bahwa jika dibandingkan
dengan fungsi keanggotaan lainnya seperti segitiga (triangular) yang sering digunakan
dalam program linier, maka tipe S yang dimodifikasi dapat memudahkan proses
perhitungan. Selain itu, fungsi ini tidak kaku dalam mengakomodasi preferensi
pengambil keputusan dalam menilai kondisi yang tidak tegas.
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah menetapkan kegunaan fungsi keanggotaan kurva-S
yang dimodifikasi dalam masalah perencanaan persediaan produksi yang terbatas
dengan variabel kontinu.
1.5 Manfaat Penelitian
Penelitian ini dapat digunakan sebagai bahan referensi yang dapat mempermudahkan
dalam menentukan kondisi yang tidak tegas dalam proses pengambilan keputusan.
Terkhusus dalam permasalahan perencanaan persediaan produksi.
1.6 Metodologi Penelitian
Metode penelitian yang digunakan dalam penelitian ini adalah :
1. Sebagai langkah awal akan dibicarakan tentang fungsi keanggotaan kurva-S
yang dimodifikasi yang akan digunakan dalam tulisan ini. Selanjutnya, akan
dimodelkan parameter-parameter fuzzy dalam program linier.
2. Mengerjakan contoh permasalahan program linier fuzzy.
BAB 2
LANDASAN TEORI
2.1 Program linier (Linier Programming)
Pemrograman linier merupakan metode matematik dalam mengalokasikan
sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan
keuntungan dan meminimumkan biaya. Program linier banyak diterapkan dalam
masalah ekonomi, industri, militer, sosial dan lain-lain. Program linier berkaitan
dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu model matematik
yang terdiri dari sebuah fungsi tujuan linier dengan beberapa kendala linier.
2.1.1 Karakteristik Pemrograman Linier
Adapun karakteristik pemrograman linier adalah sebagai berikut (Siringo-ringo,
2005) :
Sifat linearitas suatu kasus dapat ditentukan dengan menggunakan beberapa
cara. Secara statistik, dapat memeriksa kelinearan menggunakan grafik (diagram
pencar) ataupun menggunakan uji hipotesa. Secara teknis, linearitas ditujukan oleh
adanya sifat proporsionalitas, additivitas, divisibilitas dan kepastian fungsi tujuan dan
pembatas.
Sifat proporsional dipenuhi jika kontribusi setiap variabel pada fungsi tujuan
atau penggunaan sumber daya yang membatasi proporsional terhadap level nilai
variabel. Jika harga per unit produk misalnya adalah sama berapapun jumlah yang
dibeli, maka sifat proporsianal dipenuhi. Atau dengan kata lain, jika pembelian dalam
penggunaan sumber daya per unitnya tergantung dari jumlah yang diproduksi, maka
sifat proporsionalitas tidak dipenuhi.
Sifat additivitas mengasumsikan bahwa tidak ada bentuk perkalian silang
diantara berbagai aktivitas, sehingga tidak akan ditemukan bentuk perkalian silang
pada model. Sifat additivitas berlaku baik bagi fungsi tujuan maupun pembatas
(kendala). Sifat additivitas dipenuhi jika fungsi tujuan merupakan penambahan
langsung kontribusi masing-masing variabel keputusan. Untuk fungsi kendala, sifat
additivitas dipenuhi jika nilai kanan merupakan total penggunaan masing-masing
variabel keputusan. Jika dua variabel keputusan misalnya merepresentasikan dua
produk subsitusi, di mana peningkatan volume penjualan salah satu produk akan
mengurangi volume penjualan produk lainnya dalam pasar yang sama, maka sifat
additivitas tidak dipenuhi. Sifat divisibilitas berarti unit aktivitas dapat dibagi ke
dalam sembarang level fraksional, sehingga nilai variabel keputusan non integer
dimungkinkan.
Sifat kepastian menunjukkan bahwa semua parameter model berupa konstanta.
Artinya koefisien fungsi tujuan maupun fungsi pembatas merupakan suatu nilai pasti,
bukan merupakan nilai peluang tertentu.
2.1.2 Formulasi Permasalahan
Agar dapat menyusun dan merumuskan suatu persoalan atau permasalahan yang
dihadapi ke dalam model program linier, maka dimintakan lima syarat yang harus
dipenuhi sebagai berikut ini (Nasendi, 1984) :
a. Tujuan
Apa yang menjadi tujuan permasalahan yang dihadapi yang ingin dipecahkan
dan dicari jalan keluarnya. Tujuan ini harus jelas dan tegas yang disebut fungsi
tujuan. Fungsi tujuan tersebut dapat berupa dampak positif, manfaat-manfaat,
keuntungan-keuntungan, dan kebaikan-kebaikan yang ingin dimaksimumkan,
atau dampak negatif, kerugian-kerugian risiko-risiko, biaya-biaya, jarak,
7
b. Alternatif Perbandingan
Harus ada sesuatu atau berbagai alternatif yang ingin diperbandingkan;
misalnya antara kombinasi waktu tercepat dan biaya tertinggi dengan waktu
terlambat dan biaya terendah; atau antara alternatif terpadat modal dengan
padat karya; atau antara kebijakan A dengan B; atau antara proyeksi
permintaan tinggi dengan rendah; dan seterusnya.
c. Sumber daya
Sumber daya yang dianalisis harus berada dalam keadaan yang terbatas.
Misalnya, keterbatasan waktu, keterbatasan biaya, keterbatasan tenaga,
keterbatasan luas tanah, keterbatasan ruangan, dan lain-lain. Keterbatasan
dalam sumber daya tersebut dinamakan sebagai kendala atau syarat ikatan.
d. Perumusan kuantitatif
Fungsi tujuan dan kendala tersebut harus dapat dirumuskan secara kuantitatif
dalam apa yang disebut model matematika.
e. Keterkaitan peubah
Peubah-peubah yang membentuk fungsi tujuan dan kendala tersebut harus
memiliki hubungan fungsional atau hubungan keterkaitan. Hubungan
keterkaitan tersebut dapat diartikan sebagai hubungan yang saling
mempengaruhi, hubungan interaksi, interdependensi, timbal-balik, saling
menunjang, dan sebagainya.
Bentuk umum pemrograman linier adalah sebagai berikut :
Funsi tujuan :
Maksimumkan atau minimumkan z = c1x1 + c2x2 + … + cnxn
Sumber daya yang membatasi :
am1x1 + am2x2 + … + amnxn = / ≤ / ≥ bm
x
1, x2, …, xn
Bentuk di atas juga dapat ditulis sebagai berikut :
≥ 0 (2.3)
Fungsi tujuan :
Maksimum dan minimumkan :
Kendala :
Dan xj
Simbol x
≥ 0 , j = 1, 2, …, n (2.6)
1, x2, …, xn menunjukkan variabel keputusan. Jumlah variabel
keputusan oleh karenanya tergantung dari jumlah kegiatan atau aktivitas yang
dilakukan untuk mencapai tujuan. Simbol c1, c2, …, cn merupakan kontribusi
masing-masing variabel keputusan terhadap tujuan, disebut juga koefisien fungsi tujuan pada
model matematiknya. Simbol a11, ..., a1n, ...,amn merupakan penggunaan per unit
variabel keputusan akan sumber daya yang membatasi, atau disebut juga sebagai
koefisien fungsi kendala pada model matematiknya. Simbol b1, b2, …, bn
Pertidaksamaan terakhir (x
menunjukkan jumlah masing-masing sumber daya yang ada. Jumlah fungsi kendala
akan tergantung dari banyaknya sumber daya yang terbatas.
1, x2, …, xn ≥ 0) menunjukkan batasan non negatif.
Membuat model matematik dari suatu permasalahan bukan hanya menuntut
kemampuan metematik tapi juga menuntut seni pemodelan. Menggunakan seni akan
9
2.1.3 Metode Simpleks
Apabila suatu masalah linear programming hanya mengandung dua kegiatan
(variabel-variabel keputusan) saja, maka dapat diselesaikan dengan metode grafik.
Bila terdapat lebih dari dua variabel maka metode grafik tidak dapat digunakan lagi,
sehingga diperlukan metode simpleks. Metode ini lazim dipakai untuk menentukan
kombinasi dari tiga variabel atau lebih.
Masalah program linier yang melibatkan banyak variabel keputusan dapat
dengan cepat dipecahkan dengan bantuan komputer. Bila variabel keputusan yang
dikandung tidak terlalu banyak, masalah tersebut dapat diselesaikan dengan suatu
algoritma yang biasanya sering disebut metode tabel simpleks. Disebut demikian
karena kombinasi variabel keputusan yang optimal dicari dengan menggunakan
tabel-tabel.
Tabel 2.1 Bentuk Tabel Simpleks
Cj C1 … Ck … C Jawab
Basis
n
Variabel
Basis
Harga
Basis
XB1 … Xn … Xm
XB1 CB1 a11 … a1k … a1n
XBr CBr ar1 … ark … arn
XBm CBm am1 … amk … amn
Sebelum menyelesaikan suatu tabel simpleks terlebih dahulu menginisialisasikan dan
merumuskan suatu persoalan keputusan ke dalam model matematik persamaan linier,
caranya sebagai berikut :
1. Konversikan semua ketidaksamaan menjadi persamaan
Agar persamaan garis batasan memenuhi persyaratan penyelesaian pada daerah
kelayakan (feasible) maka untuk model program linier diubah menjadi suatu model
yang sama dengan menambahkan variabel slack, surplus dan variabel buatan
(artificial variable) pada tiap batasan (constraint) serta memberi harga nol pada setiap
koefisien c-nya. Batasan dapat dimodifikasi sebagai berikut :
1) Untuk batasan bernotasi (≤) dapat dimodifikasi kepada bentuk persa maan
dengan menambahkan variabel slack ke dalamnya.
2) Untuk batasan bernotasi (≥) dapat dimodifikasi kepada bentuk persamaan
dengan mengurangi variabel surplus dan kemudian menambahkan variabel
buatan (artificial variable) ke dalamnya.
3) Untuk batasan bernotasi (=) diselesaikan dengan menambahkan variabel
buatan (artificial variable) ke dalamnya.
Dengan penambahan variabel buatan ini akan merusak sistem batasan, hal ini
dapat diatasi dengan membuat suatu bilangan besar M sebagai harga dari variabel
dengan buatan tersebut dalam fungsi tujuan. Jika persoalan maksimasi maka dibuat –
M sebagai harga, dan jika persoalan minimal dibuat +M sebagai harga dari variabel
buatan. Cara pendekatan ini dikenal dengan metode M besar (Big M Method).
Penambahan variabel slack dan variabel buatan (artificial variable) pada tiap batasan
(constraint) untuk persoalan maksimal dapat dirumuskan sebagai berikut :
Maksimalkan :
11
0, 0, 0, 0 untuk semua harga i dan j
= 0, j = 1, 2, ..., n
= , i = 1, 2, ..., m
= , i = m
1
1
2. Menyusun persamaan-persamaan di dalam tabel awal simpleks.
+ 1, ..., m
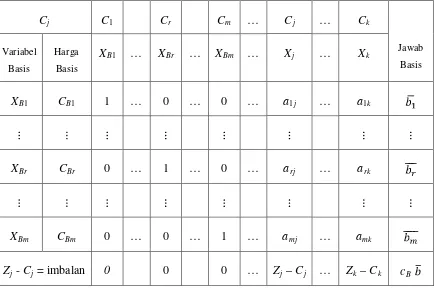
Tabel 2.2 Bentuk Awal Tabel Simpleks Sebelum Pivoting
Cj C1 Cr Cm … Cj … Ck
Jawab
Basis Variabel
Basis
Harga
Basis
XB1 … XBr … XBm … Xj … Xk
XB1 CB1 1 … 0 … 0 … a1j … a1k
XBr CBr 0 … 1 … 0 … arj … ark
XBm CBm 0 … 0 … 1 … amj … amk
Langkah-langkah yang digunakan untuk menyelesaikan suatu tabel simpleks
adalah sebagai berikut :
Langkah 1 : Mengecek nilai optimal imbalan.
Untuk persoalan maksimal : zj – cj = minimal { zj – cj : j R }. Jika zk – ck
0 maka selesai, berarti jawab atau solusi sudah optimal. Untuk persoalan minimal zj –
cj = minimal { zj – cj : j R }. Jika zk – ck
Harga-harga imbalan (z
0 maka selesai, berarti jawab atau solusi
sudah optimal.
j – cj
Untuk : c
) dapat diperoleh dengan rumus :
j
a
= Harga dari semua variabel dalam z.
ij
c
= Koefisien dari semua variabel dalam sistem batasan.
Bi = Harga dari variabel basis.
Langkah 2 : Menentukan variabel yang akan masuk dalam basis.
Untuk persoalan maksimalkan jika terdapat beberapa zj – cj 0 maka kolom
yang menjadi kolom pivot adalah kolom dengan zj – cj terkecil, dan variabel yang
sehubungan dengan kolom pivot adalah variabel yang akan masuk ke dalam basis.
Untuk persoalan minimal jika terdapat beberapa zj – cj 0 maka kolom yang menjadi
kolom pivot adalah kolom dengan zj – cj
Jika pada baris z
terbesar, dan variabel yang sehubungan
dengan kolom pivot adalah variabel yang masuk dalam basis.
j – cj terdapat lebih dari satu kolom yang mempunyai nilai
negatif yang angkanya terbesar dan sama pada persoalan maksimal atau terdapat lebih
dari satu kolom yang mempunyai nilai positif terbesar dan sama pada persoalan
minimal maka terdapat dua kolom yang bisa terpilih menjadi kolom pivot. Untuk
13
Langkah 3 : Menentukan variabel yang akan keluar dari basis.
Menetapkan variabel yang keluar dari basis yaitu : = minimum
variabel yang sehubungan dengan baris pivot yang demikian adalah variabel yang
keluar dari basis. Jika terdapat dua baris atau lebih nilai maka ada beberapa baris
yang dapat terpilih sebagai baris pivot. Dapat dipilih baris pivot secara bebas di antara
keduanya dan hasilnya akan sama.
Langkah 4 : Menyusun tabel simpleks baru.
Untuk menyusun tabel simpleks yang baru, maka harus mencari koefisien
elemen pivot dari tabel simpleks sebelumnya. Koefisien elemen pivot dapat dicari
dengan menghubungkan kolom pivot dengan baris pivot sedemikian rupa sehingga
titik potong kedua pivot ini menunjukkan koefisien, yang disebut elemen pivot.
Koefisien-koefisien baris pivot baru dapat dicari dengan menggunakan rumus
sebagai berikut : (2.12)
Untuk menghitung nilai baris baru lainnya dilakukan dengan menggunakan
rumus sebagai berikut : - (2.13)
Langkah 5 : Mengecek nilai optimal imbalan dari tabel simpleks yang baru.
Jika imbalan sudah optimal maka tafsirkan hasil penyelesaian, jika belum
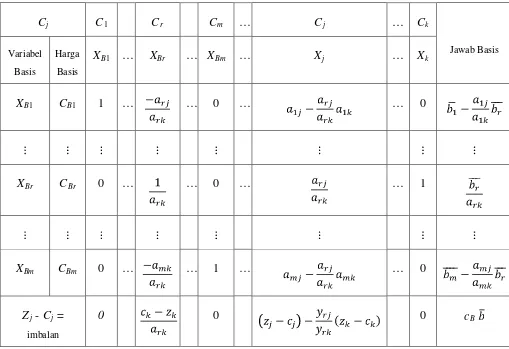
Tabel 2.3 Bentuk Awal Tabel Simpleks Sesudah Pivoting
Agar persamaan di atas memenuhi persyaratan penyelesaian dalam daerah kelayakan
(feasible), maka pada sisi kiri persamaan batasan ditambahkan variabel slack.
15
Model di atas dapat dibawa ke dalam tabel simpleks sebagai berikut : 0
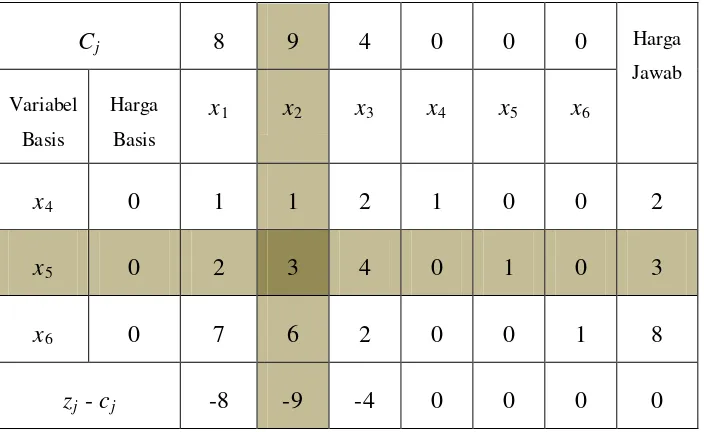
Tabel 2.4 Tabel Simpleks untuk Solusi Awal (Iterasi 0)
Cj 8 9 4 0 0 0 Harga
Dari tabel 2.4, tampak bahwa penyelesaian opitimal belum dicapai di mana harga zj –
cj terkecil dari tabel 2.4 adalah -9, sehingga variabel yang masuk basis adalah variabel
x2. Kolom variabel x2
I
menjadi kolom pivot dan perhitungan untuk indeks (I) adalah :
min
Diperoleh I =
min = 1, maka variabel yang akan meninggalkan basis adalah variabel x5
kemudian digantikan dengan variabel x2. Angka kunci (elemen pivot) yang diperoleh
Tabel 2.5 Tabel Simpleks untuk Solusi yang Baru (Iterasi 1)
Cj 8 9 4 0 0 0 Harga
Jawab
Variabel
Basis
Harga
Basis
x1 x2 x3 x4 x5 x6
x4 0 0 1 0 1
x2 9 1 0 0 1
x6 0 3 0 -6 0 -2 1 2
zj - cj -2 0 8 0 3 0 9
Dari tabel 2.5 tampak bahwa penyelesaian optimal belum tercapai di mana harga zj –
cj terkecil dari tabel di atas adalah -2, sehingga variabel yang masuk basis adalah
variabel x1. Kolom variabel x1 menjadi kolom pivot dan perhitungan untuk indeks (I)
adalah : Imin
Diperoleh I
=
min = 0,67 maka variabel yang akan meninggalkan basis adalah variabel x6
kemudian digantikan oleh variabel x1. Angka kunci (elemen pivot) yang diperoleh =
17
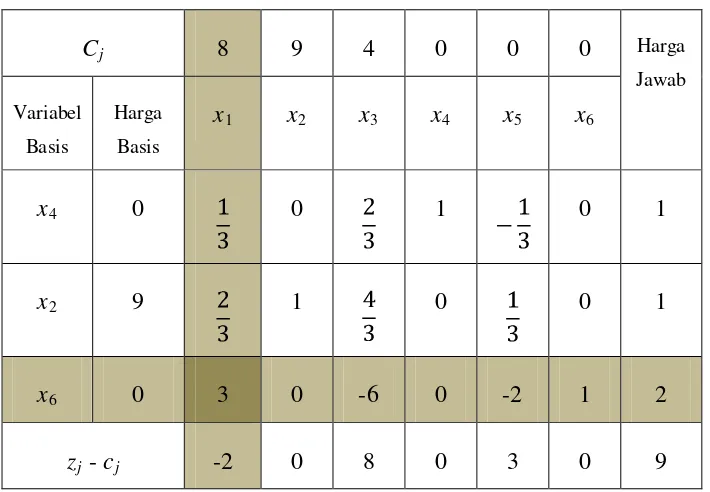
Tabel 2.6 Tabel Simpleks untuk Solusi Akhir (Iterasi 2)
Dari tabel 2.6 tidak ada lagi zj – cj
x
< 0, dengan demikian telah dicapai penyelesaian
optimal yaitu :
1
x
= = 0,67
2
x
= = 0,56
3
Z = 8 + 9 4(0) = 8(0,67) + 9(0,56) = 5,36 + 5,04 = 10,04 = 0
Cj 8 9 4 0 0 0 Harga
Jawab
Variabel
Basis
Harga
Basis
x1 x2 x3 x4 x5 x6
x4 0 0 1
x2 9 1 0
x1 8 1 0 -2 0
2.2 Teori Himpunan Fuzzy
Himpunan A dikatakan crisp jika sebarang anggota-anggota yang ada pada
himpunan A tersebut dikenakan suatu fungsi, akan bernilai 1 yakni jika a A maka
fungsi a = 1. Namun jika a A, maka nilai fungsi yang dikenakan pada a adalah 0.
Nilai fungsi yang dikenakan pada sebarang anggota himpunan A dikatakan sebagai
nilai keanggotaan. Jadi pada himpunan crisp, hanya mempunyai 2 nilai keanggotaan
yaitu 0 dan 1. Tetapi pada himpunan fuzzy, nilai keanggotaan dari
anggota-anggotanya tidak hanya 0 dan 1 saja. Tapi berada pada interval tertutup [0,1]. Dengan
kata lain himpunan A dikatakan fuzzy selama fungsi : A [0,1].
Misalkan diketahui klasifikasi harga dari sebuah barang sebagai berikut :
MURAH harga < 35.000
STANDARD 35.000 harga 55.000
MAHAL harga > 55.000
Dengan menggunakan pendekatan crisp, amatlah tidak adil untuk menetapkan
harga STANDARD. Pendekatan ini bisa saja dilakukan untuk hal-hal yang bersifat
diskontinu. Misalkan klasifikasi untuk harga 55.000 dan 56.000 sangat jauh berbeda,
harga 55.000 termasuk STANDARD, sedangkan harga 56.000 sudah termasuk
MAHAL. Demikian pula untuk kategori MURAH dan MAHAL. Barang yang seharga
34.000 dikatakan MURAH, sedangkan barang yang berharga 35.000 sudah TIDAK
MURAH lagi. Barang yang berharga 55.000 termasuk STANDARD, barang yang
berharga 55.000 lebih 1 rupiah sudah TIDAK STANDARD lagi. Dengan demikian
pendekatan crisp ini sangat tidak cocok diterapkan pada hal-hal yang bersifat kontinu,
missal harga barang. Selain itu, untuk menunjukkan suatu harga pasti termasuk
STANDARD atau tidak termasuk STANDARD, dan menunjukkan suatu nilai
kebenaran 0 dan 1, dapat digunakan nilai pecahan, dan menunjukkan 1 atau nilai yang
dekat 1 untuk harga 45.000, kemudian pecahan menurun menuju ke 0 untuk harga di
bawah 35.000 dan di atas 55.000.
Terkadang kemiripan antara keanggotaan fuzzy dengan probabilitas
19
nilainya sangat berbeda. Keanggotaan fuzzy memberikan suatu ukuran terhadap
pendapat atau keputusan, sedangkan probabilitas mengindikasikan proporsi terhadap
keseringan suatu hasil bernilai besar dalam jangka panjang. (Kusumadewi, 2004)
2.3.1 Fungsi Keanggotaan Fuzzy
Sebuah himpunan fuzzy A dari bilangan riil didefinisikan oleh fungsi keanggotaan
(dinotasikan oleh A)
: [ 0,1 ]
Jika x maka (x) dikatakan sebagai derajat keanggotaan x dalam A. Himpunan
fuzzy dalam disebut normal jika terdapat x sehingga (x) = 1. Himpunan fuzzy
A adalah himpunan fuzzy dari bilangan riil dengan normal, (fuzzy) convex dan fungsi
keanggotaan yang kontinu dari penyokong yang terbatas.
2.3.2 Bilangan Fuzzy Triangular
Sebuah himpunan fuzzy A disebut bilangan fuzzy triangular dengan nilai tengah
a, sebelah kiri > 0, dalam disebut konvex jika A adalah unimodal (sebagai sebuah
fungsi). Bilangan fuzzy dan sebelah kanan > 0.
Fungsi keanggotaannya adalah sebagai berikut :
(2.14)
Penyokong A adalah . Bilangan fuzzy triangular dengan nilai tengah a
dilihat sebagai nilai kwantitas fuzzy. “ x dekat terhadap a “atau” x hampir sama dengan
1
x
Gambar 2.1 Bilangan Fuzzy Triangular
Contoh 2.2 :
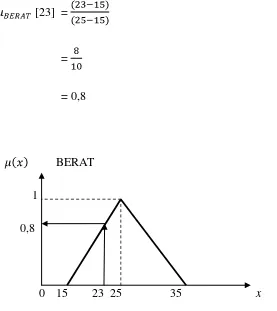
Fungsi keanggotaan triangular untuk himpunan BERAT pada variabel berat
badan (kg) seperti terlihat pada gambar 2.2.
[23] =
=
= 0,8
BERAT
1
0,8
0 15 23 25 35 x
21
2.1.3. Bilangan Fuzzy Trapezoidal
Sebuah himpunan fuzzy A disebut bilangan fuzzy trapezoidal dengan interval
toleransi [a,b], sebelah kiri dan kanan . Fungsi keanggotaannya adalah sebagai
berikut :
(2.15)
Penyokong A adalah . Bilangan fuzzy trapezoidal dapat dilihat sebagai
nilai kwantitas fuzzy. “ x mendekati pada interval [a,b] ”.
1
x
a b
Gambar 2.3 Bilangan Fuzzy Trapezoidal
Contoh 2.3 :
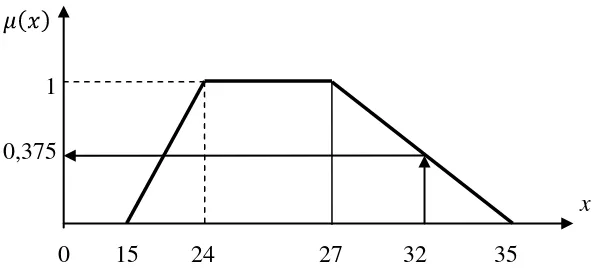
Fungsi keanggotaan trapezodial untuk himpunan BERAT pada variabel berat
badan (kg) terlihat pada gambar 2.4.
[32] =
=
1
0,375
x
0 15 24 27 32 35
Gambar 2.4 Himpunan Fuzzy : BERAT (Kurva Trapezoidal)
2.1.4. Bilangan Fuzzy Kurva-S
Kurva PERTUMBUHAN dan PENYUSUTAN merupakan kurva-S atau
sigmoid yang berhubungan dengan kenaikan dan penurunan permukaan secara tak
linier.
Kurva-S untuk PERTUMBUHAN akan bergerak dari sisi paling kiri (nilai
keanggotaan = 0) ke sisi paling kanan (nilai keanggotaan = 1). Fungsi keanggotaannya
akan bertumpu pada 50% nilai keanggotaannya yang sering disebut dengan titik
infleksi (gambar 2.5).
Gambar 2.5 Bilangan Fuzzy Kurva-S : PERTUMBUHAN
1
0
1 domain 2
Derajat keanggotaan
23
Kurva-S untuk PENYUSUTAN akan bergerak dari sisi paling kanan (nilai
keanggotaan = 1) ke sisi paling kiri (nilai keanggotaan = 0) seperti terlihat pada
gambar 2.6.
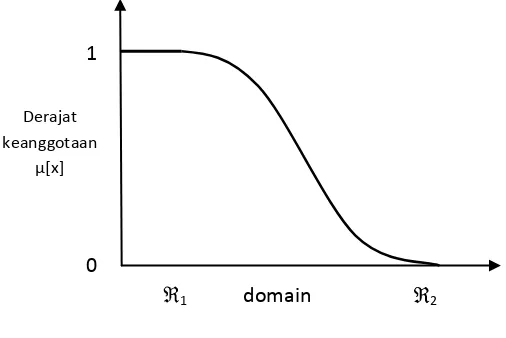
Gambar 2.6 Bilangan Fuzzy Kurva-S : PENYUSUTAN
Kurva-S didefinisikan dengan menggunakan 3 parameter, yaitu : nilai
keanggotaan nol ( ), nilai keanggotaan ( ), dan titik infleksi atau crossover ( ) yaitu
titik yang memiliki domain 50% benar. Gambar 2.7 menunjukkan karakteristik
kurva-S dalam bentuk skema.
Gambar 2.7 Karakteristik Fungsi Kurva-S
Fungsi keanggotaan pada kurva PERTUMBUHAN adalah :
Contoh 2.4 :
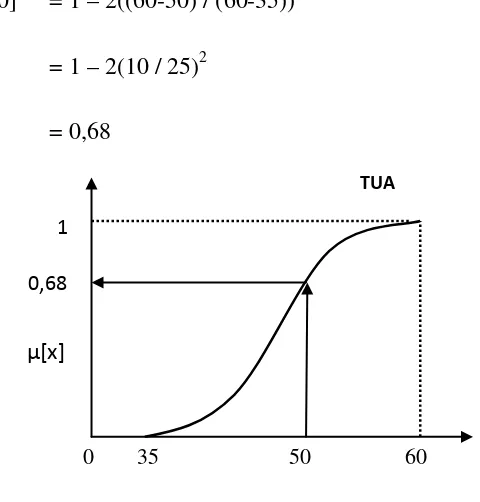
Fungsi keanggotaan untuk himpunan TUA pada variabel umur seperti terlihat pada
gambar 2.7.
[50] = 1 – 2((60-50) / (60-35))
= 1 – 2(10 / 25)
2
= 0,68
2
0 35 50 60
Gambar 2.8 Bilangan Fuzzy Kurva-S : TUA
Sedangkan fungsi keanggotaan pada kurva PENYUSUTAN adalah : µ[x]
1 0,68
Umur (tahun)
25
Contoh 2.5 :
Fungsi keanggotaan untuk himpunan MUDA pada variabel umur seperti terlihat pada
gambar 2.8.
[50] = 2((50-37) / (50-20))
= 2(13 / 30)
2
= 0,376
2
0 20 37 50
Gambar 2.9 Bilangan Fuzzy Kurva-S : MUDA
2.3 Multi Objective Fuzzy Linear Programming
Multi objective linear programming adalah metode optimasi dengan beberapa fungsi
tujuan yang tunduk pada beberapa batasan. Solusi permasalahan ini diperoleh seperti
penyelesaian optimasi dengan 1 fungsi tujuan.
Selama ini ada 2 cara untuk menyelesaikan multi objective linear
programming, yaitu :
1. Metode penjualan terbobot
Misalkan untuk permasalahan :
Umur (tahun) 1
Max f1
Max f ;
2
… ;
Max fn
Dikombinasikan menjadi : .
Max : w1f1 + w2f2 + … + wnfn.
2. Lexicographics ordering method.
Pertama kali obyek-obyek diurutkan berdasarkan pentingnya. Obyek pertama
diselesaikan sebagai :
F1 = max {f1
Kemudian, untuk setiap i > 1 diselesaikan F
(x) dengan batasan yang telah diberikan}
i = max {fi(x), fk(x) = Fk
Metode lain yang dapat digunakan adalah dengan menggunakan Himpunan
Fuzzy. Dengan menggunakan metode ini, tidak perlu menggunakan kalibrasi bobot
atau melakukan seleksi terhadap derajat pentingnya objek. Metode ini hanya
menggunakan preferensi (pilihan) khusus pada tujuan yang dapat dimodelkan dengan
menggunakan fungsi-fungsi keanggotaan fuzzy.
untuk i =
1, 2, …,i-1}. Metode ini akan cocok jika sebelumnya telah diketahui derajat
BAB 3
PEMBAHASAN
3.1 Fungsi Keanggotaan Logistik
Fungsi keanggotaan logistik untuk masalah Fuzzy Linear Programming didefinisikan
sebagai :
Dimana f(x) merupakan derajat fungsi keanggotaan dari nilai spesifik parameter x,
yaitu 0 < f(x) < 1. Parameter x dipertimbangkan menjadi anggota dari bilangan fuzzy,
xL dan xU merupakan batas bawah dan batas atas dari parameter fuzzy x. B dan C
merupakan konstanta dan parameter > 0 menentukan bentuk dari fungsi
keanggotaan. Gambar 3.1 menunjukkan bentuk dari fungsi keanggotaan logistik.
Gambar 3.1 Fungsi Keanggotaan Logistik
3.2 Modifikasi Fungsi Keanggotaan Kurva-S
Modifikasi fungsi keanggotaan kurva-S adalah sebuah kasus yang khusus dari fungsi
logistik dengan nilai spesifik B, C dan α. Nilai-nilai ini harus ditemukan. Fungsi
logistik seperti yang diberikan oleh persamaan (1) dan digambarkan dalam Gambar 1
ditunjukan sebagai fungsi keanggotaan bentuk-S oleh Zadeh (1971).
Disini didefinisikan, modifikasi fungsi keanggotaan kurva-S sebagai berikut :
= (3.2)
Di mana µ adalah derajat fungsi keanggotaan. Notasi α menentukan bentuk dari
fungsi keanggotaan , di mana α > 0. Semakin besar parameter α, semakin
berkurang kekaburan terjadi.
Gambar 3.1 menunjukkan modifikasi kurva-S. Fungsi keanggotaan ini
didefinisikan ulang sebagai 0.001 ≤ . Rentang ini dipilih karena dalam
pasokan produksi pendapatan dan polusi tidak perlu selalu 100% dari kebutuhan. Pada
saat yang sama total pendapatan dan total polusi tidak akan 0%. Oleh karena itu,
dianjurkan ada rentang antara dan sebagai 0.001 ≤ . Konsep ini
29
Gambar 3.2 Modifikasi Fungsi Keanggotaan Kurva-S
Akan diskalakan ulang sumbu x pada xa = 0 dan xb
Nilai B, C dan diperoleh dari persamaan (3.2) seperti :
= 1 untuk mencari nilai dari B, C
dan :
B = 0.999 (1 + C) (3.3)
= 0.001 (3.4)
Dengan mensubsitusikan persamaan (3.3) ke persamaan (3.4) diperoleh :
= 0.001 (3.5)
Dari persamaan (3.5) didapat :
α = ln (3.6)
Karena nilai B dan bergantung pada C, maka dibutuhkan satu kondisi untuk
mendapatkan nilai B, C dan .
= 2 (3.7)
Diperoleh :
= 2 ln
(3.8)
Subsitusi persamaan (3.6) dan persamaan (3.7) ke dalam persamaan (3.8), diperoleh :
2 ln = ln (3.9)
(0.998 + 1.998C)2
C =
(3.11)
= C(998 + 999C) (3.10)
C = 0.001001001
Dalam hal ini nilai C harus positip, jadi dari persamaan (3.11) diperoleh nilai C =
0,001001001 dan dari persamaan (3.3) dan (3.6), B = 1 dan α = 13,81350956.
Modifikasi fungsi keanggotaan kurva-S ini mempunyai bentuk yang mirip
dengan fungsi logistik dan merupakan bagian dari fungsi tangent hyperbolic. Tetapi
fungsi ini lebih mudah diatasi dari pada tangent hyperbola. Dan lagi, fungsi
keanggotaan trapezodial dan triangular merupakan penaksiran dari fungsi logistik
(Vasant, 2004). Oleh karena itu, fungsi-S ini dipertimbangkan yang lebih tepat untuk
menunjukkan level tujuan yang samar yang mana seorang pembuat keputusan
mempertimbangkan pelaksanaan solusinya. Selanjutnya, hal ini juga dapat
dimungkinkan bahwa modifikasi fungsi keanggotaan kurva-S berganti bentuknya
berdasarkan dari nilai-nilai parameternya. Maka seorang pembuat keputusan dapat
mampu menyalurkan strateginya pada perencanaan persediaan produksi yang fuzzy
menggunakan parameter-parameter ini. Karena itu, modifikasi fungsi keanggotaan
31
3.3 Parameter Sumber Daya Fuzzy
Dalam hal ini, pertama akan diambil persamaan dari parameter sumber daya fuzzy.
Persamaan ini yang akan digunakan untuk menghasilkan nilai fuzzy dari parameter
yang maksudkan.
Fuzzy Resource Parameter .
Dari persamaan (3.1), pada interval ,
Maka diperoleh :
Karena adalah variabel sumber daya yang fuzzy pada persamaan (3.12),
maka disimbolkan i
Fungsi keanggotaan dari serta interval fuzzy, ke dari diberikan
3.4 Contoh Numerik
Permasalahan Perencanaan Persediaan Produksi terbatas dengan variabel kontinu yang
dinyatakan seperti :
Sebuah Perusahaan memiliki sebuah pabrik, yang menghasilkan 3 Produk.
1. Untuk menghasilkan 1 unit Produk I, dibutuhkan 2 kg M1, 3 kg M2, dan 4 kg
M3
2. Untuk menghasilkan 1 unit Produk II, dibutuhkan 8 kg M .
1, dan 1 kg M2
3. Untuk menghasilkan 1 unit Produk III, dibutuhkan 4 kg M
.
1, 4 kg M2, dan 2 kg
M3
Banyaknya bahan baku yang tersedia adalah material M .
1 sebanyak 100 kg, material
M2 sebanyak 50 kg, dan material M3
Konstribusi keuntungan Produk I sebesar $5/unit, Produk II sebesar $10/unit, Produk
III sebesar $12/unit. Namun selama proses produksi, 1 unit produk I menghasilkan 1
satuan polusi, 1 unit produk II menghasilkan 2 satuan polusi, dan 1 unit produk III
menghasilkan 2 satuan polusi. Tujuan Perusahaan adalah ingin memaksimalkan
pendapatan sekaligus meminimalkan total polusi berbahaya yang dihasilkan. sebanyak 50 kg.
= jumlah Produk II yang dibuat;
3
Permasalahan ini dapat diekspresikan sebagai multi-objective linear
programming, sebagai berikut :
= jumlah Produk III yang dibuat;
33
Penyelesaian :
Apabila diselesaikan satu per satu :
Maksimumkan : Z
Dengan bantuan slack variabel, maka persamaan dapat ditulis menjadi :
Tabel 3.1 Tabel Simpleks untuk Solusi Awal (Kasus 1)
min = 12,5, maka variabel yang akan meninggalkan basis adalah variabel x5
kemudian digantikan dengan variabel x3. Angka kunci (elemen pivot) yang diperoleh
= 4, maka tabel simpleks yang baru adalah :
Table 3.2 Tabel Simpleks untuk Solusi yang Baru (Kasus 1)
35
Imin
Diperoleh I =
min = 7,1, maka variabel yang akan meninggalkan basis adalah variabel x4
kemudian digantikan dengan variabel x2
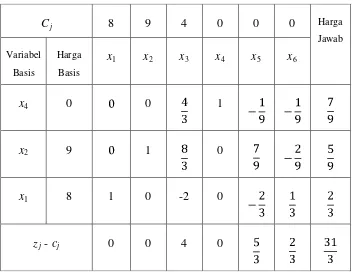
Tabel 3.3 Tabel Simpleks untuk Solusi Akhir (Kasus 1)
. Angka kunci (elemen pivot) yang diperoleh
= 7, maka tabel simpleks yang baru adalah :
Cj 5 10 12 0 0 0 Harga
< 0, dengan demikian telah dicapai penyelesaian
Dengan batasan :
Dengan bantuan slack variabel, maka persamaan dapat ditulis menjadi :
Maksimumkan : Z0 = x1 + 2x2 + 2x3 + 0x4 + 0x5 + 0x
Tabel 3.4 Tabel Simpleks untuk Solusi Awal (Kasus 2)
37
Dari tabel dapat dilihat tidak ada zj – cj
x
≥ 0, dengan demikian diperoleh penyelesaian
optimal yaitu :
Pada kasus 1 diperoleh penghasilan maksimum $200, namun disisi lain juga
menghasilkan 35,71 satuan polusi. Pada kasus 2 polusi yang diperoleh 0 satuan polusi,
namun hal itu juga menunjukkan $0 pendapatan. = 0
Seperti yang diketahui, kedua tujuan ini saling bertolak belakang satu sama
lain. Disaat memaksimumkan pendapatan, polusi meningkat. Disaat meminimumkan
polusi, pendapatanpun minim. Untuk menunjukkan sebuah solusi yang
dikompromikan yang berkenaan pada kekaburan dan derajat kepuasan, perusahaan
memberikan kebijakan sebagai berikut :
Goal 1 : Harus menahan paling sedikit 75% dari pendapatan maksimum ($150).
Goal 2 : Harus tidak melebihi 30 satuan polusi untuk total polusi, tetapi lebih baik lagi
jika tidak menimbulkan polusi sama sekali.
Goal 3 : Rentang dari total pendapatan dan total polusi berbahaya harus minim.
Rentang ini disebut sebagai fuzzy band.
Dua tujuan pertama akan dimodelkan ke dalam fuzzy linear programming dan
modifikasi fungsi keanggotaan kurva-S.
Model fuzzy linear programming untuk masalah perencanaan persediaan
Di mana , j = 1, 2, 3., 0 < < 1, 0 < < .
C = 0,001001001, B = 1, dan = 13,81.
Pada persamaan (3.13), setelah menukar antara parameter sumber daya yang
bernilai fuzzy dan parameter non-fuzzy dan , nilai terbaik dari fungsi objektif
pada level tertentu dari mencapai ketika :
untuk i = 1, 2, 3, 4. ; j = 1, 2, 3. (3.15)
Penyelesaian persamaan di atas menggunakan teknik program linier.
Tabel 3.5 Input Data untuk Pendapatan
39
x1, x2, x3
Setelah diselesaikan dengan metode simpleks menggunakan software QM diperoleh :
≥ 0
Setelah diselesaikan dengan metode simpleks menggunakan software QM diperoleh :
Tabel 3.6 Input Data untuk Polusi
Setelah diselesaikan dengan metode simpleks menggunakan software QM diperoleh :
41
Setelah diselesaikan dengan metode simpleks menggunakan software QM diperoleh :
≥ 0
total pendapatan, adalah minimum total pendapatan dan adalah jarak antara
total pendapatan. adalah maksimum total polusi, adalah minimum total
polusi dan adalah jarak untuk polusi berbahaya. Fuzzy band untuk pendapatan
dan polusi diberikan sebagai berikut :
Tabel 3.7 Fuzzy Band untuk Total Pendapatan
Tabel 3.8 Fuzzy Band untuk Total Polusi
Proses berhenti pada iterasi ke 3. Hal ini dikarenakan minimum polusi sudah
melebihi batas 30 ton meskipun nilai dari fuzzy band = 3,53 adalah yang terkecil,
namun hal itu juga berarti goal ke-2 dilanggar. Oleh karena itu, iterasi ke-3
memberikan hasil yang cukup baik untuk maksimum total pendapatan dan minimum
total polusi. Hasil dari tabel 3.8 menunjukkan bahwa total pendapatan maksimum
adalah 194,73 dan total polusi minimum adalah 23,21 pada 99% tingkat kepuasan
dengan tingkat kekaburan = 13,81.
Menurut Zimmermann dan Carlsson dalam pada Vasant (2004), solusi yang
nyata tepat berada pada tingkat kepuasan 50% dalam lingkungan fuzzy.Tabel 3.9 dan
3.10 memberikan solusi fuzzy untuk optimal pendapatan dan optimal polusi yang
berkenaan dengan kekaburan dan tingkat kepuasan.
Tabel 3.9 Optimal Polusi dan Tingkat Kepuasan
43
Tabel 3.9 Optimal Pendapatan dan Tingkat Kepuasan
( = 13.81)
Dari tabel 3.8 dan tabel 3.9 dapat dilihat bahwa total polusi pada tingkat
kepuasan 50% adalah 28,90 satuan polusi, di mana goal ke-2 terpenuhi. Total
pendapatan pada tingkat kepuasan 50% adalah $173,09, di mana goal pertama juga
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari studi literatur ini dapat disimpulkan :
1. Fuzzy Linear Programming (FLP) merupakan alat yang sederhana dan sesuai
untuk permasalahan multi-objective dibandingkan dengan metode lain.
2. Tujuan dalam memformulasikan bentuk baru dari fungsi keanggotaan kurva-S
yang modifikasi pada masalah perencanaan persediaan produksi yang terbatas
telah tercapai.
3. Kemudahan dari fungsi keanggotaan kurva-S yang modifikasi dalam aplikasinya
pada permasalahan dunia nyata telah dibuktikan melalui analisis, serta sangat
memudahkan juga dalam pengambilan keputusan.
4.2 Saran
1. Model ini dapat diperluas pada situasi lainnya tidak hanya pada perencanaan
persediaan produksi tetapi pada bidang yang lain juga dengan sedikit atau tanpa
modifikasi.
2. Model ini juga dapat diperluas untuk banyaknya tujuan dengan memasukkan
hanya satu penambahan pembatas ke dalam kumpulan pembatas untuk setiap
45
DAFTAR PUSTAKA
Hadiguna, R.A, dan Machfud., 2008. “ Model Perencanaan Produksi pada Rantai
Pasok Crude Palm Oil dengan Mempertimbangkan Preferensi Pengambil
Keputusan”. Jurnal Teknik Industri, Volume 10 Nomor 1: hal. 38-49.
Kusumadewi. Sri. dan Purnomo, Hari. 2004. Aplikasi Logika Fuzzy untuk Pendukung
Keputusan. Yogyakarta: Graha Ilmu.
Nasendi, B. D. Dan Effendi Anwar. 1985. Program Linier dan Variasinya, Jakarta : P.
T. Gramedia.
Siringoringo, Hotniar., 2005, Seri Teknik Riset Operasional. Pemrograman Linier.
Penerbit Graha Ilmu. Yogyakarta.
Sutapa, Nyoman., 2000. “Masalah Program Linier Fuzzy dengan Fungsi Keanggotaan
Linier”. Jurnal Teknik Industri, Volume 2 Nomor 1: hal. 28-33.
Zadeh, L. A., 1971. “Similiarity Relation and Fuzzy Orderings”. Information science ;
3 : 177-206.
Vasant, P.M., 2003. “Aplication of Fuzzy Linear Programing in Production Planing.”
Fuzzy Optimization and Decision Making, Volume 3, hal. 229-241.
Vasant, P.M., 2004. “Aplication of Multi Objective Fuzzy Linear Programing in
Supply Production Planing Problem.” Jurnal teknologi, 40(D) : 37-48.
Vasant, P.M., 2006. “Fuzzy Production Planing and its Application to Decision