Capm (The Capital Assets Pricing Model) N-Momen Pada Asuransi Bencana

SEPTIAWATI

G54103054

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRACT

SEPTIAWATI. CAPM (The Capital Assets Pricing Model) N-Moment On Catastrophe

Insurance. Supervised by EFFENDI SYAHRIL and DONNY CITRA LESMANA.

Skewness is a deviation that occurs to the distribution of rate of return. Skewness causes disequilibrium in premium, rate of return and risk. One of the application of skewness can be found in catastrophe insurance. Because of the rareness and randomness of catastrophe, the rate of return is asymmetrically distributed. Hence, we need an estimator model in risk and returns that is asymmetrically distributed.

Dibimbing oleh EFFENDI SYAHRIL dan DONNY CITRA LESMANA.

Skewness adalah ukuran penyimpangan yang terjadi pada nilai dari sebaran imbal hasil.

Skewness dalam suatu nilai pada sebaran imbal hasil menyebabkan terjadinya ketidakseimbangan pada nilai premi, imbal hasil, dan risiko. Contoh nyata dari sebaran yang mengalami penyimpangan adalah nilai imbal hasil perusahaan asuransi bencana. Bencana yang bersifat acak dan langka menyebabkan nilai dari sebaran imbal hasil perusahaan asuransi bencana mengalami penyimpangan dan menyebar asimetris, sehingga diperlukan suatu model penduga risiko dan imbal hasil yang menyebar asimetris.

CAPM (THE CAPITAL ASSETS PRICING MODEL) N-MOMEN

PADA ASURANSI BENCANA

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

SEPTIAWATI

G54103054

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

NIM :

G54103054

Menyetujui :

Pembimbing

I,

Pembimbing

II,

Drs. Effendi Syahril, Grad.Dipl.

Donny Citra Lesmana, M.Sc.

NIP. 131 804 163

NIP. 132 311 927

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, M.S.

NIP. 131 473 999

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 3 September 1984 dari pasangan M Yusuf dan Hilalia. Penulis merupakan anak ketiga dari empat bersaudara.

Tahun 2003 penulis lulus dari SMUN 48 Pinang Ranti Jakarta dan pada tahun yang sama diterima sebagai mahasiswi Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur SPMB (Seleksi Penerimaan Mahasiswa Baru).

Puji dan syukur kehadirat Allah SWT atas rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam tercurah kepada junjungan kita nabi besar Muhammad SAW yang telah memberikan suri tauladan kepada umatnya hingga akhir jaman.

Karya ilmiah ini disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada program studi Matematika.

Penulis mengucapkan terima kasih kepada :

1. Bapak Drs. Effendi Syahril, Grad.Dipl. selaku Pembimbing I yang telah meluangkan waktu untuk memberikan bimbingan, pengarahan, semangat, dan saran sehingga penulis dapat menyelesaikan karya ilmiah ini.

2. Bapak Donny Citra Lesmana, M.Sc. selaku Pembimbing II atas bimbingan dan saran yang telah diberikan.

3. Ibu Ir. Retno Budiarti, M.S. selaku Penguji yang telah memberikan saran dan masukannya. 4. Keluarga di Condet (Mama dan Papa, Kaka, Kiki, Mbam, dan De’Dhika) terima kasih atas

doa, cinta, semangat, dan kasih sayangnya.

5. Dian Eka Pratiwi (Iwit), Ifni Husnul Khotimah (Ifni), dan Dwi Putri Methasari (Metha) atas persahabatan, semangat, dan kebersamaannya selama di IPB.

6. Mansyur Husjaini, S.Si. atas doa, nasihat, perhatian, semangat, dan kasih sayangnya.

7. Dosen-dosen atas ilmu yang telah diberikan kepada penulis, serta staff departemen

matematika, terima kasih atas bantuan selama di Departemen Matematika.

8. Sahabat-sahabat : Vina (yang selalu memberikan keceriaan dan semangat), Gatha, Amie (makasih buat perhatian dan bantuannya), Gandronk, Mika, Icha, Achie (terima kasih atas semangat dan bantuannya), Muchie, Om Rama, Bedu, Azis, dan Rusli (terima kasih atas semangat, persahabatan, jalan-jalannya, dan keceriaannya).

9. Teman-teman tercinta : Manto, Sri (makasih atas semangatnya), Elis, Mita, Uly, Kafi, Ari, Ali, Mayang, Herni, Walidah, Sawa, Dimas, Fee, Jayu, Abay, Marlin, Nchie, Putra, Uve, Berry, Prima, Yuda, Dwi Puspa, Nisa (tetap semangat, makasih telah bersedia menjadi pembahas), Aam, Lili, Anton, Ucup, Demi. Terima kasih atas kebersamaannya selama ini.

10. Semua mahasiswa/i matematika atas dukungannya, khususnya Ka Dc 38 (terima kasih atas bantuannya), Echie, Fitri, Sita, Kuren math 41, Pipit 42. Terima kasih atas bantuannya. 11. Keluarga mungil Pondok Kencana (Venny, Ale, Anjun, dan Lalis) atas kebersamaannya dan

wisma Blobo atas semua bantuannya.

12. Semua pihak yang ikut membantu dan penulis tidak dapat menyebutkan satu persatu.

Semoga karya ilmiah ini dapat bermanfaat bagi pihak yang membaca.

Bogor, Oktober 2007

DAFTAR ISI

Halaman

PENDAHULUAN

Latar Belakang ... 1

Tujuan ... 1

Metodologi ... 1

Sistematika Penulisan ... 1

LANDASAN TEORI Ruang Contoh, Kejadian, dan Peluang ... 2

Peubah Acak, Fungsi Sebaran, dan Fungsi Kerapatan Massa ... 2

Nilai Harapan, Standar Deviasi, Koragam ... 2

Fungsi Pembangkit Momen, Momen, Momen Pusat ... 3

Skewness, Coskewness ... 3

Deret Taylor, Fungsi Utilitas Joan, Teorema Lagrange ... 3

PEMBAHASAN Model Seleksi Portofolio Markowitz ... 4

Pemilihan Portofolio ... 5

CAPM 2-Momen ... 6

CAPM 3-Momen ... 7

CAPM N-Momen ... 8

Sifat-Sifat Koragam dan Coskewness ... 8

CAPM 3-Momen pada Asuransi Bencana ... 9

CAPM N-Momen pada Asuransi Bencana ... 10

SIMPULAN ... 10

DAFTAR PUSTAKA ... 10

PENDAHULUAN

Latar Belakang

Banyak kejadian alam yang tidak dapat diduga-duga kejadiannya misalnya banjir, tanah longsor, tsunami, angin badai, gempa, dan lain-lain. Tidak seorangpun yang mengetahui kapan bencana alam yang merugikan banyak orang itu akan terjadi. Kerugian yang diderita pun cukup besar. Untuk mengatasi kerugian akibat bencana, salah satu alternatifnya adalah dengan mengikuti jaminan asuransi bencana.

Asuransi merupakan salah satu cara pembayaran ganti rugi kepada pihak yang mengalami musibah, sehingga orang yang mengalami musibah dapat mengatasi risiko yang ditimbulkan akibat suatu bencana walaupun kerugian tetap terjadi.

Bencana yang bersifat acak dan langka dapat menyebabkan nilai dari imbal hasil perusahaan asuransi menyebar asimetris. Karena itu, dapat ditemui suatu kecondongan (skewness) pada nilai sebarannya. Skewness digunakan untuk mengukur sebaran asimetris dari sebaran peluang yang memiliki peubah acak yang bernilai riil.

Dalam bencana terdapat risiko, kerugian, dan ketidakpastian. Sehingga pihak (perusahaan) asuransi bencana perlu mempertimbangkan imbal hasil yang akan didapatkan. Perusahaan asuransi bencana tidak ingin mengalami kerugian dan untuk itu diperlukan manajemen risiko, yaitu mengurangi kemungkinan kerugian atau mengurangi risiko yang diakibatkan oleh kerugian yang terjadi. Dengan demikian, diperlukan suatu model pendugaan mengenai kesetimbangan imbal hasil pada aset berisiko dan penentuan imbal hasil aset untuk menghitung imbal hasil perusahaan asuransi bencana. Dengan menggunakan model pendugaan, perusahaan asuransi dapat menghitung imbal hasil yang diharapkannya.

The Capital Assets Pricing Model (CAPM) dapat memberikan prediksi yang tepat tentang hubungan antara risiko dan imbal hasilnya. Dalam CAPM, standar deviasi dari suatu nilai imbal hasil adalah ukuran dari risiko yang dihadapi oleh investor. Standar deviasi berakibat pada risiko sistematik (beta)

yang diperhitungkan dalam pasar finansial. CAPM ini melibatkan momen pusat ke-2, sehingga CAPM dapat digunakan untuk menghitung ketidakpastian imbal hasil. Namun CAPM 2-momen hanya berlaku untuk nilai dari sebaran imbal hasil yang menyebar simetris.

Untuk menghitung suatu sebaran imbal hasil yang asimetris diperlukan momen pusat ke-3. Sehingga diperlukan pengembangan model CAPM 2-momen menjadi CAPM 3-momen. Untuk penerapan pada asuransi bencana, akan dilakukan modifikasi pada CAPM 3-momen.

Tujuan

Tujuan dari karya ilmiah ini adalah menelaah ulang pengembangan model CAPM 3-momen dan model asuransi CAPM 3-momen yang melibatkan skewness dari suatu aset untuk menghitung premi kesetimbangan pada asuransi bencana sebagai kompensasi dari biaya kecondongan yang terjadi.

Metodologi

Metode penulisan karya ilmiah ini adalah studi pustaka. Jurnal utama karya ilmiah ini merujuk pada Kozik, T. J. dan Larson, A. M. 2001. The N-Momen Insurance CAPM. Allstate Insurance Company. Bahan-bahan yang menunjang penulisan karya ilmiah ini diperoleh dari buku-buku dan jurnal yang terkait dengan tulisan.

Sistematika Penulisan

2

LANDASAN TEORI

Ruang Contoh, Kejadian, dan Peluang

Definisi 1 (Percobaan Acak)

Percobaan acak adalah suatu percobaan yang dapat diulang dalam kondisi yang sama, namun hasil pada percobaan berikutnya tidak dapat ditebak dengan tepat, tetapi dapat diketahui kemungkinan hasil yang muncul.

[Hogg dan Craig, 1995]

Definisi 2 (Ruang Contoh)

Ruang contoh adalah himpunan yang beranggotakan semua hasil yang mungkin muncul dari suatu percobaan acak dan biasa dinotasikan dengan Ω.

[Hogg dan Craig, 1995]

Definisi 3 (Medan-σ)

Medan-σ adalah suatu himpunan F yang anggotanya terdiri atas himpunan bagian ruang contoh Ω, yang memenuhi kondisi berikut:

1. ∅ ∈F ,

2. Jika A A1, 2,...∈F maka 1

i i

A

∞ =

∈

U

F,

3. Jika A∈F maka c

A ∈F.

[Grimmett dan Stirzaker, 1992]

Definisi 4 (Ukuran Peluang)

Misalkan F adalah medan-σ dari ruang contoh Ω. Ukuran peluang adalah suatu fungsi

: [0,1]

P F→ pada

(

Ω,F

)

yang memenuhi: 1. P

( )

∅ =0,P

( )

Ω =1,

2. Jika A A1, 2,...∈F adalah himpunan yang

saling lepas yaitu Ai∩Aj = ∅ untuk

setiap pasangan i≠ j, maka

( )

1 1

i i

i i

P A P A

∞ ∞

= =

⎛ ⎞₌

⎜ ⎟

⎝

U

⎠

∑

.

[Grimmett dan Stirzaker, 1992]

Peubah Acak, Fungsi Sebaran, dan Fungsi Kerapatan Massa

Definisi 5 (Peubah Acak)

Misalkan Ω adalah ruang contoh dari suatu percobaan acak. Fungsi X yang terdefinisi pada Ω yang memetakan setiap unsur ω ∈ Ω ke satu dan hanya satu bilangan real

( )

X ω =x disebut peubah acak.

Ruang dari X adalah himpunan bagian bilangan real A=

{

x x: =X( ),ω ω∈ Ω

}

.

[Hogg dan Craig, 1995]

Definisi 6 (Fungsi Sebaran)

Fungsi sebaran peubah acak X adalah fungsi

[ ]

: 0,1

F R→ , yang didefinisikan oleh

( )

P

(

)

X

F x = X ≤x .

[Grimmett dan Stirzaker, 1992]

Definisi 7 (Peubah Acak Diskret)

Peubah acak X dikatakan diskret jika himpunan semua nilai

{

x x1, 2,...

}

merupakan

himpunan tercacah.

[Grimmett dan Stirzaker, 1992]

Definisi 8 (Fungsi Kerapatan Massa)

Fungsi kerapatan massa dari peubah acak diskret X adalah fungsi p R: →

[ ]

0,1, yaitu

( )

(

)

X

p x =P X=x .

[Grimmett dan Stirzaker, 1992]

Nilai Harapan, Standar Deviasi, Koragam

Definisi 9 (Nilai Harapan)

Jika X adalah peubah acak diskret dengan fungsi kerapatan massa pX

( )

x , maka nilai

harapan dari X, dinotasikan dengan E X

[ ]

, adalah

[ ]

X

( )

x

E X = ∑x p x

asalkan jumlah di atas konvergen mutlak. Beberapa sifat dari nilai harapan

1. Jika k suatu konstanta, maka E k

[ ]

=k. 2. Jika k suatu konstanta dan v v1, 2 adalah

peubah acak, maka

[

1 1 2 2

]

1

[ ]

1 2

[ ]

2

E k v +k v =k E v +k E v . Secara umum, jika k k1, 2,...,knadalah konstanta

dan v v1, 2,...,vnadalah peubah acak, maka

[

1 1 2 2 ... n n

]

E k v +k v + +k v

[ ]

[ ]

[ ]

1 1 2 2 ... n n

k E v k E v k E v

= + + + .

[Grimmett dan Stirzaker, 1992]

Definisi 10 (Ragam)

2 2

( ) ( - [ ]) Var X E X E X

σ = _{= ⎣}⎡ ⎤_⎦

2 2

[ ] ( [ ])

E X E X

= − .

[Hogg dan Craig, 1995]

Definisi 11 (Standar Deviasi)

Jika X adalah peubah acak maka standar deviasi dari X didefinisikan sebagai berikut

( )

X Var X

σ = .

[Ghahramani, 2005]

Definisi 12 (Koragam)

Misalkan Xdan Ydua peubah acak dengan

1

( )

E X =µ dan E Y

( )

=µ2, maka

(

1

)(

2

)

( , )

Cov X Y =E⎡_⎣ X−µ Y−µ ⎤_⎦ =E XY( )−µ µ1 2

disebut koragam peubah acak Xdan Y. [Hogg dan Craig, 1995]

Fungsi Pembangkit Momen, Momen, Momen Pusat

Definisi 13 (Fungsi Pembangkit Momen)

Jika X adalah peubah acak diskret, t merupakan konstanta maka fungsi pembangkit momen didefinisikan sebagai berikut

( ) tX tx ( )

X

x

M t =E e⎡_⎣ ⎤_⎦= ∑e f x dengan − < <h t h.

Selanjutnya, turunan pertamanya sebagai nilai harapan dari peubah acak X

' _{( ) ( )}

X X

d

M t M t

dt =

'

( ) tx ( )

X x

M t = ∑xe f x

' ₍₀₎ 0x _{( ) ( )}

X

x x

M =∑xe f x =∑xf x

'

(0) [ ]

X

M =E X .

Kemudian, turunan keduanya sebagai nilai harapan dari peubah acak X2

" '

( ) ( )

X X

d

M t M t

dt =

"_{( )} 2 tx _{( )} X

x

M t = ∑x e f x

" 2 0 2

(0) x ( ) ( )

X x

M x e f x x f x

x

=∑ =∑

"_{(0) [} 2_]

X

M =E X .

[Hogg dan Craig, 1995]

Definisi 14 (Momen)

Momen ke-k dari peubah acak X didefinisikan sebagai

( k), 1, 2,3,...

k

m =E X k=

[Hogg dan Craig, 1995]

Definisi 15 (Momen Pusat)

Misalkan nilai harapan dari peubah acak X,

1

m, maka momen pusat ke-k dari peubah acak X didefinisikan sebagai

(

1

)

,

k

k p

m =E⎡_⎣ X−m ⎤_⎦ dengan k=1, 2,3,..

[Hogg dan Craig, 1995]

Skewness, Coskewness

Definisi 16 (Skewness)

Misalkan X peubah acak dengan nilai harapan µ, ragam σ2, dan momen pusat ke-3 E⎡_⎢⎣

(

X−µ

)

3⎤_⎥⎦. Dalam teori peluang dan statistik, skewness mengukur sebaran

asimetris. Nilai dari

(

)

3

3

E X µ

σ

⎡ ₋ ⎤

⎢ ⎥

⎣ ⎦ _disebut

sebagai ukuran dari skewness.

[Hogg dan Craig, 1995]

Definisi 17 (Coskewness)

Misalkan X dan Y dua peubah acak dengan ( )

E X =a dan ( )E Y =b, maka

[

][

]

(

2

)

( , , )

Cos X Y Y =E X−a Y−b disebut coskewness peubah acak X dan Y.

[Kozig dan Larson, 2001]

Deret Taylor, Fungsi Utilitas Joan, Teorema Lagrange

Definisi 18 (Deret Taylor)

Jika suatu fungsi y= f x( ) memiliki turunan maka fungsi tersebut memiliki ekspansi deret Taylor

2

( ) ( ) '( ) "( ) 2! h f x+h = f x +hf x + f x

3 '''( ) ... 3! h f x + + yaitu 2 1

( ) ( ) '( ) "( ) 2!

n n n n

h f x ₊ = f x +hf x + f x

3

"'( ) ...

3! n

h f x

+ +

( )( ) ( 1) !

p

p p

n

h

f x h

p Ο

+

4

dengan h=x_n+₁−x_n.

[Fisher, 1988]

Definisi 19 (Fungsi Utilitas Joan)

Fungsi utilitas Joan didefinisikan sebagai berikut

( )

u x = x dengan x adalah kekayaan.

[Winston, 2004]

Teorema 1 (Metode Lagrange)

Masalah dengan dua variabel dan satu kendala

Untuk memaksimumkan atau meminimumkan

1 2

( , )

f x x terhadap kendala g x x( ,1 2)=0,

selesaikan sistem persamaan berikut maksimumkan

1 2

( , ) f x x dengan kendala

1 2

( , ) 0 g x x = .

Dari masalah tersebut, maka diperoleh fungsi Lagrange sebagai berikut:

( , ) ( ) ( ) l= xλ = f x +λg x .

Syarat perlu untuk eksistensi titik ekstrim

*

X=X akan terpenuhi jika turunan parsial dari fungsi Lagrange sama dengan nol, sehingga menghasilkan:

(

1 2

)

1

, , l

x x

x λ

∂

∂

(

_{1 2}

)

(

_{1 2}

)

1 1

, , 0

f g

x x x x

x λ x

∂ ∂

= + =

∂ ∂ (a)

(

1 2

)

2

, , l

x x

x λ

∂

∂

(

1 2

)

(

1 2

)

2 2

, , 0

f g

x x x x

x λ x

∂ ∂

= + =

∂ ∂ (b)

dan

(

1, 2,

)

( ,1 2) 0

l

x x λ g x x λ

∂ _{= =}

∂ .

Dari Persamaan (a) dan (b) akan dihasilkan titik ekstrim

(

)

1 2

*_, *

x x . λ yang berpadanan dengan fungsi g x x( ,1 2)=0 disebut pengali

Lagrange.

[Rao, 1978]

Definisi 20 (Asuransi)

Asuransi atau pertanggungan adalah perjanjian antara dua pihak atau lebih. Pihak penanggung mengikatkan diri kepada pihak tertanggung dengan menerima premi asuransi untuk memberikan penggantian kepada tertanggung atas kerugian, kerusakan atau kehilangan, atau tanggung jawab hukum kepada pihak ketiga yang mungkin akan diderita tertanggung, yang timbul dari suatu peristiwa yang tidak pasti, atau untuk memberikan suatu pembayaran yang didasarkan atas meninggal atau hidupnya seseorang yang dipertanggungkan (Undang-Undang Republik Indonesia Nomor 2 Tahun 1992).

[Iskandar, 01-07-2007]

PEMBAHASAN

Model Seleksi Portofolio Markowitz

Pada tahun 1952, Markowitz mempublikasikan tulisannya yang berjudul “Portfolio Selection”. Dalam tulisannya, Markowitz memperlihatkan bagaimana membuat suatu portofolio dengan peluang yang lebih besar pada imbal hasil yang diharapkan dengan suatu tingkat risiko. Sejak saat itu, seleksi portofolio menjadi hal penting dalam ekonomi keuangan dan digunakan dalam pasar modal untuk membuat suatu portofolio efisien. Markowitz memasukkan prinsip diversifikasi, yang akhirnya membuatnya memperoleh nobel ekonomi 1990. Prinsip diversifikasi adalah suatu prinsip berinvestasi pada beragam aset.

Imbal hasil yang diharapkan dari suatu portofolio adalah penjumlahan dari imbal hasil yang diharapkan dari tiap sekuritas pembentuk portofolio dikalikan dengan bobot masing-masing sekuritas dalam portofolio. Misalkan E r

( )

p merupakan nilai harapan

imbal hasil portofolio P dan wi merupakan

bobot-bobot sekuritas dalam portofolio, maka

( )

p

E r dapat dituliskan sebagai berikut

( )

( )

1

n

p i i

i

E r w E r

=

=

∑

.

jumlah bobot dalam suatu portofolio adalah satu, atau secara matematis ditulis

1

1

n i i

w

=

=

∑

.

Ragam portofolio, 2

p

σ , mencerminkan risiko dari portofolio dan wi adalah bobot-bobot

sekuritas dalam portofolio. Secara matematis ragam dari suatu portofolio dituliskan sebagai berikut:

2

1 1

n n

p i j ij

i j

w w

σ σ

= =

=

∑∑

dengan 2

ii i

σ =σ , 2

i

σ adalah ragam sekuritas ke-i. σij adalah koragam sekuritas i dan j,

dengan σij=σji, untuk i≠ j, dan

i j j i

w w =w w. Portofolio Markowitz ini digunakan untuk memilih wi sehingga

2

p

σ minimum atau dapat dituliskan

{ }

2

min

i p

w σ

dengan kendala

1

1

n i i

w

=

=

∑

.

Pemilihan Portofolio

Pemilihan suatu sekuritas dalam pembentukan portofolio dibagi ke dalam kasus sekuritas berisiko dan bebas risiko. Ketika menunjukkan suatu peluang risiko imbal hasil yang ada bagi investor dapat ditunjukkan oleh frontier ragam minimum. Frontier adalah kurva ragam terendah yang bisa dicapai untuk imbal hasil yang diharapkan dari portofolio tertentu. Dalam menghadapi masalah pemilihan portofolio, jika diperbolehkan short sales dalam pembentukan portofolio berisiko maka portofolio berisiko yang hanya terdiri atas sebuah aset menjadi tidak efisien. Tetapi jika short sales tidak diperbolehkan maka sekuritas tunggal mungkin berada pada frontier, yaitu kurva ragam terendah yang dicapai untuk nilai harapan dari imbal hasil portofolio tertentu.

Dengan menggunakan imbal hasil yang diharapkan, ragam, dan koragam maka dapat dihitung portofolio ragam minimum untuk setiap imbal hasil yang diharapkan. Semua portofolio yang ada pada frontier ragam minimum dari portofolio ragam global dan yang di atasnya memberikan kombinasi imbal hasil risiko terbaik menjadi calon portofolio optimal.

Gambar 1: Frontier ragam minimum aset berisiko

Bagian frontier yang ada di atas portofolio minimum global disebut frontier efisien dari aset berisiko (efficient frontier of risky assets). Selanjutnya, bagian dari optimisasi adalah keterlibatan aset bebas risiko.

Garis CAL (Capital Alocation Line) adalah suatu garis yang menunjukkan semua kombinasi risiko imbal hasil yang mungkin dan tersedia dari berbagai pilihan alokasi aset. Garis ini bermula dari r_f dan lurus sampai titik M. Kemiringan CAL sama dengan kenaikan imbal hasil yang diharapkan dari portofolio lengkap untuk setiap kenaikan dari standar deviasi. Kemiringan tersebut disebut rasio imbal hasil terhadap variabilitas.

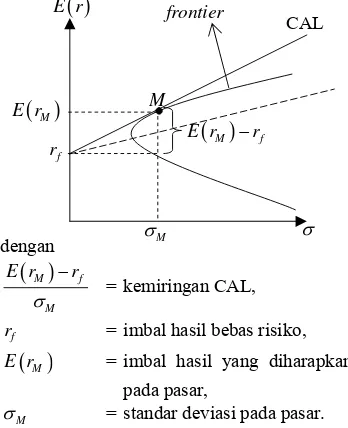
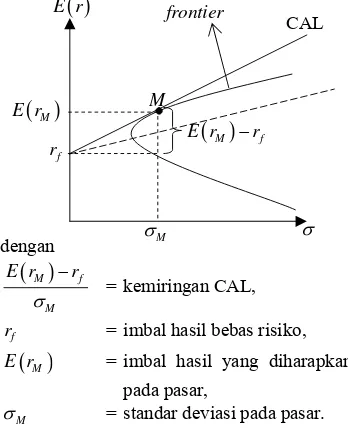
Pada Gambar 2 dapat dilihat bahwa titik M adalah titik singgung dari CAL dan frontier. Titik M merupakan titik portofolio optimal pada CAL. CAL dari portofolio optimal, M, menyinggung frontier efisien. CAL unggul di atas garis yang lain. Oleh karena itu, portofolio M merupakan portofolio optimal.

Gambar 2: CAL dan frontier

dengan

( )

M f

M

E r r σ

−

= kemiringan CAL,

f

r = imbal hasil bebas risiko,

( )

M

E r = imbal hasil yang diharapkan pada pasar,

M

σ = standar deviasi pada pasar.

( )

E r

σ portofolio

ragam minimum

global

frontier efisien

frontier ragam minimum

aset individual

M

( )

E r

( )

M

E r

M

σ

f

r

( )

M f

E r −r CAL frontier

6

Model CAPM dibentuk dari CAL yang bersinggungan dengan portofolio yang efisien. Pada garis CAL ini menunjukkan pertukaran risiko imbal hasil. CAL diperoleh dari portofolio bebas risiko dan berisiko, M. Investor akan memilih CAL yang curam karena imbal hasil yang diharapkan semakin besar.

Model CAPM 2-Momen

Kemampuan untuk mengestimasi imbal hasil suatu sekuritas individu merupakan hal yang sangat penting dan diperlukan oleh investor. Untuk dapat mengestimasi imbal hasil suatu sekuritas dengan baik diperlukan suatu model estimasi. CAPM merupakan suatu model untuk mengestimasi kesetimbangan imbal hasil yang diharapkan dari suatu aset berisiko.

Model CAPM 2-momen (klasik) sebagai berikut

( )_{i f i}[ (_M) _f]

E r =r +β E r −r (1) (lihat Lampiran 1)

dengan

f

r = nilai imbal hasil bebas risiko,

i

r = nilai imbal hasil pada aset ke-i, ( )i f

E r −r = premi risiko atas sekuritas individu,

(_M) _f

E r −r = premi risiko atas portofolio pasar, dan

i

β = risiko sistematis. Ide dasar dari CAPM (The Capital Assets Pricing Model) adalah menentukan harga kesetimbangan aset pada pasar. Model klasik CAPM telah diperkenalkan oleh Sharp (1964), Lintner (1965), dan Mossin (1966), dan itu telah dicatat sebagai kerangka dari kesetimbangan pasar modal sampai sekarang. Hubungan kesetimbangan pada imbal hasil hanya pada satu aset dan hanya pada satu faktor risiko yaitu beta. CAPM merupakan suatu alat penetapan harga aset yang memprediksi tentang bagaimana hubungan antara risiko dan imbal hasil yang diharapkan. Hubungan ini mempunyai dua fungsi penting. Pertama, menyediakan tolok ukur tingkat imbal hasil untuk mengevaluasi alternatif investasi yang mungkin. Kedua, model ini dapat digunakan untuk menduga imbal hasil yang diharapkan atas aset yang belum diperdagangkan di pasar.

CAPM mempunyai beberapa asumsi penyederhanaan untuk mengarahkan pada versi dasar CAPM sebagai berikut

1. Investor bersifat price takers. Artinya, investor tidak dapat mempengaruhi harga dan tidak ada monopoli dari investor tertentu.

2. Terdapat banyak investor, masing-masing dengan jumlah kekayaan yang sangat kecil dibandingkan dengan total kekayaan seluruh investor.

3. Seluruh investor merencanakan untuk satu periode investasi yang identik.

4. Investor yang rasional berusaha mengoptimalkan imbal hasil dan risiko. 5. Semua investor memiliki nilai harapan

yang seragam pada imbal hasil sekuritas untuk sebarang waktu periode.

6. Tidak ada pajak dan tidak ada ongkos transaksi.

Inti dari asumsi ini adalah mencoba untuk memastikan bahwa individu adalah mirip satu sama lain, kecuali dalam hal besarnya kekayaan awal dan sikap penghindaran terhadap risiko (risk aversi).

Implikasi dari model CAPM adalah

1. Setiap investor akan berinvestasi pada portofolio yang sama (portofolio pasar). 2. Portofolio pasar memuat semua aset yang

diperdagangkan di pasar dengan proporsi investasi adalah sama seperti proporsi saham dalam portofolio pasar.

3. Premi risiko pasar bergantung pada tingkat penghindaran risiko semua pelaku pasar. Premi risiko pasar merupakan selisih imbal hasil aset berisiko dan aset bebas risiko.

4. Premi risiko masing-masing saham bergantung pada koragam saham tersebut dengan pasar.

Nilai harapan imbal hasil portofolio atas aset bebas risiko pada CAPM 2-momen sama dengan premi risiko pasarnya dengan nilai β adalah sama dengan satu.

imbal hasil portofolio apapun yang mengkombinasikan kumpulan aset ini akan menyebar normal pula dan standar deviasinya akan secara penuh menunjukkan risikonya.

Model CAPM 3-Momen

Model klasik CAPM 2-momen yang diperkenalkan oleh Sharp (1964), Lintner (1965), dan Mossin (1966) mendapat banyak penolakan dan kritikan dari beberapa orang. Berdasarkan hasil empiris yang telah dilakukan menunjukkan bahwa CAPM klasik tidak konsisten. Kraus-Litzenberger memulai suatu diskusi tentang momen yang lebih tinggi dalam CAPM yang dituliskan pada sebuah tulisan berjudul “Skewness Preference and The Valuation of Risk Assets”. Kraus-Litzenberger juga menyampaikan bahwa perlu ditambahkan skewness pada CAPM untuk penilaian suatu aset.

Berdasarkan pendugaan beta dan gamma saham NYSE dari Januari 1926 sampai Desember 1935, Kraus-Litzenberger mendapatkan bukti yang melibatkan skewness pada premi risiko (dikutip dari tesis yang berjudul “Pricing Skewness and Kurtosis Risk on the Swedish Stock Market”). Sehingga CAPM 3-momen dapat lebih efektif pada proses pembentukan harga aset daripada 2-momen mean-variance. Berdasarkan tes empiris juga, bahwa CAPM 3-momen menunjukkan hubungan yang negatif antara sistematik skewness dengan imbal hasil aset. Dengan demikian, sistematik skewness positif lebih disukai dibanding dengan yang negatif. Aset dikatakan memiliki coskewness positif (negatif) apabila dapat mengurangi (melebihkan) risiko portofolio untuk imbal hasil pasar yang mutlak besar dan tingkat risiko rendah (tinggi) pada kesetimbangan.

Dengan menambahkan ruas kanan pada CAPM 2-momen dengan gamma dikali premi penyimpangan pasar, maka didapat CAPM 3-momen. Model kesetimbangan imbal hasil ini mengasumsikan bahwa nilai imbal hasil pada portofolio pasar bersifat menyebar asimetris sebagai berikut:

E R( _i)=R_f +b₁β_i+b₂γ_i (2) (lihat Lampiran 2)

dengan

f

R = 1+r_f ,

i

R = 1+ri,

M

R = 1+rM,

f

r = nilai imbal hasil bebas risiko,

i

r = nilai imbal hasil pada aset ke-i,

M

r = nilai imbal hasil pada portofolio pasar,

1

b = premi risiko pasar,

2

b = premi penyimpangan (skewness) pasar,

2 ( , ) ( ) i M RM i M i M

Cov R R R R Var R σ β σ = =

( )

( )

(

)

( )

(

2

)

i i M M

M M

E R E R R E R

E R E R

− − ⎡ ⎤ ⎡_⎣ ⎤_⎦ ⎣ ⎦ = − ⎡ ⎤ ⎣ ⎦

. (3)

Standar deviasi dinyatakan sebagai berikut:

(

( )

)

1 2 ₂

M

R E RM E RM

σ =⎡_⎢ − ⎤_⎥

⎣ ⎦ . (4)

Gamma (risiko sistematis) dinyatakan sebagai berikut:

i

γ i M₃ M RM

R R R

τ τ =

( )

( )

(

)

( )

(

)

2 3

i i M M

M M

E R E R R E R

E R E R

− − ⎡ ⎤ ⎡_⎣ ⎤_⎦ ⎣ ⎦ = − ⎡ ⎤ ⎣ ⎦

. (5)

Kemiringan dari nilai imbal hasil pada keseluruhan portofolio didefinisikan:

( )

(

)

(

)

1

3 3

M M M

R E R E R

τ ₌ ⎡ ₋ ⎤

⎣ ⎦ . (6)

Beta dan gamma pada CAPM 3-momen sama dengan ukuran risiko sistematis. Dengan menyederhanakan Persamaan (2) sebagai berikut:

1 2

( i) f i i

E R =R +b β +b γ

1 2

)

(1 i) (1 f i i

E +r = +r +b β +b γ

1 2

(1) ( )i 1 f i i

E +E r = +r +b β +b γ

1 2

( )i f i i

E r =r +b β +b γ (7) maka diperoleh Persamaan (7) sebagai model CAPM 3-momen.

Pada model CAPM 3-momen nilai imbal hasilnya (premi risiko pada investor) sama dengan penjumlahan dari premi risiko pasar dan premi penyimpangan pasar, dengan nilai βdan γ sama dengan satu. Selanjutnya, dari Persamaan (7) akan didapat portofolio pasar yaitu

8

Model CAPM N-Momen

Model kesetimbangan CAPM ini kemudian diperumum menjadi CAPM n-momen. Model kesetimbangan CAPM n-momen mengasumsikan bahwa nilai imbal hasil pada portofolio pasar adalah sebagai berikut:

( )

_{( 1)}

2

i f n ni

n

E R R ∞ b ₋ v =

= + ∑ (9) (lihat Lampiran 2)

dengan

i

R = 1+ri, f

R = 1+rf , i

r = nilai imbal hasil sekuritas ke-i,

f

r = nilai imbal hasil bebas risiko.

Kemudian, b_(n−₁₎ dan vni dapat dirumuskan

sebagai berikut:

1

(

( )

)

( 1)

n n

n n M M

b − =θ P −E R −E R . (10)

{

(

( )

)

(

( )

)

}

( )

(

)

1

n

i i M M

ni n

M M

E R E R R E R

v

E R E R

−

− −

=

− . (11)

(lihat Lampiran 2)

Dengan menyederhanakan Persamaan (9) sebagai berikut:

( )

( 1)

2

i f n ni

n

E R R ∞ b − v = = + ∑

(

)

(

)

( 1)

2

1 i 1 f n ni

n

E r r ∞ b − v

=

+ = + + ∑

( )

( 1)

2

i f n ni

n

E r r ∞ b − v =

= + ∑ (12) maka diperoleh persamaan CAPM n-momen. Dengan tidak memakai momen yang lebih tinggi dari rata-rata dan ragam tidak akan mempengaruhi nilai imbal hasil, tetapi bukan berarti bahwa kecondongan (skewness) tidak penting. Dalam hal ini, suatu imbal hasil yang asimetris, yang terkait dengan skewness, dapat dihitung dengan momen ketiga.

Sifat-Sifat Koragam dan Coskewness

Koragam menghitung potensi diversifikasi dari sebuah aset. Koragam mengukur banyaknya imbal hasil dari 2 aset berisiko bergerak bersamaan. Koragam positif artinya aset tersebut bergerak bersamaan jika imbal hasil keduanya melampaui harapan atau keduanya lebih rendah dari harapannya. Koragam negatif artinya aset tersebut bergerak berlawanan jika aset yang satu melampaui harapan dan yang satu lebih kecil dari harapannya. Menurut Kozig dan Larson, berdasarkan Campbell Harvey dan Akhtar Siddique (2000), risiko sistematik

(coskewness) adalah komponen dari suatu penyimpangan aset yang terkait pada penyimpangan portofolio pasar.

Sebagai sebuah ukuran risiko, beta bersifat linier yaitu beta pada suatu kombinasi linier atas sekuritas adalah kombinasi linier dari nilai-nilai beta pada sekuritas itu sendiri. Artinya, suatu beta dari suatu portofolio sama dengan rataan terboboti dari nilai-nilai beta suatu sekuritas pada portofolio. Misalkan

Z = portofolio dari n sekuritas,

i

S = uang yang diinvestasikan pada sekuritas ke-i,

i

r = tingkat imbal hasil pada sekuritas ke-i,

Z

r = tingkat imbal hasil dari portofolio,

M

r = imbal hasil pada portofolio pasar, S = i

i S ∑ , maka 2 Z M M r r Z r σ β σ =

( )

( )

(

)

( )

(

2

)

Z Z M M

M M

E r E r r E r

E r E r

− − ⎡ ⎤ ⎡ ⎤ ⎣ ⎦ ⎣ ⎦ = − ⎡ ⎤ ⎣ ⎦

( )

( )

(

2

)

i i i i

M M

M M

S r S r

E E r E r

S S

E r E r

⎛⎡⎛_∑ ⎞₋ ⎛_∑ ⎞⎤_{⎡ − ⎤}⎞ ⎜⎢_⎣⎜_⎝ ⎟_⎠ ⎜_⎝ ⎟_⎠⎥ ⎣_⎦ ⎦⎟ ⎝ ⎠ = − ⎡ ⎤ ⎣ ⎦

( )

( )

(

)

( )

(

2

)

i

i i M M

M M

S

E r E r r E r

S

E r E r

⎡ − ⎤⎡ − ⎤ ∑ _{⎣ ⎦⎣ ⎦} = − ⎡ ⎤ ⎣ ⎦ i i S S β ∑

= . (13) Untuk

Z

sama dengan portofolio pasar, sehingga nilai beta adalah satu, maka koragam dari tingkat imbal hasil portofolio pasar dengan portofolio pasar itu sendiri sama dengan ragam dari tingkat imbal hasil portofolio pasar. Dengan demikian, penjumlahan terboboti dari koragam-koragam pada tingkat imbal hasil semua sekuritas portofolio pasar sama dengan nilai ragam dari tingkat imbal hasil portofolio pasar.

Serupa dengan itu, nilai gamma dari suatu portofolio adalah rataan terboboti dari nilai-nilai gamma dari masing-masing sekuritas.

3 M M r M Z Z

r r r τ γ τ =

( )

(

)

(

( )

)

(

)

( )

(

)

(

)

2 3

Z Z M M

M M

E r E r r E r

E r E r

− −

=

( )

( )

(

)

(

)

2 3

i i i i

M M

M M

S r S r

E E r E r

S S

E r E r

⎛⎡⎛_∑ ⎞₋ ⎛_∑ ⎞⎤_{⎡ − ⎤} ⎞ ⎜⎢_⎣⎜_⎝ ⎟_⎠ ⎜_⎝ ⎟ ⎣_⎠⎥_⎦ ⎦ ⎟ ⎝ ⎠ = −

( )

( )

(

)

( )

(

)

2 3 i

i i M M

M M

S

E r E r r E r

S

E r E r

⎛ ⎞ _{⎡ − ⎤ ⎡ − ⎤} ∑⎜ ⎟_{⎝ ⎠} ⎣ ⎦⎣ ⎦ = − ⎡ ⎤ ⎣ ⎦ i i S S γ

= ∑ . (14) Coskewness dari imbal hasil pada portofolio pasar dengan dirinya sendiri sama dengan skewness dari imbal hasil pada portofolio pasar. Maka penjumlahan terboboti coskewness dari imbal hasil semua sekuritas dalam portofolio pasar sama dengan skewness dari imbal hasil portofolio pasar.

Model CAPM 3-Momen pada Asuransi Bencana

Menurut Kozig dan Larson pada tulisannya yang berjudul “The N-Moment Insuranse CAPM”, berdasarkan penurunan asuransi CAPM yang dikerjakan oleh D’Arcy dan Doherty, tingkat imbal hasil untuk ekuitas, r_e, tersusun atas kombinasi linier dari imbal hasil underwriting, r_u, dan imbal hasil investasi, ri.

r_e r Pu

(

1 tu

)

r Si

(

kP

)(

1 ti

)

S S

− + −

= + (15)

dengan:

e

r = tingkat imbal hasil pada ekuitas,

P = premi pada tahun yang ditentukan, S = modal pemegang saham (shareholder’s

equity),

u

r = imbal hasil penjamin (underwriting) per unit premi,

u

t = tingkat pajak pada pendapatan underwriting,

k = koefisien pembangkit dana (perbandingan antara dana cadangan terhadap premi total),

i

r = imbal hasil atas investasi per unit yang diinvestasikan,

i

t = pajak pada pendapatan investasi. Berdasarkan Persamaan (7), nilai harapan ekuitas 3-momen diperoleh

E r

( )

_e =r_f +b₁β_e+b₂γ_e. (16) Beta (gamma) dari ekuitas merupakan

kombinasi linier suatu beta (gamma) underwriting dan suatu beta (gamma) investasi dan dapat dinyatakan sebagai berikut

e u

(

1 u

) (

)

i

(

1 i

)

P t S kP t

S S

β β

β = − + − − (17)

dan

_e P u

(

1 tu

) (

S kP

)

i

(

1 ti

)

S S

γ γ

γ = − + − − . (18)

Substitusi Persamaan (15) ke Persamaan (16), maka diperoleh

( )

_u

(

1 _u

)

( )

_i

(

)(

1 _i

)

E r P t E r S kP t

S S

− + −

+

1 2

f e e

r bβ bγ

= + + . (19) Substitusi Persamaan (7), (17), dan (18) ke Persamaan (19) sehingga diperoleh

( ) (

_u 1 _u

)

E r P t

S −

(

S kP r

)

(

f b1 i b2 i

)

(

1 ti

)

S

β + γ

+ + −

+

(

1 u

)(

1 u 2 u

)

f

P t b b

r

S

β γ

= + − −

(

S kP

)(

1 ti

)(

b1 i b2 i

)

S

β γ

− − +

+ . (20)

Dengan menyederhanakan dan menyelesaikan Persamaan (20) maka diperoleh imbal hasil kesetimbangan underwriting setelah dipotong pajak sebagai berikut

( )(

_u 1 _u

)

E r −t f

(

1 i

)

i f

t r S kr t

P

= − − +

+b₁β_u

(

1−t_u

)

+b₂γ_u

(

1−t_u

)

(21) (lihat Lampiran 3)

dengan

1

b = premi risiko pasar,

2

b = premi penyimpangan pasar,

u β =

(

)

( )

, u M M

Cov r r Var r ,

u γ =

( )

( )

(

)

( )

(

)

2 3

u u M M

M M

E r E r r E r

E r E r

⎡ − ⎤⎡_⎣ − ⎤_⎦

⎣ ⎦

− .

Imbal hasil kesetimbangan underwriting setelah dipotong pajak terdiri atas empat komponen yaitu

1. Mewakili bunga yang dibayarkan ke policy holder (pemegang kebijakan untuk penggunaan dana mereka),

2. Untuk menangkap ulang penalti pajak selama menjadi underwriting,

3. Persiapan untuk kompensasi risiko, dan

4. Persiapan untuk kompensasi

10

Model CAPM N-Momen pada Asuransi Bencana

Model CAPM diperumum menjadi n-momen, dengan mengasumsikan bahwa modal pemegang saham adalah

S

, nilai imbal hasilnya

( )

( 1)

2 e

e f n

n n

E r r ∞ b − v =

= + ∑ . (22) Berdasarkan Persamaan (15) maka

(

1

)

u e

u

n n

Pv t

v

S −

=

(

S kP v

)

ni

(

1 ti

)

S

+ −

+ . (23)

Substitusi Persamaan (15) ke Persamaan (22) diperoleh kesetimbangan sebagai berikut

( ) (

_u 1 _u

)

( )(

_i

)(

1 _i

)

E r P t E r S kP t

S S

− − −

+

( 1)

2 e

f n

n n

r ∞ b ₋ v =

= + ∑ . (24) Dengan melakukan substitusi Persamaan (12) dan Persamaan (23) ke Persamaan (24) maka dihasilkan

( ) (

u 1 u

)

E r P t

S −

(

)

( 1)

(

)

2

1

i

f n i

n n

S kP r b v t

S ∞

− =

⎛ ⎞

+ ⎜_⎝ + ∑ ⎟_⎠ − +

f

r =

_{( 1)}

(

) (

)

(

)

2

1 1

i u i i

n n

n n

Pv t S kP v t

b

S S

∞ − =

− + −

⎡ ⎤

+∑ ⎢ + ⎥

⎢ ⎥

⎣ ⎦.

(25) Dengan menyederhanakan dan menyelesaikan Persamaan (25) untuk imbal hasil kesetimbangan underwriting setelah dipotong pajak, maka dihasilkan model asuransi CAPM n-momen sebagai berikut

( )(

u 1 u

)

E r −t kr_f

(

1 t_i

)

t r Si f P

= − − +

(

)

( 1) 2

1

u

n u

n n

b v t

∞ − =

+∑ − . (26)

(lihat Lampiran 4)

SIMPULAN

Suatu skewness pada tingkat sebaran imbal hasil tidak bisa diabaikan begitu saja. Munculnya sebaran-sebaran imbal hasil yang menyimpang menyebabkan terjadinya ketidakseimbangan pada premi, imbal hasil yang diharapkan serta risikonya. Karena sebaran tersebut mengalami penyimpangan, penting untuk menilai sistematik skewness (coskewness) ketika menentukan imbal hasil kesetimbangan dan premi yang dibutuhkan pada kasus jaminan asuransi bencana.

Pada CAPM 2-momen hanya melibatkan standar deviasi dan diketahui bahwa standar deviasi merupakan akar dari momen pusat ke-2. Momen pusat ke-2 hanya dapat menghitung ketidakpastian imbal hasil. Model CAPM 2-momen hanya dapat menghitung imbal hasil

yang sebarannya simetris sehingga diperumum CAPM 3-momen untuk mengukur imbal hasil yang sebarannya asimetris.

Sedangkan untuk menghitung imbal hasil underwriting pada asuransi bencana diperlukan pengembangan model asuransi CAPM 3-momen dari model CAPM 3-momen yang melibatkan suatu kecondongannya. Secara eksplisit, hal ini akan menghasilkan penentuan atas akibat dari penyimpangan terhadap premi kesetimbangan. Tetapi belum diketahui secara jelas dampak yang ditimbulkan untuk momen yang lebih tinggi dari momen ke-3 karena belum dilakukan analisis secara empiris dan masih bersifat teoritis saja.

DAFTAR PUSTAKA

Bodie, Z, Kane, A, dan Marcus, A J. 2002. Investment. Ed. ke-6. The McGraw-Hill Companies, Inc. New York.

Fisher, M. E. 1988. Introductory Numerical Methods with the NAG Software Library.

Mathematics Department. The University of Western Australia.

Grimmet, G. R. dan D.R. Stirzaker. 1992. Probability and Random Processes. Ed. ke-2. Clarendon Press. Oxford. New- York.

Hogg, R. V. dan A. T. Craig. 1995. Intoduction to Mathematical Statistics. Ed. ke-5. Prentice-Hall, Inc. New Jersey.

Johansson, Andreas. 2005. Pricing Skewness and Kurtosis Risk on the Swedish Stock Market. Master Thesis. Department of Economics, Lund University, Sweden.

Kozik, T. J. dan Larson, A. M. 2001. The N-Momen Insurance CAPM. Allstate Insurance Company.

Rao, S. S. 1978. Optimization Theory and- Applications. San Diego: San Diego State University.

Wikipedia. 2007. Definisi Asuransi. www.ryaniskandar.wordpress.com.[01 Juli 2007].

Lampiran 1

Bukti Persamaan (1)

Gambar: Kurva Frontier dan CAL

Kemiringan garis CAL adalah

( )

M f

M

E r r σ

−

, merupakan market price of risk (risiko harga pasar)

dan disebut rasio imbal hasil terhadap variabilitas.

Misalkan imbal hasil yang diharapkan pada portofolio E r

( )

P , a adalah bobot dari investor. Dapat

digambarkan dalam suatu prospek sederhana sebagai berikut:

( )

P

E r

( )

P a

( ) (

i 1 a

) ( )

M

E r = E r + − E r .

Ragam portofolio didapat sebagai berikut:

2

rp

σ =w'Vw

(

)

2

2

2 a a 1 a

1 a

i iM

rp

Mi M

σ σ

σ

σ σ

⎛ ⎞⎛ ⎞

= − ⎜ _{⎟⎜ −} ⎟

⎝ ⎠

⎝ ⎠

(

)

(

)

(

_a 2 _{1 a a 1 a} 2

)

a

1 a

i iM iM M

σ σ σ σ ⎛ ⎞

= + − + − _{⎜ ⎟}

−

⎝ ⎠

(

)

(

)

2

2 2 2

a σi a(1 a)σMi a 1 a σiM 1 a σM

= + − + − + −

(

)

2

(

)

2 2 2

a σi 1 a σM 2a 1 a σiM

= + − + −

dengan

w = vektor bobot,

w' = vektor transpose dari w,

V = matriks ragam-koragam.

Standar deviasi= =σ Varrp = a2σi2+ −

(

1 a

)

2σM2 +2a 1 a

(

−

)

σiM .

Setiap investasi akan trade off imbal hasil dan standar deviasinya merupakan perubahan imbal hasil terhadap perubahan standar deviasi sebagai berikut:

( )

( )

/ a / a

P P

p p

r r

dE r E r

dσ σ

∂ ∂

=

∂ ∂

( )

( )

( )

a P

i M

E r

E r E r ∂

= −

∂

(

)

(

)

(

2 2 2 2

)

12

(

2

(

)( )

2

)

1

a 1 a 2a 1 a 2a 2 1 a 1 2 4a

a 2

rp

i M iM i M iM iM

σ

σ σ σ − σ σ σ σ

∂

= + − + − + − − + −

∂

a E r

( )

i

( )

M

E r

M

( )

M

E r

f

r

M

σ σ

( )

M f

E r −r

CAL

frontier

( )

E r

14

(

)

(

)

(

)

2 2

2

2 2 2

a 1 a 2a

a 1 a 2a 1 a

i M iM iM

i M iM

σ σ σ σ

σ σ σ

− − + −

=

+ − + − .

Kemudian

( )

( )

/ a

/ a

P P

P P

r r

dE r E r

dσ σ

∂ ∂

=

∂ ∂

( )

( )

(

)

(

)

(

)

2 2

2

2 2 2

a 1 a 2a

a 1 a 2a 1 a

i M

i M iM iM

i M iM

E r E r

σ σ σ σ

σ σ σ

− =

− − + −

+ − + −

.

Karena setiap investor memegang portofolio yang sama yaitu portofolio pasar (pada titik ekuilibrium) maka a=0.

( )

( )

( )

2 a 0

P

i M

P

r M iM

M

E r E r dE r

dσ σ σ

σ =

− =

− + .

Kemiringan CAL sama dengan perubahan imbal hasil yang diharapkan terhadap perubahan standar deviasi maka diperoleh

( )

( )

( )

2

M f i M

M M iM

M

E r r E r E r

σ σ σ

σ

− −

=

− +

( )

M f

(

( )

i f

)

(

( )

M f

)

iM M

M M

E r r E r r

E r r

σ

σ _σ

σ

− − −

− =

− +

( )

(

)

iM

(

(

( )

)

(

( )

)

)

M f M M i f M f

M

E r r σ σ σ E r r E r r

σ

⎛ ⎞

− _⎜− + _⎟= − − −

⎝ ⎠

( )

(

M f

)

1 iM₂

(

(

( )

i f

)

(

( )

M f

)

)

M

E r r σ E r r E r r

σ

⎛ ⎞

− ⎜_⎜− + ⎟_⎟= − − −

⎝ ⎠

( )

(

)

(

( )

)

iM₂

(

(

( )

)

(

( )

)

)

M f M f i f M f

M

E r r E r r σ E r r E r r

σ

− − + − = − − −

( )

(

)

iM₂

( )

M f i f

M

E r r σ E r r

σ

− = −

( )

2

(

( )

)

iM

i f M f

M

E r r σ E r r

σ

= + −

dengan iM₂ i M

σ _β

σ = adalah risiko sistematis.

Sehingga model CAPM klasik adalah

( )

i f i

(

( )

M f

)

E r =r +β E r −r .

Lampiran 2

Bukti Persamaan (2) dan (9)

Misalkan Wj adalah kekayaan awal tahun oleh individu ke-j. Kemudian semua kekayaan

diinvestasikan dalam uang pada salah satu sekuritas ke-i. Misalkan Sij adalah banyaknya investasi

yang dilakukan pada salah satu sekuritas ke-i oleh individu ke-j. Kekayaan awal tahun didefinisikan sebagai berikut

j ij

i

W = ∑S . (L .27) Kekayaan akhir tahunnya adalah

j ij i

i

W% = ∑S R . (L.28) 1

i i

R = +r, r_i merupakan nilai imbal hasil sekuritas ke-i. Anggap bahwa setiap individu ingin memaksimumkan E Uj

(

j

( )

W%j

)

dengan kendala j ij

i

W = ∑S . Di mana Uj adalah fungsi utilitas

yang terdiferensial dan kontinu pada fungsi kekayaan oleh individu ke-j. Ekspansi deret Taylor

( )

j j

U W% di sekitar E Wj

( )

%j sebagai berikut

( )

0

~

~ ( ( )) ~ ~

( ) ( ( ))

! j

j j j

n

j j n

j j

n

U E W

U W W E W

n ∞

=

= ∑ − . (L.29)

Kemudian nilai harapan dari Persamaan (L.28) adalah

( )

0

~

~ ( ( )) ~ ~

( ( ) ( )

! j

j j j

n n

j j

j j

n

U E W

E U W E W E W

n ∞

=

⎛ ⎞

= ∑ ⎜ − ⎟

⎝ ⎠ (L.30)

dimana U( )_jn adalah turunan ke-n dari U_jyang dievaluasi pada E W_j(~_j). Dari Persamaan (L.30)

dimisalkan momen pusat ke-n dari peubah acak W~j adalah

~ ~

( )

j j

n jn E W E Wj

µ = ⎛_⎜ − ⎞_⎟

⎝ ⎠ . (L.31)

Kemudian dengan membentuk Lagrange, masing-masing individu memaksimumkan Z.

~ ( _j)

j

Z= ⎜E U W⎛ ⎞_⎟

⎝ ⎠ dengan kendala j ij

i

W = ∑∞S .

Sehingga maksimumkan

0

~

( _j( _j)) _j( _{j ij})

i

Z E U W L W ∞ S

=

= + − ∑ . (L.32)

Substitusi Persamaan (L.30) dan Persamaan (L.331) ke Persamaan (L.32) sehingga

( )

0 0

~

( ( ))

( )

! j

j

n

j j

jn j ij

n j

U E W

Z L W S

n µ

∞ ∞

= =

= ∑ + −∑ . (L.33)

Untuk penyederhanaan dimisalkan saja j=1 dan turunkan Persamaan (L.33) terhadap Si, maka

diperoleh

( ) ( )

0

0

! !

n n

n n

n

i i i

Z U U

L

S S n µ S µ n

∞

=

⎛ ⎞

∂ ₌ ∂ ₊ ∂ _{− =}

∑ ⎜_⎜ ⎟_⎟

∂ _⎝∂ ∂ _⎠ . (L.34)

Dengan j=1, kekayaan awal tahunnya menjadi _i

i

W = ∑S (L.35)

dan kekayaan akhir tahunnya ~ i i

i

W= ∑S R . (L.36)

Dimisalkan W=E W(~). (L.37) Substitusi Persamaan (L.36) ke Persamaan (L.37) diperoleh

~

( ) ( _{i j}) ( _i) _i

i i

16

Turunkan Persamaan (L.38) terhadap S_i

( _i)

i

W E R S ∂ ₌

∂ . (L.39)

Kemudian, lihat Persamaan (L.34) dan Persamaan (L.39) maka diperoleh

( ) ( 1) ( 1)

( )

! ! !

n n n

i

i i

U U W U

E R

S n n S n

+ +

⎛ ⎞

∂ ₌ ∂ ₌

⎜ ⎟

⎜ ⎟

∂ _{⎝ ⎠} ∂ . (L.40)

Lihat Persamaan (L.31) dan Persamaan (L.34) diperoleh

( )

n

i S µ ∂ ∂ = ~ ~ ( ) n i

E W E W S ⎛ ⎞ ∂ _⎜ ⎛ ₋ ⎞ _⎟ ⎜ ⎟ ⎜ ⎟ ∂ _{⎝ ⎝ ⎠ ⎠} = n

i i i i

i i

i

E S R E S R

S ⎛ ⎞ ∂ _⎜ ⎛_{∑ −} ⎛_∑ ⎞⎞ _⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ∂ _⎝ ⎝ ⎝ ⎠⎠ _⎠

= _{i i i}

( )

_i n

i i

i

E S R S E R

S ⎛ ⎞ ∂ _⎜ ⎛_{∑ −∑} ⎞ _⎟ ⎜ ⎟ ⎜ ⎟ ∂ _⎝ ⎝ ⎠ _⎠ =

( )

1 ~ n

i i i i

i i

i

nE W W S R S E R

S − ⎧_{⎛ ⎞ ∂} ⎫ ⎪ ₋ ⎛_{∑ −∑} ⎞⎪ ⎨⎜ ⎟ _{∂ ⎝}⎜ ⎟_⎠⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ =

(

( )

)

1 ~ n i i

nE W W R E R

− ⎧_{⎛ ⎞} ⎫ ⎪ _{− −} ⎪ ⎨⎜ ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

. (L.41)

Subtitusikan Persamaan (L.40) dan Persamaan (L.41) ke Persamaan (L.42) diperoleh

( ) ( )

0 ! !

n n

n n

n

i i i

Z U U

L

S S n µ S µ n

∞ = ⎛ ⎞ ∂ ₌ ∂ ₊ ∂ ₌ ∑ ⎜_⎜ ⎟_⎟ ∂ _⎝∂ ∂ _⎠

( )

(

)

1

( 1) ( )

0 ~ ( ) ! ! n n n

i n i i

n i

Z U U

E R nE R E R W W L

S n µ n

− + ∞ = ⎛ ⎧ ⎫ ⎞ ∂ _{= ∑⎜ +} ⎪ ₋ ⎛ ₋ ⎞ ⎪ _⎟= ⎨ ⎜ ⎟ ⎬ ⎜ ⎟

∂ _{⎝ ⎪⎩ ⎝ ⎠ ⎪⎭ ⎠} . (L.42)

Pada Persamaan (L.42), ekspansi deret Taylor untuk U(1) di sekitar W sebagai berikut

( 1) 0 ! n n n U n µ + ∞ =

∑ . (L.43)

Substitusi Persamaan (L.43) ke Persamaan (L.42) diperoleh

( )

( )

(

( )

)

1

(1) 2 ~ ! n n

i i i

n

U

E R U nE R E R W W L

n − ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ +∑ ⎨ − ⎜ − ⎟ ⎬= ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

( )

( )

(

( )

)

1

(1) 2 ~ ( 1)! n n

i i i

n

U

E R U nE R E R W W L

n n − ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ +∑ ₋ ⎨ − ⎜ − ⎟ ⎬= ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

. (L.44)

Lihat pada Persamaan (L.31) dengan indeks i=1 maka

~ ~

( )

n

n E W E W µ ⎛⎜ ⎞⎟

⎜ ⎟

⎝ ⎠

= − . (L.45)

Jika n=0

0

0

~ ~

E W E W µ = ⎛_⎜ − ⎛ ⎞_{⎜ ⎟}⎞_⎟

⎝ ⎠

⎝ ⎠ =E(1)=1 (L.46)

dan jika n=1

1

1

~ ~

E W E W µ = ⎛_⎜ − ⎛ ⎞_{⎜ ⎟}⎞_⎟

⎝ ⎠

⎝ ⎠

~ ~

E W⎛ E W⎛ ⎞⎞ = _{⎜ − ⎜ ⎟⎟} ⎝ ⎠

⎝ ⎠

~ ~

E W⎛ ⎞ E E W⎛ ⎛ ⎞⎞ = _{⎜ ⎟}− _{⎜ ⎜ ⎟⎟} ⎝ ⎠ ⎝ ⎝ ⎠⎠

~ ~

E W⎛ ⎞ E W⎛ ⎞ = _{⎜ ⎟}− _{⎜ ⎟}

Selanjutnya, turunkan Persamaan (L.46) dan Persamaan (L.47) terhadap S_i

( )

0

( )

1 0

i i

S µ S µ

∂ ₌ ∂ ₌

∂ ∂ . (L.48)

Persamaan (L.48) mengakibatkan n=2, 3, 4,...,∞. Kemudian kurangkan sekuritas ke-i dengan sekuritas ke-k pada Persamaan (L.44) dengan L=0, sehingga diperoleh

(

)

(1) ( )

(

(

)

)

1

2 ~ 0 ( 1)! n n

i k i k i k

n

U

E R R U E R R E R R W W

n − ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ − +∑ ₋ ⎨ − − − ⎜ − ⎟ ⎬= ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

(

)

(

)

(

)

1

( ) (1) 2 ~ ( 1)! n n

i k i k

i k

n

U E R R E R R W W

E R R

U n − ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ _{− − − −} ⎪ ⎨ ⎜ ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ − = − ∑ −

( )

( )

( )

( )

(

)

(

)

1

( ) (1) 2 ~ ( 1)! n n

i k i k

i k

n

U E R R E R E R W W

E R E R

U n − ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ _{− − − −} ⎪ ⎨ ⎜ ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ = − ∑

− . (L.49)

Pada Persamaan (L.49), misalkan

(

)

( )

(1) _{1 !}

n n

U

U n

θ = −

− (L.50)

Substitusi Persamaan (L.50) ke Persamaan (L.49)

( )

( )

(

(

( )

( )

)

)

1

2

~ n

i k n i k i k

n

E R E R θ E R R E R E R W W

− ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ = + ∑ ⎨ − − − ⎜ − ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

. (L.51)

Anggap ada sekuritas yang bebas risiko. Misalkan Rf = +1 rf . Kemudian subsitusi Rf ke Rk

pada Persamaan (L.51) diperoleh

( )

(

(

( )

)

)

1

2

~ n

i f n i f i f

n

E R R θ E R R E R R W W

− ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ = + ∑ ⎨ − − − ⎜ − ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

( )

(

)

1

2

~ n

f n i f i f

n

R θ E R R E R R W W

− ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ = + ∑ ⎨ − − + ⎜ − ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

( )

(

)

1

2

~ n

f n i i

n

R θ E R E R W W

− ∞ = ⎧ _{⎛ ⎞} ⎫ ⎪ ⎪ = + ∑ ⎨ − ⎜ − ⎟ ⎬ ⎝ ⎠ ⎪ ⎪ ⎩ ⎭

. (L.52)

Misalkan S_f adalah banyaknya investasi yang telah ditanamkan pada sekuritas bebas risiko. Banyaknya investasi yang telah ditanamkan pada portofolio dari sekuritas-sekuritas berisiko adalah