Peramalan Nilai Tukar Mata Uang Rupiah Terhadap Dolar Amerika Serikat Tahun 2014 dengan Menggunakan Jaringan Syaraf Tiruan Model Backpropagation

(1)

PERAMALAN NILAI TUKAR MATA UANG RUPIAH TERHADAP DOLAR AMERIKA SERIKAT TAHUN 2014 DENGAN

MENGGUNAKAN JARINGAN SYARAF TIRUAN MODEL BACKPROPAGATION

SKRIPSI

Diajukan untuk melengkapi dan memenuhi syarat mencapai gelar Sarjana Sains

MOHAMMAD TAUFIKURRAHMAN 120823010

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

PERSETUJUAN

Judul : Peramalan Nilai Tukar Mata Uang Rupiah

Terhadap Dolar Amerika Serikat Tahun 2014 Dengan Menggunakan Jaringan Syaraf Tiruan Model Backpropagation

Kategori : Skripsi

Nama : Mohammad Taufikurrahman

Nomor Induk Mahasiswa : 120823010

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika Dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Disetujui di Medan, Agustus 2014

Disetujui Oleh

Departemen Matematika FMIPA USU Pembimbing 1, Ketua,

(3)

PERSETUJUAN

Judul : Peramalan Nilai Tukar Mata Uang Rupiah

Terhadap Dolar Amerika Serikat Tahun 2014 Dengan Menggunakan Jaringan Syaraf Tiruan Model Backpropagation

Kategori : Skripsi

Nama : Mohammad Taufikurrahman

Nomor Induk Mahasiswa : 120823010

Program Studi : Sarjana (S1) Matematika

Departemen : Matematika

Fakultas : Matematika Dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Disetujui di Medan, Agustus 2014

Komisi Pembimbing:

Pembimbing 2, Pembimbing 1,

Drs. Gim Tarigan, M.Si Drs. Partano Siagian, M.Sc NIP. 19550202 198601 1 001 NIP. 19511227 198003 1 001

Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

(4)

PERNYATAAN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Agustus 2014

(5)

PENGHARGAAN

Puji syukur kepada Tuhan Yang Maha Kuasa atas segala rahmat dan karunia-Nya yang telah dilimpahkan, sehingga penulisan skripsi dengan judul “Peramalan Nilai Tukar Mata Uang Rupiah terhadap Dolar Amerika Serikat tahun 2014 dengan menggunakan Jaringan Syaraf Tiruan Model Backpropagation” dapat diselesaikan dengan baik. Pada kesempatan ini, penulis mengucapkan terima kasih yang sedalam-dalamnya kepada:

1. Bapak Drs. Partano Siagian, M.Sc selaku dosen dan pembimbing I yang berkenan dan rela mengorbankan waktu, tenaga dan pikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.

2. Bapak Drs. Gim Tarigan, M.Si selaku dosen dan pembimbing II yang juga berkenan dan rela mengorbankan waktu, tenaga dan pikiran guna memberikan petunjuk dan bimbingannya dalam penulisan skripsi ini.

3. Bapak Drs. Marihat Situmorang, M.Kom dan Drs. Suwarno Ariswoyo, M.Si selaku dosen pembanding atas masukan dan saran yang telah diberikan demi perbaikan skripsi ini.

4. Bapak Prof. Dr. Tulus, M.Si, Ph.D dan Ibu Dr. Mardiningsih, M.Si selaku ketua dan sekretaris Departemen Matematika FMIPA USU.

5. Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU.

6. Bapak dan Ibu dosen pengajar Departemen Matematika FMIPA USU yang telah memberikan banyak ilmu pengetahuan selama masa perkuliahan.

7. Staf pegawai Departemen Matematika FMIPA USU.

8. Kedua orang tuaku (Irman Munir dan Marleni), Odang (Zamtis Eliyati), Uda (Muhammad Arnando), dan uni-uniku (Imelda Saluza dan Happy Irzaleni) tercinta yang selalu memberikan kasih sayang, semangat dorongan dan do’a agar penulis dapat menyelesaikan skripsi ini dengan baik.

9. Sahabat-sahabat seperjuangan dan semua pihak yang telah membantu dalam penyelesaian skripsi ini yang tidak mungkin disebutkan satu persatu.

(6)

Akhir kata penulis berharap semoga tulisan ini bermanfaat bagi setiap pembaca.

Medan, Agustus 2014 Penulis

(7)

ABSTRAK

(8)

TO PREDICT THE EXCHANGE RATE RUPIAH FOR DOLLAR USA IN 2014 WITH USED NEURAL NETWORK

BACKPROPAGATION MODEL

ABSTRACT

(9)

DAFTAR ISI

DAFTAR GAMBAR xii

DAFTAR SINGKATAN xiii

DAFTAR LAMPIRAN xiv

Bab 1. PENDAHULUAN

1.1. Latar Belakang 1

1.2. Perumusan Masalah 3

1.3. Pembatasan Masalah 3

1.4. Tinjauan Pustaka 4

1.5. Tujuan Penelitian 8

1.6. Kontribusi Penelitian 9

1.7. Metodologi Penelitian 9

Bab 2. LANDASAN TEORI

2.1. Jaringan Syaraf Tiruan 12

2.2. Arsitektur Jaringan 16

2.3. Algoritma Pembelajaran dan Pelatihan 18

2.4. Jaringan Syaraf Tiruan Backpropagation 20

2.4.1. Algoritma 20

2.4.2. Fungsi Aktivasi pada Backpropagation 22

2.4.3. Pelatihan Backpropagation 24

2.5. Backpropagationdalam Peramalan 28 Bab 3. HASIL DAN PEMBAHASAN

3.1. Data Percobaan 33

3.2. Analisis Data 35

Bab 4. KESIMPULAN DAN SARAN

4.1. Kesimpulan 47

(10)

DAFTAR PUSTAKA 49

LAMPIRAN 50

(11)

DAFTAR TABEL

Nomor Tabel

Judul Halaman

2.1. 3.1.

Istilah Jaringan Syaraf Tiruan dan Statistik

Nilai Tukar Rupiah terhadap Dolar Amerika Serikat

(12)

DAFTAR GAMBAR

Sebuah Sel Jaringan Syaraf

Arsitektur Jaringan Model Backpropagation Sebuah Sel Jaringan Syaraf

Jaringan Lapisan Tunggal Jaringan Lapisan Jamak Jaringan Reccurent

Alur Kerja Jaringan Backpropagation Fungsi Linear

Fungsi Logistik Sigmoid Biner Fungsi Logistik Sigmoid Bipolar

Nilai Tukar Rupiah terhadap Dolar Amerika Serikat Hasil Pembelajaran Jaringan Syaraf Tiruan

Perbandingan Data Asli dengan Jaringan Syaraf Tiruan (JST) dari Data Pelatihan

Hasil Pembelajaran Jaringan Syaraf Tiruan

(13)

DAFTAR SINGKATAN

(14)

DAFTAR LAMPIRAN

Data Nilai Tukar Mata Uang Rupiah terhadap Dolar Amerika Serikat (1985 – 2013)

Data yang Akan Dilatih Data yang Akan Diuji

Arsitektur Jaringan yang Digunakan Data Pelatihan yang Akan Ditransformasi Data Pengujian yang Akan Ditransformasi Hasil Transformasi Data Pelatihan

Hasil Transformasi Data Pengujian

Hasil Mean Square Error (MSE) dari Data Pelatihan Hasil Mean Square Error (MSE) dari Data Pengujian

Perbandingan Antara Data Asli dengan Hasil Ramalan Jaringan Syaraf Tiruan (JST) untuk Data Pelatihan

Perbandingan Antara Data Asli dengan Hasil Ramalan Jaringan Syaraf Tiruan (JST) untuk Data Pengujian

Hasil Ramalan Jaringan Syaraf Tiruan Tahun 2014 dan 2015

(15)

ABSTRAK

(16)

TO PREDICT THE EXCHANGE RATE RUPIAH FOR DOLLAR USA IN 2014 WITH USED NEURAL NETWORK

BACKPROPAGATION MODEL

ABSTRACT

(17)

BAB 1

PENDAHULUAN

1.1. Latar Belakang

Semua negara mempunyai mata uang sebagai alat tukar. Pertukaran uang dengan barang yang terjadi disetiap negara tidak akan menimbulkan masalah mengingat nilai uang yang berlaku sudah disesuaikan dengan nilai barang. Masalah itu akan muncul jika barang berasal dari negara lain. Oleh karena itu perlu adanya mekanisme yang menyediakan akses untuk menukarkan mata uang negara dengan mata uang negara lainnya, sehingga pembayaran dari barang tersebut dapat diterima. Dengan kata lain dibutuhkan transaksi valuta asing untuk menukarkan mata uang antar negara.

Pasar valuta asing (foreign exchange market) merupakan suatu jenis perdagangan atau transaksi yang memperdagangkan terhadap mata uang negara lainnya yang melibatkan pasar-pasar uang utama di dunia selama 24 jam secara berkesinambungan. Pasar valuta asing membantu perdagangan internasional dan investasi dengan memungkinkan konversi mata uang. Salah satu mata uang yang paling banyak diperdagangkan di bursa valuta internasional adalah Dolar Amerika Serikat.

(18)

depan dilakukan berdasarkan informasi masa lalu dari suatu variabel atau kesalahan masa lalu ini dinamakan deret berkala atau time series (Makridakis, 1999:21). Teknik peramalan yang digunakan dalam metode ini antara lain Auto Regressive Integrated Moving Avarege (ARIMA) atau Box-Jenkins, ekonometri

regresi, exponential smoothing, dan lain sebagainya. Metode-metode tersebut dapat digunakan untuk meramal data pengunjung perpustakaan, volume penjualan teh hitam, dan keuangan (seperti peramalan nilai tukar (kurs), peramalan produk domestik b_{ruto, peramalan harga saham, dan lain sebagainya).}

Dalam beberapa tahun terakhir telah terjadi peningkatan yang substansial dalam volatilitas pertukaran nilai mata uang, kenaikan volatilitas ini terkait dengan peningkatan atau penurunan dalam perdagangan. Menurut Baxter dan Stockman (1989), memberikan bukti empiris bahwa peningkatan volatilitas nilai tukar memberikan dampak yang besar terhadap nilai tukar suatu negara dan inflasi. Peningkatan dari volatilitas nilai tukar ini dapat menghambat perdagangan internasional dan investasi internasional. Artinya, pasar valuta asing merupakan pasar yang paling volatil. Karena itulah akan muncul suatu masalah apabila data runtun waktu mengandung volatil atau data runtun waktu memiliki sistem pola data dengan formulasi yang selalu berubah-ubah atau dengan kata lain sistem yang memiliki tingkat kesulitan yang tinggi untuk dibuat formulasi modelnya sehingga hasil ramalan atau prediksi dengan menggunakan metode-metode statistik sebelumnya kurang memberikan hasil yang baik, karena metode-metode sebelumnya sulit untuk menangkap adanya volatilitas. Salah satu aplikasi data runtun waktu yang terkenal sulit untuk diprediksi adalah nilai tukar, hal ini dikarenakan kurs merupakan salah satu pasar yang sangat volatile (Yu et al, 2007).

(19)

sistem pemroses informasi yang memiliki karakteristik mirip dengan jaringan syaraf biologi. Salah satu metode dari jaringan syaraf tiruan yang sangat baik dalam menangani masalah pengenalan pola-pola kompleks dan juga dapat digunakan untuk peramalan adalah metode backpropagation atau propagasi balik (Puspitaningrum, 2006:125).

Berdasarkan latar belakang tersebut, maka penulis tertarik untuk mengadakan penelitian mengenai “PERAMALAN NILAI TUKAR MATA UANG RUPIAH TERHADAP DOLAR AMERIKA SERIKAT TAHUN 2014 DENGAN MENGGUNAKAN JARINGAN SYARAF TIRUAN MODEL BACKPROPAGATION”.

1.2. Perumusan Masalah

Permasalahan yang akan dibahas dalam penelitian ini adalah ”Bagaimana penggunaan jaringan syaraf tiruan model backpropagation untuk meramal nilai tukar mata uang Rupiah terhadap Dolar Amerika Serikat pada tahun 2014”.

1.3. Pembatasan Masalah

Agar permasalahan yang dikaji lebih fokus dan menjadi lebih jelas. Adapun pembatasan dalam penelitian ini adalah:

1. Peramalan pergerakan nilai tukar mata uang Rupiah terhadap Dolar Amerika Serikat tersebut dilakukan untuk tahun 2014.

2. Data yang digunakan adalah data pergerakan nilai tukar mata uang Rupiah terhadap Dolar Amerika Serikat mulai tahun 1985 – 2013.

(20)

1.4. Tinjauan Pustaka

Menurut Siang (2005:2), Jaringan syaraf tiruan atau neural network adalah sistem pemroses informasi yang memiliki karakteristik mirip dengan jaringan syaraf biologi. Menurut Fausett (1994:3), jaringan syaraf tiruan dibentuk sebagai generalisasi model matematika dari jaringan syaraf biologi dengan asumsi sebagai berikut:

1. Pemrosesan informasi terjadi pada banyak elemen sederhana (neurons). 2. Sinyal yang dikirimkan diantara neuron-neuron melalui

penghubung-penghubung.

3. Penghubung antar neuron memiliki bobot yang akan memperlemah atau memperkuat sinyal.

4. Untuk menentukan keluaran (output), setiap neuron menggunakan fungsi aktivasi yang dikenakan pada penjumlahan masukan (input) yang diterima. Besarnya keluaran ini selanjutnya dibandingkan dengan suatu batas ambang.

dan jaringan syaraf tiruan ditentukan oleh tiga hal, yakni: 1. Pola hubungan antar neuron (arsitektur jaringan).

2. Metode untuk menentukan bobot penghubung (metode training/ learning/ algoritma).

(21)

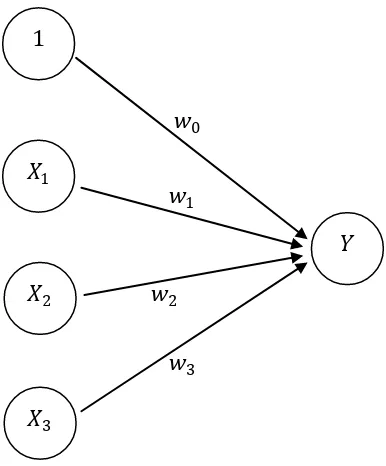
Sebagai contoh, perhatikan arsitektur jaringan pada gambar berikut:

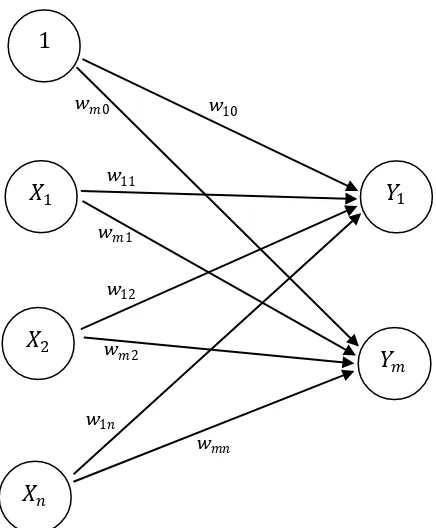
Pada gambar 1.1 terlihat sebuah sel jaringan syaraf tiruan pada simpul � menerima masukan dari neuron 1, �₁, �₂, dan �₃ dengan bobot (weight) masing-masing adalah �₀, �₁, �₂, dan �₃. Argumen fungsi aktivasi adalah net masukan (kombinasi linear masukan dan bobotnya). Keempat sinyal neuron yang ada dijumlahkan sehingga diperoleh persamaan net = 1�₀ + �₁�₁ + �₂�₂ + �₃�₃. Apabila nilai fungsi aktivasi cukup kuat, maka sinyal akan diteruskan. Nilai fungsi aktivasi (keluaran model jaringan) juga dapat digunakan sebagai dasar untuk merubah bobot.

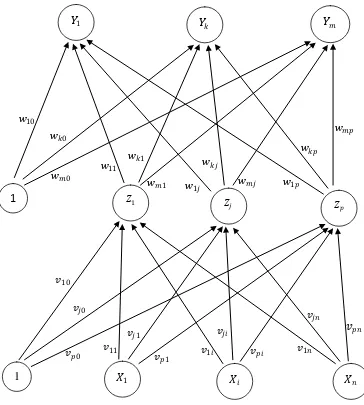
Backpropagation memiliki beberapa neuron yang ada dalam satu atau

lebih lapisan tersembunyi. Gambar 1.2 adalah arsitektur backpropagation dengan

� buah masukan (ditambah sebuah bias), sebuah lapisan tersembunyi yang terdiri dari � neuron (ditambah sebuah bias), serta � buah neuron keluaran. �_�� merupakan bobot garis dari neuron masukan �_� ke neuron lapisan tersembunyi �_� (�_�₀ merupakan bobot garis yang menghubungkan bias di neuron masukan ke neuron lapisan tersembunyi �_�). �_�� merupakan bobot dari neuron lapisan

Gambar 1.1. Sebuah Sel Jaringan Syaraf

1

(22)

tersembunyi �_� ke neuron keluaran �_� (�_�₀ merupakan bobot dari bias di lapisan tersembunyi ke neuron keluaran �_�).

Algoritma pelatihan untuk jaringan backpropagation dengan satu lapisan tersembunyi (dengan fungsi aktivasi sigmoid biner) adalah sebagai berikut:

1. Langkah 1

Inisialisasi semua bobot dengan bilangan acak kecil 2. Langkah 2

Jika kondisi penghentian belum dipenuhi, lakukan langkah 3-9

��0

Gambar 1.2. Arsitektur Jaringan Model Backpropagation

��

�1

1

(23)

3. Langkah 3

Untuk setiap pasang data pelatihan, lakukan langkah 4-9

Fase I : Propagasi maju 4. Langkah 4

Tiap unit masukan menerima sinyal dan meneruskannya ke unit tersembunyi di atasnya.

Fase II : Propagasi Mundur 7. Langkah 7

Hitung faktor � unit keluaran berdasarkan kesalahan di setiap unit keluaran

�� (� = 1, 2,…, �)

�� = (�� − ��)�′(�_��) = (�� − ��)��(1− ��)

�� = target keluaran

�� merupakan unit kesalahan yang akan dipakai dalam perubahan bobot

lapisan di bawahnya.

Hitung perubahan bobot �_�� dengan laju pemahaman

(24)

8. Langkah 8

Hitung faktor � unit tersembunyi berdasarkan kesalahan di setiap unit tersembunyi �_� (� = 1, 2, ..., �)

�_��_� = � �_��_��

�=1

Faktor � unit tersembunyi:

�� =�_��′��_��= �_��1− ��

Hitung perubahan bobot �_��

∆�� =��, (� = 1,2, … ,� ;�= 0,1, … ,�)

Fase III : Perubahan Bobot 9. Langkah 9

Hitung semua perubahan bobot. Perubahan bobot garis yang menuju ke unit keluaran, yaitu:

��(��) =��(��) +∆��, (� = 1, 2,⋯,� ;�= 0, 1, 2,⋯,�)

Perubahan bobot garis yang menuju ke unit tersembunyi adalah:

��(��) =��(��) +∆��, (� = 1, 2,⋯,� ;�= 0, 1, 2,⋯,�)

Setelah pelatihan selesai dilakukan, jaringan bisa digunakan untuk pengenalan pola. Dalam hal ini, hanya propagasi maju (langkah 5 dan 6) saja yang digunakan untuk menentukan keluaran jaringan.

1.5. Tujuan Penelitian

(25)

1.6. Kontribusi Penelitian

Hasil penelitian ini diharapkan berkontribusi bagi:

1. Penulis

a. Meningkatkan wawasan dalam bidang nilai tukar mata uang. b. Sebagai penerapan ilmu dari mata kuliah yang telah diperoleh.

2. Wisatawan/Pengamat pasar valuta asing

a. Dapat mengetahui pergerakan nilai tukar mata uang Rupiah terhadap Dolar Amerika Serikat pada tahun 2014.

b. Menjadi bahan pertimbangan bagi para pengamat valuta asing dalam mengambil keputusan yang tepat.

3. Departemen/Universitas

a. Dapat dijadikan sebagai bahan studi kasus bagi pembaca dan acuan bagi mahasiswa.

b. Dapat memberikan bahan referensi bagi pihak perpustakaan.

c. Dapat berfungsi sebagai bahan bacaan yang dapat menambah ilmu pengetahuan bagi pembacanya.

1.7. Metodologi Penelitian

Metodologi penelitian dalam penelitian ini adalah:

1. Merancang sistem peramalan nilai tukar mata uang menggunakan jaringan syaraf tiruan model backpropagation, langkah-langkahnya sebagai berikut: a. Menetapkan Tujuan Sistem

(26)

b. Memperoleh Data

Data diperoleh dari buku Kajian Ekonomi dan Keuangan di Perpustakaan Kantor Perwakilan Bank Indonesia Wilayah IX (SUMUT & ACEH), pergerakan nilai tukar mata uang Rupiah terhadap Dolar Amerika Serikat mulai tahun 1985 – 2013.

c. Transformasi Data Masukan

Transformasi data masukan bertujuan untuk menyesuaikan nilai range data dengan logsigmoid threshold function dalam sistem backpropagation. Ini berarti nilai kuadrat masukan harus berada pada

range 0 sampai 1. Sehingga range masukan yang memenuhi syarat adalah nilai data masukan dari 0 sampai 1 atau dari –1 sampai 1. Oleh karena itu keluaran yang dihasilkan pun akan berada pada range 0 sampai 1, untuk mendapatkan nilai sebenarnya dari keluaran perlu dilakukan proses detransformasi.

d. Merancang Arsitektur Jaringan

Merancang arsitektur jaringan bertujuan untuk memperoleh komposisi jumlah neuron, elemen masukan, lapisan tersembunyi, dan nilai parameter training yang optimal. Langkah-langkah untuk membangun model jaringan data ini adalah:

1) Membentuk data pelatihan (training) dan pengujian (testing).

2) Penentuan jumlah lapisan tersembunyi dan jumlah neuron ditentukan secara trial and error sampai dicapai error minimumnya.

e. Menentukan Fungsi Aktivasi

(27)

f. Penentuan koefisien laju pemahaman (�) dapat dilakukan dengan trial and error untuk memperoleh nilai bobot yang paling optimum agar Mean

Squared Error (MSE) jaringan dapat diperbaiki.

g. Mendapatkan model pelatihan yang baik digunakan untuk mendapatkan peramalan.

h. Peramalan data nilai tukar mata uang untuk data pelatihan dan data pengujian.

i. Grafik perbandingan antara data asli dengan peramalan menggunakan jaringan syaraf tiruan model backpropagation.

2. Jaringan yang dibangun akan dinilai keakuratan peramalannya. Kaedah penilaian yang akan digunakan adalah Mean Square Error (MSE). Ketepatan model diukur secara relatif menggunakan MSE yang didapat dari persamaan berikut ini:

(28)

BAB 2

LANDASAN TEORI

2.6. Jaringan Syaraf Tiruan

Jaringan syaraf tiruan atau neural network merupakan suatu sistem informasi yang mempunyai cara kerja dan karakteristik menyerupai jaringan syaraf pada makhluk hidup, yang terdiri dari elemen-elemen pemrosesan sederhana yang disebut neuron (unit atau node). Setiap neuron dihubungkan dengan neuron lain dengan hubungan komunikasi yang disebut arsitektur jaringan. Jaringan syaraf tiruan adalah sistem pemroses informasi yang memiliki karakteristik mirip dengan jaringan syaraf biologi (Siang, 2005:2).

Jaringan syaraf tiruan diilhami dari cabang ilmu biologi yang berkaitan dengan sistem syaraf. Cabang ilmu tersebut adalah neurobiology, tujuan utama dari neurobiology adalah untuk menjelaskan bagaimana sel-sel syaraf dapat membedakan dan mengembangkan hubungan khusus mereka dan bagaimana jaringan syaraf dapat mengingat kembali semua informasi.

Menurut Fausett (1994:3), jaringan syaraf tiruan dibentuk sebagai generalisasi model matematika dari jaringan syaraf biologi dengan asumsi sebagai berikut:

(29)

3. Penghubung antar neuron memiliki bobot yang akan memperkuat atau memperlemah sinyal.

4. Untuk menentukan keluaran, setiap neuron menggunakan fungsi aktivasi yang dikenakan pada penjumlahan masukan yang diterima. Besarnya keluaran ini selanjutnya dibandingkan dengan suatu batas ambang.

dan jaringan syaraf tiruan ditentukan oleh tiga hal, yakni:

1. Pola hubungan antar neuron (arsitektur jaringan).

2. Metode untuk menentukan bobot penghubung (metode training/ learning/ algoritma).

3. Fungsi aktivasi.

Neuron adalah suatu unit pemroses informasi yang menjadi dasar dalam pengoperasian jaringan syaraf tiruan (Siang, 2005:23). Neuron terdiri dari tiga elemen pembentuk yaitu:

1. Himpunan unit-unit yang dihubungkan dengan jalur koneksi.

2. Suatu unit penjumlah yang akan menjumlahkan masukan-masukan sinyal yang sudah dikalikan dengan bobotnya.

3. Fungsi aktivasi yang akan menentukan apakah sinyal dari unit masukan akan diteruskan ke unit lain ataukah tidak.

Di dalam jaringan syaraf tiruan, istilah node atau unit sering digunakan untuk menggantikan neuron. Setiap unit pada jaringan menerima atau mengirim sinyal dari atau ke unit-unit yang lainnya. Pengiriman sinyal akan disampaikan melalui suatu penghubung. Kekuatan hubungan yang terjadi antara setiap simpul yang saling terhubung dikenal dengan nama bobot.

(30)

1. Aktifitas unit-unit lapisan masukan menunjukkan informasi dasar yang kemudian digunakan dalam jaringan syaraf tiruan.

2. Aktifitas setiap unit-unit lapisan tersembunyi ditentukan oleh aktifitas dari unit masukan dan bobot dari koneksi antara unit masukan dan unit-unit dari lapisan tersembunyi.

3. Karakteristik dari unit-unit keluaran tergantung pada aktifitas unit-unit lapisan tersembunyi dan bobot antara unit lapisan tersembunyi dan unit-unit keluaran.

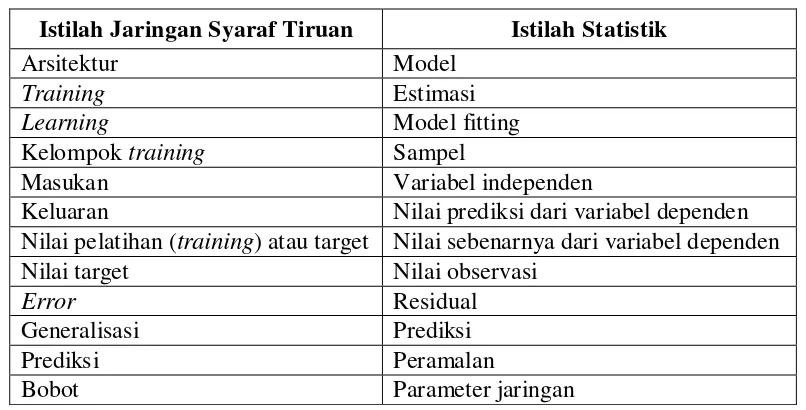
Literatur jaringan syaraf tiruan dan statistika memuat banyak konsep yang sama dengan istilah yang berbeda namun ada istilah yang sama dalam kedua literatur dengan makna yang berbeda. Daftar hubungan istilah yang banyak digunakan adalah sebagai berikut:

Tabel 2.1. Istilah Jaringan Syaraf Tiruan dan Statistik

Istilah Jaringan Syaraf Tiruan Istilah Statistik

Arsitektur Model

Training Estimasi

Learning Model fitting

Kelompok training Sampel

Masukan Variabel independen

Keluaran Nilai prediksi dari variabel dependen Nilai pelatihan (training) atau target Nilai sebenarnya dari variabel dependen

Nilai target Nilai observasi

Error Residual

Generalisasi Prediksi

Prediksi Peramalan

Bobot Parameter jaringan

(31)

Perubahan harga bobot koneksi dapat dilakukan dengan berbagai cara, tergantung pada jenis algoritma pelatihan yang digunakan. Dengan mengatur besarnya nilai bobot ini diharapkan bahwa kinerja jaringan dalam mempelajari berbagai macam pola yang dinyatakan oleh setiap pasangan masukan-keluaran akan meningkat.

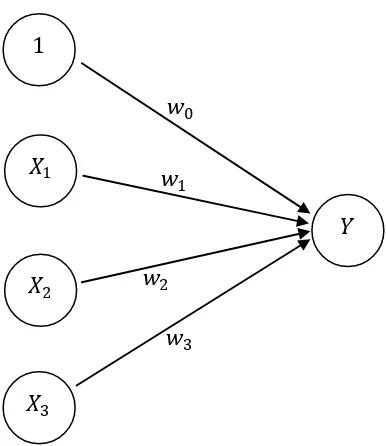
Pada gambar 2.1 terlihat sebuah sel syaraf tiruan sebagai elemen penghitung. Simpul � menerima masukan dari unit 1 (bias), �₁, �₂, dan �₃ dengan bobot masing-masing adalah �₀, �₁, �₂, dan �₃. Argumen fungsi aktivasi adalah net masukan (kombinasi linear masukan dan bobotnya). Keempat sinyal unit yang ada dijumlahkan sehingga diperoleh persamaan net = 1�0 + �1�1 + �2�2 + �3�3.

Besarnya sinyal yang diterima oleh � mengikuti fungsi aktivasi � = f(net).

Apabila nilai fungsi aktivasi cukup kuat, maka sinyal akan diteruskan. Nilai fungsi aktivasi (keluaran model jaringan) juga dapat digunakan sebagai dasar untuk merubah bobot.

�0

Gambar 2.1. Sebuah Sel Jaringan Syaraf

�1

�2

�

�3

�1

�2

(32)

2.7. Arsitektur Jaringan

Arsitektur jaringan syaraf tiruan digolongkan menjadi tiga kelompok yaitu sebagai berikut:

a. Jaringan Lapisan Tunggal (Single Layer Networks)

Pada jaringan ini, sekumpulan unit masukan dihubungkan langsung dengan sekumpulan keluarannya. Sinyal dari lapisan masukan sampai lapisan keluaran.

Setiap unit akan dihubungkan dengan unit-unit lainnya yang berada di atasnya dan di bawahnya, tetapi tidak dengan unit yang berada pada lapisan yang sama. Contohnya adalah model ADALINE, perceptron, dan lain sebagainya.

Pada gambar 2.2 akan diperlihatkan arsitektur jaringan lapisan tunggal � buah unit masukan (�₁, �₂,…, �_�) dengan 1 unit bias dan � buah unit keluaran

Gambar 2.2. Jaringan Lapisan Tunggal

1

�10

(33)

b. Jaringan Lapisan Jamak (Multi Layer Networks)

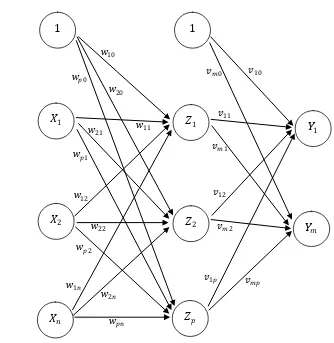
Jaringan ini adalah perluasan dari jaringan lapisan tunggal. Pada jaringan ini, selain unit masukan dan keluaran, ada unit-unit lain (lapisan tersembunyi). Lapisan tersembunyi (hidden layer) didalam jaringan ini bisa saja lebih dari satu.

Jaringan lapisan jamak dapat menyelesaikan masalah yang lebih kompleks dibandingkan dengan lapisan tunggal. Model yang termasuk dalam jaringan ini antara lain: MADALINE, backpropagation.

Pada gambar 2.3 diperlihatkan jaringan � buah unit masukan

Gambar 2.3. Jaringan Lapisan Jamak

�2

(34)

c. Jaringan Reccurent

Model jaringan reccurent (reccurent network) mirip dengan jaringan lapisan tunggal ataupun jamak. Hanya saja, ada unit keluaran yang memberikan sinyal pada unit masukan (sering disebut feedback loop). Contoh model pada jaringan ini antara lain: Hopfield network, Jordan network, Elmal network. Arsitektur jaringan recurrent dapat dilihat pada gambar 2.4:

2.8. Algoritma Pembelajaran dan Pelatihan

Jaringan syaraf tiruan merupakan hubungan antara masukan dan keluaran yang harus diketahui secara pasti dan apabila hubungan tersebut sudah diketahui maka bisa dibuat suatu model. Ide dasar jaringan syaraf tiruan adalah konsep pembelajaran atau pelatihan. Algoritma pelatihan artinya membentuk pemetaan (fungsi) yang menggambarkan hubungan antara vektor masukan dan vektor keluaran.

Agar bisa menyelesaikan suatu permasalahan, jaringan syaraf tiruan memerlukan algoritma pembelajaran atau pelatihan yaitu bagaimana sebuah konfigurasi jaringan bisa dilatih untuk mempelajari data historis yang ada. Dengan

�1 ��

(35)

pelatihan ini, pengetahuan yang terdapat dalam data bisa diserap dan direpresentasikan oleh harga-harga bobot koneksinya.

Berdasarkan cara memodifikasi bobotnya, ada 2 macam pelatihan yang dikenal yaitu:

a. Dengan Supervisi (Supervised)

Metode ini bisa digunakan jika keluaran yang diharapkan telah diketahui sebelumnya. Biasanya pembelajaran dilakukan dengan menggunakan data yang telah ada. Dalam pelatihan dengan supervisi, terdapat sejumlah pasangan data (masukan-target keluaran) yang dipakai untuk melatih jaringan. Pada setiap pelatihan, suatu masukan diberikan ke jaringan kemudian jaringan akan memproses dan mengeluarkan keluaran. Selisih antara keluaran jaringan dengan target (keluaran yang diinginkan) merupakan kesalahan yang terjadi. Kemudian jaringan akan memodifikasi bobot sesuai dengan kesalahan tersebut. Model yang menggunakan pelatihan dengan supervisi antara lain: Perceptron, ADALINE, Backpropagation.

b. Tanpa Supervisi (Unsupervised)

(36)

2.9. Jaringan Syaraf Tiruan Backpropagation

Metode backpropagation merupakan metode yang sangat baik dalam menangani masalah pengenalan pola-pola kompleks. Sama seperti model jaringan syaraf tiruan lainnya, backpropagation melatih jaringan untuk mendapatkan keseimbangan antara kemampuan jaringan untuk mengenali pola yang digunakan selama pelatihan serta kemampuan jaringan untuk memberikan respon yang benar terhadap pola masukan yang serupa (tapi tidak sama) dengan pola yang dipakai selama pelatihan.

Dalam jaringan backpropagation setiap unit yang berada di lapisan masukan akan terhubung dengan setiap unit yang berada pada lapisan tersembunyi, dan setiap unit yang berada pada lapisan tersembunyi akan terhubung dengan setiap unit yang berada pada lapisan keluaran.

Menurut Puspitaningrum (2006:125), jaringan syaraf tiruan model backpropagation terdiri dari banyak lapisan (multilayer neural networks):

1. Lapisan masukan (1 buah). Lapisan masukan terdiri dari unit atau unit-unit masukan, mulai dari unit-unit masukan 1 sampai unit-unit masukan �.

2. Lapisan tersembunyi (minimal 1). Lapisan tersembunyi terdiri unit-unit atau unit-unit tersembunyi, mulai dari unit tersembunyi 1 sampai unit tersembunyi

�.

3. Lapisan keluaran (1 buah). Lapisan keluaran terdiri dari unit-unit keluaran, mulai dari unit keluaran 1 sampai unit keluaran �.

2.9.1. Algoritma

Backpropagation merupakan salah satu algoritma pelatihan dengan supervisi,

(37)

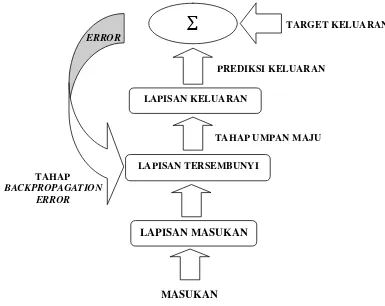
keluaran yang akan dihasilkan. Istilah ‘Backpropagation’ diambil dari cara kerja jaringan ini, berikut merupakan alur kerja jaringan backpropagation:

Dapat dilihat dari gambar 2.5 cara kerja jaringan backpropagation, mula-mula jaringan diinisialisasi dengan bobot yang diset dengan bilangan acak. Kemudian sampel pelatihan dimasukkan ke dalam jaringan. Sampel pelatihan terdiri pasangan vektor masukan dan vektor target keluaran. Keluaran dari jaringan berupa vektor prediksi keluaran. Selanjutnya vektor keluaran hasil jaringan atau prediksi keluaran dibandingkan dengan target keluaran, untuk mengetahui apakah jaringan keluaran sudah sesuai dengan yang diharapkan (prediksi keluaran sudah sama dengan target keluaran).

Error yang dihasilkan akibat adanya perbedaan antara prediksi keluaran

dengan target keluaran tersebut kemudian dihitung untuk mengupdate bobot-bobot koneksi yang relevan dengan jalan mempropagasikan kembali error. Setiap

Gambar 2.5. Alur Kerja Jaringan Backpropagation

(38)

perubahan bobot yang terjadi diharapkan dapat mengurangi besarnya error. Proses akan terus berlanjut sampai kerja jaringan mencapai tingkat yang diinginkan atau sampai kondisi perhentian dipenuhi. Pada umumnya kondisi perhentian yang sering digunakan adalah jumlah iterasi atau error. Iterasi akan berhenti jika jumlah iterasi yang dilakukan jaringan telah melebihi jumlah iterasi yang ditentukan, atau jika nilai error yang didapat lebih kecil dari batas toleransi.

2.9.2. Fungsi Aktivasi pada Backpropagation

Karakteristik yang harus dimiliki fungsi aktivasi pada backpropagation adalah sebagai berikut:

1. Kontinu.

2. Terdiferensial dengan mudah. 3. Fungsi yang tidak menurun.

Fungsi aktivasi diharapkan jenuh (mendekati nilai-nilai maksimum dan minimum secara asimtot). Fungsi aktivasi digunakan di dalam metode backpropagation adalah sebagai berikut:

1. Fungsi Identitas (Linear)

Fungsi linear mempunyai nilai keluaran yang sama dengan nilai masukannya. Fungsi linear didefinisikan sebagai berikut:

(39)

2. Fungsi Sigmoid Biner

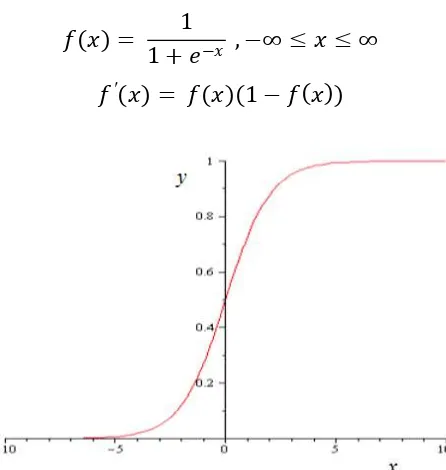
Fungsi sigmoid biner yang memiliki range (0,1). Fungsi sigmoid biner didefinisikan sebagai berikut:

�(�) = 1

1 +�−� ,−∞ ≤ � ≤ ∞

�′₍_�_{) =}_�₍_�₎₍₁_{− �}₍_�₎₎

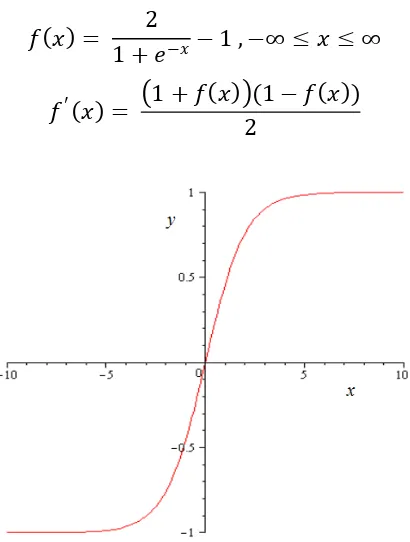
3. Fungsi Sigmoid Bipolar

Fungsi lain yang sering dipakai adalah fungsi sigmoid bipolar dengan range (-1,1) yang didefinisikan sebagai berikut:

Gambar 2.6. Fungsi Linear

(40)

�(�) = 2

1 +�−� −1 ,−∞ ≤ � ≤ ∞

�′₍_�_{) =}�1 +�(�)�(1− �(�)) 2

2.9.3. Pelatihan Backpropagation

Jaringan feedforward (umpan maju) sama seperti jaringan syaraf yang lain, pelatihan dilakukan dalam rangka perhitungan bobot sehingga pada akhir pelatihan akan didapat bobot yang baik. Selama proses pelatihan, bobot-bobot akan diatur secara iteratif untuk meminimumkan nilai error yang terjadi. Nilai error didapat dari hasil perhitungan rata-rata kuadrat kesalahan (MSE). Mean Square Error juga dijadikan dasar perhitungan unjuk kerja fungsi aktivasi.

Pelatihan untuk jaringan feedforward sering menggunakan gradien dari fungsi aktivasi untuk menentukan bagaimana mengatur bobot-bobot dalam rangka meminimumkan kinerja. Gradien ini ditentukan dengan menggunakan suatu teknik yang disebut backpropagation.

Pada dasarnya, algoritma pelatihan standar backpropagation akan menggerakkan bobot dengan arah gradien negatif. Prinsip dasar dari algoritma

(41)

backpropagation adalah memperbaiki bobot-bobot jaringan dengan arah yang membuat fungsi aktivasi menjadi turun dengan cepat.

Menurut Siang (2005:100-103), pelatihan backpropagation meliput i 3 fase yaitu sebagai berikut:

1. Fase 1, yaitu propagasi maju.

Pola masukan dihitung maju mulai dari lapisan masukan hingga lapisan keluaran menggunakan fungsi aktivasi yang ditentukan.

2. Fase 2, yaitu propagasi mundur.

Selisih antara keluaran jaringan dengan target yang diinginkan merupakan kesalahan yang terjadi. Kesalahan yang terjadi itu dipropagasi mundur. Dimulai dari garis yang berhubungan langsung dengan unit-unit di lapisan keluaran.

3. Fase 3, yaitu perubahan bobot.

Modifikasi bobot untuk menurunkan kesalahan yang terjadi. Ketiga fase tersebut diulang-ulang terus hingga kondisi penghentian dipenuhi.

Algoritma pelatihan untuk jaringan backpropagation dengan satu lapisan tersembunyi (dengan fungsi aktivasi sigmoid biner) adalah sebagai berikut:

1. Langkah 1

Inisialisasi semua bobot dengan bilangan acak kecil 2. Langkah 2

Jika kondisi penghentian belum dipenuhi, lakukan langkah 3-9 3. Langkah 3

(42)

Fase I : Propagasi maju 4. Langkah 4

Tiap unit masukan menerima sinyal dan meneruskannya ke unit tersembunyi di atasnya.

Fase II : Propagasi Mundur 7. Langkah 7

Hitung faktor � unit keluaran berdasarkan kesalahan di setiap unit keluaran

�� (� = 1, 2,..., �)

�� = (�� − ��) �′(�_��) = (�� − ��) ��(1− ��)

�� = target keluaran

�� merupakan unit kesalahan yang akan dipakai dalam perubahan bobot

lapisan di bawahnya.

Hitung perubahan bobot �_�� dengan laju pemahaman �

(43)

8. Langkah 8

Hitung faktor � unit tersembunyi berdasarkan kesalahan di setiap unit tersembunyi �_� (� = 1, 2, ..., �)

�_��_� = � �_� �_��

�=1

Faktor � unit tersembunyi:

�� =�_��′��_��= �_��1− ��

Hitung perubahan bobot �_��

∆�� =��, (� = 1,2, … ,� ;�= 0,1, … ,�)

Fase III : Perubahan Bobot 9. Langkah 9

Hitung semua perubahan bobot. Perubahan bobot garis yang menuju ke unit keluaran, yaitu:

��(��) =��(��) +∆�� , (�= 1, 2,⋯,� ;� = 0, 1, 2,⋯,�)

Perubahan bobot garis yang menuju ke unit tersembunyi adalah:

��(��) =��(��) +∆�� , (� = 1, 2,⋯,� ;� = 0, 1, 2,⋯,�)

Setelah pelatihan selesai dilakukan, jaringan dapat dipakai untuk pengenalan pola. Dalam hal ini, hanya propagasi maju (langkah 5 dan 6) saja yang digunakan untuk menentukan keluaran jaringan.

(44)

Pemilihan bobot awal sangat mempengaruhi jaringan syaraf tiruan dalam mencapai minimum global (atau mungkin lokal saja) terhadap nilai error dan cepat tidaknya proses pelatihan menuju kekonvergenan.

Apabila bobot awal terlalu besar maka masukan ke setiap lapisan tersembunyi atau lapisan keluaran akan jatuh pada daerah di mana turunan fungsi sigmoidnya akan sangat kecil. Apabila bobot awal terlalu kecil, maka masukan ke setiap lapisan tersembunyi atau lapisan keluaran akan sangat kecil. Hal ini akan menyebabkan proses pelatihan berjalan sangat lambat. Biasanya bobot awal diinisialisasi secara random dengan nilai antara -0,5 sampai 0,5 (atau -1 sampai 1 atau interval yang lainnya).

2.10. Backpropagation dalam Peramalan

Backpropagation merupakan salah satu metode jaringan syaraf tiruan yang bisa

diaplikasikan dengan baik dalam bidang peramalan (forecasting). Peramalan yang sering diketahui adalah peramalan harga saham, peramalan besarnya penjualan, nilai tukar valuta asing, prediksi besarnya aliran sungai dan lain sebagainya. Secara umum, masalah peramalan dapat dinyatakan dengan sejumlah data time series �₁, �₂,..., �_�. Masalahnya adalah memperkirakan berapa harga �_�₊₁ berdasarkan �₁, �₂,..., �_�. Langkah-langkah yang diperlukan dalam membangun arsitektur jaringan untuk peramalan adalah sebagai berikut:

1. Transformasi Data

(45)

a. Transformasi Polinomial

�′ = ln �

keterangan:

�′ = nilai data setelah transformasi polinomial.

� = nilai data aktual.

b. Transformasi Normal

�� =_��0− ��

�� − ��

keterangan:

�� = nilai data normal

�0 = nilai data aktual.

�� = nilai minimum data aktual keseluruhan.

�� = nilai maksimum data aktual keseluruhan.

c. Transformasi Linier pada Selang [�,�]

�′ ₌(� − ��)(� − �)

�� − �� +�

keterangan:

�′ _{= nilai data setelah transformasi linier.}

� = nilai data aktual.

�� = nilai minimum data aktual keseluruhan.

(46)

2. Pembagian Data

Setelah transformasi data, langkah selanjutnya adalah pembagian data. Data dibagi menjadi data pelatihan dan data pengujian. Beberapa komposisi data pelatihan dan pengujian yang sering digunakan adalah sebagai berikut:

a. 80% untuk data pelatihan dan 20% untuk data pengujian. b. 70% untuk data pelatihan dan 30% untuk data pengujian. c. 2/3 untuk data pelatihan dan 1/3 untuk data pengujian. d. 50% untuk data pelatihan dan 50% untuk data pengujian. e. 60% untuk data pelatihan dan 40% untuk data pengujian.

Aspek pembagian data harus ditekankan agar jaringan mendapat data pelatihan yang secukupnya dan data pengujian dapat menguji prestasi pelatihan yang dilakukan berdasarkan nilai MSE data pelatihan dan data pengujian. Bilangan data yang kurang untuk proses pelatihan akan menyebabkan jaringan mungkin tidak dapat mempelajari keacakan data dengan baik. Sebaliknya, data yang terlalu banyak untuk proses pelatihan akan melambatkan proses pemusatan (konvergensi).

3. Perancangan Model Pelatihan yang Baik

Langkah selanjutnya setelah pembagian data adalah penentuan bilangan unit masukan, bilangan lapisan tersembunyi, bilangan unit lapisan tersembunyi dan bilangan unit keluaran yang akan digunakan dalam jaringan. Terdapat beberapa aturan yang dapat membantu perancangan model pelatihan yang baik, yaitu sebagai berikut:

a. Jumlah unit masukan sama dengan periode di mana data berfluktuasi. b. Jumlah unit keluaran sama dengan jumlah keluaran masalah.

(47)

d. Jika menggunakan satu lapisan tersembunyi, bilangan unit tersembunyi awal adalah 75% dari bilangan simpul masukan.

Beberapa kaedah untuk memperkirakan bilangan unit tersembunyi yaitu sebagai berikut:

ℎ = �, 2�

ℎ = �

2

keterangan:

� = bilangan simpul masukan yang digunakan

ℎ = bilangan simpul tersembunyi.

Penentuan bilangan simpul tersembunyi yang terbaik diperoleh secara trial and error dari simpul 1 sampai 2�.

4. Memilih dan MenggunakanModel Pelatihan yang Baik

(48)

�� = nilai aktual pada waktu �

�� = nilai ramalan pada waktu �

Berdasarkan nilai MSE yang terendah dari proses pelatihan diperoleh model pelatihan yang baik. Keakuratan ramalan jaringan dilihat dari nilai MSE dari proses pengujian.

5. PemilihanModel Pelatihan yang Baikdan Penggunaannya untuk Peramalan

Langkah-langkah pemilihan model pelatihan yang baik sebagai berikut:

a. Proses pelatihan dilakukan terhadap data pelatihan dengan arsitektur jaringan yang memiliki bilangan unit tersembunyi berbeda akan diperoleh nilai keluaran jaringan atau prediksi keluaran, MSE-nya dihitung. Jaringan dengan nilai MSE terendah dipilih sebagai model pelatihan yang baik untuk digunakan dalam peramalan.

(49)

2. Perlu dilakukan penambahan lapisan tersembunyi, sehingga hasil ramalannya dapat dibandingkan dengan hasil ramalan yang penulis dapatkan.

(50)

DAFTAR PUSTAKA

Fausett, Laurene. 1994. Fundamentals of Neural Networks Architectures, Algorithms, and Applications. London: Prentice Hall, Inc.

Makridakis, Spyros, dkk. 1999. Metode dan Aplikasi Peramalan. Tangerang: Binarupa Aksara.

Puspitaningrum, Dyah. 2006. Pengantar Jaringan Saraf Tiruan. Yogyakarta: Andi.

Sercu, Piet, and Raman Uppal. 2000. Exchange Rate Volatility, Trade, and Capital Flows under Alternative Exchange Rate Regimes. New York: Cambridge University Press.

Siang, Jong Jek. 2005. Jaringan Syaraf Tiruan dan Pemrogrammannya menggunakan MATLAB. Yogyakarta: Andi.

(51)

Lampiran 1. Data Nilai Tukar Mata Uang Rupiah terhadap Dolar Amerika Serikat

(52)

Lampiran 2. Data yang Akan Dilatih

No. Masukan (Input) Target

t-2 t-1 t t+1

(53)

Lampiran 3. Data yang Akan Diuji

t-2 t-1 t t+1

(54)

Lampiran 4. Arsitektur Jaringan yang Digunakan

�1

�3

�1

�2

�3

�

�2

�4

�5

(55)

Lampiran 5. Data Pelatihan yang Akan Ditransformasi

No. X1 X2 X3

(56)

Lampiran 6. Data Pengujian yang Akan Ditransformasi

No. X1 X2 X3

(57)

Lampiran 7. Hasil Transformasi Data Pelatihan

No. X1 X2 X3

1 0 0 0

2 0,0556 0,0010 0,0090 3 0,0566 0,0100 0,0166 4 0,0651 0,0176 0,0287 5 0,0723 0,0297 0,0391 6 0,0836 0,0401 0,0471 7 0,0935 0,0481 0,0526 8 0,1010 0,0535 0,0629 9 0,1062 0,0638 0,0752 10 0,1159 0,0762 0,0838 11 0,1275 0,0847 0,3429 12 0,1356 0,3435 0,7286 13 0,3800 0,7289 0,6229 14 0,7439 0,6232 0,9080

15 0,6442 0,9081 1

16 0,9132 1 0,8331

(58)

Lampiran 8. Hasil Transformasi Data Pengujian

No. X1 X2 X3

1 0,4283 0,0148 0,2185

2 0,0148 0,2185 1

3 0,2185 1 0,2088

4 1 0,2088 0

5 0,2088 0 0,0393

(59)

Lampiran 9. Hasil Mean Square Error (MSE) dari Data Pelatihan

Error Pembagian Data Data Pelatihan

(60)

Lampiran 10. Hasil Mean Square Error (MSE) dari Data Pengujian

Error Pembagian Data Data Pengujian

(61)

Lampiran 11. Perbandingan Antara Data Asli dengan Hasil Ramalan Jaringan Syaraf Tiruan (JST) untuk Data Pelatihan

No. Tahun Data Asli JST

1 1985 1.125,25

2 1986 1.641,00

3 1987 1.650,00

(62)

Lampiran 12. Perbandingan Antara Data Asli dengan Hasil Ramalan Jaringan Syaraf Tiruan (JST) untuk Data Pengujian

1 2005 9.830,00 9.830,00

2 2006 9.020,00 9.020,00

3 2007 9.419,00 9.419,00

4 2008 10.950,00 10.950,00

5 2009 9.400,00 9.400,00

6 2010 8.991,00 8.991,00

7 2011 9.068,00 9.068,00

8 2012 9.670,00 9.670,00

(63)

Lampiran 13. Hasil Ramalan Jaringan Syaraf Tiruan Tahun 2014 dan 2015

No. Tahun Hasil Prediksi

1 2014 12.111,09

(64)

DAFTAR PUSTAKA

Fausett, Laurene. 1994. Fundamentals of Neural Networks Architectures, Algorithms, and Applications. London: Prentice Hall, Inc.

Makridakis, Spyros, dkk. 1999. Metode dan Aplikasi Peramalan. Tangerang: Binarupa Aksara.

Puspitaningrum, Dyah. 2006. Pengantar Jaringan Saraf Tiruan. Yogyakarta: Andi.

Sercu, Piet, and Raman Uppal. 2000. Exchange Rate Volatility, Trade, and Capital Flows under Alternative Exchange Rate Regimes. New York: Cambridge University Press.

Siang, Jong Jek. 2005. Jaringan Syaraf Tiruan dan Pemrogrammannya menggunakan MATLAB. Yogyakarta: Andi.

(65)

Lampiran 1. Data Nilai Tukar Mata Uang Rupiah terhadap Dolar Amerika Serikat

(66)

Lampiran 2. Data yang Akan Dilatih

t-2 t-1 t t+1

(67)

Lampiran 3. Data yang Akan Diuji

t-2 t-1 t t+1

(68)

Lampiran 4. Arsitektur Jaringan yang Digunakan

�1

�3

�1

�2

�3

�

�2

�4

�5

(69)

Lampiran 5. Data Pelatihan yang Akan Ditransformasi

No. X1 X2 X3

(70)

Lampiran 6. Data Pengujian yang Akan Ditransformasi

No. X1 X2 X3

(71)

Lampiran 7. Hasil Transformasi Data Pelatihan

No. X1 X2 X3

1 0 0 0

2 0,0556 0,0010 0,0090 3 0,0566 0,0100 0,0166 4 0,0651 0,0176 0,0287 5 0,0723 0,0297 0,0391 6 0,0836 0,0401 0,0471 7 0,0935 0,0481 0,0526 8 0,1010 0,0535 0,0629 9 0,1062 0,0638 0,0752 10 0,1159 0,0762 0,0838 11 0,1275 0,0847 0,3429 12 0,1356 0,3435 0,7286 13 0,3800 0,7289 0,6229 14 0,7439 0,6232 0,9080

15 0,6442 0,9081 1

16 0,9132 1 0,8331

(72)

Lampiran 8. Hasil Transformasi Data Pengujian

No. X1 X2 X3

1 0,4283 0,0148 0,2185

2 0,0148 0,2185 1

3 0,2185 1 0,2088

4 1 0,2088 0

5 0,2088 0 0,0393

(73)

Lampiran 9. Hasil Mean Square Error (MSE) dari Data Pelatihan