ABSTRAK
PENGARUH MODEL PEMBELAJARAN PROBLEM BASED
LEARNING TERHADAP KEMAMPUAN PEMECAHAN
MASALAH MATEMATIS SISWA
(Studi pada Siswa Kelas VIII SMP Negeri 1 Pagelaran T.P. 2013/2014)
Oleh
RIANITA AFRILIA
Penelitian ini bertujuan untuk mengetahui pengaruh model pembelajaran Problem Based Learning terhadap kemampuan pemecahan masalah matematis siswa. Desain penelitian yang digunakan adalah posttest only control group design. Populasi penelitian ini adalah seluruh siswa kelas VIII SMP Negeri 1 Pagelaran Tahun Pelajaran 2013/2014 yang terdistribusi dalam sepuluh kelas. Sampel penelitian adalah siswa kelas VIII1 dan VIII3 yang diambil dengan teknik
purposive random sampling. Data penelitian diperoleh melalui tes kemampuan pemecahan masalah matematis yang dianalisis menggunakan Uji Mann-Whitney.
Berdasarkan hasil analisis data, disimpulkan bahwa model pembelajaran Problem Based Learning berpengaruh terhadap kemampuan pemecahan masalah matematis siswa.
Moto
Berangkat dengan penuh keyakinan
Berjalan dengan penuh keikhlasan
Istiqomah dalam menghadapi cobaan
“ YAKIN, IKHLAS,ISTIQOMAH”
(Muhammad Zainuddin)
Jika salah maka perbaikilah namun jika kita menyerah maka kita
akan gagal.
P
ersembahan
Segala Puji Bagi Allah SWT, Dzat Yang Maha Sempurna,
Sholawat serta Salam Selalu Tercurah Kepada Rosululloh Muhammad SAW
Kupersembahkan karya kecil ini sebagai tanda cinta & kasih sayangku kepada :
Ayah (Syahroni) dan Ibu (Rohilawati), yang telah membesarkan,
mendidik dengan penuh kasih sayang yang tulus, dan selalu mendoakan
yang terbaik untuk keberhasilan dan kebahagianku.
Adik-adikku (Yoga Pratama dan Bella Puspita) serta seluruh keluarga
besar yang terus memberikan dukungan dan doanya padaku.
Para pendidik yang telah mengajar dan mendidik dengan penuh
kesabaran.
Semua Sahabat yang begitu tulus menyayangiku dengan segala
kekuranganku, yang selalu memeberikan doa dan semangat, terimakasih
atas kebersamaan selama ini. Semoga kita selalu dapat menjaga
silaturrahmi yang baik.
iii SANWACANA
Alhamdulillahi Robbil ‘Alamin, puji syukur kehadirat Allah SWT yang telah
melimpahkan rahmat dan karunia-Nya sehingga penyusunan skripsi ini dapat diselesaikan. Sholawat serta salam semoga selalu tercurah atas manusia yang akhlaknya paling mulia, yang telah membawa perubahan luar biasa, menjadi uswatun hasanah, yaitu Rasulullah Muhammad SAW.
Skripsi yang berjudul “Pengaruh Model Pembelajaran Problem Based Learning terhadap Kemampuan Pemecahan Masalah Matematis Siswa kelas VIII SMP Negeri 1 Pagelaran (Studi pada Siswa Kelas VIII SMP Negeri 1 Pagelaran T.P. 2013/2014) adalah salah satu syarat untuk memperoleh gelar sarjana pendidikan pada Fakultas Keguruan dan Ilmu Pendidikan, Universitas Lampung.
Penulis menyadari sepenuhnya bahwa terselesaikannya penyusunan skripsi ini tidak terlepas dari bantuan berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih yang tulus ikhlas kepada:
iv 2. Ibu Dr. Tina Yunarti, M.Si., selaku Dosen Pembimbing II yang telah bersedia meluangkan waktu untuk membimbing, memberikan sumbangan pemikiran, kritik, dan saran kepada penulis demi terselesaikannya skripsi ini.
3. Ibu Dra. Rini Asnawati, M.Pd., selaku dosen pembahas yang telah memberi masukan dan saran-saran kepada penulis.
4. Bapak Dr. Bujang Rahman, M.Si., selaku Dekan FKIP Universitas Lampung beserta staff dan jajarannya yang telah memberikan bantuan kepada penulis dalam menyelesaikan skripsi ini.
5. Bapak Dr. Caswita, M.Si., selaku Ketua Jurusan PMIPA yang telah mem-berikan kemudahan kepada penulis dalam menyelesaikan skripsi ini.
6. Ibu Dra. Nurhanurawati, M.Pd., selaku Ketua Program Studi Pendidikan Matematika yang telah memberikan kemudahan kepada penulis dalam menyelesaikan skripsi ini.
7. Bapak dan Ibu dosen Pendidikan Matematika di Fakultas Keguruan dan Ilmu Pendidikan yang telah memberikan bekal ilmu pengetahuan kepada penulis. 8. Bapak Suwardi SY, S.Pd., selaku Kepala SMP Negeri 1 Pagelaran beserta
Wakil, staff, dan karyawan yang telah memberikan kemudahan selama penelitian.
9. Ibu M. Sulastri, S.Pd., selaku guru mitra yang telah banyak membantu dalam penelitian.
v 11.Ayah (Syahroni) dan Ibu (Rohilawati) tercinta, atas perhatian dan kasih sayang yang telah diberikan selama ini yang tidak pernah lelah untuk selalu mendoakan yang terbaik
12.Adik-adikku (Yoga dan Bella) serta keluarga besarku yang telah memberikan doa, semangat, dan motivasi kepadaku
13.Keluarga besar di Liwa , Bapak, Ibu, Among, Ngah, Reki serta Ibu Septi dan Pak Suharto yang telah memberikan banyak dukungan dan motivasi.
14.Sahabat yang terkasih, Andriyani Mustika, Cita Bhekti, Hesti Lestari, Fitri Aprilia dan Nurul Rohmah yang selama ini memberiku semangat dan doa serta selalu menemani saat suka dan duka. Semoga persahabatan dan kebersamaan kita selalu menjadi kenangan yang indah sampai kapanpun. 15.Teman-teman karibku tersayang, seluruh angkatan 2010 Kelas A Pendidikan
Matematika: Aan, Beni, Tripau, Rusdi , Novrian, Arif, Qorry, Intan, Nurul H, Iga, Ebta, Asih, Imas, Rini, Dhea, Ria, Yulisa, Novi, Utari, Dian, Sulis, Tri.H, Fertil, Endang dan dua sahabat ku Kismon, Alji, Wira, Aulia, Valenti dan Joshua atas kebersamaannya selama ini dan semua bantuan yang telah diberikan. Semoga kebersamaan kita selalu menjadi kenangan yang terindah. 16.Teman-teman seperjuangan angkatan 2010 Kelas B, kakak-kakakku angkatan
2006, 2007, 2008 dan 2009 serta adik-adikku angkatan 2011, 2012, dan 2013 terima kasih atas kebersamaannya.
vi 18.Pak Liyanto, penjaga Gedung G, terima kasih atas bantuan dan perhatiannya
selama ini.
19.Almamater tercinta yang telah mendewasakanku.
20.Semua pihak yang telah membantu dalam penyusunan skripsi ini.
Semoga dengan kebaikan, bantuan, dan dukungan yang telah diberikan pada penulis mendapat balasan pahala yang setimpal dari Allah SWT dan semoga skripsi ini bermanfaat.
Bandar Lampung, 10 September 2014 Penulis,
vi DAFTAR ISI
Halaman
DAFTAR TABEL ... viii
DAFTAR LAMPIRAN ... x
I. PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 8
C. Tujuan Penelitian ... 8
D. Manfaat Penelitian ... 9
E. Ruang Lingkup Penelitian ... 9
II. TINJAUAN PUSTAKA ... 10
A. Teori Belajar yang Melandasi Problem Based Learning... 10
B. Model Pembelajaran Problem Based Learning ... 12
C. Kemampuan Pemecahan Masalah Matematis ... 18
D. Kerangka Pikir... ... 22
E. Anggapan Dasar... ... 25
F. Hipotesis... ... 25
III. METODE PENELITIAN ... 26
A.Populasi dan Sampel ... 26
B.Desain Penelitian ... 27
vii D. Data Penelitian ... 30 E. Teknik Pengumpulan Data ... 30 E. Instrumen Penelitian ... 30 IV. HASIL PENELITIAN DAN PEMBAHASAN
A. Hasil Penelitian ... 41 B. Pembahasan ... 44 V. SIMPULAN DAN SARAN
A. Simpulan ... 49 B. Saran ... 50 DAFTAR PUSTAKA
vi DAFTAR TABEL
Tabel 2.1 Tahap-Tahap Pelaksanaan dalam Problem Based Learning ... 16
Tabel 3.1 Rata-Rata Nilai Ujian Mid Semester Siswa Kelas VIII SMP Negeri 1 Pagelaran ... 26
Tabel 3.2 Desain Penelitian ... 28
Tabel 3.3 Pedoman Penskoran Tes Pemecahan Masalah ... 31
Tabel 3.4 Validitas Butir Item Soal ... 33
Tabel 3.5 Interpretasi Nilai Daya Pembeda... 35
Tabel 3.6 Daya Pembeda Butir Item Soal ... 36
Tabel 3.7 Interpretasi Indeks Tingkat Kesukaran ... 37
Tabel 3.8 Tingkat Kesukaran Butir Item Soal ... 37
Tabel 3.9 Hasil Uji Normalitas data Postes dengan Chi-Kuadrat ... 39
Tabel 3.10 Hasil Uji Normalitas data Gain denganuji (K-S-Z) ... 39
Tabel 4.1 Data Kemampuan AkhirPemecahan Masalah Matematis Siswa ... 42
Tabel 4.2 Data Pencapaian Indikator Kemampuan Pemecahan Masalah Matematis Siswa Setelah Pembelajaran ... 43
vi DAFTAR LAMPIRAN
Halaman
Lampiran A.1 Rencana Pelaksanaan Pembelajaran (RPP) PBL ... 54
Lampiran A.3 Rencana Pelaksanaan Pembelajaran (RPP) Konvesional ... 86
Lampiran A.4 Lembar Kerja Siswa (LKS) ... 118
Lampiran B.1 Kisi-Kisi Instrumen Tes ... 139
Lampiran B.2 Tes Kemampuan Pemecahan Masalah Matematis ... 141
Lampiran B.3 Pedoman Pemberian Skor dan Kunci Jawaban Tes Kemampuan Pemecahan Masalah Matematis ... 142
Lampiran B.4 Form Validasi Instrumen ... 145
Lampiran B.5 Pedoman Penskoran Tes Pemecahan Masalah ... 147
Lampiran B.6 Tes Kemampuan Pemecahan Masalah ... 148
Lampiran C.1 Analisis Validitas Butir Soal Tes Uji Coba... 151
Lampiran C.2 Reabilitas Butir Soal ... 152
Lampiran C.3 Daya Pembeda dan Tingkat Kesukaran ... 153
Lampiran C.4 Data Kemampuan Akhir Pemecahan Masalah Matematis PBL 154 Lampiran C.5 Data Kemampuan Awal Pemecahan Masalah Matematis Konvesional ... 155
vii Lampiran C.7 Analisi Uji Normalitas Data Posttest Kemampuan Akhir
Pemecahan Masalah Matematis Kelas Konvesional ...161 Lampiran C.8 Pencapaian Indikator Kemampuan Akhir Pemecahan Masalah . 163 Lampiran C.14 Analisis Uji Mann Whitney Data Kemampuan Akhir Pemecahan
1
I. PENDAHULUAN
A. Latar Belakang Masalah
Tujuan pendidikan nasional adalah memberikan kesempatan pada anak didik untuk mengembangkan bakat dan kemampuannya seoptimal mungkin. Pendidikan pada dasarnya merupakan suatu upaya untuk memberikan pengetahuan, wawasan, keahlian dan keterampilan kepada individu untuk mengembangkan potensi - potensi yang ada di dalam diri mereka. Hal ini sesuai pada UUD 1945 pasal 31
yang berbunyi “Setiap warga negara berhak mendapatkan pendidikan”.
Pernyataan di atas memberikan penekanan bahwa seluruh warga negara berhak dan layak mendapatkan pendidikan secara merata tanpa adanya perbedaan latar belakang. Pendidikan juga merupakan pilar utama dalam pembangunan. Untuk itu diperlukan adanya perubahan dalam dunia pendidikan guna meningkatkan mutu pendidikan itu sendiri.
Sesuai dengan tujuan pendidikan di atas, diperlukan suatu pembelajaran yang dapat meningkatkan kualitas pendidikan, salah satunya dalam bidang matematika. Standar isi Permendiknas nomor 22 tahun 2006 menyatakan bahwa pelajaran matematika bertujuan agar siswa memiliki kemampuan sebagai berikut:
2 2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika, dalam membuat generalisasi, menyusun bukti, atau menjeleaskan gagasan dan pertanyaan matematika
3. Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh
4. Mengomunikasikan gagasan dengan simbol, tabel, diagram, media lain untuk memperjelas keadaan atau masalah
5. Memiliki sikap menghargai kegunaan matematika dalam kehidupan yaitu memiliki rasa ingin tahu, perhatian, dan minat dlam mempelajari matematika, serta ulet dan percaya diri dalam memecahkan masalah matematika.
Tujuan pembelajaran matematika yang dirumuskan Kurikulum Tingkat Satuan Pendidikan (Depdiknas, 2006) menyatakan bahwa mata pelajaran matematika bertujuan agar siswa mempunyai kemampuan untuk memahami konsep matematika, menggunakan penalaran, memecahkan masalah, mengomunikasikan gagasan dengan simbol, tabel, diagram atau media lain untuk memperjelas keadaan atau masalah. Berdasarkan tujuan pembelajaran matematika tersebut, kemampuan pemecahan masalah merupakan salah satu kemampuan yang penting dan harus dimiliki oleh siswa. Untuk mencapai tujuan pembelajaran matematika, salah satu aspek yang harus dikuasai siswa adalah kemampuan pemecahan masalah matematis.
3 (Hudiono, 2005) terdapat beberapa alasan perlunya pemecahan masalah yaitu memberi kelancaran siswa dalam membangun suatu konsep dan berfikir matematis serta untuk memiliki pemahaman masalah yang kuat. Penggunaan pemecahan masalah matematis yang sesuai dengan permasalahan dapat menjadikan gagasan dan ide-ide matematika lebih konkrit dan membantu siswa untuk memecahkan suatu masalah yang kompleks menjadi lebih sederhana. Oleh sebab itu, kemampuan pemecahan masalah matematis perlu dimiliki oleh siswa karena dapat memberi kemudahan kepada siswa dalam membangun suatu konsep dan berfikir matematis.
4 TIMSS, yang subtansinya kontekstual, menuntut penalaran, argumentasi, dan kreativitas dalam penyelesaiannya Wardhani dan Rumiati (2011:2). Hal ini dikarenakan pada proses pembelajaran umumnya siswa cenderung mengikuti cara yang biasa digunakan oleh gurunya. siswa tidak dapat mengembangkan ide dan kemampuan yang mereka miliki. Akibatnya kemampuan pemecahan masalah matematis siswa menjadi tidak bekembang secara optimal.
Hasil survey tersebut menunjukkan bahwa kemampuan siswa Indonesia dalam memecahkan masalah masih tergolong rendah. Penelitian lain dilakukan oleh Rakhmasari (Kurniawati, 2013) menunjukkan bahwa siswa masih sulit untuk membuat kesimpulan, memahami permasalahan, dan memberikan alasan atas jawaban yang dihasilkan. Hal ini disebabkan karena pembelajaran matematika yang biasa dilakukan bersifat prosedural. Siswa belum terbiasa untuk menyelesaikan soal yang bersifat nonrutin sehingga kemampuan berpikir tingkat tinggi seperti kemampuan pemecahan masalah matematis mereka belum terlatih. Padahal kemampuan ini diperlukan siswa untuk dapat mengembangkan, memahami konsep-konsep, serta dapat menyelesaikan masalah matematis.
5 pemecahan masalah matematis. Selain itu siswa mengalami kesulitan jika diminta untuk menyelesaikan soal yang mengembangkan kemampuan pemecahan masalah matematis, seperti merencanakan strategi penyelesaian masalah. Berdasarkan hasil tes pendahuluan untuk mengetahui kemampuan pemecahan masalah matematis siswa di kelas VIII SMP Negeri 1 Pagelaran dengan contoh soal sebagai berikut:
“sebuah persegi panjang memiliki ukuran panjang (3x – 4) cm dan lebar (x + 1)
cm. Jika keliling 34 cm maka susunlah bentuk representatifnya dari kalimat tersebut dan tentukan luas persegi panjang tersebut!”
6 di LKS siswa. Penyelesaian soal pun masih terpaku pada satu cara, siswa cenderung mengikuti langkah-langkah yang biasa digunakan oleh gurunya dan belum terbiasa menyelesaikan soal dengan banyak kemungkinan jawaban. Dengan proses pembelajaran yang seperti itu, maka siswa akan jarang mendapatkan kesempatan untuk mengembangkan kemampuan pemecahan masalahnya. Akibatnya, tingkat pemahaman siswa terhadap materi ajar menjadi kurang optimal dan siswa menjadi pasif.
7 Menanggapi permasalahan kemampuan pemecahan masalah yang ada di atas, maka diperlukan usaha dari guru selaku pendidik untuk menciptakan suasana belajar dan menyenangkan. Salah satu cara untuk menggembangkan kemampuan pemecahan masalah matematis siswa yaitu dengan suatu model pembelajaran yang mengutamakan keaktifan pada diri siswa sehingga mampu mengembangkan kemampuan pemecahan masalah matematisnya. Selain itu diperlukan suatu model pembelajaran yang menyajikan tugas-tugas dalam bentuk masalah karena dengan adanya masalah maka siswa akan berusaha untuk mencari solusinya dengan berbagai ide dan representasi sehingga kemampuan berfikir siswa benar-benar dioptimalkan melalui proses pemecahan masalah tersebut. Berdasarkan hal tersebut perlu diterapkannya suatu model pembelajaran yang dapat meningkatkan kemampuan siswa dalam memahami dan dapat meningkatkan kemampuan pemecahan masalah matematis siswa.
8 Dalam pembelajaran PBL, siswa dihadapkan pada permasalahan-permasalahan kontekstual. Siswa dituntut untuk menyelesaikan masalah-masalah tersebut untuk memperoleh konsep matematika. Siswa juga dilatih untuk menginterpretasikan ide-idenya ke dalam simbol matematika atau gambar dan menyelesaikannya. Dalam proses tersebut, siswa tidak bekerja secara individu tetapi siswa mendiskusikannya dengan teman kelompoknya. Setelah itu, setiap kelompok mempresentasikan hasil diskusinya di depan kelas kemudian kelompok yang lain menanggapi. Oleh karena itu, dilakukan studi eksperimen menggunakan model pembelajaran PBL untuk melihat apakah model pembelajaran PBL berpengaruh terhadap kemampuan pemecahan masalah matematis siswa pada jenjang SMP.
B. Rumusan Masalah
Berdasarkan latar belakang masalah yang telah diuraikan di atas, maka rumusan masalah dalam penelitian ini adalah apakah model pembelajaran Problem Based Learning berpengaruh terhadap kemampuan pemecahan masalah matematis siswa kelas VIII semester genap SMP Negeri 1 Pagelaran tahun pelajaran 2013/2014?”
C.Tujuan Penelitian
9
D.Manfaat Penelitian
Penelitian ini diharapkan dapat bermanfaat secara teoritis dan praktis, manfaat tersebut adalah sebagai berikut:
1. Manfaat Teoritis
Penelitian ini secara teoritis diharapkan mampu memberikan sumbangan terhadap perkembangan pendidikan dan pembelajaran matematika, terutama terkait dengan model pembelajaran Problem Based Learning dan juga kemampuan pemecahan masalah matematis.
2. Manfaat Praktis
Dilihat dari segi praktis, penelitian ini memberikan manfaat antara lain: a. Bagi guru dan calon guru, untuk menambah wawasan dalam pembelajaran
matematika sebagai model alternatif yaitu dengan menggunakan model pembelajaran Problem Based Learning dan keterkaitannya dalam pemecahan masalah matematis siswa.
b. Bagi Peneliti lainnya, dalam menemukan strategi pembelajaran yang tepat dan memberi masukan bagi guru dan calon guru dalam kegiatan pembelajaran matematika dengan menerapkan pembelajaran Problem Based Learning.
E. Ruang Lingkup Penelitian
Adapun ruang lingkup dalam penelitian ini sebagai berikut :
10 sekolah yang diteliti, yaitu guru aktif memberikan informasi, sedangkan kegiatan siswa menyimak, mencatat, dan mengerjakan tugas.
2. Model pembelajaran Problem Based Learning
Problem Based Learning adalah model pembelajaran yang digunakan oleh guru untuk mengembangkan kemampuan siswa dalam memecahkan suatu masalah secara sistematis agar kemampuan berfikir siswa dioptimalkan dan memperoleh pengetahuan dan konsep dasar.
3. Kemampuan pemecahan masalah matematis siswa adalah kemampuan siswa mengidentifikasi masalah, merencanakan strategi dan prosedur pemecahan masalah, melakukan prosedur pemecahan masalah, memeriksa kembali langkah-langkah yang dilakukan.
11
II. TINJAUAN PUSTAKA
A. Kajian Teori
1. Teori Belajar yang Melandasi Problem Based Learning
Teori yang melandasi Problem Based Learning adalah teori Vygotsky, Bruner dan Dewey. Teori Vgostky menjelaskan bahwa siswa membentuk pengetahuan sebagai hasil dari pikiran dan kegiatan siswa sendiri melalui bahasa. Menurut Vygotsky, proses pembelajaran akan terjadi jika anak bekerja atau menangani tugas-tugas yang belum dipelajari, namun tugas-tugas tersebut masih berada dalam jangkauan mereka yang disebut dengan zone of proximal development,yaitu daerah tingkat perkembangan sedikit di atas daerah perkembangan seseorang saat ini. Pembelajaran terjadi melalui tantangan dan bantuan dari guru atau teman sejawat yang lebih mampu, siswa bergerak ke dalam zona perkembangan terdekat mereka dimana pembelajaran baru terjadi (Ibrahim dan Nur 2005: 19).
12 satu kemungkinan yang ia pandang terbaik untuk memecahkan masalah tersebut dan hasilnya akan membuktikan apakah kemungkinan pemecahan masalah tersebut benar atau salah.
Berbeda dengan dua pendapat di atas Bruner (Trianto, 2009:38) mengatakanbahwa belajar penemuan sesuai dengan pencarian pengetahuan secara aktif oleh manusia, dan dengan sendirinya memberi hasil yang paling baik. Konsep penting dari teori belajar yang diungkapkan oleh Bruner adalah scaffolding. Bruner memberikan scaffolding sebagai suatu proses dimana seorang siswa dibantu menuntaskan masalah tertentu melampaui kapasitas perkembangannya melalui bantuan dari seorang guru atau orang lain yang memiliki kemampuan lebih.
2. Model Pembelajaran Problem Based Learning
Penggunaan strategi pembelajaran sangat penting untuk menunjang tercapainya tujuan pembelajaran. Dalam proses pembelajaran guru harus memiliki model pembelajaran yang tepat agar siswa dapat belajar secara efektif, efisien dan mengena pada tujuan yang diharapkan. Pembelajaran Problem Based Learning (PBL) merupakan salah satu model pembelajaran yang menekankan keterlibatan siswa dalam kegiatan pembelajaran untuk mencapai tujuan pembelajaran yang diharapkan.
13 berguna untuk mengungkapkan konsepsi awal siswa dan digunakan untuk membangkitkan motivasi belajar; (2) Tahap eksplorasi, tahap ini berfungsi sebagai mediasi pengungkapan ide-ide atau pengetahuan dalam diri siswa; (3) Tahap diskusi dan penjelasan konsep, pada tahap ini siswa diupayakan untuk bekerja sama dengan temannya, berusaha menjelaskan pemahamannya kepada orang lain dan mendengar, bahkan menghargai temuan temannya; (4) Tahap pengembangan dan aplikasi konsep, tahap ini merupakan tahap untuk mengukur sejauh mana siswa telah memahami suatu konsep dengan menyelesaikan permasalahan.
Problem Based Learning didasarkan pada teori psikologi kognitif. Menurut Barrows (Jusuf, 2009:1), PBL adalah model pembelajaran berdasarkan pada prinsip penggunaan kasus (masalah) sebagai titik pangkal untuk mendapatkan dan mengintegrasi pengetahuan yang baru. Fokusnya tidak banyak pada apa yang sedang dilakukan oleh siswa, tetapi pada apa yang siswa pikirkan selama mengerjakannya.
14 Pembelajaran PBL merupakan model belajar yang menggunakan masalah sebagai langkah awal dalam mengumpulkan dan mengintegrasikan pengetahuan baru. Model ini juga berfokus pada keaktifan peserta didik dalam kegiatan pembelajaran, siswa tidak lagi belajar satu arah seperti pada model pembelajaran konvensional. Dengan model pembelajaran ini diharapkan siswa dapat mengembangkan pengetahuan mereka sendiri. sPBL memiliki ciri-ciri seperti Wee & Kek (Amir, 2009:12) “pembelajaran dimulai dengan pemberian masalah, biasanya memiliki konteks dengan dunia nyata,pemelajar secara berkelompok aktif merumuskan masalah dan mengidentifikasi kesenjangan pengetahuan mereka, mempelajari dan mencari solusi dari masalah. Sementara pendidik lebih banyak memfasilitasi. Ketimbang memberi materi, pendidik merancang sebuah sekenario masalah, memberikan clue indikasi-indikasi tentang sumber bacaan tambahan dan berbagai arahan dan saran yang diperlukan saat pelajar menjalankan proses. Meskipun bukanlah pembelajaran yang sama sekali baru, Tan (Amir, 2009:13) menyatakan bahwa penerapan model pembelajaranPBL mengalami kemajuan yang pesat di banyak sekolah dari disiplin ilmu di negara-negara maju.
Menurut Pannen (2001:23) pembelajaran PBL (pembelajaran berdasarkan masalah) mempunyai 5 asumsi utama, yaitu :
a. Pembelajaran bersifat student centered
b. Pembelajajaran terjadi pada kelompok-kelompok kecil c. Guru berperan sebagai fasilitator dan moderator
d. Masalah menjadi fokus dan sarana untuk mengembangkan ketrampilan pemecahan masalah.
15 Sedangkan menurut Rusman (2013: 232), karakteristik dari pembelajaran berbasis masalah antara lain (1) permasalahan yang digunakan menjadi starting point dalam belajar, merupakan permasalahan yang ada di dunia nyata, membutuhkan perspektif ganda dan menantang pengetahuan yang dimiliki siswa, (2) belajar pengarahan diri, (3) pembelajaran kolaboratif, komunikasi, dan kooperatif, (4) pengembangan keterampilan inquiry dan pemecahan masalah, (5) keterbukaan proses pembelajaran yang meliputi sintesis dan integrasi proses belajar, dan (6) evaluasi dan review pengalaman siswa dan proses belajar.
Menurut Sternberg (Yamin, 2013:84-86) merancang model pemecahan masalah masalah adalah sebagai berikut:
a. Pengidentifikasi masalah : pengenalan masalahkepada siswa
b. Pendefinisian masalah dan representasinya : siswa dituntut untuk mendefinisikan masalah dengan tepat dan mempresentasikannya.
c. Perumusan strategi : setelah masalah didefinisikan secara efektif, maka siswa harus menyusun atau merencanakan strategi penyelesaiannya. d. Pengorganisasian informasi: tahap ini adalah pengumpulan informasi dan
membuat struktur informasi serta mengintegrasikannya. e. Pengolahan sumber daya
f. Pemonitoran: memonitor langkah-langkah yang dilakukan untuk mencapai tujuan.
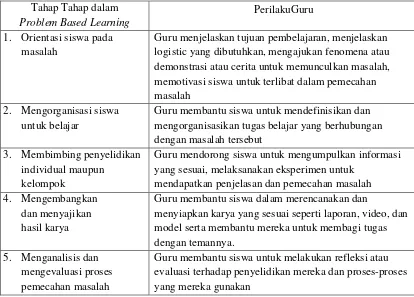
16 Tabel 2.2 Tahap-Tahap Pelaksanaan dalam Problem Based Learning
Tahap Tahap dalam
Problem Based Learning
PerilakuGuru
1. Orientasi siswa pada masalah
Guru menjelaskan tujuan pembelajaran, menjelaskan logistic yang dibutuhkan, mengajukan fenomena atau demonstrasi atau cerita untuk memunculkan masalah, memotivasi siswa untuk terlibat dalam pemecahan masalah
2. Mengorganisasi siswa untuk belajar
Guru membantu siswa untuk mendefinisikan dan mengorganisasikan tugas belajar yang berhubungan dengan masalah tersebut
3. Membimbing penyelidikan individual maupun
kelompok
Guru mendorong siswa untuk mengumpulkan informasi yang sesuai, melaksanakan eksperimen untuk
mendapatkan penjelasan dan pemecahan masalah 4. Mengembangkan
dan menyajikan hasil karya
Guru membantu siswa dalam merencanakan dan
menyiapkan karya yang sesuai seperti laporan, video, dan model serta membantu mereka untuk membagi tugas dengan temannya.
5. Menganalisis dan mengevaluasi proses pemecahan masalah
Guru membantu siswa untuk melakukan refleksi atau evaluasi terhadap penyelidikan mereka dan proses-proses yang mereka gunakan
Selain itu menurut (Amir, 2009:24) di dalam model pembelajaran ini terdapat 6 proses yang akan dilalui oleh siswa yaitu :
1. Mengklarifikasi istilah dan konsep yang belum jelas 2. Merumuskan masalah
3. Menganalisi masalah
4. Menata gagasan secara sistematis menganalisisnyadengan dalam 5. Memformulasikan tujuan pembelajaran
6. Mencari informasi tambahan dari sumber lain (di luar diskusi kelompok)
17 dihadapi. Selain itu, dibutuhkan pengembangan keterampilan kerja sama diantara siswa dan saling memerlukan bantuan guru untuk merencanakan penyelidikan dan tugas-tugas lainnya.
Penyajian masalah dalam model PBL memegang peran sentral karena ketepatan dalam memilih masalah akan menjadi kunci dalam keberhasilan proses belajar. Hal ini diungkap (Sudarman, 2007;323) bahwa masalah dalam PBL ialah suatu rangsangan dan tantangan bagi siswa untuk menggerakkan mereka belajar, yang memerlukan suatu skill khusus bagi seorang penyaji, dalam hal ini guru untuk bisa mengangkat suatu permasalahan yang baik.Dalam PBL, guru berperan sebagai pembimbing dan memberikan masalah kepada siswa untuk dipecahkan secara bersama-sama dengan menerapkan discovery learning(belajar penemuan).
Kegiatan PBL memiliki kelebihan dan kekurangan. KelebihanpembelajaranPBL menurut Wee Kek (Amir, 2009:32-33) adalah kegiatan yang membangun pengetahuan sebelumnya dan membangun pemikiran yang metakognitif dan konstruktif, meningkatkan minat dan motivasi dalam pembelajaran dan peliputan materi menjadi sasaran tetap dapat terliputi. Sedangkan kekurangan PBL diantaranya sulit mencari problem yang relevan, persiapan pembelajaran (problem dan konsep) yang komplek, dan membutuhkan waktu yang cukup lama dalam proses pendidikan (Trianto, 2009: 96).
18 mempengaruhi kecakapan siswa selain itu juga dari masalah yang diberikan siswa dapat bekerja kelompok, mencoba memecahkan masalah dengan pengetahuan yang mereka miliki dan sekaligus dapat mencari informasi-informasi baru yang relevan beserta dengan solusinya. Sehingga siswa terbiasa dalam membangun kecakapan hidup dan terbiasa berfikir dengan pikiran dan tindakannya .
3. Kemampuan Pemecahan Masalah Matematis
Menurut Dahar (1989:138), pemecahan masalah merupakan suatu kegiatan manusia yang menggabungkan konsep-konsep dan aturan-aturan yang telah diperoleh sebelumnya, dan tidak sebagai suatu keterampilan generik. Pemecahan masalah sebagai pendekatan pembelajaran merupakan upaya yang ditempuh dan diciptakan dalam proses pembelajaran yang mengembangkan ketrampilan memecahkan masalah matematika, yang secara nyata dilakukan sehingga diperoleh jawaban yang benar melalui tahapan-tahapan tertentu. Metode pemecahan masalah merupakan metode yang merangsang dan menggunakan wawasan tanpa melihat kualitas pendapat yang disampaikan siswa. Orientasi pembelajarannya adalah investigasi dan penemuan yang pada dasarnya adalah pemecahan masalah.
19 menurut Suherman dkk. (2001:92) menyatakan bahwa salah satu cara mengembangkan kemauan anak dalam pemecahan masalah melalui penyediaan pengalaman pemecahan masalah yang memerlukan strategi berbeda-beda dari suatu masalah ke masalah lainya.
Suyitno (2010:5) menyatakan bahwa suatu soal dapat dikatakan sebagai masalah bagi siswa jika memenuhi syarat sebagai berikut:
a. Siswa memiliki pengetahuan awal untuk mengerjakan soal tersebut b. Diperkirakan siswa mampu mengerjakan soal tersebut
c. Siswa belum tahu algoritma atau cara menyelesaikan soal tersebut d. Siswa mau dan berkehendak menyelesaikan soal tersebut
Polya (Suyitno, 2010:6) berpendapat :
Dalam pemecahan masalah terdapat empat langkah yang harus dilakukan yaitu:
a. Mengidentifikasi masalah
b. Merencanakan pemecahan masalah c. Menyelesaikan masalah sesuai rencana d. Memeriksa kembali hasil yang diperoleh
20 untuk digunakan dalam mengajar, khususnya dalam mengajar matematika perlu pula memperhatikan topik apa yang hendak diajarkan.
Dalam proses pembelajaran, disamping perlunya penalaran yang baik juga diperlukan menguasai langkah-langkah memecahkan masalah secara tepat. Selanjutnya menurut John Dewey (Nasution, 2003:121), langkah-langkah yang harus dicapai dalam memecahkan masalah adalah sebagai berikut :
1. Mengidenfikasi dan merumuskan masalah 2. Mengemukakan hipotesis
3. Mengumpulkan data 4. Menguji hipotesis 5. Mengambil kesimpulan
Menurut Karl Albrecht (Nasution, 2003:121), proses pemecahan masalah terdiri dari enam langkah yang dapat digolongkan dalam dua fase utama yang disebutkannya (1) fase perluasan atau ekspansi yang pada pokoknya bersifat divergen dan(2) fase penyelesaian yang bersifat konvergen. Pada fase pertama peneliti membuka diri bagi ide-ide baru untuk memperoleh pandangan yang luas mengenai masalah itu sehingga ia memahami seluk beluk atau kompleksitasnya. Namun pada saat ia harus mengambil keputusan dan memilih satu dari banyak kemungkinan lain disinilah peserta didik memasuki fase yang kedua. Dalam fase ini ia harus memusatkan perhatian kepada satu fokus tertentu.
Berdasarkan pada dokumen Peraturan Dirjen Dikdasmen tanggal 11 November 2004 (Depdiknas, 2004) dimuat beberapa pencapaian kemampuan pemecahan masalah yaitu :
21 2. Mengorganisasidata dan memilih informasi yang relevan
3. Menyajikan masalah secara tematik dalam segala bentuk
4. Memilih pendekatan dan metode pemecahan masalah secara tepat 5. Menggembangkan strategi pemecahan masalah
6. Membuat dan menafsirkan metode matematika dari suatu masalah dan, 7. Menyelesaikan masalah yang tidak rutin.
Untuk memperoleh kemampuan dalam pemecahan masalah seseorang harus memiliki banyak pengalaman dalam memecahkan berbagai masalah. Pentingnya kemampuan penyelesaian masalah oleh siswa dalam matematika ditegaskan juga oleh Rusman (2013:2), yaitu (1) kemampuan menyelesaikan masalah merupakan tujuan umum pengajaran matematika, (2) penyelesaian masalah yang meliputi metode, prosedur dan strategi merupakan proses inti dan utama dalam kurikulum matematika, dan (3) penyelesaian masalah merupakan kemampuan dasar dalam belajar matematika.
Menurut NCTM (2000), kemampuan pemecahan masalah matematis adalah kemampuan siswa memahami masalah, merencanakan strategi dan prosedur pemecahan masalah, melakukan prosedur pemecahan masalah, memeriksa kembali langkah-langkah yang dilakukan dan hasil yang diperoleh serta menuliskan jawaban akhir sesuai dengan permintaan soal.
Strategi-strategi pemecahan masalah: 1. Bekerja mundur.
2. Menemukan suatu pola.
3. Mengambil suatu sudut pandang yang berbeda.
4. Memecahkan suatu masalah yang beranalogi dengan masalah yang sedang dihadapi tetapi lebih sederhana (spesifikasi tanpa kehilangan generalisasi). 5. Mempertimbangkan kasus-kasus ekstrem.
6. Membuat gambar (representasi visual).
22 8. Memperhitungkan semua kemungkinan
9. Mengorganisasikan data. 10. Penalaran logis.
Berdasarkan dari uraian di atas, dapat disimpulkan bahwa kemampuan pemecahan masalah matematis merupakan kemampuan dalam menyelesaikan permasalahan dengan menggabungkan konsep-konsep pengetahuan dan aturan-aturan yang telah diperoleh sebelumnya dengan indikator memahami masalah, membuat rencana penyelesaian, melakukan perhitungan, dan memeriksa kembali hasil.
B. Kerangka Pikir
Penelitian tentang pengaruh Problem Based Learning (PBL) terhadap kemampuan pemecahan masalah matematis siswa ini melibatkan dua pembelajaran yang diterapkan pada dua kelas berbeda. Pada kelas pertama, yaitu kelas eksperimen menerapkan PBL dan kelas kedua sebagai kelas kontrol menerapkan pembelajaran konvesional.
23 Fase pertama adalah orientasi siswa pada masalah. Pada fase ini, siswa mendengarkan tujuan pembelajaran, motivasi, dan berbagai contoh situasi masalah yang ada di dalam kehidupan sehari-hari.Oleh karena itu, pada fase ini siswa akan terlatih dalam proses pemahaman masalah serta pemilihan informasi yang penting dalam melakukan pemecahan masalah.
24 Fase selanjutnya adalah mengembangkan dan menyajikan hasil karya. Dalam tahap ini, beberapa kelompok mempresentasikan hasil diskusi di depan kelas dengan bimbingan dari guru dan kelompok lain menanggapi. Melalui proses pembelajaran ini, siswa akan terlibat aktif dan diberikan kesempatan untuk mengemukakan ide-ide serta pendapatnya.
Fase yang terakhir adalah menganalisis dan mengevaluasi proses pemecahan masalah. Pada fase ini, guru membantu siswa melakukan refleksi atau evaluasi serta mengklarifikasi hasil diskusi kemudian guru bersama siswa menyimpulkan materi yang telah dipelajari. Dalam aktivitas ini, siswa akan menilai dirinya sendiri, apakah hasil yang ia dapat sesuai dengan harapan atau tujuan pembelajaran.
25 Berdasarkan uraian di atas diharapkan pembelajaran PBL dapat membantu siswa dalam membangun pengetahuan matematika mereka sendiri dan mempermudah penyelesaian masalah karena berhubungan langsung dengan kehidupan nyata. Dengan demikian, penerapan model pembelajaran PBL ini diharapkan dapat mempengaruhi kemampuan pemecahan masalah matematis siswa.
C. Anggapan Dasar
Anggapan dasar dalam penelitian ini adalah semua siswa kelas VIII semester genap SMP Negeri 1 Pagelaran memperoleh materi pelajaran matematika yang sama. Faktor lain yang mempengaruhi kemampuan pemecahan masalah matematis siswa selain model pembelajaran diabaikan.
D. Hipotesis .
Berdasarkan pertanyaan dalam rumusan masalah yang diuraikan sebelumnya, maka hipotesis dari penelitian ini adalah:
1. Hipotesis Umum
Model pembelajaran Problem Based Learning berpengaruh terhadap kemampuan pemecahan masalah matematis siswa.
2. Hipotesis Khusus
26
III. METODE PENELITIAN
A.Populasi dan Sampel
Penelitian ini dilakukan pada semester genap tahun ajaran 2013-2014 di SMP Negeri 1 Pagelaran. Populasi dalam penelitian ini adalah seluruh siswa kelas VIII SMP Negeri 1 Pagelaran sebanyak 326 siswa yang terdistribusi dalam sepuluh kelas (Tabel 3.1). Distribusi kelas VIII SMP Negeri 1 Pagelaran Tahun Pelajaran 2013/2014 dan rata-rata nilai ujian mid semester siswa kelas VIII SMP Negeri 1 Pagelaran sebagai berikut :
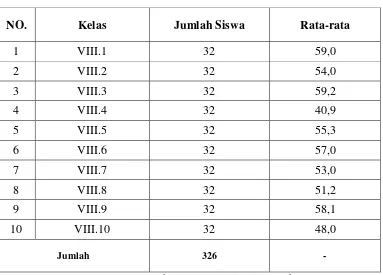
Tabel 3.1 Rata-rata Nilai Ujian Mid Semester Kelas VIII SMP Negeri 1 Pagelaran Tahun Pelajaran 2013/2014
NO. Kelas Jumlah Siswa Rata-rata
1 VIII.1 32 59,0
2 VIII.2 32 54,0
3 VIII.3 32 59,2
4 VIII.4 32 40,9
5 VIII.5 32 55,3
6 VIII.6 32 57,0
7 VIII.7 32 53,0
8 VIII.8 32 51,2
9 VIII.9 32 58,1
10 VIII.10 32 48,0
Jumlah 326 -
27 Pengambilan sampel dalam penelitian ini dilakukan dengan teknik purposive random sampling, yaitu teknik penentuan sampel dengan pertimbangan tertentu. Pertimbangan yang dimaksud adalah dengan mengambil populasi yang diajar oleh guru yang sama dan juga melihat dari nilai rata-rata kelas yang hampir sama. Kemudian mengambil dua kelas secara acak sebagai sampel. Tahap-tahap pengambilan sampel ini adalah sebagai berikut:
1. Mencari data awal (nilai ujian mid semester ganjil) dari guru kelas VIII SMP Negeri 1 Pagelaran
2. Menghitung rata-rata nilai ujian mid semester untuk setiap kelas
3. Menentukan dua kelas dengan nilai rata-rata kelas yang relatif sama. Dari dua kelas tersebut, satu kelas dipilih sebagai kelas yang menerapkan Problem Based Learning dan satu kelas lagi dipilih sebagai kelas yang menerapkan pembelajaran konvensional.
4. Diasumsikan bahwa kelas dengan nilai rata-rata yang relatif sama memiliki kemampuan awal yang sama.
Setelah memperhatikan nilai siswa pada mid semester SMP Negeri 1 Pagelaran, terlihat bahwa rata-rata nilai ujian mid semester adalah 53,7. Terpilihlah kelas VIII.1 sebagai kelas yang menggunakan model pembelajaran Problem Based Learning dan kelas VIII.3 sebagai kelas yang menggunakan pembelajaran konvesional.
B. Desain Penelitian
28 yang ada dalam penelitian, dimana setiap kelas memiliki rata-rata kemampuan pemecahan masalah matematis yang hampir sama dilihat dari rata-rata nilai test awal kemampuan pemecahan masalah dan pada penelitian ini akan diketahui pengaruh yang ditimbulkan dari pembelajaran berbeda yang diterapkan di dua kelas sampel. Pada desain ini kelas eksperimen memperoleh perlakuan dengan model pembelajaran Problem Based Learning sedangkan kelas kontrol memperoleh perlakuan dengan pembelajaran konvensional. Di akhir pembelajaran siswa diberikan posttest untuk mengetahui kemampuan pemecahan masalah matematis siswa. Sesuai dengan yang dikemukakan oleh Furchan (1982:356) desain pelaksanaan penelitian ini digambarkan sebagai berikut:
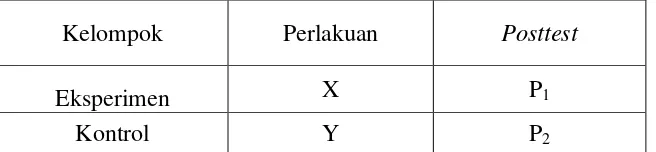
Tabel 3.2 Desain Penelitian
Keterangan:
X = Menggunakan model pembelajaran Problem Based Learning Y = Menggunakan model pembelajaran konvesional
P1 = Skor posttest siswa pada kelas eksperimen
P2 = Skor posttest siswa pada kelas kontrol
C. Prosedur Penelitian
Tahap-tahap yang dilaksanakan dalam penelitian ini adalah sebagai berikut: 1. Tahap Persiapan
a. Menyusun proposal penelitian.
Kelompok Perlakuan Posttest
Eksperimen X P1
29 b. Membuat bahan ajar, Rencana Pelaksanaan Pembelajaran (RPP), dan
instrumen penelitian.
c. Mengonsultasikan perangkat pembelajaran dan instrumen dengan dosen pembimbing .
d. Menguji coba instrumen penelitian (21 januari 2014) e. Merevisi instrumen penelitian jika diperlukan. 2. Tahap Pelaksanaan
a. Mengadakan tes kemampuan awal pemecahan masalah dalam kelas eksperimen dan kelas kontrol. (1 Februari 2014)
b. Melaksanakan pembelajaran matematika dengan menggunakan model pembelajaran PBL pada kelas eksperimen dan model pembelajaran konvensional pada kelas kontrol. (3 Februari 2014)
c. Mengadakan tes akhir kemampuan pemecahan masalah (posttest) dalam kelas eksperimen dan kelas kontrol. (27 Februari 2014)
3. Tahap Pengolahan Data
a. Mengolah dan menganalisis data yang diperoleh dari masing-masing kelas. b. Mengambil kesimpulan.
4. Tahap Laporan
a. Melaporkan hasil penelitian pada dosen pembimbing
30 D. Data Penelitian
Data dalam penelitian ini adalah data kemampuan pemecahan masalah matematis siswa yang berupa data kuantitatif dan diperoleh melalui tes (post-test) setelah mengikuti pembelajaran.
E. Teknik Pengumpulan Data
Dalam penelitian ini teknik pengumpulan data yang digunakan adalah metode tes, baik dalam pembelajaran yang menggunakan model pembelajaran PBL maupun dengan pembelajaran konvensional. Tes diberikan sesudah pembelajaran (posttest).
F. Instrumen Penelitian
Instrumen yang digunakan dalam penelitian ini berupa tes pemecahan masalah matematis yang berbentuk uraian untuk mengukur kemampuan pemecahan masalah matematis siswa. Sebelum penyusunan tes kemampuan pemecahan masalah matematis, terlebih dahulu dibuat kisi-kisi tes kemampuan pemecahan masalah matematis. Tes pemecahan masalah matematis ini menuntut siswa memberikan jawaban sesuai dengan indikator-indikator pemecahan masalah. Pemberian skor jawaban siswa disusun berdasarkan indikator kemampuan
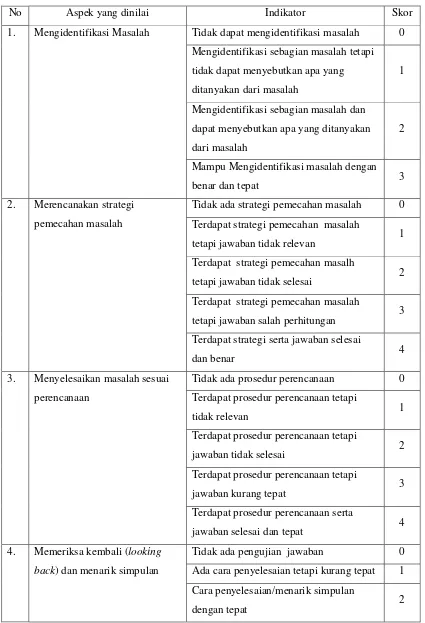
31 Tabel 3.3 Pedoman penskoran tes pemecahan masalah
No Aspek yang dinilai Indikator Skor
1. Mengidentifikasi Masalah Tidak dapat mengidentifikasi masalah 0
Mengidentifikasi sebagian masalah tetapi
tidak dapat menyebutkan apa yang
ditanyakan dari masalah
1
Mengidentifikasi sebagian masalah dan
dapat menyebutkan apa yang ditanyakan
dari masalah
Tidak ada strategi pemecahan masalah 0
Terdapat strategi pemecahan masalah
tetapi jawaban tidak relevan 1
Terdapat strategi pemecahan masalh
tetapi jawaban tidak selesai 2
Terdapat strategi pemecahan masalah
tetapi jawaban salah perhitungan 3
Terdapat strategi serta jawaban selesai
dan benar 4
3. Menyelesaikan masalah sesuai
perencanaan
Tidak ada prosedur perencanaan 0
Terdapat prosedur perencanaan tetapi
tidak relevan 1
Terdapat prosedur perencanaan tetapi
jawaban tidak selesai 2
Terdapat prosedur perencanaan tetapi
jawaban kurang tepat 3
Terdapat prosedur perencanaan serta
jawaban selesai dan tepat 4
4. Memeriksa kembali (looking
back) dan menarik simpulan
Tidak ada pengujian jawaban 0
Ada cara penyelesaian tetapi kurang tepat 1
Cara penyelesaian/menarik simpulan
32 Dalam penelitian ini, instrumen yang digunakan adalah yang memenuhi kriteria tes yang baik, yaitu memiliki validitas tes, reabilitas tes, daya pembeda butir tes dan juga tingkat kesukaran butir tes.
1. Validitas Instrumen
Validitas tes yang digunakan dalam penelitian ini adalah validitas isi dan validitas butir soal.
a) Validitas Isi
33 b) Validitas Butir Soal
Validitas butir soal dalam penelitian ini diukur menggunakan korelasi product moment dengan angka kasar sebagai berikut :
∑ ∑ ∑
√ ∑ ∑ ∑ ∑
Keterangan:
: Koefisien korelasi antara variabel X dan variabel Y N : Jumlah siswa
∑ : Jumlah skor pada siswa pada tiap butir soal
∑ : jumlah skor total siswa
∑ : Jumlah hasil perkalian skor siswa pada setiap butir dengan total skor siswa
(Widoyoko, 2012:137)
Kriteria soal yang akan digunakan dalam penelitian ini adalah butir soal yang valid yaitu butir soal dengan koefisien validitas butir soal lebih dari atau sama dengan 0,3 (Widoyoko, 2012:143). Hasil perhitungan koefisien validitas butir soal dari uji coba soal kemampuan pemecahan masalah disajikan pada tabel 3.5 berikut :
Tabel 3.4 Validitas Butir Item Soal
Nomor Item Soal 1a 1b 1c 2a 2b 3 4
xy
r 0,82 0,75 0,72 0,77 0,75 0,73 0,88 Interpretasi Valid Valid Valid Valid Valid Valid Valid
34 2. Reliabilitas
Setelah perangkat tes dinyatakan valid, kemudian instrument tes diujicobakan pada kelas sampel. Uji coba instrument tes ini ditujukan untuk mengetahui tingkat reliabilitas tes. Perhitungan untuk mencari nilai reliabilitas instrumen didasarkan pada pendapat Arikunto (2008:109) yang menyatakan bahwa untuk melindungi reliabilitas dapat digunakan rumus Alpha, yaitu :
n
: banyaknya butir soal (item)
2i
: jumlah varians dari tiap-tiap item tes : varians total Berdasarkan hasil perhitungan uji coba instrumen tes, diperoleh bahwa nilai koefisien reliabilitas tes adalah 0,88 dan didapat nilai rata-ratanya adalah 46. Hal ini menunjukkan bahwa instrumen tes yang diujicobakan memiliki reliabilitas yang tinggi sehingga instrumen tes ini layak untuk digunakan untuk mengukur kemampuan pemecahan masalah matematis siswa. Hasil perhitungan reliabilitas uji coba soal dapat dilihat pada Lampiran C.2.
2
t
35 3. Indeks Daya Pembeda
Teknik yang digunakan untuk menghitung daya pembeda bagi tes bentuk uraian adalah dengan menghitung perbedaan dua buah rata-rata yaitu antara rata-rata kelas atas dengan rata-rata kelas bawah untuk tiap-tiap item Sudijono (2008:120) mengungkapkan menghitung daya pembeda ditentukan dengan rumus yaitu:
Keterangan :
DP : indeks daya pembeda satu butir soal tertentu
JA : jumlah skor kelompok atas pada butir soal yang diolah JB : jumlah skor kelompok bawah pada butir soal yang diolah IA : jumlah skor ideal kelompok (atas/bawah).
Hasil perhitungan daya pembeda diinterpretasikan berdasarkan klasifikasi yang tertera dalam Tabel 3.5 berikut :
Tabel 3.5 Interpretasi Nilai Daya Pembeda
(Sudijono, 2008)
Kriteria soal tes yang digunakan dalam penelitian ini memiliki interpretasi baik,
yaitu memiliki nilai daya pembeda ≥ 0,30. Hasil perhitungan daya pembeda butir
item soal yang telah diujicobakan disajikan pada Tabel 3.6 sebagai berikut :
Nilai Interpretasi
Kurang dari 0,20 Buruk
0,20-0,40 Sedang
0,40-0,70 Baik
0,70-1,00 Sangat Baik
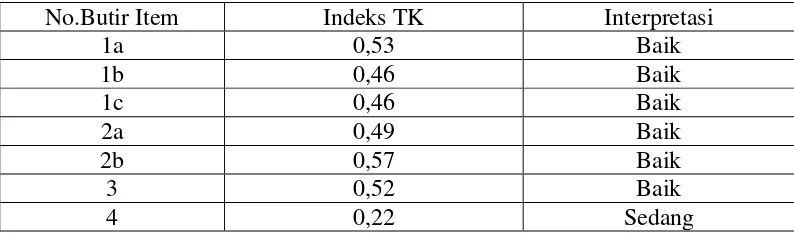
36 Tabel 3.6 Daya Pembeda Butir Item Soal
No.Butir Item Indeks TK Interpretasi
1a 0,53 Baik
1b 0,46 Baik
1c 0,46 Baik
2a 0,49 Baik
2b 0,57 Baik
3 0,52 Baik
4 0,22 Sedang
Dengan melihat hasil perhitungan daya pembeda butir item soal yang diperoleh, maka instrumen tes yang sudah diujicobakan telah memenuhi kriteria daya pembeda soal yang sesuai dengan kriteria yang diharapkan. Hasil perhitungan daya pembeda butir item soal dapat dilihat pada Lampiran C.3.
4. Tingkat Kesukaran
Sudijono (2008:372) mengatakan bahwa suatu tes dikatakan baik jika memiliki derajat kesukaran sedang, tidak terlalu sukar dan tidak terlalu mudah. Per-hitungan tingkat kesukaran suatu butir soal digunakan rumus sebagai berikut:
Keterangan:
TK : tingkat kesukaran suatu butir soal
JT : jumlah skor yang diperoleh siswa pada butir soal yang diperoleh
IT : jumlah skor maksimum yang dapat diperoleh siswa pada suatu butir soal
37
Tabel 3.7 Interpretasi Indeks Tingkat Kesukaran
Nilai Interpretasi Kriteria soal yang digunakan dalam penelitian ini adalah memiliki interpretasi
nilai tingkat kesukaran 0.16 ≤ TK ≤ 0.85. Hasil perhitungan tingkat kesukaran uji
coba soal disajikan pada Tabel 3.8.
Tabel 3.8 Tingkat Kesukaran Butir Item Soal
No Butir Item Indeks TK Interpretasi
1a 0,70 Mudah
Dengan melihat hasil perhitungan tingkat kesukaran butir item soal yang diperoleh, maka instrumen tes yang sudah diujicobakan telah memenuhi kriteria tingkat kesukaran soal yang sesuai dengan kriteria yang diharapkan. Hasil perhitungan tingkat kesukaran butir item soal dapat dilihat pada Lampiran C.3.
G. Teknik Analisis Data
38 matematis. Dari hasil tes akhir dianalisis untuk mengetahui pengaruh model pembelajaran PBL dan pembelajaran konvensional terhadap kemampuan pemecahan masalah matematis siswa. Adapun analisis data dilakukan dengan langkah-langkah berikut.
a) Uji Normalitas
Uji Normalitas dalam penelitian ini menggunakan uji Chi-Kuadrat dan uji Kolmogorov-Smirnov Z (K-S Z). Uji Chi Kuadrat menurut Sudjana (2005: 273) adalah sebagai berikut:
a) Hipotesis
H0 : data berasal dari populasi yang berdistribusi normal
H1 : data tidak berasal dari populasi yang berdistribusi normal
b) Taraf signifikansi yang digunakan α = 5%
c) Statistik Uji
O = frekuensi pengamatan x2 = Uji normalitas
i
E = frekuensi yang diharapkan
d) Keputusan Uji
Dalam hal lainnya H0 diterima.
39 Hipotesis:
Ho : sampel berasal dari populasi yang berdistribusi normal
H1 : sampel tidak berasal dari populasi yang berdistribusi normal
Kriteria pengujiannya yaitu jika nilai probabilitas (sig) dari Z lebih besar dari
, maka hipotesis Ho diterima (Trihendradi, 2005:113).
Hasil perhitungan uji normalitas diberikan pada Tabel 3.9 di bawah ini:
Tabel 3.9 Hasil Uji Normalitas data posttest dengan chi-kuadrat
Kelas Keputusan Uji
PBL 22,71
9,49 H0 ditolak Konvensional 20,47 H0 ditolak
Tabel 3.10 Hasil Uji Normalitas data posttest dengan uji (K-S-Z)
KELAS Kolmogorov-Smirnov(a) Shapiro-Wilk Statistic df Sig. Statistic df Sig. postest eksperimen .293 34 .000 .862 34 .001
kontrol . 186 33 .005 . 925 33 .025
Berdasarkan Tabel 3.9, dapat dilihat bahwa bahwa data posttest pada kelas PBL
memiliki pada taraf signifikansi = 5%, yang berarti H0 ditolak.
Sedangkan data posttest pada kelas konvesional memiliki pada
taraf signifikansi = 5%, yang berarti H0 ditolak. Hal ini juga dapat dilihat dari
40 b) Uji Hipotesis
Setelah melakukan uji normalitas dan homogenitas data, analisis berikutnya adalah menguji hipotesisnya. Berdasarkan hasil uji prasyarat, data kemampuan pemecahan masalah matematis kelas PBL dan kelas konvensional berasal dari populasi yang tidak berdistribusi normal. Russefendi (1998:401) jika data berasal dari populasi yang tidak berdistribusi normal maka uji hipotesis menggunakan uji non parametrik. Dalam penelitian ini uji yang digunakan adalah uji Mann-Whitney dengan hipotesis sebagai berikut.
a. Ho: (tidak ada perbedaan peringkat kemampuan pemecahan masalah matematis siswa yang mengikuti pembelajaran PBL dengan kemampuan pemecahan masalah matematis siswa yang mengikuti pembelajaran konvensional)
b. H1: (ada perbedaan peringkat kemampuan pemecahan masalah matematis
siswa yang mengikuti pembelajaran PBL dengan kemampuan pemecahan masalah matematis siswa yang mengikuti pembelajaran konvensional)
Rumus yang digunakan untuk menghitung nilai statistik uji Mann-Whitney adalah sebagai berikut.
∑
Keterangan:
U = Nilai uji Mann-Whitney
n1 = Jumlah sampel kelas eksperimen
49
V. SIMPULAN DAN SARAN
A.Simpulan
Berdasarkan hasil penelitian dan pembahasan, diperoleh simpulan bahwa model pembelajaran Problem Based Learning berpengaruh terhadap kemampuan pemecahan masalah matematis siswa kelas VIII SMP Negeri 1 Pagelaran. Hal ini dapat dilihat dari kemampuan pemecahan masalah matematis siswa yang mengikuti pembelajaran Problem Based Learning lebih tinggi daripada kemampuan pemecahan masalah matematis siswa yang mengikuti pembelajaran konvensional.
B.Saran
Berdasarkan kesimpulan, dikemukakan saran-saran sebagai berikut:
50 2. Peneliti lain yang ingin mengembangkan penelitian lanjutan tentang pengaruh pembelajaran PBL terhadap kemampuan pemecahan masalah matematis siswa
disarankan untuk.
a. Dalam jangka waktu yang lebih lama agar kondisi kelas sudah kondusif saat dilakukan pengambilan data, sehingga data dapat menggambarkan kemampuan siswa secara optimal.
b. Mempertimbangkan karakter siswa dalam menerapkan model pembelajaran yang sesuai.
51
DAFTAR PUSTAKA
Amir,Taufiq. 2009. Pendidikan Melalui Problem Based Learning. Jakarta : Kencana Prenada Media group.
Aqib, Zainal. 2013. Model Podel Pengajaran dan Penelitian. Yogayakarta : Pustaka pelajar
Arikunto, Suharsimi. 2008. Dasar-Dasar Evaluasi Pendidikan. Jakarta: Bumi Aksara
Dahar, R.W. 1998. Teori-teori Belajar. Jakarta : Depdikbud Depdiknas.2004. PedomanPembelajaran Tuntas. Jakarta
Djamarah dan Aswan. 2002. Strategi Belajar Mengajar. Jakarta: Rineka Cipta Furchan, Arief. 1982. Pengantar Penelitian dalam Pendidikan. Surabaya : Usaha
Nasional
Horsley, S. L. 1990. Elementary School Science for the 90S. Virginia: Association Supervision and Curriculum Development.
Hudiono. 2005. Meningkatkan Kemampuan Representasi dan Pemecahan Masalah Siswa SMA Melalui Model Pembelajaran Mathematics Project. Skripsi FPMIPA UPI Bandung: Tidak diterbitkan
Hudojo, Herman. 2005. Pengembangan Kurikulum dan Pembelajaran Matematika. Malang: Universitas Negeri Malang Press.
Ibrahim, Muslimin dan Nur Mohamad. 2005. PembelajaranBerdasarkanMasalah. Surabaya :PusatSainsdanMatematikaSekolahUniversitasNegeri Surabaya. Jusuf,Ahmad Aulia. 2009. Pendekatan spices dan Pembelajaran berdasarkan
masalah(online).Tersedia:http://staff.ui.ac.id/internal/132015140/material/s pices dan problem based Learningi
Kadir. 2010. Statistika untuk penelitian ilmu-ilmu sosial. Jakarta : Rosemata Sampurna
52
Martin, O Michael. 2012. TIMSS 2011 International Results in Science. United States: TIMSS & PIRLS International Study Center.
Nasution. 2013. Kurikulum dan Pengajaran. Jakarta : Bumi aksara
National Council of Teachers of Mathematics (NCTM). 2000. Principles and Standards for School Mathematics. Reston, USA: NCTM, Inc.
Pannen, I aulina.2001. Kontrukvisme dalam PembelajaranDirektorat Jendral Pendidikan Tinggi Departemen Pendidikan Nasional Jakarta
PISA.2012..http://en.wikipedia.org/wiki/Programme_for_International_Student_ Assessmentdonesia berada di peringkat dua terbawah untuk skor matematika dalam survei "Programme for International Student Assessment".(diaksespadatanggal 09 Desember 2013)
Pramudha. 2011. Pendidikan Non Formal dan peranannya dalam Pendidikan Anak.Yogyakarta: Kompas Gramedia
Ruseffendi. 1998. Statistika Dasar untuk Penelitian Pendidikan. Bandung: IKIP Bandung Press.
Rusman. 2013. Model-Model Pembelajaran. Jakarta: Raja Grafindo Persada. Sardiman. 2004. Interaksi dan motivasi belajar mengajar. Jakarta : Raja Grafindo
Persada
Santock. 2004. Psikologi dan Perkembangan Remaja. Jakarta. BPK Gunung Mulia
Sudarman. 2007. Problem Based Learning: Suatu Model Pembelajaran untuk Mengem-bangkan dan Meningkatkan Ke-mampuan Memecahkan Masalah. Jurnal Pendidikan Inovatif Vol. 02 No. 02 Hlm. 68-73. [online].Diaskses dhttp://physicsmaster.orgfree.com/Artikel%20&%20Jurnal/Wawasan%20Pe ndidikan/PBL%20Model.pdf pada tanggal 3 September 2013.
Suherman, Erman, dkk. (2001). Strategi Pembelajaran Matematika Kontemporer. JICA-UPI. Bandung
Sudijono, Anas. 2008. Pengantar Evaluasi Pendidikan. Jakarta: Raja Grafindo Persada.
Sudjana. 2005. Metode Statistik. Bandung : Tarsito
53 Trianto. 2009. Mendesain Model Pembelajaran Inovatif-Progresif: Konsep, Landasan, dan Implementasinya pada Kurikulum Tingkat Satuan Pendidikan (KTSP). Jakarta: Kencana
Trihendradi, Cornelius. 2005. Step by Step SPSS 17.0 Analisis Data Statistik. Yogyakarta: Andi Offset.
Wakhinuddin. 2010. Validitas Isi. (online). Tersedia: http://wakhinuddin.word- press.com/2010/08/02/validitas-isi/ [26 desember 2012]
Wardhani dan Rumiati. 2011. Instrumen Penilaian Hasil Belajar Matematika SMP: Belajar dari PISA dan TIMSS . Yogyakarta PPPPTK. [Online] Diakses di http://p4-tkmatematika.org/ pada 12 November 2013.
Widoyoko, Eko Putro. 2013. Evaluasi Program Pembelajaran. Yogyakarta: Pustaka Pelajar.