Fungsi Interpolasi untuk Tabel Mortalita

(1)

FUNGSI INTERPOLASI UNTUK TABEL MORTALITA

ANNISAA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

ANNISAA. Fungsi Interpolasi untuk Tabel Mortalita Dibimbing oleh SRI NURDIATI dan I GUSTI PUTU PURNABA.

Setiap manusia mempunyai risiko kematian. Asuransi adalah salah satu cara untuk meminimalisir risiko tersebut. Orang yang mengikuti asuransi mempunyai kewajiban untuk membayar premi, salah satu parameter untuk menghitung harga premi adalah tabel mortalita. Tujuan karya ilmiah ini adalah memodelkan tabel mortalita dengan metode interpolasi serta menganalisis perbedaan harga premi antara asuransi endowmen dengan asuransi berjangka. Metode interpolasi yang digunakan adalah metode interpolasi spline linear, kuadratik dan berderajat lebih dari dua. Metode interpolasi yang paling baik untuk tabel mortalita adalah interpolasi spline linear karena kesalahannya relatif kecil.

(3)

ABSTRACT

ANNISAA. Interpolation Function for Mortality Table. Supervised by SRI NURDIATI and I GUSTI PUTU PURNABA.

Every human has a risk of death. Insurance is a way to minimize the risk. People who join the insurance have an obligation to pay a premium. One of the parameters to calculate the premium price is the table of mortality. The purpose of this paper is to model the table of mortality with the interpolation method and analyze the difference of premium price between endowment insurance with term insurance. We use the method of linear, quadratic, and more than two degree spline interpolation. The best interpolation method for the mortality table is a linear spline interpolation because the error of calculate is relative small.

(4)

FUNGSI INTERPOLASI UNTUK TABEL MORTALITA

ANNISAA

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Judul Skripsi : Fungsi Interpolasi untuk Tabel Mortalita

Nama

: Annisaa

NIM

: G54080036

Menyetujui,

Tanggal Lulus :

Pembimbing I

Dr. Ir. Sri Nurdiati, M.Sc

NIP.

19601126 198601 2 001

Pembimbing II

Dr. Ir. I Gusti Putu Purnaba, DEA

NIP.

19651218 199002 1 001

Mengetahui,

Ketua Departemen Matematika

(6)

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya serta shalawat dan salam kepada Nabi Muhammad SAW sehingga karya ilmiah ini berhasil diselesaikan.

Penyusunan karya ilmiah ini juga tidak terlepas dari bantuan berbagai pihak. Oleh karena itu penulis mengucapkan terimakasih yang sebesar-besarnya kepada Bapak dan Ibu tersayang, terimakasih atas kasih sayang, didikan, nasihat, semangat serta doa yang tiada henti-hentinya untuk penulis. Kepada Ibu Dr. Ir. Sri Nurdiati, M.Sc dan Bapak Dr. Ir. I Gusti Putu Purnaba, DEA selaku dosen pembimbing, terimakasih atas waktu, ilmu yang diberikan dan kesabaran dalam membimbing penulis serta Bapak Dr. Ir. Hadi Sumarno, MS selaku dosen penguji terimakasih atas waktu, ilmu dan saran yang bermanfaat bagi penulis. Di samping itu, penghargaan penulis sampaikan kepada Bapak dan Ibu dosen Departemen Matematika yang telah mengajar dan memberikan bekal ilmu pengetahuan kepada penulis. Tidak lupa ungkapan terimakasih kepada seluruh keluarga atas doa dan kasih sayangnya. Terimakasih kepada keluarga besar VISION atas semangat, kesabaran, doa dukungan dan bantuannya selama ini,serta terimakasih sahabat terdekat: Nurhayati, Suwaibatul Aslamyah, Raidinal Alifahrana, Previta Widiastana, Yoppy RM Yunus, Faris Itsnartasia, Raka Abimanyu, Fahrul Irianto, Lya, Agustina, Andromeda atas semangat, doa dan dukungannya. Terimakasih kepadaTeman-teman Math 45, adik kelas angkatan 46, dan teman-teman Kos putri Nikita atas dukungan, bantuan, doa dan kebersamaannya.

Penulis menyadari bahwa karya ilmiah ini masih jauh dari sempurna, oleh karena itu penulis mengharapkan saran dan kritik yang bersifat membangun demi penyempurnaan karya ilmiah ini. Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, April 2013

(7)

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 20Agustus 1990 sebagai anak pertama dari dua bersaudara. Anak dari pasangan Sujiah dan Darmadji.

Pada tahun 1996 penulis menyelesaikan pendidikan di TK Islam Qur’an. Tahun 2002 penulis menyelesaikan pendidikan di SDN Lagoa 07 Jakarta. Tahun 2005 penulis menyelesaikan pendidikan di SLTPN 30 Jakarta Utara. Tahun 2008 penulis menyelesaikan pendidikan di SMAN 72 Jakarta pada tahun yang sama penulis diterima di Departemen Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor (IPB) malalui jalur Undangan Seleksi Masuk IPB (USMI).

(8)

viii

DAFTAR ISI

Halaman

DAFTAR TABEL

... ix

DAFTAR GAMBAR

... ix

DAFTAR LAMPIRAN

... ix

PENDAHULUAN

... 1

1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

LANDASAN TEORI

... 2

2.1 Interpolasi ... 2

2.2 Interpolasi Polinomial ... 2

2.3 Interpolasi Linear ... 2

2.4 Fungsi Spline ... 2

2.5 Spline Linear ... 2

2.6 Syarat-syarat Spline Linear ... 2

2.7 Spline Kuadratik ... 2

2.8 Syarat-syarat Spline Kuadratik ... 2

2.9 Spline Kubik... 3

2.10 Uji Kesesuaian Data ... 3

2.11 Tabel Hayat ... 3

2.12 Istilah Perhitungan Premi Asuransi ... 3

HASIL DAN PEMBAHASAN

... 4

3.1 Pemodelan Tabel Mortalita dengan Interpolasi ... 4

3.1.1 Pemotongan Selang pada Tabel Mortalita ... 4

3.1.2 Tabel Mortalita dengan Interpolasi Berderajat Banyak ... 4

3.1.3 Tabel Mortalita dengan Interpolasi Kuadratik ... 5

3.1.4 Tabel Mortalita dengan Interpolasi Spline Linear ... 5

3.2 Penerapan Model pada Asuransi ... 6

3.2.1 Asuransi Endowmen ... 6

3.2.2 Asuransi Berjangka ... 9

3.2.3 Kesalahan dari Nilai Premi Asuransi Endowmen dan Asuransi Berjangka ... 9

KESIMPULAN

... 12

DAFTAR PUSTAKA

... 12

(9)

viii

DAFTAR GAMBAR

Halaman

1 Mortalita dengan selang satu ... 4

2 Mortalita dengan selang lima ... 4

3 Hasil interpolasi spline linear ... 5

4 Hasil interpolasi berderajat banyak ... 33

DAFTAR TABEL

Halaman

1 Nilai premi asuransi endowmen seorang laki-laki dengan tingkat bunga 10% ... 7

2 Nilai premi asuransi endowmen seorang perempuan dengan tingkat bunga 10% ... 8

3 Perbedaan kesalahan premi antara asuransi endowmen dan asuransi berjangka ... 9

4 Nilai premi asuransi berjangka seorang laki-laki dengan tingkat bunga 10% ... 10

5 Nilai premi asuransi berjangka seorang perempuan dengan tingkat bunga 10% ... 11

6 Fungsi interpolasi linear spline laki-laki ... 13

7 Fungsi interpolasi linear spline perempuan ... 14

8 Tabel mortalita Indonesia 2011 ... 16

9 Proses perhitungan nilai kesalahan dengan interval sama (laki-laki) ... 19

10 Proses perhitungan nilai kesalahan dengan interval berbeda (laki-laki) ... 19

11 Proses perhitungan nilai kesalahan dengan interval sama (perempuan) ... 24

12 Proses perhitungan nilai kesalahan dengan interval berbeda (perempuan) ... 24

13 Nilai fungsi kuadratik ... 29

14 Fungsi kuadratik ... 32

15 Keterangan garis ... 33

DAFTAR LAMPIRAN

Halaman

1 Fungsi Interpolasi Spline Linear ... 13

2 Program untuk Mencari Interpolasi Linear pada MATLAB ... 15

3 Program untuk Mencari Fungsi Interpolasi Kuadratik pada MATLAB ... 15

4 Program untuk Membuat Grafik Fungsi Kuadratik pada MATLAB ... 15

5 Tabel Mortalita Indonesia 2011 ... 16

6 Perbedaan Pemecahan Selang untuk Mendapatkan Fungsi Interpolasi Spline Linear pada Laki-laki ... 19

7 Perbedaan Pemecahan Selang untuk Mendapatkan Fungsi Interpolasi Spline Linear pada Perempuan ... 24

8 Nilai Fungsi Kuadratik ... 29

9 Fungsi Kuadratik ... 32

10 Hasil Interpolasi Berderajat Banyak ... 33

(10)

PENDAHULUAN

1.1 Latar Belakang

Pada masa kini kehidupan manusia telah mengalami banyak perubahan. Perubahan tersebut disebabkan oleh berbagai faktor seperti alam dan pola hidup manusia. Dari perubahan tersebut, manusia menghadapi berbagai bentuk risiko, antara lain risiko kematian. Risiko kematian yang terjadi pada manusia dapat dihindari dengan cara mengubah pola hidup atau risiko tersebut dapat diminimalisir dengan adanya asuransi.

Asuransi dalam hukum dan ekonomi adalah bentuk menagemen risiko yang dipakai untuk proteksi terhadap kerugian. Asuransi adalah transfer sepadan dari risiko potensi kerugian dengan suatu premi. Perjanjian yang dibuat oleh seseorang yang mengikuti program asuransi dengan perusahaan asuransi disebut polis asuransi, sedangkan orang yang mengikuti program asuransi disebut pemegang polis. Para pemegang polis berkewajiban membayar sejumlah uang kepada perusahaan asuransi pada tiap periode tertentu atau dibayar lunas yang disebut premi asuransi. Perusahaan asuransi memberi jaminan terhadap risiko yang terjadi sesuai kesepakatan berupa sejumlah uang yang disebut klaim asuransi (Gunawan 2000).

Dalam menentukan nilai premi asuransi dibutuhkan peluang seseorang meninggal. Peluang seseorang meninggal terdapat pada tabel mortalita. Tabel mortalita merupakan data statistik dari suatu penduduk yang menyatakan peluang seseorang meninggal.

Fungsi atau hasil penelitian dapat disajikan dalam bentuk tabel yang memuat pasangan bilangan yang berurutan. Namun, seringkali data yang diperlukan belum bisa diperoleh, padahal kelengkapan data tersebut

sangat diperlukan untuk menghasilkan suatu analisis yang akurat. Untuk memperoleh data yang tidak ada atau hilang di antara nilai-nilai data yang diberikan diperoleh suatu metode penaksiran.

Interpolasi adalah suatu metode untuk menaksir nilai data yang tidak ada atau hilang di antara nilai-nilai data yang diberikan. Nilai data tersebut bisa berasal dari suatu parameter (dimensi satu) atau beberapa parameter (dimensi banyak). Untuk menaksir data yang hilang dalam nilai data yang berdimensi banyak, diperlukan metode interpolasi yang bekerja pada dimensi banyak pula. Interpolasi pada dimensi banyak diselesaikan dengan urutan interpolasi dimensi satu.

Salah satu interpolasi dalam dimensi satu adalah interpolasi polinomial. Interpolasi polinomial adalah metode interpolasi yang dapat menghasilkan nilai data yang mempunyai tingkat ketelitian tinggi. Dalam metode interpolasi polinomial, telah dikenal antara lain interpolasi polinomial Newton, Lagrange dan spline, dengan kelebihan atau kelemahan masing-masing.

Karya ilmiah ini, akan membahas penggunaan model dari tabel mortalita dengan metode interpolasi linear dalam menentukan besarnya premi asuransi yang akan dibayar oleh pemegang polis.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah: (i) Memodelkan tabel mortalita dengan

metode interpolasi.

(11)

LANDASAN TEORI

2.1 Interpolasi

Interpolasi adalah proses pencarian dan perhitungan suatu fungsi yang grafiknya melewati sekumpulan titik yang diberikan (Sahid 2005).

2.2 Interpolasi Polinomial

Suatu fungsi polinomial P(x) dengan p Pn adalah interpolasi polinomial jika P(x) melalui setiap titik penginterpolasi berbentuk (xi,yi) untuk dengan Pn adalah himpunan fungsi polinomial berderajat n (Philips 2003).

2.3 Interpolasi Linear

Metode interpolasi linear merupakan metode interpolasi untuk mencari nilai data di antara dua titik data, dengan membuat persamaan garis lurus dari dua titik data tersebut. Interpolasi linear hanya menggunakan dua titik data. Dengan demikian, untuk mencari nilai data yang hilang hanya diperlukan dua titik data dimana data itu ada diantaranya (Mutaqin1998). 2.4 Fungsi Spline

Fungsi spline adalah suatu fungsi yang terdiri atas beberapa potong fungsi polinomial yang dirangkaikan bersama dengan beberapa syarat kemulusan (Sahid 2005).

2.5 Spline Linear

Spline linear S(x) pada selang [x1,xn] dengan didefinisikan oleh

{

(Sahid 2005) 2.6 Syarat-syarat Spline Linear

Misalkan x1=a dan xn=b maka domain S(x) adalah [a,b]. Tahap selanjutnya adalah mensyaratkan bahwa S(x) kontinu pada [a,b]. Jadi, S(x) harus memiliki sifat-sifat sebagai berikut:

1. S(x) sepotong-sepotong linear dan 2. S(x) kontinu pada [a,b].

Untuk tujuan ekstrapolasi diasumsikan bahwa: 1. S(x) didefinisikan sama dengan S1(x)

untuk x<a, dan

2. S(x) didefinisikan sama dengan Sn-1 (x) untuk x>a.

Konstanta-konstanta ak dan bk dipilih sedemikian sehingga S(x) kontinu pada [a,b]. Syarat kontinuitas ini bersamaan dengan persamaan-persaman di bawah ini:

1.

2. atau

untuk

3.

.

(Sahid 2005) 2.7 Spline Kuadratik

Didefinisikan dengan fungsi S(x) didefinisikan sebagai

{

(Sahid 2005)

2.8 Syarat-syarat Spline Kuadratik

Suatu fungsi S(x) merupakan sebuah spline berderajat dua pada [a,b], jika S(x) memiliki sifat-sifat sebagai berikut:

1. S(x) sepotong-sepotong kuadratik pada [a,b],

2. S(x) kontinu pada [a,b], dan 3. kontinu pada [a,b].

Untuk tujuan ekstrapolasi diasumsikan bahwa: 1. S(x) didefinisikan sama dengan S1(x)

untuk x<a, dan

2. S(x) didefinisikan sama dengan Sn-1(x) untuk x>a.

(Sahid 2005) untuk x1 ≤ x≤x2

untuk x2 ≤ x≤ x3

untuk xn ≤ x ≤xn+1.

untuk x1 ≤ x≤ x2 untuk x2 ≤ x≤x3

(12)

3

2.9 Spline Kubik

Sebuah fungsi spline S(x) dikatakan spline kubik (berderajat tiga), jika S(x) memiliki sifat-sifat sebagai berikut:

1. S(x) sepotong-sepotong merupakan polinomial kubik pada selang [a,b], 2. S(x) kontinu pada selang [a,b], 3. S’(x) kontinu pada selang [a,b], dan 4. S’’(x) kontinu pada selang [a,b]. Untuk tujuan ekstrapolasi menggunakan

1. S(x) didefinisikan sama dengan S1(x) untuk x<a, dan

2. S(x) didefinisikan sama dengan Sn-1(x) untuk x>a.

{

Dengan

(1 ≤ k ≤ n-1).

(Sahid 2005) 2.10 Uji Kesesuaian Data

Untuk mengetahui kesesuaian data yang diperoleh berdasarkan suatu metode tertentu terhadap data sebenarnya perlu dilakukan uji kesesuaian data. Ada beberapa kriteria yang dapat dijadikan sebagai acuan diantaranya adalah galat mutlak (Absolute Error, AE). Misalkan yi adalah data ke-i yang sebenarnya y adalah data yang diperoleh dengan menggunakan metode tertentu sebagai nilai pendekatan untuk yi. Galat mutlak didefinisikan sebagai berikut:

AE= |yi-y|.

(Mathews 1992) 2.11 Tabel Hayat

Tabel hayat menggambarkan sejarah hidup kelompok yang dimulai dengan

kelahiran pada waktu yang dimulai dan kemudian perlahan-lahan berkurang karena kematian hingga kelompok penduduk tersebut tidak ada satu pun yang tertinggal (Siegel & Swanson 2004).

Keterangan Tabel Hayat

1. x :usia x, kolom ini berisi x=0,1,2,..., , dengan adalah usia tertua.

2. jumlah orang yang hidup pada usia x. Kolom ini dimulai dengan yang biasanya bernilai 100.000.

3. :tingkat kematian penduduk usia x, dengan rumus

4. nqx :peluang seorang akan meninggal sebelum mencapai usia x+n untuk penduduk berusia x.

5. npx :peluang seorang hidup mencapai usiax + n untuk penduduk berusia x. 6. :tingkat harapan hidup pada usia x.

(Bowers et al.1997) 2.12 Istilah Perhitungan Premi Asuransi

1. _̅̅̅:nilai sekarang aktuaria orang berumur x dari asuransi berjangka dengan pembayaran premi selama n tahun sebesar satu satuan. Pembayaran santunan dibayarkan pada saat tertanggung meninggal pada jangka n tahun.

̅̅̅ ∑ kpx.

2. ̅̅̅:nilai sekarang aktuaria dari asuransi endowmen orang berumur x dengan pembayaran premi selama n tahun sebesar satu satuan. Pembayaran santunan oleh penanggung akan di bayarkan saat tertanggung hidup sampai umur yang ditentukan atau meninggal sebelum usia itu.

(Promislow 2006) untuk x1 ≤ x≤ x2

(13)

4

HASIL DAN PEMBAHASAN

3.1 Pemodelan Tabel Mortalita dengan Interpolasi

Pemodelan tabel mortalita pada penelitian ini menggunakan interpolasi. Penelitian ini melakukan beberapa bentuk interpolasi untuk menentukan model yang tepat dalam tabel mortalita. Ketepatan interpolasi terhadap tabel mortalita dapat dilihat dari berbagai kategori, seperti jenis fungsi dan kesalahan relatif.

Beberapa jenis metode interpolasi yang akan digunakan yaitu :

1. Interpolasi berderajat banyak, 2. Interpolasi kuadratik,

3. Interpolasi linear, dan 4. Interpolasi spline.

Sebelum dilakukan analisis berdasarkan metode interpolasi, selang pada tabel mortalita dilakukan perubahan terlebih dahulu sebagai pembanding dalam menentukan metode interpolasi yang tepat digunakan untuk tabel mortalita.

3.1.1 Pemotongan Selang pada Tabel Mortalita

Sebelum mengidentifikasi metode interpolasi tersebut, dilakukan perubahan selang usia pada tabel mortalita yang bertujuan untuk melihat seberapa cocok metode interpolasi dapat digunakan pada tabel mortalita. Perubahan selang pada tabel mortalita dijadikan pembanding dari hasil interpolasi. Selang yang digunakan pada tabel mortalita selang satu, artinya setiap selang hanya punya jarak satu. Namun, dalam penelitian ini akandigunakan selang lima untuk melihat apakah fungsi dari selang lima mempunyai perbedaan dengan selang satu.

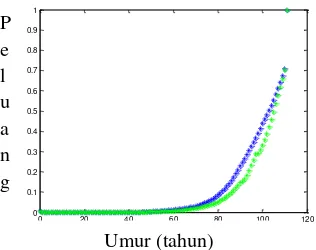
Dalam tabel mortalita sebelum dilakukan perubahan selang yang digunakan berawal dari angka nol. Namun, pada penelitian iniselang lima berawal dari angka lima. Berikut merupakan plot data dari tabel mortalita dengan selang satu dan selang lima.

Gambar 1 Tabel mortalita dengan selang satu.

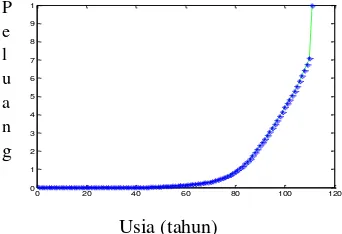
Gambar 2 Tabel mortalita selang lima.

Pada Gambar 1 dan Gambar 2 terdapat dua jenis warna yaitu birudan hijau. Warna biru menyatakan peluang seorang laki-laki meninggal dan warna hijau menyatakan peluang seorang perempuan meninggal. 3.1.2 Tabel Mortalita dengan Interpolasi

Berderajat Banyak

Penelitian ini menggunakan beberapa metode interpolasi untuk tabel mortalita. Metode interpolasi yang pertama adalah metode interpolasi berderajat banyak.

Metode interpolasi berderajat banyak menggunakan selang satu. Hasil dari metode menyatakan bahwa semakin tinggi pangkat dari persamaan maka akan mengikuti data tabel mortalita.

Langkah-langkah dari metode interpolasi berderajat banyak sebagai berikut: 1. Membuat variabel dari unsur fungsi, x

untuk usia dan y untuk peluang seseorang meninggal. Selain itu, membuat p1 untuk tempat fungsi dari interpolasi.

0 20 40 60 80 100 120

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0 20 40 60 80 100 120

(14)

5

2. Menggunakan perintah polyfit untuk membuat fungsi. Fungsi yang diperoleh di simpan pada p1. Penggunaan perintah polyfit menghasilkan polinom berderajat banyak. Fungsi yang digunakan adalah p1=polyfit(x,y,2), dengan 2 menjelaskan derajat polinom.

3. Membuat variabel y2 untuk menyimpan hasil evaluasi polinom dari p1, sehingga menghasilkan nilai baru.

Interpolasi berderajat banyak di atas kemudian dihitung kesalahan atau galat dari fungsi yang baru. Berdasarkan hasil tersebut, galat yang didapat bernilai sangat besar. Fungsi berderajat banyak diawali dengan derajat tiga dan diakhiri dengan derajat 4. Semakin besar derajat maka nilai kesalahan atau galat semakin kecil. Namun, untuk menjadi suatu fungsi akan menjadi tidak valid jika nilai kesalahan terlalu besar. Gambar dari interpolasi berderajat banyak dapat dilihat pada Lampiran 10.

3.1.3 Tabel Mortalita dengan Interpolasi Kuadratik

Percobaan pertama membuat fungsi berderajat banyak menghasilkan galat yang besar. Olehkarena itu, dilakukan percobaan kedua dengan metode interpolasi kuadratik untuk memperkecil galat dengan memotong fungsi atau menjadikan fungsi menjadi fungsi yang sepotong-sepotong.

Langkah-langkah interpolasi kuadratik sebagai berikut :

1. Membuat fungsi baru.

Mencari nilai a, b, dan c yang mengikuti pola kuadratik yaitu ax2+bx+c. Fungsi untuk menentukan nilai a, b, dan c dapat dilihat pada Lampiran 3.

2. Setelah membuat fungsi, selanjutnya memindahkan data ke dalam MATLAB R2008B agar data dapat diproses.

3. Menampilkan hasil dari interpolasi kuadratik dalam bentuk grafik. Program untuk membuat grafik dapat dilihat pada Lampiran 4.

Hasil dari interpolasi kuadratik menimbulkan adanya keanehan yang menyebabkan beberapa peluang seseorang

meninggal di usia tertentu memberikan nilai yang negatif padahal tidak mungkin negatif. Nilai negatif pada peluang. Nilai negatif dapat terjadi pada interpolasi kuadratik ketika titik-titik yang difitkan menyebabkan nilai minimum fungsi berada di bawah sumbu x. 3.1.4 Tabel Mortalita dengan Interpolasi

Spline Linear

Metode berikutnya adalah interpolasi spline linear, langkah untuk membuat interpolasi spline linear sebagai berikut: 1. Langkah pertama adalah membuat fungsi

baru.

Pertama, menentukan formula untuk nilai hasil interpolasi dengan fungsi dari nilaia dan b yang mengikuti pola linear ax+b. Kedua, mendefinisikan a dan b sebagai berikut:

,

( )

Dengan k adalah bilangan real dari 1 sampai n-1. Rincian program dapat dilihat pada Lampiran 2.

2. Setelah membuat fungsi baru maka selanjutnya data dipindahkan ke dalam MATLAB R2008B agar data diproses. 3. Setelah data dipindahkan kemudian

menghitung interpolasi spline linear dengan perintah [a,b]=spliner(x,y). Setelah itu, menemukan hasil dari nilai a dan nilai b yang membentuk suatu fungsi linear. Hasilnya dapat dilihat pada Lampiran 1.

Dari langkah-langkah di atas hasil interpolasi seperti gambar di bawah ini:

Gambar 3 Hasil interpolasi spline linear.

0 20 40 60 80 100 120

(15)

6

Pada Gambar 3 terlihat dua buah garis yaitu garis biru dan garis hijau. Garis biru menyatakan nilai peluang meninggal dari tabel mortalita sedangkan garis hijau adalah nilai dari interpolasi spline linear. Terlihat bahwa garis biru dan hijau saling berhimpit. Hal tersebut menggambarkan kesalahan dari interpolasi linear bernilai kecil.

Berdasarkan pembahasan pada 3.1.2 dan 3.1.3, metode interpolasi yang paling bisa diterima untuk model ini adalah interpolasi spline linear karena pada interpolasi spline linear hasil dari peluang bukan negatif. Selain itu, model yang didapat dari interpolasi spline linear memiliki nilai kesalahan yang relatif kecil.

3.2 Penerapan Model pada Asuransi

Model tabel mortalita ini digunakan untuk mencari harga premi asuransi, menghitung nilai premi pada asuransi berjangka dan asuransi endowmen. Dengan adanya pemodelan tabel mortalita untuk mengetahui peluang seseorang meninggal dapat digunakan fungsi dari hasil pemodelan. Perlu diketahui bahwa usia yang digunakan bukan usia bulat seperti 20 tahun melainkan 20 tahun 6 bulan yang akan dikonversi menjadi 20,5 tahun.

3.2.1 Asuransi Endowmen

Asuransi endowmen adalah gabungan antara asuransi dengan tabungan. Pada umumnya asuransi endowmen ada dua jenis

yaitu asuransi endowmen dan asuransi endowmen murni.

Perbedaan dari kedua jenis asuransi endowmen ini adalah cara pembayaran santunan perusahaan asuransi kepada tertanggung. Santunan dari asuransi endowmenn tahun dibayarkan baik setelah kematian tertanggung atau kelangsungan hidup tertanggung pada akhir masa n tahun. Namun, untuk asuransi endowmen murni n tahun santunan akan dibayarkan jika dan hanya jika tertanggung bertahan hidup setidaknya n tahun dari saat penerbitan kebijakan.

Nilai premi asuransi yang akan dihitung pada penelitian ini adalah asuransi endowmen. Misalkan orang dengan usia 20 tahun 6 bulan mengikuti asuransi endowmen, dengan jangka pembayaran 10 tahun, maka uang santunan akan diserahkan pada tertanggung saat orang tersebut masih hidup atau mati pada saat pembayaran, misalkan uang santunannya Rp 100.000.000. Sebelumnya akan dihitung ̅̅̅.

Dalam kasus di atas dihitung

̅̅̅̅̅ ∑ kp20,5q20,5+k+v20,5np20,5.

(16)

7

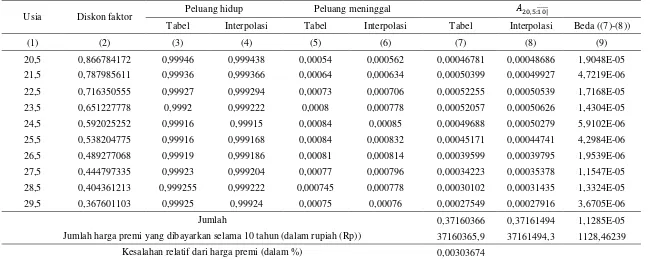
Tabel 1 Nilai premi asuransi endowmen seorang laki-laki dengan tingkat bunga 10%

Usia Diskon faktor Peluang hidup Peluang meninggal ̅̅̅̅̅

Tabel Interpolasi Tabel Interpolasi Tabel Interpolasi Beda ((7)-(8))

(1) (2) (3) (4) (5) (6) (7) (8) (9)

20,5 0,866784172 0,99946 0,999438 0,00054 0,000562 0,00046781 0,00048686 1,9048E-05 21,5 0,787985611 0,99936 0,999366 0,00064 0,000634 0,00050399 0,00049927 4,7219E-06 22,5 0,716350555 0,99927 0,999294 0,00073 0,000706 0,00052255 0,00050539 1,7168E-05 23,5 0,651227778 0,9992 0,999222 0,0008 0,000778 0,00052057 0,00050626 1,4304E-05 24,5 0,592025252 0,99916 0,99915 0,00084 0,00085 0,00049688 0,00050279 5,9102E-06 25,5 0,538204775 0,99916 0,999168 0,00084 0,000832 0,00045171 0,00044741 4,2984E-06 26,5 0,489277068 0,99919 0,999186 0,00081 0,000814 0,00039599 0,00039795 1,9539E-06 27,5 0,444797335 0,99923 0,999204 0,00077 0,000796 0,00034223 0,00035378 1,1547E-05 28,5 0,404361213 0,999255 0,999222 0,000745 0,000778 0,00030102 0,00031435 1,3324E-05 29,5 0,367601103 0,99925 0,99924 0,00075 0,00076 0,00027549 0,00027916 3,6705E-06

Jumlah 0,37160366 0,37161494 1,1285E-05

Jumlah harga premi yang dibayarkan selama 10 tahun (dalam rupiah (Rp)) 37160365,9 37161494,3 1128,46239 Kesalahan relatif dari harga premi (dalam %) 0,00303674

(17)

8

Tabel 2 Nilai premi asuransi endowmen seorang perempuan dengan tingkat bunga 10%

Tabel Interpolasi Tabel Interpolasi Tabel Interpolasi Beda((7)-(8))

(1) (2) (3) (4) (5) (6) (7) (8) (9)

20,5 0,866784172 0,999725 0,999708 0,000275 0,000292 0,0002383 0,00025303 1,4727E-05 21,5 0,787985611 0,99969 0,999676 0,00031 0,000324 0,0002442 0,00025522 1,1025E-05 22,5 0,716350555 0,99965 0,999644 0,00035 0,000356 0,00025063 0,00025493 4,2951E-06 23,5 0,651227778 0,99962 0,999612 0,00038 0,000388 0,00024737 0,00025258 5,2058E-06 24,5 0,592025252 0,999595 0,99958 0,000405 0,00042 0,00023967 0,00024855 8,8731E-06 25,5 0,538204775 0,99957 0,999556 0,00043 0,000444 0,00023133 0,00023886 7,5283E-06 26,5 0,489277068 0,99955 0,999532 0,00045 0,000468 0,00022008 0,00022887 8,7989E-06 27,5 0,444797335 0,99953 0,999508 0,00047 0,000492 0,00020896 0,00021873 9,7761E-06 28,5 0,404361213 0,999505 0,999484 0,000495 0,000516 0,00020006 0,00020854 8,483E-06 29,5 0,367601103 0,999475 0,99946 0,000525 0,00054 0,00019289 0,0001984 5,5081E-06

Jumlah 0,3696816 0,36976031 7,8706E-05

(18)

9

Dapat dilihat bahwa nilai premi pada Tabel 1 dan Tabel 2 adalah nilai premi seorang laki-laki dan perempuan yang harus dibayarkan selama 10 tahun. Namun pada kenyataannnya nilai premi yang dibayarkan oleh nasabah kepada perusahan asuransi tidak dalam jangka tahun, melainkan dalam jangka bulan. Selain itu, nilai premi yang sampai pada nasabah adalah nilai premi yang sudah dikenakan biaya administrasi, sehingga nilai premi perbulan akan lebih besar lagi.

3.2.2 Asuransi Berjangka

Asuransi berjangka adalah asuransi yang pembayarannya memiliki jangka waktu. Misalkan seseorang dengan usia 20 tahun 6 bulan mengikuti asuransi berjangka 10 tahun dengan santunan Rp 100.000.000. Pembayaran premi akan dibayarkan tertanggung selama 10 tahun dan uang santunan akan diterima tertanggung pada saat orang tersebut meninggal pada pada jangka waktu yang ditentukan dan dibayarkan di akhir tahun. Untuk menghitung harga premi harus dihitung nilai ∑

kp20,5. Hasilnya menunjukkan nilai

premi dari seorang perempuan dengan usia 20 tahun 6 bulan pada Tabel 3 dan Tabel 5. Nilai peluang meninggal dari tabel mortalita menggunakan pembulatan. Misalkan, usia 20 tahun 6 bulan maka nilai tabel mortalitanya dilihat pada usia 20 dan seterusnya.

Lebih jauh, terlihat bahwa nilai premi pada Tabel 4 dan Tabel 5 adalah nilai premi seorang laki-laki dan perempuan yang harus dibayarkan selama 10 tahun. Namun pada kenyataannya nilai premi yang dibayarkan oleh tertanggung kepada perusahan asuransi tidak dalam jangka tahun, melainkan dalam jangka bulan. Selain itu, nilai premi yang sampai pada nasabah adalah nilai premi yang sudah dikenakan biaya administrasi, sehingga nilai premi per bulan akan lebih besar lagi. 3.2.3 Kesalahan dari Nilai Premi Asuransi

Endowmen dan Asuransi Berjangka

Tabel di bawah ini menjelaskan perbedaan antara nilai kesalahan relatif dari tabel mortalita dengan kesalahan relatif dari hasil interpolasi.

Tabel 3 Perbedaan kesalahan relatif harga premi antara asuransi endowmen dengan asuransi berjangka

Asuransi Laki-laki Perempuan Endowmen 0,003% 0,020%

Berjangka 0,340% 0,020%

Tabel 3 menjelaskan bahwa nilai kesalahan dari asuransi berjangka untuk orang berjenis kelamin laki-laki memiliki kesalahan paling besar yaitu sebesar 0,340%. Hal tersebut terjadi karena nilai kesalahan dari interpolasi linear dari peluang meninggal seorang laki-laki besar, dibandingkan dengan perempuan.

Bila dilihat lagi akan ada perbedaan nilai premi asurasi antara asuransi endowmen dengan asuransi berjangka. Hal tersebut dikarenakan aturan dan proses perhitungan yang berbeda, sehingga akan menghasilkan transfer risiko yang berbeda bagi perusahaan asuransi.

Nilai premi pada asuransi endowmen akan lebih besar daripada nilai premi pada asuransi berjangka. Hal tersebut dikarenakan pada asuransi endowmen selain sistem asuransi juga memakai sistem tabungan. Artinya seorang pemegang polis dapat mengambil uangnya dari perusahaan asuransi sebelum tanggal waktu pembayaran habis. Hal ini yang membuat transfer risiko pada perusahaan asuransi lebih besar, sehingga harga premi lebih mahal.

(19)

10

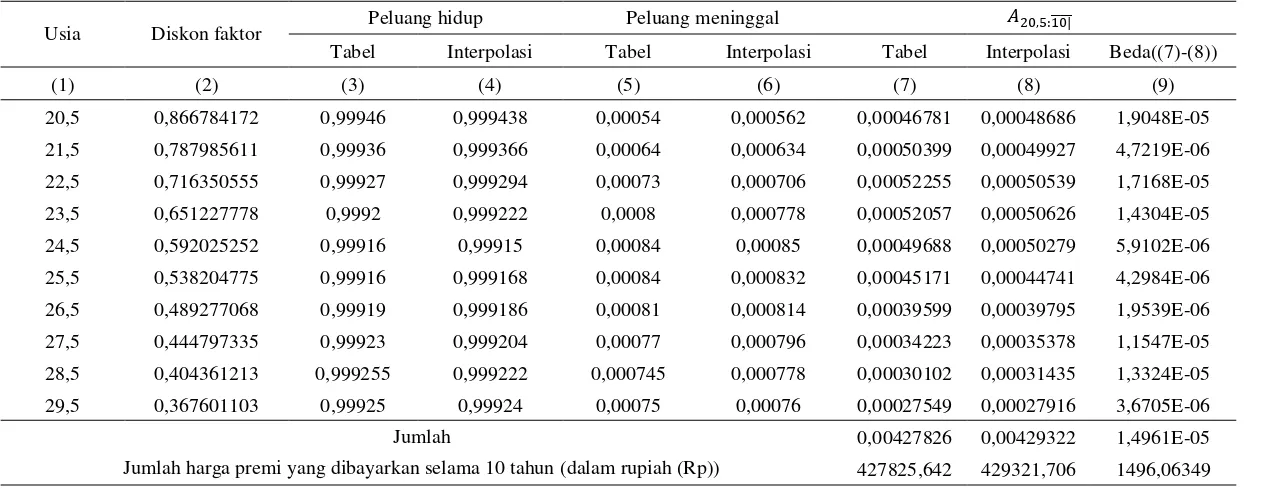
Tabel 4 Nilai premi asuransi berjangka seorang laki-lakidengan tingkat bunga 10%

(1) (2) (3) (4) (5) (6) (7) (8) (9)

20,5 0,866784172 0,99946 0,999438 0,00054 0,000562 0,00046781 0,00048686 1,9048E-05 21,5 0,787985611 0,99936 0,999366 0,00064 0,000634 0,00050399 0,00049927 4,7219E-06 22,5 0,716350555 0,99927 0,999294 0,00073 0,000706 0,00052255 0,00050539 1,7168E-05 23,5 0,651227778 0,9992 0,999222 0,0008 0,000778 0,00052057 0,00050626 1,4304E-05 24,5 0,592025252 0,99916 0,99915 0,00084 0,00085 0,00049688 0,00050279 5,9102E-06 25,5 0,538204775 0,99916 0,999168 0,00084 0,000832 0,00045171 0,00044741 4,2984E-06 26,5 0,489277068 0,99919 0,999186 0,00081 0,000814 0,00039599 0,00039795 1,9539E-06 27,5 0,444797335 0,99923 0,999204 0,00077 0,000796 0,00034223 0,00035378 1,1547E-05 28,5 0,404361213 0,999255 0,999222 0,000745 0,000778 0,00030102 0,00031435 1,3324E-05 29,5 0,367601103 0,99925 0,99924 0,00075 0,00076 0,00027549 0,00027916 3,6705E-06

Jumlah 0,00427826 0,00429322 1,4961E-05

(20)

11

Tabel 5 Nilai premi asuransi berjangka seorang perempuan dengan tingkat bunga 10%

(1) (2) (3) (4) (5) (6) (7) (8) (9)

20,5 0,866784172 0,99971 0,999708 0,00029 0,000292 0,00025129 0,00025303 1,7326E-06 21,5 0,787985611 0,99967 0,999676 0,00033 0,000324 0,00025995 0,00025522 4,7248E-06 22,5 0,716350555 0,99963 0,999644 0,00037 0,000356 0,00026495 0,00025493 1,0022E-05 23,5 0,651227778 0,99961 0,999612 0,00039 0,000388 0,00025388 0,00025258 1,3014E-06 24,5 0,592025252 0,99958 0,99958 0,00042 0,00042 0,00024855 0,00024855 5,421E-20 25,5 0,538204775 0,99956 0,999556 0,00044 0,000444 0,00023671 0,00023886 2,1509E-06 26,5 0,489277068 0,99954 0,999532 0,00046 0,000468 0,00022496 0,00022887 3,9106E-06 27,5 0,444797335 0,99952 0,999508 0,00048 0,000492 0,0002134 0,00021873 5,3324E-06 28,5 0,404361213 0,99949 0,999484 0,00051 0,000516 0,00020612 0,00020854 2,4237E-06

29,5 0,367601103 0,99946 0,99946 0,00054 0,00054 0,0001984 0,0001984 0

Jumlah 0,00235821 0,00235771 4,9777E-07

(21)

12

KESIMPULAN

Dalam penulisan karya ilmiah ini dapat

disimpulkan bahwa:

(i) Metode interpolasi dapat digunakan untuk memodelkan tabel mortalita. Interpolasi yang digunakaan adalah interpolasi berderajat banyak, interpolasi kuadratik, dan interpolasi spline linear. Dari beberapa model interpolasi di atas, interpolasi spline linear yang paling baik untuk model tabel mortalita karena hasil dari interpolasi spline linear baik untuk tabel mortalita karena hasil dari interpolasi spline linear adalah positif dan memiliki nilai kesalahan relatif

kecil jika dibandingkan dengan interpolasi berderajat banyak dan interpolasi kuadratik.

(ii) Perbedaan nilai premi asuransi endowmen dan asuransi berjangka antara tabel mortalita dengan model dari interpolasi terletak pada usia seseorang. Pada tabel mortalita hanya berselang satu, sedangkan dengan adanya model interpolasi usia dapat dihitung secara lebih spesifik. Selain itu nilai kesalahan dari asuransi berjangka untuk orang berjenis kelamin laki-laki memiliki kesalahan lebih besar dari orang berjenis kelamin perempuan.

DAFTAR PUSTAKA

Bowers NL, Gerber HU, Hickman JC, Jones

DA, Nesbitt CJ. 1997. Actuarial Mathematics Hesca. Ed ke-2. Schamburg: The Society of Actuaries.

Gunawan B. 2000. Penentuan Peluang Kebangkrutan Perusahaan Asuransi dari Peluang Survival. Skripsi, Jurusan Matematika FMIPA IPB, Bogor.

Mathews JH. 1992. Numerical Methods for Mathematics, Science, and Engineering. London: Prentice-Hall.

Mutaqin A. 1998. Interpolasi Multi Dimensi. Skripsi, Jurusan Matematika FMIPA IPB, Bogor.

Philips GM. 2003. Interpolation and Approximation by Polynomials. New York: Springer.

Promislow SD. 2006. Fundamentals of Actuarial Mathematics. England: Wiley.

Sahid. 2005. Pengantar Komputasi Numerik dengan Matlab. Ed ke-1. Yogyakarta: ANDI.

(22)

13

Lampiran 1 Fungsi Interpolasi

Spline

Linear

Keterangan:

X

: usia

Y

: nilai interpolasi tabel

Y1

: nilai interpolasi dari fungsi baru

F(x)

: fungsi dari interpolasi linear

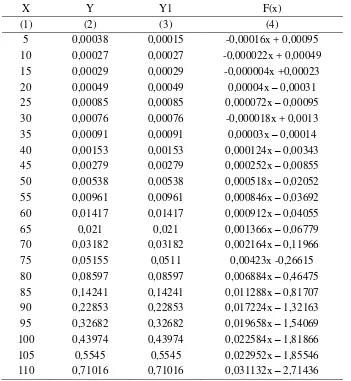
Tabel 6 Fungsi Interpolasi linear laki-laki

X

Y

Y1

F(x)

(1)

(2)

(3)

(4)

5

0,00038

0,00015

-0,00016x + 0,00095

10

0,00027

-0,000022x + 0,00049

15

0,00029

-0,000004x +0,00023

20

0,00049

0,00004x

–

0,00031

25

0,00085

0,000072x

–

0,00095

30

0,00076

-0,000018x + 0,0013

35

0,00091

0,00003x

–

0,00014

40

0,00153

0,000124x

–

0,00343

45

0,00279

0,000252x

–

0,00855

50

0,00538

0,000518x

–

0,02052

55

0,00961

0,000846x

–

0,03692

60

0,01417

0,000912x

–

0,04055

65

0,021

0,001366x

–

0,06779

70

0,03182

0,002164x

–

0,11966

75

0,05155

0,0511

0,00423x -0,26615

80

0,08597

0,006884x

–

0,46475

85

0,14241

0,011288x

–

0,81707

90

0,22853

0,017224x

–

1,32163

95

0,32682

0,019658x

–

1,54069

100

0,43974

0,022584x

–

1,81866

105

0,5545

0,022952x

–

1,85546

(23)

14

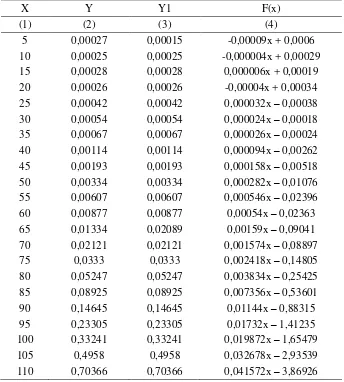
Tabel 7 Fungsi Interpolasi

Spline

Linier Perempuan

X

Y

Y1

F(x)

(1)

(2)

(3)

(4)

5

0,00027

0,00015

-0,00009x + 0,0006

10

0,00025

-0,000004x + 0,00029

15

0,00028

0,000006x + 0,00019

20

0,00026

-0,00004x + 0,00034

25

0,00042

0,000032x

–

0,00038

30

0,00054

0,000024x

–

0,00018

35

0,00067

0,000026x

–

0,00024

40

0,00114

0,000094x

–

0,00262

45

0,00193

0,000158x

–

0,00518

50

0,00334

0,000282x

–

0,01076

55

0,00607

0,000546x

–

0,02396

60

0,00877

0,00054x

–

0,02363

65

0,01334

0,02089

0,00159x

–

0,09041

70

0,02121

0,001574x

–

0,08897

75

0,0333

0,002418x

–

0,14805

80

0,05247

0,003834x

–

0,25425

85

0,08925

0,007356x

–

0,53601

90

0,14645

0,01144x

–

0,88315

95

0,23305

0,01732x

–

1,41235

100

0,33241

0,019872x

–

1,65479

105

0,4958

0,032678x

–

2,93539

(24)

15

Lampiran 2 Program untuk Mencari Interpolasi Linear pada MATLAB

function [a,b]=spliner(x,f) n=length(x);

for k=1:(n-1),

a(k)=(f(k+1)-f(k))/(x(k+1)-x(k)); b(k)=f(k)-a(k)*x(k);

end

Lampiran 3 Program untuk Mencari Fungsi Interpolasi Kuadratik pada MATLAB

function [a,b,c]=kuad(x,f) n=length(x);

a=zeros(floor(n/2),1); b=zeros(floor(n/2),1); c=zeros(floor(n/2),1); for k=1:2:(n-2),

p = polyfit([x(k) x(k+1) x(k+2)],[f(k) f(k+1) f(k+2)],2); a((k+1)/2)=p(1);

b((k+1)/2)=p(2); c((k+1)/2)=p(3); end

Lampiran 4 Program untuk Membuat Grafik Fungsi Kuadratik pada MATLAB

xx=0:1:110;

yy=zeros(1,length(xx));

yy(1)=a(1)*xx(1)^2+b(1)*xx(1)+c(1); for n=2:length(xx),

kn = ceil(xx(n)/10);

yy(n)=a(kn)*xx(n)^2+b(kn)*xx(n)+c(kn); end

plot(xx,yy,x,y);

(25)

16

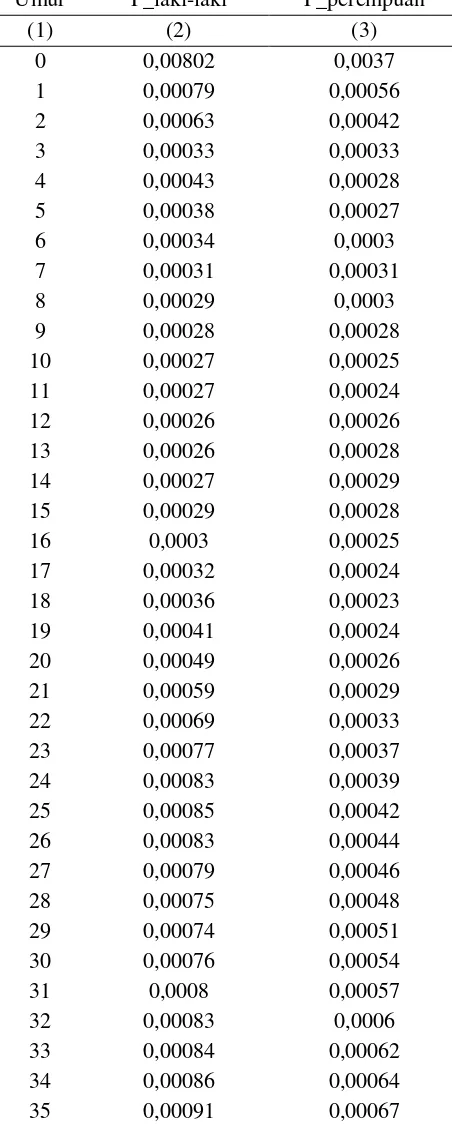
Lampiran 5 Tabel Mortalita Indonesia 2011

P_laki-laki

:peluang meninggal laki-laki

P_perempuan :peluang meninggal perempuan

Tabel 8 Tabel Mortalita Indonesia 2011

Umur

P_laki-laki

P_perempuan

(1)

(2)

(3)

0

0,00802

0,0037

1

0,00079

0,00056

2

0,00063

0,00042

3

0,00033

4

0,00043

0,00028

5

0,00038

0,00027

6

0,00034

0,0003

7

0,00031

8

0,00029

0,0003

9

0,00028

10

0,00027

0,00025

11

0,00027

0,00024

12

0,00026

13

0,00026

0,00028

14

0,00027

0,00029

15

0,00029

0,00028

16

0,0003

0,00025

17

0,00032

0,00024

18

0,00036

0,00023

19

0,00041

0,00024

20

0,00049

0,00026

21

0,00059

0,00029

22

0,00069

0,00033

23

0,00077

0,00037

24

0,00083

0,00039

25

0,00085

0,00042

26

0,00083

0,00044

27

0,00079

0,00046

28

0,00075

0,00048

29

0,00074

0,00051

30

0,00076

0,00054

31

0,0008

0,00057

32

0,00083

0,0006

33

0,00084

0,00062

34

0,00086

0,00064

(26)

17

Umur

P_laki-laki

P_perempuan

36

0,00099

0,00074

37

0,00109

0,00084

38

0,0012

0,00093

39

0,00135

0,00104

40

0,00153

0,00114

41

0,00175

0,00126

42

0,00196

0,00141

43

0,00219

0,00158

44

0,00246

0,00175

45

0,00279

0,00193

46

0,00318

0,00214

47

0,00363

0,00239

48

0,00414

0,00268

49

0,00471

0,00299

50

0,00538

0,00334

51

0,00615

0,00374

52

0,00699

0,00422

53

0,00784

0,00479

54

0,00872

0,00542

55

0,00961

0,00607

56

0,01051

0,00669

57

0,01142

0,00725

58

0,01232

0,00776

59

0,01322

0,00826

60

0,01417

0,00877

61

0,01521

0,00936

62

0,01639

0,01004

63

0,01773

0,01104

64

0,01926

0,01214

65

0,021

0,01334

66

0,02288

0,01466

67

0,02486

0,01612

68

0,02702

0,01771

69

0,02921

0,01947

70

0,03182

0,02121

71

0,03473

0,02319

72

0,03861

0,02539

73

0,04264

0,02778

74

0,04687

0,03042

75

0,05155

0,0333

76

0,05664

0,03646

(27)

18

Umur

P_laki-laki

P_perempuan

78

0,06942

0,04372

79

0,07734

0,04789

80

0,08697

0,05247

81

0,09577

0,05877

82

0,10593

0,06579

83

0,11683

0,07284

84

0,12888

0,08061

85

0,14241

0,08925

86

0,15738

0,09713

87

0,17368

0,10831

88

0,1911

0,12131

89

0,20945

0,1345

90

0,22853

0,14645

91

0,24638

0,15423

92

0,26496

0,16454

93

0,2845

0,18235

94

0,30511

0,20488

95

0,32682

0,23305

96

0,34662

0,25962

97

0,3677

0,2872

98

0,39016

0,29173

99

0,41413

0,30759

100

0,43974

0,33241

101

0,45994

0,35918

102

0,48143

0,38871

103

0,50431

0,42124

104

0,52863

0,45705

105

0,5545

0,4958

106

0,58198

0,53553

107

0,61119

0,57626

108

0,64222

0,61725

109

0,67518

0,65996

110

0,71016

0,70366

(28)

19

Lampiran 6 Perbedaan Pemecahan Selang untuk Mendapatkan Fungsi Interpolasi

Spline

Linier pada Laki-laki

Keterangan :

X

: usia seseorang dengan selang 1

X1

: usia seseorang dengan selang 5

Y

: peluang seseorang mati berdasarkan tabel mortalitas

Y1

: peluang seseorang mati berdasarkan model interpolasi linier

E

: nilai kesalahan (Y-Y1)

%

: nilai kesalahan relatif

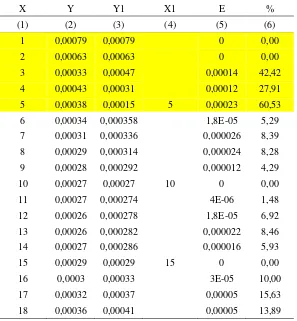
Tabel 9 Proses perhitungan nilai kesalahan dengan interval sama

Tabel 10 Proses perhitungan nilai kesalahan dengan interval bebeda

X Y Y1 X1 E % X Y Y1 X1 E %

(1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6)

1 0,00079 0,00079 0 0,00 1 0,00079 0,00079 9,75782E-19 0,00

2 0,00063 0,00063 0 0,00 2 0,00063 0,00063 1,0842E-19 0,00

3 0,00033 0,00047 0,00014 42,42 3 0,00033 0,00033 0 0,00

4 0,00043 0,00031 0,00012 27,91 4 0,00043 0,00043 5,42101E-20 0,00

5 0,00038 0,00015 5 0,00023 60,53 5 0,00038 0,00038 5 0 0,00

6 0,00034 0,000358 1,8E-05 5,29 6 0,00034 0,000358 1,8E-05 5,29

7 0,00031 0,000336 0,000026 8,39 7 0,00031 0,000336 0,000026 8,39

8 0,00029 0,000314 0,000024 8,28 8 0,00029 0,000314 0,000024 8,28

9 0,00028 0,000292 0,000012 4,29 9 0,00028 0,000292 0,000012 4,29

10 0,00027 0,00027 10 0 0,00 10 0,00027 0,00027 10 0 0,00

11 0,00027 0,000274 4E-06 1,48 11 0,00027 0,000274 4E-06 1,48

12 0,00026 0,000278 1,8E-05 6,92 12 0,00026 0,000278 1,8E-05 6,92

13 0,00026 0,000282 0,000022 8,46 13 0,00026 0,000282 0,000022 8,46

14 0,00027 0,000286 0,000016 5,93 14 0,00027 0,000286 0,000016 5,93

15 0,00029 0,00029 15 0 0,00 15 0,00029 0,00029 15 0 0,00

16 0,0003 0,00033 3E-05 10,00 16 0,0003 0,00033 3E-05 10,00

17 0,00032 0,00037 0,00005 15,63 17 0,00032 0,00037 0,00005 15,63

18 0,00036 0,00041 0,00005 13,89 18 0,00036 0,00041 0,00005 13,89

(29)

20

X Y Y1 X1 E % X Y Y1 X1 E %

19 0,00041 0,00045 4E-05 9,76 19 0,00041 0,00045 4E-05 9,76

20 0,00049 0,00049 20 0 0,00 20 0,00049 0,00049 20 0 0,00

21 0,00059 0,000562 2,8E-05 4,75 21 0,00059 0,000562 2,8E-05 4,75

22 0,00069 0,000634 5,6E-05 8,12 22 0,00069 0,000634 5,6E-05 8,12

23 0,00077 0,000706 6,4E-05 8,31 23 0,00077 0,000706 6,4E-05 8,31

24 0,00083 0,000778 5,2E-05 6,27 24 0,00083 0,000778 5,2E-05 6,27

25 0,00085 0,00085 25 0 0,00 25 0,00085 0,00085 25 0 0,00

26 0,00083 0,000832 2E-06 0,24 26 0,00083 0,000832 2E-06 0,24

27 0,00079 0,000814 2,4E-05 3,04 27 0,00079 0,000814 2,4E-05 3,04

28 0,00075 0,000796 4,6E-05 6,13 28 0,00075 0,000796 4,6E-05 6,13

29 0,00074 0,000778 3,8E-05 5,14 29 0,00074 0,000778 3,8E-05 5,14

30 0,00076 0,00076 30 0 0,00 30 0,00076 0,00076 30 0 0,00

31 0,0008 0,00079 1E-05 1,25 31 0,0008 0,00079 1E-05 1,25

32 0,00083 0,00082 0,00001 1,20 32 0,00083 0,00082 0,00001 1,20

33 0,00084 0,00085 0,00001 1,19 33 0,00084 0,00085 0,00001 1,19

34 0,00086 0,00088 2E-05 2,33 34 0,00086 0,00088 2E-05 2,33

35 0,00091 0,00091 35 0 0,00 35 0,00091 0,00091 35 0 0,00

36 0,00099 0,001034 4,4E-05 4,44 36 0,00099 0,001034 4,4E-05 4,44

37 0,00109 0,001158 6,8E-05 6,24 37 0,00109 0,001158 6,8E-05 6,24

38 0,0012 0,001282 8,2E-05 6,83 38 0,0012 0,001282 8,2E-05 6,83

39 0,00135 0,001406 5,6E-05 4,15 39 0,00135 0,001406 5,6E-05 4,15

40 0,00153 0,00153 40 0 0,00 40 0,00153 0,00153 40 0 0,00

41 0,00175 0,001782 3,2E-05 1,83 41 0,00175 0,001782 3,2E-05 1,83

42 0,00196 0,002034 7,4E-05 3,78 42 0,00196 0,002034 7,4E-05 3,78

43 0,00219 0,002286 9,6E-05 4,38 43 0,00219 0,002286 9,6E-05 4,38

44 0,00246 0,002538 7,8E-05 3,17 44 0,00246 0,002538 7,8E-05 3,17

45 0,00279 0,00279 45 0 0,00 45 0,00279 0,00279 45 0 0,00

46 0,00318 0,003308 0,000128 4,03 46 0,00318 0,003308 0,000128 4,03

47 0,00363 0,003826 0,000196 5,40 47 0,00363 0,003826 0,000196 5,40

(30)

21

X Y Y1 X1 E % X Y Y1 X1 E %

48 0,00414 0,004344 0,000204 4,93 48 0,00414 0,004344 0,000204 4,93

49 0,00471 0,004862 0,000152 3,23 49 0,00471 0,004862 0,000152 3,23

50 0,00538 0,00538 50 0 0,00 50 0,00538 0,00538 50 0 0,00

51 0,00615 0,006226 7,6E-05 1,24 51 0,00615 0,006226 7,6E-05 1,24

52 0,00699 0,007072 8,2E-05 1,17 52 0,00699 0,007072 8,2E-05 1,17

53 0,00784 0,007918 7,8E-05 0,99 53 0,00784 0,007918 7,8E-05 0,99

54 0,00872 0,008764 4,4E-05 0,50 54 0,00872 0,008764 4,4E-05 0,50

55 0,00961 0,00961 55 0 0,00 55 0,00961 0,00961 55 0 0,00

56 0,01051 0,010522 1,2E-05 0,11 56 0,01051 0,010522 1,2E-05 0,11

57 0,01142 0,011434 1,4E-05 0,12 57 0,01142 0,011434 1,4E-05 0,12

58 0,01232 0,012346 2,6E-05 0,21 58 0,01232 0,012346 2,6E-05 0,21

59 0,01322 0,013258 3,8E-05 0,29 59 0,01322 0,013258 3,8E-05 0,29

60 0,01417 0,01417 60 0 0,00 60 0,01417 0,01417 60 0 0,00

61 0,01521 0,015536 0,000326 2,14 61 0,01521 0,015536 0,000326 2,14

62 0,01639 0,016902 0,000512 3,12 62 0,01639 0,016902 0,000512 3,12

63 0,01773 0,018268 0,000538 3,03 63 0,01773 0,018268 0,000538 3,03

64 0,01926 0,019634 0,000374 1,94 64 0,01926 0,019634 0,000374 1,94

65 0,021 0,021 65 0 0,00 65 0,021 0,021 65 0 0,00

66 0,02288 0,023164 0,000284 1,24 66 0,02288 0,023164 0,000284 1,24

67 0,02486 0,025328 0,000468 1,88 67 0,02486 0,025328 0,000468 1,88

68 0,02702 0,027492 0,000472 1,75 68 0,02702 0,027492 0,000472 1,75

69 0,02921 0,029656 0,000446 1,53 69 0,02921 0,029656 0,000446 1,53

70 0,03182 0,03182 70 0 0,00 70 0,03182 0,03182 70 0 0,00

71 0,03473 0,03418 0,00055 1,58 71 0,03473 0,03418 0,00055 1,58

72 0,03861 0,03841 0,0002 0,52 72 0,03861 0,03841 0,0002 0,52

73 0,04264 0,04264 0 0,00 73 0,04264 0,04264 0 0,00

74 0,04687 0,04687 0 0,00 74 0,04687 0,04687 0 0,00

75 0,05155 0,0511 75 0,00045 0,87 75 0,05155 0,0511 75 0,00045 0,87

76 0,05664 0,058434 0,001794 3,17 76 0,05664 0,058434 0,001794 3,17

(31)

22

X Y Y1 X1 E % X Y Y1 X1 E %

77 0,06254 0,065318 0,002778 4,44 77 0,06254 0,065318 0,002778 4,44

78 0,06942 0,072202 0,002782 4,01 78 0,06942 0,072202 0,002782 4,01

79 0,07734 0,079086 0,001746 2,26 79 0,07734 0,079086 0,001746 2,26

80 0,08697 0,08597 80 0,001 1,15 80 0,08697 0,08597 80 0,001 1,15

81 0,09577 0,097258 0,001488 1,55 81 0,09577 0,097258 0,001488 1,55

82 0,10593 0,108546 0,002616 2,47 82 0,10593 0,108546 0,002616 2,47

83 0,11683 0,119834 0,003004 2,57 83 0,11683 0,119834 0,003004 2,57

84 0,12888 0,131122 0,002242 1,74 84 0,12888 0,131122 0,002242 1,74

85 0,14241 0,14241 85 0 0,00 85 0,14241 0,14241 85 0 0,00

86 0,15738 0,159634 0,002254 1,43 86 0,15738 0,159634 0,002254 1,43

87 0,17368 0,176858 0,003178 1,83 87 0,17368 0,176858 0,003178 1,83

88 0,1911 0,194082 0,002982 1,56 88 0,1911 0,194082 0,002982 1,56

89 0,20945 0,211306 0,001856 0,89 89 0,20945 0,211306 0,001856 0,89

90 0,22853 0,22853 90 0 0,00 90 0,22853 0,22853 90 0 0,00

91 0,24638 0,248188 0,001808 0,73 91 0,24638 0,248188 0,001808 0,73

92 0,26496 0,267846 0,002886 1,09 92 0,26496 0,267846 0,002886 1,09

93 0,2845 0,287504 0,003004 1,06 93 0,2845 0,287504 0,003004 1,06

94 0,30511 0,307162 0,002052 0,67 94 0,30511 0,307162 0,002052 0,67

95 0,32682 0,32682 95 0 0,00 95 0,32682 0,32682 95 0 0,00

96 0,34662 0,349404 0,002784 0,80 96 0,34662 0,349404 0,002784 0,80

97 0,3677 0,371988 0,004288 1,17 97 0,3677 0,371988 0,004288 1,17

98 0,39016 0,394572 0,004412 1,13 98 0,39016 0,394572 0,004412 1,13

99 0,41413 0,417156 0,003026 0,73 99 0,41413 0,417156 0,003026 0,73

100 0,43974 0,43974 100 0 0,00 100 0,43974 0,43974 100 0 0,00

101 0,45994 0,462692 0,002752 0,60 101 0,45994 0,462692 0,002752 0,60

102 0,48143 0,485644 0,004214 0,88 102 0,48143 0,485644 0,004214 0,88

103 0,50431 0,508596 0,004286 0,85 103 0,50431 0,508596 0,004286 0,85

104 0,52863 0,531548 0,002918 0,55 104 0,52863 0,531548 0,002918 0,55

105 0,5545 0,5545 105 0 0,00 105 0,5545 0,5545 105 0 0,00

(32)

23

X Y Y1 X1 E % X Y Y1 X1 E %

106 0,58198 0,585632 0,003652 0,63 106 0,58198 0,585632 0,003652 0,63

107 0,61119 0,616764 0,005574 0,91 107 0,61119 0,616764 0,005574 0,91

108 0,64222 0,647896 0,005676 0,88 108 0,64222 0,647896 0,005676 0,88

109 0,67518 0,679028 0,003848 0,57 109 0,67518 0,679028 0,003848 0,57

110 0,71016 0,71016 110 0 0,00 110 0,71016 0,71016 110 0 0,00

111 1 1 0 0,00 111 1 1 0 0,00

(33)

24

Lampiran 7 Perbedaan Pemecahan Selang untuk Mendapatkan Fungsi Interpolasi

Spline

Linier pada Perempuan

Keterangan :

X

: usia dengan selang 1

X1

: usia dengan selang 5

Y

: peluang seseorang mati berdasarkan tabel mortalitas

Y1

: peluang seseorang mati berdasarkan model interpolasi linier

E

: nilai kesalahan (Y-Y1)

[image:33.792.419.729.226.548.2]

%

: nilai kesalahan relatif

Tabel 11 Proses perhitungan nilai kesalahan dengan interval sama

Tabel 12 Proses perhitungan nilai kesalahan dengan interval bebeda

X Y Y1 X1 E % X Y Y1 X1 E %

(1) (2) (3) (4) (5) (6) (1) (2) (3) (4) (5) (6)

1 0,00056 0,00051 0,00005 8,93 1 0,00056 0,00056 2,1684E-19 0,00

2 0,00042 0,00042 0 0,00 2 0,00042 0,00042 0 0,00

3 0,00033 0,00033 0 0,00 3 0,00033 0,00033 5,42101E-20 0,00

4 0,00028 0,00024 4E-05 14,29 4 0,00028 0,00028 0 0,00

5 0,00027 0,00015 5 0,00012 44,44 5 0,00027 0,00027 5 1,6263E-19 0,00

6 0,0003 2,66E-04 0,000034 11,33 6 0,0003 2,66E-04 0,000034 11,33

7 0,00031 2,62E-04 0,000048 15,48 7 0,00031 2,62E-04 0,000048 15,48

8 0,0003 2,58E-04 0,000042 14,00 8 0,0003 2,58E-04 0,000042 14,00

9 0,00028 2,54E-04 0,000026 9,29 9 0,00028 2,54E-04 0,000026 9,29

10 0,00025 2,50E-04 10 0 0,00 10 0,00025 2,50E-04 10 0 0,00

11 0,00024 2,56E-04 1,6E-05 6,67 11 0,00024 2,56E-04 1,6E-05 6,67

12 0,00026 2,62E-04 2E-06 0,77 12 0,00026 2,62E-04 2E-06 0,77

13 0,00028 2,68E-04 1,2E-05 4,29 13 0,00028 2,68E-04 1,2E-05 4,29

14 0,00029 2,74E-04 1,6E-05 5,52 14 0,00029 2,74E-04 1,6E-05 5,52

15 0,00028 2,80E-04 15 0 0,00 15 0,00028 2,80E-04 15 0 0,00

16 0,00025 2,76E-04 0,000026 10,40 16 0,00025 2,76E-04 0,000026 10,40

17 0,00024 2,72E-04 0,000032 13,33 17 0,00024 2,72E-04 0,000032 13,33

18 0,00023 2,68E-04 0,000038 16,52 18 0,00023 2,68E-04 0,000038 16,52

[image:33.792.80.375.228.545.2]

(34)

25

X Y Y1 X1 E % X Y Y1 X1 E %

19 0,00024 2,64E-04 0,000024 10,00 19 0,00024 2,64E-04 0,000024 10,00

20 0,00026 2,60E-04 20 0 0,00 20 0,00026 2,60E-04 20 0 0,00

21 0,00029 2,92E-04 2E-06 0,69 21 0,00029 2,92E-04 2E-06 0,69

22 0,00033 3,24E-04 6E-06 1,82 22 0,00033 3,24E-04 6E-06 1,82

23 0,00037 3,56E-04 0,000014 3,78 23 0,00037 3,56E-04 0,000014 3,78

24 0,00039 3,88E-04 2E-06 0,51 24 0,00039 3,88E-04 2E-06 0,51

25 0,00042 4,20E-04 25 0 0,00 25 0,00042 4,20E-04 25 0 0,00

26 0,00044 4,44E-04 4E-06 0,91 26 0,00044 4,44E-04 4E-06 0,91

27 0,00046 4,68E-04 8E-06 1,74 27 0,00046 4,68E-04 8E-06 1,74

28 0,00048 4,92E-04 0,000012 2,50 28 0,00048 4,92E-04 0,000012 2,50

29 0,00051 5,16E-04 6E-06 1,18 29 0,00051 5,16E-04 6E-06 1,18

30 0,00054 5,40E-04 30 0 0,00 30 0,00054 5,40E-04 30 0 0,00

31 0,00057 5,66E-04 4E-06 0,70 31 0,00057 5,66E-04 4E-06 0,70

32 0,0006 5,92E-04 8E-06 1,33 32 0,0006 5,92E-04 8E-06 1,33

33 0,00062 6,18E-04 2E-06 0,32 33 0,00062 6,18E-04 2E-06 0,32

34 0,00064 6,44E-04 4E-06 0,62 34 0,00064 6,44E-04 4E-06 0,62

35 0,00067 6,70E-04 35 0 0,00 35 0,00067 6,70E-04 35 0 0,00

36 0,00074 7,64E-04 2,4E-05 3,24 36 0,00074 7,64E-04 2,4E-05 3,24

37 0,00084 8,58E-04 1,8E-05 2,14 37 0,00084 8,58E-04 1,8E-05 2,14

38 0,00093 9,52E-04 2,2E-05 2,37 38 0,00093 9,52E-04 2,2E-05 2,37

39 0,00104 1,05E-03 6E-06 0,58 39 0,00104 1,05E-03 6E-06 0,58

40 0,00114 1,14E-03 40 0 0,00 40 0,00114 1,14E-03 40 0 0,00

41 0,00126 0,001298 3,8E-05 3,02 41 0,00126 0,001298 3,8E-05 3,02

42 0,00141 0,001456 4,6E-05 3,26 42 0,00141 0,001456 4,6E-05 3,26

43 0,00158 0,001614 0,000034 2,15 43 0,00158 0,001614 0,000034 2,15

44 0,00175 0,001772 2,2E-05 1,26 44 0,00175 0,001772 2,2E-05 1,26

45 0,00193 0,00193 45 0 0,00 45 0,00193 0,00193 45 0 0,00

46 0,00214 0,002212 7,2E-05 3,36 46 0,00214 0,002212 7,2E-05 3,36

47 0,00239 0,002494 0,000104 4,35 47 0,00239 0,002494 0,000104 4,35

(35)

26

X Y Y1 X1 E % X Y Y1 X1 E %

48 0,00268 0,002776 9,6E-05 3,58 48 0,00268 0,002776 9,6E-05 3,58

49 0,00299 0,003058 6,8E-05 2,27 49 0,00299 0,003058 6,8E-05 2,27

50 0,00334 0,00334 50 0 0,00 50 0,00334 0,00334 50 0 0,00

51 0,00374 0,003886 0,000146 3,90 51 0,00374 0,003886 0,000146 3,90

52 0,00422 0,004432 0,000212 5,02 52 0,00422 0,004432 0,000212 5,02

53 0,00479 0,004978 0,000188 3,92 53 0,00479 0,004978 0,000188 3,92

54 0,00542 0,005524 0,000104 1,92 54 0,00542 0,005524 0,000104 1,92

55 0,00607 0,00607 55 0 0,00 55 0,00607 0,00607 55 0 0,00

56 0,00669 0,00661 8E-05 1,20 56 0,00669 0,00661 8E-05 1,20

57 0,00725 0,00715 0,0001 1,38 57 0,00725 0,00715 0,0001 1,38

58 0,00776 0,00769 7E-05 0,90 58 0,00776 0,00769 7E-05 0,90

59 0,00826 0,00823 3E-05 0,36 59 0,00826 0,00823 3E-05 0,36

60 0,00877 0,00877 60 0 0,00 60 0,00877 0,00877 60 0 0,00

61 0,00936 0,009684 0,000324 3,46 61 0,00936 0,009684 0,000324 3,46

62 0,01004 0,010598 0,000558 5,56 62 0,01004 0,010598 0,000558 5,56

63 0,01104 0,011512 0,000472 4,28 63 0,01104 0,011512 0,000472 4,28

64 0,01214 0,012426 0,000286 2,36 64 0,01214 0,012426 0,000286 2,36

65 0,01334 0,01334 65 0 0,00 65 0,01334 0,01334 65 0 0,00

66 0,01466 0,01453 0,00013 0,89 66 0,01466 0,01453 0,00013 0,89

67 0,01612 0,01612 0 0,00 67 0,01612 0,01612 0 0,00

68 0,01771 0,01771 0 0,00 68 0,01771 0,01771 0 0,00

69 0,01947 0,0193 0,00017 0,87 69 0,01947 0,0193 0,00017 0,87

70 0,02121 0,02089 70 0,00032 1,51 70 0,02121 0,02089 70 0,00032 1,51

71 0,02319 0,023628 0,000438 1,89 71 0,02319 0,023628 0,000438 1,89

72 0,02539 0,026046 0,000656 2,58 72 0,02539 0,026046 0,000656 2,58

73 0,02778 0,028464 0,000684 2,46 73 0,02778 0,028464 0,000684 2,46

74 0,03042 0,030882 0,000462 1,52 74 0,03042 0,030882 0,000462 1,52

75 0,0333 0,0333 75 0 0,00 75 0,0333 0,0333 75 0 0,00

76 0,03646 0,037134 0,000674 1,85 76 0,03646 0,037134 0,000674 1,85

(36)

27

X Y Y1 X1 E % X Y Y1 X1 E %

77 0,03991 0,040968 0,001058 2,65 77 0,03991 0,040968 0,001058 2,65

78 0,04372 0,044802 0,001082 2,47 78 0,04372 0,044802 0,001082 2,47

79 0,04789 0,048636 0,000746 1,56 79 0,04789 0,048636 0,000746 1,56

80 0,05247 0,05247 80 0 0,00 80 0,05247 0,05247 80 0 0,00

81 0,05877 0,059826 0,001056 1,80 81 0,05877 0,059826 0,001056 1,80

82 0,06579 0,067182 0,001392 2,12 82 0,06579 0,067182 0,001392 2,12

83 0,07284 0,074538 0,001698 2,33 83 0,07284 0,074538 0,001698 2,33

84 0,08061 0,081894 0,001284 1,59 84 0,08061 0,081894 0,001284 1,59

85 0,08925 0,08925 85 0 0,00 85 0,08925 0,08925 85 0 0,00

86 0,09713 0,10069 0,00356 3,67 86 0,09713 0,10069 0,00356 3,67

87 0,10831 0,11213 0,00382 3,53 87 0,10831 0,11213 0,00382 3,53

88 0,12131 0,12357 0,00226 1,86 88 0,12131 0,12357 0,00226 1,86

89 0,1345 0,13501 0,00051 0,38 89 0,1345 0,13501 0,00051 0,38

90 0,14645 0,14645 90 0 0,00 90 0,14645 0,14645 90 0 0,00

91 0,15423 0,16377 0,00954 6,19 91 0,15423 0,16377 0,00954 6,19

92 0,16454 0,18109 0,01655 10,06 92 0,16454 0,18109 0,01655 10,06

93 0,18235 0,19841 0,01606 8,81 93 0,18235 0,19841 0,01606 8,81

94 0,20488 0,21573 0,01085 5,30 94 0,20488 0,21573 0,01085 5,30

95 0,23305 0,23305 95 0 0,00 95 0,23305 0,23305 95 0 0,00

96 0,25962 0,252922 0,006698 2,58 96 0,25962 0,252922 0,006698 2,58

97 0,2872 0,272794 0,014406 5,02 97 0,2872 0,272794 0,014406 5,02

98 0,29173 0,292666 0,000936 0,32 98 0,29173 0,292666 0,000936 0,32

99 0,30759 0,312538 0,004948 1,61 99 0,30759 0,312538 0,004948 1,61

100 0,33241 0,33241 100 0 0,00 100 0,33241 0,33241 100 0 0,00

101 0,35918 0,365088 0,005908 1,64 101 0,35918 0,365088 0,005908 1,64

102 0,38871 0,397766 0,009056 2,33 102 0,38871 0,397766 0,009056 2,33

103 0,42124 0,430444 0,009204 2,18 103 0,42124 0,430444 0,009204 2,18

104 0,45705 0,463122 0,006072 1,33 104 0,45705 0,463122 0,006072 1,33

105 0,4958 0,4958 105 0 0,00 105 0,4958 0,4958 105 0 0,00

(37)

28

X Y Y1 X1 E % X Y Y1 X1 E %

106 0,53553 0,537372 0,001842 0,34 106 0,53553 0,537372 0,001842 0,34

107 0,57626 0,578944 0,002684 0,47 107 0,57626 0,578944 0,002684 0,47

108 0,61725 0,620516 0,003266 0,53 108 0,61725 0,620516 0,003266 0,53

109 0,65996 0,662088 0,002128 0,32 109 0,65996 0,662088 0,002128 0,32

110 0,70366 0,70366 110 0 0,00 110 0,70366 0,70366 110 0 0,00

111 1 1 0 0,00 111 1 1 0 0,00

(38)

29

Lampiran 8 Nilai dari Fungsi Kuadratik

P_laki-laki

:peluang meninggal laki-laki

P_perempuan :peluang meninggal perempuan

Y1 : peluang meninggal laki-laki dari fungsi kuadratik Y2 : peluang meninggal perempuan dari fungsi kuadratik

[image:38.612.71.550.214.732.2]

E1 : nilai kesalahan dari fungsi kuadratik laki-laki (P_laki-laki – Y1) E2 : nilai kesalahan dari fungsi kuadratik perempuan (P_perempuan – Y2) K1 : kesalahan relatif dari fungsi kuadaratik laki-laki ( |E1| / P_laki-laki * 100) K2 : kesalahan relatif dari fungsi kuadaratik perempuan( |E2| / P_perempuan * 100) Tabel 13 Nilai dari Fungsi Kuadratik

Usia P_laki-laki P_perempuan Y1 E1 K1 Y2 E2 K2

(1) (2) (3) (4) (5) (6) (7) (8) (9)

0 0,00802 0,0037 0,00802 0 0 0,0037 0 0

1 0,00079 0,00056 0,00589 0,0051 645,519 0,002741 0,002181 389,5 2 0,00063 0,00042 0,00406 0,00343 544,5079 0,001919 0,001499 356,8571 3 0,00033 0,00033 0,002532 0,002202 667,3939 0,001233 0,000903 273,5758 4 0,00043 0,00028 0,001306 0,000876 203,6279 0,000683 0,000403 144

5 0,00038 0,00027 0,00038 0 0 0,00027 0 0

6 0,00034 0,0003 -0,00024 0,000584 171,8824 -6,80E-06 0,000307 102,2667 7 0,00031 0,00031 -0,00057 0,000878 283,0968 -0,00015 0,000457 147,4839 8 0,00029 0,0003 -0,00059 0,00088 303,3103 -0,00015 0,000451 150,4 9 0,00028 0,00028 -0,00031 0,00059 210,8571 -1,88E-05 0,000299 106,7143 10 0,00027 0,00025 0,00027 1,03E-18 3,81E-13 0,00025 1,03E-18 4,12E-13 11 0,00027 0,00024 0,00026 1,04E-05 3,851852 0,00026 0,00002 8,333333 12 0,00026 0,00026 0,000256 3,6E-06 1,384615 0,000268 8E-06 3,076923 13 0,00026 0,00028 0,00026 4E-07 0,153846 0,000274 6E-06 2,142857 14 0,00027 0,00029 0,000272 1,6E-06 0,592593 0,000278 0,000012 4,137931

15 0,00029 0,00028 0,00029 0 0 0,00028 0 0

16 0,0003 0,00025 0,000316 1,56E-05 5,2 0,00028 0,00003 12 17 0,00032 0,00024 0,000348 2,84E-05 8,875 0,000278 0,000038 15,83333 18 0,00036 0,00023 0,000388 2,84E-05 7,888889 0,000274 0,000044 19,13043 19 0,00041 0,00024 0,000436 2,56E-05 6,243902 0,000268 0,000028 11,66667 20 0,00049 0,00026 0,00049 9,76E-19 1,99E-13 0,00026 0 0 21 0,00059 0,00029 0,000598 8E-06 1,355932 0,000295 5,2E-06 1,793103 22 0,00069 0,00033 0,000688 2E-06 0,289855 0,000329 1,2E-06 0,363636 23 0,00077 0,00037 0,00076 1E-05 1,298701 0,000361 9,2E-06 2,486486 24 0,00083 0,00039 0,000814 0,000016 1,927711 0,000391 1,2E-06 0,307692 25 0,00085 0,00042 0,00085 1,08E-18 1,28E-13 0,00042 0 0 26 0,00083 0,00044 0,000868 3,8E-05 4,578313 0,000447 7,2E-06 1,636364 27 0,00079 0,00046 0,000868 7,8E-05 9,873418 0,000473 1,28E-05 2,782609 28 0,00075 0,00048 0,00085 0,0001 13,33333 0,000497 1,68E-05 3,5 29 0,00074 0,00051 0,000814 7,4E-05 10 0,000519 9,2E-06 1,803922

(39)

30

Usia P_laki-laki P_perempuan Y1 E1 K1 Y2 E2 K2

31 0,0008 0,00057 0,000752 4,76E-05 5,95 0,000539 3,12E-05 5,473684 32 0,00083 0,0006 0,000764 6,64E-05 8 0,000551 4,88E-05 8,133333 33 0,00084 0,00062 0,000794 4,64E-05 5,52381 0,000577 4,28E-05 6,903226 34 0,00086 0,00064 0,000842 1,76E-05 2,046512 0,000617 2,32E-05 3,625 35 0,00091 0,00067 0,00091 9,76E-19 1,07E-13 0,00067 0 0 36 0,00099 0,00074 0,000996 6,4E-06 0,646465 0,000737 3,2E-06 0,432432 37 0,00109 0,00084 0,001102 1,16E-05 1,06422 0,000817 2,28E-05 2,714286 38 0,0012 0,00093 0,001226 2,56E-05 2,133333 0,000911 1,88E-05 2,021505 39 0,00135 0,00104 0,001368 1,84E-05 1,362963 0,001019 2,12E-05 2,038462

40 0,00153 0,00114 0,00153 0 0 0,00114 0 0

41 0,00175 0,00126 0,001676 7,44E-05 4,251429 0,001248 1,16E-05 0,920635 42 0,00196 0,00141 0,001874 8,56E-05 4,367347 0,001382 2,84E-05 2,014184 43 0,00219 0,00158 0,002126 6,36E-05 2,90411 0,00154 4,04E-05 2,556962 44 0,00246 0,00175 0,002432 2,84E-05 1,154472 0,001722 2,76E-05 1,577143 45 0,00279 0,00193 0,00279 9,97E-18 3,58E-13 0,00193 9,97E-18 5,17E-13 46 0,00318 0,00214 0,003202 2,16E-05 0,679245 0,002162 2,24E-05 1,046729 47 0,00363 0,00239 0,003666 3,64E-05 1,002755 0,00242 2,96E-05 1,238494 48 0,00414 0,00268 0,004184 4,44E-05 1,072464 0,002702 2,16E-05 0,80597 49 0,00471 0,00299 0,004756 4,56E-05 0,968153 0,003008 1,84E-05 0,615385 50 0,00538 0,00334 0,00538 1,99E-17 3,71E-13 0,00334 9,97E-18 2,99E-13 51 0,00615 0,00374 0,0062 4,96E-05 0,806504 0,003888 0,000148 3,967914 52 0,00699