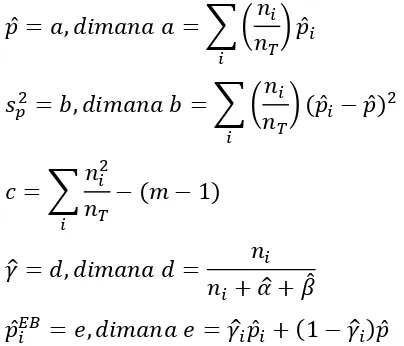PENERAPAN METODE BAYES EMPIRIK PADA PENDUGAAN
AREA KECIL
(Studi tentang Proporsi Status Kepemilikan Kartu Jaminan
Kesehatan Masyarakat (JAMKESMAS)
di Kota Takengon Kabupaten Aceh Tengah)
SKRIPSI
LINDA SAHARA
100823012
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PENERAPAN METODE BAYES EMPIRIK PADA PENDUGAAN
AREA KECIL
(Studi tentang Proporsi Status Kepemilikan Kartu Jaminan
Kesehatan Masyarakat (JAMKESMAS)
di Kota Takengon Kabupaten Aceh Tengah)
SKRIPSI
Diajukan untuk memenuhi syarat mendapat gelar Sarjana Sains
LINDA SAHARA
100823012
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Program Studi : SARJANA (S1) MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA
PERNYATAAN
PENERAPAN METODE BAYES EMPIRIK PADA PENDUGAAN AREA KECIL
(Studi tentang Proporsi Status Kepemilikan Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS) di Kota Takengon Kabupaten Aceh tengah)
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2012
LINDA SAHARA
PENGHARGAAN
Segala Puji bagi Allah SWT. Pemelihara sekalian alam, Yang Maha Bijaksana, Maha
Luas Anugerah-Nya, Maha Ilmu, Maha Rahman, Maha Pengasih yang menciptakan
manusia dalam bentuk yang paling baik dan sempurna menjadikan langit dan bumi
dengan kekuasaan-Nya serta mengatur semua urusan di dunia dan akhirat dengan
keadilan dan kebijaksanaan-Nya. Atas kehendak Nya lah penulis dapat menyelesaikan
Skripsi ini.
Dengan kerendahan hati penulis menyadari bahwa skripsi ini masih jauh dari
sempurna, tetapi penulis berharap kiranya skripsi ini dapat menambah bahan bacaan
yang bermanfaat bagi siapa saja yang membacanya. Selama proses penulisan skripsi
ini penulis banyak mendapat bantuan moril maupun materil dari berbagai pihak,
karena itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada :
1. Bapak Drs. Suwarno Ariswoyo, M.Si dan Bapak Drs. Faigiziduhu Bu’ulolo M.Si, sebagai ketua dan co pembimbing pada penyelesaian skripsi ini yang telah
memberi panduan dan penuh kepercayaan kepada saya untuk menyempurnakan
skripsi ini. Panduan ringkas dan padat serta profesional telah diberikan agar
penulis dapat menyelesaikan skripsi ini.
2. Bapak Prof.Dr.Tulus.Vordipl.Math.,M.Si.,Ph.D dan Ibu Dra. Mardiningsih, M.Si
sebagai ketua dan sekretaris Departemen Matematika FMIPA USU.
3. Dr. Sutarman, M.Sc sebagai Dekan Fakultas Matematika dan Ilmu Pengetahuan
Alam Universitas Sumatera Utara.
4. Bapak Drs. Pasukat Sembiring, M.Si dan Bapak Drs. Gim Tarigan, M.Si sebagai penguji yang telah memberikan masukan positif dalam penyelesaian skripsi ini.
5. Seluruh dosen pengajar pada Departemen Matematika FMIPA USU yang telah
membagikan ilmunya serta bimbingan dan arahan kepada penulis dan seluruh staf
pegawai yang telah memberikan bantuan dalam penyelesaian skripsi ini.
6. Ayahanda tercinta Damai dan ibunda tercinta Zuriati serta seluruh anggota
keluarga atas segala dukungan yang diberikan baik moril maupun materil selama
penyelesaian skripsi ini.
7. Sahabat-sahabatku, teman-temanku yang telah banyak memberi dorongan
semangat dan atas semua bantuannya khususnya Direstika Yolanda, Vani Gita
Pertiwi, Uci Supriana, Eka Kurniati Hasibuan, Monica Elisabet Pangaribuan dan
seluruh rekan-rekan yang lainnya.
Akhirnya penulis berharap kiranya Tuhan Yang Maha Esa membalas kebaikan
dari semua pihak dan kiranya tulisan ini bermanfaat bagi pembaca khususnya bagi
penulis.
Medan, Juli 2012 Penulis
LINDA SAHARA
ABSTRAK
Pendugaan area kecil berguna untuk menduga parameter subpopulasi (area) yang
berukuran contoh kecil. Pada data biner, model Beta-Binomial dapat digunakan untuk
menduga parameter area kecil. Ada dua metode dalam pendugaan area kecil untuk
data biner, yaitu Bayes empirik dan Bayes hierarkhi. Pada skripsi ini digunakan
metode Bayes empirik dalam menghasilkan penduga proporsi. Tujuannya adalah
menilai kinerja penduga langsung dan penduga Bayes empirik pada pendugaan area
kecil untuk kasus biner. Hasil penerapan pada proporsi status kepemilikan Kartu
Jaminan Kesehatan Masyarakat (JAMKESMAS) di kota Takengon kabupaten Aceh
Tengah menunjukkan bahwa penduga Bayes empirik dari model Beta-Binomial
memberikan hasil pendugaan dengan ketelitian yang lebih tinggi dibandingkan
penduga langsung.
ABSTRACT
Small area estimation is useful to estimate small sub population of a certain area. In
binary data, Beta-Binomial mode can be used to estimate a perimeter of a small area.
There two methods available in small area estimation using binary data, i.e empirical
Bayes and hierarchical Bayes. To get a proportional estimation result, emprical Bayes
method is used in this thesis. The purpose of this thesis is to measure the performance
of direct estimation and empirical Bayes estimation that are applied in a small area
with a binary case. The application of proportional status of “Kartu Jaminan
Kesehatan Masyarakat (Jamkesmas)” ownership in Takengon, Aceh Tengah shows
that the estimation of empirical Bayes applied in Beta-Binomial mode gives a more
detailed result than that of direct estimation.
DAFTAR ISI
BAB 2 LANDASAN TEORI 9
2.1 Pendugaan Area Kecil 9
2.2 Metode Bayes Empirik 12
2.3 Model Beta-Binomial 13
2.4 Penduga Bayes Empirik Bagi Proporsi 17
2.5 Prosedur Pendugaan Proporsi Dengan Metode Bayes Empirik 18
2.5.1 Penduga Langsung 18
2.5.2 Penduga Bayes Empirik Berdasarkan Model Beta-Binomial 19
BAB 3 PEMBAHASAN 21
3.1 Penerapan Pada Data Status Kepemilikan Kartu
Jaminan Kesehatan Masyarakat 21
3.1.1 Perhitungan Penduga Langsung 25
3.1.2 Perhitungan Penduga Bayes Empirik Bagi Proporsi 27
DAFTAR TABEL
Halaman
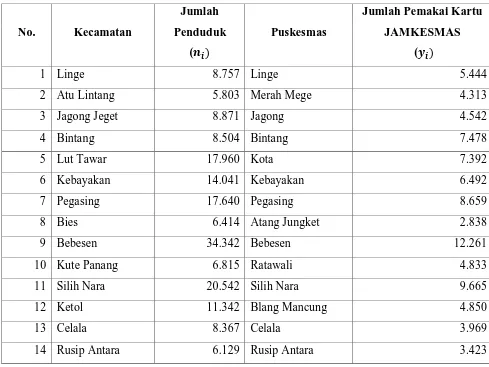
Tabel 3.1 Data Aktual Jumlah Penduduk dan Jumlah Pemakai
Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS)
di Kota takengon Kabupaten Aceh Tengah 22
Tabel 3.2 Perhitungan Penduga Langsung 24
Tabel 3.3 Perhitungan Bayes Empirik Bagi Proporsi 26
Tabel 3.4 Perhitungan Penduga Bayes Empirik Berdasarkan
Model Beta-Binomial 31
DAFTAR GAMBAR
Halaman
Gambar 3.1 Data Aktual Jumlah Penduduk dan Jumlah Pemakai
Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS)
di Kota Takengon Kabupaten Aceh Tengah 23
ABSTRAK
Pendugaan area kecil berguna untuk menduga parameter subpopulasi (area) yang
berukuran contoh kecil. Pada data biner, model Beta-Binomial dapat digunakan untuk
menduga parameter area kecil. Ada dua metode dalam pendugaan area kecil untuk
data biner, yaitu Bayes empirik dan Bayes hierarkhi. Pada skripsi ini digunakan
metode Bayes empirik dalam menghasilkan penduga proporsi. Tujuannya adalah
menilai kinerja penduga langsung dan penduga Bayes empirik pada pendugaan area
kecil untuk kasus biner. Hasil penerapan pada proporsi status kepemilikan Kartu
Jaminan Kesehatan Masyarakat (JAMKESMAS) di kota Takengon kabupaten Aceh
Tengah menunjukkan bahwa penduga Bayes empirik dari model Beta-Binomial
memberikan hasil pendugaan dengan ketelitian yang lebih tinggi dibandingkan
penduga langsung.
ABSTRACT
Small area estimation is useful to estimate small sub population of a certain area. In
binary data, Beta-Binomial mode can be used to estimate a perimeter of a small area.
There two methods available in small area estimation using binary data, i.e empirical
Bayes and hierarchical Bayes. To get a proportional estimation result, emprical Bayes
method is used in this thesis. The purpose of this thesis is to measure the performance
of direct estimation and empirical Bayes estimation that are applied in a small area
with a binary case. The application of proportional status of “Kartu Jaminan
Kesehatan Masyarakat (Jamkesmas)” ownership in Takengon, Aceh Tengah shows
that the estimation of empirical Bayes applied in Beta-Binomial mode gives a more
detailed result than that of direct estimation.
BAB 1
PENDAHULUAN
1.1Latar Belakang
Statistik area kecil (small area statistics) saat ini telah menjadi perhatian para statistisi
dunia secara sangat serius. Telah banyak penelitian yang dikembangkan baik untuk
perbaikan teknik dan pengembangan metode maupun aplikasi dalam berbagai kasus
dan persoalan nyata yang dihadapi. Fay dan Herriot (1979) merupakan peneliti
pertama yang mengembangkan pendugaan area kecil (small area estimation, SAE)
berbasis model. Model yang dikembangkannya kemudian menjadi rujukan dalam
pengembangan penelitian pendugaan area kecil lebih lanjut sampai dengan saat ini.
Perhatian yang besar ini terjadi seiring dengan meningkatnya kebutuhan
pemerintah dan para pengguna statistik (termasuk dunia bisnis) terhadap informasi
yang lebih rinci, cepat, dan handal, tidak saja untuk lingkup superpopulasi seperti
negara tetapi pada lingkup yang lebih kecil (subpopulasi) seperti kabupaten,
kecamatan dan desa/kelurahan atau subpopulasi lain yang dibangun oleh karakteristik
jenis kelamin, status sosial ekonomi, pendidikan, ras dan yang lainnya. Di Indonesia,
pentingnya statistik area kecil semakin dirasakan seiring dengan era otonomi daerah di
mana sistem ketatanegaraan bergeser dari sistem sentralisasi ke sistem desentralisasi.
Pada sistem desentralisasi, pemerintah daerah memiliki kewenangan yang lebih besar
untuk mengatur dirinya sendiri, khususnya pada level pemerintah kabupaten/kota.
Dengan demikian kebutuhan statistik sampai pada level desa/kelurahan menjadi
suatu kebutuhan dasar sebagai landasan bagi pemerintah daerah kabupaten/kota untuk
menyusun sistem perencanaan, pemantauan dan penilaian pembangunan daerah atau
Pendugaan area kecil (small area estimation) adalah suatu teknik statistika untuk
menduga parameter-parameter subpopulasi yang ukuran contohnya kecil (Rao, 2003).
Teknik pendugaan ini memanfaatkan data dari domain besar (yakni seperti data
sensus, data survei sosial ekonomi nasional) untuk menduga peubah yang menjadi
perhatian pada domain yang lebih kecil. Area kecil didefinisikan sebagai subpopulasi
yang ukuran contohnya kecil sehingga pendugaan langsung tidak dapat menghasilkan
dugaan yang teliti (Rao, 2003). Biasanya statistik diperoleh dari suatu survei yang
dirancang untuk memperoleh statistik nasional. Persoalan muncul ketika ingin
diperoleh informasi untuk area yang lebih kecil (propinsi, kabupaten, kecamatan atau
desa/kelurahan) yaitu objek survei jumlahnya kecil bahkan bisa saja area tersebut
tidak tersampling sehingga analisis yang didasarkan hanya pada objek -objek tersebut
menjadi sangat tidak dapat diandalkan (presisi rendah). Small area estimation
merupakan suatu metode yang dapat menangani permasalahan tersebut.
Pendugaan area kecil merupakan konsep terpenting dalam pendugaan parameter di
suatu area yang relatif kecil dalam percontohan survei (survey sampling). Metode
pendugaan area kecil digunakan untuk menduga karakteristik dari subpopulasi
(domain yang lebih kecil). Pendugaan langsung (direct estimation) pada subpopulasi
tidak memiliki presisi yang memadai karena kecilnya jumlah data yang digunakan
untuk memperoleh dugaan tersebut. Alternatif metode lain adalah dengan cara
menambahkan informasi pada area tersebut dari area lain melalui pembentukan model
yang tepat. Pendugaan parameter area kecil dengan pendekatan seperti ini disebut
pendugaan tidak langsung (indirect estimation) dalam arti bahwa dugaan tersebut
mencakup data dari domain yang lain. Chand dan Alexander (1995) menyebutkan
bahwa prosedur pendugaan area kecil pada dasarnya memanfaatkan kekuatan
informasi area sekitarnya (neighbouring areas) dan sumber data di luar area yang
statistiknya ingin diperoleh melalui pembentukan model yang tepat untuk
meningkatkan efektifitas ukuran data. Secara umum pendugaan area kecil dapat
dikatakan sebagai suatu metode untuk menduga parameter pada suatu area yang relatif
kecil dalam percontohan survei dengan memanfaatkan informasi dari luar area, dari
Metode Bayes empirik merupakan suatu metode pendugaan yang terdiri dari
fungsi kepekatan peluang prior, fungsi kepekatan peluang posterior dan fungsi
kepekatan peluang marginal. Salah satu model dalam metode Bayes empirik yang
digunakan adalah model Beta-Binomial, karena model ini memenuhi ketiga fungsi
kepekatan peluang tersebut. Model Beta-Binomial digunakan karena cocok untuk data
biner.
Jaminan Kesehatan Masyarakat (JAMKESMAS) adalah sebuah program jaminan
kesehatan untuk warga Indonesia yang memberikan perlindungan sosial dibidang
kesehatan untuk menjamin masyarakat miskin dan tidak mampu yang iurannya
dibayar oleh pemerintah agar kebutuhan dasar kesehatannya yang layak dapat
terpenuhi. Program ini dijalankan oleh Departemen Kesehatan sejak 2008. Program
Jaminan Kesehatan Masyarakat (Jamkesmas) diselenggarakan berdasarkan konsep
asuransi sosial. Program ini diselenggarakan secara nasional dengan tujuan untuk:
1. Mewujudkan portabilitas pelayanan sehingga pelayanan rujukan tertinggi yang
disediakan Jamkesmas dapat diakses oleh seluruh peserta dari berbagai wilayah.
2. Agar terjadi subsidi silang dalam rangka mewujudkan pelayanan kesehatan yang
menyeluruh bagi masyarakat miskin.
Dari uraian di atas serta dengan mempertimbangkan kemampuan penulis, maka
penulis ingin melakukan penelitian dengan judul “ Penerapan Metode Bayes Empirik Pada Pendugaan Area Kecil” (Studi tentang Proporsi Status Kepemilikan Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS) di Kota Takengon Kabupaten Aceh
1.2Perumusan Masalah
Dalam penulisan ini yang menjadi permasalahannya adalah menentukan proporsi
status kepemilikan Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS) di kota
Takengon Kabupaten Aceh Tengah, kemudian memperlihatkan prosedur pendugaan
proporsi status kepemilikan JAMKESMAS dengan Metode Bayes Empirik.
1.3Pembatasan Masalah
Batasan masalah dari tulisan ini diantaranya adalah:
1. Pengambilan data berasal dari kantor Dinas Kesehatan dan kantor Badan Pusat
Statistik kota Takengon Kabupaten Aceh Tengah.
2. Pendugaan proporsi dengan metode Bayes empirik.
3. Proses hitungan dilakukan dengan Microsoft Office Excel.
1.4Tujuan Penelitian
Tujuan tulisan ini adalah menjelaskan bagaimana menilai kinerja penduga langsung
dan penduga Bayes empirik pada pendugaan area kecil serta menjalankan perhitungan
dengan menggunakan Microsoft Office Excel.
1.5Manfaat Penelitian
Sebagai sarana bagaimana meningkatkan pengetahuan dan wawasan penulis mengenai
cara menggunakan metode Bayes empirik menggunakan model Beta-Binomial pada
1.6Tinjauan Pustaka
1.6.1 Penduga Langsung Bagi Proporsi
Peubah pengamatan diasumsikan mempunyai sebaran binomial ~�Binomial ( , ).
Fungsi peluang dari sebaran binomial (PROF. DR. SUDJANA, M.A.,M.Sc.) adalah:
⃒ = � − �− �,
dengan
= , … , , < < , = , … , (1.1)
Selanjutnya dengan memaksimumkan fungsi peluang tersebut diperoleh penduga
kemungkinan maksimum bagi yaitu:
̂ = �
� (1.2)
Penduga ini merupakan penduga kemungkinan maksimum yang bersifat tak bias
karena nilai harapan dari penduga sama dengan parameternya.
� ̂ = � �
� = �� = � = (1.3)
Sehingga dugaan kuadrat tengah galat sama dengan ragamnya, yaitu:
1.6.2 Penduga Bayes Empirik Bagi Proporsi
Langkah awal pada pendugaan Bayes empirik dari model Beta-Binomial oleh
Kleinman (Rao, 2003) adalah dengan membuat dugaan parameter prior dengan
menyamakan rataan contoh terboboti.
̂ = ∑ �
� ̂ (1.5)
Keterangan:
̂ = dugaan parameter prior
= banyaknya individu pada subpopulasi ke-i
� = jumlah seluruh individu
̂ = penduga proporsi
dan ragam contoh terboboti.
� = ∑ �
� ̂ − ̂ (1.6)
dengan nilai harapan masing-masing dan kemudian diselesaikan persamaan momen
̂� , = � ⃒ , , = �+
�+ + (1.9)
untuk memperoleh penduga Bayes empirik bagi yaitu:
̂�� = ̂�( ̂, ̂) = ̂ ̂ + − ̂ ̂ (1.10)
dengan ̂ = �
�+̂+̂ , ̂ = �
� sebagai penduga langsung dari , dan masing
-masing menyatakan banyaknya pengamatan dan banyaknya suatu kasus, ̂ adalah
penduga sintetik atau sebagai penduga tak langsung.
1.7Metodologi Penelitian
Metode yang digunakan dalam penelitian ini adalah metode Bayes empirik di mana
prosedur yang digunakan dalam menduga proporsi ada dua cara yaitu berdasarkan
penduga langsung dan Bayes empirik dari dua model Beta-Binomial yang diuraikan
sebagai berikut:
1.7.1 Penduga Langsung
1. Menentukan penduga proporsi.
2. Menentukan dugaan kuadrat tengah galat (ktg).
3. Menentukan galat baku.
1.7.2 Penduga Bayes Empirik Berdasarkan Model Beta-Binomial
1. Menentukan nilai dugaan parameter ̂ dan ̂ dari sebaran prior.
2. Menentukan penduga Bayes empirik ̂��.
3. Menentukan kuadrat tengah galat dengan menggunakan metode Jacknife.
4. Menentukan galat baku.
5. Proses hitungan dilakukan dengan Microsoft Office Excel.
Perbandingan kebaikan dari kedua penduga proporsi (penduga langsung dan
BAB 2
LANDASAN TEORI
2.1 Pendugaan Area Kecil
Secara umum metode pendugaan area kecil dibagi menjadi dua bagian yaitu metode
penduga langsung (direct estimation) dan metode penduga tak langsung (indirect
estimation). Metode-metode pendugaan selama ini yang sering digunakan adalah
metode pendugaan langsung.
Pendugaan langsung merupakan pendugaan yang didasarkan pada desain
penarikan yang menjadi perhatian (jumlah pemakai Jamkesmas). Dalam kasus
pendugaan area kecil, penduga langsung bagi parameter pada area kecil yang menjadi
perhatian relatif akan menghasilkan galat baku yang besar karena masalah jumlah
yang memakai kartu Jamkesmas.
Suatu pendekatan tidak langsung mampu meningkatkan efektifitas ukuran jumlah
pemakai Jamkesmas. Pada pendugaan tak langsung terdapat dua model penghubung
yang digunakan untuk menghubungkan area kecil dengan area kecil lainnya yaitu
Penduga tak langsung dengan menggunakan model penghubung implisit adalah
model yang didasarkan pada desain penarikan jumlah yang menjadi perhatian (design
based). Penduga yang dihasilkan mempunyai ragam desain yang relatif kecil
dibandingkan dengan ragam desain dari penduga langsung. Model penghubung
implisit mempunyai tiga metode yaitu, metode sintetik, komposit, dan James-Stein.
Metode sintetik adalah merupakan suatu metode dari penduga langsung untuk area
besar, yang memiliki galat baku kecil digunakan untuk memperoleh penduga tak
langsung untuk area kecil tertentu. Metode ini mengasumsikan bahwa area kecil
tersebut memiliki karateristik yang sama dengan area besar. Metode komposit
merupakan rata-rata terboboti dari penduga langsung dan penduga tak langsung.
Metode James-Stein adalah penduga komposit yang menggunakan pembobot umum
dengan meminimumkan jumlah kuadrat galat.
Model penghubung eksplisit adalah model yang didasarkan pada pengaruh acak
area kecil untuk mendapatkan keragaman antar area dan informasi peubah penyerta,
yang selanjutnya dikenal dengan model area kecil. Menurut Rao (2005) peubah
penyerta yang baik adalah peubah yang berhubungan erat dengan peubah yang
menjadi perhatian dan berasal dari data sensus atau data administratif.
Suatu peubah respons yang menyatakan “sukses” atau “gagal” disebut sebagai peubah biner. Pada pendugaan area kecil untuk kasus biner, peubah yang menjadi
perhatian berupa proporsi. Penduga langsung bagi proporsi merupakan penduga
kemungkinan maksimum yaitu ̂ = �
� , dengan mengasumsikan peubah pengamatan
diasumsikan menyebar binomial, ~� Binomial ( , ). Penduga langsung ini
mempunyai ragam yang besar karena hanya berdasarkan jumlah objek survei yang
terdapat pada area tersebut. Suatu pendugaan lain dikembangkan untuk mengatasi
permasalahan ini, yaitu pendugaan tak langsung. Pendugaan tak langsung bagi
proporsi diperoleh dari model Beta-Binomial. Model ini mempunyai dua tahap, yaitu
pada tahap pertama diasumsikan bahwa peubah yang menjadi perhatian ~�
ƒ( ⃒ , ) = � +
� ∝ � − (1- − ; > , > (Robert V. Hogg) (2.1)
Berdasarkan teorema Bayes maka penduga Bayes dan ragam posterior bagi adalah:
̂� , = � , , = +
+ + .
dan
Var ⃒ , , = , , = + + ++ − ++ + .
Bila penduga Bayes ini akan digunakan maka harus diketahui terlebih dahulu nilai
parameter sebaran priornya. Namun seringkali informasi mengenai parameter prior
belum diketahui. Pendekatan lain yang dapat digunakan adalah Bayes empirik, yaitu
pendekatan yang dilakukan untuk mendapatkan informasi parameter prior
berdasarkan datanya. Informasi parameter prior diperoleh dengan memaksimumkan
fungsi sebaran marjinal ⎹ , ~ � Beta-Binomial, namun bentuk tertutup untuk ̂
dan ̂ tidak ada (McCulloch & Searle, 2001). Pada tulisan ini bertujuan untuk
menilai kinerja penduga langsung dan penduga Bayes empirik pada pendugaan area
2.2 Metode Bayes Empirik
Metode Bayes yang ditemukan oleh Thomas Bayes dan kemudian dikembangkan
oleh Richard Price (1763) dua tahun setelah wafatnya Bayes, kemudian Laplace pada
tahun 1774 dan 1781 yang memberikan analisis secara rinci, merupakan metode yang
lebih baik untuk statistik Bayes sekarang (Gill, 2002).
Model statistik Bayes merupakan perpaduan antara sebaran prior dan posterior,
yaitu jika dimisalkan dengan sebaran percontohan �⃒ �~ ⃒ �) dan sebaran prior
�~� � diketahui maka sebaran posterior dari θ adalah:
� �⃒ ) =� ,� =� ⎹ � � �
dengan
= ∫ ⃒ � � � � (2.4)
Suatu sebaran prior dinamakan konjugate bila menghasilkan sebaran posterior
yang sama dengan dirinya. Sebaran yang masih dalam keluarga eksponensial
mempunyai prior konjugate. Seperti sebaran Poisson memiliki prior konjugate
Metode Bayes empirik merupakan suatu metode yang menggunakan data
pengamatan untuk menduga parameter prior. Pertama kali model ini diperkenalkan
oleh Fay-Herriot (1970), untuk menduga rata-rata pendapatan area kecil di Amerika
Serikat. Metode ini sesuai untuk menangani data-data biner dan cacahan pada
pendugaan area kecil. Pendekatan Bayes Empirik dalam pendugaan area kecil
mempunyai ciri-ciri sebagai berikut:
a) Memperoleh fungsi kepekatan posterior dari parameter area kecil yang teramati.
b) Pendugaan parameter model dari fungsi kepekatan marginal.
c) Menggunakan pendugaan fungsi kepekatan posterior untuk membuat inferensi
parameter area kecil.
2.3 Model Beta Binomial
Model ini merupakan suatu model yang berawal dari model Bernoulli dengan model
peluang untuk data biner yang dinyatakan dengan
~� Binomial ( , ) = 0,…, , 0< < , = , … , (2.5)
dengan model dasar
⃒ ~� � ⎹
~� � , (2.6)
dan
dengan � , menyatakan sebaran beta dengan parameter dan serta fungsi
kepekatan untuk adalah:
ƒ( ⃒ , ) = � +
� ∝ � − (1- − ; > , > (Robert V. Hogg) (2.8)
dan, � = fungsi gama
untuk menyederhanakan = , … , � � menjadi total contoh = ∑ ,
merupakan statistik cukup minimal untuk model tahap pertama. Diketahui bahwa
~� � ,
yang mempunyai fungsi kepekatan sebagai berikut:
⃒ = � − �− � (2.9)
Berdasarkan fungsi kepekatan dan fungsi kepekatan maka:
⃒ , , ~ � + , − + (2.10)
Oleh karena itu, penduga Bayes bagi adalah:
̂� , = � ⎹ , , = +
+ + .
dan ragam posterior bagi adalah:
� ⃒ , , = �+ �− �+
Sebaran penghubung , , dinamakan prior konjugate pada sebaran posterior,
⎹ , , mempunyai bentuk yang sama dengan sebaran priornya. Dari sebaran
penghubung tersebut, maka digunakan model Beta-Binomial dengan sebaran peluang
marginal:
Untuk menduga parameter dan digunakan dengan metode momen Kleinman:
dan
̂ = ̂ [�̂ −�̂ [ �−∑�( �2/ �)− − ]
���2−�̂ −�̂ − − ] [�̂− ] (2.18)
di mana ̂ dan ̂ dugaan parameter sebaran Beta-Binomial
Pensubstitusian parameter ̂ dan ̂ dari metode Kleinman ke penduga EB bagi ̂��
Langkah awal pada pendugaan Bayes empirik dari model Beta-Binomial oleh
Kleinman (Rao, 2003) adalah dengan membuat dugaan parameter prior dengan
menyamakan rataan contoh terboboti.
̂ = ∑ �
� ̂ (2.20)
Keterangan:
̂ = dugaan parameter prior
= banyaknya individu pada subpopulasi ke-i
� = jumlah seluruh individu
dan ragam contoh terboboti.
� = ∑ �
� ̂ − ̂ (2.21)
dengan nilai harapan masing-masing dan kemudian diselesaikan persamaan momen
untuk dan , dengan � = ∑ . Penduga momen ̂ dan ̂, diberikan sebagai
untuk memperoleh penduga Bayes empirik bagi yaitu:
̂�� = ̂�( ̂, ̂) = ̂ ̂ + − ̂ ̂ (2.25)
dengan ̂ = �
�+̂+̂ , ̂ = �
� sebagai penduga langsung dari , dan masing
-masing menyatakan banyaknya pengamatan dan banyaknya suatu kasus, ̂ adalah
2.5 Prosedur Pendugaan Proporsi Dengan Metode Bayes Empirik
Prosedur yang digunakan dalam menduga proporsi ada dua cara yaitu berdasarkan
penduga langsung dan penduga Bayes empirik dari model Beta-Binomial yang
diuraikan sebagai berikut:
2.5.1 Penduga Langsung
5. Menentukan penduga proporsi
̂ = �
� (2.26)
Dengan menyatakan banyaknya pengamatan suatu kasus pada subpopulasi ke-i,
menyatakan banyaknya individu pada subpopulasi ke-i. Subpopulasi ini dapat
berupa kecamatan.
6. Menentukan dugaan kuadrat tengah galat (ktg) yaitu
ktg(�̂)= ̂ − ̂ (2.27)
7. Menentukan galat baku
8. Proses hitungan dilakukan dengan Microsoft Office Excel.
2.5.2 Penduga Bayes Empirik Berdasarkan Model Beta-Binomial
6. Menentukan nilai dugaan parameter ̂ dan ̂ dari sebaran prior
~
���� , (2.28)
8. Menentukan kuadrat tengah galat dengan menggunakan metode Jacknife yaitu:
a) Anggap bahwa ̂��= ( ̂ , ̂, ̂), ̂��,− = ( ̂ , ̂− , ̂− , lalu
�̂ = − ∑ = ̂��,− – ̂��
=
.
b) Dengan mencari ̂− dan ̂− yang merupakan penduga momen yang diperoleh
dari data ke -1 yang dihapus maka dihitung
�̂ = ̂, ̂, )− − ∑ [ ( ̂= − , ̂− , ) − ̂, ̂, ] (2.30)
c) Penduga Jacknife bagi kuadrat tengah galat penduga Bayes empirik diberikan
oleh
� �̂�� = �̂ + �̂ (2.31)
9. Menentukan galat baku.
10.Proses hitungan dilakukan dengan Microsoft Office Excel.
Perbandingan kebaikan dari kedua penduga proporsi (penduga langsung dan
BAB 3
PEMBAHASAN
3.1 Penerapan Pada Data Status Kepemilikan Kartu Jaminan Kesehatan Masyarakat (Jamkesmas)
Data jumlah penduduk dan status kepemilikan Kartu Jaminan Kesehatan Masyarakat
(Jamkesmas) diperoleh dari kantor Badan Pusat Statistik (BPS) dan Kantor Dinas
Kesehatan kota Takengon Kabupaten Aceh Tengah. Data ini diambil dari 14
kecamatan di kota Takengon. Peubah yang menjadi perhatian adalah proporsi status
kepemilikan kartu Jaminan Kesehatan Masyarakat (Jamkesmas), peubah pengamatan
adalah jumlah rumahtangga pemilik kartu sehat pada kecamatan − , dan
Tabel 3.1 Data Aktual Jumlah Penduduk dan Jumlah Pemakai Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS) di Kota Takengon Kabupaten Aceh
Tengah
Sumber: Badan Pusat Statistik dan Dinas Kesehatan Kota Takengon Kabupaten Aceh
Gambar 3.1 Data Aktual Jumlah Penduduk dan Jumlah Pemakai Kartu Jaminan Kesehatan Masyarakat (JAMKESMAS) di kota Takengon Kabupaten
Aceh Tengah
0 5000 10000 15000 20000 25000 30000 35000 40000
Jumlah Penduduk
3.1.1 Perhitungan Penduga Langsung
1. Menentukan penduga proporsi
̂
=
̂ = ..
̂ = ,
2. Menentukan dugaan kuadrat tengah galat
̂ = �̂ ̂ = ̂ − ̂
̂ = . ( .
. ) ( −
.
. )
̂ = . ,
3. Menentukan galat baku
� � = √ ̂
Tabel 3.3 Perhitungan Bayes Empirik Bagi Proporsi
̂ =
�=
̂ = ̂�� =0,03102 0,01741 423,88463 0,99999708 0,62167 0,02457 0,01708 178,84974 0,99999784 0,74324 0,02588 0,01194 435,33354 0,99999859 0,51201 0,04260 0,03392 399,00508 0,99999852 0,87935 0,04211 0,01397 1824,67512 0,99999930 0,41158 0,03699 0,01447 1110,18721 0,99999911 0,46236 0,04933 0,01959 1759,77342 0,99999929 0,49087 0,01617 0,00664 221,37645 0,99999804 0,44247 0,06985 0,01614 6706,04017 0,99999963 0,35703 0,02753 0,01804 251,59875 0,99999816 0,70917 0,05506 0,02020 2391,03906 0,99999939 0,47050 0,02763 0,01034 719,88419 0,99999889 0,42761 0,02261 0,00973 385,83715 0,99999850 0,47436 0,01950 0,01014 201,01061 0,99999795 0,55849 0,49086 0,21960 17008.49513 13,99998030 7,56072
3.1.2 Perhitungan Penduga Bayes Empirik Bagi Proporsi
1. Langkah awal pada pendugaan Bayes empirik dari model Beta-Binomial oleh
Kleinman (Rao, 2003) adalah dengan membuat dugaan parameter prior dengan
menyamakan rataan contoh terboboti.
3. Dengan nilai harapan masing-masing dan kemudian diselesaikan persamaan
̂ = , (Penduga Momen)
̂ = , ,
̂ = , (Penduga Momen)
4. Lalu substitusikan penduga momen ̂ dan ̂ ke dalam rumus:
̂� , = � , , = �+
�+ +
untuk memperoleh penduga Bayes empirik bagi yaitu:
̂�� = ̂�( ̂, ̂) = ̂ ̂ + − ̂ ̂
dengan ̂ = �
�+̂+̂ , ̂ = �
� sebagai penduga langsung dari , dan masing -
masing menyatakan banyaknya pengamatan dan banyaknya suatu kasus, ̂ adalah
penduga sintetik atau sebagai penduga tak langsung.
̂ =
+ ̂ + ̂
̂ = . + ,. + ,
̂ = . . ,
Jadi, ̂�� yaitu:
̂�� = ̂�( ̂, ̂) = ̂ ̂ + − ̂ ̂
̂�� = , × , + − , ,
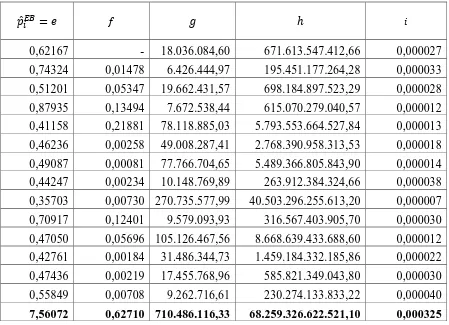
Tabel 3.4 Perhitungan Penduga Bayes Empirik Berdasarkan Model Beta-Binomial
̂��= ℎ
0,62167 - 18.036.084,60 671.613.547.412,66 0,000027
0,74324 0,01478 6.426.444,97 195.451.177.264,28 0,000033
0,51201 0,05347 19.662.431,57 698.184.897.523,29 0,000028
0,87935 0,13494 7.672.538,44 615.070.279.040,57 0,000012
0,41158 0,21881 78.118.885,03 5.793.553.664.527,84 0,000013
0,46236 0,00258 49.008.287,41 2.768.390.958.313,53 0,000018
0,49087 0,00081 77.766.704,65 5.489.366.805.843,90 0,000014
0,44247 0,00234 10.148.769,89 263.912.384.324,66 0,000038
0,35703 0,00730 270.735.577,99 40.503.296.255.613,20 0,000007
0,70917 0,12401 9.579.093,93 316.567.403.905,70 0,000030
0,47050 0,05696 105.126.467,56 8.668.639.433.688,60 0,000012
0,42761 0,00184 31.486.344,73 1.459.184.332.185,86 0,000022
0,47436 0,00219 17.455.768,96 585.821.349.043,80 0,000030
0,55849 0,00708 9.262.716,61 230.274.133.833,22 0,000040
7,56072 0,62710 710.486.116,33 68.259.326.622.521,10 0,000325
3.1.3 Perhitungan Penduga Bayes Empirik Berdasarkan Model Beta-Binomial
Nilai dugaan parameter ̂ dan ̂ dari sebaran prior dan nilai penduga Bayes empirik
̂�� yang telah didapat pada rumus (3.6), (3.7) dan (3.9) maka dapat kita cari nilai kuadrat tengah galat dengan menggunakan metode Jacknife yaitu:
d) Anggap bahwa ̂��= ( ̂ , ̂, ̂), ̂��,− = ( ̂ , ̂− , ̂− , lalu
�̂ = − ∑ = ̂��,− – ̂��
=
�̂ = − ,
�̂ = ,
e) Dengan mencari ̂− dan ̂− yang merupakan penduga momen yang diperoleh dari
data ke -1 yang dihapus maka dihitung
�̂ = ( ̂, ̂, ) − − ∑[ ( ̂− ,̂− , ) − ( ̂, ̂, )]
=
Terlebih dahulu kita cari nilai yaitu:
( ̂, ̂, ) = + + ++ − ++ +
( ̂, ̂, ) = . + ,. + ,+ , +. − .. + ,+ , + ,
�̂ = , − − ∑[− , ]
=
�̂ = ,
f) Penduga Jacknife bagi kuadrat tengah galat penduga Bayes empirik diberikan oleh
� ̂�� = �̂ + �̂
� ̂�� = , + ,
� ̂�� = ,
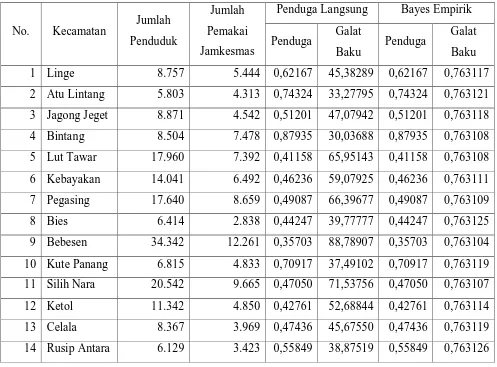
Tabel 3.5 Pendugaan Proporsi Status Kepemilikan Kartu Sehat
Dari tabel 3.5 dapat diperoleh informasi bahwa secara rata-rata banyak rumahtangga belum
memiliki kartu Jaminan Kesehatan Masyarakat (JAMKESMAS). Penduga langsung memberikan
galat baku yang besar sehingga penduga mempunyai presisi yang rendah. Sedangkan penduga
Bayes empirik memberikan hasil pendugaan dengan presisi meningkat yang ditunjukkan oleh
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil penelitian yang diperoleh dari bab-bab sebelumnya mengenai
penerapan metode Bayes empirik pada pendugaan area kecil untuk kasus biner (studi
tentang proporsi status kepemilikan Kartu Jaminan Kesehatan Masyarakat
(JAMKESMAS) di kota Takengon kabupaten Aceh Tengah adalah penduga Bayes
empirik dari model Beta-Binomial lebih dapat diandalkan daripada penduga langsung,
yang diperlihatkan dengan semakin kecilnya galat baku.
4.2 Saran
Penelitian ini menggunakan model Beta-Binomial tanpa peubah penyerta. Untuk lebih
meningkatkan keakuratan pendugaan disarankan memasukkan peubah penyerta dalam
DAFTAR PUSTAKA
Abadi, Slamet. 2011. Tesis: Pendugaan Statistik Area Kecil Menggunakan Model
Beta-Binomial. Institut Pertanian Bogor.
Brackstone, G.J. 2002. Strategies and approach for small area statistic. Survey
Methodology, 28 (2), 117-123
[BPS] Badan Pusat Statistik, Jumlah Penduduk Tahun 2010.
Carlin, B.P., & Louis, T.A. 2000. Bayes and empirical Bayes methods for data
analysis. New York: Chapman & Hall.
Dinas Kesehatan, Jumlah Pemakai Jaminan Kesehatan Masyarakat (Jamkesmas)
Tahun 2010.
Farrel, P.J., MacGibbon, B., & Tomberlin, T.J. 1997. Empirical Bayes small-area
estimation using logistic regression models and summary statistics.
Journal of Business & Economic Statistics, 15 (1), 101-108.
Farrel, P.J., MacGibbon, B., & Tomberlin, T.J. 1997. Bootstrap adjusments for
empirical Bayes interval estimates of small-area proportions. The
Canadian Journal of Statistics, 25 (1), 75-89
Fay, R.E., & Herriot, R.A. 1979. Estimates of income for small places: an
application of James-Stein procedures to census data. Journal of the
American Statistical Association, 74 (366), 269-277.
Gill, J. 2002. Bayesian Methods: a social and behavioral sciences approach. Boca
Raton: Chapman & Hall.
Gosh, M., & Rao, J.N.K. 1994. Small area estimation: an appraisal. Statistical
Science, 9 (1), 55-76.
Jiang, J., & Lahiri, P. 2001. Empirical best prediction for small area inference with
binary data. Annals of the institute of Statistical Mathematics, 53 (2),
217-243.
Jiang, J., Lahiri, P., & Wan, S.M. 2002. A unified jacknife theory for empirical best
Larsen, M.D. 2003. Estimation of small-area proportions using covariates and
survey data. Journal of Statistical Planning and inference, 112 (2003),
89-98.
Malec, D., sedransk, J., Moriarity, C.L., & LeClere, F.B. 1997. Small area
inference for binary variables in the national health interview survey.
Journal of the American Statistical Association, 92 (439), 815-826
McCulloch, C.E., & Searle, S.R.2001. Generalized linear and mixed models. New
York: Wiley.
Rao, J.N.K 1999. Some recent advances in model-based small area estimation.
Survey Methodology, 25 (2), 175-186.
Rao, J.N.K. 2003. Small area estimation. New York: John Wiley and Sons.
Robert V. Hogg. 2003. Introduction To Ma thematical Statistics. Prentice Hall,