AMIN LUKMANUL HAKIM
G54102040
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PENGHITUNGAN NILAI RESISTOR PENGGANTI MENGGUNAKAN
NILAI EIGEN DAN VEKTOR EIGEN ORTONORMAL
DARI MATRIKS LAPLACE
AMIN LUKMANUL HAKIM
G54102040
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
AMIN LUKMANUL HAKIM, Penghitungan Nilai Resistor Pengganti Menggunakan Nilai Eigen dan Vektor Eigen Ortonormal dari Matriks Laplace. Dibimbing oleh AGAH DRAJAT GARNADI dan FARIDA HANUM.
Nilai resistor pengganti dapat dihitung dengan menggunakan nilai-nilai eigen dan vektor-vektor eigen ortonormal dari matriks Laplace yang diperoleh dari hubungan suatu gambar jaringan resistor dalam bentuk graf. Karena matriks Laplace adalah suatu matriks Hermite yang real dan simetrik, juga merupakan matriks semidefinit positif maka nilai-nilai eigen dari matriks Laplace adalah real taknegatif dan vektor-vektor eigennya adalah real yang saling ortogonal.
Dalam tulisan karya ilmiah ini dibahas lima bentuk jaringan resistor (resistors network) yang hingga dalam bentuk graf :
1. Jaringan resistansi dua-simpul.
ABSTRACT
AMIN LUKMANUL HAKIM, Computing of Resistance Between Arbitrary Two Nodes within Resistor Network In Terms of Eigenvalues and Orthonormal Eigenvectors of the Laplacian Matrix. Supervised by AGAH DRAJAT GARNADI and FARIDA HANUM.
The resistance between arbitrary two nodes in a resistor network could be computed in terms of eigenvalues and orthonormal eigenvectors of the Laplacian matrix associated with the resistor network. Since the Laplacian matrix is a Hermitean, it is symmetric and real, also positive semidefinite, hence the eigenvalues of the Laplacian matrix are nonnegative real and the eigenvectors are real and orthogonal.
In this work, five finite resistor networks are studied : 1. Two-point resistance network.
PENGHITUNGAN NILAI RESISTOR PENGGANTI MENGGUNAKAN
NILAI EIGEN DAN VEKTOR EIGEN ORTONORMAL
DARI MATRIKS LAPLACE
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Oleh :
AMIN LUKMANUL HAKIM
G54102040
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Penghitungan Nilai Resistor Pengganti Menggunakan Nilai Eigen dan
Vektor Eigen Ortonormal dari Matriks Laplace
Nama
: Amin Lukmanul Hakim
NIM : G54102040
Menyetujui,
Mengetahui,
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Tanggal Lulus : ...
Pembimbing I
Drs. Agah D. Garnadi Grad, Dipl.
NIP. 131 842 411
Pembimbing II
Dra. Farida Hanum, M.Si.
NIP. 131 956 709
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Allah SWT yang selalu memberikan nikmat, karunia dan kekuatan yang sangat besar, sehingga penulis dapat menyelesaikan skripsi ini. Shalawat serta salam semoga senantiasa tercurah kepada Nabi Muhammad SAW beserta keluarganya, sahabatnya serta segenap umatnya.
Skripsi ini berjudul Penghitungan Nilai Resistor Pengganti Menggunakan Nilai Eigen dan Vektor Eigen Ortonormal dari Matriks Laplace.
Ucapan terima kasih kepada Bpk. Drs. Agah Drajat Garnadi, Grad. Dipl. Sci. selaku Pembimbing I yang telah meluangkan tenaga dan waktunya untuk memberikan bimbingan, pengarahan, semangat, dan saran sehingga penulis dapat menyelesaikan karya ilmiah ini.
Terima kasih juga kepada Ibu Dra. Farida Hanum M. Si. selaku Pembimbing II atas bimbingan dan saran sehingga penulis dapat menyelesaikan skripsi ini. Terima kasih juga kepada Bpk. Dr. Ir. I G. Putu Purnaba, DEA selaku Penguji yang telah memberikan saran dan masukannya, serta kepada saudara Ari Septian dan saudari Mita yang telah beresedia menjadi Pembahas pada acara seminar. Ucapan terima kasih kepada kedua orang tua tercinta, Bapak Memed dan Ibu Euis Masruroh di Tasikmalaya, yang telah memberikan kasih sayang, semangat, dorongan, dan doa untuk kelancaran penyelesaian skripsi ini.
Penulis mengucapkan terima kasih kepada kedua kakak tercinta, Yani Suryani serta suaminya A Haris, yang telah memberikan semangat dan dorongan serta memberikan bantuan biaya untuk kelancaran penulisan skripsi ini.
Terima kasih juga kepada adik tercinta, Muhammad Luthfi, serta kakak-kakak tercinta yang lainnya A Endang, A Ade Abduh, Ceu Yayah, Totoh Tohariah, dan A Dadi di Bengkulu, beserta seluruh keluarganya dan anak-anak tercintanya yang telah memberikan dorongan, semangat, dan doa untuk keberhasilan penulis.
Terima kasih juga kepada teman-teman Angkatan 39 masuk tahun 2002 yang telah memberikan kasih sayang dan semangat selama masa-masa kuliah di Jurusan Matematika, Institut Pertanian Bogor. Tidak lupa ucapan terima kasih kepada dosen-dosen Departemen Matematika yang telah memberikan ilmunya, juga kepada staf Departemen Matematika (Bu Susi, Mas Bono, Mas Yono, Mas Deni, Bu Ade, Bu Marisi juga kepada staf pegawai Departemen Matematika), serta kepada seluruh pihak yang telah membantu dalam penyelesaian skripsi ini yang tidak dapat disebutkan satu per satu.
Bogor, September 2007
RIWAYAT HIDUP
Penulis dilahirkan di Kota Tasikmalaya pada tanggal 27 Januari 1982 sebagai anak ketujuh dari delapan bersaudara dari pasangan Memed dan Euis Masruroh.
ix
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... x
1 PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
2 LANDASAN TEORI 2.1 Matriks ... 1
2.2 Graf ... 2
2.3 Aljabar Linear ... 3
2.4 Jaringan Listrik dan Jaringan Resistor ... 7
2.5 Sifat-Sifat Matriks Laplace L dan L(ε) dari Graf Jaringan Resistor ... 9
2.6 Teorema-Teorema tentang Matriks Laplace L dan L(ε) ... 10
3 PEMBAHASAN 3. 1 Teorema Resistansi Dua Simpul ... 13
3. 2 Jaringan Resistansi Dua Simpul ... 16
3. 3 Jaringan Satu Dimensi dengan Kondisi Batas Bebas ... 17
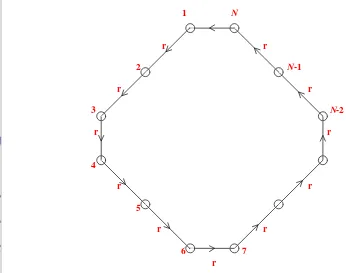
3. 4 Jaringan Satu Dimensi dengan Kondisi Batas Periodik ... 18
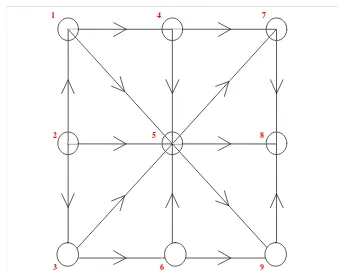
3. 5 Jaringan Dua Dimensi dengan Kondisi Batas Bebas ... 18
3. 6 Jaringan Dua Dimensi dengan Kondisi Batas Silindrik ... 20
3. 7 Penghitungan Nilai Resistor Pengganti Menggunakan Nilai Eigen dan Vektor Eigen Ortonormal dari Matriks Laplace dengan Scilab 4.1 ... 21
3. 8 Penghitungan Nilai Arus Listrik dengan Menggunakan Scilab 4.1 ... 21
4 SIMPULAN ... 25
DAFTAR PUSTAKA ... 25
x
DAFTAR GAMBAR
Halaman
1. Graf dengan 4 simpul dan 5 sisi ... 2
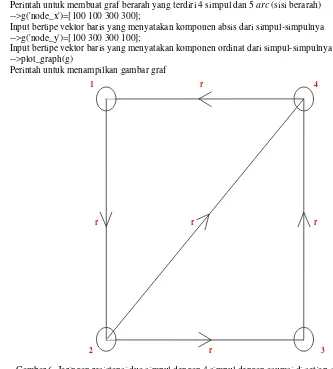
2. Digraf dengan 4 simpul dan 5 arc (sisi berarah) ... 3
3. Jaringan resistor dengan 4 simpul ... 8
4. Jaringan listrik ... 8
5. Jaringan resistor dengan 4 simpul dan nilai resistor pada setiap sisi sebesar 10 Ω ... 8
6. Jaringan resistansi dua simpul dengan 4 simpul dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r ohm ... 28
7. Jaringan resistor satu dimensi dengan kondisi batas bebas dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r ohm ... 29
8. Jaringan resistor satu dimensi dengan kondisi batas periodik dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r ohm ... 29
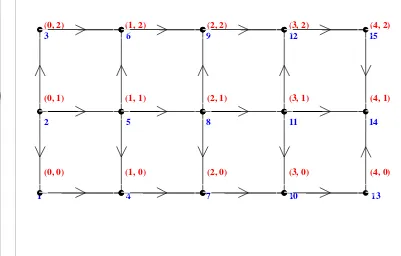
9. Jaringan resistor dua dimensi dengan kondisi batas bebas dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r ohm ... 30
10. Jaringan resistor dua dimensi dengan kondisi batas silindrik dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r ohm ... 31
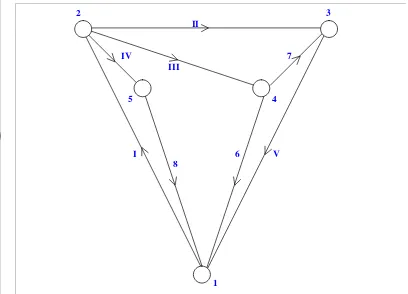
11. Jaringan listrik di hoteldengan asumsi di arc (sisi berarah) I, II, III, IV, V terdapat resistor pengganti masing-masing sebesar RI, RII, RIII, RIV, dan RV serta di arc 6, 7, 8 terdapat sumber tegangan awal masing-masing sebesar 1000 V, 500 V, 500 V ... ... 32
12a. Jaringan resistor di hotel ruangan I dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 20 ohm ... 33
12b. Jaringan resistor di hotel ruangan I dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 20 ohm ... 33
13. Jaringan resistor di hotel ruangan II dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 25 ohm ... 34
14. Jaringan resistor di hotel ruangan III dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 20 ohm ... 35
15. Jaringan resistor di hotel ruangan IV dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 25 ohm ... 36
16a. Jaringan resistor di hotel ruangan V dengan asumsi di setiap arc (sisi berarah) terdapat resistor sebesar r = 50 ohm ... 37
xi
DAFTAR LAMPIRAN
Halaman 1. Pembuatan graf jaringan resistor dengan Scilab 4.1 ... 28 2. Matriks Laplace L dari gambar jaringan resistor di ruangan I, II, III, IV, dan V ... 39 3. Pembuatan matriks Laplace L dengan Scilab 4.1 ... 43 4. Penentuan nilai-nilai eigen dan vektor-vektor eigen ortonormal dari matriks Laplace
dengan Scilab 4.1 ... 49 5. Formula (rumus) untuk menghitung nilai resistor pengganti RI, RII, RIII, RIV, dan RV ... 59
6. Penghitungan nilai resistor pengganti Rαβmenggunakan Scilab 4.1 ... 62
7. Penghitungan nilai arus listrik (i) pada jaringan listrik menggunakan Scilab 4.1 ... 65 8. Penyelesaian masalah pada jaringan listrik menggunakan matriks Laplace L dengan
Scilab 4.1 ... 67 9. Pembuktian akhir Teorema Resistansi Dua-Simpul ... 69 10. Pembuktian penghitungan nilai-nilai eigen dan vektor-vektor eigen ortonormal dari
matriks
T
Nfree ... 71 11. Pembuktian penghitungan nilai-nilai eigen dan vektor-vektor eigen ortonormal darimatriks
T
Nper ... 81 12. Pembuktian Teorema 6 tentang sifat-sifat kronecker product matriks ... 8513. Pembuktian Teorema 2 tentang nilai-nilai eigen dan vektor-vektor eigen dari
1.1 Latar Belakang
Selama ini, untuk menghitung nilai arus listrik (I) dari suatu jaringan listrik sering menggunakan perhitungan rumus-rumus fisika. Mungkin jaringan listrik yang diberikan sangat sederhana terdiri dari beberapa resistor dan sumber tegangan listrik. Tetapi jika jaringan listrik yang diberikan terdiri dari banyak jaringan resistor, maka penentuan besarnya nilai arus listrik (I) yang mengalir pada jaringan listrik tersebut, mungkin memerlukan waktu yang cukup lama.
Salah satu cara yang digunakan untuk menghitung nilai arus listrik (I) pada suatu jaringan listrik yang sangat kompleks yaitu dengan menggunakan perpaduan antara perhitungan matriks dan penggunaan Scilab 4.1. Resistor Pengganti di antara dua simpul α dan β, yaitu Rαβ dari jaringan resistor dapat
dihitung dengan menggunakan nilai-nilai eigen dan vektor-vektor eigen yang ortonormal dari matriks Laplace L. Matriks Laplace L dapat diperoleh dari hubungan gambar jaringan resistor. Setelah diperoleh nilai Resistor Pengganti Rαβ, maka dapat dihitung besarnya nilai arus listrik (I) dari jaringan listrik tersebut dengan menggunakan Scilab 4.1.
1.2 Tujuan
Tujuan dari penulisan skripsi ini adalah untuk mengetahui bagaimana hubungan antara nilai-nilai eigen dan vektor-vektor eigen yang ortonormal dari suatu matriks Laplace L dalam mencari nilai Resistor Pengganti di antara dua simpul dan nilai arus listrik (I) yang mengalir pada suatu jaringan listrik yang kompleks. Jaringan listrik yang kompleks terdiri dari beberapa jaringan resistor dan beberapa sumber tegangan listrik (V).
II LANDASAN TEORI
2.1 Matriks
Berikut ini diberikan beberapa definisi tentang matriks yang menjadi landasan teori untuk bab pembahasan.
Definisi 1 (Operasi Baris Dasar Matriks) I. Saling menukarkan baris ke-i dengan baris
ke-j, diberi notasi Eij, dengan i≠ j.
II. Mengalikan baris ke-i dengan suatu konstanta k≠ 0, diberi notasi Ei(k).
III. Menempatkan atau mengisikan baris ke-i
dengan k kali baris ke-j ditambah baris ke-i, diberi notasi Eij(k) dengan i≠j.
[Leon, 1998]
Definisi 2 (Bentuk Eselon Baris Tereduksi)
Suatu matriks dikatakan memiliki bentuk eselon baris jika
(i) entri bukan nol pertama dalam setiap baris adalah 1.
(ii) jika baris k tidak seluruhnya mengandung nol, maka banyaknya entri nol di bagian muka pada baris k + 1 lebih besar dari banyaknya entri nol di bagian muka pada baris k,
(iii) jika terdapat baris-baris yang entrinya semuanya adalah nol, maka baris-baris ini berada di bawah baris-baris yang memiliki entri-entri bukan nol.
Suatu matriks dikatakan memiliki bentuk eselon baris tereduksi jika :
(i) matriks memiliki bentuk eselon baris, (ii) entri bukan nol pertama dalam setiap baris
adalah satu-satunya entri bukan nol dalam kolom yang bersangkutan.
[Leon, 1998]
Definisi 3 (Matriks Hermite)
Misalkan M = (mij) adalah suatu matriks m × n dengan mij = aij + ibij untuk setiap i dan j, maka M dapat dituliskan dalam bentuk M = A + iB
dengan A = (aij) dan B = (bij) mempunyai entri bilangan real. Dapat didefinisikan matriks sekawan M dengan M =A−iB.
Tranpos dari Mdilambangkan sebagai MH. Suatu matriks M disebut Hermite jika M = MH.
[Leon, 1998] Ilustrasi :
3 2 3 2
maka
2 4 2 4
T H
i i
M M
i i
− −
= =
+ +
⎛
⎞
⎛
⎞
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
3 2 3 2
2 4 2 4
T
i i
M
i i
+ −
= = =
− +
⎛
⎞
⎛
⎞
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
Definisi 4 (Kronecker Products ⊗)
Misalkan A = (amn) mempunyai orde m×n dan B = (bst) mempunyai orde s×t, maka
A⊗B =
11 12 1
21 22 2
1 2
n
n
m m mn
a B a B a B a B a B a B
a B a B a B
⎛
⎞
⎜
⎟
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
dengan ukuran matriks A⊗B adalah ms×nt. Secara khusus, untuk u = (u1, u2, … , un)T, v = (v1, v2, … , vn)T ∈Cn , dengan Cn adalah himpunan bilangan kompleks maka
T n n n
n u v u v v
u v u v
dan
1 2 1 2 3
3 4 4 5 6
A=
⎛
⎜
⎞
⎟
B=⎛
⎜
⎞
⎟
⎝
⎠
⎝
⎠
maka⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⊗= ⊗
6 5 4
3 2 1 4 3
2 1 B A
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
==
24 20 16 18 15 12
12 8 4 9 6 3
12 10 8 6 5 4
6 4 2 3 2 1
4 3
2 1
B B
B B
Definisi 5 (Kronecker Sum)
Misalkan untuk suatu bilangan bulat r, s, k, matriks A ∈Rr,r, B ∈Rs,s dan Ik adalah suatu matriks identitas yang berorde k. Jumlah
B
A⊗Is+Ir⊗ disebut sebagai Kronecker Sum dari matriks A dan B.
2.2 Graf
Berikut ini diberikan beberapa definisi tentang graf yang akan menjadi landasan (dasar) untuk pembahasan materi selanjutnya.
Definisi 6 (Graf)
Suatu graf adalah pasangan terurut (V, E) dengan V adalah himpunan berhingga dan takkosong dari elemen-elemen graf yang disebut simpul (node, verteks) dan E adalah himpunan pasangan takterurut dari simpul-simpul berbeda di V. Setiap {p, q}
∈
E (dengan p, q∈
V) disebut sisi (edge) dan dikatakan menghubungkan simpul-simpul p dan q. Misalkan diberikan graf G = (V, E). Jika e = {p, q} ∈E maka p dan q masing-masing dikatakan incident dengan e.Misalkan diberikan graf G = (V, E). Jika e = {p, q} ∈ E maka p dikatakan adjacent dengan q, dan sebaliknya.
Derajat simpul(vi) yaitu banyaknya sisi yang incident dengan simpul vi.
[Foulds, 2002]
Definisi 7 (Digraf)
Suatu graf berarah/digraf (directed graph) adalah pasangan terurut (V,A), dengan V adalah himpunan takkosong dan hingga dan A adalah himpunan pasangan terurut elemen-elemen berbeda di V. Elemen dari A biasa disebut arc (sisi berarah).
Misalkan diberikan digraf D = (V, A). Jika e = {p, q} ∈A maka p dan q masing-masing dikatakan incident dengan e.
Misalkan diberikan digraf D = (V,A). Jika e = {i,j} maka i incident dari e jika sisi berarah e menjauhi simpul i dan j incident ke e jika sisi berarah e mendekati simpul j.
[Foulds, 2002]
Suatu walk pada graf G = (V, E) yang menghubungkan simpul v1 dengan vn adalah suatu barisan simpul (verteks) dan sisi (edge) dari G dengan bentuk <v1, {v1, v2}, v2, {v2, v3}, v3, ..., vn-1, {vn-1, vn}, vn> dan dapat dituliskan sebagai <v1, v2, ..., vn> atau v1, v2, ..., vn. Suatu walk yang menghubungkan v1 dengan vn dikatakan tertutup (closed walk) jika v1 = vn. Jika tidak (v1 ≠ vn) maka walk tersebut dikatakan terbuka.
[Foulds, 2002]
Definisi 9 (Matriks Derajat/Degree Matrix)
Matriks Derajat D untuk suatu graf
G = (V,E) dengan V = n adalah suatu matriks persegi yang didefinisikan sebagai
{
deg ( ) jika :0 selainnya i ij
v i j
d = =
dengan deg(vi) adalah derajat simpul(vi) yaitu banyaknya sisi yang incident dengan simpul vi dan V menyatakan banyaknya simpul di G.
[Skiena, 1990]
Definisi 10 (Matriks Adjacency)
Suatu matriks adjacency dari graf G = (V, E) adalah A = (aij)n×n dengan
1, jika dengan
0, jika selainnya
i j
ij
v adjacent v
a ⎧⎪⎨ ⎪⎩
=
untuk vi, vj ∈V dan (vi, vj) ∈E.
[Foulds, 2002]
Definisi 11 (Matriks Laplace)
Matriks Laplace untuk suatu graf G didefinisikan sebagai L = D – A
dengan D adalah matriks derajat dari graf G dan A adalah matriks adjacency dari G. Dengan perkataan lain, jika diberikan suatu graf G dengan n simpul, maka matriks Laplace L = (lij)n×n didefinisikan sebagai
⎪
⎩
⎪
⎨
⎧
≠ = =
selainnya 0,
dan jika
1,
-jika ), deg(
: i j
i
ij i j v adjacentv j
i v l
[Bendito, et al., 2000] Ilustrasi :
Perhatikan gambar graf berikut.
G :
Gambar 1. Graf dengan 4 simpul dan 5 sisi. v1 v2
Dari gambar graf tersebut dapat diperoleh matriks derajat D dan matriks adjacency A.
2 0 0 0
0 3 0 0
0 0 2 0
0 0 0 3
D
⎛ ⎞
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
= dan
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
0 1 1 1
1 0 1 0
1 1 0 1
1 0 1 0 A
Maka matriks Laplace L = D – A
2 1 0 1
1 3 1 1
0 1 2 1
1 1 1 3
L
− −
− − −
=
− −
− − −
⎛
⎞
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
.
Berikut ini dibahas matriks yang diperoleh dari suatu digraf D = (V,A).
Definisi 12 (Matriks Incidence)
Matriks incidence pada suatu digraf adalah matriks berukuran n×m yang merepresentasikan hubungan antara simpul dan arc (sisi berarah) pada suatu graf berarah. Jika n adalah banyaknya simpul dan m adalah banyaknya arc (sisi berarah) maka untuk komponen baris i dan kolom j pada matriks incidence adalah
⎪
⎩
⎪
⎨
⎧
i incident
j arc
i incident
j arc
i incident
j arc
simpul dengan tidak
jika 0,
simpul ke jika
1,
-simpul dari jika
, 1
[Watkins & Wilson, 1990] Ilustrasi :
D :
v1 v2
a
d e b
c
v4 v3 Gambar 2. Digraf dengan 4 simpul dan 5 arc
(sisi berarah).
Dari digraf D pada Gambar 2. di atas dapat diperoleh matriks incidenceB :
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− −
− −
−
=
1 1 1 0 0
0 0 1 1 0
1 0 0 1 1
0 1 0 0 1 B
2.3 Aljabar Linear
Berikut ini diberikan beberapa definisi tentang materi aljabar linear yang menjadi landasan teori untuk pembahasan selanjutnya.
Definisi 13 (Ruang Vektor)
Misalkan V adalah himpunan di mana didefinisikan operasi-operasi penjumlahan dan perkalian dengan skalar. Himpunan V
bersama-sama dengan operasi-operasi penjumlahan dan perkalian dengan skalar dikatakan membentuk suatu ruang vektor jika aksioma-aksioma berikut dipenuhi.
A1. x + y = y + x untuk setiap x dan y di V.
A2. (x + y) + z = x + (y + z) untuk setiap x, y,
z di V.
A3. Terdapat elemen 0 di V sehingga x + 0 = x
untuk setiap x
∈
V.A4. Untuk setiap x
∈
V terdapat elemen –x diV sehingga x + (–x) = 0.
A5. α(x + y) = αx + αy untuk setiap skalar α
dan setiap x dan y di V.
A6. (α + β)x = αx + βx untuk setiap skalar α
dan β dan setiap x
∈
V.A7. (αβ)x = α(βx) untuk setiap skalar α dan β
dan setiap x
∈
V.A8. 1 . x = x untuk setiap x
∈
V.[Leon, 1998]
Definisi 14 (Ruang Vektor Bagian)
Jika S adalah himpunan bagian takkosong dari suatu ruang vektor V, dan S memenuhi syarat :
(i) αx
∈
S, untuk semua x∈
S, dan α adalah sembarang skalar,(ii) x + y
∈
S, untuk semua x dan y∈
S, maka S disebut ruang bagian dari V.[Leon, 1998]
Definisi 15 (Ruang Nol dan Nulitas A)
Misalkan A adalah matriks m×n. Himpunan semua penyelesaian dari sistem homogen
Ax = 0 membentuk ruang bagian dari Rn yang disebut ruang nol (nullspace) dari A dan dinotasikan dengan
N(A) = {x
∈
Rn | Ax = 0}.Nulitas(A) adalah banyaknya anggota (ukuran) dari ruang nol (nullspace) dari A.
[Leon, 1998]
Definisi 16 (Kombinasi Linear)
Jika a1, a2, ..., an adalah vektor-vektor dalam Rm dan c1, c2, ..., cn adalah skalar-skalar, maka jumlah berbentuk c1a1 + c2a2 + ... + cnan disebut suatu kombinasi linear (linear combination) dari vektor-vektor a1, a2, ..., an.
[Leon, 1998]
Definisi 17 (Bebas Linear)
Vektor-vektor v1, v2, ..., vn dalam ruang vektor V disebut bebas linear (linearly independent) jika c1v1 + c2v2 + ... + cnvn = 0 mengakibatkan semua skalar c1, ..., cn harus sama dengan nol.
Vektor-vektor v1, v2, ..., vn dalam ruang vektor V disebut bergantung linear (linearly dependent) jika terdapat skalar-skalar c1, c2, ..., cn yang tidak semuanya nol sehingga c1v1 + c2v2 + ... + cnvn = 0.
[Leon, 1998]
Teorema 1
Misalkan A matriks persegi. Jika det(A) = 0 maka A1, A2, ..., An adalah saling bergantung linear.
Catatan : A1, A2, ..., An adalah vektor-vektor kolom ke-j dari matriks A.
BUKTI :
(
⇒
) Diketahui det(A) = 0 maka A singular, sehingga Ax = 0 mempunyai penyelesaian taktrivial untuk setiap x≠0. Jadi x11A1 + x21A2 + ... + xn1An = 0. Karena x ≠0 maka x11, x21, x31, ..., xn1 adalah skalar tidak semuanya nol. Jadi, A1, A2, ..., An adalah saling bergantung linear. (Terbukti)Definisi 19 (Nilai Eigen dan Vektor Eigen)
Misalkan A adalah suatu matriks n×n. Skalar λ disebut sebagai suatu nilai eigen atau nilai karakteristik (characteristic value) dari A jika terdapat suatu vektor taknol v, sehingga memenuhi Av = λv. Vektor v disebut vektor eigen atau vektor karakteristik dariλ. Misalkan A adalah matriks n×n dan λ adalah suatu skalar. Pernyataan-pernyataan berikut ini adalah ekuivalen.
(a)λ adalah nilai eigen dari A.
(b) (A – λI)v = 0 mempunyai penyelesaian taktrivial.
(c) N(A – λI) ≠ {0}. (d) A – λI adalah singular. (e) det(A – λI) = 0.
[Leon, 1998]
Teorema 2
Misalkan A dan B adalah matriks persegi dengan entri bilangan kompleks yang masing-masing berorde m×m dan n×n dengan nilai-nilai eigen λi dan µj, i = 1, ... , m, j = 1, ... , n. Maka nilai-nilai eigen dari A⊗Badalah
i j
λ µ , i = 1, ... , m, j = 1, ... ,n, dan nilai-nilai eigen dari A⊗In+Im⊗B adalah
i j
λ +µ , i = 1, ... , m, j = 1, ... , n. [Zhang, 1999]
BUKTI : lihat di Lampiran 13.
Teorema 3
Misalkan A∈Rr,r dan B∈Rs,s dan
Aui = λiui, i = 1, ... , r, Bvj = µjvj, j = 1, ... , s, maka untuk i = 1, ... , r, j = 1, ... , s
) ( ) )(
(A⊗B ui⊗vj =λiµj ui⊗vj
) )( (
) )(
(A⊗Is+Ir⊗B ui⊗vj = λi+µj ui⊗vj [Lyche, 2006]
BUKTI :
Dari Teorema 2 diperoleh ) )(
(A⊗B ui⊗vj =(Aui)⊗(Bvj) ) ( ) (λiui ⊗ µjvj =
) )( ( i⊗ j ui⊗vj
= λ µ
) ( i j j i u ⊗v
=λµ .■
Dari persamaan di atas dapat diperoleh ) ( ) )(
(A⊗Is ui⊗vj =λi ui⊗vj , dan
) ( ) )(
(Ir ⊗B ui ⊗vj =µj ui ⊗vj
hasilnya sekarang digunakan untuk membuktikan persamaan kedua
) )(
(A⊗Is +Ir ⊗B ui⊗vj ) )( (A⊗ s ui⊗vj
= I +(Ir⊗B)(ui⊗vj) )
( ) (Aui ⊗ Isvj
= +(Irui)⊗(Bvj) )
( ) ( iui ⊗ Isvj
= λ +(Irui)⊗(µjvj) )
)( ( i⊗ s ui⊗vj
= λ I +(Ir⊗µj)(ui⊗vj) )
( i j i u ⊗v
=λ +µj(ui⊗vj) ) )( ( i+ j ui⊗vj
= λ µ .■
Jadi nilai-nilai eigen dari suatu Kronecker product (sum) adalah products (sums) dari nilai-nilai eigen yang berbeda milik matriks A dan B. Vektor-vektor eigen dari suatu Kroneckerproduct (sum) adalah hasil kali dari vektor-vektor eigen milik matriks A dan B.
(Terbukti)
Selanjutnya akan dibahas suatu teorema tentang nilai-nilai eigen dan vektor-vektor eigen dari proses Kronecker product matriks.
Teorema 4
Misalkan A
∈
Rn×n mempunyai nilai-nilai eigenλi, i
∈
[1,n], dan misalkan B∈
Rm×m mempunyai nilai-nilai eigen µj, j∈
[1,m]. Maka mn nilai-nilai eigen dari (A⊗B)adalahλ1µ1, ... , λ1µm, λ2µ1, ... , λ2µm, ... , λnµm. Selanjutnya, jika x1, ... ,xp adalah vektor-vektor eigen kanan yang bebas linear dari A bersesuaian dengan λ1, ... , λp (p≤n), dan z1, ..., zq adalah vektor-vektor eigen kanan yang bebas linear dari B bersesuaian dengan µ1, ... ,
µq (q ≤ m), maka xi⊗zj
∈
R mnadalah vektor-vektor eigen kanan yang bebas linear dari
)
(A⊗B bersesuaian dengan λiµj, i
∈
[1,p], j∈
[1,q].BUKTI :
Catatan : vektor-vektor eigen kanan adalah vektor-vektor eigen yang terletak (ditulis) di sebelah kanan suatu matriks atau skalar.
Misalkan A mempunyai nilai-nilai eigen λi, 1 ≤ i ≤ n, maka Axi = λixi, 1 ≤ i ≤ n dan misalkan B mempunyai nilai-nilai eigen µj, 1 ≤ j≤m, maka Bzj = µjzj, 1 ≤j≤m.
Misalkan juga x1, ... , xp adalah vektor-vektor eigen kanan yang bebas linear dari A bersesuaian dengan nilai-nilai eigen λ1, ... , λp (p ≤ n) akan terdapat matriks X dengan xj vektor eigen kolom ke-j untuk j = 1, ... , n sehingga berlaku X-1AX = D1 dan z1, ... , zq adalah vektor-vektor eigen kanan yang bebas linear dari B bersesuaian dengan µ1, ... , µq (q≤ m) akan terdapat matriks Z dengan zj vektor eigen kolom ke-j untuk j = 1, ... , n sehingga berlaku juga X-1AX = D2.
). )( ( ) (
) )( )( (
) )( (
) ( ) (
1 1 1
1 1
1 1
2 1
Z X B A Z X
Z X B A Z X
Z X B Z A X
BZ Z AX X D D
⊗ ⊗ ⊗
=
⊗ ⊗ ⊗
=
⊗ ⊗
=
⊗ =
⊗
− − −
− −
− −
Jadi, (X⊗Z)adalah suatu matriks yang mempunyai nm vektor kolom yang bebas linear dengan xi⊗zjvektor eigen kolom ke-j untuk j = 1, ... , nm.
Selanjutnya ) )(
(A⊗B xi⊗zj =(Axi)⊗(Bzj) =(λixi)⊗(µjzj)
) )( ( i⊗ j xi⊗zj
= λ µ
) ( i j j i x ⊗z
=λµ .
Jadi, mn nilai-nilai eigen dari (A⊗B)adalah
λ1µ1, ... , λ1µm, λ2µ1, ... , λ2µm, ... , λnµm. Begitu juga
) )(
(A⊗B X⊗Z =(AX)⊗(BZ) =(Axi)⊗(Bzj) =(λixi)⊗(µjzj) =(λi⊗µj)(xi⊗zj) =λiµj(xi⊗zj)
Jadi xi⊗zj
∈
Rmn adalah vektor-vektor eigen kanan yang bebas linear berbeda dari)
(A⊗B bersesuaian dengan λiµj, i ≤ p ≤ n, j≤q≤m.
(Terbukti)
Teorema 5
Suatu matriks A
∈
Mn adalah singular jika dan hanya jika 0∈
σ(A).Catatan : σ(A) adalah himpunan nilai-nilai eigen dari matriks A.
[Horn & Johnson, 1985]
BUKTI :
Matriks A adalah singular jika dan hanya jika Ax = 0 untuk setiap x≠0. Hal ini terjadi jika dan hanya jika Ax = 0x untuk setiap x≠0, Ax
= 0x berlaku, jika dan hanya jika λ = 0 adalah suatu nilai eigen.
(Terbukti)
Definisi 20 (Hasil Kali Dalam)
Hasil Kali Dalam pada ruang vektor V adalah
sebuah operasi pada V yang memadankan setiap pasang vektor-vektor x dan y di dalam V
dengan sebuah bilangan real <x,y> yang memenuhi syarat berikut :
(i) <x, x> ≥ 0 dengan persamaan berlaku jika dan hanya jika x = 0.
(ii) <x, y> = <y, x> untuk semua x dan y di dalam V.
(iii) <αx + βy, z> = α<x, z> + β<y, z> untuk semua x, y, z di dalam V dan semua skalar α dan β.
Sebuah ruang vektor V dengan hasil kali dalamnya disebut ruang hasil kali dalam. Hasil kali dalam baku untuk Rn adalah hasil kali skalar <x, y> = xTy.
[Leon, 1998]
Definisi 21 (Norma)
Sebuah ruang vektor V dikatakan ruang linear bernorma (normed linear space) jika untuk setiap vektor v ∈V dikaitkan dengan sebuah bilangan real v yang disebut norma dari v
yang memenuhi :
(i) v > 0 dengan kesamaan berlaku jika dan hanya jika v = 0.
(ii) α =v α v untuk tiap skalar α.
(iii) v+w ≤ v + w untuk semua v, w∈V. [Leon, 1998]
Definisi 22 (Himpunan Ortogonal dan Ortonormal)
Misalkan v1, v2, …, vn adalah vektor-vektor di dalam sebuah ruang hasil kali dalam
V. Jika <vi, vj> = 0 bilamana i≠j, maka {v1,
v2, …, vn} dikatakan sebagai sebuah himpunan ortogonal dari vektor-vektor.
Sebuah himpunan ortonormal dari
vektor-vektor adalah sebuah himpunan ortogonal dari vektor-vektor satuan.Himpunan {u1, u2, …, un} akan menjadi ortonormal jika dan hanya jika <ui, uj> = ij dengan
⎩
⎨
⎧
=
≠ =
j i
j i ij
jika 0
vektor taknol {v1, v2, … , vn}, maka dimungkinkan untuk membentuk sebuah himpunan ortonormal dengan mendefinisikan
i i v v u
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
= 1 untuk i = 1, 2, …, n dengan
> <
= i i
i v v
v , .
[Leon, 1998]
Definisi 23 (Matriks Ortogonal)
Sebuah matriks Q yang berorde n×n dikatakan sebagai matriks ortogonal jika vektor-vektor kolom dari Q membentuk sebuah himpunan ortonormal di dalam Rn, maka Q dapat dibalik dan QT = Q-1 sehingga QTQ = I.
[Leon, 1998] Ilustrasi :
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
− − = 6 / 1 2 / 1 3 / 1 6 / 2 0 3 / 1 6 / 1 2 / 1 3 / 1Q maka
1 6 / 1 6 / 2 6 / 1 2 / 1 0 2 / 1 3 / 1 3 / 1 3 / 1 − = − − =
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
Q QTDapat ditunjukkan bahwa vektor-vektor kolom dari Q membentuk sebuah himpunan ortonormal yaitu
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
= 3 / 1 3 / 1 3 / 1 1 u ,⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
− = 2 / 1 0 2 / 1 2 u ,⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
− = 6 / 1 6 / 2 6 / 1 3 umaka <u1,u2> = <u1,u3> = <u2,u3> = 0, <u1,u1> = <u2,u2> = <u3,u3> = 1, dan
1 3 2
1 = u = u =
u .
Definisi 24 (Matriks Uniter)
Matriks uniter Un × n adalah suatu matriks kompleks atau real yang memenuhi UHU =
UUH = I, jika vektor-vektor kolomnya membentuk suatu himpunan ortonormal dalam
Cn, dengan UH = U-1 dan |detU| = 1 untuk suatu matriks uniter U, maka suatu matriks uniter sesungguhnya adalah matriks ortogonal. Catatan : matriks UH =
T U . [Zhang, 1999] Ilustrasi :
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
− − = 6 / 1 2 / 1 3 / 1 6 / 2 0 3 / 1 6 / 1 2 / 1 3 / 1U maka
1 6 / 1 6 / 2 6 / 1 2 / 1 0 2 / 1 3 / 1 3 / 1 3 / 1 − = − − =
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
U UT Teorema 6Untuk matriks-matriks A, B, C, dan D dengan ukuran yang berbeda, berlaku
1. (A⊗B)(C⊗D)=(AC)⊗(BD),
2. (A⊗B)*= A*⊗B*, dengan A*= ATdan T
B B*= ,
3. (A⊗B)−1=A−1⊗B−1 jika A dan B adalah matriks taksingular,
4. (A⊗B)≠(B⊗A),
5. A⊗B adalah uniter jika A dan B adalah uniter.
[Zhang, 1999]
BUKTI : lihat di Lampiran 12.
Definisi 25 (Matriks Definit)
Suatu matriks simetrik real A disebut
(i) definit positif jika xTAx > 0 untuk semua x
taknol dalam Rn.
(ii) definit negatif jika xTAx < 0 untuk semua
x taknol dalam Rn .
(iii) semidefinit positif jika xTAx ≥ 0 untuk semua x taknol dalam Rn.
(iv) semidefinit negatif jika xTAx ≤ 0 untuk
semua x taknol dalam Rn .
[Leon, 1998]
Definisi 26 (Matriks Definit Positif)
Sifat-Sifat Matriks Definit Positif Simetrik :
Sifat I. Jika A adalah matriks definit positif
simetrik, maka A taksingular.
Sifat II. Jika A adalah suatu matriks definit
positif simetrik, maka det(A) > 0.
Sifat III. Semua nilai-nilai eigen matriks
definit positif simetrik A adalah positif.
Sifat IV. Jika A adalah suatu matriks definit
positif simetrik, maka submatriks utama A1, A2, ... , An dari A adalah definit positif.
Sifat V. Jika A adalah matriks definit positif
simetrik, maka A dapat direduksi menjadi matriks segitiga atas hanya dengan menggunakan operasi baris III dan semua elemen-elemen porosnya adalah positif.
Sifat VI. Jika A adalah suatu matriks definit
yang entri-entri diagonalnya positif semua.
Sifat VII. (Dekomposisi Cholesky) Jika A
adalah matriks definit positif simetrik, maka A dapat difaktorkan ke dalam suatu hasil kali LLT, dengan L adalah matriks segitiga bawah dengan elemen-elemen diagonal positif.
[Leon, 1998]
2.4 Jaringan Listrik dan Jaringan Resistor
Berikut ini beberapa definisi tentang jaringan listrik dan jaringan resistor yang akan menjadi landasan teori untuk materi bab pembahasan selanjutnya.
Definisi 27 (Kondisi Batas Bebas)
Kondisi Batas Bebas adalah suatu walk terbuka yang mengandung setidaknya tiga simpul dan semua simpulnya berbeda yang menghubungkan x1 dengan xn dengan syarat x1
≠xn.
[Tzeng & Wu, 2000]
Definisi 28 (Kondisi Batas Periodik)
Kondisi Batas Periodik adalah suatu walk tertutup yang mengandung setidaknya tiga simpul dan semua simpulnya berbeda yang menghubungkan x1 dengan xn dengan syarat x1 = xn.
[Tzeng & Wu, 2000]
Definisi 29 (Penurunan Tegangan V)
Penurunan tegangan atau beda potensial V adalah perbedaan antara jumlah elektron yang berada dalam suatu materi (misalkan dalam suatu kawat listrik atau benda penghambat). Terdapat hubungan V = RI jika
V adalah beda potensial antara kedua ujung benda penghambat.
R adalah resistor tahanan atau penghambat, adalah suatu komponen elektronik yang dapat menghambat gerak lajunya arus listrik. I adalah besar arus yang melalui benda
penghambat.
Misalkan diberikan graf jaringan resistor yang terdiri dari n sisi (edge), di setiap sisi ke-i, i = 1, …, n masing-masing terdapat satu resistor dengan nilai resistansi sebesar R ohm. Maka berdasarkan Hukum Ohm dapat diperoleh penurunan tegangan V di setiap sisi ke-i dalam bentuk notasi matriks yaitu V = RI , dengan
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
= =
=
n n
n R
R R R i i i I v v v V
0 0
0 0
0 0
,
, 2
1 2
1 2
1
V suatu matriks berorde n×1 dengan
komponennya merupakan nilai beda potensial di setiap sisi.
R suatu matriks diagonal berorde n×n dengan
komponen pada poros diagonal utama merupakan nilai-nilai resistansi resistor di setiap sisi.
I suatu matriks berorde n×1 dengan
komponennya merupakan nilai arus listrik di setiap sisi.
[Noble, 1969]
Definisi 30 (Hukum Kirchhoff / Kirchhoff’s Laws)
1. Pada setiap simpul, maka jumlah dari kuat arus yang masuk sama dengan jumlah dari kuat arus yang keluar. (Kirchhoff Current Law /KCL)
2. Di sekeliling setiap simpul (loop) tertutup, maka jumlah aljabar dari tegangan harus sama dengan jumlah aljabar penurunan tegangan. (Kirchhoff Voltage Law /KVL)
[Leon, 1998]
Definisi 31 (Resistor Pengganti)
Resistor pengganti adalah suatu resistor gabungan dari beberapa resistor yang terletak di antara dua simpul, misalkan α dan β, dengan penurunan tegangan masing-masing Vα dan Vβ maka
_
V V R
I
α β
αβ= …… (1),
dengan Rαβ adalah nilai resistor pengganti di
antara simpul α dan β, dan
I adalah nilai arus listrik yang mengalir di antara simpul α dan β.
[Wu, 2004]
Definisi 32 (Jaringan Resistor)
Jaringan resistor adalah network (jaringan) berbentuk graf yang terdiri dari N simpul yang bernomor dengan i = 1 , 2, … , N. Di setiap sisi di antara simpul i dan j yang saling adjacent terdapat satu resistor. Misalkan rij = rji adalah nilai resistansi dari resistor yang dihubungkan oleh simpul i dan j. Maka, nilai konduktansinya adalah cij = rij
1
−
= cji sehingga nilai cij = 0 jika tidak ada resistor penghubung antara simpul i dan j.
[Cserti, 2002] Ilustrasi :
4 r34 3
Gambar 3. Jaringan resistor dengan 4 simpul.
Definisi 33 (Jaringan Listrik)
Jaringan listrik adalah suatu digraf D = (V, A) yang mempunyai tiga bagian yang bersesuaian dengan setiap arc (sisi berarah) k :
(i) suatu elemen sumber listrik Ek, (ii) suatu variabel arus listrik ik(t),
dan
(iii) suatu variabel beda potensial (voltase) vk(t).
dengan t menunjukkan waktu.
Untuk suatu elemen Ek, ada tiga bagian yang dapat dirangkai sebagai suatu rangkaian sederhana, yaitu :
1. Resistor dengan Ohm’s Law-nya. 2. Induktor.
3. Kapasitor.
4. Sumber tegangan (Voltage supply).
[Foulds, 2002] Ilustrasi :
Perhatikan gambar jaringan listrik berikut. E
4 3
V
Gambar 4. Jaringan listrik. Dengan asumsi di setiap arc mengalir arus listrik (i).
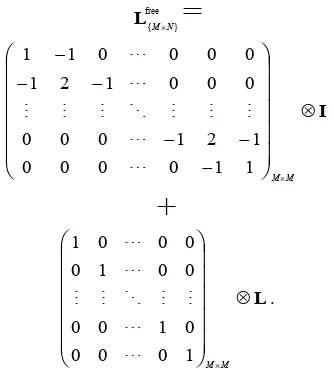
Maka matriks Laplace dari graf jaringan resistor adalah sebagai berikut.
Definisi 34 (Matriks Laplace L dari Graf Jaringan Resistor)
Misalkan diberikan suatu graf jaringan resistor yang terdiri dari N simpul, maka dapat
jaringan resistor tersebut yaitu :
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− − − − − − = N N N N N c c c c c c c c c 2 1 2 2 12 1 12 1 Ldengan cij akan bernilai
1/ jika dua simpul yang saling dihubungkan oleh satu resistor. 0 jika dua simpul yang tidak saling tidak dihubungkan oleh satu resistor.
ij r adjacent adjacent ⎧ ⎪ ⎪ ⎨ ⎪ ⎪⎩
dan ci =∑
= N j ij c 1
' , jika notasi
1
' N
j=
∑ menunjukkan bahwa persamaan ruas kanan tidak berlaku untuk i = j tetapi harus i≠j. Maka
kolom. setiap untuk 0 dan baris setiap untuk 0 1 1
'
'
= ∑ − = ∑ − = = N i ij j N j ij i c c c cdengan rijadalah nilai resistansi dari resistor di antara simpul i dan j yang saling adjacent.
[Wu, 2004] Ilustrasi :
Perhatikan gambar jaringan resistor berikut. 1 r 2
4 r 3
Gambar 5. Jaringan resistor dengan 4 simpul dan nilai resistor pada setiap sisi sebesar 10 Ω. Jika diketahui nilai r = 10 Ω. Maka nilai konduktansinya adalah 1/r = 1/10 = 0,1. Jadi matriks Laplace L dari gambar jaringan resistor tersebut adalah
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− − − − − − − − − − = 3 1 1 1 1 2 1 0 1 1 3 1 1 0 1 2 * 1 . 0 L⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− − − − − − − − − − = 3 . 0 1 . 0 1 . 0 1 . 0 1 . 0 2 . 0 1 . 0 0 1 . 0 1 . 0 3 . 0 1 . 0 1 . 0 0 1 . 0 2 . 0 L r24 r i r r r1 2
r r
Definisi 35 (Matriks L(ε) dari Graf Jaringan Resistor)
Matriks L(ε) adalah bentuk taksingular (determinannya bukan nol) dari L dengan menambahkan suatu matriks εI, L(ε) merupakan modifikasi dari L yang berbentuk
L(ε) = L + εI dengan ε > 0 suatu skalar atau 0 > ε > -λi untuk nilai ε yang negatif, 1 ≤i≤n dengan -λi adalah nilai-nilai eigen ke-i dari matriks Laplace L dan I suatu matriks identitas.
[Wu, 2004] Ilustrasi :
Misalkan untuk nilai ε = 0.9 > 0, maka dapat diperoleh suatu matriks L(ε) yaitu
L(0.9) = L + 0.9I
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+ − − − − − − − − − − = 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 * 9 . 0 3 . 0 1 . 0 1 . 0 1 . 0 1 . 0 2 . 0 1 . 0 0 1 . 0 1 . 0 3 . 0 1 . 0 1 . 0 0 1 . 0 2 . 0⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− − − − − − − − − − = 2 . 1 1 . 0 1 . 0 1 . 0 1 . 0 1 . 1 1 . 0 0 1 . 0 1 . 0 2 . 1 1 . 0 1 . 0 0 1 . 0 1 . 1 ) (ε LDefinisi 36 (Fungsi Green G(ε))
Fungsi green G(ε) adalah invers dari L(ε).
Jadi G(ε) = L-1(ε), jika diketahui L(ε) = L + εI, dengan skalar ε > 0 atau 0 > ε > -λi untuk nilai
ε yang negatif, 1 ≤ i ≤ n dengan -λi adalah nilai-nilai eigen ke-i dari matriks Laplace L
dan I suatu matriks identitas.
[Katsura, etal., 1971]
2.5 Sifat-Sifat Matriks Laplace L dan L(ε)
dari Graf Jaringan Resistor
Sebelum membahas tentang sifat-sifat matriks Laplace L dan L(ε) dari graf jaringan resistor, akan dibicarakan tentang penjelasan lain dari matriks Laplace L yaitu mengenai hubungan antara matriks Laplace dengan matriks incidence yang diperoleh dari suatu graf G = (V,E) yang berarah. Ternyata matriks Laplace dapat diperoleh dari perkalian suatu matriks incidence dengan transposenya. Bentuk umum yang lain dari suatu matriks Laplace L adalah L = BBT dengan B suatu matriks incidence yang diperoleh dari suatu graf G = (V,E) yang berarah. Sedangkan,
matriks Laplace dari suatu jaringan resistor yaitu L = C = BCBB
T
, untuk B suatu matriks incidence dari suatu graf G = (V,E) yang berarah dan CB suatu matriks diagonal dengan nilai-nilai pada poros utamanya nilai dari konduktansi resistor di setiap sisi. Jika L = BCBB
T
maka nilai dari komponen untuk baris i dan kolom j dari matriks L adalah
Ljj = jumlah dari semua nilai ci pada sisi-sisi yang bertemu pada simpul j.
⎪
⎪
⎩
⎪⎪
⎨
⎧
− = adjacent adjacent k j i c L i jk yang simpul -simpul antara di sisi ada tidak jika 0 yang dan simpul kan menghubung sisi jikaDengan ci adalah nilai konduktansi dari resistor pada sisi i.
Berikut beberapa sifat tentang matriks Laplace
L dan L(ε) yang diperolah dari suatu graf jaringan resistor.
1. Matriks Laplace diperoleh dari hubungan gambar jaringan resistornya.
[Donev]
BUKTI :
Bentuk umum dari matriks Laplace jaringan resistor adalah suatu conductance matrix yang berbentuk L = C = BCBBT dengan B adalah suatu matriks incidence node-arc dari suatu graf G yang berarah, dan CB adalah suatu matriks diagonal dengan elemen-elemen diagonal utamanya adalah nilai konduktansi (invers dari nilai resistansi resistor) di setiap arc (sisi berarah) dari graf jaringan resistor G yang berarah. Karena matriks B dan CB masing-masing diperoleh dari suatu gambar graf dan jaringan resistor, maka matriks Laplace diperoleh dari hubungan gambar jaringan resistor.
2. Setiap entri bukan nol selain entri-entri pada diagonal utama, dari matriks Laplace adalah nilai dari konduktansi resistornya sehingga lij = 1/rij dengan rij nilai resistansi di antara simpul i dan j yang adjacent.
3. Jumlah komponen setiap kolom dalam satu baris sama dengan nol dan jumlah komponen setiap baris dalam satu kolom sama dengan nol.
4. Matriks L hanya mempunyai satu nilai eigen dengan nilai 0.
BUKTI :
Andaikan matriks L mempunyai lebih dari satu nilai eigen yang bernilai 0. Maka berlaku Lxi = λixi, untuk i = 1, …, n dan λ1 = … = λn = 0 yang bersesuaian dengan vektor-vektor eigen xi. Selanjutnya dapat diperoleh
anggota yaitu vektor x = α(1, 1, …, 1)T, α suatu skalar. Maka untuk x = α(1, 1, …, 1)T persamaan Lxi = 0 = λixi berlaku jika dan hanya jika λ = 0. Jadi, matriks L hanya mempunyai satu nilai eigen dengan nilai 0. Hal ini kontradiksi dengan pengandaian. 5. Matriks L adalah matriks semidefinit positif
simetrik sedang matriks L(ε) adalah matriks definit positif simetrik.
BUKTI : Untuk bukti lengkap lihat di Bab
pembahasan 3.1.
Akan ditunjukkan bahwa L adalah suatu matriks semidefinit positif. Untuk setiap x≠ 0 dalam Rn maka xTLx = xTλx = λxTx > 0 untuk λ suatu nilai eigen dari L (penjelasan penghitungannya di Pembahasan 3.1). Karena λ = 0 adalah salah satu nilai eigen dari L yang bersesuaian dengan vektor eigen
x = α(1, 1, …,1) ≠0 dengan α suatu skalar maka ada nilai xTLx yang bernilai xTLx = 0xTx = 0. Jadi, jika untuk suatu matriks L
mempunyai nilai xTLx ≥ 0 maka L
semidefinit positif.
6. L adalah matriks singular sedang L(ε) adalah matriks taksingular.
BUKTI :
Setelah dilakukan operasi baris dasar yang berhingga banyaknya terhadap matriks L
maka dapat diperoleh suatu matriks U = EkEk – 1…E1L yang merupakan suatu
matriks eselon baris. Karena matriks U memiliki satu baris terakhir yang seluruhnya bernilai 0, maka det(U) = 0. Jadi, dapat disimpulkan bahwa det(L) = det(U) = 0. Berarti L adalah matriks singular.
Diketahui bahwa L(ε) = L + εI, maka setelah dilakukan operasi baris dasar yang berhingga banyaknya terhadap matriks L(ε) maka dapat diperoleh suatu matriks segitiga atas V yang semua elemen-elemen porosnya (elemen diagonalnya) adalah positif. Hal ini dapat terjadi karena L(ε) merupakan suatu matriks simetrik definit positif (lihat sifat kelima dari matriks definit positif simetrik di landasan teori). Jadi, det(V) = det(L(ε)) ≠ 0 berarti matriks L(ε) adalah taksingular. 7. Matriks L(ε) mempunyai nilai-nilai eigen
bernilai positif.
BUKTI : Untuk bukti lengkap lihat di
Teorema 9, lihat juga sifat ketiga dari matriks definit positif simetrik di landasan teori.
8. Pada matriks L(ε) nilai skalar ε harus ε > 0 atau 0 > ε > -λi untuk nilai ε yang negatif, 1
≤i≤n dengan -λi adalah nilai-nilai eigen ke-i dari matriks Laplace L karena jika ε < -λi <
adalah matriks definit negatif simetrik.
BUKTI :
Untuk bukti lengkap bahwa matriks L(ε) adalah matriks definit positif dan proses penghitungan xTL(ε)x untuk setiap x≠0 di Rn yang lengkap lihat di pembahasan 3.1. Jika L(ε) adalah suatu matriks definit positif maka nilai xTL(ε)x = xT(λi + ε)x = (λi + ε)xTx
> 0 untuk setiap x ≠0 di Rn dengan ε > 0. Misalkan untuk nilai ε < -λi < 0
⇔
ε + λi < 0 maka xTL(ε)x = (λi + ε)xTx = (ε + λi)xTx < 0. Jadi, untuk nilai ε < -λi < 0 maka matriksL(ε) adalah matriks definit negatif.
2.6 Teorema-Teorema tentang Matriks
Laplace L dan L(ε)
Berikut ini teorema-teorema yang berhubungan dengan sifat-sifat matriks Laplace.
Teorema 7
Misalkan
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
− −
− −
−
− −
=
n n n
n
n n
l l
l
l l
l
l l
l
2 1
2 22
21
1 12
11
L suatu
matriks Laplace. Jika }
..., , 1 { , 0 1
n i
l N
j
ij= ∀ ∈
∑
=
maka 0 adalah nilai eigen dari L.
Catatan : Matriks Laplace L dapat dinyatakan oleh vektor-vektor kolomnya, yaitu
[
L1 Lj Ln]
=L ; dengan
n j
l l L
j n j
j
≤ ≤
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
1
1
.
Karena jumlah dari setiap komponen pada kolom-kolom matriks Laplace L sama dengan nol, maka berlaku
∑
=0=
N
j j L 1
.
BUKTI 1 :
(
⇒
) Diketahui1 2
1
11 12 1
21 22 2
31 32 3
1 2
... 0, {1, ..., } ... 0
... 0 ... 0
... 0 N
ij i i
j
n
n
n
n n nn
in
l l l l i n
l l l l l l l l l
l l l
= = + + + = ∀ ∈
∑
+ + + = + + + = + + + =
+ + + =
11 12 1
21 22 2
31 32 3
1 2 0 0 ... 0 0 n n n
n n nn
l l l
l l l
l l l
l l l
+ + + =
⎡ ⎤
⎡ ⎤ ⎡ ⎤
⎡ ⎤
⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥
⎣ ⎦
⎣ ⎦ ⎣ ⎦
⎣ ⎦
Misalkan λ adalah salah satu nilai eigen dari L yang bersesuaian dengan vektor eigen
0
≠
v
. Akan ditunjukkan (L−λI)v=0Ù Lv−λIv=0
Ù Lv= +0 λIv=λIv=λv. Maka Lv=λv, sehingga diperoleh
11 11 12 21 1 1 11
21 11 22 21 2 1 21
31 11 32 21 3 1 31
1
1 11 2 21 1
...
...
...
...
n n n n n n nn n nn n
l v
l v
l v
v
l v
l v
l v
v
l v
l v
l v
v
v
l v
l v
l v
λ
λ
λ
λ
+
+ +
⎡
⎤ ⎡
⎤
⎢
+
+ +
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
+
+ +
⎥ ⎢
=
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
+
+ +
⎥ ⎢
⎣
⎥
⎦
⎣
⎦
dengan⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
= 1 11 n v v v .Jadi L1v11 + L2v21 + ... + Lnvn1 = λv.
Dapat diperoleh kesimpulan bahwa det(L) = det(Ln) = 0. Dengan menggunakan operasi baris dasar yang berhingga banyaknya terhadap matriks L maka dapat diperoleh hasil seperti berikut ini.
___________________________________________________________________________________ n n n n n n n n n n n n n n n n n n n n n n n n n nn n n n n l l l l l l l l l l l l l l l l l l l l l E l l l l l l l l l l l l E l l l l l l l l l L L = − − − − = − − − − + − − − − − + − − − − − − − − − − − + − − − − − − − − =
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
2 1 2 22 21 2 1 2 22 21 2 1 2 22 12 1 21 11 ) 1 ( 1 2 1 2 22 12 2 1 22 12 21 11 ) 1 ( 12 2 1 2 22 21 1 12 11 0 0 0 ... ... ... ~ ~ __________________________________________________________________________________ Karena det(L) = 0 berarti L1, L2, L3, ..., Lnadalah saling bergantung linear. Maka ada suatu skalar v11, v21, v31, ..., vn1 yang tidak semuanya nol, sehingga
v11L1 + v21L2 + ... + vn1Ln = 0 ... (2). Serta
v11L1 + v21L2 + ... + vn1Ln = λv ... (3), maka dari persamaan-persamaan (2) dan (3) dapat diperoleh 0 = λv.
Karena
v
≠
0
, maka supaya persamaan0 = λv dipenuhi, jika dan hanya jika haruslah
λ = 0. Jadi 0 harus menjadi nilai eigen dari L.
(Terbukti)
BUKTI 2 :
Setelah diperoleh kesimpulan bahwa det(L) = 0. Dapat diketahui bahwa L adalah matriks singular. Jika L matriks singular maka berdasarkan Teorema 5 0 adalah salah satu nilai eigen dari matriks L.
(Terbukti)
Teorema 8
Jika L(ε) memiliki n nilai eigen maka L(ε) memiliki n vektor eigen.
BUKTI :
(
⇒
) Misalkan λi nilai eigen yang dimiliki oleh L(ε) dengan i = 1, 2, ..., n (beberapa dariλi boleh sama). Maka berlaku L(ε)xj = λjxj, untuk setiap j, adalah vektor kolom ke-j dari
L(ε)X dengan X adalah matriks dimana vektor kolom ke-j adalah xj, jika xj adalah vektor eigen yang dimiliki oleh λj, berarti X adalah bebas linear. Andaikan untuk xj dengan j = 1, 2, ..., m dengan m > n maka diperoleh bahwa X adalah bergantung linear. Kontradiksi dengan fakta bahwa X bebas linear. Jadi haruslah m = n. Maka untuk setiap j, λj adalah nilai eigen dari L(ε) dan xj adalah vektor eigen yang dimiliki oleh λj. Maka berlaku
L(ε)xj = λjxj dan
L(ε)X = (L(ε)x1, L(ε)x2, ..., L(ε)xn) = (λ1x1, λ2x2, ..., λnxn)
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
n n x x x λ λ λ 2 1 2 1, ,..., )(
linear, maka L(ε) mempunyai n vektor eigen yang bebas linear. (Terbukti)
Teorema 9
Jika λ1, ..., λn adalah nilai eigen dari L maka
λ1 + ε, ..., λn + ε adalah nilai eigen dari L(ε).
BUKTI :
(
⇒
) Misalkan λ1, ..., λn adalah nilai eigen dariL yang bersesuaian dengan vektor eigen ortonormal x1, ..., xn. Karena λ1, ..., λn adalah n nilai eigen yang berbeda dari L dan L
mempunyai n vektor eigen berbeda yang saling bebas linear. Maka terdapat matriks pendiagonal X dengan X = (x1, ..., xn) dan suatu matriks diagonal D. Matriks pendiagonal X adalah matriks taksingular dengan vektor-vektor kolom dari X merupakan n vektor eigen berbeda yang saling bebas linear. X dapat mendiagonalisasi L sehingga berlaku X-1
LX = D. Karena L(ε) juga mempunyai n vektor eigen ortonormal yang sama dengan milik L, maka X juga dapat mendiagonalisasi L(ε) = L
+ εI akan berlaku juga
X-1L(ε)X = D(ε) ↔
X-1L(ε)X = X-1(L(ε)x1, L(ε)x2, ..., L(ε)xn). Karena X
![Gambar 9. Jaringan resistor dua dimensi dengan kondisi batas bebas dengan asumsi di setiap arc-->g=make_graph('duper',1,36,[1 1 1 2 2 3 3 4 4 5 5 5 6 6 7 7 8 8 9 9 10 11 12 13 13 14 14 15 16 17 17 18 18 19 19 20 20 21 22 23 23 24 24 25 25 26 26 27 27 28 29 29 30 30 31 31 32 33 34 35],[2 5 13 3 6 4 7 8 18 6 9 14 7 10 8 11 12 17 10 15 11 12 16 14 19 15 20 21 22 16 23 17 24 20 33 21 29 25 28 22 32 (sisi berarah) terdapat resistor sebesar r ohm 23 36 26 29 27 30 28 31 32 30 33 31 34 32 35 36 34 35 36]);](https://thumb-ap.123doks.com/thumbv2/123dok/557181.339240/41.612.106.504.180.480/gambar-jaringan-resistor-dimensi-berarah-terdapat-resistor-sebesar.webp)
![Gambar 10. Jaringan resistor dua dimensi dengan kondisi batas silindrik dengan asumsi di setiap arc� (sisi berarah) terdapat resistor sebesar r ohm g=make_graph('hotel',1,5,[1 2 2 2 3 4 4 5],[2 3 4 5 1 1 3 1]);](https://thumb-ap.123doks.com/thumbv2/123dok/557181.339240/42.612.103.503.64.359/gambar-jaringan-resistor-silindrik-berarah-terdapat-resistor-sebesar.webp)
![Gambar 14. Jaringan resistor di hotel ruangan III dengan asumsi di setiap -->g=make_graph('empat',1,15,[1 2 2 2 3 4 5 5 5 6 7 8 8 8 9 10 11 11 11 12 13 15],[4 1 3 5 6 7 4 6 8 9 10 7 9 11 12 13 10 12 14 15 14 14]); arc (sisi berarah) terdapat resistor sebesar r = 20 ohm](https://thumb-ap.123doks.com/thumbv2/123dok/557181.339240/46.612.139.467.80.345/gambar-jaringan-resistor-ruangan-berarah-terdapat-resistor-sebesar.webp)