Analisis Problem Pengiriman Informasi Dengan Error Correcting Codes

ANALISIS PROBLEM PENGIRIMAN INFORMASI DENGAN ERROR CORRECTING CODES

SKRIPSI

MEIDIANA TANADI 060803005

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

ANALISIS PROBLEM PENGIRIMAN INFORMASI DENGAN ERROR CORRECTING CODES

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MEIDIANA TANADI 060803005

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2010

Judul : ANALISIS PROBLEM PENGIRIMAN INFORMASI DENGAN ERROR CORRECTING CODES

Kategori : SKRIPSI

Nama : MEIDIANA TANADI

Nomor Induk Mahasiswa : 060803005

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, 14 Juni 2010

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Prof. Dr. Drs. Iryanto, M.Si Prof. Dr. Herman

Mawengkang

NIP. 19460404 197107 1 001 NIP. 19461128 197403 1

001

Diketahui oleh

Departemen Matematika FMIPA USU

Ketua,

Dr. Saib Suwilo, M.Sc

PERNYATAAN

ANALISIS PROBLEM PENGIRIMAN INFORMASI DENGAN

ERROR CORRECTING CODES

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.

Medan, 14 Juni 2010

MEIDIANA TANADI

PENGHARGAAN

Puji dan syukur panjatkan kepada Tuhan yang Maha Penyayang, atas kemurahan dan berkat yang telah diberikan sehingga penulis dapat menyelesaikan skripsi dengan judul ”Analisis Problem Pengiriman Informasi dengan Error Correcting Codes” guna melengkapi syarat memperoleh gelar sarjana Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam di Universitas Sumatera Utara.

Pada kesempatan ini, penulis menyampaikan terima kasih yang sedalam – dalamnya kepada :

1. Bapak Prof. Dr. Eddy Marlianto, M.Sc selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

2. Bapak Dr. Saib Suwilo, M.Sc, Bapak Drs. Henry Rani Sitepu, M.Sc selaku Ketua dan sekretaris Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

3. Bapak Prof. Dr. Herman Mawengkang selaku Dosen Pembimbing I dan Bapak Prof. Dr. Drs. Iryanto selaku Dosen Pembimbing II yang telah membimbing, mengarahkan dan meluangkan waktunya untuk penulis dalam menyelesaikan skripsi.

4. Seluruh Staf Pengajar dan Pegawai Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

5. Kedua orang tua serta kedua abang penulis yang telah memberikan doa, bimbingan dan dorongan serta bantuan baik material maupun nonmaterial kepada penulis sehingga selesainya skripsi ini.

6. Senior matematika Hindra, Darwin, Alice, Josephine dan teman – teman ’06 terutama Erwin serta teman dekat penulis,Rudy, yang senantiasa memberikan doa dan semangat kepada penulis untuk menyelesaikan skripsi ini.

ABSTRAK

Suatu kelas yang penting dari multiple – error – correcting codes adalah kelas Bose – Chaudhuri – Hocquengham codes, atau BCH codes. BCH codes adalah family dari cyclic codes dan oleh karena itu dapat didecode dengan teknik untuk decoding cyclic codes. Penelitian ini memberikan proses encoding dan decoding untuk BCH codes.

ANALYSIS PROBLEM SENDING INFORMATION WITH ERROR CORRECTING CODES

ABSTRACT

An important class of multiple – error – correcting codes is the class of Bose – Chaudhuri – Hocquengham codes, or BCH codes. BCH codes are a family of cyclic codes and hence can be decoded by any technique for decoding cyclic codes. This paper determine encoding and decoding procedure for general BCH codes.

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv

ABSTRACT v

DAFTAR ISI vi

DAFTAR TABEL vii

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 3

1.3. Tinjauan Pustaka 3

1.4. Tujuan Penelitian 4

1.5. Manfaat Penelitian 4

1.6. Metodologi Penelitian 4

2. LANDASAN TEORI 5

2.1. Ring dan Field 5

2.2. Ring Polinomial 6

2.3. Mengubah codeword dalam bentuk codeword 14

2.4. Cyclic codes 15

2.5. Generating Matrix dan Check Matrix 16

2.6. Istilah Matrix 18

3. PEMBAHASAN 20

3.1. Deteksi dan Koreksi kesalahan 20

3.2. Proses Encoding 20

3.3. Proses Decoding 25

4. KESIMPULAN DAN PENELITIAN LANJUTAN 33

4.1. Kesimpulan 33

4.2. Penelitian Lanjutan 34

DAFTAR TABEL

Tabel

2.1 RepresentasiGF(24) 13

3.1 RepresentasiGF(25) 23

ABSTRAK

Suatu kelas yang penting dari multiple – error – correcting codes adalah kelas Bose – Chaudhuri – Hocquengham codes, atau BCH codes. BCH codes adalah family dari cyclic codes dan oleh karena itu dapat didecode dengan teknik untuk decoding cyclic codes. Penelitian ini memberikan proses encoding dan decoding untuk BCH codes.

ANALYSIS PROBLEM SENDING INFORMATION WITH ERROR CORRECTING CODES

ABSTRACT

An important class of multiple – error – correcting codes is the class of Bose – Chaudhuri – Hocquengham codes, or BCH codes. BCH codes are a family of cyclic codes and hence can be decoded by any technique for decoding cyclic codes. This paper determine encoding and decoding procedure for general BCH codes.

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Sejak permulaan komunikasi, selalu dihadapkan pada adanya gangguan pada saat pengiriman

informasi mengakibatkan isi dari informasi yang dikirim berubah. Informasi yang dikirim

berupa barisan binary digit (0 dan 1). Karena adanya gangguan dalam proses pengiriman, 1

yang dikirim kemungkinan yang diterima 0, dan 0 yang dikirim kemungkinan yang diterima

1. Akibatnya terjadi perubahan pada isi informasi yang dikirim. Atau dengan kata lain,

informasi yang dikirim akan berbeda dengan informasi yang diterima. Sehingga muncul

persoalan bagaimana cara memastikan informasi yang diterima merupakan informasi yang

dikirimkan.

Untuk memecahkan persoalan ini diperlukan suatu metode yang mampu mengetahui

adanya kesalahan sekaligus memperbaikinya ketika terjadi gangguan dalam proses

pengiriman. Salah satu cabang ilmu dalam bidang matematika yang dapat menganalisis

permasalahan ini adalah teorierror correcting codes.

Error correcting codes merupakan studi tentang metode – metode pengiriman informasi secara efisien dan tepat dari satu tempat ke tempat lain. Error correcting codes

pertama kali ditemukan oleh Claude Shannon [4]. Error correcting codes selain digunakan dalam penyimpanan data computer, juga digunakan dalam pengiriman informasi [5]. Suatu

kelas penting dari multiple - error correcting codes adalah kelas Bose – Chaudhuri – Hocquengham codes, atau BCH codes. BCH codesmampu memperbaiki banyak kesalahan.

Informasi yang dikirim berupa barisan binary digit 0 dan 1 disebut information digit. Panjang dari suatu informasi n, adalah jumlah digit yang terdapat pada informasi. Distance

dari dua information digit adalah jumlah posisi digit yang berbeda dari duainformation digit. Suatu binary code adalah himpunan dari information digit. Suatu block code adalah kode yang memiliki semua information digit dengan panjang yang sama; besarnya panjang ini disebut juga panjang dari kode. Istilah kode berartibinary block code.Information digityang merupakan elemen dari kode disebut codeword. BCH codes menggunakan teori field dan polynomial atas finite field(field berhingga). MisalkanF adalahGF(q), finite field dengan q

elemen. Suatu binary code adalah kode atas GF(2). Suatu (n,k) code atas GF(q) adalah k-dimensional subcpace dariFn, space dari semuan-tuples dengan komponen dariF = GF(q). Jelas suatu (n,k) binary code memiliki 2k vector atau codeword didalamnya. Jumlah dari komponen tidak nol dari suatu vector disebut weight dari suatu kode, yang dinotasikan dengan d, adalah weight dari vector tak nol dengan weight terkecil dalam kode. Suatu (n,k) code denganminimum weight ddisebut suatu (n,k,d) code [6]

Suatu kode yang “baik” adalah kode yang pada dasarnya dapat memperbaiki banyak

kesalahan [6]. Untuk mendeteksi adanya kesalahan, semuaerror correcting codesmemiliki prinsip yang sama yaitu menambahkan digit tambahan padainformation digituntuk

memperoleh suatu barisan kode ataucodewordyang disebut denganproses encoding.

Dengan kata lain,information digitselalu muncul dalamkposisi dari suatucodeword. Sisan – kdigit dalamcodewordmerupakan digit tambahan.Codewordini membentuk suatu kode. Berarti suatu kode merupakan himpunan daricodeword – codeword. Dengan adanya digit tambahan ini, kesalahan yang terjadi dalam proses pengiriman dapat dideteksi dan dikoreksi.

Ini disebut denganproses decoding. Jadi, suatu system komunikasi meliputi tiga langkah :

1. Encoding information digit ke dalam codeword,

2. mengirim codeword,

3. decoding codeword.

1.2 Perumusan Masalah

Masalah yang akan diangkat penulis adalah bagaimana kode BCH menyelesaikan

persoalan dalam proses pengiriman informasi yang sering terjadi kesalahan dengan proses

encoding dan decoding sehingga informasi yang sebenarnya dikirim dapat diketahui.

1.3 Tinjauan Pustaka

Blahut [1] menyatakan, andaikan bahwa semua informasi dapat ditunjukkan sebagai

informasi biner; yaitu sebagai barisan digit nol dan satu. Informasi biner ini dikirimkan

melalui suatu channel (saluran) yang kadang – kadang menyebabkan kesalahan. Tujuan dari kode adalah menambahkan digit tambahan ke information digit sehingga kesalahan dapat ditemukan dan diperbaiki pada penerima. Yaitu, barisan digit yang ditunjukkan dengan

barisan digit yang lebih panjang dengan redundancy (kelebihan) yang cukup untuk melindungi informasi. Suatu kode biner berukuran M danblocklenght n adalah himpunanM information digit yang panjangnya n yang disebut codeword. Oleh karena M = 2k untuk bilangan bulatk, dan kode ditunjukkan sebagai suatu (n,k)binary code.

Pless [6] menyatakan, secara umum, misalkan F adalah GF(q), finite field dengan q

elemen. Maka q adalah pangkat dari suatu bilangan prima. Jika q adalah bilangan prima p, katakan q = 2 atau 3, maka F dapat dikatakan sebagai himpunan p elemen 0, 1, …, p – 1 dengan operasi aritmatika dengan mod p. Suatu binary code adalah kode atas GF(2). Suatu (n,k) code atas GF(q) adalah k-dimensional subspace Fn, space dari semua n-tuples dengan komponen – komponen dari F= GF(q). Jelas suatu (n,k) binary codememiliki 2k codeword didalamnya. Suatu (n,k) code denganminimum distance ddisebut dengan suatu (n,k,d) code.

Hankerson [4] menyatakan, jika informasi yang diterima bukanlah suatu codeword, dengan jelas kesalahan telah terjadi selama proses pengiriman. Namun jika informasi yang

diterima suatu codeword, maka tidak ada kesalahan yang terjadi selama pengiriman, jadi tidak akan ditemukan kesalahan.

Durbin [2] menyatakan, encoding merupakan proses penambahan digit tambahan ke

decoding) akan menerima codeword ini setelah ditentukan kemungkinan perubahan pada informasi dalam proses pengiriman.Decoderharus membuat keputusan seperti apa informasi yang dikirimkan didasarkan pada informasi yang diterima.

1.4 Tujuan Penelitian

Tujuan yang ingin dicapai penulis adalah mengetahui bagaimana proses encoding dan

decoding dari kode BCH sehingga informasi yang sebenarnya dapat diketahui ketika terjadi kesalahan dalam proses pengiriman.

1.5 Manfaat Penelitian

Penelitian ini dapat dimanfaatkan untuk mengatasi permasalahan dalam bidang komunikasi,

dan hasil penelitian ini juga dapat diaplikasikan untuk melindungi data dalam memori

komputer.

1.6 Metodologi Penelitian

Metodologi penelitian ini bersifat literatur atau kepustakaan dengan langkah – langkah

sebagai berikut :

1. Melakukan studi dari beberapa buku di perpustakaan

2. Memaparkan beberapa definisi, akibat dan teorema yang mendukung dalam

memperoleh hasil utama penelitian ini

3. Memaparkan proses encoding dan decoding dari BCH codes dengan tahapan sebagai berikut :

a. Memaparkan proses encoding, yaitu dengan menentukan generator polynomial g(x) dari (n,k,d)BCH codes.

BAB 2

LANDASAN TEORI

Pada bab ini akan dijelaskan mengenai teori – teori yang berhubungan dengan penelitian

sehingga dapat dijadikan sebagai landasan berfikir dalam melakukan penelitian dan akan

mempermudah dalam hal pembahasan hasil utama pada bab berikutnya. Adapun teori – teori

tersebut mencakup pengertian dari ring, field, polynomial, generating matrix, dan check

matrix.

2.1 Ring dan Field

Pada bagian ini akan diberikan beberapa definisi dan teorema dasar tentang field dan ring.

Definisi 2.1 :

Suatu ring adalah suatu himpunan tak kosong R dengan dua operasi biner yang dinotasikan dengan operasi “penjumlahan” dan “perkalian” sehingga memenuhi aksioma – aksioma

1. untuk semua , berlaku

2. untuk semua , berlaku

3. R mempunyai unsur identitas relatif terhadap operasi penjumlahan, yakni terdapat

suatu unsur sehingga untuk semua

4. untuk setiap , terdapat sehingga

5. untuk semua , berlaku

6. untuk semua , dipenuhi, a)

b)

Dari definisi 2.1 juga dapat dikatakan bahwa suatu himpunan tak kosong R dengan operasi biner “+” dan “ ” dikatakan suatu ring bila

1. adalah suatu grup komutatif 2. adalah suatu semigrup

3. operasi perkalian adalah distributif terhadap penjumlahan, yakni untuk semua

Jika operasi perkalian dari R adalah komutatif, maka R disebut sebagai ring komutatif. Jika terdapat suatu unsur yang dinotasikan dengan 1 sedemikian hingga untuk

semua , maka R disebut sebagai ring dengan unsur kesatuan, dan unsur 1 disebut

sebagai unsur kesatuan. Selanjutnya apabila memungkinkan penulisan notasi cukup

dituliskan saja.

Definisi 2.2 :

Suatu ring komutatif F dengan unsur kesatuan disebut sebagai field bilamana setiap unsur tak nol adalah unsur satuan.

Definisi di atas juga dapat dinyatakan sebagai berikut. Suatu field F adalah suatu struktur aljabar dengan dua operasi biner “+” dan “ ” sehingga

1. adalah suatu grup komutatif 2. adalah suatu semigrup

3. operasi perkalian adalah distributif terhadap penjumlahan, yakni untuk semua

dan

2.2 Ring Polinomial

AndaikanRadalah suatu ring komutatif. Himpunan

R[x] = {a0+a1x+a2x2+ … +anxn;ai Rdann Z+}

disebut sebagai ring polynomial atasRdalam indeterminatex.

Pada definisi di atas, symbol x, x2, …, xn tidak menyatakan suatu variabel yang berasal dari ringR, tetapi symbol – symbol tersebut semata – mata hanyalah sebagai suatu tempat penyimpanan yang pada suatu saat mungkin saja digantikan dengan unsur R. Dua unsur diR[x]

Selanjutnya perhatikan suatu polynomial

a(x) =a0+a1x+a2x2+ … +anxn

di R[x]. Pada polynomial ini, bentuk akxk disebut sebagai suku dari polynomial a(x) dan

untuk setiap suku akxk, k = 0,1,…,n, ak disebut sebagai koefisien dari xk. Derajat dari suatu

polynomial a(x) adalah bilangan bulat positif terbesar n sehingga an 0. Dengan kata lain

suatu polynomiala(x) = a0 +a1x+a2x2+ … + anxndikatakan berderajat s, jikaas 0 danan

0 untuk semuak>s. Derajat daria(x) ditunjukkan dengan deg(a), atau deg[a(x)]. Deg(a) = 0 jika dan hanya jika a(x) adalah polynomial konstan (constant polynomial) yang tak nol, yaitu, jika dan hanya jika a(x) adalah polynomial ao, untuk tak nol a0 R. Bila a(x) adalah

polynomial berderajats, maka koefisienasdisebut sebagaikoefisien utama(leading coefisien)

dari a(x). Polinomial a(x) dikatakan sebagai polynomial monic jika koefisien utamanya adalah 1. Himpunan semua polynomial atasRditunjukkan denganR[x].

Selanjutnya akan dilakukan abstraksi dari konsep pembagian polynomial, yakni

konsep pembagian pada polynomial atas suatu field F. Teorema berikut ini memperlihatkan secara umum bahwa dapat dilakukan pembagian polynomial atas sebarang fieldF.

Teorema 2.1 :

Andaikan F adalah suatu field. Bila f(x), g(x) F[x] dengan g(x) 0, maka terdapat polynomial q(x)dan r(x)di F[x]yang tunggal sehingga f(x) =g(x)q(x) +r(x)dengan r(x) = 0

atau derajat r(x)lebih kecil dari derajat g(x). Bukti :

Dengan menggunakan induksi pada derajat polynomial f(x) akan diperlihatkan keberadaan polynomialq(x) danr(x). Jikaf(x) = 0 atau derajatf(x) lebih kecil dari derajatg(x), makaq(x) dan r(x) diperoleh r(x) = f(x) dan q(x) = 0. Selanjutnya, andaikan f(x) berderajat n dan g(x) berderajatmdengann>m. Misalkan

f(x) =a0+a1x+a2x2+ … +anxn

Dengan menggunakan teknik pembagian seperti di atas, misalkan

h(x)= f(x) –anb-1mxn-mg(x)

Sehinggah(x) = 0 atau derajath(x) lebih kecil dari derajatf(x). Dengan menggunakan asumsi pada induksi, untuk polynomial h(x) terdapat polynomial q1(x) dan r1(x) sehingga h(x) = g(x)q1(x) +r1(x) denganr1(x) = 0 atau derajatr1(x) lebih kecil dari derajatg(x).

Hal ini berakibat f(x) =anbm-1xn-mg(x) +h(x)

=anbm-1xn-mg(x) +g(x)q1(x) +r1(x)

=g(x) [anbm-1xn-m+q1(x)] +r1(x)

Dengan mengambilq(x) =anbm-1xn-m+q1(x) danr(x) =r1(x), diperoleh f(x) =g(x)q(x) +r(x)

Denganr(x) = 0 atau derajatr(x) lebih kecil dari derajatg(x).

Selanjutnya akan diperlihatkan ekspresi f(x) = g(x) q(x) + r(x) adalah tunggal. Misalkanf(x) juga dapat ditulis sebagaif(x) =g(x)s(x) +t(x) dengant(x) = 0 atau derajatt(x) lebih kecil dari derajatg(x). Perlihatkan bahwa

g(x)q(x) +r(x) =g(x)s(x) +t(x) Sehingga

g(x) [q(x) –s(x)] =t(x) –r(x)

Karena derajat t(x) – r(x) lebih kecil dari derajat g(x), maka haruslah q(x) – s(x) = 0. Yakni,

q(x) =s(x) dan tentunyar(x) =t(x).

Polinomial q(x) disebut quotient dan r(x) disebut remainder (sisa) dalam pembagian

Akibat langsung dari teorema di atas diperoleh hasil sebagai berikut.

Akibat 2.1 :

Andaikan F adalah suatu field. Bila a F dan f(x) F[x], maka f(a) adalah sisa hasil bagi dari f(x)oleh(x– a).

Bukti :

Menurut teorema 2.1 untuk polynomial f(x) dan (x– a) terdapat polynomial q(x), r(x) F[x] sehinggaf(x) = (x– a)q(x) +r(x) dengan derajatr(x) lebih kecil dari derajat (x– a). Akibatnya

r(x) adalah suatu konstanta yang berada di F, sehingga f(x) = (x– a) q(x) + r. Karena f(x)

F[x], untukx Fkita dapat memandang fsebagai suatu pemetaan f:F F. Sehinggaf(x) = (a– a)q(a) +r, yakni sisa hasil bagir=f(a).

Akibat 2.2 :

Andaikan F adalah suatu field, dan misalkan a F dan f(x) F[x]. Unsur a adalah pembuat nol dari f(x)jika dan hanya jika(x – a)adalah faktor dari f(x).

Bukti :

Dengan menggunakan algoritma pembagian, maka polynomial f(x) dapat ditulis sebagai

f(x) = (x– a)q(x) +r(x)

denganr(x) = 0 atau derajat dari r(x) adalah 0. Bilaapembuat nol darif(x) maka

f(a) = 0 = (a– a)q(x) +r,

yang berakibatr= 0. Jadi (x–a) adalah faktor darif(x).

Sebaliknya jika (x – a) adalah faktor darif(x), maka terdapat polynomial q(x) F[x] sehingga f(x) = (x– a) q(x). Hal ini berakibat f(a) = (a– a) q(a) = 0q(a) = 0. Jadi a adalah pembuat nol darif(x).

Akibat 2.3 :

Bukti :

Andaikanf(x) adalah suatu polynomial berderajatndiF[x]. Akan diperlihatkan pernyataan di atas dengan menggunakan induksi pada derajat darif(x).

Andaikan f(x) adalah polynomial berderajatn= 1. Misalkanf(x) =ax+b, dengana,b Fdana 0. Akibatnyaab-1adalah akar darif(x). Sekarang andaikanf(x) berderajat n > 1. Andaikan adalah pembuat nol darif(x). Menurut akibat 2.1,f(x) dapat ditulis sebagaif(x) = (x– a) g(x) dengang(x) adalah polynomial berderajat n – 1. Jika adalah akar dari f(x), maka

0 =f( ) = ( – )g( ).

Karena – , maka g( ) = 0. Yakni adalah pembuat nol dari g( ). Tetapi menurut hipotesis induksig( ) mempunyai banyakn– 1 akar. Sehinggafmempunyai paling banyakn

akar.

Definisi 2.3 :

Andaikan f(x) = a0 + a1x + a2x2 + … + anxn adalah suatu polynomial di Z[x]. Isi dari f(x)

didefinisikan sebagai pembagi persekutuan terbesar dari a(x) = a0 , a1 , …, an. Suatu

polynomial f(x) Z[x]dikatakan primitip jika isi dari f(x)adalah1.

Contoh 2.2.1 :

Isi dari polynomialf(x) = 6 + 4x+ 10x2+ 18x6adalah 2, karena pembagi persekutuan terbesar dari 6, 4, 10 dan 18 adalah 2. Sementara isi dari polynomial g(x) = 3x + 9x3+ 4x5 adalah 1. Sehinggag(x) adalah primitip.

Definisi 2.4 :

Selanjutnya, a(x) kongruens ke b(x) modulo f(x), ditunjukkan dengan a(x) b(x) (modulo ), jika dan hanya jika terdapatc(x) dengana(x) =c(x)f(x) +b(x). Untuk setiap polynomial monik f(x) dengan derajat tak nol, misalkan F(x) / yang menunjukkan himpunan kelas – kelas kongruens dari polynomial di F[x] modulo f(x). Ini disebut ring polynomial modulo f(x). Ini adalah suatu ring yang terdiri dari semua polynomial dengan derajat yang lebih kecil dari derajatf(x).

Teorema 2.2 :

F(x)/ adalah field jika dan hanya jika f(x)irreducible. Bukti :

Misalkan I merupakan principal ideal f(x). Andaikan f(x) reducible atas F, katakan f(x) =

a(x)b(x) dengan a(x) dan b(x) keduanya berderajat lebih rendah dari p(x). F[x]/I bukan suatu field. Derajat polynomial tak nol diIharus paling sedikit sebesar degf(x), jadia(x) Idanb(x)

I. Oleh karena ituI+a(x) danI+b(x) keduanya elemen tak nolF[x]/I. Tetapi (I+a(x))(I+b(x)) =I+a(x)b(x) =I+f(x) =I,

elemen nol dariF[x]/I. Disimpulkan,F[x]/Imemiliki pembagi nol sehinggaF[x]/Ibukan field (bukan juga daerah integral). Ini membuktikan bahwaF[x]/Isuatu field, makaf(x) irreducible.

Andaikan f(x) irreducible. F[x]/I komutatif dan I + e adalah unsur kesatuan untuk

F[x]/I (dengan e unsure kesatuan dari F). Jadi ini mencukupi untuk membuktikan setiap elemen tak nol dari F[x]/I memiliki perkalian inverse diF[x]/I. AmbilI+F[x] tak nol. Maka

Definisi 2.5 :

Suatu elemen primitip dari field GF(q)adalah elemen sehingga setiap elemen field kecuali nol dapat ditulis sebagai pangkat dari .

Contoh 2.2.2 :

FieldGF(5)

21= 2, 22= 4, 23= 3, 24= 1

Dan dengan demikian 2 adalah elemen primitip dariGF(5).

Jadi, adalah elemen primitip dari F jika setiap elemen tak nol di F adalah pangkat dari . Suatu elemen primitip di field dengan q elemen memiliki order q – 1. Tidak selalu akar dari polynomial irreducible adalah elemen primitip. Suatu polynomial irreducible yang

memiliki elemen primitip sebagai akar disebutpolynomial primitip.

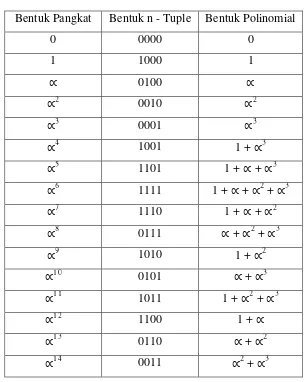
Tabel 2.1 Representasi GF (24)

Bentuk Pangkat Bentuk n - Tuple Bentuk Polinomial

0 0000 0

1 1000 1

0100

2

0010 2

3

0001 3

4

1001 1 + 3

5

1101 1 + + 3

6

1111 1 + + 2+ 3

7

1110 1 + + 2

8

0111 + 2+ 3

9

1010 1 + 2

10

0101 + 3

11

1011 1 + 2+ 3

12

1100 1 +

13

0110 + 2

14

0011 2+ 3

Dengan menentukan setiap pangkat dari , mempermudah menentukan invers dari

suatu elemen dan mengalikan dua elemen. Contoh, invers dari 3 + 1. Karena 3 + 1 = 4 dan 4 11= 15= 1 sehingga ( 3+ 1)–1= 11= 3+ 2+ 1.

Teorema 2.3 :

Misalkan m(x)adalah minimal polynomial dengan elemen di finite field GF(pr). Maka yang fakta – fakta berikut diperoleh :

1. m(x)irreducible.

2. Jika adalah akar dari polynomial f(x) dengan koefisien – koefisien di GF(p), maka m(x)membagi f(x).

3. m(x)membagi

r

p x =x.

4. Jika m(x)adalah primitip,maka derajatnya adalah r.Dalam suatu kasus derajat m(x)

[image:24.595.144.449.92.474.2]

Bukti :

1. Jikam(x) irreducible, makam(x) =a(x)b(x) danm( ) = 0, salah satunyaa(x) ataub(x) adalah 0 menyangkal fakta bahwa m(x) adalah polynomial dengan derajat terkecil dengan sebagai akar.

2. Dengan algoritma pembagian, f(x) = a(x)m(x) + r(x) dengan derajat r(x) lebih kecil dari derajatm(x). Karenaf( ) =m( ) = 0,r( ) = 0 dan karena derajatr(x) lebih kecil dari derajatm(x),r(x) sama dengan 0.

3. Ini mengikuti dari (2) karena suatu elemen di GF(pr) adalah akar dari persamaan

r

p x

=x.

4. Karena di GF(pr) dan GF(pr) adalah r – dimensional vector space atas GF(p), himpunan 1, , …, r adalah linierly independent dan juga memenuhi persamaan

derajat lebih kecil dari atau sama dengan r. Jika m(x) adalah primitip membangkitkan semuaGF(pr) dan jugam(x) memiliki derajatr.

Jikaf(x) adalah polynomial berderajatm,reciprocal polynomialdarif(x) didefinisikan menjadixmf(x-1). Jika f(x) = anxn+ an-1xn-1+…+ a0,reciprocal polynomialnya sama dengan

a0xn+ a1xn-1+…+ an.

2.3 Mengubah Codeword dalam Bentuk Polinomial

Information digit yang berupa barisan digit 0 dan 1 merupakan elemen dari kode yang disebut

codeword. Misalkan, suatu kode yang terdiri dari semua codeword dengan panjang dua

adalah

C = {00, 01, 10, 11}

Suatu codeword v = a0a1a2…an-1 dengan panjang n dapat diubah dalam bentuk

polynomial f(x) = a0 + a1x + a2x2 + … + an-1xn-1 berderajat n.Contoh, codeword dengan

panjang 7;v= 1000111 diubah dalam polynomial

f(x)= 1 + x4+ x5+ x6.

2.4 Cyclic Codes

Cyclic codes adalah kelas yang penting dari kode. Salah satu alasannya adalah dapat

diencode secara efisien dengan memakai shift register. Begitu juga dengan pola decoding

yang memakai shift register. Polinomialv(x) = a0+ a1x + a2x2+ … + an-1xn-1dapat dianggap

sebagai codewordv = a0a1a2…an-1.

Suatu (n,k) code C disebut cyclic jika x = (a0,a1,a2,… ,an-1) di C, begitu juga cyclic

shift pertamanya y = (an-1,a0,a1,…, an-2). Ini berarti (an-2,an-1,a0,…, an-3), cyclic shift dari y

yang pertama, dan semuacyclic shift yang lain darixjuga diC.

Misalkan suatu vector (a0,a1,a2,… ,an-1) dapat disamakan dengan polynomiala0+ a1x

+ a2x2 + … + an-1xn-1. Maka (an-1,a0,a1,…, an-2) dapat disamakan dengan an-1 + a0x + a1x2

+ … + an-2xn-1. Jadi polynomial ini sama dengan polynomial

(a0+ a1x + a2x2+ … + an-1xn-1)x(modulo ).

Misalkan v adalah codeword dengan panjang n. Cyclic shift dari v adalah codeword dengan panjang n yang diperoleh dari v dengan mengambil digit terakhir dari v dan memindahkan nya menjadi digit paling awal, semua digit yang lain berpindah satu posisi ke kanan. Suatu

kode dikatakan cyclic code jika cyclic shiftdari setiapcodeword juga merupakancodeword. Untuk cyclic code, elemen dari kode bisa dikatakan sebagai codeword dan polynomial. Diberikan suatu codeword vdengan panjang n, misalkan codeword dapat disamakan dengan polynomial v(x), maka cyclic shift dari v dapat disamakan dengan polynomial xiv(x) (mod

) untuki= 0, 1, …,n– 1.

Cyclic codes didasarkan pada Rn = F[x]/ , yang terdiri dari kelas – kelas

kongruens dari polynomial – polynomial berderajat lebih kecil dari n di F[x] tetapi perkaliannya adalah modulo (xn– 1). Secara eksplisit, jika terdapat dua polynomial a(x) dan

b(x), hasil kalinya di F[x] adalah a(x)b(x) =c(x(xn – 1) +r(x) dengan derajat r(x) lebih kecil dari derajatxn– 1 dengan algoritma pembagian. Jadir(x) dianggap sebagai hasil kali daria(x) dan b(x) dengan Rn adalah himpunan semua polynomial di F[x] berderajat yang lebih kecil

dari n dengan perkalian modulo (xn– 1).

Misalkan , …, r adalah elemen di field F = GF(qm) dan misalkan f1(x), …, fr(x)

dari semua polynomialh(x) di F[x]/ sehinggah( i) = 0, i = 1, …,r. MakaCadalah

cyclic codes dengan generator polynomial g(x) = lcm(f1(x), …, fr(x)). Jelas bahwa cyclic

codes C dapat ditentukan dengan cara ini karena f1(x) dapat diambil sebagai factor yang

irreducibledarigenerator polynomialdariCdan iadalah akar darif1(x).

2.5 Generating Matrix dan Check Matrix

Suatu ideal I di Rn = F[x]/ disebut principal ideal jika setiap elemen di I adalah

perkalian dari polynomial g(x) tertentu. Jika I adalah principal, maka I = {c(x)g(x); c(x) di

Rn}. Ditunjukkan denganI= . Suatu ring disebutprincipal ideal ring(PIR) jika setiap

ideal adalah principal.

Teorema 2.4 :

Jika C adalah ideal (yaitu suatu cyclic code dengan panjang n) di Rn, misalkan g(x) adalah

polynomial monik dengan derajat terkecil di C.Maka g(x)tunggal dan C= . Bukti :

Akan ditunjukkan bahwa Rn adalah suatu P.I.R dan monic generator dengan derajat terkecil

dari ideal adalah tunggal sekalipun ideal dapat memiliki generator lain.

Pertama ditunjukkan Rn adalah PIR. Misalkan g(x) adalah polynomial monik dengan

derajat terkecil diCdan misalkana(x) polynomial lain diC. Dengan algoritma pembagian di

F[x], a(x). Dengan definisi ideal r(x) di C. Tetapi ini menyangkal pilihan g(x) kecuali kalau

r(x) sama dengan nol sehinggaa(x) =g(x)b(x). Oleh karena ituRnadalah PIR.

Jika g(x) dan h(x) adalah polynomial monik dengan derajat yang sama dan keduanya diC, makag(x) –h(x) adalah polynomial diCdengan derajat yang lebih rendah darig(x) atau

Teorema berikut memberitahukan bagaimana menemukan generator daricyclic code. Teorema 2.5 :

Jika C adalah suatu ideal, monic generator tunggal, g(x), dari C dengan derajat terkecil yang membagi xn – 1 dan sebaliknya jika polynomial g(x) di C membagi xn – 1, maka g(x)

memiliki derajat terrendah di . Bukti :

Pertama andaikan bahwag(x) adalah polynomial monik dengan derajat terkecil diC. Dengan algoritma pembagian di F[x], xn – 1 = a(x)g(x) + r(x) dengan derajat r(x) lebih kecil dari derajatg(x). r(x) = – a(x)g(x) modulo (xn – 1) dan jadi r(x) di . Ini kontradiksi kecuali kalaur(x) sama dengan nol. Jadig(x) membagixn– 1.

Sebaliknya, andaikan g(x) membagi xn – 1 dan b(x) di tetapi memiliki derajat yang lebih rendah dari g(x). Maka b(x) = c(x)g(x) + (xn – 1)d(x) di F[x] karena b(x) di C. Bagaimanapun, karenag(x) membagixn– 1,g(x) membagib(x), ini kontradiksi.

Polinomial monik g(x) dengan derajat terkecil diCdisebut generator polynomial dari

C. Dengan teorema sebelumnya diketahuiC= dang(x) membagixn– 1.

Teorema 2.6 :

Jika derajat g(x)adalah n – k, maka dimensi dari C = adalah k. Jika g(x)= g0+ g1x

+ g2x2+ … + gn-kxn-k,maka generator matrix dari C sebagai berikut.

k n-1 0 k n-1 -k n-0 k n-1 0

g

0

0

0

...

...

...

...

g

0

0

g

g

0

...

0

0

...

0

0

g

...

g

0

g

...

g

g

Bukti :

Vektor – vektor g(x), g(x)x,g(x)x2, …, g(x)xk-1 adalah linierly independent jika tidak maka terdapat elemen – elemen fieldai, 0 i k– 1, sehingga

Tetapi hasil kali ini memiliki derajat lebih kecil darin jadi ini tidak dapat menjadi 0 modulo (xn – 1) kecuali kalau setiap ai adalah 0. Untuk melihat bahwa vektor – vektor ini span C,

catatan bahwa s(x) di C dapat diekspresikan sebagai c(x)g(x) dengan derajat c(x) lebih kecil dari atau sama dengank– 1. Karena itu

c(x)g(x) = (c0+ c1x + c2x2+ … + ck-1xk-1)g(x)

=c0gx+ c1gxx + … + ck-1gxxk-1

Dari sini bahwa generator matrix dari C adalah matrix yang baris pertamanya adalah

g(x), baris keduanyag(x)x, baris ketigag(x)x2, …, hinggag(x)xk-1.

Andaikang(x) adalah generator polynomial dari cyclic codeC. Diketahui bahwa g(x) membagi g(x) membagi xn – 1 sehingga xn – 1 = g(x)h(x). Jika g(x) memiliki derajat h(x) membagi xn – 1, ini adalah generator polynomial dari cyclic code C’ dengan dimensin – k.

! _{memiliki dimensi n – k dan ini tentu sesuai jika h(x) generator polynomial dari} !_. g(x)h(x) = 0 diRn tetapi ini tidak mengikuti dari ini bahwa inner product dari dua vectorg(x) dan h(x) adalah 0. Pada kenyataannya tidak benar pada umumnya bahwah(x) generator dari

!_.

Jikaxn– 1 = g(x)h(x), dang(x) adalahgenerator polynomialdaricyclic code C, maka

h(x) disebutcheck polynomialdariC.

2.6 Istilah Matrix

Misalkan diberikan matriks

=

d

b

c

a

A

maka berlaku aturan berikut.

• Transpose

=

=

=

d

c

b

a

A

A

A

'

T

• Determinan matriks

ad

bc

d

b

c

a

A

A

=

=

=

−

• Invers matriks

−

−

=

=

=

−

a

b

c

d

A

A

adj

A

A

A

1

1

.

1

• Matriks identitas

=

1

0

0

1

I

• Determinan matriks berukuran

3

×

3

.

=

i

h

g

f

e

d

c

b

a

A

_{, maka (aei bfg cdh) (bdi afh ceg)}

f g i h g

e d f e d

b a c b a

BAB 3 PEMBAHASAN

Pada bab ini akan diperlihatkan hasil utama dari penelitian ini. Hasil utama yang diperoleh

berdasarkan penjelasan – penjelesan yang telah dipaparkan pada bab – bab sebelumnya. Hasil

utama dari tulisan ini yaitu proses encoding dan proses decoding.

3.1 Deteksi dan Koreksi kesalahan

Dalam pengiriman suatu informasi dari sumber melalui saluran pengirim menuju ke tujuan,

sering terjadi gangguan yang dapat mengakibatkan informasi yang diterima di tujuan tidak

sama dengan informasi yang dikirim. Oleh karena itu diperlukan pendeteksian kesalahan

pada informasi, yang kemudian kesalahan yang telah terdeteksi akan dikoreksi sehingga

informasi yang diterima sama seperti informasi yang dikirim.

Error correcting codes merupakan studi tentang metode – metode pengiriman informasi secara efisien. Semua error correcting codes didasarkan pada prinsip dasar yang sama yaitu menambahkan redundant digit (digit tambahan) ke information digit, agar kesalahan yang terjadi dalam proses pengiriman dapat dideteksi. Penambahan digit ini

disebut dengan proses encoding. Sedangkan mengkoreksi kesalahan yang telah terdeteksi disebutproses decoding.

Cyclic codeadalah kelas darierror correcting codes yang dapat diencode dan decode secara efisien dengan menggunakan shift – registers, yang didasarkan pada penggunaan polynomial. BCH codes ditemukan oleh R. C. Bose dan D. K. Ray – Chaudhuri dan secara

bebas oleh A. Hocquenghem.

3.2 Proses Encoding

Dimensi dari binary cyclic (n,k) code diperlihatkan oleh

k=n–deg[g(x)]

dengang(x)generator polynomial. Karena suatucyclic code Cjuga linier, himpunankvector linearly independent dapat dipilih sebagai generator matrix. Khususnya, vector – vector biner

dihubungkan dengan g(x), xg(x), …, xk-1g(x) adalah linearly independent. Vektor – vector ini dapat digunakan sebagai baris – baris dari generator matrix dari C. Dalam kasus ini non –

systematicencoding dicapai. Yaitu, information digit tidak tampak dalam posisi codeword. Contoh 3.2.1 :

Cyclic (7,4,3) code, dengan generator polynomial g(x) = 1 + x + x3_#g(1101). Generator matrix untuk kode ini adalah

=

1

0

0

0

0

1

0

0

1

0

1

0

1

0

0

0

1

1

0

0

0

1

1

0

1

0

1

1

G

Sebagai kemungkinan lain, parity sub – matrix dari generator matrix dari cyclic code

dapat dibentuk dengan vector – vector yang dihubungkan dengan polynomial – polynomial

berikut :

xn– 1 modg(x) $

xn-k+1– 1 modg(x),

xn-k– 1 modg(x) dansystematic encoding diperoleh.

Contoh 3.2.2 :

Misalkan cyclic (7,4,3) code. Makag(x) =x3+x+ 1, dan

x6(mod % ) =x2+ 1,

x4(mod % ) =x2+x,

x3(mod % ) =x+ 1.

Systematic generator matrix dari C adalah

=

1

0

1

1

1

1

1

0

0

1

1

1

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

G

Misalkan u(x) merupakan information digit yang akan diencode. Encoding

information digitdapat dilakukan dengan dua cara : 1. Non – systematic encoding

v(x) =u(x)g(x) 2. Systematic encoding

v(x) =xn-ku(x) + [xn-ku(x)(mod )]

Contoh, membentuk generator polynomial untuk BCH(31,16). Kode ini memiliki 31 digitcodeword, 15 digit tambahan, memperbaiki 3 kesalahan (t= 3), dan memilikiminimum distance antara codeword adalah 7 digit atau lebih. Oleh karena itu dibutuhkan 2t – 1 = 5

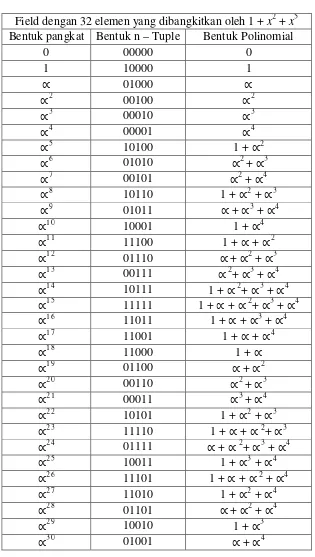
Tabel 3.1 Representasi GF(25)

Field dengan 32 elemen yang dibangkitkan oleh 1 +x2+x5

Bentuk pangkat Bentuk n – Tuple Bentuk Polinomial

0 00000 0

1 10000 1

01000

2

00100 2

3

00010 3

4 ₀₀₀₀₁ 4

5

10100 1 + 2

6 ₀₁₀₁₀ 2

+ 3

7

00101 2+ 4

8

10110 1 + 2+ 3

9 ₀₁₀₁₁

+ 3+ 4

10 ₁₀₀₀₁

1 + 4

11

11100 1 + + 2

12

01110 + 2+ 3

13

00111 2+ 3+ 4

14 ₁₀₁₁₁

1 + 2+ 3+ 4

15 ₁₁₁₁₁

1 + + 2+ 3+ 4

16

11011 1 + + 3+ 4

17 ₁₁₀₀₁

1 + + 4

18

11000 1 +

19

01100 + 2

20

00110 2+ 3

21 ₀₀₀₁₁ 3

+ 4

22

10101 1 + 2+ 3

23

11110 1 + + 2+ 3

24

01111 + 2+ 3+ 4

25

10011 1 + 3+ 4

26 ₁₁₁₀₁

1 + + 2+ 4

27

11010 1 + 2+ 4

28

01101 + 2+ 4

29

10010 1 + 3

30

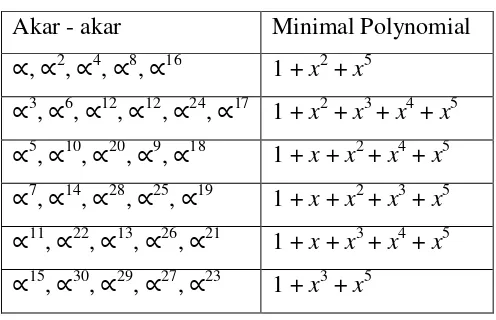
[image:34.595.156.471.94.651.2]

Berikut ini diberikan tabel minimal polynomial

Tabel 3.2 Minimal Polinomial di GF(25) Akar - akar Minimal Polynomial

, 2, 4, 8, 16 1 +x2+x5 3

, 6, 12, 12, 24, 17 1 +x2+x3+x4+x5 5

, 10, 20, 9, 18 1 +x+x2+x4+x5 7

, 14, 28, 25, 19 1 +x+x2+x3+x5 11

, 22, 13, 26, 21 1 +x+x3+x4+x5 15

, 30, 29, 27, 23 1 +x3+x5

Dari tabel minimal polynomial di atas, dapat ditentukan tiga pangkat ganjil pertama

minimal polinomialnya adalah :

:m1(x) = 1 +x2+x5 3

:m3(x) = 1 +x2+x3+x4+x5 5

:m5(x) = 1 +x+x2+x4+x5

Oleh karena itu,g(x) = lcm(m1(x),m3(x),m5(x)) =m1(x)m3(x)m5(x).

Jadi,g(x) = (1 +x2+x5)( 1 +x2+x3+x4+x5)( 1 +x+x2+x4+x5) = 1 +x+x2+x3+x5+x7

+x8+x9+x10+x11+x15.

Untuk mengencode information digit, misalkan informasi yang dipilih 1000001 dan disebut dengan f(x), ditempatkan dalam 16 – digit informasi. Selanjutnya, ditambahkan lima belas digit nol yang sama dengan derajat dari generator polynomial. Ini sama dengan mengalikan f(x) dengan x15. Kemudian dibagi dengan generator polynomial, 1111010111110001. Information digit yang telah diencode adalah 0000000000000001000001000000000. Quotient tidak digunakan. Remainder (sisa) adalah 010001000101001, ataux+ x5 +x9+x11+x14dalam bentuk polynomial, dan berderajat lebih rendah darigenerator polynomial. Jadicodewordadalah

[image:35.595.174.422.128.288.2]

Metode ini disebutsystematic encoding.

Untuk non systematic encoding, posisi dariinformation digitdan digit tambahan tidak ditentukan. Untuk memeriksa apakah terjadi kesalahan, codeword yang diterima dibagi

dengangenerator polynomial.

Remainder (sisa) adalah nol jika tidak terdapat kesalahan. Ini berarti digit tambahan (r(x)) dihitung dariinformation digit(f(x)), yaitu :

F(x)xn=q(x)g(x) +r(x)

3.3 Proses Decoding

Algoritma decoding untuk binary codes pertama kali dikembangkan oleh Peterson. Namun disini akan diberikan algoritma decoding yang dikembangkan oleh Gorenstein dan Zierler,

dan dapat memperbaikitkesalahan. Namun, yang akan dibahas hanya kode biner.

Andaikan bahwa BCH codes dibentuk berdasarkan elemen field . Polinomial

kesalahan adalah

e(x) =etxt+ et-1xt-1+ … +e1x + e0.

Andaikan r kesalahan terjadi 0 r t, dan terjadi di lokasi i1, i2, …, ir yang tak diketahui.

Polinomial kesalahan dapat ditulis

e(x) =ei1xi1+ ei2xi2+ … +eirxir,

denganei1 adalah besar dari kesalahan kel(ei1= 1 untuk binary codes). Baiki1, i2, …,irdan

ei1, ei2, …, eir keduanya tidak diketahui. Menilai polynomial yang diterima dalam untuk

memperoleh syndromeS1:

S1=v( ) =c( ) +e( ) =e( ) =ei1 i1+ ei2 i2+ … +eir ir.

Untuk mempersingkatnya, besarnya kesalahan dinotasikan dengan Yl = eil untuk l =

1, …,rdan lokasi kesalahanXl= iluntukl= 1, …,r,iladalah lokasi kesalahan kel.

S1= Y1X1+ Y2X2+ … + YrXr.

Demikian pula, polynomial yang diterima dapat dinilai dalam setiap pangkat dari yang

digunakan untuk menentukan generator polynomial g(x). Syndrome untuk j = 1, …, 2t

dinotasikan dengan

S1=v( j) =c( j) +e( j) =e( j)

Kemudian terdapat himpunan 2t persamaan simultan dalam r lokasi kesalahan yang tak diketahuiX1, …,Xrdanrbesar kesalahan yang tak diketahuiY1, …,Yr:

S1= Y1X1+ Y2X2+ … + YrXr

S1= Y1X12+ Y2X22+ … + YrXr2

$

S2t= Y1X12t+ Y2X22t+ … + YrXr2t

Himpunan persamaan ini memiliki satu solusi. Himpunan persamaan non linier terlalu

sulit untuk diselesaikan dengan tepat.

Selanjutnya, polynomial penentu letak kesalahan (error locator polynomial),

s(x) =srxr+ sr-1xr-1+ … +s1x+ 1, (3.1)

dan s(x) memiliki akar – akar pada invers lokasi – lokasi kesalahan Xl-1 untuk l = 1, …, r,

yaitu :

s(x) = (1 –xX1) (1 –xX2)… (1 –xXr).

Kemudian, s1, …, srdapat dihitung dari syndromeS1, …, S2t. Jika koefisien – koefisien dari

s(x) diketahui, maka akar – akar daris(x) dapat ditemukan, dan digunakan untuk memperoleh lokasi – lokasi kesalahan.

Kemudian, kedua sisi persamaan (3.1) di atas, dikalikan denganYlXlj+r dan ambil x=

Xl-1. Maka sisi kiri adalah nol, dan

Yl(Xlj+r+s1Xlj+-1r+ … +srXlj) = 0.

Persamaan yang demikian memenuhi untuk setiap l dan setiap j. Kemudian persamaan ini ditambahkan daril= 1 sampail=r, dan diperoleh.

= +

=

+

+

−

+

+

v l j l r r j l j l

l

X

r

s

X

s

X

Y

1

1

1

...

)

0

(

Atau

0

...

1 1 1 1 1

=

+

+

+

= = − + = + v l j l l r v l r j l l v l r j l

l

X

s

Y

X

s

Y

X

Y

Persamaan di atas diketahui sebagai persamaan

Sj+r+ s1Sj+r-1+ s2Sj+r-2+… + srSj= 0,

danSjdiperoleh jikaj 2t. Sehingga diperoleh persamaan berikut,

s1Sj+r-1+ s2Sj+r-2+… + srSj= –Sj+runtukj= 1, …,r. (3.2)

Ini adalah himpunan persamaan linier yang menghubungkan syndrome ke koefisien –

koefisiens(x). Persamaan ini dituliskan dalam bentuk matriks :

)

3

.

3

(

S

-S

S

s

s

s

S

...

S

S

...

S

...

S

S

S

...

S

S

2r 2 r 1 r 1 1 r r 1 2r 1 r r 1 r 3 2 r 2 1

−

−

=

+ + − + + +

Persamaan ini dapat diselesaikan dengan menginvers matriks, hanya apabila matriks ini

nonsingular. Akan dibuktikan bahwa matriks adalah nonsingular jika terdapat r kesalahan.

Teorema 3.1 :

Matriks Vandermonde, didefinisikan sebagai suatu matriks dengan bentuk:

=

− −

− 1 1

2 1 1 2 2 2 2 1 2 1

1

1

1

µ µ µ µ µ µ

X

X

X

X

X

X

X

X

X

A

Memiliki determinan tidak nol jika dan hanya jika semua Xiberbeda untuk i= 1, …,9.

Bukti:

Akan ditunjukkan bahwa determinan dari matriks |A| 0, jika dan hanya jika Xi berbeda

untuki= 1, …,9.

( ) |A| 0 makaXiberbeda untuki= 1, …,9.

JikaXiada yang sama, maka menurut sifat – sifat determinan, |A| = 0. Sehingga terbukti |A|

0 jikaXiberbeda untuki= 1, …,9.

(_:) jika Xi berbeda untuki = 1, …,9maka |A| 0. Untuk9= 1, maka |A| = |1| = 1,

|A| 0.

Diasumsikan benar untuk₉– 1, maka ini juga benar untuk₉dengan₉matriks Vandermonde.

KemudianX1digantikan dengan indeterminatex. Maka determinan adalah fungsi darixyang diberikan oleh

=

− − − 1 2 1 2 2 2 2 1

1

1

1

det

)

(

2 µ µ µ µ µ µ

X

X

X

X

X

X

x

x

x

x

D

Determinan dapat diperluas sebagai elemen dari baris pertama kali kofaktor dari elemen –

Yang memiliki paling banyak ₉ – 1 pembuat nol. Koefisien_;<=> adalah determinan dari

matriks Vandermonde dan dengan hipotesis induksi adalah tak nol. Jika untuki, 2 i ₉, ganti x = Xi, maka dua baris dari matriks adalah sama, dan D(Xi = 0). Jadi setiap Xi(i 1)

adalah suatu pembuat nol dariD(x), dan karena semuanya berbeda dan terdapat sebanyak₉– 1, polynomial dengan mudah dapat difaktor :

−

=

∏

= − µ µ 2

1

(

)

)

(

i i

X

x

d

x

D

Oleh karena itu determinan matriks Vandermonde adalah

−

=

∏

= − µ µ 2 1

1

(

)

)

(

i i

X

X

d

x

D

Ini tidak nol karena _;<=> tak nol dan X1 berbeda dari setiap sisa Xi. Oleh karena itu,

determinan dari ₉ dengan ₉ matriks vandermonde adalah tak nol, dan dengan induksi

teorema benar untuk semua9.

Teorema berikut memperlihatkan bagaimana menentukan r, jumlah kesalahan yang terjadi.

Teorema 3.2 :

Matriks dari sindrom

S

...

S

...

S

...

S

S

S

...

S

S

1 2m n 1 m 3 2 m 2 1

=

+ +

M

Bukti : Misalkan

=

−

−1 1

1 1

1

1

m m m m

X

X

X

X

V

dan

=

m m

X

Y

X

Y

X

Y

D

0

0

0

0

0

2 2 1 1

Maka M = VDVT. Fakta ini dapat dibuktikan dengan menghitung elemen ke ij dari

VDVTdan ini adalah elemen keijdariM. Oleh karena |M| = |V||D||V|. Jikam>r, maka |D| = 0 sehingga |M| = 0. Jika m = r, |D| 0 dan |V| 0 serta Xi yang berbeda – beda dan tak nol

yang hanya terjadim r. Oleh karena itu |M| 0.

Teorema 3.2 memberikan dasar bagi algoritma decoding. Pertama, menemukan

banyaknya kesalahan r yaitu dengan menentukan nilai r dimulai dengan nilai terbesar yang mungkin, r = t dan menghitung determinan M. Jika hasilnya tidak sama dengan nol, maka merupakan nilai dari r. Sebaliknya, jika determinannya nol, nilai r dikurangi 1 dan diulangi. Cara ini dilanjutkan sampai diperoleh determinan tidak nol. Nilai atau jumlah kesalahan r

akan diketahui. Kemudian, mencari M invers dan dengan persamaan (3.3) diperoleh (sr, s r-1,…, s1)T = M-1(–Sr+1, –Sr+2, …, –S2r)T. Kemudian, s(x) dihitung dan akar – akar dari s(x)

dicari untuk menemukan lokasi kesalahan. Jika kode adalah biner, algoritma selesai.

Sebaliknya, kembali ke persamaan – persamaan syndrome dan menemukan besarnyaYi.

S1= Y1X1+ Y2X2+ … + YrXr

S1= Y1X12+ Y2X22+ … + YrXr2

$

Dari persamaan di atas, dapat diubah ke dalam bentuk matriks,

S

S

S

Y

Y

Y

...

...

...

...

r 2 1 r 2 1 r r r 2 r 1 2 r 2 2 2 1 r 2 1

=

X

X

X

X

X

X

X

X

X

Misalkan matriks

...

...

...

X

...

X

X

_{1 2 r}

=

r r r r r

X

X

X

X

X

X

X

2 1 2 2 2 2 1

Selanjutnya dengan menginverse matriks Xdan dengan persamaan – persamaan syndrome di atas, diperoleh

S

S

S

Y

Y

Y

r 2 1 r 2 1

=

−1

X

Dari sini besarnyaYluntukl= 1, …,r, bilangan kesalahan akan diketahui.

Contoh, proses decoding dari BCH(15,5) dengan generator polynomial

g(x) =x10+x8+x5+x4+x2+x+ 1

Misalkan codeword yang diterima v(x) = x7 + x2. Langkah pertama adalah menghitung syndrome dengan menggunakan table 2.1.

S1=v( ) = 7+ 2= 1 + + 2+ 2= 1 + 2= 12

S2=v( 2) =v( )2=_?>@ = 9

S3=v( 3) = 21+ 6= 6+ 6= 0

S4=v( 4) = 28+ 8= 13+ 8= 2+ + + 2+ 3= 3

S6=v( 6) = 42+ 12= 12+ 12= 0.

Untuk menemukan jumlah kesalahanr,ambilr= 3. Maka

3 3 9 9 12

=

=

1

0

0

0

5 4 3 4 3 2 3 2 1

α

α

α

α

α

S

S

S

S

S

S

S

S

S

M

Determinan M adalah nol, oleh karena itu ambilr= 2. Maka

= = 0 9 9 12 3 2 2 1 α α α S S S S M

Determinan tidak nol, oleh karena itu dua kesalahan terjadi. Selanjutnya, untuk menemukan

lokasi kesalahan, , 0 9 6 6 1 = − α α α M

Dan dari persamaan (3.3)

= = = − 12 9 3 9 6 6 4 3 1 1 2 0 0 α α α α α α s s M s s

Oleh karena itu, polynomial penentu letak kesalahan (error locator polynomial)s(x) = s2x2+

s1x+ 1 = 9x2+ 12x+ 1. Reciprocaldari polynomials(x) adalahx2+ 12x+ 9= (x+ 7)(x

Bab 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Penelitian ini telah memperlihatkan bagaiman BCH code mampu menyelesaikan persoalan

dalam mendeteksi dan mengkoreksi t kesalahan yang terjadi dalam proses pengiriman informasi. Dimana di dalam penelitian ini diperoleh :

(1) Untuk mendeteksi kesalahan (proses encoding) ada dua cara :

1. Non – systematic encoding

v(x) =u(x)g(x). 2. Systematic encoding

v(x) =xn-ku(x) + [xn-ku(x) modg(x)]

(2) Untuk mengkoreksi kesalahan (proses decoding) dengan algoritma decoding dapat

dibentuk dengan :

1. Menghitung syndrome Sj=v( j),j= 1,…, 2t.

2. Menentukan jumlah maksimum r untuk menemukan jumlah kesalahan yang terjadi dengan menghitung determinan dari

S

...

S

S

...

S

...

S

S

S

...

S

S

1 2r 1 r r 1 r 3 2 r 2 1

=

+ + +

M

Ambil nilair = t. Jika determinan Mtak nol, maka determinan M adalah nilair. Tetapi jika determinan M nol, kurangi nilai r dengan 1 dan ulangi sampai diperoleh determinan yang tak nol.

3. Menemukan lokasi kesalahan dengan cara menginvers M dan dengan (3.3) diperoleh (sr, sr-1,…, s1)T= M-1(–Sr+1, –Sr+2, …, –S2r)T. Kemudian hitung s(x) dan

menemukan akar – akar dari s(x). Maka akan diketahui lokasi kesalahan. Jika kode adalah biner, maka algoritma selesai. Jika sebaliknya, maka dilanjutkan

4.2 SARAN

Penelitian ini telah menunjukkan bagaimana proses encoding dan decoding dengan

kode BCH. Saran dalam penelitian ini adalah bagaimana menentukan proses encoding

PUSTAKA

[1] Blahut, R. E. 1983.Theory And Practice of Error Control Codes. Massachusetts: Addison – Wesley Publishing Company, Inc.

[2] Durbin, J. R. 1979.Modern Algebra. 3rdEdition. New York: John Wiley & Sons, Inc. [3] Fraleigh, J. B. 1982.A first Course In Abstract Algebra. 5thEdition. Massachusetts :

Addison – Wesley Publishing Company.

[4] Hankerson, D. R. and Hoffman, D. G. 2000.Coding Theory And Cryptography, 2nd Edition, Revised And Expanded. Auburn. Alabama. Marcel Dekker, Inc.

[5] Morales, R. H. 2002.The Art of Error Correcting Coding. New York: John Wiley & Sons, Inc.