PENDUGAAN PARAMETER DISTRIBUSI GENERALIZED BETA II (GB2) DENGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE)

(1)

ABSTRAK

PENDUGAAN PARAMETER DISTRIBUSI GENERALIZED BETA II (GB2) DENGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE)

Oleh

WARYOTO

Generalized Beta II (GB2) mempunyai empat parameter yaitu parameter skala ( ), dan parameter bentuk ( , , ). Parameter dari GB2 diduga dengan meneggunakan metode Maximum Likelihood Estimation (MLE). MLE merupakan metode estimasi parameter suatu distribusi, dengan cara memilih penduga-penduga yang nilai-nilai parameternya diestimasi dengan memaksimumkan fungsi kemungkinannya. Karena tidak dapat diselesaikan secara analitik, sehingga digunakan metode iterasi untuk mendapatkan dugaan bagi parameter-parameternya. Metode iterasi yang digunakan adalah Metode Newton Raphson, dan dengan bantuan software R. Penelitian ini bertujuan untuk menduga parameter distribusi GB2, membandingkan bias, dan ragam. Berdasarkan simulasi hasilnya menunjukkan bahwa bias menjadi lebih kecil dan selang kepercayaan menjadi lebih pendek ketika ukuran sampel lebih besar.

(2)

Oleh

WARYOTO

Tesis

Sebagai Salah Satu Syarat untuk Memperoleh Gelar MAGISTER SAINS

Pada

Jurusan Matematika Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(3)

Tesis

Oleh

WARYOTO

MAGISTER MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

(4)

DAFTAR GAMBAR

Gambar Halaman

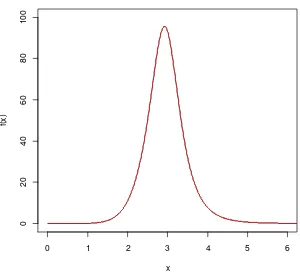
1. Grafik fungsi Kepekatan Peluang Generalized Beta II (GB2)

dengan = , = , = , = ... 9

2. Diagram Alir Membangkitkan Sampel Sebanyak 100 GB2 ... 17

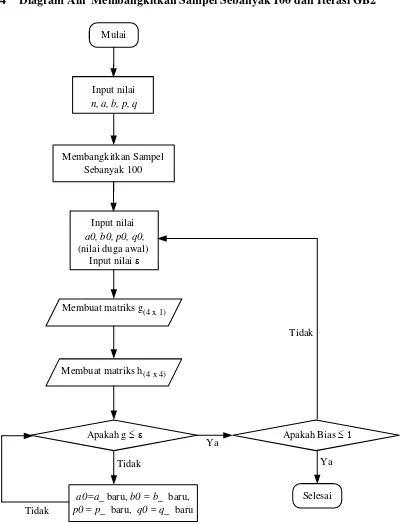
3. Diagram Alir Membangkitkan Sampel Sebanyak 100 dan Iterasi GB2 ... 18

4. Grafik a duga terhadap Selang Kepercayaan (SK) ... 48

5. Grafik b duga terhadap Selang Kepercayaan (SK) ... 49

6. Grafik p duga terhadap Selang Kepercayaan (SK) ... 49

7. Grafik q duga terhadap Selang Kepercayaan (SK) ... 50

8. Grafik Bias untuk n = {20, 30, 50, 100 dan 500} Generalized Beta II (GB2) ... 50

(5)

DAFTAR ISI

2.7 Metode Pendugaan Maksimum Likelihood Estimation (MLE) ... 11

2.8 Metode Newton Raphson ... 13

2.9 Software R ... 14

III. METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 16

3.2 Metode Penelitian ... 16

3.3 Diagram Alir Membangkitkan Sampel Sebanyak 100 ... 17

(6)

IV. HASIL DAN PEMBAHASAN

4.1 Pendugaan Parameter GB2 dengan Menggunakan Metode

Maxsimum Likelihood Estimation (MLE) ... 19

4.1.1 Pendugaan Parameter Persamaan (4.6) Terhadap ̂ ... 22

4.1.2 Pendugaan Parameter Persamaan (4.6) Terhadap (̂) ... 23

4.2 Metode Newton Raphson untuk Pendugaan Parameter , , dan 27

4.2.1 Turunan Kedua Parameter dari fungsi Logaritma Natural GB2 Terhadap Parameter , , dan ... 29

4.3 Menghitung Bias ... 40

4.4 Menghitung Ragam ... 43

4.5 Menghitung Selang Kepercayan (SK) ... 44

4.6 Grafik Dugaan Terhadap Selang Kepercayaan (SK) ... 48

(7)

DAFTAR TABEL

Tabel Halaman

1. Nilai Dugaan, Selang Kepercayaan (SK), Bias dan Ragam Generalized Beta II (GB2) untuk nilai parameter = 2; = 1,5;

(8)

(9)

(10)

(11)

MOTTO

“Tak ada rahasia untuk menggapai sukses. Sukses itu dapat terjadi

karena persiapan, kerja keras, dan mau belajar dari kegagalan”

(General Colin Powell)

“Jadilah yang sedikit dari hal-hal yang positif”

(Waryoto)

“Lebih baik mencoba tapi gagal, dari pada gagal mencoba”

(12)

PERSEMBAHAN

Seiring do’a dan rasa syukur kehadirat Allah SWT

Kupersembahkan karya kecilku ini kepada:

Orang tuaku (Wartim – Dayimah) dan (Muji – Paenah) atas limpahan kasih sayang, do’a dan motivasinya selama ini

Istriku tercinta (Munah Nuryatri, SKM)

yang senantiasa mendampingi hidupku, yang sabar menanti akan keberhasilanku

Anak kami tersayang (Raisya Nadia Eka Putri)

Semua saudaraku yang telah menyayangiku dan memberikan banyak hal dalam hidupku

(13)

RIWAYAT HIDUP

Penulis dilahirkan di Bumi Raharjo, pada tanggal 16 Juli 1980, merupakan anak pertama dari pasangan Bapak Wartim dan Ibu Dayimah, penulis mempunyai satu adik laki-laki yaitu Warsono, dan dua adik perempuan yaitu Susinawati dan Lilik Yulita. Pada saat tesis ini ditulis, penulis telah menikah dengan Munah Nuryatri dan telah dikaruniai seorang anak perempuan yaitu Raisya Nadia Eka Putri.

(14)

Pada Tahun 2004 sampai dengan saat ditulis tesis ini penulis mengajar di MTs Wali Songo Bumi Ratu Nuban Lampung Tengah. Pada Tahun 2007 sampai dengan saat ditulis tesis ini penulis mengajar di SMA Muhammadiyah 1 Metro. Pada Tahun 2008 sampai dengan saat ditulis tesis ini penulis mengajar di Primagama cabang kota Metro.

(15)

SANWACANA

Puji syukur penulis panjatkan kehadirat Allah SWT karena atas berkat rahmat dan hidayah-Nya penulis dapat menyelesaikan tesis ini yang berjudul “PENDUGAAN PARAMETER DISTRIBUSI GENERALIZED BETA II (GB2) DENGAN METODE MAXIMUM LIKELIHOOD ESTIMATION (MLE)” sebagai salah satu syarat meraih gelar Magister Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

Terima kasih yang tulus penulis ucapkan kepada:

1. Bapak Warsono, Ph.D., selaku Dosen Pembimbing I yang selalu mengarahkan, membimbing dan memotivasi penulis dalam menyelesaikan tesis ini.

2. Bapak Mustofa Usman, P.hD., selaku Dosen Pembimbing II yang dengan sabar membimbing, mengarahkan dan memotivasi penulis dalam menyelesaikan tesis ini, dan sekaligus selaku ketua jurusan matematika.

3. Bapak Suharsono, Ph.D., selaku Pembimbing Akademik yang telah mendampingi penulis selama perkuliahan, dan sekaligus sebagai dosen penguji yang telah memberikan kritik, saran, dan nasehat-nasehat dalam penulisan tesis ini.

(16)

5. Bapak Prof. Suharso, Ph.D., selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

6. Seluruh dosen yang telah mendidik dan membimbing penulis selama menyelesaikan masa studi.

7. Orang tuaku tercinta (Bp Wartim dan Ibu Dayimah), (Bp Muji dan Ibu Paenah), yang senantiasa dengan tulus menyayangi, mendo’akan dan memotivasiku

dalam menggapai cita-citaku.

8. Istri tercinta (Munah Nuryatri, SKM) yang senantiasa mendampingiku memberiku semangat dan motivasi. Anak kami tersayang (Raisya Nadia Eka Putri) yang telah banyak mensuportku.

9. Teman-teman Pasca (Kris, Rahman, Anton, Malik, Herli, Ade, Ike, Ana, Viviana, Nurman, Dwi, Fauzan, Agus, Suli, Guiana, Rini, Ayu, Permata, Edi, Cut, Wahid, dan Recand), teman-teman MIPA (Mas Geri, dan Mbak Reni) 10. Keluarga Besar Primagama Kota Metro (Mas Ronal, Mas Tikno, Mas Jojok,

Mas Bowo, dan Mbak Vita). serta semua pihak yang tidak mungkin saya sebut satu persatu namanya.

Semoga senantiasa memberikan kebaikan dan balasan atas jasa dan budi baik yang telah diberikan kepada penulis. Penulis mohon maaf atas segala kekurangan dan ketidaksempurnaan dalam penulisan tesis ini. Semoga tesis ini bermanfaat bagi kita semua. Amiin.

Bandar Lampung, Januari 2016 Penulis,

(17)

1

I. PENDAHULUAN

1.1 Latar Belakang

Statistik adalah metode atau ilmu yang mempelajari suatu proses dalam merencanakan, mengumpulkan, menganalisis, dan mempresentasikan data. Statistik dikelompokkan menjadi dua macam, yaitu statistik deskriptif dan statistik inferensia. Statistik deskriptif adalah metode-metode yang berkaitan dengan pengumpulan dan penyajian suatu gugus data sehingga memberikan informasi yang berguna, sedangkan statistik inferensia mencakup semua metode yang berhubungan dengan analisis sebagian data untuk kemudian sampai pada peramalan atau penarikan kesimpulan mengenai keseluruhan gugus data populasinya.

(18)

2

Kemungkinan maksimum atau sering dikenal dengan sebutan Maximum Likelihood Estimation (MLE).

Penggunaan metode MLE merupakan metode yang paling efisien dan sering memberikan pendugaan yang baik, karena prinsip dari metode MLE adalah memilih salah satu nilai dari parameternya untuk memaksimumkan fungsi kemungkinan atau memaksimumkan informasi. Dalam penduga parameter dari suatu distribusi ada penduga parameter yang tidak dapat diselesaikan secara analitik, sehingga perlu diselesaikan dengan cara numerik. Salah satu cara yang digunakan adalah dengan teknik iteratif yaitu Metode Newton Raphson. Metode Newton Raphson sering digunakan karena metode ini lebih sederhana dan mempunyai konvergensi yang cepat.

(19)

3

Dengan demikian peneliti tertarik untuk melakukan penelitian mengenai pendugaan parameter distribusi Generalized Beta II empat parameter (GB2) menggunakan metode Maximum Likelihood Estimation (MLE).

1.2 Batasan Masalah

Pada penelitian ini, permasalahan dibatasi pada pendugaan, selang kepercayaan, ketakbiasan, dan ragam penduga parameter GB2 dari masing-masing ukuran data dengan dengan bantuan Software R.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini adalah:

1. Menduga parameter distribusi GB2 dengan menggunakan metode Maximum Likelihood Estimation (MLE)

(20)

4

1.4 Manfaat Penelitian

(21)

5

II. LANDASAN TEORI

Dalam proses penelitian penduga parameter dari suatu distribusi diperlukan beberapa konsep dan teori yang mendukung dari ilmu statistika. Berikut ini akan dijelaskan beberapa konsep dan teori yang berkaitan dengan penduga parameter distribusi GB2 menggunakan metode Maximum Likelihood Estimation (MLE) dengan bantuan Software R.

2.1 Fungsi Gamma

Fungsi Gamma merupakan salah satu dari beberapa fungsi khusus di dalam matematika. Fungsi Gamma merupakan perluasan dari transformasi laplace yang sangat penting dalam matematika dan sebagai dasar dalam perkembangan teknologi dan sains modern.

Definisi 2.1

Fungsi Gamma yang dinotasikan dengan Γ yaitu:

Γ = ∫ − � − _{, >}

∞

(22)

6

Pada sub-bab selanjutnya akan dijelaskan tentang fungsi digamma yang akan digunakan uantuk menyelesaikan persamaan yang nantinya akan dijumpai pada saat melakukan turunan (derivatif) pada saat mencari penduga suatu parameter.

2.2 Fungsi Digamma

Fungsi Digamma merupakan hasil turunan (derivatif) pertama dari fungsi Gamma.

Definisi 2.2

Fungsi Digamma didefinisikan sebagai berikut:

� =� ln Γ_� =Γ_Γ′ , >

(Abramowitz, and Stegun,1972)

Sub-bab berikutnya akan dijelaskan tentang fungsi polygamma yang merupakan hasil turunan (derivatif) pertama dari fungsi digamma

2.3 Fungsi Polygamma

(23)

7

Definisi 2.3

Fungsi Polygamma didefinisikan sebagai berikut:

�� ₌��

� � =

� �+ _{ln Γ}

� �+ , >

(Abramowitz, and Stegun,1972)

Selain fungsi Gamma, Digamma maupun Polygamma pada penelitian ini juga menggunakan fungsi Beta yang digunakan untuk menyelesaikan integral khusus.

2.4 Fungsi Beta

Fungsi Beta juga merupakam salah satu fungsi khusus yang ada di dalam matematika. Fungsi Beta digunakan untuk mengevaluasi integral tentu.

Definisi 2.4

Fungsi Beta adalah suatu fungsi bernilai real dengan dua peubah, didefinisikan oleh suatu bentuk integral, yaitu:

� , = ∫ − ₋ − _{, > , >}

� , = ∫ ₊ − ₊ , > , >

∞

(24)

8

Sifat: � , = � , Bukti

� , = ∫ − ₋ −

= ∫ − − −

= ∫ − ₋ −

= � ,

Fungsi Beta dapat juga dinyatakan dengan fungsi Gamma yaitu: Dengan

� ,

=

Γ .Γ

Γ +

(Ross, 2010)

2.5 Distribusi Generalized Beta II GB2)

Definisi 2.5

Suatu variabel acak dikatakan memiliki distribusi Generalized Beta II (GB2) dengan parameter , , , jika fungsi kepekatan peluangnya adalah:

= � � −

(25)

9

Gambar 1. Grafik Fungsi Kepekatan Peluang Generalized Beta II (GB2) dengan

= , = , = , =

Statistik inferensia terdiri dari pengujian hipotesis dan pendugaan. Pada penelitian ini akan dilakukan pendugaan parameter. Pendugaan parameter dilakukan untuk menduga

(26)

10

ukuran dari suatu populasi yang belum diketahui. Definisi pendugaan parameter akan dijelaskan pada Subbab 2.6.

2.6 Penduga Parameter

Dalam statistik inferensia dibutuhkan pemahaman mengenai kaidah-kaidah pengambilan kesimpulan tentang suatu parameter populasi berdasarkan karakteristik sampel. Hal ini membangun apa yang disebut dengan pendugaan titik dari fungsi kepekatan peluang parameter yang tidak diketahui.

Definisi 2.6

Misal suatu peubah acak X memiliki fungsi kepekatan peluang yang bergantung pada suatu parameter tak diketahui  dengan sembarang nilai dari suatu himpunan ruang parameter , maka dinotasikan dengan

f (x; ), .

Definisi 2.7

Misal X1, X2, ..., Xn berdistribusi bebas stokastik identik dengan fungsi kepekatan

peluang f (x; ), . Suatu statistik U(X1, X2, ..., Xn) = U(X) yang digunakan untuk

(27)

11

Untuk menduga parameter dari suatu distribusi dapat dilakukan dengan beberapa metode. Dalam penelitian ini pendugaan parameter distribusi GB2 akan dilakukan dengan menggunakan metode MLE. Definisi metode MLE akan dijelaskan pada Subbab 2.7.

2.7 Metode Pendugaan Maximum Likelihood Estimation (MLE)

Definisi 2.8

Misalkan X1, X2, ..., Xn adalah sampel acak berukuran n yang saling bebas stokastik

identik dari suatu distribusi yang mempunyai fungsi kepekatan peluang f (x; ), 

. Fungsi kepekatan peluang bersama dari X1, X2, ..., Xn adalah f (x1; ) f (x2; ) ... f

(xn; ) yang merupakan fungsi kemungkinan (Likelihood Function).

Untuk x1, x2, ..., xn tetap, fungsi kemungkinan merupakan fungsi dari  dan

dilambangkan dengan L() dan dinotasikan sebagai berikut: L() = f ( ̅ ; )

= f (x1, x2, ..., xn ; )

= f (x1; ) f (x2; ) ... f (xn; ), 

(28)

12

Definisi 2.9

L() = f (x1, x2, ..., xn ; ),   merupakan fungsi kepekatan peluang dari x1, x2, ...,

xn. Untuk hasil pengamatan x1, x2, ..., xn, nilai �̂ berada dalam  (�̂), dimana L()

maksimum yang disebut sebagai Maximum Likelihood Estimation (MLE) dari �. Jadi,

�̂ merupakan penduga dari �.

Jika f (x1, x2, ..., xn ; �̂) = max f (x1, x2, ..., xn ; ),  maka untuk memaksimumkan

L() terhadap parameternya. Biasanya mencari turunan dari L() terhadap parameternya relatif sulit, sehingga dalam penyelesainnya dapat diatasi dengan menggunakan logaritma atau fungsi ln dari L() yaitu: ln L() = ∑�_�= ln _�; � . Untuk memaksimumkan ln L() adalah dengan mencari turunan dari ln L() terhadap parameternya, kemudian hasil turunannya dibuat sama dengan nol.

� ln L �

�� = (Hogg and Craig, 1995)

(29)

13

2.8 Metode Newton Raphson

Apabila proses pendugaan parameter didapat persamaan akhir yang non linear maka tidak mudah memperoleh pendugaan parameter tersebut, sehingga diperlukan suatu metode numerik untuk memecahkan persamaan non linear tersebut. Salah satu metode yang digunakan untuk memecahkan sistem persamaan non linear adalah Metode Newton Raphson. Metode Newton Raphson adalah metode untuk menyelesaikan persamaan non linear secara iteratif. Jika 0 merupakan nilai awal (inisialisasi) dari 

atau 0 merupakan nilai ke 1 dari , maka dapat dimisalkan 0 = i dan 1 = i + 1 dengan

i awal 0.

Metode ini dapat diperluas untuk menyelesaikan sistem persamaan dengan lebih dari satu parameter. Misal 1, 2, . . . p ... maka iterasinya sebagai berikut:

(30)

14

Matriks Hessian atau matriks turunan kedua dari fungsi logaritma natural terhadap parameter , , dan dilambangkan dengan H  yaitu:

Untuk memudahkan melakukan proses iterasi dengan metode Newton Raphson akan digunakan Software R. Penjelasan mengenai Software R akan dijelaskan pada Subbab 2.9.

2.9 Software R

(31)

15

modeling, pengujian analisis klasik, analisis time-series, klasifikasi dan lainnya, serta perangkat lunak yang umumnya digunakan untuk manipulasi data, perhitungan, dan tampilan grafik yang mencakup antara lain:

a. Penanganan data yang efektif dan penyimpangan data

b. Rangkaian operator untuk perhitungan array dalam matrik tertentu

c. Fasilitas grafik untuk analisis data dan menampilkannya, baik pada layar maupun hardcopy

(32)

16

III. METODE PENELITIAN

3.1 Waktu dan Tempat Penelitian

Penelitian ini dilakukan pada semester ganjil tahun akademik 2015/2016 di Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.

Metode penelitia brtujuan untuk menjelaskan langkah-langkah yang dilakukan saat penelitian. Berikut ini akan dijelaskan metode penelitian dan langkah-langkah yang dilakukan dalam menduga parameter distribusi GB2.

3.2 Metode Penelitian

Penelitian ini untuk menduga parameter distribusi GB2 yaitu , , , dan dengan metode Maximum Likelihood Estimation (MLE) dengan menggunakan software R. Adapun langkah-langkah yang dilakukan adalah sebagai barikut:

1. Menduga parameter GB2 , , , dan dengan metode Maximum Likelihood Estimation (MLE) dengan langkah-langkah sebagai berikut:

a. Membentuk fungsi kemungkinan yang berasal dari fungsi kepekatan peluang GB2.

(33)

17

c. Dugaan parameter dari metode MLE dengan mencari turunan pertama dari logaritma natural fungsi kepekatan peluang terhadap parameter-parameter yang akan diduga dan disama dengankan nol.

2. Menyelesaikan dugaan parameter yang tidak dapat diselesaikan secara analitik menggunakan Metode iterasi Newton Raphson.

3. Menggunakan Software R untuk mendapatkan nilai dugaan parameter GB2. 4. Membandingkan dugaan dengan nilai parameter, selang kepercayaan, bias, dan

ragam, untuk data berukuran 20, 30, 50, 100 dan 500 dengan masing-masing sampel dilakukan pengulangan sebanyak 100 kali.

3.3 Diagram Alir Membangkitkan Sampel Sebanyak 100

Mulai

Selesai Input nilai n, a, b, p, q

Membangkitkan Sampel Sebanyak 100

(34)

18

3.4 Diagram Alir Membangkitkan Sampel Sebanyak 100 dan Iterasi GB2

Mulai

Membuat matriks g_{(4 x 1)}

Membuat matriks h_{(4 x 4)}

Apakah g £ e

(35)

52

V. KESIMPULAN

5.1. Kesimpulan

Dari hasil penelitian ini dapat diperoleh beberapa kesimpulan sebagai berikut: 1. Penduga parameter Generalized Beta II empat parameter (GB2) dengan

metode Maximum Likelihood Estimation (MLE) menghasilkan penduga yang tidak dapat diselesaikan secara analitik, sehingga perlu diselesaikan dengan cara numerik menggunakan metode Newton Raphson.

2. Dugaan parameter {a, b, p, q} mempunyai nilai yang semakin mendekati parameter yang sebenarnya, jika ukuran sampel semakin besar.

3. Semakin besar ukuran sampel maka selang kepercayaan akan semakin pendek. 4. Semakin besar ukuran sampel maka bias cenderung semakin kecil atau selisih

(36)

53

5.2. Saran

(37)

DAFTAR PUSTAKA

Abramowitz, Milton. and Stegun, Irene 1972. Handbook of Mathematical Functions with Formulas, Graphs, and mathematical Tables. U.S. Goverment, Washington.

Hoog, V Robert and Craig, T Allen. 1995. Introduction of Mathematical Statistic Fifth Edition. New Jersey: The United States of America.

Kleiber, C. and Kotz, S. 2003. Statistical Size Distributions in Economics and Actuarial Sciences. Hoboken, NJ, USA: Wiley-Interscience.

Ross, Sheldon. 2010. A First Course in Probability Eighth Edition. Univerity of Southern California. United States of America