ABSTRACT
Edge Maximal Graphs Having Cycles with Locating-Chromatic Number Three
By
Dini Wulandari
ABSTRAK
Graf Maksimal Sisi Memuat Siklus Berbilangan Kromatik Lokasi Tiga
Oleh
Dini Wulandari
GRAF MAKSIMAL SISI MEMUAT SIKLUS BERBILANGAN KROMATIK LOKASI TIGA
Oleh Dini Wulandari
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
RIWAYAT HIDUP
Penulis dilahirkan di Padang Cermin pada tanggal 17 April 1994. Penulis merupakan anak pertama dari empat bersaudara dari pasangan Bapak Idris dan Ibu Adriani.
Penulis telah menyelesaikan pendidikan sekolah dasar di SD Negeri 4 Wates pada tahun 2005, pendidikan sekolah menengah pertama di SMP Negeri 2 Padang Cermin pada tahun 2008 dan pendidikan sekolah menengah atas di SMA Perintis 2 Bandar Lampung pada tahun 2011. Setelah menamatkan sekolah menengah atas, penulis melanjutkan pendidikan ke perguruan tinggi dan terdaftar sebagai mahasiswi Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung melalui jalur ujian mandiri. Selama menempuh pendidikan di perguruan tinggi penulis juga ikut serta dalam organisasi kemahasiswaan yaitu pada periode 2011/2012 terdaftar sebagai anggota GEMATIKA ( Generasi Muda Himpunan Mahasiswa Matematika) FMIPA Unila. Pada periode tahun 2012/2013 –2013/2014 penulis terdaftar sebagai anggota HIMATIKA biro Dana dan Usaha.
Dengan rasa syukur yang tiada terkira...
Kupersembahkan karya kecilku ini sebagai hadiah
sederhana atas keringat, waktu, doa, dan air mata dari
dua orang hebat dalam hidupku, yang selalu
menjagaku sejak nafas pertama yang di anugerahkan
Tuhan hingga saat ini.
SANWACANA
Puji syukur kehadirat Tuhan Yang Maha Esa atas segala limpahan rahmat dan hidayahNya sehingga penulis dapat menyelesaikan skripsi yang berjudul“Graf Maksimal Sisi Memuat Siklus Berbilangan Kromatik Lokasi Tiga”.
Dalam penyusunan skripsi ini, penulis menyadari banyak pihak yang telah terlibat sehingga skripsi ini dapat terselesaikan dengan baik dan tepat waktu. Untuk itu penulis ingin mengucapkan terimakasih kepada :
1. Ibu Dr. Asmiati, S.Si., M.Si., selaku pembimbing I yang setia membimbing, memberikan arahan, saran, dan dukungan kepada penulis dalam menyelesaikan skripsi ini.
2. Ibu Dr. Wamiliana, M.A., Ph.D., selaku pembimbing II yang dengan sabar memberikan kesempatan bagi penulis untuk belajar lebih banyak selama proses pembuatan skripsi ini.
3. Bapak Agus Sutrisno, M.Si., selaku penguji yang telah memberikan kritik dan saran yang membangun dalam proses pembuatan skripsi ini.
5. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku Ketua Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam.
6. Bapak Prof. Suharso, Ph.D., selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam.
7. Seluruh dosen, staf, dan karyawan Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam yang telah memberikan ilmu pengetahuan dan bantuan kepada penulis.
8. Kedua orang tua beserta keluarga yang selalu memberikan semangat, doa dan kasih sayang.
9. Opi, Debi, dan Didi, jagoan-jagoan yang selalu memberikan motivasi, semangat dan juga keceriaan bagi penulis.
10. Ayu, Anissa, Faiga, Triani, dan Haidir yang senantiasa memberikan semangat dan bantuan selama masa perkuliahan kepada penulis.
11. Arifah dan Sabrina yang selalu memberikan semangat dan motivasi kepada penulis.
12. Semua pihak yang telah membantu penulis dalam menyelesaikan skripsi.
Penulis menyadari bahwa skripsi masih jauh dari kesempurnaan. Oleh karena itu, penulis mengharapkan kritik dan saran yang bersifat membangun agar lebih baik dimasa yang akan datang.
Bandar Lampung, April 2015 Penulis,
i DAFTAR ISI
Halaman
DAFTAR ISI... .i
DAFTAR GAMBAR...iii
BAB I PENDAHULUAN 1.1Latar Belakang Masalah...1
1.2Batasan Masalah...3
1.3Tujuan Penelitian...3
1.4Manfaat Penelitian...3
BAB II TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf...5
2.2 Bilangan Kromatik Lokasi...7
BAB III METODE PENELITIAN 3.1 Waktu dan Tempat Penelitian...16
ii BAB IV HASIL DAN PEMBAHASAN
4.1 Karakterisasi Graf Maksimal Sisi Memuat Siklus Ganjil
Berbilangan Kromatik Lokasi Tiga...17
4.2 Karakterisasi Graf Maksimal Sisi Memuat Siklus Genap
Berbilangan Kromatik Lokasi Tiga...29
BAB V KESIMPULAN DAN SARAN
5.1 Kesimpulan...35
5.2 Saran...35
iii
DAFTAR GAMBAR
Halaman
Gambar 1. Contoh graf dengan 5 titik dan 7 sisi...5
Gambar 2. Graf ...7
Gambar 3. Contoh graf berbilangan kromatik tiga...8
Gambar 4. Pewarnaan lokasi minimum pada graf G...10
Gambar 5. Pewarnaan lokasi minimum pada , 3...11
Gambar 6. Pewarnaan lokasi minimum dari , ...12
Gambar 7. Pewarnaan lokasi minimum pada ...13
Gambar 8. Empat type graf maksimal sisi di yang memuat siklus ganjil ...23
Gambar 9. Graf maksimal sisi di yang memuat siklus genap...33 G
BAB I PENDAHULUAN
1.1 Latar Belakang Masalah
Teori graf merupakan salah satu cabang dari ilmu matematika yang pertama kali diperkenalkan oleh seorang matematikawan Swiss yang bernama Leonhard Euler pada tahun 1736. Banyaknya jembatan yang menghubungkan antar wilayah di Konigsberg melahirkan pemikiran mungkin tidaknya melewati ketujuh jembatan yang menghubungkan keempat kota tersebut masing-masing tepat satu kali dan kembali ke tempat semula.
Permasalahan jembatan Konigsberg direpresentasikan oleh Euler dengan memisalkan daratan yang ada dengan titik (vertex) dan jembatan-jembatan yang menghubungkan daratan tersebut dengan garis (edge). Kemudian Euler menyimpulkan bahwa tidak mungkin dapat melalui ketujuh jembatan yang ada tepat satu kali dikarenakan derajat (banyaknya garis yang menempel pada suatu titik) titiknya adalah ganjil. Kisah Jembatan Konigsberg inilah yang melatarbelakangi sejarah lahirnya Teori Graf.
2 adalah jaringan internet, peta rangkaian listrik, meminimumkan biaya dengan memilih rute terpendek, dan sebagainya.
Graf G didefinisikan sebagai himpunan (V,E) dengan V merupakan himputan titik (vertex) yang tidak boleh kosong dan E merupakan himpunan pasangan sisi tak terurut dari titik-titik di V. Pewarnaan titik adalah pemberian warna titik-titik suatu graf dengan syarat dua titik yang bertetangga tidak boleh memiliki warna yang sama, sedangkan dimensi partisi dari G adalah kardinalitas minimum dari k-partisi di V(G). Pengembangan dari kedua konsep inilah yang melatarbelakangi munculnya konsep bilangan kromatik lokasi pada graf G.
Kajian tentang pewarnaan lokasi merupakan kajian yang cukup baru dalam teori graf. Konsep pewarnaan lokasi pertama kali diperkenalkan oleh Chartrand dkk. pada tahun 2002 dengan definisi sebagai berikut:
Misalkancadalah suatu pewarnaan titik pada grafGdengan menggunakan warna-warna 1,2,...,kuntuk suatu bilangan bulat positif k. Secara ekuivalen,cmerupakan suatu partisi Π dari V(C) ke dalam kelas-kelas warna yang saling bebas , , , dimana titik-titik pada diberi warna i, 1≤ i ≤ k. Kode warna ( )
dari suatu titik ( )didefinisikan sebagai k-vektor yaitu:
( ) = ( ( , ), ( , ), , ( , ))
dengan ( , ) = min{ ( , )| } untuk 1 . Jika setiap titik di G
memiliki kode warna yang berbeda terhadap partisi Π, maka cdisebut pewarnaan
3 Pada pengkarakterisasian graf berbilangan kromatik lokasi tertentu Chartrand dkk. (2003) telah berhasil mengkarakterisasi graf berbilangan kromatik n-1 atau n-2. Baskoro dan Asmiati (2013) telah berhasil mengkarakterisasi graf pohon berbilangan kromatik lokasi tiga. Pada tulisan ini akan dilakukan pengkajian graf maksimal sisi memuat siklus berbilangan kromatik lokasi tiga berdasarkan paper Asmiati dan Baskoro (2012).
1.2 Batasan masalah
Pada penelitian ini akan dikaji graf maksimal sisi memuat siklus berbilangan kromatik lokasi tiga.
1.3 Tujuan Penelitian
Tujuan dari penelitian ini adalah menganalisis karakterisasi graf memuat siklus berbilangan kromatik lokasi tiga.
1.4 Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah:
a. Memberikan pemahaman dan wawasan mengenai teori graf terutama tentang bilangan kromatik lokasi pada graf yang memuat siklus.
4 c. Untuk menjadi referensi penelitian lanjutan dalam menentukan
BAB II TINJAUAN PUSTAKA
Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini.
2.1 Konsep Dasar Graf
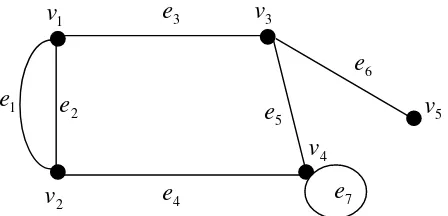
Beberapa konsep dasar yang digunakan dalam penelitian ini diambil dari Deo (1989). Suatu graf G dinotasikan dengan G = (V, E) dibangun dari suatu himpunan V = { }yang menyatakan himpunan titik tak kosong dari G dan E = { }himpunan sisi yang merupakan pasangan tak terurut dari titik-titik diV.
Gambar 1. Contoh graf dengan 5 titik dan 7 sisi
Dua titik u dan v pada graf G dikatakan bertetangga (adjacent) jika dihubungkan oleh sebuah sisi e. Sisi e juga dikatakan menempel (incident) pada titik u jika titik u merupakan salah satu titik ujung dari sisi e. Dua sisi atau lebih yang menghubungkan pasangan titik yang sama pada suatu graf disebut sisi paralel (multiple edges). Pada Gambar 1. titik bertetangga
6 dengan dan . Sisi menempel pada dan . Sisi paralel dari gambar tersebut adalah sisi dan .
Derajat dari titik v suatu graf G adalah banyaknya sisi yang menempel pada titik v yang dinotasikan dengan d(v).Titik yang berderajat satu disebut dengan daun (pendant), sedangkan titik yang berderajat nol disebut dengan titik terasing (isolated vertex). Pada Gambar 1. ( )✁ ( )✁ ( )✁ ( )✁ 3dan adalah daun karena berderajat satu.
Loopmerupakan sisi yang memiliki titik awal dan akhir yang sama. Pada suatu graf sederhana tidak terdapat loop maupun sisi paralel . Graf pada Gambar 1. bukan graf sederhana karena memiliki loop yaitu pada titik , sedangkan sisi paralel yaitu dan .
Jalan (walk) merupakan himpunan berhingga yang memuat titik dan sisi dari suatu graf dimana setiap sisi menempel dengan titik sebelum dan sesudahnya Pada Gambar 1. contoh jalan adalah
.
Lintasan (path) adalah jalan yang semua sisi dan semua titik yang dilalui harus berbeda. Graf G dikatakan graf terhubung jika terdapat lintasan yang menghubungkan setiap dua titik yang berbeda. Pada Gambar 1. yang
merupakan lintasan adalah .
7 disebut siklus ganjil. Contoh siklus genap pada Gambar 1. adalah
.
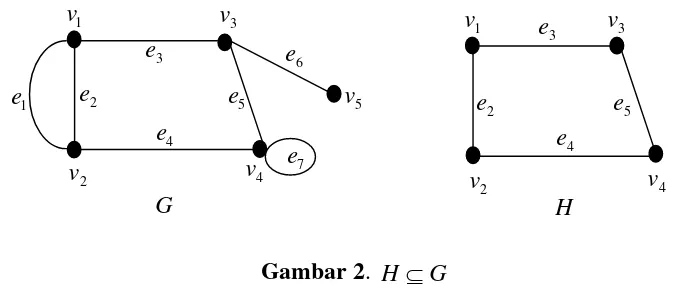
Suatu graf H dikatakan subgraf dari G, dinotasikan dengan jika dan
hanya jika dan .
Gambar 2.
2.2 Bilangan Kromatik Lokasi
Pada bagian ini akan diberikan definisi yang berkaitan dengan bilangan kromatik lokasi pada suatu graf yang diambil dari Chartrand dkk.(2002). Bilangan kromatik lokasi merupakan pengembangan dari dua konsep dalam graf yaitu pewarnaan titik dan dimensi partisi graf.
Pewarnaan titik graf G adalahc : V(G) {1, 2, 3, ..., k}dengan syarat dua titik yang bertetangga tidak boleh memiliki warna yang sama. Minimum banyaknya warna yang diperlukan untuk mewarnai suatu graf itulah yang disebut bilangan kromatik dan dinotasikan dengan ( ).
8 Gambar 3.Contoh graf berbilangan kromatik tiga
Selanjutnya diberikan definisi dan teorema mengenai bilangan kromatik lokasi. Konsep bilangan kromatik lokasi pertama kali dikaji oleh Chartrand dkk. (2002). Misalkan c suatu pewarnaan titik di G dan merupakan himpunan titik yang diberi warnai, maka = { ✂ ✂ ✂ } merupakan himpunan yang
terdiri dari kelas-kelas warna pada V(G). Kode warna ( )dari vmerupakan k-pasang terurut ( ( ✂ )✂ ( ✂ )✂ ✂ ( ✂ )) dengan ( ✂ ) ✄ m
in { ( ✂ )| } untuk 1 . Jika setiap titik di G memiliki kode warna yang berbeda maka c disebut pewarnaan lokasi dari G yang kemudian dinotasikan dengan ( ).
Berikut ini akan diberikan lemma dan teorema penting mengenai bilangan kromatik lokasi pada suatu graf yang telah dibuktikan oleh Chartrand dkk. (2002). Lingkungan dari suatu titik v pada graf G yang dinotasikan dengan N(v)adalah himpunan titik-titik di G yang bertetangga denganv.
9 Bukti:
Misalkan c merupakan suatu pewarnaan lokasi pada graf terhubung G dan misalkan ☎ { ✆ ✆ ✆ } merupakan partisi titik-titik G ke dalam kelas warna . Jikau,v V(G),misalkanc(u) = c(v)sedemikian sehingga titik u dan v berada dalam kelas warna yang sama, misal dari Π maka ( ✆ ) ☎ ( ✆ ) ☎0. Jika d(u,w) = d(v,w) untuk setiap w V(G) – {u,v}, maka
, = ( , ) untuk setiap j i, 1 j k. Akibatnya, ( ) = ( )
sehingga c bukan pewarnaan lokasi. Jadi c(u) c(v).
Akibat 2.1 Jika G adalah graf terhubung dengan suatu titik yang bertetangga dengan k daun, maka ( ) + 1.
Bukti:
Misalkan adalah titik yang bertetangga dengan k daun yaitu , , , di G. Berdasarkan Teorema 2.1 bahwa setiap pewarnaan lokasi pada graf G mempunyai warna yang berbeda untuk setiap , = 1, 2, , . Jika v bertetangga dengan semua maka v harus memiliki warna yang berbeda
10 Berikut ini diberikan contoh menentukan bilangan kromatik lokasi pada suatu graf.
Gambar 4.Pewarnaan lokasi minimum pada graf G
Terlebih dahulu akan ditentukan batas bawah bilangan kromatik lokasi graf G. Karena titik yang mempunyai 3 daun maka berdasarkan Akibat 2.1 ,
( ) 4 (1)
Selanjutnya ditentukan batas atas bilangan kromatik lokasi graf G. Titik-titik pada V(G) dipartisi sebagai berikut:
= { }; = { , }; = { , }; = { , }. Kode warnanya adalah
( ) = (0,1,1,1) ; ( ) = (1,0,2,2) ; ( ) = (1,2,0,2) ; ( ) =
(1,2,2,0); ( ) = (1,0,1,2); ( ) = (2,1,0,1); ( ) = (3,2,1,0).
Karena semua titik di G mempunyai kode warna berbeda, maka c merupakan
pewarnaan lokasi . jadi, ( ) 4 (2)
Berdasarkan Persamaan (1) dan (2), maka ( ) = 4.
11 Bukti:
Misalkan c adalah pewarnaan lokasi pada G dan misalkan v adalah titik yang mempunyai derajat maksimum k. Maka v bertetangga dengan titik
✝ ✝ ✝ sehingga ( ✝ )✞ ( ✝ )✞ = ( , ) = 1. Menurut Teorema 2.1, diperoleh ( ) ( ) ( ) sehingga , , ,
mempunyai warna berbeda, dan karena v bertetangga dengan , , , maka v mempunyai warna yang berbeda dari , , , Jadi warna yang dibutuhkan adalah (1 + k) warna. Akibatnya, ( ) 1 + .
Berikut ini diberikan bilangan kromatik lokasi beberapa graf yang diambil dari Chartrand dkk. (2002) .
Teorema 2.3bilangan kromatik lokasi graf lintasan , n 3 adalah 3.
Bukti:
Diketahui bahwa ( ) = 1 dan ( ) = 2. Jelas bahwa untuk n 3 maka ( ) 3. Berdasarkan Teorema 2.2 ( ) 1 + , dengankadalah derajat
titik maksimum. Karena , = 2, maka ( ) 1 + 2. Akibatnya, ( )
3. Jadi terbukti ( ) = 3.
Gambar 5. Pewarnaan lokasi minimum pada , 3
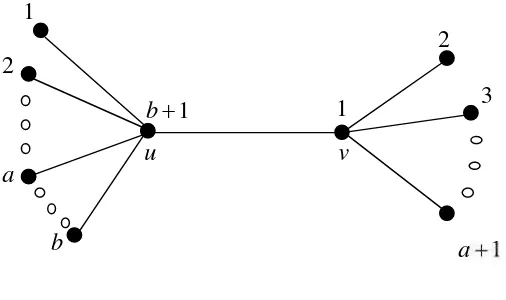
Teorema 2.4 Untuk bilangan bulat a dan b dengan 1 dan 2
, = + 1.
12 Bukti:
Berdasarkan Akibat 2.1 didapat batas bawah dari ✟ yaitu ✟ + 1.
Selanjutnya, ditentukan batas atasnya yaitu , + 1. Misalkan c
merupakan pewarnaan titik dengan (b+1) warna seperti yang terlihat pada Gambar 6. Perhatikan bahwa kode warna dari setiap titik , berbeda,
sehinggacmerupakan pewarnaan lokasi. Jadi , = + 1.
Gambar 6.Pewarnaan lokasi minimum dari ,
Selanjutnya akan diberikan beberapa definisi tentang titik dominan dan clear pathyang diambil dari Asmiati dkk. (2013).
Misalkan c merupakan pewarnaan lokasi graf G (V,E) dan diberikan = { , , , } adalah partisi V(G) terhadap c. Suatu titik v G disebut titik
dominan jika ( , ) = 0 jika dan 1 untuk yang lainnya. Suatu lintasan yang menghubungkan dua titik dominan di G disebut dengan clear path jika semua titik internalnya bukan titik dominan.
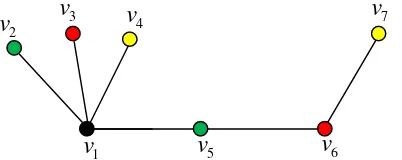
13 Berikut ini akan ditentukan bilangan kromatik lokasi dan titik dominan yang terdapat pada suatu graf G:
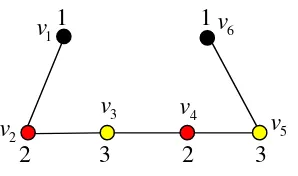
Gambar 7.Pewarnaan lokasi minimum pada
Pada Gambar 8. diperoleh bilangan kromatik lokasi dari graf tersebut adalah 3 dengan kode warna dari tiap-tiap titik sebagai berikut:
( )✠ {0,1,2} , ( ) = {1,0,1} , ( ) = {2,1,0} , ( ) = {2,0,1} , ( ) = {1,1,0}, ( ) = {0,2,1}
Berdasarkan teorema sebelumnya, maka graf pada Gambar 8. yang menjadi titik dominan adalah dan . Contoh clear path pada Gambar 8. adalah
.
Lemma 2.1 Diberikan suatu graf G dengan ( )= k. Terdapat paling banyak k titik dominan di G dan semuanya harus memiliki warna yang berbeda.
Bukti:
Misalkan merupakan titik dominan dan G adalah graf terhubung maka ( , ) = 0 untuk dan ( , ) = 1untuk . Karena ( ) = ,
maka kelas partisi Π memuat k kelas warna, misalkan , , , dan setiap
memiliki kode warna yang berbeda. Akibatnya, G memuat paling banyakktitik dominan dan masing-masing memiliki kode warna yang berbeda.
14 Lemma 2.2diberikan graf G dengan ( )= 3. Maka panjang dari setiapclear pathnya ganjil.
Bukti:
Diberikan 3 pewarnaan lokasi pada G. Diberikan P suatu clear path yang menghubungkan dua titik dominan x dan y pada G. Misalkan c(x) =1 danc(y) = 2 . jika semua titik internal P bukan dominan maka warna masing-masing titik haruslah 1 atau 2. Akibatnya, banyaknya titik internalnya harus genap. Jadi, panjang dari P adalah ganjil.
Lemma 2.3 Diberikan graf G yang memuat siklus dengan ( )✡ 3 dan c adalah pewarnaan dengan menggunakan tiga titik. Pernyataan berikut adalah ekuivalen:
a. Jika G memuat siklus ganjil maka G tepat memiliki 3 titik dominan dan ketiganya berada di siklus ganjil.
b. Jika G memuat siklus genap maka G memiliki paling banyak 3 titik dominan dan dua diantaranya haruslah titik yang bertetangga dalam suatu siklus.
Bukti:
15 b. Jika G memuat siklus genap, berdasarkan Lemma 2.1 dan 2.2 semua titik dari setiap siklus C di G harus menerima dua warna. Oleh karena itu, terdapat paling banyak dua titik dominan di C. Misalkan hanya terdapat satu titik dominan di C yaitu x , titik x harus mempunyai tetangga ketiga (diluar siklus C) yang menerima warna ketiga yang berbeda dari C. Akibatnya, dua titik lain yang bertetangga dengan xdi C akan mempunyai warna yang sama, kontradiksi.
BAB III METODE PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini dilakukan pada semester ganjil tahun ajaran 2014/2015
bertempat di jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
3.2 Metode Penelitian
Metode yang dilakukan untuk menganalisis graf maksimal sisi memuat siklus berbilangan kromatik lokasi tiga adalah:
1. Menentukan graf maksimal sisi memuat siklus berbilangan kromatik lokasi tiga.
2. Menganalisis graf maksimal sisi memuat siklus berbilangan kromatik lokasi tiga.
BAB V KESIMPULAN
5.1 Kesimpulan
1. Terdapat empat tipe graf maksimal sisi memuat siklus ganjil berbilangan kromatik lokasi tiga. Graf-graf tersebut diperoleh berdasarkan letak dari ketiga titik dominannya.
2. Graf maksimal sisi memuat siklus genap berbilangan kromatik lokasi tiga juga diperoleh. Hanya terdapat satu tipe graf yang memenuhi kondisi tersebut.
5.2 Saran
DAFTAR PUSTAKA
Asmiati, Assiyatun, H.and Baskoro, E.T. 2011. Locating-Chromatic Number of Amalgamation of Stars.ITB J.Sci.Vol 43A (1), 1-8.
Asmiati, and Baskoro, E.T. 2012. Characterizing All Graphs Containing Cycle with Locating – Chromatic Number 3. AIP Conf. Proc.Vol 1450, 351-357.
Baskoro, and Asmiati, E.T. 2013. Characterizing All Trees with Locating-Chromatic Number 3. Electronic Journal of Graph Theory and Application.Vol 1(2), 109-117.
Chartrand, G.et al. 2003. Graphs of Order n with Locating Chromatic Number n-1.Dicrete Mathemathics.Vol 269, 65-79.
Chartrand, G.et al. 2002. The Locating Chromatic Number of Graph. Bull Inst. Combin.Appl.Vol 36, 89-101.