PENYELESAIAN MASALAH ROTASI ALIRAN FLUIDA
KENTAL VON KARMAN MENGGUNAKAN METODE
SPEKTRAL HOMOTOPI
PARARAWENDY INDARJO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Spektral Homotopi adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, April 2015
Pararawendy Indarjo
ii
ABSTRAK
PARARAWENDY INDARJO. Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Spektral Homotopi. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.
Masalah rotasi aliran fluida kental Von Karman sering muncul pada masalah rotasi bahan bakar pesawat ruang angkasa yang diluncurkan oleh NASA. Pengendalian besaran kecepatan rotasi pada aliran Von Karman penting dilakukan. Persamaan yang menjelaskan rotasi aliran pada fluida kental yang disebabkan oleh cakram yang berputar terus-menerus adalah persamaan Von Karman. Pada karya ilmiah ini, pendekatan analitik untuk menyelesaikan persamaan Von Karman dilakukan dengan metode spektral homotopi. Dalam metode ini, dikombinasikan metode spektral dan metode homotopi. Sebagaimana metode homotopi, diperlukan parameter bantu untuk mengontrol daerah kekonvergenan penyelesaian. Penyelesaian yang dihasilkan merupakan suatu rumus rekursif dengan suatu hampiran awal yang diberikan. Menggunakan perangkat lunak berbasis fungsional, diperoleh penyelesaian berupa besaran komponen kecepatan yang konvergen ke suatu nilai.
Kata kunci: persamaan Von Karman, metode spektral homotopi, masalah taklinear
ABSTRACT
PARARAWENDY INDARJO. Solution of Von Karman Rotation Viscous Fluid Flow Problem using Spectral Homotopy Method. Supervised by JAHARUDDIN and ALI KUSNANTO.
Von Karman viscous fluid flow rotation problem appears frequently on spacecraft’s fuel rotation problem launched by NASA. The control of speed magnitude is important to be performed. The equation which explains viscous fluid flow rotation induced by infinite disk rotation is Von Karman equation. In this work, an analytic approximation solution of this equation is obtained by spectral homotopy method. This method consists of a combination between spectral method and homotopy method. In homotopy method, an embedded parameter is needed to control the solution’s convergence region. The solution of this problem is then expressed in term of a recursive formula with a given initial approximation. Using functional-based software, it is shown that velocity components converge to a particular value.
iii
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PENYELESAIAN MASALAH ROTASI ALIRAN FLUIDA
KENTAL VON KARMAN MENGGUNAKAN METODE
SPEKTRAL HOMOTOPI
PARARAWENDY INDARJO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian ini ialah metode penyelesaian sistem persamaan diferensial, dengan judul Penyelesaian Masalah Rotasi Aliran Fluida Kental Von Karman Menggunakan Metode Spektral Homotopi.
Terima kasih penulis ucapkan kepada Bapak Dr Jaharuddin MS dan Bapak Drs Ali Kusnanto MSi selaku pembimbing, serta kepada Ibu Elis Khatizah SSi MSi selaku dosen penguji. Penghargaan tertinggi penulis berikan kepada kedua orang tua beserta seluruh keluarga, atas segala doa dan dukungan yang tak ternilai harganya. Di samping itu, penulis juga mengucapkan terimakasih kepada seluruh rekan di Departemen Matematika, terutama angkatan 48, atas kebersamaan dalam lebih dari tiga tahun ini.
Semoga karya ilmiah ini bermanfaat.
Bogor, April 2015
Pararawendy Indarjo
DAFTAR ISI
DAFTAR GAMBAR iii
DAFTAR LAMPIRAN iii
PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
Persamaan Navier Stokes 2
Metode Homotopi 4
Metode Mean Weight Residual 5
HASIL DAN PEMBAHASAN 7
Aplikasi Metode 8
Studi Kasus 12
SIMPULAN DAN SARAN 16
Simpulan 16
Saran 16
DAFTAR PUSTAKA 17
LAMPIRAN 18
RIWAYAT HIDUP 28
DAFTAR GAMBAR
1 Domain fluida dalam koordinat silinder 3
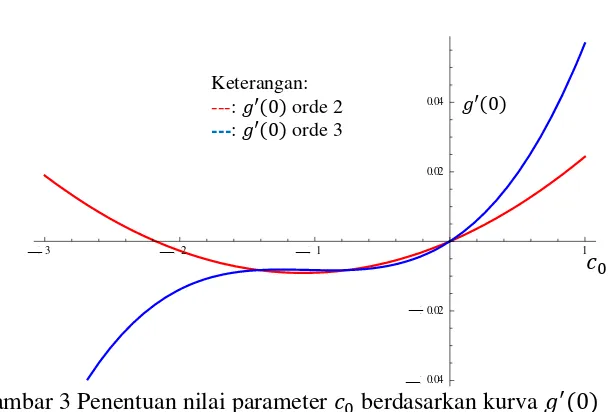
2 Penentuan nilai parameter berdasarkan kurva ℎ′ 12 3 Penentuan nilai parameter c berdasarkan kurva g' 13
4 Kurva terhadap dengan = − 14
5 Kurva terhadap dengan = − 15
DAFTAR LAMPIRAN
1 Penurunan persamaan (10)-(11) 18
2 Penurunan persamaan (56)-(59) 20
3 Penurunan persamaan (65)-(68) 22
4 Penurunan persamaan (74)-(76) 27
PENDAHULUAN
Latar Belakang
Rotasi aliran fluida kental Von Karman merupakan masalah yang terkenal dalam mekanika fluida. Salah satu aplikasinya adalah rotasi bahan bakar pesawat ruang angkasa yang diluncurkan oleh NASA. Rotasi aliran fluida kental Von Karman digunakan untuk menganalisis karakteristik bahan bakar pesawat ruang angkasa yang mudah terbakar dalam keadaan sedikit gravitasi. Kecepatan rotasi bahan bakar sangat memengaruhi timbulnya percikan api pada media bahan bakar. Aliran Von Karman mengontrol besaran kecepatan rotasi agar bahan bakar tidak menimbulkan percikan api yang dapat memengaruhi media bahan bakar (Williams dan Nayagam 2002). Secara umum, persamaan Von Karman menjelaskan tentang aliran fluida kental yang disebabkan oleh cakram yang berputar terus-menerus. Dengan menganggap aliran tunak dan laminar, aliran fluida kental tak-termampatkan ini berputar terus-menerus di atas cakram dengan suatu kecepatan sudut. Persamaan gerak dari fluida ini dinyatakan dalam persamaan kontinuitas dan persamaan Navier-Stokes dengan suatu kondisi batas tertentu. Von Karman mengubah persamaan diferensial parsial pada persamaan kontinuitas dan persamaan Navier-Stokes menjadi persamaan diferensial biasa menggunakan suatu transformasi (Liao 2004).
Pada kenyataannya, persamaan rotasi aliran fluida kental Von Karman merupakan persamaan taklinear yang masih sulit untuk ditemukan penyelesaian eksaknya. Beberapa peneliti telah menggunakan pendekatan numerik atau kombinasi analitik dan numerik untuk menyelesaikan masalah tersebut, diantaranya metode pendekatan numerik untuk menyelesaikan persamaan Von Karman (Benton 1966), metode homotopi (Liao 2004), dan metode homotopi tetapi dengan pendekatan deret polinomial (El-Nahhas 2007).
Di sisi lain, terdapat metode spektral yang juga dapat digunakan untuk menyelesaikan suatu persamaan diferensial. Metode ini telah digunakan peneliti untuk menyelesaikan berbagai permasalahan diferensial. Beberapa diantaranya adalah analisis kestabilan arus fluida yang berputar (Khorrami et al. 1989), penentuan penyelesaian numerik dari persamaan Navier-Stokes pada aplikasi aliran Taylor-Coutte (Moser et al. 1983), dan penyelesaian persamaan Schrodinger (Feit et al. 1982).
Di dalam karya ilmiah ini, dibahas penyelesaian masalah rotasi aliran fluida kental menggunakan metode spektral homotopi. Metode ini adalah modifikasi dari metode homotopi dengan penyelesaian persamaan deformasi di masing-masing orde ditentukan menggunakan metode spektral.
Perumusan Masalah
2
homotopi untuk mendapatkan penyelesaian pendekatan dari persamaan tersebut. Didefinisikan suatu fungsi homotopi yang akan diterapkan pada analisis homotopi.
Tujuan Penelitian
Penelitian dalam karya ilmiah ini bertujuan untuk:
1. Mengkonstruksi ulang penurunan persamaan kontinuitas fluida dan persamaan Navier-Stokes dalam sistem koordinat silinder yang merupakan persamaan Von Karman.
2. Menggunakan metode spektral homotopi untuk menyelesaikan persamaan Von Karman.
3. Menggambarkan kurva penyelesaian persamaan Von Karman dengan perangkat lunak berbasis fungsional, kemudian memberikan tafsiran terhadap hasil-hasil tersebut.
TINJAUAN PUSTAKA
Dalam penelitian ini, model matematis yang ditinjau adalah persamaan Von Karman. Persamaan ini diturunkan dari persamaan Navier Stokes yang diuraikan berikut ini.
Persamaan Navier Stokes
Persamaan Navier-Stokes diturunkan berdasarkan persamaan gerak pada fluida. Persamaan gerak ini berpadanan dengan kekekalan momentum yang menyatakan bahwa rata perubahan momentum merupakan selisih antara rata-rata momentum yang masuk dengan rata-rata-rata-rata momentum yang keluar kemudian dijumlahkan dengan jumlah gaya-gaya yang terjadi pada sistem.
Penurunan persamaan Navier-Stokes dilakukan dengan asumsi-asumsi sebagai berikut:
1. Fluida memiliki koefisien kekentalan yang konstan. 2. Fluida memiliki sifat tak termampatkan.
3. Kecepatan aliran fluida pada suatu titik tidak bergantung terhadap waktu (tunak).
4. Aliran fluida bersifat kontinu dan tidak saling berpotongan (laminar). 5. Gaya gravitasi diabaikan.
Berdasarkan asumsi di atas, persamaaan Navier-Stokes dituliskan dalam persamaan vektor (Streeter dan Wiley 1985) berikut:
��
� = � � − �̃
3
� berturut-turut merupakan rapat massa fluida, tekanan fluida, dan koefisien kekentalan kinematik. Kemudian, didefinisikan operator �
� sebagai berikut
Berdasarkan asumsi bahwa kecepatan aliran fluida bersifat tunak, � tidak bergantung pada t. Akibatnya, suku pertama di ruas kanan persamaan (2) akan
Berdasarkan persamaan (3), persamaan (1) dapat diuraikan menjadi:
[ �� + �� + �� ] = � [�� +�� +�� ] − ��̃� , [ �� + �� + �� ] = � [�� +�� +�� ] − ��̃� , [ �� + �� + �� ] = � [�� +�� +�� ] − ��̃� .
Di sisi lain, tinjau persamaan kontinuitas fluida yang diberikan sebagai berikut
�
� = −� . � .
Berdasarkan asumsi bahwa fluida bersifat tak termampatkan, ruas kiri persamaan (7) akan bernilai nol. Kemudian, karena � bernilai positif, persamaan (7) dapat
Elemen volume yang dilalui fluida dapat berbentuk sebarang. Tinjau fluida dalam bentuk silinder dengan bagian alas ditunjukkan pada Gambar 1.
Gambar 1 Domain fluida dalam koordinat silinder
Selanjutnya, persamaan kontinuitas fluida pada persamaan (8) akan dinyatakan dalam koordinat silinder. Sistem koordinat silinder dinyatakan sebagai pasangan terurut , , . Transformasi koordinat kartesian menuju koordinat silinder diberikan sebagai berikut
4
Jika transformasi variabel pada persamaan (9) dan aturan rantai digunakan, maka akan diperoleh persamaan berikut
� = cos + sin , � = − sin + cos ,
dengan � dan � berturut-turut menyatakan komponen kecepatan dalam arah dan . Selanjutnya, dengan menggunakan transformasi (9) dan persamaan (10), diperoleh persamaan (8) dalam koordinat silinder sebagai berikut
� � persamaan (10) dan (11) diberikan pada Lampiran 1.
Tinjau kembali persamaan Navier-Stokes dalam koordinat kartesian yang diberikan pada persamaan (4)-(6). Dengan cara yang serupa pada penurunan persamaan (11), diperoleh persamaan Navier-Stokes yang dinyatakan dalam koordinat silinder sebagai berikut:
� ���
Persamaan (11)-(14) akan diselesaikan dengan metode spektral homotopi. Konsep metode homotopi diberikan sebagai berikut.
Metode Homotopi
Berikut ini diberikan ilustrasi konsep metode homotopi yang disarikan dari (Liao 2004). Misalkan diberikan persamaan diferensial berikut
�[ ] = ,
dengan N operator turunan, t variabel bebas dan u(t) fungsi yang akan ditentukan. Selanjutnya, didefinisikan pula suatu operator linear L yang memenuhi
L[ f] = 0, bila f = 0.
Misalkan merupakan pendekatan awal dari penyelesaian persamaan (15) dan q [0,1] suatu parameter. Didefinisikan suatu fungsi H sebagai berikut
[�; ] = − �[� − ] + �[�].
� ; = masing-masing merupakan penyelesaian dari persamaan
[� : ; ] = dan [� : ; ] = .
Dengan demikian peningkatan nilai q dari 0 sampai 1 menyatakan perubahan nilai
5 dengan adalah pendekatan awal, dan B(t) masing-masing merupakan parameter bantu dan fungsi bantu. Jika q = 0 dan q = 1, maka dari persamaan (18) akan diperoleh � ; = dan �[� ; = ]. Selanjutnya, karena parameter q bernilai dari 0 sampai 1, maka � ; memetakan dari penduga awal ke penyelesaian eksak u(t). Dengan menggunakan konsep deret Taylor,
� ; dapat diuraikan menjadi
� ; = + ∑+∞
Untuk = , maka persamaan (19) menjadi
� ; = + ∑
+∞
=
.
Hasil ini menunjukkan adanya hubungan antara penyelesaian eksak dengan pendekatan awal dan , n = 1, 2, 3, … yang akan ditentukan.
Penyelesaian pendekatan ,n = 1, 2, 3, … diperoleh dari persamaan (20) dengan terlebih dahulu menentukan operator linear L. (Liao 2004).
Metode spektral homotopi adalah gabungan antara metode homotopi dan metode spektral. Metode spektral adalah salah satu bentuk khusus dari metode
mean weight residual yang diberikan sebagai berikut.
Metode Mean Weight Residual
Metode Mean Weight Residual (selanjutnya disingkat MWR) adalah metode yang umum digunakan untuk mendapatkan penyelesaian persamaan diferensial. Penyelesaian yang akan ditentukan diuraikan dalam bentuk deret dari fungsi-fungsi basis yang dapat ditentukan berdasarkan persamaan diferensial sedemikian sehingga diperoleh penyelesaian persamaan diferensial tersebut.
Misalkan diberikan suatu masalah nilai batas sebagai berikut:
, = ; , Ω
, ,��� ,��� = ; , Γ, batas dari Ω. Misalkan penyelesaian masalah nilai batas (23) diambil dalam bentuk
= + ∑
�
=
,
6 penyelesaian eksak. Dalam MWR konstanta ditentukan sedemikian sehingga rata-rata sisaan (25) menjadi nol. Integral terboboti dari sisaan diatur menjadi nol:
, = ∫� �= = , , … , �.
Berdasarkan persamaan (26), maka persamaan (25) dapat ditulis sebagai berikut dan fungsi pembobot telah didefinisikan, dapat dibalik untuk mendapatkan
, yang akhirnya memberikan pendekatan penyelesaian persamaan (23).
Terdapat banyak cara untuk memilih fungsi pembobot dan setiap pilihan bersesuaian pada kriteria tertentu MWR. Domain Ω dibagi ke dalam � subdomain yang lebih kecil, Ω , maka salah satu cara mendefinisikan adalah sebagai berikut
= { , Ω, Ω .
Seiring dengan bertambahnya �, persamaan diferensial (23) terpenuhi secara rata-rata dalam subdomain yang semakin kecil, dan dapat dianggap mendekati nol dimana-mana.
Dalam perkembangannya, MWR dikembangkan ke dalam beberapa metode yang lebih spesifik. Diantaranya adalah metode collocation, Galerkin, dan spektral.
Pada metode collocation, fungsi pembobot dipilih sebagai fungsi delta Dirac
= �( − ),
yang memenuhi kondisi berikut
∫ � = | �
� ,
sehingga sisaan bernilai nol pada sejumlah � tertentu titik-titik collocation .
Saat � meningkat, sisaan akan bernilai nol di semakin banyak titik dan dapat dianggap mendekati nol di mana-mana.
Pada metode Galerkin, fungsi pembobot dipilih sama dengan fungsi basis,
= . Fungsi basis harus dipilih sebagai anggota-anggota dari himpunan fungsi yang lengkap. Sebuah himpunan fungsi { } disebut lengkap jika fungsi manapun dari kelas yang diberikan dapat diuraikan dalam suku-suku dari himpunan tersebut,
= ∑ . Sehingga deret dalam persamaan (24) dapat merepresentasikan penyelesaian eksak yang ingin ditentukan. Selanjutnya, metode Galerkin (25)
7 memaksa sisaan menjadi nol dengan membuatnya ortogonal terhadap setiap anggota dari fungsi himpunan lengkap (saat � → ∞) (Finlayson 1972).
Metode terakhir, metode spektral, dikembangkan berdasarkan konsep bahwa dalam MWR, penyelesaian , diuraikan dalam deret berikut
, = ∑
∞
=
dengan menjadi koefisien urai dan adalah himpunan fungsi basis yang saling ortogonal. Pada praktiknya, ekspresi deret dijumlahkan hingga batas � tertentu dan fungsi basis yang umum digunakan adalah polinomial Chebyshev atau Legendre (Ogundare 2009).
HASIL DAN PEMBAHASAN
Tinjau persamaan Von Karman untuk tunak, berlapis, simetrik terhadap pusat koordinat yang terinduksi oleh cakram putar tunak takhingga dengan kecepatan sudut Ω berpusat di sumbu-z pada fluida terisolasi pada separuh-ruang
> di atas cakram. Persamaan Von Karman dalam koordinat silinder , , adalah persamaan (11)-(14) dengan kondisi batas yang rata dan licin pada cakram dan kondisi batas di ketakhinggaan berikut
� = Ω � = � = , saat = ,
� = � = , saat = +∞,
dengan � adalah kerapatan fluida, � adalah koefisien kekentalan kinematik, �̃ adalah tekanan, � , � , dan � secara berurut adalah komponen kecepatan dalam arah jari-jari , sudut , dan sumbu- , serta Ω adalah konstanta kecepatan sudut.
Langkah pertama yang akan dilakukan adalah penyederhanaan persamaan (11)-(14). Untuk itu, digunakan transformasi Von Karman berikut:
� = � , � = � ,
� = √�� , �̃ = −���� ,
dengan = √�/� besaran nondimensional yang menyatakan jarak sepanjang sumbu rotasi.
Jika transformasi (29) digunakan, maka persamaan (11)-(14) menjadi persamaan diferensial biasa berikut:
′′ − ′ − + = ,
′′ − ′ − = ,
′′ − ′ + �′ = ,
+ ′ = .
Kondisi batas (28) menjadi
= ∞ = , = , ∞ = , = .
Dari persamaan (33) diperoleh
= − �′ .
Jika persamaan (35) disubstitusikan ke dalam persamaan (30) dan (31), maka diperoleh persamaan berikut:
8
′′ − ′ + ′ = ,
dan kondisi batas (34) menjadi
= ′ = ′ ∞ = , = ∞ = .
Dalam karya ilmiah ini akan dibahas penyelesaian persamaan (36) dan (37) dengan kondisi batas (38) menggunakan metode spektral homotopi.
Aplikasi Metode
Berikut ini akan dibahas penggunaan metode spektral homotopi yang telah diuraikan sebelumnya. Dimulai dengan mentransformasi daerah asal masalah dari
[ , ∞ ke [− , ] menggunakan metode pemotongan daerah asal. Sebelum transformasi dilakukan, untuk alasan komputasi, selang [ , ∞ digantikan dengan
[ , �] dengan � adalah konstanta yang dipilih sedemikian sehingga lebih besar dari ketebalan lapisan fluida. Selang [ , �] kemudian ditransformasi ke daerah asal [− , ] menggunakan transformasi berikut
� = � − , � [− , ].
Penyelesaian persamaan (36) – (38) dimisalkan dalam bentuk
= ℎ � + = � +
dengan dan adalah fungsi-fungsi yang memenuhi kondisi batas (38). Aturan rantai memberikan
Substitusi persamaan (40)-(43) ke dalam persamaan (36) dan (37) menghasilkan
9 Selanjutnya, berdasarkan persamaan (44) dan (45), didefinisikan operator-operator linear berikut:
�ℎ[ℎ̃ �; , ̃ �; ] = � ℎ̃�� + � ℎ̃�� + �ℎ̃��+ ̃ + ℎ̃,
��[ℎ̃ �; , ̃ �; ] = � �̃�� + �ℎ̃��+ ��̃��+ ℎ̃ + ̃,
Penyelesaian awal diperoleh dengan menyelesaikan bagian linear dari (44) dan (45), yaitu
Sistem (49)-(51) diselesaikan dengan metode spektral Chebyshev dengan fungsi-fungsi tak diketahui ℎ � dan � didekati oleh deret berhingga dari polinomial Chebyshev dalam bentuk
ℎ � ≈ ℎ�(� ) = ∑� ℎ̂
= , (� ), = , , … , �,
� ≈ �(� ) = ∑� ̂
= , (� ), = , , … , �,
dengan , dan , adalah polinomial Chebyshev ke-k. Koefisien-koefisien secara berurutan ℎ̂ dan ̂ , � , � , … , �� adalah titik-titik collocation Gauss-Lobatto yang didefinisikan sebagai berikut
� = cos� , = , , … , �,
dan � + adalah jumlah titik collocation. Turunan fungsi ℎ � dan � pada titik-titik collocation � direpresentasikan sebagai
��ℎ
���� = ∑�= � ℎ � , ���
���� = ∑�= � � ,
dengan adalah orde turunan dan � adalah matriks diferensial spektral Chebyshev. Substitusi (52)-(55) ke dalam (49)-(51) menghasilkan
10
yang juga memberikan pendekatan awal dari penyelesaian (44) dan (45).
Selanjutnya, akan dicari penyelesaian orde tinggi dari (44) dan (45). Berdasarkan persamaan (44) dan (45), didefinisikan operator taklinear �ℎ dan �� sebagai berikut:
Bedasarkan persamaan (18), persamaan deformasi orde nol diberikan sebagai berikut
− �ℎ[ℎ̃ �; − ℎ � ] = (�ℎ[ℎ̃ �; , ̃ �; ] − � ),
− ��[ ̃ �; − � ] = (��[ℎ̃ �; , ̃ �; ] − � ),
dengan [ , ] adalah parameter bantu dan adalah parameter taknol yang mengontrol kekonvergenan.
Kemudian, berdasarkan persamaan (20)-(22), persamaan orde ke-m
diberikan sebagai berikut
11 Berdasarkan persamaan (47), (48), (65), (66) dan (56), diperoleh
��� = + ���− − − � + �− , sebagaimana pada penyelesaian awal. Baris-baris yang bersesuaian, semua kolom, dari �di ruas kanan (69), �dan �− semua diatur menjadi nol. Ini akan menghasilkan formula rekursif berikut, untuk :
= �− [ + �̃� dengan menggunakan persamaan (73).
Selanjutnya, koefisien-koefisien ℎ̂ dan ̂ orde ke-m, pada persamaan (52) dan (53) dapat diperoleh dengan persamaan
12
= ( � , � , … �� )�.
Penurunan persamaan (74)-(76) diberikan pada Lampiran 4. Dengan demikian, diperoleh penyelesaian pendekatan dari persamaan Von Karman (36) dan (37) dalam bentuk deret orde ke-m sebagai berikut:
≈ ∑ = ∑�= ℎ̂, , � + ,
≈ ∑ = ∑�= ̂ , , � + .
Studi Kasus
Pada bagian ini akan dibahas suatu studi kasus penyelesaian persamaan Von Karman dengan menggunakan metode spektral homotopi. Berdasarkan uraian pada bagian aplikasi metode, berikut ini prosedur untuk menentukan penyelesaian dari persamaan Von Karman (36) dan (38):
1 Misalkan diberikan fungsi-fungsi pendekatan awal dan sebagai berikut
= − + − − ,
= − .
Jelas bahwa dan memenuhi kondisi batas (38). 2 Mencari nilai-nilai koefisien fungsi ℎ � dan � ,
menggunakan persamaan (74) dan (75), dengan terlebih dahulu mencari
, secara rekursif menggunakan persamaan (60) (untuk = ) dan (73) (untuk ).
3 Membentuk penyelesaian persamaan Von Karman (36) dan (37) menggunakan persamaan (77) dan (78).
Misalkan � = dan � = , maka berdasarkan persamaan (59) diperoleh matriks segi dengan dimensi 24. Kemudian persamaan (60) memberikan
= − . . , . , . , . , . , . , . , . , . , . ,
. , , , . , . , − . , . , − . , . , . , . , . , . , �.
Selanjutnya akan ditentukan nilai parameter yang sesuai. Nilai diperoleh dari kurva fungsi ℎ′ dan ′ untuk orde 2 dan orde 3. Kurva fungsi
ℎ′ dan ′ diberikan pada Gambar 2 dan Gambar 3 secara berurutan sebagai berikut.
Gambar 2 Penentuan nilai parameter berdasarkan kurva ℎ′
13
Gambar 3 Penentuan nilai parameter berdasarkan kurva ′
Berdasarkan Gambar 2 dan Gambar 3, dipilih nilai parameter = − . Kemudian, berdasarkan persamaan (73), diperoleh penyelesaian untuk =
, , , sebagai berikut oleh persamaan (74) dan (75) sebagai berikut
14
̂ = − . . , − . , − . , . , − . , . , . , − . , . , − . ,
− . , − . �,
̂ = − . − . , . , − . , − . , . , − . , . , − . , − . , . ,
− . , . �,
̂ = − . . , − . , . , − . , . , . , − . , . , − . , . ,
. , − . �,
̂ = − . . , − . , . , . , − . , . , − . , − . , . , − . ,
. , − . �.
Akhirnya diperoleh bentuk penyelesaian persamaan (36) dan (37) menggunakan persamaan (77) dan (78) sebagai berikut
≈ . + . � − . � − . � + . � + . � − . �
− . � + . � − . � − . � + . � +
≈ . − . � − . � + . � + . � − . � − . �
+ . � + . � − . � − . � + . � +
Berdasarkan persamaan (81) diperoleh kurva fungsi sebagai berikut.
Gambar 4 Kurva terhadap dengan = −
Berdasarkan Gambar 4, dimulai dari nol, nilai semakin menurun seiring dengan bertambahnya nilai . Nilai kemudian konvergen menuju -0.875024575 saat
→ ∞. Dengan kata lain, kecepatan partikel dalam arah sumbu yaitu � adalah
− . × √�Ω dengan � adalah koefisien kekentalan kinematik fluida dan Ω konstanta kecepatan sudut. Tanda negatif berarti bahwa arah gerak fluida pada sumbu adalah menuju titik pusat koordinat.
Berikut ini diberikan Tabel 1 yang menyatakan galat antara nilai dengan literatur (Putri 2013) dengan = − hingga orde ke-4.
2 4 6 8 10
0.8 0.6 0.4 0.2
H
(81)
(82)
−
−
−
15 Tabel 1 Perbandingan hasil penyelesaian ∞ terhadap literatur beserta galat orde ∞ Sp��tra� Ho�otopi ∞ �it�ratur Putri galat 1 -0.876244931 -0.859257831 0.0169871 2 -0.876350528 -0.864152428 0.0121981 3 -0.874753263 -0.868545963 0.0062073 4 -0.875024575 -0.876812375 0.0017878
Berdasarkan Tabel 1 dapat disimpulkan bahwa penyelesaian yang diperoleh dalam karya tulis ini cukup baik. Terbukti mengacu pada hasil yang diperoleh literatur (Putri 2013), galat yang dihasilkan oleh metode spektral homotopi pada karya tulis ini cenderung semakin kecil untuk setiap orde (hingga orde 4). Nilai galat yang terkecil dihasilkan pada orde 4, yakni kurang dari 0.002.
Gambar 5 Kurva terhadap dengan = −
Berdasarkan Gambar 5, kurva semakin menurun seiring membesarnya . Sehingga dapat disimpulkan konvergen ke 0 saat → ∞. Dikaitkan dengan konteks permasalahan, partikel fluida hampir tidak bergerak dalam arah tangensial yaitu � untuk fluida yang hampir takkental � → . Untuk fluida yang hampir kental � → ∞ , kecepatan partikel dalam arah sumbu
yaitu � adalah Ω dengan Ω merupakan kecepatan sudut.
1 2 3 4 5 6 7
0.2 0.4 0.6 0.8 1.0
16
SIMPULAN DAN SARAN
Simpulan
Metode spektral homotopi adalah suatu metode pendekatan analitik untuk menyelesaikan suatu sistem persamaan diferensial taklinear. Metode ini secara sederhana dapat dipandang sebagai pemasukan konsep spektral ke dalamanalisis homotopi. Metode ini dapat digunakan untuk menyelesaikan persamaan Von Karman berkenaan dengan rotasi aliran fluida kental. Penggunaan metode spektral homotopi untuk persamaan Von Karman memerlukan suatu operator taklinear yang ditentukan berdasarkan bentuk taklinear dari persamaan tersebut. Berdasarkan operator ini, diperoleh suatu rumus rekursif untuk memperoleh penyelesaian persamaan Von Karman yang dinyatakan dalam polinomial Chebyshev orde tertentu. Semakin tinggi orde yang digunakan, maka penyelesaian hampiran persamaan ini semakin mendekati penyelesaian eksaknya.
Dalam penelitian ini, diperoleh penyelesaian masalah berupa besaran komponen kecepatan fluida dalam arah sumbu- dan komponen kecepatan sudut. Untuk fuida yang takkental, partikel fluida tidak bergerak dalam arah sudut 0, namun bergerak dengan kecepatan dalam arah sumbu- sebesar . × √�Ω mendekati pusat koordinat. Pemilihan nilai parameter dalam metode spektral homotopi ikut menentukan kekonvergenan dari penyelesaian masalah tersebut.
Saran
17
DAFTAR PUSTAKA
Benton ER. 1966. On the flow due to a rotating disk. J.Fluid Mech. 24:781-800. Doi: http://dx.doi.org/10.1017/S002211206001009.
El-Nahhas A. 2007. Analytic approximations for Von Karman swirling flow.
Science. 44(3):181-187.
Feit MD, Fleck JA, Steiger A. 1982. Solution of the Schrodinger equation by a spectral method. Journal of Computanional Physics, 47, 412-433. doi:10.1016/0021-9991(82)90091-2.
Finlayson BA. 1972. The Method of Mean Weight Residual and Variational Principles. London: Academic Press.
Khorrami MR, Malik MR, Ash RL. 1989. Application of spectral collocation techniques to the stability of swirling flows. Journal of Computanional Physic. 81(1), 206-229. doi:10.1016/0021-9991(89)90071-5.
Liao S. 2004. Beyond Perturbation: Introduction to The Homotopy Analysis Method. New York (US): Boca Raton.
Moser RD, Moin P, Leonard A. 1983. A spectral numerical method for the Navier-Stokes equations to Taylor-Couette flow. Journal of Computational Physics. 52(3), 524-544. doi:10.1016/0021-9991(83)90006-2.
Ogundare BS. 2009. On the pseudo-spektral method of solving linear ordinary differential equations. Journal of Mathematics and Statistics. 5(2): 136-140. Putri, RG. 2013. Penyelesaian masalah rotasi aliran fluida kental Von Karman
menggunakan metode homotopi [Skripsi]. Bogor (ID): Institut Pertanian Bogor.
Siddiqui AM, Farooq AA, Haroon T, Babcock BS. 2013. A variant of the classical VonKarman flow for a Jeffrey fluid. Journal of Applied Mathematical Sciences. 7(20): 983-991.
Streeter VL, Wiley EB. 1985. Mekanika Fluida Jilid 1. Prijono A, penerjemah. Jakarta(ID): Penerbit Erlangga. Terjemahan dari: Fluid Mechanics, Ed ke-8. Williams FA, Nayagam V. 2002. Dynamics of diffusion flames in Von Karman
18
Lampiran 1 Penurunan persamaan (10) dan (11)
Pertama, akan diturunkan persamaan (10). Tinjau transformasi variabel yang diberikan pada persamaan (9) berikut
= cos , = sin .
Berdasarkan transformasi (9), diperoleh turunan-turunan parsial dari dan sebagai berikut:
Untuk mengawali penurunan, akan ditentukan turunan total dari terhadap yang dinyatakan sebagai komponen kecepatan arah sumbu , yaitu sebagai berikut
=�� =�� �� +�� �� .
Berdasarkan turunan-turunan parsial pada persamaan (83) dan � =�
� dan � = �
� , maka persamaan (84) dapat ditulis sebagai berikut
= cos � − sin � .
Dari persamaan (85) dan (86), diperoleh persamaan (10) sebagai berikut
� = cos + sin , � = − sin + cos .
Selanjutnya, akan diturunkan persamaan (11) yang merupakan hasil transformasi dari persamaan (8) ke dalam koordinat silinder. Langkah pertama, perhatikan bahwa transformasi (9) dapat dituliskan sebagai berikut:
= + ,
Kemudian tinjau persamaan (8) yang akan diturunkan berikut
�
Akan ditentukan representasi suku-suku pada ruas kiri persamaan (8) tersebut dalam koordinat silinder. Dengan menggunakan aturan rantai, diperoleh
19 sumbu , maka diperoleh hubungan berikut
= � ,
Jika persamaan (88)-(90) dijumlahkan, maka diperoleh persamaan berikut
cos �� − sin �� + sin �� + cos �� +��� = .
Kemudian sisipkan ekspresi
cos + sin + − cos − sin
pada persamaan (90), diperoleh
cos �� − sin �� + cos + sin + sin �� + cos �� +
− cos − sin +���
� = .
Ruas kiri persamaan (92) adalah penjabaran dari ekspresi berikut
�( cos + sin )
Berdasarkan persamaan (10), ekspresi (92) dapat dituliskan sebagai berikut
� � berdasarkan persamaan (92), telah diturunkan persamaan kontinuitas fluida dalam koordinat silinder sebagai berikut
20
Lampiran 2 Penurunan persamaan (56)-(59) Substitusikan (52) dan (53) berikut
ℎ � ≈ ℎ�(� ) = ∑ ℎ̂
ke dalam persamaan (49) berikut
ℎ′′′ � + ℎ′′ � + ℎ′ � + � + ℎ � = � diagonal. Selanjutnya, diperoleh persamaan matriks berikut
� + � + � + � + �
= [� , � , … , � � ]�
atau setara dengan
� + � + � + � � � = [� , � , … , �
� ]�. Persamaan ini merupakan bentuk matriks dari (49). Dengan menerapkan cara yang serupa, diperoleh bentuk matriks dari persamaan (50).
Berdasarkan persamaan (49) dan (50) diperoleh
21
= diag [ , , … , �− , � ] , = , , , , .
Selanjutnya penurunan kondisi batas yang bersesuaian. Dimulai dengan kondisi batas yang diberikan oleh persamaan (51) berikut
ℎ − = �ℎ′
− = �ℎ′ = , − = , = .
Perhatikan titik-titik collocation � , = , , … , � . Berdasarkan definisi titik
collocation pada (54), diketahui � = − saat = � dan � = saat = . Kemudian, dengan menerapkan fakta bahwa ��ℎ
���� = ∑�= � ℎ � , maka kondisi batas (51) memberikan
� ∑ � ℎ � = , �
�
=
∑ �� ℎ � = , ℎ �� = ,
�
=
22
Lampiran 3 Penurunan persamaan (65)- (68)
Untuk mendapatkan persamaan deformasi orde ke-m, kedua ruas pada persamaan deformasi orde nol (63) dan (64) diturunkan terhadap q sebanyak m
kali, kemudian dibagi dengan m! dan substitusikan nilai q=0.
Pertama, tinjau persamaan deformasi orde nol untuk fungsi h pada persamaan (63) berikut
− �ℎ[ℎ̃ �; − ℎ � ] = (�ℎ[ℎ̃ �; , ̃ �; ] − � ).
Turunan pertama persamaan (63) terhadap q adalah
−�ℎ[ℎ̃ �; − ℎ � ] + − �ℎ[�� ℎ̃ �; ]
= (�ℎ[ℎ̃ �; ,̃ �; ]− � ) + � (� �ℎ[ℎ̃ �; ,̃ �; ]− � ).
Substitusi nilai q=0 memberikan
�ℎ[ℎ ] = �ℎ[ℎ , ] − � .
Turunan kedua persamaan (63) terhadap q adalah
− �ℎ[�� ℎ̃ �; ]+ − �ℎ[�� ℎ̃ �; ]
= � (� �ℎ[ℎ̃ �; ,̃ �; ]− � ) + � (� �ℎ[ℎ̃ �; ,̃ �; ]− � ).
Substitusi nilai q=0 memberikan
�ℎ[ℎ − ℎ ] = �� (�ℎ[ℎ̃ �; , ̃ �; ] − � )| =
yang ekuivalen dengan
�ℎ[ℎ − ℎ ] = �� (�ℎ[ℎ̃ �; , ̃ �; ] − � )| = .
Turunan ketiga persamaan (63) terhadap q adalah
− �ℎ[�� ℎ̃ �; ]+ − �ℎ[�� ℎ̃ �; ]
= �
� (�ℎ[ℎ̃ �; , ̃ �; ] − � )+ �
23 Substitusi nilai q=0 memberikan
�ℎ[ℎ − ℎ ] = �� (�ℎ[ℎ̃ �; , ̃ �; ] − � )| =
yang ekuivalen dengan
�ℎ[ℎ − ℎ ] = �� (�ℎ[ℎ̃ �; , ̃ �; ] − � )| =
.
Turunan keempat persamaan (63) terhadap q adalah
− �ℎ[�� ℎ̃ �; ]+ − �ℎ[�� ℎ̃ �; ]
= (�ℎ[ℎ̃ �; , ̃ �; ] − � )+ �� (�ℎ[ℎ̃ �; , ̃ �; ] − � ).
Substitusi nilai q=0 memberikan
! �ℎ[ℎ − ℎ ] = � (� �ℎ[ℎ̃ �; ,̃ �; ]− � )| =
yang ekuivalen dengan
�ℎ[ℎ − ℎ ] = ! � (� �ℎ[ℎ̃ �; ,̃ �; ]− � )| =
.
Untuk turunan ke-m dengan , diperoleh
− �ℎ[� −
� − ℎ̃ �; ]+ − �ℎ[
�
� ℎ̃ �; ]
= �� −− (�ℎ[ℎ̃ �; , ̃ �; ] − � )+ �� (�ℎ[ℎ̃ �; , ̃ �; ] − � ).
Substitusi nilai q=0 memberikan
! �ℎ[ℎ − ℎ − ] = �
−
� − (�ℎ[ℎ̃ �; ,̃ �; ]− � )|
=
yang ekuivalen dengan
�ℎ[ℎ − ℎ − ] = − ! �
−
� − (�ℎ[ℎ̃ �; ,̃ �; ]− � )|
=
24
Cara yang serupa diterapkan pada persamaan (64), diperoleh
��[ − − ] = ,
25
Telah diturunkan bagian pertama persamaan (68). Selanjutnya, bagian kedua persamaan (68) dapat diturunkan dengan cara serupa.
26
yang ekuivalen dengan
� = ′′+ ℎ′ + ′ + ℎ +
+ �ℎ′
+ �ℎ′
+ �ℎ′
− � ′
ℎ − � ′
ℎ − � ′ℎ
�
= !( ′′+ ℎ′ + ′ + ℎ +
+ � ℎ′
+ � ℎ′
+ � ℎ′
+ � ℎ′
− � ′
ℎ − � ′
ℎ − � ′ℎ
− � ′ℎ )
yang ekuivalen dengan
� = ′′+ ℎ′ + ′ + ℎ +
+ �ℎ′
+ �ℎ′
+ �ℎ′
+ �ℎ′
− � ′
ℎ − � ′
ℎ − � ′
ℎ − � ′ℎ
atau secara umum � � =
−
′′ + ℎ
−
′ +
−
′ + ℎ
− + −
+ � ∑(ℎ′
− − − ′ℎ − − ) − � − .
−
27 Lampiran 4 Penurunan persamaan (74) – (76)
Telah diketahui bahwa untuk setiap orde m, , ℎ didekati sebagai fungsi polinom berorde N dengan masing-masing sukunya adalah polinomial Chebysev berorde 0,1,...,N. Kemudian untuk setiap suku, polinomial Chebyshev ini dievaluasi pada titik-titik collocation � , = , , … , �,sehingga diperoleh sistem persamaan linear berikut
� ℎ̂ � � ℎ̂�
⋱
�� ℎ̂ � �� ℎ̂�
= (ℎ � , ℎ � , … ℎ �� )�
dengan vektor variabel yang ingin dicari adalah koefisien-koefisien
(ℎ̂ , ℎ̂ , … , ℎ̂�)� . Sistem persamaan linear tersebut dapat dituliskan sebagai berikut
( � ⋱ � �
�� � ��
) (ℎ̂ , ℎ̂ , … , ℎ̂�)� = (ℎ � , ℎ � , … ℎ �� )�.
Selanjutnya, jelas bahwa (ℎ̂, ℎ̂, … , ℎ̂)� � dapat dicari dengan persamaan
(ℎ̂ , ℎ̂ , … , ℎ̂�)� = (
� � �
⋱
�� � ��
)
−
(ℎ � , ℎ � , … ℎ �� )�.
ekuivalen dengan yang ingin diturunkan. Serupa untuk penurunan koefisien ̂ ,� diperoleh
̂� = − ,
̂�= − ,
dengan
̂�= (ℎ̂ , ℎ̂ , … , ℎ̂�)�, ̂�= ̂ , ̂ , … , ̂� �,
= ( � ⋱ � �
�� � ��
),
= (ℎ � , ℎ � , … ℎ �� )�,
28
RIWAYAT HIDUP
Penulis dilahirkan pada tanggal 19 Januari 1994 di Sampit, Kalimantan Tengah sebagai anak kedua dari tiga bersaudara dari pasangan Sularjo dan Asih Indarti. Pendidikan formal yang ditempuh penulis dimulai dari TK Tunas Rimba (lulus pada 1999), kemudian dilanjutkan di SDN 2 Mentawa Baru Hilir (lulus pada 2005). Selanjutnya, pendidikan tingkat menengah ditempuh penulis di SMPN 1 (lulus tahun 2008) dan SMAN 1 (lulus tahun 2011) yang semuanya berada di Sampit. Pada tahun 2011, penulis diterima menjadi mahasiswa Departemen Matematika IPB melalui jalur SNMPTN Undangan.
Selama berkuliah di IPB, penulis aktif mengikuti kegiatan ekstra-kurikuler yang tersedia di lingkungan kampus. Beberapa organisasi yang pernah penulis ikuti adalah Klub Asrama Tutor Sebaya (2011-2012), Lembaga Dakwah Kampus Al-Hurriyyah (2011-2012) dan Gugus Mahasiswa Matematika (2012-2014). Selain organisasi, penulis juga sempat berpartisipasi dalam beberapa kepanitian antara lain MPKMB (Masa Perkenalan Kampus Mahasiswa Baru) IPB 49, Matematika Ria (2013, 2014) dan IPB Mathematics Challenge (2013, 2014). Penulis juga pernah aktif menjadi asisten responsi untuk matakuliah Kalkulus III dan Pemrograman Linear.
Selanjutnya, berikut ini adalah beberapa pencapaian, akademik maupun non-akademik, yang pernah ditorehkan penulis selama menjadi mahasiswa S-1 Departemen Matematika IPB:
Ketua Klub Asrama terbaik (2012)
Mahasiswa Berprestasi Asrama TPB IPB (2012) Juara I GumatikaCalculus Cup (2012)
Juara II Lomba Debat “Nasionalisme” Fateta se-IPB (2012) Juara II Kompetisi Statistika Dasar, Statistika Ria 2013 Mahasiswa Berprestasi Departemen Matematika IPB (2014)
Delegasi Kopertis III dalam ON-MIPA tingkat Nasional bidang Matematika (2014)