ANALISIS CURAH HUJAN UNTUK PENDUGAAN DEBIT
PUNCAK DENGAN METODE RASIONAL PADA
DAS PERCUT KABUPATEN DELI SERDANG
SKRIPSI
Oleh:
MACHAIRIYAH
DEPARTEMEN TEKNOLOGI PERTANIAN
FAKULTAS PERTANIAN
UNIVERSITAS SUMATERA UTARA
2007
PUNCAK DENGAN METODE RASIONAL PADA
DAS PERCUT KABUPATEN DELI SERDANG
SKRIPSI
Oleh:
MACHAIRIYAH
030308008/TEKNIK PERTANIAN
Skripsi Sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana di Fakultas Pertanian
Universitas Sumatera Utara
Diketahui Oleh: Komisi Pembimbing
Prof. Dr. Ir. Sumono, MS Ir. Edi Susanto, M.Si
Ketua Anggota
DEPARTEMEN TEKNOLOGI PERTANIAN
FAKULTAS PERTANIAN
UNIVERSITAS SUMATERA UTARA
2007
Nama : Machairiyah
NIM : 030308008
Departemen : Teknologi Pertanian Program Studi : Teknik Pertanian
Disetujui Oleh:
Komisi Pembimbing
(Prof. Dr. Ir. Sumono, MS) (Ir. Edi Susanto, M.Si)
Ketua Anggota
Mengetahui :
(Ir. Saipul Bahri Daulay, M.Si) Ketua Departemen
ABSTRACT
Rainfall is the most important input component in the hydrologic process. Rainfall characteristics, such as intensity (I), duration (t), depth (d) and frequency. Intensity that is related to duration and frequency can be expressed by Intensity-Duration-Frequency (IDF) curve. Data used in this research comprised of rainfall and land use data. The data of rainfall used were daily rainfall recorded in Saentis station. In the research, daily rainfall depth was calculated by frequency analysis, which was started by determining the daily maximum mean rainfall with partial series method, followed by calculating the statistical parameter to choose the best distribution. Intensity could be calculated by Mononobe method and to calculate flood discharge using the rational method.
The result of this study indicated that the Log Pearson Type III distribution fit to most of data in the Percut DAS and flood discharge with return period can be calculated .
Keywords : rainfall, intensity, the flood discharge, rational method
ABSTRAK
Hujan adalah komponen masukan penting dalam proses hidrologi. Karakteristik hujan diantaranya intensitas, durasi, kedalaman dan frekuensi. Intensitas yang berhubungan dengan durasi dan frekuensi dapat diekspresikan dengan kurva Intensity -Duration- Frequency (IDF). Data yang diperlukan berupa data curah hujan dan data tata guna lahan. Data curah hujan yang digunakan adalah data curah hujan harian yang tercatat pada stasiun Saentis. Dalam penelitian ini, curah hujan harian dihitung dengan analisis frekuensi yang dimulai dengan menentukan curah hujan harian maksimum rata-rata dengan metode parsial, kemudian menghitung parameter statistik untuk memilih distribusi yang paling cocok. Intensitas dihitung dengan mempergunakan metode mononobe dan untuk menghitung debit puncak dengan metode rasional.
Hasil penelitian menunjukkan bahwa distribusi Log Pearson Type III sangat cocok dengan sebaran data di wilayah studi DAS Percut dan debit puncak dengan kala ulang tertentu dapat dihitung.
RINGKASAN PENELITIAN
MACHAIRIYAH, “Analisis Curah Hujan untuk Pendugaan Debit Puncak dengan Metode Rasional pada DAS Percut Kabupaten Deli Serdang’’ di bawah bimbingan Sumono, selaku ketua komisi pembimbing dan Edi Susanto selaku anggota komisi pembimbing.
Penelitian ini bertujuan untuk mengetahui pola distribusi yang tepat dan
menghitung debit puncak dengan metode rasional pada DAS Percut Kabupaten
Deli Serdang. Dari penelitian yang dilakukan menghasilkan kesimpulan sebagai
berikut :
Kondisi DAS Percut
Secara geografis DAS Percut terletak pada 03o18’- 03o40’ LU dan 98o30’
– 99o00 BT, sungai utama yang dilaluinya adalah sungai Percut. Luas total daerah
pengaliran sungai Percut (A) sebesar 276,8 km2, Lebar Maksimum sungai 45 m,
panjang sungai Percut 70 km dan kelerengan/kemiringan (S) sungai Percut
sebesar 0,02500 m. Ada tiga stasiun penakar curah hujan pada DAS Percut yaitu
Saentis, Batang Kuis dan Medan Amplas. Dari ketiga stasiun penakar hujan yang
ada hanya Saentís dan Batang Kuis yang berfungsi dengan baik. Curah hujan di
daerah pengaliran sungai Percut dapat diwakili oleh stasiun (pos) hujan Saentis.
Kondisi tata guna lahan pada DAS Percut didominasi daerah pertanian dan
permukiman.
Analisis Curah Hujan
Curah hujan maksimum tertinggi sebesar 210 mm dan curah hujan
maksimum terendah sebesar 95 mm. Berdasarkan parameter statistika yang
diperoleh dan setelah diuji dengan uji Chi-Square dan Smirnov Kolmogorov,
jenis distribusi yang cocok dengan sebaran data curah hujan harian maksimum di
wilayah studi adalah distribusi Log Pearson Type III. Besarnya curah hujan
rancangan berbagai periode ulang 1, 2, 5, 10, 15, 20, 25, 30, 40, 50, 100, 200
(tahun) diperoleh sebesar 86,98 mm; 110,78 mm; 136,61 mm; 157,62 mm; 164,08
mm; 170,83 mm; 177,86 mm; 184,77 mm; 199,34 mm; 215,12 mm; 244,65 mm;
277,7 mm.
Intensitas Hujan
Salah satu syarat yang harus dipenuhi dalam penggunaan rumus
menghitung debit puncak (banjir) dengan metode rasional adalah nilai intensitas
hujan dengan durasi tertentu harus sama dengan waktu konsentrasi. Hal ini
terpenuhi dimana waktu konsentrasi diperoleh sebesar 7,24 jam yang tidak
melebihi durasi hujan yang umum terjadi 1-6 jam dan 12 jam paling maksimum.
Intensitas hujan yang diperoleh berdasarkan waktu konsentrasi untuk kala ulang
sama sebesar 8,18 mm/jam; 10,42 mm/jam; 12,84 mm/jam; 14,82 mm/jam; 15,55
mm/jam; 16,06 mm/jam; 16,69 mm/jam; 17,37 mm/jam; 18,74 mm/jam; 20,23
Debit Puncak
Koefisien limpasan sangat mempengaruhi debit puncak yang terjadi.
Pada DAS Percut, koefisien limpasan diperoleh sebesar 0,305, hal ini berarti
bahwa DAS Percut dalam kondisi baik. Perubahan tata guna lahan yang terjadi
harus bersamaan dengan upaya pelestarian lingkungan. Debit Puncak yang
diperoleh untuk masing-masing kala ulang sebesar 192,05 m3/detik; 244,68
m3/detik; 301,57 m3/detik; 348,03 m3/detik; 365,16m3/detik; 377,18 m3/detik;
391,93 m3/detik; 407,91 m3/detik; 440,15 m3/detik; 475,00 m3/detik; 540,17
m3/detik; dan 613,24 m3/detik.
RIWAYAT HIDUP
Penulis dilahirkan di Medan pada tanggal 13 Desember 1985 dari ayah
Abdul Khair dan ibu Mardiah. Penulis merupakan putri pertama dari empat
bersaudara.
Tahun 2003 penulis lulus dari SMU Negeri 1 Binjai dan pada tahun 2003
lulus seleksi masuk USU melalui jalur SPMB. Penulis memilih program studi
Teknik Pertanian, Departemen Teknologi Pertanian, Fakultas Pertanian.
Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Satuan
Operasi Dasar, Ilmu Ukur Wilayah dan Hidrologi Teknik. Penulis mengikuti
kegiatan organisasi ATM dan IMATETA pada tahun 2003-2007. Penulis
KATA PENGANTAR
Puji dan syukur penulis panjatkan kehadirat Allah SWT atas rahmat dan
karunia-Nya sehingga skripsi ini berhasil diselesaikan.
Skripsi ini berjudul “Analisis Curah Hujan untuk Pendugaan Debit
Puncak dengan Metode Rasional pada DAS Percut Kabupaten Deli Serdang”
Terima kasih penulis sampaikan kepada Bapak Prof. Dr. Ir. Sumono, MS
selaku ketua komisi pembimbing dan Bapak Ir. Edi Susanto, M.Si selaku
anggota komisi pembimbing yang telah banyak membimbing penulis selama
melaksanakan penelitian. Ungkapan terima kasih juga disampaikan kepada ayah,
ibu, seluruh keluarga serta sahabat terbaikku atas segala doa dan perhatiannya.
Semoga skripsi ini bermanfaat.
Medan, September 2007
DAFTAR ISI
Hal
ABSTRACT ... ii
RINGKASAN PENELITIAN ... iii
RIWAYAT HIDUP ... vi
KATA PENGANTAR ... vii
DAFTAR TABEL ... x
DAFTAR GAMBAR ... xi
DAFTAR LAMPIRAN ... xii
PENDAHULUAN Latar Belakang ... 1
Tujuan Penelitian ... 4
Kegunaan Penelitian ... 4
TINJAUAN PUSTAKA Siklus Hidrologi ... 5
Daerah Aliran Sungai (DAS) ... 6
Analisis Frekuensi ... 8
Distribusi Normal ... 11
Distribusi Gumbel ... 13
Distribusi Log Normal ... 14
Distribusi Log Pearson Type III ... 14
Uji Kecocokan ... 16
Intensitas Curah Hujan ... 18
Waktu Konsentrasi ... 20
Koefisien Limpasan ... 21
Metode Rasional ... 24
METODOLOGI PENELITIAN Lokasi dan Waktu Penelitian ... 26
Bahan dan Alat Penelitian ... 26
Bahan ... 26
Alat ... 26
Metode Penelitian ... 26
Pelaksanaan Penelitian ... 27
Kerangka Pelaksanaan Penelitian ... 28
Pengolahan Data ... 28
HASIL DAN PEMBAHASAN Kondisi DAS Percut ... 32
Analisis Curah Hujan ... 34
Curah Hujan Harian Maksimum ... 34
Penentuan Pola Distribusi Hujan ... 35
Curah Hujan Rencana ... 38
Intensitas Hujan ... 39
Analisis Debit Banjir ... 42
Waktu Konsentrasi ... 42
Koefisien Limpasan (Run Off Coeffisient) ... 43
Debit Puncak ... 44
KESIMPULAN DAN SARAN Kesimpulan ... 46
Saran ... 47
DAFTAR PUSTAKA ... 48
DAFTAR TABEL
Hal
1 Parameter Statistik Analisis Frekuensi ... 10
2 Nilai Koefisien Aliran untuk Berbagai Penggunaan Lahan ... 23
3 Data Penggunaan Lahan yang Dilalui DAS Percut ... 33
4 Data Curah Hujan Harian Maksimum Tahunan
Periode 1985-2006 di Stasiun Saentis ... 35
5 Parameter Statistik Analisis Frekuensi ... 35
6 Hasil Uji Chi Square dan Smirnov-Kolmogorov ... 37
7 Parameter Statistik Analisis Frekuensi
Distribusi Log Pearson Type III ... 38
8 Hujan Rancangan Berbagai Periode Ulang ... 39
9 Intensitas Hujan Jam-jaman (mm/jam) untuk
Berbagai Periode Ulang ... 40
10 Perhitungan Koefisien Limpasan ... 43
11 Debit Puncak (banjir) di DAS Percut ... 45
DAFTAR GAMBAR
Hal
1 Siklus Hidrologi ... 6
2 Berbagai Macam Bentuk DAS ... 8
3 Kurva Distribusi Frekuensi Normal ... 11
4 Kerangka Pelaksanaan Penelitian ... 28
5 Distribusi Frekuensi Hujan DAS Percut ... 36
LAMPIRAN
Hal
1 Kerangka Pemikiran Penelitian ... 50
2 Data Curah Hujan Bulanan Maksimum (mm) Pos Hujan Saentis ... 51
3 Nilai Faktor Frekuensi K ... 52
4 Nilai Kritis untuk Distribusi Chi-Kuadrat (Uji Satu Sisi) ... 54
5 Nilai Kritis Do untuk uji Smirnov-Kolmogorov ... 55
6 Tabel Distribusi Normal ... 56
7 Peta DAS Percut ... 57
8 Peta Tata Guna Lahan Kabupaten Deli Serdang ... 58
PENDAHULUAN
Latar Belakang
Pertumbuhan penduduk dan pembangunan yang begitu cepat telah
menyebabkan perubahan tata guna lahan. Banyak lahan yang semula berupa lahan
terbuka atau hutan berubah menjadi areal pemukiman maupun industri. Hal ini
tidak hanya terjadi di kawasan perkotaan, namun sudah merambah ke kawasan
budidaya dan kawasan lindung yang berfungsi sebagai daerah resapan air.
Dampak dari perubahan tata guna lahan tersebut adalah meningkatnya aliran
permukaan langsung sekaligus menurunnya air yang meresap ke dalam tanah.
Akibat selanjutnya adalah distribusi air yang makin timpang antara musim
penghujan dan musim kemarau, debit banjir meningkat dan ancaman kekeringan
semakin menjadi-jadi.
Sejumlah sungai dan pantai di Sumatera Utara dewasa ini dalam kondisi
kritis dan mengancam kehidupan masyarakat. Di samping kualitas dan kuantitas
air sungainya yang semakin menurun untuk penyediaan air baku pada musim
kemarau, hal itu juga menimbulkan bahaya banjir pada musim hujan. Luas daerah
pengaliran sungai yang telah kritis di kota Medan lebih kurang 592.000 hektar,
tersebar di satuan wilayah sungai (SWS) Wampu-Besitang, SWS
Belawan-Belumai-Ular, SWS BahBolon, SWS Barumun Kualah, dan SWS Batang
Gadis-Batang Toru. Sedangkan yang rawan terhadap banjir mencapai seluas 115.903
hektar, terdiri dari perkotaan 7.996 hektar, daerah industri 4.549 hektar, dan
daerah pertanian/pedesaan 103.903 hektar, serta sarana transportasi yang rawan
antara lain sungai pada SWS Wampu-Besitang dan SWS Belawan-Belumai-Ular,
yaitu Sungai Deli, Sungai Percut, dan Sungai Belawan (Anonimous, 2006).
Menurut Sudjarwadi (1987), banjir adalah aliran/genangan air yang
menimbulkan kerugian ekonomi atau bahkan kehilangan jiwa. Aliran atau
genangan air ini dapat terjadi karena adanya luapan-luapan pada daerah di kanan
atau kiri sungai/saluran akibat alur sungai tidak memiliki kapasitas yang cukup
bagi debit aliran yang lewat.
Kejadian banjir dan kekeringan di suatu Daerah Aliran Sungai (DAS)
sebenarnya memiliki fenomena yang tidak sesederhana. Suatu DAS terdiri dari
berbagai unsur penyusun utama yang di satu pihak bertindak sebagai objek atau
sasaran fisik alamiah, seperti sumber daya alam tanah, vegetasi dan air, dan di lain
pihak adalah subjek atau pelaku pendayagunaan unsur-unsur tersebut, yaitu
manusia. Diantara unsur-unsur itu terjadi proses hubungan timbal balik dan saling
mempengaruhi, yang pada akhirnya akan menghasilkan suatu kondisi hidrologis
dari wilayah DAS tersebut (Asdak, 1995).
Bencana banjir selain akibat kerusakan ekosistem ataupun aspek
lingkungan yang tidak terjaga tetapi juga disebabkan karena bencana alam itu
sendiri seperti curah hujan yang tinggi. Curah hujan sangat berpengaruh pada
besarnya debit air yang mengalir pada suatu sungai. Curah hujan yang diperlukan
untuk analisis hidrologi adalah curah hujan rata-rata dari seluruh daerah yang
bersangkutan, bukan curah hujan pada suatu titik tertentu (stasiun). Curah hujan
ini disebut curah hujan wilayah/daerah dan dinyatakan dalam mm. Analisis
hidrologi memerlukan data curah hujan yang akurat, namun data curah hujan ini
jumlah alat yang dipasang dan tidak semua data tercatat secara lengkap. Dalam
perencanaan bangunan pengendali banjir seperti saluran drainase, tanggul dan
lain-lain, data masukan curah hujan sangat diperlukan.
Analisis frekuensi adalah prosedur memperkirakan frekuensi suatu
kejadian pada masa lalu atau masa yang akan datang. Prosedur tersebut dapat
digunakan menentukan hujan rancangan dalam berbagai kala ulang berdasarkan
distribusi yang paling sesuai. Menurut Sri Harto (1993), analisis frekuensi dapat
dilakukan dengan seri data yang diperoleh dari rekaman data baik data hujan
maupun data debit. Analisis ini sering dianggap cara analisis yang paling baik,
karena dilakukan terhadap data yang terukur langsung yang tidak melewati
pengalihragaman terlebih dahulu. Perhitungan debit banjir rencana dengan metode
rasional untuk perancangan bangunan keairan memerlukan data intensitas hujan
dalam durasi dan periode ulang tertentu yang dapat diperoleh dari kurva IDF
(Intensity Duration Frequency).
Menurut Gunawan (1991), bahwa pendugaan debit puncak dengan
menggunakan metode rasional merupakan penyederhanaan besaran-besaran
terhadap suatu proses penentuan aliran permukaan yang rumit akan tetapi metode
tersebut dianggap akurat untuk menduga aliran permukaan dalam rancang bangun
yang relatif murah, sederhana dan memberikan hasil yang dapat diterima
(reasonable). Selain itu metode rasional merupakan metode empiris yang lazim
digunakan dibandingkan dengan rumus-rumus empiris lainnya dimana rumus ini
menggunakan berbagai variabel yang berhubungan dengan debit banjir yaitu
faktor daerah pengaliran, curah hujan, koefisien limpasan dan perubahan tata guna
Sungai Percut merupakan salah satu dari beberapa sungai yang ada di kota
Medan yang termasuk dalam kategori kritis. Daerah aliran sungai ini merupakan
daerah rawan banjir pada saat musim penghujan datang, banyak hal yang
menyebabkan daerah ini rawan banjir salah satunya adalah perubahan tata guna
lahan di sekitar aliran sungai Percut. Untuk mengatasi hal tersebut dibutuhkan
langkah-langkah penanggulangan yang tepat, antara lain dengan adanya suatu
bangunan pengendali banjir.
Pendugaan debit puncak Sungai Percut dengan metode rasional dalam kala
ulang tertentu dapat dimanfaatkan sebagai bahan dasar perencanaan bangunan
pengendali banjir. Hal inilah yang menjadi dasar penulis melakukan penelitian.
Tujuan Penelitian
1. Untuk mengetahui pola distribusi frekuensi yang tepat pada DAS
Percut.
2. Untuk menghitung debit puncak aliran sungai pada DAS Percut
dengan menggunakan metode rasional.
Kegunaan Penelitian
1. Sebagai salah satu syarat bagi penulis untuk menyelesaikan
pendidikan S1 di Program Studi Teknik Pertanian Departemen
Teknologi Pertanian Fakultas Pertanian Universitas Sumatera Utara.
TINJAUAN LITERATUR
Siklus Hidrologi
Siklus hidrologi adalah suatu rangkaian proses yang terjadi dengan air
yang terdiri dari penguapan, presipitasi, infiltrasi dan pengaliran keluar (outflow).
Air menguap ke udara dari permukaan tanah dan laut. Penguapan dari daratan
terdiri dari evaporasi dan transpirasi. Evaporasi merupakan proses menguapnya
air dari permukaan tanah, sedangkan transpirasi adalah proses menguapnya air
dari tanaman. Uap yang dihasilkan mengalami kondensasi dan dipadatkan
membentuk awan-awan yang nantinya dapat kembali menjadi air dan turun
sebagai presipitasi. Sebelum tiba di permukaan bumi presipitasi tersebut sebagian
langsung menguap ke udara, sebagian tertahan oleh tumbuh-tumbuhan (intersepsi)
dan sebagian lagi mencapai permukaan tanah. presipitasi yang tertahan oleh
tumbuh-tumbuhan sebagian akan diuapkan dan sebagian lagi mengalir melalui
dahan (stem flow) atau jatuh dari daun (trough fall) dan akhirnya sampai ke
permukaan tanah.
Air yang sampai ke permukaan tanah sebagian akan berinfiltrasi dan
sebagian lagi mengisi lekuk-lekuk permukaan tanah kemudian mengalir ketempat
yang lebih rendah (runoff), masuk ke sungai-sungai dan akhirnya ke laut. Dalam
perjalanannya menuju laut sebagian akan mengalami penguapan. Air yang masuk
ke dalam tanah sebagian akan keluar lagi menuju sungai yang disebut dengan
tanah yang keluar sedikit demi sedikit dan masuk ke dalam sungai sebagai aliran
bawah tanah (groundwater flow), dan begitu seterusnya. Proses mengenai siklus
hidrologi dapat dilihat pada gambar :
Gambar 1. Siklus Hidrologi
Karena siklus hidrologi merupakan suatu sistem tertutup, maka air yang
masuk selalu sama dengan yang keluar. Hal ini dikenal dengan istilah neraca air
(Soemarto,1987).
Daerah Aliran Sungai (DAS)
Daerah Pengaliran Sungai adalah suatu kesatuan wilayah tata air yang
terbentuk secara alamiah, dimana air meresap atau mengalir melalui sungai dan
anak-anak sungai yang bersangkutan. Sering disebut dengan DAS (daerah aliran
sungai) atau DTA (daerah tangkapan air). Menurut Sri Harto (1993), daerah aliran
sungai merupakan daerah yang dimana semua airnya mengalir ke dalam sungai
yang dimaksudkan. Daerah ini umumnya dibatasi oleh topografi yang berarti
ditetapkan berdasarkan aliran air permukaan.
DAS disebut juga sebagai watershed atau catchment area. DAS ada yang
kecil dan ada juga yang sangat luas. DAS yang sangat luas bisa terdiri dari
tergantung banyaknya anak sungai dari cabang sungai yang ada, yang merupakan
bagian dari suatu sistem sungai utama (Asdak, 1995).
DAS merupakan ekosistem yang terdiri dari berbagai macam komponen
dan terjadi keseimbangan dinamik antara komponen yang merupakan masukan
(input) dan komponen yang merupakan keluaran (output), dimana keadaan atau
pengaruh yang berlaku pada salah satu bagian di dalamnya akan mempengaruhi
wilayah secara keseluruhan (Hartono, dkk, 2005).
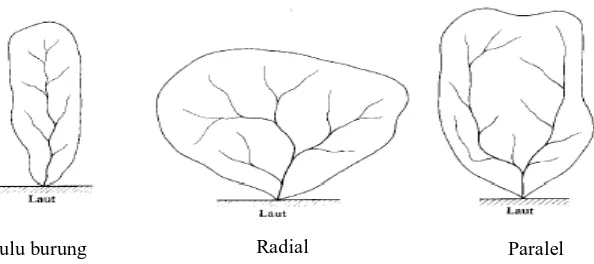
Menurut Sosrodarsono dan Takeda (2003), berdasarkan perbedaan debit
banjir yang terjadi, bentuk DAS dapat dibedakan menjadi tiga bentuk, yaitu :
1. Bulu burung
Suatu daerah pengaliran yang mempunyai jalur daerah di kiri kanan sungai
utama dimana anak-anak sungai mengalir ke sungai utama. Daerah pengaliran
demikian mempunyai debit banjir yang kecil, oleh karena waktu tiba banjir dari
anak-anak sungai itu berbeda-beda. Sebaliknya banjirnya berlangsung agak lama.
2. Radial
Daerah pengaliran yang berbentuk kipas atau lingkaran dan dimana
anak-anak sungainya mengkonsentrasi ke suatu titik secara radial. Daerah pengaliran
semacam ini mempunyai banjir yang besar di dekat titik pertemuan anak-anak
sungai.
3. Pararel
Daerah pengaliran seperti ini mempunyai corak dimana dua jalur daerah
pengaliran yang bersatu di bagian hilir. Banjir itu terjadi di sebelah hilir titik
Gambar 2. Berbagai macam bentuk DAS.
Sungai mempunyai fungsi untuk mengumpulkan curah hujan dalam suatu
daerah tertentu dan mengalirkannya ke laut. Daerah pengaliran sebuah sungai
adalah daerah yang mengalirkan airnya ke sungai tersebut. Luas daerah pengaliran
diperkirakan dengan pengukuran daerah itu pada peta topografi. Luas daerah
pengaliran berpengaruh terhadap besarnya debit yang terjadi. Semakin besar
daerah pengaliran maka debit pengaliran akan semakin besar.
Analisis Frekuensi
Dalam proses pengalihragaman hujan menjadi aliran ada beberapa sifat
hujan yang penting untuk diperhatikan, antara lain adalah intensitas hujan (I),
lama waktu hujan (t), kedalaman hujan (d), frekuensi (f) dan luas daerah pengaruh
hujan (A). Komponen hujan dengan sifat-sifatnya ini dapat dianalisis berupa hujan
titik maupun hujan rata-rata yang meliputi luas daerah tangkapan (catchment
area) yang kecil sampai yang besar (Soemarto, 1987).
Sistem hidrologi kadang-kadang dipengaruhi oleh peristiwa-peristiwa luar
biasa (ekstrim), seperti hujan lebat, banjir, dan kekeringan. Tujuan analisis
frekuensi data hidrologi adalah berkaitan dengan besaran peristiwa-peristiwa
ekstrim yang berkaitan dengan frekuensi kejadiannya melalui penerapan distribusi
kemungkinan. Data hidrologi yang dianalisis diasumsikan tidak terikat
(independent), terdistribusi secara acak dan bersifat stokastik (peluang).
Ada dua macam seri data yang dipergunakan dalam analisis frekuensi
yaitu:
1. Data maksimum tahunan: tiap tahun diambil hanya satu besaran
maksimum yang dianggap berpengaruh pada analisis selanjutnya. Series
data ini sering disebut seri data maksimum (maximum annual series).
2. Seri parsial: dengan menetapkan besaran tertentu sebagai batas bawah,
selanjutnya semua besaran data yang lebih besar dari batas bawah tersebut
diambil kemudian dianalisis dengan cara yang lazim. Metode ini lebih
realitis dibandingkan metode maximum annual series sehingga beberapa
ahli menyarankan menggunakan cara partial series.
(Suripin, 2004).
Analisis frekuensi adalah suatu analisa data hidrologi dengan
menggunakan statistika yang bertujuan untuk memprediksi suatu besaran hujan
atau debit dengan masa ulang tertentu. Frekuensi hujan adalah besarnya
kemungkinan suatu besaran hujan disamai atau dilampaui. Sebaliknya, kala ulang
(return period) diartikan sebagai waktu dimana hujan atau debit dengan suatu
besaran tertentu akan disamai atau dilampaui sekali dalam jangka waktu tersebut.
Dalam hal ini tidak berarti bahwa selama jangka waktu ulang tersebut (misalnya T
tahun) hanya sekali kejadian yang menyamai atau melampaui, tetapi merupakan
perkiraan bahwa hujan ataupun debit tersebut akan disamai atau dilampaui K kali
dalam jangka panjang L tahun, dimana K/L kira-kira sama dengan 1/T
Dalam analisis frekuensi, hasil yang diperoleh tergantung pada kualitas
dan panjang data. Makin pendek data yang tersedia, makin besar penyimpangan
yang terjadi. Menurut Soemarto (1987), dalam ilmu statistik dikenal beberapa
macam distribusi dan empat jenis distribusi yang umum digunakan dalam bidang
hidrologi adalah :
1. Distribusi Normal
2. Distribusi Log Normal
3. Distribusi Log-Pearson Type III dan
4. Distribusi Gumbel
Dalam statistik dikenal beberapa parameter yang berkaitan dengan analisis
data yang meliputi :
Tabel 1. Parameter Statistik Analisis Frekuensi
Parameter Sampel
Rata-rata
X = i
n
i
X n
∑
=11
Simpangan baku
s =
(
)
2 / 1 2 1 1 1 − −
∑
− X X n i n i Koefisien variasi Cv = x s Koefisien skewness Cs =(
)
( )( )
3 31
2
1 n s
n X X n i n i − − −
∑
= Koefisien kurtosisCk =
(
)
( )( )(
)
4 4 i n 1 i 2 s 3 n 2 n 1 n X X n − − − −∑
=Distribusi Normal
Distribusi normal atau kurva normal disebut pula distribusi Gauss.
Distribusi ini mempunyai probability density function sebagai berikut:
− − = 2 2 2 ) ( exp 2 1 ) ( ' σµ π σ x X
P ………...….. (1)
dimana:
P(X) = fungsi densitas peluang normal (ordinat kurva normal).
X = Variabel acak kontinu
µ = Rata-rata nilai X
σ = Simpangan baku dari X
Analisis kurva normal cukup menggunakan parameter statistik µ dan σ . Bentuk kurvanya simetris terhadap X = µ, dan grafiknya selalu di atas sumbu
datar X serta mendekati sumbu datar X dan di mulai dari X = µ+ 3σ dan X = µ - 3σ, nilai mean = median = modus.
Gambar 3. Kurva distribusi frekuensi normal
Luas 99,73 % Luas 96, 45 %
Dari gambar diatas dapat ditarik kesimpulan bahwa :
1) Kira-kira 68,27 % terletak di daerah satu deviasi standart sekitar nilai
rata-ratanya yaitu antara (µ - σ) dan (µ +σ ).
2) Kira-kira 95,45 % terletak di daerah dua deviasi standart sekitar nilai
rata-ratanya yaitu antara (µ - 2σ) dan (µ + 2σ).
3) Kira-kira 99,73 % terletak di daerah tiga deviasi standart sekitar nilai
rata-ratanya yaitu antara (µ - 3σ) dan (µ + 3σ).
Rumus yang umum digunakan untuk distribusi normal adalah:
XT = X + KT.s ……….. (2)
di mana:
XT = Perkiraan nilai yang diharapkan terjadi dengan periode ulang T-tahunan
X = Nilai rata-rata hitung sampel
s = Deviasi standard nilai sampel
KT = Faktor frekuensi, merupakan fungsi dari peluang atau yang digunakan
periode ulang dan tipe model matematik distribusi peluang yang
digunakan untuk analisis peluang.
(Suripin, 2004).
Menurut Jayadi (2000), sifat khas lain yaitu nilai asimetris (koefisien
skewness) hampir sama dengan nol dan dengan kurtosis 3 selain itu kemungkinan:
P
( )
x−σ =15,87%P
( )
x =50%Distribusi Gumbel
Menurut Chow (1964), rumus umum yang digunakan dalam metode
Gumbel adalah sebagai berikut:
X = X +s.K ... (3)
Dengan : X = nilai rata-rata atau mean; s = standard deviasi
Faktor frekuensi K untuk nilai-nilai ekstrim Gumbel ditulis dengan rumus
berikut ini:
n n Tr
S Y Y
K= − ... (4)
dimana :
Yn = reduced mean yang tergantung jumlah sampel/data n
Sn = reduced standard deviation yang juga tergantung pada jumlah sampel/
data n
Tr = Fungsi waktu balik (tahun)
YTr = reduced variate yang dapat dihitung dengan persamaan berikut:
YTr = -In
− −
r r
T T
In 1 ……….... (5)
Ciri khas statistik distribusi Gumbel adalah nilai asimetris (koefisien
skewness) sama dengan 1,396 dan dengan kurtosis (Ck) = 5,4002.
Distribusi Log Normal
Jika variabel acak Y = Log x terdistribusi secara normal, maka x
dikatakan mengikuti distribusi Log Normal. Ini dapat dinyatakan dengan model
matematik dengan persamaan :
YT = Y + KTS ………. (6)
dimana:
YT = Perkiraan nilai yang diharapkan terjadi dengan periode ulang T- tahunan
Y = Nilai rata-rata hitung sampel
S = Standard deviasi nilai sampel
KT = Faktor frekuensi, merupakan fungsi dari peluang atau yang digunakan
periode ulang dan tipe model metematik distribusi peluang yang
digunakan untuk analisis peluang.
(Singh, 1992)
Menurut Jayadi (2000), ciri khas statistik distribusi Log Normal adalah
nilai asimetris (koefisien skewness) sama dengan tiga kali nilai koefisien variasi
(Cv) atau bertanda positif.
Distribusi Log Pearson Type III
Parameter penting dalam Log Pearson Type III yaitu harga rata-rata,
simpangan baku dan koefisien kemencengan. Jika koefisien kemencengan sama
Langkah-langkah penggunaan distribusi Log Pearson Type III adalah
sebagai berikut.
1. Ubah data ke dalam bentuk logaritmis, X = log X.
2. Hitung harga rata-rata:
Log X = i
n i X n log 1 1
∑
= ... (7)3. Hitung harga simpangan baku:
s =
(
)
2 / 1 2 1 log log 1 1 − −
∑
= X X n i n i ... (8)4. Hitung koefisien kemencengan:
Cs =
(
)
( )( )
3 3 1 2 1 log log s n n X X n i n i − − −∑
= ... (9)5. Hitung logaritma hujan dengan periode ulang T:
Log XT = log X + K.s ... (10)
(Linsley, et al, 1975).
Menurut Jayadi (2000), ciri khas statistik distribusi Log Pearson Type III
adalah:
1. Jika tidak menunjukkan sifat-sifat seperti ketiga distribusi diatas
2. Garis teoritis probabilitasnya berupa garis lengkung.
Ada dua cara untuk mengetahui ketepatan distribusi probabilitas data
hidrologi yaitu data yang ada diplot pada kertas probabilitas yang sudah desain
garis lurus yang mempresentasikan sebaran data-data yang diplot kemudian
ditarik sedemikian rupa berupa garis linier. Metode pengeplotan data dapat
dilakukan secara empiris, persamaan yang umum digunakan adalah persamaan
Weibull :
Tr =
m n+1
………. (11)
dimana :
m = Nomor urut (peringkat) data setelah diurutkan dari besar ke kecil.
n = Banyaknya data atau jumlah kejadian.
(Soedibyo, 2003).
Menurut Sri Harto (2000), menyebutkan bahwa masing-masing distribusi
mempunyai sifat yang khas, sehingga data curah hujan harus diuji kecocokannya
dengan sifat statistik masing-masing distribusi tersebut. Pemilihan distribusi yang
tidak benar dapat menimbulkan kesalahan perkiraan yang cukup besar, baik over
estimate maupun under estimate.
Uji kecocokan
Diperlukan penguji parameter untuk menguji kecocokan (the goodness of
fittest test) distribusi frekuensi sampel data terhadap fungsi distribusi peluang
yang diperkirakan dapat menggambarkan atau mewakili distribusi frekuensi
tersebut. Pengujian parameter yang sering dipakai adalah Chi-Square dan
1. Uji Chi-Square
Menurut Danapriatna dan Setiawan (2005), pada dasarnya uji ini
merupakan pengecekan terhadap penyimpangan rerata data yang dianalisis
berdasarkan distribusi terpilih. Penyimpangan tersebut diukur dari perbedaan
antara nilai probabilitas setiap varian X menurut hitungan distribusi frekuensi
teoritik (diharapkan) dan menurut hitungan dengan pendekatan empiris. Teknik
pengujiannya yaitu menguji apakah ada perbedaan yang nyata antara data yang
diamati dengan data berdasarkan hipotesis nol (H0).
Uji Chi-Square dimaksudkan untuk menentukan apakah persamaan
distribusi yang telah dipilih dapat mewakili distribusi statistik sampel data yang
dianalisis. Parameter Xh2 merupakan variabel acak. Parameter X2 yang digunakan
dapat dihitung dengan rumus:
Xh2 =
∑
(
)
=
−
n
i Ei
Ei Oi
1
2
... (12)
Dimana : Xh2 = parameter Chi-Square terhitung
G = jumlah sub kelompok
Oi = jumlah nilai pengamatan pada sub kelompok i
Ei = jumlah nilai teoritis pada sub kelompok i
(Suripin, 2004).
Cara memberikan interpretasi terhadap Chi-Square adalah dengan
menentukan df atau db (derajat kebebasan). Uji ini digunakan untuk data yang
variabelnya tidak dipengaruhi oleh varibel lain dan diasumsikan bahwa sampel
2. Uji Smirnov-Kolmogorov
Dalam statistika, uji smirnov-kolmogorov dipakai untuk membedakan dua
buah sebaran data yaitu membedakan sebaran berdasarkan data hasil pengamatan
sebenarnya dan populasi atau sampel yang diandaikan atau diharapkan. Dengan
kata lain, uji smirnov-kolmogorov menguji apakah dua sampel independen berasal
dari populasi yang sama atau dari populasi-populasi yang memiliki distribusi yang
sama. Nilai-nilai parameter populasi yang dipakai untuk menghitung frekuensi
yang diharapkan atau frekuensi teoritik ditaksir berdasarkan nilai-nilai statistik
sampel. Uji statistik ini dapat dirumuskan:
Dn = max { F0(x)-SN(x)} ………. (13)
Dimana F0(x) menyatakan sebaran frekuensi kumulatif yaitu sebaran frekuensi
teoritik berdasarkan H0. Untuk setiap harga x, F0(x) merupakan proporsi harapan
yang nilainya sama atau lebih kecil dari x. SN(x) adalah sebaran frekuensi
kumulatif dari suatu sampel sebesar N pengamatan. Uji ini menitikberatkan pada
perbedaan antara nilai selisih yang terbesar (Wikipedia, 2006).
Chakravart, et al (1967), menyatakan bahwa uji smirnov-kolmogorov
dipergunakan untuk mengambil keputusan jika sampel tidak diperoleh dari
distribusi spesifik. Tujuannya untuk menguji perbedaan distribusi kumulatif dari
variabel kontinu, sehingga merupakan test of goodness of fit. Uji
smirnov-kolmogorov (KS-tes) mencoba untuk memutuskan jika dua data berbeda secara
signifikan.
Menurut Danapriatna dan Setiawan (2005), Uji smirnov-kolmogorov
hipotesis. Uji ini ditegaskan berdasarkan H0: data mengikuti distribusi yang
ditetapkan, Ha: data tidak mengikuti distribusi yang ditetapkan.
Intensitas Curah Hujan
Perhitungan debit banjir dengan metode rasional memerlukan data
intensitas curah hujan. Intensitas curah hujan adalah ketinggian curah hujan yang
terjadi pada kurun waktu dimana air tersebut terkonsentrasi (Loebis, 1992).
Intensitas curah hujan dinotasikan dengan huruf I dengan satuan mm/jam.
Durasi adalah lamanya suatu kejadiaan hujan. Intensitas hujan yang tinggi
pada umumnya berlangsung dengan durasi pendek dan meliputi daerah yang tidak
sangat luas. Hujan yang meliputi daerah yang luas, jarang sekali dengan intensitas
yang tinggi, tetapi dapat berlangsung dengan durasi cukup panjang. Kombinasi
dari intensitas hujan yang tinggi dengan durasi yang panjang jarang terjadi, tetapi
apabila terjadi berarti sejumlah besar volume air bagaikan ditumpahkan dari langit
(Sudjarwadi, 1987).
Kurva frekuensi intensitas-lamanya adalah kurva yang menunjukan
persamaan dimana t sebagai absis dan I sebagai ordinat. Kurva ini digunakan
untuk perhitungan debit puncak dengan menggunakan intensitas curah hujan yang
sebanding dengan waktu pengaliran curah hujan dari titik paling atas ke titik yang
ditinjau di bagian hilir daerah pengaliran itu (Sosrodarsono dan Takeda, 2003).
Analisis hubungan dua parameter hujan yang penting berupa intensitas dan
durasi dapat dihubungkan secara statistik dengan suatu frekuensi kejadiannya.
Penyajian secara grafik hubungan ini adalah berupa kurva
Sri Harto (1993), menyebutkan bahwa analisis IDF memerlukan analisis
frekuensi dengan menggunakan seri data yang diperoleh dari rekaman hujan. Jika
tidak tersedia waktu untuk mengamati besarnya intensitas curah hujan atau
disebabkan oleh karena alatnya tidak ada, dapat ditempuh cara-cara empiris
dengan mempergunakan rumus-rumus eksperimental seperti rumus Talbot,
Mononobe, Sherman dan Ishgura.
Menurut Loebis (1992), intensitas hujan (mm/jam) dapat diturunkan dari
data curah hujan harian (mm) empiris menggunakan metode mononobe, intensitas
curah hujan (I) dalam rumus rasional dapat dihitung berdasarkan rumus :
3 / 2 24 24
24
=
t R
I ……… (14)
dimana: R = Curah hujan rancangan setempat (mm)
t = Lamanya curah hujan (jam)
I = Intensitas curah hujan (mm/jam)
Besar intensitas curah hujan tidak sama di segala tempat, hal ini
dipengaruhi oleh topografi, durasi dan frekuensi di tempat atau lokasi yang
bersangkutan. Ketiga hal ini dijadikan pertimbangan dalam membuat lengkung
IDF (IDF curve = Intensity-Duration Frequency Curve). Lengkung IDF ini
digunakan dalam menghitung debit puncak dengan metode rasional untuk
menentukan intensitas curah hujan rata-rata dari waktu konsentrasi yang dipilih
(Sosrodarsono dan Takeda, 2003).
Menurut Suripin (2004), waktu konsentrasi adalah waktu yang diperlukan
oleh air hujan yang jatuh untuk mengalir dari titik terjauh sampai ke tempat
keluaran DAS (titik kontrol) setelah tanah menjadi jenuh. Dalam hal ini
diasumsikan bahwa jika durasi hujan sama dengan waktu konsentrasi, maka setiap
bagian DAS secara serentak telah menyumbangkan aliran terhadap titik kontrol.
Salah satu metode untuk memperkirakan waktu konsentrasi adalah rumus yang
dikembangkan oleh Kirpich (1940) yang dapat ditulis sebagai berikut :
tc=
385 , 0 2
1000 87 , 0
xS xL
………... (15)
dimana: tc = Waktu konsentrasi dalam jam,
L = Panjang sungai dalam Km,
S = Kemiringan sungai dalam m/m.
Durasi hujan yang biasa terjadi 1-6 jam bahkan maksimum 12 jam pun
jarang terjadi. Durasi hujan sering dikaitkan dengan waktu konsentrasi sehingga
sangat berpengaruh pada besarnya debit yang masuk ke saluran atau sungai. Jika
tidak diperoleh waktu konsentrasi sama dengan intensitas hujan maka perlu
digunakan metode rasional yang dimodifikasi (Suroso, 2006).
Koefisien Limpasan
Koefisien limpasan adalah persentase jumlah air yang dapat melimpas
melalui permukaan tanah dari keseluruhan air hujan yang jatuh pada suatu daerah.
Semakin kedap suatu permukaan tanah, maka semakin tinggi nilai koefisien
kondisi tanah, laju infiltrasi, kemiringan lahan, tanaman penutup tanah dan
intensitas hujan (Eripin, 2005).
Besarnya aliran permukaan dapat menjadi kecil, terlebih bila curah hujan
tidak melebihi kapasitas infiltrasi. Selama hujan yang terjadi adalah kecil atau
sedang, aliran permukaan hanya terjadi di daerah yang impermabel dan jenuh di
dalam suatu DAS atau langsung jatuh di atas permukaan air. Apabila curah hujan
yang jatuh jumlahnya lebih besar dari jumlah air yang dibutuhkan untuk
evaporasi, intersepsi, infiltrasi, simpanan depresi dan cadangan depresi, maka
barulah bisa terjadi aliran permukaan. Apabila hujan yang terjadi kecil, maka
hampir semua curah hujan yang jatuh terintersepsi oleh vegetasi yang lebat
(Kodoatie dan Sugiyanto, 2002).
Pengaruh tata guna lahan pada aliran permukaan dinyatakan dalam koefisien
aliran permukaan (C), yaitu bilangan yang menampilkan perbandingan antara
besarnya aliran permukaan dan besarnya curah hujan. Angka koefisien aliran
permukaan itu merupakan salah satu indikator untuk menentukan kondisi fisik
suatu DAS. Nilai C berkisar antara 0 – 1. Nilai C = 0 menunjukkan bahwa semua
air hujan terintersepsi dan terinfiltrasi ke dalam tanah, sebaliknya untuk nilai C =
1 menunjukkan bahwa air hujan mengalir sebagai aliran permukaan. Pada DAS
yang baik harga C mendekati nol dan semakin rusak suatu DAS maka harga C
semakin mendekati satu (Kodoatie dan Syarief, 2005).
Di Indonesia penelitian untuk menentukan nilai C masih memberikan
peluang yang cukup besar sesuai jenis penggunaan lahan dan curah hujan. Tabel
diatas merupakan contoh nilai koefisien limpasan yang sesuai dengan kondisi
memilih nilai C maka tidak benar pula debit puncak banjir yang dihitung dengan
metode rasional. Setiap daerah memiliki nilai koefisien limpasan yang berbeda
(Soewarno, 2000).
[image:37.595.115.442.308.585.2]Nilai koefisien limpasan disajikan pada Tabel 2 berikut ini.
Tabel 2. Nilai Koefisien Aliran untuk Berbagai Penggunaan Lahan
Penggunaan Lahan atau Bentuk Struktur Nilai C (%)
Hutan Tropis < 3
Hutan Produksi 5
Semak Belukar 7
Sawah-sawah 15
Daerah Pertanian, Perkebunan 40
Jalan aspal 95
Daerah Permukiman 50 - 70
Bangunan Padat 70 - 90
Bangunan Terpencar 30 - 70
Atap rumah 70 - 90
Jalan tanah 13 - 50
Lapis keras kerikil batu pecah 35 - 70
Lapis keras beton 70 - 90
Taman,halaman 5 - 25
Tanah lapang, tegalan 10 - 30
Kebun, ladang 0 - 20
Sumber : Majalah Geografi Indonesia No.14-15 ( Soewarno, 2000).
Jika DAS terdiri dari berbagai macam penggunaan lahan dengan koefisien
aliran permukaan yang berbeda, maka C yang dipakai adalah koefisien DAS yang
dapat dihitung dengan persamaan berikut :
CDAS =
∑
∑
= = n i i n i i i A A C 1 1dimana : Ai = luas lahan dengan jenis penutup tanah i
Ci = koefisien aliran permukaan jenis penutup tanah i
n = jumlah jenis penutup lahan.
(Suripin, 2004).
Metode Rasional
Menurut Gunawan (1991), bahwa pendugaan debit puncak dengan
menggunakan metode rasional merupakan penyederhanaan besaran-besaran
terhadap suatu proses penentuan aliran permukaan yang rumit akan tetapi metode
tersebut dianggap akurat untuk menduga aliran permukaan dalam rancang bangun
yang relatif murah, sederhana dan memberikan hasil yang dapat diterima
(reasonable).
Metode rasional adalah metode lama yang masih digunakan hingga
sekarang untuk memperkirakan debit puncak (peak discharge). Ide yang
melatarbelakangi metode rasional adalah jika curah hujan dengan intensitas I
terjadi secara terus-menerus, maka laju limpasan langsung akan bertambah sampai
mencapai waktu konsentrasi tc. Waktu konsentrasi tc tercapai ketika seluruh
bagian DAS telah memberikan konstribusi aliran di outlet. Laju masukan pada
sistem adalah hasil curah hujan dengan intensitas I pada DAS dengan luas A. Nilai
perbandingan antara laju masukan dengan laju debit puncak (Qp) yang terjadi
pada saat tc dinyatakan sebagai run off coefficient (C) dengan nilai 0≤C≤1
Rumus ini adalah rumus yang tertua dan yang terkenal di antara
rumus-rumus empiris lainnya. Rumus ini banyak digunakan untuk sungai-sungai biasa
dengan daerah pengaliran yang luas dan juga untuk perencanaan drainase daerah
pengaliran yang relatif sempit. Metode rasional dapat dipandang sebagai salah
satu cara praktis dan mudah. Selain itu, penerapannya di Indonesia masih
memberikan peluang untuk dikembangkan. Metode ini cocok dengan kondisi
Indonesia yang beriklim tropis (Soewarno, 2000).
Bentuk umum rumus rasional ini adalah sebagai berikut :
Q = 0,278.C.I.A ... (17)
dimana: Q = Debit banjir maksimum (m3/dtk)
C = Koefisien pengaliran/limpasan
I = Intensitas curah hujan rata-rata (mm/jam)
A = Luas daerah pengaliran (km2)
Arti rumus ini dapat segera diketahui yakni, jika terjadi curah hujan
selama 1 jam dengan intensitas 1 mm/jam dalam daerah seluas 1 km2, maka debit
banjir sebesar 0,2778 m3/dtk dan melimpas selama 1 jam
(Sosrodarsono dan Takeda, 2003).
Menurut Wanielista (1990), beberapa asumsi dasar untuk menggunakan
metode rasional adalah :
1. Curah hujan terjadi dengan intensitas yang tetap dalam jangka waktu
tertentu, setidaknya sama dengan waktu konsentrasi.
2. Limpasan langsung mencapai maksimum ketika durasi hujan dengan
3. Koefisien run off dianggap tetap selama durasi hujan
4. Luas DAS tidak berubah selama durasi hujan.
METODOLOGI PENELITIAN
Lokasi dan Waktu Penelitian
Penelitian ini dilaksanakan pada bulan Juni - Agustus 2007 di DAS Percut,
Kabupaten Deli Serdang.
Bahan dan Alat
Bahan
Adapun data yang digunakan dalam penelitian ini adalah:
1. Data curah hujan harian selama 22 tahun terakhir (1985 – 2006) yang
diperoleh dari Bagian Penelitian Tebu Tembakau Deli (BPTTD) Sampali,
Medan.
2. Data kondisi DAS Percut yang diperoleh dari Badan Pusat Statistik Deli
Serdang.
3. Peta tata guna lahan kabupaten Deli Serdang.
4. Peta DAS Percut.
Sedangkan alat yang digunakan dalam penelitian ini adalah :
1. Perlengkapan kerja seperti alat tulis, kalkulator, komputer.
2. Grafik Skala logaritma.
3. Planimeter.
Metode Penelitian
Penelitian ini menggunakan metode deskriptif dengan menggunakan data
sekunder dan peta.
Pelaksanaan Penelitian
Tahapan pelaksanaan penelitian sebagai berikut :
1. Menentukan curah hujan harian maksimum untuk tiap-tiap tahun data
dengan metode “partial series”.
2. Menentukan parameter statistik dari data yang telah diurutkan dari kecil ke
besar yaitu Mean X , Standard Deviation S, Coefisient of Variation Cv,
Coefisient of Skweness Cs, Coefisient of Kurtosis Ck.
3. Menentukan jenis distribusi yang sesuai berdasarkan parameter statistik
yang ada.
4. Lakukan pengujian Chi-square dan Smirnov-Kolmogorov untuk
mengetahui apakah distribusi yang dipilih sudah tepat.
5. Dari jenis distribusi yang terpilih dapat dihitung besaran hujan rancangan
untuk kala ulang tertentu.
6. Menentukan intensitas curah hujan harian dengan metode Mononobe
dalam kala ulang tertentu.
7. Penggambaran lengkung identitas curah hujan harian dengan kala ulang
8. Menghitung debit puncak.
Kerangka Pelaksanaan Penelitian
Pengolahan Data
1. Dilakukan penentuan parameter statistik dari data curah hujan maksimum.
Mulai Hujan harian
maksimum
Parameter statistik
Ditentukan jenis distribusi
Kurva IDF
Intensitas hujan Hitung nilai C
Dan Luas DAS
Selesai
Hujan Rencana
Ya
Tepat
Tidak
Hitung debit puncak
Uji Chi-Square dan Smirnov Kolmogorov
Prosedur :
- Dihitung nilai mean X
X = i
n
i
X n
∑
=11
- Dihitung standard deviasi S
s =
(
)
2 / 1 2 1 1 1 − −
∑
= X X n i n i- Dihitung koefisien varians
Cv =
x s
- Dihitung Coefisient of Skweness Cs,
Cs =
(
)
( )( )
3 31
2
1 n s
n X X n i n i − − −
∑
=- Dihitung Coefisient of Kurtosis Ck.
Ck =
(
)
( )( )(
)
4 4 i n 1 i 2 s 3 n 2 n 1 n X X n − − − −∑
=2. Penentuan pola distribusi yang tepat diantara distribusi Gumbel, distribusi
Log Normal, distribusi Log Pearson Type III dan distribusi Normal.
Rumus umum yang digunakan: XT = X + KT.S
Nilai K dapat dilihat pada Tabel K (Lampiran 3).
3. Dilakukan pengujian distribusi dengan uji Chi-Square dan Smirnov-
Hipotesis: Ho : Distribusi frekuensi hasil observasi sesuai (fit) dengan
distribusi teoritis tertentu (diharapkan).
Hi : Distribusi frekuensi hasil observasi tidak sesuai dengan
distribusi teoritis tertentu (diharapkan).
Kriteria Pengujian :
Ho diterima apabila : χ2hitung ≤ χ2(a;db)
Ho ditolak apabila : χ2hitung > χ2(a;db)
db = G-1
a. Uji Chi-Square
Adapun prosedur uji Chi-Square adalah :
− Urutkan data pengamatan (dari besar ke kecil atau sebaliknya).
− Kelompokkan data menjadi beberapa G sub-group (interval kelas).
− Ditentukan frekuensi pengamatan sebesar Oi dan frekuensi yang
diharapkan sebesar Ei untuk tiap-tiap sub-grup.
− Dihitung besarnya frekuensi untuk masing–masing sub grup
minimal 5 dengan menggunakan Tabel kurva normal (Lampiran 6).
− Pada tiap sub-group hitung nilai (Oi – Ei)2 dan
i i
E
E 2
i )
(O − .
− Jumlah seluruh G sub-grup nilai
i i
E
E 2
i )
(O −
untuk menentukan nilai
Chi-Square hitung.
− Tentukan derajat kebebasan dk = G-1. Nilai kritis untuk distribusi
b. Uji Smirnov-Kolmogorov :
Prosedur pelaksanaannya adalah :
− Urutkan data (dari besar ke kecil atau sebaliknya) dan tentukan
besarnya peluang dari masing-masing data tersebut X1 = P(X1).
− Urutkan masing-masing peluang teoritis dari hasil penggambaran
data (persamaan distribusi) X1 = P’(X1).
− Dari kedua nilai peluang tersebut, tentukan selisih terbesarnya antar
peluang pengamatan dengan peluang teoritis.
D = maksimum (P(Xn) – P’(Xn).
− Berdasarkan tabel nilai kritis (Smirnov-Kolmogorov test) tentukan
harga D0 (lihat Lampiran 5). Bila nilai D dan jumlah data yang
tersedia pada tabel nilai kritis D0 sesuai, maka distribusi yang
dipilih telah tepat.
4. Penentuan intensitas curah hujan harian dalam kala ulang tertentu dengan
metode mononobe:
I =
3 / 2 24 24
24
t R
.
5. Penentuan debit puncak (Qp):
HASIL DAN PEMBAHASAN
Kondisi DAS Percut
Daerah Aliran Sungai (DAS) Percut merupakan salah satu kawasan di
Sumatera Utara yang kondisinya kritis atau rawan banjir. Secara geografis DAS
Percut terletak pada 03o18’- 03o40’ LU dan 98o30’ – 99o00 BT, dengan sungai
utama yang melaluinya adalah Sungai Percut. Sungai Percut ini mengalir dari
daerah hulu yang terletak di sebagian kecil kecamatan STM Hulu dan kecamatan
Sibolangit, hingga bermuara pada daerah hilir di kecamatan Percut Sei Tuan dan
kemudian terus mengalir sampai ke Selat Malaka (Pantai Timur Sumatera Utara).
Daerah pengaliran (catchment area) Sungai Percut berbentuk bulu burung
yang meliputi beberapa bagian dari kecamatan Percut Sei Tuan, Batang Kuis,
Pantai Labu, Sibolangit, Tanjung Morawa, Patumbak, Biru-biru, STM Hulu dan
STM Hilir. Tidak seluruh luasan dari masing-masing kecamatan tersebut masuk
ke dalam daerah pengaliran Sungai Percut, akan tetapi hanya beberapa bagian
Ada tiga stasiun penakar curah hujan pada DAS Percut yaitu Saentis,
Batang Kuis dan Medan Amplas. Dari ketiga stasiun penakar hujan yang ada
hanya Saentís dan Batang Kuis yang berfungsi dengan baik. Kedua stasiun
penakar hujan ini letaknya berdekatan sehingga data curah hujan untuk daerah
pengaliran Sungai Percut diwakili oleh salah satu penakar saja. Dalam hal ini
penulis menggunakan data curah hujan harian dari stasiun penakar hujan Saentis.
Data kondisi DAS Percut yang diperoleh dari Badan Pusat Statistik
Kabupaten Deli Serdang adalah sebagai berikut.
Luas total daerah pengaliran Sungai Percut (A) = 276,8 km2
Lebar Maksimum sungai = 45 m
Panjang sungai Percut (L) = 70 km.
Kelerengan/kemiringan (S) = 0,02500 m
Kondisi tata guna lahan di Daerah Aliran Sungai (DAS) Percut terdiri dari
permukiman, perkebunan, sawah, tegalan, hutan dan tambak. Permukiman di
kawasan DAS Percut dapat digolongkan pada kawasan dengan kepadatan yang
sedang, sebagian besar kawasan DAS Percut berupa kawasan pertanian, hutan dan
perkebunan. Berdasarkan peta tata guna lahan yang ada, DAS Percut dapat
dikelompokkan ke dalam beberapa penggunaan lahan yang luas masing-masing
[image:47.595.114.286.678.748.2]lahan adalah sebagai berikut.
Tabel 3. Data Penggunaan Lahan pada DAS Percut
Tata Guna Lahan Luas (km2)
Permukiman 86,8
Hutan 23,5
Sawah 38,6
Tegalan 4,2 Perkebunan
- Tebu
- Kelapa Sawit - Coklat
26,3 34,5 5,4
Tambak 2,2
Lainnya 2,7
Luas Total 276,8
Sumber : Data Primer
Dari data diatas dapat diketahui bahwa kondisi tata guna lahan pada DAS
Percut didominasi daerah pertanian dan permukiman.
Analisis Curah Hujan
Curah Hujan Harian Maksimum
Untuk mengetahui besarnya curah hujan rencana yang terjadi di daerah
pengaliran Sungai Percut, diperlukan data curah hujan harian selama beberapa
tahun terakhir pada stasiun penakar hujan yang terdekat. Data curah hujan harian
yang digunakan diperoleh dari Bagian Penelitian Tebu Tembakau Deli (BPTTD)
Sampali, Medan yang merupakan data curah hujan harian selama 22 tahun
terakhir (1985-2006), dari stasiun penakar hujan Saentís.
Data curah hujan harian yang diperoleh terlebih dahulu dianalisis untuk
mendapatkan data curah hujan harian maksimum. Penentuan data curah hujan
maksimum ini mengunakan metode partial series yang merupakan metode terbaik
dibandingkan dengan metode annual maximum series. Hal ini sesuai dengan
pernyataan Suripin (2004) mengatakan bahwa metode annual maximum series
merupakan metode yang kurang realitis sebab dalam metode ini, besaran data
maksimum kedua dalam satu tahun yang mungkin lebih besar dari besaran data
analisis. Oleh karena itu, beberapa ahli menyarankan untuk menggunakan metode
Partial Series.
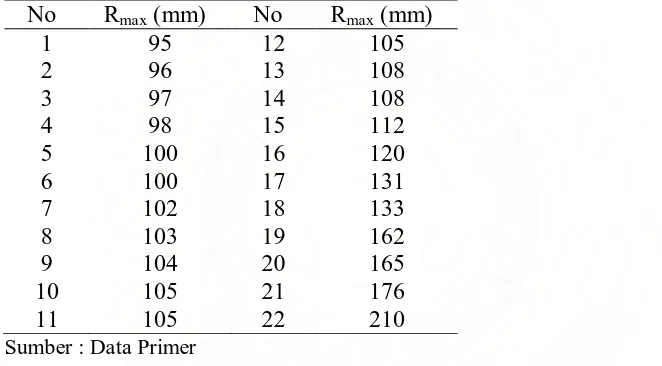
Setelah dilakukan analisis, diperoleh data curah hujan harian maksimum
[image:49.595.111.442.318.501.2]selama 22 tahun terakhir.
Tabel 4. Data Curah Hujan Harian Maksimum Tahunan Periode 1985-2006 di Stasiun Saentis.
No Rmax (mm) No Rmax (mm)
1 95 12 105
2 96 13 108
3 97 14 108
4 98 15 112
5 100 16 120
6 100 17 131
7 102 18 133
8 103 19 162
9 104 20 165
10 105 21 176
11 105 22 210
Sumber : Data Primer
Berdasarkan pada Tabel 4 di atas diperoleh bahwa curah hujan harian
maksimum tertinggi sebesar 210 mm dan curah hujan harian maksimum
terendah sebesar 95 mm.
Penentuan Pola Distribusi Hujan
Penentuan pola distribusi atau sebaran hujan dilakukan dengan
menganalisis data curah hujan harian maksimum yang diperoleh dengan
menggunakan analisis frekuensi. Dari hasil perhitungan diperoleh nilai untuk
Machairiyah : Analisis Curah Hujan Untuk Pendugaan Debit Puncak Dengan Metode Rasional Pada Das Percut Kabupaten Deli Serdang, 2007.
[image:50.595.114.313.114.228.2]USU Repository © 2008
Tabel 5. Parameter Statistik Analisis Frekuensi
Parameter Nilai
Rata-rata X = 119,7727
Simpangan baku s = 31,0329 Koefisien variasi Cv = 0,259098 Koefisien skewness Cs = 1,735077
Koefisien kurtosis Ck = 2,370905
Berdasarkan hitungan parameter statistik yang diperoleh pada Tabel 5
tersebut ditetapkan bahwa jenis distribusi yang cocok dengan sebaran data curah
hujan harian maksimum di wilayah studi adalah distribusi Log Pearson Type III
untuk menghitung curah hujan rancangan dengan berbagai kala ulang. Hal ini
ditunjukkan oleh nilai parameter statistik yang diperoleh tidak mengikuti pola
distribusi untuk ketiga metode lainnya dan penggambaran garis teoritiknya berupa
garis lengkung (dapat dilihat pada Gambar 5). Hal ini sesuai dengan pernyataan
Jayadi (2000), ciri khas statistik distribusi Log Pearson Type III adalah:
1. Jika tidak menunjukkan sifat-sifat seperti ketiga distribusi yaitu distribusi
Gumbel, Normal maupun Log Normal
2. Garis teoritis probabilitasnya berupa garis lengkung.
Penggambaran garis teoritiknya dapat dilakukan dengan melakukan
pengeplotan data secara empiris dengan metode Weibull. Pengeplotan ini
bertujuan untuk mengetahui ketepatan distribusi probabilitas dan penggambaran
garis teoritik data hidrologi. Setelah dilakukan pengeplotan, data curah hujan
maksimum digambarkan di kertas probabilitas.
100 1000
aksi
m
u
m
Uji Kecocokan (Goodness Of Fit)
Dari distribusi yang telah diketahui, maka dilakukan uji statistik untuk
mengetahui kesesuaian distribusi yang dipilih dengan hasil empiris. Pada
penelitian ini uji statistik dilakukan dengan metode Chi-Square dan Smirnov
Kolmogorov. Menurut Sri Harto (1993), setiap distribusi mempunyai sifat yang
khas, sehingga data curah hujan harus diuji kecocokannya dengan metode
Chi-Square dan Smirnov Kolmogorov. Pemilihan distribusi yang tidak benar dapat
menimbulkan kesalahan perkiraan yang cukup besar, baik over estimate maupun
[image:51.595.113.385.539.606.2]under estimate.
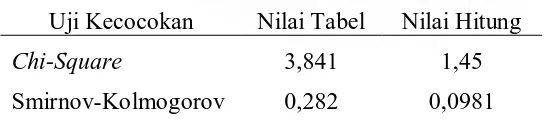
Tabel 6. Hasil Uji Chi Square dan Smirnov-Kolmogorov
Uji Kecocokan Nilai Tabel Nilai Hitung
Chi-Square 3,841 1,45
Smirnov-Kolmogorov 0,282 0,0981
Dari Tabel 6 dapat dilihat bahwa dengan uji Chi-Square diperoleh nilai
χ2
hitung < χ2tabel sedangkan Smirnov Kolmogorov diperoleh nilai Dhitung < Dtabel
sehingga dapat ditarik kesimpulan bahwa Ho terima. Hal ini berarti bahwa
berbeda secara nyata atau dapat dinyatakan pola distribusi yang digunakan sudah
tepat yaitu distribusi Log Pearson Type III.
Curah Hujan Rencana
Berdasarkan analisis frekuensi yang dilakukan pada data curah hujan
harian maksimum diperoleh bahwa jenis distribusi yang paling cocok dengan
sebaran data curah hujan harian maksimum di daerah pengaliran Sungai Percut
adalah distribusi Log Pearson Type III. Untuk itu, data curah hujan harian
maksimum yang diperoleh diubah dalam bentuk logaritmik sehingga parameter
[image:52.595.112.327.499.622.2]statistik berubah sesuai dengan Tabel 7 di bawah ini :
Tabel 7. Parameter Statistik Analisis Frekuensi Distribusi Log Pearson Type III
Parameter Nilai
Rata-rata X = 2,06687
Simpangan baku s = 0,09787
Koefisien variasi Cv = 0,04735
Koefisien skewness Cs = 1,426049
Koefisien kurtosis Ck = 1,057912
Setelah itu, dilakukan penghitungan curah hujan rancangan pada periode
ulang tertentu dengan persamaan Log XT = LogX + K . Ssehingga :
Berdasarkan persamaan diatas dapat dihitung hujan rancangan untuk
[image:53.595.114.442.297.578.2]berbagai periode ulang. Hujan rancangan ini dapat dilihat pada Tabel 8 berikut.
Tabel 8. Hujan Rancangan Berbagai Periode Ulang
No Kala Ulang
(Tahun)
Hujan Rancangan (mm)
1 1 86,98
2 2 110,78
3 5 136,61
4 10 157,62
5 15 164,08
6 20 170,83
7 25 177,86
8 30 184,77
9 40 199,34
10 50 215,12
11 100 244,65
12 200 277,7
Intensitas Hujan
Untuk mendapatkan intensitas hujan dalam periode 1 jam dari data curah
hujan harian maksimum digunakan rumus mononobe. Hal ini disebabkan karena
data curah hujan jangka pendek tidak tersedia, yang ada hanya data curah hujan
Machairiyah : Analisis Curah Hujan Untuk Pendugaan Debit Puncak Dengan Metode Rasional Pada Das Percut Kabupaten Deli Serdang, 2007.
USU Repository © 2008
persamaan (14) sesuai dengan pernyataan Loebis (1992) bahwa intensitas hujan
(mm/jam) dapat diturunkan dari data curah hujan harian (mm) empiris
menggunakan metode mononobe. Hasil analisis ditunjukkan dengan Tabel 9 di
bawah ini.
Hasil analisis berupa intensitas hujan dengan durasi dan periode ulang
tertentu dihubungkan ke dalam sebuah kurva Intensity Duration Frequency (IDF).
Kurva IDF menggambarkan hubungan antara dua parameter penting hujan yaitu
durasi dan intensitas hujan yang selanjutnya dapat dimanfaatkan untuk
menghitung debit puncak dengan metode rasional. Hal ini sesuai dengan
pernyataan Sosrodarsono dan Takeda (2003), yang mengatakan bahwa Lengkung
Intensity Duration Frequency (IDF) ini digunakan dalam menghitung debit
puncak dengan metode rasional untuk menentukan intensitas curah hujan rata-rata
dari waktu konsentrasi yang dipilih.
Dari Tabel 9 di atas dapat dibuat kurva Intensity Duration Frequency
(IDF) seperti Gambar 6 di bawah ini.
Dari kurva Intensity Duration Frequency (IDF) terlihat bahwa intensitas
hujan yang tinggi berlangsung dengan durasi pendek. Hal ini menunjukkan bahwa
hujan deras pada umumnya berlangsung dalam waktu singkat namun hujan tidak
deras (rintik-rintik) berlangsung dalam waktu lama. Interpretasi kurva Intensity
Duration Frequency (IDF) diperlukan untuk menentukan debit banjir rencana
mempergunakan metode rasional.
Analisis Debit Banjir
Waktu Konsentrasi
Waktu konsentrasi digunakan untuk menentukan lamanya air hujan
mengalir dari hulu sungai hingga ke tempat keluaran DAS. Waktu konsentrasi (tc)
dihitung dengan menggunakan rumus Kirpich (1940) pada persamaan (15).
Berdasarkan data panjang dan kemiringan sungai sebelumnya, diperoleh nilai
waktu konsentrasi sebesar 7,24 jam. Hal ini berarti bahwa waktu yang diperlukan
oleh air hujan untuk mengalir dari titik terjauh (hulu) sampai ke tempat keluaran
DAS (hilir) sebesar 7,24 jam. Hal ini sesuai dengan pernyataan Suroso (2006),
[image:55.595.115.440.415.516.2]maksimum 12 jam pun jarang terjadi. Durasi hujan sering dikaitkan dengan waktu
konsentrasi sehingga sangat berpengaruh pada besarnya debit yang masuk ke
saluran atau sungai. Hal ini menunjukkan bahwa durasi hujan dengan intensitas
tertentu sama dengan waktu konsentrasi dapat terpenuhi sehingga metode rasional
layak digunakan untuk wilayah studi.
Koefisien Limpasan
Dalam perhitungan debit banjir menggunakan metode rasional diperlukan
data koefisien limpasan (run off coeffisient). Koefisien limpasan ini diperoleh
dengan menghitung data luasan dari masing-masing tata guna lahan yang ada.
Luasan diperoleh dengan mengukur masing-masing kondisi tata guna lahan pada
peta dengan planimeter. Penulis menghitung nilai koefisien limpasan hanya
berdasarkan pada peta tata guna lahan yang dikeluarkan oleh Badan Perencanaan
Pembangunan Daerah (Bappeda) Kabupaten Deli Serdang. Ada kawasan-kawasan
tertentu yang sifatnya minoritas tidak terdapat di dalam peta tersebut, sehingga
tidak turut diperhitungkan dalam menentukan koefisien limpasan.
Berdasarkan pada Tabel 3 dapat dihitung nilai koefisien limpasan untuk
[image:56.595.113.426.647.747.2]masing-masing luasan yaitu:
Tabel 10. Perhitungan Koefisien Limpasan
Tata Guna lahan C A (km2) C x A
Pemukiman 0,5 86,8 43,4
Hutan 0,03 23,5 0,705
Sawah 0,15 38,6 5,79
Perkebunan 0,4 66,2 26,48
Tegalan 0,2 4,2 0,84
Jumlah 273,9 82,675
Nilai C 0,305186
Dari Tabel 10 di atas dan dengan menggunakan persamaan (16) dapat
dihitung nilai koefisien limpasan yaitu sebesar 0,305. Dari nilai koefisien
limpasan ini dapat diketahui bahwa 0,305 dari air hujan yang turun akan melimpas
ke permukaan yang kemudian akan mengalir menuju daerah hilir.
Nilai koefisien limpasan dapat juga digunakan untuk menentukan kondisi fisik
dari suatu DAS. Dari nilai koefisien limpasan sebesar 0,305 maka dapat
dinyatakan bahwa DAS Percut memiliki kondisi fisik yang baik. Hal ini sesuai
dengan pernyataan Kodoatie dan Syarief (2005), yang mengatakan bahwa
angka koefisien aliran permukaan itu merupakan salah satu indikator untuk
menentukan kondisi fisik suatu DAS. Nilai C berkisar antara 0 – 1. Nilai C = 0
menunjukkan bahwa semua air hujan terintersepsi dan terinfiltrasi ke dalam
tanah, sebaliknya untuk nilai C = 1 menunjukkan bahwa air hujan mengalir
sebagai aliran permukaan. Pada DAS yang baik harga C mendekati nol dan
semakin rusak suatu DAS maka harga C semakin mendekati satu.
Perubahan tata guna lahan yang terjadi secara langsung mempengaruhi debit
puncak (banjir) yang terjadi pada suatu DAS. Kondisi fisik DAS Percut
sekarang harus terus dilestarikan, perkembangan dan kemajuan suatu daerah
yang terus meningkat harus disertai dengan upaya peningkatan pelestarian
lingkungan agar nilai koefisien limpasan tidak meningkat secara drastis.
Berdasarkan berbagai data yang telah diperoleh di atas maka dapat
dihitung debit puncak Sungai Percut dengan metode rasional sesuai persamaan
(17) untuk berbagai kala ulang tertentu. Lama hujan dengan intensitas tertentu
sama dengan waktu konsentrasi. Untuk itu, penulis melakukan interpolasi
terhadap data intensitas hujan jam-jaman sehingga diperoleh data yang terlihat
[image:58.595.111.442.295.508.2]pada Tabel 11.
Tabel 11. Debit Puncak (banjir) di DAS Percut
Kala Ulang (tahun)
Intensitas Hujan (mm/jam)
Debit Puncak (m3/detik)
1 8,18 192,05
2 10,42 244,68
5 12,84 301,57
10 14,82 348,03
15 15,55 365,16
20 16,06 377,18
25 16,69 391,93
30 17,37 407,91
40 18,74 440,15
50 20,23 475,00
100 23,00 540,17
200 26,11 613,24
Berdasarkan perhitungan di atas dapat dinyatakan bahwapada kala ulang 1
tahun selama durasi hujan (waktu konsentrasi) 7,24 jam dengan intensitas hujan
8,18 mm/jam seluas 276,8 km2 maka debit puncak yang diperoleh pada DAS
Percut sebesar 192,05 m3/detik. Debit puncak yang diperoleh dapat dijadikan
sebagai bahan dasar untuk perencanaan bangunan pengendali banjir, dimana
dibangun suatu bangunan pengendali banjir yang dapat menampung debit puncak
suatu aliran air sehingga dapat menghemat biaya dan waktu dalam pelaksanaan
KESIMPULAN DAN SARAN
Kesimpulan
1. Pola distribusi yang tepat untuk DAS Percut adalah distribusi Log Pearson
Type III.
2. Hujan rancangan berbagai periode ulang 1, 2, 5, 10, 15, 20, 25, 30, 40, 50,
100, 200 tahun adalah sebesar 86,98 mm/jam; 110,78 mm/jam; 136,61
mm/jam; 157,62 mm/jam; 164,08 mm/jam; 170,83 mm/jam; 177,86
mm/jam; 184,77 mm/jam; 199,34 mm/jam; 215,12 mm/jam; 244,65
mm/jam dan 277,7 mm/jam.
3. Waktu yang diperlukan oleh hari