BAB 1
PENDAHULUAN
1.1 Latar Belakang
Pengambilan keputusan diperlukan pada semua tahap administrasi dan manajemen. Misalnya dalam tahap perencanaan, diperlukan banyak kegiatan pengambilan keputusan sepanjang proses perencanaan tersebut. Keputusan-keputusan yang dibuat dalam proses perencanaan ditujukan kepada pemilihan alternatif program dan prioritasnya.
Prosedur pembuatan keputusan diawali dengan mengidentifikasi berbagai alternatif yang akan dipertimbangkan dalam pembuatan keputusan. Penentuan keputusan yang terbaik tergantung kepada peneliti dengan memperhitungkan situasi yang mungkin terjadi di masa depan. Seringnya masa depan tersebut merupakan sesuatu yang tidak pasti. Ada berbagai kemungkinan situasi masa depan, dimana peneliti tidak yakin tentang situasi mana yang akan terjadi. (Azhar Kasim, 1994)
Jadi, selanjutnya adalah mengidentifikasi situasi masa depan yang mungkin terjadi. Situasi masa depan ini dikenal dengan “state of nature”, yang berdasarkan pada asumsi bahwa tiap macam situasi masa depan yang dikemukakan meliputi seluruh situasi yang dapat terjadi (collectively exhaustive), dan tiap situasi tidak dapat terjadi secara bersamaan dengan situasi lain (mutually exclusive).
ABSTRAK
Prosedur pembuatan keputusan diawali dengan mengidentifikasi berbagai alternatif yang akan dipertimbangkan dalam pembuatan keputusan. Selanjutnya mengidentifikasi situasi masa depan yang mungkin terjadi. Situasi masa depan ini
ABSTRACT
Making Decision Procedures begin with identify some alternatives which must be considered in making decision. Then identify the future may be happened. The future
is called “State of Nature” according to assumption that every situation in the future
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Pengambilan keputusan diperlukan pada semua tahap administrasi dan manajemen. Misalnya dalam tahap perencanaan, diperlukan banyak kegiatan pengambilan keputusan sepanjang proses perencanaan tersebut. Keputusan-keputusan yang dibuat dalam proses perencanaan ditujukan kepada pemilihan alternatif program dan prioritasnya.
Prosedur pembuatan keputusan diawali dengan mengidentifikasi berbagai alternatif yang akan dipertimbangkan dalam pembuatan keputusan. Penentuan keputusan yang terbaik tergantung kepada peneliti dengan memperhitungkan situasi yang mungkin terjadi di masa depan. Seringnya masa depan tersebut merupakan sesuatu yang tidak pasti. Ada berbagai kemungkinan situasi masa depan, dimana peneliti tidak yakin tentang situasi mana yang akan terjadi. (Azhar Kasim, 1994)
Jadi, selanjutnya adalah mengidentifikasi situasi masa depan yang mungkin terjadi. Situasi masa depan ini dikenal dengan “state of nature”, yang berdasarkan pada asumsi bahwa tiap macam situasi masa depan yang dikemukakan meliputi seluruh situasi yang dapat terjadi (collectively exhaustive), dan tiap situasi tidak dapat terjadi secara bersamaan dengan situasi lain (mutually exclusive).
mungkin berkeinginan mencari informasi tambahan tentang terjadinya situasi masa depan.
Informasi hasil penelitian ini dapat digunakan untuk merevisi atau memperbarui Probabilitas Prior sehingga keputusan akhirnya dibuat berdasarkan perkiraan probabilitas tentang masa depan yang lebih akurat. Cara memperoleh informasi tambahan ini sering dilakukan melalui eksperimen yang khusus didesain untuk memperoleh data yang paling baru dan lengkap tentang situasi masa depan atau tentang apa yang akan terjadi.
Perlu disadari bahwa eksperimen yang biasanya didasarkan atas data hasil penelitian sampel acak tidak 100% benar, hasil penelitian ini mengandung unsur ketidakpastian, ini disebabkan karena adanya kesalahan sampling. Misalnya promosi yang diusulkan oleh ahli riset pemasaran ternyata tidak dapat meningkatkan penjualan. Walaupun informasinya tidak sempurna tetapi hasil eksperimen tetap masih bermanfaat.
Suatu hasil eksperimen yang tidak baik (unfavourable test) dapat meningkatkan probabilitas untuk menolak suatu keputusan yang tidak menguntungkan, sebaliknya, yang baik (unfavourable) meningkatkan probabilitas untuk menolak suatu keputusan yang menguntungkan. (Azhar Kasim, 1994)
Dengan adanya informasi hasil eksperimen diharapkan kemungkinan besar akan dihasilkan keputusan yang mendekati ketepatan. Pengambilan keputusan dengan informasi tambahan akan mempengaruhi probabilitas terjadinya kejadian tak pasti yang menentukan hasil dari tindakan atau pemilihan alternatif. Banyaknya informasi yang dapat diperhitungkan ke dalam keputusan akan membantu Pengambil keputusan untuk mengambil keputusan yang lebih baik.
probabilitas digabungkan dengan semua komponen keputusan dengan menggunakan diagram pohon keputusan.
Sebelum keputusan diambil, perlu dilakukan analisa sensitivitas untuk menganalisa sejauh mana perubahan dapat terjadi pada keputusan. Dengan informasi ini Pengambil keputusan dapat mempertimbangkan keputusan yang akan diambil.
1.2 Rumusan Masalah
Dalam analisa ini akan dicari alternatif terbaik untuk mendapatkan keuntungan maksimal dengan metode pengambilan keputusan yang berdasarkan nilai ekspektasi, dimana terdapat informasi tambahan. Kemudian akan dilihat sejauh mana perubahan dapat terjadi pada keputusan berdasarkan analisa sensitivitas, dan bagaimana keterlibatan pertimbangan subjektif dalam proses pengambilan keputusan.
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah:
1. Menentukan alternatif terbaik yang dapat memaksimalkan keuntungan, yaitu alternatif dengan hasil Expected Payoff tertinggi.
2. Mengevaluasi apakah layak memanfaatkan informasi sampel untuk meningkatkan keakuratan penelitian atau tidak, yaitu yang dilihat dari tingkat efisiensinya.
3. Menganalisa kekonsistenan penelitian sebelumnya, dengan melakukan analisa sensitivitas.
1.4 Kontribusi Penelitian
Kontribusi dari penelitian ini adalah:
1. Pengambilan keputusan diperlukan pada tahap administrasi dan manajemen. Misalnya tahap perencanaan dalam bidang perbankan, proyek, dan pemasaran diperlukan analisa pengambilan keputusan untuk memperkirakan strategi optimal yang dapat dilakukan untuk mencapai keuntungan dan meminimalisir kerugian. 2. Revised information diperlukan pada polling, misalnya polling pemilihan umum
untuk mengetahui informasi terkini, di sini konsep probabilitas Bayes sangat berperan.
1.5 Metode Penelitian
Metode penelitian yang dilakukan penulis dalam pengerjaan tugas akhir ini adalah: 1. Mengidentifikasi alternatif dan situasi masa depan (state of nature) yang relevan
yang akan dipertimbangkan dalam pembuatan keputusan, dimana masing-masing bersifat mutually exclusive, yaitu apabila satu kejadian terjadi maka tidak mungkin.
2. Melakukan analisa prior tanpa adanya informasi, berdasarkan Expected Value. 3. Melakukan analisa preposterior menggunakan konsep probabilitas Bayes untuk
mengevaluasi penting atau tidaknya informasi tambahan sampel, yaitu informasi yang diperoleh dari hasil riset.
4. Jika keputusan adalah menggunakan informasi sampel, maka selanjutnya melakukan analisa sensitivitas untuk melihat besar perubahan terhadap keputusan. 5. Jika hasil analisa mendukung keputusan sebelumnya, maka selanjutnya melakukan
1.6 Tinjauan pustaka
Mangkusubroto, Kuntoro, dan Trisnadi, Listiarini menyatakan bahwa Keputusan adalah suatu kesimpulan dari suatu proses untuk memilih tindakan yang terbaik dari sejumlah alternatif yang ada. Pengambilan keputusan adalah proses yang mencakup semua pemikiran dan kegiatan yang diperlukan guna membuktikan dan memperlihatkan pilihan terbaik. (Kuntoro Mangkusubroto dkk, 1987)
Teorema Bayes digunakan untuk menghitung probabilitas terjadinya suatu peristiwa berdasarkan pengaruh yang didapat dari hasil observasi. Pada teorema ini terdapat beberapa bentuk probabilitas, yaitu Probabilitas Awal (Probabilitas Prior), Probabilitasan Bersyarat, Probabilitas Ganda, Probabilitas Posterior. (M. Iqbal Hasan, 2002)
Spiegel, Murray R, Schiller John, Srinivasan R. Alu [10] nilai Harapan atau nilai rata-rata merupakan nilai ringkasan untuk mewakili sekelompok nilai. Kalau x adalah variabel acak, maka Nilai Harapan sama dengan jumlah hasil kali setiap variabel dengan probabilitasnya, seperti rumus berikut:
Supranto, Johannes [11] menjelaskan struktur persoalan keputusan dalam menentukan Payoff yang diperoleh dari Alternatif Tindakan dengan Kejadian tak Pasti tertentu dan Probalitasnya, ke dalam Tabel Keputusan.
Bunn, Derek W [1] Expected Value of Perfect Information (EVPI) adalah jumlah maksimum yang wajar dibayar oleh pengambil keputusan untuk memperoleh informasi sempurna, dihitung dengan:
EVPI = EPPI –EV dimana :
EV : adalah nilai harapan terbesar dari tiap alternatif tindakan.
EPPI : adalah hasil perkalian maksimum baris (pay off tertinggi) dengan probabilitas. yang dihitung dengan:
Jika informasi tentang probabilitas secara pasti, maka biaya yang boleh dikeluarkan maksimum sama dengan EVPI (Kasim Azhar, 1994).
Kuntoro Mangkusubroto, dkk memberikan contoh dan penjelasan tentang Perbaikan Nilai Kemungkinan Dengan Adanya Informasi Tambahan, bahwa ada umumnya dalam menghadapi suatu persoalan, pengambil keputusan telah mempunyai informasi awal. Bila informasi awal dirasakan telah memadai, maka keputusan dapat langsung dibuat. Tapi bila informasi awal dirasakan belum cukup, maka diperlukan suatu usaha untuk mendapatkan informasi tambahan.
Selanjutnya bila kemudian telah diperoleh informasi tambahan, maka pembuat keputusan perlu menggunakan informasi tambahan ini bersama dengan informasi awal, untuk mendapatkan informasi yang lebih baik untuk pengambilan keputusan.
Probabilitas suatu peristiwa yang ditentukan dengan perasaan atau kepercayaan individu atau kelompok yang didasarkan pada fakta atau peristiwa masa lalu yang ada dinamakan Probabilitas Subjektif. (Sri Mulyono, 1996)
perkiraan probabilitas state of nature dapat berubah ke strategi lain. Jika perkiraan perubahannya terlalu besar, maka tidak layak untuk membeli penelitian itu.
Bab 2
LANDASAN TEORI
2.1. Definisi Dasar
Himpunan semua hasil (outcome) yang mungkin dari suatu percobaan disebut ruang sampel (sample space) dinyatakan dengan lambang T dan setiap hasil dalam ruang sample disebut sebagai titik sampel (sample point). Kejadian atau peristiwa (event) adalah himpunan bagian dari ruang sampel.
Contoh:
Dua buah uang logam setimbang dilemparkan ke atas, maka yang dimaksud dengan: Percobaan : pelemparan dua uang logam.
Ruang sampel : {A,G}, {A,A}, {G,A},{G,G} Titik sampel : G (gambar) dan A (angka)
Peristiwa yang mungkin adalah: AA (angka dengan angka), AG (angka dengan gambar), G (gambar dengan gamba
Kejadian majemuk adalah dua kejadian atau lebih yang terjadi secara bersamaan. Kejadian majemuk ada dua, yaitu (Adler Haymans,1991):
1. Gabungan, yang disimbolkan dengan
Untuk kejadian A dan B, gabungan dari ruang hasil kejadian A dengan ruang hasil kejadian B, adalah ruang hasil yang unsur-unsurnya terdiri dari semua unsur ruang hasil kejadian A saja, atau B saja, atau semua unsur di ruang hasil kejadian A dan kejadian B ini dinyatakan dengan symbol .
Contoh:
2. Irisan, yang disimbolkan dengan ∩
Untuk dua kejadian A dan B, irisan ruang hasil kejadian A dengan ruang hasil kejadian B adalah ruang hasil yang unsur-unsurnya terdiri dari unsur-unsur yang dimiliki oleh ruang hasil kejadian A dan juga dimiliki oleh kejadian B. Simbol untuk kejadian ini adalah:
Contoh:
Misalkan A = {a, e, i, o, u} dan B = {a, e}; maka A ∩ B = {i, o, u}
Dalam percobaan tertentu tidak jarang didefinisikan dua kejadian A dan B yang tidak mungkin terjadi sekaligus. Kedua kejadian A dan B seperti itu dikatakan saling meniadakan atau saling terpisah (mutually exclusive), dirumuskan sebagai:
Kejadian A dan B saling meniadakan atau terpisah yakni, bila A dan B tidak memiliki unsur persekutuan.
Contoh:
Misalkan A = {a, b, c, d} dan B = {e, f}; maka A ∩ B = Ø.
2.2. Konsep Probabilitas
2.2.1. Peluang Kejadian
Untuk menentukan peluang suatu kejadian A, semua bobot titik sampel dalam A dijumlahkan. Jumlah ini dinamakan peluang A dan dinyatakan dengan P(A).
Jika A adalah suatu kejadian, maka probabilitas kejadian A dapat ditulis dengan: 0 ≤ P(A) ≤ 1, P(Ø) = 0, dan P(T) = 1
Contoh:
Sebuah mata uang dilantunkan dua kali. Berapakah peluangnya bahwa paling sedikit muncul muka sekali?
Ruang sampel percobaan ini adalah:
T = {MM, MB, BM, BB}
Bila mata uang tersebut setangkup, maka tiap hasil mempunyai kemungkinan muncul yang sama. Karena itu tiap titik sampel diberi bobot b sehingga 4b = 1 atau b = 1/4. Bila A menyatakan kejadian bahwa paling sedikit satu muka muncul, maka:
A = {MM, MB, BM} Dan,
Bila ruang sampel suatu percobaan berisi unsur, dan masing-masing dapat terjadi dengan peluang yang sama, maka tiap titik mendapat peluang . Peluang setiap kejadian N yang berisi n dari ke N titik sample adalah nisbah dari banyaknya unsur di A dengan unsur di T.
Teorema:
Bila suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan sama, dan bila tepat sebanyak n dari hasil berkaitan dengan kejadian A, maka peluang kejadian A adalah:
P(A) =
2.2.2. Aturan Penjumlahan
Teorema : Bila A dan B dua kejadian sembarang maka: P(A B) = P(A) + P(B) P(A
2.2.3. Aturan Perkalian
Teorema: Untuk dua kejadian A dan B dapat terjadi pada satu percobaan, maka: P(A B) = P(A) P(B|A)
Teorema: Dua kejadian A dan B bebas jika dan hanya jika: P(B|A) = P(B)
Dan
P(A|B) = P(A) Jika tidak demikian, A dan B tak bebas.
Teorema: bila dalam suatu percobaan, kejadian A1, A2, A3, …, , dapat terjadi, maka:
P( ) =
P( )
Bila kejadian A1, A2, A3, …, bebas, maka:
P( ) = P(
2.2.4. Probabilitas Bersyarat
Misalkan A dan B adalah dua kejadian sedemikian rupa sehingga P(A) > 0, maka
Probabilitas Bersyarat adalah probabilitas B akan terjadi dengan syarat A telah terjadi. Teorema: Peluang bersyarat B bila A diketahui, dinyatakan dengan P(A), ditentukan
oleh:
bila P(A) > 0
2.3. Perbaikan Nilai Kemungkinan Dengan Adanya Informasi Tambahan
keputusan dapat langsung dibuat. Tapi bila informasi awal dirasakan belum cukup, maka diperlukan suatu usaha untuk mendapatkan informasi tambahan. Selanjutnya bila kemudian telah diperoleh informasi tambahan, maka pembuat keputusan perlu menggunakan informasi tambahan ini bersama dengan informasi awal, untuk mendapatkan informasi yang lebih baik untuk pengambilan keputusan. (Kuntoro Mangkusubroto, 1987)
Contoh:
Pabrik W memproduksi bagian-bagian mesin mobil yang akan digunakan dalam industri perakitan mobil. Oleh sebab itu, ketelitian tinggi sangat diperlukan di pabrik W tersebut. Setiap bagian harus dibuat tepat sama dengan standar yang sudah ditetapkan oleh pemesan.
Untuk menjamin ketepatan ini, Pabrik W mempunyai bagian khusus yang bernama bagian Pengendalian Kualitas, yang bertugas untuk memeriksa produk pada tiap tahapan proses, dan menghentikan proses apabila produk yang dihasilkan tidak memenuhi standar yang ditetapkan, sehingga kesalahan yang berkepanjangan dapat dihentikan. Salah satu tahapan yang harus dilakukan adalah melakukan pengecekan pengaturan mesin produksi sebelum mesin tersebut digunakan untuk memproduksi.
Salah seorang staf bagian Pengendalian Kualitas, Dedi, mendapat tugas untuk memeriksa pengaturan mesin sebelum mesin tersebut digunakan. Dari pengalamannya bekerja slama ini, Dedi mengetahui bahwa besarnya kemungkinan pengaturan mesin sudah benar adalah 0,8. Walaupun begitu, Dedi merasa ragu untuk menyetujui pengaturan mesin tersebut dengan hanya mengandalkan informasi tersebut.
Dari hasil terakhir itulah, Dedi akan mengambil keputusan berkenaan dengan pengaturan mesin tersebut. Bila dari hasil terakhir tersebut, mesin dapat dikatakan telah dipengaturan dengan benar, maka mesin tersebut sudah dapat digunakan untuk menghasilkan produk selanjutnya. Tapi bila pengaturan mesin tersebut tidak benar maka mesin tersebut akan dipengaturan lagi.
2.3.1. Nilai kemungkinan Prior dan Posterior
Dalam contoh kasus di atas, Dedi telah mempunyai suatu informasi awal, bahwa kemungkinan pengaturan mesin sudah benar adalah 0,8. Informasi awal tentang nilai kemungkinan ini disebut sebagai nilai kemungkinan Prior.
Bila sampel produk yang diukur ternyata ukurannya tidak tepat, pastinya dedi akan berpendapat bahwa nilai kemungkinan pengaturan mesin tersebut benar lebih kecil dari 0,8. Sebaliknya, jika sampel tersebut ternyata bagus, tentunya akan memperkuat dugaan Dedi bahwa pengaturan mesin sudah benar.
Persoalan yang timbul adalah bagaimana caranya agar Dedi dapat memperbaiki kemungkinan Prior-nya, setelah dia mendapatkan informasi baru, sehingga dia pada akhirnya bisa mendapatkan nilai kemungkinan yang telah diperbaiki. Nilai kemungkinan akhir ini yang disebut sebagai nilai kemungkinan Posterior.
Dalam hal ini dapat diambil definisi bahwa:
1. Nilai kemungkinan Prior adalah nilai adalah nilai kemungkinan mesin tersebut pengaturannya telah benar (B) atau dinyatakan sebagai P(B).
2.3.2. Penghitungan Nilai Kemungkinan Posterior
Untuk dapat menghitung nilai kemungkinan Posteriornya, terlebih dahulu diagram kemungkinan untuk situasi tersebut akan digambarkan.
Gambar 2.3.2.1 Diagram Kemungkinan
Nilai kemungkinan Prior adalah P(B) = 0,8 dan P(S) = 0,2. Kemudian juga diketahui bahwa bila pengaturan mesin telah benar, kemungkinan hasilnya tepat adalah 0,9, tetapi bila pengaturan mesin salah, kemungkinan hasilnya tepat hanya sebesar 0,4. Hal ini disebut likelihood.
Likelihood-nya adalah sebagai berikut:
P(T|B) = 0,9 P(T|S) = 0,4
Jika setelah diperiksa, sampel produk tersebut tenyata tepat (T), nilai kemungkinan Posteriornya adalah P(B|T), dan nilainya dapat diperoleh dengan menggunakan perhitungan untuk kemungkinan bersyarat:
Dapat dilihat bahwa dengan mengetahui sampel yang diperiksa ternyata ukurannya tepat, maka perkiraan nilai kemungkinan pengaturan mesin sudah tidak benar, meningkat dari 0,8 menjadi 0,9.
Sebaliknya bila ternyata sampel tersebut ternyata ukurannya tidak tepat ( )
__ T , maka nilai kemungkinan Posteriornya adalah:
Terlihat bahwa bila sampel yang diambil ternyata tidak tepat, nilai kemungkinan bahwa pengaturan mesin adalah benar, yang semula 0,8 turun menjadi 0,4.
Cara perhitungan nilai kemungkinan Posterior dengan menggunakan perhitungan nilai kemungkinan bersyarat, sering juga disebut perbaikan nilai kemungkinan Bayes.
2.4. Teorema bayes
Bukti:
Menurut definisi peluang bersyarat:
diperoleh bentuk:
Buktinya selesai.
Teorema Bayes digunakan untuk menghitung probabilitas terjadinya suatu peristiwa berdasarkan pengaruh yang didapat dari hasil observasi. Pada teorema ini terdapat beberapa bentuk probabilitas, yaitu sebagai berikut: (Azhar Kasim, 1994)
1. Probabilitas Awal (Probabilitas Prior), yaitu probabilitas berdasarkan informasi yang tersedia (sebelum ada tambahan informasi).
2. Probabilitasan Bersyarat yaitu probabilitas dimana terjadinya suatu peristiwa didahului oleh terjadinya peristiwa lain.
3. Probabilitas Ganda, yaitu gabungan dari beberapa probabilitas (probabilitas gabungan)
4. Probabilitas Posterior, yaitu probabilitas yang diperbaiki dengan adanya informasi tambahan.
2.5. Teorema Jumlah Peluang atau Aturan Penghapusan
Misalkan kejadian B1, B2, …, Bk merupakan suatu partisi dari ruang sampel T dengan
Perhatikan diagram Venn di gambar terlihat bahwa kejadian A merupakan gabungan dari sejumlah kejadian yang saling terpisah
2.6. Nilai Kemungkinan Objektif dan Subjektif 2.6.1. Nilai Kemungkinan Objektif
Bila membicarakan persoalan kemungkinan, biasanya yang ada dalam bayangan adalah distribusi frekuensi, data masa lalu, dan sebagainya. Dalam contoh klasik maka pertanyaan nya selalu, berapakah kemungkinan munculnya sisi gambar dalam suatu percobaan munculnya mata uang.
Sebagian besar orang akan setuju bahwa nilai kemungkinan tersebut adalah sebesar 0,5. Pada kenyataannya, bila mata uang tersebut benar (atau bukan mata uang yang diberi sesuatu agar tak seimbang), maka dalam pelemparan berkali-kali, frekuensi relatif dari munculnya sisi gambar adalah 0,5. Analisa frekuensi relatif inilah yang pada dasarnya mendasari nilai kemungkinan pada pelemparan mata uang, sehingga dikatakan sebagai nilai kemungkinan objektif.
Nilai kemungkinan objektif digunakan dalam beberapa bidang dimana data dapat diperoleh dengan mudah, misalnya dalam bidang biologi dan pertanian, pengendalian kualitas dalam pabrik, atau dalam menguji kualitas beras impor dan sebagainya.
situasi yang belum pernah terjadi sebelumnya. Misalnya, apakah suatu produk baru akan berhasil dalam pemasaran? Atau, apakah suatu teknologi proses pembuatan yang baru akan berhasil?
Untuk menghadapi persoalan semacam ini, dibutuhkan konsep nilai kemungkinan yang lain, yang dapat menerangkan ketidakpastian tanpa harus menggunakan berbagai data atau percobaan sebelum dapat menyatakan suatu nilai kemungkinan.
2.6.2. Nilai Kemungkinan Subjektif (Intuisi)
Untuk menentukan suatu peluang kejadian terkadang harus menggunakan intuisi, keyakinan, dan pengalaman peristiwa masa lalu. Misalnya peluang seseorang menang main tennis, maka harus diperhatikan prestasi orang tersebut dan lawannya dalam main tenis sebelumnya, di sini intuisi turut menentukan.
Probabilitas suatu peristiwa yang ditentukan dengan perasaan atau kepercayaan individu atau kelompok yang didasarkan pada fakta atau peristiwa masa lalu yang ada dinamakan Probabilitas Subjektif (Sri Mulyono, 1996).
Pernahkah mendengar seorang dokter yang berkata, “Kemungkinan operasi ini
berhasil adalah lebih besar dari 0,9.” Atau kalimat, “ Saya kurang yakin bahwa penawaran ini akan diterima, rasanya kemungkinannya kecil sekali, kurang dari 0,2.”
Dan kalimat lain yang senada. Apakah arti kemungkinan dalam kalimat-kalimat tersebut diatas?
Salah satu cara yang umum digunakan dalam menentukan pilihan di antara dua alternatif yang ada adalah dengan membandingkan keduanya secara langsung kemudian menentukan pilihan berdasarkan nilai kemungkinan subjektif.
Ciri utama nilai kemungkinan subjektif, adalah kenyataan bahwa logika dari nilai kemungkinan subjektif tidak dapat ditelusuri secara rasional. Bila seorang direktur perusahaan mengambil keputusan berdasarkan nilai kemungkinan subjektif, mugkin direktur perusahaan tersebut akan berkata, “Saudara sekalian, saya telah membaca semua laporan yang masuk, dan setelah mempertimbangkannya
masak-masak, saya kira sebaiknya bergabung dengan Perusahaan X”.
Meskipun mungkin keputusan tersebut adalah hasil pemikiran yang cemerlang, tetapi keputusan tersebut tidak dapat dievaluasi. Tidak ada jalan atau alat analisa untuk memeriksa langkah demi langkah untuk menentukan apakah keputusan tersebut adalah suatu konsekuensi logis dari pilihan-pilihan, dan informasi yang tersedia. Semua itu hanya berlangsung dalam pikiran saja, dan mungkin jika direktur perusahaan tersebut diminta untuk menjelaskannya kepada orang lain, mungkin direktur perusahaan tersebut tidak mampu.
2.7. Nilai Ekspektasi
2.7.1. Nilai Harapan (Expexted Values)
Bila pilihan secara langsung tidak dapat atau sukar untuk dilakukan, maka cara yang sering digunakan adalah dengan menggunakan nilai ekspektasi sebagai dasar pemilihan.
2.7.2. Struktur Persoalan Keputusan
Struktur persoalan keputusan sebagai berikut:
Tabel Payoff (Tabel Keputusan). (Johanes Supranto,1998)
Tabel 2.7.2.1 Tabel Keputusan Kejadian dan Probabilitas
Nj= Kejadian tak pasti j, pj=probabilitas kejadiankolom j
aij= Payoff yang diperoleh pada tindakan Aidankejadian tak pasti Nj , dimana i = 1, 2, 3, …, m dan j = 1, 2, 3, …, n.
Dari masing-masing tindakan dapat dihitung nilai harapan payoff . Untuk hal-hal yang sifatnya menguntungkan, seperti laba, hasil penjualan, penerimaan, dan sebagainya, nilai harapan (EV) dinyatakan dengan Expected Payoff (EP).
2.7.3. Expected Value of Perfect Information (EVPI)
Expected Value of Perfect Information (EVPI) adalah jumlah maksimum yang wajar dibayar oleh pengambil keputusan untuk memperoleh informasi sempurna, dihitung dengan: (Derek W. Bunn. 1984)
EVPI = EPPI –EV dimana :
EV : adalah nilai harapan terbesar dari tiap alternatif tindakan.
EPPI : adalah hasil perkalian maksimum baris (pay off tertinggi) dengan probabilitas. yang dihitung dengan:
Dengan Pr(Ni) adalah probabilitas dari Ni dan P adalah strategi dengan hasil tertinggi ketika Ni terjadi.
Penelitian yang dilakukan tidak dapat menghasilkan informasi yang sempurna, tetapi mendapatkan informasi tambahan harus tidak boleh mencapai biaya lebih atau sama denga EVPI. Berdasarkan hasil perhitungan EVPI ini, pembuat keputusan dapat membandingkan antara biaya maksimum untuk memperoleh biaya informasi tambahan, dengan biaya yang sebenarnya bagi keperluan mendapatkan informasi tersebut. Suatu rencana penelitian survei untuk memperoleh informasi tambahan layak untuk dipertimbangkan asalkan biaya yang dibutuhkan lebih kecil dari pada EVPI.
2.7.4. Expected Value Of Sample Information (EVSI)
Agar dapat dicapai keputusan yang optimal, sebelumnya dapat dilakukan penelitian atau riset terlebih dahulu untuk mendapatkan tambahan informasi, dan ini memerlukan tambahan biaya. Masalah yang dihadapi adalah jumlah biaya maksimum yang dapat dialokasikan untuk keperluan riset tersebut. Biaya maksimum ini mencerminkan nilai informasi yang diperoleh melalui riset itu.
Rumus untuk mencari EVSI atau nilai maksimum informasi sampel adalah : EVSI = EV dengan informasi sampel - EV tanpa informasi sampel
Untuk mengukur nilai informasi ini dapat digunakan rumus efisiensi sebagai berikut:
Suatu efisiensi yang tinggi menunjukkan informasi yang baik, yaitu hampir sama baiknya dengan informasi yang sempurna, sedangkan tingkat efisiensi yang rendah memungkinkan pengambil keputusan mencari jenis informasi yang lain.(Sri Mulyono, 1996)
2.7.5. Pohon Keputusan (Decision Tree)
Tujuan penggunaan pohon keputusan ini adalah untuk memudahkan penggambaran situasi keputusan secara sistematik dan komprehensip. Pada pohon keputusan ini biasanya digunakan notasi/simbol seperti berikut: (Azhar Kasim, 1994)
: simbol keputusan : simbol kejadian tidak pasti
PILIHAN KEJADIAN HASIL
Gambar 2.7.5.1 Pohon Keputusan (Decision Tree)
Keterangan:
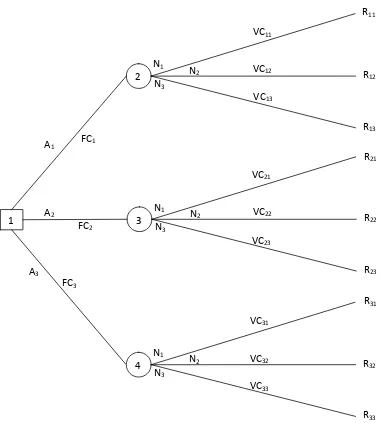
Ai : alternatif ke-i
Nj : state of nature ke-j, j = 1, 2, 3, …
Menurut Huber dalam Kasim [1] Penggunaan diagram pohon keputusan dalam proses pembuatan keputusan secara ideal harus menurut prosedur sebagai berikut: (Azhar Kasim, 1994)
Tahap 1 : Membentuk pohon keputusan, menggambarkan cabang. 1. Gambarkan alternatif-alternatif sebagai cabang dari titik pilihan.
2. Pada ujung dari masing-masing cabang alternatif, buat titik situasi masa depan (state of nature).
3. Dari tiap titik masa depan ini, buat cabang-cabang tentang situasi masa depan yang mungkin terjadi.
4. Kalau pada ujung cabang-cabang situasi masa depan ini masih ada alternatif keputusan lain maka buatlah titik keputusan baru.
5. Ulangi langkah 1,2,3,4 sampai di akhir tiap titik situasi masa depan dan tidak ada lagi titik keputusan baru.
Tahap 2 : Membentuk sebuah pohon keputusan, menyisipkan daun.
1. Untuk masing-masing alternatif keputusan, tuliskan biaya pelaksanaannya (seringkali biaya ini tidak dituliskan karena dianggap sudah diperhitungkan dalam perhitungan pay off buatan titik pilihan).
2. Untuk masing-masing hasil (outcome), tulislah probabilitas dari peristiwanya. 3. Tentukan hasil kotor (gross pay off) dari masing-masing cabang hasil
(outcome) yang paling kanan.
Tahap 3 : memotong cabang keputusan, memproses informasi
1. Hitung net expected value (expected monetary value) dari tiap garpu tala. 2. Ubah masing-masing titik hasil (outcome) yang paling kanan dengan nilai
bersih (EMV) yang diharapkan pada cabang tersebut.
3. Pada masing-masing titik pilihan, buang masing-masing cabang alternatif kecuali cabang dengan nilai bersih yang diharapkan paling besar yang telah dihitung pada langkah 2 dan ambil nilai bersih (EMV) yang terbesar sebagai payoff untuk cabang hasil (outcome) mendahului titik pilihan.
2.8. Analisa Sensitivitas
Sebelum keputusan dibuat, perlu diperiksa seberapa besar perkiraan probabilitas state of nature dapat berubah ke strategi lain. Jika perkiraan perubahannya terlalu besar, maka tidak layak untuk membeli penelitian itu. Untuk mengetahui seberapa sensitif suatu keputusan terhadap perubahan faktor atau parameter yang mempengaruhinya maka setiap pengambilan keputusan seharusnya disertai dengan analisa sensitivitas. Analisa sensitivitas akan memberikan gambaran sejauh mana suatu keputusan akan konsisten.
Analisa sensitivitas dilakukan dengan mengubah nilai suatu parameter pada suatu saat untuk selanjutnya dilihat bagaimana pengaruhnya terhadap akseptabilitas suatu alternatif. Analisa sensitivitas ini memberikan kekuatan/keyakinan sebelum mengambil keputusan.
Prosedur analisa sensitivitas dapat dilakukan dengan tahapan sebagai berikut: (Robert dkk, 1981)
1. Pilih variabel yang akan dianalisa 2. Identifikasi alternatif terbaik
3. Samakan nilai harapan dari dua strategi ini, yakni, cari titik indiferensi.
4. Hitung nilai dari variabel yang dipilih dalam langkah 1 sehingga langkah 3 dipenuhi.
BAB 3
PEMBAHASAN
3.1. Analisis Keputusan (Decision Analysis)
Kasus: (Robert, dkk, 1981)
Selkirk Winter Recreation Complex
Divisi Taman Rekreasi Hutan Dramun telah memperoleh sebagian lahan di gunung-gunung bagian barat negaranya. Lahan itu terbukti ideal untuk ski dan kegiatan-kegiatan musim dingin lainnya dan berpotensi untuk kegiatan-kegiatan musim panas juga. Letak lahan itu dekat dengan pusat metropolitan barat dan mudah diakses ke pasar timur. Lahan kini berada dalam produksi timber komersial. Firma memutuskan untuk menggunakan properti sebagai pengembangan rekreasi.
Pak Dramun menyatakan bahwa proyek Selkirk, nama proyek komplek rekreasi yang diusulkan, akan selesai dalam beberapa fase. Fase pertama akan berhubungan dengan bentuk perumahan penduduk. Ibu William menjelaskan, “Kami memiliki tiga pilihan. Kami dapat membangun komplek apartemen, komplek sewaan, atau kombinasi komplek apartemen - sewaan.”
Akan ditentukan pendekatan manakah yang mungkin menimbulkan nilai bersih tertinggi dari arus kas untuk proyek selama sepuluh tahun kedepan. Pak Dramun hanya akan menerima salah satu dari pilihan tersebut dan beliau mengharapkan pilihan tersebut akan mendatangkan keuntungan tertinggi dengan modal seminim mungkin.
Dapat dipilih salah satu dari ketiga level permintaan, lanjut Ibu William. Level pertama, sesuai dengan pengembangan apartemen, yang kedua sesuai untuk pengembangan rental, dan yang ketiga perpaduan keduanya. Kemungkinan tiap level permintaan diharapkan dalam urutan 0,3, 0,4 , 0,3. Dengan demikian, Firma hanya berkeyakinan 30% permintaan akan cocok untuk unit apartemen.
Sekarang , jika Firma mengikuti pilihan pertama (yaitu hanya membangun unit apartemen) dan permintaan sesuai dengan unit apartemen, Firma mengharapkan dapat menjual $22.273.670 unit apartemen. Proyeksi perolehan lainnya, yang dinyatakan dalam nilai bersih ditunjukkan dalam tabel 3.1.1. Angka ini diramalkan oleh Departemen Penelitian Pasar Hutan Dramun dan didasarkan pada reaksi konsumen yang mungkin terhadap masing-masing alternatif.
Tabel 3.1.1 Perolehan Berdasarkan Pilihan Perolehan Jika Permintaan Sesuai Dengan Pilihan yang
diambil Apartemen Rental
Kombinasi keduanya Apartemen $22.273.670 $12.273.670 $16.109.191
Rental $12.862.541 $20.097.720 $16.748.100 Kombinasi
keduanya $16.665.030 $16.968.100 $19.511.537
Sebelum membuat keputusan, biaya proyek harus dipertimbangkan. Walaupun setiap pilihan akan menghasilkan komplek yang sama secara fisik, tetapi biaya tetap dan biaya variabel akan berbeda. Biaya-biaya ini akan ditunjukkan pada tabel 3.1.2.
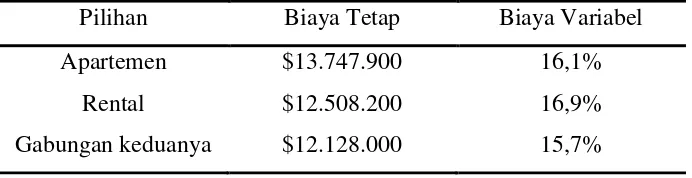
Tabel 3.1.2 Biaya Proyek Selkirk
Pilihan Biaya Tetap Biaya Variabel
Apartemen $13.747.900 16,1%
Rental $12.508.200 16,9%
Presiden perusahaan, Pak Dramun, telah menyatakan bahwa beliau ingin memilih alternatif yang memaksimumkan nilai bersih dari arus kas sambil mengevaluasi kesempatan-kesempatan mencapai arus kas tersebut secara eksplisit.
3.2. Memecahkan Model Satu Keadaan (Single-State Model) – Pendekatan Tabel Payoff
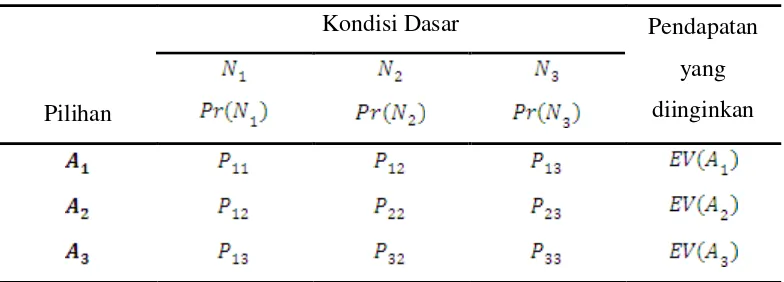
Tabel 3.2.1 Tabel Payoff Umum
Kondisi Dasar Pendapatan
yang diinginkan Pilihan
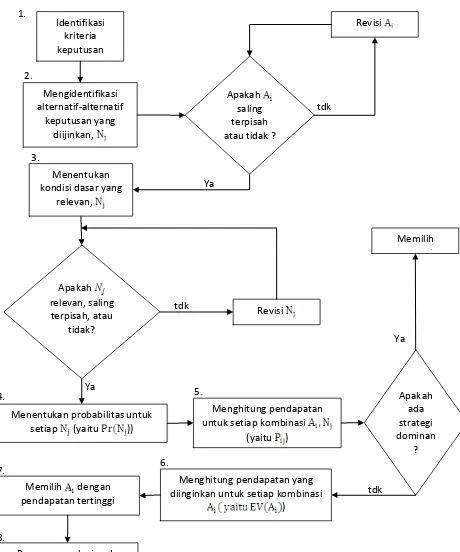
Berdasarkan tabel 3.2.1 dan gambar 3.2.1 diperoleh analisa: 1. Identifikasi kriteria keputusan.
Tujuan Pak Dramun secara jelas bersesuaian dengan kriteria nilai yang diharapkan sebelumnya. Dengan demikian, pilih alternatif yang menghasilkan nilai bersih tertinggi yang diharapkan dari arus kas.
2. Identifikasi alternatif-alternatif keputusan yang mungkin.
Pak Dramun secara jelas telah menentukan tiga alternatif yang mungkin: A1: bangun komplek apartemen dan jual setiap unit secara individu.
A2: bangun komplek rental dan sewakan tiap unit.
A3: bangun kombinasi keduanya, jual separuh unit dan menyewakan separuh lagi.
3. Menentukan kondisi dasar “State of Nature” yang relevan (N1).
beberapa pengaruh lingkungan dari masalah dan mengkonsolidasinya ke dalam tiga keadaan yang mungkin:
N1: permintaan sesuai dengan apartemen. N2: permintaan sesuai dengan unit rental. N3: permintaan sesuai dengan unit kombinasi. 4. Menentukan probabilitas untuk setiap Nj. Perkiraan probabilitas ini adalah:
Pr(N1) = 0,3 Pr(N2) = 0,4 Pr(N3) = 0,3
Harus mengakui bahwa ini adalah perkiraan probabilitas benar yang paling baik dari setiap kondisi dasar “State of Nature”. Untuk sementara, ujilah karakteristik probabilitas-probabilitas ini. Setiap unit saling terpisah, dengan demikian:
Pr(N1 N2) = 0 dan
5. Menghitung tiap Pij.
Pij adalah nilai bersih yang baru dari mengusahakan alternatif i dan kondisi dasar j terjadi. P11 (yangtelah dihitung sebelumnya) adalah sama dengan $4.939.709. Beberapa pendapatan lainnya adalah:
Pij = Revenueij – Fixed Cost – Variable Cost
P11 = $22.273.670 $13.747.900 $3.586.061 = $4.939.709
P12 = $12.273.670 $13.747.900 ($12.273.670 0,161) = $3.450.291
Tabel 3.2.2 Tabel Pij = Revij FCi VCij
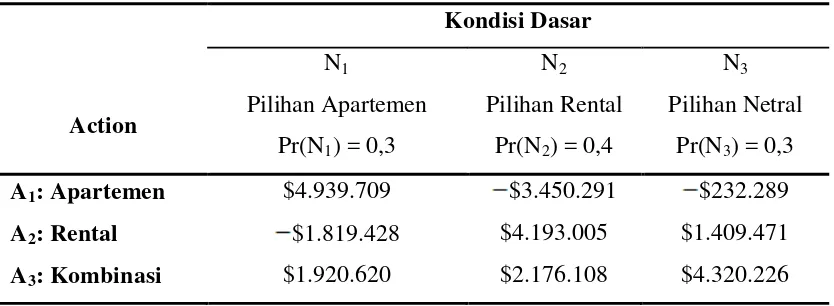
Tabel 3.2.3 Tabel Inisial Payoff untuk Proyek Selkirk Kondisi Dasar
N1 N2 N3
Action Pilihan Apartemen
Pr(N1) = 0,3
6. Menghitung pendapatan yang diinginkan untuk tiap alternatif.
Tujuannya adalah untuk melengkapi perhitungan sehingga dapat direkomendasikan strategi ataupun kriteria. Dengan kata lain, apakah suatu strategi memiliki pendapatan tertinggi dari seluruh kondisi dasar ? Jika demikian, itu adalah strategi dominan dan akan selalu dipilih atas alternatif alternatif.
Tabel 3.2.4 Tabel Final Payoff Kondisi Dasar
N1 N2 N3
Aksi Pr(N1) Pr(N2) Pr(N3) EV(Ai) Choice A1 P11 P12 P13
EV(A1) = P11[(Pr(N1)] + P12[(Pr(N2)] + P13[(Pr(N3)]
A2 P21 P22 P23
EV(A2) = P21[(Pr(N1)] + P22[(Pr(N2)] + P23[(Pr(N3)]
A3 P31 P32 P33
EV(A1) = P31[(Pr(N1)] + P32[(Pr(N2)] + P33[(Pr(N3)]
Menghitung nilai harapan, EV, atau nilai rata-rata dari Ai, dimana m adalah jumlah kondisi dasar. Nilai yang diharapkan dari A1 adalah:
($4.939.709)(0,3) + ( $3,450,291)(0,4) + ( $232.289)(0,3) $32.109,60 atau $32.110
EV(A2) dan EV(A3) ditunjukkan dalam tabel 3.2.5.
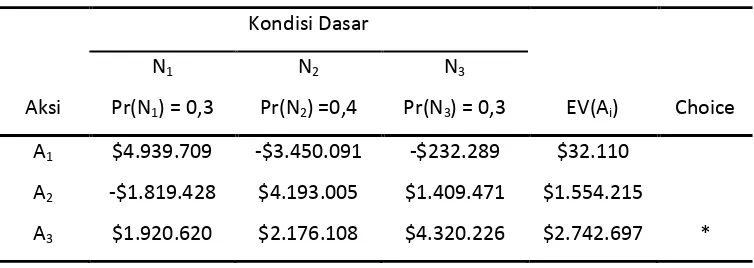
Tabel 3.2.5 Tabel Final Payoff untuk Proyek Selkirk Kondisi Dasar
N1 N2 N3
Aksi Pr(N1) = 0,3 Pr(N2) =0,4 Pr(N3) = 0,3 EV(Ai) Choice A1 $4.939.709 -$3.450.091 -$232.289 $32.110
A2 -$1.819.428 $4.193.005 $1.409.471 $1.554.215
A3 $1.920.620 $2.176.108 $4.320.226 $2.742.697 *
Dengan kembali ke langkah 1, ditentukan bahwa kriteria keputusan adalah untuk memilih alternatif dengan nilai harapan yang paling tinggi alternatif ketiga, bangun unit kombinasi, memiliki harapan tertinggi $2.742.607. Dengan demikian, ini adalah alternatif yang akan direkomendasikan kepada Pak Dramun.
8. Penerapan hasil.
Gambar 3.2.1 Flowchart – Prosedur Analisa Keputusan
3.3. Pendekatan Pohon Keputusan
Gambar 3.3.1 Pohon Keputusan Single-State secara Umum
Prosedurnya mengikuti tahap-tahap berikut selain dari langkah 1 pada gambar 3.3.1: Langkah 5 : Gambarkan pohon keputusan.
Langkah 6 : Tentukan Rij untuk setiap kombinasi kondisi dasar. Langkah 7 : Tentukan arus kas parsial sepanjang tiap cabang pohon.
Langkah 8 : Hitung nilai yang diharapkan untuk node yang ada dengan mengkaji biaya variabel, probabilitas, perolehan, dan biaya tetap.
Langkah 9 : Eliminasi seluruh nya kecuali node yang memiliki nilai tertinggi. Langkah 10 : Majukan nilai yg diharapkan dari node terbaik ke node keputusan.
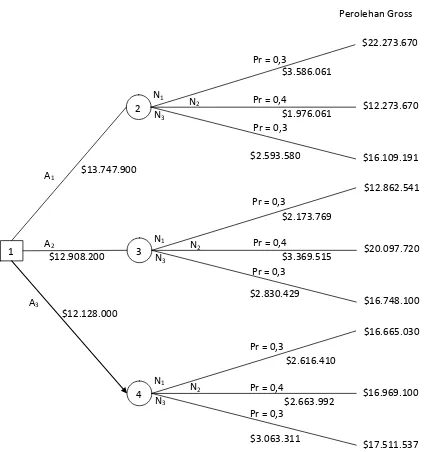
Gambar 3.3.2 Pohon Keputusan Parsial – Proyek Selkirk
Gambar 3.3.2 mengilustrasikan penyelesaian parsial dari keputusan proyek Selkirk melalui langkah 7. Perolehan (langkah 6) dimasukkan secara langsung dari tabel 3.1.1. Biaya variabel dan biaya tetap (langkah 7) bisa dihitung dari tabel 3.1.2 seperti yang dicontohkan. Biaya variabel A1N1 dapat ditentukan dari tabel 3.1.2.
VC12 = R12 0,161
= $12.273.670 0,161 = $1.976.061
VC13 = R13 0,161
= $16.109.191 0,161 = $2.593.580
Biaya-biaya variabel lainnya juga dapat dihitung. Nilai yang diharapkan dari setiap node peristiwa harus dihitung sesuai hubungannya (langkah 8).
EV2 = [($22.273.670 $3.586.061) 0,3] + [($12.273.670 $1.976.061) 0,4] +
[($16.109.191 $2.593.580) 0,3] $13.747.900 = $32.109,60 atau $32.110
VC21 = R21 0,169
= $16.749.100 0,169 = $2.830.429
VC22 = R22 0,169
= $20.097.720 0,169 = $3.396.515
VC23 = R23 0,169
= $16.749.100 0,169 = $2.830.429
EV2 = [($12.862.541 $2.173.769) 0,3] + [($20.097.720 $3.396.515) 0,4] + [($16.749.100 $2.830.429) 0,3] $12.508.200
VC31 = R31 0,157
= $16.968.157 0,157 = $2.616.410
VC32 = R32 0,157
= $16.968.157 0,157 = $2.663.992
VC33 = R33 0,157
= $19.511.537 0,157 = $3.063.311
EV4 = [($16.665.030 $2.616.410) 0,3] + [($16.968.157 $2.663.992) 0,4] +
[($19.511.537 $3.063.311) 0,3] $12.508.200 = $2.742.697
Dapat dengan mudah mengamati bahwa node keempat memiliki nilai harapan yang paling tinggi, sehingga dipiilih A3 sebagai alternatif dan membawa nilai dari node keempat ke node pertama (langkah 10).
3.4. Proposal Raken untuk Proyek Selkirk
Tugas selanjutnya adalah untuk mengevaluasi proposal yang digambarkan di sini dan untuk membuat beberapa rekomendasi terhadap Pak Dramun.
3.4.1. Elemen-elemen Masalah
Masalah utama: Apakah menerima proposal penelitian Pak Raken?
Kriteria Presisi: Akan menerima proposal jika hasil yang diantisipasi dari penelitian lebih berharga daripada biaya proyek penelitian.
Selain dari informasi yang diberikan, informasi lain yaitu: Biaya Proyek: $125.000
Reliabilitas informasi: 90%
Sebelumnya telah menentukan, dengan informasi yang ada sekarang dipilih alternatif ketiga, yaitu proyek kombinasi rental-apartemen. Dengan demikian, nilai yang diharapkan dari informasi sekarang adalah $2.742.697. Proposal Raken memberikan informasi berdasarkan kondisi-kondisi probabilitas untuk memilih kemungkinan alternatif lain atau tidak.
3.4.2. Prosedur Keputusan
Urutan analisis adalah: 1. Analisis sebelumnya.
Menentukan strategi terbaik dengan menggunakan kriteria nilai yang diharapkan dengan probabilitas sebelumnya (subjektif) dan menghasilkan tabel 3.2.5
2. Expected Value of Perfect Information (EVPI).
3. Analisis Preposterior.
Hitung payoff yang diharapkan dari penelitian yang diusulkan dengan menggunakan reabilitas yang dinyatakan peneliti dan probabilitas-probabilitas sebelumnya.
4. Analisis sensitivitas.
Tentukan berapa banyak probabilitas kondisi dasar yang harus berubah sebelum keputusan diubah.
5. Analisis Posterior.
Setelah mengumpulkan informasi sampel yang objektif, kombinasikan dengan informasi sebelumnya untuk merevisi probabilitas dan hitung kembali payoff yang diharapkan.
3.4.3. Expected Value of Perfect Information (EVPI)
EVPI = EPPI EV (Alternatif keputusan sekarang) Dimana:
EVPI = Expected Value of Perfect Information. EPPI = Expected Payoff of Perfect Information. EV = Nilai harapan dari Perfect Information.
(Strategi optimum yang diberikan oleh Ni)
Dimana Pr(Ni) adalah probabilitas Ni dan P adalah strategi optimum. Dalam kasus ini, EPPI = ($4.939.709)(0,3) + ($4.193.005)(0,4) + ($4.320.226)(0,3)
= $4.455.182,50 atau = $4.455.183
Artinya, jika diketahui bahwa kondisi dasar N1 akan terjadi maka diilih A1
3.4.4. Menghitung Expected Value of Perfect Information
EVPI = EPPI EV (alternatif terbaru)
= $4.455.183 $2.742.697 = $1.712.486
Jika biaya lebih tinggi, maka Proposal Raken ditolak.
3.4.5. Probabilitas Preposterior
Perhatikan pada bagian ini akan membahas tabel probabilitas bukan tabel payoff.
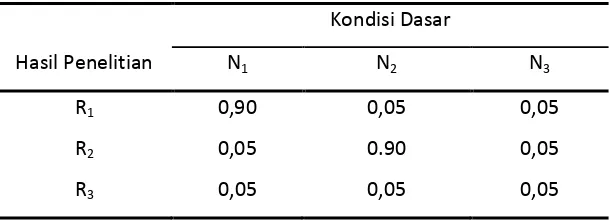
Tabel 3.4.5.1 Tabel Prediksi Probabilitas Kondisi Dasar
Hasil Penelitian N1 N2 N3
R1 0,90 0,05 0,05
R2 0,05 0.90 0,05
R3 0,05 0,05 0,05
Dimana,
N1, N2, N3 = kondisi dasar yang dibahas sebelumnya. R1 = hasil penelitian yang menunjukkan N1.
R2 = hasil penelitian yang menunjukkan N2.
R3 = hasil penelitian yang menunjukkan N3.
Rumus Bayes:
Tabel 3.4.5.2 Tabel Probabilitas Preposterior Umum untuk R1
N1 Pr(N1) Pr(R1|N1) Pr(R1|N1)Pr(N1) Probabilitas Gabungan Probabilitas Total N2 Pr(N2) Pr(R1|N2) Pr(R1|N2)Pr(N2) Probabilitas Gabungan
Probabilitas Total N3 Pr(N3) Pr(R1|N3) Pr(R1|N3)Pr(N3) Probabilitas Gabungan
Probabilitas Total
Tabel 3.4.5.3 Tabel Probabilitas Preposterior Umum untuk R2
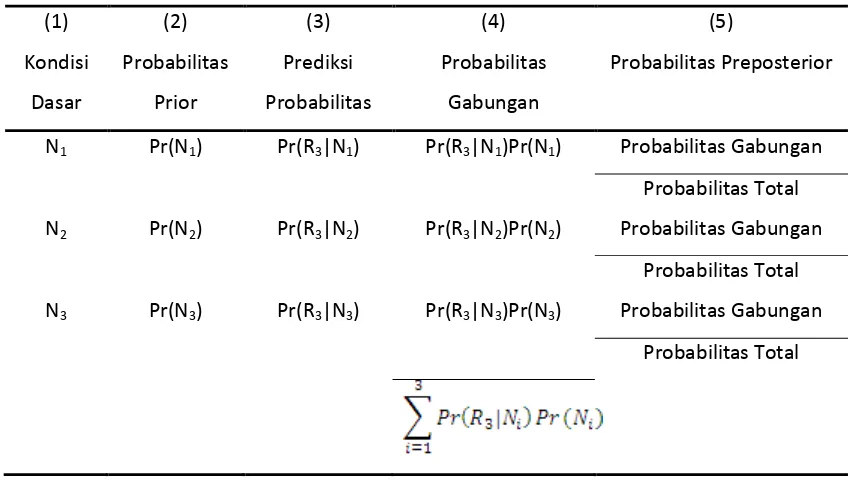
Tabel 3.4.5.4 Tabel Probabilitas Preposterior Umum untuk R3
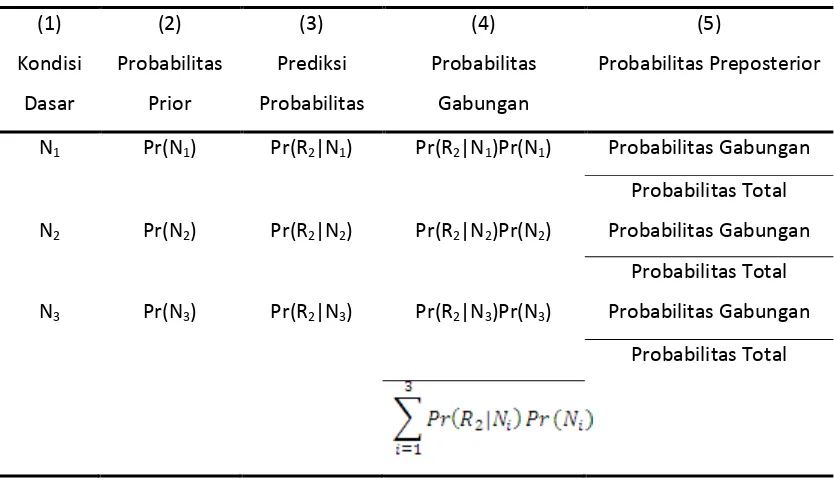
Langkah-langkah yang berikut akan memperjelas tabel 3.4.5.2. Ikuti langkah-langkah ini untuk membuat tabel 3.4.5.5:
1. Tentukan hasil penelitian yang pertama yang mungkin, R1.
2. Masukkan probabilitas sebelumnya (Prior) dari tabel 3.2.5 ke dalam kolom 2. 3. Masukkan probabilitas kondisional atau yang diprediksi dari baris 1, tabel 3.4.5.1
ke kolom 3.
Tabel 3.4.5.5 Tabel Probabilitas Preposterior dari Pengeluaran R1
Tabel 3.4.5.6 Tabel Probabilitas Preposterior dari Pengeluaran R2
Tabel 3.4.5.7 Tabel Probabilitas Preposterior dari Pengeluaran R3
(1) (2) (3) (4) (5)
3.4.6. Keputusan Preposterior
Penyelesaian analisis Preposterior membutuhkan baik pohon keputusan maupun tabel keputusan. Pohon keputusan pada umumnya lebih mudah dibangun dan digunakan di sini. Pohon keputusan dasar ditunjukkan dalam gambar 3.4.6.1. Pada tahap analisis ini, hanya mensubstitusikan probabilitas Preposteror sepanjang cabang pohon keputusan. Ini pada dasarnya adalah probabilitas kondisional Pr(Ni|Rj) yang dihasilkan dengan menggunakan teorema Bayes.
Perbedaan mendasar antara pohon ini dan pohon sebelumya terletak dalam tingkat probabilitas kondisi dasarnya. Ujilah probabilitas dengan mengikuti node 3 yang menunjukkan hasil penelitian. Jika memutuskan untuk melakukan penelitian dan hasil penelitian adalah R1, maka probabilitas N1 meningkat dari 0,30 ke
Tabel 3.4.6.1 Pohon Keputusan Preposterior dengan Arus Kas yang Dipilih
Tabel 3.4.6.1 Tabel Perhitungan EV
N1 N2 N3 EV(Ai)
A1 P11 P12 P13 EV(A1) = P11[Pr(N1)] + P12[Pr(N2)] + P13[Pr(N3)] A2 P21 P22 P23 EV(A2) = P21[Pr(N1)] + P22[Pr(N2)] + P23[Pr(N3)] A3 P31 P32 P33 EV(A3) = P31[Pr(N1)] + P32[Pr(N2)] + P33[Pr(N3)]
Tabel 3.4.6.2 Tabel Perhitungan EV5,
N1 N2 N3
EV5
0,885 0,066 0,049
A1 Apartemen 4.939.709 -3.450.291 232.289 4.132.541 A2 Rental -1.819.428 4.193.005 1.409.471 -1.264.391 A3 Kombinasi 1.920.620 2.176.108 4.320.226 2.055.063
Tabel 3.4.6.3 Tabel Perhitungan EV6
N1 N2 N3
EV6
0,885 0,066 0,049
A1 Apartemen 4.939.709 -3.450.291 -232.289 -3.005.737
A2 Rental -1.819.428 4.193.005 1.409.471 3.854.565 A3 Kombinasi 1.920.620 2.176.108 4.320.226 2.245.700
Tabel 3.4.6.4 Tabel Perhitungan EV7
N1 N2 N3
EV6
0,885 0,066 0,049
Tabel 3.4.6.5 Tabel Payoff EV dengan Biaya Menerima Penelitian
Pr EV Pr EV
R1 0,3 4.132.541 1.239.762
R2 0,4 3.854.565 1.541.826
R3 0,3 4.061.134 1.218.340
Jumlah 3.999.928
EV(dengan biaya penelitian) 3.874.928
3.4.7. Analisis Sensitivitas
Prosedur analisis sensitivitas membutuhkan langkah-langkah seperti berikut: 1. Pilih variabel yang akan dianalisis.
2. Identifikasi strategi optimum dan strategi kedua yang paling baik.
3. Samakan nilai harapan dari dua strategi ini, cari titik indiferensi (Indifference Point).
4. Hitunglah nilai variabel yang dipilih pada langkah 1 sehingga langkah 3 terpenuhi. 5. Bandingkan nilai yang dihitung dari langkah 4 dengan nilai aktual untuk variabel.
Perhatikan tabel 3.2.5 untuk data strategi. Lalu lakukan langkah-langkah berikut: Langkah 1:
Karena masih mempertimbangkan apakah membeli atau tidak membeli proyek penelitian, maka harus terus fokus kepada kondisi dasar “State of Nature”. Dengan demikian, perlu menentukan seberapa sensitifkah keputusan sekarang terhadap perubahan dalam probabilitas kondisi dasar.
Langkah 2:
Dua strategi terbaik yang adalah A3 (EV = $2.742.697) dan A2 (EV = $1.554.215). Makna dari analisis sensitivitas adalah untuk menemukan titik yang indifferent secara lengkap (completely indifferent) antara A3 dan A2. Dengan demikian hanya menyamakan A3 dan A2, sehingga:
Langkah 3:
Identifikasi probabilitas-probabilitas kondisi dasar, yaitu kondisi dasar yang paling
sesuai untuk strategi optimum dan yang sesuai dengan strategi “terbaik kedua”.
N3 sesuai A3 N2 sesuai A2
Langkah 4:
Menentukan nilai variabel. Dalam kasus ini dicari kemungkinan yang diperbolehkan dari N3 sampai N2, sehingga:
Pr(N3 )+ Pr(N2) = 0,3 + 0,4 = 0,7
Langkah 5:
Dengan demikian, dapat fokus mengubah maksimum dari 0,7 dengan mengabaikan probabilitas konstan N1 karena tidak berpengaruh pada hasil analisis. Untuk melengkapi langkah ini harus dengan mengkombinasikan konsep di atas dengan langkah 3, sehingga:
Pr(N3) = P
Dan
Pr(N2) = 0,7 Pr(N2)
Karena EV(A3) = EV(A2),
Dapat dilihat bahwa:
($1.920.620)(0,3) + ($2.176.108)(0,7 P) + ($2.599.705)(P) = ( $1.819.428)(0,3) + ($4.193.005)(0,7 P) + ($1.409.471)(P)
$2.099.461,6 + $423.097 P = $2.389.275,1 $2.783.534 P $3.206.631 P = $289.813,5
P = 0,09 untuk N3
Dan
Tabel 3.4.7.1 Tabel Analisa Sensitivitas Payoff
Aksi N1 N2 N3 EV(Ai)
A2 P21 P22 P23 EV(A2) = P21[(Pr(N1)] + P22[(Pr(N2)] + P23[(Pr(N3)] A3 P31 P32 P33 EV(A3) = P31[(Pr(N1)] + P32[(Pr(N2)] + P33[(Pr(N3)]
Tabel 3.4.7.2 Tabel Analisa Sensitivitas Payoff Kondisi Dasar
N1 N2 N3
Aksi Pr = 0,30 Pr = 0,61 Pr = 0,09 Payoff Aksi A2 $1.819.428 $4.193.005 $1.409.471 $2.138.757 * A3 $1,920,620 $2.176.108 $2.599.205 $2.137.540 *
Dengan demikian,ketika probabilitas N2 meningkat melewati 0,61 dan probabilitas N3 bergerak ke turun ke 0,09, maka preferensi untuk A2 lebih tinggi dari pada A3.
Selama analisis ini Pr(N1) dipertahankan konstan sedangkan Pr(N2) dan Pr(N3)) dimanipulasi. Selanjutnya, mengkaji Pr(N1)) seperti yang dilakukan pada Pr(N2). Selama analisis yang berikut Pr(N2) dipertahankan konstan.
N3 sesuai A3 dan N1 sesuai A1: Pr(N3) + Pr(N1) = 0,3 + 0,3 = 0,6
Pr(N1) = P
Pr(N3) = 0,6 P
EV(A3) = EV(A1)
($1,920.620)(0,6 P ) + ($2.176.108)(0,4) + ($A.599.205)(P) = ($4.939.709)(0,6 P) + ( $3.450.291)(0,4) + ($232.289)(P)
$2.022.815,2 + $678.585 P = $1.583.709 $4.707.420 $5.386.005 P = $439.106
Probabilitas yang dihasilkan adalah negatif, sehingga disimpulkan bahwa A1 tidak akan pernah menjadi strategi optimum selama A2 dan N2 adalah faktor yang signifikan.
Pr(N3) harus jatuh dari 0,30 ke 0,09, Perubahan sebesar 21 poin, atau 70 persen.
Dengan demikian, dapat disimpulkan bahwa Penelitian tidak akan dibeli, terlepas dari kriteria nilai yang diharapkan menunjukkan keputusan sebaliknya.
Tabel 3.4.7.3 Range Pr(N3)
Pr(N3) Strategi Optimum Pr(N2) Pr(N1)
0,3 A3 0,4 0,3
0,09 Indifferen antara A2 dan A3
0,61 0,3
0,6 A3 0,4 0
< 0,09 A2 1 < Pr(N2) < 0 0,3
Pada awalnya, diputuskan untuk membeli penelitian,tetapi sekarang keputusan menjadi kurang meyakinkan berdasarkan analisis sensitivitas.
Pertimbangan tambahan bisa dievaluasi sebelum membuat keputusan pembelian penelitian. Pertama, berapa biaya kesalahan,dan, kedua, berapa biaya dari menunda keputusan sehingga proyek penelitian bisa diselesaikan ? Pertimbangan pertimbangan ini bisa sangat mempengaruhi keputusan pembelian.
3.4.8. Penerapan Nilai Kemungkinan Subjektif
Rekomendasi ‘menolak’ diarahkan pada Pak Draman. Nilai EVPI $1.712.486 dan payoff yang di harapkan pada penelitian adalah $3.254.787, yang lebih besar dari payoff yang diharapkan karena tidak melakukan penelitian. Pak Norbert membuat
“Terima kasih ata analisismu”, respon PakNorbert. “Namun demikian,kita harus cepat membuat keputusan, dan kita tidak ingin membangun jenis unit
perumahan yang salah”. Dengan memperhatikan batasan tambahan ini Pak Norbert memutuskan untuk membeli proyek penelitian.
Peneliti semata - mata menasihatkan pembuat keputusan. Tidak semua informasi bisa dipadukan ke dalam model, seperti yang diilustrasikan dalam situasi ini. Akan dipakai untuk apakah analisis yang ada jika Pak Norbert memilih untuk mengabaikannya? Pak Norbert mampu menggunakan informasi tambahan untuk mengklarisikasi keputusan ini. dalam kasus ini, dia bisa secara subjektif mempertimbangkan EVPI, analisis preposterior,dan analisis sensitivitas (yang menunjukkan kesimpulan yang berbeda). Pak Norbert membuat sebuah keputusan berdasarkan data dan tafsiran intuitifnya.
3.4.9. Analisis Posterior
Tabel 3.4.9.1 Hasil Penelitian Raken
Ni Jumlah Responden Frekuensi Relatif Probabilitas
N1 4.500 0,25
N2 7.200 0,70
N3 900 0,15
Total 18.000 1,00
Tabel 3.4.9.2 Tabel Probabilitas Posterior
Tabel 3.4.9.3 Tabel Probabilitas Posterior
Tabel 3.4.9.4 Tabel Revisi Payoff
Kondisi Dasar
Strategi N1 Pr(N1) = 0,20
N2 Pr(N2) = 0,76
N3 Pr(N3) = 0,04
Pendapatan yang diharapkan
Keputusan
A1 $4.939.709 $3.450.291 $232.289 $1.624.988
A2 $1.819.428 $4.193.005 $1.409.471 $2.879.117 * A3 $1.920.620 $2.176.108 $2.599.205 $2.141.934
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Kesimpulan yang dapat diperoleh pada kasus Selkirk Winter Recreation Complex yaitu:
1. EVPI lebih besar dari biaya proyek penelitian maka proposal itu diterima.
2. Analisis Preposterior, mengkaji reliabilitas firma penelitian dan dampak yang mungkin yang ditimbulkan oleh penelitian terhadap keputusan. Berbekal informasi ini, diputuskan bahwa penelitian masih akan dibeli.
3. Analisa sensitivitas, mengkaji dampak yang mungkin yang diunculkan oleh perubahan besar dalam probabilitas terhadap keputusan. ketika probabilitas N2 meningkat melewati 0,61 dan probabilitas N3 turun ke 0,09, sehingga preferensi untuk A2 meningkat dari pada A3.
4. Karena Pr(N3) harus berubah secara besar, tingkat keyakinan untuk membeli penelitian menurun.
5. Dalam kasus ini, Pak Norbert secara subjektif mempertimbangkan EVPI, analisis preposterior,dan analisis sensitivitas. Pak Norbert membuat sebuah keputusan berdasarkan data dan tafsiran intuitifnya. Pak Norbert akhirnya memutuskan untuk membeli penelitian berdasarkan penilaian subjektifnya.
6. Dari Analisa Posterior, keputusan yang dipilih adalah A2. Hal ini didasarkan pada informasi subjektif, informasi Prior dan sampel objektif.
4.2 Saran
1. Diharapkan kepada pembaca untuk mengembangkan kajian ini, dengan melibatkan analisa resiko dalam pengambilan keputusan.
2. Diharapkan kepada pembaca agar dapat mengembangkan lebih lanjut untuk menetapkan batasan seberapa jauh kriteria diturunkan dan dinaikkan sehingga dapat mempengaruhi keputusan yang akan diambil.
Daftar Pustaka
1. Bunn, Derek W. 1984. Applied Decision Analysis. San Fransisco: McGraw Hill Book Company.
2. Dunn A, Robert, and Ramsing, Kenneth D. 1981. Teori Pembuatan Keputusan. New York: Macmilan Publishing Co, Inc.
3. Hasan, M. Iqbal. 2002. Pokok-pokok Materi Teori Pengambilan Keputusan. Indonesia, Jakarta: Ghalia.
4. Kasim, Azhar. 1994. Teori Pembuatan Keputusan. Jakarta: FEUI.
5. Mangkusubroto, Kuntoro, dan Trisnadi, Listiarini. 1987. Analisa Keputusan Pendekatan Sistem dalam Manajemen Usaha dan Proyek. Bandung: Ganeca Exact.
6. Manurung, Adler Haymans. 1991. Pengambilan Keputusan Pendekatan Kuantitatif. Jakarta: Rineka Cipta.
7. Mulyono, Sri. 1996. Teori Pengambilan Keputusan. Jakarta: FEUI.
8. Nasution, Misdawardana. 2010. Kajian Analisis Keputusan Menggunakan Analisis Sensitifitas dengan Fungsi Utility Eksponensial. Medan: FMIPA USU.
9. Paul, E. Moody. 1983. Decision Making : Proven Methods for Better Decision. New York: McGraw Hill.