KONFIGURASI BIPLOT BIASA DAN BIPLOT KANONIK
DENGAN BERBAGAI UKURAN CONTOH
RIKA PUTRA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
RIKA PUTRA. Konfigurasi Biplot Biasa dan Biplot Kanonik dengan Berbagai Ukuran Contoh. Dibimbing oleh SISWADI dan TONI BAKHTIAR.
Studi ini memberikan konfigurasi 18 provinsi di Indonesia berdasarkan kinerja lulusan Madrasah Aliyahnya. Data yang digunakan ialah nilai mutu mata kuliah dan IPK mahasiswa Beasiswa Utusan Daerah Departemen Agama Tingkat Persiapan Bersama Institut Pertanian Bogor (BUD DEPAG TPB IPB) tahun akademik 2009/2010 lulusan Madrasah Aliyah dari 18 provinsi di Indonesia. Konfigurasi diperoleh melalui biplot biasa dengan menggunakan data asal maupun agregat dan biplot kanonik. Ketaksesuaian antarkonfigurasi diperoleh melalui analisis Procrustes. Konfigurasi yang diperoleh dari biplot biasa dengan data agregat lebih sesuai dengan konfigurasi biplot biasa dengan data asal dibandingkan dengan konfigurasi yang diperoleh dari biplot kanonik. Dari biplot kanonik diperoleh hasil bahwa provinsi Jakarta, Bali dan Lampung merupakan provinsi yang relatif baik, sedangkan provinsi NAD, Banten, NTB dan Gorontalo relatif rendah kinerja lulusan Madrasah Aliyahnya. Provinsi Jakarta dan Bali secara umum memiliki nilai yang relatif baik pada mata kuliah yang berhubungan dengan pengetahuan alam, sedangkan provinsi Lampung memiliki nilai yang relatif baik dalam pengetahuan sosial. Untuk menelusuri kemungkinan perubahan konfigurasi yang dihasilkan biplot kanonik, dilakukan simulasi dengan berbagai ukuran contoh. Hasil yang diperoleh memberikan gambaran adanya perubahan konfigurasi akibat perbedaan ukuran contoh yang digunakan.
ABSTRACT
RIKA PUTRA. Configuration of Classical Biplot and Canonical Biplot with Various Sample Sizes. Supervised by SISWADI and TONI BAKHTIAR.
This study provides a configuration of 18 provinces in Indonesia based on the performance of Islamic High School graduates. The data used in this study are scores of subjects and GPA from the IPB first year students who receive provincial representing scholarship from the Ministry of Religious Affairs (BUD DEPAG) in 2009/2010 academic year. Configurations obtained through classical biplot with original data, aggregate data, and canonical biplot. The dissimilarity of inter-configurations is obtained via Procrustes analysis. Configuration obtained from classical biplot with aggregate data is more in line with configuration obtained by the original data as compared to configuration obtained from canonical biplot. The canonical biplot result reveals that the provinces of DKI Jakarta, Bali, and Lampung are relatively good, while the provinces of NAD, Banten, NTB, and Gorontalo have relatively low performance of Islamic High School graduates. The provinces of Jakarta and Bali in general have relatively good scores on subjects related to the natural sciences, while the province of Lampung has relatively good scores of subjects related to the socials sciences. To explore possibility of configuration changes obtained by the canonical biplot, a simulation with various sample sizes is then conducted. The results obtained provide configuration changes due to the differences in the sample size used.
KONFIGURASI BIPLOT BIASA DAN BIPLOT KANONIK
DENGAN BERBAGAI UKURAN CONTOH
RIKA PUTRA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS METEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Konfigurasi Biplot Biasa dan Biplot Kanonik dengan Berbagai
Ukuran Contoh
Nama
: Rika Putra
NIM
: G54080007
Menyetujui,
Pembimbing I,
Pembimbing II,
Dr. Ir. Siswadi, M.Sc.
NIP. 19490609 197412 1 001
Dr. Toni Bakhtiar, M.Sc.
NIP. 19720627 199702 1 002
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS.
NIP. 19650505 198903 2 004
PRAKATA
Bismillahirrahmanirrahim, puji dan syukur penulis panjatkan kepada Allah SWT atas karunia-Nya sehingga karya ilmiah yang berjudul Konfigurasi Biplot Biasa dan Biplot Kanonik dengan Berbagai Ukuran Contoh dapat penulis selesaikan. Shalawat serta salam semoga selalu tercurahkan untuk nabi besar Muhammad SAW, keluarga, sahabat dan para pengikutnya sampai akhir zaman.
Terima kasih penulis ucapkan kepada Bapak Dr. Ir. Siswadi, M.Sc. dan Bapak Dr. Toni Bakhtiar, M.Sc. atas ilmu, kesabaran, motivasi, dan saran selama penulis melakukan bimbingan tugas akhir, Bapak Ir. N. K. Kutha Ardana, M.Scyang telah bersedia menjadi dosen penguji pada saat sidang tugas akhir, serta tidak lupa pula untuk seluruh dosen Departemen Matematika atas ilmu yang telah diberikan, dosen dan tenaga kependidikan Departemen Matematika atas bantuannya selama ini.
Karya ilmiah ini penulis persembahkan untuk Papa, Mama, Adik-adikku, dan Kakak-kakakku. Terima kasih atas pengorbanan, doa, semangat, dan motivasinya. Terima kasih penulis ucapkan kepada teman-teman Matematika 45, keluarga besar Pondok Nirvana, dan teman-teman lainnya untuk kebersamaan yang berharga, doa, semangat, dan motivasinya. Terima kasih penulis ucapkan kepada Kak Mariyam dan Pak Kusnandar atas bantuannya dalam penulisan karya ilmiah ini. Terima kasih penulis juga ucapkan kakak-kakak Matematika Angkatan 44 dan adik-adik Matematika Angkatan 46, serta semua pihak yang turut membantu penulis dalam menyelesaikan karya ilmiah ini.
Akhir kata, penulis menyadari masih banyak kekurangan dalam penulisan karya ilmiah ini. Oleh karena itu, penulis sangat berharap dan menghargai semua saran dan kritik yang diberikan. Semoga karya ilmiah ini bermanfaat bagi pembacanya.
Bogor, September 2012
RIWAYAT HIDUP
Penulis dilahirkan di Kampung Rimbo pada tanggal 27 April 1989 dari bapak Bukhari dan ibu Erlita. Penulis merupakan anak kelima dari delapan bersaudara.
Penulis menyelesaikan pendidikan di SMAN 1 Nan Sabaris pada tahun 2008 dan pada tahun yang sama lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis memilih mayor Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam dengan mengambil mata kuliah tambahan supporting course yaitu Perdagangan Pertanian, Ekonomi Sumber Daya Alam dan Lingkungan, Perancangan Percobaan I, Analisis Regresi I, dan Metode Penarikan Contoh.
DAFTAR ISI
Halaman
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... ix
PENDAHULUAN ... 1
Latar Belakang ... 1
Tujuan ... 1
TINJAUAN ANALISIS... 1
Analisis Biplot Biasa ... 1
Ukuran Kesesuaian Analisis Biplot Biasa ... 3
Analisis Peubah Kanonik ... 4
Analisis Biplot Kanonik ... 6
Analisis Procrustes ... 8
METODE PENELITIAN ... 9
Sumber Data ... 9
Peubah Penelitian ... 10
Objek Penelitian ... 10
Metode Penelitian ... 10
PEMBAHASAN ... 11
Konfigurasi Biplot Biasa dan Biplot Kanonik Data Asal ... 11
Simulasi Biplot Kanonik dengan Berbagai Ukuran Contoh... 11
Kesesuaian Antarkonfigurasi dengan Analisis Procrustes ... 13
Analisis Biplot Biasa dengan Data Agregat, Biplot Biasa dengan Data Asal, dan Biplot Kanonik dengan Data Asal ... 13
Analisis Hasil Simulasi Biplot Kanonik dengan Berbagai Ukuran Contoh... 15
KESIMPULAN ... 16
DAFTAR PUSTAKA ... 17
DAFTAR TABEL
Halaman
1 Analisis ragam antarkelompok dan dalam kelompok ... 5
2 Objek penelitian berdasarkan provinsi ... 10
3 Kesesuaian antarkonfigurasi untuk matriks data pendekatan berdimensi dua... 13
4 Kesesuaian antarkonfigurasi untuk matriks koordinat objek/kelompok berdimensi dua ... 13
5 Kesesuaian antarkonfigurasi untuk matriks koordinat peubah berdimensi dua ... 13
DAFTAR GAMBAR
Halaman 1 Biplot biasa dengan data agregat ... 112 Biplot biasa dengan data asal ... 11
3 Biplot kanonik dengan data asal ... 11
4 Biplot kanonik dengan matriks �data asal dikalikan konstanta = 2 ... 12
5 Biplot kanonik dengan matriks = diag 3, . . ,3 = 3� ... 12
6 Biplot kanonik dengan matriks = diag 3, . . ,3 = 3� dikalikan konstanta = 2 ... 12
7 Biplot kanonik dengan matriks data asal dengan urutan terbalik ... 12
DAFTAR LAMPIRAN
Halaman 1 Data nilai mata kuliah dan IPK mahasiswa BUD DEPAG TPB IPB 2009/2010 ... 192 Matriks rata-rata objek/kelompok ... 22
3 Matriks jumlah kuadrat dan hasil kali data antarkelompok pada data asal ... 23
4 Matriks jumlah kuadrat dan hasil kali data dalam kelompok pada data asal ... 24
5 Matriks jumlah kuadrat dan hasil kali total data kelompok pada data asal ... 25
6 Matriks indikator ... 26
7 Matriks ... 27
8 Matriks koordinat objek/kelompok ... 28
9 Matriks koordinat peubah ... 29
10 Biplot biasa dengan data agregat ... 30
11 Biplot biasa dengan data asal ... 31
12 Biplot kanonik dengan data asal ... 32
13 Biplot kanonik dengan matriks data asal dikalikan konstanta = 2 ... 33
14 Biplot kanonik dengan matriks = diag 3, . . ,3 = 3� ... 34
15 Biplot kanonik dengan matriks = diag 3, . . ,3 = 3� dikalikan konstanta = 2 ... 35
PENDAHULUAN
Latar BelakangAnalisis biplot diperkenalkan oleh Gabriel pada tahun 1971. Analisis biplot biasa merupakan salah satu bentuk analisis peubah ganda yang dapat memberikan antara lain: gambaran secara grafik tentang kedekatan antarobjek, keragaman peubah, korelasi antarpeubah, serta keterkaitan peubah dengan objek. Selain itu, analisis biplot juga dapat digunakan untuk menggambarkan hubungan antara peubah dan objek yang berada pada ruang berdimensi tinggi ke dalam ruang berdimensi rendah (dua atau tiga). Dari biplot diperoleh tiga matriks pendekatan yang terkait dengan data, peubah, dan objek. Ukuran kesesuaian dari ketiga matriks tersebut dikemukakan oleh Gabriel (2002) yang kemudian untuk matriks peubah dirumuskan oleh Siswadi dan Bakhtiar (2011) menggunakan analisis Procrustes.
Analisis paling umum untuk diskriminasi antarkelompok, dengan menggunakan beberapa peubah yang diamati, adalah analisis peubah kanonik (APK, Canonical Variate Analysis) yang diperkenalkan oleh Fisher (1936). APK juga merupakan salah satu teknik statistika untuk analisis data dengan peubah ganda yang berbasis analisis pengelompokan data sehingga ragam antarkelompok maksimum dan ragam di dalam kelompok minimum (Varas et al. 2005). APK digunakan untuk memperoleh kombinasi linear dari peubah-peubah asal yang akan memberikan nilai sedekat mungkin bagi objek-objek dalam kelompok yang sama dan sebesar mungkin bagi objek-objek antarkelompok (Varas et al. 2005).
Analisis biplot kanonik merupakan representasi grafik dari APK, dikembangkan oleh Gabriel (1995) untuk memperoleh representasi secara serempak antara rata-rata kelompok dan peubah di mana
dimungkinkan tidak hanya untuk menetapkan perbedaan antarkelompok tetapi juga untuk menggambarkan peubah yang dianggap dominan dalam membedakan antarkelompok (Vallejo-Arboleda et al. 2007).
Analisis Procrustes adalah alat analisis berdasarkan asas kuadrat terkecil yang dapat digunakan untuk mengukur kemiripan maksimal antarkonfigurasi titik melalui serangkaian transformasi linear (Bakhtiar dan Siswadi 2011). Bentuk transformasi tersebut adalah translasi, rotasi dan dilasi. Analisis ini bertujuan untuk membandingkan dua konfigurasi yang mewakili unit pengamatan yang sama sebagai nilai numerik. Nilai numerik yang dihasilkan dapat digunakan sebagai ukuran kesesuaian (goodness of fit) antarkonfigurasi. Untuk melihat kesamaan bentuk dan ukuran dari dua konfigurasi maka setelah kedua konfigurasi dilakukan translasi salah satu konfigurasi dibuat tetap sementara konfigurasi yang lainnya dirotasi dan didilasi sehingga paling sesuai dengan konfigurasi pertama.
Merujuk pada Kusnandar (2011) maka permasalahan yang muncul ialah bagaimana perubahan konfigurasi biplot biasa dengan menggunakan data asal dan agregatnya dan bagaimana perubahan konfigurasi biplot kanonik dengan berbagai ukuran contoh.
Tujuan
Tujuan penulisan karya ilmiah ini ialah ingin mendapatkan gambaran perubahan konfigurasi biplot biasa dengan menggunakan data asal dan agregatnya dan gambaran perubahan konfigurasi biplot kanonik dengan berbagai ukuran contoh.
TINJAUAN ANALISIS
Analisis Biplot BiasaAnalisis biplot pertama kali diperkenalkan oleh Gabriel pada tahun 1971 yang kemudian dibahas panjang lebar dalam Greenacre (2010). Biplot berupa suatu peragaan grafik dari matriks data X dalam plot dengan menumpangtindihkan vektor-vektor dalam ruang berdimensi rendah,
biasanya dua (atau tiga) yang mewakili vektor-vektor baris matriks X (gambaran objek) dengan vektor-vektor kolom matriks
X (gambaran peubah).
1. Kedekatan antarobjek.
Dua objek dengan karakteristik yang relatif sama akan digambarkan sebagai dua titik yang posisinya berdekatan. 2. Keragaman peubah.
Peubah dengan keragaman kecil digambarkan sebagai vektor yang pendek, sedangkan peubah dengan keragaman besar digambarkan sebagai vektor yang panjang.
3. Korelasi antarpeubah.
Peubah digambarkan sebagai vektor. Jika sudut antara dua peubah lancip < 90°
maka korelasinya bernilai positif. Apabila sudut antara dua peubah tumpul
> 90° maka korelasinya bernilai negatif. Sedangkan jika sudut dua peubah siku-siku maka tidak saling berkorelasi.
4. Keterkaitan peubah dengan objek. Karakteristik suatu objek bisa disimpulkan dari posisi relatifnya dengan peubah. Jika posisi objek searah dengan arah vektor peubah maka objek tersebut nilainya di atas rata-rata, jika berlawanan maka nilainya di bawah rata-rata, dan jika hampir di tengah-tengah maka nilainya mendekati rata-rata.
Analisis biplot dikembangkan atas dasar Dekomposisi Nilai Singular (DNS) atau Singular Value Decomposition (SVD). Misalkan n ∗ adalah matriks data dengan n
objek dan p peubah. Selanjutnya ∗ dikoreksi terhadap nilai rata-ratanya sehingga diperoleh matriks X,
= ∗−1 T ∗ , (1)
dengan 1 adalah vektor × 1 yang semua elemennya bernilai 1. Matriks koragam
= (s ) yang diperoleh dari matriks ialah
= 1 −1
T (2)
dan matriks korelasi = ,
=�−1 2 �−1 2 , (3)
dengan �−1 2= diag 1 11,
1
22, . . , 1
. Misalkan matriksn ∗ = �1,�2,…,� T
maka didefinisikan jarak Euclid antara objek ke-i dan ke-j sebagai �,� =
� − � T
� − � dan jarak Mahalanobis antara objek ke-i dan ke-j sebagai
� �,� = � − �
T −
1 � − � .
Matriks berpangkat r dengan
min , dapat dinyatakan sebagai SVD berikut:
n =n� T (4)
(Aitchison & Greenacre 2002) dengan U dan
A merupakan matriks-matriks ortonormal kolom, yaitu �T�= T = . Matriks A
adalah matriks yang kolom-kolomnya terdiri atas vektor eigen yang berpadanan dengan nilai eigen positif � dari matriks
T . Matriks U adalah matriks yang
kolom-kolomnya merupakan vektor eigen-vektor eigen yang berpadanan dengan nilai eigen-nilai eigen positif dari matriks T. Dapat ditulis
r = diag λ1 , λ2 , . . . , λ (5)
p = 1, 2,…, (6)
n� =
1
λ1 1, 1
λ2 2, . . . , 1
λ (7)
dengan λ1 λ2 λ > 0 dan
λ disebut nilai singular dari matriks . Dalam Jolliffe (2002), persamaan (4) dapat diuraikan menjadi
=� α 1−α T, α ∈[0,1]. (8)
Misalkan =� α= 1, 2,…, T
dan = 1−α=
1, 2,…, T
maka persamaan (8) menjadi
= T= λ � T =1
. (9)
Dengan demikian setiap elemen ke-(i,j) unsur matriks Y dapat dinyatakan sebagai
x = T . Vektor merepresentasikan
berpangkat dua, sehingga persamaan dapat ditulis menjadi
x = ∗T ∗,
dengan ∗dan ∗ masing-masing mengandung dua unsur pertama vektor dan . Dengan pendekatan tersebut matriks
X dapat disajikan dalam ruang dimensi dua. Nilai � yang digunakan dapat merupakan nilai sebarang � ∈ 0, 1 , tetapi pengambilan nilai-nilai ekstrem yaitu �= 0 dan �= 1 berimplikasi pada interpretasi biplot. a. Jika �= 0, maka =�dan = ,
akibatnya
T = T T T
= T T = �T� T
= T,
sehingga diperoleh
T = ( −1)
, dengan adalah koragam peubah ke-i dan ke-j.
= −1 , dengan =
menggambarkan keragaman peubah ke-i.
Korelasi antara peubah ke-i dan ke-j dijelaskan oleh kosinus sudut antara
h dan h (misal: �), yaitu
cos � = T
= =
Jika X berpangkat p maka
� − � T −1 � − � = ( −1)
− T − artinya kuadrat jarak Mahalanobis antara � dan
� sebanding dengan kuadrat jarak Euclid antara dan , serta adalah matriks koragam yang diperoleh dari X.
b. Jika �= 1, maka =� dan = , akibatnya
T = T T T = T T
= T T
= T
Artinya, � − � T � − � =
− T − atau kuadrat jarak Euclid antara � dan � akan sama dengan kuadrat jarak Euclid antara dan .
Ukuran Kesesuaian Analisis Biplot Biasa
Menurut Gabriel (2002), biplot tidak hanya sebagai representasi matriks data X
dengan menggunakan matriks T, tetapi
juga matriks T sebagai representasi dari
matriks T yang berkaitan dengan ragam
koragam dan korelasi antarpeubah dan matriks T sebagai representasi bagi X T
yang berkaitan dengan ukuran ketakmiripan antar objek. Secara umum dapat ditulis
= T ≈ T,
di mana Tmerupakan matriks berpangkat < sehingga − T minimum.
Rumus umum yang dikemukakan oleh Gabriel untuk ukuran kesesuaian analisis biplot ini adalah sebagai berikut:
GF , = 1−min� −� 2
2 . (10)
Persamaan di atas dapat ditulis menjadi:
GF , = tr
2 T
tr T tr T
di mana Y merupakan pendekatan X. Ukuran kesesuaian analisis biplot sebagai ukuran kedekatan dari tiga bentuk matriks dengan tr dinamakan teras dari matriks segi = ( ), yaitu tr = =1 ,
ialah:
1. Kesesuaian data:
GF , T = tr
2 T T
tr T tr( T T)
2. Kesesuaian peubah:
GF T , T = tr
2 T T
tr T T tr( T T)
3. Kesesuaian objek:
GF T, T = tr
2 T T
tr T T tr( T T)
Bila dikaitkan dengan analisis Procrustes, Gabriel hanya melakukan transformasi dilasi untuk ukuran kesesuaian matriks data, objek, dan peubah. Sementara Siswadi dan Bakhtiar (2011) menggunakan analisis Procrustes dengan melakukan transformasi dilasi, translasi dan rotasi yang menghasilkan ukuran kesesuaian yang sama dengan Gabriel untuk matriks data dan objek. Khusus untuk matriks peubah, ukuran kesesuaiannya dinyatakan sebagai berikut:
GF T , T = tr
2 � �T� T
tr � T� tr(� T� )
dengan
� = T−1 T T ,
�= �T, dan � T adalah dekomposisi
nilai singular bentuk lengkap (DNSBL) dari matriks � T� .
Analisis Peubah Kanonik
Tinjauan analisis peubah kanonik ini merujuk pada Kusnandar (2011). Pendekatan standar untuk perlakuan data peubah ganda dengan beberapa objek diidentifikasi a piori, yang memiliki sejarah panjang dalam literatur statistika, adalah
analisis peubah kanonik (APK, Canonical
Variate Analysis) yang diperkenalkan oleh
Fisher (1936). APK merupakan salah satu teknik statistika untuk analisis data dengan peubah ganda yang berbasis analisis pengelompokan data sehingga ragam antarkelompok maksimum dan ragam di dalam kelompok minimum (Varas et al. 2005).
Salah satu pendekatan dalam APK ialah mencari peubah kanonik yang merupakan kombinasi linear dari peubah asal yang akan menghasilkan cara terbaik dalam pemisahan kelompok-kelompok tersebut. Peubah ini akan memberikan nilai sedekat mungkin bagi objek-objek dalam kelompok yang sama dan sebesar mungkin bagi objek-objek antarkelompok.
Andaikan ada n objek dari m kelompok contoh acak dengan masing-masing berukuran 1, 2,…, ( 1+ 2+ +
= ) dengan p peubah yang diamati,
1, 2,…, . Misalnya = ( 1, ,…, �)′
adalah vektor yang mewakili peubah, n
adalah matriks data asal yang telah terkoreksi terhadap nilai rata-rata kolomnya, dan n = ( ) adalah matriks indikator m
kelompok (peubah dummy) yang diberikan oleh:
=
1, jika ∈k kelompok ke− dengan
= 1,2,…, = 1,2,…,
0, selainnya
�
sehingga dapat ditulis
′=
1…1 0…0 … 0…0 0…0 1…1 …
… 0…0 0…0 0…0 … 1…1
(11)
= ′ = diag( 1, 2,…, ), (12)
yaitu matriks diagonal berukuran ×
dengan elemen diagonal utamanya merupakan banyaknya objek dari setiap kelompok.
Ilustrasi:
Misalkan ada 5 objek yang dikelompokkan menjadi 2 kelompok, dengan kelompok pertama berisi 3 objek dan kelompok kedua berisi 2 objek, maka matriks indikator untuk kasus ini dapat ditulis = 1 0 1 0 1 0 0 0 1 1
, dengan = ′ = 30 02 .
Matriks m merupakan matriks yang
setiap barisnya merupakan vektor rata-rata dari peubah dalam setiap kelompok, yaitu:
= −1 ′ . (13)
Analisis ragam antarkelompok dan dalam kelompok dapat dikonstruksi seperti pada Tabel 1.
Untuk matriks jumlah kuadrat dan hasil kali (JKK, sums of squares and products) data dalam kelompok dapat ditulis juga sebagai:
= ′ − ′ = =1 , (14) dengan adalah matriks JKK data dalam kelompok k, untuk = 1,2,…, , yaitu
�= w ′ untuk , ′ = 1,2,…, , dan
w ′didefinisikan oleh:
w ′= ∈� ( − )( ′− ′), (15) dengan
�1= 1,2,…, 1 ,
�2= 1+ 1, 2+ 2,…, 1+ 2 ,…,
� = + 1, −1 + 2,…, =1
−1
=1 ,
adalah rata-rata dari peubah j dalam kelompok k, yaitu = 1 ∈� dan adalah banyaknya objek dari kelompok k dengan =1 = .
Sedangkan matriks JKK data antarkelompok dapat ditulis sebagai:
�= ′
Tabel 1 Analisis ragam antarkelompok dan dalam kelompok
Sumber Keragaman Derajat Bebas
db
Jumlah Kuadrat dan Hasil Kali JKK
Antarkelompok (between group)
−1 �= ′
Dalam kelompok
(within group) −
= ′ − ′
Total −1 = ′
dengan merupakan rata-rata keseluruhan dari peubah j, yaitu =1 =1 dan
=�+ .
Tujuannya, berdasarkan pengukuran peubah 1, 2,…, secara serempak, akan
memaksimumkan rasio antara ragam antarkelompok dengan ragam dalam kelompok. Untuk mencapai tujuan ini, transformasikan peubah vektor x, ke dalam peubah baru, yang membuat ragam yang tinggi antarkelompok terhadap ragam dalam kelompok. Jika transformasi dilambangkan oleh =�′ , maka yang dicari ialah vektor
v sehingga � = �′��
�′ � maksimum dengan
kendala �′ �= 1, yaitu solusi dibatasi untuk vektor dengan panjang satu satuan terhadap matriks W. Fungsi � yang akan dimaksimumkan merupakan rasio antara ragam antarkelompok dengan ragam dalam kelompok.
Definisikan fungsi Lagrange dengan �2 sebagai pengganda Lagrange yang akan dimaksimumkan.
Fungsi Lagrange:
ℒ=�′�� − �2 �′ � −1 , (17)
dengan syarat orde-1:
�ℒ
��2= 0↔ �′ �= 1, (18)
�ℒ
� = 0↔2�� −2�2 �= 0. (19)
Syarat (18) taklain adalah kendala dan dari syarat (19) diperoleh
� − �2 �= 0 ��=�2 �
�′��=�2�′ �.
Karena (18) diperoleh
�′��=�2,
yang menyatakan bahwa � maksimum jika � memenuhi �′��=�2.
Matriks merupakan matriks taksingular, sehingga dengan mengalikan persamaan (18) dengan −1, diperoleh −1� − �2 �= 0
Artinya, vektor � atau bobot kanonik yang dapat memaksimumkan � adalah vektor eigen dari matriks −1� yang berpadanan
dengan nilai eigen terbesar �2. Transformasi
yang diperoleh dari vektor eigen yang
berpadanan dengan nilai eigen terbesar disebut peubah kanonik pertama. Peubah kanonik kedua diperoleh dari vektor eigen yang bersesuaian dengan nilai eigen terbesar kedua, dan begitu pula untuk mencari peubah kanonik yang lainnya. Banyaknya peubah kanonik yang mungkin diperoleh adalah
= pangkat −1� = min , −1 .
Semua penyelesaian dari (19) dapat dikumpulkan bersama dalam bentuk
� = �, (20) dengan = [ 1, 2,…, ] dan �= diag(�12,�22,…,�2), di mana �12 �22
�2> 0, sehingga ′ = . Jika = ,
maka dapat ditulis ′= −1 dan
−1= ′ .Dengan mengalikan persamaan
(20) dengan ′ diperoleh
′� =�.
Jika matriks −1� tidak simetris, perhitungan vektor eigen dan peubah kanonik secara komputasi lebih menguntungkan menggunakan matriks simetris −1/2� −1/2 berukuran ×
daripada matriks −1� (Gittins, 1985).
Dekomposisi spektral dari matriks
−1/2� −1/2 diberikan oleh:
−1/2� −1/2= ′,
dengan adalah suatu matriks berukuran
× yang kolom-kolomnya merupakan vektor eigen yang berpadanan dengan nilai eigen dan � adalah matriks diagonal yang diagonal utamanya merupakan nilai eigen.
Berdasarkan asumsi tersebut persamaan (18) dapat ditulis menjadi
−1/2 � − �2 �= 0 ( −1/2� − �2 / )�= 0
( −1/2� −1/2 1/2− �2 / )�= 0 ( −1/2� −1/2− �2 ) 1/2�= 0.
Jadi, persamaan tersebut dapat ditulis sebagai
( −1/2� −1/2− �2 ) = 0 (21)
dengan = 1/2�dan ′ = 1.
�= −1/2 , sehingga, �′ �= ′ − / − / = ′ = 1.
Semua kombinasi linear untuk sebuah objek dengan nilai-nilai x diberikan oleh:
= ′ .
Hal ini memberikan sebuah transformasi dari peubah asal menjadi himpunan peubah baru yang dikenal sebagai peubah kanonik. Ruang yang dihasilkan oleh peubah-peubah ini disebut ruang kanonik. Rata-rata kelompok pada ruang kanonik disebut juga rata-rata kanonik diberikan oleh:
∗= ,
dan transformasi seluruh himpunan objek pada ruang kanonik diberikan oleh , sehingga:
∗ ∗′ = ′ ′= −1 ′.
Artinya, jarak Euclid antara rata-rata dalam ruang peubah kanonik bersesuaian dengan jarak Mahalanobis dalam ruang peubah asal. Jadi, ruang peubah kanonik dapat dianggap sebagai ruang Euclid.
Peubah kanonik yang diperoleh,
1, 2,…, merupakan kombinasi linear
yang dipilih sehingga 1merefleksikan perbedaan terbesar antarkelompok, peubah
2 merefleksikan perbedaan terbesar
antarkelompok yang tidak dapat dicakup oleh 1 dan 2, dan seterusnya. Diharapkan
beberapa peubah kanonik pertama, misalnya dua peubah kanonik pertama, cukup layak digunakan sehingga masing-masing objek dan rata-ratanya dapat digambarkan dalam ruang berdimensi dua. Bila hal ini dimungkinkan maka bagaimana baiknya upaya pemisahan antarkelompok dan penentuan objek ke suatu kelompok akan lebih mudah dilakukan.
Analisis Biplot Kanonik
Tinjauan analisis biplot kanonik ini merujuk pada Kusnandar (2011). Analisis biplot kanonik merupakan representasi grafik dari APK, dikembangkan oleh Gabriel (1995) untuk memperoleh representasi secara serempak antara rata-rata kelompok dan peubah di mana dimungkinkan tidak hanya untuk menetapkan perbedaan antarkelompok tetapi juga untuk menggambarkan peubah yang dianggap dominan dalam membedakan antarkelompok (Vallejo-Arboleda et al. 2007).
Misalnya n adalah matriks data asal
yang terkoreksi terhadap rata-rata kolomnya dan n adalah matriks indikator m
kelompok (peubah dummy). Analisis biplot
kanonik merupakan peragaan secara grafik dari baris dan kolom sebuah matriks m ,
dengan baris mewakili rata-rata kelompok dan kolom mewakili peubah. Matriks merupakan rata-rata objek masing-masing kelompok untuk setiap peubah yang diamati dan terkoreksi terhadap nilai rata-rata keseluruhan.
Untuk memperhitungkan pengaruh penyebaran objek dan skala pengukuran peubah, diperkenalkan pembobotan sehubungan dengan matriks JKK data dalam kelompok dan yang lainnya berkaitan dengan banyaknya objek, hal ini karena akurasi rata-rata bergantung pada ukuran yang telah dihitung, sehingga dapat didefinisikan sebagai:
= 1/2 −1/2. (22)
Artinya, baris dari terboboti oleh banyaknya objek dan peubah pada kolom terboboti oleh invers dari matriks JKK dalam kelompok (Gabriel, 1972), dengan
′ = −1/2 ′ 1/2 1/2 −1/2 = −1/2 ′ −1/2
= −1/2� −1/2, (23)
sehingga ′ memiliki vektor eigen
= 1/2� dan nilai eigen �2, dengan
−1/2 −1/2= −1.
Mengkonstruksi biplot dari matriks dengan ukuran tersebut akan setara dengan mengkonstruksi biplot untuk matriks . Biplot representasi dari matriks diperoleh dari DNS, yaitu
m =m � ′ = λ=1 ′ (24)
dengan � adalah matriks diagonal yang elemen diagonal utamanya merupakan akar dari nilai eigen-nilai eigen positif matriks
′ atau ′ , yaitu �= diag(λ1,λ2,…,λr), dengan λ1 λ2 λr > 0. Nilai
λ1,λ2,…,λr disebut nilai singular dari dan
λ12,λ22,…,λr2 merupakan nilai eigen-nilai
eigen positif matriks ′ atau ′ . Matriks dan adalah matriks ortonormal kolom, sehingga ′ = ′ = (matriks identitas berdimensi r). Matriks adalah matriks yang kolom-kolomnya merupakan vektor eigen yang berpadanan dengan nilai eigen positif dari matriks ′ , yaitu = ( 1, ,…, ) dan adalah matriks yang kolom-kolomnya merupakan vektor eigen-vektor eigen yang berpadanan dengan nilai eigen-nilai eigen positif dari matriks ′ , dengan hubungan
= 1, ,…, = 1
λ1 , λ2 ,…, λr .
= 1, ,…, = ( 1/2�
1, 1/2� ,…, 1/2� ) = 1/2(�
1,� ,…,� )
= 1/2 . (25) Penyelesaian diperoleh dengan mensubstitusi persamaan (22) ke persamaan (24), sehingga
1/2 −1/2
= � ′
atau
= −1/2 � ′ 1/2 (26)
yang ekivalen dengan dekomposisi nilai singular umum (DNSU, Generalized Singular Value Decomposition) dari matriks
dalam matriks dan −1 , yaitu: = −1/2 � ′ 1/2= � ′
dengan = −1/2 dan = 1/2 .
Dengan memilih matriks definit positif
�= dan �= −1, sehingga ′� =
′ −1/2 −1/2
= ′ = , dan
′� = ′ 1/2 −1 1/2 = ′ = .
PNSU menyediakan pendekatan terbaik pangkat rendah dari matriks menggunakan nilai dan vektor singular pertama.
Dekomposisi pada (26) memungkinkan untuk mengkonstruksi representasi biplot untuk matriks rata-rata kelompok, yaitu:
= ′, (27) dengan
= −1/2 �, dan = 1/2 ,
di mana ′ = ′ 1/2 1/2 = .
Elemen ke-(i,j) dari matriks dapat ditulis sebagai:
, = ′ ,
dengan ′ merupakan vektor baris ke-i dari matriks , = 1,2,…, dan ′ merupakan vektor baris ke-j dari matriks , = 1,2,…, ; di mana vektor dan mempunyai r elemen.
Untuk menggambarkan pada ruang dimensi < , dapat didekati menggunakan matriks berpangkat s,
( )= ( ) ′( ),
dengan mengambil s kolom pertama matriks sebagai penanda baris (rata-rata kelompok m) dan s kolom pertama matriks sebagai penanda kolom (peubah p). Biasanya digunakan = 2, sehingga koordinat-koordinat dan dapat digambarkan dalam ruang berdimensi dua. Pada diagram pencar, penanda baris diwakili sebagai titik dan penanda kolom sebagai vektor.
Matriks dan pada biplot kanonik memenuhi sifat sebagai berikut:
1. Berdasarkan DNS matriks yang diberikan dalam persamaan (24), diperoleh
= �−1 dan = ′ �−1.
Oleh karena itu, matriks dapat dinyatakan dengan mengganti ekspresi dan pada (22) sebagai
= −1/2 � = −1/2 �−1� = −1/2 1/2 −1/2
= −1/2 (28)
dan mengganti dalam persamaan (25) kemudian mensubstitusikannya ke (28) diperoleh:
= . (29) Persamaan (29) dapat menafsirkan matriks sebagai proyeksi pada daerah pemisahan maksimum dari kelompok, yang dihasilkan oleh kolom dari matriks , dan
− ′ − = ( − )′ −1( − ),
dengan adalah matriks JKK data dalam kelompok, adalah vektor rata-rata kelompok i. Artinya, kuadrat jarak Euclid antara vektor dan pada biplot sama dengan kuadrat jarak Mahalanobis antara dan .
2. Perkalian ′ dari penanda baris dengan penanda kolom merupakan pendekatan rata-rata , dari kelompok ke-k pada peubah ke-j yang telah terkoreksi terhadap rata-rata terboboti seluruh objek, sehingga memungkinkan untuk karakterisasi perbedaan antarkelompok,
, = ′ = proj( , ) .
3. Kualitas representasi (atau ukuran kesesuaian dari matriks data) dapat didekati oleh:
�2 =1
�2 =1
4. Matriks sebagai pendekatan matriks JKK data dalam kelompok, yaitu:
′= 1/2 ′ 1/2=
5. Panjang penanda kolom sebanding dengan keragaman dalam kelompok-kelompok, = dengan =
.
Analisis Procrustes
Dalam Bakhtiar dan Siswadi (2011) analisis Procrustes adalah alat analisis berdasarkan asas kuadrat terkecil yang dapat digunakan untuk mengukur kemiripan maksimal antarkonfigurasi titik melalui serangkaian transformasi linear. Analisis ini bertujuan untuk membandingkan dua konfigurasi yang mewakili unit pengamatan yang sama. Untuk melihat kesamaan bentuk dan ukuran dari dua konfigurasi maka setelah kedua konfigurasi dilakukan translasi salah satu konfigurasi dibuat tetap sementara konfigurasi yang lainnya ditransformasikan sehingga paling sesuai dengan konfigurasi pertama.
Misalnya ∈ ℝ × adalah konfigurasi
titik dalam ruang Euclid berdimensi dengan koordinat diberikan oleh matriks
× berikut
= 1′∙
2∙ ′
∙ ′
, (30)
dengan ∙= 1 , 2, ,
′
, untuk
= 1, 2, , dan konfigurasi ∈ ℝ ×
yang merupakan konfigurasi titik dalam ruang Euclid berdimensi . Konfigurasi ini akan dipasangkan dengan konfigurasi dalam bentuk baris, dengan masing-masing baris dari konfigurasi dipasangkan dengan baris konfigurasi yang bersesuaian. Diasumsikan bahwa dimensi kedua konfigurasi dan adalah sama, dengan demikian tiap matriks memiliki jumlah kolom yang sama. Jika > maka − kolom nol dapat ditambahkan pada matriks
sehingga kedua konfigurasi berada pada ruang dimensi yang sama. Perubahan kolom yang merupakan vektor 0 di kolom mana saja, telah dijelaskan panjang lebar oleh Siswadi et al. (2012). Dengan demikian tanpa mengurangi perumuman dapat diasumsikan bahwa = . Diasumsikan pula bahwa salah satu konfigurasi, , dibuat tetap dan konfigurasi yang lain, , akan ditransformasi agar sesuai dengan konfigurasi .
Dalam menentukan tingkat kesesuaian dua konfigurasi, analisis Procrustes mendasarkan penghitungannya pada jumlah kuadrat jarak antartitik yang bersesuaian, disebut juga jarak Procrustes, yaitu
, = − =1 =1 2
= tr − ′ − . (31)
Dengan mempertimbangkan perubahan posisi, orientasi, dan skala dua konfigurasi yang dibandingkan, analisis Procrustes mensyaratkan tiga bentuk transformasi geometris harus dilakukan untuk mendapatkan E yang optimal. Ketiga bentuk transformasi ini adalah translasi, rotasi dan dilasi.
Translasi
Translasi dalam analisis Procrustes merupakan proses penggeseran semua titik pada konfigurasi dan konfigurasi dengan jarak yang tetap dan arah yang sama sehingga kedua konfigurasi memiliki sentroid (titik berat) yang sama.
Penguraian jumlah kuadrat persamaan (31) menghasilkan
,
= − − − =1 =1 +
− 2
= − − − =1 =1 2+ 2 − − − −=1 =1
+ − =1 2. (32) Karena bentuk kedua dari ruas kanan persamaan (32) bernilai nol, maka diperoleh
, = �, � + , (33) di mana
� = −1� , � = −1� ,
= − =1 2,
dengan 1 adalah vektor berukuran × 1
yang semua elemennya bernilai 1, � dan � menyatakan sentroid dari masing-masing konfigurasi dan yang dinyatakan sebagai � =1 ′ dan � =1 ′ .
Penyesuaian optimal dengan translasi diperoleh dengan menghimpitkan sentroid X
dan Y ( = 0). Jadi, norma kuadrat perbedaan minimum dua konfigurasi setelah penyesuaian dengan translasi adalah:
� , = �, �
= − − − =1 =1 2. (34)
Rotasi
Rotasi adalah proses pemindahan seluruh titik dengan sudut yang tetap tanpa mengubah jarak setiap titik terhadap sentroidnya. Dalam analisis Procrustes rotasi dilakukan dengan cara menggandakan konfigurasi dengan matriks ortogonal
yang meminimumkan jarak
Norma kuadrat perbedaan kedua konfigurasi setelah penyesuaian dengan rotasi adalah
� , =
Q
inf , . (35)
Secara aljabar, berdasarkan (31) diperoleh:
( , ) = tr − ′ − = tr ′− ′ ′ ( − )
= tr ′ + ′ ′ − ′ − ′ ′ = tr ′ + tr ′ ′ −tr ′
− tr ′ ′ = tr ′ + tr ′ ′ −tr ′
−tr ′ ′ ′ = tr ′ + tr ′ −tr ′
−tr ′
= tr ′ + tr ′ −2tr ′ . (36) Untuk memperoleh nilai ( , ) yang minimum harus dipilih matriks ortogonal Q
yang memaksimumkan nilai tr ′ . Misalnya � ′ merupakan hasil penguraian nilai singular bentuk lengkap dari matriks ′ , sehingga ′ = � ′, dengan �= � adalah matriks diagonal dan , merupakan matriks ortogonal, maka
tr ′ = tr � ′ = tr ′ �
= tr � , (37) dengan = ′ merupakan perkalian matriks ortogonal, sehingga = ℎ juga matriks ortogonal dan berlaku –1 ≤ hij ≤ 1.
Sehingga diperoleh
tr ′ = tr � = ℎ �=1
tr � . Jadi, E minimum ketika tr ′ � = tr � , mengakibatkan
′ �= �,atau = ′.
Jadi, jarak Procrustes oleh rotasi yang optimal diberikan oleh:
� , = tr ′ + tr ′ −2 tr �.
Dilasi
Dilasi adalah pembesaran/pengecilan jarak setiap titik dalam konfigurasi terhadap
sentroidnya. Dilasi Y terhadap X dilakukan dengan menggandakan konfigurasi Y dengan suatu skalar c. Norma kuadrat perbedaan kedua konfigurasi setelah penyesuaian dengan dilasi adalah
, =
c
inf
, . (38)Secara aljabar, berdasarkan (31) diperoleh:
,
= tr − ′ −
= tr ′− ′ − = tr ′ − ′ − ′ + 2 ′ = tr ′ + 2tr ′ − tr ′
− tr ′
= tr ′ + 2tr( ′ )− tr( ′ ′)
− tr( ′ ) = tr ′ + 2tr( ′ )− tr ′
− tr( ′ )
= 2tr ′ −2 tr ′ + tr ′ .
yang dapat dilihat sebagai fungsi kuadrat dalam c, sehingga nilai minimum ,
diperoleh dengan memilih
=tr ( ′ ) tr ( ′ ) .
Jadi, jarak Procrustes oleh dilasi yang optimal diberikan oleh:
, = tr ′ −tr2( ′ )
tr ( ′ ) . (39)
Bakhtiar dan Siswadi (2011) telah menunjukkan bahwa urutan optimal transformasi linear dalam analisis Procrustes ialah translasi, rotasi dan dilasi, dengan jarak Procrustes diberikan oleh:
�� ,
= �, �
= tr ′� � −tr
2 ′
� ′
�
tr ′� � . (40)
Untuk memperoleh posisi yang paling sesuai sehingga kedua matriks menjadi semakin dekat dilakukan penyesuaian seperti di atas. Ukuran kesesuaian dua konfigurasi menggambarkan kedekatan (kesesuaian) antara dua matriks. Semakin kecil nilai �� maka semakin besar kemiripan atau kedekatan antarkonfigurasi.
METODE PENELITIAN
Sumber DataData yang digunakan dalam penelitian ini adalah data sekunder mengenai mahasiswa Beasiswa Utusan Daerah Departemen Agama (BUD DEPAG) yang
diperoleh dari Direktorat Pendidikan
Tingkat Persiapan Bersama Institut Pertanian Bogor (TPB IPB), yang terdiri
diikuti bersama dan IPK mahasiswa BUD DEPAG TPB IPB tahun akademik 2009/2010.
Peubah Penelitian
Peubah yang digunakan dalam penelitian ini ialah:
1. Nilai mutu mata kuliah Agama (AG), 2. Nilai mutu mata kuliah Biologi (BI), 3. Nilai mutu mata kuliah Ekonomi Umum
(EK),
4. Nilai mutu mata kuliah Fisika (FI), 5. Nilai mutu mata kuliah Bahasa Indonesia
(ID),
6. Nilai mutu mata kuliah Bahasa Inggris (IG),
7. Nilai mutu mata kuliah Kalkulus (KA), 8. Nilai mutu mata kuliah Kimia (KI), 9. Nilai mutu mata kuliah Pengantar
Kewirausahaan (KW),
10.Nilai mutu mata kuliah Pengantar Matematika (PM),
11.Nilai mutu mata kuliah Olahraga dan Seni (OR),
12.Nilai mutu mata kuliah Pengantar Ilmu Pertanian (PI),
13.Nilai mutu mata kuliah Sosiologi Umum (SO),
14.Nilai mutu mata kuliah Pengantar Kewarganegaraan (PK), dan
15.Nilai mutu Indeks Prestasi Kumulatif (IP).
Objek Penelitian
Objek penelitian adalah provinsi yang terwakili oleh mahasiswa BUD DEPAG TPB IPB tahun akademik 2009/2010 yang berjumlah 18 provinsi asal dari 69 mahasiswa seperti disajikan dalam Tabel 2.
Tabel 2 Objek penelitian berdasarkan provinsi
No Asal Provinsi Kode Jumlah mahasiswa
1 NAD 1 3
2 SUMUT 2 3
3 SUMBAR 3 2
4 RIAU 4 1
5 JAMBI 5 1
6 SUMSEL 6 1
7 LAMPUNG 7 1
8 DKI JAKARTA 8 3
9 JABAR 9 18
10 BANTEN 10 5
11 JATENG 11 6
12 DIY 12 1
13 JATIM 13 17
14 BALI 14 1
15 NTB 15 2
16 SULSEL 16 2
17 SULBAR 17 1
18 GORONTALO 18 1
Total Mahasiswa 69
Metode Penelitian
Langkah-langkah dalam penelitian ini ialah:
1. Menentukan biplot biasa dari data asal dan data agregat dalam dimensi dua dengan menggunakan paket BiplotPack Ver. 4.1.0 dan memilih �= 0 (Ardana, 2011) dengan software Mathematica 8.0. 2. Menentukan matriks indikator dan
matriks yang terkait pada data asal (dalam hal ini = 18).
3. Menentukan biplot kanonik dari data asal dengan menggunakan algoritme dan paket BiplotGH Ver. 1.0 (Ardana, 2009) dengan software Mathematica 8.0. Adapun algoritme untuk memperoleh biplot kanonik ialah:
i. 69 15∗ adalah matriks data asal, dan 69 18 adalah matriks indikator 18
kelompok.
ii. Menentukan matriks data asal yang terkoreksi terhadap nilai rata-rata kolomnya dengan rumus = ∗−
1
69( ′
∗).
iii. Menentukan matriks rata-rata kelompok, yaitu = −1 ′ .
iv. Menentukan matriks JKK data dalam kelompok, yaitu = ′ − ′ . v. Menentukan matriks rata-rata
kelompok terboboti, yaitu = 1/2 −1/2.
vi. Matriks diurai menjadi = � ′
dengan dekomposisi nilai singular. vii. Menentukan koordinat rata-rata
kelompok dengan rumus =
−1/2
� dan koordinat peubah dengan rumus = 1/2 .
viii. Koordinat rata-rata kelompok dan peubah yang diperoleh kemudian diplot menggunakan paket BiplotGH Ver. 1.0 (Ardana, 2009).
a. Matriks data asal dikalikan dengan konstanta (dalam hal ini
= 2).
b. Matriks dengan jumlah objek setiap kelompok sama ( 1= 2=
= = ), di mana = 3. c. Matriks dengan jumlah objek
setiap kelompok sama yang dikalikan dengan konstanta sehingga
( 1= 2= = = ), (dalam
hal ini = 2 dan = 3).
d. Matriks data asal dengan urutan terbalik.
Dalam hal ini matriks indikator, matriks JKK data dalam kelompok ( ), dan matriks rata-rata kelompok ( ) yang
digunakan tetap. Untuk mendapatkan biplot kanonik dengan berbagai ukuran contoh yang lain, maka dilakukan pengulangan biplotnya pada bagian 3.v. 5. Menelusuri ketepatan biplot biasa dan
biplot kanonik dengan menggunakan ukuran kesesuaian dari Gabriel (2002) dan Siswadi dan Bakhtiar (2011). 6. Menentukan kesesuaian antarkonfigurasi
dengan analisis Procrustes dari Bakhtiar dan Siswadi (2011) dalam dimensi dua. 7. Melakukan perbandingan analisis biplot
biasa dan kanonik dengan data asal, serta melakukan perbandingan analisis biplot kanonik dengan berbagai ukuran contoh.
PEMBAHASAN
Konfigurasi Biplot Biasa dan BiplotKanonik Data Asal
Konfigurasi untuk biplot biasa diperoleh dengan melakukan pendekatan yang berbeda terhadap matriks data asal. Adapun pendekatan yang digunakan yaitu: (1) biplot biasa dengan data agregat yang diperoleh dari matriks data asal yang telah dirata-ratakan terhadap objek/kelompok dan (2) biplot biasa dengan data asal yang diperoleh dari rata-rata koordinat objek/kelompok. Selanjutnya untuk biplot kanonik diperoleh dengan menggunakan data asal. Adapun hasil biplotnya yang diperoleh disajikan pada Gambar 1, Gambar 2 dan Gambar 3.
Simulasi Biplot Kanonik dengan Berbagai Ukuran Contoh
Untuk mengetahui sejauh mana perubahan konfigurasi pada biplot kanonik
dengan berbagai ukuran contoh dilakukan simulasi. Simulasi pada biplot kanonik diperoleh dengan menggunakan matriks yang bervariasi. Adapun variasi matriks yang digunakan yaitu: (1) matriks data asal dikalikan dengan konstanta = 2, (2) matriks dengan jumlah objek setiap kelompok sama atau berdiagonal utama
= 3 sehingga 1= 2= = = = 3, (3) matriks dengan jumlah objek setiap kelompok sama atau berdiagonal utama = 3 dikalikan dengan konstanta
= 2 sehingga 1= 2= = = = 6, dan (4) matriks data asal dengan urutan terbalik. Adapun hasil biplotnya yang diperoleh disajikan pada Gambar 4 sampai dengan Gambar 7.
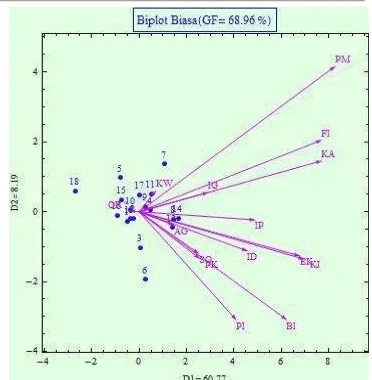
Gambar 3 Biplot kanonik dengan data asal
Gambar 4 Biplot kanonik dengan matriks data asal dikalikan konstanta = 2
Gambar 5 Biplot kanonik dengan matriks
= diag 3, . . ,3 = 3�
Gambar 6 Biplot kanonik dengan matriks
= diag 3, . . ,3 = 3�
dikalikan konstanta = 2
Kesesuaian Antarkonfigurasi dengan Analisis Procrustes
Bakhtiar dan Siswadi (2011) telah menunjukkan bahwa urutan optimal transformasi linear dalam analisis Procrustes ialah translasi, rotasi dan dilasi dengan jarak Procrustes diberikan pada persamaan (40). Semakin kecil jarak antarkonfigurasi maka
semakin banyak kesamaan bentuk dan ukuran dari dua konfigurasi tersebut. Dalam kasus ini kesesuaian konfigurasi yang digunakan yaitu matriks data, matriks koordinat objek/kelompok berdimensi dua dan matriks koordinat peubah berdimensi dua dari berbagai ukuran contoh. Adapun hasilnya dapat dilihat pada tabel berikut.
Tabel 3 Kesesuaian antarkonfigurasi untuk matriks data pendekatan berdimensi dua
A1 A2 A3 A4 A5 A6 A7
A1 0 2.62 6.74 6.74 6.11 6.11 9.63
A2 0 31.83 31.83 29.78 29.78 40.34
A3 0 0 1.18 1.18 7.67
A4 0 1.18 1.18 7.67
A5 0 0 7.70
A6 0 7.70
A7 0
Tabel 4 Kesesuaian antarkonfigurasi untuk matriks koordinat objek/kelompok berdimensi dua
A1 A2 A3 A4 A5 A6 A7
A1 0 1.11 0.94 0.94 0.90 0.90 1.20
A2 0 0.22 0.22 0.23 0.23 0.20
A3 0 0 0.02 0.02 0.18
A4 0 0.02 0.02 0.18
A5 0 0 0.15
A6 0 0.15
A7 0
Tabel 5 Kesesuaian antarkonfigurasi untuk matriks koordinat peubah berdimensi dua
A1 A2 A3 A4 A5 A6 A7
A1 0 3.33 1.42 1.42 1.13 1.13 4.41
A2 0 80.76 80.76 80.05 80.05 60.61
A3 0 0 0.71 0.71 6.56
A4 0 0.71 0.71 6.56
A5 0 0 6.17
A6 0 6.17
A7 0
Keterangan:
A1 : Biplot biasa dengan data agregat A2 : Biplot biasa dengan data asal A3 : Biplot kanonik dengan data asal
A4 : Biplot kanonik dengan matriks data asal dikalikan konstanta = 2
A5 : Biplot kanonik dengan matriks berdiagonal utama 3
A6 : Biplot kanonik dengan matriks berdiagonal utama 3 dikalikan konstanta = 2
A7 : Biplot kanonik dengan matriks data asal dengan urutan terbalik
Analisis Biplot Biasa dengan Data Agregat, Biplot Biasa dengan Data Asal, dan Biplot Kanonik Data Asal
Kesesuaian antarkonfigurasi dari biplot biasa dengan data agregat, biplot biasa dengan data asal dan biplot kanonik dengan matriks data asal terhadap matriks data pendekatan, matriks koordinat
relatif dekat jika dibandingkan dengan biplot kanonik dengan data asal, di mana nilai = 2.62. Sedangkan kesesuaian antarkonfigurasi untuk matriks koordinat objek/kelompok berdimensi dua, terlihat bahwa biplot biasa dengan data asal dan biplot kanonik dengan data asal memiliki kesamaan bentuk dan ukuran yang relatif dekat jika dibandingkan dengan biplot biasa dengan data agregat, di mana nilai = 0.22. Kesesuaian antarkonfigurasi untuk koordinat peubah berdimensi dua, terlihat bahwa biplot biasa dengan data agregat dan biplot kanonik dengan data asal memiliki kesamaan yang relatif dekat jika dibandingkan dengan biplot biasa dengan data asal, di mana nilai = 1.42. Implikasi dari kesesuaian antarkonfigurasi ini dapat dilihat pada biplotnya. Adapun interpretasinya antara lain:
1. Kedekatan Antarobjek (Provinsi)
Kedekatan antarobjek atau kedekatan letak posisi dua objek yang digambarkan sebagai dua titik yang berdekatan diinterpretasikan sebagai kemiripan karakteristik dua objek. Gambar 1, Gambar 2 dan Gambar 3 memberikan gambaran adanya persamaan dan perbedaan posisi objek. Beberapa kemiripan karakteristik yang terdapat antara lain provinsi Jakarta (8) dengan Bali (14) pada biplot biasa dengan data agregat maupun data asal, tetapi pada biplot kanonik dengan data asal tidak memiliki kemiripan. Provinsi Riau (4) dengan Sumatera Selatan (6) pada biplot biasa dengan data agregat memiliki kesamaan, tetapi pada biplot biasa dengan data asal dan biplot kanonik dengan data asal tidak memiliki kesamaan karakteristik.
2. Keragaman Peubah
Keragaman peubah pada analisis biplot digambarkan oleh panjang pendeknya vektor peubah. Peubah dengan keragaman kecil digambarkan dengan vektor yang pendek, sebaliknya jika keragamannya besar digambarkan dengan vektor yang panjang. Berdasarkan Gambar 1, Gambar 2 dan Gambar 3 terlihat bahwa mata kuliah yang memiliki keragaman nilai yang relatif sama dan lebih tinggi dibandingkan mata kuliah lainnya yaitu Pengantar Matematika (PM). Mata kuliah Kalkulus (KA) pada biplot kanonik dengan data asal memiliki keragaman relatif besar sebanding dengan mata kuliah Pengantar Matematika (PM), tetapi pada biplot biasa dengan data asal
tidak memiliki keragaman yang begitu besar jika dibandingkan dengan mata kuliah PM. Mata kuliah Kewirausahaan (KW) pada biplot biasa dengan data agregat memiliki keragaman nilai yang relatif kecil, sedangkan pada biplot biasa dengan data asal yaitu mata kuliah Olahraga dan Seni (OR). Berbeda halnya biplot kanonik dengan matriks data asal, mata kuliah yang memiliki keragaman nilai yang relatif kecil yaitu mata kuliah Sosiologi Umum (SO) dan Agama (AG). Perubahan yang terjadi terlihat pada mata kuliah Olahraga dan Seni (OR) bahwa mata kuliah ini memiliki keragaman relatif besar pada biplot biasa dengan data agregat dan biplot kanonik dengan data asal, tetapi pada biplot biasa dengan data asal memiliki keragaman yang kecil.
3. Korelasi Antarpeubah
Sudut antara dua vektor peubah menggambarkan korelasi dua peubah tersebut. Semakin sempit (lancip) sudut yang dibuat antara dua peubah, maka semakin tinggi korelasinya. Jika sudut yang dibuat tegak lurus maka tidak berkorelasi, sedangkan jika sudutnya tumpul atau berlawanan arah maka korelasinya negatif. Jika ditinjau berdasarkan peubah IPK (IP), dalam biplot biasa dengan data agregat korelasi terbesar dari peubah IPK dibentuk oleh peubah Kalkulus (KA), artinya semakin tinggi nilai IPK maka besar kemungkinan mendapatkan nilai Kalkulus yang tinggi pula. Sedangkan pada biplot biasa dengan data asal korelasi terbesar dari peubah IPK dibentuk oleh peubah Ekonomi Umum (EK). Pada biplot kanonik dengan data asal peubah IPK memiliki korelasi terbesar dengan Pengantar Ilmu Pertanian (PI). Perubahan yang terjadi yaitu peubah Pengantar Kewarganegaraan (PK) dengan Kimia (KI) bahwa pada biplot biasa dengan data agregat dan biplot kanonik dengan data asal memiliki korelasi yang besar, sedangkan pada biplot biasa dengan data asal tidak memiliki korelasi yang besar. Peubah yang tidak memiliki korelasi pada biplot biasa dengan data agregat dan biplot kanonik dengan data asal yaitu peubah IPK dengan Olahraga dan Seni (OR), akan tetapi pada biplot biasa dengan data asal berkorelasi negatif.
4. Keterkaitan Objek dengan Peubah
Lampung merupakan provinsi yang relatif baik, sedangkan provinsi NAD, Banten, NTB dan Gorontalo relatif rendah kinerja lulusan Madrasah Aliyahnya. Provinsi DKI Jakarta dan Bali secara umum memiliki nilai yang relatif baik pada mata kuliah yang berhubungan dengan pengetahuan alam, sedangkan provinsi Lampung memiliki nilai yang relatif baik dalam pengetahuan sosial.
Analisis Hasil Simulasi Biplot Kanonik dengan Berbagai Ukuran Contoh
Kesesuaian antarkonfigurasi dari biplot biplot kanonik dengan matriks data asal dengan berbagai ukuran contoh lainnya terhadap matriks data pendekatan, matriks koordinat objek/kelompok dan matriks koordinat peubah dalam dimensi dua memberikan kesamaan dan ketaksamaan. Perbedaan ukuran contoh yang digunakan mengakibatkan terjadinya perubahan konfigurasi yang diperoleh. Pada Tabel 3, 4 dan 5 terlihat bahwa biplot kanonik dengan data asal memiliki kesamaan yang relatif dekat dengan biplot kanonik dengan matriks berdiagonal utama 3, di mana nilai
= 1.18 untuk matriks data pendekatan, = 0.02 untuk koordinat objek/kelompok dan = 0.71 untuk koordinat peubah derdimensi dua. Sedangkan biplot kanonik dengan data asal dengan biplot kanonik dengan matriks data asal urutan terbalik memiliki kesamaan dan bentuk yang relatif jauh. Hal ini dapat dilihat pada nilai -nya yang besar Implikasi dari kesesuaian antarkonfigurasi ini dapat dilihat pada biplotnya. Adapun kesamaan bentuk dan ukuran dari konfigurasi ini, namun memberikan perbedaan yang cukup ekstrem. Perbedaan ini di interpretasikan antara lain:
1. Kedekatan Antarobjek (Provinsi)
Gambar 3, Gambar 5 dan Gambar 7 memberikan gambaran adanya perbedaan posisi objek dari biplot kanoniknya. Beberapa perbedaan yang terlihat dalam hal kedekatan antarobjek, antara lain provinsi Sumatera Selatan (6) dengan Jambi (5) dan Sulawesi Barat (17) pada biplot kanonik dengan data asal dan berdiagonal utama3 memiliki kemiripan karakteristik, akan tetapi pada biplot kanonik dengan matriks data asal urutan terbalik relatif tidak memiliki kemiripan.
2. Keragaman Peubah
Berdasarkan Gambar 3, Gambar 5 dan Gambar 7 terlihat bahwa mata kuliah Pengantar Matematika (PM) dan Kalkulus (KA) pada biplot kanonik dengan data asal dan matriks berdiagonal utama 3 memiliki keragaman yang relatif tinggi dibandingkan pada biplot kanonik dengan matriks data asal urutan terbalik. Di mana pada biplot kanonik dengan matriks data asal urutan terbalik, mata kuliah yang memiliki keragaman yang relatif tinggi yaitu mata kuliah Pengantar Matematika (PM) dan Fisika (FI).
3. Korelasi Antarpeubah
Gambar 3, Gambar 5 dan Gambar 7 menunjukkan adanya perbedaan korelasi antarpeubah, antara lain peubah Pengantar Matematika (PM) dengan Kalkulus (KA) pada biplot kanonik dengan matriks data asal dan berdiagonal utama tiga memiliki korelasi yang relatif besar dibandingkan pada biplot kanonik dengan matriks data asal urutan terbalik, justru berkorelasi besar dengan peubah Pengantar Kewarganegaraan (PK). Peubah Olahraga dan Seni (OR) dengan Agama (AG) pada biplot kanonik dengan matriks data asal urutan terbalik memiliki korelasi relatif besar. Sementara pada biplot kanonik dengan matriks data asal dan berdiagonal utama 3 tidak memiliki korelasi yang besar. Meski biplot kanonik dengan data asal dan biplot kanonik dengan matriks berdiagonal utama 3 memiliki kesamaan bentuk dan ukuran yang relatif dekat, tetapi juga memberika perbedaan korelasi antarpeubah, di antaranya: pada biplot kanonik dengan data asal peubah yang memiliki korelasi relatif besar yaitu peubah Sosiologi Umum (SO) dengan Ekonomi Umum (EK), sedangkan pada biplot kanonik dengan matriks berdiagonal utama 3 yaitu peubah Ekonomi Umum (EK) dengan Bahasa Indonesia (ID).
4. Keterkaitan Objek dengan Peubah
KESIMPULAN
Konfigurasi yang diperoleh dari biplot biasa dengan data agregat lebih sesuai dengan konfigurasi biplot biasa dengan data asal dibandingkan dengan konfigurasi yang diperoleh dari biplot kanonik. Dari biplot kanonik diperoleh hasil bahwa provinsi DKI Jakarta, Bali dan Lampung merupakan provinsi yang relatif baik, sedangkan provinsi NAD, Banten, NTB dan Gorontalo relatif rendah. Provinsi DKI Jakarta dan Bali secara umum memiliki nilai yang relatif baik pada
mata kuliah yang berhubungan dengan pengetahuan alam, sedangkan provinsi Lampung memiliki nilai yang relatif baik dalam pengetahuan sosial.
Untuk mengetahui kemungkinan perubahan konfigurasi yang dihasilkan biplot kanonik, dilakukan simulasi dengan berbagai ukuran contoh. Hasil yang diperoleh memberikan gambaran adanya perubahan konfigurasi akibat perbedaan ukuran contoh yang digunakan.
DAFTAR PUSTAKA
Aitchison J, Greenacre M. 2002. Biplots for Compositional Data. Applied Statistics. 51: 375−392.
Ardana NKK. 2009. BiplotGH Ver. 1.0 – A Multivariate Data Visualization-Application Package Mathematica Based. Bogor: Departemen Matematika FMIPA IPB.
Ardana NKK. 2011. BiplotPack Ver. 4.1.0 − A Mathematica Package for Multivariate Data Visualization. Bogor: Departemen Matematika FMIPA IPB.
Bakhtiar T, Siswadi. 2011. Orthogonal Procrustes Analysis: Its Transformation Arrangement and Minimal Distance. International Journal of Applied Mathematics and Statistics. 20:
16−24.
Gabriel KR. 1971. The Biplot Graphic Display of Matrices with Application to Principal Component Analysis. Biometrika. 58: 453−467.
Gabriel KR. 1995. MANOVA Biplots for Two-Way Contingency Tables. Oxford Science Publications. 268-277.
Gabriel KR. 2002. Goodness of Fit of Biplots and Correspondence Analysis. Biometrika. 89: 423−436.
Greenacre M. 2010. Biplot in Practice. Madrid: BBVA Foundation.
Gittins R. 1985. Canonical Analysis: A Review with Applications in Ecology. Berlin: Springer-Verlag.
Kusnandar. 2011. Biplot Biasa dan Kanonik untuk Pemetaan Provinsi Berdasarkan Prestasi Mahasiswa IPB [Tesis]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Krzanowski WJ. 1989. On Confidence Regions in Canonical Variate Analysis. Biometrika. 76: 107−116.
Krzanowski WJ. 1990. Principles of
Multivariate Analysis, A User’s
Perspective. New York: Oxford University Press.
Leon SJ. 2001. Aljabar Linear dan Aplikasinya. Ed ke-5. Bondan A, penerjemah; Hardani HW, editor. Jakarta: Erlangga, Terjemahan dari: Linear Algebra with Applications, 5ℎ
Ed.
Mariyam. 2011. Ukuran Kesesuaian dalam Analisis Biplot Biasa dan Analisis Biplot Imbuhan [Skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Siswadi, Bakhtiar T. 2011. Goodness-of-Fit of Biplots via Procrustes Analysis. Far East Journal of Mathematical Sciences. 52: 191−201.
Siswadi, Bakhtiar T, Maharsi R. 2012. Procrustes Analysis and the Goodness-of-fit of Biplots: Some Thoughts and Findings. Applied Mathematical Sciences. 6: 3579−3590.
Siswadi, Suharjo B. 1999. Analisis Eksplorasi Data Peubah Ganda. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Vallejo-Arboleda A, Vicente-Villardon, Galindo-Villardon. 2007. Canonical Statis: Biplot Analysis of Multi-Table Group Structured Data Based on Statis-Act Methodology. Computational Statistics & Data Analysis. 51: 4193− 4205.
Lampiran 1 Data nilai mata kuliah dan IPK Mahasiswa BUD DEPAG TPB IPB 2009/2010 (Matriks data asal)
Kode Provinsi No AG BI EK FI ID IG KA KI KW PM OR PI SO PK IP
1 NAD
1 4.00 1.00 2.00 1.00 1.00 2.00 0.00 0.00 4.00 0.00 4.00 2.00 2.00 2.00 1.56 2 3.00 3.00 3.00 3.00 3.00 3.00 2.00 2.00 3.00 2.00 4.00 4.00 3.00 2.00 2.75 3 4.00 3.00 4.00 4.00 4.00 4.00 3.00 3.00 4.00 3.00 4.00 4.00 4.00 3.00 3.58
2 SUMUT
1 4.00 3.00 4.00 2.00 3.00 4.00 2.00 1.00 3.00 2.00 4.00 3.00 3.00 3.00 2.86 2 4.00 4.00 4.00 3.00 4.00 4.00 3.00 3.00 4.00 4.00 4.00 3.00 3.00 3.00 3.53 3 4.00 1.00 2.00 1.00 3.00 2.00 1.00 1.00 3.00 1.00 4.00 3.00 2.00 2.00 1.94
3 SUMBAR
1 3.00 2.00 4.00 2.00 3.00 3.00 1.00 2.00 4.00 2.00 4.00 3.00 3.00 2.00 2.56 2 4.00 3.00 4.00 3.00 4.00 4.00 2.00 3.00 4.00 2.00 4.00 4.00 4.00 3.00 3.33 4 RIAU 1 3.00 3.00 4.00 3.00 3.00 3.00 2.00 3.00 4.00 3.00 3.00 3.00 3.00 3.00 3.03 5 JAMBI 1 3.00 2.00 3.00 2.00 3.00 2.00 2.00 2.00 4.00 2.00 4.00 2.00 2.00 2.00 2.33 6 SUMSEL 1 4.00 4.00 4.00 2.00 3.00 3.00 2.00 3.00 3.00 2.00 4.00 3.00 3.00 3.00 3.03 7 LAMPUNG 1 4.00 3.00 4.00 4.00 4.00 3.00 3.00 2.00 3.00 4.00 4.00 3.00 3.00 3.00 3.33
8 JAKARTA
1 4.00 4.00 4.00 4.00 4.00 4.00 4.00 4.00 4.00 3.00 3.00 4.00 3.00 4.00 3.81 2 3.00 3.00 4.00 3.00 3.00 4.00 2.00 2.00 4.00 3.00 3.00 3.00 3.00 3.00 3.03 3 4.00 4.00 4.00 4.00 4.00 4.00 4.00 4.00 4.00 4.00 3.00 4.00 3.00 4.00 3.89
9 JABAR
8 3.00 4.00 3.00 3.00 2.00 4.00 2.00 2.00 4.00 4.00 4.00 3.00 3.00 3.00 3.08 9 3.00 2.00 2.00 1.00 3.00 2.00 1.00 1.00 4.00 1.00 4.00 3.00 4.00 2.00 2.14 10 3.00 2.00 3.00 1.00 3.00 3.00 1.00 2.00 4.00 2.00 4.00 3.00 3.00 2.00 2.31 11 3.00 3.00 4.00 2.00 4.00 3.00 2.00 3.00 4.00 2.00 4.00 3.00 3.00 3.00 2.94 12 4.00 4.00 4.00 3.00 4.00 4.00 3.00 3.00 4.00 3.00 4.00 3.00 3.00 3.00 3.44 13 4.00 2.00 4.00 2.00 3.00 3.00 2.00 3.00 4.00 2.00 4.00 3.00 3.00 3.00 2.89 14 4.00 3.00 4.00 4.00 3.00 3.00 2.00 3.00 3.00 3.00 4.00 3.00 3.00 3.00 3.19 15 3.00 2.00 2.00 2.00 3.00 3.00 2.00 2.00 3.00 2.00 4.00 2.00 2.00 2.00 2.31 16 4.00 2.00 3.00 1.00 3.00 4.00 2.00 2.00 3.00 3.00 4.00 3.00 3.00 3.00 2.78 17 4.00 4.00 4.00 3.00 3.00 3.00 2.00 3.00 4.00 2.00 3.00 3.00 3.00 3.00 3.11 18 4.00 3.00 4.00 4.00 4.00 3.00 3.00 3.00 4.00 4.00 4.00 3.00 3.00 2.00 3.36
10 BANTEN
1 4.00 1.00 4.00 3.00 3.00 4.00 1.00 2.00 4.00 4.00 4.00 1.00 3.00 2.00 2.78 2 4.00 3.00 4.00 3.00 3.00 3.00 2.00 3.00 3.00 2.00 4.00 4.00 3.00 3.00 3.08 3 3.00 3.00 3.00 2.00 4.00 4.00 1.00 2.00 4.00 1.00 4.00 3.00 3.00 2.00 2.61 4 4.00 2.00 4.00 2.00 3.00 3.00 2.00 2.00 4.00 1.00 4.00 3.00 3.00 2.00 2.64 5 3.00 2.00 3.00 1.00 3.00 3.00 2.00 2.00 4.00 2.00 4.00 2.00 2.00 2.00 2.33
11 JATENG
1 4.00 3.00 3.00 2.00 4.00 3.00 2.00 2.00 4.00 3.00 4.00 4.00 4.00 3.00 3.08 2 3.00 2.00 2.00 2.00 2.00 3.00 1.00 2.00 4.00 2.00 4.00 3.00 2.00 3.00 2.33 3 4.00 4.00 4.00 3.00 4.00 4.00 2.00 4.00 4.00 3.00 4.00 4.00 3.00 4.00 3.58 4 4.00 4.00 4.00 4.00 3.00 4.00 2.00 3.00 4.00 3.00 4.00 3.00 4.00 3.00 3.47 5 4.00 2.00 4.00 4.00 4.00