Model penyakit menular dengan periode latent dan Relapse:

MODEL PENYAKIT MENULAR DENGAN PERIODE

LATENT

DAN

RELAPSE

ABDI SUKAMTO

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS

DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis dengan judul Model Penyakit MenuIar dengan Periode Latent dan Relapse adalah karya saya sendiri dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi dari karya yang diterbitkan maupun yang tidak diterbitkan dari penulis lain disebutkan dalam teks dan dicanturnkan dalam Dafiar Pustaka di bagian akhir tesis ini.

Bogor, Juli 2009

ABSTRACT

ABDI SUKAMTO. Modeling of lnfected Diseases with Latent and Relapse Supervised by PAIAN SIANTURI and ALI KUSNANTO.

ABDI SUKAMTO. Model Penyakit Menular dengan Periode Latent dan Relapse. Dibimbing oleh PAIAN SIANTURI dan ALI KUSNANTO.

Seseorang yang terinfeksi oleh penyakit menular, berarti kuman tersebut berada di dalam tubuh dalam bentuk tidak aktif sampai jangka waktu tertentu, ha1 ini dikarenakan sistem kekebalan tubuh mampu mengontrol kurnan tersebut. Dengan melakukan pengobatan, maka orang tersebut mungkin akan sembuh. Pengobatan yang tidak sempurna mungkin akan mengakibatkan kambuhnya kembali penyakit tersebut.

Dalam tulisan ini akan dikaji jenis penyakit yang bersifat relapse, yaitu peristiwa karnbuh kembali setelah sembuh dan memiliii periode latent, yaitu masa bersembunyinya penyakit tersebut di dalam tubuh ketika sistem kekebalan tubuh dalam kondisi baik. Penelitian sebelumnya telah dilakukan oleh Driessehe dan Zou (2007) untuk mengkaji model relapse pada penyakit infeksi, dan Feng et al. (1999) membuat aturan periode latent pada model matematika untuk TBC. Disini pemodelan terhadap penyebaran penyakit yang bersifat latent dan relapse dipelajari. Salah satu penyakit yang memiliki ciri-~iri latent dan relapse adalah tuberculosis (TBC).

Pemodelan penyakit menular ini dilakukan untuk melihat dinarnika masing-masing populasi yaitu populasi rentan, populasi menular dan populasi sembuh. Selain itu model asumsi juga diterapkan gum membandmgkan terhadap model asli dengan cara malakukan analisis kestabilan dengan menggunakan metode Routh-Hurwitz dan menguji teori tersebut melalui simulasi dengan menggunakan software computer Mathematica 7.0.

Hasil simulasi yang telah dilakukan terhadap ketiga model yaitu model asli, model asumsi eksponensial negatif, dan asumsi fungsi tangga diperoleh dua titik tetap yaitu : P(S,I,R) = (l,O,O) dan P'(s',I*,R') dengan S* adalah proporsi manusia rentan, I* proporsi manusia menular, dan R' proporsi manusia sembuh. Analisis kestabilan titik tetap tersebut bergantung pada nilai

R,,

,

dengan

4

adalah bilangan reproduksi dasar. Jika

R,,

c

1, maka titik tetap bebas penyakit

P bersifat stabil sedangkan pada titik tetap endemik~' bersifat stabil jika

R,,

> l .

bilangan reproduksi maka semaki cepat masing-masing populasi untuk mencapai kestabilannya.

O

Hak Cipta milik Institut Pertanian Bogor, tahun 2009

Hak Cipta dilindungi undang-undang

I . Dilarang mengutip sebagian atair seltmih hasil kalya tttlis ini tanpa mencantumkan atair menyebiitkan suniber.

a. Penprtipan hanya tintuk kepentingan pendidikan, penelitian, penzilisan kalya ilmiah, penyustinan laporan, penulisan kritik, atatr tiizjauan stratu masalah

b. Pengzitipan tidak menigikan kepentingan yang wajar Institzrt Pertanian Bogor.

MODEL PENYAKIT MENULAR DENGAN PERIODE LATENT

DAN RELAPSE

ABDl SUKAMTO

Tesis

Sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOEAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

Judul Tesis : Model Penyakit Menular Dengan Periode Latent dan Relapse

Nama : Abdi Sukamto

NRP : G551070261

Program Studi : Matematika Terapan

Disetujui, Koinisi Pembimbing

Dr. Paian Sianturi Ketua

Drs.Ali Kusnanto M.Si Anggota

Diketahui

Ketua Program Studi olah Pasca Sarjana IPB

Matematika Terapan

&i-

Dr.Ir.Endar.H.Nugrahani,MS

I

airil A. Notodiputro, M.S.

PRAKATA

Puji dan syukur kepada Allah SWT yang telah memberikan karuniaNya sehingga telah dapat menyelesaikan karya tulis ini. Judul yang saya teliti adalah :

Model Penyakit Menular dengan Periode Latent dan Relapse yang telah saya pilih dalam penelitian ini sejak bulan Desember 2009.

Terima kasili penulis ucapkan kepada Bapak Dr. Paian Sianturi dan Bapak Drs. Ali Kusnanto M.Si selaku pembimbing yang telah banyak membimbing dan mengarahkan serta Bapak Drs. Siswandi, M.Si selaku penguji yang telah banyak memberikan saran. Ungkapan terima kasih juga penulis sampaikan kepada Departemen Agama Republik Indonesia terhadap beasiswa yang diberikan dan kepada rekan-rekan mahasiswa yang telah memberikan motivasi dan sarannya. Semoga Allah memberikan balasan yang lebih baik bagi kita semua.

Terzkhir kepada abang, kakak, serta istri dan anak-anak yang tercinta yang bersedia melepaskan kepergian saya dengan penuh keyakinan dan kesabaran dalam kerangka menuntut ilmu pengetahuan.

Semoga karya ilmiah ini bermanfaat.

RIWAYAT

HIDUP

Penulis dilahirkan di Pangkalan Berandan pada tanggal 23 Maret 1969 dari ayah Salijo dan ibu Painem. Penulis merupakan putra kesebelas dari dua belas bersaudara.

Tahun I990 penulis lulus dari SMU Muhammadiyah-4 Pangkalan Berandan Sumatera Utara dan pada tahun yang sama lulus seleksi masuk I A N Medan melalui seleksi masuk IAIN. Penulis memilih jurusan Tadris Matematika Fahltas Tarbiyah. Kesempatan untuk melanjutkan program magister pada program studi Matematika Terapan dan pada perguruan tinggi IPB diperoleh pada tahun 2009.

DAFTAR IS1

Halaman

. .

DAFTAR TABEL

...

XII

. .

.

DAFTAR GAMBAR

...

xi11 DAFTAR LAMPIRAN

... ... ... ...,. .

...

...

,

. .... ... .. .. . ... ..

.... ... .

.xiv

I PENDAHULUAN

1.1 Latar Belakang

...

1

.

.

1.2 Tujuan Penelltian

...

2 1.3 Metode

...

2

I1 TINJAUAN PUSTAKA

2.1 Sistem Persamaan Diferensial

...

3 2.2 Titik Tetap

...

4 2.3 Bilangan Reproduksi Dasar

(&

)

...

7 I11 MODEL MATEMATIKA

3.1 Model Matematika

...

8

3.1.1 Asumsi Peluang Tetap Tinggal di Kelas Exposed Menyebar Eksponensial Negatif

...

10 3.1.2 Asumsi Peluang Tetap Tinggal di Kelas Exposed Merupakan

Fungsi Tangga

...

1 1 IV HASIL DAN PEMBAHASAN

. .

4.1 Penentuan Titik Tetap

...

12

.

,

4.2 Analisis Kestabilan

...

14 4.2.1 Perilaku di Sekitar Titik Tetap

P

(1,0,O) pada Model Asli

...

14 4.2.2 Perilaku di Sekitar Titik Tetap

P'

(s*, I ' , R')

pada Model Asli.

...

15 4.2.3 Perilaku di Sekitar Titik Tetap

P'

(s*,

I*,

R') dengan Asumsi

Eksponensial Negatif

...

16 4.2.4 Perilaku di sekitar Titik Tetap

P*

(S'

,

I * , R' ) dengan Asumsi

Fungsi Tangga

...

.

....

. . ... ....

...

...

...

...

... ...

... ..

I8 4.3 Simulasi Model

...

... .

....

.

..

...

...

...

...

.

....

... .

...

..

...

...

..

19

V SIMPULAN DAN SARAN

5.1 Simpulan

...

30

5.2 Saran

...

30

DAFTAR PUSTAKA

...

31

DAFTAR TABEL

Halaman

1

.

Perbandingan titik tetap antara model asli dengan model asurnsi

sebagai fungsi eksponensial negatif dan fungsi tangga

...

13

2 Perbandingan ketiga titik tetap bebas penyakit dan bilangan Reproduksi

...

'26

3 Perbandingan ketiga titik tetap endemik dan bila~gan reproduksi

...

26

4 Hubungan antara model asli dengan parameter

...

58

5 Hubungan antara model eksponensial negatif dengan parameter

...

59

6 Hubungan antara model fungsi tangga dengan parameter

...

60

DAFTAR GAMBAR

Halaman

1 Diagram flow untuk model SEIRI

...

8 2 Proporsi populasi rentan (5'). menular

(4.

dan sembuh (R) dari model

asli dengan titik tetap bebas penyakit (DFE) untuk Ro = 0.25

...

20 3 Tipe kestabilan titik tetap bebas penyakit (DFE) dari model asli

...

21 4 Proporsi populasi rentan

(9.

menular

(4.

dan sembuh (R) dari model

asli dengan titik tetap endemik (EE) untuk Ro = 1.37

...

21 5 Tipe kestabilan titik tetap endemik (EE) dari model asli

...

22 6 Proporsi populasi rentan (S). menular

(4.

dan sembuh (R) dari model

Asumsi eksponensial negatif dengan titik tetap bebas penyakit (DFE)

Untuk Ro = 0.48

...

22

7 Tipe kestabilan DFE dari model ssumsi eksponensial negatif

...

23 8 Proporsi populasi rentan (S). menular

(4.

dan sembuh (R) dari model

Asumsi eksponensial negatif dengan EE untuk Ro = 2.89

...

23 9 Tipe kestabilan EE dari model asumsi eksponensial negatif

...

24 10 Proporsi populasi rentan (S). menular (I). dan sembuh ( R ) dari model

Asumsi fungsi tangga dengan DFE untuk Ro = 0.55

...

24

11 Tipe kestabilan DFE dari model asumsi fungsi tangga

...

25 12 Proporsi populasi rentan (S). menular

(4.

dan sembuh (R) dari model

Asumsi fungsi tangga dengan EE untuk Ro = 3.04

...

25 13 Tipe kestabilan EE dengan asumsi hngsi tangga

...

26 14 Plot gabungan Proporsi populasi rentan ( S ). proporsi populasi

Menular (I). dan sembuh ( R ) dari titik tetap bebas penyakit

...

27 15 Tipe kestabilan DFE dengan model gabungan

...

27 16 Plot gabungan Proporsi populasi rentan ( S ). proporsi populasi

Menular ( I ) . dan sembuh ( R ) dari titik tetap endemik

...

28 17 Tipe kestabilan EE dengan model gabungan

...

28

DAFTAR LAMPIRAN

Halaman

1 Mencari titik tetap dan bilangan reproduksi dari model asli

...

32

2 Mencari titik tetap dan bilangan reproduksi dari model asumsi eksponensial negative

...

33

3 Mencari titik tetap dan bilangan reproduksi dari model asumsi

...

fungsi tangga 34 4 Menganalisis kestabilan titik tetap bebas penyakit pada model asli

...

35

5 Menganalisis kestabilan titik tetap endemik pada model asli

...

39

6 Menganalisis kestabilan titik tetap endemik pada model asumsi eksponensial negatif

...

41

...

7 Pembuktian mencari r ( t ) pada model asli 44

...

8 Pembuktian mencari E'( t ) pada model asli 46 9 Pembuktian mencari ?( t ) pada asumsi eksponensial negatif

...

47

10 Pembuktian mencari

T(

t ) pada asumsi fungsi tangga

...

48

1 1 Mencari nilai N=l pada persamaan (8)

...

49

12 Program untuk simulasi model asli

...

50

...

13 Program untuk simulasi model asumsi eksponensial negatif 52 14 Program untuk simulasi model asumsi fungsi tangga

...

54

15 Program untuk simulasi model gabungan

...

56

16 Mencari Bilangan reproduksi

...

57

17 Tabel 4 hubungan antara model asli dengan parameter

...

58

18 Tabel 5 hubungan antara model eksponensiai negatif dengan

...

parameter 59 19 Tabel 6 hubungan antara model fungsi tangga dengan parameter

...

60

I PENDAHULUAN

1.1 Latar Belakang

Salah satu permasalahan yang dihadapi di dalam kehidupan sehari-hari adalah menyebarnya suatu penyakit pada suatu rnasyarakat dengan tingkat penyebaran yang lebih cepat dari biaanya. Jenis penyakit tersebut biasanyz digolongkan ke dalam penyakit menular. Hal ini disebabkan oleh kuman ymg dapat berupa virus, bakteri, amuba ataupun jamur. Cara penularannya ada bermacam-macam, salah satu di antaranya melalui kontak langsung antara orang yang sehat dengan si penderita.

Seseorang yang terinfeksi oleh penyakit, berarti kuman berada di dalam tubuh dalam bentuk tidak aktif sampai waktu tertentu, ha1 ini dikarenakan sistem kekebalan tubuh mampu mengontrol kuman tersebut, tetapi jika sistem kekebalan tubuh lemah maka menyebabkan aktifnya kuman tersebut sehingga dapat menularkan kepada orang lain. Dengan melakukan pengobatan, maka seseorang tersebut akan menjadi sembuh. Pada manusia, pengobatan yang tidak sempurna akan mengakibatkan kambuh kembali (Driessche et al. 2007).

1.2 Tujuan Penelitian

1 Mengkaji model penyebaran penyakit menular yang bersifat latent1 exposed dan kemungkinan relapse.

2 Melakukan analisis kestabilan.

3 Mengimplementasikan model dalam pemrograman berbasis fungsional 4 Membandingkan perilaku model asli dan model asumsi.

1.3 Metode

Langkah-langkah yang digunakan dalam metode tersebut adalah :

1 Merekonstruksi model penyebaran penyakit menular yang bersifat

latent /exposed dan kemungkinan relapse.

2

Mengkaji model dengan cara menentukan titik tetap serta menganalisis kestabilan di titik tetapnya guna mengetahui perilaku di sekitar titik tetap, dengan inenggunakan kriteria Routh-Hunvitz.

3 Mengkaji model yang menggunakan asumsi, yaitu :

a Peluang tetap tinggal di kelas exposed diasumsikan menyebar secara eksponensial negatif.

11. TINJAUAN PUSTAKA

2.1 Sistem Persamaan Diferensial

Definisi 1 [ Sistem Persamaan Diferensial Linear (SPDL) ]

Jika suatu sistem persamaan diferensial dinyatakan sebagai berikut :

x = A x + b , x ( 0 ) = x 0 , x ~ % " (1)

dengan A adalah matriks koefisien berukuran n x n dan vektor konstan b E W

,

maka sistem tersebut dinamakan SPD linear orde 1 dengan kondisi awal x(0) =no. Sistem ini disebut homogen jika b = 0 , dan non homogen jika b # 0.

[Tu 19941 Definisi 2 [ Sistem Persamaan Diferensial Tak Linear ]

Suatu sistem persamaan diferensial dinyatakan sebagai berikut :

x = f ( t , x ) (2)

dengan

J;(t,xl>x,,...>x,,)

X = ["?';&nf(t,x) =[ ]fhgsi tak linear pada ~.-....,xn. x,, ( t ) ~ , ( ~ > x , , x , , . . . , x " )

Sistem ini disebut sebagai sistem persamaan diferensial tak linear.

[Braun 19831 Defiisi 3 [ Sistem Persamaan Diferensial Mandiri ]

Misalkan suatu sistem persamaan diferensial (SPD) dinyatakan sebagai berikut :

x = f(x), X E % ~ (3)

dengan f merupakan fungsi kontinu bemilai real dari x dan mempunyai tumnan parsial kontinu. Persamaan ini disebut sebagai persamaan diferensial mandiri (autonomous), jika tidak memuat t secara eksplisit di dalarnnya.

Definisi 4 [ Sistem Persamaan Diferensial Delay (DDE) ]

Persamaan diferensial delay dapat ditulis sebagai berikut :

P- dN(t) - f (N(t), N(t - z)),dengan z > 0

.

dt (4)

N(t) adalah total populasi pada waktu t, z adalah delay/ tunda danN(t-z)

merupakan total populasi pada periode exposed.

[ Murray 1989 ]

2.2 Titik Tetap

Defiiisi 5

1

Titik Tetap ]

Diberikan SPD

Titik x' disebut titik tetap jika f (x*) = 0. Titik tetap disebut juga titik kritis atau kesetimbangan.

[Tu 19941

Definisi 6 [ Titik Tetap Stabil]

Misalkan

x

adalah titik tetap sebuah persamaan diferensial dan x(t) adalah solusi dengan kondisi awal x(0) =xo, dimana xo

z

2. Titik

x

dikatakan titik tetap stabil, jika untuk setiap E > 0, terdapat r z 0, sedemikian sehingga

Ino

-XI

<

r

,

maka lx(t)

-xi

< E untuk t > 0.

[ Vershult 19901

Definisi 7 [ Analisis Kestabilan Titik Tetap ]

Analisis kestabilan titik tetap yang berbeda untuk setiap nilai eigen yaitu :

1 Sistem

x

= Ax adalah stabil asimtotik global jika dan hanya jika setiap nilai eigen dari A bagian realnya bernilai negatif.

2 Sistem x = Ax adalah stabil netral jika dan hanya jika setiap nilai eigen dari A mempunyai bagian real yang tidak positif dan sekurang- kurangnya satu nilai eigen mempunyai bagian real nol.

3 Sistem .t = Ax adalah tidak stabil jika dan hanya jika beberapa nilai eigen dari A bagian realnya bernilai positif.

Definisi 8 [ Komunitas Multi-Spesies dan Kriteria Routll-Hurvvitz ]

Suatu model populasi dengank spesies yang berinteraksi dalam komunitas dapat dituliskan dalam bentuk persamaan :

atau dapat ditulis dalam notasi vektor

denganX = (x, ,x,

,...,

x,),

f

= (f;,

f,

,...,

f,) fungsi tak linear pada x, ,x2

,...,

x, Kestabilan sistem tersebut dapat ditentukan dengan urutan sebagai berikut :

1 Menentukan titik tetap ( x ) yang memenuhi f ( x ) = 0

2 Pelinearan dengan menentukan matriks Jacobi pada titik tetap, yaitu :

af

-

J = - ( x ) atau ax

3 Menentukan nilai eigen, dengan menyelesaikandet ( 2 1 - J) = 0 . Nilai eigen(2) ini akan memenuhi persamaan karakteristik berikut :

2" +alln-I +a,/Z"-, +...+ak = O .

Kriteria Routh-Hurwitz

Diberikan persamaan karakteristik :

A"

+

a,An-'

+

a2AnM2

+

...

+

ak =; 0 .

Selanjutnya didefmisikan matriks sebagai berikut :

HI = (a,), H, =

i

i

' 2 1 - m untuk 0 < 21 - m 5 k, Misalkan H, = (h,) dengan h, = 1 untuk 21 = 7n,

0 untuk 21 < Tn atau 21 > k

+

m.

Titik tetap

x

stabil jika dan hanya jika determinan dari semua matriks Routh- Hurwitz bernilai positif, yaitu : det H , > 0

Catatan :

Kriteria Routh-Hurwitz

untuk

k = 2,3,4 disebutkan bahwa titik tetap

;

stabii jika dan hanya jika :

k = 2,3,4

k = 2 , a, >O, a, >O

k = 3 , a,>O, a 3 > 0

,

a,a,>a3

k = 4 , 2 2

a, >0, a, >O , a, >O

,

a,a2a3 > a, +a, a,

pdelstein-Keshet 19881

Detinisi 9 [ Fungsi Eksponensial Negatif ]

Suatu peubah acak kontinu x disebut fungsi eksponensial negatif dengan parameter A > 0, jika fungsi kepekatannya diberikan sebagai berikut :

Ae-*, t

>

0

f

( t ) = F '(t) =

0 , t < O

2.3 Definisi 10 ( Bilangan Reproduksi Dasar (

Ro

))

Bilangan reproduksi dasar ditulis R,, adalah nilai harapan dmi kasus kedua yang dihasilkan pada suatu populasi yang seluruhnya rentan oleh suatu jenis individu yang terinfeksi/ menular. Kondisi yang akan timbul adalah :

1 Jika R, <

1,

berarti setiap individu yang menular akan menginfeksi kurang dari satu individu ham, dan penyakit tidak akan berkembangl punah.

2 r i a & > 1, berarti setiap individu yang menular akan menginfeksi lebih dari satu individu

bam,

dan penyakit tersebut dapat menyerang populasi sehingga menjadi wabah.

I11 MODEL MATEMATIKA

3.1 Model Matematika

Populasi individu dibagi ke dalam empat kelas yaitu: Susceptible (S),

Exposed (E), Infected ( I ) , Recovered (R). Susceptible yaitu populasi yang rentan terhadap penyakit, Exposed/ Laten adalah populasi yang terinfeksi penyakit tetapi tidak menular, Infected adalah populasi yang terinfeksi oleh penyakit dan meaular, serta Recovered adalah populasi yang sembuh dari penyakit tetapi suatu saat mungkin kambuh kembali dan masuk ke kelas Infected.

Misalkan saja ada populasi rentan sebagian di antaranya melakukan kontak dengan populasi menular, maka ketika itu sebagian populasi rentan sudah dikatakan terinfeksi. Saat itu, populasi yang terinfeksi tadi masuk ke dalam kelas E. Populasi yang berada di kelas E akan tetap berada di kelas ini sampai selang waktu tertentu, dan akan berpindah ke kelas I jika sistem kekebalan tubuh lemah. Dengan melakukan proses pengobatan, mungkin populasi tersebut akan sembuh. Kesembuhan ini bisa menjadi sembuh total jika pengobatan berjalan secara sempurna, tetapi mun&n kambuh kembali jika pengobatan tidak sempurna.

Secara skematis, pola penyebaran penyakit dapat digambarkan dalam diagram flow berikut ini :

[image:23.585.54.473.45.809.2]

Laju perubahan S tergantung pada laju kelahirar dan kematian yang diasumsikan sama yakni b. Sebagian populasi yang rentan (S) akan masuk kelompok E, artinya populasi sehat mungkin akan beresiko tertular penyakit. Proporsi ini tergantung nilai

P

(koefisien pemindahan) dan total populasi N.

Banyaknya populasi kelasE tergantung pada laju kematian yakni b. Laju perubahan ini juga dipengaruhi oleh proporsi populasi S yang terkonversi ke kelas

E, serta dipengamhi oleh P(t), yakni peluang individu masih bertahan di kelas E

.

Laju perubahan I tergantung pada laju kematian b, laju kesembuhan y, dan laju kambuh kembali

a,

serta adanya pengamh P(t).

Laju perubahan R tergantung pada laju kematian b. dan dipengaruhi juga dari sebagian populasi I yang sembuh

(3.

Sebagian populasi yang sembuh (R) akan masuk kembali ke kelompok I, artinya sebagian populasi sembuh mungkin akan kanlbuh kembali.

Misalkan bahwa P(t) merupakan peluang populasi E masih tetap tinggal di kelas exposed pada waktu t. Nilai P(t) memenuhi sifat berikut ini :

P :[O,m)+[ 0,l ] adalah tidak naik, kontinu sepotong-sepotong dengan keterbatasan dan banyak loncatan serta memenuhi P(O')=l, limP(t)=O dengan

I-+m

m

I ~ ( u ) d z t positif dan terbatas,

0

Dari penjelasan diagram, diperoleh model matematika yang disebut model SEIRI berikut :

I(t)

S '(t) = bN - PS(t) - - bS(t)

N

dengan N = S(t)

+

E(t)

+

I(t)

+

R(t)

rentan terhadap penyakit, E ( t ) populasi yang terinfeksi oleh penyakit, I ( t )

populasi yang menular, R(t) populasi yang sembuh dari penyakit, P(t) peluang tetap bertahannya populasi di kelas exposed.

Dengan menggunakan penskalaan yaitu :

persamaan (1) menjadi :

S '(t) = b - PS(t)I(t) - bS(t)

Laju perubahan E(t) dan I(t) diperoleh sebagai turunannya terhadap waktu yakni,

Selanjutnya dirubah menjadi model umum yaitu S , I dan R ditulis :

S'(t) = b - pS(t)I(t) - bS(t)

I yt) = - ~ P S ( ( ) I ( ( ) ~ ~ ~ ( ~ ' ~ , P ( ( ) d ( + a R ( t ) ( y

+

b)I(t) 0

(9)

R '(t) = y I ( t )

-(a

+

b)R(t)

Dalam tulisan ini juga akan ditarnpilkan model lain dengan beberapa asumsi terhadap hngsi tersebut, yaitu :

3.1.1 Asumsi Peluang Tetap Tinggal di Kelas Exposed Menyebar

Eksponensial Negatif

.

S '(t) = b - ,DS(t)I(t) - bS(t)

I'(t) =aR(t)

+

~ ( 1 -S(t) - I(t) -R(t)) -(y +b)I(t) ₍₁₀₎

R '(t) = yI(t) - ( a

+

b)R(t)

Selanjutnya E1(t) = ,DS(t)I(t) - ( E

+

b)E(t) didapat dari persamaan (8)

.

3.1.2 Asumsi Peluang Tetap Tinggal di Kelas Exposed Merupakan Fungsi Tangga

.

Ada dua kondisi yang pertama bahwa kuinan dalam posisi tidak aktif sampai beberapa tahun karena mampu dikontrol oleh sistem kekebalan tubuh dan yang kedua kuman muncul ke pennukaan dari persembunyiannya dikarenakan tubuh dalam kondisi lemah. Hal ini dijelaskankan seperti adanya loncatan, maka dibuatlah asumsi mempakan fungsi tangga yang menggunakan waktu delay/ tundaan. Dengan persamaan :

1 , I E L O , ~ I

P

(

t

) =

{ ,

,

dengan -r adalah waktu delay/ tundaan.

Untuk t ~ [ O , z ]

S'(t) = b - ,BS(t)I(t) - bS(t)

I'(t) =aR(t) - (y

+

b)I(t) R'(t) = yI(t) - ( a

+

b)R(t) E'(t) = ,DS(t)I(t) - bE(t)

Dari model (11) menggambarkan bahwa kuman tersebut masih dalam kondisi bersembunyi dan tidak aktif, karena mampu dikontrol oleh sistem kekebalan tubuh, ha1 ini terlihat dari laju perubahan pada E'(t)danI1(t) tidak adanya tundaan sehingga mengakibatkan populasi tersebut hanya terinfeksi.

Untuk t > r

IV HASIL DAN PEMBAHASAN

4.1 Penentuan Titik Tetap

Untuk menentukan titik tetap pada sistem persamaan diferensial (9) yang

. .

dS d l dR

merupakan model asli, dzpat dican dengan menentukan - = 0,- = 0,- = 0. dt dt dt

Dari hasil analisis didapat dua jenis titik tetap, yaitu titik tetap bebas penyakit

(Disease-free equilibrium-DFE) yang memuat I = 0 dan R = 0 serta titik tetap endemik yang memuat I # 0 dan R

+

0.

Titik tetap tersebut yaitu P ( S , I , R ) = (l,O,O) yang merupakan titik tetap

bebas penyakit, dan P'(s*,I*,R') = b

a + b

merupakan titik tetap endemik dengan n = S ( { ) I ( { ) dan R -

O - P Q

b ( a + y + b )

merupakan bilangan reproduksi dasar (lihat pada lampiran I), deagan

I

Q=-r

~ r n

f

e - b " - S ) d l ~ ( t - { ) d 5 = I - b k E (0,l) adalah bagian yang mempertahan

l+m

0

a + b

kan kelas E, dan adalah rata-rata lamanya kematian setiap individu

b ( a + y + b )

I

di kelas I, serta = lim e-b" ~ ( u ) d z c merupakan rata-rata lamanya individu

I-+=

0

tinggal di kelas E sebelum menular ataupun mati.

Selanjutnya untuk menentukan titik tetap bebas penyakit dan titik tetap endemik berdasarkan asumsi yang ada, didapat yaitu :

Asumsi 1 :

Jika peluang individu yang masuk dan masih bertahan di kelas exposed

( a

+

b)

RO =8(&)(b(a+u+b))

,

u n t u k ~ merupakan parameter dari fungsi

"

eksponensial negatif, dan Q = bagian yang mempertahankan kelas E.

Asumsi 2 :

Jika peluang individu yang masuk d m masih bertahan di kelas E diasumsikan sebagai fungsi tangga, maka dari persamaan (12) didapat yaitu (1,0,0) yang merupakm titik tetap bebas penyakit, dan titik tetap endemiknya yaitu :

denganc=S(t - z)I(t - z), =,Be-h ( a +b)

,

dan Q = e-br, dengan z adalah b ( a + y + b )

periode E (lihat pada lampiran 1).

Secara ringkas, perbandingan titik tetap bebas penyakit dan titik tetap endemik dari model asli dan asumsi yang ada ditampilkan pada tabel berikut ini :

ENDEMIK

P*( s*, I*,R* )

b MODEL ASLI

[image:28.582.29.461.16.804.2]

ASUMSI EKSPONENSlAL NEGATIF

Tabel 1

.

Perbandingan titik tetap antara model asli dengan model asumsi sebagai fungsi eksponensial negatif dan fungsi tangga.

BEBAS PENYAKIT

P ( S , I , R )

( 1 , 0 , 0 )

ASUMSI SEBAGAI

FUNGSI TANGGA

( 1,03 0 )

1 b

(LO, 0 b

Dari tabel di atas dapat diketahui bahwa baik pada model asli maupun pada model yang menggunakan asumsi sebagai fungsi eksponensial negatif dan fbngsi tangga memiliki titik tetap bebas penyakit yang sama, yaitu populasi total hanya terdiri dari individu yang rentan(S), sedangkan individu pada kelas populasi lainnya tidak ada.

4. 2 Analisis Kestabilan

4.2.1 Perilaku di Sekitar Titik Tetap P(l,O,O) pada Model Asli Misalkan sistem persamaan (9) ditulis sebagai berikut :

f ( S , I, R) = b - PS(t)I(t) - bS(t)

Dengan - melakukan pelinearan pada persarnaan (16) dan mensubsitusi titik tetap

(1,0,O) ke persamaan tersebut, diperoleh matriks Jacobi sebagai berikut :

Sistem ini akan stabil jika nilai eigen pada matriks Jacobi bernilai negatif. Dengan menyelesaikan det (11 - J ) = 0 pada persamaan ( l 7 ) , didapat :

/2+b

P

0

0 A+B(/Z)+y+b

-a

0 -Y /2+a+b = O

(/2+b)[(;l+ B(A)+ y+b)(/l+a+b)-ay] = 0 _{( 1 8)}

Dari persamaan ( 1 8) dapat diketahui bahwa A, = -b

.

Untuk mencari

4,

yaitu :

h,(/2):=h2+(a+yt2b);l+b(a+y+b)+(;l+a+b)B(;l)=0 (19)

Ill2 + g l l + b r l = I l l + a + b l l ~ ( l l ) I S 1 l l + a + b / ~ ~

Ill2

+

gll

+

brI2 _<

(PQ)'

Ill

+ a

+

br (20)

Jika pada persamaan (20) dimisalkanll=x

+

yi untuk x 2 0 , dengan mas kiri

F,

( x , y ) serta mas kanan F2 ( x , y) ,inaka didapat :

2

~ , ( x , y ) = 1 ; 1 ~ + g l l + b r / = y 4 + [ 2 x 2 + 2 g x + r 2 + b 2 ] y 2 + [ x 2 +gx+brI2

F,(x,Y)

=(pel2

l(a

+

a

+

b)/2 =(PQ)'[(x

+

(Y

+

b12

+

y2

I

(21)

Dan persamaan (20) dan (21), diketahui bahwa

F,

( x , y ) S F2 ( x , y). Selanjutnya

dengan asumsi bahwa

4

< 1, dan bilangan reproduksi

4

= PQ a + b

b ( a + y + b )

maka didapat PQ = b ( a + y + b )

& <

b ( a + y + b )

.

_{Selanjutnya didapat :}

a + b a + b

(a

+

b)'

4

(x, y ) 2 [((a

+

b)' {2x2

+

2gx

+

r2

+

b2}y2

+

(a

+

b)' (x2

+

gx

+

br)' 2 [br]' y2

+

[brx

+

b(a

+

b)rI2

=[brI2[(x+a+b)'

+

y 2 ] (23)

Jadi hasil pada persamaan (23) ini kontradiksi dengan persamaan (22) di atas. Oleh karena itu berdasarkan asumsi x > 0, maka seharusnya bagian real x

kurang dari no1 ( x < 0). Sehingga DFE Stabil Asimtotik Lokal untuk R,, 1 1 .

4.2.2 Perilaku di Sekitar Titik Tetap P'(s',I*,R') Pada Model Asli

Berdasarkan persarnaan (9) pada titik tetap P', maka diperoleh matriks Jacobi sebagai berikut :

Jika nilai eigen yang diperoleh mempunyai bilangan real negatif, maka solusi terhadap titik tetap akan stabil. Selanjutnya dengan menerapkan

Dengan melakukan proses seperti pada persamaan (18), untuk Ro > 1 didapat :

(;l+npi$ + b ) ( ( , I + ~ ( ; l ) + y + b ) ( A + a + b ) - q ) = 0

(25)

dengan A, =-

(np&

+

b ) < 0

Untuk mencari

4,

dilakukan dengan cara kriteria R o u t h - H d t z , yaitu :

Dengan mengambil nilai-nilai koefisien, didapat : c, = a + 2 b + y + B ( ; 1 ) > 0

Hal ini sangat sesuai dengan criteria Routh-Hurwitz pada landasan teori persamaan (6) sehingga menyebabkan

4,

< 0. Jadi kesimpulannya bahwa titik keseimbangan endemik stabil.

4.2.3 Perilaku di Sekitar Titik Tetap P'(S', I', R') dengan Asumsi Eksponensial Negatif.

Dari persamaan (27) dapat ditulis sebagai :

P

((A

+

b&)(A

+

E

+

y

+

b)(A

+

a

+

b)) - ((A

+

b&)(-y)(& - a)

+

( A + a

+

b)(-)(&)) ₍₂₈₎

&

Dengan menyederhanakan persamaan di atas, didapat :

dengan nilai koefisien yakni :

a, =a+2b+e++y+bR0>O

&'(ba+b2 +yb+yb2 + b 2 A + b 3 ) - p ( a + b )

=

,541

4'

l > O

Sesuai dengan kriteria Routh-Hunvitz bahwa titik tetap akan stabil jika :

a,a2 - a, > 0 pada persamaan : A" +all"1

+

a2;l"-' +...+a, = 0 dengan k = 3

a,a2 -a3 =(a+2b+s+y+b&)[&a+&b+cy+ sb'2-Ep+by+ba+ b2

&

4.2.4 Perilaku di Sekitar Titik Tetap P'(S*, 1', R') dengan Asumsi Fungsi Tangga.

Dengan melakukan pelinearan dan untuk menentukan kestabilan seperti pada persamaan (16) dan (17) didapat :

PS

*

n

+

r

+

b -

ps

*

_{(3 0)}

-Y i l + a + b

Dari persamaan (30) dapat ditulis sebagai :

4(il):=i13 +a,i12 +a2il+a3 +(a4i12 +aSil+a,)e-"' = O _{(3 1)}

Dengan nilai koefisien

a, = r + b ( l + & ) , a , =br(l+&)+02&,a, =b2r&,a4 =-,Be-"~*=-k,r b

a, = - p e - k ~

*

(a

+2b) = -k4(a

+

2b)r,

a,

= -b2r, k, = - < 1 (32) a + b

untuk r = a + y + b

Dengan mengganti il = 0 pada persamaan (31), didapat :

h,(o)=b2r(&-1)>0 (33)

Selanjutnya jika persamaan (31) diganti z = 0, maka didapat :

h,(il) =i13 +(aI +a4)i12 +(a2 +a,)il+a3 +a, ₍₃₄₎

U n t u k c l = a , + a , , c 2 = a 2 + a , , c 3 = a , + a , ,

h,

(il)=i13

+

cl;lZ

+

c2;1

+

c3

.

Sehingga dapat digunakan Kriteria Routh- Hurwitz.

Karena semua pembuat no1 dari h(;l)rnempunyai bagian real negative untuk z = 0, sehingga mengakibatkan persamaan tersebut akan stabil.

Misalkan ;l= io dengan

w

> 0, disubsitusikan ke persamaan (3 1 ) maka

Pada persamaan (35) jika y = w 2 , rnaka akan menjadi :

~ ( Y ) : = Y 3 + q ! Y 2 + ~ 2 Y + 4 ~ = 0 (37)

untuk :

2 2 2 2 2 2

q ! = a ! - 2 a 2 - a 4 , q 2 = a 2 - 2 a p , + 2 a 4 a , - a , , q , = a , - a , ₍₃

8)

Dengan mensubsitusikan persamam (32) ke persamaan (38) akan menghasilkan :

q, = r 2 [ 1 - ( k 4 ) Z ] + b 2 [ 1 + & 2 ] > 0

q2 =((a+ b)2&2 = b2)(k4r)Z f b 4 h 2 > 0 q3 = b4r2

(4'

- 1 ) > 0

Ini mengakibatkan

h,

(y) = 0 tidak mempunyai akar real negatif. Sehingga semua akar dari

h,

( A ) = 0 mempunyai bagian real negatif untuk semua z

>

0 sepanjang _{- . .}

&

>

1 . Sehingga stabil asimtotic global.

4.3 Simulasi Model

Untuk meliiat bagaimana perilaku dari kedua jenis titik tetap perlu dilakukan dinamika tersebut dengan parameter yang sudah diketahui.

4.3.1 Nilai-nilai parameter

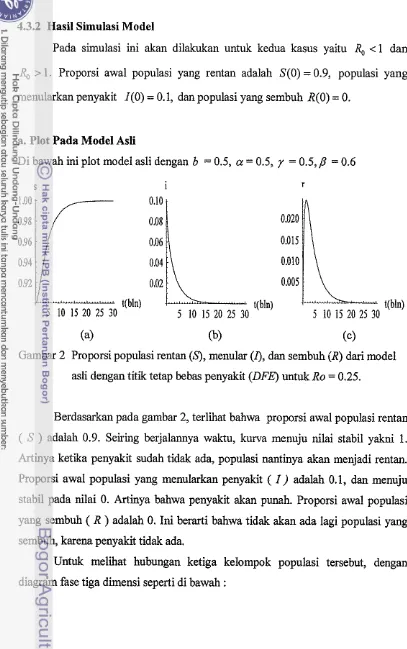
4.3.2 Hasil Simulasi Model

Pada simulasi ini akan dilakukan untuk kedua kasus yaitu

4

< 1 dan

&

> 1. Proporsi awal populasi yang rentan adalah S(0) = 0.9, populasi yang menularkan penyakit I(0) = 0.1, dan populasi yang sembuh R(0) = 0.

a. Plot Pada Model Asli

Di bawah ini plot model asli dengan b = 0.5, a = 0.5, y = 0.5,P = 0.6

S I I

(a) (b) (c)

Gambar 2 Proporsi populasi rentan

(8,

meiiular (I), dan sembuh (R) dari model asli dengan titik tetap bebas penyakit (DICE) untuk Ro = 0.25.

Berdasarkan pada gambar 2, terlihat bahwa proporsi awal populasi rentan

( S ) adaiah 0.9. Seiring berjalamya waktu, kurva menuju nilai stabil yakni 1.

Artiiya ketika penyakit sudah tidak ada, populasi nantinya akan menjadi rentan. Proporsi awal populasi yang menularkan penyakit ( I ) adalah 0.1, dan menuju stabil pada nilai 0. Artinya bahwa penyakit akan punah. Proporsi awal populasi yang sembuh ( R ) adalah 0. Ini berarti bahwa tidak akan ada lagi populasi yang sembuh, karena penyakit tidak ada.

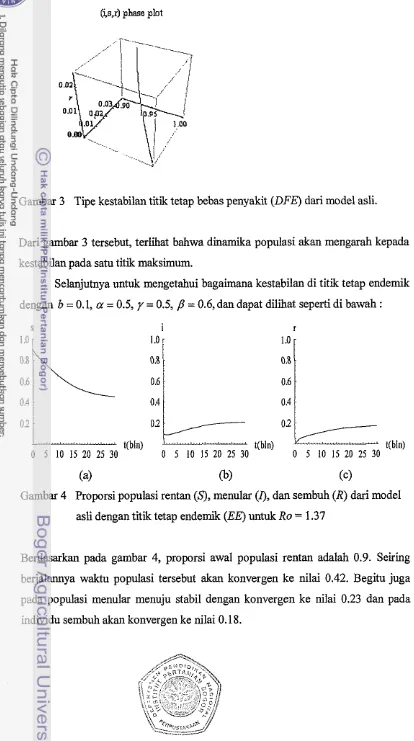
[image:35.577.46.453.35.684.2]

Gambar 3 Tipe kestabilan titik tetap bebas penyakit (DFE) dari model asli.

Dari gambar 3 tersebut, terlihat bahwa dinamika populasi akan mengarah kepada

kestabian pada satu titik maksimum.

Selanjutnya untuk mengetahui bagaimana kestiibilan di titik tetap endemik dengan b = 0. I,

a

= 0.5, y = 0.5, ,5 = 0.6, dan dapat diiihat seperti di bawah : [image:36.582.48.462.50.791.2]

(a> (b) (c)

Gambar 4 Proporsi populasi rentan

(9,

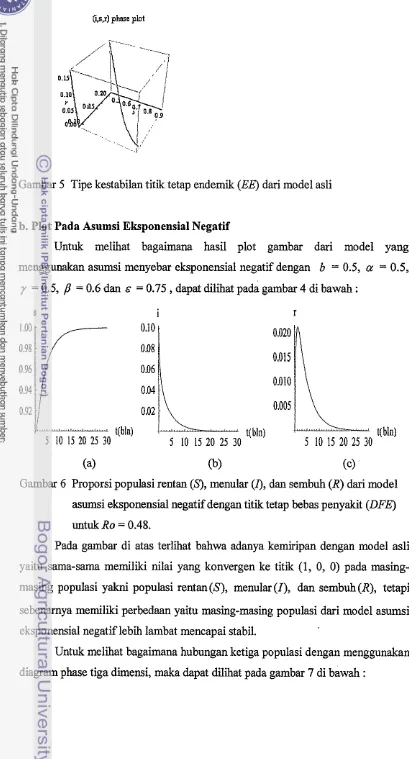
menular (I), dan sembuh (R) dari model asli dengan titii tetap endemik (EE) untuk Ro = 1.37

Gambar 5 Tipe kestabilan titik tetap endemik (BE) dari model asli

b. Plot Pada Asumsi Eksponeusial Negatif

Untuk inelihat bagaimana hasil plot gambar dari model yang menggunakan asumsi menyebar eksponensial negatif dengan b = 0.5,

a

= 0.5,

y = 0.5,

p

= 0.6 dan E = 0.75

,

dapat dilihat gambar

4

di bawah :

S I r

[image:37.577.47.456.42.801.2]

(a)

Cb)

(4

Gambar 6 Proporsi populasi rentan

(8,

menular (I), dan sembuh (R) dari model asumsi eksponensial negatifdengan titik tetap bebas penyakit (DFE) untuk Ro = 0.48.

Pada gambar di atas terlihat bahwa adanya kemiripan dengan model asli yaitu sama-sama memiliki nilai yang konvergen ke titik (1, 0, 0) pada masing- masing populasi yakni populasi rentan@), menular ( I ) , dan sembuh (R), tetapi sebenamya memiliki perbedaan yaitu masing-masing populasi dari model asumsi eksponensial negatiflebi lambat mencapai stabil.

Gambar 7 Tipe kestabilan DFE dari model asumsi eksponensial negatif

Untuk melihat hasil plot titik tetap endemik pada model asumsi eksponensial negatif dengan E = 0.75, b = 0.1,

a

= 0.5, y = 0.5, ,D = 0.6, dapat dilihat pada gawbar di bawah :

(a) ( b ) (c)

Gambar 8 Proporsi populasi rentan (S), menular (I), dan sembuh (R) dari model asumsi eksponensial negatif dengan EE untuk Ro = 2.89.

[image:38.585.45.464.44.798.2]

Gambar 9 Tipe kestabilan EE dari model asumsi eksponensial negatif.

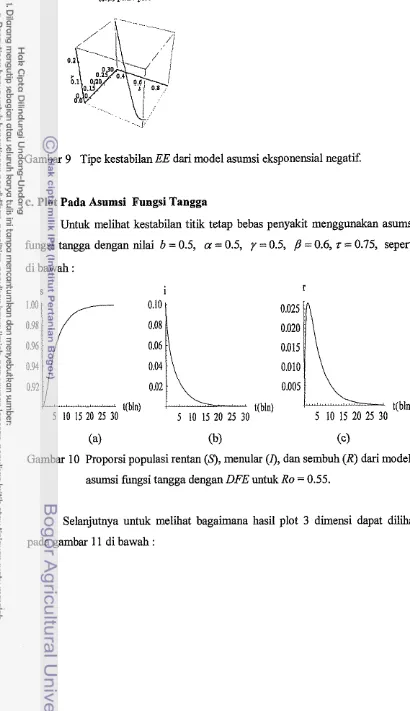
c.

Plot Pada Asumsi Fungsi Tangga

Untuk melihat kestabilan titik tetap bebas penyakit menggunakan asumsi fungsi tangga dengan nilai b = 0.5, a = 0.5, y = 0.5,

P

= 0.6, 2 = 0.75, seperti

(a)

Co)

(c)

Gambar 10 Proporsi populasi rentan

(9,

menular (I), dan sembuh (R) dari model asumsi fungsi tangga dengan DFE untuk Ro = 0.55. [image:39.585.41.451.62.773.2]

[image:40.577.36.467.36.816.2]

Gambar 11 Tipe kestabilan DFE dari model asumsi h g s i tangga.

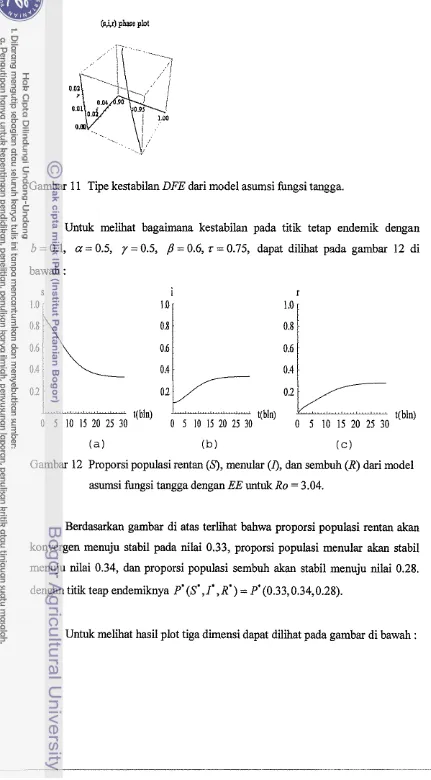
Untuk meliiat bagaimana kestabilan pada titik tetap endemik dengan b=0.1, a=0.5, y=0.5, /J=0.6,r=0.75, dapat dilihat pada gambar 12 di bawah :

Gambar 12 Proprsi populasi rentan

(9,

menular (I), dan sembuh (R) dari model asumsi fungsi tangga dengan EE untuk Ro = 3.04.

Berdawkan gambar di atas terlihat bahwa proporsi populasi rentan akan konvergen menuju stabil pada nilai 0.33, proporsi populasi menular akan stabil menuju nilai 0.34, dan proporsi populasi sembuh akan stabil menuju nilai 0.28. dengan titik teap endemiknya P'(s*, I * , R') =

P*

(0.33,0.34,0.28).

Gambar 13 Tipe kestabilan EE dengan asurnsi fungsi tangga.

Dari hasil simulasi pada ketiga model di atas, didapat perbandingan terhadap titik tetap dan bilangan reproduksi yaitu :

a. Titik Tetap Bebas Penyakit ( DFE )

Tabel 2 Perbandingan ketiga titik tetap bebas penyakit dan bilangan reproduksi.

b. Titik Tetap Endemik ( EE ) No

1 2 3

Tabel 3 Perbandingan ketiga titik tetap endemik dan bilangan reproduksi. Model Asli Eksponensial Negatif Fungsi Tangga No 1

2

3 Model Asli Eksponensial Negatif Fungsi Tangga Bilangan Reproduksi (

%)

0.25 0.48 0.55 Titik Tetap Bebas Penyakit

S*

1

1 1

Bilangan Reproduksi ( R,, )

1.37 2.89 3.04 Titik Tetap Endemik

I* 0 0 0 S* 0.42 0.35 0.33 R* 0 0 0 I* 0.23 0.3 1

0.34

[image:41.577.40.457.33.803.2]

Dari tabel 2 dan 3 di atas diketahui bahwa semakin tinggi bilangan reproduksi maka semakin cepat pula mencapai kestabilannya.

Untuk melihat hasil plot gabungan dari ketiga titik tetap seperti dibawah :

s i

r

I .OO 0.10 0.025

0.98 0.08 0.020

0.96 0.06 0.015

0.94 0.04 0010

0.92 0.02 0.005

tidin1

t

din.

t Ulnl [image:42.577.25.448.21.771.2]

5 10 15 20 25 30 5 10 15 20 25 30 5 10 15 20 25 30 Gambar 14 Plot gabungan proporsi populasi rentan ( S ) , proporsi populasi

menular ( I ), dan sembuh ( R ) dari titik tetap bebas penyakit.

Untuk melihat hasil plot tiga dimensi dapat dilihat pada gambar di bawah :

Untuk melihat bagaimana kestabilan titik tetap endemik dapat dilihat sebagai berikut :

Gambar 16 Plot gab~mgan proporsi populasi rentan ( S ), proporsi populasi menular ( I ), dan sembuh ( R ) dari titik tetap endemik.

= Asumsi Eksponensial Negatif

Untuk melihat hasil plot gabungan dari ketiga titik tetap endemik seperti dibawah

(js,r) phase plot

[image:43.577.37.460.0.815.2]

V

SIMPULAN

DAN

SARAN

Berdasarkan hasil pembahasan, dapat disimpulkan bahwa hasil analisis yang telah dilakukan terhadap model asli dan asurnsi terhadap model penyakit dengan periode latent dan relupe diperoleh dua titik tetap yaitu P(S, I, R) = (1,0,0) dan P'(S', I., R')

.

Analisis kestabilan titik tetap tersebut bergantung pada nilai

4 ,

yakni bilangan reproduksi dasar. J'ia

4

<

1, rnaka titik tetap P bersifat stabil. Pada titik tetap P' bersifat stabil jika

4

> 1

Selanjutnya dari hasil simulasi untuk kasus

4

>

1, diperoleh informasi tentang pengaruh kelahii-an(b), koefisien pemindahan(P), infeksi kembali penyakit tersebut(a), dan laju kesembuhan(y) sebagai berikut :

1 Semakin besar tingkat kelahiran maka proporsi populasi rentan semakin banyaklmeningkat, sedangkan proporsi populasi menular dan sembuh akan semakin berkurang

.

2 Semakin besar tingkat kontakkoefisien pemindahm maka proporsi populasi rentan semakin berkurang, sedangkan proporsi populasi menular dan sembuh semakin meningkat.

3 Semakin besar tingkat kambuh kembali maka proporsi populasi rentan akan semakii berkurang dan proporsi menular dan sembuh akan semakin meningkat.

4 Semakii besar faktor kesembuhan maka proporsi populasi rentan akan semakin meningkat dan proporsi populasi menular dan sembuh akan semakii berkurang.

5 Semakin besar bilangan reproduksi maka masing-masing populasi semakin cepat mencapai kestabilannya.

5.2 Saran

Dalam penulisan thesis ini pengamh obat dan vaksinasi diabaikan karena

DAFTAR PUSTAKA

Borelli RL, Coleman CS. 1998. Dzfferential Equations. USA: John Wiley and Sons, Inc.

Braun M. 1983. D~fferential Equations and Their Applications. New York :

Springer-Verlag.

Driessche PVD, Watmough J. 2005. Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartemental Models of Disease Transmission. Math. Biosci : 1-21.

Driessche PVD, Wang L, Zou X. 2007. Modeling Diseases with Latency and Relapse. Mathematical Biosciences and Engineering 4: 205-219.

Driessche PVD, Zou X. 2007. Modelmg Relapse in Infectious Diseases. Mathematical Biosciences 207: 89-103.

Edelstein-Keshet L. 1988. Mathematical Models in Biology. New York: Random House.

Feng Z, Castilo-Chavez C, Huang W. 1999. On the Role Variable Latent Periods in Mathematical Models for TB. IMA Preprint Series 1612: 1-23.

Ghahramani S. 2005. Fundamentals of Probability with Stochastic Prochesses. America: Pearson Education.

Murray JD. 1989. Mathematical Biology. New York: Springer-Verlag.

Tu PNV. 1994. Dynamical Systems. An Introduction with Applications in Economics and Biology. New York: Springer-Verlag.

Lampiran ( 1 ) Mencari Titik Tetap dan Bilangan Reproduksi dari Model Asli

Dari persamaan (9) pada model asli diketahui :

Untuk mencari titik tetap dari model tersebut dapat dilakukan dengan cara menyelesaikan S1(r) = 0

,

I '(t) = 0

,

Rt(t) = 0

.

Sehingga persamaan di atas menjadi :

I

dengan w = - / ~ ~ ( < ) l ( { ) e - * " - " d , ~ ( t - <)d<.

0

Selanjutnya dengan melakukan pemfaktoran yakni :

..

Untuk mencari titik tetap dari persamaan (9) dengan cara :

T,:S+O,I=O,R=O,

b b

(--/?I-b)=O+-=b+S=l.

S S

Sehingga didapat titik tetap bebas penyakit yaitu : T,(l,O,O)

Untuk mencari titik tetap endemik dari persamaan (9) yaitu :

T,:S+O,I+O,R+O,

b

w

a R Y I

(--PI-b)=O,(-+--(y+b))=O, (--(a+b))=O

S I I R

Dengan mensubsitusikan R ke I pada persamaan (1.5) didapat :

w ( a

+

b) I

I =

b ( a + y + b ) dengan w = - ₀ [,B~({)l({)e-~"-"d, ~ ( t - { ) d { . Misalkann = S({)I(<)pada persamaan (1.6), sehingga didapat :

a + b I = S({)I({)Ro = nRo dengan Ro = PQ

b ( a + y + b ) '

Selanjutnya dengan mensubsitusi persamaan (1.5) dan (1.6) didapat :

R =- yn Ro, ( a + 6 ) dan S = b

n ~ ~ o + b '

Jadi titik tetap endemik yaitu : T2( b

,

nRo, -

npRo

+

b

(a

yn _{+ b)} Ro).

Lampiran (2) Mencari Titik Tetap dan Bilangan Reproduksi Model Asumsi Eksponensiai Negatif.

Dari persamaan (10) pada model asli dietahui :

Untuk mencari titik tetap dari sestem persamaan (13) dapat diakukan dengan cara yang sama seperti persamaan (8), selanjutnya didapat :

Dengan mensubsitusikan S ke E dan R ke I pada persamaan (1.8) akan didapat :

I = bE(&

+

b )

P(b - EE - bE) (1.9)

I = &E(a

+

b ) ( a b

+

yb

+

b Z )

Dengan mensubsitusi kedua persamaan (1.9) dan (1.10) didapat :

E = P ~ b ( a

+

b )

-

b ( ~

+

b)(ab

+

yb

+

b 2 ) (1.11) /?&(a

+

b ) ( ~

+

b )

Mensubsitusi persamaan (1 .I 1) ke (1 .lo) akan mendapatkan :

b E

I* = -

(4

-

1)

dengan

4

=

P

Selanjutnya dengan mensubsitusi persamaan(l.12) ke S dan ke R pada persamaan (1.8) didapat :

1

S =-dm R * = yb

(4

- 1). Sehingga didapat titik endemik yaitu :

Ro

P ( a + b)

Lampiran (3) Mencari Titik Tetap dan Bilangan Reproduksi dari Model

Asumsi Fungsi Tangga.

Diketahui persamaan (1 1) dan (12) dari model asli yaitu :

a.Untuk t E [O,z]

S1(t) = b - pS(t)I(t)

-

bS(t) I '(t) = aR(t) - (y

+

b)I(t) R '(t) = yZ(t) - (a

+

b)R(t) E '(t) = pS(t)I(t) - bE(t)

Untuk mencari titik tetap pada persamaan (1.13) dan (1.14) dapat dilakukan seperti persamaan (1.2) yakni :

Dengan mernisallcan m = e - b r ~ ( t - z)I(t - z), didapat :

I* = eRo,dengan e=S(t - r ) I ( t - z). dengan

4

=,Be-h ( a + b)

.

(1.17) b ( a + y + b )

Selanjutnya dengan mensubsitusi persamaan ( 1 .l7) ke S dan ke R didapat :

* - b

S = dan R* =- ye Ro,dengan c=S(t - r ) l ( t - 7).

( b

+

,mi, a + b

Sehingga didapat titik tetap endemik yaitu : b

,

cRo, - R o ) a + b

Lampiran (4)

MENGANALISIS I(ESTAB1LAN TITIK TETAP BEBAS PENYAKIT PADA MODEL ASLI.

Titik Keseimbangan Bebas Penyakit IDiseade Free Equilibriurn(DFE) dengan

( 1

,o,o

Misalkan sistem pada (2.1) dirubah menjadi :

f (&',I) = b - pS(t)I(t) - bS(t)

I

f

(S,I,R) = - ~ ~ ~ ( { ) l ( { ) e - ~ " - " d t ~ ( t -5)d{ +aR(t) -( y +b)I(t)

0

(2.2)

f

(I$) = yI(t) - (a

+

b)R(t)

Untuk titik keseimbangan di ( S,I,R ) = (l,O,O),diperoleh matriks Jacobian dari persamaan (2.3).

-P

J =

iL

0 -(B(A)+(y

+

b))

Y

-(a

+

b)

Sehingga diperoleh sistem linear

dengan menentukan determinan, dapat ditulis seperti :

Dimana B ( 1 ) = limj,De-(b+z)(1-6)dt ~ ( t - nd< untuk ( A

+

b)h, ( A ) = 0 ,+m

0

h , ( A ) : = ( A + B ( A ) + y + b ) ( A + a + b ) - a y

,I2 +aa+ba+aB(a)+aB(a)+bB(/Z)+ya+ay+by+bA+ba+b2 - a y

l 2 + a A + y3. +bA+ bA+ b a

+

by +b2 +AB(;l) + a B ( A ) + bB(/Z)

A 2 + ( a + y + 2 b ) A + b ( a + y + b ) + ( / Z + a + b ) ~ ( ; 1 )

Karena hl(?) = 0, sehingga dapat ditulis seperti :

b,(/2):=A2 + ( a + y + 2 b ) / l i b ( a + y + b ) + ( A + a + b ) B ( A ) = O ;t2 +(a+y+2b);l+b(a+y+b)=-(A+a+b)B(A)

karena x 2 0

maka1;12+(a+y+2b)~+b(a+y+b)l=1;1+a+bll~(~)I$1/2+a+bl~~

1;12+(a+y+2b);l+b(a+y+b)12 < ( p ~ ) ~ I ~ + a + b l ~

Misalkan di ruas kiri F,(x,y) dan ruas kanan Fz(x) m a k a 4 ( x 7 y ) < F , ( x , y )

Misalkan ? = x

+

iy , maka

/ x 2 + 2 x y i - y 2 +(a+y+2b)(x)+(a+y+2b)(iy)+b(a+y+b)12

dengan melakukan penyederhanaan didapht F,(x,y) =

Dari

rumus bilangan reproduksi Ro = ,BQ a + b untuk Ro < 1, sehingga

b(a+y+b)

PQ

di dapat :

a + b Ro =

pQ

b ( a + y + b ) b ( a + y + b )

PQ

= RO

a + b

b ( a + y + b ) b ( a + y + b )

PQ=

a + b Ro < a + b

Oleh karena itu :

( c ~ + b ) ~ E ; ( x , y ) ~ ( a + b ) ~ F ~ ( x , y ) < [ b ( a + y + b ) ] ~ [ ( x + a + b ) ~ + y ~ ] ( a + b ) 2 1 ; ; ( x > ~ )

2

[(a

+

b)' (2x2

+

2(a

+

y

+

2b)x

+

(a

+

y

+

b)2

+

b2)ly2

+[(a

+

b)(x2

+

(a+y+2b)x+b(a+y+b))l2

2 [b(a

+

y

+

b)12 y2 +[(a

+

b)(a

+

y

+

2b)x

+

b(a

+

b)(a

+

y

+

b)12 2 [ b ( a + y+b)12y2 +[b(a+y+b)x+b(a+b)(a+y+b)12 = [ b ( a + y + b ) ~ ~ [ ( x + a + b ) ~ + y 2 ]

Lampiran (5)

MENGANALISIS KESTABILAN TITIK TETAP ENDEMIK PADA MODEL ASLI

Untuk menganalisis kestabilannya maka dapat dilakukan dari model persamaan ketiga(9) seperti di bawah :

dengan titik keseimbangan endemik yaitu :

Selanjutnya dapat ditulis seperti di bawah :

dan dilakukan proses pelinearan sebagai berikut :

f ( S , I) = b - pS(t)I(t) - bS(t)

f (S,I,R) = -j/3~({)I(()e-~('-<)dtP(t -{)d{+aR(t)-(y +b)I(t)

O

f

(123

=

YW)

-

(a

+b)R(t)

I

a ( - J p s ( ( ) ~ ( t ) e - ~ ( ' - ~ j d t p ( t - ( ) d t

+

a ~ ( t ) - ( y

+

b)r(t))

af

( S > I , R ) - - 0

dl dI

= -B(z) - ( y

+

b) = -(B(z)

+

(y

+

b))

bP

npRo+b 0

det 0 A+B(;l)+y+b -a =O 0 -Y A + a + b

\ 1

dari persamaan (3.4) di atas didapat penyederhanaan yaitu

(A+np&+b)((A+B(;l)+y+b)(A+a+b)-ay)=O

dengan

4

= -(np&

+

b)

.

Untuk mencari

4,

seperti di bawah :

h , ( A ) : = ( ( A + B ( A ) + y + b ) ( ; l + a + b ) - q ) = 0

;lZ

+

a A

+

b;l

+

AB(A)

+

aB(;l)

+

bB(A)

+

y;l

+

ya

+

yb+b;l+ba+bZ -ay=O

; 1 2 + ( a + 2 b + ~ ( ; l ) + y ) ; l + a ~ ( A ) + b B ( ; l ) + y b + b a + b Z =O

Sesuai dengan kriteria Routh-Hurwitz didapat masing-masing koefisien bernilai lebih besar dari nol, yaitu :

c, = a + 2 b + y + B ( A ) > O

c, =aB(;l)+bB(A)+yb+ba+b2 >O

Lampiran ( 6 )

Menganalisis Kestabilan Titik Tetap Endemik pada Model Asumsi Ekesponensial Negatif . -

Titik Keseimbangan Endemik yaitu :

Untuk menganalisis kestabilannya dapat dilakukan dari model persamaan (10)

seperti di bawah :

S '(t) = b - pS(t)Z(t)

-

bS(t)

Z'(t) = aR(t)

+

~ ( 1 - S(t) - Z(t) - R(t)) - (y

+

b)Z(t) R '(t) = yZ(t) - ( a

+

b)R(t)

Sistem persamaan d5ensial pada persamaan (4.2) dapat ditulis menjadi :

f ( S , I) = b - pS(t)Z(t) - bS(t)

f ( S , I, R) = a R ( t )

+

~ ( 1 - S(t) - Z(t) - R it)) - ( y

+

b)Z(t) _(4.3)

f

( 1 3 ) = yI(t) - ( a

+

b)R(f)

af

(s,

I,R) - a ( a R ( t )

+

E - E S ( ~ ) - &I(t) - E R ( ~ ) - ( y

+

b ) ~ ( t ) )

- = a - E

dR dR (4.4)

Dengan mensubsitusi titik P*

(s*,

I*, R*) = P' diperoleh matriks Jacobian yakni :

Sehingga diperoleh sistem linear :

detl

;

A + ( ~ + y + b ) z - a -Y A + ( a + b )

Dengaii melakukan penyederhanaan didapat :

P

( ( A

+

b&)(A

+

F i y

+

b)(A + a

+

b)) - ( ( A

+

bRo)(-?I)(& - a )

+

( A

+

a

+

b)(-)(&))

4

dengan nilai koefisien :

&'(ba+b2 +yb+yb2 +b2;1+b3)-/(a+b)

=%I

%'

I > O

Sesuai dengan kriteria Routh-Hurwitz bahwa titik tetap akan stabil jika :

karena kriteria di atas terpenuhi, maka disimpulkan bahwa titik tetap tersebut stabil asimtotik global dengan 2 1.

Lampiran ( 7 ) pada persamaan 9.

Pembuktian Meneari I'(t) pada Model Asli Jumlah seluruh populasi adalah :

S(t)

+

E(t)

+

I ( t )

+

R(t) = N _(5.1)

Dengan menggunakan penskalaan sehingga didapat N = 1. akibatnya :

S(t)

+

E(t)

+

I ( t )

+

R(t) = 1 _(5.2)

Persamaan (5.2) di atas diturunkan dan menjadi :

S '(t)

+

E '(t) + I '(t)

+

R(t) = 0

Jika mas kiri hanya I'(t ), rnaka persamaan menjadi :

I '(t) = -5' '(t) - E '(t) - R '(t)

-

(s

'(t)

+

E '(t)

+

R '(t)) _(5.3)

1

Buktiian bahwa : 19(t) =- j p ~ ( e ) l ( c ) e - ~ ( ' - ' ) d , ~ ( ~ - < ) d t

+

a R ( t ) - ( y

+

b)I(t)

0

Dengan mensubsitusi S'(t) = b

-

PS(t)I(t) - bS(t) R1(t) = yI(t)-

(a

+

b)R(t)

I

~ ' ( t ) = p s ( t ) ~ ( t )

+

j p s ( { ) ~ ( < ) e - ~ ( ~ - t ) d , ~ ( t - 5 ) d c - b ~ ( t )

0

Lampiran ( 8) pada persamaan (9).

Pembuktian Untuk Mencari E'(t) pada Model Asli Jurnlah seluruh populasi :

S ( t )

+

E(t)

+

I ( t )

+

R(t) = 1

Lampiran ( 9 ) pada persamaan 10

Pembuktian Untuk Mencari I'(t) pada Asumsi Eksponensial Negatif Fungsi Eksponensial Negatif

Dik:

S '(t) = b - /3S(t)I(t) - bS(t)

R '(t) = yI(t) -

(a

+

b)R(t)

E '(t) = ,BS(t)I(t) - ( E

+

b)E(t)

Dit :

I '(t) =

S ( t )

+

E(t)

+

I ( t )

+

R(t) = 1 s y t ) + E ' ( t ) + I ' ( t ) + R y t ) = o I!(?) = -S '(t) - E ' ( t ) - R '(t) I '(t) = - ( S '(t)

+

E '(t)

+

R '(t))

-

( b - pS(t)I(t) - bS(t)

+

PS(t)I(t)

-

( E

+

b)E(t)

+

yI(t)

-(a

+

b ) ~ ( t ) )

- ( b - bS(t) - &E(t) - bE(t)

+

yI(t) -

(a

+

b ) ~ ( t ) )

- ( b - bS(t)- s E ( t ) - bE(t)

+

yI(t) - a R ( t ) - bR(t)

- ( b - &E(t)

+

yI(t) - a R ( t )

-

bR(t) - bS(t) - bE(t))

- (b - &E(t)

+

yI(t) - a R ( t ) - b[R(t)

+

S(t)

+

E(t)])

- ( b - ~ E ( t ) + y I ( t ) - a R ( t ) - b [ l - I @ ) ] )

- (b - cE(t)

+

yI(t) - a R ( t ) - b

+

bI(t))

Lampiran ( 10) pada persamaan 11

Pembuktian Untuk Mencari I'(t) pada Asumsi Fungsi Tangga

Fungsi Tangga untuk t E [O, T] Dik:

S'(t) = b - / S $ ) I ( t ) - bS(t) R1(t) = yI(t)

-

(a

+

b)R(t)

F

'(t) = / S ( t ) I ( t ) - bE(t) Dit :

r

'(t) =

S(t)

+

E(t)

+

I ( t )

+

R(t) =

1

S '(t)

+

E '(t)

+

I '(t)

+

R '(t) = 0 I '(t) = -S '(t) - E '(t) - R '(t)

I '(t) = - ( S '(t)

+

E '(1)

+

R '(t))

-(b - / S ( t ) I ( t ) - bS(t)

+

/S(t)I(t) - bE(t)

+

yI(t) -

(a

+

b ) ~ ( t ) )

- ( b - bS(t)

-

bE(t)

+

yI(t) -

(a

+

b ) ~ ( i ) )

- (b - bS(t) - bE(t)

+

yI(t)

-

a R ( t ) - bR(t))

- (b

+

yI(t) - aR(t)

-

bR(t) - bS(t) - bE(t))

- (b

+

yI(t) - aR(t)

-

b[R(t)

+

S(t)

+

E(t)])

- (b

+

y I(t) - aR(t)

-

b[l - I(t)])

- (b

+

yI(t) - a R ( t )

-

b

+

bI(t))

Fungsi Tangga

untukt > T

Dik :

S'(t) = b - pS(t)I(t) - bS(t)

I y t ) = p e - " ~ ( t -s)I(t - 5 ) +aR(t) -( y + b)I(t) R'(t) = yI(t) - (rr

+

b)R(t)

E'(t) = PS(t)I(t) - ,L?e-b'S(f - r)I(t - T ) - bE(t)

Dit : I'(t) =

S(t) +E(t)

+

I(t)

+

R(t) = 1 S'(t)

+

E'(t) + l ' ( t )

+

R 1 ( f ) = 0 I '(t) = -S'(t) - E'(t) - R '(1) I r ( t ) = -(S'(t)

+

E'(t)

+

R'(t))

-(b-PS(t)l(t) - bS(t) +/?S(t)l(t) -pe-6'S(t - t ) l ( t - t ) -bE(t)

+

yl(t)-(a + b ) ~ ( t ) )

-

( b - bS(t) - bE(t)

+

PS(t)I(t) - pe-brS(t - T ) I ( ~ - t )

+

yI(t) - ( a

+

b ) ~ ( t ) )

-

(b -bS(t) - bE(t) +pS(t)I(t) - ,fXb'S(t -r)l(t - r )

+

yI(t) - aR(t) - bR(t))

-

(b

+

yI(t) - aR(t)

+

,BS(t)l(t) - /3e-"S(t - z)l(t - t ) - bR(t) - bS(t) - bE(t))

- (b

+

y l ( t ) - aR(t)

+

PS(t)I(t) -,Be-b'S(t -r)I(t - T ) - b[R(t) + S ( t ) +E(t)])

- (b

+

TI(!) - aR(t) +PS(t)l(t) - pe-"S(t - r ) l ( t - z) - b[l - l ( t ) ] )

- (b

+

yI(t) - aR(t)

+

PS(t)l(t) - pe-"S(t - t ) I ( t - T ) - b

+

bl(t))

- (yI(t) -aR(t)

+

bI(t)

+

/3S(t)I(t) - pe-*'S(t - r)l(t - T ) )

- yI(t)

+

a R ( t ) - bl(t) - PS(t)l(t)

+

,L?e-b'S(t -z)I(t - T )

=

p

e 4' S(t - r)I(t - T )

+

aR(t) - ( y

+

b)l(t)

Terbukti

Lampiran ( 1 1 )

Mencari N = 1 pada persamaan (8)

s ( t ) E(t) I ( t ) R(t)

N=-+-+-+--+N= S(t)

+

E(t)

+

I ( t )

+

R(t)

Lampiran (12 ) Program Untuk Simulasi Model Asli

Program Titik Tetap Bebas Penynkit (1,0,O) Fungsi Kontinu

Quiet@TableForm[{{TableForm[IIParametricPlot3D[Evaluate [{s[t],i[t],r[t]}/.sol],(t,O,Tfin},PlotPoints-t5OO,Axes Label-t(s,i,r},ImageSize-f2OO,FaceGrids-tAll,AxesEdge+{{l

,O}, {O,O}, {O,O}},ImagePadding*25,BoxRatios+(l,l,l),Box

ed+True,BoxStyle+Directive[0pacity[0.6]],FaceGridsStyl

e+Directive[Opacity [0.005], Darker [Gray, 0.0011 ] ,PlotLab

el+" (i, s,r)phaseplot"l

I }

I, ({Plot [EvaluateLs [tl /.sol], { t, 0, Tfin}

,

PlotRange+AI.l,AxesLabel-t( t, s

1 ,

PlotStyle+Dark

er [Blue, 0.51, ImageSize+1OO,AspectRatio+l]

1,

[Plot [Evalu

ate[i[t]/.sol], {t,O,Tfin},PlotRange+All,AxesLabel+(t,i },PlotStyle-tDarker[Blue,0.5l,ImageSize+lOO,AspectRatio

+I]}, (Plot[Evaluate[r[t]/.sol],{t,0,Tfin},PlotRange~Al

l,AxesLabel+{t,r}, PlotStyle-tDarker [Blue, 0.51, Imagesize

-+lOO,AspectRatio-tll

I } ,

( { ParametricPlot [Evaluate [(s [t]

,

i[t] }/.sol], {t,O,Tfin},AxesLabel+{s,i},PlotStyle+Darke

r [Red, 0.31, ImagePadding+25, PlotRange-tAll, PlotPoints-t20

0, ImageSize-tl50,AspectRatio-tO. 85, PlotLabe1-t" (s, i) phase plot"] 1, (ParametricPlot [Evaluate[(i[tl

,

r[t]

I / .

sol], {t, 0

,Tfin},AxesLabel+{i,r},PlotStyle+Darker[RedrO.3],Image Padding+25,PlotRange+A11,PlotPoints-t2OO,ImageSize+l50, AspectRatio-tO. 85, PlotLabel*" (i, r) phaseplot"] }, ( Paramet ricPlot[Evaluate[{s[tl,r[t] }/.soll,{t,0,T£in},AxesLabel

-t{s,r}, PlotStyle+Darker [Red, 0.31, ImagePadding-t25, PlotR

ange-tA11,PlotPoints+2OO,ImageSize+l5O,AspectRatio+O.85

,

PlotLabel*" ( s , r) phase plot"]

1 ) 1

I], Style ["length of simulation(time) ",Bold], ({Tfin, 30,""}, 1,100, Imagesize* Tiny},Delimiter,Style["parameters",Bold],{(b,O.5},0,1,1

mageSize+Tiny}, {{a, 0.5},0,0.5, ImageSize-tTiny}, ( (/3,0.6}

Program Titik Tetap Endemik Fungsi Kontinu

Manipulate [sol=Quiet@NDSolve [{s

'

[t] =b-fi (s [t] *i [t] ) -b

ar [t]

-

(y+b) i [t]

,

r' [t] =:yi [t]

-

(y+b) r [t]

,

s [O] =a1

,

r 101 ==a3 ,i[O]==a2},{s,i,r},{t,O,Tfin),MaxSteps+o31;

Quiet@TableForm[{{TableForm[{{Pa~ametricPlot3D[Evaluate

[[s[t] ,i[t] ,r[t] }/.sol], W , T f i n } , PlotPoints+5OO,Axes

L a b e l + { s , i , r } , I m a g e S i z e + 2 O O , F a c e G r i d s ~ { { l

,O}, {O,O}, {O,O}},ImagePadding+25,BoxRatios+{l,l,l},Box

ed+True,BoxStyle+Directive[Opacity[O.6]],FaceGridsStyl

e+Directive [Opacity [O. 0051, Darker [Gray, 0.0011 1, PlotLab el+" (i, s, r)phaseplotl'] } I], { {Plot [Evaluate [s [t] /.sol], { t, 0, Tfin}

,

PlotRange+All,AxesLabel+{ t, s 1, PlotStyle+Dark

er [Blue, 0.51, 1mageSize+1OOrAspectRatio+l]

1 ,

{Plot [Evalu

ate[i[t]/.sol], {t,O,Tfin},PlotRange+All,AxesLabel+{t,i

~,PlotStyle+Darker[Blue,0.5],ImageSize+lOO,AspectRatio +l]

1,

{Plot [Evaluate [r [t] / . sol], {t, 0 , T f i A l

l,AxesLabel+{t,r), PlotStyle-tDarker [Blue, 0.51, Imagesize

+lOO,AspectRatio+l] 1 1, { {ParametricPlot [Evaluate [ {s [tl

,

i[t] }/.sol], [t, O,Tfin},AxesLabel+{s,i},PlotStyle+Darke

r[Red,0.3],ImagePadding+25,PlotRange+All,PlotPoints+2O 0, ImageSize+150,AspectRatio+O. 85, PlotLabel+" (s, i)

phaseplot"] } , { ParametricPlot [Evaluate [{i [t]

,

r [t] }/.sol]

,

{t, 0,Tfin) ,AxesLabel+{i, r}, PlotStyle+Darker [Red, 0.31,

ImagePadding+25,PlotRange+A11,PlotPoints+2OO,ImageSize +150,AspectRatio+O. 85, PlotLabel+" (i, r}phaseplot"] 1 , {Pa