METHOD DAN MAXIMUM LIKELIHOOD ESTIMATOR; SUATU TERAPAN DATA PARUH WAKTU DAN DATA SIMULASI SEBAGAI PERBANDINGAN
SKRIPSI
REHDAMENTA S TARIGAN 080803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MOMENTS METHOD DAN MAXIMUM LIKELIHOOD ESTIMATOR; SUATU TERAPAN DATA PARUH WAKTU DAN DATA SIMULASI SEBAGAI
PERBANDINGAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
REHDAMENTA S TARIGAN 080803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Kajian Estimasi Parameter Distribusi Gamma Dengan Penduga Metode Momen dan Penduga Kemungkinan Maksimum; Suatu Terapan Data Paruh Waktu dan Simulasi Sebagai Perbandingan
Kategori : Skripsi
Nama : Rehdamenta S NomorIndukMahasiswa : 080803067
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematikadan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2015
Komisi Pembimbing :
Pembimbing 2, Pembimbing 1,
Dr. Pasukat Sembiring, M.Si
NIP. 19511227198503 1 002 NIP. 1964104199103 1 004
Dr. Open Darnius Sembiring, M.Sc
Disetujui oleh
DepartemenMatematika FMIPA USU Ketua,
NIP. 196209011988031 002
PERNYATAAN
KAJIAN ESTIMASI PARAMETER BERDISTRIBUSI GAMMA DENGAN PENDUGA METODE MOMEN DAN KEMUNGKINAN MAKSIMUM; SUATU TERAPAN DATA PARUH WAKTU DAN SIMULASI SEBAGAI PERBANDINGAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2015
PENGHARGAAN
Puji dan syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa sehingga penulis dapat menyelesaikan skripsi ini.
ABSTRAK
Estimasi adalah suatu proses untuk menemukan karakteristik yang dapat menggambarkan suatu keadaan secara efektif dan efisien. Karakteristik yang diperoleh bisa bernilai yang sebenarnya atau nilai pendekatan. Dalam prakteknya, hasil estimasi merupakan nilai pendekatan terhadap keadaan yang sebenarnya.
Metode estimasi momen dan maksimum likelihood diterapkan kedalam distribusi gamma. Tahapan penyelesaian menghasilkan karakteristik yang disebut dengan parameter �̂ dan �. Pada kedua estimasi momen diperoleh λ �̂= 4.09016193 , �λ= 0.002513199 , E[X] = 1627.475 dan V[X] = 647569.9189. Estimasi maksimum menghasilkan �̂= 3.860568854 , λ� = 1627.475, E[X] = 1627.475 dan V[X] = 687313.0827.
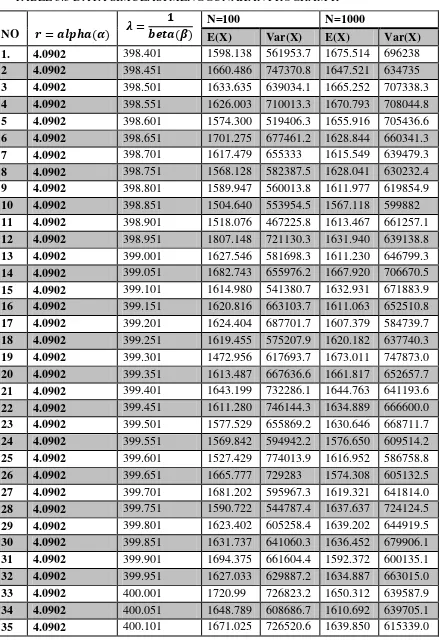
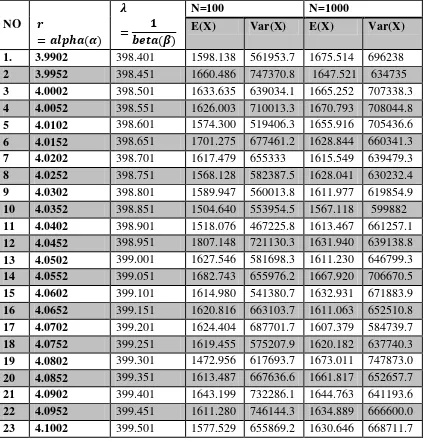
Berdasarkan bangkitan data pada R, diperoleh nilai ekspektasi dan varians yang mendekati nilai ekspektasi dan varians yang diestimasi pada data sebelumnya. Data tersebut dibangkitkan dengan n=100 dan n=1000 selanjutnya dengan menentukan nilai �̂ dan � yang dimodifikasi selanjutnya dibandingkan λ
ABSTRACT
Estimation is a process finding charakteristics and process in describe a phenomen effectively and efficiently. Charakteristics can be an approximation number or true one. Practically, the yield of estimation was an approaching number into the true phenomen.
Moments method and maximum likelihood estimation applied into gamma distribution. The solving steps result characteristics called with parametrics �̂ dan �. Moments estimaton yield λ �̂= 4.09016193 , �λ= 0.002513199 , E[X] = 1627.475 dan V[X] = 647569.9189. Maximum likelihood estimation yield �̂= 3.860568854 , �λ= 1627.475, E[X] = 1627.475 dan V[X] = 687313.0827.
DAFTAR ISI
Halaman
Persetujuan iii
Pernyataan iv
Penghargaan v
Abstrak vi
Abstract vii
Daftar Isi viii
Daftar Tabel ix
Daftar Gambar x
Daftar Lampiran xi
Bab 1 Pendahuluan 1.1 LatarBelakang 1
1.2 RumusanMasalah 4
1.3 BatasanMasalah 4
1.4 TujuanPenelitian 4
1.5 KontribusiPenelitian 4
1.6 MetodologiPenelitian 5
1.7 TinjauanPustaka 6
Bab 2 LandasanTeori 2.1 Probabilitas Dasar 9
2.2 Peubah Acak 10
2.2.1 peubah acak diskrit 10
2.2.2 pubah acak kontinu 11
2.3 Ekspektasi dan Varians 11
2.3.1Ekspektasi 14
2.3.2Varians 14
2.4 Distribusi Gamma dan Turunan Kalkulus 15
2.4.1 Distribusi dan Fungsi gamma 17
2.5 Estimasi 25
2.5.1 Moments estimator 25
2.5.1.1 Prosedur Metode Moments 26
2.5.2 Maximum Likelihood Estimator 27
2.5.2.1 Prosedur Metode MLE 28
2.5.3 Sifat-sifat Estimator 29
Bab 3 Hasil dan Pembahasan 31
3.1 Metode Moments Estimator 31
3.2 Metode Maximum Likelihood Estimator 39
3.3 Aplikasi terhadap data 45
3.3.1 Aplikasi Estimasi Moments 45
3.3.2 Aplikasi Estimasi Maksimum Likelihood 48
3.4 Simulasi Data 52
Bab 4 Kesimpulan dan Saran 4.1 Kesimpulan 54
4.2 Saran 55
DAFTAR TABEL
DAFTAR GAMBAR
DAFTAR LAMPIRAN
LAMPIRAN A xii
LAMPIRAN B xiii
LAMPIRAN C xiv
ABSTRAK
Estimasi adalah suatu proses untuk menemukan karakteristik yang dapat menggambarkan suatu keadaan secara efektif dan efisien. Karakteristik yang diperoleh bisa bernilai yang sebenarnya atau nilai pendekatan. Dalam prakteknya, hasil estimasi merupakan nilai pendekatan terhadap keadaan yang sebenarnya.
Metode estimasi momen dan maksimum likelihood diterapkan kedalam distribusi gamma. Tahapan penyelesaian menghasilkan karakteristik yang disebut dengan parameter �̂ dan �. Pada kedua estimasi momen diperoleh λ �̂= 4.09016193 , �λ= 0.002513199 , E[X] = 1627.475 dan V[X] = 647569.9189. Estimasi maksimum menghasilkan �̂= 3.860568854 , λ� = 1627.475, E[X] = 1627.475 dan V[X] = 687313.0827.
Berdasarkan bangkitan data pada R, diperoleh nilai ekspektasi dan varians yang mendekati nilai ekspektasi dan varians yang diestimasi pada data sebelumnya. Data tersebut dibangkitkan dengan n=100 dan n=1000 selanjutnya dengan menentukan nilai �̂ dan � yang dimodifikasi selanjutnya dibandingkan λ
ABSTRACT
Estimation is a process finding charakteristics and process in describe a phenomen effectively and efficiently. Charakteristics can be an approximation number or true one. Practically, the yield of estimation was an approaching number into the true phenomen.
Moments method and maximum likelihood estimation applied into gamma distribution. The solving steps result characteristics called with parametrics �̂ dan �. Moments estimaton yield λ �̂= 4.09016193 , �λ= 0.002513199 , E[X] = 1627.475 dan V[X] = 647569.9189. Maximum likelihood estimation yield �̂= 3.860568854 , �λ= 1627.475, E[X] = 1627.475 dan V[X] = 687313.0827.
BAB I \
PENDAHULUAN
1.1 Latar Belakang
Informasi-informasi faktual yang diperoleh berdasarkan hasil observasi maupun penelitian sangatlah beragam. Informasi yang dirangkum sedemikian rupa disebut dengan data.. Data yang akan diteliti pada umumnya memiliki karakteristik yang spesifik, sehingga ketika data dianalisa diperoleh model yang sesuai dengan karakteristik data tersebut. Fungsi yang menggambarkan data tersebut dikatakan sebagai distribusi data. Variasi distribusi data dalam statistika menunjukkan bahwa data-data memiliki karakteristik tertentu yang hanya bisa dijelaskan oleh distibusi yang bersesuaian. Misalkan data yang berdistribusi seragam akan sulit dijelaskan oleh distribusi gamma, data yang berdistribusi normal akan sulit dijelaskan oleh distribusi beta maupun sebaliknya.
Bermacam-macam distribusi memperlihatkan betapa banyaknya variasi data. Kajian distribusi statistik yang spesifik akan memperlihatkan karakteristik dari suatu distribusi. Maka, kaidah-kaidah dalam statistik diperlukan untuk memahami kajian distribusi statistik.
dan hukum. Aplikasi statistik melibatkan penggunaan teorema, rumus, aturan, hukum untuk menyelesaikan permasalahan kehidupan nyata.
Statistika secara didikotomi menjadi statistika deskriptif dan statistika inferesia. Statistika deskriptif meliputi metode pengumpulan, pengelompokan, pengolahan dan penyajian data, sedangkan statistika inferensia meliputi metode analisis, interpretasi dan prediksi berdasarkan hasil sampel dalam membantu penarikan kesimpulan suatu populasi. Statistika inferensia dapat dibagi menjadi dua kategori umum yaitu estimasi parameter dan pengujian hipotesis. Teknik ini menggunakan informasi sampel dalam menentukan kesimpulan. Dalam teori keputusan, inferensi didasarkan pada kombinasi informasi sampel beserta bagian-bagian lainnya yang dianggap relevan dengan suatu persoalan tertentu agar dihasilkan keputusan terbaik. Hal yang dianggap relevan dengan informasi sampel adalah konsekuensi yang timbul dari keputusan yang diambil.
Dalam pendekatan klasik, inferensi didasarkan sepenuhnya pada informasi yang diperoleh melalui sampel acak yang diambil dari suatu populasi yang berdistribusi tertentu. Adalah penting menentukan keputusan dan kebijakan berdasarkan hasil analisis data sehingga hasil yang diperoleh sesuai harapan atau setidaknya dapat meminimumkan resiko akibat kegagalan suatu perlakuan. Kesimpulan yang akurat memerlukan informasi sebanyak mungkin. Sebaik mengambil populasi untuk dianalisis, namun jika ukuran populasi sangat besar akan menjadi masalah baru. Apakah berkaitan dengan dana maupun sumber daya yang dimiliki. Pada kondisi tersebut, penggunaan sampel adalah alternatif terbaik menentukan karakteristik populasi dalam mengefektifkan dan mengefisienkan baik sumber daya dan waktu. Sampel diharapkan dapat mewakili karakteristik populasi sedekat sebisa mungkin, sehingga keputusan yang diperoleh sahih dan tepat.
tersebut bisa saja tidak terobservasi secara langsung. Observasi dari satu atau lebih peubah acak yang distribusinya bergantung kepada karakteristik yang diperlukan sehingga akan mempermudah memahaminya. Untuk mengembangkan metode yang digunakan dalam menyelidiki nilai peubah acak berdasarkan sampel data dan menggali informasi mengenai karakteristik populasi yang tidak diketahui dan tidak terobservasi maka dibutuhkan kajian mendalam mengenai hal tersebut.
Estimasi merupakan suatu metode dimana peneliti dapat memperkirakan nilai populasi dengan menggunakan nilai sampel atau aturan yang pada umumnya diekspresikan sebagai sebuah formula yang menyatakan bagaimana menghitung nilai estimasi berdasarkan muatan pengukuran dalam sampel. Estimator adalah suatu statistik yang dapat berupa mean, median, modus varians, simpangan baku maupun ukuran proporsi lainnya. Di mana sampel digunakan untuk melakukan penaksiran suatu parameter populasi. Konsep populasi dan variabel acak sangatlah penting terhadap interpretasi yang tepat pada data statistik dan analisnya.
Karakteristik suatu populasi dapat diketahui dengan melakukan estimasi terhadap sampelnya. Sedangkan nilai sampel statistik yang digunakan untuk mengestimasi parameter populasi disebut dengan estimator. Tujuan dari banyak investigasi statistik adalah untuk mengestimasi satu atau lebih parameter yang relevan. Karakteristik yang berkaitan dengan sampel disebut sebagai statistik, sedangkan karakteristik yang berkaitan dengan populasi disebut dengan parameter. Parameter adalah ukuran seluruh populasi yang diwakili oleh nilai estimasi. Parameter populasi pada umumnya tidak diketahui karena banyaknya anggota populasi.
Perhatikan bahwa proses antrian, waktu tunggu, paruh waktu merujuk kepada distribusi Poisson. Pembahasan lebih lanjut menunjukkan bahwa proses Poisson dapat ditransformasikan kedalam distribusi gamma. Untuk mengetahui karakteristik distribusi gamma diperlukan analisa. Analisa yang digunakan adalah dengan melakukan penaksiran terhadap parameternya.
.
Berdasarkan uraian diatas maka penulis mengajukan judul :”Kajian estimasi parameter distribusi gamma berdasarkan moments method estimator (MMEs) dan maximum likelihood estimator (MLE); suatu terapan pada data paruh waktu dan Simulasi sebagai perbandingan.”
2. Rumusan Masalah
Akan dikaji estimasi parameter distribusi gamma dengan metode moments estimator dan maximum likelihood estimator dengan melakukan perbandingan
berdasarkan data paruh waktu dan data simulasi
3. Batasan Masalah
Pembatasan masalah pada tulisan ini yakni fungsi padat peluang berdistribusi gamma dengan parameter r dan λ. Hasil penurunan kedua metode estimasi diterapakan dalam rata-rata time travel kerja pekerja. Membandingkan hasil kedua estimasi tersebut dengan data yang telah ditetapkan Dengan memperhatikan sifat-sifat penduga yaitu tidak bias, efisien dan konsisten. Dan dengan melakukan bangkitan data dengan nilai r dan λ tertentu.
4. Tujuan penelitian
Berdasarkan penjabaran sebelumnya, maka tujuan penelitian adalah sebagai berikut:
b) Mengetahui hasil dari kedua estimasi tersebut
c) Melihat karakteristik terhadap kasus tertentu pada kedua metode estimasi yang telah diberikan.
5. Kontribusi Peneltian
a) Bagi penulis
Kontribusi penelitian bagi penulis adalah menambah dan memperdalam pemahaman tentang statistika inferensia khususnya estimasi parameter pada distribusi gamma serta aplikasinya statistiknya dalam kehidupan sehari-hari, sehingga menambah minat memperdalam ilmu dalam bidang statistik.
b) Bagi pembaca
Menambah pustaka kepada pembaca yang ingin memahami tentang estimasi kedua parameter yang diajukan. Serta pembanding untuk peneliti yang ingin parameter pada distribusi yang serupa dalam menambah cakrawala ilmu pengetahuan didalam analisis statistik khususnya dengan disribusi yang berkaitan.
6. Metode Penelitian
Berdasarkan buku Fundamental of Research Methodology and Statistics, Kumar mengemukakan tiga aspek penelitian, yakni:
a) Aspek teoretis b) Aspek faktual c) Aspek terapan
Berdasarkan aspek tersebut maka metode yang digunakan penulis adalah sebagai berikut:
a) Menentukan permasalahan yang akan diteliti
c) Telaah teori pada literatur utama dan tambahan
d) Untuk mengarahkan peneltian maka penulis, melaksanakan prosedur sebagai
berikut:
1. Mendefinisikan fungsi densitas distribusi gamma
2. Melakukan estimasi momen estimator:
a) Menentukan persamaan umum momen populasi dan momen
sampel
b) Momen pertama , momen kedua pupulasi dan momen sampel
disamakan
c) Melakukan manipulasu aljabar untuk memperoleh hasil
penyelesaian sistem pertidaksamaan yaitu nilai dari parameter
� dan λ
3. Melakukan estimasi maksimum likelihood
a) Menentukan fungsi likelihood fungsi densitas
b) Menentukan fungsi maksimum likelihood fungsi distribusi
c) Melakukan diferensial ��� likelihood sebagai konsekuensi memaksimumkan parameter distribusi gamma terhadap
parameter � dan λ
4. Mensubstitusi data paruh waktu dari lightbulbs kedalam kedua estimasi,
sehingga diketahui parameter �̂ dan λ�
5. Berdasarkan hasil pada kedua estimasi dilakukan simulasi data secara acak
pada distribusi gamma dengan menggunakan program R, dimodifikasi
sebanyak empat puluh kali dengan bangkitan data �= 100 dan �= 1000 kali
e) Penarikan kesimpulan
7.) Tinjauan Pustaka
dikonfigurasi. Pengambilan keputusan dilakukan berdasarkan estimasi yang diperoleh menggunakan model alternatif.
Suatu Model adalah representasi yang ditaksir berdasarkan keadaan fisik. Model diharapkan dapat menjelaskan sifat-sifat pengamatan menggunakan sekelompok aturan sederhana dan dimerngerti. Aturan tersebut diharapkan dapat memprediksi keluaran dari sebuah eksperimen yang melibatkan keadaan fisik sebelumnya. Model bermanfaat menjelaskan segala aspek relevan dari situasi yang diberikan.
Model matematis digunakan pada kejadian observasional yang memiliki sifat-sifat mengukuran. Model matematis terdiria atas sekelompok asumsi tenatang bagaimana suatu sistem atau proses fisik bekerja. Asumsi tersebut diterapkan dalam bentuk relasi matematis yang melibatkan parameter dan variabel penting.
Untuk lebih memahami terapan statistika ini adalah lebih baik untuk memahami karakteristik distribusi statistika sebelum diaplikasikan kedalam berbagai permasalahan sehari-hari.
Fungsi Kepadatan peluang atau probability density function p.d.f merupakan variabel acak kontinu dan terdefenisi pada himpuan bilangan riil, jika:
1. �(�)≥ 0, ∀� ∈ ℝ 2. � �(�)�� = 1
∞
−∞
3. �(�< �<�) =� �(�) �
� ��
Andaikan bahwa barisan kejadian saling bebas terjadi dalam konstanta λ
perunit waktu. Jika variabel acak � menyatakan interval antara jarak kejadian ��(�) =��−��, �> 0, maka X dapat diintrepretasikan sebagai waktu tunggu
untuk kejadian pertama. Bagian ini membangkitkan hubungan Poisson/eksponensial dan terpusat pada interval, atau waktu tunggu, yang dibutuhkan untuk terjadinya kejadian ke-r.
�
Definisi 1.1
Diberikan bilangan riil r > 0 dan λ > 0, variabel acak X dikatakan sebagai gamma p.d.f dengan parameter r dan λ jika:
�
�(
�
) =
��
(�−1)!
�
�−1
�
−��,
�
> 0
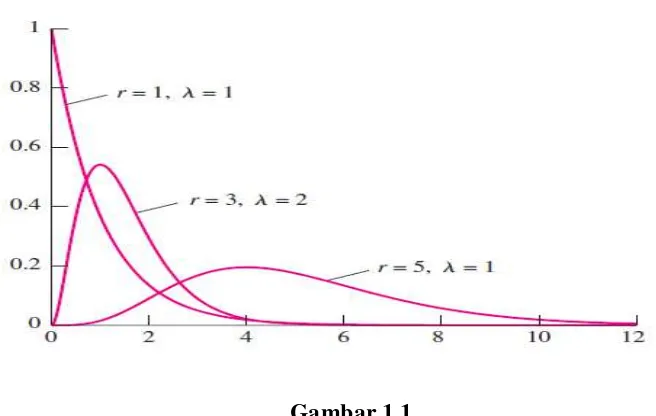
Gambar 1.1
BAB II
LANDASAN TEORI
2.1 Probabilitas Dasar
Andrei Kolgomorov (1903-1987) meletakkan landasan matematis teori peobabilitas dan teori acak. Dalam tulisannya, Kolgomorov menggunakan teori probabilitas dalam mempelajari pergerakan planet dan turbulensi aliran udara. Kontribusi penting lainnya adalah proses stokastik, informasi, mekanika statistik dan dinamika nonlinear.
ke-18, ketika Pierre de Laplace dan Karl F Gauss menggunakan aturan dasar probabilitas terhadap masalah fisis lainnya.
Beberapa definisi dan aksioma yang akan digunakan dalam hal ini berkaitan dengan peristiwa dan probabilitas acak.
Definisi 2.1
Eksperimen adalah suatu proses yang hasil dari keluarannya tidak diketahui secara pasti di mana eksperimen tersebut diasumsikan dapat di ulang dalam suatu waktu dan dibawah kondisi yang identik. Setiap pengulangan disebut sebagai repetisi. Eksperimen acak memenuhi tiga keadaan berikut:
a) Himpunan seluruh keluaran tidak diketahui pasti dalam tiap percobaan. b) Dalam kedaan khusus, tidak diketahui keluaran mana yang akan terjadi. c) Eksperimen dapat diulang dengan keadaan yang mirip.
2.2 Peubah Acak
Suatu eksperimen memuat sejumlah karakteristik yang terukur. Tetapi peneliti pada umumnya berkonsentrasi pada beberapa karakteristik tertentu pada suatu eksperimen. Apakah pada nilai karakteristik di sekitar pusat data atau pada penyebaran data. Pengelompokan keluaran suatu eksperimen diwakili oleh bilangan sederhana bertujuan untuk memudahkan deskripsi. Deskripsi tersebut diperlukan, tetapi di lain kasus hal itu berguna untuk menyatakan suatu bilangan sebagai perwakilan suatu keluaran di ruang sample.
Definisi 2.2
Peubah acak adalah seluruh nilai bernilai riil yang tiap-tiap nilainya diasosiasikan dengan keluaran dari suatu eksperimen acak.
2.2.1 Peubah Acak Diskrit
Jika himpunan seluruh nilai yang mungkin dari peubah acak � adalah suatu himpunan yang dapat dicacah sedemikian rupa, �1, �2, �3, … ,�� atau �1, �2, �3, … sehingga X disebut sebagai variabel acak diskrit. Bagi suatu peubah acak diskrit �, didefinisikan fungsi massa peluang ��(�) sebagai:
��(�) =�(�=
�) 2.
Fungsi massa peluang �(�) bernilai positif , untuk sejumlah nilai � tercacah. Dengan kata lain, jika � mengambil salah satu dari nilai�1,�2, … maka peubah acak diskrit X dengan nilai yang mungkin �1, �2, �3, … ,�� fungsi massa peluang adalah fungsi yang memenuhi kriteria berikut:
1). �(��)≥0, �= 1,2, …
2). � �(��) �
�=1
= 1
3). �(��) =�(�= ��)
2.2.2 Peubah Acak Kontinu
Definisi 2.5
Suatu peubah acak � berdistribusi kontinu jika terdapat fungsi � taknegatif, terdefinisi pada garis bilangan riil, sehingga setiap interval pada bilangan riil (berbatas atau tak berbatas), probabilitas bahwa X yang berada pada interval tersebut merupakan jumlahan daerah f pada interval tersebut. Sebagai contoh, keadaan yang menggambarkan definisi diatas, dengan batas dalam interval tertutup [�,�].
�(� ≤ � ≤ �) =∫ ��� (�)��
�(� ≥ �) =∫ ��∞ (�) dan �(� ≤ �) =
∫ �−∞� (�)�� 2.2
Berdasarkan karakteristik f distribusi variabel acak kontinu dengan cara yang sama menyatakan bahwa fungsi probabilitas berkarakteristik distribusi peubah acak kontinu. Fungsi kepadatan peluang � dapat digunakan untuk menggambarkan distribusi probabibilitas peubah acak kontinu. Jika suatu interval memuat kemiripan nilai X, probabilitasnya besar dan berkorespondensi dengan �(�). Memenuhi ketiga kaidah berikut:
1). �(�)≥ 0
2). � �(�) �� = 1 ∞
−∞
3). �(� ≤ � ≤ �) = � �(�) �� �
�
Distribusi probabilitas adalah visualisasi peubah acak � dalam bentuk kurva. Ketika � merupakan peubah acak berbatas, himpunan probabilitas yang digambarkan terhadap nilai yang mungkin disebut distribusi probablitas �.
Jika � adalah peubah acak berbatas, dengan nilai-nilai �1,�2, …
maka daftar
distribusi probabilitas berkaitan dengan
�= �1, �= �2, …. Jumlah seluruh probabilitas selalu sama dengan 1.Ingat bahwa � merupakan variabel acak, sedangkan � merupakan nilai spesifik dari variabel acak �. Berakibat jika �= 2 maka probabilitas �(�=�) berarti �(�= 2), probabilitas bahwa � adalah 2. Hal yang sama jika � merupakan peubah acak maka �(�=�) probabilitas � dengan nilai khusus �.
Dalam suatu pengukuran eksperimen, hasil pengukuran eksperimen seringkali menghasilkan variasi. Ukuran-ukuran yang menggambarkan karakteristik sampel berkorespondensi dengan karakteristik populasi. Secara sederhana karakteristik tersebut digambarkan sebagai nilai harapan atau lebih dikenal dengan mean. Secara matematis dinyatakan oleh formula berikut:
1). Peubah acak diskrit �� =�[�]
=� ���(��) �
�=1
2.3
2). Peubah acak kontinu �� =�[�]
= � ��(�)�� ∞
−∞
2.4
Sifat-sifat nilai ekspektasi 1. �[�] =�
2. �[��+�] =��[�] +�
3. �[�1+⋯+��] =�[�1] +⋯+�[��]
4. �[�(�,�) ± h(�,�)] = �[�(�,�)] ± E[h(�,�)]
5. �[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
6. �(�.�) =�(�) E(�)
Bukti sifat 1.
Pada peubah acak kontinu berlaku;
�[�] = � ��(�)�� ∞
−∞ �[�] =�
Sustitusi �= � maka �[�] =∫ ��−∞∞ (�)�� , karena b merupakan konstanta berlaku
�[�] =� � �(�)�� ∞
� �(�)�� ∞
−∞
= 1
�[�] =�
Bukti sifat 5.
�[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
�[�] = � ��(�)�� ∞
−∞
Substitusi Y = �(�) ± h(�)
�[�] = � ��(�)�� ∞
−∞
= �[ �(�) ± h(�)]�(�)�� ∞
−∞
Berlaku
�[�] = � �[�]�(�)��± � ℎ[�]�(�)�� ∞
−∞ ∞
−∞
�[�(�) ± h(�)] = � �[�]�(�)��± � ℎ[�]�(�)�� ∞
−∞ ∞
−∞
�[�(�) ± h(�)] =�[�(�)] ±�[ℎ(�)]
2.3.2 Varians.
Pengukuran suatu variabel memungkinkan untuk mempermudah pemahaman mengenai suatu data. Untuk mengetahui seberapa besar tingkat variabilitas sampel yang berhubungan dengan populasi dinyatakan didefinisikan oleh
Var[X] =�[(� − �)2], secara jelas diperlihatkan oleh: 1). Variabel acak diskrit
�2
� = Var[X] = �(� �
�=10
− �)2�(��) 2.5
�2
� = Var[X] = �(�
∞
−∞
− �)2�(�)�� 2.6
Varians untuk kasus kontinu dapat dijabarkan sebagai berikut
Var[X] = �[(� − �)2]
Var[X] = �(� − �)2�(�)��
∞
−∞
= �(�2−2��+�2)�(�)�� ∞
−∞
= � �2�(�)�� −2� � ��(�)��+�2 � �(�)�� ∞
−∞ ∞
−∞ ∞
−∞
Var[X] = �[�2]−2��[�] +�2 Karena �=�[X] maka diperoleh:
Var[X] =
�[�2]−(�[X])2 2.7 Sifat-sifat varians:
1. Var[c] = 0
2. Var[�X] =�2 Var[X]
3. Var[X + c] = Var[X]
4. Var[X1+⋯+ X�] = Var[X1] +⋯+ Var[X�]
Jika � adalah sebuah fungsi dan � merupakan satu titik interior pada domain �. Jika � memiliki nilai maksimum atau minimum lokal di �, maka
�′(�) = 0 atau �′(�) tidak ada
2.8
Teknik pengintegralan parsial �
��[�(�)�(�)]
=�(�)�′(�)
+�(�)�′(�) 2.9
Misalkan
�= �(�) dan �= �(�)
��=�′(�) dan ��= �′(�)��
Persamaan 2.9 menjadi
�
��[��]
=�′�
+��′
Perhatikan persamaan (2.9) untuk memperoleh formula integral parsial, ruas kiri dan kanan dilakukan pengintegralan, sehingga diperoleh:
���� [�(�)�(�)] =� �(�)�′(�)��+� �(�)�′(�)��
� �′(�)�(�)��+� �(�)�′(�)��= �(�)�(�)
� �(�)�′(�)��= �(�)�(�)
� ���
= �� − � ��� 2.10
Definisi improper integral tipe-I
(a) Jika ∫ ��� (�)�� ada untuk setiap bilangan � ≥ �, maka; � �(�)��
∞
�
= lim
�→∞� �(�)�� �
�
Menyatakan bahwa limit tersebut eksis.
(b) Jika ∫ ��� (�)�� eksis untuk setiap bilangan � ≤ �, maka � �(�)��
�
−∞
= lim
�→−∞� �(�)�� �
�
Menyatakan limit tersebut eksis
Improper integral ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� dikatakan konvergen jika limit yang dikaitkan ada dan divergen jika limitnya tidak ada.
(c) Jika ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� konvergen, maka didefinisikan: � �(�)��= � �(�)��
�
−∞ ∞
−∞
+� �(�)�� ∞
�
2.4.1 Distribusi dan Fungsi Gamma
Andaikan suatu peristiwa Poisson terjadi dengan konstanta rate � per unit waktu. Misalkan variabel acak X menyatakann sebagai waktu tunggu kejadian ke− �. Maka X memiliki pdf ��(�), di mana
��(�) = �
�
(�−1)!�
�−1�−� ,
Pembuktian formula untuk ��(�) dilakukan dengan mendifferensialkan fungsi kumulatif, ��(�). Misalkan � sebagai waktu tunggu peristiwa ke-r. Maka,
��(�) =�(� ≤ �) = 1− �(�> �)
= 1−(sedikitnya ada � kejadian terjadi pada interval [0,�])
��(�) = 1 − � �−(��)(��)� �! �−1 �=0 2.11
Untuk memperoleh fungsi padat peluannya maka fungsi kumulatif pada kejadian yang berlangsung dalam interval [0, x] adalah variabel acak Poisson dengan
parameter λx, diturunkan terhadap x, diperoleh fungsi padat peluang sebagai berikut
��(�) =�′�(�)
= �
�� �1
− � �−��(��)�
�! �−1
�=0
� 2.12
Berdasarkan aturan differensial dari perkalian dua buah fungsi pada persamaan
(2.9), misalkan � =�−��,�= (��)�
�! ��(�) =��� ��−�� (��)� �! �−1 �=0
� − �� ��−�� (��)�−1 (� −1)! �−1 �=0 �� =� ���−��(��) � �! � − � ���
−�� (��)�−1 (� −1)!� �−1 �=1 �−1 �=0 =���� ��−��(��) � �! �−2 �=0 �+���−�� (��) �−1
(� −1)!�� − �� ��
−��(��)� �! �−2 �=0 �� =���∑ ��−��(���)� ! �−2
�=0 �+���−��
(��)�−1
(�−1)!�� − �∑ ��
−�� (��)�
�!
�−2
�=0 ��
=���−�� (��) �−1
=��
−��(�)�−1(�)�−1
(� −1)! =(�)
�−1+1(�)�−1�−��
(� −1)!
��(�) = � �
(� −1)!�
�−1�−�� ,�> 0
Definisi 2.5
Diberikan bilangan riil r > 0 dan λ > 0, peubah acak X dikatakan sebagai fungsi gamma pdf dengan parameter r dan λ jika:
��(�) = � �
(� −1)!�
�−1�−�� ,�> 0 atau �(�:�,�) = �� Γ(�)�
�−1�−�� ,�> 0 Fungsi Gamma
Γ(�)
=� ��−1�−��� ∞
0
2.13
Beberapa pembuktian fungsi gamma untuk membantu penurunan rumus dalam distribusi gamma. Mula-mula akan dicari nilai dari Γ�1
2�, substitusi nilai �= 1 2 ke pers. (2.13)
Γ�1
2�=� �
1
2−1�−���
∞
0
Γ�1
2�
= lim �→∞� �
−12�−��� �
0
2.14
Fungsi diatas dijadikan kedalam bentuk polar, maka pertama-tama misalkan sebagai berikut:
Substitusi �=�2 →���� = 2� ke persamaan (2.14)
Γ �1
2�= lim�→∞�(�
2)−12�−�21
2��� �
0
Γ �1
2�= lim�→∞� �−
1�−�21
2��� �
0
=1
2�→∞lim � �−� 2
��
�
0
�2 =� �−�2�� � �−�2��= � �� �∞ −�2−�2�� 0 � �� ∞ 0 ∞ 0 ∞ 0
�2 =� � �∞ −�2����� 0
2�
0
= � �� � �−�22��� ∞
0 2�
0
= 4π
Γ�12�= lim �→∞� �−
1�−�21
2��� �
0
=1
2�→lim∞� �−�
2
��
�
0
=1
2�2√��
Dihasilkan Γ �1
2�=√�
Substitusi �= 1 ke pers (2.13) diperoleh: Γ(1) =� �1−1�−���
∞ 0 =� �−��� ∞ 0 = lim �→∞� �−��� � 0 = lim �→∞�−� −�| 0
��= lim �→∞{(−�
−�)−(−�−0)}
=− 1
�∞+�0 = 0 + 1
= 1 Dihasilkan Γ(1) = 1
Substitusi �= 2 ke pers (2.13) diperoleh: Γ(2) =� �2−1�−���
∞
Γ (2) =� ��−��� ∞ 0 = lim �→∞� �� −��� � 0 = lim �→∞− ��
−�+ lim �→∞� � −��� � 0 = lim �→∞�−�� −�| 0
��+ lim �→∞� � −��� � 0 = lim �→∞� � −��� � 0 = 1
Γ(2) = (−∞�−∞+ 0�0) + lim �→∞� �
−��� �
0
= (0 + 0) + 1
Γ(2 ) = � ��−��� ∞
0
Diperoleh nilai Γ(2) =� ��−��� ∞
0
= 1
Substitusi �= 3 ke pers (2.13) diperoleh: Γ(3) =� �3−1�−���
∞
0
Γ(3) = lim �→∞� �
2�−���
�
0
= −lim �→∞� �
2��−�
�
0
= −lim �→∞�
2�−� + 2 lim
�→∞� �� −��� �
Γ(3) =−lim �→∞��
2�−�| 0
��+ lim
�→∞� ��−��� �
0
Γ(3) =−{(∞2�−∞)−(02�−0)} + 2 lim
�→∞� ��−��� �
0
Γ(3) = (0 + 0) + 2 lim
�→∞� ��−��� �
0
Γ(2) =∫ ��∞ −���
0 = 1 maka Γ(3) = 2� ��−���
∞
0 Γ(3) = 2Γ(2)
Γ(3) = 2
Diperoleh Γ(3) =� �3−1�−���
∞
0
= 2
Substitusi �= 4 ke pers (2.13) diperoleh: Γ(4) =� �4−1�−���
∞
0
Γ(4) = lim �→∞� �
3�−���
�
0
Γ(4) = lim �→∞� �
3�−���
�
0
= −lim �→∞� �
3��−�
�
0
= −lim �→∞�
3�−�| 0
�+ 3 lim �→∞� �
2�−���
�
0
= −lim �→∞�
3�−�| 0
� + 3 lim �→∞� �
2�−���
�
0
= lim �→∞(−�
3�−� + 03�−0) + 3 lim
�→∞� �
2�−���
�
= −∞3�−∞ + 03�−0+ 3 lim �→∞� �
2�−���
�
0
= (0 + 0) + 3 lim �→∞� �
2�−���
�
0 Γ(4) = (0 + 0) + 3Γ(3)
Γ(4) = 6
Diperoleh Γ(4) =� �4−1�−��� ∞
0
= 6
Akan dicari formula ke-r untuk fungsi gamma sebagai berikut:
�(�) =� ��−��−��� ∞
�
Γ(�) = lim �→∞� �
�−1�−���
�
0
= −lim �→∞� �
�−1��−�
�
0
Γ(�) =−lim �→∞�
�−1�−�| 0
� + lim �→∞� �
−����−1
�
0
= −∞�−1�−∞+ 0�−1�0+ (� −1)� ��−2�−��� ∞
0
Γ(�) = 0 + 0 + (� −1) lim
�→∞� ��−
2�−���
�
0
Γ(�) =−(� −1) lim
�→∞� ��−
2��−�
�
0
Γ(�) =−(� −1)�lim �→∞�
�−2�−�| 0
� −(� −2) lim �→∞� �
�−3�−���
�
0
Γ(�)
=−(� −1)�(∞�−2�−∞)−(0�−2�−0)
−(� −2) lim
�→∞� ��−
3�−���
�
0
�
Γ(�) =−(� −1)�0−0−(� −2) lim �→∞� �
�−3�−���
�
0
�
Γ(�) = (� −1)(� −2)�lim �→∞� ��−
3�−���
�
0
�
Γ(�) =−(� −1)(� −2)�lim �→∞� �
�−3��−�
�
0
�
Γ(�)
=−(� −1)(� −2)�lim �→∞�
�−3�−�| 0
� −(�
−3) lim �→∞� �
�−4�−���
�
0
�
Γ(�) =−(� −1)(� −2)�(∞�−3�−∞)−(0�−3�−0)−(�
−3) lim �→∞� �
�−4�−���
�
0
�
Γ(�) =−(� −1)(� −2)�0−0−(� −3) lim �→∞� �
�−4�−���
�
0
�
Γ(�) = (� −1)(� −2)(� −3)�lim �→∞� �
�−4�−���
�
0
�
Γ(�) = (� −1)(� −2)(� −3)�� �(�−3)−1�−��� ∞
0
Pada persamaan terakhir diketahui bahwa nilai terakhir adalah perkalian berulang menurun maka untuk nilai �> 1 maka gamma � menjadi:
Γ(�) = (� −1)(� −2)(� −3){Γ(� −3)}
Γ(�) = (� −1)Γ(� −1)
Γ(�) = (� −1)(� −2)(� −3) … 3.2.1
Γ(�) = (� −1)!, di mana �> 1
Γ(�+ 1) = �Γ(�) =�!
Γ(�) =Γ(�+ 1)
�
Γ(�) = Γ(�+�)
�(�+ 1) … (�+� −1) �+� > 0
�! = (�+�)! (�+ 1)�
di mana (�+ 1)� =�(�+ 1) … (�+� −1) untuk � > 0
�! =�! (�+ 1)� (�+ 1)� =
�!�� (�+ 1)�
(�+ 1)�
�� lim
�→∞
�!��
(�+ 1)� = lim�→∞
�!��
�(�+ 1) … (�+� −1)
Diperoleh identitas Γ(�) = lim
�→∞
�!��
�(�+ 1) … (�+� −1)
Identitas Weierstrass �!��
�(�+ 1) … (�+� −1)
=�����(�)−1−
1 2−
1 3−⋯−
1
��1
� ��1
1 +�/1
��2
1 +�/2⋯
lim �→∞
�!��
�(�+ 1) … (�+� −1)
= lim �→∞�
����(�)−1−12−13−⋯−1��1 �
��1
1 +�/1
��2
1 +�/2⋯
��� 1 +�/�
Γ(�) = lim �→∞�
����(�)−1−1 2− 1 3−⋯− 1 ��1 � ��1
1 +�/1
��2
1 +�/2⋯
��� 1 +�/�
Γ(�) =�−��1
��→lim+∞� ��/�
1 +�/� �=�
�=1
Γ(�) =�−��1
� � ��/�
1 +�� ∞
�=1
Kedua ruas dilogaritmakan diperoleh ��{Γ(�)} =−log(�)− γ�+� ��
� − �� �1 + � ���
∞
�=1
Berdasarkan persamaan terakhir diperoleh ��� atau ������������� yang dinotasikan oleh ψ(�) untuk suatu bilangan bulat tak nol atau negatif dinyatakan dalam turunan logaritma Γ(�)
ψ(x) = �
��{log[Γ(�)]} ψ(x) =Γ′(�)
Γ(�) =−γ − 1 �+� 1 � − 1 �+� ∞ �=1 Γ′(�) Γ(�) =−γ+� 1 � − 1
�+� −1 ∞
�=1
� ≠0, 1, 2, …
� = lim �→∞�1 +
1
2+⋯+ 1
� −log(�)�= 0.5772156649 …
2.5 Estimasi
Estimator dalah kuantitas yang didasarkan dari observasi sampel yang nilainya diambil
sebagai indikator dari nilai parameter populasi yang tidak diketahui (sebagai contoh, rata-rata
parameter tak diketahui yang memiliki nilai dalam himpunan yang disebut ruang parameter.
Dalam estimasi, sampel acak diambil dari distribusi untuk memperoleh beberapa informasi dari parameter tak diketahui. Dilakukan perulangan sebanyak � eksperimen independen, sampel observasi �1,�2, … ,�� dan lakukan pendugaan nilai parameter menggunakan observasi �1,�2, … ,��. Fungsi �1,�2, … ,�� digunakan menduga nilai parameter, statistik �(�1,�2, … ,��) disebut sebagai penduga parameter yang dicari. Perhitungan �(�1,�2, … ,��) dilakukan mendekati nilai parameter sebenarnya. Karakteristik populasi oleh bilangan tunggal berdasarkan pada sampel data dan mewakili nilai yang menggambarkan karakteristik populasi disebut dugaan titik.
2.5.1 Moments Estimator (MMes)
Definisi 2.9
Secara sederhana estimasi � parameter berdasarkan metode momen adalah dengan menyamakan momen populasi dengan momen sampel yang bersesuaian, dituliskan oleh:
�
�1 = �1 �2 = �2
⋮
�� = ��
Persamaan di sisi sebelah kiri bergantung kepada distribusi parameternya. Persamaan di sisi sebelah kanan dapat dihiting berdasarkan data yang digunakan. Momen populasi ke− � didefinisikan sebagai
�� = E(��)
Momen sampel ke− � disefinisikan oleh: �� =
1 n� ��
�
n
i=1
Misalkan �1, �2, … ,�� adalah peubah acak kontinu dan ��(�) merupakan fungsi padat peluang dengan � parameter tidak diketahui, �1,�2, … ,��. Momen � pertama peubah �, jika ada diberikan oleh integral berikut:
�����= � �∞ � −∞ ��
(�,�1,�2, … ,��)��, �= 1,2, … ,�
Momen sampel ke− � merupakan aproksimasi terhadap moment teoretis ke− �.
Metode momen mengestimasi parameter tidak diketahui ��1,��2, … dan ��� terhadap model yang parameternya tidak diketahui adalah
penyelesaian dari � persamaan simultan
� ���(�,�1,�2, … ,��)��=�
1
��
∞
−∞
� �� �
�=1
� �2��(�,�1,�2, … ,��)��= �1
��
∞
−∞
� ��2 �
�=1
⋮ ⋮
� ���
�(�,�1,�2, … ,��)��= �
1
��
∞
−∞
� �� �
�=1
Peubah acak diskrit dengan pmf ��(�:�1,�2, … ,�� ) metode momen mengestimasi penyelesaian persamaan simultan
� �� �
��(�:�1,�2, … ,��) =�
1
�� � �� �
2.5.1.1 Prosedur Metode Moments
Tahapan pendugaan metode moments melibatkan tiga langkah dasar berikut ini: Misalkan terdapat � paramerter yang akan diestimasi, msalkan �= (�1, … ,��).
2.Tentukan hubungkan � momen sampel , ��, � = 1, 2, … ,�.
Banyaknya sampel moment harus sama banyak dengan parameter yang akan di estimasi.
3.Dari sistem persamaan, �� = ��, � = 1, 2, … ,�, selesaikan parameter � = (�1, … ,��) yang merupakan penduga momen untuk ��.
2.5.2 Maximum Likelihood Estimation (MLE)
Definisi 2.6
Misalkan �1,�2, … ,�� merupakan sampel acak berukuran n dengan variabel acak diskrit pmf ��(�,�), di mana �(�1,�2, … ,��) adalah parameter tidak diketahui. Fungsi likelihood, L(θ), adalah perkalian pmf yang dikaitkan dengan n ke-k.
�(�) =�(�1 = �1, … ,�� =��)
�(�) =� �(�� = ��) �
�=1
�(�) =� ��(��:�) �
�=1
Andaikan �1,�2, … ,�� adalah sampel acak berukuran n dari pdf kontinu, ��(�,�) di mana �(�1,�2, … ,��) merupakan parameter tak diketahui, fungsi likelihood dituliskan:
�(�) =�(�1 =�1, … ,�� = ��)
�(�) =�(�1;�1,�2, … ,��).�(�2;�1,�2, … ,��) … .�(��;�1,�2, … ,��) Pandang sebagai fungsi �1,�2, … ,�� , disebut sebagai fungsi likelihood. Misalkan
[�1( �1,�2, … ,��), �2 ( �1,�2, … ,��), … ,��( �1,�2, … ,��)] Adalah tupel-k yang memaksimalkan � ( �1,�2, … ,�� ) sehingga:
��2 = �2(�1,�2, … ,��) ��3 = �3(�1,�2, … ,��)
⋮
��� = ��(�1,�2, … ,��)
Adalah penduga kemungkinan maksimum dari �1,�2, … ,��. Secara umum dapat dituliskan sebagai berikut
�(�) =� ��(��,�) �
�=1
2.5.2.1 Prosedur untuk menentukan MLE
1. Definisikan Fungsi Likelihood, �(�). 2. Gunakan logaritma natural, ln[�(�)].
3. Ketika diterapkan, differensialkan ln[�(�)] terhadap �, dan samakan dengan nol.
4. Selesaikan parameter � dan akan diperoleh ��.
2.5.3 Sifat-sifat estimator
Sifat yang diharapkan dari sebuah penduga adalah bahwa penduga tersebut berada sedekat-dekatnya dengan nilai sebenarnya parameter yang tidak diketahui. Bila diperhatikan mean bukanlah satu-satunya lokasi yang mungkin parameter dimana parameter berada.. Untuk praktisi statisi, pertanyaan penting adalah mendapatkan sampel statistik seperti mean, median, observasi terkecil atau obeservasi terbesar, sebaiknya dipilih mempersentasikan seluruh sampel. Untuk memahami matematika pendugaan, maka pertama-tama ingat bahwa setiap penduga adalah fungsi dari sekelompok peubah acak
Estimator tidak bias adalah estimator yang nilai harapannya sama dengan nilai sesungguhnya dari parameter yang akan ditaksir.
Didefinisikan sebagai berikut
Andaikan �� merupakan estimasi titik untuk suatu parameter �. Maka �� disebut sebagai estimator tidak bias apabila �����= �. Jika ����� ≠ �, maka �� dikatakan bias. Bias suatu penaksir titik �� diberikan oleh �����= ����� − �.
2. Efisien
Jika distribusi Sampling dari dua buah statistik mempunyai mean atau ekspektasi yang sama, maka statistik varians yang lebih kecil disebut sebagai estimator efisien dari mean, sementara statistik yang kedua adalah estimator tak efisien. Nilai dari kedua statistik masing-masing disebut estimasi efisien dan estimasi tak efisien. Dan dinotasikan andaikan bahwa ��1 dan ��2 adalah dua penduga takbias untuk parameter �. suatu penduga adalah efisien terhadap � apabila penduga memiliki varians yang lebih kecil.
Ef(��2 ,��1) =
��� (��1)
��� (��2)
Ef���2 ,��1� =
E���1− �� 2
E���2− ��2
Ef���2 ,��1� =
E���1− ����1�� 2
E���2− ����2�� 2
Jika �� > 1 maka ��1 >��2 artinya secara relative ��2 lebih efisien daripada ��1, dan jika �� < 1 maka ��1 < ��2 secara relative ��1 lebih efisien daripada ��2.
3. Konsisten
meskipun ukuran sampel semakin lama semakin besar.
Suatu penduga dikatakan konsisten jika memenuhi syarat berikut:
1. Jika ukuran sampel bertambah maka penduga akan mendekati nilai parameter sebenarnya. Jika sampel menjadi tak terhingga maka penduga konsisten harus dapat memberi suatu titik yang sempurna terhadap parameternya. Sehingga, ��� � merupakan penduga konsisten, jika dan hanya jika:
� �θ� −E(θ)�2 →0 ������� → ∞
BAB III
PEMBAHASAN
Untuk dapat menyelesaikan estimasi parameter dengan dua metode yang akan dibahas maka perhatikan kembali distribusi gamma dengan parameter
�
dan
�
, yaitu:��(�) = � �
(� −1)!�
�−1�−�� atau �(�:�,�) = ��
Γ(�)�
�−1�−�� ,�> 0
3.1 Metode Moments Estimator (MMEs)
Misalkan �1, �2, … ,�� adalah sampel acak distribusi probabilitas gamma dengan parameter �dan λ. Di mana moment ke-� �� bersesuaian dengan parameter yang
akan dicari.
�
�1 = �1 �2 = �2
⋮
�� = ��
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪
⎧ � ���(�,�1,�2, … ,��)��= �
1 �� � �� � �=1 ∞ −∞
� �2�
�(�,�1,�2, … ,��)��= �
1
�� � ��2
� �=1 ∞ −∞ ⋮ ⋮ � ���
�(�,�1,�2, … ,��)�� =�
1 �� ∞ −∞ � �� � �=1
Prosedur melakukan estimasi menggunakan moment estimator adalah sebagai berikut:
1. Momen Pertama
Momen pertama adalah ketika nilai � = 1, sehingga saat � = 1 maka momen pertama adalah nilai ekspektasi sebagai berikut:
�1 =�1
� ���(�;�,�)�� ∞
−∞
= �1
�� � ��
�
�=1
3.1
Persamaan disisi sebelah kiri merupakan momen pertama populasi, diselesaikan dengan
�1 = �(�) =� �
λ���−1�−�� Γ(�) �� ∞
−∞
�1 = �
λ����−λx Γ(�) ∞
−∞ ��
= � λ
����−λx Γ(�)
0
−∞ ��
+� λ
����−λx Γ(�) ∞
0
��
Momen pertama adalah nilai ekspektasi distribusi gamma, maka:
�1 = �(�)
�1 = � �
Karena λ�
Γ(�) adalah konstanta maka ∫
λ�
Γ(�)�
��−�� ∞
0 �� menjadi
= λ � Γ(�) � � ��−�� �� ∞ 0 =− λ �
λΓ(�)�→∞lim� ����−�� �
0
=− λ �
λΓ(�)��→∞lim�� ��−��]
0
�� − �lim �→∞� �
�−1�−����
�
0
�
=
−
λ
�
λΓ
(
�
)
�→∞lim��
�
�
−��]
0
�
�
+
λ
��
λΓ
(
�
)
�→∞lim� �
�−1
�
−����
�
0
=
− λ
�λΓ
(�
)�→∞lim��
�
�
−��−
0
��
−�0� + �λ�→∞lim�
λ�
Γ(�)��−
1�−����
�
0
=− λ �
λΓ(�)�∞
��−�∞−0��−�0� + �
λ�→∞lim�
λ�
Γ(�)�
�−1�−����
�
0
�1 =
− λ
�
λΓ
(�
)(0−0) +� λ ��
λ�
Γ(�)�
�−1�−����
∞
0
�
Berdasarkan kaidah peubah acak kontinu pada distribusi gamma, yaitu:
�∞Γλ(��)��−1�−����= 1 0
�1 = − λ�
λΓ(�)�∞
��−�∞−0��0�+� λ ��
λ�
Γ(�)�
�−1�−����= 1
∞
0
�
�1 = − λ�
λΓ(�)(0−0) +
� λ(1)
�1 = � �
Dengan menyamakan hasil pengintegralan di sebelah kiri dan penjumlahan disebelah kanan diperoleh momen pertama sebagai berikut:
� ��(�)��= �1 �� � �� � �=1 ∞ −∞ � λ= � 1 �� � �� � �=1
= X�
� λ= � 1 �� � �� � �=1
atau �
=λ �1
�� � ��
�
�=1
3.2
2. Momen kedua
Momen kedua adalah ketika nilai � = 2, sehingga saat �= 2 maka momen kedua adalah nilai ekspektasi sebagai berikut:
�2 = �2 �(�2)
=� �2��(�;�,�)�� ∞
−∞
=�1
�� � ��2
�
�=1
3.3
�2 =�(�2) =� �2
λ���+1�−�� Γ(�) �� ∞
−∞
�2 =� �2
λ���−1�−�� Γ(�) ��
0
−∞ +� �
2λ���− 1�−�� Γ(�) �� ∞
0
�2 = λ�
Γ(�)� �
�+1�−����
∞
0
= − λ �
�Γ(�)�→∞lim � ��
+1� � 0 �−�� =− λ �
�Γ(�)�→∞lim ��
�+1�−��
]
0
�− �+ 1� �∞ ��−��� 0
=− λ �
�Γ(�)�→∞lim ��
�+1�−��
]
0
��+�+ 1
� �→∞lim � � �� � 0 �−�� =− λ �
�Γ(�)��→∞lim��
�+1�−�� −0�+1�−�0�
+�+ 1
� �→∞lim��
��−�� − � � �� �−1�−��� 0
���
=�− λ �
�Γ(�)��→∞lim�
�+1�−��
]
0
�� −λ�(�+ 1)
�2Γ(�) ��→∞lim���−��
]
0��
+λ
��(�+ 1)
�2Γ(� �→∞lim � ��−
1�−���
�
0
��
=− λ �
�Γ(�)�→∞lim���
+1�−�� −0�+1�−�0�
−λ��(2�Γ+ 1)(�) lim �→∞��
��−�� −0��−�0�
+λ
��(�+ 1)
�2Γ(� �→∞lim � ��−
1�−���
� 0 � = − λ � �Γ(�)�∞
�+1�−�∞−0�+1�0� −λ�(�+ 1)
�2Γ(�) �∞��−�∞−0�� 0�
+(�+ 1)�
�2 �→∞lim� λ�
Γ(�)�
�−1�−���
∞
0
�
= λ �
�Γ(�)(0−0)−
λ�(�+ 1)
�2Γ(�) (0−0)
+(�+ 1)�
�2 � λ�
Γ(�)�
�−1�−���
∞
0
�
�2 =
(�+ 1)�
�2 �� λ�
Γ(�)�
�−1�−���
∞
0
� �
�2 = �(�2) =� �2�(�)��
∞
�2 =�
λ���+1�−�� Γ(�) �� ∞
−∞
�2 =�
λ���+1�−�� Γ(�) �� ∞
−∞
=(�+ 1)�
�2 3.4 Dengan menyamakan hasil pada persamaan (3.4) dengan momen sampel diperoleh
�2 =�2
(�+ 1)�
�2 =�
1
�� � ��2 �
�=1
Substitusikan (3.2) kepersamaan (3.4), diperoleh:
��� � �1 �2 �
�=1
=
����� ∑λ ��=1��� ���� ∑λ ��=1��+ 1��
λ2
�λ 2
� � � ��2
� �=1 =���λ �� � �� � �=1 � ���� � �λ � � �=1
+ 1��
�λ 2
� � � ��2
� �=1 =��λ �� 2 �� �� � �=1 � 2 +�λ �� � �� � �=1 � ��� � �λ � � �=1 =���λ 2 �
�2� � �� 2
�
�=1
� −λ 2
�2�� ��
� �=1 � 2 � ��� � �λ � � �=1 =�λ 2
�2�� �� �� 2 � �=1 � − �� �� � �=1 � 2 �� λ� =� ∑ �� � �=1 �(∑� ��2
�=1 )− �
1
�(∑��=1��)2��
� 3.5
λ�
=� X�
�(1/�)(∑� ��2
�=1 )−X�2�
� 3.6
Estimasi parameter untuk r
�̂=�λ� �� � �� � �=1 ���� �̂
=� X�
2
�(1/�)(∑� ��2
�=1 )−X�2�
� 3.7
3. Momen ke-n
Momen ke-n maka momen ke-n adalah nilai ekspektasi sebagai berikut: �� =��
�� = �(��) =� ����(�;�,�)�� ∞
−∞
=�1
�� � ��� �
�=1
3.8
�� =� ��λ
���−1�−�� Γ(�) �� ∞
−∞
�� =� λ
���−1+��−�� Γ(�) ��
0
−∞
+� λ
���−1+��−�� Γ(�) �� ∞
0
�� =� λ
���+�−1�−�� Γ(�) �� ∞ 0 �� = λ � Γ(�)� �
(�+�)−1�−����
∞ 0 �� =− 1 � λ�
Γ(�)�→∞lim � �
(�+�)−1��−��
�
=−1
� λ�
Γ(�)��→∞lim�
(�+�)−1�−��| 0
�
−((�+�)−1) lim �→∞� �
(�+�)−2�−����
� 0 � =1 � λ� Γ(�)�−
(�+�)−1
� ��(�+�)−2�−�� −(�+� −2) lim
�→∞� �
(�+�)−3�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
� �−
(�+� −2)
� ���(�+�)−3�−���
−(�+� −3) lim �→∞� �
(�+�)−4�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
�
(�+� −2)
� �−
(�+� −3)
� ���(�+�)−4�−���
−(�+� −4) lim �→∞� �
(�+�)−5�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
�
(�+� −2)
�
(�+� −3)
� (�+� −4) lim
�→∞�� �
(�+�)−5�−����
�
� �
=1
�
(�+�)−1
�
(�+� −2)
�
(�+� −3)
� (�+� −4) lim
�→∞��
λ�
Γ(�)�
(�+�)−5�−����
�
0
�
��
=(�+�)−1
�
(�+� −2)
�
(�+� −3)
�
(�+� −4)
� ��
λ�
Γ(�)�
(�+�−4)−1�−����
∞
0
Atau �� = �(��) = λ
�
Γ(�)� �
(�+�)−1�−����
∞
0
3.9
Sederhanakan persamaan terakhir kedalam fungsi gamma sebagai berikut: misalkan
�
=
��
,
�
=
� � �� �� =� → �� = 1 � �� �� = λ � Γ(�)�� � � ��(�+�)−1 �−�1
� ∞ 0 � �� �� =λ �−1 Γ(�)��
�(�+�)−1
(λ)(�+�)−1�−���
∞ 0 � �� =λ �−1 Γ(�)(λ)
−((�+�)−1)�� �∞ (�+�)−1�−��� 0
�
�� =λ
−�+�−�−1+1 Γ(�) �� �
(�+�)−1�−���
∞ 0 � �� = λ −� Γ(�)�� �
(�+�)−1�−���
∞
0
�
�� = �(��) = 1
λ�Γ(�)�� �(�+�)−1�−��� ∞
0
�
Berdasarkan definisi fungsi gamma Γ(�) =� �∞ �−1�−��� 0
= (� −1)!
Moment ke-n
�� = � 1
�(��) =� 1
λ�Γ(�)[Γ(�+�)]�
= 1
� �� ��
�
�=1
� 3.11
3.2 Metode Maximum Likelihood Estimator (MLE)
Prosedural penyelesaian dengan menggunakan maximum likelihood estimator adalah sebagai berikut:
I. Prosedur Pertama
Misalkan �1,�2, … ,�� adalah sampel acak berukuran n dari pdf kontinu, ��(�: �,�), didefinisikan fungsi likelihood distribusi gamma sebagai berikut:
�(�:�,�)
=� �(��;�,�) �
�=1
3.13
�(�:�,�) =�(�1;�,�).�(�2;�,�).�(�3;�,�) …�(��;�,�)
�(�:�,�) =��λ ��
1�−1�−��1 Γ(�) � �
�
2�−1�−��2 Γ(�) � �
�
3�−1�−��3 Γ(�) �…�
�
��−1�−���
Γ(�) ��
�(�:�,�) =� (λ �)� (Γ(�))�(�1
�−1.�
2�−1�3�−1…���−1)(�−��1�−��2�−��3…�−���)� �(�:�,�)
=� (λ �)�
�Γ(�)��(�1.�2.�3…��)
�−1(�−� ∑��=1��)�
II. Prosedur kedua
����(�:�,�)�=��� � (λ �)�
(Γ(�))�(�1.�2.�3…��)
�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�(Γ(�))−�(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�(Γ(�))−�(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�+��(Γ(�))−�+��(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=�(��)��� − ���Γ(�) + (� −1)���1.�2.�3…��
+−� � �� �
�=1
� 3.15
III. Prosedur ketiga
Jika � adalah sebuah fungsi dan � merupakan satu titik interior pada domain �. Jika � memiliki nilai maksimum atau minimum lokal di �, maka
�′(�) = 0 atau �′(�) tidak ada 2.6
Berdasarkan definisi di atas maka logaritma natural fungsi likelihood didiferensialkan terhadap parameter � dan �.
�����(�:�,�)�
�� = 0 dan
����(�(�:�,�)�
�� = 0
Differensialkan loglikelihood ��{�(�:�,�)} terhadap λ
����(�(�:�,�)�
��
= ��((��)��� − ���Γ(�) +����1.�2.�3…�� − ���1.�2.�3…�� +−� ∑ �� � �=1 )
�� �
= ��(��)���
�� −
����Γ(�)
�� +
�����1.�2.�3…�� − ���1.�2.�3…��
�� −
�� ∑��=1��
�� �
= ��
� −0 + 0−0 +− � ��
�
�=1
= ��
� − � ��
�
�=1
Turunan fungsi diruas kanan disamakan dengan nol. ��
� − � �� = 0
�
�=1 ��
� =� ��
�
�=1 �
�
=�1
�� � ��
�
�=1
3.17
Berdasarkan turunan dari (3.17) ekspektasi untuk penduga kemungkinan maksimum adalah
E[�] = �
� =�
1
�� � ��
�
�=1
Nilai ekspektasi dengan moments estimator dan maksimum likelihood adalah sama.
Differensialkan ��{�(�:�,�)} terhadap r
�����(�:�,�)�
��
=���(��)��� − ���Γ(�) + (� −1)���1.�2.�3…�� ±� ∑ �� � �=1 �
�� �
=��((��)��� − ���Γ(�) +����1.�2.�3…�� − ���1.�2.�3…�� ±� ∑ �� � �=1 )
�� �
=�(�)��� − � Γ ′(�)
Γ(�) +���1.�2.�3…�� −0 + 0�
=�(�)��� − � Γ ′(�)
Γ(�) +���1.�2.�3…��� =�(�)��� − � Γ
′(�)
Γ(�) +���1+���2 +���3+⋯+�����
=�(�)��� − � Γ ′(�