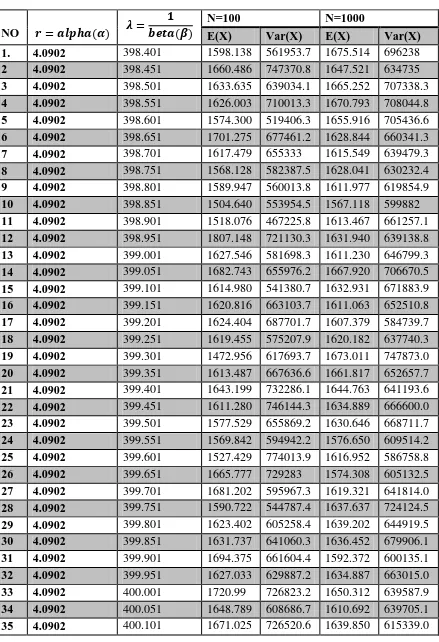
LAMPIRAN A
TABEL 3.3 DATA SIMULASI MENGGUNAKAN PROGRAM R
NO �=�����(�) �= � ����(�)
N=100 N=1000
E(X) Var(X) E(X) Var(X)
1. 4.0902 398.401 1598.138 561953.7 1675.514 696238
2 4.0902 398.451 1660.486 747370.8 1647.521 634735
3 4.0902 398.501 1633.635 639034.1 1665.252 707338.3
4 4.0902 398.551 1626.003 710013.3 1670.793 708044.8
5 4.0902 398.601 1574.300 519406.3 1655.916 705436.6
6 4.0902 398.651 1701.275 677461.2 1628.844 660341.3
7 4.0902 398.701 1617.479 655333 1615.549 639479.3
8 4.0902 398.751 1568.128 582387.5 1628.041 630232.4
9 4.0902 398.801 1589.947 560013.8 1611.977 619854.9
10 4.0902 398.851 1504.640 553954.5 1567.118 599882
11 4.0902 398.901 1518.076 467225.8 1613.467 661257.1
12 4.0902 398.951 1807.148 721130.3 1631.940 639138.8
13 4.0902 399.001 1627.546 581698.3 1611.230 646799.3
14 4.0902 399.051 1682.743 655976.2 1667.920 706670.5
15 4.0902 399.101 1614.980 541380.7 1632.931 671883.9
16 4.0902 399.151 1620.816 663103.7 1611.063 652510.8
17 4.0902 399.201 1624.404 687701.7 1607.379 584739.7
18 4.0902 399.251 1619.455 575207.9 1620.182 637740.3
19 4.0902 399.301 1472.956 617693.7 1673.011 747873.0
20 4.0902 399.351 1613.487 667636.6 1661.817 652657.7
21 4.0902 399.401 1643.199 732286.1 1644.763 641193.6
22 4.0902 399.451 1611.280 746144.3 1634.889 666600.0
23 4.0902 399.501 1577.529 655869.2 1630.646 668711.7
24 4.0902 399.551 1569.842 594942.2 1576.650 609514.2
25 4.0902 399.601 1527.429 774013.9 1616.952 586758.8
26 4.0902 399.651 1665.777 729283 1574.308 605132.5
27 4.0902 399.701 1681.202 595967.3 1619.321 641814.0
28 4.0902 399.751 1590.722 544787.4 1637.637 724124.5
29 4.0902 399.801 1623.402 605258.4 1639.202 644919.5
30 4.0902 399.851 1631.737 641060.3 1636.452 679906.1
31 4.0902 399.901 1694.375 661604.4 1592.372 600135.1
32 4.0902 399.951 1627.033 629887.2 1634.887 663015.0
33 4.0902 400.001 1720.99 726823.2 1650.312 639587.9
34 4.0902 400.051 1648.789 608686.7 1610.692 639705.1
36 4.0902 400.151 1687.111 679290.2 1664.018 649804.7
37 4.0902 400.201 1474.283 547981.8 1625.877 666851.2
38 4.0902 400.251 1647.881 732988 1689.153 693847.5
39 4.0902 400.301 1635.947 645336.2 1614.837 637229.0
40 4.0902 400.351 1684.227 601005.5 1635.401 674738.2
LAMPIRAN B
Tabel 3.4 DATA SIMULASI MENGGUNAKAN PROGRAM R
NO �
=�����(�) �
= �
����(�)
N=100 N=1000
E(X) Var(X) E(X) Var(X)
1. 3.9902 398.401 1527.046 572266.0 1574.048 549768.8
2 3.9952 398.401 1541.640 648613.3 1573.576 623145.6
3 4.0002 398.401 1496.475 453328.0 1603.118 614076.3
4 4.0052 398.401 1508.523 537611.3 1580.227 551884.7
5 4.0102 398.401 1610.603 561945.4 1579.716 625462.8
6 4.0152 398.401 1584.964 752948.4 1609.335 616387.9
7 4.0202 398.401 1622.256 669094.7 1624.030 644750.6
8 4.0252 398.401 1676.418 646093.2 1579.945 605474.6
9 4.0302 398.401 1720.881 1017922 1607.242 656087.3
10 4.0352 398.401 1672.840 704580.2 1605.874 662898.0
11 4.0402 398.401 1638.088 582177.7 1617.575 641810.4
12 4.0452 398.401 1666.779 691366.7 1606.448 615097.3
13 4.0502 398.401 1604.338 625357.3 1598.146 580384.5
14 4.0552 398.401 1682.189 729193.5 1620.53 658834.6
15 4.0602 398.401 1702.154 793063.7 1586.053 625068.4
16 4.0652 398.401 1556.422 659861.4 1584.501 644549.4
17 4.0702 398.401 1672.257 559013.6 1621.853 609416.4
18 4.0752 398.401 1654.126 580475 1688.478 753897.9
19 4.0802 398.401 1628.359 701560.3 1634.323 625817.0
20 4.0852 398.401 1624.058 800784 1609.191 617399.0
21 4.0902 398.401 1659.832 479894.2 1640.756 626264.3
22 4.0952 398.401 1506.366 608552.3 1666.759 673903.0
23 4.1002 398.401 1618.63 1093616 1632.114 663613.0
24 4.1052 398.401 1569.842 594942.2 1665.548 702278.9
25 4.1102 398.401 1569.015 504496.2 1628.19 675704.3
26 4.1152 398.401 1625.067 537602.6 1641.446 769968.0
27 4.1202 398.401 1597.348 509946.7 1578.309 599140.7
28 4.1252 398.401 1638.113 724311.8 1638.587 640491.5
30 4.1352 398.401 1735.920 817420.5 1619.191 671769.9
31 4.1402 398.401 1674.372 616203.4 1673.539 627841.1
32 4.1452 398.401 1595.511 505259 1652.601 706484.6
33 4.1502 398.401 1803.212 1002436 1684.700 652979.1
34 4.1552 398.401 1739.005 724615.6 1608.383 570895.8
35 4.1602 398.401 1684.398 726520.6 1657.421 712554.2
36 4.1652 398.401 1684.499 632458.1 1663.924 665045.6
37 4.1702 398.401 1611.154 530376.9 1628.982 622447.1
38 4.1752 398.401 1680.615 654685.4 1667.854 670082.0
39 4.1802 398.401 1726.906 702444 1674.860 696738.6
40 4.1852 398.401 1641.203 596904.5 1691.498 650611.9
LAMPIRAN C
Tabel 3.5 DATA SIMULASI MENGGUNAKAN PROGRAM R
NO �
=�����(�) �
= �
����(�)
N=100 N=1000
E(X) Var(X) E(X) Var(X)
1. 3.9902 398.401 1598.138 561953.7 1675.514 696238
2 3.9952 398.451 1660.486 747370.8 1647.521 634735
3 4.0002 398.501 1633.635 639034.1 1665.252 707338.3
4 4.0052 398.551 1626.003 710013.3 1670.793 708044.8
5 4.0102 398.601 1574.300 519406.3 1655.916 705436.6
6 4.0152 398.651 1701.275 677461.2 1628.844 660341.3
7 4.0202 398.701 1617.479 655333 1615.549 639479.3
8 4.0252 398.751 1568.128 582387.5 1628.041 630232.4
9 4.0302 398.801 1589.947 560013.8 1611.977 619854.9
10 4.0352 398.851 1504.640 553954.5 1567.118 599882
11 4.0402 398.901 1518.076 467225.8 1613.467 661257.1
12 4.0452 398.951 1807.148 721130.3 1631.940 639138.8
13 4.0502 399.001 1627.546 581698.3 1611.230 646799.3
14 4.0552 399.051 1682.743 655976.2 1667.920 706670.5
15 4.0602 399.101 1614.980 541380.7 1632.931 671883.9
16 4.0652 399.151 1620.816 663103.7 1611.063 652510.8
17 4.0702 399.201 1624.404 687701.7 1607.379 584739.7
18 4.0752 399.251 1619.455 575207.9 1620.182 637740.3
19 4.0802 399.301 1472.956 617693.7 1673.011 747873.0
20 4.0852 399.351 1613.487 667636.6 1661.817 652657.7
21 4.0902 399.401 1643.199 732286.1 1644.763 641193.6
22 4.0952 399.451 1611.280 746144.3 1634.889 666600.0
24 4.1052 399.551 1569.842 594942.2 1576.650 609514.2
25 4.1102 399.601 1527.429 774013.9 1616.952 586758.8
26 4.1152 399.651 1665.777 729283 1574.308 605132.5
27 4.1202 399.701 1681.202 595967.3 1619.321 641814.0
28 4.1252 399.751 1590.722 544787.4 1637.637 724124.5
29 4.1302 399.801 1623.402 605258.4 1639.202 644919.5
30 4.1352 399.851 1631.737 641060.3 1636.452 679906.1
31 4.1402 399.901 1694.375 661604.4 1592.372 600135.1
32 4.1452 399.951 1627.033 629887.2 1634.887 663015.0
33 4.1502 400.001 1720.99 726823.2 1650.312 639587.9
34 4.1552 400.051 1648.789 608686.7 1610.692 639705.1
35 4.1602 400.101 1671.025 726520.6 1639.850 615339.0
36 4.1652 400.151 1687.111 679290.2 1664.018 649804.7
37 4.1702 400.201 1474.283 547981.8 1625.877 666851.2
38 4.1752 400.251 1647.881 732988 1689.153 693847.5
39 4.1802 400.301 1635.947 645336.2 1614.837 637229.0
40 4.1852 400.351 1684.227 601005.5 1635.401 674738.2
LAMPIRAN D
DAFTAR PUSTAKA
[1] Andrews, George E. et al. 1999. Encyclopedia of Mathematics and Its Aplication. Cambridge University Press. UK
[2] Brase, Henri & Pelilo. 2012. Understandable Statistics: Concepts and Methods. Tenth Edition. Brooks/Cole: Boston
[3] Dekking, F.M., et al. 2005. A Modern Introduction to Probability and Statistics. Springer Verlag: USA
[4] Evans, Michael J. & Rosenthal. 2010. Probability and Statistics. WH Freeman: New York
[5] Hayter, Anthony. 2012. Probability and Statistics. 4th edition. Brooks/Cole: Boston
[6] Larsen, R.J & Marx, M.L. 2012. An Introduction to Mathematical Statistics and Its Applications. Fifth Edition. Prentice Hall: Canada
[7] Montgomery, D.C & Runger. 2014. Applied Statistics and Probability for Engineers. 6th edition. John Wiley & Sons: New Jersey
[8] Ramachandran, K.M., et al. Mathematical Statistics with Applications. Academic Press: California.
[9] Rice, John. A. 2007. Mathematical Statistics and Data Analysis. 3rd Edition. Duxbury Press: Boston
[10] Spiegel,Murray R. et al. 2009. Mathematical Handbook of Formulas and Tables. McGrawHill. USA
[11] Stewart, James. 2012. Calculus. Seventh Edition. Cengage: Belmont, USA [12] Salas, et al. 2007. Calculus. Tenth Editions. John Wiley & Sons: USA [13] Ross, S.M. 2009. Introduction to Probability and Statistics for Engineers and Scientists. Fourth Edition. Academic Press: Canada
[14] Wackerly, D.D., et al. 2008. Mathematical Statistics with Applications.Seventh Edition. Duxbury Press: Boston
BAB III
PEMBAHASAN
Untuk dapat menyelesaikan estimasi parameter dengan dua metode yang akan dibahas maka perhatikan kembali distribusi gamma dengan parameter
�
dan
�
, yaitu:��(�) = � �
(� −1)!�
�−1�−�� atau �(�:�,�) = �� Γ(�)�
�−1�−�� ,�> 0
3.1 Metode Moments Estimator (MMEs)
Misalkan �1, �2, … ,�� adalah sampel acak distribusi probabilitas gamma dengan
parameter �dan λ. Di mana moment ke-� �� bersesuaian dengan parameter yang
akan dicari.
�
�1 = �1
�2 = �2
⋮
�� = ��
⎩ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪
⎧ � ���(�,�1,�2, … ,��)��= �
1 �� � �� � �=1 ∞ −∞
� �2�
�(�,�1,�2, … ,��)��= �
1
�� � ��2
� �=1 ∞ −∞ ⋮ ⋮ � ���
�(�,�1,�2, … ,��)�� =�
1 �� ∞ −∞ � �� � �=1
Prosedur melakukan estimasi menggunakan moment estimator adalah sebagai berikut:
1. Momen Pertama
Momen pertama adalah ketika nilai � = 1, sehingga saat � = 1 maka momen pertama adalah nilai ekspektasi sebagai berikut:
�1 =�1
� ���(�;�,�)�� ∞
−∞
= �1
�� � ��
�
�=1
3.1
Persamaan disisi sebelah kiri merupakan momen pertama populasi, diselesaikan dengan
�1 = �(�) =� �
λ���−1�−��
Γ(�) �� ∞
−∞
�1 = �
λ����−λx
Γ(�) ∞
−∞ ��
= � λ
����−λx
Γ(�)
0
−∞ ��
+� λ
����−λx
Γ(�) ∞
0
��
Momen pertama adalah nilai ekspektasi distribusi gamma, maka:
�1 = �(�)
�1 = � �
λ���−1�−��
Karena λ�
Γ(�) adalah konstanta maka ∫
λ� Γ(�)�
��−�� ∞
0 �� menjadi
= λ � Γ(�) � � ��−�� �� ∞ 0 =− λ �
λΓ(�)�→∞lim� ����−�� �
0
=− λ �
λΓ(�)��→∞lim�� ��−��]
0
�� − �lim �→∞� �
�−1�−����
�
0
�
=
−
λ
�
λΓ
(
�
)
�→∞lim��
�
�
−��]
0�
�
+
λ
��
λΓ
(
�
)
�→∞lim� �
�−1
�
−����
�0
=
− λ
�λΓ
(�
)�→∞lim��
�
�
−��−
0
��
−�0� + �λ�→∞lim�
λ�
Γ(�)��−
1�−����
�
0
=− λ �
λΓ(�)�∞
��−�∞−0��−�0� + �
λ�→∞lim�
λ�
Γ(�)�
�−1�−����
�
0
�1 =
− λ
�
λΓ
(�
)(0−0) +� λ ��
λ�
Γ(�)�
�−1�−����
∞
0
�
Berdasarkan kaidah peubah acak kontinu pada distribusi gamma, yaitu:
�∞Γλ(��)��−1�−����= 1 0
�1 = −
λ�
λΓ(�)�∞
��−�∞−0��0�+�
λ �� λ�
Γ(�)�
�−1�−����= 1
∞
0
�
�1 = −
λ�
λΓ(�)(0−0) +
� λ(1)
�1 =
� �
Dengan menyamakan hasil pengintegralan di sebelah kiri dan penjumlahan disebelah kanan diperoleh momen pertama sebagai berikut:
� ��(�)��= �1 �� � �� � �=1 ∞ −∞ � λ= � 1 �� � �� � �=1
= X�
� λ= � 1 �� � �� � �=1
atau �
=λ �1
�� � ��
�
�=1
3.2
2. Momen kedua
Momen kedua adalah ketika nilai � = 2, sehingga saat �= 2 maka momen kedua adalah nilai ekspektasi sebagai berikut:
�2 = �2
�(�2)
=� �2��(�;�,�)�� ∞
−∞
=�1
�� � ��2
�
�=1
3.3
�2 =�(�2) =� �2
λ���+1�−��
Γ(�) �� ∞
−∞
�2 =� �2
λ���−1�−��
Γ(�) ��
0
−∞ +� �
2λ���− 1�−��
Γ(�) �� ∞
0
�2 =
λ�
Γ(�)� �
�+1�−����
∞
0
= − λ �
�Γ(�)�→∞lim � ��
+1� � 0 �−�� =− λ �
�Γ(�)�→∞lim ��
�+1�−��
]
0
�− �+ 1� �∞ ��−���
0
=− λ �
�Γ(�)�→∞lim ��
�+1�−��
]
0
��+�+ 1
� �→∞lim � � �� � 0 �−�� =− λ �
�Γ(�)��→∞lim��
�+1�−�� −0�+1�−�0�
+�+ 1
� �→∞lim��
��−�� − � � �� �−1�−��� 0
���
=�− λ �
�Γ(�)��→∞lim�
�+1�−��
]
0
�� −λ�(�+ 1)
�2Γ(�) ��→∞lim���−��
]
0 ��+λ
��(�+ 1)
�2Γ(� �→∞lim � ��−
1�−���
�
0
��
=− λ �
�Γ(�)�→∞lim���
+1�−�� −0�+1�−�0�
−λ��(2�Γ+ 1)(�) lim �→∞��
��−�� −0��−�0�
+λ
��(�+ 1)
�2Γ(� �→∞lim � ��−
1�−���
� 0 � = − λ � �Γ(�)�∞
�+1�−�∞−0�+1�0� −λ�(�+ 1)
�2Γ(�) �∞��−�∞−0�� 0�
+(�+ 1)�
�2 �→∞lim�
λ�
Γ(�)�
�−1�−���
∞
0
�
= λ �
�Γ(�)(0−0)−
λ�(�+ 1)
�2Γ(�) (0−0)
+(�+ 1)�
�2 �
λ�
Γ(�)�
�−1�−���
∞
0
�
�2 =
(�+ 1)�
�2 ��
λ�
Γ(�)�
�−1�−���
∞
0
� �
�2 = �(�2) =� �2�(�)��
∞
�2 =�
λ���+1�−��
Γ(�) �� ∞
−∞
�2 =�
λ���+1�−��
Γ(�) �� ∞
−∞
=(�+ 1)�
�2 3.4
Dengan menyamakan hasil pada persamaan (3.4) dengan momen sampel diperoleh
�2 =�2
(�+ 1)�
�2 =�
1
�� � ��2 �
�=1
Substitusikan (3.2) kepersamaan (3.4), diperoleh:
��� � �1 �2
�
�=1
=
����� ∑λ ��=1��� ���� ∑λ ��=1��+ 1��
λ2
�λ
2
� � � ��2
� �=1 =���λ �� � �� � �=1 � ���� � �λ � � �=1
+ 1��
�λ
2
� � � ��2
� �=1 =��λ �� 2 �� �� � �=1 � 2 +�λ �� � �� � �=1 � ��� � �λ � � �=1 =���λ 2 �
�2� � �� 2
�
�=1
� −λ
2
�2�� ��
� �=1 � 2 � ��� � �λ � � �=1 =�λ 2
�2�� �� �� 2 � �=1 � − �� �� � �=1 � 2 �� λ� =� ∑ �� � �=1
�(∑� ��2
�=1 )− �
1
�(∑��=1��)2��
� 3.5
λ�
=� X�
�(1/�)(∑� ��2
�=1 )−X�2�
� 3.6
Estimasi parameter untuk r �̂=�λ� �� � �� � �=1 ���� �̂
=� X�
2
�(1/�)(∑� ��2
�=1 )−X�2�
� 3.7
3. Momen ke-n
Momen ke-n maka momen ke-n adalah nilai ekspektasi sebagai berikut:
�� =��
�� = �(��) =� ����(�;�,�)�� ∞
−∞
=�1
�� � ��� �
�=1
3.8
�� =� ��λ
���−1�−��
Γ(�) �� ∞
−∞
�� =� λ
���−1+��−��
Γ(�) ��
0
−∞
+� λ
���−1+��−��
Γ(�) �� ∞
0
�� =� λ
���+�−1�−��
Γ(�) �� ∞ 0 �� = λ � Γ(�)� �
(�+�)−1�−����
∞ 0 �� =− 1 � λ�
Γ(�)�→∞lim � �
(�+�)−1��−��
�
=−1
� λ�
Γ(�)��→∞lim�
(�+�)−1�−��| 0
�
−((�+�)−1) lim �→∞� �
(�+�)−2�−����
� 0 � =1 � λ� Γ(�)�−
(�+�)−1
� ��(�+�)−2�−��
−(�+� −2) lim �→∞� �
(�+�)−3�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
� �−
(�+� −2)
� ���(�+�)−3�−���
−(�+� −3) lim �→∞� �
(�+�)−4�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
�
(�+� −2)
� �−
(�+� −3)
� ���(�+�)−4�−���
−(�+� −4) lim �→∞� �
(�+�)−5�−����
� 0 �� =1 � λ� Γ(�)
(�+�)−1
�
(�+� −2)
�
(�+� −3)
� (�+�
−4) lim �→∞�� �
(�+�)−5�−����
�
� �
=1
�
(�+�)−1
�
(�+� −2)
�
(�+� −3)
� (�+�
−4) lim �→∞��
λ�
Γ(�)�
(�+�)−5�−����
�
0
�
��
=(�+�)−1
�
(�+� −2)
�
(�+� −3)
�
(�+� −4)
� ��
λ�
Γ(�)�
(�+�−4)−1�−����
∞
0
Atau
�� = �(��)
= λ �
Γ(�)� �
(�+�)−1�−����
∞
0
3.9
Sederhanakan persamaan terakhir kedalam fungsi gamma sebagai berikut: misalkan
�
=
��
,
�
=
� � �� �� =� → �� = 1 � �� �� = λ � Γ(�)�� � � ��(�+�)−1
�−�1
� ∞ 0 � �� �� =λ �−1 Γ(�)��
�(�+�)−1
(λ)(�+�)−1�−���
∞ 0 � �� =λ �−1 Γ(�)(λ)
−((�+�)−1)�� �∞ (�+�)−1�−��� 0
�
�� =λ
−�+�−�−1+1
Γ(�) �� �
(�+�)−1�−���
∞ 0 � �� = λ −� Γ(�)�� �
(�+�)−1�−���
∞
0
�
�� = �(��) = 1
λ�Γ(�)�� �(�+�)−1�−��� ∞
0
�
Berdasarkan definisi fungsi gamma Γ(�) =� �∞ �−1�−��� 0
= (� −1)!
Moment ke-n
�� = � 1
�(��) =� 1
λ�Γ(�)[Γ(�+�)]�
= 1
� �� ��
�
�=1
� 3.11
3.2 Metode Maximum Likelihood Estimator (MLE)
Prosedural penyelesaian dengan menggunakan maximum likelihood estimator adalah sebagai berikut:
I. Prosedur Pertama
Misalkan �1,�2, … ,�� adalah sampel acak berukuran n dari pdf kontinu,
��(�: �,�), didefinisikan fungsi likelihood distribusi gamma sebagai berikut:
�(�:�,�)
=� �(��;�,�) �
�=1
3.13
�(�:�,�) =�(�1;�,�).�(�2;�,�).�(�3;�,�) …�(��;�,�)
�(�:�,�) =��λ ��
1�−1�−��1
Γ(�) � �
�
2�−1�−��2
Γ(�) � �
�
3�−1�−��3
Γ(�) �…�
�
��−1�−���
Γ(�) ��
�(�:�,�) =� (λ �)�
(Γ(�))�(�1 �−1.�
2�−1�3�−1…���−1)(�−��1�−��2�−��3…�−���)�
�(�:�,�)
=� (λ �)�
�Γ(�)��(�1.�2.�3…��)
�−1(�−� ∑��=1��)�
II. Prosedur kedua
����(�:�,�)�=��� � (λ �)�
(Γ(�))�(�1.�2.�3…��)
�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�(Γ(�))−�(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�(Γ(�))−�(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=����(λ�)�+��(Γ(�))−�+��(�1.�2.�3…��)�−1(�−� ∑��=1��)��
����(�:�,�)�=�(��)��� − ���Γ(�) + (� −1)���1.�2.�3…��
+−� � �� �
�=1
� 3.15
III. Prosedur ketiga
Jika � adalah sebuah fungsi dan � merupakan satu titik interior pada domain �. Jika � memiliki nilai maksimum atau minimum lokal di �, maka
�′(�) = 0 atau �′(�) tidak ada 2.6
Berdasarkan definisi di atas maka logaritma natural fungsi likelihood didiferensialkan terhadap parameter � dan �.
�����(�:�,�)�
�� = 0 dan
����(�(�:�,�)�
�� = 0
Differensialkan loglikelihood ��{�(�:�,�)} terhadap λ
����(�(�:�,�)�
��
= ��((��)��� − ���Γ(�) +����1.�2.�3…�� − ���1.�2.�3…�� +−� ∑ �� � �=1 )
�� �
= ��(��)���
�� −
����Γ(�)
�� +
�����1.�2.�3…�� − ���1.�2.�3…��
�� −
�� ∑��=1��
�� �
= ��
� −0 + 0−0 +− � ��
�
�=1
= ��
� − � ��
�
�=1
Turunan fungsi diruas kanan disamakan dengan nol.
��
� − � �� = 0
�
�=1
��
� =� ��
�
�=1
� �
=�1
�� � ��
�
�=1
3.17
Berdasarkan turunan dari (3.17) ekspektasi untuk penduga kemungkinan maksimum adalah
E[�] = �
� =�
1
�� � ��
�
�=1
Nilai ekspektasi dengan moments estimator dan maksimum likelihood adalah sama.
Differensialkan ��{�(�:�,�)} terhadap r
�����(�:�,�)�
��
=���(��)��� − ���Γ(�) + (� −1)���1.�2.�3…�� ±� ∑ �� � �=1 �
�� �
=��((��)��� − ���Γ(�) +����1.�2.�3…�� − ���1.�2.�3…�� ±� ∑ �� � �=1 )
�� �
=�(�)��� − � Γ ′(�)
Γ(�) +���1.�2.�3…�� −0 + 0�
=�(�)��� − � Γ ′(�)
Γ(�) +���1.�2.�3…���
=�(�)��� − � Γ ′(�)
Γ(�) +���1+���2 +���3+⋯+�����
=�(�)��� − � Γ ′(�)
Γ(�)
+�ln(��) �
�=1
� 3.19
Nilai untukΓ ′(�)
Γ(�) adalah sebagai beriku
Γ′(�)
Γ(�) = −�+��1− 1
��+�
1 2−
1
�+ 1�+� 1 3−
1
�+ 2�+ … +� 1
� −
1
�+� −1�
+⋯ � Γ′(�) Γ(�) =−�+�� � 1 � ∞ �=1
−�+� −1 1�� 3.20
Substitusikan Γ′(�)
Γ(�) =−�+∑ � 1
� −
1
�+�−1�
∞
�=1 ke pers (3.18) turunan fungsi
logaritma natural terhadap nilai �. =�(�)��� − � �−�+� �1
� −
1
�+� −1� ∞
�=1 �
+�ln(��) �
�=1
�
�(�)��� − � �−�+� �1
� −
1
�+� −1� ∞
�=1 �
+�ln(��) �
�=1
�
= 0 3.21
Substitusi persamaan (3.18)
� � =� 1 �� � �� � �=1 atau �̂ = �̂
�1�� ∑��=1��
ke dalam persamaan (3.22)
�(�)�� � �
�1�� ∑��=1��
�+�ln(��) =� �−�+� �1
� −
1
�+� −1� ∞
�=1 �
�
�=1
�
��� ��(��)�+1
�(ln�1+ ln�2 +⋯+ ln��) = �−�+� �
1
� −
1
�+� −1� ∞
�=1 ��
���(�)−ln�(�) +1
�(ln(�1�2…��)) = �−�+� �
1
� −
1
�+� −1� ∞
�=1 ��
���(�) + ln(�1�2…��)
1
�
�(�)
= �−�+� �1
� −
1
�+� −1� ∞
�=1 ��
3.22
3.3 Aplikasi terhadap data berdistribusi gamma
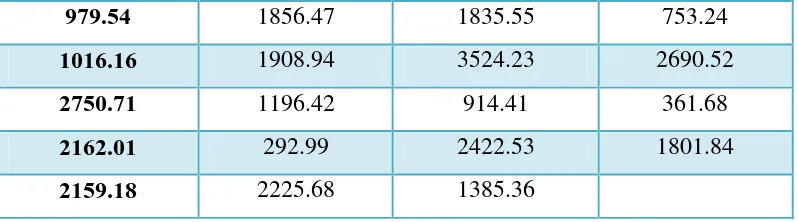
Tabel 3.1 Paruh hidup pemakaian bola lampu (Jam)
336.87 1666.71 1397.96 2618.51
979.54 1856.47 1835.55 753.24
1016.16 1908.94 3524.23 2690.52
2750.71 1196.42 914.41 361.68
2162.01 292.99 2422.53 1801.84
2159.18 2225.68 1385.36
Sumber: Probability & Statistics, Evans
Tabel 3.2 Perhitungan Paruh hidup pemakaian bola lampu (Jam)
No Data ke-i (xi)
��− �� (��− ��)� (��)� ��(��)
23 1548.48 -78.99222222 6239.771172 2397790.31 7.345029084 24 753.24 -874.2322222 764281.9784 567370.4976 6.624383902 25 2690.52 1063.047778 1130070.578 7238897.87 7.897489762 26 361.68 -1265.792222 1602229.95 130812.4224 5.890759843 27 1801.84 174.3677778 30404.12193 3246627.386 7.496563644 SU
M
43941.75
0 17484387.81 88998365.33 195.1486559
3.3.1 Aplikasi Estimasi Moments
Berdasarkan persamaan (3.6) diperoleh parameter yang diestimasi pada data paruh waktu, perhitungan data tabel 3.2. di mana jumlah sampel yang diambil adalah
� = 27
Estimasi untuk nilai λ sebagai berikut:
λ�= ∑ ��
� �=1
�(∑��=1��2)−�1(∑��=1��)2�
atau λ�= X�
�(1/�)(∑��=1��2)−X�2�
λ�= ∑ �� � �=1
�(∑� ��2
�=1 )−
1
�(∑��=1��)2�
λ�= 43941.75
�88998365.33−271 (43941.75)2�
λ�= 43941.75
�88998365.33−271 1930877393�
λ�= 43941.75
(88998365.33−71513978.52)
λ�= 43941.75 (17484387.81)
Estimasi untuk nilai �
�̂=�λ�
�� � ��
�
�=1
�̂= X�
2
�(1/�)(∑� ��2
�=1 )−X�2�
�̂=�λ�
�� � ��
�
�=1
�̂=�0.002513199
27 �(43941.75)
�̂= 4.090161938
E[X] =�
λ= �
1
�� � ��
�
�=1
Dengan menyesuaikan nilai E[X] dengan data diperoleh: E[X] = �1
�� � ��
�
�=1
=(336.87 + 710.64 + 1016.16 +⋯+ 2690.52 + 361.68 + 1801.84) 27
E[X] = 1627.472
atau
E[X] =�
λ
E[X] =4.090161938 0.002513199 E[X] = 1627.472
Var[X] =�1
n� �xi
2 n
i=1
− ��1n� �xi n
i=1
�
Var[X] =n∑ xi
2 n
i=1 −{∑ni=1xi}2
n2
Var[X] =27(88998365.33)−{43941.75}
2
272
Var[X] =2402955863.91−1930877393.0625 729
Var[X] =472078470.8 729 Var[X] = 647569.9189
3.3.2 Aplikasi Estimasi Maksimum Likelihood
Hasil maksimum akan diperoleh apabila memenuhi kaidah berikut:
����(�(�:�,�)�
�� = 0
Didapatkan
�
�= �(�) = X�=
∑��=1��
� �
�=
(�1+�2+�3+⋯+�46+�47 +�48+�49+�50) 50
� �
=(336.87 + 710.64 + 1016.16 +⋯+ 2690.52 + 361.68 + 1801.84) 27
� �=
43941.75 27
�
�= 1627.472 atau �= 1627.472�
E[X] =�
Akan dicari � dengan mensubstitusi �= �
1627 .472 kedalam persamaan berikut:
(�)�� � �
�1�� ∑��=1��
� − � ��+� �1
� −
1
�+� −1� ∞
�=1 �
+�ln(��) = 0 �
�=1
� = 27
(27)�� � �
1627.472� −27�−0.55772156649 +� � 1
� −
1
�+� −1� ∞
�=1 �
+�ln(��) = 0 �
�=1
(27)�� � �
1627.472� −27�−0.55772156649 +� � 1
� −
1
�+� −1�
27
�=1 �
+�ln(��) = 0 �
�=1
(27){ln(�)− ��(1627.472)}
−27�−0.55772156649 +� �1
� −
1
�+� −1�
27
�=1 �
+�ln(��) = 0 �
�=1
(27)(ln(�)−7.394783)−27�−0.55772156649 +� �1
� −
1
�+� −1�
27
�=1 �
+ 195.1486559 = 0
(ln(�)−7.394783)− �−0.55772156649 +� �1
� −
1
�+� −1�
27
�=1 �
+ 7.227729 = 0
ln(�)−7.934783 + 0.55772156649− � �1
� −
1
�+� −1�
27
�=1
+ 7.22772996
= 0
ln(�)− � �1
� −
1
�+� −1�= 0.149331474
27
�=1
ln(�)− ��1−1
��+�
1 2−
1
�+ 1�+� 1 3−
1
�+ 2�+⋯+� 1 27−
1
Nilai � dapat di dekati dengan melakukan taksiran dengan interpolasi linear diperoleh ,
�= 3.860568854
� �=
43941.75 27
�= 3.8605�27 43941.75
�= 0.00237
Var(X) = E[X2]−E[X]2
Var(X) =(�+ 1)�
�2 − �
� ��
2
Var(X) = �
�2
Var(X) =3.860568854 0.002372
Plot distribusi gamma dengan �= 4.0901 dan � = 0.0025 di R
.� <−���(0.001, 0.035,�����ℎ.��� = 100)
plot(.�, dgamma(. x, shape = 4.0901, scale = 0.0025), xlab = "�", ylab
= "Density",
main = "Gamma Distribution: shape = 4.0901, scale
= 0.0025", type = "l")
abline(h = 0, col = "gray")
remove(.�)
Plot distribusi gamma dengan �= 3.86 dan �= 0.00237 di R
.� <−���(0.001, 0.032, length. out = 100)
plot(.�, dgamma(.�, shape = 3.86, scale = 0.00237), xlab = "x", ylab
= Density,
main = "Gamma Distribution: shape = 3.86, scale = 0.0023", type
= "l")
abline(h = 0, col = "gray")
remove(.�)
3.4 Simulasi Data
Dengan menggunakan bantuan program R, akan dilakukan data bangkitan secara acak dengan algoritma sebagai berikut:
#generate gamma r. v
� =⋯ alpha =⋯ beta =⋯
�= rgamma(n, shape = alpha, scale = beta)
�
Karena: ��(�) = ��
(�−1)!�
�−1�−� ,�> 0, sehingga harus dilakukan transformasi
yaitu �= � (alpha) dan nilai λ= 1 � (����)
Untuk mendapatkan nilai ekspektasi dan nilai varians pada program R, dilakukan simulasi dengan modifikasi parameter � dan λ, di mana data dibangkitkan
�1 = 100 kali dan �2 = 1000 kali. Dengan ketentuan sebagai berikut:
SIMULASI PERTAMA nilai �� ditentukan konstan
nilai λk = λk−1+ 0.005 untuk perulangan berikutnya dimana
hasil simulasi data pada lampiran A SIMULASI KEDUA
nilai�� = ��−1+ 0.005 nilai λkditentukan konstan di mana
simulasi data pada lampiran B SIMULASI KETIGA
nilai�� = ��−1+ 0.005
nilai λkdλk−1 + 0.005
di mana
simulasi data pada lampiran C
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan pembahasan diatas, dapat disimpulkan bahwa:
1. Estimasi parameter distribusi gamma dengan parameter � dan � tidak diketahui sehingga parameter tersebut diestimasi dengan menggunakan dua metode yaitu metode Estimasi Momen dan Maksimum Likelihood yang langkah-langkahnya tertera pada pembahasan sebelumnya. Dari hasil perhitungan diperoleh hasil estimasi untuk parameter � dan �. Sehingga didapatkan untuk distribsusi gamma
�[�] adalah �
� dan �[�] adalah �
�2 . Oleh sebab itu , �̂ �� dan
� �
����2 adalah penduga
yang bagi � � dan
� �2.
2. Hasil yang diestimasikan pada lightbulb adalah sebagai berikut:
Moments Estimator Maximum Likelihood Estimator
Parameter � 4.090161938 3.860568854
Parameter � 0.002513199 0.00237
Persamaan
�
�(
�
) =
0.0025134.09
Γ
(
4.09)�
3.09
�
−��
�(
�
) =
0.002373.86
Γ
(
3.86)�
2.86
�
−�Ekspektasi
E(X)
1627.475
1627.475
Varians
V(X)
647569.9189
687313.0827
3. Pada aplikasi program R, data yang telah dibangkitkan untuk nilai � dan � yang telah dimodifikasi sebelumnya di mana � dan � di buat sedemikian dekat dengan nilai � dan � yang telah diestimasi pada sebelumnya. Hasilnya diperoleh ekspektasi dan varians yang nilai dekat terhadap nilai ekspektasi dan varians data yang di estimasi.
4.2 Saran
Estimasi pada tulisan ini masih terbatas pada data yang berdistribusi gamma, dengan menggunakan estimasi Momen dan Maksimum Likelihood. Bagi pembaca yang ingin melakukan penelitian penulis menyarankan agar membandingkan metode dengan membangkitkan data simulasi dengan menggunakan algoritma program R.
Gambar 1.1
BAB II
LANDASAN TEORI
2.1 Probabilitas Dasar
Andrei Kolgomorov (1903-1987) meletakkan landasan matematis teori peobabilitas dan teori acak. Dalam tulisannya, Kolgomorov menggunakan teori probabilitas dalam mempelajari pergerakan planet dan turbulensi aliran udara. Kontribusi penting lainnya adalah proses stokastik, informasi, mekanika statistik dan dinamika nonlinear.
ke-18, ketika Pierre de Laplace dan Karl F Gauss menggunakan aturan dasar probabilitas terhadap masalah fisis lainnya.
Beberapa definisi dan aksioma yang akan digunakan dalam hal ini berkaitan dengan peristiwa dan probabilitas acak.
Definisi 2.1
Eksperimen adalah suatu proses yang hasil dari keluarannya tidak diketahui secara pasti di mana eksperimen tersebut diasumsikan dapat di ulang dalam suatu waktu dan dibawah kondisi yang identik. Setiap pengulangan disebut sebagai repetisi. Eksperimen acak memenuhi tiga keadaan berikut:
a) Himpunan seluruh keluaran tidak diketahui pasti dalam tiap percobaan. b) Dalam kedaan khusus, tidak diketahui keluaran mana yang akan terjadi. c) Eksperimen dapat diulang dengan keadaan yang mirip.
2.2 Peubah Acak
Suatu eksperimen memuat sejumlah karakteristik yang terukur. Tetapi peneliti pada umumnya berkonsentrasi pada beberapa karakteristik tertentu pada suatu eksperimen. Apakah pada nilai karakteristik di sekitar pusat data atau pada penyebaran data. Pengelompokan keluaran suatu eksperimen diwakili oleh bilangan sederhana bertujuan untuk memudahkan deskripsi. Deskripsi tersebut diperlukan, tetapi di lain kasus hal itu berguna untuk menyatakan suatu bilangan sebagai perwakilan suatu keluaran di ruang sample.
Definisi 2.2
Peubah acak adalah seluruh nilai bernilai riil yang tiap-tiap nilainya diasosiasikan dengan keluaran dari suatu eksperimen acak.
2.2.1 Peubah Acak Diskrit
Jika himpunan seluruh nilai yang mungkin dari peubah acak � adalah suatu himpunan yang dapat dicacah sedemikian rupa, �1, �2, �3, … ,�� atau �1,
�2, �3, … sehingga X disebut sebagai variabel acak diskrit. Bagi suatu peubah acak diskrit �, didefinisikan fungsi massa peluang ��(�) sebagai:
��(�) =�(�=
�) 2.
Fungsi massa peluang �(�) bernilai positif , untuk sejumlah nilai � tercacah. Dengan kata lain, jika � mengambil salah satu dari nilai�1,�2, … maka peubah acak diskrit X dengan nilai yang mungkin �1, �2, �3, … ,�� fungsi massa peluang adalah fungsi yang memenuhi kriteria berikut:
1). �(��)≥0, �= 1,2, …
2). � �(��)
�
�=1
= 1
3). �(��) =�(�= ��)
2.2.2 Peubah Acak Kontinu
Definisi 2.5
Suatu peubah acak � berdistribusi kontinu jika terdapat fungsi � taknegatif, terdefinisi pada garis bilangan riil, sehingga setiap interval pada bilangan riil (berbatas atau tak berbatas), probabilitas bahwa X yang berada pada interval tersebut merupakan jumlahan daerah f pada interval tersebut. Sebagai contoh, keadaan yang menggambarkan definisi diatas, dengan batas dalam interval tertutup [�,�].
�(� ≤ � ≤ �) =∫ ��� (�)��
�(� ≥ �) =∫ ��∞ (�) dan �(� ≤ �) =
∫ �−∞� (�)�� 2.2
Berdasarkan karakteristik f distribusi variabel acak kontinu dengan cara yang sama menyatakan bahwa fungsi probabilitas berkarakteristik distribusi peubah acak kontinu. Fungsi kepadatan peluang � dapat digunakan untuk menggambarkan distribusi probabibilitas peubah acak kontinu. Jika suatu interval memuat kemiripan nilai X, probabilitasnya besar dan berkorespondensi dengan
�(�). Memenuhi ketiga kaidah berikut:
1). �(�)≥ 0
2). � �(�) �� = 1
∞
−∞
3). �(� ≤ � ≤ �) = � �(�) ��
�
�
Distribusi probabilitas adalah visualisasi peubah acak � dalam bentuk kurva. Ketika � merupakan peubah acak berbatas, himpunan probabilitas yang digambarkan terhadap nilai yang mungkin disebut distribusi probablitas �.
Jika � adalah peubah acak berbatas, dengan nilai-nilai �1,�2, …
maka daftar
distribusi probabilitas berkaitan dengan
�= �1, �= �2, …. Jumlah seluruhprobabilitas selalu sama dengan 1.
Ingat bahwa � merupakan variabel acak, sedangkan � merupakan nilai spesifik dari variabel acak �. Berakibat jika �= 2 maka probabilitas �(�=�) berarti
�(�= 2), probabilitas bahwa � adalah 2. Hal yang sama jika � merupakan peubah acak maka �(�=�) probabilitas � dengan nilai khusus �.
Dalam suatu pengukuran eksperimen, hasil pengukuran eksperimen seringkali menghasilkan variasi. Ukuran-ukuran yang menggambarkan karakteristik sampel berkorespondensi dengan karakteristik populasi. Secara sederhana karakteristik tersebut digambarkan sebagai nilai harapan atau lebih dikenal dengan mean. Secara matematis dinyatakan oleh formula berikut:
1). Peubah acak diskrit
�� =�[�]
=� ���(��)
�
�=1
2.3
2). Peubah acak kontinu
�� =�[�]
= � ��(�)��
∞
−∞
2.4
Sifat-sifat nilai ekspektasi 1. �[�] =�
2. �[��+�] =��[�] +�
3. �[�1+⋯+��] =�[�1] +⋯+�[��]
4. �[�(�,�) ± h(�,�)] = �[�(�,�)] ± E[h(�,�)] 5. �[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
6. �(�.�) =�(�) E(�) Bukti sifat 1.
Pada peubah acak kontinu berlaku; �[�] = � ��(�)��
∞
−∞
�[�] =�
Sustitusi �= � maka �[�] =∫ ��−∞∞ (�)�� , karena b merupakan konstanta berlaku
�[�] =� � �(�)��
∞
� �(�)��
∞
−∞
= 1
�[�] =�
Bukti sifat 5.
�[�(�) ± h(�)] =�[�(�)] ± E[h(�)]
�[�] = � ��(�)��
∞
−∞
Substitusi Y = �(�) ± h(�)
�[�] = � ��(�)��
∞
−∞
= �[ �(�) ± h(�)]�(�)��
∞
−∞
Berlaku
�[�] = � �[�]�(�)��± � ℎ[�]�(�)��
∞
−∞ ∞
−∞
�[�(�) ± h(�)] = � �[�]�(�)��± � ℎ[�]�(�)��
∞
−∞ ∞
−∞
�[�(�) ± h(�)] =�[�(�)] ±�[ℎ(�)]
2.3.2 Varians.
Pengukuran suatu variabel memungkinkan untuk mempermudah pemahaman mengenai suatu data. Untuk mengetahui seberapa besar tingkat variabilitas sampel yang berhubungan dengan populasi dinyatakan didefinisikan oleh Var[X] =�[(� − �)2], secara jelas diperlihatkan oleh:
1). Variabel acak diskrit
�2
� = Var[X] = �(� �
�=10
− �)2�(��) 2.5
�2
� = Var[X] = �(�
∞
−∞
− �)2�(�)�� 2.6
Varians untuk kasus kontinu dapat dijabarkan sebagai berikut
Var[X] = �[(� − �)2]
Var[X] = �(� − �)2�(�)��
∞
−∞
= �(�2−2��+�2)�(�)��
∞
−∞
= � �2�(�)�� −2� � ��(�)��+�2 � �(�)��
∞
−∞ ∞
−∞ ∞
−∞
Var[X] = �[�2]−2��[�] +�2
Karena �=�[X] maka diperoleh: Var[X] =
�[�2]−(�[X])2 2.7
Sifat-sifat varians: 1. Var[c] = 0
2. Var[�X] =�2 Var[X] 3. Var[X + c] = Var[X]
4. Var[X1+⋯+ X�] = Var[X1] +⋯+ Var[X�]
Jika � adalah sebuah fungsi dan � merupakan satu titik interior pada domain �. Jika � memiliki nilai maksimum atau minimum lokal di �, maka
�′(�) = 0 atau �′(�) tidak ada
2.8
Teknik pengintegralan parsial
�
��[�(�)�(�)]
=�(�)�′(�)
+�(�)�′(�) 2.9
Misalkan
�= �(�) dan �= �(�) ��=�′(�) dan ��= �′(�)�� Persamaan 2.9 menjadi
�
��[��]
=�′�
+��′
Perhatikan persamaan (2.9) untuk memperoleh formula integral parsial, ruas kiri dan kanan dilakukan pengintegralan, sehingga diperoleh:
���� [�(�)�(�)] =� �(�)�′(�)��+� �(�)�′(�)��
� �′(�)�(�)��+� �(�)�′(�)��= �(�)�(�)
� �(�)�′(�)��= �(�)�(�)
� ���
= �� − � ��� 2.10
Definisi improper integral tipe-I
(a) Jika ∫ ��� (�)�� ada untuk setiap bilangan � ≥ �, maka;
� �(�)��
∞
�
= lim
�→∞� �(�)�� �
�
Menyatakan bahwa limit tersebut eksis.
(b) Jika ∫ ��� (�)�� eksis untuk setiap bilangan � ≤ �, maka
� �(�)��
�
−∞
= lim
�→−∞� �(�)�� �
�
Menyatakan limit tersebut eksis
Improper integral ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� dikatakan konvergen jika limit yang dikaitkan ada dan divergen jika limitnya tidak ada.
(c) Jika ∫ ��∞ (�)�� dan ∫ �−∞� (�)�� konvergen, maka didefinisikan:
� �(�)��= � �(�)��
�
−∞ ∞
−∞
+� �(�)��
∞
�
2.4.1 Distribusi dan Fungsi Gamma
Andaikan suatu peristiwa Poisson terjadi dengan konstanta rate � per unit waktu. Misalkan variabel acak X menyatakann sebagai waktu tunggu kejadian ke− �. Maka X memiliki pdf ��(�), di mana
��(�) = �
�
(�−1)!�
�−1�−� ,
�> 0 2.10
Pembuktian formula untuk ��(�) dilakukan dengan mendifferensialkan fungsi kumulatif, ��(�). Misalkan �sebagai waktu tunggu peristiwa ke-r. Maka,
��(�) =�(� ≤ �) = 1− �(�> �)
= 1−(sedikitnya ada � kejadian terjadi pada interval [0,�])
��(�) = 1 − � �−(��)(��)� �! �−1 �=0 2.11
Untuk memperoleh fungsi padat peluannya maka fungsi kumulatif pada kejadian yang berlangsung dalam interval [0, x] adalah variabel acak Poisson dengan
parameter λx, diturunkan terhadap x, diperoleh fungsi padat peluang sebagai berikut
��(�) =�′�(�)
= �
�� �1
− � �−��(��)�
�!
�−1
�=0
� 2.12
Berdasarkan aturan differensial dari perkalian dua buah fungsi pada persamaan (2.9), misalkan � =�−��,� = (��)�
�! ��(�) =��� ��−�� (��)� �! �−1 �=0
� − �� ��−�� (��)�−1
(� −1)!
�−1 �=0 �� =� ���−��(��) � �! � − � ���
−�� (��)�−1
(� −1)!�
�−1 �=1 �−1 �=0 =���� ��−��(��) � �! �−2 �=0 �+���−�� (��) �−1
(� −1)!�� − �� ��
−��(��)� �! �−2 �=0 �� =���∑ ��−��(���)� ! �−2
�=0 �+���−��
(��)�−1
(�−1)!�� − �∑ ��
−�� (��)�
�!
�−2
�=0 ��
=���−�� (��)
�−1
=��
−��(�)�−1(�)�−1
(� −1)!
=(�)
�−1+1(�)�−1�−��
(� −1)!
��(�) = � �
(� −1)!�
�−1�−�� ,�> 0
Definisi 2.5
Diberikan bilangan riil r > 0 dan λ > 0, peubah acak X dikatakan sebagai fungsi gamma pdf dengan parameter r dan λ jika:
��(�) = � �
(� −1)!�
�−1�−�� ,�> 0 atau �(�:�,�) = ��
Γ(�)�
�−1�−�� ,�> 0
Fungsi Gamma
Γ(�)
=� ��−1�−���
∞
0
2.13
Beberapa pembuktian fungsi gamma untuk membantu penurunan rumus dalam distribusi gamma. Mula-mula akan dicari nilai dari Γ�1
2�, substitusi nilai �= 1 2 ke pers. (2.13)
Γ�1
2�=� � 1
2−1�−���
∞
0
Γ�1
2�
= lim
�→∞� �
−12�−��� �
0
2.14
Fungsi diatas dijadikan kedalam bentuk polar, maka pertama-tama misalkan sebagai berikut:
Substitusi �=�2 →���� = 2� ke persamaan (2.14)
Γ �1
2�= lim�→∞�(�
2)−12�−�21 2���
�
0
Γ �1
2�= lim�→∞� �−
1�−�21 2���
�
0
=1
2�→∞lim � �−�
2
��
�
0
�2 =� �−�2�� � �−�2�� = � �� �∞ −�2−�2�� 0 � �� ∞ 0 ∞ 0 ∞ 0
�2 =� � �∞ −�2����� 0
2�
0
= � �� � �−�22���
∞
0 2�
0
= 4π
Γ�12�= lim
�→∞� �−
1�−�21 2���
�
0
=1
2�→lim∞� �−� 2
��
�
0
=1
2�2√��
Dihasilkan Γ �1
2�=√�
Substitusi �= 1 ke pers (2.13) diperoleh:
Γ(1) =� �1−1�−���
∞ 0 =� �−��� ∞ 0 = lim �→∞� �−��� � 0 = lim �→∞�−� −�| 0
��= lim �→∞{(−�
−�)−(−�−0)}
=− 1
�∞+�0
= 0 + 1
= 1
Dihasilkan Γ(1) = 1
Substitusi �= 2 ke pers (2.13) diperoleh:
Γ(2) =� �2−1�−���
∞
Γ (2) =� ��−��� ∞ 0 = lim �→∞� �� −��� � 0 = lim �→∞− ��
−�+ lim �→∞� � −��� � 0 = lim �→∞�−�� −�| 0
��+ lim �→∞� � −��� � 0 = lim �→∞� � −��� � 0 = 1
Γ(2) = (−∞�−∞+ 0�0) + lim
�→∞� � −��� �
0
= (0 + 0) + 1
Γ(2 ) = � ��−���
∞
0
Diperoleh nilai Γ(2) =� ��−���
∞
0
= 1
Substitusi �= 3 ke pers (2.13) diperoleh:
Γ(3) =� �3−1�−���
∞
0
Γ(3) = lim
�→∞� �
2�−���
�
0
= −lim
�→∞� �
2��−�
�
0
= −lim
�→∞�
2�−� + 2 lim
�→∞� �� −��� �
Γ(3) =−lim
�→∞��
2�−�| 0
��+ lim
�→∞� ��−��� �
0
Γ(3) =−{(∞2�−∞)−(02�−0)} + 2 lim
�→∞� ��−��� �
0
Γ(3) = (0 + 0) + 2 lim
�→∞� ��−��� �
0
Γ(2) =∫ ��∞ −���
0 = 1 maka
Γ(3) = 2� ��−���
∞
0
Γ(3) = 2Γ(2)
Γ(3) = 2
Diperoleh Γ(3) =� �3−1�−���
∞
0
= 2
Substitusi �= 4 ke pers (2.13) diperoleh:
Γ(4) =� �4−1�−���
∞
0
Γ(4) = lim
�→∞� �
3�−���
�
0
Γ(4) = lim
�→∞� �
3�−���
�
0
= −lim
�→∞� �
3��−�
�
0
= −lim
�→∞�
3�−�| 0
�+ 3 lim �→∞� �
2�−���
�
0
= −lim
�→∞�
3�−�| 0
� + 3 lim �→∞� �
2�−���
�
0
= lim
�→∞(−�
3�−� + 03�−0) + 3 lim
�→∞� �
2�−���
�
= −∞3�−∞ + 03�−0+ 3 lim
�→∞� �
2�−���
�
0
= (0 + 0) + 3 lim
�→∞� �
2�−���
�
0
Γ(4) = (0 + 0) + 3Γ(3)
Γ(4) = 6
Diperoleh Γ(4) =� �4−1�−���
∞
0
= 6
Akan dicari formula ke-r untuk fungsi gamma sebagai berikut:
�(�) =� ��−��−���
∞
�
Γ(�) = lim
�→∞� �
�−1�−���
�
0
= −lim
�→∞� �
�−1��−�
�
0
Γ(�) =−lim
�→∞�
�−1�−�| 0
� + lim �→∞� �
−����−1
�
0
= −∞�−1�−∞+ 0�−1�0+ (� −1)� ��−2�−���
∞
0
Γ(�) = 0 + 0 + (� −1) lim
�→∞� ��−
2�−���
�
0
Γ(�) =−(� −1) lim
�→∞� ��−
2��−�
�
0
Γ(�) =−(� −1)�lim
�→∞�
�−2�−�| 0
� −(� −2) lim �→∞� �
�−3�−���
�
0
Γ(�)
=−(� −1)�(∞�−2�−∞)−(0�−2�−0)
−(� −2) lim
�→∞� ��−
3�−���
�
0
�
Γ(�) =−(� −1)�0−0−(� −2) lim
�→∞� �
�−3�−���
�
0
�
Γ(�) = (� −1)(� −2)�lim
�→∞� ��−
3�−���
�
0
�
Γ(�) =−(� −1)(� −2)�lim
�→∞� �
�−3��−�
�
0
�
Γ(�)
=−(� −1)(� −2)�lim
�→∞�
�−3�−�| 0
� −(�
−3) lim
�→∞� �
�−4�−���
�
0
�
Γ(�) =−(� −1)(� −2)�(∞�−3�−∞)−(0�−3�−0)−(�
−3) lim
�→∞� �
�−4�−���
�
0
�
Γ(�) =−(� −1)(� −2)�0−0−(� −3) lim
�→∞� �
�−4�−���
�
0
�
Γ(�) = (� −1)(� −2)(� −3)�lim
�→∞� �
�−4�−���
�
0
�
Γ(�) = (� −1)(� −2)(� −3)�� �(�−3)−1�−���
∞
0
Pada persamaan terakhir diketahui bahwa nilai terakhir adalah perkalian berulang menurun maka untuk nilai �> 1 maka gamma � menjadi:
Γ(�) = (� −1)(� −2)(� −3){Γ(� −3)}
Γ(�) = (� −1)Γ(� −1)
Γ(�) = (� −1)(� −2)(� −3) … 3.2.1
Γ(�) = (� −1)!, di mana �> 1
Γ(�+ 1) = �Γ(�) =�!
Γ(�) =Γ(�+ 1)
�
Γ(�) = Γ(�+�)
�(�+ 1) … (�+� −1) �+� > 0
�! = (�+�)! (�+ 1)�
di mana (�+ 1)� =�(�+ 1) … (�+� −1) untuk � > 0
�! =�! (�+ 1)� (�+ 1)� =
�!�� (�+ 1)�
(�+ 1)�
��
lim
�→∞
�!��
(�+ 1)� = lim�→∞
�!��
�(�+ 1) … (�+� −1) Diperoleh identitas
Γ(�) = lim
�→∞
�!��
�(�+ 1) … (�+� −1) Identitas Weierstrass
�!��
�(�+ 1) … (�+� −1)
=�����(�)−1− 1 2−
1 3−⋯−
1
��1
� ��1 1 +�/1
��2 1 +�/2⋯
���
lim
�→∞
�!��
�(�+ 1) … (�+� −1)
= lim
�→∞�
����(�)−1−12−13−⋯−1��1
� ��1 1 +�/1
��2 1 +�/2⋯
���
1 +�/�
Γ(�) = lim
�→∞�
����(�)−1−1 2− 1 3−⋯− 1 ��1 � ��1 1 +�/1
��2 1 +�/2⋯
���
1 +�/�
Γ(�) =�−��1
��→lim+∞�
��/� 1 +�/�
�=�
�=1
Γ(�) =�−��1
� � ��/� 1 +��
∞
�=1
Kedua ruas dilogaritmakan diperoleh
��{Γ(�)} =−log(�)− γ�+� ��
� − �� �1 + � ���
∞
�=1
Berdasarkan persamaan terakhir diperoleh ��� atau ������������� yang dinotasikan oleh ψ(�) untuk suatu bilangan bulat tak nol atau negatif dinyatakan dalam turunan logaritma Γ(�)
ψ(x) = �
��{log[Γ(�)]} ψ(x) =Γ′(�)
Γ(�) =−γ − 1 �+� 1 � − 1 �+� ∞ �=1 Γ′(�) Γ(�) =−γ+� 1 � − 1
�+� −1
∞
�=1
� ≠0, 1, 2, …
� = lim
�→∞�1 +
1
2+⋯+ 1
� −log(�)�= 0.5772156649 …
2.5 Estimasi
Estimator dalah kuantitas yang didasarkan dari observasi sampel yang nilainya diambil
sebagai indikator dari nilai parameter populasi yang tidak diketahui (sebagai contoh, rata-rata
parameter tak diketahui yang memiliki nilai dalam himpunan yang disebut ruang parameter.
Dalam estimasi, sampel acak diambil dari distribusi untuk memperoleh beberapa informasi dari parameter tak diketahui. Dilakukan perulangan sebanyak
� eksperimen independen, sampel observasi �1,�2, … ,�� dan lakukan pendugaan nilai parameter menggunakan observasi �1,�2, … ,��. Fungsi
�1,�2, … ,�� digunakan menduga nilai parameter, statistik �(�1,�2, … ,��) disebut sebagai penduga parameter yang dicari. Perhitungan �(�1,�2, … ,��) dilakukan mendekati nilai parameter sebenarnya. Karakteristik populasi oleh bilangan tunggal berdasarkan pada sampel data dan mewakili nilai yang menggambarkan karakteristik populasi disebut dugaan titik.
2.5.1 Moments Estimator (MMes)
Definisi 2.9
Secara sederhana estimasi � parameter berdasarkan metode momen adalah dengan menyamakan momen populasi dengan momen sampel yang bersesuaian, dituliskan oleh:
�
�1 = �1
�2 = �2
⋮
�� = ��
Persamaan di sisi sebelah kiri bergantung kepada distribusi parameternya. Persamaan di sisi sebelah kanan dapat dihiting berdasarkan data yang digunakan. Momen populasi ke− � didefinisikan sebagai
�� = E(��)
Momen sampel ke− � disefinisikan oleh:
�� =
1 n� ��