Estimasi Parameter µ Dan Σ2 Pada Distribusi Eksponensial Tergeneralisir Dua Variabel Menggunakan Fungsi Pembangkit Momen

ESTIMASI PARAMETER µ DAN σ

2

PADA DISTRIBUSI

EKSPONENSIAL TERGENERALISIR DUA

VARIABEL MENGGUNAKAN FUNGSI

PEMBANGKIT MOMEN

SKRIPSI

GHAZALI WARDHONO

090823040

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

ESTIMASI PARAMETER µ DAN σ2

PADA DISTRIBUSI EKSPONENSIAL TERGENERALISIR DUA VARIABEL MENGGUNAKAN FUNGSI

PEMBANGKIT MOMEN SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

GHAZALI WARDHONO 090823040

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : ESTIMASI PARAMETER µ DAN σ2 PADA

DISTRIBUSI EKSPONENSIAL TERGENERALISIR

DUA VARIABEL MENGGUNAKAN FUNGSI

PEMBANGKIT MOMEN

Kategori : SKRIPSI

Nama : GHAZALI WARDHONO

Nomor Induk Mahasiswa : 090823040

Program Studi : SARJANA (S1) MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

Diluluskan di

Medan,

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Pangeran Sianipar, MS Drs. Pasukat Sembiring, M.Si NIP. 19470208 197403 1 001 NIP. 19531113 198503 1 002

Diketahui oleh

Departemen Matematika FMIPA USU Ketua

Prof.Dr.Tulus, M.Si

PERNYATAAN

ESTIMASI PARAMETER µ DAN σ2

PADA DISTRIBUSI EKSPONENSIAL

TERGENERALISIR DUA VARIABEL MENGGUNAKAN

FUNGSI PEMBANGKIT MOMEN

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa

kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan,

GHAZALI WARDHONO

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, atas segala berkat

dan kasih karunia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah

ditetapkan.

Ucapan terima kasih penulis ucapkan kepada Drs. Pasukat Sembiring, M.Si

dan Drs. Pangeran Sianipar, MS selaku dosen pembimbing pada penyelesaian skripsi

ini yang telah memberikan panduan dan penuh kepercayaan kepada penulis untuk

menyempurnakan kajian ini. Panduan ringkas dan padat dan professional telah

diberikan kepada penulis agar penulis dapat menyelesaikan skripsi ini. Ucapan terima

kasih juga ditunjukan kepada Ketua dan Sekretaris Departemen yaitu Prof.Dr.Tulus,

M.Si. dan Dra. Mardiningsih, M.Si. Dekan pada FMIPA USU, Pegawai di FMIPA

USU serta rekan-rekan kuliah. Akhirnya, tidak terlupakan kepada orang tua saya

ibunda (Siti Rohana) dan ayahanda (Alm. Triman Wardhono), adik saya (M Ishan

Wardhono), serta kedua kakak saya (Mutiah dan Siti Aisyah) dan semua keluarga

yang selama ini memberikan bantuan dan dorongan yang diperlukan. Semoga Tuhan

ABSTRAK

Dalam sebuah distribusi, rata-rata dan variansi merupakan parameter yang penting diestimasi setelah parameter distribusinya sudah diketahui. Dari estimasi kedua parameter tersebut, distribusi dapat lebih mudah dikaji, mengetahui karakteristik, dan mencari ukuran parameter lain seperti kemiringan dan kurtosis dari distribusi tersebut. Dalam mengestimasi kedua parameter tersebut dengan benar, metode yang paling tepat

digunakan adalah fungsi pembangkit momen. Kegunaan yang jelas dari fungsi

pembangkit momen ialah untuk menentukan momen distribusinya. Bila fungsi pembangkit momen dari suatu peubah acak ada, fungsi itu dapat dipakai untuk mentransformasikan dan menemukan seluruh momen dari peubah acak tersebut, dengan menurunkan fungsi pembangkit momen hingga n kali. Dapat diketahui bahwa turunan pertamanya adalah rata-rata dan turunan kedua adalah variansinya. Untuk peubah acak X1 dan X2 yang kontinu, maka fungsi pembangkit momen gabungannya

dinotasikan dengan :

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

M_xx tx+tx ∝

−∝ ∝

−∝

∫ ∫

=

Dalam penelitian ini, distribusi yang akan diestimasi parameter rata-rata dan variansinya adalah distribusi baru yang diperkenalkan Gupta dan Kundu pada tahun 1999, yakni distribusi eksponensial tergeneralisir. Jika terdapat dua peubah acak (X1,X2) yang berdistribusi eksponensial tergeneralisir dengan asumsi saling bebas,

maka distribusi eksponensial tergeneralisir dua variabel (fungsi kepadatan peluang gabungan dari (X1,X2)), untuk x1 > 0, x2 > 0 adalah :

)

,

(

x

₁

x

₂

F

1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

ABSTRACT

From some distribution, the mean and variance is an important parameter estimates after the parameters distribution are known. From estimates of these parameters we can more easily review, investigate the characteristics, and found all of other measurement parameters such as skewness and kurtosis of these distribution. In estimating these parameters correctly, the most appropriate method used is the moment generating function.Obvious usefulness from the moment generating function is to determine the moment of it’s distribution. If the moment generating function of a random variable exists, the function can be used to transform and find all the moments of these random variables, moment generating function by deriveded to n-times. Can be seen that the first derivative is average and the second derivative is the variance. For random variables X1 and X2 are continuous, then the joint moment generating

function is denoted by:

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

M_xx tx+tx ∝

−∝ ∝

−∝

∫ ∫

=

In this research, distributions will be estimated parameter mean and variance is a new distribution introduced by Gupta and Kundu (1999), named a Generalized Exponential Distribution. If there are two random variables (X1,X2) a Generalized Exponential

Distribution with the assumptions are mutually independent, then the Generalized Exponential distribution of two variables (joint probability density function of (X1,X2)), for x1 > 0, x2 > 0 is:

)

,

(

x

₁

x

₂

F

1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

Bab 1 Pendahuluan 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Tinjauan Pustaka 2

1.4 Tujuan Penelitian 5

1.5 Kontribusi Penelitian 5

1.6 Metode Penelitian 6

Bab 2 Landasan Teori 7

2.1 Peluang 7

2.1.1 Peluang Bersyarat 8

2.1.2 Peluang Dua Peristiwa yang Saling Bebas 9

2.2 Peubah Acak dan Distribusinya 9

2.2.1 Peubah Acak 9

2.2.2 Distribusi Peubah Acak 10

2.2.2.1 Distribusi Peubah Acak Diskrit 10 2.2.2.2 Distribusi Peubah Acak Kontinu 11 2.2.3 Distribusi Peubah Acak Gabungan 11

2.3 Defenisi Momen 12

2.3.1 Momen di Sekitar Titik Asal 12

2.3.2 Momen di Sekitar Rataan 13

2.4 Konversi Momen di Sekitar Titik Asal ke

Momen di Sekitar Rataan. 14

2.5 Fungsi Pembangkit 15

2.5.1 Fungsi Pembangkit Eksponensial 15

2.5.2 Fungsi Pembangkit Momen 16

2.5.3 Fungsi Pembangkit Momen Gabungan 19 2.6 Distribusi Eksponensial Tergeneralisir Dua Variabel 21

2.7 Estimasi 22

2.7.1 Estimasi Titik 24

Bab 3 Pembahasan 25 3.1 Transformasi Distribusi Eksponensial Tergeneralisir

Dua Variabel Dengan Fungsi Pembangkit Momen 25 3.2 Fungsi Pembangkit Momen Marginal dari X1 dan X2 26

3.3 Estimator Rata-rata (µ) Pada Distribusi Ekponensial

Tergeneralisir dengan Fungsi Pembangkit Momen 27 3.4 Estimator Variansi (σ2) Pada Distribusi Ekponensial

Tergeneralisir dengan Fungsi Pembangkit Momen 28

3.5 Contoh Kasus 28

3.5.1 Nilai Rata-rata Peubah Acak X1 dan X2 30

3.5.2 Nilai Variansi Peubah Acak X1 dan X2 31

3.5.3 Nilai Estimasi Rata-rata X1 dan X2 dengan Estimator

Rata-rata Fungsi Pembangkit Momen 34 3.5.4 Nilai Estimasi Variansi X1 dan X2 dengan Estimator

Variansi Fungsi Pembangkit Momen 34

Bab 4 Kesimpulan dan Saran 36

4.1 Kesimpulan 36

4.2 Saran 37

Daftar Pustaka 38

DAFTAR TABEL

Tabel 2.1 Momen di Sekitar Titik Asal 13

DAFTAR GAMBAR

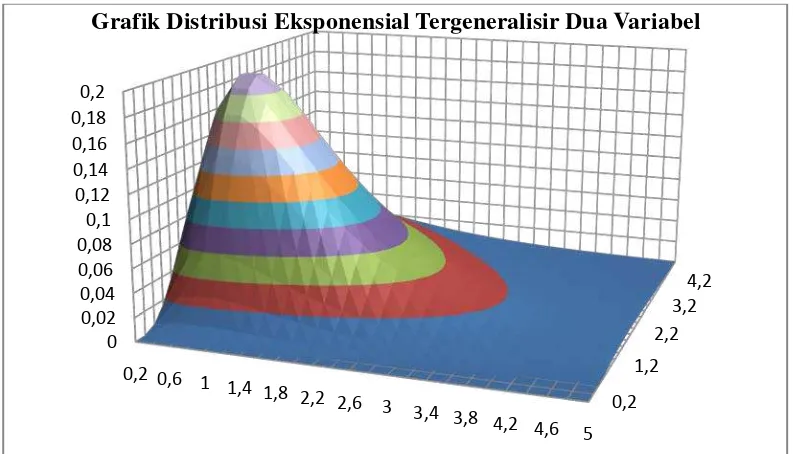
Gambar 3.1 Grafik Distribusi Eksponensial Tergeneralisir

Dua Variabel dengan α = 16 29

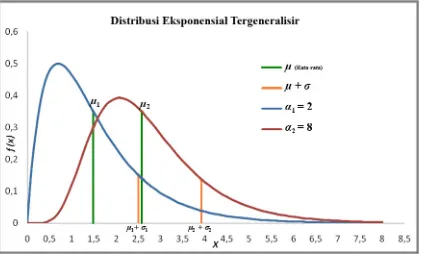
Gambar 3.2 Grafik Distribusi Eksponensial Tergeneralisir

dengan α1 = 2 dan α2 = 8 29

Gambar 3.3 Grafik Peubah Acak X1 dan X2 dengan Garis

ABSTRAK

Dalam sebuah distribusi, rata-rata dan variansi merupakan parameter yang penting diestimasi setelah parameter distribusinya sudah diketahui. Dari estimasi kedua parameter tersebut, distribusi dapat lebih mudah dikaji, mengetahui karakteristik, dan mencari ukuran parameter lain seperti kemiringan dan kurtosis dari distribusi tersebut. Dalam mengestimasi kedua parameter tersebut dengan benar, metode yang paling tepat

digunakan adalah fungsi pembangkit momen. Kegunaan yang jelas dari fungsi

pembangkit momen ialah untuk menentukan momen distribusinya. Bila fungsi pembangkit momen dari suatu peubah acak ada, fungsi itu dapat dipakai untuk mentransformasikan dan menemukan seluruh momen dari peubah acak tersebut, dengan menurunkan fungsi pembangkit momen hingga n kali. Dapat diketahui bahwa turunan pertamanya adalah rata-rata dan turunan kedua adalah variansinya. Untuk peubah acak X1 dan X2 yang kontinu, maka fungsi pembangkit momen gabungannya

dinotasikan dengan :

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

M_xx tx+tx ∝

−∝ ∝

−∝

∫ ∫

=

Dalam penelitian ini, distribusi yang akan diestimasi parameter rata-rata dan variansinya adalah distribusi baru yang diperkenalkan Gupta dan Kundu pada tahun 1999, yakni distribusi eksponensial tergeneralisir. Jika terdapat dua peubah acak (X1,X2) yang berdistribusi eksponensial tergeneralisir dengan asumsi saling bebas,

maka distribusi eksponensial tergeneralisir dua variabel (fungsi kepadatan peluang gabungan dari (X1,X2)), untuk x1 > 0, x2 > 0 adalah :

)

,

(

x

₁

x

₂

F

1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

ABSTRACT

From some distribution, the mean and variance is an important parameter estimates after the parameters distribution are known. From estimates of these parameters we can more easily review, investigate the characteristics, and found all of other measurement parameters such as skewness and kurtosis of these distribution. In estimating these parameters correctly, the most appropriate method used is the moment generating function.Obvious usefulness from the moment generating function is to determine the moment of it’s distribution. If the moment generating function of a random variable exists, the function can be used to transform and find all the moments of these random variables, moment generating function by deriveded to n-times. Can be seen that the first derivative is average and the second derivative is the variance. For random variables X1 and X2 are continuous, then the joint moment generating

function is denoted by:

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

M_xx tx+tx ∝

−∝ ∝

−∝

∫ ∫

=

In this research, distributions will be estimated parameter mean and variance is a new distribution introduced by Gupta and Kundu (1999), named a Generalized Exponential Distribution. If there are two random variables (X1,X2) a Generalized Exponential

Distribution with the assumptions are mutually independent, then the Generalized Exponential distribution of two variables (joint probability density function of (X1,X2)), for x1 > 0, x2 > 0 is:

)

,

(

x

₁

x

₂

F

1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

BAB 1

PENDAHULUAN

1.1Latar Belakang

Distribusi eksponensial tergenaralisir (Generalized Exponential Distribution) pertama

kali diperkenalkan oleh Gupta dan Kundu pada tahun 1999. Distribusi ini diambil dari salah satu fungsi kepadatan kumulatif yang digunakan pada pertengahan abad 19

(Gompertz-Verhulst) untuk membandingkan tabel kematian dan menghasilkan laju

pertumbuhan penduduk. Dimana salah satu dari tiga parameternya distandarisasi

menjadi satu.

Distribusi eksponensial tergenaralisir memilki parameter α sebagai alat untuk

mengestimasi nilai kegagalan awal, dimana semakin besar nilai α maka distribusi

tersebut mendekati distribusi normal. Berbeda dengan distribusi eksponensial biasa

yang memiliki parameter λ, dimana semakin besar nilai λ maka distribusi tersebut

berbentuk linier negatif.

Dalam kajiannya Gupta dan Kundu menggunakan maksimum likelihood estimator untuk menghitung estimasi dari parameter α nya. Dan kemudian

memperoleh observasi, dimana satu set data telah dianalisis ulang dan diamati bahwa

distribusi eksponensial tergeneralisir memberikan hasil yang lebih baik daripada

distribusi eksponensial biasa.

Untuk itu penulis ingin mengkaji lebih mendalam lagi distribusi eksponensial

tergenaralisir dengan mencari estimator parameter µ dan σ2. Banyak metode yang digunakan untuk mencari estimator parameter µ dan σ2, diantaranya dengan menggunakan metode momen, fungsi pembangkit momen, fungsi karakteristik, dan

estimasi maksimum likelihood. Tetapi dalam penelitian ini hanya akan digunakan

dan estimator parameter µ dan σ2 pada distribusi eksponensial tergenaralisir dua variabel.

Dua variabel digunakan tidak hanya untuk harapan estimasi tersebut tidak

berbias, tetapi juga untuk membandingkan bahwa kedua variabel tersebut memiliki

hasil yang sama dari nilai rata-rata dan variansi keseluruhan distribusinya.

Menurut Walpole (1995) kegunaan yang jelas dari fungsi pembangkit momen ialah untuk menentukan momen distribusi. Bila fungsi pembangkit momen suatu

peubah acak memang ada, fungsi itu dapat dipakai untuk membangkitkan atau

menemukan seluruh momen dari peubah acak tersebut, dengan menurunkan fungsi

pembangkit momen hingga n kali. Dapat diketahui bahwa turunan pertamanya adalah

rata-rata dan turunan kedua adalah variansinya.

Dari latar belakang di atas, penulis akan mengkaji tentang “Estimasi Parameter µ dan σ2

Pada Distribusi Eksponensial Tergeneralisir Dua Variabel Menggunakan

Fungsi Pembangkit Momen”

1.2 Perumusan Masalah

Pada penelitian ini rumusan masalah yang dibahas adalah bagaimanakah transformasi

distribusi eksponensial tergeneralisir dua variabel dengan menggunakan fungsi

pembangkit momen untuk mencari marginal fungsi pembangkit momennya, kemudian

mencari estimator parameter rata-rata (µ) dan parameter variansinya (σ2) dan mengestimasi kedua parameter tersebut.

1.3Tinjauan Pustaka

Dijelaskan oleh Gupta dan Kundu (1999) bahwa distribusi ekponensial tergeneralisir

kumulatif (fkk) dan fungsi kepadatan peluang (fkp) dengan x > 0, adalah sebagai

berikut :

α λ

λ

α

, ) (1 )

;

( x

GE x e

F = − −

1

) 1

( )

, ;

(

α

λ

=

αλ

−λx − −λx α−

GE x e e

F

Dengan :

x

= peubah acak

α

= parameter bentuk

λ

= parameter skala

e

= 2,7183

Jika (X1,X2) merupakan distribusi eksponensial tergeneralisir dua variabel

dengan asumsi saling bebas, maka fungsi kepadatan peluang gabungan dari (X1,X2),

untuk x1 > 0, x2 > 0 adalah :

) , (x1 x2

F 1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

Untuk mentransformasi distribusi eksponensial tergeneralisir dua variabel di

atas dengan fungsi pembangkit momen. Maka akan disubtitusikan dengan persamaan

fungsi pembangkit momen yang di jelaskan sebagai berikut :

Dijelaskan oleh Walpole dan Myers (1995) bahwa fungsi pembangkit momen atau Moment generating function (MGF) dari sebuah peubah acak X dapat

didefinisikan sebagai:

) ( )

( tx

x t E e

M = _untuk t dalam R

di mana T = {t ∈R : M_x(t) < ∞}.

Karena distribusi yang akan ditransformasi merupakan distribusi gabungan

maka fungsi pembangkit momennya harus dalam bentuk gabungan (Joint Moment

Generating Function), yang di notasikan sebagai berikut:

) (

) ,

( 11 22

2

1 1 2

x t x t x

x t t E e

Untuk peubah acak X1 dan X2 yang kontinu dan bebas satu sama lain (saling

lepas), dinotasikan dengan :

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

Mxx tx tx + ∝ −∝ ∝ −∝

∫ ∫

=

Berdasarkan fungsi pembangkit momen gabungan dari X1 dan X2, dapat

ditentukan fungsi pembangkit momen masing-masing dari X1 dan X2 yang dinamakan

fungsi pembangkit momen marginal dari X1 dan fungsi pembangkit momen marginal

dari X2

Fungsi pembangkit momen marginal dari X

.

1 diperoleh dari fungsi pembangkit

momen gabungan dengan mensubstitusikan t2 = 0, sehingga:

) ( ) ( ) 0 ,

( 11

1 1 x t e E t M t

M = = _{, dan}

Fungsi pembangkit momen marginal dari X2 diperoleh dari fungsi pembangkit

momen gabungan dengan mensubstitusikan t1 = 0, sehingga:

) ( ) ( ) , 0

( 2 2

2 2 x t e E t M t

M = =

Kemudian dapat ditentukan momen – momen dari peubah acak X1 berdasarkan

fungsi pembangkit momen marginalnya. Dimana momen ke-1 yang juga merupakan

nilai parameter rata-rata (µ), dihitung dengan meggunakan rumus :

1 0

1

1,0) (0,0)

( ) ( 1 t M t t M X E t x _∂ ∂ = ∂ ∂ = = =

µ

Dan momen ke-2nya dihitung dengan menggunakan rumus:

2 1 0 2 1 1 2

2 ( ,0) (0,0)

Dari rumus momen ke-1 dan momen ke-2, maka dapat di hitung nilai parameter

variansi (σ2)nya dengan menggunakan rumus :

2

1 2

1 2

2 (0,0) (0,0)

)

( _

  

 

∂ ∂ − ∂

∂ =

t M t

M Var

σ

_x

Perhitungan yang sama juga dapat dilakukan dalam menentukan nilai parameter

rata-rata (µ) dan nilai parameter variansi (σ2) dari peubah acak X2 berdasarkan fungsi

pembangkit momen marginalnya dengan menggunakan rumus di atas.

1.4Tujuan Penelitian

Penelitian ini bertujuan untuk mentransformasi distribusi eksponensial tergeneralisir

dua variabel dengan menggunakan fungsi pembangkit momen untuk mencari marginal

fungsi pembangkit momennya, kemudian mencari estimator parameter rata-rata (µ)

dan parameter variansinya (σ2

) dan mengestimasi kedua parameter tersebut.

1.5

Kontribusi Penelitian

Kesimpulan yang diperoleh setelah dilakukan penelitian, diharapkan :

1. Memudahkan penggunaan distribusi eksponensial tergeneralisir dua variabel

secara praktis.

2. Sebagai bahan kajian untuk menganalisis distribusi eksponensial tergeneralisir dua

variabel lebih mendalam.

3. Memperkaya literatur dalam bidang statistika terutama yang berhubungan dengan

1.6Metode Penelitian

Metode yang digunakan dalam penelitian ini adalah:

1. Dengan melakukan studi literatur terlebih dahulu mengenai fungsi pembangkit

momen dan distribusi eksponensial tergeneralisir dua variabel.

2. Memaparkan dan menjelaskan pengertian fungsi pembangkit momen dan

distribusi eksponensial tergeneralisir dua variabel.

3. Mensubtitusi persamaan fungsi pembangkit momen dengan persamaan

distribusi eksponensial tergeneralisir dua variabel.

4. Mentransformasikan persamaan yang didapat dari hasil subtitusi dengan

mengintegralkan persamaan tersebut.

5. Mencari estimator parameter rata-rata (µ) dan parameter variansi (σ2) dengan mencari turunan pertama dan turunan kedua dari hasil transformasi

persamaannya.

6. Mengestimasi parameter rata-rata (µ) dan parameter variansi (σ2) dengan menguji nilai kedua parameter tersebut pada contoh kasus.

BAB 2

LANDASAN TEORI

2.1 Peluang

Peluang adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu

peristiwa (event) akan terjadi di masa mendatang yang hasilnya tidak pasti (uncertain

event). Peluang dinyatakan antara 0 (nol) sampai 1 (satu) atau dalam persentase.

Peluang 0 menunjukkan peristiwa yang tidak mungkin terjadi, sedangkan peluang 1

menunjukkan peristiwa yang pasti terjadi. P(A) = 0,99 artinya probabilitas bahwa

kejadian A akan terjadi sebesar 99 % dan peluang A tidak terjadi adalah sebesar 1%.

Ada tiga hal penting dalam rangka membicarakan peluang, yaitu percobaan

(experiment), ruang sampel (sample space), kejadian (event), dan titik sampel (sample point).

Percobaan (experiment) adalah pengamatan terhadap beberapa aktivitas atau

proses yang memungkinkan timbulnya paling sedikit 2 (dua) peristiwa tanpa

memperhatikan peristiwa mana yang akan terjadi.

Ruang sampel (sample space) atau semesta (universe) merupakan himpunan dari

semua hasil (outcome) yang mungkin dari suatu percobaan (experiment). Jadi ruang

sampel adalah seluruh kemungkinan peristiwa yang akan terjadi akibat adanya suatu

percobaan atau kegiatan.

Kejadian (event) adalah kumpulan dari satu atau lebih hasil yang terjadi pada

sebuah percobaan atau kegiatan. Kejadian menunjukkan hasil yang terjadi dari suatu

percobaan. Dalam setiap percobaan atau kegiatan hanya ada satu hasil. Pada kegiatan

jual beli saham, kalau tidak membeli berarti menjual. Pada perubahan harga terjadi

Besarnya nilai kemungkinan bagi munculnya suatu kejadian adalah selalu

diantara 0 (nol) dan 1 (satu). Pernyataan ini dapat ditulis sebagai 0 ≤P(A) ≤ 1, dimana

P(A) menyatakan nilai kemungkinan bagi munculnya kejadian A. Jika suatu percobaan

dapat menghasilkan N macam hasil yang berkemungkinan sama (equally likely) dan

jika tepat terdapat sebanyak n hasil yang berkaitan dengan kejadian A, maka peluang

kejadian A adalah :

N

n A P( )=

(2.1)

Titik sampel (sample point) merupakan tiap anggota atau elemen dari ruang

sampel. Jika suatu operasi dapat dilakukan dengan n1 cara, dan bila untuk setiap cara

ini operasi kedua dapat dilakukan dengan n2 cara, dan bila untuk setiap cara ini operasi

ketiga dapat dilakukan dengan n3 cara, dst, maka deretan k operasi dapat dilakukan

dengan n1,n2,...,nk cara. Dalam penelitian ini akan dibahas teori peluang bersyarat dan

peluang dua peristiwa yang saling bebas, sebagai berikut :

2.1.1 Peluang Bersyarat

Jika A dan B adalah dua buah peristiwa yang di bentuk dari ruang sampel S, maka

peluang bersyarat dari A diberikan B didefenisikan sebagai :

) (

) (

) | (

B P

B A P B A

P = ∩ Dengan 0 ≤P(A) ≤ 1 (2.2)

Dalam hal ini, P(A|B) adalah perhitungan peluang peristiwa A, apabila

peristiwa B sudah terjadi. Atau dapat dinyatakan bahwa peluang peristiwa A dan B

kedua-duanya terjadi sama dengan peluang peristiwa B terjadi dikalikan dengan

2.1.2 Peluang Dua Peristiwa yang Saling Bebas

Dalam pembicaraan sehari-hari, dua buah peristiwa dikatakan bebas, jika terjadinya

atau tidak terjadinya peristiwa yang satu tidak dipengaruhi oleh terjadinya peristiwa

yang lain.

Perumusan dua peristiwa yang saling bebas didasarkan pada perumusan

perkalian dari peluang bersyarat, yaitu :

P(A∩B)=P(B).P(A|B)

Karena dua peristiwa A dan B bebas, maka dalam perhitungan P(A|B)

terjadinya peristiwa A tidak dipengaruhi oleh terjadinya peristiwa B. Sehingga

peristiwa A diberikan peristiwa B akan merupakan peristiwa A itu sendiri. Akibatnya,

) ( ) |

(A B P A

P = . Dengan demikian :

) ( ). ( )

(A B P B P A P ∩ =

(2.3)

2.2 Peubah Acak dan Distribusinya

2.2.1 Peubah Acak

Peubah acak atau variabel acak merupakan hasil-hasil prosedur penyampelan acak

(random sampling) atau eksperimen acak dari suatu data yang telah dianalisis secara

statistik. Peubah acak dapat dinyatakan dengan huruf besar (X), sedangkan nilai dari

peubah acak dinyatakan dengan huruf kecil (x).

Definisi 2.1 :

Peubah acak ialah suatu fungsi yang mengaitkan suatu bilangan real pada setiap unsur

2.2.2 Distribusi Peubah Acak

2.2.2.1 Distribusi Peubah Acak Diskrit

Seringkali untuk memudahkan suatu perhitungan semua peluang peubah acak

dinyatakan dalam suatu fungsi nilai-nilai X seperti f(X) yaitu f(X)=P(X =x). Pada peubah acak diskrit, setiap nilainya dikaitkan dengan peluang. Himpunan pasangan

berurutan (x,f(X)) disebut distribusi peluang peubah acak X. Sebuah distribusi yang

mencantumkan semua kemungkinan nilai peubah acak diskrit berikut peluangnya

disebut peluang diskrit, (Wibisono, 2005: 224).

Suatu peubah acak diskrit dapat dinyatakan sebagai:

∑

= ( ) )

(X p X

f ( 2.4)

Definisi 2.2 :

Himpunan pasangan terurut (x,f(X)) merupakan suatu fungsi peluang, fungsi massa

peluang, atau distribusi peluang peubah acak diskrit X bila, untuk setiap kemungkinan

hasil x:

1. f(X)≥0

2.

∑

=

x x f( ) 1

3. f(X)=P(X =x) (Walpole & Myers, 1995 :54)

Definisi 2.3 :

Jika peubah X dapat menerima suatu himpunan diskrit dari nilai-nilai X1, X2, . . . ,Xn

dengan peluang masing-masing P1,P2, . . . Pn, dimana P1+P2+ . . . + Pn = 1, maka suatu

fungsi f(X) yang mempunyai nilai masing - masing P1,P2, . . . Pi untuk X1, X2, . . . ,Xi

disebut fungsi peluang. Sehingga dapat dituliskan dengan f(X) = P(X = Xi), yaitu

2.2.2.2 Distribusi Peubah Acak Kontinu

Distribusi peluang bagi peubah acak kontinu tidak dapat disajikan dalam bentuk tabel,

akan tetapi distribusinya dapat dinyatakan dalam persamaan yang merupakan fungsi

nilai-nilai peubah acak kontinu dan digambarkan dalam bentuk kurva,

(Wibisono,2005:226).

Suatu peubah acak kontinu dapat dinyatakan sebagai:

( )

∫

∝

∝ −

= f x dx X

f( ) (2.5)

Definisi 2. 4 :

Fungsi f(x) adalah fungsi padat peluang peubah acak kontinu X, yang didefinisikan

atas himpunan semua bilangan real R, bila

1. f(x) ≥ 0 untuk semua x ∈ R.

2.

∫

( )

=1

∝

∝ −

dx x f

3. P(a < x < b)=

∫

( )

b

a

dx x

f (Walpole & Myers, 1995 :60)

2.2.3 Distribusi Peubah Acak Gabungan

Seperti yang dijelaskan pada subbab sebelumnya ada dua macam peubah acak, yaitu

peubah acak diskrit dan peubah acak kontinu. Tetapi karena distribusi yang akan

diteliti dalam penelitian ini merupakan distribusi kontinu, maka hanya akan dibahas

peubah acak kontinu.

Jika S merupakan ruang sampel dari sebuah eksperimen, maka pasangan (X,Y)

dinamakan peubah acak gabungan, jika X dan Y masing-masing menghubungkan

(X,Y) disebut peubah acak gabungan kontinu, jika banyak nilai-nilai yang

mungkin dari X dan Y masing-masing berbentuk sebuah interval. Perhitungan peubah

acak kontinu yang masing-masing berharga tertentu, memerlukan sebuah fungsi yang

dinamakan fungsi kepadatan gabungan. Yang didefenisikan sebagai berikut :

( )

∫∫

= ∈

A

dy dx y x f A

X

P[( ) ] ,

(2.6)

Dengan A terletak dalam bidang-xy.

Sebuah fungsi dari dua peubah acak kontinu X dan Y dapat digunakan sebagai

fungsi kepadatan gabungan, jika nilai-nilainya yaitu f(x,y), memenuhi sifat-sifat

sebagi berikut :

1. f(x,y)≥0 untuk −∝<x<∝,−∝< y<∝

2. [( )∈ ]=

∫ ∫

( )

, =1

∝

∝ −

∝

∝ −

dy dx y x f A

X P

2.3 Defenisi Momen

Dalam menentukan nilai ekspektasi rata-rata dan nilai ekspektasi variansi, dimana

nilai – nilai kedua ukuran diatas merupakan pangkat ke-1 dan pangkat ke-2 dari nilai

ekspektasi. Sehingga dapat ditentukan perumusan umum untuk menghitung nilai

ekspektasi dari pangkat ke-r yang biasa disebut dengan momen. Momen terdiri dari 2

jenis, yaitu:

2.3.1 Momen di Sekitar Titik Asal

Momen ke-r di sekitar titik asal dari sebuah random variabel X dapat didefinisikan

sebagai µ_r' =E[(X −0)r]=E[(X)r]asalkan nilai ekspektasi itu ada. Untuk X diskrit, maka fungsi peluang f(X) :

] ) [(X r

E = 1 ( 1) 2 ( 2) ... ( n)

r n r

r

x f X x

f X x f

] ) [(X r

E =

∑

=

n

i r i f x

X

1

1)

(

(2.7)

Untuk X kontinu, maka fungsi peluang f(X) :

] ) [(X r

E =

∫

∝

∝ −

) (x₁ f X_ir

(2.8)

Dalam hal ini, E[(Xr)] merupakan momen ke-r. Sehingga dapat diperoleh momen ke-0

sampai ke-4 di sekitar titik asal, sebagai berikut :

Tabel 2.1 Momen di Sekitar Titik Asal

Momen Momen di Sekitar Titik Asal

Momen ke-0 ' _{[( )}0_{] 1}

0 =E X =

µ

Momen ke-1 µ' = _{[( )}1_]= _{( )}=µ

1 E X E X

Momen ke-2 ' _{[( )}2_]

2 =E X

µ

Momen ke-3 ' _{[( )}3_]

3 =E X

µ

Momen ke-4 ' _{[( )}4_]

4 =E X

µ

Dari tabel di atas dapat dilihat momen pertama di sekitar titik asal dari suatu

distribusi adalah nilai rata-rata.

2.3.2 Momen di Sekitar Rataan

Momen ke-r di sekitar rataan dari sebuah random variabel X dapat didefinisikan

sebagai µ_r =E[(X −µ)r].

Teorema 2.1 :

Momen pertama dari momen di sekitar rataan bernilai 0.

Bukti: [( )1] [( )] [ ] 0

1 = −µ = −µ = −µ =

µ E X E X E X

Sehingga dapat diperoleh momen ke-0 sampai ke-4 di sekitar rataan, sebagai

Tabel 2.2 Momen di Sekitar Rataan

Momen Momen di Sekitar Rataan

Momen ke-0 _{[( )}0_{] 1}

0 = −µ =

µ E X

Momen ke-1 _{[( )}1_{] 0}

1 = −µ =

µ E X

Momen ke-2 _{[( )}2_]

2 µ

µ =E X −

Momen ke-3 _{[( )}3_]

3 µ

µ =E X −

Momen ke-4 _{[( )}4_]

4 µ

µ =E X −

Dari tabel di atas dapat dilihat momen kedua di sekitar rataan dari suatu

distribusi adalah nilai variansi.

2.4 Konversi Momen di Sekitar Titik Asal ke Momen di Sekitar Rataan

Dengan menggunakan dalil binomial, maka dapat diperoleh konversi momen pusat

ke-r di sekitar titik asal ke momen pusat ke-r di sekitar rataan sebagai berikut:

] )

[( r

r E X µ

µ = − = _i r i

r i i r ₋ = −      

∑

'( ) 0 µ µ (2.9)

Kemudian dengan mensubtitusikan beberapa nilai r ke dalam rumus di atas,

maka akan didapat nilai variansi, kemiringan dan kurtosisnya. Dimana nilai

variansinya didapat dari subtitusi nilai r = 2, sebagai berikut :

2

µ = i

i i i − = −      

∑

' 2

2 0 ) ( 2 µ µ

= ₀' 2 ₁' 1 ₂' ( )0

2 2 ) ( 1 2 ) ( 0 2 µ µ µ µ µ µ _ −      + −       + −      

= 2' ' 1 2

2µ µ µ

µ − +

2

µ = ' 2

2 µ

µ −

(2.10)

Sehingga didapat nilai variansinya, yaitu hasil dari pengurangan momen pusat

ke-r di sekitar titik asal ke-2 dikurang kuadrat dari momen pusat ke-r di sekitar titik

asal ke-1. Atau sering di notasikan dengan :

) (X

Var = E(X2)−E(X)2

2.5 Fungsi Pembangkit

Fungsi Pembangkit adalah salah satu metode yang dapat digunakan untuk

menyelesaikan permasalahan. Dengan men-translasi persoalan ke dalam Fungsi

Pembangkit, maka kita dapat menggunakan sifat-sifat khusus dari Fungsi Pembangkit

sebagai jalan untuk memecahkan masalah. Fungsi Pembangkit ini bisa kita perlakukan

sebagaimana fungsi-fungsi pada umumnya. Misal saja melakukan operasi diferensial.

Fungsi Pembangkit memiliki banyak penggunaan, misalnya untuk menyelesaikan

permasalahan rekurensi, counting, membuktikan identitas kombinatorika, maupun

aplikasi-aplikasi lain yang beragam. Dalam penerapannya, banyak metode yang

menggunakan Fungsi Pembangkit sebagai alat penyelesaian masalah.

Fungsi pembangkit dari barisan bilangan S (terhingga atau takhingga)

,... , , , _{1 2 3} 0 a a a

a dapat didefenisikan dalam bentuk deret sebagai berikut :

i i i

i

ix a a x a x a x a x

a x

A =

∑

= + + + + +

∝

=

... )

( _{0 1} 1 ₂ 2 ₃ 3

0

(2.12)

Pada deret tersebut, pangkat dari variabel x merupakan indikator sedemikian

hingga koefisien dari xi adalah harga fungsi numerik pada i. Untuk sebuah fungsi

numerik ai digunakan nama A(x) untuk menyatakan fungsi pembangkitnya.

Walaupun ada banyak jenis-jenis fungsi pembangkit, tetapi dalam penelitian ini

hanya akan di bahas fungsi pembangkit eksponensial dan fungsi pembangkit momen.

2.5.1 Fungsi Pembangkit Eksponensial

Fungsi pembangkit eksponensial merupakan salah satu alat penyelesaian masalah dari

beberapa jenis fungsi pembangkit. Dimana fungsi pembangkit ini diambil dari Deret

Maclaurin sebagai berikut :

∑

∝

= = +

+ +

+ +

o r

r r r

r

r x a r

x a x

a x a x a a

! !

... ! 3 !

2 !

1

Jika nilai a₀,a₁,a₂,a₃,...,a_r =1, maka dapat didefenisikan fungsi pembangkit

eksponensial adalah sebagai berikut

∑

∝ = = + + + + + = o r r r x r x r x x x x e ! ! ... ! 3 ! 2 1 3 2 (2.13)

Dan untuk e−xdidefenisikan sebagai berikut :

∑

∝ = − _{= − + − + + − = −} o r r r r r x r x r x x x x e ! ) 1 ( ! ) 1 ( ... ! 3 ! 2 1 3 2 (2.14)

Dalam penelitian ini hanya akan dibahas satu ekspansi binomial dalam bentuk

fungsi pembangkit eksponensial sebagai berikut :

Teorema 2.2 :

∑

= − −       − = − n i ix i n x _e i n e 0 ) 1 ( ) 1 (

Bukti :

Dengan menggunakan rumus Binom Newton :

∑

= −       = + n i i i n n b a i n b a 0 ) ( (2.15) Maka : n x e ) 1 ( − − =

∑

= − − ₋       n i i x i n e i n 0 )) )( 1 (( ) 1 ( =

∑

= − −       n i i x i e i n 0 ) ( ) 1 ( =

∑

= −       − n i ix i e i n 0 ) 1 (

2.5.2 Fungsi Pembangkit Momen

Menurut Ronald dan Raymond (1995). Kegunaan yang jelas dari fungsi pembangkit

momen ini adalah untuk menentukan momen-momen distribusi. Akan tetapi,

kegunaan yang terpenting adalah untuk mencari distribusi dari fungsi peubah acak.

Definisi 2.5 :

Fungsi pembangkit momen dari suatu peubah acak X didefinisikan untuk setiap

bilangan riil t sebagai M_X(t)=E(etx)

(Dudewich & Mishra, 1995 : 300)

Dari definisi 2.5, dapat diuraikan dalam 2 kasus yang berbeda, yaitu untuk

peubah acak diskrit dan peubah acak kontinu.

Fungsi pembangkit momen untuk peubah acak diskrit dari X di x yaitu:

M (t) E(e ) e f(x)

x tx tx

x = =

∑

(2.16)

Fungsi pembangkit momen untuk peubah acak kontinu dari X di x yaitu:

∫

∝

∝ − =

= ( ) ( ) )

(t E e e f x

M_x tx tx (2.17)

(Spiegel, 1991:80)

Teorema 2.3 :

Bila fungsi pembangkit momen M_x(t) dari peubah acak X ada untuk t ≤ T, untuk T

> 0, maka E(Xr)dengan (n = 1,2,3,…), makaE(Xr) = M(_Xr)(0).

) (Xr

E = M_X(r)(0)

=

0 ) (

=

t X r r

t M dt

d

(Dudewich & Mishra, 1995 : 300)

Bukti :

Diketahui bahwa M_X(t)=E(etx)_, Dengan menggunakan deret Maclaurin :

! ... ! 3 ! 2 1

3 2

r y y

y y e

r

y = + + + + +

Jika y diganti tX maka :

! ) ( ... ! 3

) ( ! 2

) ( 1

3 2

r tX tX

tX tX e

r

y _{= + + + + +}

Sehingga diperoleh :

) (t

= _      + + + + + ! ) ( ... ! 3 ) ( ! 2 ) ( 1 3 2 r tX tX tX tX E r =

( ) ( )

_      + +       +       + + ! ) ( ... ! 3 ) ( ! 2 ) ( 1 3 2 r tX E tX E tX E tX E E r

=

( )

( )

( )

( )

r

r X E r t X E t X E t X tE ! ) ( ... ! 3 ) ( ! 2 ) ( 1 3 3 2 2 + + + + +

=

( )

( )

( )

( )

r

r X E r t X E t X E t X tE ! ) ( ... ! 3 ) ( ! 2 ) ( 1 3 3 2 2 + + + + +

JikaM_X(t)diturunkan terhadap t, kemudian harganya sama dengan nol, maka

akan diperoleh:

) ( '

t

M_X =

( )

( )

( )

( )

r

r X E r t r X E t X E t X E ! . ... ! 3 3 ! 2

2 3 1

2 2 − + + + + ) 0 ( ' X

M = E

( )

X =µ₁' momen pusat ke-1 di sekitar titik asal

) ( ' ' _t

M_X =

( )

( )

( )

r

r X E r t r r X E t X E ! ) 1 ( ... ! 3

6 3 2

2 − − + + + ) 0 ( ' ' X

M = E

( )

X2 =µ₂' momen pusat ke-2 di sekitar titik asal

) ( ' ' ' t

M_X =

( )

( )

r

r X E r t r r r X E ! ) 2 )( 1 ( ... 3 3 − − − + + ) 0 ( ' ' ' X

M =

( )

' 3 3 =µ

X

E momen pusat ke-3 di sekitar titik asal

. . .

Sampai turunan ke-r

Jadi untuk mendapatkan momen ke-r dari suatu peubah acak X adalah dengan

menurunkan fungsi pembangkit momen sebanyak r kali dan memasukkan nilai t = 0,

sehingga terbukti bahwa:

) (Xr E =

Teorema 2.4 :

Jika M_X(t)adalah fungsi pembangkit momen dari peubah acak X dan a adalah suatu

konstanta, maka fungsi pembangkit momen dari aX adalah:

) (t

M_aX = MX(at)

(Spiegel, 1991 : 80)

Bukti:

) (t

M_aX = E(etaX)

= E(e(ta)X)

= MX(at)

Teorema 2.5 :

Jika M_X(t)adalah fungsi pembangkit momen dari peubah acak X, a dan b adalah

suatu konstanta, maka fungsi pembangkit momen dari aX + b adalah:

) (t

M_aX+b = M_X(at)ebt

Bukti :

) (t

M_aX+b = E(e(aX+b)t)

= _E(_eatX+bt)

= E(eatX).E(ebt)

= M_X(at).ebt

2.5.3 Fungsi Pembangkit Momen Gabungan

Fungsi pembangkit momen gabungan atau Joint MGF dapat didefinisikan sebagai

fungsi pembangkit momen yang diperoleh berdasarkan fungsi peluang gabungan atau

fungsi densitas gabungan dari dua peubah acak. Dalam hal ini, fungsi pembangkit

momen gabungan dapat digunakan untuk memperoleh momen-momen, baik untuk

Sehingga fungsi pembangkit momen gabungan dari (X1, X2)didefinisikan untuk

bilangan riil (t1, t2) sebagai:

) , ( _{1 2}

, 2

1 t t

M_{X X} = _E(_et1X1+t2X2) _(2.18)

(Dudewicz & Mishra, 1995 : 305)

Teorema 2.6 :

Misal fungsi pembangkit momen gabungan dari (X1, X2) ada, maka X1 dan X2

merupakan peubah acak yang saling bebas jika _, (₁, ₂)

2 1 t t

M_{X X} = (₁). ( ₂) 2

1 t M t

M_{X X}

Bukti:

) , ( _{1 2}

, 2 1 t t

M_{X X} = _E(_et1X1+t2X2)

= _E(_et1X1._et2X2)

= _E(_et1X1)._E(_et2X2)

= ( ₁). ( ₂) 2

1 t M t

M_{X X}

Untuk peubah acak X1 dan X2 yang kontinu, maka fungsi pembangkit momen

gabungannya dinotasikan dengan :

2 1 2 2 1 1 2

1, ) ( ) ( )

( 11 2 2

2

1 t t e f x f x dxdx

M_xx tx+tx ∝

−∝ ∝

−∝

∫ ∫

= _(2.19)

Berdasarkan fungsi pembangkit momen gabungan dari X1 dan X2, dapat

ditentukan fungsi pembangkit momen masing-masing dari X1 dan X2 yang dinamakan

fungsi pembangkit momen marginal dari X1 dan fungsi pembangkit momen marginal

dari X2

Fungsi pembangkit momen marginal dari X

.

1 diperoleh dari fungsi pembangkit

momen gabungan dengan mensubstitusikan t2

) ( ) ( ) 0 ,

( 11

1 1

x t e E t M t

M = =

= 0, sehingga :

(2.20)

Fungsi pembangkit momen marginal dari X2 diperoleh dari fungsi pembangkit

momen gabungan dengan mensubstitusikan t1

) ( ) ( ) , 0

( 2 2

2 2

x t e E t M t

M = =

= 0, sehingga :

Sehingga didapat hasil transformasinya, yang kemudian dapat ditentukan

momen – momen dari peubah acak X1

1 0

1

1,0) (0,0) (

) (

1 t

M t

t M X

E

t

x _∂

∂ = ∂

∂ = =

=

µ

berdasarkan fungsi pembangkit momen

marginalnya. Dimana momen ke-1 yang juga merupakan nilai parameter rata-rata (µ),

dihitung dengan meggunakan rumus :

(2.22)

Dan momen ke-2nya dihitung dengan menggunakan rumus:

2 1 0

2 1

1 2

2 ( ,0) (0,0) )

(

1 t

M t

t M X

E

t ∂

∂ = ∂

∂ =

= (2.23)

Dari hasil hitung momen ke-1 dan momen ke-2, maka dapat dihitung nilai

parameter variansi (σ2

2

1 2

1 2

2 (0,0) (0,0) )

( _

  

 

∂ ∂ − ∂

∂ =

t M t

M Var σ_x

)nya dengan menggunakan rumus :

(2.24)

Perhitungan yang sama juga dapat dilakukan dalam menentukan nilai parameter

rata-rata (µ) dan nilai parameter variansi (σ2) dari peubah acak X2 berdasarkan fungsi

pembangkit momen marginalnya dengan menggunakan rumus di atas.

2.6 Distribusi Eksponensial Tergeneralisir Dua Variabel

Distribusi eksponensial tergenaralisir (Generalized Exponential Distrubution) pertama

kali diperkenalkan oleh Gupta dan Kundu pada tahun 1999. Distribusi ini diambil dari salah satu fungsi kepadatan kumulatif yang digunakan pada pertengahan abad 19

(Gompertz-Verhulst) untuk membandingkan tabel kematian dan menghasilkan laju

pertumbuhan penduduk. Yang didefeniskan sebagai berikut :

α λ

ρ

)

1

(

)

(

t

e

t

G

=

−

−

Kemudian dengan menstandarisasikan ρ = 1 dan x = t, maka didapat distribusi

Distribution) dengan fungsi kepadatan kumulatif (fkk) dan x > 0, adalah sebagai

berikut :

α λ

λ

α

,

)

(

1

)

;

(

x

GE

x

e

F

=

−

−

dari turunan fungsi kepadatan kumulatif di atas, juga didapat fungsi kepadatan

peluangnya (fkp) adalah sebagai berikut :

1

) 1

( )

, ;

(

α

λ

=

αλ

−λx − −λx α−

GE x e e

F _(2.25)

Dengan :

x

= peubah acak

α

= parameter bentuk

λ

= parameter skala

e

= 2,7183

Dimana α > 0 dan λ > 0 masing – masing adalah parameter bentuk dan parameter

skala. Ini jelas bila α = 1, maka distribusi diatas merupakan distribusi eksponensial. Sekarang untuk memfokuskan pada kajian parameter α, maka λ = 1. Sehingga

distribusi eksponensial tergeneralisir dengan parameter bentuk di notasikan dengan

GE(α).

Jika terdapat dua peubah acak (X1,X2) yang berdistribusi eksponensial

tergeneralisir dengan asumsi saling bebas, maka distribusi eksponensial tergeneralisir

dua variabel (fungsi kepadatan peluang gabungan dari (X1,X2)), untuk x1 > 0, x2 > 0

adalah :

)

,

(

x

₁

x

₂

F

1 1 1 2 2 1 1 2

2

1

(

1

)

(

1

)

x x x

x

e

e

e

− −

−

− − − −

−

=

α

α

α α

(2.26)

2.7 Estimasi

Estimasi adalah menaksir ciri-ciri tertentu dari populasi atau memperkirakan

nilai populasi (parameter) dengan memakai nilai sampel (statistik). Dengan statistika

berusaha menyimpulkan populasi. Cara pengambilan keputusan tentang parameter

sebenarnya yang tidak diketahui akan diestimasi berdasarkan statistik sampel yang

diambil dari populasi yang bersangkutan.

Sifat atau ciri estimator yang baik yaitu tidak bias, efisien dan konsisten:

1. Estimator yang tidak bias

Estimator dikatakan tidak bias apabila ia dapat menghasilkan estimasi yang

mengandung nilai parameter yang diestimasikan. Misalkan, estimator θˆ

dikatakan estimator yang tidak bias jika rata-rata semua harga θˆ yang

mungkin akan sama dengan θ. Dalam bahasa ekspektasi ditulis E

( )

θˆ =θ.

Misalkan X adalah variabel random dengan rata-rata µ dan varian σ2 ,

n X X

X₁, ₂,..., adalah sampel random yang besarnya n dari X , maka rata-rata

sampel X dan varian sampel S2 adalah estimator yang tidak bias dari µ dan 2

σ .

2. Estimator yang Efisien

Estimator dikatakan efisien apabila hanya dengan rentang nilai estimasi yang

kecil saja sudah cukup mengandung nilai parameter. Estimator bervarians

minimum ialah estimator yang efisien diantara semua estimator untuk

parameter yang sama. Jika θˆ₁ dan θˆ₂ dua estimator untuk θ dimana varians

untuk θˆ₁ lebih kecil dari varians untuk θˆ₂, maka θˆ₁ merupakan estimator yang efisien.

3. Estimator yang konsisten

Estimator dikatakan konsisten apabila sampel yang diambil beberapa pun

besarnya, pada rentangnya tetap mengandung nilai parameter yang sedang

diestimasi. Misalkan, θˆ estimator untuk θ yang dihitung berdasarkan sebuah

sampel acak berurutan n. Jika ukuran sampel n makin besar mendekati

ukuran populasi menyebabkan θˆ mendekati θ, maka θˆ disebut estimator

Estimasi nilai parameter memiliki dua cara, yaitu estimasi titik (point

estimation) dan estimasi selang (interval estimation).

2.7.1 Estimasi Titik

Estimasi titik adalah estimasi yang dalam nilai populasinya (parameter) ditentukan

hanya oleh satu nilai saja. Nilai yang dipakai menduga populasi tersebut dinamakan

estimator. Misalkan x₁,x₂,...,x_n merupakan sampel acak berukuran n dari X , maka

statistik θˆ=h

(

x₁,x₂,...,x_n

)

yang berkaitan dengan θ dinamakan penaksir dari θ.

Setelah sampel diambil, nilai-nilai yang dihitung dari sampel itu digunakan sabagai

taksiran titik θ.

2.7.2 Estimasi Interval

Estimasi interval adalah estimasi dalam suatu interval dimana interval tersebut

ditentukan batas atas dan batas bawah suatu estimator. Metode ini memuat nilai-nilai

estimator yang masih dianggap benar dalam tingkat (selang) kepercayaan tertentu

BAB 3

PEMBAHASAN

3.1 Transformasi Distribusi Eksponensial Tergeneralisir Dua Variabel Dengan Fungsi Pembangkit Momen

Dalam membentuk hubungan fungsional dari suatu hasil percobaan. Maka diperlukan

fungsi pendekatan untuk menggambarkan hasil percobaan tersebut, yang sering

disebut fungsi distribusi. Dari fungsi distribusi tersebut, maka kita dapat melakukan

analisis statistik terhadap populasi yang diamati. Termasuk mengestimasi nilai

rata-rata dan variansi dari hasil percobaan tersebut dengan fungsi distribusi.

Jika terdapat peubah acak yang berdistribusi tertentu, maka kita dapat

mengestimasi parameter rata-rata dan parameter variansinya dengan menggunakan

berbagai macam metode, diantaranya dengan menggunakan metode momen, fungsi

pembangkit momen, fungsi karakteristik, estimasi maksimum likelihood, dll. Dengan

asumsi bahwa estimasi yang diperoleh tidak jauh berbeda (tidak bias) dari nilai

rata-ratanya dan nilai variansinya. Dalam penelitian ini akan digunakan fungsi pembangkit

momen dalam mengestimasi parameter rata-rata dan parameter variansi pada distribusi

ekponensial tergeneralisir dua variabel.

Dengan mensubtitusikan fungsi pembangkit momen gabungan pada persamaan

(2.19) dengan fungsi distribusi eksponensial tergeneralisir dua variabel pada

persamaan (2.26), maka diperoleh transformasi distribusi eksponensial tergeneralisir

dua variabel dengan fungsi pembangkit momen sebagai berikut:

)

,

(

t

₁

t

₂

M

1 2

) 1 ( ) 1 ( 1 1

0 0 2 1

2 2 1 1 2 2 1

1

)

(

1

)

1

(

e

−x −

e

−x −

e

−x −t

e

−x −t

dx

dx

∝ ∝

−

−

Untuk memudahkan dalam proses pengintegralan. Maka, dengan menggunakan

ekspansi binomial dalam bentuk fungsi pembangkit eksponensial pada teorema (2.2),

fungsi diatas dapat dibentuk menjadi :

) , (t₁ t₂

M 1 2

) 1 ( 1 0 2 ) 1 ( 1 0 1 0 0 2 1 2 2 2 1 1 1

1

)

1

(

1

)

1

(

e

dx

dx

j

e

i

j t x j j i t x i

i − − +

− = + − − − = ∝ ∝

∑

∑

∫∫

−





 −







−







−







=

α

α

α

α

α

α

Kemudian dengan mengintegral fungsi integral ganda diatas terhadap x1 dan x2.

Maka didapat transformasi distribusi eksponensial tergeneralisir dua variabel dengan

fungsi pembangkit momen sebagai berikut :

) , (t₁ t₂ M

)

1

(

1

1

)

1

(

)

1

(

1

1

)

1

(

2 1 0 2 2 1 1 0 1 1 2 1

j

t

j

i

t

i

j j i i

+

−













−

−

+

−











 −

−

=

∑

∑

− = − = α α

α

α

α

α

(3.1)

3.2 Fungsi Pembangkit Momen Marginal dari X1 dan X2

Berdasarkan transformasi diatas, dapat ditentukan fungsi pembangkit momen

masing-masing dari X

1 dan X2 yang dinamakan fungsi pembangkit momen marginal dari X1

dan fungsi pembangkit momen marginal dari X2

Fungsi pembangkit momen marginal dari X

pada distribusi eksponensial

tergeneralisir dua variabel.

1 diperoleh dari fungsi pembangkit

momen gabungan dengan mensubstitusikan t2 = 0, sehingga fungsi diatas menjadi :

) 0 , (t1

M

)

1

(

1

1

)

1

(

)

1

(

1

1

)

1

(

1 0 2 2 1 1 0 1 1 2 1

j

j

i

t

i

j j i i

+













−

−

+

−











 −

−

=

∑

∑

− = − = α α

α

α

α

α

Dengan nilai :

(

1

1

)

1

1

)

1

(

1 0 2 2 1

=

+













−

−

∑

−

=

j

j

j

j

α

α

α

Sehingga, fungsi pembangkit momen marginal dari X1 adalah :

Dengan cara yang sama, dapat ditentukan juga fungsi pembangkit momen

marginal dari X2 dengan mensubstitusikan t1 = 0. Sebagai berikut :

) , 0 ( t₂ M

)

1

(

1

1

)

1

(

2 1

0

2 2

2

j

t

j

j

j

+

−













−

−

=

∑

−

=

α

α

α

(3.3)

Dari kedua fungsi pembangkit momen diatas dapat dibuktikan bahwa distribusi

eksponensial tergeneralisir dua variabel merupakan distribusi gabungan yang saling

bebas, karena masing-masing fungsi pembangkit momen marginalnya membentuk

distribusi eksponensial tergeneralisir satu variabel. Sehingga dapat dimisalkan

α

α

α

₁ = ₂ = dant₁ =t₂ =t. kemudian dapat ditentukan estimator parameter

rata-ratanya dan parameter variansinya sebagai berikut :

3.3 Estimator Rata-rata (µ) Pada Distribusi Eksponensial Tergeneralisir dengan Fungsi Pembangkit Momen

Dari kedua fungsi pembangkit momen marginal di atas, dengan nilai

α

₁ =

α

₂ =

α

dan t1 =t2 =t. Maka, fungsi pembangkit momennya menjadi :

M(t)

(

1

)

1

1

)

1

(

1

0

i

t

i

i

i

+

−











 −

−

=

∑

−

=

α

α

α

Untuk mendapatkan momen ke-r dari distribusi eksponensial tergeneralisir di

atas, fungsi pembangkit momennya diturunkan sebanyak r kali dan memasukkan nilai

t = 0. Dalam hal ini untuk mendapatkan estimator rata-ratanya, fungsi pembangkit

momennya diturunkan sekali. Sehingga didapat estimator rata-ratanya adalah sebagai

berikut :

∧

µ 2

1

0

(

1

)

1

1

)

1

(

i

i

i

i

+











 −

−

=

∑

−

=

α

α

α

3.4 Estimator Variansi (σ2) Pada Distribusi Eksponensial Tergeneralisir dengan Fungsi Pembangkit Momen

Dari momen ke-1 atau estimator rata-rata diatas, dapat juga dihitung momen ke-2nya

adalah sebagai berikut :

) (t

M 3

1

0

(

1

)

1

2

1

)

1

(

i

i

i

i

+











 −

−

=

∑

−

=

α

α

α

Sehingga dengan menggunakan rumus variansi pada persamaan (), yaitu hasil

pengurangan momen ke-2 dengan momen ke-1 kuadrat, didapat estimator variansinya

adalah sebagai berikut :

∧

2

σ 3 2

1

0

)

(

)

1

(

1

2

1

)

1

(

∧ −

=

−

+











 −

−

=

∑

α

α

α

µ

i

i

i

i

(3.5)

3.5 Contoh Kasus

Misalkan terdapat dua peubah acak X1 dan X2 yang berdistribusi eksponensial

tergeneralisir, dengan asumsi kedua peubah acak saling bebas. Peubah acak X1

memiliki parameter kegagalan awal (α1) = 2, dan peubah acak X2 memiliki parameter

kegagalan awal (α2) = 8. Sehingga luas kedua peubah acak tersebut dapat

diperlihatkan pada distribusi ekponensial tergeneralisir dua variabel sebagai berikut :

)

,

(

x

₁

x

₂

F

1 2

0 0

7 1 2

2

1

)

(

1

)

1

(

16

e

x

e

x

e

x x

dx

dx

∫ ∫

∝ ∝

− − −

−

−

−

=

Gambar 3.1 Grafik Distribusi Eksponensial Tergeneralisir Dua Variabel dengan α = 16

Berdasarkan peluang dua peristiwa yang saling bebas pada subbab (2.1.2),

dimana f(X1∩X2)= f(X1).f(X2), maka dapat diketahui dua marginal distribusinya adalah:

)

(

x

₁

F

1

0

1 1

)

1

(

2

e

−x

e

−x

dx

∝

−

=

∫

_{, dan}

)

(

x

₂

F

∫

∝

− −

−

=

0

2

7 2

2

)

1

(

8

e

x

e

x

dx

[image:42.595.119.516.83.310.2]

Dengan gambaran 2 grafik berdimensi 2nya adalah sebagai berikut

Gambar 3.2 Grafik Distribusi Eksponensial Tergeneralisir dengan α1 = 2 dan α2 = 8

0,2 1,2

2,2 3,2

4,2

0 0,02 0,04 0,06 0,08 0,1 0,12 0,14 0,16 0,18 0,2

0,2 0,6 1

1,4 1,8 2,2 _2,6 3

3,4 3,8 _4,2

4,6 ₅

Grafik Distribusi Eksponensial Tergeneralisir Dua Variabel

-0,1 0 0,1 0,2 0,3 0,4 0,5 0,6

0 1 2 3 4 5 6 7 8 9

f (

x

)

X

Grafik Distribusi Eksponensial Tergeneralisir

[image:42.595.112.528.555.748.2]

Dalam hal ini, akan di cari nilai rata-ratanya dan nilai variansinya. Kemudian

akan dibandingkan dengan estimator fungsi pembangkit momennya.

3.5.1 Nilai Rata-rata Peubah Acak X_{1 dan} X₂

Pada subbab (2.3.1) dijelaskan bahwa nilai rata-rata dari sebuah peubah acak adalah

)] [(X E

=

µ . Sehingga nilai ekspektasi rata-rata peubah acak X adalah sebagai berikut:

µ = E[(X)] = x.f(x)dx

0

∫

∝

= x e x e x 1dx

0 ) 1 ( . − − ∝ −

∫

_α − α

=

x

e

dx

i

i x x i i

∫∑

∝ − − − =











 −

−

0 1 0

.

1

)