PERBANDINGAN REGRESI ROBUST LEAST MEDIAN OF
SQUARES (LMS) DAN LEAST TRIMMED SQUARES (LTS)
DALAM MENGATASI MASALAH PENCILAN
SKRIPSI
IDA HUSNA
100803007
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERBANDINGAN REGRESI ROBUST LEAST MEDIAN OF SQUARES (LMS) DAN LEAST TRIMMED SQUARES (LTS) DALAM MENGATASI
MASALAH PENCILAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
IDA HUSNA 100803007
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Perbandingan Regresi Robust Least Median Of
Squares (LMS)dan Least Trimmed Squares
(LTS) Dalam Mengatasi Masalah Pencilan
Kategori : Skripsi
Nama : Ida Husna
Nomor Induk Mahasiswa : 100803007
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
(FMIPA) Universitas Sumatera Utara
Disetujui di
Medan, Januari 2015
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dr. Suwarno Ariswoyo, M.Si. Dr. Open Darnius, M.Sc NIP. 195003211980031001 NIP. 19641014 199103 1 004
Diketahui oleh:
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
PERBANDINGAN REGRESI ROBUST LEAST MEDIAN OF SQUARES (LMS)
DAN LEAST TRIMMED SQUARES (LTS) DALAM MENGATASI
MASALAH PENCILAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya
Medan, Januari 2015
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Allah SWT yang Maha Pemurah dan
Maha Penyayang,yang telah senantiasa memberikan rahmat dan hidayah-Nya
sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul
Perbandingan Regresi Robust Least Median Of Squares dan Least Trimmed
Squares dalam Mengatasi Masalah Pencilan.
Terimakasih penulis sampaikan kepada Bapak Dr. Open Darnius,
M.Scselaku pembimbing 1dan BapakDr.Suwarno Ariswoyo, M.Siselaku
pembimbing 2 yang telah dengan sabar meluangkan waktunya untuk
membimbing penulis selama penulisan skripsi ini. Penulis juga mengucapkan
terima kasih kepada Ibu Asima Manurung, S.Si, M.Si dan Bapak Dr. Faigiziduhu
Bu’ulolo, M.Siselaku dosen penguji penulis yang telah memberikan kritik dan
saran yang sangat penting dalam penyempurnaan penulisan skripsi ini.
Terimakasih kepada Bapak Prof. Dr.Tulus, M.Si danIbu Dr. Mardiningsih, M.Si
selaku ketua dan Sekretaris Departemen Matematika FMIPA USU, Dekan dan
Pembantu Dekan FMIPA USU, seluruh Staf dan Dosen Matematika FMIPA USU,
Pegawai FMIPA USU dan rekan-rekan kuliah khususnya Komutatif 2010.
Akhirnya Penulis mengucapkan terimakasih yang teristimewa kepada orangtua
tercinta Ibunda Arni Dawati dan Ayahanda Zakaria (Almarhum), Bapak T. Abdul
Manan serta adik penulis yang senantiasa memberikan dorongan, do’a dan
motivasi sehingga penulis selalu bersemangat dalam menyelesaikan skripsi ini.
Semoga segala bentuk bantuan yang telah diberikan kepada penulis mendapatkan
PERBANDINGAN REGRESI ROBUST LEAST MEDIAN OF SQUARES (LMS) DAN LEAST TRIMMED SQUARES (LTS) DALAM
MENGATASI MASALAH PENCILAN
ABSTRAK
Analisis regresi digunakan untuk mengetahui hubungan antar variabel. Salah satu metode penaksir parameter dalam model regresi adalah metode kuadrat terkecil (OLS). Dalam penelitian ini digunakan empat kelompok data dengan letak pencilan berbeda-beda yang terdiri atas 100 observasi. Kemudian tulisan ini bertujuan untuk membandingkan dua metode regresi robust yaitupenaksir least median of squares (LMS) dan penaksirleast trimmed squares(LTS). Berdasarkan hasil yang diperoleh pada penelitian ini, regresi robustpenaksir LTSmemberikan hasil yang lebih baik daripada penaksir LMS dan metode OLS dengan kriteria pembandingannya menggunakan rata-rata kuadrat sisa.
THE COMPARISON OF ROBUST REGRESSION LEAST MEDIAN OF SQUARES (LMS) AND LEAST TRIMMED SQUARES (LTS) IN
OVERCOMING OUTLIER
ABSTRACT
Regression analysis was usedto determine the relationshipbetween variables. One of methodparameterestimatorin the regression modelis ordinary least
squares(OLS). This research usedfour groupsof
datawithdifferentoutlierlayoutconsisting of100observations. Then,this paperaimstocomparethetwomethods ofrobustregressionleastmedian ofsquares
(LMS) estimator andleasttrimmed ofsquares(LTS) estimator. Based on the resultsobtained inthis research, the LTSestimatorrobustregressiongivesbetter resultsthantheLMSestimator andOLS, the comparisoncriterionisthe averagesquaredresidual.
DAFTAR ISI
DAFTAR TABEL viii
DAFTAR GAMBAR ix
DAFTAR LAMPIRAN x
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Pembatasan Masalah 3
1.4 Tujuan Penelitian 3
1.5 Kontribusi Penelitian 3
1.6 Metodologi Penelitian 3
1.6.1 Bidang Penelitian 4
2.1.3 Pendeteksian Pencilan 5
2.2 Metode Kuadrat Terkecil 7
3.2 Pendeteksian Pencilan 19
3.3 Metode Kuadrat Terkecil 28
3.4 Rata-rata Kuadrat Sisa untuk MKT 41
BAB 4 KESIMPULAN DAN SARAN 73
4.1 Kesimpulan 73
4.2 Saran 73
DAFTAR PUSTAKA 75
DAFTAR TABEL
3.5 Pendeteksian Pencilan untuk Data Kelompok 1 dan Data Kelompok 2
22
3.6 Pendeteksian Pencilan untuk Data Kelompok 3 dan Data Kelompok 4
25
3.7 Perkalian Variabel Bebas dan Variabel Terikat untuk Data Kelompok 1
28
3.8 Perkalian Variabel Bebas dan Variabel Terikat untuk Data Kelompok 2
31
3.9 Perkalian Variabel Bebas dan Variabel Terikat untuk Data Kelompok 3
35
3.10 Perkalian Variabel Bebas dan Variabel Terikat untuk Data Kelompok 4
37
3.11 Nilai Sisaan Terurut 43
3.12 Data kelompok 1 untuk penaksir LTS 46
3.13 Data kelompok 2 untuk penaksir LTS 48
3.14 Data kelompok 3 untuk penaksir LTS 49
3.15 Data kelompok 4 untuk penaksir LTS 50
3.16 Data Iterasi Ke-1 57
3.23 Hasil Perhitungan Fungsi Pembobot untuk Data Kelompok 1
66
3.24 Hasil Estimasi Koefisien Regresi dan Rata-rata Kuadrat Sisa
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
3.1 Scatterplot Data Kelompok 1 20
3.2 Scatterplot Data Kelompok 2 20
3.3 Scatterplot Data Kelompok 3 21
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lampiran
1 Program untuk membangkitkan data menggunakan Software R
77
2 Program MINITAB regresi robust dengan pembobot fungsi Huber
78
3 Hasil output program MINITAB untuk masing-masing kelompok data berdasarkan penaksir LMS
PERBANDINGAN REGRESI ROBUST LEAST MEDIAN OF SQUARES (LMS) DAN LEAST TRIMMED SQUARES (LTS) DALAM
MENGATASI MASALAH PENCILAN
ABSTRAK
Analisis regresi digunakan untuk mengetahui hubungan antar variabel. Salah satu metode penaksir parameter dalam model regresi adalah metode kuadrat terkecil (OLS). Dalam penelitian ini digunakan empat kelompok data dengan letak pencilan berbeda-beda yang terdiri atas 100 observasi. Kemudian tulisan ini bertujuan untuk membandingkan dua metode regresi robust yaitupenaksir least median of squares (LMS) dan penaksirleast trimmed squares(LTS). Berdasarkan hasil yang diperoleh pada penelitian ini, regresi robustpenaksir LTSmemberikan hasil yang lebih baik daripada penaksir LMS dan metode OLS dengan kriteria pembandingannya menggunakan rata-rata kuadrat sisa.
THE COMPARISON OF ROBUST REGRESSION LEAST MEDIAN OF SQUARES (LMS) AND LEAST TRIMMED SQUARES (LTS) IN
OVERCOMING OUTLIER
ABSTRACT
Regression analysis was usedto determine the relationshipbetween variables. One of methodparameterestimatorin the regression modelis ordinary least
squares(OLS). This research usedfour groupsof
datawithdifferentoutlierlayoutconsisting of100observations. Then,this paperaimstocomparethetwomethods ofrobustregressionleastmedian ofsquares
(LMS) estimator andleasttrimmed ofsquares(LTS) estimator. Based on the resultsobtained inthis research, the LTSestimatorrobustregressiongivesbetter resultsthantheLMSestimator andOLS, the comparisoncriterionisthe averagesquaredresidual.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Analisis regresi digunakan untuk membuat model yang menjelaskan hubungan
fungsional antara variabel terikat dengan satu atau lebih variabel bebas dari data
pengamatan. Kemudian jika dalam sebuah data pengamatan terdapat pencilan,
maka model yang dihasilkan perlu dianalisis lebih lanjut, keberadaan pencilan
pada suatu data dapat mengganggu proses analisis data, sehingga pendeteksian
pencilan merupakan hal yang sangat penting untuk dilakukan.
Ada banyak cara pendeteksiannya, dan penyajiannya dapat berupa grafik
atau nilai. Adanya pencilan dalam data dapat mengakibatkan estimasi koefisien
regresi yang diperoleh tidak tepat. Hal ini dapat ditunjukkan dengan nilai standar
error yang besar apabila menggunakan metode kuadrat terkecil. Kemudian
tindakan membuang begitu saja suatu pencilan bukanlah tindakan yang bijaksana
karena ada kalanya pencilan memberikan informasi yang cukup berarti. Oleh
karena itu, diperlukan suatu estimasi yang bersifat robust atau tahan terhadap
pencilan yang dikenal dengan regresi robust.Regresi robustmerupakan metode
regresi yang digunakan ketika distribusi dari sisaan tidak normal atau adanya
beberapa pencilan yang berpengaruh pada model. Metode ini merupakan alat
penting untuk menganalisa data yang dipengaruhi oleh pencilan sehingga
dihasilkan model yang robust atau resistance terhadap pencilan. Suatu estimasi
yang resistance adalah relatif tidak terpengaruh oleh perubahan besar pada bagian
kecil data atau perubahan kecil pada bagian besar data.
Menurut Draper dan Smith (1992), adakalanya pencilan memberikan
informasi yang tidak bisa diberikan oleh titik data lainnya, misalnya karena
pencilan timbul dari kombinasi keadaan yang tidak biasa yang mungkin saja
Menurut Chen (2002), regresi robustadalah metode yang penting untuk
menganalisis data yang terkontaminasi oleh pencilan. Untuk menaksir parameter
regresi robust dapat digunakan beberapa metode antara lain: M-estimator, Least
Median of Squares(LMS)-estimator, Least Trimmed Squares(LTS)-estimator,
S-estimator, dan MM-estimator. Least median of squares (LMS) adalah metode
penaksir parameter regresi robustdengan meminimumkan median dari kuadrat
sisaan sedangkanleast trimmed squares (LTS) adalah metode penaksir parameter
regresi robustdengan meminimumkan jumlah sisaan kuadrat terhadap sebaran data
yang sudah terpotong.
Regresi robust least median of squares (LMS) diperkenalkan oleh
Rousseeuw pada tahun 1984. Metode least median of squares menduga koefisien
regresi dengan meminimumkan median dari kuadrat galat. Prinsip dasar metode
regresi robust pendugaleast median of squares adalahmencocokkan sebagian
besar data setelah pencilan teridentifikasi sebagai titik yang tidak berhubungan
dengan data (Rosseeuw dan Leroy, 1987).
Kemudian menurut (Akbar dan Maftukhah, 2007) least trimmed squares
merupakan salah satu metode penaksir dalam regresirobust yang digunakan untuk
mengatasi pencilan. Metode penaksir ini adalah metode penaksiran parameter
regresi robust dengan menggunakan konsep pengepasan metode kuadrat
terkecil(ordinary least squares) untuk meminimumkan jumlah kuadrat sisaan.
Berdasarkan uraian di atas, maka dalam penelitian tugas akhir ini penulis
akan membandingkan metode regresi robust penaksirleast median of squares
(LMS) dan least trimmed squares (LTS) dalam mengatasi permasalahan data
pencilan.
1.2 Perumusan Masalah
Keberadaan pencilan dalam suatu data dapat mengakibatkan estimasi koefisisen
tahan terhadap pencilan yaitu regresi robust. Dalam penelitian ini akan diselidiki
empat tipe pencilan data pada regresi linier sederhana yang akan diselesaikan
dengan dua metode robust yakni least median of squares(LMS) dan least trimmed
squares (LTS) dalam membandingkan metode yang lebih baik.
1.3 Pembatasan Masalah
Data yang digunakan dalam penelitian ini adalah membangkitkanempat kelompok
data dengan satu variabel bebas dan satu variabel terikat yang mempunyai jenis
pencilan berbeda-beda, kemudian akan ditanggulangi dengan metode regresi
robust penaksirleast median of squares dan least trimmed squares.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah memilih salah satu dari dua metode least median of
squares dan least trimmed squaressehingga dapat mengatasi masalah pencilan.
1.5 Kontribusi Penelitian
Manfaat dari penelitian ini adalah:
1. Memberikan pengetahuan tentang tindakan yang harus dilakukan dalam
mengidentifikasi dan menanggulangi pencilan.
2. Memberikan pengetahuan dasar tentang regresi robust penduga least median
of squares dan penduga least trimmed squares.
3. Hasil penelitian ini dapat dijadikan sebagai bahan referensi untuk
peneliti-peneliti berikutnya.
1.6.1 Bidang Penelitian
Penelitian ini dikelompokkan dalam penelitian tinjauan literatur pada bidang ilmu
statistika matematika.
1.6.2 Sumber Data
Data yang akan dianalisis pada penelitian ini adalah menggunakan data bangkitan
yang dibangkitkan dengan menggunakan software R 3.1.0 terdiri dari satu
variabel bebas (X) dan satu variabel terikat (Y) sebanyak n = 100 observasi.
1.6.3 Teknik Analisis Data
Dalam mengolah data secara cepat dan akurat akan digunakan bantuan software
Minitab 16 dan SPSS 16.0 sehingga dapat dipastikan keakuratan perhitungan dan
penyajian data. Langkah-langkah yang dilakukan dalam menganalisis data adalah:
1. Mendeteksi adanya pencilan dengan menentukan nilai Leverage, DfFITS
dan Cook’s Distance.
2. Menentukan nilai �0 dan �1 serta rata-rata kuadrat sisa dengan metode
kuadrat terkecil.
3. Menentukan nilai �0 dan �1 dengan regresi robust yaitu penaksir LMS dan
LTS serta menentukan nilai rata-rata kuadrat sisa dari kedua penaksir.
4. Membandingkan nilai rata-rata kuadrat sisa dari metode kuadrat terkecil dan
regresi robust.
1.6.4 Membuat Kesimpulan
Berdasarkan hasil analisis data yang diperoleh akan dibuat kesimpulan sekaligus
memberikan saranyang berkaitan dengan pengembangan penelitian ini, yaitu
BAB 2
TINJAUAN PUSTAKA
2.1 Pencilan
2.1.1Pengertian Pencilan
Secara umum pencilan (outlier) adalah data yang tidak mengikuti pola umum
model. Pencilan juga dapat diartikan sebagai suatu keanehan atau keganjilan pada
data amatan yang menunjukkan ketidaksesuaian dengan sisa data (Sembiring,
1995). (Hair, dkk, 1995) juga menyatakan bahwa pencilan adalah data yang
muncul memiliki karakteristik unik yang terlihat sangat jauh berbeda dari
observasi lainnya dan muncul dalam bentuk nilai ekstrim baik untuk sebuah
variabel tunggal ataupun variabel kombinasi.
2.1.2 Dampak Pencilan
Berdasarkan pengertian pencilan yaitu jika dalam suatu data terdapat pencilan
maka analisis data yang akan dihasilkan akan tidak tepat karena pencilan dapat
menyebabkan munculnya nilai rata-rata dan simpangan baku yang tidak konsisten
terhadap mayoritas data. Kemudian estimasi koefisien garis regresi yang
dihasilkan tidak tepat, disamping itu pada beberapa analisa inferensia dapat
menyebabkan kesalahandalam pengambilan keputusan dan kesimpulan. Oleh
karena itu dibutuhkan suatu regresi yang robust terhadap pencilan yang dikenal
dengan regresi robust.
2.1.3 Pendeteksian Pencilan
Terdapat beberapa metode dan nilai yang digunakan untuk mendeteksi pencilan
1. Metode Grafik
Diagram Pencar (Scatter Plot)merupakan salah satu metode untuk melihat apakah
terdapat pencilan pada data, dapat dilakukan dengan memplot data dengan
observasi ke-i (i=1,2,…,n). Kemudian setelah diperoleh model regresi maka dapat
dilakukan dengan cara memplot antara residual dengan nilai prediksi Y(��). Jika
terdapat satu atau beberapa data yang terletak jauh dari pola kumpulan data
keseluruhan maka hal ini mengindikasikan adanya pencilan. Kemudian,
kelemahan metode ini yaitu yang menentukan data tersebut sebagai pencilan atau
tidak tergantung pada kebijakan (judgement) peneliti.
2. Leverage Values, DfFITS, Cook’s Distancedan DfBETA(s)
Untuk mendeteksi ada atau tidak adanya pencilan dapat juga dengan menentukan
Leverage Values, DfFITS, Cook’s Distance, dan DfBETA(s).Berikut definisi dari masing-masing nilai tersebut yaitu:
a. Leverage Value adalah menampilkan nilai leverage (pengaruh) terpusat.
b. DfFITSatau Standardized DfFIT adalah menampilkan nilai perubahan
dalamhargayang diprediksi bilamana case tertentu dikeluarkan dan sudah
distandarkan.
c. Cook’s Distance adalah menampilkan nilai jarak Cook
d. DfBETA(s) adalah menampilkan nilai perubahan koefisienregresi
sebagaihasilperubahan yang disebabkan oleh pengeluaran case tertentu.
Digunakan untuk mendeteksi pencilan pada variabel bebas.
.
Ketentuan dalam pendeteksian pencilan denganLeverage Value,
DfFITS,Cook’s Distance,DfBETA(s)adalah:
a. Jika Leverage Value> (2�−1)
� maka dikatakan pencilan.
b. Jika DfFITS> 2��� maka dikatakan pencilan.
c. Jika Cook’s D> � (0,5; p, n-p) maka dikatakan pencilan.
d. Jika DfBETA (s) > 2
keterangan:
n =jumlah observasi (sampel)
p = jumlah parameter
2.2 Metode Kuadrat Terkecil
Analisis regresidigunakan untuk melihat hubungan antara variabel terikatdengan
satu atau lebih variabel bebas. Model yang dihasilkan menggunakan analisis
regresi adalah model regresi. Kemudian metode kuadrat terkecil merupakan salah
satumetode yang sering digunakan untuk mendapatkannilai-nilai penduga
(penaksir) parameter dalam pemodelan regresi(Cahyawati, 2009).
Menurut Sumodiningrat (1994) dalam analisis regresi yang menggunakan
satu variabel terikat (Y) dan satu variabel bebas (X) disebut regresi linier
sederhana. Model regresi linier sederhana dapat dituliskan sebagai berikut:
�� =�0+�1�� + �� 2.1
keterangan:
i = 1, 2, ...,n
Yi= variabel terikat
Xi= variabel bebas
�0= koefisien regresi
�1= koefisien regresi
��= sisaan
nilai�0 dan �1 adalah parameter regresi yang akan diestimasi.
Kemudian model penaksir regresi linier sederhana untuk persamaan (2.1)
adalah sebagai berikut:
��� = �̂0 +�̂1�� 2.2
keterangan:
���= nilai Yiyang diestimasi
�̂0,�̂1= penaksir parameter
Dari persamaan regresi linier sederhana (2.1), nilai residu (sisaan) ke-i
pada model merupakan selisih antara data sebenarnya dengan data dugaan, yaitu:
�� =�� − ��� 2.3
�� = ��− ��̂0+�̂1��� 2.4
Dalam melakukan penaksiran �0 dan �1 dengan metode kuadrat terkecil
adalah menemukan nilai-nilai taksiran yang meminimumkan jumlah kuadrat
residu yaitu:
dengan menurunkan persamaan (2.6) terhadap �̂0 dan �̂1 kemudian menyamakan
tiap turunannya dengan nol, diperolehlah nilai sebagai berikut:
��
Dari persamaan (2.7) maka akan dicari nilai �̂0 sebagai berikut:
� ��
Selanjutnya, dari persamaan (2.8) akan dicari nilai �̂1sebagai berikut:
� ����
Rata-rata kuadrat sisa S2 adalah salah satu cara untuk menentukan kecocokan
model, jika semakin kecil rata-rata kuadrat sisa yang dihasilkan maka semakin
baik model tersebut (Sembiring, 1995). Metode ini diperoleh dengan menghitung
banyaknya parameter dalam model melalui pembagian dengan derajat
kebebasannya. Rata-rata kuadrat sisa dapat ditentukan dengan rumus berikut:
�2 = ���
� − �
�2 = ��� − ���
� − �
�2 = ∑ (�� − ��) 2
�
� − ∑��(��� − ��)2
� − �
2.11
keterangan:
JKS = jumlah kuadrat sisa
JKT = jumlah kuadrat total
JKR = jumlah kuadrat regresi
n = jumlah sampel
p = jumlah parameter
�� = data sebenarnya
�
�� = data dugaan
��� = rata-rata data sebenarnya
2.4 Regresi Robust
Regresirobustadalah suatu metode yang digunakan untuk mengatasi masalah
pencilan (Rousseeuw dan Leroy, 1987). Metode ini merupakan alat penting untuk
menganalisis data yang dipengaruhi oleh pencilan (outlier) sehinggadapat
menghasilkan model yang robust atau resistance terhadap pencilan (Wulandari,
2013).
Dalam regresi robust terdapat salah satu cara yang digunakan untuk
point. Breakdown pointmerupakan kelompok terkecil adanya pencilan yang
mengakibatkan suatu penaksir menghasilkan penaksiran yang jauh berbeda atau
bias. Konsep breakdown dilakukan untuk mengetahui kemampuan suatu penaksir
dalam menghasilkan nilai taksiran yang resisten terhadap adanya pencilan dalam
jumlah tertentu (Akbar dan Maftukhah, 2007).
Banyak metode estimasi yang bisa digunakan dalam regresi robustyaitu
penaksir Least Median Of Squares (LMS),Least Trimmed Squares (LTS),
penaksir M (M–Estimator), penaksir S dan penaksir MM. Least median of squares
(LMS) adalah metode penaksir parameter regresi robust dengan meminimumkan
median dari kuadrat sisaan sedangkan least trimmed squares (LTS) adalah metode
penaksir parameter regresi robust untuk meminimumkan jumlah kuadrat residual
yang sudah terpotong.
2.5 Metode Penaksir Least Median Of Square (LMS)
Least Median Of Squaremerupakan salah satu metode penaksir dalam regresi
robust yang digunakan untuk mengatasi masalah pencilan. Dengan menggunakan
median dari kuadrat sisaannya penduga yang dihasilkan akan lebih kekar dalam
menghadapi pencilan (Rousseeuw, 1984). Dalam penelitian (Parmikanti, 2013)
menyebutkan LMS merupakan salah satu metode estimasi dalam regresi robust,
dengan metode ini data pencilan tidak dibuang begitu saja tetapi diproses
dieliminasi melalui sebuah iterasi. Kemudian jika pada metode kuadrat terkecil
hal yang perlu dilakukan adalah meminimumkan kuadrat sisa (∑��=1(��)2) maka
pada LMS yang perlu dilakukan adalah meminimumkan median kuadrat sisa
yaitu:
�= min {��������2} = min {�1,�2, … ,��} 2.12
Untuk nilai �1,�2, … ,�� adalah median dari setiap hi pengamatan atau
untuk mendapatkan nilai �1 dicari himpunan bagian data sejumlah hi pengamatan
ℎ� = ��2+ (�+1 )2 � 2.13
dengan n= banyaknya data dan p= banyaknya parameter, demikian seterusnya
sampai iterasi berakhir pada iterasi ke-syaitu saat hs = hs+1, sehingga akan
diperoleh nilai M seperti pada (2.12).
Kemudian karena LMS merupakan penduga (penaksir) pada regresi
robust, maka sama halnya dengan penaksir lain pada regresi robust, prinsip dasar
dari LMS adalah dengan memberikan bobot (wii)pada data sehingga data pencilan
tidak mempengaruhi model parameter taksiran.
Berdasarkan Rousseeuw (1987), bobot wii dirumuskan dengan ketentuan
sebagai berikut:
Setelah bobot wii dihitung, dapat dibentuk matriks W sebagai berikut:
� = �
pembobot yang disarankan oleh Huber memakai fungsi obyektif (Montgomery
dan Peck,1982: 369) yaitu:
��(�∗) = �
dengan fungsi influence
ψ�(�∗) = �
��∗ ����� |��∗|≤ �
� �������∗> �
−� �������∗ <−� dan fungsi pembobot
��� =ψ(εi
∗)
dengan ��∗=��
�0, r= 2,5 dan setelah bobot wii dihitung maka dibentuk matriks W,
sehingga penaksir parameter regresi LMS dapat dihitung dengan menggunakan
rumus:
����� = (����)−1 (����) 2.15
2.6 Metode Penaksir Least Trimmed Squares (LTS)
Salah satu metode penaksir dalam regresirobust yang sering digunakan untuk
mengatasi pencilan adalah least trimmed squares. Metode penaksir ini adalah
metode penaksiran parameter regresi robustdengan menggunakan konsep
pengepasan metode kuadrat terkecil (ordinary least squares) untuk
meminimumkan jumlah kuadrat sisaan (Akbar dan Maftukhah, 2007). Penaksir
least trimmed squaresdapat dinyatakan sebagai berikut:
Minimum∑ℎ�=1�(2�:�) 2.16
keterangan:
�(2�:�)= kuadrat residual (sisaan kuadrat) yang terurut dari terkecil hingga terbesar. 2
) 1 (
ε
<ε
(22)<ε
(23)< …. <ε
(2i)< … <ε
(2h)< … <ε
(2n)n = jumlah pengamatan
p= jumlah parameter
ℎ = ��
2+
(�+ 1 )
2 �=
[�+�+ 1]
2
Jumlah h menunjukkan sejumlah subset data dengan kuadrat fungsi obyektif
terkecil. Nilai h pada persamaan akan membangun breakdown point yang besar
sebanding dengan 50%.Kuadrat sisa pada persamaan (2.16) berasal dari
persamaan estimasi regresi linier menggunakan konsep metode kuadrat terkecil
dengan banyaknya sisaan kuadrat (�(2�:�))yang akan diolah adalah sebanyak h
BAB 3
PEMBAHASAN
3.1 Data
Data yang digunakan dalam penelitian ini adalah data bangkitan yang terdiri dari
satu variabel bebas dan satu variabel terikat (program untuk membangkitkan data
dengan menggunakan bantuan software R 3.1.0 dapat dilihat pada Lampiran 1).
Data yang digunakan dalam penelitian ini terdiri atas empat kelompok data,
masing-masing kelompok data mempunyai letak pencilan yang berbeda-beda dan
setiap kelompok data terdiri atas 100 observasi.
Tabel 3.1Data Kelompok 1
Data ke- X Y
(1) (2) (3)
1 24,74459 25,49922 2 25,94975 34,56932 3 27,21102 44,89028 4 20,06318 35,16295 5 39,26117 55,17023 6 30,95748 32,41692 7 38,69946 57,61637 8 24,71633 33,82560 9 32,22099 52,10756 10 35,63591 44,01251 11 22,38679 32,36768
Data ke- X Y
(1) (2) (3)
30 25,71962 27,28854
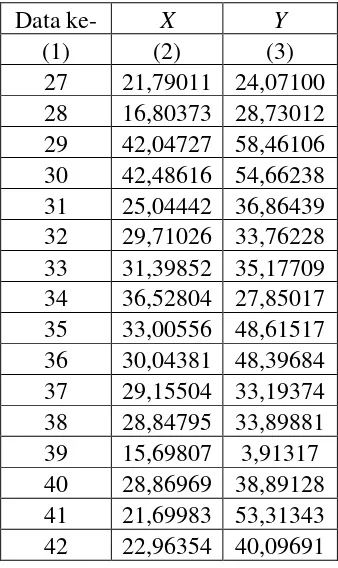
Tabel 3.4 Data Kelompok 4
17 14,65998 30,75306
3.2 PendeteksianPencilan
Pendeteksian pencilan dapat dilakukan dengan metode grafis yaitu scatter plotdan
Pendeteksian pencilan dengan menggunakan scatter plotuntuk masing-masing
kelompok data adalah:
50 40
30 20
10 0
70
60
50
40
30
20
10
0
X
Y
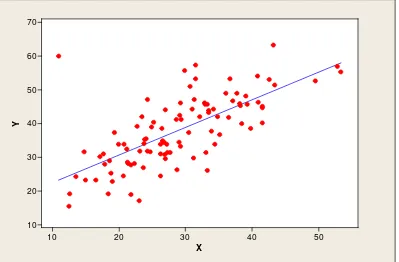
Gambar 3.1Scatter PlotData Kelompok 1
50 40
30 20
10 70
60
50
40
30
20
10
X
Y
60 50
40 30
20 10
70
60
50
40
30
20
10
X
Y
Gambar 3.3Scatter PlotData Kelompok 3
60 50
40 30
20 10
70
60
50
40
30
20
10
0
X
Y
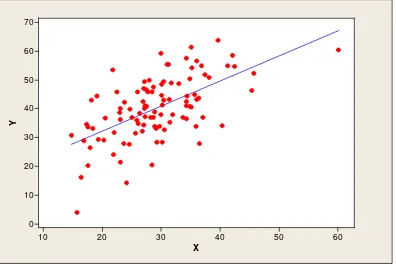
Berdasarkan hasil scatter plot pada Gambar 3.1, Gambar 3.2, Gambar 3.3
dan Gambar 3.4 yang diperoleh menunjukkan bahwa data pada Tabel 3.1, Tabel
3.2, Tabel 3.3 dan tabel 3.4masing-masing memilikiletak pencilan yang
berbeda-beda. Kemudian pendeteksian pencilan yang akan digunakan adalah menentukan
nilai leveragedanDfFITS(Difference fitted value FITS).
Kemudian menurut (Soemartini, 2007) jika diperoleh nilai leveragelebih
besar dari (2�−1)
� maka data dapat dinyatakan sebagai pencilan, selanjutnya jika
nilai |DFFITS| lebih besar dari 2��
� maka data dapat dinyatakan sebagai pencilan
dengan n = jumlah observasi dan p = jumlah parameter, diperoleh nilai (2�−1)
100 = 0,28284. Berikut hasil
pendeteksian pencilan dengan menggunakan nilai leveragedanDfFITS untuk
masing-masing kelompok data yaitu:
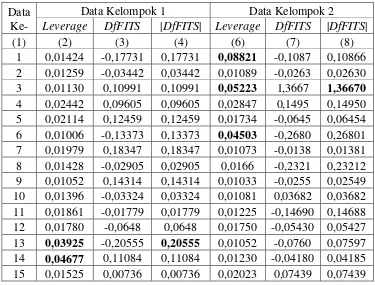
Tabel 3.5 Pendeteksian Pencilan untuk Data Kelompok 1 dan Data Kelompok 2
Data Ke-
Data Kelompok 1 Data Kelompok 2
(1) (2) (3) (4) (6) (7) (8) 100 0,06371 0,20861 0,20861 0,01775 0,01619 0,01619
Berdasarkan hasil pendeteksian pencilan pada Tabel 3.5 data yang
termasuk pencilan untuk data kelompok 1 dilihat berdasarkan nilai yang lebih
besar dari nilai leverage adalah data ke-13, 14, 26, 36, 39, 40, 41, 43, 52, 54, 71,
78, 87, 93 dan 100. Kemudian berdasarkan nilai yang lebih besar dari |DfFITS|
adalah data ke-13, 20 dan 87. Selanjutnya yang termasuk pencilan untuk data
kelompok 2 berdasarkan nilai leverage adalah data ke-1, 3, 6, 19, 21, 22, 23, 33,
49, 52, 61, 71, 72, 87 dan 99. Kemudian berdasarkan nilai |DfFITS| adalah data
ke-3 dan 87.
Tabel 3.6 Pendeteksian Pencilan untuk Data Kelompok 3 dan Data Kelompok 4
Data Ke-
Data Kelompok 3 Data Kelompok 4
Leverage DfFITS |DfFITS| Leverage DfFITS |DfFITS|
(1) (2) (3) (4) (5) (6) (7)
(1) (2) (3) (4) (6) (7) (8)
Selanjutnya hasil pendeteksian pencilan pada Tabel 3.6 data yang
termasuk pencilan untuk data kelompok 3 dilihat dari nilai leverage adalah data
ke-1, 4, 26, 31, 33, 45, 62, 69, 70, 71, 74, 86, 93, 99 dan 100. Kemudian
data kelompok 4 yang termasuk pencilan dilihat berdasarkan nilai leverageadalah
data ke-10, 17, 18, 21, 22, 28, 29, 30, 39, 58, 62, 67, 68, 73, 98 dan 100.
Sedangkan jika dilihat berdasarkan nilai |DfFITS| maka data yang termasuk
pencilan adalah data ke-26, 34, 39, 41, 62, 64, 67 dan 100.
3.3 Metode Kuadrat Terkecil
Prinsip dasar metode kuadrat terkecil adalah untuk meminimumkan jumlah
kuadrat sisaan dari model regresi yang terbentuk. Model regresi yang akan
dibentuk yaitu regresi linier sederhana dengan persamaan sebagai berikut:
�� = �0+�1�� + ��
dengan model penaksir regresinya adalah:
��� = �̂0 +�̂1��
Berikut ini perhitungan nilai penaksir paramater �̂0 dan �̂1sehingga model
penaksiran dengan metode kuadrat terkecil berdasarkan rumus pada (2.9) dan
(2.10) adalah:
1. Model penaksir untuk persamaan regresi linier sederhana dengan metode
kuadrat terkeciluntuk data kelompok 1 adalah:
Tabel 3.7 Perkalian Variabel Bebasdan Variabel Terikat untuk Data Kelompok 1
Data ke- X Y XY X2
(1) (2) (3) (4) (5)
(1) (2) (3) (4) (5) 96 34,66952 39,24439 1.360,58442 1.201,97580 97 29,75051 38,82558 1.155,08053 885,09261 98 23,90947 20,76767 496,54397 571,66261 99 27,00098 34,18201 922,94786 729,05297 100 50,00000 65,00000 3.250,00000 2.500,00000 Jumlah 3.028,179 4.080,565 13.0493,451 98.938,252 Rata-rata 30,29179 40,80563
�̂1 =
∑��=1���� −
∑��=1��∑��=1��
�
�−1
�[∑��=1��]2+∑��=1��2�
�̂1 =
130.493,451− �4.080,565�3.028,179
100 �
− 1
100(3.028,179)
2+ 98.938,252
�̂1 =
130.493,451−123.566,812
7.239,5927
�̂1 = 0,95677
dan
�̂0 =�� − �̂1��
�̂0 = 40,80563 −0,95677(30,28179)
�̂0 = 11,83277
Jadi, model penduga (penaksir) untuk persamaan regresi linier sederhana
dengan metode kuadrat terkecil adalah:
��� = �̂0 +�̂1��
��= 11,83277 + 0,95677��
2. Model penaksir untuk persamaan regresi linier sederhana dengan metode
kuadrat terkecildata kelompok 2 adalah:
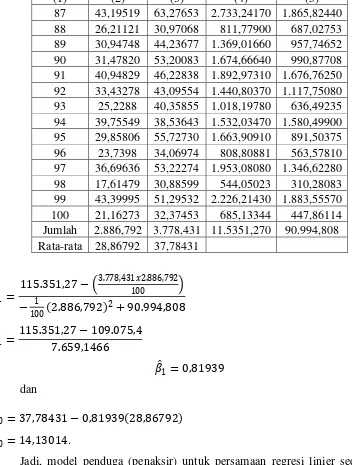
Tabel 3.8 Perkalian Variabel Bebasdan Variabel Terikat untuk Data Kelompok2
Data ke- X Y XY X2
(1) (2) (3) (4) (5)
(1) (2) (3) (4) (5) 87 43,19519 63,27653 2.733,24170 1.865,82440 88 26,21121 30,97068 811,77900 687,02753 89 30,94748 44,23677 1.369,01660 957,74652 90 31,47820 53,20083 1.674,66640 990,87708 91 40,94829 46,22838 1.892,97310 1.676,76250 92 33,43278 43,09554 1.440,80370 1.117,75080 93 25,2288 40,35855 1.018,19780 636,49235 94 39,75549 38,53643 1.532,03470 1.580,49900 95 29,85806 55,72730 1.663,90910 891,50375 96 23,7398 34,06974 808,80881 563,57810 97 36,69636 53,22274 1.953,08080 1.346,62280 98 17,61479 30,88599 544,05023 310,28083 99 43,39995 51,29532 2.226,21430 1.883,55570 100 21,16273 32,37453 685,13344 447,86114 Jumlah 2.886,792 3.778,431 11.5351,270 90.994,808 Rata-rata 28,86792 37,78431
�̂1 =
115.351,27− �3.778,431�2.886,792
100 �
− 1
100(2.886,792)
2+ 90.994,808
�̂1 =
115.351,27−109.075,4
7.659,1466
�̂1 = 0,81939
dan
�̂0 = 37,78431−0,81939(28,86792)
�̂0 = 14,13014.
Jadi, model penduga (penaksir) untuk persamaan regresi linier sederhana
dengan metode kuadrat terkecil adalah:
��� = �̂0 +�̂1��
��= 14,13014 + 0,81939��
3. Model penaksir untuk persamaan regresi linier sederhana dengan metode
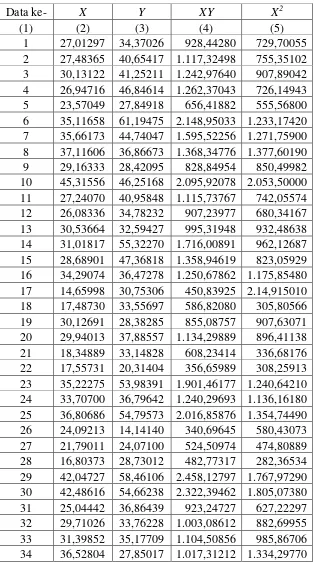
kuadrat terkeciluntuk data kelompok 3 adalah:
untuk Data Kelompok3
Data ke- X Y XY X2
(1) (2) (3) (4) (5)
1 16,60849 36,78474 610,93895 275,84194 2 20,99639 40,84729 857,64557 440,84839 3 35,76885 42,97343 1.537,11010 1.279,41060 4 47,50563 59,98169 2.849,46780 2.256,78490 5 25,52563 43,70598 1.115,62270 651,55779 6 32,65760 43,52522 1.421,42910 1.066,51880 7 34,63220 49,00489 1.697,14720 1.199,38930 8 35,30503 43,83961 1.547,75860 1.246,44510 9 35,74264 37,17254 1.328,64470 1.277,53630 10 34,38473 45,17666 1.553,38740 1.182,30970 11 29,91268 23,16619 692,96274 894,76842 12 33,49929 44,06404 1.476,11400 1.122,20240 13 20,43011 36,55776 746,87900 417,38939 14 26,57563 44,49170 1.182,39490 706,26411 15 33,08429 46,09861 1.525,13970 1.094,57020 16 27,69186 52,26243 1.447,24380 766,83911 17 32,20885 39,98075 1.287,73390 1.037,41000 18 31,57274 23,02997 727,11929 996,83791 19 25,35646 34,97857 886,93258 642,95006 20 32,25274 39,92474 1.287,68210 1.040,23920 21 26,49884 42,13870 1.116,62660 702,18852 22 18,92887 39,16833 741,41230 358,30212 23 20,61227 31,18401 642,77325 424,86567 24 33,80334 39,58782 1.338,20050 1.142,66580 25 27,97932 24,24846 678,45551 782,84235 26 15,04196 20,75603 312,21142 226,26056 27 29,53431 36,99399 1.092,59210 872,27547 28 42,26966 45,44611 1.920,99170 1.786,72420 29 35,31827 42,19785 1.490,35520 1.247,38020 30 25,71962 27,28854 701,85078 661,49885 31 10,05847 14,91350 150,00701 101,17282 32 24,86370 43,03724 1.070,06500 618,20358 33 46,99963 55,72772 2.619,18240 2.208,96520 34 38,70424 57,32921 2.218,88340 1.498,01820 35 31,45907 41,66349 1.310,69470 989,67309 36 43,35575 48,17687 2.088,74420 1.879,72110 37 29,39431 40,21297 1.182,03260 864,02546 38 37,35673 43,39702 1.621,17060 1.395,52530
39 31,62098 40,42059 1.278,13860 999,88638 40 31,03240 51,63043 1.602,21620 963,00985 41 40,75897 32,67099 1.331,6360 1.661,29360 42 29,48946 30,84335 909,55377 869,62825 43 37,73232 44,15409 1.666,03630 1.423,72800 44 30,80963 17,44293 537,41010 949,23330 45 11,19797 24,03819 269,17889 125,39453 46 40,49931 46,90160 1.899,48260 1.640,19410 47 27,67897 36,79854 1.018,54580 766,12538 48 24,97487 33,10301 826,74342 623,74413 49 31,43041 35,67424 1.121,25580 987,87067 50 41,36430 53,94065 2.231,21740 1.711,00530 51 18,42851 26,32006 485,03943 339,60998 52 35,68648 51,18505 1.826,61420 1.273,52490 53 26,08254 32,85181 856,85857 680,29889 54 21,35571 37,15159 793,39858 456,06635 55 33,08343 39,24751 1.298,4422 1.094,5133 56 39,45915 49,36376 1.947,85200 1.557,0245 57 32,26371 46,58488 1.503,00100 1.040,94700 58 29,77752 31,85549 948,57749 886,70070 59 40,52360 39,00853 1.580,76610 1.642,16220 60 35,20957 39,93557 1.406,11410 1.239,71380 61 19,00883 24,70060 469,52945 361,33562 62 15,60287 36,05882 562,62113 243,44955 63 27,28392 33,82839 922,97117 744,41229 64 22,25923 44,21626 984,21997 495,47332 65 39,57518 46,56289 1.842,73480 1.566,19490 66 33,32347 42,77791 1.425,50840 1.110,45370 67 19,08901 39,89865 761,62579 364,39030 68 17,27758 32,60186 563,28130 298,51477 69 13,33586 8,986635 119,84451 177,84516 70 47,58513 65,97605 3.139,47910 2.264,34460 71 48,24881 55,37938 2.671,98910 2.327,94770 72 28,35026 29,01599 822,61092 803,73724 73 27,93389 36,96822 1.032,66630 780,30221 74 14,04516 33,04512 464,12394 197,26652 75 33,79499 45,29251 1.530,65980 1.142,10130 76 29,74637 42,89407 1.275,94280 884,84653 77 18,15913 23,56968 428,00481 329,75400 78 27,49074 38,14234 1.048,56120 755,74079 79 37,79537 37,62058 1.421,88390 1.428,49000 80 29,23991 47,06033 1.376,03970 854,97234
81 31,93475 50,37412 1.608,68490 1.019,82830 82 22,39107 30,01924 672,16286 501,36002 83 22,28542 32,68675 728,43784 496,63994 84 37,29705 56,30928 2.100,17000 1.391,06990 85 43,30303 52,26282 2.263,13830 1.875,15240 86 16,69417 19,44500 324,61817 278,69531 87 37,16748 37,36955 1.388,93200 1.381,42160 88 24,30172 39,76316 966,31316 590,57359 89 27,25944 25,22295 687,56349 743,07707 90 28,88071 40,26224 1.162,80200 834,09541 91 27,13596 50,27035 1.364,13420 736,36033 92 34,36808 35,02501 1.203,74240 1.181,16490 93 16,39683 27,57033 452,06600 268,85603 94 42,53627 50,37801 2.142,89280 1.809,33430 95 42,04388 49,79590 2.093,61280 1.767,68780 96 28,74595 38,29136 1.100,72160 826,32964 97 17,67922 30,00145 530,40229 312,55482 98 35,87051 49,82878 1.787,38380 1.286,69350 99 60,77202 10,77202 654,63741 3.693,23840 100 51,81691 67,62898 3.504,32470 2.684,99220 Jumlah 3.038,096 3.920,031 125.014,720 101.098,800 Rata-rata 30,38096 39,20031
�̂1 =
125.014,72− �3.920,031�3.038,096
100 �
−1001 (3.038,096)2+ 101.098,8
�̂1 =
125.014,72−119.094,3
8.798,5109
�̂1 = 0,67289
dan
�̂0 = 39,20031−0,67289(30,38096)
�̂0 = 18,75735
Jadi, model penduga (penaksir) untuk persamaan regresi linier sederhana
dengan metode kuadrat terkecil adalah:
��� = �̂0 +�̂1��
4. Model penaksir untuk persamaan regresi linier sederhana dengan metode
kuadrat terkeciluntuk data kelompok 4 adalah:
Tabel 3.10 Perkalian Variabel Bebasdan Variabel Terikat untuk Data Kelompok4
Data ke- X Y XY X2
(1) (2) (3) (4) (5)
(1) (2) (3) (4) (5) 77 27,18383 37,05706 1.007,35282 738,96061 78 21,99154 31,67718 696,62997 483,62783 79 35,02418 40,57255 1.421,02029 1.226,69320 80 24,70347 39,75115 981,99134 610,26143 81 23,04234 21,41075 493,35378 530,94943 82 25,97825 45,76960 1.189,01411 674,86947 83 34,28952 42,43533 1.455,08710 1.175,77120 84 26,71742 32,06980 856,82232 713,82053 85 31,26519 55,32701 1.729,80948 977,51211 86 23,71397 42,07665 997,80442 562,35237 87 35,96028 56,50225 2.031,83673 1.293,14170 88 35,90696 33,70689 1.210,31195 1.289,30980 89 26,92559 42,37279 1.140,91237 724,98740 90 30,38130 42,93243 1.304,34304 923,02339 91 38,12271 50,67338 1.931,80657 1.453,34100 92 25,78838 36,01918 928,87631 665,04054 93 31,62336 48,91462 1.546,84464 1.000,03690 94 36,33426 43,50603 1.580,75941 1.320,17840 95 27,74841 45,75707 1.269,68594 769,97426 96 28,15924 36,79820 1.036,20935 792,94280 97 34,27644 40,85242 1.400,27552 1.174,87430 98 18,07238 42,77081 772,97033 326,61092 99 30,36756 49,26409 1.496,03021 922,18870 100 60,08562 60,40087 3.629,22372 3.610,28170 Jumlah 2.915,319 4.018,501 122.004,196 90.595,901 Rata-rata 29,15319 40,18501
�̂1 =
122.004,196− �4.018,501�2.915,319
100 �
�̂0 = 40,18501−0,86566(29,15319)
�̂0 = 14,94827
Jadi, model penduga (penaksir) untuk persamaan regresi linier sederhana
dengan metode kuadrat terkecil adalah:
��= 14,94827 + 0,86566��
3.4 Rata-rata Kuadrat Sisa untuk MKT
Berdasarkan model yang telah terbentuk dengan metode kuadrat terkecil, akan
dihitung nilai sisaan dan sisaan kuadrat untuk metode kuadrat terkecil. Kemudian
akan dihitung jumlah kuadrat regresi dan kuadrat total untuk mendapatkan nilai
rata-rata kuadrat sisa (Mean Square Error). Nilai rata-rata kuadrat sisa diperoleh
dengan rumus:
�2 = ���
� − �
�2 = ��� − ���
� − �
�2 = ∑ (�� − ��) 2
�
� − ∑��(��� − ��)2
� − �
keterangan:
JKS = jumlah kuadrat sisa
JKT = jumlah kuadrat total
JKR = jumlah kuadrat regresi
n = jumlah sampel
p = jumlah parameter
�� = data sebenarnya
��� = data dugaan
��� = rata-rata data sebenarnya
Berikut perhitungan nilai rata-rata kuadrat sisa dari masing-masing
kelompok data pada Lampiran 2 yakni:
1. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 1 adalah:
n = 100
p = 2
�2 =��� − ���
� − �
�2 =11.256,33−6.627,187
100−2
�2 =4.629,147
98
= 47,23620
Jadi, nilai rata-rata kuadrat sisa yang diperoleh adalah 47,23620.
2. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 2 adalah:
n = 100
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =10.706−5.142,351
100−2
�2 =5.563,651
98
= 56,77195
Jadi, nilai rata-rata kuadrat sisa yang diperoleh adalah 56,77195.
3. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 3 adalah:
n = 100
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =11.919,72−3.983,798
100−2
�2 =7.935,918
98
= 80,97875
Jadi, nilai rata-rata kuadrat sisa yang diperoleh adalah 80,97875.
n = 100
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =11.704,68−4.200,224
100−2
�2 =7.504,454
98
= 76,57607
Jadi, nilai rata-rata kuadrat sisa yang diperoleh adalah 76,57607.
3.5 Regresi Robustdengan Penaksir LTS
Metode regresi robust merupakan metode yang digunakan untuk mengatasi
permasalahan pencilan dan dikembangkan dengan tujuan untuk mendapatkan sifat
robust (kuat) yang mampumengenali dan mengatasi adanya pencilan. Metode
penaksir ini adalah metode penaksiran parameter regresi robust dengan
menggunakan konsep pengepasan metode kuadrat terkecil (ordinary least
squares) untuk meminimumkan jumlah kuadrat sisaan.
Kemudian untuk mendapatkan model penaksiran dengan metode least
trimmed squaresmaka nilai sisaan kuadrat (��2)akandiurutkan dari terkecil hingga
terbesar.
Tabel 3.11 Nilai Sisaan Terurut
Data ke-
Data Kelompok
1 2 3 4
(1) (2) (3) (4) (5)
1 0,003548 0,074807 4,96E-05 0,048597 2 0,004025 0,176716 0,021779 0,055775 3 0,0892 0,189662 0,036538 0,106772 4 0,164641 0,237603 0,060451 0,58441
(1) (2) (3) (4) (5)
6 0,781626 0,378577 0,148839 1,098987 7 1,165704 0,551434 0,202154 1,163665 8 1,549662 0,739456 0,247312 1,267894 9 2,157473 0,816964 0,286398 1,570157 10 2,165564 0,998034 0,340715 1,926633 11 2,226300 1,094220 0,342883 2,025397 12 2,722483 1,678518 0,425192 2,778398 13 2,739075 2,115219 0,707102 2,836812 14 2,808784 2,167448 0,786322 3,664941 15 3,125331 2,173721 0,796864 4,822442 16 3,276170 2,467772 1,136870 5,328187 17 3,669603 2,486798 1,382504 5,364365 18 3,985129 2,571838 1,757890 5,459880 19 4,197617 2,715994 2,082622 5,687898 20 4,373918 2,791787 2,552100 5,900166 21 4,392065 3,531529 2,678780 6,382685 22 4,549632 3,560550 2,810601 7,336394 23 4,778134 3,633644 3,019418 7,419113 24 4,929928 3,746901 3,076760 7,536515 25 5,317741 4,070956 3,137685 8,383084 26 5,342192 4,234808 3,668985 8,617399 27 5,374886 4,671093 4,290479 8,884411 28 6,448912 4,878774 4,922196 9,627112 29 8,042407 5,069138 4,929661 9,698439 30 8,324162 5,139768 5,081265 11,46787 31 9,727852 5,393854 6,050017 11,68323 32 10,19759 6,373787 6,319957 12,04537 33 10,83648 6,831817 7,549545 12,36656 34 11,36165 7,032910 7,647170 14,19476 35 11,97112 7,226844 7,800260 14,46413 36 12,02730 7,953893 8,990602 15,62077 37 12,14165 9,197032 10,77266 15,69790 38 12,89624 9,302952 10,81117 16,33570 39 13,18984 9,526791 11,94548 16,94239 40 13,26188 10,63623 14,40086 17,39625 41 17,09269 11,14970 14,47680 18,88103 42 17,64465 12,32027 16,19416 18,97884 43 17,67667 12,56643 16,42835 21,25491 44 19,35492 13,05619 16,44094 21,31337 45 20,47646 13,27603 16,98003 22,04069 46 20,9324 15,02327 17,27139 25,96215
(1) (2) (3) (4) (5)
48 22,41784 17,59443 19,07322 27,77313 49 23,98557 18,14327 21,65436 31,25962 50 26,93114 18,21694 23,39578 36,08010 51 28,09787 18,42749 23,40289 36,26420 52 28,11259 18,46771 25,79796 39,38813 53 28,39536 18,76820 28,56680 43,04827 54 30,20114 18,87613 30,80851 43,44487 55 31,79687 19,68957 31,76084 43,56191 56 33,16764 20,76621 37,42504 46,07846 57 33,33395 21,49865 40,92705 47,67866 58 40,32964 22,54896 43,15036 48,32506 59 40,46799 23,77431 46,27343 48,90040 60 40,51127 26,20106 46,88969 50,61113 61 43,06387 26,26129 46,94581 53,73845 62 43,18379 27,20614 47,03595 55,36618 63 44,75268 27,38743 48,08760 56,29682 64 46,02750 29,66613 48,14771 57,53195 65 46,91319 29,85440 48,21748 59,09035 66 49,32006 30,63292 49,23471 62,79703 67 50,16865 30,87118 54,01780 63,76396 68 53,60989 32,32758 54,86026 64,44618 69 55,48199 38,18069 56,99277 66,57927 70 56,88829 39,43151 58,88930 69,43886 71 59,11793 42,17777 60,17356 73,01214 72 63,20569 44,32642 60,41471 73,45847 73 63,59411 45,02059 61,65187 75,71435 74 66,50375 45,07248 63,38829 77,23506 75 66,64570 47,97749 65,98153 94,86948 76 68,33522 53,42503 68,83190 96,68574 77 69,18249 53,61155 70,80585 104,2733 78 70,30151 59,39894 74,43778 108,6724 79 73,11570 64,21790 77,00570 116,4247 80 76,68711 66,51469 77,75650 117,0462 81 79,15408 66,73192 85,71563 128,5229 82 81,63177 72,67790 102,5803 138,6000 83 89,24040 72,79158 109,8493 148,3038 84 93,32309 81,43203 111,2115 151,8957 85 99,09122 82,14561 112,6165 159,8981 86 100,1688 96,85158 141,0632 161,8068 87 105,2295 98,55170 143,8006 164,5831 88 116,1437 102,0549 155,1299 166,9627
(1) (2) (3) (4) (5)
90 122,4567 132,1944 175,6549 181,8278 91 126,4589 135,6328 177,8460 182,8780 92 127,9715 173,0923 182,5920 208,5212 93 137,8887 174,3270 196,1274 248,0440 94 145,2201 176,2991 221,1615 251,1420 95 149,2686 189,1363 231,0140 330,6187 96 182,7497 233,6117 247,0903 350,3996 97 189,7404 253,7983 288,0610 365,9783 98 194,3503 293,4973 351,3481 383,3954 99 203,0297 298,7103 486,0224 469,2623 100 237,2016 1365,449 2.389,08 606,3557
Berdasarkan nilai sisaan kuadrat yang telah terurut akan diambil sebanyak
h pengamatan, nilai h diperoleh dari rumus ℎ= ��
Berikut ini data masing-masing kelompok yang telah diambil sebanyak h
pengamatan.
Tabel 3.12 Data Kelompok 1 untuk Penaksir LTS
Data ke- X Y �� �� ��2
(1) (2) (3) (4) (5) (6)
1 29,55657 40,17118 40,11161 0,059569 0,003548 2 21,14061 31,99603 32,05947 -0,06344 0,004025 3 27,78347 38,71382 38,41516 0,298663 0,089200 4 24,11822 35,31412 34,90836 0,40576 0,164641 5 24,27338 35,88895 35,05682 0,832133 0,692446 6 22,38679 32,36768 33,25178 -0,88410 0,781626 7 23,64163 35,53205 34,45237 1,079678 1,165704 8 36,4755 45,48658 46,73144 -1,24485 1,549662 9 29,0238 41,07071 39,60187 1,468834 2,157473 10 29,75051 38,82558 40,29716 -1,47159 2,165564 11 33,01645 44,91400 43,42192 1,492079 2,226300 12 29,29285 41,50928 39,85929 1,649995 2,722483 13 24,71633 33,82560 35,48061 -1,65502 2,739075 14 40,58374 48,98613 50,66208 -1,67594 2,808784 15 29,39212 41,72213 39,95427 1,767861 3,125331
(1) (2) (3) (4) (5) (6)
17 35,63591 44,01251 45,92813 -1,91562 3,669603 18 38,58055 46,74921 48,74549 -1,99628 3,985129 19 30,7637 43,31536 41,26655 2,048809 4,197617 20 25,94975 34,56932 36,66071 -2,09139 4,373918 21 27,81915 36,35357 38,44929 -2,09573 4,392065 22 30,24056 38,63304 40,76603 -2,13299 4,549632 23 37,11979 49,53376 47,34787 2,185894 4,778134 24 28,46568 41,28822 39,06787 2,220344 4,929928 25 40,90212 53,27272 50,96669 2,306023 5,317741 26 44,16298 51,77527 54,08659 -2,31132 5,342192 27 29,45897 42,33661 40,01822 2,31838 5,374886 28 22,10428 35,52095 32,98148 2,539471 6,448912 29 30,38004 38,06357 40,89948 -2,83591 8,042407 30 47,48107 54,37607 57,26123 -2,88516 8,324162 31 29,71313 43,38035 40,2614 3,118951 9,727852 32 44,36028 57,46872 54,27536 3,193367 10,19759 33 22,7689 30,32549 33,61737 -3,29188 10,83648 34 46,59793 59,78697 56,41627 3,370704 11,36165 35 35,94319 49,68207 46,22214 3,45993 11,97112 36 32,11075 39,08733 42,55537 -3,46804 12,02730 37 27,00098 34,18201 37,6665 -3,48449 12,14165 38 27,71680 41,94250 38,35137 3,591134 12,89624 39 31,47927 45,58298 41,95119 3,631782 13,18984 40 23,99872 31,15234 34,79403 -3,64169 13,26188 41 20,06318 35,16295 31,02862 4,134331 17,09269 42 27,62597 34,06391 38,26447 -4,20055 17,64465 43 34,23751 40,38583 44,5902 -4,20436 17,67667 44 35,79879 41,68456 46,08398 -4,39942 19,35492 45 19,24524 34,77113 30,24604 4,525093 20,47646 46 29,25879 35,25151 39,82671 -4,57519 20,93240 47 22,64944 38,22674 33,50308 4,723667 22,31303 48 46,81812 51,89220 56,62695 -4,73475 22,41784 49 35,34783 40,75501 45,65252 -4,89751 23,98557 50 29,04652 44,81313 39,62361 5,189522 26,93114 51 30,75822 46,56205 41,26131 5,300743 28,09787 52 34,22317 39,27434 44,57647 -5,30213 28,11259
Data ke- X Y �� �� ��2
(1) (2) (3) (4) (5) (6)
1 38,20033 45,1576 45,43111 -0,27351 0,074807 2 38,12793 45,79216 45,37178 0,420375 0,176716 3 18,59265 28,92927 29,36477 -0,4355 0,189662 9 21,16273 32,37453 31,47067 0,903861 0,816964 10 26,50885 34,85221 35,85123 -0,99902 0,998034 11 13,50086 24,14656 25,19261 -1,04605 1,094220 12 23,13152 31,7883 33,08388 -1,29558 1,678518 13 40,94829 46,22838 47,68276 -1,45438 2,115219 14 32,08192 41,88997 40,41774 1,472226 2,167448 15 26,63582 34,48091 35,95526 -1,47435 2,173721 16 33,43278 43,09554 41,52463 1,570914 2,467772 17 23,80648 35,21389 33,63693 1,576958 2,486798 18 43,39995 51,29532 49,69163 1,603695 2,571838 19 24,06255 35,49478 33,84675 1,648027 2,715994 20 26,75824 34,38471 36,05557 -1,67086 2,791787 21 30,45736 37,20736 39,0866 -1,87924 3,531529 22 26,25136 33,7533 35,64024 -1,88694 3,56055 23 17,15792 30,09538 28,18917 1,906212 3,633644 24 34,20891 44,09627 42,16058 1,935691 3,746901 25 39,0443 48,14031 46,12265 2,017661 4,070956 26 49,4608 52,59996 54,65782 -2,05786 4,234808 27 33,46781 43,7146 41,55333 2,161271 4,671093 28 37,08485 46,72589 44,5171 2,208795 4,878774 29 36,41086 41,71336 43,96483 -2,25147 5,069138 30 24,2726 31,75176 34,01887 -2,26711 5,139768 31 17,61479 30,88599 28,56352 2,322467 5,393854 32 53,34214 55,31352 57,83816 -2,52464 6,373787 33 27,19714 33,80143 36,4152 -2,61377 6,831817 34 26,38167 38,39898 35,74702 2,651963 7,03291 35 20,70278 33,78207 31,09379 2,688279 7,226844 36 24,67059 31,52471 34,34497 -2,82026 7,953893 37 29,30558 41,1755 38,14284 3,032661 9,197032 38 21,29077 28,52551 31,57558 -3,05007 9,302952 39 41,50944 45,05601 48,14256 -3,08655 9,526791
(1) (2) (3) (4) (5) (6)
41 19,86411 33,74571 30,40659 3,339117 11,14970 42 28,63277 41,10157 37,59155 3,510025 12,32027 43 29,04005 34,38035 37,92527 -3,54492 12,56643 44 41,51401 44,53297 48,1463 -3,61333 13,05619 45 21,37247 27,9989 31,64253 -3,64363 13,27603 46 37,71788 48,91178 45,03579 3,875986 15,02327 47 42,57739 53,04641 49,01763 4,028782 16,23109 48 33,24595 45,56611 41,37154 4,194571 17,59443 49 29,1598 42,28288 38,02339 4,259491 18,14327 50 22,24937 28,09292 32,36105 -4,26813 18,21694 51 21,7661 27,67234 31,96506 -4,29272 18,42749 52 24,8516 38,7907 34,49329 4,297407 18,46771
Tabel 3.14 Data Kelompok 3 untuk Penaksir LTS
Data ke- X Y �� �� ��2
(1) (2) (3) (4) (5) (6)
1 37,73232 44,15409 44,14705 0,007041 4,96E-05 2 35,76885 42,97343 42,82585 0,147576 0,021779 3 28,74595 38,29136 38,10021 0,19115 0,036538 4 43,35575 48,17687 47,931 0,245867 0,060451 5 35,31827 42,19785 42,52266 -0,32481 0,105499 6 31,62098 40,42059 40,03479 0,385797 0,148839 7 32,20885 39,98075 40,43036 -0,44962 0,202154 8 37,35673 43,39702 43,89432 -0,49731 0,247312 9 32,25274 39,92474 40,4599 -0,53516 0,286398 10 27,67897 36,79854 37,38225 -0,58371 0,340715 11 27,93389 36,96822 37,55379 -0,58556 0,342883 12 17,67922 30,00145 30,65352 -0,65207 0,425192 13 25,35646 34,97857 35,81946 -0,84089 0,707102 14 27,49074 38,14234 37,25559 0,886748 0,786322 15 40,49931 46,90160 46,00893 0,892672 0,796864 16 22,28542 32,68675 33,75299 -1,06624 1,136870 17 39,57518 46,56289 45,38709 1,175799 1,382504 18 35,30503 43,83961 42,51375 1,325854 1,757890 19 20,61227 31,18401 32,62714 -1,44313 2,082622 20 33,32347 42,77791 41,18038 1,597529 2,55210 21 29,53431 36,99399 38,63069 -1,6367 2,67878 22 29,39431 40,21297 38,53649 1,676485 2,810601 23 31,45907 41,66349 39,92584 1,737647 3,019418 24 42,26966 45,44611 47,20018 -1,75407 3,07676
(1) (2) (3) (4) (5) (6)
26 33,80334 39,58782 41,50328 -1,91546 3,668985 27 28,88071 40,26224 38,19089 2,071347 4,290479 28 17,27758 32,60186 30,38326 2,218602 4,922196 29 16,39683 27,57033 29,79061 -2,22028 4,929661 30 11,19797 24,03819 26,29235 -2,25417 5,081265 31 24,97487 33,10301 35,56269 -2,45968 6,050017 32 35,20957 39,93557 42,44952 -2,51395 6,319957 33 42,04388 49,7959 47,04826 2,747644 7,549545 34 33,49929 44,06404 41,29869 2,765352 7,64717 35 32,6576 43,52522 40,73232 2,792895 7,80026 36 42,53627 50,37801 47,37958 2,998433 8,990602 37 34,38473 45,17666 41,89449 3,282173 10,77266 38 27,28392 33,82839 37,11643 -3,28803 10,81117 39 26,08254 32,85181 36,30803 -3,45622 11,94548 40 33,79499 45,29251 41,49766 3,794846 14,40086 41 22,39107 30,01924 33,82408 -3,80484 14,4768 42 21,35571 37,15159 33,12739 4,024196 16,19416 43 20,43011 36,55776 32,50457 4,05319 16,42835 44 39,45915 49,36376 45,30902 4,054743 16,44094 45 29,74637 42,89407 38,77338 4,120683 16,98003 46 48,24881 55,37938 51,22349 4,155886 17,27139 47 31,43041 35,67424 39,90656 -4,23232 17,91256 48 43,30303 52,26282 47,89553 4,36729 19,07322 49 24,30172 39,76316 35,10973 4,653425 21,65436 50 14,04516 33,04512 28,2082 4,836918 23,39578 51 18,42851 26,32006 31,15771 -4,83765 23,40289 52 33,08429 46,09861 41,01944 5,079169 25,79796
Tabel 3.15 Data Kelompok 4 untuk Penaksir LTS
Data ke- X Y �� �� ��2
(1) (2) (3) (4) (5) (6)
1 30,13122 41,25211 41,03166 0,220448 0,048597 2 25,04442 36,86439 36,62822 0,236167 0,055775 3 34,40308 44,40288 44,72964 -0,32676 0,106772 4 16,80373 28,73012 29,49459 -0,76447 0,584410 5 26,24908 38,44191 37,67105 0,770861 0,594227 6 28,86969 38,89128 39,93961 -1,04833 1,098987 7 35,66173 44,74047 45,8192 -1,07873 1,163665 8 31,27615 43,14879 42,02278 1,126008 1,267894 9 25,78838 36,01918 37,27224 -1,25306 1,570157
(1) (2) (3) (4) (5) (6)
11 27,18383 37,05706 38,48022 -1,42316 2,025397 12 27,13237 40,10253 38,43568 1,666853 2,778398 13 30,3813 42,93243 41,24815 1,684284 2,836812 14 27,48365 40,65417 38,73977 1,914404 3,664941 15 34,28952 42,43533 44,63134 -2,19601 4,822442 16 21,99154 31,67718 33,98547 -2,30829 5,328187 17 18,34889 33,14828 30,83217 2,31611 5,364365 18 45,72712 52,19577 54,53241 -2,33664 5,45988 19 19,2204 29,20167 31,5866 -2,38493 5,687898 20 27,2407 40,95848 38,52945 2,429026 5,900166 21 28,15924 36,7982 39,3246 -2,5264 6,382685 22 28,5982 36,99601 39,70459 -2,70858 7,336394 23 38,12271 50,67338 47,94958 2,723805 7,419113 24 26,08336 34,78232 37,52759 -2,74527 7,536515 25 36,33426 43,50603 46,40139 -2,89536 8,383084 26 42,48616 54,66238 51,72684 2,935541 8,617399 27 29,94013 37,88557 40,86624 -2,98067 8,884411 28 36,03373 43,03847 46,14123 -3,10276 9,627112 29 14,65998 30,75306 27,63883 3,114232 9,698439 30 20,22499 29,06981 32,45623 -3,38642 11,46787 31 24,70347 39,75115 36,33308 3,418074 11,68323 32 17,4873 33,55697 30,08633 3,470644 12,04537 33 30,08584 44,50899 40,99238 3,516612 12,36656 34 34,27644 40,85242 44,62001 -3,76759 14,19476 35 22,90638 38,58058 34,77741 3,803173 14,46413 36 20,45595 36,60848 32,65617 3,952312 15,62077 37 27,01297 34,37026 38,33232 -3,96206 15,6979 38 17,86739 26,37361 30,41535 -4,04174 16,3357 39 26,92559 42,37279 38,25668 4,116114 16,94239 40 41,30349 54,87393 50,70305 4,170881 17,39625 41 37,461 51,72199 47,37676 4,345231 18,88103 42 34,79871 40,71565 45,07212 -4,35647 18,97884 43 17,31506 34,54753 29,93722 4,610305 21,25491 44 31,90844 37,95349 42,57013 -4,61664 21,31337 45 35,02418 40,57255 45,2673 -4,69475 22,04069 46 33,00556 48,61517 43,51986 5,095307 25,96215 47 34,86972 50,28486 45,13359 5,151268 26,53556 48 22,96354 40,09691 34,82689 5,270022 27,77313 49 25,60622 31,52352 37,11455 -5,59103 31,25962 50 26,71742 32,0698 38,07647 -6,00667 36,08011 51 28,84795 33,89881 39,92079 -6,02198 36,2642
(1) (2) (3) (4) (5) (6)
Kemudian untuk memperoleh nilai �̂0 dan �̂1 digunakan data dengan nilai
sisaan kuadrat yang telah diurutkan sebanyak h. Berikut perhitungan
masing-masing kelompok data berdasarkan rumus pada (2.9) dan (2.10) diperoleh:
1. Perhitungan nilai �̂0 dan �̂1untuk data kelompok 1 yaitu:
�̂1 =
∑��=1����−
∑��=1��∑��=1��
�
�−1
�[∑��=1��]2+∑��=1��2�
�̂1 =
68.961,834−2.152,039�1.612,814
52
−521 (1.612,814)2+ 52.565,719
�̂1 =
68.961,834−66.746,907
2.543,241
�̂1 = 0,87091
dan
�̂0 =�� − �̂1��
�̂0 = 41,38537−0,87091(31,01565)
�̂0 = 14,37361
Jadi, diperoleh model penaksir metodeleast trimmed squaresadalah:
��� = �̂0 +�̂1��
��� = 14,37361 + 0,87091 �
2. Perhitungan nilai �̂0 dan �̂1untuk data kelompok 2 yaitu:
�̂1 =
63.946,642−2.008,979�1.555,445
52
−521 (1.555,445)2+ 51.182,623
�̂1 =
63.946,642−3.853,264
4.655,538
�̂1 = 0,82677
dan
�̂0 = 38,63421−0,82677(29,9124)
�̂0 = 13,87651
Jadi, diperoleh model penaksir metodeleast trimmed squaresadalah:
��� = 13,87651 + 0,82677 �
3. Perhitungan nilai �̂0 dan �̂1untuk data kelompok 3 yaitu:
�̂1 =
65.715,796−2.070,464�1.584,089
52
− 1
52(1.584,089)
2+ 51.756,837
�̂1 =
65.715,796−63.073,087
3.500,300
�̂1 = 0,75500
dan
�̂0 = 39,81662−0,75500(30,46326)
�̂0 = 16,81700
Jadi, diperoleh model penaksir metodeleast trimmed squaresyaitu:
��� = �̂0 +�̂1��
��� = 16,81700 + 0,75500 �
4. Perhitungan nilai �̂0 dan �̂1untuk data kelompok 4 yaitu:
�̂1 =
60.473,622−2.056,963�1.476,857
52
−521 (1.476,857)2+ 44.428,899
�̂1 =
60.473,622−58.419,986
2.484,558
�̂1 = 0,82656
dan
�̂0 = 39,55698−0,82656(28,40109)
�̂0 = 16,08177
Jadi, diperoleh model penaksir metodeleast trimmed squaresyaitu:
��� = �̂0 +�̂1��
��� = 16,08177 + 0,82656 �
Dari model penaksir least trimmed squares yang diperoleh, selanjutnya akan
dihitung nilai rata-rata kuadrat sisa untuk masing-masing data kelompok yaitu:
1. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 1 adalah:
n = 52
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =2.391,516−1.929,008
52−2
�2 =462,507
50
= 9,25014
Jadi, diperoleh rata-rata kuadrat sisa dengan penaksirLTS adalah 9,25014.
2. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 2 adalah:
n = 52
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =3.522,075−3.182,324
52−2
�2 =339,751
50
= 6,79503
Jadi, diperoleh rata-rata kuadrat sisa dengan penaksir LTSadalah 6,79503
3. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 3 adalah:
n = 52
p = 2
sehingga:
�2 =��� − ���
�2 =2.327,632−1.601,226
52−2
�2 =726,407
50
= 14,32813
Jadi, diperoleh rata-rata kuadrat sisa dengan penaksir LTS adalah 14,32813.
4. Perhitungan nilai rata-rata kuadrat sisa untuk data kelompok 4 adalah:
n = 12
p = 2
sehingga:
�2 =��� − ���
� − �
�2 =2.303,745−1.861,874
52−2
�2 =441,872
50
= 8,83743
Jadi, diperoleh rata-rata kuadrat sisa dengan penaksir LTS adalah 8,83743.
3.7 Regresi Robust dengan PenaksirLMS
LMS merupakan salah satu penaksir dalam regresi robustyang digunakan untuk
mengatasi masalah pencilan. Hal yang perlu diperhatikan pada penaksir LMS
adalah meminimumkan median kuadrat sisa yaitu:
�= min {��������2} = min {�1,�2, … ,��}
kemudian dalam menentukan nilai �1,�2,…,��yaitu median dari kuadrat sisa
pada iterasi ke-i, terlebih dahulu dicari nilai kuadrat sisa metode kuadrat terkecil
dan jumlah pengamatan pada iterasi ke-i, sehingga diperoleh nilai M.
Jumlah pengamatan pada setiap iterasi ditentukan dengan mencari nilai