Solusi Persamaan Boltzmann Dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik

PENDEKATAN ANALITIK DAN NUMERIK

YOANITA HISTORIANI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Dengan ini saya menyatakan bahwa tesis dengan judul Solusi Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik adalah karya saya sendiri dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain disebutkan di dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini

Bogor, Agustus 2007

Bobylev Initial Condition using Analitycal and Numerical Approach. Under the supervision from ENDAR H. NUGRAHANI and SRI NURDIATI.

A gas flow may be modeled at either a microscopic or a macroscopic level. The microscopic model recognizes the particular structure of the gas as collection of discrete molecules and ideally provides position, velocity and state of every molecule at all times. The position, velocity, and state of each molecules can be modeled as a probability distribution function. The mathematical model at this level is called Boltzmann equation. The macroscopic level recognizes some physical properties like temperature, volume, average velocity, energy, and impul.

Mathematical model contained in Boltzmann equation is complicated, involves high dimensional differential and integral form, so it is relatively difficult to find a solution of this equation. This thesis use Bobylev initial condition which takes a general form of normal distribution function.

YOANITA HISTORIANI. Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik. Dibimbing oleh ENDAR H. NUGRAHANI dan SRI NURDIATI.

Pergerakan molekul pada suatu sistem gas dapat dimodelkan dari 2 sudut pandang yang berbeda, yaitu secara mikroskopik dan makroskopik. Dari sudut pandang mikroskopik, suatu sistem gas diamati sebagai sekumpulan molekul tunggal yang identik yang saling berinteraksi satu dengan lainnya. Setiap molekul gas berada pada posisi tertentu, kecepatan tertentu, pada saat t yang dimodelkan dalam suatu fungsi distribusi peluang. Model matematik yang menggambarkan evolusi distribusi peluang suatu molekul gas terhadap waktu, posisi, kecepatan serta interaksi antar molekul dikenal dengan persamaan Boltzmann. Dari sudut pandang makroskopik, gerak partikel dapat diamati secara lebih jelas dengan melakukan pengukuran besaran fisika pada sistem, antara lain kecepatan rata-rata, tekanan, temperatur, energi dan suhu.

Rumusan matematik persamaan Boltzmann melibatkan fungsi diferensial dan integral dengan dimensi variabel bebas yang tinggi, sehingga persamaan ini relatif sulit dicari solusi meskipun fungsi sebaran yang dipergunakan sebagai nilai awal merupakan fungsi sebaran yang paling sederhana. Pada tesis ini, fungsi sebaran yang dipilih sebagai nilai awal adalah fungsi distribusi Bobylev, yang merupakan bentuk umum dari fungsi distribusi normal.

©

Hak Cipta milik Institut Pertanian Bogor, tahun 2007

Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.

PENDEKATAN ANALITIK DAN NUMERIK

YOANITA HISTORIANI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

NIM : G551050141

Disetujui Komisi Pembimbing

Dr. Ir. Endar H. Nugrahani, MS Dr. Ir. Sri Nurdiati, MSc

Ketua Anggota

Diketahui

Ketua Departemen Matematika Dekan Sekolah Pascasarjana

Dr. Berlian Setiawaty, MS Prof. Dr. Ir. Khairil Anwar Notodiputro, MS

Puji syukur kehadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini dapat dilaksanakan dan diselesaikan dengan baik. Judul yang dipilih pada penelitian yang dilaksanakan sejak bulan Januari 2007 ini adalah Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik.

Terima kasih penulis ucapkan kepada Ibu Dr. Ir. Endar H. Nugrahani, MS dan Ibu Dr. Ir. Sri Nurdiati, MSc selaku pembimbing serta Bapak Dr. Ir. Putu Purnaba, DEA yang telah banyak memberikan saran.

Semoga karya ilmiah ini bermanfaat.

Penulis dilahirkan di Kebumen pada tanggal 29 Agustus 1982 sebagai anak pertama dari pasangan Turisno dan Tri Rujiati. Pendidikan sarjana ditempuh di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor, lulus pada tahun 2004.

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... x

PENDAHULUAN Latar Belakang ... 1

Tujuan Penelitian ... 2

Batasan Penelitian ... 2

TINJAUAN PUSTAKA Persamaan Lioville(Persamaan Transport) ... 4

Persamaan Boltzmann ... 6

Besaran Makroskopik Gas ... 8

METODE ... 10

HASIL DAN PEMBAHASAN Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev ... 11

Besaran Makroskopik Gas ... 15

Simulasi dengan Metode DSMC ... 16

KESIMPULAN DAN SARAN ... 21

DAFTAR PUSTAKA ... 22

PENDEKATAN ANALITIK DAN NUMERIK

YOANITA HISTORIANI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Dengan ini saya menyatakan bahwa tesis dengan judul Solusi Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik adalah karya saya sendiri dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain disebutkan di dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini

Bogor, Agustus 2007

Bobylev Initial Condition using Analitycal and Numerical Approach. Under the supervision from ENDAR H. NUGRAHANI and SRI NURDIATI.

A gas flow may be modeled at either a microscopic or a macroscopic level. The microscopic model recognizes the particular structure of the gas as collection of discrete molecules and ideally provides position, velocity and state of every molecule at all times. The position, velocity, and state of each molecules can be modeled as a probability distribution function. The mathematical model at this level is called Boltzmann equation. The macroscopic level recognizes some physical properties like temperature, volume, average velocity, energy, and impul.

Mathematical model contained in Boltzmann equation is complicated, involves high dimensional differential and integral form, so it is relatively difficult to find a solution of this equation. This thesis use Bobylev initial condition which takes a general form of normal distribution function.

YOANITA HISTORIANI. Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik. Dibimbing oleh ENDAR H. NUGRAHANI dan SRI NURDIATI.

Pergerakan molekul pada suatu sistem gas dapat dimodelkan dari 2 sudut pandang yang berbeda, yaitu secara mikroskopik dan makroskopik. Dari sudut pandang mikroskopik, suatu sistem gas diamati sebagai sekumpulan molekul tunggal yang identik yang saling berinteraksi satu dengan lainnya. Setiap molekul gas berada pada posisi tertentu, kecepatan tertentu, pada saat t yang dimodelkan dalam suatu fungsi distribusi peluang. Model matematik yang menggambarkan evolusi distribusi peluang suatu molekul gas terhadap waktu, posisi, kecepatan serta interaksi antar molekul dikenal dengan persamaan Boltzmann. Dari sudut pandang makroskopik, gerak partikel dapat diamati secara lebih jelas dengan melakukan pengukuran besaran fisika pada sistem, antara lain kecepatan rata-rata, tekanan, temperatur, energi dan suhu.

Rumusan matematik persamaan Boltzmann melibatkan fungsi diferensial dan integral dengan dimensi variabel bebas yang tinggi, sehingga persamaan ini relatif sulit dicari solusi meskipun fungsi sebaran yang dipergunakan sebagai nilai awal merupakan fungsi sebaran yang paling sederhana. Pada tesis ini, fungsi sebaran yang dipilih sebagai nilai awal adalah fungsi distribusi Bobylev, yang merupakan bentuk umum dari fungsi distribusi normal.

©

Hak Cipta milik Institut Pertanian Bogor, tahun 2007

Hak Cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.

PENDEKATAN ANALITIK DAN NUMERIK

YOANITA HISTORIANI

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

NIM : G551050141

Disetujui Komisi Pembimbing

Dr. Ir. Endar H. Nugrahani, MS Dr. Ir. Sri Nurdiati, MSc

Ketua Anggota

Diketahui

Ketua Departemen Matematika Dekan Sekolah Pascasarjana

Dr. Berlian Setiawaty, MS Prof. Dr. Ir. Khairil Anwar Notodiputro, MS

Puji syukur kehadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini dapat dilaksanakan dan diselesaikan dengan baik. Judul yang dipilih pada penelitian yang dilaksanakan sejak bulan Januari 2007 ini adalah Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev menggunakan Pendekatan Analitik dan Numerik.

Terima kasih penulis ucapkan kepada Ibu Dr. Ir. Endar H. Nugrahani, MS dan Ibu Dr. Ir. Sri Nurdiati, MSc selaku pembimbing serta Bapak Dr. Ir. Putu Purnaba, DEA yang telah banyak memberikan saran.

Semoga karya ilmiah ini bermanfaat.

Penulis dilahirkan di Kebumen pada tanggal 29 Agustus 1982 sebagai anak pertama dari pasangan Turisno dan Tri Rujiati. Pendidikan sarjana ditempuh di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor, lulus pada tahun 2004.

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... x

PENDAHULUAN Latar Belakang ... 1

Tujuan Penelitian ... 2

Batasan Penelitian ... 2

TINJAUAN PUSTAKA Persamaan Lioville(Persamaan Transport) ... 4

Persamaan Boltzmann ... 6

Besaran Makroskopik Gas ... 8

METODE ... 10

HASIL DAN PEMBAHASAN Solusi Eksak Persamaan Boltzmann dengan Nilai Awal Bobylev ... 11

Besaran Makroskopik Gas ... 15

Simulasi dengan Metode DSMC ... 16

KESIMPULAN DAN SARAN ... 21

DAFTAR PUSTAKA ... 22

1 Kurva solusi eksak dan numerik dengan nilai awal Bobylev ... 18

2 Kurva komponen kecepatan x ... 19

3 Kurva komponen kecepatan y ... 20

1 Integral Gauss ... 24 2 Bukti Persamaan 10 ... 25 3 Bukti Persamaan 11 ... 25 4 Bukti Persamaan 26 ... 26

5 Bukti ₃

3 4

2

I d

S

T ₌ π

∫

ee e ... 29

6 Bukti Persamaan 29 ... 31 7 Bukti Persamaan 30 ... 32 8 Bukti Persamaan 33 ... 32 9 Bukti Persamaan 34 ... 33 10 Bukti Persamaan 35 ... 33 11 Bukti Persamaan 37 ... 36 12 Bukti Persamaan 38 ... 41 13 Bukti Persamaan 39 ... 42 14 Bukti Persamaan 40 ... 42 15 Bukti Persamaan 42 ... 43 16 Bukti Persamaan 43 ... 44 17 Bukti Persamaan 0 ... 45

2

=

∫

S

ede

Latar Belakang

Menurut teori molekuler benda, satu unit volume makroskopik gas (misalkan 1 cm3) merupakan suatu sistem yang terdiri atas sejumlah besar

molekul (kira-kira sebanyak buah molekul) yang bergerak dengan arah yang tidak menentu. Karena jumlahnya yang sangat besar, maka secara matematis, untuk memodelkan gerak dan sifat setiap molekul tidak mudah, sehingga perilaku setiap molekul gas pada suatu sistem didekati dengan menggunakan sifat partikel.

20

10

Pergerakan partikel gas yang tidak melibatkan interaksi dengan partikel lainnya disebut aliran. Model matematika yang menyatakan peristiwa ini dikenal dengan persamaan transport. Di sisi lain, model pergerakan partikel yang melibatkan interaksi dengan partikel gas lain disebut persamaan Boltzmann, yang pertama kali diungkapkan oleh seorang ahli fisika bernama Ludwig Boltzmann

pada tahun 1898 (Cercignani 1975).

Persamaan Boltzmann merupakan persamaan diferensial integral yang menggambarkan evolusi distribusi peluang suatu partikel gas sebagai fungsi dari waktu, posisi dan kecepatannya, serta interaksi antar partikel karena adanya tumbukan antar partikel gas. Persamaan Boltzmann telah dikenal luas karena banyak aplikasi dan perluasannya antara lain dalam bidang fisika, biologi, ekonomi, ekonofisika dan sosial. Pada bidang fisika, aplikasi dari solusi persamaan Boltzmann dapat digolongkan menjadi dua jenis. Aplikasi yang pertama berkaitan dengan penarikan kesimpulan mengenai sifat-sifat makroskopik gas yang didekati dari sifat-sifat mikroskopiknya. Hasilnya memberi banyak manfaat dalam bidang mekanika statistika, yaitu menjembatani perbedaan antara sifat-sifat yang terdapat pada struktur atom benda dengan sifat benda pada tingkat makroskopik. Aplikasi yang kedua berkaitan dengan pengembangan model untuk jenis zat lain seperti zat padat dan zat cair (Bellomo & Pulvirenti 2000).

Besaran makroskopik gas adalah sifat-sifat gas yang dapat diamati secara fisis pada suatu sistem, seperti suhu, tekanan, dan volume (Cercignani 1975).

Karena rumusan matematis persamaan Boltzmann melibatkan fungsi dengan dimensi variabel bebas yang tinggi, maka persamaan ini relatif sulit dicari solusi, meskipun fungsi sebaran yang dipergunakan sebagai nilai awal merupakan fungsi sebaran yang paling sederhana. Fungsi sebaran yang pernah dipilih sebagai nilai awal antara lain adalah fungsi sebaran Maxwell, fungsi sebaran Bobylev, fungsi sebaran Bobylev Cercignani I ,serta fungsi sebaran Bobylev Cercignani II (Nugrahani 2003).

Secara umum, terdapat 2 jenis solusi persamaan Boltzmann, yaitu solusi eksak dan solusi numerik. Solusi eksak diperoleh dengan menyelesaikan persamaan secara matematis, sedangkan solusi numerik diperoleh melalui suatu simulasi. Salah satu metode yang banyak digunakan untuk melakukan simulasi adalah metode Monte Carlo, sedemikian sehingga vektor posisi dan kecepatan partikel dibangkitkan secara stokastik (Liboff 1990).

Tujuan Penelitian

Tujuan dari penelitian ini adalah:

1. Merekonstruksi solusi eksak persamaan Boltzmann dengan menggunakan distribusi awal Bobylev.

2. Memanfaatkan solusi eksak persamaan Boltzmann untuk menghitung besaran makroskopik gas.

3. Mencari solusi numerik dengan menggunakan simulasi aliran dan tumbukan partikel gas dengan menggunakan metode Direct Simulation Monte Carlo. Batasan Penelitian

Penelitian ini dibatasi oleh beberapa asumsi, antara lain:

1. Pengamatan gerak molekul hanya dilakukan pada gerak linear, dengan mengabaikan gerak angular.

2. Sifat-sifat molekul gas didekati dengan menggunakan sifat partikel. 3. Pada sistem, gas dimodelkan sebagai gas ideal, tunggal dan identik. 4. Tumbukan yang terjadi adalah tumbukan antara 2 partikel.

TINJAUAN PUSTAKA

Definisi 1 Gas

Gas adalah suatu sistem dinamik yang terdiri atas sejumlah besar N partikel dengan massa partikel yang relatif kecil m.

(Cercignani 1975) Definisi 2 Gas Ideal

Suatu gas dikatakan ideal jika energi potensial dari gaya intermolekulernya diabaikan, meskipun partikel-partikel tersebut berada pada jarak yang lebih dekat dari diameter partikel tersebut.

(Cercignani 1975) Definisi 3 Gas Tunggal

Gas tunggal adalah gas yang molekulnya tidak mempunyai derajat bebas internal, sedemikian sehingga derajat bebas yang dimiliki hanya berasal dari vektor posisi dan vektor kecepatan.

(Cercignani 1975)

Definisi 4 Teori Kinetik

Teori kinetik adalah suatu cabang ilmu fisika yang mempelajari sifat-sifat mikroskopik molekul dan interaksi yang berhubungan dengan sifat-sifat makroskopik benda seperti hukum gas ideal. Asumsi-asumsi yang mendasari teori kinetik adalah:

1. Jumlah molekul sangat banyak.

2. Molekul-molekul tersebut merupakan molekul tunggal yang identik.

3. Molekul bergerak secara acak.

4. Gerak molekul tidak melanggar hukum gerak Newton.

5. Molekul mengalami tumbukan elastis dengan molekul lainnya. 6. Gaya gravitasi antar molekul diabaikan.

7. Sifat-sifat molekul didekati dengan menggunakan sifat-sifat partikel dengan tidak mengabaikan hukum-hukum mekanika klasik.

Definisi 5 Hukum Kekekalan Momentum

Misal terdapat 2 partikel yang bergerak pada suatu sistem. Massa partikel

pertama bergerak dengan kecepatan , serta massa partikel kedua

bergerak dengan kecepatan . Maka hukum kekekalan momentum menyatakan

bahwa:

1

m v₁ m₂

2

v

konstan.

2 2 1

1v +m v =P=

m

(Kibble & Berkshire 1996)

Definisi 6 Hukum Kekekalan Energi

Misalkan suatu partikel yang bergerak mempunyai energi kinetik T dan energi potensial P. Maka berlaku T+V =C =konstan.

(Kibble & Berkshire 1996)

Definisi 7 Fungsi Kepekatan Peluang

Misalkan X peubah acak satu dimensi dalam ruang Ω yang terdiri dari selang atau gabungan selang. Misal terdapat fungsi f

( )

x tak negatif yang memenuhi:

( )

=1

∫

Ω

dx x

f .

Jika fungsi peluang P

( )

A denganA∈Ω dapat dinyatakan dalam bentuk f

( )

x sedemikian sehingga P

( )

A

(

X

)

∫

f

( )

xdx

Α

= Ω ∈

=Pr , maka X merupakan peubah

acak kontinu dan f

( )

x merupakan fungsi kepekatan peluang dari X.

(Hogg & Craig 1995)

Definisi 8 Persamaan Lioville (Persamaan Transport)

Misalkan pada suatu sistem terdapat N buah partikel gas ideal tunggal. Misalkan setiap partikel berada pada posisi xi bergerak dengan kecepatan vi,

dengan . Maka setelah waktu t, persamaan gerak dari partikel tersebut dapat dituliskan sebagai:

N i =1 ,2 ,...,

, ,

i i

i i

dt d

dt d

v x

a v

= =

(1)

Pada sistem, partikel gas bergerak pada suatu bidang fase dengan dimensi ruang 6N, yaitu 3N merupakan dimensi komponen vektor posisi xi dan 3N lainnya merupakan dimensi dari komponen vektor kecepatan vi. Misalkan vektor z menyatakan dimensi ruang 6N. Maka persamaan evolusi z terhadap waktu adalah:

i i dt d

y z

= . (2)

Jika nilai awal diketahui untuk semua partikel gas, maka nilai untuk

semua partikel dapat diketahui, yaitu dengan menggunakan konsep persamaan diferensial biasa. Akan tetapi, karena jumlah partikel gas yang terdapat pada sistem tersebut sangat banyak, maka untuk mengidentifikasi posisi awal x

0

z z_t

0 dan

kecepatan awal dari setiap partikel akan menjadi sulit dilakukan dan

membutuhkan waktu yang tidak sedikit. Oleh karena itu, dirumuskan teknik lain untuk menggambarkan posisi dan pergerakan awal partikel, yaitu dengan

menggunakan fungsi sebaran

0

v

( )

(

, 0

)

0 = f t=

f z z yang menyatakan fungsi kepekatan peluang pada saat t = 0.

Jika setiap partikel bergerak tanpa bertumbukan satu sama lain dan banyaknya partikel yang keluar dari sistem sama dengan banyaknya partikel yang masuk sistem, maka persamaan gerak partikel dapat dinyatakan sebagai:

( )

=0 ∂

∂ + ∂

∂f t z fy (3)

yang dikenal sebagai persamaan Liouville atau persamaan aliran. Perhatikan

bahwa ∂ ∂z

( )

fy = y∂f ∂z+ f ∂ ∂z

( )

y , sehingga:

( )

=0

∂ ∂ + ∂ ∂ + ∂

∂f t y f z f f z y . (4)

Oleh karena ∂/∂z y =0, maka persamaan (4) dapat dituliskan kembali dalam

bentuk: ∂f ∂t+ y∂f ∂z =0, (5)

atau :

(

)(

)

(

)(

)

0,

1 1

= ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂

∂

∑

∑

= =

N i

i i

i N

i

i t f t f

t

f x x v v

(

)

(

)

0

1 1

= ∂ ∂ +

∂ ∂ +

∂

∂

∑

∑

=

= i

N i

i i

N i

i f f

t

f v x a v

Definisi 9 Persamaan Boltzmann

Pada persamaan Liouville, setiap partikel diasumsikan hanya bergerak, tanpa bertumbukan satu dengan lainnya, sehingga nilai ruas kanan persamaan Liouville bernilai nol. Jika pada sistem terjadi tumbukan antar 2 partikel, maka nilai ruas kanan berubah, menjadi model matematis yang merepresentasikan tumbukan antar 2 partikel tersebut yang disebut collision integral dan dilambangkan I[ f, f], dituliskan:

] , [f f I f t f

= ∂ ∂ + ∂ ∂

x

v (7)

Misalkan terdapat 2 buah partikel yang saling bertumbukan. Sebelum

tumbukan, partikel 1 melaju dengan kecepatan v, sedangkan partikel 2 melaju

dengan kecepatan . Kecepatan partikel setelah tumbukan masing-masing dan

didefinisikan sebagai berikut:

w v'

' w

e w v w v v'

2 2

− + +

= . (8)

e w v w v w'

2 2

− − +

= . (9)

Vektor e merupakan vektor normal bidang tumbukan yang dinyatakan dengan

(

)

j i

j i

x x

x x e

− −

= dengan i≠ j, i,j=1,2,...,N sedemikian sehingga resultan kedua vektor kecepatan setelah tumbukan memenuhi:

1. Hukum kekekalan momentum

.

w v w

v' + ' = + (10)

Bukti persamaan ini dapat dilihat pada Lampiran 2.

2. Hukum kekekalan energi

.

2 2

2 2

w v

w

v' + ' = + (11)

Dengan mengasumsikan bahwa =0

∂ ∂

v

f

, maka persamaan (6) dapat

dituliskan sebagai:

] , [f f I f t

f ₌

∂ ∂ + ∂ ∂

x

v , (12)

dengan:

(

cos

)

[ ( ) ( ) ( ) ( )] , ]

, [

2 3

'

' _{w v w w e}

v f f f d d

f g

f f I

S R

∫ ∫

−

= θ (13)

dan

u = v – w,

(

cosθ

)

g = parameter tumbukan antar 2 partikel, e = vektor normal tumbukan,

de = sin θ dθ dϕ,

x = vektor posisi partikel.

yang dikenal dengan persamaan Boltzmann.

(Cercignani 1975)

Definisi 10 Distribusi Kecepatan Maxwell

Menurut Maxwell, pada suatu sistem yang diam, distribusi kecepatan partikel yang ada di dalamnya simetris di sekitar titik nol. Artinya, jumlah partikel yang bergerak ke arah kanan dan ke arah kiri adalah sama, sedemikian sehingga peluang untuk menemukan partikel yang bergerak dengan kecepatan sangat besar adalah kecil sekali. Jika peristiwa tersebut digambarkan dalam bentuk kurva, maka diperoleh suatu kurva yang menyerupai kurva sebaran normal, atau Gauss exp(-x2). Distribusi kecepatan tersebut dikenal dengan distribusi kecepatan Maxwell dan dinyatakan sebagai:

( )

_⎟⎟

⎠ ⎞ ⎜

⎜ ⎝ ⎛ − ⎟

⎠ ⎞ ⎜

⎝ ⎛ =

kT m kT

m n f

2 exp 2

4

2 2

2 3

v v

v

π

π . (14)

Definisi 11 Besaran Makroskopik Gas

Salah satu manfaat dari solusi persamaan Boltzmann adalah dapat menjelaskan beberapa sifat makroskopik benda, khususnya gas dengan menggunakan pandekatan mikroskopiknya. Sifat makroskopik gas adalah sifat gas yang dapat teramati secara fisis. Sifat tersebut meliputi densitas, impuls, aliran impuls, aliran energi, energi, volume, tekanan dan suhu. Sifat mikroskopik gas berhubungan dengan struktur dan sifat atomik dari gas tersebut.

Misalkan adalah fungsi kepekatan peluang partikel yang berada

pada posisi x dan bergerak dengan kecepatan v pada waktu t. Fungsi kepekatan peluang di atas dapat dimanfaatkan untuk memperoleh besaran makroskopik.

) , , (t x v

f

1. Fungsi Densitas

Fungsi densitas (kerapatan) partikel pada ruangR3didefinisikan sebagai:

. (15)

( )

t x f

(

t x v

)

dv

d

R

∫

=

3

, , ,

2. Impuls

Impuls merupakan hasil perkalian antara fungsi densitas dengan vektor

kecepatan massa

( )

ξ . Kecepatan massa didefinisikan sebagai:

(

)

(

)

∫

∫

=

3 3

, ,

, ,

R R

d t f

d t f

v v x

v v x v

ξ , (16)

sehingga

( )

(

)

(

)

(

)

∫

∫

∫

=

3 3

3 , ,

, ,

, , ,

R R

R f t d

d t f d t f t

d

v v x

v v x v

v v x

ξ

x ,

m

( )

t x vf

(

t x v

)

dv. (17)

R

∫

=

3

, , ,

3. Aliran Impuls

M

( )

t x vv f

(

t x v

)

dv. (18)

R T

∫

=

3

4. Aliran Energi

( )

t x v v f

(

t x v

)

dv

r

R

∫

=

3

, , 2

1

, 2 . (19)

5. Energi

( )

t x v f

(

t x v

)

dv

E

R

∫

=

3

, , 2

1

, 2 . (20)

6. Volume

( )

(

)

(

)

∫

∫

= =

3 3

, ,

, ,

,

R R

d t f

d t f d

t

v v x

v v x v m x

V . (21)

7. Suhu

( )

x v V

( ) (

t x f t x v

)

dv

Gd t

T

R

, , ,

3 1 ,

3

2

∫

−

= . (22)

dengan G adalah konstanta gas.

8. Tekanan

P

( )

t x v V

( ) (

t x f t x v

)

dv

R

, , ,

3 1 ,

3

2

∫

−

= (23)

(Cercignani 1975)

Definisi 12 Simulasi

Simulasi merupakan suatu proses membuat desain logika matematika dari suatu sistem real dengan melibatkan batasan-batasan tertentu untuk memecahkan suatu masalah.

(Pritsker 1999) Definisi 13 Metode Monte Carlo

Metode Monte Carlo adalah suatu metode algoritma komputasi yang banyak digunakan dalam simulasi untuk menggambarkan berbagai sistem pada bidang matematika dan fisika dengan melibatkan bilangan acak sebagai pembangkit variabel-variabel yang terdapat pada sistem.

METODE PENELITIAN

Pada penelitian ini, persamaan Boltzmann disederhanakan menjadi

Persamaan Boltzmann spasial homogen, yaitu dengan menetapkan ∂f ∂x dari persamaan (12) bernilai nol. Artinya, sebaran kecepatan f(v,t) setelah waktu t dianggap tidak bergantung pada vektor posisinya. Karena ruas kiri persamaan Boltzmann mengandung bentuk diferensial, maka solusi masalah tersebut sangat bergantung pada nilai awal yang dipilih.

Langkah-langkah untuk mencari solusi eksak dan numerik persamaan

Boltzmann dapat dituliskan sebagai berikut:

1. Memilih fungsi distribusi peluang tertentu sebagai nilai awal.

2. Mencari solusi eksak persamaan Boltzmann dengan mengintegralkan ruas kiri serta mengevaluasi integral ruas kanan Persamaan (12) dan (13), sehingga diperoleh fungsi distribusi partikel gas pada saat t, t≠0.

3. Solusi numerik diperoleh dengan melakukan simulasi gerak dan tumbukan partikel gas menggunakan metode DSMC (Direct Simulation Monte Carlo) satu dimensi dengan asumsi bahwa gerak dan proses tumbukan hanya

diperhatikan dalam sumbu x saja (Bird 1994). Software yang digunakan untuk melakukan simulasi adalah MATLAB 7.0.

4. Dengan menggunakan metode Monte Carlo, vektor posisi dan kecepatan molekul dibangkitkan secara stokastik.

PEMBAHASAN

Pada karya ilmiah ini, persamaan Boltzmann yang akan dicari solusinya adalah persamaan Boltzmann spasial homogen, yaitu persamaan Boltzmann

dengan ∂f ∂x bernilai nol, dituliskan:

(

cos

)

[ ( ) ( ) ( ) ( )] .

2 3

'

' _{w v w w e}

v f f f d d

f g

t f

S R

∫ ∫

−

= ∂

∂ θ (24)

Ruas kiri persamaan Boltzmann mengandung bentuk diferensial, sehingga

solusi masalah tersebut bergantung pada nilai awal yang dipilih. Selanjutnya akan dicari solusi eksak dan solusi numerik dari persamaan Boltzmann dengan menggunakan nilai awal Bobylev. Solusi numerik akan dicari dengan simulasi menggunakan Metode DSMC satu dimensi.

Solusi Eksak Persamaan Boltzman dengan Nilai Awal Bobylev Misalkan dipilih nilai awal Bobylev berikut:

⎟ ⎠ ⎞ ⎜

⎝ ⎛− +

=

= 2

0 2

0 0

0( ) ( )exp

) 0 ,

(v f v A B v C v

f , (25)

dengan dan A₀,B₀ ≥0 C₀ >0.

Selanjutnya, akan dicari nilai dan hubungan antara koefisien dan

dengan memanfaatkan sifat-sifat sebagai berikut:

0 0,B

A C₀

1. Karena f₀(v) merupakan fungsi kepekatan peluang, maka:

∫

f₀(v)dv=1. 2. Dari Persamaan (20), v f v dv

d

T =

∫

( )

2 1 2 3

0 2

,

3. 1β₀ =2TC₀ − .

Maka, dari sifat 1,2 dan 3 (lihat Lampiran 4) diperoleh:

⎥⎦ ⎤ ⎢⎣

⎡ +

− ⎭ ⎬ ⎫ ⎩

⎨ ⎧

⎥⎦ ⎤ ⎢⎣

⎡ + ₋

+ ⎥⎦ ⎤ ⎢⎣

⎡ + =

= 0 2 0 2

0 2

3 0 0

2 ) 1 ( exp 2 3 2

) 1 ( 1

2 ) 1 ( ) , ( ) 0 ,

(v v v v

T T

T F

f β β β

π β β

dengan parameter β₀ =2TC₀ −1,

3 2

0≤β₀ ≤ menunjukkan simpangan kesetimbangan dari sebaran awal.

Selanjutnya, akan dicari solusi spasial homogen Persamaan Boltzmann,

yaitu fungsi kepekatan peluang partikel pada saat t, yaitu f(v,t)=F(v,β

( )

t ), dengan β

( )

t merupakan simpangan dari sebaran awal pada saat t danβ

( )

0 =β₀.

Pertama, akan dihitung nilai integral dari fungsi kerapatan partikel pada saat t = 0 terhadap v. Dengan melakukan substitusi koordinat bola (lihat Lampiran 4), diperoleh:

(

2 3

2 ) , 0

( _{0 0 0}

2 5 0

2 3

3

B C A C

d f

R

+ =

∫

v v π

)

. (27)

Dengan demikian, fungsi kerapatan partikel pada waktu t didefinisikan sebagai:

(

∫

= +

=

3

3 2

2 ) , (

2 5

2 3

R

B AC C

d t f

d v v π

)

. (28)

Akan dicari nilai A, B, C yang memenuhi persamaan di atas. Nilai tersebut dapat diperoleh dari dua fungsi lainnya, yaitu dari aliran impuls dan temperatur. Dari Persamaan (18), aliran impuls didefinisikan sebagai:

∫

=

3

) , ( R

T _{f t d}

M vv v v ,

sehingga M (aliran impuls) dapat dinyatakan dalam bentuk:

(

)

3 2 7 2

3

5 2

4 I

C B AC

M =π + , (29)

Bukti persamaan ini dapat dilihat pada Lampiran 6. Di sisi lain, temperatur (T) didefinisikan sebagai (lihat lampiran 7):

(

)

2 7 2

3

5 2

4 3

1

C B AC d

trM d

T = =π + , (30)

⎟ ⎠ ⎞ ⎜

⎝ ⎛ −

= dC TC

A 3

2 5

2 3

2 3

π

, (31)

dan

(

2 1

2 3

2 5

−

= dC TC

B

π

)

. (32)

Dengan demikian, fungsi kerapatan partikel pada saat t, , dapat dinyatakan sebagai:

) , (t v

f

⎟ ⎠ ⎞ ⎜

⎝ ⎛− ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

+ ⎟ ⎠ ⎞ ⎜

⎝ ⎛ ₊ −

= 2 7₂ 2 5₂ 3₂ 2

2

3 ₂ exp

5 3

2 )

,

(t v d T v C T v C C C v

f

π

, (33)

sedemikian sehingga, fungsi sebaran partikel pada saat t sangat bergantung pada kecepatan partikel tersebut.

Ruas kiri persamaan Boltzmann (24) merupakan turunan fungsi sebaran

partikel terhadap waktu t, dengan f

( )

t,v pada persamaan (33) diperoleh:

(

CT

)

C C C C t

C d t

f ⎟∂ ∂

⎠ ⎞ ⎜

⎝ ⎛− ⎥⎦ ⎤ ⎢⎣

⎡ _{− +}

− =

∂

∂ 1₂ 2 4 2 2

2

3 ₄ exp

15 5

2

1 v v v

π

. (34)

Selanjutnya, akan dicari nilai ruas kanan dari persamaan Boltzmann secara bertahap sebagai berikut:

(

cos

)

[ ( ) ( ) ( ) ( )] . ]

, [

2 3

'

' _{w v w w e}

v f f f d d

f g

f f I

S R

∫ ∫

−

= θ

⎟ ⎠ ⎞ ⎜

⎝

⎛ _⎟

⎠ ⎞ ⎜

⎝

⎛ ₊

− ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

− =

− 2 ' 2 ' 2 2 2 2 2

'

'_{) ( ) ( ) ( ) exp}

(v f w f v f w B v w v w C v w

f

. exp

, 2 2 2 2

2 _⎟

⎠ ⎞ ⎜

⎝

⎛ _⎟

⎠ ⎞ ⎜

⎝

⎛ ₊

− ⎥⎦ ⎤ ⎢⎣

⎡ ₋

=B U V v UTeeTU C v w (35)

Dengan memanfaatkan substitusi dan penyederhanaaan pada persamaan (8), (9) dan (11), maka:

(

cos

)

(

3 ,

2

2

µ η µ

θ = + −

∫

v UU e

ee

T T

S

I d

g

)

(36)

(

θ

)

θ θ η π

(

θ

)

θ θ π

µ πg cos sin d , 2 πg cos sin d ,

2

0 3

0

∫

∫

=

= +

= v w

U .

Ruas kanan persamaan Boltzmann dapat dituliskan kembali dalam bentuk (lihat Lampiran 11):

(

)

exp .

4 15 5

2

, 2 4 2 2

2 7

2 3 2

⎟ ⎠ ⎞ ⎜

⎝ ⎛− ⎥⎦ ⎤ ⎢⎣

⎡ _{− +}

= C v C v Cv

C B f f

I π µ (37)

Dengan mempergunakan bentuk baru ruas kanan (37) dan kiri persamaan Boltzmann (34), diperoleh:

(

)

, 2 exp

4 15 2 5 4 2 2 7

2 3 2

2 4

15 2 5 4 2 2

1 2 1 2 3

⎟ ⎠ ⎞ ⎜

⎝ ⎛ ⎥⎦ ⎤ ⎢⎣

⎡

⎥⎦ ⎤ ⎢⎣

⎡

− +

− =

∂ ∂ − + −

−

v v

v

v v

v

C C

C C

B

t C C e C

C CT C

d

µ π

π

(

2 1

)

2 −

− = ∂

∂C t dµC CT . (38)

Substitusiβ =2TC−1 dan

2

µ

α = d , menghasilkan:

(

β

)

β α

β

1

+ − = ∂ ∂

t . (39)

Persamaan (39) merupakan persamaan diferensial biasa, sehingga solusinya adalah:

(

t

)

t

Ae Ae

t _α

α

β −₋

− =

1 )

( , A konstanta. (40)

Dengan melakukan substitusi t = 0, pada Persamaan (40), diperoleh:

) 1 ( )) 0 ( 1 (

) 0 (

0 0

β β β

β

+ = +

=

A , (41)

sehingga,

) 1

( 1 ) (

0 0

t t

e e

t _α

α β

β

β − ₋

− +

= . (42)

Jadi, solusi eksak persamaan Boltzmann homogen spasial mengambil bentuk yang

( )

( )

( )

( )

( )

, 2 ) 1 ( exp 2 3 2 ) 1 ( 1 2 ) 1 ( ) , ( ) , ( 2 2 2 3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ + ₋ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = = v v v v T t T t t T t d t F t f β β β π β β (43)

dengan β

( )

t dari Persamaan (42) serta

3 2 0 , 0 ,

0 > < <

> T _t

d β .

Besaran Makroskopik Gas

Jika fungsi sebaran partikel pada saat t diketahui, maka besaran makroskopik dari masalah nilai awal Bobylev dapat dihitung, sebagai berikut:

1. Fungsi Densitas

( )

(

)

( )

( )

( )

( ) . 1 2 3 2 ) 1 ( 1 2 ) 1 ( , , , 3 2 3 2 ) 1 ( 2 2 3 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ + ₋ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = =

∫

∫

⎥⎦ ⎤ ⎢⎣ ⎡ + − R T t R d e T t t T t d d t f t d v v v v x x v β β β π β

2. Kecepatan Rata-rata:

( )

( )

( )

( )

( )

( )

. 0 2 ) 1 ( exp 2 3 2 ) 1 ( 1 2 ) 1 ( 1 , 1 , 3 3 2 2 2 3 = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛₋ + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ + ₋ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = =

∫

∫

R R d T t T t t T t d d d t f d x t V v v v v v v v β β β π β

3. Aliran Impuls

( )

(

)

( )

( )

( )

( ) . 2 3 2 ) 1 ( 1 2 ) 1 ( , , , 3 2 ) 1 ( 2 2 3 3 2 3 dTI d e T t t T t d d t f t M R T t T R T = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎥⎦ ⎤ ⎢⎣ ⎡ + ₋ + ⎥⎦ ⎤ ⎢⎣ ⎡ + = =

∫

∫

⎥⎦ ⎤ ⎢⎣ ⎡ + − v v vv v v x vv x v β β β π β

( )

(

)

( )

( )

( )

( )

. 0

2 ) 1

( exp 2 3 2

) 1

( 1

2 ) 1

( 2

1

, , 2

1 ,

3 3

2 2

2 3 2

2

=

⎟ ⎠ ⎞ ⎜

⎝

⎛ +

− ⎭ ⎬ ⎫ ⎩

⎨ ⎧

⎥⎦ ⎤ ⎢⎣

⎡ + ₋

+ ⎥⎦ ⎤ ⎢⎣

⎡ + =

=

∫

∫

R R

d T

t T

t t

T t d

d t f t

r

v v v

v v

v v x v

v x

β β

β π

β

5. Energi

( )

(

)

( )

( )

( )

( )

. 2

3

2 ) 1

( exp 2 3 2

) 1

( 1

2 ) 1

( 2

1

, , 2

1 ,

3 3

2 2

2 3 2

2

dT

d T

t T

t t

T t d

d t f t

E

R R

=

⎟ ⎠ ⎞ ⎜

⎝

⎛ +

− ⎭ ⎬ ⎫ ⎩

⎨ ⎧

⎥⎦ ⎤ ⎢⎣

⎡ + ₋

+ ⎥⎦ ⎤ ⎢⎣

⎡ + =

=

∫

∫

v v v

v

v v x v

x

β β

β π

β

Simulasi dengan menggunakan metode DSMC satu dimensi

Metode DSMC merupakan salah satu metode yang dapat digunakan untuk mensimulasikan mekanisme tumbukan secara langsung. Inti dari metode ini adalah membuat representasi sederhana mengenai sebaran awal partikel, gerak, tumbukan dan pemberian indeks terhadap setiap partikel. Seperti program simulasi yang lainnya, program ini juga mengalami beberapa penyederhanaan, antara lain pada jumlah partikel yang dijadikan subjek pengamatan dan pada dimensi posisi yang digunakan. Posisi partikel diperhatikan hanya berdasarkan sumbu x saja. Misalkan ruang yang dipergunakan sebagai sistem ada pada

, 1

0≤x≤ 0≤ y≤1 dan 0≤ z≤1. Untuk memudahkan proses inisialisasi posisi awal partikel, sumbu x dibagi menjadi beberapa sel dan setiap selnya dibagi lagi menjadi beberapa sub sel (Bird 1994).

Proses simulasi dilakukan dengan menggunakan MATLAB 7.0. Program utama diberi nama NSBIC.m, yaitu program untuk menguji prosedur tumbukan pada gas seragam sederhana. Program NSBIC.m dibuat dengan algoritma sebagai berikut:

3. Mendeskripsikan pergerakan sejumlah partikel pada selang waktu tertentu. 4. Menentukan urutan partikel dalam sel dan sub sel.

5. Menghitung banyaknya tumbukan selama selang waktu tertentu. 6. Menentukan contoh aliran partikel.

7. Menampilkan hasil.

Sistem dibagi menjadi beberapa sel dan subsel. Pada simulasi kali ini, sistem akan dibagi menjadi 50 sel dan 400 sub sel dengan jumlah partikel maksimal 1000 partikel. Secara keseluruhan, program cukup besar sehingga perlu dipecah menjadi beberapa subroutine. Pada program NSBIC.m, terdapat 8 buah subroutine yaitu sebagai berikut:

1. DATAOS.m

Subroutine ini berisi data awal yang berkaitan dengan sifat-sifat fisis partikel gas seperti kerapatan, suhu, banyak partikel sebenarnya yang disimulasikan oleh partikel simulasi, interval waktu (time step), jumlah subsel pada masing-masing sel, massa serta diameter partikel, tetapan kekentalan, serta scattering parameter.

2. INITOS4.m

Subroutine ini berisi nilai variabel awal dan sebaran partikel pada saat . Nilai awal yang didefinisikan antara lain adalah konstanta Boltzmann,

, collision cross section, informasi geometri setiap sel dan sub sel (termasuk nomor sel dan sub sel), serta kecepatan awal masing-masing partikel.

0 = t

23 3806 .

1 −

= e

k

3. SAMPIOS.m

SAMPIOS.m merupakan sub routine yang berisi inisialisasi seluruh variabel sampling, antara lain: banyaknya tumbukan pada t = 0, jumlah sampel, banyaknya partikel yang berpindah posisi, serta banyaknya partikel yang terseleksi untuk bertumbukan dan terpisah lagi.

4. MOVEOS.m

pembatas merupakan tumbukan lenting sempurna, sedemikian sehingga gerakan pantulnya mengikuti sifat pantulan cermin.

5. INDEXS.m

Subroutine INDEX.m mengatur penomoran partikel berdasarkan susunan sel dan sub selnya.

6. COLLS3.m

COLLS3.m merupakan subroutine yang mensimulasikan tumbukan antara dua partikel, yaitu mengatur partikel partikel yang akan bertumbukan serta menghitung kecepatan relatif partikel, sudut elevasi, azimuth, sudut defleksi, serta kecepatan partikel setelah tumbukan.

7. SAMPLEOS.m

SAMPLEOS.m melakukan sample terhadap partikel dalam aliran. 8. OUTOS.m

OUTOS.m bertugas menampilkan hasil output pada setiap langkah waktu tertentu secara terus menerus.

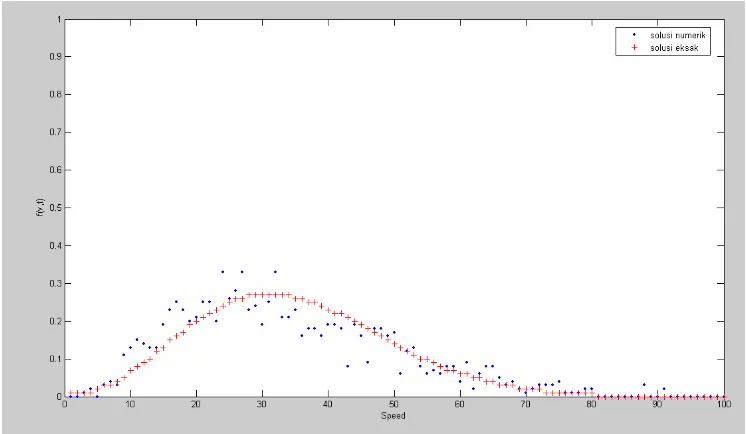
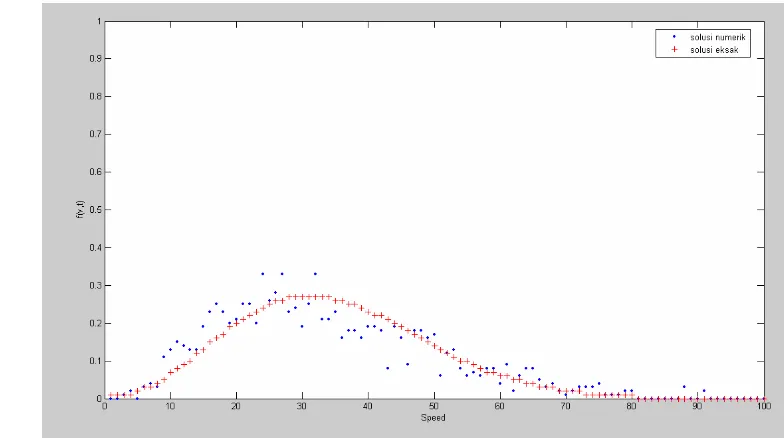
[image:40.595.125.498.457.674.2]

Hasil dari simulasi selama selang waktu t tertentu menghasilkan pola sebaran sebagai berikut:

Kurva merah menunjukkan sebaran kecepatan yang diperoleh melalui solusi eksak. Kurva biru menunjukkan solusi hasil simulasi.

Karena fungsi sebaran partikel terhadap kecepatan dan waktu dari hasil simulasi telah diketahui, maka dihitung nilai beberapa besaran makroskopik, antara lain:

1. Fungsi Kepekatan Peluang Dengan menggunakan algoritma:

Density = sum(fPV)/1000,

Diperoleh Density = 1, yang sesuai dengan hasil yang diperoleh secara eksak.

Keterangan:

fPV = frekuensi speed partikel. 1000 = jumlah partikel.

2. Kecepatan Rata-rata

Dari hasil simulasi diperoleh: Vrata = [0.2407, 0.5707, 0.0044]

yang hasilnya mendekati nol, sesuai dengan hasil yang diperoleh secara

eksak.

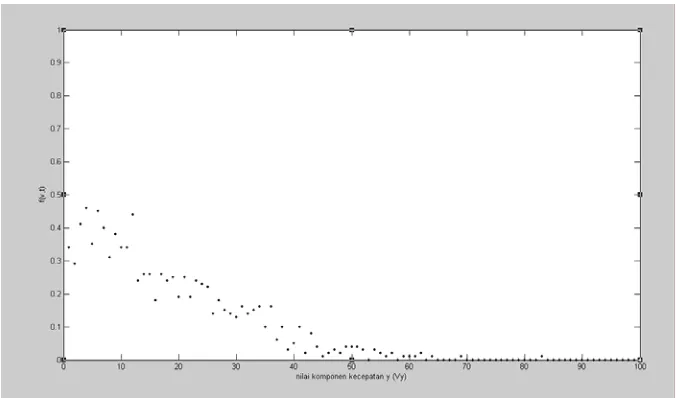
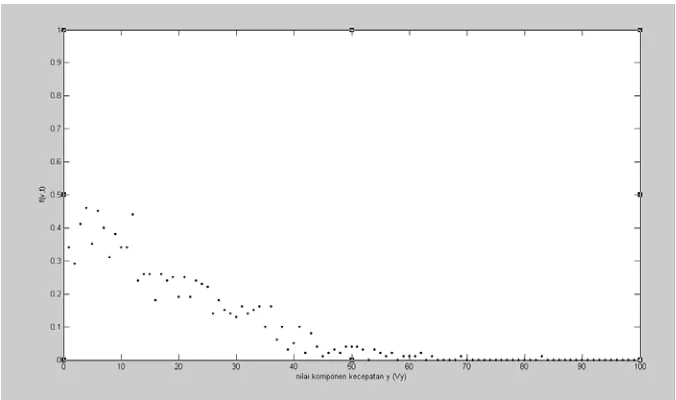
Dibawah ini adalah kurva yang menunjukkan sebaran partikel terhadap masing-masing komponen kecepatan partikel.

[image:42.595.158.496.83.282.2]

Gambar 3 Kurva sebaran komponen kecepatan y hasil simulasi.

KESIMPULAN DAN SARAN

Solusi eksak persamaan Boltzmann homogen spasial dengan nilai awal Bobylev berhasil diperoleh dengan bentuk sebagai berikut:

( )

( )

( )

( )

( )

⎥⎦ ⎤ ⎢⎣

⎡ +

−

⎭ ⎬ ⎫ ⎩

⎨ ⎧

⎥⎦ ⎤ ⎢⎣

⎡ + ₋

+ ⎥⎦ ⎤ ⎢⎣

⎡ + = =

2

2 ) 1 ( 2

2 3

2 3 2

) 1

( 1

2 ) 1

( ) , ( ) , (

v

v v

v T

t e

T t t

T t d

t F t f

β

β β

π β β

dengan

( )

3 2 0

, 0 ,

0 > < <

> T t

d β . Dari hasil tersebut, dapat dihitung nilai dari

beberapa besaran makroskopik seperti fungsi densitas, kecepatan rata-rata, impuls, dan energi.

Solusi numerik persamaan Boltzmann dengan menggunakan metode DSMC satu dimensi dapat diperoleh, sedemikian sehingga nilai dari beberapa besaran makroskopik dapat dihitung, antara lain fungsi densitas dan rata-rata.

DAFTAR PUSTAKA

Bird, G.A. 1994. Molecular Gas Dynamics and The Direct Simulation of Gas Flow. New York: Oxford University Press.

Bobylev, A.V. 1975. Exact Solutions of The Boltzmann Equation. Sov. Phys. Dokl. 20(12):822-824.

Bollomo, Pulvirenti. 2000. Modelling in Applied Science. New York: Birkhaeuser Boston.

Boltzmann, L. 1964. Lectures on Gas Theory. New York: Dover Publications, Inc.

Cercignani, C.1975. Theory and Application of The Boltzmann Equation. London: Scootish Academic Press.

Harris, S. 1971. An Introduction of The Boltzmann Equation. New York: Dover Publications, Inc.

Kibble, Berkshire. 1996. Classical Mechanics. England: Addison Wesley Longman Limited.

Krane, K. S. 1992. Fisika Modern. Wospakrik HJ, penerjemah; Jakarta: UI-Pres. Liboff, R.L. 1990. Kinetic Theory. New York: Prentice-Hall, Inc

Nugrahani, E.H. Beitraege zur Numerik der Boltzmann Gleichung (Some Contributions to Numerical Solution of the Boltzmann Equation) [disertasi]. Saarbruecken: Universitaet des Saarlandes; 2003.

Lampiran 1. Integral Gauss

Integral Gauss merupakan integral dari fungsi Gauss, yaitu fungsi yang mengandung bentuk exp(-x2), yang sering muncul dalam mekanika statistik. Integral Tak Tentu dari

∫

exp(−x2)dx tidak dapat dicari solusinya dengan mengintegralkan seperti biasa. Misalkan:

( )

,

exp x2 dx

I

∫

∞

∞ −

−

= (44)

Maka integral ini dapat dicari nilainya dengan menggunakan sifat fungsi eksponensial. Bentuk I di atas dapat dituliskan kembali dengan menggunakan variabel yang lain:

( )

y dy

I

∫

∞

∞ −

−

= _exp 2 ₍₄₅₎

Selanjutnya, dengan mengalikan persamaan (44) dan (45), diperoleh:

( )

x dx

( )

y dy

I

∫

∫

∞

∞ − ∞

∞ −

− −

= 2 2

2 _{exp exp}

( ) ( )

(

)

(

x y

)

dxdy dy dx y x

∫ ∫

∫ ∫

∞ ∞ − ∞

∞ −

∞ ∞ − ∞

∞ −

+ − =

− −

=

2 2

2 2

exp

exp exp

Integral lipat dua tersebut dapat dinyatakan dalam koordinat polar

( )

r,θ dengan ,

∞ < <r

0 0<θ <2π dan r2 = x2 +y2.

( )

( )

( )

π π π

θ π

=

⎥⎦ ⎤ ⎢⎣

⎡_{− −}

=

− =

− =

∞ ∞

∞

∫

∫

∫

0 2 0

2 0

2 2

0 2

exp 2 1 2

exp 2

exp

r rdr r

Dengan demikian, =

∫

_exp

( )

− 2 =π12

∞

∞ −

dx x

I . Karena fungsi exp(-x2)

simetris di sekitar 0, maka terdapat nilai yang sama antara x dan –x, sehingga

( )

2 exp

2 1

0

2 ₌π

−

∫

∞

dx

x .

Dengan cara yang sama, solusi untuk fungsi

∫

( )

ax dx adalah

∞

−

0

2

exp .

2

1 2

1

⎟ ⎠ ⎞ ⎜ ⎝ ⎛

a π

Lampiran 2. Bukti Persamaan 10 Persamaan 10:

w v w

v' + ' = +

Bukti:

w v e w v w v e w v w v w

v + = + + − + + − − = +

2 2

2 2

' '

Lampiran 3. Bukti Persamaan 11 Persamaan 11:

2 2

2 ' 2 '

w v

w

v + = +

Bukti:

2 2

2 ' 2 '

2 2

2

2 e

w v w v e w v w v w

v + = + + − + + − −

2 2

2 2

2 2

, 2 2 2

2 2

, 2 2 2

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ − + −

+ − ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ + +

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ − + −

+ + ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ + =

e w v e w v w v w

v

e w v e w v w v w

v

2 2

2 2

2 2

2

2 ⎟⎟_⎠

⎞ ⎜⎜

⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ + + ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ − + ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ +

2

2 2

2

2 e

w v w

v

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛ − + + =

2 , 2 2

,

2 2 2 2

2

w w v v

w w v

v − +

+ +

+ =

= v 2 + w 2

Lampiran 4. Bukti Persamaan 26 Persamaan 26:

⎥⎦ ⎤ ⎢⎣

⎡ +

− ⎭ ⎬ ⎫ ⎩

⎨ ⎧

⎥⎦ ⎤ ⎢⎣

⎡ + ₋

+ ⎥⎦ ⎤ ⎢⎣

⎡ + =

= 0 2 0 2

0 2

3 0 0

2 ) 1 ( exp 2 3 2

) 1 ( 1

2 ) 1 ( ) , ( ) 0 ,

(v v v v

T T

T F

f β β β

π β β

Bukti:

Asumsi 1.

∫

f₀(v)dv =1

∫

∫

⎟

⎠ ⎞ ⎜

⎝ ⎛− +

=

3 3

2 0 2

0

0 )exp

( )

, 0 (

R R

d C

B A d

f v v v v v

Dengan melalukan transformasi ke dalam koordinat permukaan bola, v =ρe, diperoleh:

(

)

∫ ∫

∫

= ∞ + −

2

3 ₀

2 0 2

2 0

0 ) exp

( )

, 0 (

S R

d d C B

A d

f v v ρ ρ ρ ρ e

(

)

∫ ∫

∞ + −

=

2 ₀

2 0 4

0 2

0 )exp

(

S

d C B

A

de ρ ρ ρ ρ

∫

∫

(

)

∫

⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣ ⎡

+ −

=

∞ ∞

− 2

2 0

0 0

4 0 2

0 2

0 exp

S

C d e

B d C A

de ρ ρ ρ ρ ρ ρ

(

)

(

)

∫

∫

∫

_⎥⎥

⎦ ⎤ ⎢

⎢ ⎣ ⎡

− +

− =

∞ ∞

2 _{0 0}

2 0 3

0 2

0

0 exp exp

S

d C B

d C A

Dengan mengintegralkan secara parsial, diperoleh: ) 2 1 2 1 2 3 ( 2 1 2 1 ( ) , 0 ( 2 1 0 0 0 0 2 1 0 0 0 2 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =

∫

∫

B _{C C C}

C C A d d f S R π π e v v ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 0 2 0 0 2 1 0 0 0 8 3 4 4 C C B C C

A π π

π

(

_{0 0 0}

)

2 5 0 2 3 3 2 2 B C A C + = π .

Karena f merupakan fungsi kepekatan peluang, maka

∫

= , sehingga: 3 1 ) , 0 ( R d

f v v

(

2 3

)

1

2 52 0 0 0

0 2 3 = + B C A C π .

Asumsi 2. v f v dv d

T =

∫

( )

2 1 2 3 0 2

∫

= 3 ) , 0 ( 2 2 3 2 R d f

T v v v

∫

+ ⎜_⎝⎛− ⎟_⎠⎞ = 3 2 0 2 0 0 2 exp ) ( 2 R d C B

A v v v

v

Dengan melakukan transformasi ke dalam koordinat permukaan bola, maka:

(

)

∫ ∫

∞ + − = 2 ₀ 2 2 0 2 0 0

2_{( )exp}

2 1 2 3 S d d C B A

T ρ ρ ρ ρ ρ e

(

)

∫ ∫

∞ + − = 2 ₀ 2 0 6 0 4

0 )exp

( 2 1 S d C B A

de ρ ρ ρ ρ

(

)

(

)

∫

∫

∫

_⎥⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − = ∞ ∞

2 _{0 0}

2 0 6 0 2 0 4

0 exp exp

2 1 S d C B d C A

de ρ ρ ρ ρ ρ ρ

(

)

(

)

∫

∫

∫

_⎥⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + − = ∞ ∞

2 _{0 0}

2 0 5 0 2 0 3

0 exp exp

2 1 S d C B d C A

Dengan menggunakan teknik pengintegralan parsial, diperoleh ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 1 0 3 0 0 2 1 0 2 0 0 2 1 8 15 2 1 4 3 2 4 T 2 3 C C B C C

A π π

π ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 3 0 0 2 0 0 2 1 0 16 15 8 3 4 3T C B C A C π π ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 0 0 0 0 0 2 1 0 4 15 2 3 4 1 4 3T C B C A C C π π ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 2 0 0 0 0 2 3 0 4 15 2 3 3T C B C A C π ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 0 0 2 3 0 0 2 15 3 2 1 3 C B A C C T π 0 0 0 2 3 0 0 2 15 3 6 C B A C

TC ⎟ = +

⎠ ⎞ ⎜ ⎝ ⎛ π atau 2 3 0 0 0 0 0 6 2 15 3 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = + π C TC C B A

Asumsi 3. β₀ =2TC₀ −1 T C 2 1 0 0 + = β .

Dengan melakukan substusi hasil asumsi 1, 2 dan 3, diperoleh:

diperoleh: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− + = = 2 0 2 0 0

0( ) ( )exp

) 0 ,

(v f v A B v C v

f ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− ⎪⎭ ⎪ ⎬ ⎫ ⎪⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 0 2 0 0 2 3 0 0 2 3

0 _{3 (2 1) exp}

2 5 v v C TC C C TC C π π

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛− ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{+ −} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 0 2 0 0 0 2 3

0 _{3 (2 1) exp}

2 5 v v C TC C TC C π

(

) (

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛− ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{− − + −} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 0 2 0 0 0 2 3

0 _{2 1 (2 1) exp}

2 3

1 TC C TC v C v

C π

(

)

(

)

⎜_⎝⎛− ⎟_⎠⎞ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ _{+ − − −} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 0 0 2 0 0 2 3

0 _{2 1 exp}

2 3 ) 1 2 (

1 C TC v TC C v

C π

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

= ₀ 2

0 2 0 0 2 3 0 2 1 exp 1 2 2 3 ) 1 2 ( 2 1 1 2 1 v v T T C TC T T β β π β

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

= 0 2

0 2 0 0 2 3 0 2 1 exp 2 3 2 1 1 2 1 v v T T T β β β β π β ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +

= 0 2 0 2

0 2 3 0 2 1 exp 2 3 2 1 1 2 1 v v T T T β β β π β

Lampiran 5. Bukti ₃

3 4 2 I d S

T ₌ π

∫

ee e

Bukti:

(

θ ϕ θ ϕ θ

)

θ ϕ θ θ ϕ θ ϕ θ π π d d d S

T _{sin cos sin sin cos sin} cos sin sin cos sin 0 2 0

2

∫ ∫

θ ϕ θ θ ϕ θ θ ϕ θ θ θ ϕ θ ϕ θ ϕ ϕ θ ϕ θ θ ϕ ϕ θ ϕ θ π π d d

∫ ∫

⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 0 2

0 2 2 2

Lampiran 6. Bukti Persamaan 29 Persamaan 29:

(

)

3 2 7 2 3 5 2 4 ) , ( 3 I C B AC d t f M R

T ₌ +

=

∫

vv v v π

Bukti:

∫

= 3 ) , ( R

T _{f t d}

M vv v v

Substitusi koordinat permukaan bola v=ρe, menghasilkan:

( )( )

e e

(

A B

) (

C

)

d de

M ρ ρ T ρ ρ2 ρ2 ρ

S 2 0 exp 2 − + =

∫ ∫

∞

ρ eeT

(

A Bρ

) (

Cρ2

)

ρ2dρde

S 2 0 2 _exp 2 − + =

∫ ∫

∞

Td ρ

(

A Bρ

) (

Cρ2 dρ

S 2 0 4 _exp 2 − + =

∫

∫

∞ e ee

)

)

Td

(

Aρ Bρ

) (

Cρ2 dρ

0 6 4 S exp 2 − + =

∫

∫

∞ e ee

(

)

(

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − =

∫

∫

∫

∞ ∞ ρ ρ ρ ρ ρ

ρ C d B C d

Lampiran 7. Bukti Persamaan 30 Persamaan 30:

(

)

2 7 2 3 5 2 4 3 1 C B AC d trM d

T = =π +

Bukti:

Dari Persamaan (29), aliran impuls (M) dituliskan:

(

)

3 2 7 2 3 5 2 4 I C B AC

M =π + ,

Dengan demikian,

( )

(