Penerapan Metode Potensial dalam Menentukan Biaya Distribusi Minimum (Studi Kasus : PT. Mitra Perkasa Dhian Abadi)

(1)

PENERAPAN METODE POTENSIAL DALAM

MENENTUKAN BIAYA DISTRIBUSI MINIMUM

(STUDI KASUS : PT. MITRA PERKASA DHIAN ABADI)

SKRIPSI

JELLY LUIS

100803029

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(2)

PENERAPAN METODE POTENSIAL DALAM

MENENTUKAN BIAYA DISTRIBUSI MINIMUM

(STUDI KASUS : PT. MITRA PERKASA DHIAN ABADI)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar sarjana sains

JELLY LUIS

100803029

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

(3)

PERSETUJUAN

Judul : Penerapan Metode Potensial dalam Menentukan Biaya Distribusi Minimum (Studi Kasus : PT. Mitra Perkasa Dhian Abadi)

Kategori : Skripsi Nama : Jelly Luis Nomor Induk Mahasiswa : 100803029

Program Studi : Sarjana (S1) Matematika Departemen : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara

Disetujui di

Medan, Agustus 2014

Komisi Pembimbing :

Pembimbing 2, Pembimbing 1,

Dr. Suwarno Ariswoyo, M.Si. Dr. Faigiziduhu Bu’ulolo, M.Si.

NIP. 195003211980031001 NIP. 195312181980031003

Disetujui Oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si. Ph.D NIP 196209011988031002

(4)

PENERAPAN METODE POTENSIAL DALAM MENENTUKAN

BIAYA DISTRIBUSI MINIMUM

(STUDI KASUS : PT. MITRA PERKASA DHIAN ABADI)

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Agustus 2014

(5)

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi ini dengan judul “Penerapan Metode Potensial dalam Menentukan Biaya Distribusi

Minimum (Studi Kasus : PT. Mitra Perkasa Dhian Abadi)”.

(6)

PENERAPAN METODE POTENSIAL DALAM MENENTUKAN BIAYA DISTRIBUSI MINIMUM

(STUDI KASUS : PT. MITRA PERKASA DHIAN ABADI)

ABSTRAK

Permasalahan transportasi termasuk permasalahan program linier khusus yang dapat diselesaikan dengan metode transportasi. PT. Mitra Perkasa Dhian Abadi merupakan perusahaan yang bergerak di bidang penjualan sepeda motor Yamaha. Dalam bidang penjualan, perusahaan ini memerlukan biaya operasi untuk mendistribusikan produknya. Salah satu masalah yang ditemukan dalam biaya operasi perusahaan ini yaitu besarnya biaya transportasi yang dikeluarkan oleh perusahaan dalam mendistribusikan sepeda motor Yamaha. Untuk itu, diperlukan suatu metode transportasi untuk menentukan biaya distribusi minimum pada PT. Mitra Perkasa Dhian Abadi yang bertujuan dapat menghemat biaya operasi perusahaan. Metode yang digunakan dalam penulisan ini adalah metode sudut barat laut untuk solusi awal dan metode potensial untuk mencari solusi optimal. Biaya transportasi dari perusahaan pada tahun 2013 sebesar Rp 58.743.000,00, sedangkan hasil perhitungan biaya transportasi dengan metode potensial pada tahun 2013 menghasilkan biaya transportasi optimal sebesar Rp 45.519.000,00. Dengan menggunakan metode potensial, pada tahun 2013 perusahaan dapat menghemat biaya sebesar Rp 13.224.000,00.

(7)

APPLICATION OF POTENTIAL METHOD IN DETERMINING MINIMUM DISTRIBUTION COST

(CASE STUDY : PT. MITRA PERKASA DHIAN ABADI)

ABSTRACT

Transportation problem is one of the specific linear program problems that can be solved by using the method of transportation. PT. Mitra Perkasa Dhian Abadi is a company engaged in selling the Yamaha motorcycles. In selling and distributing its products, the company needs the operation cost. One of the problems found inside the company's operating cost is the high cost of transportation incurred by the company in distributing Yamaha motorcycles. Therefore, its need a method of transportation to determine the minimum distribution costs at PT. Mitra Perkasa Dhian Abadi that aimed to save the cost of operation. The research methodology used in this paper is Northwest Corner Rule for the initial solution and the Potential Method to find the optimal solution. The company’s cost of transportation in 2013 is Rp 58.743.000,00 while there sults of transportation costs in 2013 calculated by using the potential method generates optimal cost for Rp 45.519.000,00. By using the potential method, in 2013 companies can save the cost for Rp 13.224.000,00.

(8)

DAFTAR ISI

Daftar Tabel viii

Daftar Gambar x

Daftar Lampiran xi

Bab 1 Pendahuluan

1.1 Latar belakang 1 2.4 Keseimbangan Transportasi 10 2.5 Metode Transportasi 13

Bab 3 Hasil dan Pembahasan

3.1 Pengumpulan Data 18

3.2 Pengolahan Data 20

3.3 Perumusan Fungsi Tujuan dan Fungsi Kendala 23 3.4 Penentuan Solusi Optimal 27 3.4.1 Penyelesaian dengan Metode Sudut Barat Laut 27 3.4.2 Penyelesaian dengan Metode Biaya Terendah 30 3.4.3 Penyelesaian Optimal dengan Metode Potensial 33

Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan 47

4.2 Saran 47

Daftar Pustaka 48

(9)

DAFTAR TABEL

Nomor Judul Halaman

Tabel

2.1 Tabel Persoalan Transportasi Seimbang 12 2.2 Tabel Persoalan Transportasi Tidak Seimbang 12 2.3 Tabel Persoalan Transportasi Tidak Seimbang 13 3.1 Data Persediaan Sepeda Motor Yamaha Tahun 2013 18 3.2 Data Permintaan Sepeda Motor Yamaha Tahun 2013 19 3.3 Data Biaya Transportasi Sepeda Motor Yamaha Tahun 2013 20 3.4 Data Permintaan yang Dikirim dari Tiap Sumber ke Tiap Tujuan 21 3.5 Data Biaya Transportasi Per Unit dari Tiap Sumber ke Tiap Tujuan 21 3.6 Tabel Transportasi PT. Mitra Perkasa Dhian Abadi 22 3.7 Tabel Transportasi PT. Mitra Perkasa Dhian Abadi setelah

ditambah dummy 26

3.8 Alokasi Awal dengan Metode Sudut Barat Laut 29 3.9 Alokasi Awal dengan Metode Biaya Terendah 32

3.10 Matriks Biaya Awal 34

3.11 Matriks Alokasi Awal 34

3.12 Matriks Biaya 35

(10)

(11)

DAFTAR GAMBAR

Nomor Judul Halaman Gambar

(12)

DAFTAR LAMPIRAN

Nomor Judul Halaman Lamp

1 Surat Izin Pengumpulan Data di Perusahaan PT. Mitra

Perkasa Dhian Abadi 49

2 Data Persediaan dan Permintaan Sepeda Motor Yamaha

Tahun 2013 50

3 Data Biaya Transportasi Pengiriman Sepeda Motor

Yamaha Tahun 2013 51

(13)

PENERAPAN METODE POTENSIAL DALAM MENENTUKAN BIAYA DISTRIBUSI MINIMUM

(STUDI KASUS : PT. MITRA PERKASA DHIAN ABADI)

ABSTRAK

Permasalahan transportasi termasuk permasalahan program linier khusus yang dapat diselesaikan dengan metode transportasi. PT. Mitra Perkasa Dhian Abadi merupakan perusahaan yang bergerak di bidang penjualan sepeda motor Yamaha. Dalam bidang penjualan, perusahaan ini memerlukan biaya operasi untuk mendistribusikan produknya. Salah satu masalah yang ditemukan dalam biaya operasi perusahaan ini yaitu besarnya biaya transportasi yang dikeluarkan oleh perusahaan dalam mendistribusikan sepeda motor Yamaha. Untuk itu, diperlukan suatu metode transportasi untuk menentukan biaya distribusi minimum pada PT. Mitra Perkasa Dhian Abadi yang bertujuan dapat menghemat biaya operasi perusahaan. Metode yang digunakan dalam penulisan ini adalah metode sudut barat laut untuk solusi awal dan metode potensial untuk mencari solusi optimal. Biaya transportasi dari perusahaan pada tahun 2013 sebesar Rp 58.743.000,00, sedangkan hasil perhitungan biaya transportasi dengan metode potensial pada tahun 2013 menghasilkan biaya transportasi optimal sebesar Rp 45.519.000,00. Dengan menggunakan metode potensial, pada tahun 2013 perusahaan dapat menghemat biaya sebesar Rp 13.224.000,00.

(14)

APPLICATION OF POTENTIAL METHOD IN DETERMINING MINIMUM DISTRIBUTION COST

(CASE STUDY : PT. MITRA PERKASA DHIAN ABADI)

ABSTRACT

Transportation problem is one of the specific linear program problems that can be solved by using the method of transportation. PT. Mitra Perkasa Dhian Abadi is a company engaged in selling the Yamaha motorcycles. In selling and distributing its products, the company needs the operation cost. One of the problems found inside the company's operating cost is the high cost of transportation incurred by the company in distributing Yamaha motorcycles. Therefore, its need a method of transportation to determine the minimum distribution costs at PT. Mitra Perkasa Dhian Abadi that aimed to save the cost of operation. The research methodology used in this paper is Northwest Corner Rule for the initial solution and the Potential Method to find the optimal solution. The company’s cost of transportation in 2013 is Rp 58.743.000,00 while there sults of transportation costs in 2013 calculated by using the potential method generates optimal cost for Rp 45.519.000,00. By using the potential method, in 2013 companies can save the cost for Rp 13.224.000,00.

(15)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Sistim perdagangan saat ini semakin luas, seakan tak dibatasi oleh batas wilayah tertentu. Hal ini mengakibatkan setiap perusahaan harus dapat mengikuti sistim perdagangan dan menghindari dampak buruk yang ditimbulkan dari sistim tersebut. Setiap perusahaan di dunia selalu mengharapkan keuntungan yang maksimal agar perusahaan dapat tetap beroperasi. Apabila perusahaan dapat mempertahankan dan meningkatkan penjualannya, maka tujuan tersebut dapat tercapai.

Salah satu faktor yang dapat mempengaruhi penjualan suatu perusahaan adalah bidang distribusi. Saat ini semakin banyak perusahaan yang bergerak di bidang distribusi. Distribusi dapat diartikan sebagai proses penyaluran barang atau jasa dari produsen ke konsumen. Untuk menyalurkan barang suatu perusahaan, maka diperlukan alat transportasi dan biaya distribusi untuk mengirim barang tersebut.

(16)

Perusahaan distribusi merupakan suatu perusahaan yang membeli barang dari produsen (pembuat barang langsung) dan kemudian menjual kembali barang tersebut untuk memperoleh laba. PT. Mitra Perkasa Dhian Abadi termasuk salah satu perusahaan distribusi sebagai sub dealer dari PT. Alfa Scorpii yang mendistribusikan produk sepeda motor Yamaha yang terletak di Propinsi Sumatera Utara. PT. Mitra Perkasa Dhian Abadi memiliki tiga gudang dan tujuh toko konsumen dengan lokasi yang berbeda

Permasalahan yang dihadapi oleh PT. Mitra Perkasa Dhian Abadi adalah jumlah biaya distribusi yang dikeluarkan oleh perusahaan cukup besar. Oleh karena itu, PT. Mitra Perkasa Dhian Abadi membutuhkan metode yang tepat agar produk tersebut dapat didistribusikan dari beberapa gudang (sumber) ke beberapa konsumen (tujuan), sehingga menghasilkan biaya transportasi yang minimum. Untuk pemecahan solusi ini, maka dapat digunakan salah satu metode transportasi yaitu metode potensial. Metode transportasi ini diharapkan dapat menentukan biaya transportasi yang optimal.

Berdasarkan uraian tersebut, penulis memberi judul penelitian ini dengan

“Penerapan Metode Potensial dalam Menentukan Biaya Distribusi Minimum (Studi Kasus : PT. Mitra Perkasa Dhian Abadi)”.

1.2 Perumusan Masalah

(17)

1.3 Batasan Masalah

Agar penelitian yang dilakukan dapat menghasilkan penelitian yang fokus dan akurat, maka diberikan batasan masalah sebagai berikut:

1. Penelitian ini hanya fokus dalam meminimumkan biaya transportasi pada PT. Mitra Perkasa Dhian Abadi.

2. Data yang diperoleh dari PT. Mitra Perkasa Dhian Abadi pada tahun 2013 meliputi:

a. Data persediaan sepeda motor Yamaha di tiap gudang (sumber). b. Data permintaan tiap konsumen (tujuan).

c. Biaya transportasi yang dikeluarkan perusahaan dari tiap gudang ke tiap konsumen.

3. Biaya transportasi yang diambil dari perusahaan meliputi: a. Biaya pergudangan.

b. Biaya pengurusan dan pengepakan barang. c. Biaya pengangkutan dan lalu lintas.

d. Biaya tak terduga yang diperkirakan oleh perusahaan.

1.4 Tujuan Penelitian

Penelitian ini bertujuan untuk meminimumkan biaya transportasi pada PT. Mitra Perkasa Dhian Abadi dengan menganalisa jumlah unit barang yang harus dikirim dari tiap gudang ke tiap konsumen dengan metode potensial, sehingga memperoleh keuntungan yang maksimal.

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai berikut:

(18)

2. Memberikan informasi dan menambah pengetahuan mengenai model transportasi bagi para pembaca.

3. Menjadi faktor pendukung bagi peningkatan kualitas dan pengetahuan penulis.

1.6 Lokasi Penelitian

PT. Mitra Perkasa Dhian Abadi berlokasi di Jalan H.O.S. Cokroaminoto No. 144 Kisaran (Asahan), Sumatera Utara.

1.7 Metodologi Penelitian

Langkah-langkah yang digunakan dalam penelitian ini adalah sebagai berikut: 1. Studi pustaka.

Pada tahap ini, penulis mengumpulkan bahan referensi, mempelajari serta menggali informasi baik dari buku, jurnal, makalah, karya ilmiah lainnya maupun situs internet mengenai distribusi dan metode transportasi.

2. Melakukan pengamatan dan pengambilan data pada PT. Mitra Perkasa Dhian Abadi secara langsung.

3. Analisa dan pengolahan data.

a. Data yang diperoleh diubah ke dalam bentuk model transportasi.

b. Model transportasi yang diperoleh diselesaikan dengan menggunakan metode transportasi, yaitu metode sudut barat laut dan metode biaya terendah untuk menentukan solusi awal.

(19)

BAB 2

LANDASAN TEORI

2.1 Pengertian Model dan Metode Transportasi

Hamdy A Taha (1996) mengemukakan bahwa dalam arti sederhana, model transportasi berusaha menentukan sebuah rencana transportasi sebuah barang dari sejumlah sumber ke sejumlah tujuan. Data dalam model ini mencakup:

1. Tingkat penawaran di setiap sumber dan jumlah permintaan di setiap tujuan. 2. Biaya transportasi per unit barang dari setiap sumber ke setiap tujuan.

Menurut Tamin (2000), model transportasi adalah suatu metode yang digunakan untuk mengatur distribusi suatu produk (barang-barang) dari sumber-sumber yang menyediakan produk (misalnya pabrik) ke tempat-tempat tujuan (misalnya gudang) secara optimal. Tujuan dari model ini adalah menentukan jumlah yang harus dikirim dari setiap sumber ke setiap tujuan sedemikian rupa dengan total biaya transportasi minimum.

Metode transportasi merupakan suatu metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama, ke tempat-tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa, karena terdapat perbedaan biaya-biaya alokasi dari satu sumber ke tempat tujuan berbeda-beda, dan dari beberapa sumber ke tempat-tempat tujuan juga berbeda-beda (Subagyo et al. 1990).

(20)

permintaan pasar pun telah diketahui maka persoalan bagaimana cara pengalokasian terbaiknya dapat dikerjakan.

Metode transportasi adalah metode yang paling efisien dibandingkan dengan metode simpleks. Penggunaan metode transportasi ini dipelopori oleh FL. Hitchcock (1941), TC. Koopmans (1949) dan GB. Dantzig (1951). Beberapa permasalahan yang dapat diselesaikan dengan metode transportasi adalah mengalokasikan barang/jasa dari suatu tempat (sumber/supply) ke tempat lainnya (demand/destination) secara optimal dengan mempertimbangkan biaya minimal, pengalokasian periklanan yang efektif, pembelanjaan modal dan alokasi dana untuk investasi, analisis pemilihan lokasi usaha yang tepat, keseimbangan lini perakitan, dan penjadwalan produksi (Zulfikarijah, 2004).

2.2 Persoalan Transportasi

Agustini dan Rahmadi (2004) mengemukakan bahwa kasus transportasi timbul ketika dicoba menentukan cara pengiriman (distribusi) suatu jenis barang (item) dari beberapa sumber (lokasi penawaran) ke beberapa tujuan (lokasi permintaan) yang dapat meminimumkan biaya. Biasanya jumlah barang yang dapat disalurkan dari setiap lokasi penawaran adalah tetap atau terbatas, namun jumlah permintaan pada setiap lokasi permintaan adalah bervariasi.

(21)

Menurut Siagian (2006), gambaran umum dari persoalan angkutan dapat dijelaskan sebagai berikut:

1. Sebuah perusahaan yang menghasilkan barang atau komoditi tertentu melalui sejumlah pabrik pada lokasi yang berbeda, akan mengirim barang ke berbagai tempat yang memerlukan dengan jumlah kebutuhan yang sudah tertentu. 2. Sejumlah barang atau komoditi hendak dikirim dari sejumlah pelabuhan asal

kepada sejumlah pelabuhan tujuan, masing-masing dengan tingkat kebutuhan yang sudah diketahui.

3. Sasaran dalam masalah transportasi ini ialah mengalokasikan barang yang ada pada pelabuhan asal sedemikian rupa hingga terpenuhi semua kebutuhan pada pelabuhan tujuan. Sedangkan tujuan utama dari persoalan angkutan ini ialah untuk mencapai jumlah biaya yang serendah-rendahnya (minimum) atau mencapai jumlah laba yang sebesar-besarnya (maksimum).

Pada umumnya, masalah transportasi berhubungan dengan distribusi suatu produk tunggal dari beberapa sumber, dengan penawaran terbatas, menuju beberapa tujuan dengan permintaan tertentu, pada biaya transportasi minimum. Karena bentuk masalah transportasi yang khas untuk menghitung minimasi biaya transportasi dalam bentuk tabel khusus yang dinamakan tabel transportasi (Mulyono, 2004).

2.3 Model Transportasi

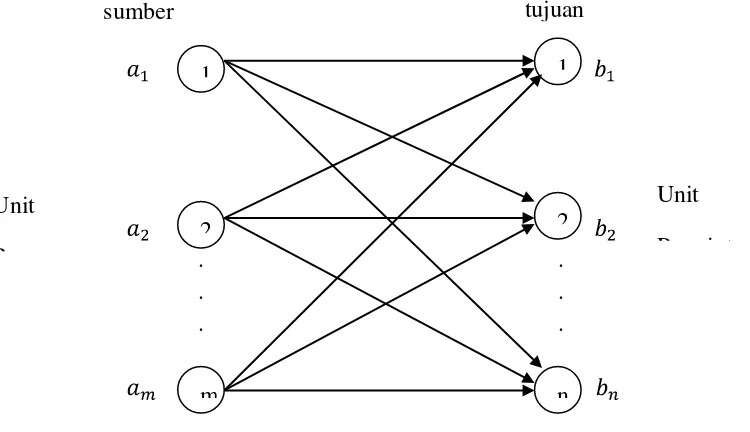
Model transportasi dari sebuah jaringan dengan m sebagai sumber dan n sebagai tujuan dapat dilihat pada Gambar 2.1. Sumber dan tujuan diwakili dengan sebuah node, dan rute pengiriman barang dari yang menghubungkan sumber ke tujuan diwakili dengan busur yaitu:

1. Masing-masing sumber mempunyai kapasitas 2. Masing-masing tujuan mempunyai kapasitas

3. : jumlah satuan unit yang dikirim dari sumber i ke tujuan j

(22)

5. Z : total keseluruhan biaya distribusi/transportasi

. .

Gambar 2.1 Model Transportasi dari Sumber ke Tujuan

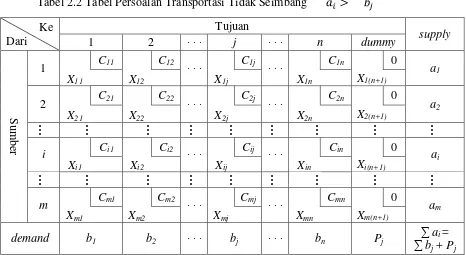
Model transportasi yang digambarkan pada Gambar 2.1 dapat dibuat ke dalam bentuk tabel yaitu tabel transportasi yang dapat dilihat pada Tabel 2.1. Dengan demikian, formulasi program liniernya dari persoalan transportasi adalah sebagai berikut:

Fungsi Tujuan: Meminimumkan

dengan batasan:

, untuk semua i dan j

Kelompok batasan pertama menetapkan bahwa jumlah pengiriman dari sebuah sumber tidak dapat melebihi penawarannya. Demikian pula, kelompok batasan

m 2 1

n 2 1

sumber tujuan

Unit

Penawaran

Unit

Permintaan

(23)

kedua mengharuskan bahwa jumlah pengiriman ke sebuah tujuan harus memenuhi permintaannya (Taha, 1996).

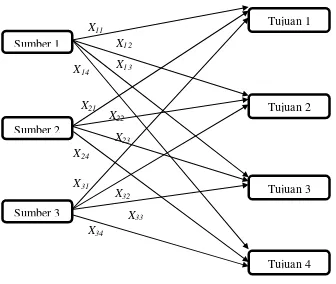
Sebagai ilustrasi, Gambar 2.2 akan memodelkan persoalan transportasi dengan 3 sumber dan 4 tujuan ( ).

Gambar 2.2 Representasi Model Persoalan Transportasi

(24)

2.4 Keseimbangan Transportasi

Problema transportasi seimbang adalah problema biaya angkutan barang di mana jumlah barang yang dipasok dari tempat asal sama dengan jumlah barang yang diminta di tempat tujuan. Problema transportasi tidak seimbang adalah suatu problema transportasi di mana jumlah permintaan lebih besar daripada pemasokan atau jumlah pemasokan lebih besar daripada permintaan (Sitorus, 1997).

Model Gambar 2.2 pada subbab 2.3 menyiratkan bahwa penawaran total harus setidaknya sama dengan permintaan total. Ketika penawaran total sama dengan permintaan total , formulasi yang dihasilkan disebut model transportasi berimbang (balanced transportation model). Formulasi ini berbeda dengan formulasi sebelumnya hanya terletak pada batasannya yaitu bahwa semua batasan adalah persamaan, dituliskan sebagai berikut:

Dalam kehidupan nyata, tidak selalu dapat dipastikan bahwa penawaran sama dengan permintaan atau melebihinya. Tetapi, sebuah model transportasi dapat selalu berimbang. Pengimbangan ini, di samping kegunaannya dalam pemodelan situasi praktis tertentu, adalah penting untuk pengembangan sebuah metode pemecahan yang sepenuhnya memanfaatkan struktur khusus dari model transportasi ini (Taha, 1996).

(25)

supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah

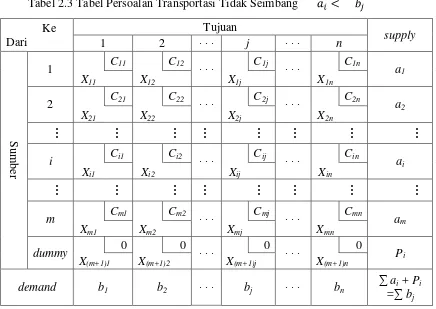
demand. Jika hal ini terjadi, maka model persoalan disebut sebagai model transportasi tidak seimbang (unbalanced transportation model). Setiap persoalan transportasi dapat dibuat seimbang dengan memasukkan kolom dummy atau baris

dummy. Ada 2 kemungkinan yang terjadi pada persoalan transportasi tidak seimbang yaitu:

1. Bila supply lebih besar daripada demand , persoalan ini diselesaikan dengan cara menetapkan dummy pada tujuan (kolom) untuk menyerap kelebihan demand sebesar

2. Bila supply lebih kecil daripada demand , persoalan ini diselesaikan dengan cara menetapkan dummy pada sumber (baris) untuk

men-supply kekurangan demand sebesar

dengan

Pi = dummy untuk baris Pj = dummy untuk kolom

(26)

Tabel 2.1 Tabel Persoalan Transportasi Seimbang

(27)

Tabel 2.3 Tabel Persoalan Transportasi Tidak Seimbang

Metode transportasi yang dapat digunakan untuk mencari solusi awal adalah Metode Sudut Barat Laut (North West Corner Method) dan Metode Biaya Terendah (Least-Cost Method).

1. Metode Sudut Barat Laut (North West Corner Method)

Metode sudut barat laut adalah metode yang paling sederhana untuk mencari solusi awal dari transportasi. Ciri dari metode ini adalah alokasi satuan belum memandang biaya transportasi (Rangkuti, 2013).

Langkah-langkah penyelesaiannya adalah:

(28)

b. Proses pertama akan menghabiskan penawaran pada sumber 1 dan atau permintaan pada tujuan 1. Akibatnya, tak ada lagi barang yang dapat dialokasikan ke kolom atau baris yang telah dihabiskan dan kemudian baris atau kolom itu dihilangkan. Kemudian pengalokasian sebanyak mungkin ke kotak di dekatnya pada baris atau kolom yang dapat dihilangkan. Jika kolom maupun baris telah dihabiskan, pindahlah secara diagonal ke kotak berikutnya. c. Lanjutkan dengan cara yang sama sampai semua penawaran telah dihabiskan

dengan keperluan permintaan telah dipenuhi.

Metode North West Corner Rule atau yang dikenal dengan metode sudut barat laut merupakan salah satu pemecahan awal yang digunakan dalam menyelesaikan persoalan transportasi.

2. Metode Biaya Terendah (Least-Cost Method)

Metode biaya terendah atau Least-Cost Method berusaha mencapai tujuan minimalisasi biaya dengan alokasi sistematik kepada kotak-kotak sesuai dengan besarnya biaya transportasi per unit (Rangkuti, 2013).

Prosedur metode ini adalah:

a. Pilih variabel (kotak) dengan biaya transport terkecil dengan alokasikan sebanyak mungkin. Untuk terkecil, minimal . Ini akan menghabiskan baris atau kolom .

b. Dari kotak-kotak sisanya yang layak (yaitu yang tidak terisi atau tidak dihilangkan) pilih nilai terkecil dan alokasikan sebanyak mungkin.

c. Lanjutkan proses ini sampai semua penawaran dan permintaan terpenuhi. Apabila telah diperoleh sebuah solusi fisibel awal atau feasible solution, maka tahap berikutnya adalah menguji apakah jawaban tersebut sudah optimal.

(29)

1. Metode Batu Loncatan (Stepping Stone Method)

Salah satu metode transportasi adalah metode batu loncatan (stepping stone method) yang digunakan untuk menghasilkan pemecahan layak bagi masalah dengan biaya-biaya operasi (biaya pabrik dan biaya transportasi), sehingga mendapatkan biaya pengiriman relatif minimal. Jumlah rute atau sel yang mendapat alokasi harus sebanyak .

Langkah penyelesaian adalah:

a. Pemecahan fisibel yang pertama dengan menggunakan metode sudut barat laut.

b. Kotak yang terisi disebut kotak basis, nilainya diberi tanda kurung buka dan tutup seperti ( ), melambangkan baris dan untuk kolom.

c. Kotak yang tidak terisi disebut kotak bukan basis (non-basis cell).

d. Semua kotak memuat biaya angkut per unit barang sebesar di mana 1 unit barang diangkut dari sumber m ke tujuan n.

tersebut harus merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.

h. Dihitung jumlah pada loop dengan koefisien ( ) dan ( ) secara bergantian.

i. Menentukan variabel yang masuk menjadi basis (entering variable) dengan cara memilih nilai yang terbesar atau .

j. Menentukan variabel yang keluar dari basis dengan cara: 1) Dibuat loop yang memuat yang terbesar.

(30)

3) Variabel yang keluar basis bila dan hanya bila minimal dari jalur

loop.

k. Menentukan harga variabel basis (yang berada di dalam loop yang baru) di mana nilai untuk variabel yang baru masuk basis diambil dari nilai variabel minimal dalam loop.

l. Untuk variabel-variabel basis yang lain yang juga berada dalam loop yaitu: 1)

2)

m. Untuk variabel-variabel basis yang lain di luar loop harganya tetap dan hitung kembali nilai untuk variabel non-basis.

n. Diperoleh tabel optimal jika semua .

o. Jika masih ada nilai , maka dapat ditentukan kembali entering variable dan leaving (variabel yang masuk dan yang keluar).

2. Metode Potensial

Dalam memecahkan masalah transportasi, metode potensial dapat juga dipergunakan untuk mencari solusi optimum. Metode potensial (metode U-V) melakukan evaluasi dari suatu lokasi transportasi secara matriks. Solusi dengan menggunakan metode potensial adalah suatu variasi dari metode stepping stone

yang didasarkan pada rumusan dual. Perbedaan utama dari metode potensial dengan metode stepping stone ialah cara mengevaluasi setiap sel dalam matriks. Dalam stepping stone, lingkaran evaluasi harus dicari untuk semua sel, yaitu sebanyak sel, yang tidak terletak dalam basis (Sudradjat, 2008).

(31)

Berdasarkan alokasi basis, maka sel dari basis dinyatakan dengan . Sel-sel ini mempunyai jumlah sebanyak . Selanjutnya dicari harga-harga untuk setiap baris dan harga-harga untuk setiap kolom, dengan perantara persamaan:

Telah diketahui bahwa jumlah sel yang mendapat alokasi awal atau jumlah sel yang menjadi basis adalah sebanyak , sehingga dengan demikian terdapat persamaan. Supaya persamaan ini dapat dipecahkan, sebenarnya diperlukan satu persamaan lagi, dan untuk itu diperoleh dengan memilih salah satu harga dari atau dengan konstanta tertentu (biasanya dipilih salah satu dari harga berikut atau ). Setelah harga-harga dan diketahui, maka dicari harga-harga sel lain yang tidak menjadi basis, yaitu dengan menggunakan persamaan: . Matriks yang diperoleh adalah matriks perubahan biaya yang disimbolkan dengan matriks .

Adapun langkah-langkah dalam metode potensial (U-V) adalah:

a. Menentukan nilai untuk setiap baris dan nilai-nilai untuk setiap kolom dengan menggunakan hubungan untuk semua variabel basis dan menentukan nilai

b. Menghitung matriks perubahan biaya untuk setiap variabel non basis dengan menggunakan rumus .

c. Apabila hasil perhitungan terdapat nilai negatif, maka solusi belum optimal. Selanjutnya dipilih dengan nilai negatif terbesar sebagai entering

variabel.

d. Mengalokasikan sejumlah nilai ke entering variabel sesuai dengan proses

(32)

BAB 3

HASIL DAN PEMBAHASAN

3.1 Pengumpulan Data

Pengumpulan data dilakukan pada PT. Mitra Perkasa Dhian Abadi yang terletak di H.O.S. Cokroaminoto No. 144 Kisaran – Sumatera Utara. Sesuai dengan izin yang diberikan oleh pimpinan PT. Mitra Perkasa Dhian Abadi, data yang dikumpulkan adalah data distribusi sepeda motor Yamaha pada tahun 2013 yang meliputi:

a. Data persediaan sepeda motor Yamaha

Data persediaan yang diperoleh dari PT. Mitra Perkasa Dhian Abadi adalah data lokasi dan kapasitas persediaan sepeda motor Yamaha di masing-masing gudang.

Jumlah persediaan sepeda motor Yamaha di tiap gudang selama tahun 2013 dapat dilihat pada Tabel 3.1.

Tabel 3.1 Data Persediaan Sepeda Motor Yamaha Tahun 2013

No Gudang Alamat Sepeda Motor Yamaha 1 Kisaran Jl. Cokroaminoto – Kisaran 375 unit 2 Tebing Tinggi Jl. Sudirman – Tebing Tinggi 260 unit 3 Lubuk Pakam Jl. Raya Medan 435 unit Sumber : PT. Mitra Perkasa Dhian Abadi

b. Data permintaan sepeda motor Yamaha

(33)

permintaan sepeda motor Yamaha dari tiap konsumen dan jumlah pengiriman yang dilakukan oleh perusahaan dari tiap gudang ke masing-masing konsumen.

Jumlah permintaan sepeda motor Yamaha dari tiap konsumen selama tahun 2013 dapat dilihat pada Tabel 3.2.

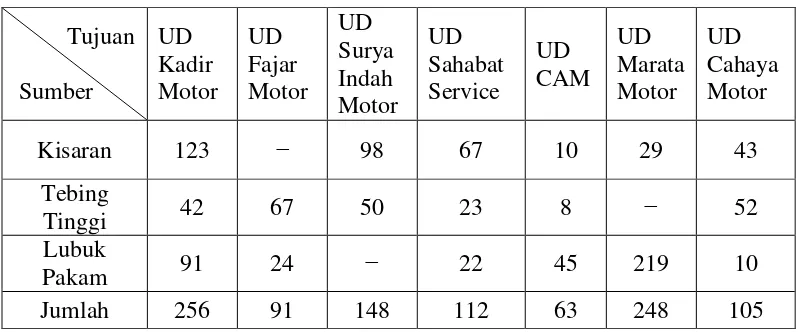
Tabel 3.2 Data Permintaan Sepeda Motor Yamaha Tahun 2013

Konsumen

Gudang (satuan dalam unit)

Jumlah

Kisaran Tebing Tinggi

Lubuk Pakam

UD Kadir Motor 123 42 91 256 UD Fajar Motor − 67 24 91 UD Surya Indah Motor 98 50 − 148 UD Sahabat Service 67 23 22 112

UD CAM 10 8 45 63

UD Marata Motor 29 − 219 248 UD Cahaya Motor 43 52 10 105 Sumber : PT. Mitra Perkasa Dhian Abadi

c. Data biaya transportasi sepeda motor Yamaha

Data biaya transportasi yang diperoleh dari PT. Mitra Perkasa Dhian Abadi adalah biaya pengiriman satu unit sepeda motor Yamaha dari tiap gudang ke masing-masing konsumen. Biaya transportasi ini meliputi semua ongkos yang berhubungan dengan biaya pendistribusian sepeda motor Yamaha dari gudang ke konsumen.

(34)

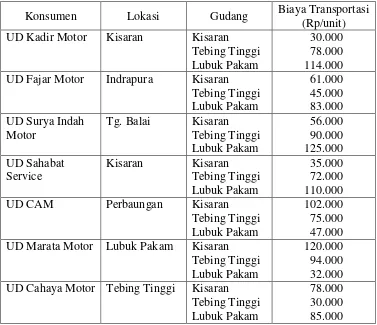
Tabel 3.3 Data Biaya Transportasi Sepeda Motor Yamaha Tahun 2013

Konsumen Lokasi Gudang Biaya Transportasi (Rp/unit) UD Kadir Motor Kisaran Kisaran

Tebing Tinggi Lubuk Pakam

30.000 78.000 114.000 UD Fajar Motor Indrapura Kisaran

Tebing Tinggi UD CAM Perbaungan Kisaran

102.000 75.000 47.000 UD Marata Motor Lubuk Pakam Kisaran

120.000 94.000 32.000 UD Cahaya Motor Tebing Tinggi Kisaran

78.000 30.000 85.000 Sumber : PT. Mitra Perkasa Dhian Abadi

3.2 Pengolahan Data

Pengolahan data untuk menyelesaikan masalah transportasi pada PT. Mitra Perkasa Dhian Abadi akan dilakukan melalui beberapa tahap. Tahap awal dalam pengolahan data ini yaitu mengolah data-data yang telah diperoleh dari PT. Mitra Perkasa Dhian dibuat menjadi matriks atau tabel transportasi dengan tujuan agar data-data tersebut lebih ringkas dan disajikan lebih terperinci.

(35)

Tabel 3.4 Data Permintaan yang Dikirim dari Tiap Sumber ke Tiap Tujuan

Tabel 3.5 Data Biaya Transportasi Per Unit dari Tiap Sumber ke Tiap Tujuan

Tujuan

Sumber

Biaya Transportasi Per Unit (Rp/unit)

(36)

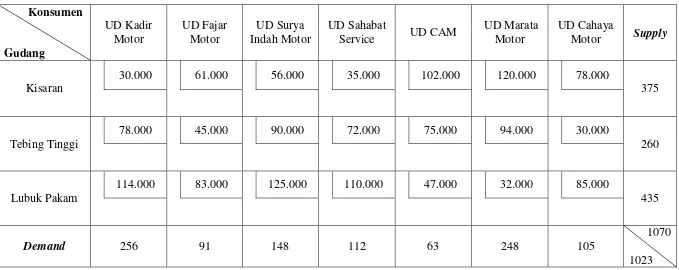
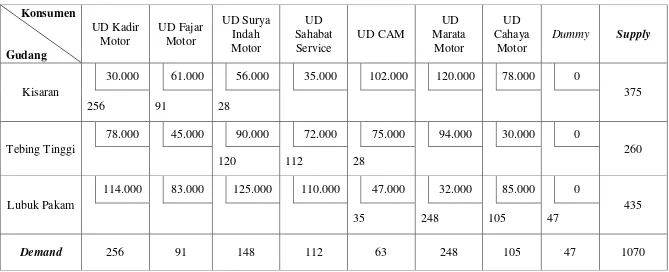
Tabel 3.6 Tabel Transportasi PT. Mitra Perkasa Dhian Abadi

Konsumen

Gudang

UD Kadir Motor

UD Fajar Motor

UD Surya Indah Motor

UD Sahabat

Service UD CAM

UD Marata Motor

UD Cahaya

Motor Supply

Kisaran

30.000 61.000 56.000 35.000 102.000 120.000 78.000

375

Tebing Tinggi

78.000 45.000 90.000 72.000 75.000 94.000 30.000

260

Lubuk Pakam

114.000 83.000 125.000 110.000 47.000 32.000 85.000

435

Demand 256 91 148 112 63 248 105

1070

(37)

3.3 Perumusan Fungsi Tujuan dan Fungsi Kendala

Dari Tabel 3.6 akan dirumuskan ke dalam model matematis dengan fungsi tujuan dan fungsi kendala sebagai berikut:

dengan batasan:

(38)

Dari Tabel 3.6 diketahui bahwa jumlah persediaan (supply) lebih besar dari jumlah permintaan (demand), hal ini dapat diselesaikan dengan cara menambahkan dummy pada tujuan untuk menyeimbangkan persediaan dan permintaan. Fungsi kendala yang awalnya terdapat tanda pertidaksamaan berubah menjadi bentuk persamaan. Karena ditambahkan dummy, maka formulasinya berubah menjadi:

dengan batasan:

(39)

(40)

(41)

3.4 Penentuan Solusi Optimal

Dalam menentukan solusi optimal pada masalah transportasi, digunakan metode sudut barat laut dan metode biaya terendah untuk menentukan solusi fisibel awal.

3.4.1. Penyelesaian dengan Metode Sudut Barat Laut

Dalam menyelesaikan persoalan transportasi dengan metode sudut barat laut dapat diselesaikan dengan langkah sebagai berikut:

a. Dimulai dari sel kosong paling kiri atas (sudut barat laut) yaitu sel , bandingkan nilai dan . Karena , maka alokasi . Permintaan pada tujuan pertama telah terpenuhi.

b. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai

dan . Karena , maka alokasi . Permintaan pada tujuan kedua telah terpenuhi.

c. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai dan Karena maka alokasi

. Persediaan pada sumber pertama telah habis.

d. Dilanjutkan ke arah bawah yaitu sel kosong , bandingkan nilai dan Karena maka alokasi

Permintaan pada tujuan ketiga telah terpenuhi.

e. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai

dan Karena maka alokasi Permintaan pada tujuan keempat telah terpenuhi.

f. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai dan Karena maka alokasi

. Persediaan pada sumber kedua telah habis.

g. Dilanjutkan ke arah bawah yaitu sel kosong , bandingkan nilai dan Karena maka alokasi

(42)

h. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai

dan Karena maka alokasi Permintaan pada tujuan keenam telah terpenuhi.

i. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai dan Karena maka alokasi Permintaan pada tujuan ketujuh telah terpenuhi.

j. Dilanjutkan ke arah kanan yaitu sel kosong , bandingkan nilai dan Karena maka alokasi

Permintaan pada tujuan kedelapan telah terpenuhi dan persediaan pada sumber ketiga telah habis.

(43)

(44)

Untuk penyelesaian dengan metode sudut barat laut, diperoleh biaya total transportasi adalah:

3.4.2 Penyelesaian dengan Metode Biaya Terendah

Dalam menyelesaikan persoalan transportasi dengan metode biaya terendah dapat diselesaikan dengan langkah sebagai berikut:

a. Untuk langkah pertama, bandingkan biaya pada baris pertama dan pilih biaya terendah pada baris pertama yaitu . Jumlah yang dialokasikan pada Alokasi ini menghabiskan permintaan pada tujuan ke-8, maka dan tidak dapat dialokasikan lagi. Biaya terendah selanjutnya pada baris pertama adalah Jumlah yang dialokasikan pada . Permintaan pada tujuan pertama telah terpenuhi, maka dan tidak dapat dialokasikan lagi. Biaya terendah selanjutnya pada baris pertama adalah . Jumlah yang dialokasikan pada . Alokasi ini belum memenuhi permintaan tujuan ke-4, tetapi persediaan pada sumber pertama telah terpenuhi. Karena itu, tidak dapat dialokasikan lagi. Sisa permintaan pada tujuan ke-4 dialokasikan ke , sehingga permintaan tujuan ke-4 telah terpenuhi dan tidak dapat dialokasikan lagi.

(45)

pada tujuan ke-5 telah terpenuhi, maka tidak dapat dialokasikan lagi. Biaya terendah selanjutnya adalah . Jumlah yang dialokasikan

pada Persediaan pada

sumber kedua telah habis, maka tidak dapat dialokasikan lagi. Sisa permintaan pada tujuan ke-3 yang belum terpenuhi dialokasikan ke

.

c. Langkah terakhir adalah mengisi kotak yang layak dengan sisa permintaan yang ada dan dengan tujuan menghabiskan sumber ketiga yaitu

dan .

(46)

(47)

Untuk penyelesaian dengan metode biaya terendah, diperoleh biaya total transportasi adalah:

3.4.3 Penyelesaian Optimal dengan Metode Potensial

Metode potensial (metode U-V) melakukan evaluasi dari suatu lokasi transportasi secara matriks. Solusi dengan menggunakan metode potensial adalah suatu variasi dari metode stepping stone yang didasarkan pada rumusan dual. Dalam metode potensial, lingkaran evaluasi hanya dicari untuk sel yang mempunyai harga paling negatif pada matriks evaluasi. Dalam proses mencari harga-harga sel evaluasi matriks, metode potensial terlebih dahulu harus menyusun satu matriks perubahan biaya. Matriks biaya awal dari transportasi dinyatakan dengan matriks perubahan biaya yang akan dijelaskan dinyatakan dengan , sedangkan matriks evaluasi dinyatakan dengan .

Dalam menentukan solusi optimal dengan metode potensial, terlebih dahulu ditentukan solusi awal yang harus digunakan. Solusi awal yang digunakan adalah biaya total transportasi yang lebih rendah, hal ini bertujuan mengurangi banyaknya jumlah iterasi pada perhitungan solusi optimal. Dari hasil perhitungan biaya total transportasi, yang cocok digunakan untuk solusi awal adalah dengan metode sudut barat laut. Oleh karena itu, tabel yang digunakan adalah Tabel 3.8.

(48)

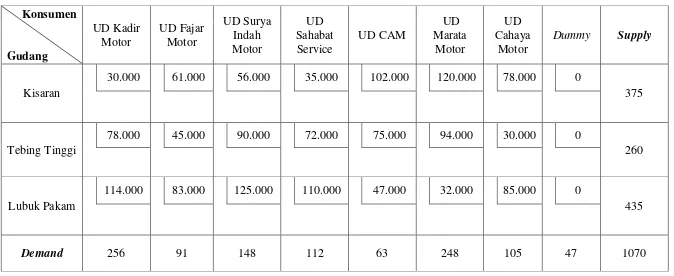
Tabel 3.10 Matriks Biaya Awal

Cij K1 K2 K3 K4 K5 K6 K7 K8 ai

G1 30.000 61.000 56.000 35.000 102.000 120.000 78.000 0 375

G2 78.000 45.000 90.000 72.000 75.000 94.000 30.000 0 260

G3 114.000 83.000 125.000 110.000 47.000 32.000 85.000 0 435

bj 256 91 148 112 63 248 105 47 1170

dengan: Biaya per unit pengiriman sepeda motor Yamaha (Rp / unit) Gudang 1 (Kisaran)

Gudang 2 (Tebing Tinggi) Gudang 3 (Lubuk Pakam) Konsumen 1 (UD Kadir Motor) Konsumen 2 (UD Fajar Motor) Konsumen 3 (UD Surya Indah Motor) Konsumen 4 (UD Sahabat Service) Konsumen 5 (UD CAM)

Konsumen 6 (UD Marata Motor) Konsumen 7 (UD Cahaya Motor)

Dummy

jumlah persediaan sepeda motor Yamaha di gudang i (unit) jumlah permintaan sepeda motor Yamaha oleh konsumen j (unit)

Selanjutnya, dari solusi awal dengan metode sudut barat laut pada Tabel 3.8, dibentuk matriks alokasi awal pada Tabel 3.11.

Tabel 3.11 Matriks Alokasi Awal

G1 256 91 28 375

G2 120 112 28 260

G3 35 248 105 47 435

(49)

Kemudian dari Tabel 3.11 dapat diperoleh tabel matriks biaya pada Tabel 3.12.

Tabel 3.12 Matriks Biaya

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 61.000 56.000 u2 90.000 72.000 75.000 u3 47.000 32.000 85.000 0

Dari Tabel 3.12 akan dicari nilai dan nilai dengan menggunakan rumus dan pilih , maka diperoleh matriks perubahan biaya 1

pada Tabel 3.13.

Tabel 3.13 Matriks Perubahan Biaya 1

Cij v1 =

(50)

Karena , solusi belum optimal. Selanjutnya dipilih nilai negatif terbesar yaitu terdapat pada , sehingga terjadi perubahan pada sel dan Tabel 3.11 juga terjadi perubahan alokasi. Perubahan nilai alokasi dapat dilihat pada Tabel 3.14.

Tabel 3.14 Matriks Perubahan Alokasi 1 (Iterasi 1)

G1 256 91 28 375

G2 120 112 28 260

G3 63 248 77 47 435

bj 256 91 148 112 63 248 105 47 1170

Selanjutnya, dari Tabel 3.14 dibentuk tabel matriks biaya iterasi 1 pada Tabel 3.15.

Tabel 3.15 Matriks Biaya Iterasi 1

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 61.000 56.000 u2 90.000 72.000 30.000 u3 47.000 32.000 85.000 0

(51)

Cij v1= 30.000 v2 = 61.000 v3= 56.000 v4= 38.000 v5= -42.000 v6= -57.000 v7= -4.000 v8= -89.000

u1= 0 30.000 61.000 56.000 38.000 -42.000 -57.000 -4.000 -89.000

u2= 34.000 64.000 95.000 90.000 72.000 -8.000 -23.000 30.000 -55.000

u3= 89.000 119.000 150.000 145.000 127.000 47.000 32.000 85.000 0

(52)

G1 256 14 105 375

G2 43 112 105 260

G3 77 63 248 47 435

bj 256 91 148 112 63 248 105 47 1170

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 61.000 56.000 u2 90.000 72.000 30.000 u3 83.000 47.000 32.000 0

(53)

Selanjutnya dihitung matriks evaluasi dengan rumus .

G1 256 119 375

G2 14 29 112 105 260

G3 77 63 248 47 435

(54)

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 56.000

u2 45.000 90.000 72.000 30.000 u3 83.000 47.000 32.000 0

(55)

Cij v1= 30.000 v2 = 11.000 v3= 56.000 v4= 38.000 v5= -25.000 v6= -40.000 v7= -4.000 v8= -72.000

u1= 0 30.000 11.000 56.000 38.000 -25.000 -40.000 -4.000 -72.000

u2= 34.000 64.000 45.000 90.000 72.000 9.000 -6.000 30.000 -38.000

u3= 72.000 102.000 83.000 128.000 110.000 47.000 32.000 68.000 0

(56)

Karena , solusi belum optimal. Selanjutnya dipilih nilai negatif terbesar, pada iterasi ini terdapat dua sel yang memiliki nilai negatif terbesar maka dapat dipilih salah satu dari dua sel tersebut. Dipilih sel

, sehingga terjadi perubahan pada sel dan Tabel 3.20 juga terjadi perubahan alokasi. Perubahan nilai alokasi dapat dilihat pada Tabel 3.23.

G1 256 7 112 375

G2 14 141 105 260

G3 77 63 248 47 435

bj 256 91 148 112 63 248 105 47 1170

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 56.000 35.000 u2 45.000 90.000 30.000 u3 83.000 47.000 32.000 0

(57)

Cij v1= 30.000 v2 = 11.000 v3= 56.000 v4= 35.000 v5= -25.000 v6= -40.000 v7= -4.000 v8= -72.000

u1= 0 30.000 11.000 56.000 35.000 -25.000 -40.000 -4.000 -72.000

u2= 34.000 64.000 45.000 90.000 69.000 9.000 -6.000 30.000 -38.000

u3= 72.000 102.000 83.000 128.000 107.000 47.000 32.000 68.000 0

(58)

G1 256 7 112 375

G2 91 64 105 260

G3 77 63 248 47 435

bj 256 91 148 112 63 248 105 47 1170

Cij v1 v2 v3 v4 v5 v6 v7 v8

u1 30.000 56.000 35.000 u2 45.000 90.000 30.000 u3 125.000 47.000 32.000 0

(59)

Cij v1= 30.000 v2 = 11.000 v3= 56.000 v4= 35.000 v5= -22.000 v6= -37.000 v7= -4.000 v8= -69.000

u1= 0 30.000 11.000 56.000 35.000 -22.000 -37.000 -4.000 -69.000

u2= 34.000 64.000 45.000 90.000 69.000 12.000 -3.000 30.000 -35.000

u3= 69.000 99.000 80.000 125.000 104.000 47.000 32.000 65.000 0

(60)

Karena , artinya tidak terdapat lagi nilai yang negatif pada matriks . Maka iterasi telah selesai dan solusi optimal dari permasalahan transportasi telah dicapai. Biaya transportasi optimal dengan metode potensial adalah:

Setelah diperoleh penyelesaian optimal dengan metode potensial, dapat dibandingkan biaya transportasi optimal yang diperoleh dengan biaya transportasi yang dikeluarkan perusahaan selama tahun 2013. Biaya transportasi optimal adalah Rp 45.519.000,00 sedangkan biaya transportasi yang dikeluarkan oleh perusahaan (sesuai Lampiran 5) sebesar Rp 58.743.000,00. Jadi, selisih biaya totalnya adalah Rp 13.224.000,00. Dapat disimpulkan bahwa PT. Mitra Perkasa Dhian Abadi pada tahun 2013 dapat menghemat biaya transportasi sebesar Rp 13.224.000,00.

(61)

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Berdasarkan hasil perhitungan dan pengolahan data yang dilakukan pada PT. Mitra Perkasa Dhian Abadi, diperoleh beberapa kesimpulan sebagai berikut: 1. Dari hasil perhitungan dengan menggunakan metode potensial, diperoleh

biaya transportasi optimal pada tahun 2013 sebesar Rp 45.519.000,00.

2. Perbandingan biaya transportasi optimal yang dihitung dengan menggunakan metode sudut barat laut untuk solusi awal dan menggunakan metode potensial untuk solusi optimal adalah Rp 45.519.000,00 dengan biaya transportasi yang dikeluarkan oleh perusahaan pada tahun 2013 sebesar Rp 58.743.000,00 (Lampiran 5), diperoleh selisih biaya total transportasi pada tahun 2013 sebesar Rp 13.224.000,00.

3. Perhitungan biaya transportasi dengan menggunakan metode potensial lebih menguntungkan perusahaan.

4.2 Saran

1. Diharapkan perusahaan dapat menerapkan metode potensial dalam menentukan biaya transportasi optimal, agar dapat menghemat biaya operasi perusahaan.

(62)

DAFTAR PUSTAKA

Agustini, D.H. dan Rahmadi, Y.E. 2004. Riset Operasional Konsep-Konsep Dasar. PT Rineka Cipta. Jakarta.

Mulyono, Sri. 2004. Riset Operasi (Edisi Revisi). Fakultas Ekonomi Universitas Indonesia. Jakarta.

Noer, Bustanul Arifin. 2010. Belajar Mudah Riset Operasional. ANDI. Yogyakarta.

Prihastuti, E.S. 2012. Efisiensi Biaya Transportasi dengan Pendekatan Metode North West Corner dan Stepping Stone (Studi Kasus Industri Air Minum Kemasan di Lampung). Jurnal Organisasi dan Manajemen. 2: 120-126.

Rangkuti, Aidawayati. 2013. 7 Model Riset Operasi & Aplikasinya. Brilian Internasional. Surabaya.

Siagian, P. 2006. Penelitian Operasional: Teori dan Praktek. Universitas Indonesia (UI-Press). Jakarta.

Sitorus, Parlin. 1997. Program Linier. Penerbit Universitas Trisakti. Jakarta.

Subagyo, P., Asri, M. dan Handoko, T.H. 1990. Dasar-Dasar Operations Research. BPFE-Yogyakarta. Yogyakarta.

Sudradjat. 2008. Pendahuluan Penelitian Operasional (Model Transportasi). Universitas Padjadjaran. Jawa Barat.

Taha, H.A. 1996. Riset Operasi, Jilid I. Ed ke-5. Editor: Dr. Lyndon Saputra. Binarupa Aksara. Jakarta.

Tamin, O.Z. 2000. Perencanaan dan Permodelan Transportasi. Erlangga. Jakarta.