Eksponen Vertex Dari Digraph Dwi-Warna Dengan Dua Loop

(1)

SKRIPSI

NURUL HIDAYATI 060803032

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2011

(2)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

(3)

PERSETUJUAN

Judul : EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DENGAN DUA LOOP

Kategori : SKRIPSI

Nama : NURUL HIDAYATI

Nomor Induk Mahasiswa : 060803032

Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, Nopember 2011

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Dr. Saib Suwilo, M.Sc. NIP.19630405 198811 2 001 NIP. 19640109 198803 1 004

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si NIP. l9620901 198803 1 002

(4)

PERNYATAAN

EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DENGAN DUA LOOP

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

(5)

PENGHARGAAN

Alhamdulillahirabbil’alamiin, penulis panjatkan ke hadirat ALLAH Subhana-hu Wa Ta’aladengan tidak putus-putusnya, yang telah mencurahkan rahmat dan hidayah-Nya kepada penulis sehingga penulis dapat menyelesaikan skripsi yang berjudul”EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DE-NGAN DUA LOOP” ini dengan baik. Tak lupa juga Sholawat beriring salam kepada junjungan Nabi MuhammadShallallahu ’Alaihi Wassalambeserta keluarga dan para sahabat.

Pada kesempatan ini penulis mengucapkan terima kasih yang sebesar-besar-nya kepada semua pihak yang basebesar-besar-nyak membantu, memotivasi dan mendo’akan penulis dari awal penulis memulai sampai menyelesaikan skripsi ini, yaitu kepada:

1. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

2. Bapak Prof. Dr. Tulus, M.Si dan Ibu Dra. Mardiningsih, M.Si, selaku Ketua dan Sekretaris Departemen Matematika F-MIPA USU Medan.

3. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Ibu Dra. Mar-diningsih, M.Si, selaku dosen pembimbing II, yang telah banyak membantu dan memberi dukungan baik berupa nasehat maupun ilmu pengetahuan, ser-ta dukungan moril dan motivasi bagi penulis dalam menyelesaikan penelitian ini.

4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakul-tas Matematika dan Ilmu Pengetahuan Alam, UniversiFakul-tas Sumatera Utara. 5. Guru-guru yang telah sabar mendidik penulis di SD Negeri 101896 Kiri Hulu

khususnya ibu kami Buk Ros yang telah meninggalkan dunia ini, di SLTP Swasta Tanjungmorawa Bersubsidi khususnya Ibu Lindawati Pakpahan, ser-ta di SMA Negeri 5 Medan khususnya Ibu Farawiati Adrianti.

6. Ibunda Sunariyah, S.Pd dan Ayahanda Djumianto Wardhana yang telah begitu sabar dan penuh cinta mendo’akan penulis, memberikan dukungan moril dan materiil serta motivasi kepada penulis untuk segera menyelesaikan tulisan ini. Dan juga kepada abangda Fitrayadi Eka Wardhana, S.E beserta kakanda Sunarseh, abangda Dwiyanto Setiawan, S.T beserta kakanda Yani Farahdina Nasution, S.P, yang juga telah menyemangati dan mendo’akan penulis serta kepada keponakan-keponakan penulis Halwa Aulia Wardhana, Wardah Annisa Wardhana dan Muhammad Luthfi Setiawan yang telah mem-berikan rona ceria di hari-hari penulis pada saat menyelesaikan penelitian ini. 7. Nurlinda Sari Butarbutar dan Tuti Larasati yang senantiasa bersama penulis dalam suka dan duka, bersama-sama dalam menyelesaikan skripsi serta saling mendo’akan, saling memotivasi dan saling membantu.

(6)

Penulis juga berterima kasih kepada Mohammad Amin yang begitu banyak memberikan semangat dan mendo’akan kebaikan penulis, abangda Heri Risdianto, pak Agustin, serta sahabat-sahabat Reza, Cory, Jo, Ulfa, Tanti, Eko, Satria, Tantri, Rani, Agung, Rini, Ayu, Sari, Tika dan Andi dan sepupu-sepupu yang tergabung dalam Wagiran’s Club khususnya Mbak Tia, Puput, Anis, Dita, Dini dan Nanda. Juga kepada Aghni, Bayu, bang Zuhri, kak Nenna, bang Deni, kak Masnah, kak Rima, kak Diana, bang Budi, kak Nana, Putri, Rina, bang Nanang yang telah membantu dan menyemangati penulis. Teman-teman seperjuangan anak-anak Murni 2006, serta teman-teman stambuk 2006, abangda dan kakan-da stambuk 2002, 2003, 2004 kakan-dan 2005, serta adinkakan-da stambuk 2007, 2008 kakan-dan 2009, anggota IM-KUBIK, ukhti-ukhti di musholah UKMI AL-FALAK dan semua teman-teman penulis baik dirumah, SD, SMP maupun SMA dan di lingkungan USU yang telah mendukung dan menyemangati penulis yang tidak dapat dise-butkan satu persatu, terimakasih semuanya.

Penulis menyadari masih ada kekurangan dalam penelitian ini, penulis meng-harapkan kritik dan saran yang membangun dari pembaca sekalian.

Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini dapat bermanfaat bagi semua dan di dunia pendidikan.

Medan, 01 Oktober 2011 Penulis,

(7)

ABSTRAK

Suatu digraph D yang setiap arc-nya berwarna merah atau biru disebut digraph dwi-warna. Suatu digraph dwi-warna terhubung kuat dikatakan primitif jika ter-dapat bilangan bulat tak negatif m dan b sehingga untuk setiap pasangan vertex udan vdiD terdapat walk dariu kevdengan panjangm+b, dimana banyaknya arc merah adalah m dan banyaknya arc biru adalah b. Misalkan D adalah di-graph dwi-warna dengan V(D) = {v1, v2,· · · , vn} untuk setiap vk ∈ V(D), maka

eksponen vertex dari D adalah bilangan bulat positif terkecil m+b sedemikian hingga terdapat walk dengan panjang m+b dari vk ke masing-masing vertex di

D. Andaikan D adalah suatu digraph dwi - warna yang terdiri darin vertex den-gan n ≥ 3 dan memiliki 2 loop, dan jika vk, k = 1,2, ..., n adalah vertex di D,

tulisan ini akan memperlihatkan pola dari eksponen vertex diDtepat 2n−2 untuk k= 1,2,3 dan tepat 2n−5 +k untuk 4≤ k≤n.

(8)

VERTEX EXPONENT OF A TWO-COLOURED DIGRAPH

WITH 2 LOOPS

ABSTRACT

A digraph D in which each of its arcs is coloured by either red or blue is called two-coloured digraph. A strongly connected of two-coloured digraph is primitive provided there are nonnegative integersmand bsuch that for each pair of vertices u and v in D there is a walk with length m+b, in which m arcs coloured by red and b arcs coloured by blue. Let D is a two-coloured digraph with V(D) = {v1, v2,· · · , vn} for each vk ∈ V(D), the vertex exponent of D is the smallest

nonnegative integerm+b such that there is a walk with lengthm+bfrom vk to

each vertex inD. Let D is a two-coloured digraph on n vertex with n ≥ 3 and 2 loops, if vk, k= 1,2, ..., n is vertex of D, this paper will give the general of vertex

(9)

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK v

ABSTRACT vi

DAFTAR ISI vii

DAFTAR GAMBAR ix

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 4

1.3. Tujuan Penelitian 4

1.4. Manfaat Penelitian 4

1.5. Metodologi Penelitian 4

2. DIGRAPH DAN 2-DIGRAPH 6

2.1. Definisi 6

2.2. Matriks Adjacency 11

2.3. Primitifitas dari Digraph dan 2-Digraph Terhubung Kuat 12 2.4. Eksponen Digraph dan 2-Digraph 16 2.5. Eksponen Vertex Digraph dan 2-Digraph 24 3. DIGRAPH DWI-WARNA DENGAN 2 LOOP 29 3.1. Eksponen 2-Digraph dengan 2 Loop 29 3.2. Eksponen Vertex 2-Digraph dengan 2 Loop 32

4. KESIMPULAN DAN SARAN 41

4.1. Kesimpulan 41

4.2. Saran 41

DAFTAR PUSTAKA 42

(10)

LAMPIRAN

A. FUNGSI MATLAB ”VERT 2EXP LOOPS” 43

(11)

DAFTAR GAMBAR

Gambar Halaman

1.1 Digraph dengan 2 Loop 3

2.1 Digraph dengan 6 vertex dan 9 arc 7 2.2 Digraph dengan walk, path, cycle dan loop 8 2.3 2-Digraph dengan 6 vertex dan 9 arc 9 2.4 2-Digraph dengan walk, path, cycle dan loop 10 2.5 (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat 13 2.6 Digraph terhubung kuat dan primitif 14 2.7 (a) 2-digraph terhubung kuat (b) 2-digraph tidak terhubung kuat 15 2.8 2-Digraph terhubung kuat dan primitif 16 2.9 Digraph Wielandt Wn dengan n vertex 27

3.1 2-Digraph dengan 2 Loop 36

(12)

ABSTRAK

(13)

VERTEX EXPONENT OF A TWO-COLOURED DIGRAPH

WITH 2 LOOPS

ABSTRACT

exponent ofD exactly 2n−2 fork = 1,2,3 and exactly 2n−5 +k for 4≤k ≤n.

(14)

SKRIPSI

(15)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MEDAN 2011

(16)

PERSETUJUAN

Judul : EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DENGAN DUA LOOP

Kategori : SKRIPSI

Nama : NURUL HIDAYATI

Nomor Induk Mahasiswa : 060803032

Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Dra. Mardiningsih, M.Si Dr. Saib Suwilo, M.Sc. NIP.19630405 198811 2 001 NIP. 19640109 198803 1 004

Diketahui oleh

Departemen Matematika FMIPA USU Ketua,

(17)

PERNYATAAN

EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DENGAN DUA LOOP

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

(18)

PENGHARGAAN

Alhamdulillahirabbil’alamiin, penulis panjatkan ke hadirat ALLAH Subhana-hu Wa Ta’aladengan tidak putus-putusnya, yang telah mencurahkan rahmat dan hidayah-Nya kepada penulis sehingga penulis dapat menyelesaikan skripsi yang berjudul”EKSPONEN VERTEX DARI DIGRAPH DWI-WARNA DE-NGAN DUA LOOP” ini dengan baik. Tak lupa juga Sholawat beriring salam kepada junjungan Nabi MuhammadShallallahu ’Alaihi Wassalambeserta keluarga dan para sahabat.

Pada kesempatan ini penulis mengucapkan terima kasih yang sebesar-besar-nya kepada semua pihak yang basebesar-besar-nyak membantu, memotivasi dan mendo’akan penulis dari awal penulis memulai sampai menyelesaikan skripsi ini, yaitu kepada:

1. Bapak Dr. Sutarman, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

2. Bapak Prof. Dr. Tulus, M.Si dan Ibu Dra. Mardiningsih, M.Si, selaku Ketua dan Sekretaris Departemen Matematika F-MIPA USU Medan.

3. Bapak Dr. Saib Suwilo, M.Sc, selaku dosen pembimbing I dan Ibu Dra. Mar-diningsih, M.Si, selaku dosen pembimbing II, yang telah banyak membantu dan memberi dukungan baik berupa nasehat maupun ilmu pengetahuan, ser-ta dukungan moril dan motivasi bagi penulis dalam menyelesaikan penelitian ini.

4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakul-tas Matematika dan Ilmu Pengetahuan Alam, UniversiFakul-tas Sumatera Utara. 5. Guru-guru yang telah sabar mendidik penulis di SD Negeri 101896 Kiri Hulu

khususnya ibu kami Buk Ros yang telah meninggalkan dunia ini, di SLTP Swasta Tanjungmorawa Bersubsidi khususnya Ibu Lindawati Pakpahan, ser-ta di SMA Negeri 5 Medan khususnya Ibu Farawiati Adrianti.

(19)

Penulis juga berterima kasih kepada Mohammad Amin yang begitu banyak memberikan semangat dan mendo’akan kebaikan penulis, abangda Heri Risdianto, pak Agustin, serta sahabat-sahabat Reza, Cory, Jo, Ulfa, Tanti, Eko, Satria, Tantri, Rani, Agung, Rini, Ayu, Sari, Tika dan Andi dan sepupu-sepupu yang tergabung dalam Wagiran’s Club khususnya Mbak Tia, Puput, Anis, Dita, Dini dan Nanda. Juga kepada Aghni, Bayu, bang Zuhri, kak Nenna, bang Deni, kak Masnah, kak Rima, kak Diana, bang Budi, kak Nana, Putri, Rina, bang Nanang yang telah membantu dan menyemangati penulis. Teman-teman seperjuangan anak-anak Murni 2006, serta teman-teman stambuk 2006, abangda dan kakan-da stambuk 2002, 2003, 2004 kakan-dan 2005, serta adinkakan-da stambuk 2007, 2008 kakan-dan 2009, anggota IM-KUBIK, ukhti-ukhti di musholah UKMI AL-FALAK dan semua teman-teman penulis baik dirumah, SD, SMP maupun SMA dan di lingkungan USU yang telah mendukung dan menyemangati penulis yang tidak dapat dise-butkan satu persatu, terimakasih semuanya.

Penulis menyadari masih ada kekurangan dalam penelitian ini, penulis meng-harapkan kritik dan saran yang membangun dari pembaca sekalian.

Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini dapat bermanfaat bagi semua dan di dunia pendidikan.

Medan, 01 Oktober 2011 Penulis,

Nurul Hidayati

(20)

ABSTRAK

(21)

VERTEX EXPONENT OF A TWO-COLOURED DIGRAPH

WITH 2 LOOPS

ABSTRACT

exponent ofD exactly 2n−2 fork = 1,2,3 and exactly 2n−5 +k for 4≤k ≤n.

(22)

DAFTAR ISI

Halaman

PERSETUJUAN i

PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK v

ABSTRACT vi

DAFTAR ISI vii

DAFTAR GAMBAR ix

BAB

1. PENDAHULUAN 1

1.1. Latar Belakang 1

1.2. Perumusan Masalah 4

1.3. Tujuan Penelitian 4

1.4. Manfaat Penelitian 4

1.5. Metodologi Penelitian 4

2. DIGRAPH DAN 2-DIGRAPH 6

2.1. Definisi 6

2.2. Matriks Adjacency 11

2.3. Primitifitas dari Digraph dan 2-Digraph Terhubung Kuat 12 2.4. Eksponen Digraph dan 2-Digraph 16 2.5. Eksponen Vertex Digraph dan 2-Digraph 24 3. DIGRAPH DWI-WARNA DENGAN 2 LOOP 29 3.1. Eksponen 2-Digraph dengan 2 Loop 29 3.2. Eksponen Vertex 2-Digraph dengan 2 Loop 32

4. KESIMPULAN DAN SARAN 41

4.1. Kesimpulan 41

4.2. Saran 41

(23)

LAMPIRAN

A. FUNGSI MATLAB ”VERT 2EXP LOOPS” 43

B. OUTPUT DARI FUNGSI MATLAB ”VERT 2EXP LOOPS” 47

(24)

DAFTAR GAMBAR

Gambar Halaman

1.1 Digraph dengan 2 Loop 3

2.1 Digraph dengan 6 vertex dan 9 arc 7 2.2 Digraph dengan walk, path, cycle dan loop 8 2.3 2-Digraph dengan 6 vertex dan 9 arc 9 2.4 2-Digraph dengan walk, path, cycle dan loop 10 2.5 (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat 13 2.6 Digraph terhubung kuat dan primitif 14 2.7 (a) 2-digraph terhubung kuat (b) 2-digraph tidak terhubung kuat 15 2.8 2-Digraph terhubung kuat dan primitif 16 2.9 Digraph Wielandt Wn dengan n vertex 27

(25)

PENDAHULUAN

1.1 Latar Belakang

Digraph merupakan hubungan antara titik-titik yang disebut dengan vertex dari digraph dengan garis berarah yang disebut dengan arc dari digraph. Vertex dari digraph direpresentasikan dalam bentuk titik atau lingkaran kecil dan arc dari digraph direpresentasikan dalam bentuk garis berarah.

Suatu walk dengan panjang m dari suatu digraph D yang menghubungkan vertexu dan vertexv adalah suatu barisan arc di D dalam bentuk

u=v0 →v1 →...→vm−1 →vm =v

dengan v0 = u dan vm = v. Jika u = v maka walk tersebut dikatakan walk

tertutup, dan jika u 6= v maka walk tersebut dikatakan walk terbuka. Suatu pathadalah suatu walk tanpa adanya perulangan vertex. Suatu path tertutup uv disebutcycle. Dan suatu cycle dengan panjang 1 disebut loop.

Suatu digraph dikatakan terhubung kuat jika untuk setiap pasangan vertex udan v terdapat walk dari u kev dan walk dari v keudan primitif jika terdapat suatu bilangan bulat positiflsedemikian hingga untuk setiap pasangan vertex dari udanvdiD terdapat walk yang panjangnya ldari ukev. Bilangan bulat terkecil dari l tersebut merupakan eksponen dari D yang dinotasikan dengan exp(D).

Konsep tradisional dari eksponen digraph primitif telah digeneralisasikan oleh Brualdi dan Liu (1990) dengan memperkenalkan tiga tipe generalisasi ekspo-nen. Misalkan D adalah sebuah digraph primitif dengan himpunan vertex V(D) = (v1, v2,· · · , vn). Untuk suatuvi ∈V(D) danX ⊆V(D),eksponen vertexγD(vk)

(26)

panjang l dari vi kesetiap vertex di D, dan himpunan eksponen expD(X) adalah

bilangan bulat positif terkecil p sehingga untuk setiap vertex vj di D terdapat

sebuah walk dari paling sedikit satu vertex diX kevj dengan panjang p.

Misalkan D adalah digraph primitif dengan orde n. Jika vertex - vertex di D adalah (v1, v2,· · · , vn) sedemikian hingga

γD(v1)≤γD(v2)≤ · · · ≤γD(vn)

makaγD(vk) adalah tipe pertama generalisasi eksponen ke - k dariD, dinotasikan

expD(vk).

Digraph dwi-warna atau 2-digraph adalah suatu digraph yang setiap arc-nya diwarnai merah atau biru (Fornasini dan Valcher (1997)). Suatu (m,b)-walk pada 2 digraph D dari vertex u kev adalah barisan arc yang terdiri dari m arc merah danbarc biru yang menghubungkan vertexudanv. Suatu 2-digraph Ddikatakan primitif jika terdapat bilangan bulat m dan b sehingga untuk setiap pasangan vertex u dan v di D terdapat (m, b)-walk dari u ke v dan sebaliknya, bilangan bulat positif terkecil darim+btersebut merupakan 2-eksponen dari 2-digraph D primitif yang dinotasikan dengan exp2(D).

Penelitian tentang 2-eksponen 2-digraph dimulai oleh Shader dan Suwilo (2003) yang memperlihatkan bahwa bila D adalah digraph dwi-warna primitif atas n vertex, maka 2-eksponen terbesar dari D terletak pada interval [1₂(n3 − 5n2₎_,1

2(3n

3 _{+ 2}_n2₋₂_n_)].

Eksponen dari 2-digraph dengan 2-loop dan n vertex dapat diketahui dari komposisi warna arc yang adjacent dengan loop merah maupun loop biru pada 2-digraph tersebut. Dalam penelitiannya Richard Albert Nasution (2007) mem-perlihatkan bentuk umum 2-eksponen dari 2-digraph dengan 2 loop dengan jumlah vertexn yaitu tepat 2n, 2n−1, dan 2n−2 dengan syarat:

(27)

merah adalah sepasang arc yang berwarna merah dan untuk loop biru adalah sepasang arc yang berwarna biru, atau sebaliknya.

2. 2-digraph dengan eksponen tepat 2n−1 didapat jika arc yang adjacent ke loop merah adalah sepasang arc berwarna merah dan arc yang adjacent ke loop biru adalah sepasang arc yang berbeda warna, atau sebaliknya.

3. 2-digraph dengan eksponen tepat 2n−2 didapat kedua loop terletak pada vertex yang sama.

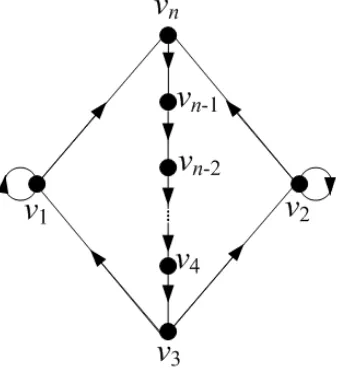
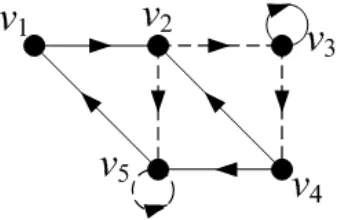
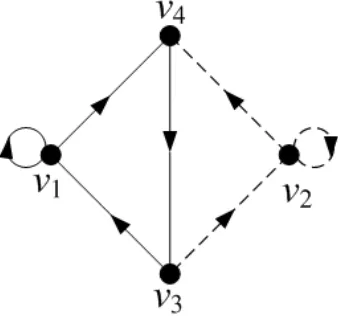
Suatu 2-digraphDterhubung kuat dengann ≥2 vertex yang memuat sebuah loop merah dan sebuah loop biru memiliki eksponenexp2(D)≤3n−3. Andaikan D adalah 2-digraph yang terdiri dari cycle v1 → vn → ... → v3 → v1 dan vn →

vn−1 →...→v3 →v2 →vn, loop (v1, v1) dan loop (v2, v2) yang diperlihatkan pada gambar

Gambar 1.1 : Digraph dengan 2 Loop

memilikiexp2(D)≤3n−5. Dan jika pewarnaan diD menjadi (v1, v1) adalah loop merah, (v2, v2) adalah loop biru, v1 → vn → vn−1 → ... → v3 → v1 adalah cycle merah danv3 →v2 →vn adalah path biru, maka 2-eksponennya tepat 3n−5.

(28)

primitif. Misalkan D adalah suatu digraph dwi-warna primitif dengan V(D) = {v1, v2, . . . , vn} untuk setiap vi ∈ V(D), maka eksponen vertex expD(vi) adalah

bilangan bulat positif terkecilm1+m2 sedemikian hingga terdapat (m1, m2)-walk dari vi ke setiap vertex di D. Penelitian ini bertujuan untuk mencari generalisasi

dari eksponen vertex dari 2-digraph dengan 2 loop pada Gambar 1.1.

1.2 Perumusan Masalah

AndaikanDadalah suatu digraph dwi - warna yang terdiri darinvertex dan memi-liki 2 loop seperti pada Gambar 1.1 dengan (v1, v1) adalah loop merah, (v2, v2) adalah loop biru, v1 → vn → vn−1 → · · · → v3 → v1 adalah cycle merah dan v3 → v2 → vn adalah path biru dari D. Masalah dari penelitian ini adalah

bagaimana menentukan pola eksponen vertexv diD.

1.3 Tujuan Penelitian

Tujuan dari penelitian ini yaitu untuk memperoleh generalisasi eksponen vertex dari 2-digraph dengan 2 loop seperti pada Gambar 1.1.

1.4 Manfaat Penelitian

Penelitian ini bermanfaat untuk memperkaya literatur dalam bidang eksponen dari digraph primitif.

1.5 Metodologi Penelitian

Untuk mencari pola eksponen vertex digraph dwi-warna dengan 2 loops dilakukan dengan cara sebagai berikut:

(29)

2. Dengan bantuan program matlab ”vert 2exp loops” yang dibuat oleh Dr. Saib Suwilo, M.Sc, yaitu suatu program yang digunakan untuk menentukan eksponen verteks dari digraph dwi-warna dengan loop. Melalui program ini peneliti memasukkan banyaknya vertex yang diinginkan lalu akan dihasilkan eksponen vertex dari masing-masing vertex serta komposisinya.

3. Mencari pola dari eksponen verteks digraph dwi-warna primitif dari hasil-hasil yang telah diperoleh tersebut secara kombinatorial.

4. Memberikan suatu pembuktian dari pola eksponen verteks yang telah diper-oleh tersebut.

(30)

DIGRAPH DAN 2-DIGRAPH

Pada bab ini akan diberikan beberapa konsep dasar seperti teorema dan definisi sebagai landasan dalam penelitian ini. Konsep dasar yang dimaksud adalah yang berkaitan dengan permasalahan dalam penelitian ini seperti definisi, keterhubung-an, primitifitas, eksponen dan eksponen vertex dari digraph dan 2-digraph. 2.1 Definisi

Pada sub-bab ini akan diberikan beberapa definisi tentang digraph dan 2-digraph serta notasi-notasi yang akan digunakan dalam pembahasan selanjutnya.

2.1.1 Digraph

Secara sederhana graph adalah kumpulan titik atau lingkaran kecil yang dihu-bungkan oleh garis tak berarah. Jika garis penghubung diberi arah, maka graph yang demikian dinamakan digraph (directed graph).

Andaikan V adalah suatu himpunan objek berhingga yang tak kosong, se-buah digraph D adalah suatu objek yang dibentuk oleh himpunan V yang un-surnya disebut vertex dari D, dan himpunan A ⊆V ×V yang unsurnya disebut arc dari D. Jika diberikan u, v∈ A, maka terdapat arc dari u ke v di D, dimana udisebut sebagai vertex awal dan v disebut sebagai vertex akhir. Arc (u,v) dapat juga dinotasikan dengan u→v.

(31)

[image:31.612.241.403.162.318.2]

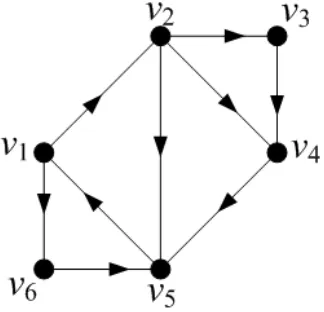
Contoh 2.1.1 : Himpunan vertexV =v1, v2, v3, v4, v5, v6 dan himpunan arcA = (v1, v2),(v1, v6),(v2, v3),(v2, v4),(v2, v5),(v3, v4),(v4, v5),(v5, v1),(v6, v5) adalah su-atu digraph dengan 6 vertex dan 9 arc dan direpresentasikan secara grafis sebagai berikut:

Gambar 2.1 : Digraph dengan 6 vertex dan 9 arc

Diberikan suatu digraph D dengan u dan vadalah vertex di D. Suatu walk dengan panjang m dari u kev adalah suatu barisan arc diD dalam bentuk

v0 →v1 →v2 →...→vm−1 →vm

denganm > 0,v0 =udan vm=v. Jika u=v maka walk tersebut dikatakan walk

tertutup dan jika u 6=v maka walk tersebut dikatakan walk terbuka. Suatu path didefinisikan sebagai suatu walk tanpa adanya perulangan vertex, namun vertex awal dan vertex akhir boleh berulang yang kemudian disebut path tertutup. Suatu path tertutup uv disebut dengan cycledan sebuah cycle dengan panjang 1 dise-but loop. Berikut ini akan diberikan representasi dari digraph untuk menjelaskan beberapa definisi di atas.

(32)

[image:32.612.232.406.103.222.2]

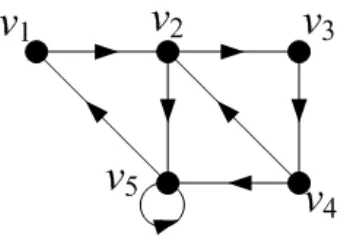
Contoh 2.1.2 : Diberikan digraph sebagai berikut:

Gambar 2.2 : Digraph dengan walk, path, cycle dan loop

Digraph pada gambar di atas memiliki walk, path, cycle dan loop sebagai berikut:

a. v1 → v2 → v3 → v4 → v2 → v5 → v1 adalah sebuah walk tertutup tetapi bukan path.

b. v1 → v2 → v5 → v5 → v1 → v2 → v3 adalah sebuah walk terbuka tetapi bukan path.

c. v1 →v2 →v5 adalah sebuah path terbuka.

d. v1 →v2 →v3 →v4→v5 →v1 adalah sebuah cycle atau path tertutup.

e. v5 →v5 adalah sebuah loop.

2.1.2 2-Digraph

2-Digraph atau digraph dwi-warna merupakan suatu digraph yang setiap arc-nya diberi warna merah atau biru.

Andaikan V adalah suatu himpunan objek berhingga yang tak kosong, se-buah 2-digraph D adalah suatu objek yang dibentuk oleh himpunan V yang un-surnya disebut vertexdari D, dan himpunan R ⊆V ×V yang unsurnya disebut arc merahdari D dan himpunanB ⊆V ×V yang unsurnya disebutarc birudari D. Jika diberikan u1, v1 ∈ R dan u2, v2 ∈ B, maka terdapat arc merah dari u1

(33)

ke v1 di D dan terdapat arc biru dari u2 ke v2 di D, dimana u1 dan u2 disebut sebagai vertex awal danv1 danv2 disebut sebagai vertex akhir. Arc merah (u1,v1) dapat juga dinotasikan denganu1

r

−

→v1 dan arc biru (u2,v2) dapat juga dinotasikan dengan u2

b

− →v2.

Vertexv dari 2-digraph direpresentasikan dalam bentuk titik atau lingkaran kecil yang diberi tandav, arc merah (u1,v1) dari 2-digraph direpresentasikan dalam bentuk garis atau kurva berarah tak putus dari titik u1 ke titik v1 dan arc biru (u2,v2) dari 2-digraph direpresentasikan dalam bentuk garis atau kurva berarah putus-putus dari titiku2 ke titikv2.

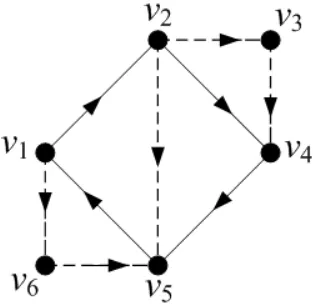
[image:33.612.245.402.431.585.2]

Contoh 2.1.3 : Himpunan vertex V = v1, v2, v3, v4, v5, v6, himpunan arc R = {(v1, v2), (v2, v4), (v4, v5), (v5, v1)}dan himpunan arcB={(v1, v6), (v2, v3), (v2, v5), (v3, v4), (v6, v5) } adalah suatu digraph dengan 6 vertex, 4 arc merah dan 5 arc biru dan direpresentasikan secara grafis sebagai berikut:

Gambar 2.3 : 2-Digraph dengan 6 vertex dan 9 arc

(34)

h r(w)

b(w)

i

disebut sebagai komposisi dari w.

Sama seperti digraph,pathmerupakan suatu walk tanpa adanya perulangan vertex, namun vertex awal dan vertex akhir boleh berulang yang kemudian disebut path tertutup atau cycle. Loop merupakan suatu cycle dengan komposisi ₁

0

atau₀

1

.Berikut ini akan diberikan representasi dari 2-digraph untuk menjelaskan beberapa definisi di atas.

[image:34.612.232.401.277.387.2]

Contoh 2.1.4 : Diberikan 2-digraph sebagai berikut:

Gambar 2.4 : 2-Digraph dengan walk, path, cycle dan loop

Digraph pada gambar di atas memiliki walk, path, cycle dan loop sebagai berikut:

a. v1

r

− → v2

b

− → v3

b

− → v4

r

− → v2

b

− → v5

r

−

→ v1 adalah sebuah walk tertutup tetapi bukan path.

b. v1

r

− → v2

b

− → v5

b

− → v5

r

− → v1

r

− → v2

b

− → v3

r

−

→ v3 adalah sebuah walk terbuka tetapi bukan path.

c. v1

r

− →v2

b

−

→v5 adalah sebuah path terbuka.

d. v1

r

− →v2

b

− →v3

b

− →v4

r

− →v5

r

−

→v1 adalah sebuah cycle atau path tertutup.

e. v5

b

−

→v5 adalah sebuah loop dengan komposisi

₀

1

.

f. v3

r

−

→v3 adalah sebuah loop dengan komposisi

₁

0

(35)

2.2 Matriks Adjacency

Digraph dan 2-Digraph dapat juga direpresentasikan dalam bentuk matriks. Suatu digraphDdan 2-DigraphDdengannvertex dapat direpresentasikan dalam bentuk matriks berordo n ×n dengan entri-entrinya berupa 1 dan 0. Matriks tersebut merupakan matriks adjacency.

2.2.1 Matriks Adjacency Digraph

Suatu matriks adjacency A = [aij] dari Digraph D dengan n vertex dapat kita

representasikan dengan entri sebagai berikut:

ai,j = 

  

  

1, jika terdapat arc dari vi ke vj

0, jika sebaliknya. untuki, j = 1,2,· · · , n.

Contoh 2.2.1 : Berikut ini adalah matriks adjacency yang diperoleh dari digraph pada Gambar 2.2 :



       

0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 1 1 0 0 0 1



       

2.2.2 Matriks Adjacency 2-Digraph

Suatu matriks adjacency dari 2-Digraph D dengan n vertex dapat kita represen-tasikan dalam 2 matriks adjacency, yaitu matriks adjacency merah dan matriks adjacency biru.

Matriks adjacency merah, R = [rij] pada D adalah matriks n ×n dengan

entri sebagai berikut:

ri,j = 

  

  

1, jika terdapat arc merah 0, jika sebaliknya

(36)

Matriks adjacency biru,B = [bij] padaD adalah matriksn×n dengan entri

sebagai berikut:

bi,j =       

1, jika terdapat arc biru 0, jika sebaliknya

untuki, j = 1,2,· · · , n

Contoh 2.2.2 : Berikut ini adalah matriks adjacency yang diperoleh dari 2-digraph pada Gambar 2.4 :

R =         

0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0

        

adalah matriks adjacency merah ;

B =         

0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1

        

adalah matriks adjacency biru.

2.3 Primitifitas dari Digraph dan 2-Digraph Terhubung Kuat

Pada sub-bab ini akan dibahas tentang digraph dan 2-digraph terhubung kuat dan primitif.

2.3.1 Digraph Primitif

(37)

[image:37.612.175.461.144.300.2]

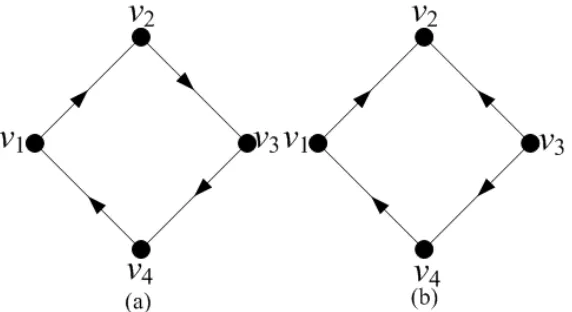
Contoh 2.3.1 : Berikut ini adalah representasi dari digraph terhubung kuat dan digraph tidak terhubung kuat.

Gambar 2.5 : (a) Digraph terhubung kuat (b) Digraph tidak terhubung kuat

Gambar 2.5 (a) merupakan suatu digraph terhubung kuat karena terdapat walk dari satu vertex ke vertex lainnya, dan Gambar 2.5 (b) bukan merupakan suatu digraph terhubung kuat atau dengan kata lain tidak terhubung kuat karena tidak terdapat walk dariv2 kev3.

Suatu digraph D terhubung kuat dikatakan primitif jika terdapat bilangan bulat positifl sehingga untuk setiap pasangan vertexudan vdiD terdapat suatu walk yang panjangnya l.

Lemma 2.1 Andaikan D adalah digraph terhubung kuat maka setiap vertex v di D terletak pada cycle.

Bukti: Ambil sebarang vertex v di D dan sebarang arc dari vertex u ke v di D. Karena D terhubung kuat, maka terdapat path dari vertexu kev yang berakibat akan diperoleh suatu path tertutup diD yang dibentuk oleh arc dari vertexukev dan path dari vertexvkeu diD. Oleh definisi bahwa path tertutup adalah suatu cycle danv sebarang vertex di D, maka setiap vertexv di D terletak pada suatu

(38)

Andaikan himpunan C ={c1, c2,...,ct} adalah himpunan semua cycle di D.

MisalkanM adalah suatu matriks baris dengan kolom keiuntuki= 1, 2,...,tdan entri-entri dariM adalah panjang cycleci (ℓ(ci)). Misalkan hMisebagai subgrup

dari grup bilangan bulat Z yang dibangun oleh kolom-kolom dariM yakni

hMi={z1ℓ(c1) +z2ℓ(c2) +...+ztℓ(ct) :zi ∈Z, i= 1,2,3, ..., t}

AndaikanD adalah digraph imprimitif dengan indeks imprimitifitask, maka k = gcd(ℓ(c1), ℓ(c2), ... , ℓ(ct)). Kemudian suatu digraph dikatakan primitif jika

k = 1 dan imprimitf jika k 6= 1.

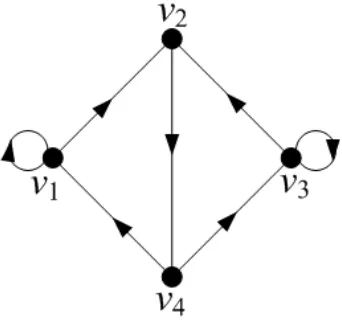
[image:38.612.231.402.351.512.2]

Contoh 2.3.2 : Representasi dari digraph terhubung kuat yang primitif

Gambar 2.6 : Digraph terhubung kuat dan primitif

Digraph pada Gambar 2.6 merupakan digraph terhubung kuat dengan 4 cycle yaitu : v1 → v1 dengan panjang 1, cyclev1 → v2 → v4 → v1 dengan panjang 3, cycle v2 → v4 → v3 → v2 dengan panjang 3 dan cyclev3 → v3 dengan panjang 1. Pembagi persekutuan terbesar dari panjang cycle-cycle pada digraph tersebut adalah 1. Dengan demikian, digraph tersebut primitif.

2.3.2 2-Digraph Primitif

(39)

[image:39.612.176.459.178.333.2]

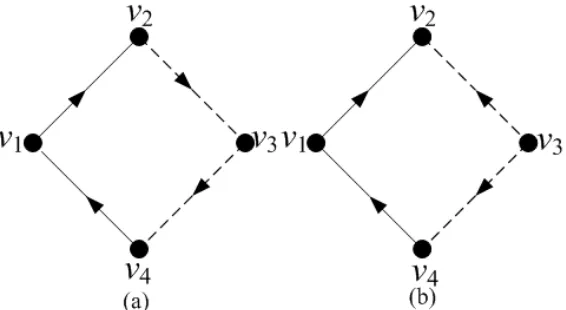
keu, dengan tidak memperhatikan komposisi warna arc dari walk tersebut. Contoh 2.3.3 : Berikut ini adalah representasi dari 2-digraph terhubung kuat dan 2-digraph tidak terhubung kuat.

Gambar 2.7 : (a) 2-digraph terhubung kuat (b) 2-digraph tidak terhubung kuat

Gambar 2.7 (a) merupakan suatu 2-digraph terhubung kuat karena terdapat walk dari satu vertex ke vertex lainnya, dan Gambar 2.7 (b) bukan merupakan suatu 2-digraph terhubung kuat atau dengan kata lain tidak terhubung kuat karena tidak terdapat walk dariv2 kev3.

Suatu 2-digraphD terhubung kuat dikatakanprimitifjika terdapat bilangan bulatmdanbsehingga untuk setiap pasangan vertexudanvdiD terdapat (m, b )-walk dariukevdan sebaliknya. AndaikanD adalah digraph dwi-warna terhubung kuat dan andaikanC ={γ1, γ2, . . . , γt}adalah himpunan semua cycle yang berada

di D. Suatu matriks cycleM dari D adalah suatu matriks berordo 2×t dengan kolom-kolomnya adalah komposisi dari cycle-cycleγi, i= 1,2,· · · , t yakni

M =

"

r(γ1) r(γ2) ... r(γt)

b(γ1) b(γ2) ... b(γt) #

disebut sebagai cycle matriks D. Suatu 2-digraph D dikatakan primitif jika dan hanya jika pembagi persekutuan terbesar dari determinan submatriks 2×2 dari M adalah 1 (Fornasini dan Valcher, 1997).

(40)

[image:40.612.232.402.113.274.2]

Contoh 2.3.3 : Representasi dari 2-digraph terhubung kuat yang primitif

Gambar 2.8 : 2-Digraph terhubung kuat dan primitif

Pada gambar terdapat 4 buah cycle, sehingga diperoleh cycle matriks sebagai berikut

M =

"

1 3 1 0 0 0 2 1

#

dan submatriksnya adalahM1 =

"

1 3 0 0

#

,M2 =

"

1 1 0 2

#

,M3 =

"

1 0 0 1

#

,dst. Dikare-nakan det(M3)=1, hal ini mengakibatkan pembagi persekutuan terbesar dari se-mua determinan submatriksnya akan bernilai 1. Dengan demikian 2-digraph terse-but 2-primitif.

2.4 Eksponen Digraph dan 2-Digraph

Pada sub-bab ini akan dibahas tentang definisi eksponen digraph dan 2-digraph serta contoh bagaimana menentukan eksponen dari digraph dan 2-digraph terse-but.

2.4.1 Eksponen Digraph

(41)

Zaini dan Suwilo (2005), menyatakan bahwa vertex vi ke vj di Ak memiliki

walk dengan panjangk. Berikut ini diperlihatkan hubungan antara suatu digraph dengan matriks.

Proposisi 2.2 Andaikan Aadalah suatu matriks adjacency dari digraphD. Entri ak

ij dari Ak menyatakan banyaknya walk dari vi ke vj yang panjangnya k di D.

Bukti: AndaikanA adalah suatu matriks adjacency dari digraph D, maka setiap entri (i, j) dari A menyatakan arc dari vi ke vj di digraph D. Hal ini berakibat

untukk = 1, maka setiap entria1

ij dari A1 menyatakan banyaknya walk dari vi ke

vj yang panjangnya satu.

Asumsikan setiap entri a(_ijk) dan Ak _{menyatakan banyaknya walk dari}_v i dan

vj yang panjangnya k di D, untuk k ≥1. Berikut ini diperlihatkan a

(k+1)

ij adalah

banyaknya walk dari vi ke vj yang panjangnya k+ 1 di D, untukk ≥1.

Perhatikan setiap walk darivi kevj di D dengan panjang k+ 1 yang terdiri

dari walk dari vi ke vj dengan panjang k untuk l = 1,2, . . . , n dan dilanjutkan

dengan arc darivikevj. Sehinggaa(_ilk)aljadalah menyatakan walk yang panjangnya

k+ 1 dari vi ke vj di D, untuk k = 1,2, . . . , n. Jika tidak terdapat walk yang

panjang k dari vi ke vj diD, maka a_il(k) = 0 sehingga a(_ilk)alj = 0. Hal ini berarti

tidak terdapat walk dengan panjangk+1 darivikevjyang melaluivldiDsehingga

diperoleh banyaknya walk yang panjangnya k+ 1 dari vi ke vj diD adalah

a(i1k)a1j+a( k)

i2 a2j+· · ·+a( k)

inanj = n X

i=1

a(_ilk)alj

karena

Ak+1 ₌_Ak_A

maka

a(_ijk) =

n X

i=1

a(_ilk)alj

(42)

Hal ini berakibata(_ijk+1) adalah benar menyatakan banyaknya walk darivi ke

vj yang panjangnyak+ 1 diD. Jadi, elemen (i, j) dariAk adalah banyaknya walk

yang panjangnya k dari vi ke vj.

Contoh 2.4.1 : Matriks adjacency dari digraph pada Gambar 2.6 adalah A =

     

1 1 0 0 0 0 0 1 0 1 1 0 1 0 1 0

     

, kemudian akan dicari eksponen dari digraph tersebut.

Berdasarkan Proposisi 2.2, banyaknya walk dari vertexvi kevj dengan

pan-jang k adalah entri dari matriksAk

ij dari Ak, dengan demikian nilai k merupakan

eksponen dari digraph bila matriksAk _{adalah matriks positif. Perhatikan matriks}

Ak _berikut:

a. Untukk = 1 ; diperolehA1 ₌

     

1 1 0 0 0 0 0 1 0 1 1 0 1 0 1 0

     

, maka bukan merupakan

ekspo-nen digraph, karena tidak terdapat walk dengan panjang 1 dari v1 kev3, v1 kev4, v2 kev1,v2 kev2, v2 kev3, v3 ke v1, v3 kev4, v4 kev2 dan v4 kev4.

b. Untukk = 2 ; diperolehA2 ₌

     

1 1 0 1 1 0 1 0 0 1 1 1 1 2 1 0

     

ekspo-nen digraph, karena tidak terdapat walk dengan panjang 2 dari v1 kev3, v2 kev2, v2 kev4,v3 kev1, dan v4 ke v4.

c. Untukk = 3 ; diperolehA3 ₌

     

2 1 1 1 1 2 1 0 1 1 2 1 1 2 1 2

     

ekspo-nen digraph, karena tidak terdapat walk dengan panjang 3 dariv2 kev4.

d. Untuk k = 4 ; diperoleh A4 ₌

     

3 3 2 1 1 2 1 2 2 3 3 1 3 2 3 2

     

(43)

panjang 4 dari tiap pasangan verteks diD, maka eksponen dari digraph pada Gambar 2.6 adalah 4.

2.4.2 2-Eksponen 2-Digraph

Pada 2-digraph, 2-eksponen dari 2-digraph D didefinisikan sebagai bilangan bulat positif terkecilm+bsehingga untuk setiap pasangan vertexudanv diD terdapat walk berarah dariukevdengan panjang m+byang terdiri darim arc merah dan barc biru. Eksponen dari 2-digraph tersebut dinotasikan dengan exp2(D).

Suwilo (2008) juga melakukan riset tentang digraph dwi - warna primitif yang dikhususkan pada lollipop dwi - warna.

Lemma 2.3 Andaikan D adalah sebuah 2-digraph atas n verteks dan misalkan R dan B masing-masing adalah matriks adjacency merah dan biru dari digraph

dwi-warna D. Maka elemen (i, j) dari (R, B)(m,b) _{adalah banyaknya} ₍_{m, b}_)-walk dari verteks vi ke verteks vj.

Bukti. Akan dibuktikan dengan induksi pada (m+b) dan (m+b+ 1), jikam= 0 maka b = 1 atau jika m = 1 maka b = 0. Jika m = 0 maka elemen (i, j) dari (R, B)(0,1)₌ _B _{adalah walk dengan komposisi}

"

0 1

#

di 2-digraph D. Dengan cara yang sama, jika b = 0 maka (R, B)(1,0) ₌ _R _{adalah walk dengan elemen (}_{i, j}₎ menyatakan walk dengan komposisi

"

1 0

#

di 2-digraph D.

Andaikan Lemma 2.3 benar untuk semua bilangan bulat tak negatif m′ dan b′ denganm′+b′ ≤m+bakan diperlihatkan untukm+b+ 1 adalah benar dengan catatan sebagai berikut.

(R, B)(m+1,b) ₌_R₍_{R, B}₎(m,b)₊_B₍_{R, B}₎(m+1,b−1)

Oleh hipotesis induksi, elemen (i, j) pada R(R, B)(m,b) _{adalah walk dari} _v

i ke vj

yang dimulai dengan arc merah dan diikuti oleh (m, b)-walk, dan elemen (i, j) padaB(R, B)(m+1,b−1)_{adalah walk dari}_v

i kevj yang dimulai dengan arc biru dan

(44)

diikuti oleh (m+ 1, b−1)-walk sedemikian hingga elemen (i, j) dari (R, B)(m+1,b) adalah jumlah (m+ 1, b)-walk dari vi ke vj. Jadi, elemen (i, j) dari (R, B)(m,b)

adalah jumlah (m, b)-walk dari verteksvi ke verteks vj.

Contoh 2.4.1 : Matriks adjacency merah dari 2-digraph pada Gambar 2.8 adalah

R =      

1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0

     

dan matriks adjacency biru dari 2-digraph pada Gambar 2.8

adalahB =

     

0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0

     

, kemudian akan dicari eksponen dari 2-digraph tersebut.

Berdasarkan Lemma 2.3, banyaknya walk dari vertexvikevj dengan panjang

m+badalah entri (i, j) dari (R, B)(m,b)_{, dengan demikian nilai}_m₊_b_merupakan eksponen dari digraph bila matriks (R, B)(m+b) _{adalah matriks positif. Perhatikan} matriks (R, B)(m,b) _berikut:

a. Untuk m+b= 1, maka diperoleh:

1. (R, B)(1,0)₌_R ₌

     

1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0

     

2. (R, B)(0,1)₌_B ₌

     

0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0

     

b. Untuk m+b= 2, maka diperoleh:

1. (R, B)(2,0)₌_R2 ₌

     

1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0

(45)

2. (R, B)(1,1)₌_RB₊_BR₌      

0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0

     

3. (R, B)(0,2)₌_B2 ₌

     

0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0

     

c. Untuk m+b= 3, maka diperoleh:

1. (R, B)(3,0)₌_R3 ₌

     

2 0 1 1 0 0 0 0 1 0 1 1 1 0 0 1

     

2. (R, B)(2,1)₌_R₍_{R, B}₎(1,1)₊_BR2 ₌

     

0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0

     

3. (R, B)(1,2)₌_RB2₊_B₍_{R, B}₎(1,1)₌

     

0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 1

     

4. (R, B)(0,3)₌_B3 ₌

     

0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0

     

d. Untuk m+b= 4, maka diperoleh:

1. (R, B)(4,0)₌_R4 ₌

     

3 0 1 2 0 0 0 0 2 0 1 1 1 0 1 1

     

2. (R, B)(3,1)₌_R₍_{R, B}₎(2,1)₊_BR3 ₌

     

0 1 0 0 1 0 0 1 0 1 0 0 0 0 0 0

     

(46)

3. (R, B)(2,2)₌_R₍_{R, B}₎(1,2)₊_B₍_{R, B}₎(2,1)₌      

0 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0

     

4. (R, B)(1,3)₌_RB3₊_B₍_{R, B}₎(1,2)₌

     

0 0 0 0 0 2 1 1 0 1 1 0 0 1 0 1

     

5. (R, B)(0,4)₌_B4 ₌

     

0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0

     

e. Untuk m+b= 5, maka diperoleh:

1. (R, B)(5,0)₌_R5 ₌

     

4 0 2 3 0 0 0 0 3 0 1 2 2 0 1 1

     

2. (R, B)(4,1)₌_R₍_{R, B}₎(3,1)₊_BR4 ₌

     

0 1 0 0 1 0 1 1 0 1 0 0 0 1 0 0

     

3. (R, B)(3,2)₌_R₍_{R, B}₎(2,2)₊_B₍_{R, B}₎(3,1)₌

     

0 1 1 1 1 0 0 1 1 1 0 2 1 0 0 0

     

4. (R, B)(2,3)₌_R₍_{R, B}₎(1,3)₊_B₍_{R, B}₎(2,2)₌

     

0 1 0 1 1 0 1 0 1 0 0 0 0 1 1 0

     

5. (R, B)(1,4)₌_RB4₊_B₍_{R, B}₎(1,3)₌

     

0 0 0 0 0 3 1 2 0 2 1 1 0 1 0 1

(47)

6. (R, B)(0,5)₌_B5 ₌      

0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0

     

f. Untuk m+b= 6, maka diperoleh:

1. (R, B)(6,0)₌_R6 ₌

     

6 0 3 4 0 0 0 0 4 0 2 3 3 0 1 2

     

2. (R, B)(5,1)₌_R₍_{R, B}₎(4,1)₊_BR5 ₌

     

0 2 0 0 2 0 1 1 0 1 0 0 0 1 0 0

     

3. (R, B)(4,2)₌_R₍_{R, B}₎(3,2)₊_B₍_{R, B}₎(4,1)₌

     

1 1 1 1 1 1 1 1 1 1 2 2 1 1 0 2

     

4. (R, B)(3,3)₌_R₍_{R, B}₎(2,3)₊_B₍_{R, B}₎(3,2)₌

     

0 2 1 1 2 0 0 1 1 1 0 2 1 0 0 0

     

5. (R, B)(2,4)₌_R₍_{R, B}₎(1,4)₊_B₍_{R, B}₎(2,3)₌

     

0 1 0 1 1 1 2 0 1 0 1 0 0 2 1 1

     

6. (R, B)(1,5)₌_RB5₊_B₍_{R, B}₎(1,4)₌

     

0 0 0 0 0 4 1 3 0 3 1 2 0 1 0 1

     

7. (R, B)(0,6)₌_B6 ₌

     

0 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0

     

(48)

1. (R, B)(7,0)₌_R7 ₌



    

9 0 4 6 0 0 0 0 6 0 3 4 4 0 2 3



    

2. (R, B)(6,1)₌_R₍_{R, B}₎(5,1)₊_BR6 ₌



    

0 3 0 0 3 0 1 2 0 2 0 0 0 1 0 0



    

3. (R, B)(5,2)₌_R₍_{R, B}₎(4,2)₊_B₍_{R, B}₎(5,1)₌



    

2 2 1 3 2 1 1 1 3 1 2 2 1 1 2 2



    

Karena terdapat walk dengan panjang 7 dari tiap pasangan verteks di 2-digraph D, maka 2-eksponen dari 2-digraph pada Gambar 2.8 adalah 7,dengan komposisi

5 2

, 5 arc merah dan 2 arc biru.

2.5 Eksponen Vertex Digraph dan 2-Digraph

Pada sub-bab ini akan dibahas tentang definisi eksponen vertex dari digraph dan 2-digraph serta contoh bagaimana menentukan eksponen dari 2-digraph dan 2-2-digraph tersebut.

2.5.1 Eksponen Vertex Digraph

Misalkan D adalah sebuah digraph primitif dengan himpunan vertex V(D) = (v1, v2,· · · , vn). Untuk suatu vi ∈ V(D) dan X ⊆ V(D), eksponen vertex γD(vi)

adalah bilangan bulat positif terkecil l sedemikian hingga terdapat walk dengan panjang l dari vi kesetiap vertex di D, dan himpunan eksponen expD(X) adalah

bilangan bulat positif terkecil p sehingga untuk setiap vertex vj di D terdapat

sebuah walk dari paling sedikit satu vertex diX kevj dengan panjang p.

(49)

D adalah (v1, v2,· · · , vn) sedemikian hingga

γD(v1)≤γD(v2)≤ · · · ≤γD(vn)

expD(vk).

Contoh 2.5.1 : Berikut ini akan dicari eksponen vertex dari masing-masing vertex di digraph pada Gambar 2.6 berdasarkan Proposisi 2.2 yaitu dengan melihat entri Ak

ij dari Ak, dimana entri pada baris ke-iharus bernilai positif.

Pada Contoh 2.4.1 telah diperoleh matriks-matriks dari Ak_{, kita perhatikan}

untuk k = 3 diperoleh matriks A3 ₌



    

2 1 1 1 1 2 1 0 1 1 2 1 1 2 1 2



    

, dimana pada baris ke-1, ke-3

dan ke-4 seluruh entrinya bernilai positif, maka expD(v1) = 3, expD(v3) = 3 dan

expD(v4) = 3.

Kemudian perhatikan untuk k = 4 diperoleh matriks A4 ₌



    

3 3 2 1 1 2 1 2 2 3 3 1 3 2 3 2



    

,

dimana pada baris ke-2 seluruh entrinya bernilai positif, maka expD(v2) = 4.

Dengan demikian keempat vertex digraph pada Gambar 2.6 telah memper-oleh eksponen vertex masing-masing, yakni expD(v1) = 3, expD(v2) = 4, expD(v3)

= 3 dan expD(v4) = 3.

2.5.2 Eksponen Vertex 2-Digraph

Misalkan D adalah suatu 2-digraph primitif dengan himpunan vertex V(D) = {v1, v2,· · · , vn}. Untuk setiap vi ∈V(D) dan X ⊆V(D), eksponen vertex γD(vi)

adalah bilangan bulat positif terkecilm1+m2sedemikian hingga terdapat (m1, m 2)-walk dari vi ke setiap vertex di D, dan himpunan eksponen expD(X) adalah

bi-langan bulat positif terkecilp1+p2 sehingga untuk setiap vertexvj di D terdapat

sebuah (p1, p2)-walk dari paling sedikit satu vertex diX kevj.

(50)

Misalkan D adalah 2-digraph primitif dengan orde n. Jika vertex - vertex di D adalah (v1, v2,· · · , vn) sedemikian hingga

γD(v1)≤γD(v2)≤ · · · ≤γD(vn)

expD(vk).

Untuk mencari eksponen vertex dari suatu 2-digraph primitif D, dimana terdiri atas m arc berwarna merah danbarc berwarna biru, maka akan dilakukan operasi (m, b)-matriks Hurwitz Product R dan B yang dapat didefinisikan secara rekurensif. Untuk suatu bilangan bulat tak negatif terkecilm danb, dank adalah vertex di D, maka untuk baris ke-k dari matriks tersebut yang seluruh entrinya bernilai positif, eksponen vertex-nya adalah m+b.

Contoh 2.5.2 : Berikut ini akan dicari eksponen vertex dari masing-masing vertex di 2-digraph pada Gambar 2.8 yaitu dengan melihat entri (i, j) dari (R, B)(m,b)_, dimana entri pada baris ke-i harus bernilai positif.

Pada Contoh 2.4.2 telah diperoleh matriks-matriks dari (R, B)(m,b)_{, kita} perhatikan untuk m + b = 6 pada (R, B)(4,2) _{diperoleh matriks (}_{R, B}₎(4,2) ₌

R(R, B)(3,2)₊_B₍_{R, B}₎(4,1)₌



    

1 1 1 1 1 1 1 1 1 1 2 2 1 1 0 2



    

, dimana pada baris ke-1, ke-2 dan ke-3

seluruh entrinya bernilai positif, maka expD(v1) = 6, expD(v2) = 6 dan expD(v3)

= 6 dengan komposisi₄

2

.

Kemudian perhatikan untuk m +b = 7 pada (R, B)(5,2) _{diperoleh matriks}

(R, B)(5,2)₌ _R₍_{R, B}₎(4,2)₊_B₍_{R, B}₎(5,1)₌



    

2 2 1 3 2 1 1 1 3 1 2 2 1 1 2 2



    

, dimana pada baris ke-4

seluruh entrinya bernilai positif, maka expD(v4) = 7 dengan komposisi ₅

2

.

(51)

oleh eksponen vertex masing-masing, yakni expD(v1) = 6, expD(v2) = 6, expD(v3)

= 6 dan expD(v4) = 7.

2.5.3 Digraph Wielandt

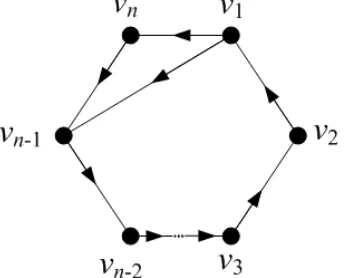
Digraph Wielandt Wn dengan orde n ≥ 3 adalah suatu digraph dengan vertex

v1, v2, . . . vn yang terdiri dari cycle vn → vn−1 → · · · → v2 → v1 → vn dan arc

[image:51.612.232.404.234.373.2]

v1 →vn−1. Digraph Wielandt direpresentasikan sebagai berikut.

Gambar 2.9 : Digraph Wielandt Wn dengan n vertex

Digraph Wielandt Wn dengan orde n mempunyai eksponen terbesar dari

digraph primitif dengan orde n tersebut, yaitu n2 ₋₂_n _{+ 2. Didefinisikan} _W(2)

n

sebagai suatu digraph dwi-warna yang diperoleh dengan mewarnai arc dengan digraph WielandtWndengan merah dan biru. Suatu digraph Wielandt dwi-warna

Wn(2) dengan orde n adalah primitif jika dan hanya jika matriks cycle dari Wn(2)

adalah

M =

"

n−1 n−2

1 1

#

Hal ini mengimplikasikan bahwa untuk suatu digraph WielandtWn(2)yang primitif

dengan orde n, n-cycle dari Wn(2) terdiri dari tepat satu arc biru dan (n −

1)-cycle dari Wn(2) juga terdiri dari tepat satu arc biru. Jadi ada dua kemungkinan.

Sebut bahwa Wn(2) tipe I, jika arc v1 → vn atau arc vn → vn−1 adalah biru, arc v1 → vn−1 adalah biru, dan yang lainnya merah; dan Wn(2) disebut tipe II, jika

pathvn−1 →vn−2 → · · · →v1 yang terdiri dari tepat satu arc biru dan selebihnya

(52)

Beberapa fakta tentang eksponen digraph dwi-warna primitif Wielandt yang telah digeneralisasikan (Gao dan Shao, 2009).

1. Misalkan Wn(2) adalah sebuah digraph dwi-warna Wielandt primitif dengan

orde n. Jika Wn(2) adalah tipe I dengan arc biru v1 → vn dan v1 → vn−1, maka untuk 1≤k ≤n, berlaku

exp_W(2)

n =γWn(2)(vk) =n

2₋₂_n₊_k.

orde n. Jika Wn(2) adalah tipe I dengan arc biru vn →vn−1 dan v1 →vn−1, maka untuk 1≤k ≤n, berlaku

exp_W(2)

n =γWn(2)(vk) =n

2₋₂_n₊_k_{+ 1}

orden. JikaWn(2)adalah tipe II dengan arc biruvj →vj−1, dimana 2 ≤j ≤ n−1, maka untuk 1≤k ≤n, berlaku

exp_W(2)

n =γWn(2)(vk) =n

(53)

DIGRAPH DWI-WARNA DENGAN 2 LOOP

Pada bab ini akan diperlihatkan hasil utama dari penelitian ini. Adapun hasil utama dari tulisan ini yaitu pola dari eksponen vertex dari 2-digraph dengan 2 loop. Sebelumnya akan dibahas tentang eksponen dari 2-digraph dengan 2 loop.

3.1 Eksponen 2-Digraph dengan 2 Loop

AndaikanD adalah digraph terhubung kuat dengann vertex, Holladay dan Varga menyatakan bahwa eksponen dari D dinyatakan dengan exp2(D) ≤ 2n− p−1, dimanap merupakan banyaknya loop diD.

Selanjutnya akan diberikan batas dari 2-eksponen dari 2-digraph khusus de-ngan sebuah loop merah dan sebuah loop biru. Kita mulai dede-ngan batas umum untuk eksponen dari 2-digraph terhubung kuat dengan sebuah loop merah dan sebuah loop biru.

Teorema 3.1 Misalkan D adalah 2-digraph terhubung kuat dengan n ≥ 2 vertex yang memuat sebuah loop merah dan sebuah loop biru. Maka exp2(D) ≤3n−3.

Bukti: Andaikan i dan j vertex di D yang saling berhubungan, dan terdapat loop merah dan loop biru di D. Untuk setiap pasangan vertex u dan v di D, diberikan walk wuv, u

pui

−→i−→pij j −pjv−→ v, dariu kev, dimana pui adalah path dari

uke i, pij adalah path dari i kej, dan pjv adalah path dari j kev. Diberikan

ℓr= max

u∈V {r(pui} dan ℓb = maxu∈V {b(pui},

ℓ′

r = max

v∈V {r(pjv} dan ℓ

′

b = max

v∈V {b(pjv}.

Maka untuk setiap pasangan vertexu danvterdapat walkwuv dariu kev dengan "

r(wuv)

b(wuv) #

≤

"

ℓr+r(pij) +ℓ′r

ℓb+b(pij) +ℓ′b #

(54)

dimana insiden terhadap loop merah dan loop biru. Karena walk wuv insiden ke

loop merah dan loop biru, maka walk wuv dapat diperpanjang menjadi walk dari

uke v dengan komposisi

"

ℓr+r(pij) +ℓ′r

ℓb+b(pij) +ℓ′b #

, sedemikian hingga

ℓr+ℓb, r(pij) +b(pij), ℓ′r+ℓ

′

b ≤n−1

akibatnya exp2(D)≤3n−3.

Selanjutnya akan diberikan 2-digraph terhubung kuat yang terdiri dari se-buah loop merah dan sese-buah loop biru dengan 2-eksponen hampir mendekati batas atas yang diberikan pada Teorema 3.1. Andaikan D adalah 2-digraph sedemikian hingga digraph tersebut dijamin memiliki cycle v1 → vn → ... → v3 → v1 dan vn → vn−1 → ... → v3 → v2 → vn, loop (v1, v1) dan loop (v2, v2) yang diperli-hatkan pada Gambar 1.1. Diberikanγ1 adalah cyclev1 →vn →...→v3 →v1 dan γ2 adalah cyclevn →vn−1 → ...→v3 →v2 →vn.

Proposisi 3.2 Andaikan D adalah 2-digraph 2-primitif dengan n≥3vertex yang mana digraph tersebut seperti pada Gambar 1.1. Jika D diwarnai dengan v1 → vn →...→v3 →v1 adalah cycle merah, (v1, v1) adalah loop merah, (v2, v2)adalah loop biru, dan v3 →v2→vn adalah path biru, maka exp2(D) = 3n−5

Bukti: Diberikan pn,3 merupakan path dari vn ke v3, p3,n merupakan path

v3 → v1 → vn, dan p′₃,n merupakan path v3 → v2 → vn. Andaikan wn,3 adalah walk dari vn ke v3 diberikan oleh

vn pn,3

−−→v3

p3,n

−−→vn pn,3

−−→v3

p′ 3,n

−−→vn pn,3

−−→v3

dengan komposisi

"

n−3 0 # + " 2 0 # + "

n−3 0 # + " 0 2 # + "

n−3 0

#

=

"

3n−7 2

#

.

Akan diperlihatkan untuk setiap pasangan vertexvi danvj diD terdapat walkwij

dari vi kevj dengan komposisi "

3n−7 2

#

(55)

Dengan menunjukkan bahwa walkwij darivi kevj insiden ke kedua loop dan "

r(wi,j)

b(wi,j) #

≤

"

3n−7 2

#

, kemudian dengan menggunakan loop merah dan loop biru, wij yaitu walk dari vi ke vj dapat diperpanjang sehingga komposisinya menjadi "

3n−7 2

#

.

Untuk setiap vertex vi di D terdapat path khusus dari vi ke v3. Jika i = 1

danj = 2 atau i= 2 danj = 1, akan diambil walk wij dari vi kevj menjadi path

khusus darivi kevj yaitu p1,2 dan p2,1 yang insiden ke kedua loop. Jikai=j = 1 atau i = j = 2, akan diambil walk wij menjadi path p1,2 diikuti oleh path p2,1 atau path p2,1 diikuti oleh p1,2,maka wij insiden ke 2 loop. Untuk setiap vertex

i /∈ {1,2} diD, setiap walk v1

p1,3

−−→ v3

p′ 3,n

−−→vn→vi,

vi →v3

p′ 3,n

−−→vn→v1,

v2 →v3

p3,n

−−→vn→vi,

dan vi→ v3

p3,n

−−→vn →v2

adalah insiden ke kedua loop sehingga memiliki komposisi batas atas

"

3n−7 2

#

.

Andaikan vi dan vj merupakan sembarang vertex di D sedemikian hingga

i /∈ {1,2} dan j /∈ {1,2}. Jika i < j, maka walk wij, vi γ1

−→vi γ2

−→vi pij

−→vj, insiden

ke kedua loop sehingga

"

r(wi,j)

b(wi,j) #

≤

"

3n−7 2

#

. Jika i > j, maka walk wij, vi pi,3

−−→

v3

p′ 3,n

−−→ vn pnj

−−→ vj γ1

−→ vj, insiden ke kedua loop sehingga "

r(wi,j)

b(wi,j) #

≤

"

3n−7 2

#

. Oleh karena itu, untuk setiap pasangan vertexvi dan vj di D, terdapat walk wij

diD dengan

"

r(wi,j)

b(wi,j) #

≤

"

3n−7 2

#

. Hal ini berakibat, exp2(D) ≤3n−5.

Selanjutnya akan diperlihatkan bahwa exp2(D) ≥ 3n −5. Andaikan untuk setiap pasangan vertex vi dan vj di D terdapat (s, t)-walk dari vi ke vj. Dengan

memperhatikan path dari v1 ke v2, yaituv1 →vn pn,3

−−→v3 →v2 dengan komposisi

" 1 0 # + "

n−3 0 # + " 0 1 # = "

n−2 1

#

(56)

sehingga diperoleh " s t # ≥ "

n−2 1

#

. Hal ini berakibat walk terpendek dari vn

ke v1 yang memuat paling sedikit n −2 arc merah dan 1 arc biru adalah walk vn

pn,3

−−→v3

p′ 3,n

−−→vn pn,3

−−→v3 →v1, dengan komposisi

"

n−3 0 # + " 0 2 # + "

n−3 0 # + " 1 0 # = "

2n−5 2 # . sehingga " s t # ≥ "

2n−5 2

#

. Jadi walk terpendek dari vn kev3 yang memuat paling sedikit 2n−5 arc merah dan 2 arc biru haruslah diantara walk vn

pn,3

−−→ v3

p′ 3,n

−−→

vn pn,3

−−→v3

p′ 3,n

−−→vn pn,3

−−→v3, dengan komposisi

"

n−3 0 # + " 0 2 # + "

n−3 0

#

=

"

3n−9 4

#

.

atau walk vn pn,3

−−→v3

p′ 3,n

−−→vn pn,3

−−→v3

p3,n

−−→vn pn,3

−−→v3, dengan komposisi

"

n−3 0 # + " 0 2 # + "

n−3 0 # + " 2 0 # + "

n−3 0

#

=

"

3n−7 2 # . sehingga " s t # ≥ "

3n−9 4 # atau " s t # ≥ "

3n−7 2

#

.

Hal ini berakibat exp2(D)≥3n−5.

Karena exp2(D)≤3n−5 dan exp2(D)≥3n−5, akibatnya exp2(D) = 3n−5.

Selanjutnya akan ditentukan eksponen vertex dari 2-digraph pada Gambar 1.1 yang memiliki exp2(D) = 3n−5.

3.2 Eksponen Vertex 2-Digraph dengan 2 Loop

Pada sub-bab ini akan ditunjukkan bentuk umum dari eksponen vertex dari 2-digraph dengan 2 loop.

Dengan menggunakan program matlab ”vert 2exp loops”, akan diinput banyak vertex yang ingin dicari dengan perintah

(57)

dengan n merupakan banyaknya vertex. Untukn = 3, akan diinput perintah

>> vert_2exp_loops (3)

dan akan diperoleh keluaran menjadi

ans =

1 2 3

2 2 2

4 4 4

dengan keterangan:

a. Baris pertama 1, 2 dan 3 menyatakan vertex ke-1, vertex ke-2 dan vertex ke-3.

b. Baris kedua menyatakan banyaknya arc merah yang dilalui.

c. Baris ketiga menyatakan banyaknya arc biru yang dilalui.

d. Baris keempat merupakan eksponen vertex dari setiap vertexnya. e. Baris kelima merupakan eksponennya.

Dari keluaran dapat ditentukan bahwa expD(v1) = 4 dengan komposisi 2

2

, expD(v2) =

4 dengan komposisi 2 2

, dan expD(v3) = 4 dengan komposisi 2

2

.

Selanjutnya dengan cara yang sama, untuk n= 4 diperoleh: expD(v1) = 6, dengan komposisi

4 2

, expD(v2) = 6, dengan komposisi

4 2

(58)

expD(v3) = 6, dengan komposisi 4

2

5 2

.

Untukn = 5, diperoleh: expD(v1) = 8, dengan komposisi

₆

2

₆

2

₆

2

₇

2

₈

2

.

₁₆

2

₁₆

2

₁₆

2

17 2

18 2

19 2

20 2

21 2

22 2

23 2

.

18 2

19 2

20 2

21 2

22 2

23 2

(59)

expD(v9) = 26, dengan komposisi 24

2

25 2

26 2

.

Sehinga untuk n =n, diperoleh: expD(v1) = 2n−2, dengan komposisi

₂_n−4 2

, expD(v2) = 2n−2, dengan komposisi

₂_n−4 2

, expD(v3) = 2n−2, dengan komposisi

₂n−4 2

, expD(v4) = 2n−2 + 1, dengan komposisi

₂n−4+1 2

₂n−4+2 2

₂n−4+3 2

, ...

expD(vk) = 2n−2 + (k−3) = 2n−5 +k, dengan komposisi

₂n−7+k

2

, expD(vk+1) = 2n−2+(k+1−3) = 2n−5+(k+1), dengan komposisi

h

2n−7+(k+1) 2

i

, ..

.

expD(vn) = 2n−2 + (n−3) = 2n−5 +n= 3n−5, dengan komposisi ₃n−7

2

.

Proposisi 3.3 Andaikan D adalah 2-digraph primitif dengan vertex v1, v2,· · · , vn

dan jika v adalah vertex di D dengan eksponen expD(v). Untuk sebarang vertex

vk, k = 1,2,· · · , n di D diperoleh bahwa expD(vk)≤ expD(v) +d(vk, v).

Bukti: Andaikan pk,v adalah (r(pk,v), b(pk,v))-path dari vk ke v dengan panjang

d(vk, v). Karena eksponen vertex v adalah expD(v), terdapat (s, t)-walk dengan

panjang expD(v) =s+t darivke setiap vertexvj,j = 1,2, ..., n. Ini menunjukkan

bahwa untuk setiap vertexvkdiD terdapat sebuah (s+r(pk,v), t+b(pk,v))-walk dari

vertexvk ke setiap vertexvj, j = 1,2, ..., n, dikatakan dengan walk yang berawal

dari vk, menuju ke v melewati (r(pk,v), b(pk,v))-path dan menuju ke vj melewati

sebuah (s, t)-walk dari v kevj. Oleh karena itu, expD(vk)≤ expD(v) +d(vk, v).

(60)

[image:60.612.218.415.138.353.2]

Teorema 3.4 Andaikan D adalah suatu digraph dwi - warna yang terdiri dari n vertex dengan n≥3 dan memiliki 2 loop seperti pada gambar berikut:

Gambar 3.1 : 2-Digraph dengan 2 Loop

jikavk, k= 1,2, ..., n adalah vertex di D maka

expD(vk) =       

2n−2 , k= 1,2,3 2n−5 +k ,4≤k ≤n.

Bukti: Diberikanpn,3 merupakan path darivn kev3,pn,k merupakan path darivn

kevk dan pk,3 merupakan path dari vk kev3. Pertama akan diperlihatkan bahwa

expD(vk) = 2n−2 untuk k = 1,2,3.

a. Untuk k = 1, path terpendek dari v1 ke v2 adalah v1 → vn pn,3

−−→ v3 → v2, dengan komposisi: " 1 0 # + "

n−3 0 # + " 0 1 # = "

n−2 1

#

.

Hal ini berakibat walk terpendek dari v1 ke v1 yang memuat paling sedikit n−2 arc merah dan 1 arc biru adalah walkv1 →vn

pn,3

−−→v3 →v2 →vn pn,3

−−→

v3 →v1, dengan komposisi:

" 1 0 # + "

n−3 0 # + " 0 1 # + " 0 1 # + "

n−3 0 # + " 1 0 # = "

2n−4 2

#

(61)

sehingga expD(v1)≥

"

2n−4 2

#

yakni expD(v1)≥2n−2.

Untuk setiapvk,k = 1,2, ..., n, terdapat (s, t)-walk dengan " s t # = "

2n−4 2

#

yang memuat loop merah dan loop biru. Dengan memperhatikan walk dari v1 kevn, yaitu v1 →vn

pn,3

−−→v3 →v2 →vn, komposisinya yaitu: " 1 0 # + "

n−3 0 # + " 0 1 # + " 0 1 # = "

n−2 2

#

,

dengan demikian walk tersebut harus melalui loop merah sebanyak n −2 kali sedemikian hingga komposisi dari walk tersebut menjadi

"

2n−4 2

#

, hal

ini berakibat terdapat walk yang nilainya lebih kecil dari

"

s t

#

, sedemikian

hingga expD(v1)≤ "

2n−4 2

#

yakni expD(v