Skripsi
Diajukan untuk Memenuhi Salah Satu Persyaratan Memperoleh Gelar Sarjana Pendidikan (S.Pd)
pada Fakultas Ilmu Tarbiyah dan Keguruan
Disusun Oleh:
ISMA HASANAH
NIM 106017000526
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH
JAKARTA
Skripsi berjudul ” Pengaruh Metode Pembelajaran SQ3R Terhadap Kemampuan Pemahaman Konsep Matematika Siswa”, disusun oleh Isma Hasanah, Nomor Induk Mahasiswa 106017000526, Jurusan Pendidikan Matematika, Fakultas Ilmu Tarbiyah dan Keguruan, Universitas Islam Negeri
Syarif Hidayatullah Jakarta. Telah melalui bimbingan dan dinyatakan sah sebagai
karya ilmiah yang berhak untuk diujikan pada sidang munaqasah sesuai ketentuan
yang ditetapkan oleh fakultas.
Jakarta, Desember 2010
Yang Mengesahkan,
Pembimbing I Pembimbing II
Abdul Mu’in, S.Si.,M.Pd Maifalinda Fatra, M.Pd
Konstruktivisme Strategi REACT Terhadap Pemahaman Konsep Matematika Siswa”, diajukan kepada Fakultas Ilmu Tarbiyah dan Keguruan Universitas Islam Negeri Syarif Hidayatullah Jakarta, dan telah dinyatakan lulus
dalam Ujian Munaqasah pada tanggal 27 Desember 2010 dihadapan dewan
penguji. Karena itu, penulis berhak memperoleh gelar Sarjana S1 (S.Pd) dalam
bidang Pendidikan Matematika.
Jakarta, Desember 2010
Panitia Ujian Munaqasah
Tanggal Tanda Tangan
Ketua Panitia (Ketua Jurusan)
Maifalinda Fatra, M.Pd ... ...
NIP. 19700528 199603 2 002
Sekretaris (Sekretaris Jurusan)
Otong Suhyanto, M.Si ... ...
NIP. 19681104 199903 1 001
Penguji I
Dra. Afidah Mas’ud ... ...
NIP. 19610926 198603 2 004
Penguji II
Otong Suhyanto, M.Si ... ...
NIP. 19681104 199903 1 001
Mengetahui
Dekan Fakultas Ilmu Tarbiyah dan Keguruan
Nama : Isma Hasanah
NIM : 106017000526
Jurusan : Pendidikan Matematika
Angkatan Tahun : 2006
Alamat : Jl. Anggrek Cakra No.15 Rt 006 Rw 09
Kebon Jeruk Jakarta Barat 11530
MENYATAKAN DENGAN SESUNGGUHNYA
Bahwa skripsi yang berjudul Pengaruh Metode Pembelajaran SQ3R Terhadap Kemampuan Pemahaman Konsep Matematika Siswa, adalah benar hasil karya sendiri di bawah bimbingan dosen:
1. Nama : Abdul Mu’in, S.Si., M.Pd
NIP : 19751201 200604 1 003
Dosen Jurusan : Pendidikan Matematika
2. Nama : Maifalinda Fatra, M.Pd
NIP : 19700528 199603 2 002
Dosen Jurusan : Pendidikan Matematika
Demikian surat pernyataan ini saya buat dengan sesungguhnya dan saya siap
menerima segala konsekuensi apabila terbukti bahwa skripsi ini bukan hasil karya
sendiri.
Jakarta, Desember 2010
Yang Menyatakan
i
Fakultas Ilmu Tarbiyah dan Keguruan, Universitas Islam Negeri Syarif Hidayatullah Jakarta.
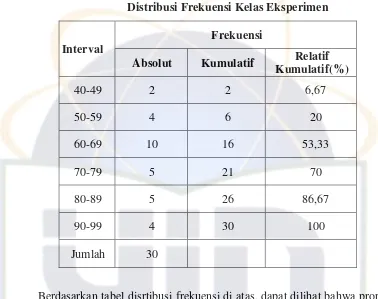
Penelitian ini dilakukan di MTs. Al-Falah Kebayoran Lama Jakarta Selatan dari tanggal 11 Oktober – 8 November 2010. Tujuan penelitian adalah untuk mengetahui pengaruh metode SQ3R terhadap pemahaman konsep matematika siswa. Metode yang digunakan adalah quasi eksperimen dengan desain penelitian Post Test Only Control group Design. Teknik pengambilan sampel menggunakan cluster random sampling. Intrumen penelitiannya berupa tes essay sebanyak 7 soal. Untuk teknik analisa data peneliti menggunakan uji perbandingan satu arah dengan uji “t”. Berdasarkan hasil perhitungan uji hipotesis diperoleh nilai thitung sebesar 2,018 dan ttabel sebesar 1,673 . Karena thitung > ttabel (2,018 > 1,673), maka Ha diterima, artinya rata-rata pemahaman konsep matematika yang diajarkan dengan metode SQ3R lebih tinggi dari rata-rata pemahaman konsep matematika yang diajarkan dengan metode konvensional. Dengan demikian dapat disimpulkan pembelajaran dengan menggunakan metode SQ3R berpengaruh terhadap pemahaman konsep matematika siswa
ii
Isma Hasanah., The Influence of SQ3R learning method through student’s understanding of mathematical concept. The thesis of Mathematic Education Department, Faculty of Tarbiyah and Teachers Training Syarif Hidayatullah State Islamic University Jakarta.
The research was held in MTs. Al-Falah junior high school Kebayoran Lama, South Jakarta on October 11th to November 8th 2010. The purpose of this rasearch is to know the influence of SQ3R method through student’s understanding of mathematical concept. The method used is quasi eksperiment with post test only control group design. To take the sample, the researcher used cluster random sampling. The research instrument is essay which content only seven questions. The technic of data analysis is one tail test with T-test. According to the calculation resulst of the hypotesis test, the researcher got ttest was 2,018 and ttabel was 1,673.Since ttest > ttabel (2,018 > 1,673),that Ha is accepted. This means that the
average of the stuent’s understanding of mathematical concept by using SQ3R learning methode is higher than which tought by conventional method. Therefore
learning math by using SQ3R methode have influence on student’s understanding of
mathematical concept.
iii
membuat skripsi ini dengan lancar. Skripsi ini masih banyak kekurangan, oleh
karena itu saya selalu mencurahkan do’a kepada-Nya untuk memohon bantuan
dan pertolongan dalam menyelesaikan skripsi ini agar selalu diberikan
kemudahan dalam segala urusan baik lahiriyah maupun batiniyah.
Selama penyusunan ini tidak sedikit hambatan yang penulis alami, karena
berkat do’a, kesungguhan hati, kerja keras, dan bantuan dari berbagai pihak
skripsi ini dapat terselesaikan. Tidak ada kata selain terima kasih penulis ucapkan
atas bimbingan, dorongan, masukan-masukan positif yang diberikan untuk
skripsi ini, lebih khusus lagi penulis mengucapkan rasa terima kasih kepada:
1. Bapak Prof. Dr. Dede Rosyada, M.A., Dekan Fakultas Ilmu Tarbiyah dan
Keguruan UIN Syarif Hidayatullah Jakarta.
2. Ibu Maifalinda Fatra, M.Pd., Ketua Jurusan Pendidikan Matematika.
3. Bapak Otong Suhyanto, M.Si., Sekretaris Jurusan Pendidikan Matematika.
4. Bapak Abdul Muin, S.Si, M.Pd., dosen Pembimbing I dan Ibu Maifalinda
Fatra M.Pd., dosen Pembimbing II . Dengan kesabaran dan keikhlasannya
telah membimbing, memberikan saran, masukan serta mengarahkan penulis,
sehingga penulis dapat menyelesaikan skripsi ini.
5. Seluruh dosen yang telah membimbing, mendidik dan memberikan ilmunya
kepada penulis dalam perkuliahan. Semoga ilmu yang telah diberikan kepada
penulis menjadi amal ibadah dan pahala di sisi Allah SWT. Dan semoga ilmu
yang telah diberikan menjadi ilmu yang bermanfaat bagi penulis. Staff
Jurusan (K. Dede) yang telah melayani penulis dalam pembuatan surat-surat.
6. Kedua orangtua tercinta yang tidak henti-hentinya mencurahkan do’a dan terus memberikan dorongan moril maupun materil sampai penyusunan skripsi
ini. Semoga amal ibadahnya dibalas dengan pahala yang berlipat ganda.
7. Kakak-kakak tercinta yang telah memberikan dorongan baik secara moril
iv
9. Ibu Lu’Luul Khusna, S.Pd, guru mata pelajaran matematika kelas VIII yang
telah membantu penulis dalam penelitian.
10.Teman-teman seperjuangan di Jurusan Pendidikan Matematika kelas B,
khususnya Rina, Lilis dan Yuli, teman-teman angkatan 2006 yang tak dapat
disebutkan satu persatu, teman-teman BEMJ Pend. Matematika 2008 – 2009, dan panitia LCCM IX, yang selalu memberikan motivasi, persahabatan dan
kenangan yang tak terlupakan.
11.Semua pihak yang terkait yang tidak bisa penulis sebutkan satu-persatu nama,
jabatan serta sumbangsihnya, penulis ucapkan rasa terima kasih yang
sebesar-besarnya.
Hanya do’a yang penulis haturkan semoga semua pihak yang telah membantu dalam menyelesaikan skripsi ini mendapat balasan dan pahala yang
berlipat ganda dari Allah SWT.
Akhirnya penulis mengharapkan skripsi ini dapat bermanfaat bagi penulis
dan bagi semua pihak yang membacanya. Amiin Yaa Rabbal ‘Alamiin
Jakarta, Desember 2010
v
ABSTRAK ………. i
KATA PENGANTAR ……….iii
DAFTAR ISI ...v
DAFTAR TABEL ………vii
DAFTAR GAMBAR ………..viii
DAFTAR LAMPIRAN ………ix
BAB I PENDAHULUAN A. Latar Belakang Masalah ………. 1
B. Identifikasi Masalah ………... 6
C. Pembatasan Masalah ……….. 6
D. Rumusan Masalah... ……… 6
E. Tujuan Penelitian ……… 7
F. Manfaat Penelitian ...………. 7
BAB II LANDASAN TEORITIK, KERANGKA BERPIKIR DAN HIPOTESIS PENELITIAN A. Deskripsi Teoretik ………... 8
1. Belajar dan Pembelajaran .………..8
2. Pembelajaran Matematika ………11
3. Pemahaman Konsep Matematika...………...14
4. Berbagai Metode Pembelajaran Matematika ………19
5. Metode SQ3R ...21
6. Metode Konvensional...29
B. Hasil Penelitian yang Relevan ………... 31
C. Kerangka Berpikir ………. 32
D. Hipotesis Penelitian ………...………..34
BAB III METODOLOGI PENELITIAN A. Tempat dan Waktu Penelitian ……….35
vi
1. Uji Validitas …...………... 38
2. Uji Reliabilitas ...………... 39
3. Tingkat Kesukaran Soal ………... 40
4. Daya Pembeda Soal ………. 41
F. Analisis Data ……….. 43 1. Uji Normalitas ………43 2. Uji Homogenitas ……….. 44 3. Pengujian Hipotesis ……….. 44 G. Hipotesis Statistik ………... 47
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Deskripsi Data ……… 47
B. Pengujian Persyaratan Analisis ……….. 53
1. Uji Normalitas ……….. 53
2. Uji Homogenitas ………....54
C. Pengujian Hipotesis ...……… 55
D. Pembahasan ...57
E. Keterbatasan Penelitian ……….. 60
BAB V KESIMPULAN DAN SARAN A. Kesimpulan ………. 61
B. Saran ……….. .62
DAFTAR PUSTAKA ………...63
vii
2. Tabel 2. Perbandingan Metode SQ3R dengan Metode Konvensional…….. 31
3. Tabel 3. Rancangan Penelitian...………... 35
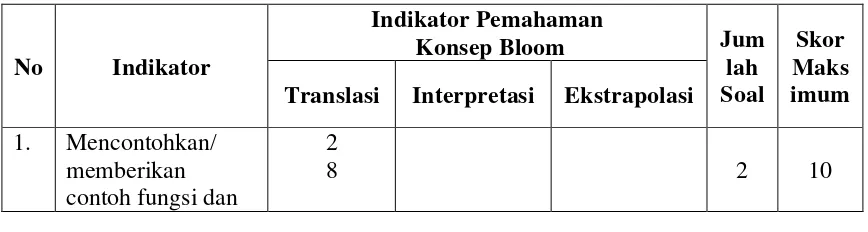
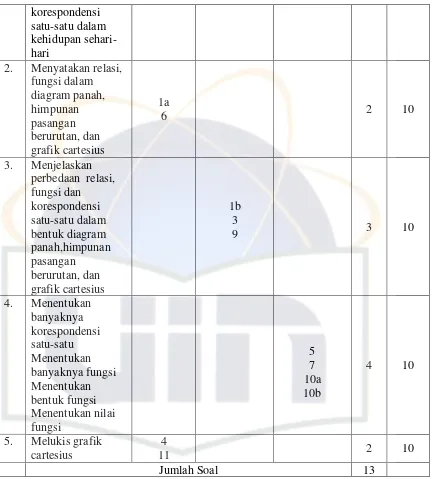
4. Tabel 4. Kisi-Kisi Instrument...……….... 36
5. Tabel .5 Klasifikasi Daya Pembeda...………... 42
6. Tabel 6. Distribusi Frekuensi Kelas Eksperimen...…...48
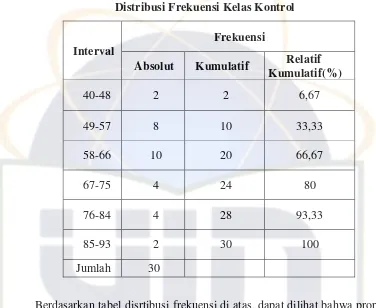
7. Tabel 7. Distribusi Frekuensi kelas Kontrol ………...………. 50
8. Tabel 8. Statistik Deskriptif Skor Hasil Pemahaman Konsep matematika Kelas Eksperimen dan Kontrol... 52
9. Tabel. 9 Hasil Uji Normalitas Kelas Eksperimen dan Kelas Kontrol...54
viii
...………... 49 2. Gambar 2. Ogive Hasil Pemahaman Konsep Matematika Kelas Eksperimen
ix
2. Lampiran 2. RPP Kelas Eksperimen ……… 77
3. Lampiran 3 Contoh Materi Fungsi (Eksperimen)... 94
4. Lampiran 4. Latihan Soal (Eksperimen) ………... 97
5. Lampiran 5. Uji Coba Tes Matematika Pada Pokok Bahasan Fungsi ...106
6. Lampiran 6. Soal Posttest Matematika Pada Pokok Bahasan fungsi ...108
7. Lampiran 7. Kunci Jawaban posttest Pada Pokok Bahasan fungsi...110
8. Lampiran 8. Perhitungan Validitas Tes ...………. 117
9. Lampiran 9. Perhitungan Reliabilitas Tes ...………...119
10.Lampiran 10. Perhitungan Daya Pembeda .... ...………...122
11.Lampiran 11. Perhitungan Tingkat Kesukaran ... ...………….124 12.Lampiran 12. Hasil Perhitungan Validitas, Daya Pembeda dan Tingkat Kesukaran Tes ………..126 13.Lampiran 13. Nilai Posttest Kelas Eksperimen dan Kelas Kontrol ………….126
14.Lampiran 14. Distribusi Frekuensi, Kelas Eksperimen ………...127
15.Lampiran 15. Distribusi Frekuensi, Kelas Kontrol... ……….. 128
16.Lampiran 16. Perhitungan Mean, Median, Modus, Varians, Simpangan Baku, Kemiringan Kurva, Kurtosis, Kelas Eksperimen dan kontrol...……… 130
17.Lampiran 17. Uji Normalitas Kelompok Eksperimen ……… 134
18.Lampiran 18. Uji Normalitas Kelompok Kontrol ………... 135
19.Lampiran 19. Perhitungan Uji Normalitas, Uji Homogenitas, Uji Hipotesis..136
20.Lampiran 20. Surat Bimbingan Skripsi ………...139
BAB I
PENDAHULUAN
A.Latar Belakang Masalah
Pendidikan merupakan interaksi antara guru dengan siswa dan interaksi
siswa dengan siswa. Interaksi pendidikan tidak hanya terjadi di sekolah, tetapi
juga terjadi di lingkungan keluarga ataupun masyarakat. Tanpa interaksi
pendidikan tidak dapat terlaksana. Manusia membutuhkan pendidikan untuk
mewujudkan dirinya menjadi manusia yang memiliki mental, fisik, emosional,
sosial, dan etika yang lebih baik.
Pendidikan bukanlah suatu hal yang statis atau tetap melainkan suatu hal
yang dinamis. Oleh karena itu pendidikan diupayakan adanya
perubahan-perubahan atau perbaikan secara terus menerus. Pendidikan di Indonesia
banyak mengalami perubahan, seperti perubahan kurikulum dari kurikulum
1994 sampai KTSP. Perubahan tersebut membawa dampak besar dalam proses
pembelajaran. Pembaharuan kurikulum akan lebih bermakna bila diikuti oleh
perubahan proses pembelajaran di dalam kelas maupun diluar kelas.
Pendidikan dalam lingkungan sekolah lebih bersifat formal, karena
sekolah merupakan sarana formal bagi siswa untuk menimba berbagai ilmu
pengetahuan. Salah satu ilmu pengetahuan yang dipelajari di sekolah adalah
matematika. Matematika merupakan bidang studi yang dipelajari oleh semua
siswa dari tingkat SD sampai SMA bahkan perguruan tinggi.
Matematika merupakan salah satu bagian yang penting dalam ilmu
pengetahuan, karena matematika banyak dibutuhkan dalan ilmu pengetahuan
dan teknologi. Hampir semua kegiatan manusia terutama yang berkaitan
dengan ilmu pengetahuan melibatkan matematika di dalamnya, seperti bidang
ekonomi, sosial, kedokteran bahkan budaya, oleh sebab itu matematika pantas
disebut sebagai Ratu Ilmu Pengetahuan.1 Peran penting matematika diakui oleh
1
Sri Anitah dan Janet Trineke, Strategi Pembelajaran Matematika, (Jakarta:UT, 2007), h. 7.11
Cockcroft yaitu: “it would be verry difficult perhaps impossible to live a normal life in very many parts of the world in the twentieth century without
making use of mathematics of some kind”. Akan sangat sulit atau tidaklah mungkin bagi seseorang untuk hidup di bagian bumi ini pada abad ke-20 tanpa
sedikitpun memanfaatkan matematika.2
Prestasi matematika siswa Indonesia cukup menggembirakan. Beberapa
siswa Indonesia dari tingkat SD, SMP, dan SMA berhasil meraih kejuaraan
dalam rangka olimpiade matematika di tingkat international. Seperti tim
olimpiade matematika Indonesia berhasil meraih satu medali emas, lima perak
dan tiga perunggu serta dua gelar honorable mention di Madrid Spanyol, tahun
2008,3 kemudian tim Indonesia juga menjadi juara umum dalam Kompetisi
Matematika Internasional III-2009 atau "The 3rd WIZMIC 2009 (Wizard at Mathematic International Competition 2009)" di Lucknow, India. Peringkat juara umum itu diraih tim Indonesia setelah menyabet 10 medali emas,
sembilan perak, dan lima perunggu dalam 3rd WIZMIC 2009.4
Prestasi ini patut kita syukuri dan kita banggakan. Ternyata siswa
Indonesia dapat berhasil di bidang matematika dan bersaing dengan
negara-negara lain. Hal ini membuktikan bahwa prestasi bangsa Indonesia di bidang
ilmu pengetahuan, terutama matematika tidaklah mengecewakan. Bangsa
Indonesia mampu mengukir prestasi yang sama seperti negara-negara lainnya.
Prestasi tersebut hanyalah diraih secara individual belum seluruhnya siswa
Indonesia berhasil meraihnya. Pendidikan matematika di Indonesia belum
menampakkan hasil yang diharapkan. Hal ini ditunjukkan dengan hasil studi
TIMSS tahun 2007 untuk siswa kelas VIII, menempatkan siswa Indonesia pada
urutan ke 41 dari 49 negara dengan nilai rata-rata kemampuan matematika
2
Fadjar Shadiq, “Apa dan Mengapa Matematika Begitu Penting?”, dari: www. Fadjarp3g.woordpress.com, diakses Selasa 22 Juni 2010, pukul: 10.00
3
Luxsman, “Prestasi Anak Bangsa Indoesia” dari: http://luxsman.blogspot.com/2009/08/prestasi-anak-bangsa-indonesia.html ,diakses Jum’at, 2 Juli 2010,pukul 10.00
4Hilda Sabri, “ RI Juara Umu Kompertisi The 3rd WIZMIC 2009”
secara umum adalah 397. Nilai tersebut masih jauh dari standar minimal nilai
rata-rata kemampuan matematika yang ditetapkan TIMSS yaitu 500.5
Keadaan ini sangat ironis dengan kedudukan dan peran matematika untuk
pengembangan ilmu dan pengetahuan. Mengingat matematika merupakan
induk ilmu pengetahuan, ternyata matematika hingga saat ini belum menjadi
pelajaran yang difavoritkan. Berhasil atau gagalnya dalam mempelajari
matematika disebabkan karena tingkat kesulitan materi pelajaran, metode
pembelajaran yang digunakan, penguasaan konsep dasar, minat siswa dan
bakat siswa.
Berdasarkan pengamatan penulis di sekolah tempat Praktek Profesi
Keguruan Terpadu (PPKT) pada tahun 2010, menunjukkan bahwa siswa hanya
mampu mengerjakan soal dengan mengikuti langkah-langkah yang diberikan
guru dan siswa terbiasa menghafal suatu konsep tanpa tahu bagaimana
pembentukan konsep itu berlangsung. Siswa mampu menghafal dengan baik
tentang materi ajar, namun pada kenyataannya mereka belum memahaminya.
Selain itu, ketika siswa diberikan soal siswa kurang mencermati isi soal. Hal ini
disebabkan karena siswa kurang teliti dalam membaca soal, sehingga siswa
tidak bisa menentukan konsep yang tepat untuk menjawab soal yang diberikan.
Pelajaran matematika merupakan salah satu pelajaran yang disegani siswa,
karena matematika bagi mereka merupakan pelajaran yang sulit dan identik
dengan simbol-simbol dan rumus-rumus. Sering kali siswa kesulitan belajar
matematika karena mereka belum memahami konsep matematika yang mereka
pelajari. Siswa hanya sekedar mengetahui konsep matematikanya, tetapi
mereka tidak bisa menerapkannya dalam memecahkan masalah. Untuk
memahami suatu pokok bahasan matematika siswa harus menguasai
konsep-konsep matematika serta keterkaitan antara konsep-konsep yang satu dengan yang
lainnya.
5
Herlanti, “Prestasi Sains Indonesia”, dari:http://yherlanti.wordpress.com/2009/01/17/prestasi-sains-indonesia-di-timss/, diakses Jum’at, 2 Juli 2010
Pemahaman konsep merupakan landasan dasar belajar matematika.
Depdiknas menyatakan bahwa tujuan mata pelajaran matematika di SD, SMP,
SMA dan SMK salah satunya adalah “agar peserta didik memiliki kemampuan pemahaman konsep matematik, menjelaskan keterkaitan antar konsep dan
mengaplikasikan konsep atau algoritma secara luwes, akurat, efisien, dan tepat
dalam pemecahan masalah”.6 Oleh karena itu dalam pembelajaran matematika yang harus ditekankan terlebih dahulu adalah pemahaman konsep yang baik
dan benar. Sehingga siswa dapat mengetahui konsep itu berlangsung dan dapat
menempatkan konsep dalam memecahkan masalah.
Pemahaman dapat diperoleh salah satunya adalah dengan membaca,
karena dengan membaca siswa akan mendapatkan pengetahuan baru serta
mengalami proses berpikir untuk mendapatkan pemahaman. Namun, dalam
membaca siswa tidak hanya melafalkan kata demi kata, kalimat demi kalimat
tanpa arti, tetapi siswa juga dapat memahami makna yang dibacanya.
Keterampilan membaca mempunyai peranan penting dalam pembelajaran
matematika. Membaca matematika berbeda dengan membaca novel. Ketika
membaca matematika siswa harus memahami istilah dan simbol-simbol
matematika. Menurut Siegel, Borasi, Pozi, Sanrige, dan Smith mengatakan
melalui membaca matematika siswa dapat mengkonstruksi makna matematik,
sehingga siswa belajar bermakna dan aktif.7
Usaha yang harus dilakukan untuk meningkatkan pemahaman konsep
matematika siswa adalah dengan cara memperbaiki proses belajar mengajar,
yaitu proses belajar mengajar yang biasanya Teacher Centered menjadi Student Centered. Jadi, di dalam proses pembelajaran siswa dilibatkan secara aktif baik dalam mental maupun fisik. Keabstrakan objek-objek matematika perlu
diupayakan agar dapat diwujudkan secara lebih konkret, sehingga akan
mempermudah siswa memahaminya. Guru perlu melakukan suatu cara
6
Fadjar Shadiq, “Apa dan Mengapa Matematika Begitu Penting?”, dari: www. Fadjarp3g.woordpress.com, diakses Selasa 22 Juni 2010, pukul: 10.00
7
penyajian konsep-konsep yang dapat memudahkan peserta didik memusatkan
perhatian dan menggunakan pengetahuan yang sudah ada dalam benaknya.
Guru matematika bertugas untuk memberi informasi kepada siswa yang
belajar matematika. Sudah seharusnya penguasaan materi pelajaran dan
kemampuan menyajikan materi pelajaran dengan berbagai metode merupakan
kunci utama kewibawaan dan keberhasilan sebagai guru matematika. Tugas
dan peran guru matematika tidak hanya mentransfer pengetahuan, tetapi
menuntun siswa untuk mengkonstrusikan ilmu pengetahuan itu sendiri. Siswa
dapat mengkonstruksikan ilmu pengetahuan itu dalam berbagai akvitas seperti
memahami, bernalar, berkomunikasi dan memecahkan masalah.
Solusi untuk masalah-masalah yang diuraikan di atas, diperlukan metode
pembelajaran yang melibatkan siswa menjadi aktif dalam mengkonstruksi ilmu
pengetahuan. Pembelajaran matematika yang melibatkan siswa untuk aktif,
dapat melatih kemampuannya untuk berfikir memahami konsep matematika
dengan pola pikir mereka. Pembelajaran tersebut dapat dilakukan dengan
menggunakan metode pembelajaran SQ3R.
Metode SQ3R adalah metode membaca yang efisien dan membantu siswa
untuk lebih berkonsentrasi terhadap teks yang dibaca. Metode SQ3R dapat
mendorong siswa untuk lebih memahami apa yang dibacanya, terarah pada
intisari yang tersirat dalam suatu buku atau teks. Metode SQ3R mempunyai 5
langkah yaitu survey, question, read, recite, dan review. Langkah-langkah metode SQ3R yang sistematis dapat membuat siswa menggunakan kemampuan
berpikirnya dalam memahami ide-ide pokok/konsep-konsep yang ada dalam
teks.
Penerapan metode belajar SQ3R dalam pembelajaran matematika dapat
digunakan untuk memahami materi ajar ataupun memecahkan masalah.
Metode SQ3R melibatkan siswa untuk aktif dalam menemukan konsep yang
ada pada suatu pokok bahasan dan menentukan konsep yang tepat dalam
Berdasarkan uraian di atas, maka penulis tertarik untuk meneliti “Pengaruh Metode Pembelajaran SQ3R Terhadap Pemahaman Konsep Matematika Siswa”.
B. Identifikasi Masalah
Berdasarkan permasalahan yang telah diuraikan di atas, maka
masalah-masalah yang diidentifikasi sebagai berikut:
1. Pembelajaran matematika masih berpusat pada guru
2. Guru cenderung menggunakan metode pembelajaran konvensional dan
tidak variatif
3. Pemahaman konsep matematik siswa masih rendah
4. Siswa kurang teliti dalam membaca soal
5. Prestasi belajar matematika yang masih rendah dibandingkan dengan
pelajaran lain
C.Pembatasan Masalah
Agar penelitian ini lebih jelas dan terarah, maka perlu pembatasan
masalah:
1. Penelitian yang dilakukan untuk mengukur kemampuan pemahaman
konsep matematik siswa yang sesuai dengan landasan Taksonomi Bloom
2. Metode pembelajaran yang digunakan adalah metode SQ3R
3. Pokok bahasan yang diteliti adalah fungsi
D.Rumusan Masalah
1. Bagaimana pemahaman konsep matematika siswa yang diajarkan dengan
metode SQ3R dan metode konvensional?
2. Apakah kemampuan pemahaman konsep matematika siswa yang diajarkan
dengan metode SQ3R lebih tinggi dari kemampuan pemahaman konsep
E.Tujuan Penelitian
Berdasarkan rumusan masalah di atas, tujuan penelitian ini adalah:
1. Untuk mengetahui dan mendeskripsikan data tentang kemampuan
pemahaman konsep matematik siswa dengan menggunakan metode SQ3R
dan metode konvensional
2. Untuk mengetahui apakah pemahaman konsep matematika yang
menggunakan metode SQ3R lebih tinggi dari pemahaman konsep
matematika siswa yang diajarkan dengan metode konvensional.
F. Manfaat Penelitian
1. Bagi guru
a. Memperoleh pengetahuan tentang pembelajaran dengan metode SQ3R
b. Dapat memperbaiki dan meningkatkan sistem pembelajaran di kelas
dengan baik.
2. Bagi peneliti
a. Memperoleh pengalaman langsung dalam praktek metode SQ3R
b. Memperoleh bekal tambahan sebagai calon guru matematika sehingga
diharapkan dapat bermanfaat kelak ketika terjun di lapangan.
3. Bagi Pembaca
a. Memperoleh pengetahuan tentang Pengaruh Metode SQ3R terhadap
Pemahaman Konsep Matematika Siswa
BAB II
Landasan Teoretik, Kerangka Berpikir
dan Hipotesis Penelitian
A.Deskripsi Teoretik
1. Belajar dan Pembelajaran
Belajar merupakan kegiatan berproses yang dilakukan di dalam
pendidikan. Belajar dapat membuat siswa dari yang tidak tahu menjadi tahu,
dari yang tidak bisa menjadi bisa dan siswa banyak mendapatkan informasi
dari proses belajar. Ini berarti berhasil atau gagalnya siswa sangat
bergantung pada proses belajar yang dialami siswa baik ketika berada di
sekolah, maupun lingkungan di rumah atau keluarganya sendiri.
Pengertian belajar yang dikemukakan oleh Fontana yaitu “suatu proses perubahan relatif tetap dalam perilaku individu sebagai hasil dari
pengalaman”.1
Chaplin membatasi belajar dengan 2 macam rumusan yaitu:2
a. Acquisition of any relatively permanent change in behaviour as result of practice and experience. Belajar adalah perolehan perubahan tingkah laku yang relatif menetap sebagai akibat praktik dan pengalaman.
b. Process of acquiring responses as a result of special practice.
Belajar ialah proses memperoleh respon-respon sebagai akibat adanya pelatihan khusus.
Kegiatan proses belajar dapat membuat siswa mengalami
perubahan-perubahan menuju kearah yang lebih baik. Perubahan tersebut tidak hanya
pada aspek kognitif, tetapi juga pada aspek sikap (afektif) dan keterampilan
(psikomotorik). Perubahan-perubahan akibat proses belajar adalah
perubahan yang relatif menetap atau tidak mudah hilang, karena ketika
siswa melakukan proses belajar siswa akan dilatih segala aspek kognitif,
afektif dan psikomotorik sehingga akan terjadi peningkatan. Oleh karena itu
1
Paulina Panen, Belajar dan Pembelajaran, (Jakarta: UT, 2001), h.1.2
2
Muhibbin Syah, Psikologi Pendidikan Dengan Pendekatan Baru, (bandung: PT Remaja Rosda Karya, 2010), ed. 15, h. 88
perubahan yang terjadi pada diri siswa tidak mudah hilang bahkan terus
berkembang apabila siswa sering melakukan kegiatan belajar.
Menurut Hakim belajar adalah “suatu perubahan di dalam kepribadian manusia, dan perubahan tersebut di tampakkan dalam bentuk peningkatan
kualitas dan kuantitas tingkah laku seperti peningkatan kecakapan,
pengetahuan, sikap, kebiasaan pemahaman, keterampilan, daya fikir”.3 Sedangkan Hilgard dan Marquist berpendapat bahwa “belajar merupakan proses mencari ilmu yang terjadi dalam diri seseorang melalui latihan,
pembelajaran, dan sebagainya sehingga terjadi perubahan dalam diri”. 4
Berdasarkan pendapat para ahli di atas dapat disimpulkan bahwa
belajar adalah proses perubahan tingkah laku yang mengakibatkan siswa
dapat merespon ilmu pengetahuan yang diberikan sehingga terjadi
peningkatan daya pikir, keterampilan, pemahaman, sikap, pengetahuan, dan
lain-lain yang dilakukan melalui pembelajaran.
Belajar merupakan aktivitas yang berproses yang di dalamnya banyak
perubahan-perubahan yang bertahap. Menutut Wittig (Syah, 2009) setiap
proses belajar selalu berlangsung dalam tahapan-tahapan yang mencakup:
Acquistion (tahap perolehan/peneriman informasi), Storage (tahap penyimpanan informasi), dan Retrieval (tahap mendapatkan kembali informasi).5 Pada tahap acquition, siswa mulai menerima informasi dan mengembangkan hasil informasi itu hingga menimbulkan pemahaman.
Apabila pada tahap ini gagal, maka siswa akan kesulitan untuk melalui
tahap storage. Tahap storage adalah tahap penyimpanan informasi yang telah didapat pada tahap acquistion. Selanjutnya pada tahap retrieval, siswa akan mengaktifkan kembali memorinya untuk memecahkan masalah.
Misalnya ketika siswa melakukan evaluasi setelah belajar, UAS, UN, siswa
akan berusaha memanggil informasi-informasi yang telah dipahaminya
untuk menjawab pertanyaan-pertanyaan.
3
Pupuh Fathurrohman, Strategi Belajar Mengajar Melalui Penanaman Konsep Umum dan Konsep Islami, (Bandung:PT. Refika Aditama, 2007), Cet. I, h.6.
4
Syaiful Sagala, Konsep dan Makna Pembelajaran, (Bandung: Alfabeta, 2009), h. 13
5
Perubahan-perubahan yang dialami siswa karena akibat dari proses
pembelajaran. Pembelajaran berdasarkan makna leksikal berarti proses, cara
perbuatan mempelajari.6 Menurut Gagne, Brigss, dan Wager pembelajaran adalah “serangkaian kegiatan yang dirancang untuk memungkinkan
terjadinya proses belajar pada siswa”.7
Pada pembelajaran guru telah
merancang kegiatan-kegiatan apa saja yang harus dilakukan dalam proses
belajar, seperti materi, metode, dan media sehingga dapat memudahkan
siswa untuk memahami materi dan rancangan kegiatan tersebut harus sesuai
dengan tujuan pembelajaran.
Pembelajaran mempunyai 2 karakteristik, yaitu (1) dalam proses
pembelajaran melibatkan proses mental siswa secara maksimal, bukan
hanya menuntut siswa sekedar mendengar, mencatat, akan tetapi
menghendaki siswa dalam proses berpikir, (2) dalam pembelajaran
membangun suasana dialogis dan proses tanya jawab terus menerus yang
diarahkan untuk memperbaiki dan meningkatkan kemampuan berpikir
siswa, yang pada gilirannya kemampuan berfikir itu dapat membantu siswa
untuk memperoleh pengetahuan yang mereka konstruksi sendiri.8
Kesimpulan yang dapat diambil dari berbagai pendapat di atas,
pembelajaran adalah usaha yang dilakukan guru agar siswa melakukan
belajar melalui rancangan yang telah dibuat. Pada pembelajaran siswa yang
lebih banyak berperan dari pada guru, guru hanya menjadi fasilitator saja.
Oleh karena itu dalam pembelajaran siswa dituntut untuk aktif baik secara
mental maupun fisik sehingga siswa dapat menggunakan kemampuan
berfikir dan keterampilan-keterampilan dalam proses belajar.
6
Agus Suprijono, Cooperative Learning Teori dan Aplikasi Paikem, (Surabaya:Pustaka Belajar, 2009), h. 13
7
Paulina Panen, Belajar dan Pembelajaran,...,h. 1.5
8
2. Pembelajaran Matematika
Menurut Suhendar istilah kata matematika menurut berbagai bahasa
antara lain mathematics (bahasa Inggris), mathematik (bahasa Jerman),
mathematique (bahasa Perancis), matematico (bahasa Italia), matematiceski
(bahasa Rusia) dan mathematick (bahasa Belanda). Istilah matematika yang dinyatakan dalam berbagai ungkapan tersebut berasal dari bahasa Yunani,
yaitu mathematike yang mengandung pengertian hal-hal yang berhubungan (relating to learning). Kata tersebut mempunyai akar kata mathema yang artinya pengetahuan atau ilmu. Kata ini pun berhubungan erat dengan kata
lain, yaitu mathamein yang maknanya adalah belajar.9
Terdapat beberapa pengertian matematika menurut para ahli,
diantaranya seperti yang diungkapkan Paling (Abdurrahman, 2002) yaitu
matematika adalah suatu cara untuk menemukan jawaban terhadap masalah
yang dihadapi manusia, suatu cara menggunakan informasi, menggunakan
pengetahuan tentang bentuk dan ukuran, menggunakan pengetahuan tentang
menghitung, dan yang paling penting adalah memikirkan dalam diri
manusia itu sendiri dalam melihat dan menggunakan hubungan-hubungan.10
Sedangkan James dan James (Suherman, 2003) mengatakan bahwa
matematika adalah ilmu tentang logika mengenai bentuk, susunan, besaran,
dan konsep-konsep yang berhubungan satu dengan yang lainnya dengan
jumlah yang banyak yang terbagi ke dalam tiga bidang, yaitu aljabar,
analisis, dan geometri.11
Berdasarkan pendapat di atas matematika adalah ilmu yang berisi
struktur-struktur, konsep yang saling berhubungan satu sama lainnya. Agar
siswa mengetahui dan memahami konsep-konsep serta struktur-struktur
yang ada di matematika, maka diperlukan belajar matematika. Menurut Skemp inti belajar matematika adalah “agar siswa memiliki pemahaman
9 Suhendar, Perkembangan kurikulum dan Pembelajaran Matematika, (Jakarta: Universitas Terbuka, 2007), h. 7.4
10
Mulyono Abdurrahman, Pendidikan Bagi Anak Berkesulitan Belajar, (Jakarta: PT Rineka Cipta, 2002), cet. 1, h. 252
relasional dimana para siswa dapat melakukan sesuatu namun ia juga harus
dapat menjelaskan mengapa ia harus melakukan”.12
Cornelius mengemukakan lima alasan perlunya belajar matematika, yaitu:13
1) Sarana berpikir yang jelas dan logis
2) Sarana untuk memecahkan masalah dalan kehidupan sehari-hari 3) Sarana mengenal pola-pola hubungan dan generalisasi
pengalaman
4) Sarana untuk mengembangkan kreativitas
5) Sarana untuk meningkatkan kesadaran terhadap perkembangan budaya.
Pada proses pembelajaran matematika, para guru matematika harus
memberikan kesempatan kepada siswa untuk dapat berpikir sesuai dengan
kreativitasnya, karena pengetahuan tidak dapat dipindahkan begitu saja dari
otak seorang guru ke otak siswanya. Setiap siswa harus membangun
pengetahuan itu di dalam otaknya sendiri-sendiri berdasar pada pengetahuan
atau pengalaman yang sudah dimiliki atau pernah dialami siswa.
Menurut Gagne (Suherman, 2003) mengatakan bahwa dalam belajar
matematika ada 2 objek yang diperoleh siswa, yaitu objek langsung dan
objek tak langsung.14 Objek langsung adalah objek yang diterima secara
langsung oleh siswa melalui penjelasan guru atau diskusi, seperti fakta,
konsep, definisi dan lain-lain. Jadi, secara langsung siswa mendapatkan
pemahaman tentang konsep-konsep, aturan-aturan yang ada di dalam
matematika. Sedangkan objek tidak langsung adalah ketika siswa
mempunyai pengetahuan dan pemahaman tentang matematika secara tidak
langsung siswa mampu memecahkan masalah, dapat belajar mandiri dengan
menggunakan proses berpikir dan kreativitas-kreativitas yang mereka miliki
untuk memecahkan masalah.
Belajar matematika merupakan belajar konsep-konsep dan
struktur-struktur yang ada di matematika. Hendaknya seorang guru sebelum
memulai materi, siswa diberikan motivasi terlebih dahulu, seperti
12 Fadjar Shadiq, “Apa Implikasi dari inti Psikologi Kognitif Terhadap Pembelajaran
Matematika?” dari : Limas, No. 22, April 2009
13
Mulyono Abdurrahman, Pendidikan Bagi Anak Berkesulitan Belajar, ..., h. 253
14
menceritakan mengapa konsep itu dimunculkan, manfaat konsep itu di
dalam atau di luar matematika. Tujuannya agar siswa tertarik untuk belajar
matematika. Pada pembelajaran matematika diperlukan keterampilan untuk
dapat mewujudkan objek-objek yang abstrak menjadi yang lebih konkret,
sehingga siswa dapat lebih mudah memahaminya.
Brownell mengemukakan bahwa salah satu cara agar anak-anak dapat
mengembangkan pemahaman tentang matematika adalah dengan
menggunakan benda-benda yang telah mereka kenal dan relevan dengan
konsep yang dibahas.15 Contohnya: guru menjelaskan konsep perkalian.
Guru bisa menggunakan benda-benda yang mereka kenal, seperti: pensil,
gelas, kelereng, dan lain-lain. Benda-benda tersebut dapat disusun dengan
cara mereka sendiri hingga terbentuk formasi perkalian.
Menurut Kilpatrick, Swatford, dan Findell (Suhendar, 2007) terdapat
lima kompetensi dalam matematika, yaitu: pemahaman konsep, pemahaman
prosedur, kemampuan strategis, bernalar secara adaptif, dan disposisi yang
produktif.16 Pemahaman konsep adalah kompetensi awal yang diperlukan
dalam belajar matematika. Pahamnya siswa terhadap suatu konsep siswa
akan mampu menerapkan suatu konsep dalam suatu masalah. Selanjutnya
adalah pemahaman prosedur, kemampuan siswa menerapkan konsep dengan
urutan atau langkah-langkah kerja secara logis dan sistematis serta
memecahkan masalah. Kemampuan strategis adalah kemampuan siswa
dalam memecahkan masalah dengan memilih strategi yang tepat untuk
masalah tersebut. Bernalar secara adaptif adalah kemampuan siswa untuk
berpikir secara logis, kreatif, serta dapat menjelaskan hasil pekerjaanya
dengan argumen-argumen yang logis. Disposisi produktif adalah
kemampuan siswa untuk menilai bahwa matematika itu adalah pelajaran
yang bermanfaat, bermakna, dan selalu bersikap positif untuk memahami
dan menguasai matematika.
15
Suhendar, Perkembangan kurikulum dan Pembelajaran Matematika, ..., h. 8.13
16
Kompetensi-kompetensi tersebut dimulai dari kompetensi yang paling
dasar, yaitu pemahaman konsep. Oleh karena itu dalam pembelajaran
matematika perlu diberi penekanan pada pemahaman konsep yang baik dan
benar. Agar kompetensi-kompetensi tersebut dapat dicapai dengan baik,
maka dalam pembelajaran matematika perlu dilakukan belajar yang
bermakna. Teori Ausabel ( Suherman, 2003) dikenal dengan teori belajar
bermakna, pada belajar bermakna materi yang telah diperoleh
dikembangkan lagi dengan keadaan lain sehingga belajarnya dapat lebih
dimengerti. 17 Pengetahuan atau pengalaman baru yang di dapat siswa
berkaitan dengan pengetahuan lama yang sudah diketahui atau dialami
siswa sebelumnya.
3. Pemahaman Konsep Matematika
Pemahaman merupakan salah satu tolak ukur keberhasilan dalam
proses belajar mengajar. Proses pemahaman dapat terjadi ketika siswa sudah
melakukan tahap pengetahuan atau mengenal. Seperti yang dikatakan
Bloom (Hamalik, 2009), salah satu taksonomi tujuan pendidikan adalah
kompetensi kognitif yaitu pengetahuan, pemahaman, penerapan, analisis,
sintesis, dan evaluasi.18
Begitu banyak definisi pemahaman diantaranya: pemahaman
(Hamalik, 2009) adalah kemampuan untuk menguasai pengertian.
Pemahaman tampak pada alih bahan/perubahan-perubahan dari satu bentuk
ke bentuk lainnya, penafsiran dan memperkirakan, contoh: memahami fakta
dan prinsip, menafsirkan bahan lisan, menafsirkan bagan, menerjemahkan
bahan verbal ke rumus matematika.19 Sedangkan Menurut Bloom (Rosyada,
2004) pemahaman adalah kemampuan untuk memahami apa yang sedang
dikomunikasikan dan mampu mengimplementasikan ide tanpa harus
17
Erman Suherman, Strategi Pembelajaran Matematik Kontemporer,..., h. 32
18
Oemar Hamalik, Kurikulum dan Pembelajaran, (Jakarta: Bumi Aksara, 2009) cet. 9, Ed. 1, h. 79
19
mengaitkan dengan ide lain, dan juga tanpa harus melihat ide itu secara
mendalam.20
Supaya siswa memahami objek secara mendalam, siswa harus
benar-benar mengenal atau mengetahui objek itu sendiri dari sifat-sifat atau
perbedaan antara objek tersebut. Dengan demikian siswa dapat lebih mudah
untuk mengetahui relasi antara objek yang satu dengan yang lainnya.
Menurut Bloom pemahaman dapat dibedakan menjadi 3 kategori,
yaitu:21
1) Pengubahan (translation), kemampuan dalam memahami suatu objek yang dinyatakan dengan cara lain dari pernyataan asal yang dikenal
sebelumnya. Pada pembelajaran matematika pemahaman translation
berkaitan dengan kemampuan siswa menterjemahkan kalimat dalam soal
menjadi bentuk lain. Misalnya dapat menyebutkan variabel-variabel yang
diketahui dan ditanya.
2) Pemberian arti (interpretation), yaitu pemahaman yang berkaitan dengan kemampuan siswa dalam menentukan konsep-konsep yang tepat untuk
digunakan dalam menyelesaikan masalah. Misalnya dalam membedakan
relasi, fungsi, dan korespondensi satu-satu dalam diagram panah maka
konsep dasar yang harus dipahami siswa adalah definisi relasi, fungsi,
dan korespondensi satu-satu.
3) Pembuatan ekstrapolasi (extrapolation), yaitu pemahaman yang berkaitan dengan kemampuan siswa menerapkan konsep dalam perhitungan
matematis untuk menyelesaikan soal. Misalnya menentukan banyak
fungsi dengan anggota himpunan tidak dirincikan, maka langkah pertama
yang harus dilakukan adalah merincikan anggota himpunan,menentukan
banyak anggota, kemudian menentukan banyak fungsi.
20
Dede Rosyada, Paradigma Pendidikan Demokratis, (Jakarta: Kencana, 2004), cet.1, h. 69
21
Seorang guru dapat menguji siswanya untuk memahami sejauh mana
siswa sudah memahami suatu materi tes dengan memberikan tes yang
mengacu pada indikator-indikator yang ada dalam materi tersebut. Moore
(Rosayada, 2004) mengatakan insikator-indikator pemahaman adalah
menerjemah, mengubah, menggeneralisasi, menguraikan (dengan kata-kata
sendiri), menulis, meringkas, membedakan, mempertahankan,
menyimpulkan, berpendapat, dan menjelaskan.22
Berdasarkan beberapa pendapat di atas dapat disimpulkan pemahaman
adalah kemampuan siswa untuk dapat memahami suatu objek dengan
menyatakan suatu objek dengan cara lain, misalnya menggunakan gambar,
grafik, menjelaskan dengan kalimat sendiri serta siswa mampu
mengimplementasikan suatu objek ke dalam hal yang sesuai.
Selama proses belajar matematika kita harus memahami
konsep-konsep yang ada dalam matematika, sehingga kita dapat mempelajari
struktur-struktur atau hubungan-hubungannya. Konsep dalam matematika
(Ansyar, 2001) berasal dari peristiwa-peristiwa nyata.23 Contohnya
pemahaman konsep tentang bilangan. Awalnya untuk menggambarkan
bilangan dalam suatu lambang, manusia menggunakan benda-benda yang
ada disekitarnya, seperti batu, ranting, dll. Akhirnya manusia itu berpikir
untuk menggambarkan sebuah lambang bilangan, karena menurut mereka
cara yang mereka lakukan tidak praktis. Lambang untuk menulis sebuah
bilangan disebut angka, seperti angka dua dilambangkan dengan 2, dan
bangsa Cina Kuno menulis bilangan dengan membuat garis seperti batang.24
Setiap negara mempunyai lambang bilangan sendiri untuk menulisnya.
Konsep-konsep yang ada di matematika merupakan hasil buah pikiran
manusia terdahulu.
22
Dede Rosyada, Paradigma Pendidikan Demokratis, ...,h.140
23
Tim Penulis Pekerti Bidang MIPA, Hakikat Pembelajaran MIPA dan Kiat Pembelajaran Biologi di Perguruan Tinggi, (Jakarta: PAU-PPAI, 2001),h.7
24
Pengertian konsep adalah ide atau pengertian umum yang disusun
dengan kata, simbol, dan tanda.25 Sedangkan menurut Rosser (Sagala, 2009)
konsep adalah suatu abstraksi yang mewakili satu kelas objek-objek,
kejadian-kejadian, kegiatan-kegiatan, atau hubungan-hubungan yang
mempunyai atribut yang sama.26
Mempelajari konsep merupakan kemampuan untuk mengelompokkan
benda atau peristiwa yang mempunyai relasi. Konsep menunjuk pada
pemahaman dasar. Siswa dapat mengembangkan suatu konsep ketika
mereka mampu mengklasifikasikan benda-benda atau ketika mereka dapat
mengasosiasikan suatu nama dengan kelompok benda tertentu.
Konsep dalam matematika adalah ide abstrak yang memungkinkan
orang dapat mengklasifikasikan objek-objek atau peristiwa-peristiwa dan
menentukan apakah objek atau peristiwa itu merupakan contoh atau bukan
contoh dari ide abstrak tersebut, konsep dalam matematika dapat
diperkenalkan melalui definisi, gambar, model/ alat peraga. 27
Menurut Suherman ditinjau dari fungsinya, konsep dapat
dikelompokkan ke dalam 3 golongan yaitu: konsep klasifikasional, konsep
kolerasional, dan konsep teoritik:28
1) Konsep klasifikasional adalah mengklasifikasikan konsep-konsep. Siswa
mengkelompokkan suatu konsep ke dalam suatu peristiwa. Contoh:
mengklasifikasikan konsep segitiga, konsep trigonometri, dan konsep
logaritma.
2) Konsep kolerasional adalah menghubungkan konsep yang satu dengan
konsep yang lainnya dua atau lebih objek. Misalnya konsep luas persegi
panjang sebagai hasil kali dari panjang dan lebar.
25
Agus Suprijono, Cooperative Learning Teori dan Aplikasi Paikem,...,h. 9
26
Syaiful Sagala, Konsep dan Makna Pembelajaran,..., h. 73
27
Sri Anitah dan Janet Trineke Manoy, Strategi Pembelajaran Matematika, (Jakarta: UT, 2007), cet. 1, h. 7.6
28
3) Konsep teoretik adalah menjelaskan konsep berdasarkan fakta. Misalnya
konsep titik, bilangan dan himpunan.
Jadi, pengertian konsep adalah ide abstrak yang memunginkan siswa
dapat mengklasifikasikan objek ke dalam contoh atau bukan-contoh dan
menghubungkan ide abstrak tersebut ke dalam obyek atau peristiwa yang
memiliki relasi. Memahami sebuah konsep diperlukan belajar konsep yang
baik dan benar, agar siswa dapat menempatkan sebuah konsep dalam suatu
masalah atau peristiwa.
Belajar konsep adalah belajar memahami objek yang abstrak melalui
contoh, bukan contoh, serta sifat dan ciri-ciri objek tersebut. Agar belajar
konsep berlangsung optimal yaitu dipersiapkan supaya siswa sudah mampu
membedakan secara pasti suatu objek dengan objek lain.
Sejak tahun 1960-an belajar konsep mendapat perhatian istimewa.
Ada beberapa keuntungan dari hasil belajar konsep, yaitu:29
1) Mengurangi beban berat bagi memori, karena kemampuan manusia
dalam mengkategorisasi berbagai stimulus terbatas;
2) Konsep-konsep merupakan batu-batu pembangunan berpikir;
3) Konsep-konsep merupakan dasar untu proses mental yang lebih tinggi;
4) Konsep perlu untuk memecahkan masalah.
Penggunaan suatu konsep biasanya digunakan secara
berkesinambungan untuk menjelaskan suatu konsep yang lain dalam
matematika. Oleh karena itu siswa harus benar-benar dapat
mengklasifikasikan suatu konsep dalam suatu masalah, dan memahami
relasinya. Kesalahan konsep yang salah diterima oleh siswa berakibat fatal
untuk mempelajari konsep-konsep berikutnya yang terkaitan dengan konsep
tersebut.
Pada belajar konsep matematika, siswa tidak hanya mengetahui
perubahan suatu konsep tetapi siswa harus memahami pembentukan konsep
29
itu berlangsung. Seseorang dikatakan memahami suatu konsep matematika
bila telah mampu melakukan beberapa hal, yaitu:30
a. Menemukan kembali suatu konsep yang sebelumya diketahui
berlandaskan pada pengetahuan dan pengalaman yang tidak diketahui
dan dipahami sebelumnya;
b. Mendefinisikan atau mengungkapkan suatu konsep dengan cara kalimat
sendiri namun tetap memenuhi ketentuan berkenaan dengan ide atau
gagasan konsep tersebut;
c. Mengidentifikasi hal-hal yang relevan dengan suatu konsep dengan
cara-cara yang tepat;
d. Memberikan contoh dan bukan contoh atau ilustrasi yang berkaitan
dengan suatu konsep guna memperjelas konsep tersebut.
Berdasarkan uraian di atas dapat disimpulkan bahwa pemahaman
konsep matematika adalah kemampuan siswa untuk memahami suatu ide
matematika, mengaitkan suatu konsep dengan konsep lain, serta
menerapkan suatu konsep dalam memecahkan masalah. Pahamnya siswa
terhadap suatu konsep dapat dilihat dari indikator pemahaman konsep.
Misalnya siswa dapat memberikan contoh dan bukan contoh, menerapkan
konsep/ rumus dan menjelaskan kembali suatu konsep dengan kata-kata
sendiri.
4. Berbagai Metode Pembelajaran Matematika
Melakukan proses pembelajaran adalah aktivitas guru sehari-hari.
Seorang guru dalam melakukan pembelajaran harus menentukan metode
yang akan digunakan. Pemilihan metode pembelajaran harus disesuaikan
dengan materi pembelajaran yang akan diajarkan agar tujuan-tujuan dalam
pembelajaran tercapai.
Metode menurut Winarno Surakhmad adalah cara, yang di dalam
fungsinya merupakan alat untuk mencapai suatu tujuan. 31 Sehingga dengan
30Suhendar, Perkembangan kurikulum dan Pembelajaran Matematika, ..., h. 7.21
menggunakan metode kegiatan pembelajaran akan lebih terarah. Semakin
baik metode yang digunakan, makin efektif pula pencapaian tujuan.
Metode pembelajaran adalah cara menyajikan materi yang masih
bersifat umum, misalnya seorang guru menyajikan materi dengan
penyampaian secara lisan atau disebut dengan metode ceramah. Seorang
guru matematika dalam pembelajaran pasti menjelaskan suatu konsep secara
detail, karena tanpa guru menjelaskan siswa akan kesulitan untuk
memahaminya. Namun, sebaiknya guru juga melibatkan siswa dalam
mengkonstruksi pengetahuan dengan pola pikir mereka. Sehingga guru tidak
perlu lagi menjelaskan secara panjang lebar. Oleh karena itu guru
matematika juga harus mempunyai variasi metode mengajar lain sehingga
siswa tidak terasa jenuh dalam proses pembelajaran. Berikut ini adalah
contoh metode-metode pembelajaran kooperatif yang dapat digunakan
dalam pembelajaran matematika:32
1) Think Pair Share, metode ini termasuk metode pembelajaran kooperatif. Langkah-langkahnya guru menyajikan materi, berikan
persoalan kepada siswa dan siswa bekerja kelompok dengan cara
berpasangan sebangku-sebangku (think-pairs), dan presentasi kelompok (share)
2) STAD (Student Teams Achievement Division), kegiatan pembelajaran STAD adalah guru menyampaikan materi, kemudian para siswa
bergabung dalam kelompoknya yang terdiri dari 4-5 orang untuk
memastikan bahwa seluruh anggota tim telah menguasai materi
tersebut. Selanjutnya guru memberikan kuis, dalam mengerjakan kuis
siswa dilarang kerja sama satu sama lainnya, guru memberikan reward
kepada kelompok yang mendapatkan skor tertinggi.
3) TTW (Think Talk Write), pembelajaran ini dimulai dengan berpikir melalui bahan bacaan, hasil bacaanya dikomunikasikan dengan
presentasi, dan kemudian buat laporan hasil presentasi.
32
Metode-metode tersebut dapat melibatkan siswa menjadi aktif dan
siswa dapat mengeksplor kemampuan yang mereka miliki. Supaya siswa
aktif, gembira, dan senang dalam belajar matematika, hendaknya seorang
guru berperan sebagai fasilitator dan siswa sebagai pusat belajar (centered learning).
Setiap metode tidak dapat berdiri sendiri tanpa terlibatya metode lain.
Misalnya pada metode STAD terlibat metode ceramah, diskusi.
Masing-masing metode mempunyai kelemahan dan keunggulan. Pemilihan variasi
metode mengajar yang tepat dapat lebih meningkatkan hasil proses belajar
mengajar.
5. Metode SQ3R
Ada beberapa metode membaca yang telah dikembangkan dan
diterapkan dalam berbagai penelitian, salah satunya adalah metode SQ3R.
Metode SQ3R adalah metode memabaca untuk memahami bahan
ajar/materi, soal-soal cerita, dan lain-lain. Metode SQ3R telah banyak
terbukti bahwa dengan metode SQ3R dapat meningkatkan memahami
bacaan baik itu materi pelajaran, cerita, novel.
Metode SQ3R dikembangkan oleh Francis P. Robinson pada tahun
1946 di Universitas Ohio Amerika Serikat.33 Metode SQ3R dapat
digunakan dalam pembelajaran untuk membantu memahami materi, seperti
di perguruan tinggi ataupun sekolah-sekolah. Dahulu metode SQ3R
digunakan sebagai sistem belajar untuk mahasiswa di perguruan tinggi
tetapi metode ini juga cocok untuk alat belajar siswa, karena metode ini
mudah diadaptasikan untuk teks cerita nyata yang lebih sederhana.34
Metode ini dirancang untuk membantu siswa memahami materi yang
digunakan beberapa tahap untuk membimbing siswa selama membaca dan
belajar. Langkah-langkah metode SQ3R disusun secara sistematis dan
bertahap hingga memudahkan siswa untuk memahami materi.
33
Muhibbin Syah, Psikologi Pendidikan dengan Pendekatan Baru,....h.128
34
langkah pada metode SQ3R yaitu Survey, Question, Read, Recite, dan Review.35
Pada proses belajar, ada beberapa siswa yang mengalami kesulitan
dalam memahami definisi, cerita, atau bacaan lainya, sehingga mereka
terhambat untuk mendapatkan informasi dari apa yang dibacanya. Tidak
jarang untuk memahami suatu bacaan kita membaca lebih dari satu kali.
Faktor-faktor yang mempengaruhi siswa dalam membaca dapat
dipengaruhi karena kondisi lingkungan keluarga, sekolah, tingkat materi
pelajaran, dan minat membaca.
Metode SQ3R dikenal untuk mempelajari suatu bacaan pada mata
pelajaran yang banyak mengandung bacaan, seperti mata pelajaran
geografi, sejarah, bahasa inggris. Padahal setelah dilakukan beberapa
penelitian, metode SQ3R juga dapat diterapkan pada pelajaran eksakta
seperti fisika, matematika, kimia, dan biologi. Penerapan pada pelajaran
eksakta sama halnya dengan pelajaran yang bukan eksakta. Seperti yang
dikatakan oleh Sagala (2009) metode SQ3R dapat digunakan untuk mata
pelajaran apa saja.36
Pada penerapan metode SQ3R siswa tidak sekedar menghafal dan
mengulang tanpa pemahaman makna, tetapi juga dapat melibatkan siswa
pada proses berpikir dan mencari pemahaman makna dari informasi yang
sedang dipelajari. Untuk memperoleh pemahaman dari informasi yang
dipelajari, siswa harus terampil membaca materi yang disajikan guru.
Adapun langkah-langkah metode SQ3R yaitu:
1) Survey
Survey adalah aktivitas siswa untuk mengamati atau
mengidentifikasi seluruh teks dari segi judul, subjudul, kata-kata yang
bercetak miring, kata-kata yang dibold atau kata-kata yang dianggap
penting. Pada aktivitas survey ini guru membantu dan mendorong siswa
35
Soedarso, Speed Reading Sistem Membaca Cepat dan Aktif, (Jakarta: Garamedia Pustaka, 2004), h. 59
36
untuk memeriksa dan meneliti secara singkat seluruh teks yang dibaca.
Survey ini dilakukan hanya beberapa menit. Pada langkah survey,
siswa dianjurkan menyiapkan pensil, kertas, stabilo untuk menandai
bagian-bagian tertentu. Bagian-bagaian tertentu ini akan dijadikan dan
mempermudah menyusun bahan pertanyaan pada langkah berikutnya.
2) Question
Question adalah aktivitas siswa untuk menyusun
pertanyaan-pertanyaan yang relevan dengan teks. Pada langkah ini guru
memberikan petunjuk atau contoh kepada siswa untuk membuat
pertayaan-pertanyaan yang jelas, singkat, dan relevan, misalnya dengan
menggunakan kata tanya apa, bagaimana, mengapa, kapan, dimana,
siapa, dll. Misalnya, jika judul bacaan itu relasi dan cara penyajian
relasi, pertanyaan yang bisa muncul adalah apakah yang dimaksud dengan relasi? atau bagaimanakah cara penyajian relasi? Jumlah pertanyaan bergantung pada panjang-pendeknya teks dan kemampuan
siswa dalam memahami teks.
3) Read
Read adalah aktivitas membaca teks secara aktif. Aktivitas ini
dilakukan untuk mencari ide pokok dan jawaban atas
pertanyaan-pertanyaan yang telah dibuat pada langkah kedua. Tandailah kata kunci
dengan menggaris bawahi, memberikan warna, atau membuat catatan
dipinggir halaman.
4) Recite
Recite adalah aktivitas menjawab setiap jawaban yang telah
ditemukan. Pada langkah ini siswa menyebutkan jawaban atas
pertanyaan-pertanyaan yang telah disusun. Siswa harus merubah
informasi yang telah dibaca dengan menggunakan kata-kata sendiri dan
mengatakannya dengan lantang. Pada langkah ini siswa dilatih untuk
tidak membuka catatan jawaban. Jika sebuah pertanyaan tidak terjawab,
siswa tetap menjawab pertanyaan berikutnya hingga seluruh pertanyaan
mendemonstrasikan pemahaman tentang materi ajar yang sedang
dipelajari.
5) Review
Review adalah aktivitas siswa untuk meninjau ulang seluruh
pertanyaan dan jawaban secara singkat. Siswa membaca kembali bagian
materi untuk mengkonfirmasi jawaban-jawaban sebelumnya. Aktivitas
review digunakan untuk memastikan siswa menangkap informasi dan
memahami ide pokok dari bahan bacaan yang diberikan. Pada aktivitas
review ini, guru bisa memberikan quis untuk menguji pemahaman
siswa pada materi yang diajarkan.
Metode SQ3R dapat mendorong siswa untuk lebih memahami buku
teks yang mereka pelajari dan lebih terarah pada intisari yang terdapat
dalam buku teks. Selain itu, tahapan-tahapan yang sistematis pada metode
SQ3R membuat siswa untuk aktif dalam proses berpikir. Sehingga
diharapkan setiap informasi yang dipelajari dapat tersimpan dengan baik
dalam sistem memori jangka panjang siswa. Menurut Soedarso usaha yang
efektif untuk memahami dan mengingat lebih lama dapat dilakukan
dengan (1) mengorganisasikan bahan yang dibaca dalam kaitan yang
mudah dipahami, (2) mengaitkan fakta yang satu dengan yang lain atau
dengan menghubungkan pengalaman atau konteks yang anda hadapi.37
Para siswa mengaplikasikan metode ini dengan bimbingan dan
bantuan guru dan melatihnya dalam bentuk kelompok atau berpasangan.38
Pembentukan kelompok atau berpasangan berguna agar siswa dapat
mendiskusikan suatu konsep dengan teman-teman
Ada beberapa keuntungan menerapkan metode SQ3R dalam proses
pembelajaran, yaitu:39
37
1) Pendekatan tugas melalui membaca teks dapat membuat siswa lebih
percaya diri
2) Membantu konsentrasi siswa
3) Metode ini bisa membantu siswa untuk memfokuskan bagian-bagian
yang tersulit dalam membaca, bila sebuah pertanyaan tidak dapat
dijawab atau tidak dimengerti, siswa bisa mengidentifikasi kesulitannya
dan mendapatkan jawabannya.
4) Melatih memberikan jawaban dalam pertanyaan tentang materi
5) Membantu mempersiapkan catatan dalam bentuk tanya jawab
Metode SQ3R dalam pembelajaran matematika dapat digunakan
untuk membaca materi matematika dan membaca soal matematika. Suatu
hal yang harus diperhatikan untuk memiliki keterampilan membaca
matematika dengan baik, yaitu siswa harus memahami hakikat matematika
seperti simbol-simbol matematika dan istilah-istilah matematika. Begitu
pula saat menemukan tabel, bagan, diagram-diagram atau contoh-contoh
siswa harus secara utuh menangkap maksudya. Keterampilan dalam
membaca matematika dapat digolongkan menjadi dua jenis yaitu:40
1) Keterampilan membaca matematika yang tingkat rendah (low order mathematical doing). Contohnya: membaca teks yang memuat operasi sederhana, menerapkan rumus matematika secara langsung, mengikuti
prosedur algoritma yang baku.
2) Keterampilan membaca matematika yang tingkat tinggi (high order mathematical doing). Contohnya: membaca matematika yang memuat kemampuan memahami ide matematik secara mendalam, mengamati
data dan menggali teks yang tersirat, menyusun konjektur, analogi dan
generalisasi, menalar secara logik, menyelesaikan masalah,
berkomunikasi secara matematik dan mengkait ide matematik dengan
kegiatan intelektual lainnya tergolong pada cara berpikir tingkat tinggi.
40
Berdasarkan pendapat-pendapat diatas, metode SQ3R mampu
meningkatkan pemahaman siswa tehadap materi ajar. Adapaun
langkah-langkah metode SQ3R dapat disimpulkan melalui tabel di bawah ini:
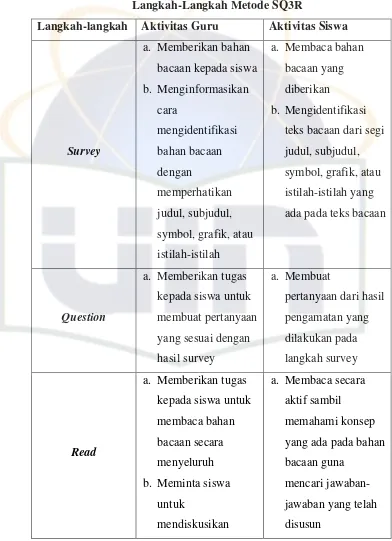
Tabel 1
Langkah-Langkah Metode SQ3R
Langkah-langkah Aktivitas Guru Aktivitas Siswa
Contoh Penerapan Metode SQ3R dalam Pembelajaran Matematika
Langkah-langkah membaca menggunakan metode SQ3R
1) Langkah pertama : Survey/mengamati bacaan
a. Materi Bacaan : Relasi
b. Judul Bacaan : Relasi
c. Subjudul Bacaan : Pengertian Relasi
d. Kata Kunci : Relasi dan Himpunan
2) Langkah kedua : Question/membuat pertanyaan
a. apakah yang dimaksud dengan relasi?
b. apakah yang dimaksud dengan himpunan?
3) Langkah ketiga : Read/membaca keseluruhan teks dengan teliti
4) Langkah keempat : Recite/menjawab pertanyaan
a. relasi adalah adanya hubungan antara himpunan A dengan himpunan B
b. himpunan adalah kumpulan anggota-anggota yang sejenis
Relasi 1. Pengertian Relasi
Banyak kasus di dalam kehidupan yang sering kita jumpai adanya
hubungan (relasi) antara himpunan yang satu dengan himpunan lainnya.
Hubungan tersebut disebut relasi. Untuk memahami pengertian relasi,
perhatikan uraian berikut:
Suatu kumpulan anak Tino, Ayu, Togar, dan Nia ditanya ibu guru tentang
jenis minuman yang mereka sukai. Ternyata Tino dan Ayu suka minum teh,
Ayu dan Togar suka minum susu, Togar dan Nia suka minum kopi.
Berdasarkan keterangan di atas dapat dibentuk 2 himpunan, yaitu:
Himpunan anak, A = {Tino, Ayu, Togar, Nia}
Himpunan jenis minuman yang disukai, B = {Teh, susu, kopi}.
Berdasarkan uraian di atas dapat disimpulkan sebagai berikut:
5) Langkah kelima : Review/ meninjau ulang
Catatan bermakna :
Relasi adalah hubungan antara himpunan A dengan himpunan B dan
himpunan A boleh lebih dari satu mempunyai hubungan dengan
himpunan B.
6. Metode Pembelajaran Konvensional
Pembelajaran konvensional adalah pembelajaran yang sering
dilakukan guru dengan langkah-langkah sebagai berikut:
1. Guru memberikan penjelasan materi
2. Guru memberikan contoh dan penyelesaiannya
3. Guru melakukan tanya jawab tentang materi yang mereka pelajari
4. Siswa menyimak, mencatat, dan mengerjakan tugas-tugas serta
ulangan yang diberikan guru.
Pada pembelajaran konvensional mengakibatkan siswa menjadi pasif
atau kurang mengembangkan kemampuan-kemampuan yang mereka
miliki. Pembelajaran konvensional yang diutamakan adalah hasil bukan
proses.
Metode mengajar yang lebih banyak digunakan guru dalam
pembelajaran konvensional adalah metode ekspositori. Menurut Suherman
(2003) metode ekspositori sama seperti metode ceramah tetapi pada
metode ini dominasi guru banyak berkurang, karena tidak terus menerus
bicara, guru berbicara pada awal pelajaran, menerangkan materi,
memberikan contoh soal, serta pada waktu yang diperlukan saja.41 Metode
ekspositori adalah metode pembelajaran konvensional yang terdiri dari
metode ceramah, tanya jawab, drill dan metode lainnya yang dapat
digabungkan dalam pembelajaran di kelas.
41
Ada beberapa langkah –langkah pembelajaran dengan metode ekspositori, yaitu:42
1) Persiapan (preparation)
Tahap persiapan berkaitan dengan mempersiapkan siswa untuk
menerima pelajaran.
2) Penyajian (presetation)
Langkah penyajian adalah langkah penyampaian materi sesuai dengan
persiapan yang telah dilakukan.
3) Menghubungkan (correlation)
Langkah korelasi adalah langkah menghubungkan materi pelajaran
dengan pengalaman siswa atau dengan hal-hal lain yang
memungkinkan siswa dapat menangkap keterkaitannya dalam struktur
pengetahuan yang dimilikinya.
4) Menyimpulkan (generalization)
Menyimpulkan adalah untuk memahami inti dari materi pelajaran yang
telah disajikan.
5) Penerapan (aplication)
Langkah aplikasi adalah langkah unjuk kemampuan siswa setelah
mereka menyimak penjelasan guru.
Metode ekspositori sering kali digunakan guru matematika dalam
proses pembelajaran. Metode ekspositori menempatkan guru sebagai pusat
pengajaran, karena guru lebih aktif memberikan informasi, menerangkan
suatu konsep, mendemonstrasikan keterampilan dalam memperoleh
konsep, serta memberikan contoh soal beserta penyelesaiannya.
Sedangkan siswa hanya menerima saja informasi yang diberikan oleh
guru. Pengajaran telah disiapkan oleh guru sehingga siap disampaikan
kepada siswa, dan siswa diharapkan belajar dari informasi yang
diterimanya. Berikut ini adalah perbandingan antara metode SQ3R dengan
metode konvensional:
42
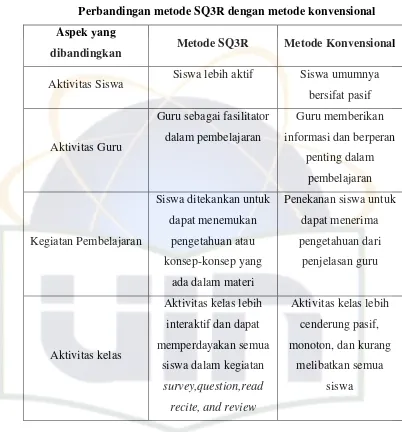
Tabel 2
Perbandingan metode SQ3R dengan metode konvensional Aspek yang
dibandingkan Metode SQ3R Metode Konvensional
Aktivitas Siswa Siswa lebih aktif Siswa umumnya
bersifat pasif
B.Hasil Penelitian yang Relevan
Penelitian yang dilakukan didukung oleh beberapa hasil penelitian
sebelumnya dan menunjukkan bahwa metode SQ3R dapat meningkatkan hasil
yang lebih baik dalam proses belajar mengajar, diantaranya:
1) Penelitian Sudrajat (2002) yang berjudul “Pengaruh Penerapan Model
Pembelajaran SQ3R terhadap Kemampuan Komunikasi Siswa dalam