Upaya Penerapan Strategi Mathematical Habits of Mind
Terhadap Kemampuan Berpikir Kreatif Matematis Siswa
SKRIPSI
OLEH :
ANGGIA ISTI PRASETYANI
NIM : 107017002995
JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS ILMU TARBIYAH DAN KEGURUAN
UNIVERSITAS ISLAM NEGERI JAKARTA
SURAT PERNYATAAN KARYA ILMIAH
Yang bertanda tangan di bawah ini:
Nama : ANGGIA ISTI PRASETYANI
NIM : 107017002995
Jurusan : Pendidikan Matematika
Angkatan Tahun : 2007
Alamat : Jl. Salak III No. 106 Rt. 03 Rw. 09 Kel. Abadijaya Kec.
Sukmajaya Depok Timur 16417
MENYATAKAN DENGAN SESUNGGUHNYA
Bahwa skripsi yang berjudul Upaya Penerapan Strategi Mathematical habits of Mind Terhadap Kemampuan Berpikir Kreatif Matematis Siswa adalah benar hasil karya sendiri di bawah bimbingan dosen:
1. Nama : Dr. Kadir, M.Pd
NIP : 19670812 199402 1 00 1
Dosen Jurusan : Pendidikan Matematika
2. Nama : Najmi Ulya, M.Pd
NIP :19670623 199703 2 00 1
Dosen Jurusan : Pendidikan Matematika
Demikian surat pernyataan ini saya buat dengan sesungguhnya dan saya siap
menerima segala konsekuensi apabila terbukti bahwa skripsi ini bukan hasil karya
sendiri.
Jakarta, Juli 2014
Yang Menyatakan,
Anggia Isti Prasetyani
i ABSTRAK
Anggia Isti Prasetyani (107017002995), Upaya Penerapan Strategi
Mathematical Habits of Mind (MHM) terhadap Kemampuan Berpikir Kreatif Matematis Siswa. (Penelitian Tindakan Kelas di SMP YAPPA Yayasan Pondok Pesantren AR Roudhoh Depok), Skripsi Jurusan Pendidikan Matematika Fakultas Ilmu Tarbiyah dan Keguruan UIN Syarif Hidayatullah Jakarta, 2014.
Penelitian ini bertujuan untuk menganalisis: (1) penerapan strategi MHM dalam meningkatkan kemampuan berpikir kreatif matematis, (2) aktivitas siswa dalam kemampuan berpikir kreatif matematis dengan penerapan strategi MHM, dan (3) respon siswa selama penerapan strategi MHM. Penelitian dilakukan di SMP YAPPA Yayasan Pondok Pesantren AR Roudhoh Depok tahun pelajaran 2012/2013. Metode penelitian yang digunakan adalah Penelitian Tindakan Kelas (PTK) yang dilaksanakan dalam dua siklus. Instrumen penelitian yang digunakan adalah lembar observasi aktivitas belajar siswa, jurnal harian siswa, pedoman wawancara, tes kemampuan berpikir kreatif matematis, dan dokumentasi.
Hasil penelitian mengungkapkan bahwa penerapan strategi MHM Mathematical Habits of Mind mencapai kemampuan berpikir kreatif matematis siswa dengan perolehan nilai rata-rata sebesar 64 pada siklus I meningkat menjadi 73,3 pada siklus II. Selanjutnya rata-rata persentase aktivitas belajar siswa dalam pembelajaran dengan strategi Mathematical Habits of Mind (MHM) mencapai 64,65% pada siklus I meningkat menjadi 75,68% pada siklus II aktivitas belajar siswa tersebut meliputi oral activities, writing activities, drawing activities, dan visual activities. Selain itu juga diperoleh respon siswa terhadap strategi pembelajaran Mathematical Habits of Mind (MHM) mencapai 63,75% pada siklus I menjadi 80,625% pada siklus II. Kesimpulan penelitian ini adalah bahwa penerapan strategi Mathematical Habits of Mind (MHM) dapat meningkatkan kemampuan berpikir kreatif matematis siswa.
ii ABSTRACT
Anggia Isti Prasetyani (107017002995), “Improving Students’ Mathematical Creative Thinking Activities Through Mathematical Habits of Mind (MHM) strategy Approach” (A Classroom Action Research at State Junior High School YAPPA Yayasan Pondok Pesantren AR Roudhoh Depok), Skripsi of Mathematic Education at Faculty of Tarbiyah and Teachers Training of State Islamic University Syarif Hidayatullah Jakarta, 2014.
This research is aimed for analyzing: 1) the implementation of MHM strategy in improving students’ the creative thinking ability, 2) students’ the creative thinking ability activities in implementing MHM, 3) students’ responses during the implementation of MHM. This research was held at State Junior High School YAPPA (Yayasan Pondok Pesantren AR Roudhoh) Depok in period 2012/2013. The strategy which was used in this research is action research which was done in two cycles. Meanwhile, the instruments of the research are observation, questioner, interview guidance, test, and documentation.
The finding of the research is the implementation of Mathematical Habits of Mind (MHM) strategy can improve the students’ mathematical creative thinking activities. The ability of mathematical creative thinking in cycle 1 which was only 64 had improved up to 73.3 in cycle 2.
In cycle 1, the average percentage of students’ mathematical creative thinking learning activities is 64.65% then it was increasing in cycle 2 up to 75.68%. Not only the percentage was increasing but also the students’ activity was improved in oral activities, writing activities, drawing activities, and visual activities. Besides learning activities, creative thinking stage, students’ responses, and the ability of students’ mathematical creative thinking showed enhancement, the average percentage of creative thinking in cycle 1 achieved 63.75% then it increased up to 80.625% in cycle 2. So, This research is the implementation of MHM strategy in improving students’ was increasing the creative thinking ability.
vi
G. Teknik Pengumpulan Data... 42
H. Instrumen penelitian ... 42
I. Hasil intervensi yang diharapkan ... 44
J. Teknik pemeriksaan kepercayaan ... 44
K. Analisis data ... 45
L. Pengembangan perencanaan tindakan ... 45
BAB IV DESKRIPSI, ANALISIS DATA, DAN PEMBAHASAN ... 47
A. Deskripsi Data ... 47
1. Observasi Pendahuluan ... 47
2. Tindakan Pembelajaran Siklus I ... 50
3. Tindakan Pembelajaran Siklus II ... 73
B. Analisis Data ... 95
1. Analisis Hasil Observasi ... 95
2. Analisis Hasil Tanggapan Siswa terhadap Penerapan Strategi MHM ... 98
3. Analisis Hasil Kemampuan Berpikir Kreatif Matematis...99
C. Intrepretasi Hasil Analisis ... 100
D. Pembahasan... 102
BAB V KESIMPULAN DAN SARAN ... 115
A. Kesimpulan ... 105
B. Saran ... 106
vii
DAFTAR TABEL
Tabel 2.1: Indikator Kemampuan Berpikir Kreatif ... 24
Tabel 2.2: Indikator Kemampuan Berpikir Kreatif yang Diteliti ... 28
Tabel 4.1: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan I ... 55
Tabel 4.2: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan II ... 58
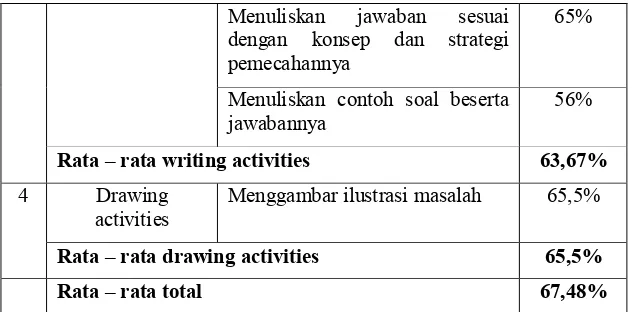
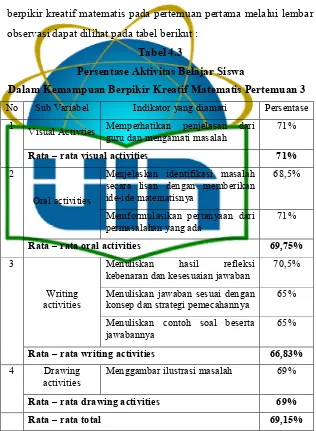
Tabel 4.3: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan III ... 61
Tabel 4.4: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan IV ... 63
Tabel 4.5: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis pada Pembelajaran Siklus I ... 65
Tabel 4.6: Persentase Indikator Kemampuan Berpikir Kreatif Matematis Siswa pada Pembelajaran Matematika Siklus I ... 70
Tabel 4.7: Tanggapan Siswa terhadap Pembelajaran siklus I ... 71
Tabel 4.8: Hasil Kemampuan Berpikir Kreatif Matematis Siklus I ... 73
Tabel 4.9: Refleksi Tindakan Siklus I... 75
Tabel 4.10: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan VI ... 81
Tabel 4.11: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan VII ... 84
Tabel 4.12: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan VIII ... 87
Tabel 4.13: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis Pertemuan IX ... 90
Tabel 4.14: Persentase Aktivitas Belajar Siswa dalam Kemampuan Berpikir Kreatif Matematis pada Pembelajaran Siklus II ... 92
viii
Tabel 4.16: Tanggapan Siswa terhadap Pembelajaran siklus II ... 96
Tabel 4.17: Hasil Kemampuan Berpikir Kreatif Matematis Siklus II ... 97
Tabel 4.18: Persentase Peningkatan Aktivitas Belajar Siswa dalam Kemampuan
Berpikir Kreatif Matematis Siklus I dan Siklus II ... 100
Tabel 4.19: Persentase Skor Indikator Kemampuan Berpikir Kreatif Matematis
Siswa pada Pembelajaran Matematika Siklus I dan Siklus II 101
Tabel 4.20: Persentase Respon Siswa terhadap Pembelajaran Matematika
Dengan srtategi MHM pada siklus I dan siklus II ... 103
Tabel 4.21: Statistik Deskriptif Peningkatan Kemampuan Berpikir Kreatif
ix
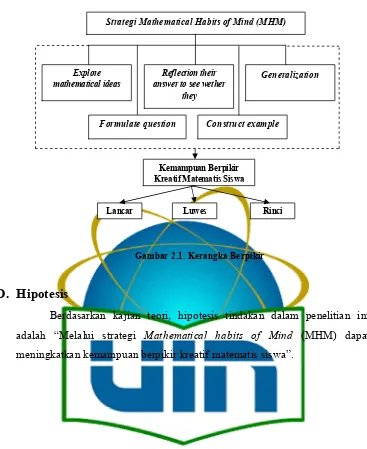
DAFTAR GAMBAR
Gambar 2.1: Kerangka Berpikir ... 35
Gambar 3.1: Desain Penelitian Tindakan Kelas ... 39
Gambar 3.2: Tahap Intervensi Tindakan ... 43
Gambar 4.1: Aktivitas siswa saat belajar dengan metode tutor sebaya .... 74
Gambar 4.2: Aktivitas siswa saat mengerjakan ujian tes Kemampuan
Berpikir Kreatif Matematis siklus I... 74
Gambar 4.3: Aktivitas siswa saat mengerjakan soal di papan tulis ... 75
Gambar 4.4: Aktivitas siswa saat mengerjakan ujian tes Kemampuan
Berpikir Kreatif Matematis siklus II ... 91
x
DAFTAR DIAGRAM
Diagram 4.1: Persentase Aktivitas Belajar dalam Berpikir Kreatif Matematis
Siklus I dan Siklus II ... 101
Diagram 4.2: Persentase Skor Indikator Kemampuan Berpikir Kreatif Matematis
Siklus I dan Siklus II ... 102
Diagram 4.3: Persentase Skor Respon Siswa terhadap strategi MHM .... 103
Diagram 4.4: Persentase Skor Kemampuan Berpikir Kreatif Matematis
xi
DAFTAR LAMPIRAN
Lampiran 1: Rancangan Pelaksanaan Pembelajaran ... 116
Lampiran 2: Lembar Kerja Siswa... 146
Lampiran 3: Pedoman Penskoran Kemampuan Berpikir Kreatif Matematis Siswa ... 169
Lampiran 4: Instrumen soal Tes Kemampuan Berpikir Kreatif Matematis Siswa Siklus I dan II ... 170
Lampiran 5: Lembar Tes Kemampuan Berpikir Kreatif Matematis Siswa Siklus I ... 178
Lampiran 6: Lembar Tes Kemampuan Berpikir Kreatif Matematis Siswa Siklus II ... 180
Lampiran 7: Lembar Observasi Aktivitas Siswa Siklus I dan II ... 182
Lampiran 8: Lembar Jurnal Harian Siswa ... 198
Lampiran 9: Lembar Pedoman Wawancara Guru ... 199
Lampiran 10: Lembar Pedoman Wawancara Siswa ... 201
Lampiran 11: Lembar Observasi Guru ... 203
Lampiran 12: Hasil Kemampuan Berpikir Kreatif Matematis Siswa Siklus I dan II ... 204
Lampiran 13: Perhitungan persentase aktivitas belajar siswa berdasarkan Kemampuan Berpikir Kreatif Matematis ... 206
Lampiran 14: Daftar Distribusi Frekuensi Kemampuan Berpikir Kreatif Matematis Siklus I ... 209
Lampiran 15: Daftar Distribusi Frekuensi Kemampuan Berpikir Kreatif Matematis Siklus II ... 211
Lampiran 16: Penghitungan Uji validitas, Reliabilitas, Taraf Kesukaran dan Daya Pembeda ... 213
Lampiran 17: Uji Validitas ... 215
Lampiran 18: Daya Pembeda ... 217
Lampiran 19: Taraf Kesukaran ... 219
xii
Lampiran 21: Hasil Tanggapan Siswa ... 223
Lampiran 22: Jawaban Tes Kemampuan Berpikir Kreatif
Matematis Siklus I ... 224
Lampiran 23: Jawaban Tes Kemampuan Berpikir Kreatif
Matematis Siklus II ... 226
Lampiran 24: Hasil Wawancara dengan Guru ... 229
1 BAB I PENDAHULUAN
A. Latar Belakang Masalah
Dewasa ini kemajuan IPTEK di berbagai Negara menjadi perbincangan
yang hangat. Di Negara berkembang seperti Indonesia perkembangan IPTEK
sudah mendapat perhatian dan dikembangkan. Ilmu pengetahuan sangat
dibutuhkan setiap manusia sebagai petunjuk dalam kehidupan. Melalui
pendidikan manusia memperoleh ilmu pengetahuan dan pengalaman.
Pendidikan merupakan suatu wadah dimana manusia mendapatkan hak untuk
mendapat pengajaran. Sesuai dengan program pemerintah yang
menganjurkan warga Indonesia mendapatkan pendidikan “wajar” (wajib
belajar) sembilan tahun. Dengan meningkatnya pendidikan di Indonesia,
diharapkan dapat menjadi Negara yang maju di segala aspek.
Dalam pendidikan, kegiatan belajar mengajar menjadi hal yang utama
dilakukan. Belajar adalah kegiatan yang berproses dan merupakan unsur yang
sangat fundamental dalam penyelenggaraan setiap jenis dan jenjang
penidikan.1 Untuk mewujudkan suatu tujuan pendidikan sangat berpengaru pada proses kegiatan anak saat belajar. Proses pembelajaran tidak melulu di
sekolah melainkan dapat terjadi di lingkungan keluarga ataupun linkungan
sosial lainnya. Setiap manusia berhak mendapat pendidikan yang layak hal ini
juga sesuai dengan isi dari UUD 1945 pasal 31 ayat 1. “ Tiap-tiap warga
negara berhak mendapatkan pengajaran”. 2
Proses pembelajaran di sekolah yang melibatkan peran guru sebagai
pendidik sangat berpengaruh pada anak didik. Untuk itu, kemampuan berpikir
kritis, kreatif, logis, dan sistematis harus diajarkan kepada siswa demi meningkatkan SDM Indonesia yang berkompeten.
1
Muhibin Syah, Psikologi Pendidikan dengan pendekata baru, (Bandung: PT. Remaja Rosdakaya Offset, 2010), hal. 87.
2
2
Kemampuan ini dapat dikembangkan melalui kegiatan pembelajaran
matematika karena tujuan pembelajaran matematika di sekolah menurut
Depdiknas (2004) adalah: (1) melatih cara berpikir dan bernalar dalam menarik
kesimpulan, (2) mengembangkan aktivitas kreatif yang melibatkan imajinasi,
intuisi, dan penemuan dengan mengembangkan pemikiran divergen, orisinil,
rasa ingin tahu, membuat prediksi dan dugaan, serta mencoba-coba, (3)
mengembangkan kemampuan memecahkan masalah, dan (4) mengembangkan
kemampuan menyampaikan informasi dan mengkomunikasikan gagasan.3 Salah satu target mempelajari matematika adalah mengembangkan kemampuan
siswa dalam berpikir matematis. Dengan belajar matematika diharapkan dapat
membantu untuk memajukan IPTEK dengan menciptakan sumber daya
manusia yang berkualitas.
Dalam kehidupannya, tiap individu senantiasa menghadapi masalah,
dalam skala sempit maupun luas, sederhana maupun kompleks. Kesuksesan
individu antara lain ditentukan oleh kreativitasnya dalam menyelesaikan
masalah. Individu kreatif memiliki beberapa karakteristik yang berbeda dengan
individu biasa. Individu kreatif memandang masalah sebagai tantangan yang
harus dihadapi, bukan dihindari. Individu kreatif juga memandang masalah dari
berbagai perspektif yang memungkinkannya memperoleh berbagai alternatif solusi.4
Pentingnya seorang siswa dalam mengembangkan kemampuan
kreativitasnya dalam penddikan diperkuat oleh UU SISDIKNAS No. 20 Tahun
2003 bab III pasal 4, sebagai berikut : “Pendidikan diselenggarakan dengan
3
Tatang Herman, 2007, Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan
Berpikir Matematis Tingkat Tinggi Siswa Sekolah Menengah Pertama, EDUCATIONIST No. I
Vol. I 4
Mahmudi, Ali.”Pengaruh strategi mhm berbasis masalah terhadap kemampuan berpikir kreatif
3
memberi keteladanan, membangun kemauan, dan mengembangkan kreativitas
peserta didik dalam proses pembelajaran”.5
Walaupun telah adanya pernyataan yang menjelaskan tentang pentingnya
mengembangkan kreativitas dalam pendidikan, tetapi masih saja ada siswa
tidak menyukai belajar matematika, karena mereka memandang matematika
sebagai mata pelajaran yang paling sulit diantara pelajaran lainnya. Padahal
bukan karena sulitnya pelajaran ini, namun pada saat menerima pelajaran ini
penerapan kebiasaan berpikir kreatif belum maksimal dilakukan. Faktor
lainnya bisa berasal dari faktor guru dan juga faktor siswa itu sendiri.
Untuk menciptakan siswa yang memiliki hasil belajar yang baik tentunya
membutuhkan pengajaran yang baik. Di SMP YAPPA Yayasan Pondok
Pesantren AR Roudhoh Depok, guru cenderung masih senang menyampaikan
materi pelajaran dengan memberikan pengetahuan hanya berdasarkan
informasi yang terdapat pada buku pelajaran yang disampaikan oleh guru saja
atau biasa dikenal dengan metode ceramah. Menurut Slavin, guru yang
intensional atau guru yang memiliki tujuan adalah orang yang terus-menerus
memikirkan hasil yang mereka inginkan bagi siswanya dan bagaimana tiap-tiap
keputusan yang mereka ambil membawa siswa ke arah hasil tersebut.6
Berdasarkan hasil observasi proses belajar mengajar yang dilakukan di
SMP YAPPA (Yayasan Pondok Pesantren AR Roudhoh) Depok, peneliti
memperoleh keterangan bahwa aktivitas belajar siswa kelas VIII-1 pada saat
pembelajaran matematika masih kurang maksimal. Hal ini terlihat dari rasa
ingin tahu siswa terhadap materi yang disampaikan guru masih sangat rendah.
Pada saat menyelesaikan soal yang diberikan guru pun, siswa cenderung
mengabaikan proses penyelesaiannya secara sistematis. Di sekolah pun, siswa
tidak dibiasakan untuk melakukan habits of mind (kebiasaan berpikir). Selain itu, guru jarang memberikan soal-soal yang menuntut siswa menggunakan pola
5
Undang-undang, SISDIKNAS (UU RI No.20 Th. 2003), www.hukumonline.com
6
4
pikirnya yang kreatif sehingga kemampuan berpikir kreatif matematis siswa
terbilang rendah Secara umum kendala yang dialami guru dalam proses
pembelajaran matematika lebih dikarenakan karena kurangnya pemahaman
siswa terhadap materi yang disampaikan dan sulitnya guru mengkondusifkan
siswa yang mengobrol ataupun sering membuat keributan di dalam kelas. Cara
penyampaian materi pelajaran yang guru sampaikan masih menggunakan
model pembelajaran ceramah, ekspositori, tanya jawab dan penugasan. Cara ini
juga kurang membuat siswa terlibat aktif. Karena siswa lebih sering hanya
mendengarkan penyampaian materi dari guru dan mengerjakan tugas yang
diberikan.
Hasil wawancara yang peneliti peroleh dari siswa di SMP YAPPA kelas
VIII-1 menunjukkan bahwa hampir sebagian siswa enggan mengikuti dan
memperhatikan proses pembelajaran matematika jika materi yang sedang
dipelajari dirasa sulit untuk dipahami. Hanya beberapa siswa yang tertarik dan
senang belajar matematika. Pada saat pembelajaran berlangsung pun tidak
semua siswa terlibat aktif dan memperhatikan penjelasan dari guru. Aktivitas
siswa dalam menyelesaikan masalah yang tertera pada soal hampir semua
siswa lebih menyukai menyelesaikan masalah dengan bentuk soal pilihan
ganda daripada bentuk soal uraian atau essay. Apabila siswa mengerjakan soal
berbentuk essay pun siswa lebih senang menjawab dengan cara singkat dan
yang penting jawaban mereka benar.
Dari hasil observasi yang diperoleh, maka dapat disimpulkan bahwa
untuk meningkatkan aktivitas belajar siswa diperlukan suatu metode atau pola
pembelajaran yang lebih bersifat student centre, dimana pada saat kegiatan belajar mengajar berlangsung, siswa yang lebih berperan aktif dalam
pembelajaran di kelas sehingga siswa dapat mengurangi aktivitas-aktivitas lain
yang kurang terarah. Sementara itu aktivitas siswa khususnya aktivitas belajar
siswa dalam berpikir kreatif matematis perlu diperhatikan dan ditingkatkan,
karena ini nantinya akan dapat membiasakan siswa menggunakan kemampuan
5
Pada masalah seperti yang terdapat di SMP YAPPA kelas VIII-1 dapat
diatasi dengan penggunaan strategi atau model pembelajaran yang sesuai
dengan memfokuskan model pengajarannya pada siswa agar melatih siswa
berperan aktif dan kreatif. Salah satu strategi pembelajaran yang dilihat dapat
diberikan untuk memfasilitasi pendukung kemampuan berpikir kreatif
matematis siswa adalah strategi Mathematical Habits of Mind (MHM).
Strategi Mathematical Habits of Mind (MHM)merupakan suatu strategi pembelajaran yang membantu siswa mengeksplorasikan ide-ide matematis
yang mereka ketahui sebelumnya. Strategi ini mempunyai enam tahapan yang
menuntut siswa untuk melakukan kebiasaan-kebiasaan berpikir. Dengan tahap
awal (explore mathematical ideas) yaitu dimana siswa harus menggunakan pemikirannya untuk memberikan ide-ide matematisnya yang sesuai dengan
konsep materi yang disampaikan guru, (reflect on their answer to see wether they) merefleksi kebenaran dan kesesuaian jawaban, (identify problem solving approaches) mengidentifikasi strategi pemecahan masalah yang dapat diterapkan dalam menyelesaikan masalah yang ada, (generalization) membuat kesimpulan, (formulate question) memformulasi pertanyaan, dan (constuct example) merekonstruksi contoh.
Dalam pembelajaran dengan strategi Mathematical Habits of Mind
(MHM), aktifitas mengeksplorasi ide-ide matematis akan sangat membantu
siswa dalam memahami masalah dengan baik. Aktivitas merefleksi kesesuaian
dan kebenaran jawaban juga dapat membuat siswa bisa mengerti dan
memahami cara penyelesaian suatu masalah dengan tepat. Strategi MHM ini
juga berpontensi untuk mengembangkan kemampuan kreativitas siswa dalam
menyelesaikan masalah. Generalisasi pada tahap strategi MHM sesungguhnya
adalah penggabungan dua komponen antara mengidentifikasikan strategi pemecahan masalah yang dapat diterapkan dalam skala lebih luas dan
identifikasi kesimpulan dari penyampaian konsep pembelajaran. Pada strategi
ini memformulasi pertanyaan dapat menumbuhkan kemampuan berpikir kreatif
siswa. Karena dengan ini lebih cenderung memberi kesempatan siswa untuk
6
sesuatu hal yang belum dipahami siswa. Terakhir didukung dengan tahapan
merekonstruksi contoh, siswa yang mampu merekonsruksi contoh sesuai
kriteria tertentu akan memiliki kepercayaan diri dan dapat menumbuhkan
disposisi matematis siswa. Penggunaan strategi Mathematical Habits of Mind
(MHM) dengan tahapan-tahapan seperti diatas akan dapat membantu
menumbuhkan kemampuan berpikir kreatif matematis siswa dalam
menghadapi soal yang mengedepankan kreativitas dalam berpikir.
Selain memfokuskan pengamatan pada peningkatan kemampuan
berpikir kreatif matematis siswa, aktivitas dan tanggapan siswa terhadap
pembelajaran matematika merupakan salah satu hal yang penting untuk
diamati. Karena dalam belajar matematika, kepercayaan diri yang tinggi sangat
dibutuhkan karena dapat menentukkan keberhasilan maupun pengalaman siswa
dalam mempelajari matematika. Oleh sebab itu perlunya menstimulus aktivitas
dan tanggapan siswa pada saat proses belajar mengajar di kelas dilakukan.
Berdasarkan latar belakang masalah yang telah diuraikan, peneliti
terdorong untuk melakukan penelitian dengan judul “Penerapan Strategi
Mathematical Habits of Mind untuk Meningkatkan Kemampuan Berpikir Kreatif Matematis Siswa”.
B. Identifikasi Masalah
Mengacu pada latar belakang yang telah diuraikan maka dapat
diidentifikasi beberapa masalah, yaitu: 1. Proses pembelajaran terpusat pada guru
2. Siswa tidak memahami soal yang mengacu pada kreativitas
3. Siswa terbiasa menunggu informasi yang diberikan guru
4. Siswa tidak membiasakan diri untuk berpikir secara matematis
5. Siswa tidak terbiasa mengerjakan soal matematika yang berbentuk uraian /
essay dengan cara tersistematis
C. Fokus Penelitian
Agar penelitian terarah dan memberikan arah yang tepat dalam
7
1. Penggunaan strategi Mathematical Habits of Mind (MHM) dalam penelitian ini adalah dengan menggunakan kebiasaan berpikirnya dalam
menghadapi permasalahan dimana hal yang dilakukan lebih mengasah pola
pikir yang kreatif dalam berbagai tahapan yang melibatkan pemikiran diri
sendiri dan diberi kesempatan untuk mengkonstruksi sendiri pengetahuan
matematikadengan melalui masalah-masalah yang ada.
2. Kemampuan berpikir kreatif matematis yang dimaksud dalam penelitian ini
adalah kemampuan dalam menemukan dan menyelesaikan suatu
masalah-masalah matematika secara lancar, luwes, rinci, dan keaslian. Kemampuan
berpikir kreatif matematis yang akan diamati pada siswa dibatasi hanya
pada kemampuan berpikir lancar (fluency), berpikir luwes (flexibility) dan kemampuan berpikir rinci (elaboration).
Pokok bahasan yang digunakan sebagai bahan penelitian yaitu lingkaran.
D. Perumusan Masalah
Berdasarkan masalah yang telah dibatasi diatas, maka perumusan
masalah yang akan diteliti adalah:
1. Apakah penerapan strategi strategi Mathematical Habits of Mind dapat meningkatkan kemampuan berpikir kreatif matematis siswa?
2. Bagaimana aktivitas belajar siswa terhadap proses pembelajaran
matematika dengan penerapan strategi Mathematical Habits of Mind ? E.
Tujuan Penelitian
Tujuan yang ingin dicapai dalam penelitian tindakan kelas (PTK) ini
adalah :
1. Untuk mengetahui dan mendeskripsikan kemampuan berpikir kreatif
matematis siswa setelah diterapkan strategi pembelajaran Mathematical Habits of Mind.
2. Untuk mengetahui dan mendeskripsikan aktivitas belajar siswa selama proses pembelajaran dengan menggunakan strategi pembelajaran
8
F.
Manfaat Penelitian
Adapun manfaat yang penulis harapkan dari penelitian ini adalah sebagai
berikut:
1. Manfaat Teoritis
a. Salah satu alternatif untuk meningkatkan kemampuan berpikir kreatif
matematis siswa dalam proses pembelajaran.
b. Sebagai pembanding bagi peneliti-peneliti lain yang ingin meneliti,
sebagai salah satu sumber informasi untuk mengadakan penelitian
lanjutan tentang strategi Mathematical Habits of Mind (MHM) dalam pembelajaran matematika, dan untuk meningkatkan kemampuan
berpikir kreatif matematis.
2. Manfaat Praktis
a) Bagi Peneliti
1. Dapat memunculkan sikap peka terhadap permasalahan pendidikan.
2. Memotivasi peneliti untuk melakukan penelitian lainnya sebagai
sumbangan khazanah ilmiah dalam pembelajaran matematika.
b) Bagi Siswa
1. Dapat meningkatkan motivasi siswa untuk belajar matematika.
2. Dapat mengembangkan daya kreatifitas siswa.
3. Dapat menjadikan siswa menjadi lebih aktif dan mandiri.
c) Bagi guru dan sekolah
1. Dapat memperbaiki dan meningkatkan kualitas pembelajaran
matematika dengan suasana kelas yang kondusif dan atraktif.
2. Dapat memberikan masukan yang berarti/bermakna pada sekolah
9
BAB II
LANDASAN TEORITIS, KERANGKA BERPIKIR
DAN HIPOTESIS PENELITIAN
A.
Landasan Teoritis
1.
Pembelajaran dengan Strategi
Mathematical Habits of Mind
(MHM)
a.
Pengertian Belajar
Belajar secara sederhana dikatakan sebagai proses perubahan dari
belum mampu menjadi sudah mampu yang terjadi dalam waktu tertentu.
Belajar merupakan hasil yang relatif tetap dalam diri seseorang tersebut.
Belajar dapat pula dikatakan serangkaian latihan yang dilakukan sehingga
hasil belajar akan nampak dalam keterampilan-keterampilan tertentu.
Setiap individu mempunyai beragam sudut pandang mengenai belajar dan
pandangan seseorang tentang belajar itu akan mempengaruhi
tindakan-tindakan yang berhubungan dengan belajar itu sendiri.
Skinner, seperti yang dikutip Barlow (1985) dalam bukunya
Educatonal Psychology: The Teachin- Learing Process, berpendapat bahwa belajar adlah suatu proses aaptasi aau penyesuaian tingkah aku
yang belangsung secara progresif.1
Hintzman dalam bukunya The Psycologhy of Learning and Memory
berpendapat Learning is change in organism due to experience which can affect the organism’s behavior. Artinya belajar adalah suatu perubahan
1
10
yang terjadi dalam diri organisme (manusia atau hewan) disebakan oleh
pengalaman yang dapat mempengaruhi tingkah laku organisme tersebut.2
Wittig dalam bukunya Psycologhy of Learning mendefinisikan belajar sebagai : any relatively permanent change in an organism’s behavioral repertoire that occurs as a result of experience. Belajar adalah perubahan yang relatif menetap dan terjadi dalam segala
macam/keseluruhan tingkah laku organisme sebagai hasil pengalaman. 3 Keberhasilan seseorang dalam pendidikan pun tergantung pada
proses belajar yang berlangsung, apakah berlangsung dengan efektif atau
tidak. Meskipun belajar mempunyai arti yang sangat luas, namun tidak
sedikit orang yang masih mempunyai asumsi bahwa belajar adalah
kegiatan yang semata-mata hanya untuk mengumpulkan dan
menghafalkan fakta-fakta yang tersaji dalam bentuk informasi/ materi
pelajaran. Hal tersebut sungguh jelas berbeda dengan apa yang telah
didefinisikan oleh sebagian para ahli mengenai makna belajar itu sendiri
yang pada intinya lebih menekankan kepada aspek proses.
b.
Pengertian Pembelajaran
Sistem pembelajaran adalah suatu kombinasi terorganisasi yang
meliputi unsur-unsur manusiawi, material, fasilitas, perlengkapan dan
prosedur yang berinteraksi untuk mencapai suatu tujuan (Hamalik,2003).4 Pembelajaran itu sendiri adalah proses yang sengaja dirancang dengan tujuan untuk menciptakan suasana lingkungan yang
memungkinkan seseorang melaksanakan kegiatan belajar mengajar. Pada
pembelajaran matematika harus memberikan peluang kepada siswa untuk
berusaha dan mencari pengalaman dalam belajar matematika. Berdasarkan
hal tersebut, dapat dikatakan bahwa ada sebuah perbedaan antara belajar
dan pembelajaran. Pembelajaran merupakan suatu sistem yang kompleks
2
Muhibin Syah, Psikologi Pendidikan dengan pendekata bau, (Bandung: PT. Remaja Rosdakaya Offset, 2010), hal. 88
3
Muhibin Syah, Psikologi Pendidikan dengan pendekata bau, (Bandung: PT. Remaja Rosdakaya Offset, 2010), hal. 89
4
11
yang keberhasilannya dapat dilihat dari dua aspek, yakni aspek produk dan
proses. Pada proses belajar, yang terlibat aktif di dalamnya hanyalah
siswa. Sedangkan pada proses pembelajaran, terkandung dua aktivitas
sekaligus, yaitu aktivitas guru dalam mengajar dan aktivitas siswa dalam
belajar.
Keberhasilan sistem pembelajaran adalah keberhasilan pencapaian
tujuan pembelajaran. Selanjutnya, yang harus mencapai tujuan adalah
siswa sebagai subjek belajar.5 Keberhasilan pembelajaran dilihat dari sisi produk adalah keberhasilan siswa mengenai hasil yang diperoleh dengan
mengabaikan proses pembelajaran. Keberhasilan pembelajaran dilihat dari
sisi hasil memang mudah dilihat dan ditentukan kriterianya, akan tetapi hal
ini dapat mengurangi makna proses pembelajaran sebagai proses yang
mengandung nilai-niolai pendidikan. Dengan kata lain keberhasilan
pembelajaran yang hanya melihat sisi hasil sama halnya dengan
mengerdilkan makna pembelajaran itu sendiri.6 Pembelajaran adalah suatu sistem, oleh sebab itu pembelajaran sangat dipengaruhi oleh berbagai
komponen yang mendukung. Seperti faktor dari guru, faktor siswa, sarana
dan prasarana, serta faktor lingkungan.
Dari beberapa definisi yang telah dikemukakan oleh para ahli dapat
disimpulkan bahwa pembelajaran adalah suatu proses interaksi dan
komunikasi antara berbagai komponen pembelajaran seperti guru, siswa,
dan sumber belajar sehingga dapat terjadi perubahan perilaku,
pengetahuan, dan keterampilan berpikir siswa.
c.
Strategi
Mathematical Habits of Mind
Mathematical Habits of Mind atau kebiasaan berpikir secara matematis adalah suatu strategi yang mengedepankan perilaku berpikir
seseorang dalam menyelesaikan persoalan matematika.
Kebiasaan-kebiasaan baik yang dilakukan seorang individu akan sangat
5
Dr. Wina Sanjaya, M.Pd, Perencanaan dan Desain Sistem Pembelajaran, (Jakarta : Kencana, 2008) cet ke 1 hal 6
6
12
mempengaruhi hidupnya. Sebelum berbicara jauh tentang kebiasaan
berpikir matematis ada baiknya kita mengenal tentang kebiasaan.
Kebiasaan adalah pola perilaku yang dibentuk oleh pengulangan
yang berkelanjutan. Kebiasaan yang dilakukan secara terus menerus akan
semakin kuat dan menetap pada diri individu sehingga sulit diubah. Dalam
hal ini kebiasaan tersebut telah membudaya pada diri individu.
Dalam ilmu psikologi, tingkah laku seseorang dapat diubah dengan
suatu tindakan yang dilakukan secara berulang-ulang.
Dari kutipan yang dinyataakan oleh William B. Allen menyebutkan bahwa ... informasi yang digambarkan kebiasaan berpikir itu adalah cepat dan jauh yang sangat berpengaruh dalam menentukan tingkah laku seseorang, dalam bukunya yang menyebutkan “... informed by the view that habits of mind are far and away the most influential determinants of human conduct in our time...”.7
Psikologi sekolah menerapkan kedisiplinan yang meliputi pendekatan ilmiah pada prilaku dan tindakan siswanya. Meskipun ada beberapa perbedaan antara pendekatan secara psikologi (dengan penelitian yang empirik), dan penerapan psikologi (menghubungkan sebuah angka pada suatu area). Seluruh tindakan psikologi membagi pada satu keadaan inti, seperti yang dinyatakan oleh Stanovich berikut : “ ... Psychology is an academic and applied discipline involving the scientific study of mental processes and behavior. Although there is some tension between scientific psychology (with its program of empirical research) and applied psychology (dealing with a number of areas), all psychologists share a common core”.8 Ada banyak kegiatan untuk menerapkan kebiasaan berpikir di kelas dan berbagai cara menyiapkan siswa untuk lebih lama lagi mendengarkan materi. Suatu tindakan itu diantara dua adalah menentukan atau mendefinisikan. Semua itu adalah langkah awal dari penerapan kebiasaan berpikir. Tidak semua menjaminkan kesuksesan. Kesuksesan dari kebiasaan berpikir akan menjadi penambahan dan serangkaian waktu penuh, selalu mengedepankan selama berlangsungnya kemampuan individual guru yang profesional dalam meningkatkan kapasitas dan kemampuan mereka yang sedang mengembangkan kecerdasan pribadinya. Dengan kata lain yang terpenting adalah suatu kerjasama dan sinergi yang secara
7
Allen, William B. And Carol M. Allen. (2003). “ Habits of Mind : Fostering access and excellence in higher education”. (New Jersey : Transaction Publishers). Hal xi - xii
8
Ciccone, Anthony A. (2009). “Exploring Signature Pedagogies Approache to Teaching
13
kolektif mendukung dari guru lain, dukungan staff pengajar, administrasi, orangtua, dan seluruh siswa, seperti yang dikatakan oleh Arthur L. Costa berikut : “...It describes various actions for implementing the Habits of Mind in the classroom and thereby preparing students for lifelong learning. The actions should not, however, be seen as either prescriptive or definitive. They are starting points. None of them guarantees instant success. Success in implementing the Habits of Mind will be incremental and sequential over time, always dependent upon the professional skill of the individual teachers in increasing their capacities and capabilities— developing their intrapersonal intelligence. Equally important is the collaboration with and the synergy of collegial support from other teachers, support staff, administrators, parents, and the students themselves.” 9
Ada banyak sekali macam-macam kebiasaan yang dapat
mempengaruhi hidup seseorang untuk menuju kesuksesan, salah satunya
adalah kebiasaan berpikir (habit of mind). Kesuksesan individu sangat ditentukan oleh kebiasaan-kebiasaan yang dilakukan oleh individu
tersebut. Kebiasaan-kebiasaan positif yang dilakukan secara konsisten
akan dapat berpotensi membentuk kemampuan-kemampuan positif.
Menurut Millman dan Jacobbe 2008, strategi Mathematical Habits of Mind (MHM) terdiri atas 5 komponen, yaitu :10
1. Mengeksplorasi ide-ide matematis, siswa menyampaikan pengetahuan
yang dimilikinya dan menambahkan hal-hal baru yang saling berkaitan
berkenaan dengan pembahasan yang sedang dibicarakan;
2. Merefleksi kebenaran atau kesesuaian jawaban, siswa mengulas
kembali dan memeriksa ulang jawaban yang sudah ada melalui cara
penyelesaian yang lain dan menyamakan kembali;
3. Generalisasi, siswa mengaitkan sebuah permasalahan dengan mencari
cara penyelesaian apa yang tepat untuk menyelesaikannya;
4. Memformulasi pertanyaan, siswa membuat pertanyaan baru dari
sebuah soal yang sudah diberikan;
9
Costa, Arthur L. And Bena Kallick. (2009). “Habits of Mind across the curuculum : practical and creative strategies for teachers”. (Alexandria : ASCD). Hal : 17
14
5. Menginstruksi contoh soal, siswa diberikan penjelasan dan contoh soal
tentang materi yang akan dibahas kemudian siswa diminta untuk
membuat soal dan pembahasan sendiri dengan mengacu pada contoh
soal yang diberikan oleh guru.
Kegiatan-kegiatan ini dapat dipandang sebagai
kebiasaan-kebiasaan berpikir matematis yang apabila dilakukan secara konsisten
berpotensi dapat membentuk kemampuan berpikir kreatif matematis.
Menjadikan kebiasan berpikir akan dapat membantu untuk
mengembangkan kemampuan berpikir kreatif. Pernyataan ini sejalan
dengan pendapat Stenberg (2006) yang memandang kreativitas sebagai
kebiasaan. Tentu saja suatu kebiasaan yang dilakukan secara terus menerus
akan mampu menjadikan itu sebagai kebisaan. Tak ubahnya dengan
melakukan kebiasaan yang kreatif jika dilakukan secara terus menerus
akan dapat membentuk kemampuan berpikir yang kreatif.
Berikut diuraikan masing-masing aktivitas dalam strategi MHM
tersebut.11
1. Mengeksplorasi ide-ide matematis
Eksplorasi ide-ide matematis dapat meliputi aktivitas mengeksplorasi
berbagai data, informasi, atau strategi pemecahan masalah. Aktivitas
demikian dapat mendorong siswa berpikir fleksibel, yakni
mengidentifikasi berbagai cara atau strategi pemecahan masalah. Dengan
aktivitas demikian dimungkinkan diperoleh strategi yang bersifat unik atau
baru. Hal demikian merupakan salah satu aspek kemampuan berpikir
kreatif. Guru dapat menstimulasi siswa untuk mengeksplorasi ide-ide
matematis dengan mengajukan beberapa pertanyaan seperti: data apa saja
yang diperlukan untuk menyelesaikan masalah ini?, apakah data yang diperlukan sudah tersedia?, strategi atau cara apa saja yang dapat
11
Ali Mahmudi.”Strategi Mathematical Habits of Mind (MHM) untuk Mengembangkan
Kemampuan Berpikir Kreatif Matematis. Disampaikan dalam makalah pada Konferensi Nasional
15
digunakan?, konsep apa saja yang diperlukan untuk menyelesaikan
masalah ini?, konsep-konsep apa saja yang saling berkaitan?, apakah
terdapat cara lain untuk menyelesaikannya, dan sebagainya.
2. Merefleksi kesesuaian solusi atau strategi pemecahan masalah
Memeriksa atau merefleksi kesesuaian solusi atau strategi pemecahan
masalah merupakan representasi dari tahap looking back (evaluate solution) pada tahap pemecahan masalah yang dikemukakan Polya (1973), yakni mengevaluasi atau menelaah kembali kesesuaian solusi masalah.
Terkait dengan kegiatan refleksi, Brownell (McIntosh, 2000) menyatakan
bahwa suatu masalah baru benar-benar dikatakan telah diselesaikan jika
individu telah memahami apa yang ia kerjakan, yakni memahmi proses
pemecahan masalah dan mengetahui mengapa solusi yang telah diperoleh
sesuai. Hal ini berarti refleksi merupakan tahapan yang sangat penting
dalam kegiatan pemecahan masalah. Guru dapat mendorong siswa
melakukan kegiatan refleksi dengan mengajukan pertanyaan-pertanyaan
seperti bagaimana kamu menyelesaikan masalah itu?, bagaimana kamu
mengetahui bahwa jawabanmu telah sesuai?, adakah cara lain untuk
menyelesaikan masalah ini?, dan sebagainya.
3. Generalisasi dan mengidentifikasi strategi penyelesaian masalah
yang dapat diterapkan pada masalah lain
Komponen strategi MHM berikutnya adalah mengidentifikasi apakah terdapat “sesuatu yang lebih” dari aktivitas yang telah dilakukan dan
mengidentifikasi pendekatan masalah yang dapat digunakan atau
diterapkan pada masalah lain dalam skala lebih luas. Aktivitas demikian
mengarah pada generalisasi ide-ide matematis yang telah dieksplorasi dan
mengarah pada konstruksi konsep-konsep matematika. Aktivitas demikian juga terkait dengan identifikasi dan analisis apakah strategi penyelesaian
masalah yang telah digunakan dapat juga diterapkan pada masalah lain
dalam skala yang lebih luas. Aktivitas demikian merupakan aktivitas
kreatif, yakni mengkonstruksi konsep matematis atau strategi penyelesaian
16
menggunakan strategi-strategi informal sebelum mereka mengenal strategi
formal. Menurut Lim (2009), hendaknya guru tidak mengajarkan
algoritma atau formula formal terlalu dini. Siswa perlu diberikan
kesempatan untuk menggunakan strategi mereka sendiri berdasarkan
pengetahuan yang mereka ketahui. Selanjutnya siswa didorong untuk
mengidentifikasi apakah strategi yang mereka gunakan berlaku untuk
masalah lain lebih umum. Beberapa pertanyaan yang dapat digunakan
membantu siswa melakukan generalisasi adalah: apa yang terjadi jika ...?,
bagaimana jika tidak?, dapatkah kamu melihat polanya?, dapatkah kamu
mempredisksi pola berikutnya?, apakah strategi itu dapat digunakan pada
masalah lain?, dan sebagainya.
4. Memformulasi pertanyaan
Komponen strategi MHM berikutnya adalah memformulasi pertanyaan. Mengembangkan kebiasaan bertanya mempunyai peranan penting dalam
pembelajaran matematika. Pertanyaan dapat menstimulasi siswa
mengembangkan kemampuan berpikir kreatif. Siswa didorong untuk
mengajukan berbagai pertanyaan terkait situasi atau masalah tertentu.
Menurut Einstein (Costa dan Kallick, 2008), memformulasi pertanyaan
kadang lebih esensial daripada solusi masalah itu sendiri. Mengajukan
pertanyaan baru dan melihat kemungkinan baru dari masalah lama
memerlukan imajinasi kreatif. Mengajukan pertanyaan adalah aktivitas
yang biasa dilakukan oleh guru. Di sisi lain, siswa relatif jarang diberikan
kesempatan untuk mengembangkan kemampuan bertanya. Sesuai dengan
kecenderungan pembelajaran matematika saat ini yang mengedepankan
aktivitas siswa, guru perlu memberikan kesempatan kepada siswa untuk
secara aktif membangun kemampuan bertanya. Salah satu jenis pertanyaan yang perlu dikembangkan agar menjadi kebiasaan siswa adalah pertanyaan
“what if not ...?” atau “what happen if ...?”. Mengajukan pertanyaan demikian akan mendorong siswa untuk menghasilkan ide-ide kreatif
(Gillman, 2008). Jenis pertanyaan ini dapat digunakan untuk memodifikasi
17
dapat mengubah informasi soal semula dengan tetap mempertahankan
situasi soal atau sebaliknya mengubah situasi soal dengan tetap
mempertahankan informasi soal semula. Kemampuan bertanya merupakan
salah satu indikator kemampuan berpikir kreatif. Haylock (1997)
mengemukakan cara mengukur kemampuan berpikir kreatif dengan
memberikan tugas kepada siswa untuk membuat pertanyaan-pertanyaan
berdasarkan informasi yang diberikan. Dengan demikian dengan
mengembangkan kebiasaan siswa untuk mengajukan pertanyaan
merupakan salah satu cara untuk mengembangkan kemampuan berpikir
kreatifnya.
5. Mengkonstruksi contoh
Aktivitas berikutnya dalam strategi MHM adalah mengkonstruksi contoh. Menurut Liz et al (2006), pemberian contoh berperan penting dalam pembelajaran matematika. Suatu konsep yang abstrak dan kompleks
menjadi lebih mudah dipahami bila diberikan contoh yang sesuai.
Penggunaan contoh dalam pembelajaran matematika merujuk pada istilah
eksemplifikasi (exemplification). Menurut Liz et al (2005), eksemplifikasi adalah mendeskripsikan suatu situasi menjadi lebih sepesifik untuk
merepresentasikan suatu situasi yang bersifat umum. Contoh merupakan
deskripsi atau ilustrasi spesifik dari suatu konsep yang menjadikan konsep
tersebut lebih dikenal dan dipahami siswa. Menurut Liz et al (2006), terdapat 3 jenis contoh, yaitu contoh umum (generic example), contoh penyangkal, dan atau non-contoh. Contoh generik adalah contoh suatu
konsep, prosedur, atau teorema yang bersifat umum. Contoh penyangkal
digunakan untuk menguji berlakunya suatu dugaan atau konjektur.
Sedangkan noncontoh digunakan untuk memperjelas definisi suatu konsep. Memberikan contoh merupakan aktivitas yang biasa dilakukan
guru. Di sisi lain, siswa relatif jarang diberikan kesempatan untuk
mengkonstruksi contoh-contoh mereka sendiri. Terdapat beberapa manfaat
yang dapat diperoleh dengan memberikan kesempatan kepada siswa untuk
18
dapat digunakan untuk mendeteksi ketidakpahaman siswa terhadap suatu
konsep. Sedangkan menurut Dahlberg dan Housman (Liz et al, 2005), mengkonstruksi contoh merupakan tugas yang kompleks yang menuntut
kemampuan siswa untuk mengaitkan beberapa konsep. Jika siswa tidak
diberikan kesempatan untuk mengkonstruksi berbagai jenis contoh,
terlebih contoh penyangkal atau noncontoh, maka siswa dapat membuat
generalisasi yang tidak tepat. Dalam mengkonstruksi contoh, siswa
mengeksplorasi dan mengkombinasikan berbagai konsep yang telah
mereka ketahui untuk membuat contoh yang menarik dan menantang.
Aktivitas demikian akan mendorong siswa untuk membuat sebanyak
mungkin contoh yang memenuhi kriteria tertentu yang bersifat unik dan
beragam. Hal ini memenuhi aspek-aspek kemampuan berpikir kreatif,
yakni kelancaran, fleksibilitas, dan keunikan.
2.
Kemampuan Berpikir Kreatif Matematis
a.
Pengertian Kemampuan Berpikir Kreatif Matematis
Apa itu berpikir kreatif? Isaksen et al (Grieshober, 2004) mendefinisikan berpikir kreatif sebagai proses konstruksi ide yang
menekankan pada aspek kelancaran, keluwesan, kebaruan, dan keterincian.
Menurut McGregor (2007), berpikir kreatif adalah berpikir yang mengarah
pada pemerolehan wawasan baru, pendekatan baru, perspektif baru, atau
cara baru dalam memahami sesuatu. Sementara menurut Martin (2009),
kemampuan berpikir kreatif adalah kemampuan untuk menghasilkan ide
atau cara baru dalam menghasilkan suatu produk. Pada umumnya, berpikir
kreatif dipicu oleh masalah-masalah yang menantang.12
Berpikir kreatif merupakan suatu proses yang digunakan ketika kita
mendatangkan atau memunculkan suatu ide baru. Hal itu menggabungkan
ide-ide yang sebelumnya belum dilakukan.13 Berpikir kreatif juga dapat
12
Ali Mahmudi, 2010, Megukur Kemampuan Berpiki treatf Matematis, hal 2 pdf 13
Tatang Yuli Eko Siswono.”Desain Tugas untuk Mengidentifikasi Kemampuan Berpikir Kreatif Siswa dalam Matematika” Jurusan Matematika FMIPA.Universitas Negeri Surabaya.hal: 1.
19
diartikan sebagai suatu kombinasi dari berpikir logis dan berpikir divergen
yang didasarkan pada intuisi tetapi masih dalam kesadaran (Pehkonen,
1997).14 Pandangan lain tentang berpikir kreatif disampaikan oleh Krulik dan Rudnick (1999), yang menjelaskan bahwa berpikir kreatif merupakan
pemikiran yang bersifat keaslian dan reflektif dan menghasilkan suatu
produk yang komplek. Berpikir tersebut melibatkan sintesis ide-ide,
membangun ide-ide baru dan menentukan efektivitasnya.15
Badan Standar Nasional Pendidikan (BSNP) tahun 2006
merekomendasikan bahwa dalam pembelajaran perlu diciptakan suasana
aktif, kritis, analisis, dan kreatif dalam pemecahan masalah. Oleh karena
itu perlu dikaji secara teoritis tentang keterkaitan kemampuan berfikir
kreatif terhadap kemampuan matematika.16
Menurut Langrehr (2006), untuk melatih berpikir kreatif siswa harus
didorong untuk menjawab pertanyaan-pertanyaan yang berkaitan dengan
hal-hal sebagai berikut :17
1. Membuat kombinasi dari beberapa bagian sehingga terbentuk hal yang
baru
2. Menggunakan ciri-ciri acak dari suatu benda sehingga terjadi
perubahan dari desain yang sudah ada menjadi desain yang baru
3. Mengeliminasi suatu bagian dari sesuatu hal sehingga diperoleh
sesuatu hal yang baru
4. Memikirkan kegunaan alternatif dari sesuatu hal sehingga diperoleh
kegunaan yang baru
14
Tatang Yuli Eko Siswono.”Desain Tugas untuk Mengidentifikasi Kemampuan Berpikir Kreatif Siswa dalam Matematika” Jurusan Matematika FMIPA.Universitas Negeri Surabaya.hal: 1.
http://tatagyes.files.wordpress.com/2007/10/tatag_jurnal_unej.pdf (23 September 2013) 15
Tatang Yuli Eko Siswono.”Desain Tugas untuk Mengidentifikasi Kemampuan Berpikir Kreatif Siswa dalam Matematika” Jurusan Matematika FMIPA.Universitas Negeri Surabaya.hal: 2.
http://tatagyes.files.wordpress.com/2007/10/tatag_jurnal_unej.pdf (23 September 2013) 16
Akhmad jazuli,Seminar Nasional Matematika dan Pendidikan Matematika Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009.hal 209 pdf 17
20
5. Menyusun ide-ide yang berlawanan dengan ide-ide yang sudah biasa
digunakan orang sehingga diperoleh ide-ide baru
6. Menentukan kegunaan bentuk ekstrim dari suatu benda sehingga
ditemukan kegunaan baru dari benda tersebut.
Menurut Learning and Teaching Scotland (LTS, 2004) bila kemampuan berpikir kreatif berkembang pada seseorang, maka akan
mengasilkan banyak ide, membuat banyak kaitan, mempunyai banyak
perspektif terhadap suatu hal, membuat dan melakukan imajinasi, dan
peduli akan hasil.18
Kemampuan berpikir kreatif merupakan salah satu kemampuan yang
dikehendaki dunia kerja (Career Center Maine Department of Labor USA, 2001).19 Selain itu, pengembangan kemampuanberpikir kreatif merupakan salah satu fokus pembelajaran matematika. Melalui pembelajaran
matematika, siswa diharapkan memiliki kemampuan berpikir logis,
analitis, sistematis, kritis, dan kreatif, serta memiliki kemampuan bekerja
sama (Depdiknas, 2004).20
Kemampuan berpikir kreatif sangat diharapkan dapat digunakan dan
diterapkan siswa dalam pelaksanaan kegiatan belajar dikelas. Karena
ketika diterapkannya berpikir kreatif pada suatu pemecahan masalah, maka
pemikiran akan menyebar dan menghasilkan banyak ide-ide. Hal ini
tentunya akan sangat berguna dalam menemukan penyelesaian dan dapat
menyelesaikannya dengan beragam cara.
Hasil dari berpikir kreatif adalah kreativitas. Secara umum, terdapat
dua pandangan berbeda mengenai kreativitas. Pandangan pertama
menyatakan bahwa kreativitas hanya dimiliki oleh individu dengan
18
Hedi Budiman.”Peningkatan Kemampuan Berpikir Kritis dan Berpikir Kreatif Matematis Siswa Melalui Pendekatan Pembelajaran Berbasis Masalah Berbantua Software Cabri 3D” Mahasiswa Pendidikan Matematika, SPs UPI Bandung. hal: 1.
http://www.pustaka.ut.ac.id/dev25/pdfprosiding2/fmipa201141.pdf (23 September 2013) 19
Mahmudi, Ali.”Pengaruh Strategi Mathematical Habits of Mind (MHM) Berbasis Masalah Terhadap Kreativitas Siswa ...., hal:2 pdf
20
21
karakteristik tertentu (Berg, 1999; Getzel & Jackson dalam Alexander,
2007; Briggs dan Davis, 2008).21
Sementara itu, Torrance (1969) mendefinisikan secara umum
kreativitas sebagai proses dalam memahami sebuah masalah, mencari
solusi-solusi yang mungkin, menarik hipotesis, menguji dan mengevaluasi,
serta mengkomunikasikan hasilnya kepada orang lain.22
Berdasarkan beberapa definisi di atas dapat disimpulkan bahwa
kreativitas merupakan suatu proses mental individu yang melahirkan
gagasan, proses, ataupun produk baru yang efektif dan berdaya guna untuk
pemecahan masalah.
b.
Indikator Kemampuan Berpikir Kreatif Matematis
Haylock (1997) mengatakan bahwa berpikir kreatif selalu tampak
menunjukkan fleksibilitas (keluwesan). Bahkan Krutetskii (1976)
mengidentifikasi bahwa fleksibilitas dari proses mental sebagai suatu
komponen dari kemampuan kreatif matematis dalam sekolah. Haylock
(1997) menunjukkan kriteria sesuai tipe Tes Torrance dalam kreativitas,
yaitu kefasihan (banyaknya respon-respon yang diterima), fleksibilitas
(banyaknya berbagai macam respon yang berbeda), dan keaslian
(kejarangan respon-respon dalam kaitan dengan sebuah kelompok
pasangannya).23
Menurut William (dalam Killen,1998) menyatakan bahwa ada 8 prilaku siswa terkait dengan kreativitas atau berfikir tingkat tinggi, yaitu
:24
21
Mahmudi, Ali.”Pengaruh Strategi Mathematical Habits of Mind (MHM) Berbasis Masalah Terhadap Kreativitas Siswa ...., hal:2
22
Hedi Budiman.”Peningkatan Kemampuan Berpikir Kritis dan Berpikir Kreatif Matematis Siswa Melalui Pendekatan Pembelajaran Berbasis Masalah Berbantua Software Cabri 3D” Mahasiswa Pendidikan Matematika, SPs UPI Bandung. hal: 2.
http://www.pustaka.ut.ac.id/dev25/pdfprosiding2/fmipa201141.pdf (23 September 2013) 23
Tatang Yuli Eko Siswono.”Desain Tugas untuk Mengidentifikasi Kemampuan Berpikir Kreatif Siswa dalam Matematika” Jurusan Matematika FMIPA.Universitas Negeri Surabaya.hal: 2. http://tatagyes.files.wordpress.com/2007/10/tatag_jurnal_unej.pdf (23 September 2013)
24
22
(1) fluency : kemampuan untuk menghasilkan sejumlah besar ide,
produk dan respon
(2) flexibility : kemampuan untuk memperoleh pendekatan yang berbeda,
membangun berbagai ide, mengambil jalan memutar
dalam jalan pikirannya, dan mengadopsi situasi baru.
(3) originality : kemampuan untuk membangun ide, yang tidak biasa, ide
cerdas yang mengubah cara dari yang nyata.
(4) elaboration : kemapuan untuk memotong, mengembangkan atau
membubuhi ide atau produk.
(5) risk taking : mempunyai keberanian untuk menyatakan sendiri
kesalahan atau kritikan, tebakan dan
mempertahankan ide sendiri
(6) complexity : mencari berbagai alternatif, membawa keluar dari
kekacauan, dan menyelidiki ke dalam masalah atau ide
yang rumit.
(7) curiosity : keinginan untuk tahu dan kagum, bermain dengan suatu
ide, membuka situasi teka teki dan mempertimbangkan
sesuatu yang misteri
(8) imaginaton : mempunyai kekuatan untuk visualisasi dan membangun
mental image dan meraih di luar lingkungan nyata.
Menurut Alvino (dalam Cotton, 1991), kreatif adalah melakukan
suatu kegiatan yang ditandai oleh empat komponen, yaitu : fluency
(menurunkan banyak ide), flexibility (mengubah perspektif dengan mudah), originality (menyusun sesuatu yang baru), dan elaboration
(mengembangkan ide lain dari suatu ide). Rincian cirri-ciri dari fluency, flexibility, originality, dan elaboration dikemukan oleh Munandar (1999):25
Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009.hal 213 pdf
25
http://file.upi.edu/Direktori/FPMIPA/JUR._PEND._MATEMATIKA/195101061976031-TATANG_MULYANA/File_24_Kemampuan_Berpikir_Kritis_dan_Kreatif_Matematik.pdf .
23
1. Ciri-ciri fluency diantaranya adalah:
a. Mencetuskan banyak ide, banyak jawaban, banyak penyelesaian
masalah, banyak pertanyaan dengan lancar
b. Memberikan banyak cara atau saran untuk melakukan berbagai hal
c. Selalu memikirkan lebih dari satu jawaban.
2. Ciri-ciri flexibility diantaranya adalah:
a. Menghasilkan gagasan, jawaban, atau pertanyaan yang bervariasi,
dapat melihat suatu masalah dari sudut pandang yang berbeda-beda
b. Mencari banyak alternatif atau arah yang berbeda-beda
c. Mampu mengubah cara pendekatan atau cara pemikiran
3. Ciri-ciri originality diantaranya adalah:
a. Mampu melahirkan ungkapan yang baru dan unik
b. Memikirkan cara yang tidak lazim untuk mengungkapkan diri
c. Mampu membuat kombinasi-kombinasi yang tidak lazim dari
bagian-bagian atau unsur-unsur
4. Ciri-ciri elaboration diantarnya adalah:
a. Mampu memperkaya dan mengembangkan suatu gagasan atau
produk
b. Menambah atau memperinci detil-detil dari suatu obyek, gagasan,
atau situasi sehingga menjadi lebih menarik.
Munandar merincikan ciri-ciri dari indikator berpikir kreatif sebagai berikut :26
a. ciri-ciri fluency diantaranya adalah:
(1) Mencetuskan banyak ide, banyak jawaban, banyak penyelesaian masalah, banyak pertanyaan dengan lancar;
(2) Memberikan banyak cara atau saran untuk melakukan berbagai hal; (3) Selalu memikirkan lebih dari satu jawaban.
b. ciri-ciri flexibility diantaranya adalah :
(1) Menghasilkan gagasan, jawaban, atau pertanyaan yang bervariasi;
26
24
(2) Melihat suatu masalah dari sudut pandang yang berbeda-beda; (3) Mencari banyak alternatif atau arah yang berbeda-beda; (4) Mampu mengubah cara pendekatan atau cara pemikiran. c. ciri-ciri originality diantaranya adalah :
(1) Mampu melahirkan ungkapan yang baru dan unik;
(2) Memikirkan cara yang tidak lazim untuk mengungkapkan diri; (3) Mampu membuat kombinasi-kombinasi yang tidak lazim dari bagian-bagian atau unsur-unsur.
d. ciri-ciri elaboration diantarnya adalah :
(1) Mampu memperkaya dan mengembangkan suatu gagasan atau produk; (2) Menambah atau memperinci detil-detil dari suatu obyek, gagasan, atau situasi sehingga menjadi lebih menarik.
Kemampuan berpikir kreatif pada anak merupakan dasar penting
bagi kemampuannya menghadapi perubahan zaman di masa depan. Untuk
menjadi individu yang kreatif, dibutuhkan kemampuan berpikir yang
mengalir lancar, bebas dan ide-ide yang orisinil.
Indikator kemampuan berpikir kreatif menurut Utami Munandar
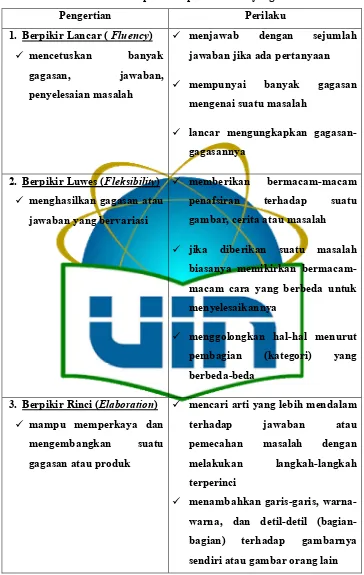
[image:40.612.135.508.236.684.2]adalah sebagai berikut:27
Tabel 2.1
Indikator Kemampuan Berpikir Kreatif
Pengertian Perilaku
1. Berpikir Lancar :
mencetuskan banyak gagasan, jawaban, penyelesaian masalah memberikan banyak cara atau
saran untuk melakukan berbagai hal
Selalu memikirkan lebih dari satu jawaban
mengajukan banyak pertanyaan
menjawab dengan sejumlah jawaban jika ada pertanyaan
mempunyai banyak gagasan mengenai suatu masalah
lancar mengungkapkan gagasan-gagasannya
27
25
bekerja lebih cepat dan melakukan lebih banyak dari orang lain
dapat dengan cepat melihat kesalahan dan kekurangan dari suatu objek atau situasi
2. Berpikir Luwes :
menghasilkan gagasan atau jawaban yang bervariasi
dapat melihat suatu masalah dari sudut pandang yang berbeda
mencari banyak alternatif atau arah yang berbeda
mampu mengubah cara pedekatan atau pemikiran
memberikan aneka ragam penggunaan yang tidak lazim terhadap suatu objek memberikan bermacam-macam
penafsiran terhadap suatu gambar, cerita atau masalah
menerapkan suatu konsep atau asas dengan cara yang berbeda-beda
memberikan pertimbangan terhadap situasi yang berbeda dari yang diberikan orang lain
dalam membahas/mendiskusikan suatu situasi selalu mempunyai posisi yang bertentangan dengan mayoritas kelompok
jika diberikan suatu masalah biasanya memikirkan bermacam-macam cara yang berbeda untuk menyelesaikannya menggolongkan hal-hal menurut
pembagian (kategori) yang berbeda-beda
Mampu mengubah arah berpikir secara spontan
hal-26
mampu melahirkan ungkapan baru dan unik
memikirkan cara yang tidak lazim untuk mengungkapkan diri
mampu membuat kombinasi-kombinasi yang tidak lazim dari bagian-bagian atau unsur-unsur
hal yang tidak terpikirkan oleh orang lain
mempertanyakan cara-cara yang lama dan memikirkan cara-cara yang baru memilih a-simetris dalam menggambar
atau membuat desain
memiliki cara berpikir yang lain dari pada yang lain
mencari pendekatan yang baru dari yang
streotype
setelah membaca atau mendengar gagasan-gagasan, bekerja untuk menemukan penyelesaian yang baru lebih senang mensintesis daripada
menganalisis sesuatu 4. Elaboratif :
mampu memperkaya dan mengembangkan suatu gagasan atau produk
menambahkan atau memperinci detil-detil dari suatu obyek, gagasan, atau situasi sehingga menjadi lebih menarik
mencari arti yang lebih mendalam terhadap jawaban atau pemecahan masalah dengan melakukan langkah-langkah terperinci
mengembangkan atau memperkaya gagasan orang lain
mencoba atau menguji detil-detil untuk melihat arah yang akan ditempuh mempunyai rasa keindahan yang kuat
sehingga tidak puas dengan penampilan yang kosong atau sederhana
[image:42.612.138.499.105.705.2]27
5. Menilai (Mengevaluasi)
menentukan patokan penilaian sendiri dan menentukan apakah suatu pernyataan benar, suatu rencana sehat, atau suatu tindakan bijaksana
mampu mengambil keputusan terhadap situasi yang terbuka tidak hanya mencetuskan
gagasan, tetapi juga melaksanakannya
memberi pertimbangan atas dasar sudut pandangnya sendiri
menentukan pendapat sendiri mengenai suatu hal
menganalisis masalah atau penyelesaian secara kritis dengan selalu menanyakan “Mengapa”?
mempunyai alasan (rasionale) yang dapat dipertanggungjawabkan untuk mencapai suatu keputusan
merancang suatu rencana kerja dari gagasan-gagasan yang tercetus
pada waktu tertentu tidak menghasilkan gagasan-gagasan tetapi menjadi peneliti atau penilai yang kritis
menentukan pendapat dan bertahan terhadapnya.
Dari penjelasan di atas, dapat diketahui bahwa indikator
kemampuan berpikir kreatif matematis meliputi kelancaran berpikir,
keluwesan, elaborasi dan keaslian pemikiran. Jadi dapat disimpulkan
bahwa semakin tinggi tingkat kelancaran berpikir, keluwesan, elaborasi
dan keaslian pemikirannya maka semakin tinggi pula tingkat kreativitas
berpikirnya.
Pada penelitian ini, peneliti menggunakan beberapa indikator
kemampuan berpikir kreatif menurut Utami Munandar dan membatasi
dalam 3 indikator yang akan dijadikan tolak ukur kemampuan berpikir
28
Tabel 2.2
Indikator Kemampuan Berpikir Kreatif yang diteliti
Pengertian Perilaku
1. Berpikir Lancar ( Fluency)
mencetuskan banyak
gagasan, jawaban,
penyelesaian masalah
menjawab dengan sejumlah
jawaban jika ada pertanyaan
mempunyai banyak gagasan
mengenai suatu masalah
lancar mengungkapkan
gagasan-gagasannya
2. Berpikir Luwes (Fleksibility)
menghasilkan gagasan atau
jawaban yang bervariasi
memberikan bermacam-macam
[image:44.612.137.501.137.712.2]penafsiran terhadap suatu
gambar, cerita atau masalah
jika diberikan suatu masalah
biasanya memikirkan bermacam-macam cara yang berbeda untuk menyelesaikannya
menggolongkan hal-hal menurut
pembagian (kategori) yang
berbeda-beda
3. Berpikir Rinci (Elaboration)
mampu memperkaya dan
mengembangkan suatu
gagasan atau produk
mencari arti yang lebih mendalam
terhadap jawaban atau
pemecahan masalah dengan
melakukan langkah-langkah
terperinci
menambahkan garis-garis,
warna-warna, dan detil-detil (bagian-
bagian) terhadap gambarnya
29
Pembelajaran dengan menggunakan strategi MHM tertuju kepada
aspek berpikir. Dimana kebiasaan-kebiasaan positif yang dilakukan secara
konsisten akan berpotensi membentuk kemampuan-kemampuan positif,
termasuk salah satunya kebiasaan berpikir secara matematis. Sementara
itu, kemampuan berpikir kreatif adalah kemampuan mengemukakan,
menghasilkan berbagai macam ide, mampu mengarahkan ide tersebut
dengan lebih terinci dan mampu memberikan respons yang baru dan unik
untuk memecahkan suatu masalah. Berdasarkan pemaparan penjelasan
mengenai strategi MHM dan kemampuan berpikir kreatif ditemukan suatu
kesamaan dalam hal penerapannya. Dimana kedua variabel tersebut
sama-sama mengedepankan cara berpikir seseorang. Diharapkan dengan
menerapkan strategi MHM pada penelitian ini dengan membiasakan siswa
untuk melakukan kebiasaan berpikir secara matematis akan dapat
meningkatkan kemampuan berpikir kreatif matematisnya dalam
menyelesaikan suatu masalah. Hubungan antara strategi MHM dengan
kemampuan berpikir kreatif matematis pada penelitian ini diteliti dengan
mengamati ragam aktivitas yang dilakukan oleh siswa.
Ada banyak jenis aktivitas yang dapat dilakukan oleh siswa di
sekolah. Paul B. Diedrich membuat suatu daftar yang berisi 177 macam
kegiatan siswa yang antara lain dapat digolongkan sebagai berikut:28 1. Visual activities, yang termasuk di dalamnya misalnya, membaca, memperhatikan gambar demonstrasi, percobaan, pekerjaan orang lain dan
sebagainya.
2. Oral activities, seperti: menyatakan, merumuskan, bertanya, memberi saran, mengeluarkan pendapat, mengadakan wawancara, diskusi, interupsi
dan sebagainya.
3. Listening activities, sebagai contoh, mendengarkan: uraian, percakapan diskusi, musik, pidato, dan sebagainya.
28
30
4. Writing activities, seperti menulis: cerita, karangan, laporan, tes, angket, menyalin, dan sebagainya.
5. Drawing activities, misalnya: menggambar, membuat grafik, peta, diagram, pola, dan sebagainya.
6. Motor activities, yang termasuk di dalamya antara lain: melakukan percobaan, membuat konstruksi, model, mereparasi, bermain, berkebun,
memelihara binatang, dan sebagainya.
7. Mental activities, sebagai contoh misalnya: menganggap, mengingat, memecahkan soal, menganalisis, melihat hubungan, mengambil keputusan,
dan sebagainya.
8. Emotional activities, seperti misalnya: menaruh mi