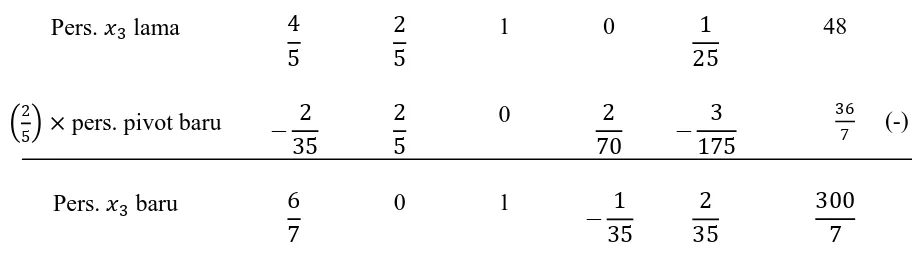F UZZY LINEAR PROGRAMMING
(FLP) DENGAN KONSTANTA
SEBELAH KANAN BERBENTUK BILANGAN
F UZZY
DAN
BERBENTUK TRAPEZOIDAL
SKRIPSI
DEWI YANNI FRANSISKA SAMOSIR
070803046
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
FUZZY LINEAR PROGRAMMING (FLP) DENGAN KONSTANTA SEBELAH KANAN BERBENTUK BILANGAN FUZZY DAN BERBENTUK TRAPEZOIDAL
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
DEWI YANNI FRANSISKA SAMOSIR
070803046
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : FUZZY LINEAR PROGRAMMING (FLP) DENGAN KONSTANTA SEBELAH KANAN BERBENTUK BILANGAN FUZZY DAN BERBENTUK
TRAPEZOIDAL
Kategori : SKRIPSI
Nama : DEWI YANNI FRANSISKA SAMOSIR
Nomor Induk Mahasiswa : 070803046
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, September 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Ujian Sinulingga, M.Si Drs. Faigiziduhu Bu‟ulölö, M.Si
NIP 19560303 198403 1 004 NIP 19531218 198003 1 003
Diketahui/ Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus, M.Si
PERNYATAAN
FUZZY LINEAR PROGRAMMING (FLP) DENGAN KONSTANTA SEBELAH KANAN BERBENTUK BILANGAN FUZZY DAN BERBENTUK TRAPEZOIDAL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan,
PENGHARGAAN
Hanya pujian dan ucapan syukur yang bisa penulis panjatkan kepada Tuhan Yang Maha Kuasa, buat setiap kebaikan, pertolongan dan penyertaan-Nya yang boleh dirasakan penulis dalam keseluruhan hidup yang dipercayakan-Nya, terkhusus buat pertolongan-Nya dalam pengerjaan skripsi ini mulai dari awal sampai akhir. Terpuji termulialah DIA.
Penulis juga mengucapkan terimakasih kepada pihak-pihak yang turut membantu baik dalam dukungan dana, pemikiran dan doa sehingga skripsi ini dapat selesai. Penulis mengucapkan terimakasih kepada Bapak Drs. Faigiziduhu Bu‟ulölö, M.Si dan Drs. Ujian Sinulingga, M.Si sebagai Dosen Pembimbing, Bapak Drs. Suyanto, M.Kom dan Drs. Rachmad Sitepu, M.Si sebagai Dosen Pembanding/ Penguji, atas bimbingan, kritikan dan saran untuk perbaikan skripsi ini. Dan juga kepada Bapak O. Samosir dan Ibu L. Hutapea sebagai orangtua tercinta, yang dengan penuh kesabaran memberikan dukungan kepada penulis, dan kepada adik-adik yaitu Delviana, Dollian, Dian yang juga selalu memberikan semangat, dan juga seluruh keluarga besar Samosir dan Hutapea yang terus mendukung dan mendoakan. Dan kepada KTB Florence dan KK Diselva, dan juga teman-teman seperjuangan di Matematika 2007 USU.
Penulis menyadari masih banyak kekurangan dalam pengerjaan skripsi ini. Oleh karena itu penulis juga mengaharapkan kritik dan saran yang bersifat membangun. Akhir kata penulis berharap skripsi ini dapat bermanfaat bagi yang membacanya.
Medan, September 2011
Penulis
ABSTRAK
Salah satu asumsi yang harus dipenuhi dalam permasalahan program linier adalah asumsi kepastian (Deterministik/ Certainty), di mana asumsi ini menyatakan bahwa semua parameter dalam program linier harus bernilai tetap dan diketahui secara pasti. Akan tetapi dalam kenyataannya asumsi ini jarang dipenuhi karena pada umumnya permasalahan program linier diselesaikan untuk memilih suatu tindakan atau keputusan yang akan digunakan untuk waktu yang akan datang. Maka parameter-parameter yang digunakan adalah suatu prediksi untuk waktu yang akan datang yang bersifat tidak pasti. Dengan adanya faktor ketidakpastian tersebut, maka permasalahan program linier dengan kondisi parameter yang tidak pasti di dekati dengan teori himpunan fuzzy dalam pengerjaannya. Dalam tulisan ini dibahas suatu bentuk fuzzy linear programming (FLP) di mana hanya konstanta sebelah kanan berbentuk bilangan fuzzy dan juga berbentuk trapezoidal beserta contoh numeriknya, di mana permasalahan dikonversikan ke dalam bentuk program linier biasa dan juga menggunakan variabel dummy dan 0 1. Selanjutnya untuk memperoleh solusi optimalnya digunakan bantuan metode simpleks dan program QM.
ABSTRACT
One of assumption that must be fulfilled in linear programming problem is the certainty assumption (Deterministic/ Certainty) where this assumption declares that all parameters in linear programming must have permanent value and known surely. But practically, this assumption is seldom to be fulfilled because in generally linear programming problem is finished to choose an action or a decision that will be used for in the future. So parameters are the prediction that will be used for an uncertainty time in future. Because of the existence of the uncertainty factor, so linear programming problem with the uncertainty parameter condition was discussed with fuzzy set theory. In this writing, was discussed about a form of fuzzy linear programming (FLP) where only right side constanta formed fuzyy numeral and Trapezoidal along with the numeric example, and the problem was conversed into classic linear programming and also use dummy variable and 0
1. The next is to get the optimal solution using simplex method and QM software.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel ix
Daftar Gambar x
Bab 1 Pendahuluan 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Batasan Masalah 3
1.4 Tinjauan Pustaka 3
1.5 Tujuan Penelitian 5
1.6 Kontribusi Penelitian 5
1.7 Metodologi Penelitian 5
Bab 2 Landasan Teori 6
2.1 Program Linier 6
2.2 Asumsi-asumsi Yang Harus Dipenuhi Dalam Program Linier 8
2.3 Metode Simpleks 9
2.3.2 Program QM 13
2.4 Teori Himpunan Crisp Dan Teori Himpunan Fuzzy 13
2.5 Fungsi Keanggotaan Trapezoidal (Trapesium) 14
2.6 Fuzzzy Linear Programming (FLP) 15
2.6.1 Program Linier Dengan Koefisien Teknologi
Berbentuk Bilangan Fuzzy 16
2.6.2 Program Linier Dengan Koefisien Teknologi
Dan Konstanta Sebelah Kanan Berbentuk Bilangan
Fuzzy 19
Bab 3 Pembahasan 23
3.1 Program Linier dengan Hanya Konstanta Sebelah
Kanan Berbentuk Bilangan Fuzzy 23
3.2 Pembahasan Contoh Numerik 25
Bab 4 Kesimpulan dan Saran 40
4.1 Kesimpulan 40
4.2 Saran 40
Daftar Pustaka 42
Lampiran
DAFTAR TABEL
Halama n
Tabel 2.1 Bentuk Umum Tabel Simplek Awal 11
Tabel 3.1 Tabel Simplek Awal 1 34
Tabel 3.2 Tabel Simplek Iterasi Pertama 1 35
Tabel 3.3 Tabel Simplek Iterasi Kedua 1 36
Tabel 3.4 Tabel Simplek Iterasi Ketiga 1 37
Tabel 3.5 Tabel Simplek Awal 2 38
Tabel 3.6 Tabel Simplek Iterasi Pertama 2 39
Tabel 3.7 Tabel Simplek Iterasi Kedua 2 40
DAFTAR GAMBAR
Halaman
ABSTRAK
Salah satu asumsi yang harus dipenuhi dalam permasalahan program linier adalah asumsi kepastian (Deterministik/ Certainty), di mana asumsi ini menyatakan bahwa semua parameter dalam program linier harus bernilai tetap dan diketahui secara pasti. Akan tetapi dalam kenyataannya asumsi ini jarang dipenuhi karena pada umumnya permasalahan program linier diselesaikan untuk memilih suatu tindakan atau keputusan yang akan digunakan untuk waktu yang akan datang. Maka parameter-parameter yang digunakan adalah suatu prediksi untuk waktu yang akan datang yang bersifat tidak pasti. Dengan adanya faktor ketidakpastian tersebut, maka permasalahan program linier dengan kondisi parameter yang tidak pasti di dekati dengan teori himpunan fuzzy dalam pengerjaannya. Dalam tulisan ini dibahas suatu bentuk fuzzy linear programming (FLP) di mana hanya konstanta sebelah kanan berbentuk bilangan fuzzy dan juga berbentuk trapezoidal beserta contoh numeriknya, di mana permasalahan dikonversikan ke dalam bentuk program linier biasa dan juga menggunakan variabel dummy dan 0 1. Selanjutnya untuk memperoleh solusi optimalnya digunakan bantuan metode simpleks dan program QM.
ABSTRACT
One of assumption that must be fulfilled in linear programming problem is the certainty assumption (Deterministic/ Certainty) where this assumption declares that all parameters in linear programming must have permanent value and known surely. But practically, this assumption is seldom to be fulfilled because in generally linear programming problem is finished to choose an action or a decision that will be used for in the future. So parameters are the prediction that will be used for an uncertainty time in future. Because of the existence of the uncertainty factor, so linear programming problem with the uncertainty parameter condition was discussed with fuzzy set theory. In this writing, was discussed about a form of fuzzy linear programming (FLP) where only right side constanta formed fuzyy numeral and Trapezoidal along with the numeric example, and the problem was conversed into classic linear programming and also use dummy variable and 0
1. The next is to get the optimal solution using simplex method and QM software.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Konsep program linier ditemukan dan diperkenalkan pertamakali oleh George Dantzig
yang berupa metode mencari solusi masalah program linier dengan banyak variabel
keputusan. Dantzig bekerja di bidang penelitian teknis matematis untuk memecahkan
masalah logistik militer angkatan udara Amerika Serikat selama perang dunia II.
Penelitiannya didukung oleh J. Von Neumann, L. Hurwich dan T. C. Koopmans yang
bekerja dalam bidang yang sama. Adapun teknik yang asli adalah program saling
ketergantungan kegiatan-kegiatan dalam suatu struktur linier dan kemudian
disederhanakan menjadi program linier.
Penerapan program linier pertama kalinya adalah dalam bidang perencanaan
militer, khususnya dalam perang Perang Dunia II oleh angkatan bersenjata Amerika
Serikat dan Inggris. Sejak itulah seiring dengan berkembangnya waktu, dalam bidang
teknologi dan pembangunan, teknik-teknik analisis program linier dengan cepat sekali
menjalar dan diterapkan dalam berbagai bidang dan disiplin ilmu dalam rangka
memecahkan berbagai permasalahan yang dihadapi.
Model program linier mengandung asumsi-asumsi implisit tertentu yang harus
dipenuhi agar definisinya sebagai suatu masalah program linier menjadi absah. Dan salah
satu asumsi dasar dalam permasalahan program linier adalah asumsi kepastian
(deterministik/ certainty), di mana setiap parameter yaitu data-data dalam pemodelan
program linier yang terdiri dari koefisien-koefisien fungsi tujuan, konstanta-konstanta
sebelah kanan dan koefisien-koefisien teknologi diketahui secara pasti. Tetapi dalam
persoalan program linier diselesaikan untuk memilih suatu tindakan atau sebuah
keputusan yang bisa dipergunakan untuk waktu yang akan datang. Jadi
parameter-parameter yang digunakan didasarkan atas suatu prediksi mengenai kondisi di waktu yang
akan datang (belum terjadi/ tidak pasti). Dengan adanya ketidakpastian tersebut maka
biasanya akan dilakukan analisa kepekaan (sensitivitas) setelah diperoleh penyelesaian
optimalnya, supaya dari hasil analisa sensitivitas itu dapat dilihat parameter-parameter
yang sensitif. Hasil dari analisa sensitivitas ini juga akan dijadikan acuan dalam
memprediksi parameter-parameter untuk kondisi yang akan datang tersebut. Dalam
pengambilan keputusan dari suatu permasalahan program linier yang semakin kompleks,
kadang-kadang tingkat ketidakpastian yang muncul juga akan semakin kompleks untuk
melakukan analisa sensitivitas. Untuk mengakomodasikan tingkat ketidakpastian tersebut
maka akan didekati dengan teori himpunan fuzzy. Dan dengan adanya tingkat
ketidakpastian tersebut, maka permasalahan program linier pun mengalami
perkembangan menjadi permasalahan fuzzy linier programming (FLP). Dalam tulisan ini
akan diselesaikan suatu permasalahan fuzzy linear programming (FLP) di mana hanya
konstanta sebelah kanan yang berbentuk bilangan fuzzy dan berbentuk trapezoidal.
Dengan alasan di atas maka penulis mengerjakan skripsi ini dengan judul: “F uzzy
Linear Programming (FLP) dengan Konstanta Sebelah Kanan Berbentuk Bilangan
F uzzydan Berbentuk Trapezoidal”.
1.2 Perumusan Masalah
Dalam tulisan ini penulis menyelesaikan suatu permasalahan fuzzy linear programming
(FLP) dengan salah satu parameternya (konstanta sebelah kanan) tidak pasti dengan
menggunakan pendekatan teori himpunan fuzzy sehingga permasalahan dapat dibuat ke
dalam bentuk program linier biasa dan dengan menggunakan metode simpleks dan
program QM diperoleh solusi optimal dari permasalahan fuzzy linear programming (FLP)
1.3 Batasan Masalah
Tulisan ini dibatasi pada permasalahan fuzzy linear programming (FLP) dengan
parameter-parameter yaitu hanya konstanta sebelah kanan yang berupa bilangan fuzzy dan
konstanta sebelah kanan tersebut juga berbentuk trapezoidal. Penulis juga membatasi
kasus yang dibahas yaitu hanya kasus maksimasi.
1.4 Tinjauan Pustaka
Sri Mulyono (2004) dalam bukunya „Riset Operasi‟ mengatakan bahwa program linier
adalah salah satu teknik operasi riset atau metode matematik dalam mengalokasikan
sumber daya yang langka untuk mencapai tujuan tunggal seperti memaksimumkan
keuntungan atau meminimumkan biaya,
Fien Zulfikarijah (2004) dalam bukunya „Operation Research‟ mengatakan bahwa dalam model linear programming terdapat asumsi-asumsi yang harus dipenuhi agar
permasalahan linear programming menjadi absah, yaitu kesebandingan (proportionality),
penambahan (additivity), pembagian (divisibility), dan kepastian (deterministic/
certainty).
Basuki Rahmat, dkk dalam jurnal (2005) „Aplikasi Fuzzy Linear Programming Untuk Optimasi Hasil Perencanaan Produksi‟ mengatakan bahwa fuzzy linear programming (FLP) adalah metode linear programming yang diaplikasikan dalam
lingkungan fuzzy. Dalam fuzzy linear programming (FLP), fungsi objektif dan batasan
tidak lagi mempunyai arti yang benar-benar tegas karena ada beberapa hal yang perlu
mendapat pertimbangan dalam sistem.
Sri Kusuma Dewi dan Hari Purnomo (2004) dalam bukunya „Aplikasi Logika Fuzzy Untuk Pendukung Keputusan‟ mengatakan bahwa salah satu model program linier
klasik, adalah:
=
Dengan batasan (kendala):
� , 0
Di mana , ∈ , ∈ ,� ∈ ×
Atau untuk kasus minimasi, adalah:
Minimumkan:
=
Dengan batasan (kendala):
� , 0
Dimana , ∈ , ∈ ,� ∈ ×
�, , adalah bilangan-bilangan crisp, tanda “ ” pada kasus maksimasi dan tanda “ ”
pada kasus minimasi juga bermakna tegas/ jelas (crisp), demikian juga perintah
“maksimumkan” dan “minimumkan” merupakan bentuk imperatif tegas. Jika di
asumsikan bahwa keputusan permasalahan program linier akan dibuat pada kondisi/
lingkungan fuzzy, maka model klasik permasalahan program linier di atas akan
mengalami sedikit perubahan, yaitu:
1. Bentuk imperatif pada fungsi objektif tidak lagi benar-benar “maksimumkan” atau
“minimumkan”, karena adanya beberapa hal yang perlu mendapat pertimbangan
dalam suatu sistem.
2. Tanda “ ” pada batasan dalam kasus maksimasi dan tanda “ ” pada batasan
dalam kasus minimasi tidak lagi bermakna tegas (crisp) secara matematis, namun
sedikit mengalami pelanggaran makna. Hal ini juga disebabkan karena adanya
beberapa hal yang perlu dipertimbangkan dalam sistem yang mengakibatkan
batasan tidak dapat didekati secara tegas.
Pada umumnya pemecahan permasalahan fuzzy linear programming (FLP)
klasik. Hasil akhirnya diperoleh dalam bentuk bilangan nyata yang menggambarkan
kompromi dari bilangan-bilangan fuzzy yang diproses didalamnya.
1.5 Tujuan Penelitian
Dalam tulisan ini penulis memusatkan pembicaraan pada permasalahan fuzzy linear
programming (FLP) dengan tujuan untuk memperlihatkan bagaimana mengatasi suatu
permasalahan fuzzy linear programming (FLP) dengan hanya konstanta sebelah kanan
yang berupa bilangan fuzzy dan berbentuk trapezoidal sehingga memperoleh solusi
optimal.
1.6 Kontribusi Penelitian
Tulisan ini diharapkan dapat digunakan sebagai bahan referensi dalam penyelesaian
permasalahan program linier dengan kondisi parameter-parameter yang tidak pasti (fuzzy
linear programming) dan salah satunya parameter konstanta sebelah kanan yang
berbentuk bilangan fuzzy dan berbentuk trapezoidal.
1.7 Metodologi Penelitian
Tulisan ini bersifat literatur dengan menggunakan tahapan-tahapan berikut dalam
pengerjaannya, yaitu:
1. Menjelaskan tentang program linier, asumsi-asumsi dasar dalam program linier,
metode simpleks, program QM, teori himpunan crisp dan teori himpunan fuzzy,
fungsi keanggotaan trapezoidal dan fuzzy linear programming (FLP).
2. Menjelaskan tentang program linier dengan hanya konstanta sebelah kanan yang
3. Menyelesaikan suatu contoh permasalahan program linier dengan hanya konstanta
sebelah kanan yang berbentuk bilangan fuzzy dan berbentuk trapezoidal.
4. Menarik kesimpulan yang berupa solusi optimal dari permasalahan fuzzy linear
BAB 2
LANDASAN TEORI
2.1 Program linier
Program linier adalah suatu teknik penyelesaian optimal atas suatu problema keputusan
dengan cara menentukan terlebih dahulu fungsi tujuan (memaksimalkan atau
meminimalkan) dan kendala-kendala yang ada ke dalam model matematik persamaan
linier. Metode analisis yang paling bagus untuk menyelesaikan persoalan alokasi sumber
ialah metode program linier. Pokok pikiran yang utama dalam menggunakan program
linier ialah merumuskan masalah dengan jelas dengan menggunakan sejumlah informasi
yang tersedia. Sesudah masalah terumuskan dengan baik, maka langkah berikutnya ialah
menerjemahkan masalah yang ada ke dalam model matematika.
Program linier sering digunakan dalam menyelesaikan problema-problema alokasi
sumber daya, seperti dalam bidang manufacturing, pemasaran, keuangan, personalia,
administrasi dan lain sebagainya.
Bentuk standar dari permasalahan program linier adalah:
a. Penulisan dalam bentuk skalar untuk kasus maksimasi
Maksimumkan :
1, 2,…, = = 1 1+ 2 2+ + (2.1)
Dengan kendala :
11 1+ 12 2+ + 1 = 1
21 1+ 22 2+ + 2 = 2
1, 2, , 0
Atau dapat juga ditulis dengan menggunakan lambang penjumlahan yaitu:
Maksimumkan :
1, 2,…, = = =1 (2.2)
Dengan kendala:
=1 = , = 1, 2, ,
0, = 1, 2, ,
Di mana , dan diketahui konstan.
Keterangan:
= parameter yang dijadikan kriteria optimisasi, atau koefisien peubah pengambilan
keputusan dalam fungsi tujuan. Untuk kasus maksimasi menunjukkan
keuntungan atau penerimaan per unit, sementara dalam kasus minimasi
menunjukkan biaya per unit.
� = peubah pengambilan keputusan atau kegiatan (yang ingin dicari; yang tidak diketahui). Karena = 1, 2, , berarti dalam hal ini terdapat variabel keputusan.
= koefisien teknologi peubah pengambilan keputusan dalam kendala ke- .
= sumber daya yang terbatas, yang membatasi kegiatan atau usaha yang
bersangkutan; disebut juga konstanta sebelah kanan dari kendala ke- . Karena
= 1, 2, , berarti dalam hal ini terdapat jenis sumber daya. = Nilai skalar kriteria pengambilan keputusan nilai fungsi tujuan.
b. Penulisan dalam bentuk matriks untuk kasus maksimasi
Maksimumkan :
= � (2.3)
Dimana � =
2.2 Asumsi-asumsi yang Harus Dipenuhi dalam Program Linier
Ada beberapa asumsi yang harus dipenuhi dalam merumuskan suatu problema keputusan
ke dalam model matematik persamaan linier sehingga problema itu dapat dikatakan absah
menjadi suatu permasalahan program linier, yaitu:
a. Asumsi Linierity (Linieritas)
Asumsi ini menyatakan bahwa fungsi tujuan dan semua kendala harus berbentuk linier.
Dengan kata lain, apabila suatu kendala melibatkan dua variabel keputusan maka dalam
diagram dimensi dua kendala tersebut akan berupa suatu garis lurus. Demikian juga
apabila suatu kendala melibatkan tiga variabel akan menghasilkan suatu bidang datar dan
kendala yang melibatkan variabel akan menghasilkan hyperplane (bentuk geometris
yang rata) dalam ruang berdimensi .
b. Asumsi Additivity (Aditivitas/ Penambahan)
Asumsi ini menyatakan bahwa nilai parameter suatu kriteria optimasi (koefisien variabel
keputusan dan fungsi tujuan) merupakan jumlah dari individu-individu dalam program
linier. Misalnya, keuntungan total yang merupakan variabel keputusan, sama dengan
jumlah keuntungan yang diperoleh dari masing-masing kegiatan ( ). Dan juga, seluruh
sumber daya yang digunakan untuk semua kegiatan harus sama dengan jumlah sumber
daya yang digunakan untuk masing-masing kegiatan.
c. Asumsi Proportionality (Proporsionalitas/ Kesebandingan)
Asumsi ini menyatakan bahwa jika variabel keputusan ( ) mengalami perubahan, maka
( ) dan juga pada kendalanya ( ). Misalnya, apabila variabel keputusan dinaikkan
dua kali. Maka secara proporsional (seimbang dan serasi) nilai-nilai fungsi tujuan dan
kendalanya juga akan menjadi dua kali lipat.
d. Asumsi Divisibility (Divisibilitas/ Pembagian)
Asumsi ini menyatakan bahwa nilai variabel keputusan ( ) yang diperoleh tidak harus
berupa bilangan bulat, artinya nilai variabel keputusan bisa diperoleh pada nilai pecahan.
e. Asumsi Certainty (Deterministik/ Kepastian)
Asumsi ini menghendaki bahwa semua parameter dalam program linier ( , dan ) harus bernilai tetap dan diketahui atau ditentukan secara pasti.
2.3 Metode Simpleks
Pada umumnya permasalahan program linier dapat diselesaikan dengan menggunakan
metode grafik dan metode simpleks. Kedua metode ini tentunya memiliki kebaikan dan
kelemahannya. Aplikasi kedua metode ini tergantung atas problema yang dihadapi.
Metode grafik digunakan apabila jumlah variabel keputusan hanya dua dan jumlah
kendala dalam model sedikit (pada umumnya tidak lebih dari 4 kendala). Apabila jumlah
kendalanya banyak (> 4 kendala), maka akan sukar untuk melukiskan garis kendalanya
dalam grafik.
Sehingga meskipun permasalahan program linier dapat diselesaikan dengan
menggunakan metode grafik, akan tetapi untuk permasalahan program linier dengan lebih
dari 3 variabel maka metode grafik ini tidak dapat digunakan. Oleh karena itu, pada tahun
1947 George Dantzig mengajukan satu metode yang paling berhasil untuk menyelesaikan
suatu permasalahan program linier, dan metode itu dinamakan metode simpleks dan telah
Metode simpleks adalah suatu metode yang secara sistematis dimulai dari suatu
pemecahan dasar yang fisibel ke pemecahan dasar fisibel (feasible) lainnya dan ini
dilakukan berulang-ulang (dengan jumlah ulangan yang terbatas) sehingga akhirnya
tercapai suatu pemecahan dasar yang optimum dan pada setiap step/ iterasi menghasilkan
suatu nilai dari fungsi tujuan yang selalu lebih besar atau sama dari step-step sebelumnya
(Supranto, 1983).
2.3.1 Langkah-langkah Metode Simpleks
Mengubah bentuk baku model program linier ke dalam bentuk tabel akan memudahkan
proses perhitungan simpleks. Langkah-langkah perhitungan dalam algoritma simpleks
adalah:
a. Berdasarkan bentuk baku, tentukan solusi awal (initial basic feasible solution)
dengan menetapkan n-m variabel nonbasis sama dengan nol. Di mana n jumlah variabel
dan m banyaknya kendala.
b. Kemudian dipilih sebuah entering variable (variabel yang masuk) di antara yang
sedang menjadi variabel nonbasis, yang jika dinaikkan di atas nol, dapat memperbaiki
nilai fungsi tujuan. Apabila tidak ada maka berhenti, berarti solusi sudah optimal. Jika
tidak, maka lanjutkan ke langkah c.
c. Selanjutnya pilih sebuah leaving variable (variabel yang keluar) di antara yang
sedang menjadi variabel basis yang harus menjadi nonbasis (nilainya menjadi nol) ketika
entering variable menjadi variabel basis.
d. Tentukan solusi yang baru dengan membuat entering variable dan leaving
variable menjadi nonbasis. Selanjutnya kembali ke langkah b.
Selanjutnya akan dijelaskan langkah-langhkah penyelesaian persoalan yang
formulasinya mempunyai bentuk sebagai berikut:
Maksimumkan:
=1 ,
0, = 1, 2, , , = 1, 2, ,
Perhitungan simpleks yang lebih rinci akan diterangkan dengan langkah berikut:
Langkah 1 : Mengubah fungsi tujuan dan fungsi kendala.
Fungsi tujuan diubah menjadi bentuk implisit dengan jalan menggeser semua ke kiri.
Fungsi kendala selain kendala nonnegatif diubah menjadi bentuk persamaan dengan
menambahkan variabel slack, yaitu suatu variabel yang mewakili tingkat pengangguran
kapasitas yang merupakan batasan.
Langkah 2 : Mentabulasikan persamaan-persamaan yang diperoleh pada langkah 1.
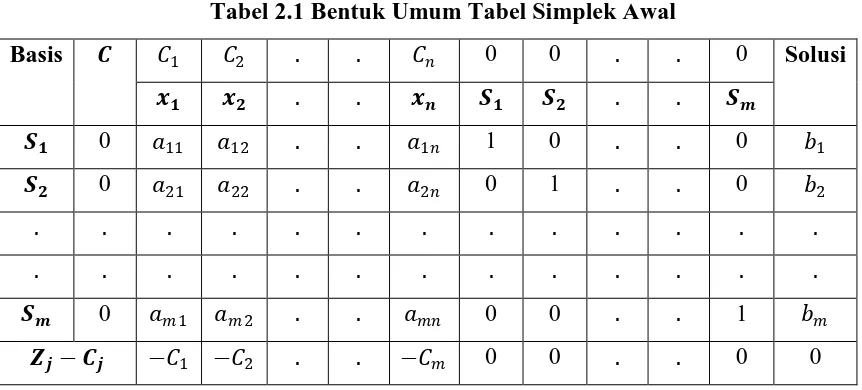
Tabel 2.1 Bentuk Umum Tabel Simplek Awal
Basis 1 2 . . 0 0 . . 0 Solusi
� � . . � . .
0 11 12 . . 1 1 0 . . 0 1
0 21 22 . . 2 0 1 . . 0 2
. . . .
. . . .
0 1 2 . . 0 0 . . 1
− − 1 − 2 . . − 0 0 . . 0 0
Kolom baris menunjukkan variabel yang sedang menjadi basis yaitu 1, 2, , yang
nilainya ditunjukkan oleh kolom solusi. Secara tidak langsung ini menunjukkan bahwa
variabel nonbasis 1, 2, , (yang tidak ditunjukkan pada kolom basis) sama dengan
Langkah 3 : Menentukan entering variable (variabel yang masuk).
Tabel di atas memperlihatkan bahwa pada baris − kolom 1, 2, , nilainya
negatif. Untuk persoalan dengan fungsi maksimasi, baris − dapat diperbaiki dengan
meningkatkan nilai 1, 2, , pada baris − menjadi tidak negatif. Untuk itu pilihlah kolom pada baris − (termasuk kolom slack) yang mempunyai nilai negatif
terbesar, selanjutnya kolom ini digunakan sebagai entering variable. Jika ditemukan lebih
dari satu nilai negatif angka terbesar pilihlah salah satu, sebaliknya jika tidak ditemukan
nilai negatif berarti solusi sudah optimal.
Sebaliknya untuk kasus minimasi, pilihlah kolom pada baris − yang nilainya positif
terbesar. Jika tidak ditemukan nilai positif berarti solusi sudah optimal.
Dan pada persoalan di atas kolom 2 merupakan entering variable.
Langkah 4 : Menentukan leaving variable (variabel yang keluar).
Leaving variable dipilih dari rasio yang nilainya positif terkecil. Rasio diperoleh dengan
cara membagi nilai solusi dengan koefisien pada kolom entering nya.
= (2.5)
Baris yang memiliki rasio yang nilainya positif terkecil selanjutnya akan digunakan
sebagai leaving variable. Jika tidak ada elemen yang nilainya positif dalam kolom kunci
(kolom entering variable) ini, maka persoalan tidak memiliki pemecahan.
Kolom pada entering variable dinamakan entering column, dan baris yang berhubungan
dengan leaving variable dinamakan persamaan pivot. Elemen pada perpotongan entering
column dan persamaan pivot dinamakan elemen pivot.
Langkah 5 : Menentukan persamaan pivot baru.
Langkah 6 : Menentukan persamaan-persamaan baru selain persamaan pivot baru.
Persamaan baru = (Persamaan lama) – (Koefisien kolom entering x persamaan pivot
baru) (2.7)
Langkah 7 : Lanjutkan perbaikan-perbaikan.
Lakukan langkah perbaikan dengan cara mengulang langkah 3 sampai langkah 6 hingga
diperoleh hasil optimal.
2.3.2 Program QM
Program QM adalah paket program komputer untuk menyelesaikan persoalan-persoalan
metode kuantitatif, manajemen sains atau riset operasi. Program QM juga adalah salah
satu software yang dapat digunakan untuk membantu perhitungan masalah program
linier.
2.4 Teori Himpunan Crisp Dan Teori Himpunan F uzzy
Himpunan Crisp A didefinisikan oleh item-item yang ada pada himpunan itu. Pada teori
himpunan Crisp, keberadaan suatu elemen pada suatu himpunan A, hanya akan memiliki
dua kemungkinan keanggotaan, yaitu menjadi anggota A atau tidak menjadi anggota A
(Chak, 1998). Suatu nilai yang menunjukkan seberapa besar tingkat keanggotaan suatu
elemen dalam suatu himpunan A, sering disebut dengan nama nilai keanggotaan atau derajat keanggotaan, dinotasikan dengan � . Pada himpunan Crisp, hanya ada 2 nilai keanggotaan, yaitu � = 1 untuk menjadi anggota A, dan � = 0 untuk bukan anggota A.
Teori himpunan fuzzy yang ditemukan oleh Lotfi A. Zadeh pada tahun 1965
merupakan kerangka matematis yang digunakan untuk mempresentasikan ketidakpastian,
ketidakjelasan, ketidaktepatan, kekurangan informasi, dan kebenaran parsial (Tettamanzi,
2001). Himpunan fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi
karakteristik sedemikian hingga fungsi tersebut akan mencakup bilangan real pada
interval 0, 1 . Nilai keanggotaannya menunjukkan bahwa suatu item dalam semesta pembicaraan tidak hanya berada pada 0 atau 1, namun juga nilai yang terletak
diantaranya. Dengan kata lain, nilai kebenaran suatu item tidak hanya bernilai benar atau
salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar, dan masih ada nilai-nilai
yang terletak antara benar dan salah.
Menurut (Kusumadewi, 2002)
Misalkan dimiliki variabel umur yang dibagi menjadi 3 kategori, yaitu:
MUDA umur < 35 tahun
SETENGAH BAYA 35 tahun umur 55 tahun
TUA umur > 55 tahun
Dengan menggunakan pendekatan himpunan Crisp, amatlah tidak adil untuk
menetapkan nilai SETENGAH BAYA. Pendekatan ini bisa saja dilakukan untuk hal-hal
sangatlah jauh berbeda, di mana umur 55 tahun termasuk dalam setengah baya,
sedangkan umur 56 tahun termasuk sudah tua. Demikian juga halnya untuk klasifikasi
muda dan tua. Orang yang berumur 34 tahun dikatakan muda, sedangkan orang yang
berumur 35 tahun sudah tidak muda lagi. Orang yang berumur 55 tahun termasuk stengah
baya menurut pengklasifikasian, tetapi orang yang berumur 55 tahun lebih 1 hari sudah
tidak setengah baya lagi tetapi sudah termasuk tua.
2.5 Fungsi Keanggotaan Trapezoidal (Trapesium)
Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan
pemetaan titik-titik input data ke dalam nilai keanggotaannya (sering juga disebut dengan
derajat keanggotaan) yang memiliki interval antara 0 sampai 1. Atau dapat dinotasikan
sebagai berikut :
�: � → 0, 1
Untuk x ∈� maka µA(x) adalah derajat keanggotaan x dalam A.
Suatu fungsi keanggotaan himpunan fuzzy disebut fungsi keanggotaan trapezoidal
jika mempunyai empat buah parameter, yaitu , , , ∈ ℝ dengan < < < , dan dinyatakan dengan , , , , dengan aturan:
−
− untuk (2.8)
1 untuk
; , , , = −
− untuk
0 untuk lainnya
Fungsi keanggotaan tersebut dapat juga dinyatakan dengan formula sebagai
; , , , = −
− , 1, −
− , 0 (2.9)
2.6 F uzzy Linear Programming (FLP)
Dalam fuzzy linear programming akan dicari suatu nilai yang merupakan fungsi
objektif yang akan dioptimasikan sedemikian hingga tunduk pada batasan-batasan yang
dimodelkan dengan menggunakan himpunan fuzzy.
Bentuk umum dari fuzzy linear programming (FLP) untuk kasus maksimasi
adalah:
Maksimumkan:
= =1 (2.10) Dengan kendala:
=1 , = 1, 2, , 0 , = 1, 2, ,
Di mana , , dan semuanya adalah bilangan fuzzy.
Keterangan:
= Fungsi tujuan
= Nilai kontribusi
= Variabel keputusan
= Koefisien teknologi
= Konstanta sebelah kanan (sumber daya)
2.6.1 Program Linier Dengan Koefisien Teknologi Berbentuk Bilangan F uzzy
Bentuk umum dari program linier dengan koefisien teknologi berbentuk bilangan fuzzy
Maksimumkan:
= =1 (2.11) Dengan kendala:
=1 , = 1, 2, ,
0, = 1, 2, ,
Untuk kasus program linier dengan koefisien teknologi berbentuk bilangan fuzzy,
terdapat beberapa asumsi yang harus dipenuhi, yaitu:
Asumsi 1: Koefisien teknologi dikatakan berbentuk bilangan fuzzy apabila memenuhi syarat fungsi keanggotaan linier berikut:
1 jika < (2.12)
= + − jika <
0 jika +
di mana ∈ dan > 0 untuk semua = 1, 2, , , = 1, 2, , .
Defuzzyfikasi adalah perubahan dari suatu besaran fuzzy ke suatu besaran
numerik, sedangkan fuzzyfikasi adalah perubahan dari besaran numerik ke suatu besaran
fuzzy.
Untuk mendefuzzyfikasi permasalahan ini, pertama-tama fungsi objektif (tujuan)
harus diubah ke dalam kondisi fuzzy, yaitu dengan menghitung batas bawah ( ) dan batas
atas ( ) dari nilai optimal awal. Batas-batas dari nilai optimal ini akan diperoleh dengan
menyelesaikan permasalahan program linier standar berikut:
Maksimumkan:
1 = =1 (2.13) Dengan kendala:
0, = 1, 2, ,
Dan juga
Maksimumkan:
2 = =1 (2.14) Dengan kendala:
=1 + , = 1, 2, ,
0, = 1, 2, ,
Dari persamaan di atas, nilai dari fungsi objektif (tujuan) berada di antara 1 dan 2 di
mana nilai koefisien teknologi mengalami perubahan di antara dan + . Dengan nilai batas bawah = 1, 2 dan nilai batas atas = 1, 2 .
Asumsi 2: Permasalahan linier crisp yaitu persamaan 1 dan 2 di atas memiliki nilai optimal yang terbatas. Pada kasus ini nilai optimal dari himpunan fuzzy �, di mana merupakan himpunan bagian dari , dalam buku Klir dan Yuan didefinisikan sebagai:
0 jika =1 < (2.15)
� =
=1 −
− jika =1 <
1 jika =1
Himpunan fuzzy dari kendala ke- , yaitu yang merupakan himpunan bagian dari ,
didefinisikan ke dalam persamaan:
0 , < =1 (2.16) = − =1
=1
, =1 < =1 +
Dengan menggunakan definisi keputusan fuzzy yang diperkenalkan oleh Bellman dan
Zadeh, maka terdapat:
= � , min (2.17)
Untuk kasus ini keputusan fuzzy yang optimal adalah solusi dari permasalahan:
max 0 = max 0 � , min (2.18)
Dengan demikian bentuk umum dari program linier dengan koefisien teknologi
berbentuk bilangan fuzzy menjadi permasalahan optimisasi:
Maksimumkan:
= (2.19) Dengan kendala:
�
, = 1, 2, ,
0, 0 1
Dengan menggunakan persamaan (2.15) dan (2.16), permasalahan di atas dapat ditulis ke
dalam bentuk:
Maksimumkan:
= (2.20) Dengan kendala:
− − =1 + 0
=1 + − 0, = 1, 2, , , = 1, 2, ,
0, 0 1
Dengan catatan kendala dalam permasalahan ini mengandung aturan cross product yaitu
penyelesaian khusus yang diadopsi dari penyelesaian permasalahan optimisasi
nonkonveks.
2.6.2 Program Linier Dengan Koefisien Teknologi Dan Konstanta Sebelah Kanan Berbentuk Bilangan F uzzy
Bentuk umum dari program linier dengan koefisien teknologi dan konstanta sebelah
kanan berbentuk bilangan fuzzy untuk kasus maksimasi adalah:
Maksimumkan:
= =1 (2.21) Dengan kendala:
=1 , = 1, 2, ,
0, = 1, 2, ,
Untuk kasus program linier dengan koefisien teknologi dan konstanta sebelah kanan
berbentuk bilangan fuzzy, terdapat beberapa asumsi yang harus dipenuhi, yaitu:
Asumsi 1: Koefisien teknologi dan konstanta sebelah kanan dikatakan berbentuk bilangan fuzzy apabila memenuhi syarat fungsi keanggotaan linier berikut:
1 jika < (2.22)
= + − jika < +
0 jika +
1 jika < (2.23)
= + − jika < +
0 jika +
Di mana ∈ . Untuk mendefuzzyfikasi permasalahan ini, pertama-tama akan dicari nilai optimal dari batas atas dan batas bawah permasalahan tersebut. Nilai batas-batas tersebut akan diperoleh dengan menyelesaikan permasalahan program linier
standar, dengan mengasumsikan bahwa batas-batas tersebut memiliki nilai optimal yang
terbatas.
Untuk 1 , persamaannya adalah:
Maksimumkan:
1 = =1 (2.24) Dengan kendala:
=1 + , = 1, 2, ,
0, = 1, 2, ,
Untuk 2 , persamaannya adalah:
Maksimumkan:
2 = =1 (2.25) Dengan kendala:
=1 + , = 1, 2, ,
0, = 1, 2, ,
Untuk 3, persamaannya adalah:
Maksimumkan:
3 = =1 (2.26) Dengan kendala:
0, = 1, 2, ,
Dan untuk 4, persamaannya adalah:
Maksimumkan:
4 = =1 (2.27) Dengan kendala:
=1 , = 1, 2, ,
0, = 1, 2, ,
Maka batas bawah = 1, 2, 3, 4 dan batas atas = 1, 2, 3, 4 .
Nilai dari fungsi objektif berada di antara batas bawah dan batas atas sementara nilai
koefisien teknologi berada di antara dan + , dan nilai konstanta sebelah kanan berada di antara dan + .
Asumsi 2: Nilai optimal himpunan fuzzy�, didefinisikan sebagai:
0 jika =1 < (2.28)
� = =1 − − jika =1 <
1 jika =1
Himpunan fuzzy dengan kendala ke- yaitu yang merupakan himpunan bagian dari
didefinisikan ke dalam:
0 , < =1 (2.29) = − =1
=1
, =1 =1 +
1 , =1 + +
Dengan menggunakan metode defuzzyfikasi, permasalahan direduksi menjadi:
Maksimumkan:
Dengan kendala:
− − =1 + 0
=1 + + − 0, = 1, 2, , , = 1, 2, , 0, 0 1
Dengan catatan seperti pada kasus program linier dengan koefisien teknologi berupa
BAB 3
PEMBAHASAN
3.1 Program Linier dengan Hanya Konstanta Sebelah Kanan Berbentuk Bilangan
F uzzy
Salah satu bentuk dari fuzzy linear programming (FLP) adalah program linier dengan
hanya konstanta sebelah kanan yang berbentuk bilangan fuzzy.
Bentuk umum dari program linier dengan konstanta sebelah kanan berbentuk
bilangan fuzzy untuk kasus maksimasi adalah:
Maksimumkan:
= =1 (3.1) Dengan kendala:
=1 , = 1, 2, ,
0, = 1, 2, ,
Program linier dengan konstanta sebelah kanan yang berbentuk bilangan fuzzy maka
harus memenuhi asumsi berikut:
Asumsi 1: Konstanta sebelah kanan dikatakan berbentuk bilangan fuzzy apabila mengikuti fungsi keanggotaan linier berikut:
1 jika <
= + − jika + (3.2)
Di mana ∈ . Untuk mendefuzzyfikasi permasalahan ini, pertama-tama akan dicari nilai optimal dari batas atas dan batas bawah permasalahan tersebut. Nilai batas-batas tersebut akan diperoleh dengan menyelesaikan permasalahan program linier
standar, dengan mengasumsikan bahwa batas-batas tersebut memiliki nilai optimal yang
terbatas.
Untuk 1 , persamaannya adalah:
Maksimumkan:
1 = =1 (3.3) Dengan kendala:
=1 , = 1, 2, ,
0, = 1, 2, ,
Dan untuk 2 , persamaannya adalah:
Maksimumkan:
2 = =1 (3.4) Dengan kendala:
=1 + , = 1, 2, ,
0, = 1, 2, ,
Maka batas bawah = 1, 2 dan batas atas = 1, 2 . Nilai
dari fungsi objektif berada di antara batas bawah dan batas atas sementara nilai konstanta
sebelah kanan berada di antara dan + .
Asumsi 2: Permasalahan linier crisp yaitu persamaan (3.3) dan (3.4) di atas memiliki nilai optimal yang terbatas. Pada kasus ini nilai optimal dari himpunan fuzzy �, di mana merupakan himpunan bagian dari , dalam buku Klir dan Yuan didefinisikan sebagai:
0 jika =1 <
1 jika =1
Sehingga untuk setiap solusi layak , tingkat pencapaian fungsi objektif diperoleh dengan
memaksimumkan tingkat pencapaian �, yaitu dengan menggunakan variabel dummy
yaitu , di mana 0 1.
Dengan demikian bentuk umum dari program linier dengan koefisien teknologi
berbentuk bilangan fuzzy menjadi permasalahan optimisasi:
Maksimumkan:
= (3.6) Dengan kendala:
�
0, 0 1
Dengan menggunakan (3.5) , permasalahan (3.6) dapat ditulis ke dalam bentuk:
Maksimumkan:
= (3.7) Dengan kendala:
− − =1 + 0
+ =1 − + 0, = 1, 2, , , = 1, 2, ,
0, (0 1)
Dengan catatan kendala dalam permasalahan ini mengandung aturan cross product yaitu
adalah bukan konveks. Oleh Karena itu solusi dari permasalahan ini memerlukan
penyelesaian khusus yang diadopsi dari penyelesaian permasalahan optimisasi
3.2 Pembahasan Contoh Numerik
Pabrik Alfa-Beta memproduksi 3 jenis produk yaitu �1, �2, dan �3 dalam sehari di mana ketiga produk tersebut dibuat dengan menggunakan dua bahan baku dan . Informasi
yang tersedia untuk menyelesaikan persoalan produksi ialah:
Jenis Bahan
Berdasarkan pengalaman produksi sebelumnya, bahan baku masih bisa ditambah
sampai dengan 900 per hari, dan bahan baku masih bisa ditambah sampai dengan 1.200
per hari. Untuk memaksimumkan keuntungan bersih, berapa unit produk �1, �2 dan �3 yang harus diproduksi setiap harinya oleh pabrik Alfa-Beta.
Dari permasalahan di atas diperoleh:
1. Variabel keputusan
Variabel keputusan adalah jumlah produk �1, �2 dan �3 yang diproduksi per hari. Ini berarti ada tiga variabel keputusan yang akan dicari besar nilainya.
1 = jumlah unit produk �1 yang diproduksi setiap hari 2 = jumlah unit produk �2 yang diproduksi setiap hari 3 = jumlah unit produk �3 yang diproduksi setiap hari
2. Nilai kontribusi
Nilai kontribusi adalah laba yang diharapkan dari penjualan produk �1, �2 dan �3
per unit.
1 = laba yang diharapkan dari penjualan produk �1 per unit
= Rp 30.000,-/ unit
= Rp 20.000,-/ unit
3 = laba yang diharapkan dari penjualan produk �3 per unit
= Rp 35.000,-/ unit
3. Koefisien teknologi
Koefisien teknologi adalah jumlah bahan baku masing-masing dan yang
dibutuhkan untuk memproduksi setiap unit produk �1, �2 dan �3. Dengan demikian dapat disusun koefisien teknologi untuk masing-masing produk dan
jenis bahan baku.
11 = jumlah jenis bahan baku untuk memproduksi produk �1
= 10
12 = jumlah jenis bahan baku untuk memproduksi produk �2
= 20
13 = jumlah jenis bahan baku untuk memproduksi produk �3
= 15
21 = jumlah jenis bahan baku untuk memproduksi produk �1
= 20
22 = jumlah jenis bahan baku untuk memproduksi produk �2
= 10
23 = jumlah jenis bahan baku untuk memproduksi produk �3
= 25
4. Sumber daya/ Konstanta sebelah kanan
Sumber daya yang tersedia adalah jumlah bahan baku dan yang dibutuhkan
untuk memproduksi produk �1, �2 dan �3. Letak sumber daya dalam model matematik program linier adalah pada sisi bagian kanan kendala masing-masing
jenis bahan baku
1 = jumlah bahan baku untuk memproduksi produk �1, �2 dan �3
dalam satu hari
2 = jumlah bahan baku untuk memproduksi produk �1, �2 dan �3
dalam satu hari
= 1.000 2 1.200
5. Tanda ketidaksamaan kendala
Karena sumber daya yang tersedia untuk memproduksi produk �1, �2 dan �3 sifatnya terbatas, maka tanda ketidaksamaan dalam setiap kendala adalah lebih
kecil atau sama dengan .
Permasalahan di atas merupakan bentuk permasalahan program linier dengan hanya
konstanta sebelah kanan yang berbentuk bilangan fuzzy dan berbentuk trapezoidal.
Dikatakan berbentuk bilangan fuzzy karena konstanta sebelah kanannya tidak merupakan
suatu bilangan yang pasti, tetapi dalam bentuk interval yaitu 800 1 900 dan
1.000 2 1.200. Dikatakan berbentuk trapezoidal karena terdapat empat buah
parameter < < < yaitu 800 < 900 < 1.000 < 1.200 yang merupakan parameter untuk konstanta sebelah kanan dari permasalahan tersebut.
Selanjutnya akan dibuat ke dalam bentuk matematis fuzzy linear programming
(FLP) berikut:
Maksimumkan:
= 30.000 1+ 20.000 2+ 35.000 3
Dengan kendala:
10 1+ 20 2+ 15 3 1
20 1+ 10 2+ 25 3 2
Dengan 1, 2, 3 0.
Karena konstanta sebelah kanan berbentuk bilangan fuzzy, maka dalam
permasalahan di atas dapat didefinisikan ke dalam fungsi keanggotaan linier (menurut
1 , < 800 permasalahan tersebut. Nilai batas-batas tersebut akan diperoleh dengan menyelesaikan
permasalahan program linier standar, dengan mengasumsikan bahwa batas-batas tersebut
memiliki nilai optimal yang terbatas.
Untuk 1, persamaannya adalah:
Maksimumkan:
Untuk mencari solusi optimal dari permasalahan ini maka akan digunakan metode
simpleks, yaitu:
Bentuk kanonik untuk persamaan 1 adalah:
Maksimumkan:
1−30.000 1 −20.000 2−35.000 3 = 0
Dengan kendala:
Dengan 1, 2, 3, 1, 2 0.
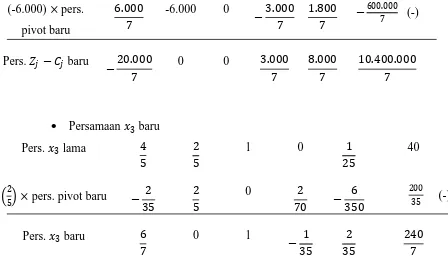
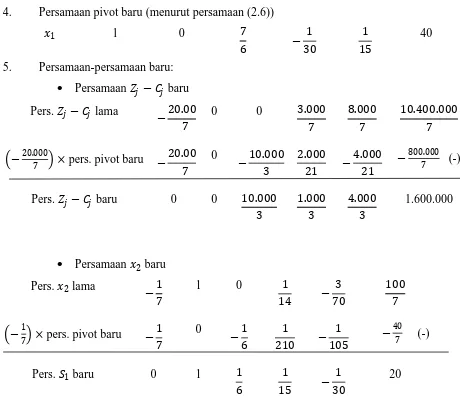
4. Persamaan pivot baru (menurut persamaan (2.6))
(15) × pers. pivot baru 12 6 15 0 3 5
600 (-)
Pers. 1 baru -2 14 0 1
−35 200
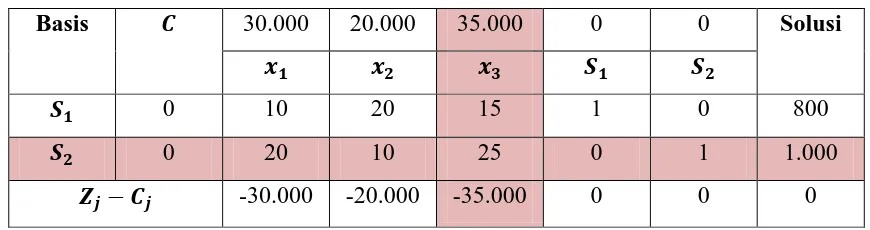
Persamaan-persamaan di atas dapat dibuat ke dalam tabel simplek iterasi pertama berikut:
Tabel 3.2 Tabel Simplek Iterasi Pertama
Basis 30.000 20.000 35.000 0 0 Solusi
1. Dari tabel simplek iterasi pertama di atas diperoleh entering variable yaitu -6.000
pada kolom 2
dan nilai positif terkecil yaitu 200
14, maka leaving variable adalah
1
3. Elemen pivot adalah 14
4. Persamaan pivot baru (menurut persamaan (2.6))
(-6.000) × pers.
Persamaan-persamaan di atas dapat dibuat ke dalam tabel simplek iterasi kedua berikut:
Tabel 3.3 Tabel Simplek Iterasi Kedua
Basis 30.000 20.000 35.000 0 0 Solusi
1. Dari tabel simplek iterasi kedua di atas diperoleh entering variable yaitu −20.000
7
dan nilai positif terkecil yaitu 240
6 , maka leaving variable adalah 3
3. Elemen pivot adalah 6
4. Persamaan pivot baru (menurut persamaan (2.6))
Persamaan-persamaan di atas dapat dibuat ke dalam tabel simplek iterasi ketiga berikut:
Tabel 3.4 Tabel Simplek Iterasi Ketiga
− 0 0 10.000
Karena baris − sudah tidak ada yang negatif, maka pada iterasi ketiga sudah dicapai
kondisi optimal. Dan dari tabel simplek iterasi ketiga di atas diperoleh nilai 1 = 40,
2 = 20, 3 = 0, dan 1 = 1.600.000.
Untuk 2, persamaannya adalah:
Maksimumkan:
Untuk mencari solusi optimal dari permasalahan ini maka akan digunakan metode
simpleks, yaitu:
Bentuk kanonik untuk persamaan 2 adalah:
Catatan:
4. Persamaan pivot baru (menurut persamaan (2.6))
3 4
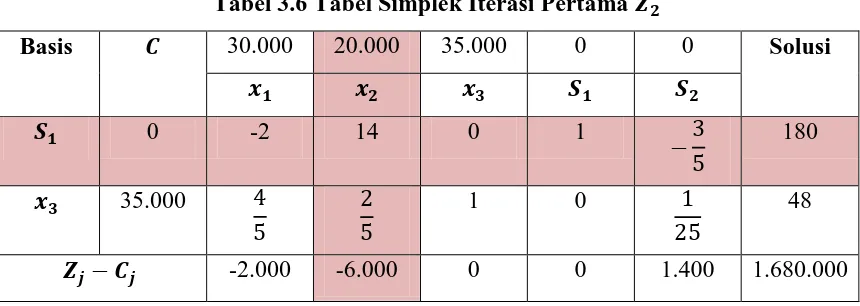
Tabel 3.6 Tabel Simplek Iterasi Pertama
1. Dari tabel simplek iterasi pertama di atas diperoleh entering variable yaitu -6.000
pada kolom 2
dan nilai positif terkecil yaitu 180
14, maka leaving variable adalah
1
3. Elemen pivot adalah 14
4. Persamaan pivot baru (menurut persamaan (2.6))
Pers. 3 lama 4
Persamaan-persamaan di atas dapat dibuat ke dalam tabel simplek iterasi kedua berikut:
Tabel 3.7 Tabel Simplek Iterasi Kedua
Basis 30.000 20.000 35.000 0 0 Solusi
1. Dari tabel simplek iterasi kedua di atas diperoleh entering variable yaitu −20.000
7
pada kolom 1
2. Rasio = 300
6 dan nilai positif terkecil yaitu 50, maka leaving variable adalah 3
3. Elemen pivot adalah 6
7
4. Persamaan pivot baru (menurut persamaan (2.6))
Pers. − lama
Persamaan-persamaan di atas dapat dibuat ke dalam tabel simplek iterasi ketiga berikut:
Tabel 3.8 Tabel Simplek Iterasi Ketiga
Basis 30.000 20.000 35.000 0 0 Solusi
Karena baris − sudah tidak ada yang negatif, maka pada iterasi ketiga sudah dicapai
kondisi optimal. Dan dari tabel simplek iterasi ketiga di atas diperoleh nilai 1 = 50,
Dengan demikian diperoleh nilai batas bawah , yaitu:
= 1, 2
= 1.600.000 , 1.900.000 = 1.600.000
Dan nilai batas atas , yaitu:
= 1, 2
= 1.600.000 , 1.900.000 = 1.900.000
Selanjutnya permasalahan dibuat ke dalam bentuk persamaan (3.7), sebagai berikut:
Maksimumkan:
=
Dengan kendala:
1.900.000−1.600.000 − 30.000 1+ 20.000 2+ 35.000 3 −1.600.000
100 + 10 1+ 20 2+ 15 3−900 0
200 + 20 1 + 10 2 + 25 3−1.200 0
Dengan , 1, 2, 3 0
Dapat juga dibuat ke dalam bentuk berikut:
Maksimumkan:
=
Dengan kendala:
30.000 1+ 20.000 2+ 35.000 3−300.000 1.600.000 10 1+ 20 2+ 15 3+ 100 900
20 1+ 10 2+ 25 3+ 200 1.200
Untuk mencari solusi optimal dari permasalahan ini tidak dapat digunakan langkah
metode simpleks biasa, maka digunakan bantuan program QM. Dengan memisalkan
= 4, maka permasalahan menjadi:
Maksimumkan:
= 4
Dengan kendala:
30.000 1+ 20.000 2 + 35.000 3−300.000 4 1.600.000 10 1+ 20 2+ 15 3+ 100 4 900
20 1+ 10 2+ 25 3+ 200 4 1.200
Dengan 1, 2, 3, 4 0.
Berdasarkan penyelesaian dengan menggunakan program QM (dapat dilihat pada
lampiran), pada iterasi keenam sudah diperoleh solusi optimalnya yaitu, = 4 = 0,5 , 1 = 45 , 2 = 20, dan 3 = 0.
Sehingga jumlah produk �1, �2, dan �3 yang harus diproduksi per hari adalah: �1 = 1 = 45 unit
�2 = 2 = 20 unit �3 = 3 = 0 unit
Untuk memperoleh total laba maksimum per hari maka jumlah produk �1, �2, dan �3 disubstitusikan ke persamaan fungsi tujuan awal yaitu:
= 30.000 1+ 20.000 2+ 35.000 3
Dengan demikian total laba maksimum per hari yang akan diperoleh adalah:
= 30.000 45 + 20.000 20 + 35.000 0 = 1.350.000 + 400.000 + 0
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Permasalahan fuzzy linear programming (FLP) dapat diselesaikan dengan pendekatan
teori himpunan fuzzy sehingga dapat diselesaikan dengan mengkonversikan ke dalam
bentuk program linier biasa dan dengan menggunakan variabel dummy . Dan untuk
fuzzy linear programming dengan parameter konstanta sebelah kanan yang berbentuk
bilangan fuzzy pada persoalan ini diselesaikan dengan lebih dahulu dikonversikan ke
dalam bentuk program linier biasa dengan menggunakan data pada proses produksi
sebelumnya dan untuk memperoleh solusi optimalnya digunakan bantuan metode
simpleks dan program QM.
Hasil perhitungan dari contoh numerik yang dikerjakan dalam skripsi ini diperoleh
jumlah produk �1,�2 dan �3 yang harus diproduksi per hari yaitu �1 sebanyak 45 unit, �2
sebanyak 20 unit, dan �3 sebanyak 0 unit artinya tidak memproduksi produk �3. Dan laba total yang akan diperoleh per hari adalah sebesar Rp 1.750.000,-.
4.2 Saran
Dalam skripsi ini penulis hanya membahas program linier dengan hanya konstanta
sebelah kanan yang berbentuk bilangan fuzzy dan berbentuk trapezoidal. Penulis
menyarankan pembaca dapat melanjutkan pembahasan untuk bentuk fuzzy linear
programming (FLP) lainnya, seperti program linier di mana hanya koefisien teknologi
sebelah kanan berbentuk bilangan fuzzy, dan juga program linier di mana fungsi tujuan,
koefisien teknologi, dan juga konstanta sebelah kanan berbentuk bilangan fuzzy. Dan
permasalahan fuzzy linear programming (FLP) juga dapat dikembangkan dengan bentuk
DAFTAR PUSTAKA
Gasimov, R. N. dan Yenilmez, K. 2002. “Solving Fuzzy Linear Programming Problems
With Linear Membership Functions”. Jurnal Turk J Math, halaman 375-396.
Klir, G. J. dan B. Yuan. 1995. Fuzzy Sets And Fuzzy Logic – Theory And Application.
Prentice Hall.
Kusumadewi, Sri. 2002. Analisis Desain Sistem Fuzzy Menggunakan Tool Box Matlab.
Yogyakarta. Graha Ilmu.
Kusumadewi, Sri. dan Hari, P. 2004. Aplikasi Logika Fuzzy Untuk Pendukung Keputusan.
Edisi Pertama. Yogyakarta. Graha Ilmu.
Kusumadewi, Sri. dkk. 2006. Fuzzy Multi-Atributte Decision Making (Fuzzy MADM.
Edisi Pertama. Yogyakarta. Graha Ilmu.
Lieberman, G. J. dan F. S. Hittler. 1990. Introduction to Operation Research. Fifth
Edition, Mc Graw – Hill.
Mulyono, Sri. 2004. Riset Operasi. Edisi Revisi. Jakarta. Fakultas Ekonomi Universitas
Indonesia.
Mustafa, Zainal. Dan Parkhan, Ali. 2000. Belajar Cepat Linear Programming dengan QS
(Quantitative Systems). Edisi Pertama. Yogyakarta. Ekonisia.
Nasendi, B. D. dan Anwar Affendi. 1984. Program Linier dan Variansinya. Bogor.
Fakultas Kehutanan, Fakultas Pertanian, Fakultas Pasca Sarjana Institu Pertanian
Bogor.
Rao, S. S. 1977. Optization – Theory And Aplications. Second Edition. San Diego, USA.
Siagian, P. 1987. Penelitian Operasional, Teori dan Praktek. Cetakan 2006. Jakarta.
UI-Press.
Supranto, J. 1983. Linear Programming. Edisi Kedua. Jakarta. Fakultas Ekonomi
Universitas Indonesia.
Susilo, Frans. 2006. Himpunan dan Logika Kabur serta Aplikasinya. Edisi kedua.
Yogyakarta. Graha Ilmu.
Sutapa, Nyoman. 2000. “Masalah Programa Linier Fuzzy Dengan Fungsi
Keanggotaan Linier”. Jurnal Teknik Industri Volume 2, nomor 1: halaman 28-33.
Zulfikarijah, Fien. 2004. Operation Research. Malang. Bayumedia Publishing.