PENYELESAIAN PERMAINAN SUDOKU,
CHALLENGER
PUZZLE
, DAN
N-QUEENS PROBLEM
MENGGUNAKAN
INTEGER PROGRAMMING
ALI VIKRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Permainan
Sudoku,
Challenger Puzzle
, dan
N-Queens Problem
menggunakan
Integer
Programming
adalah benar karya saya dengan arahan dari komisi pembimbing
dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun.
Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun
tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan
dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut
Pertanian Bogor.
Bogor, Februari 2014
Ali Vikri
ABSTRAK
ALI VIKRI. Penyelesaian Permainan Sudoku,
Challenger Puzzle,
dan
N-Queens
Problem
menggunakan
Integer Programming
. Dibimbing oleh FARIDA
HANUM dan MUHAMMAD ILYAS.
Banyak orang menganggap matematika itu sulit sehingga mereka tidak
tertarik untuk mempelajarinya. Menyajikan matematika dalam bentuk teka-teki
merupakan salah satu cara untuk menarik orang mempelajari matematika secara
tidak langsung. Teka-teki akan mengundang rasa ingin tahu seseorang untuk
memecahkan masalah. Ketika seseorang dapat menyelesaikan teka-teki, maka
secara tidak langsung dia sebenarnya telah mempelajari matematika. Dalam karya
ilmiah ini akan diformulasikan beberapa masalah teka-teki matematika yaitu
Sudoku,
Challenger Puzzle
, dan
N-Queens Problem
menggunakan
integer
programming
dan diselesaikan menggunakan LINGO 11.0
Kata kunci:
Challenger Puzzle, Integer Programming, N-Queens Problem,
Sudoku
ABSTRACT
ALI VIKRI.
Completion Sudoku Games, Puzzles Challenger, and the N-Queens
Problem using Integer Programming. Supervised by FARIDA HANUM and
MUHAMMAD ILYAS.
Many people think that mathematics is complicated so they are not
interested to learn it. Presenting mathematics in the form of a puzzle is one way to
attract people to study mathematics. The puzzle will attract curiosity of someone
to solve problems. When someone can solve the puzzle, then it implies that he in
fact has studied mathematics. In this paper, some mathematical puzzles are
formulated, such as Sudoku, Puzzle Challenger, and the N-Queens Problem using
integer programming and are solved by using LINGO 11.0
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains
pada
Departemen Matematika
PENYELESAIAN PERMAINAN SUDOKU,
CHALLENGER
PUZZLE
, DAN
N-QUEENS PROBLEM
MENGGUNAKAN
INTEGER PROGRAMMING
ALI VIKRI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Penyelesaian Permainan Sudoku,
Challenger Puzzle, dan N-Queens
Problem
Menggunakan
Integer Programming
Nama
: Ali Vikri
NIM
: G54080032
Disetujui oleh
Dra Farida Hanum, MSi
Pembimbing I
Muhammad Ilyas, MSi MSc
Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc
Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas
segala karunia-Nya sehingga penelitian dengan judul Penyelesaian permainan
Sudoku,
Challenger Puzzle,
dan
N-Queens Problem
menggunakan
Integer
Programming
dapat diselesaikan.
Terima kasih penulis ucapkan kepada Ibu Dra Farida Hanum, M.Si dan
Bapak Muhammad Ilyas, MSi MSc selaku pembimbing, serta Bapak Dr Ir I Gusti
Putu Purnaba, DEA yang telah banyak memberi saran. Ungkapan terima kasih
juga disampaikan kepada ayah, ibu, serta seluruh keluarga, atas segala doa dan
kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Februari 2014
DAFTAR ISI
DAFTAR GAMBAR
vi
PENDAHULUAN
1
Latar Belakang
1
Tujuan Penelitian
1
TINJAUAN PUSTAKA
1
DESKRIPSI DAN FORMULASI MASALAH
2
Deskripsi Masalah
2
Formulasi Masalah
4
HASIL DAN PEMBAHASAN
17
Sudoku
17
Challenger Puzzle
20
N-Queens Problem
21
SIMPULAN
23
DAFTAR PUSTAKA
23
LAMPIRAN
24
DAFTAR GAMBAR
Contoh Sudoku yang belum diselesaikan ... 2
Contoh
grid
pada Sudoku ... 3
Contoh
Challenger Puzzle
yang belum diselesaikan ... 3
Contoh
N-Queens Problem
yang belum diselesaikan ... 4
Contoh Sudoku Tipe 1 ... 5
Contoh Sudoku Tipe 2 ... 6
Contoh Sudoku Tipe 3 ... 7
Contoh Sudoku Tipe 4 ... 8
Contoh Sudoku Tipe 5 ... 9
Contoh Sudoku Tipe 6 ... 10
Contoh Sudoku Tipe 7 ... 11
Contoh
Challenger Puzzle
Tipe A ... 12
Contoh
Challenger Puzzle
Tipe B ... 13
Contoh
Challenger Puzzle
Tipe C ... 13
Contoh
Challenger Puzzle
Tipe D ... 14
Posisi untuk penjumlahan sel miring pada
N-Queens Problem
... 16
Sudoku Tipe 1 ... 17
Sudoku Tipe 2 ... 17
Sudoku Tipe 3 ... 18
Sudoku Tipe 4 ... 18
Sudoku Tipe 5 ... 19
Sudoku Tipe 6 ... 19
Sudoku Tipe 7 ... 20
Challenger Puzzle
Tipe A ... 20
Challenger Puzzle
Tipe B ... 21
Challenger Puzzle
Tipe C ... 21
Challenger Puzzle
Tipe D ... 21
N-Queens Problem
Tipe I ... 22
N-Queens Problem
Tipe II ... 22
1
PENDAHULUAN
Latar Belakang
Banyak orang menganggap matematika itu sulit sehingga tidak tertarik
untuk mempelajarinya. Padahal matematika sama saja dengan pelajaran lainnya
jika berminat mempelajarinya. Menyajikan matematika dalam bentuk teka-teki
merupakan salah satu jalan untuk menarik orang mempelajari matematika secara
tidak langsung. Karena dengan teka-teki ini akan mengundang rasa ingin tahu
seseorang untuk memecahkan masalah. Ketika seseorang dapat menyelesaikan
teka-teki, maka secara tidak langsng dia sebenarnya telah mempelajari
matematika.
Riset Operasi dapat digunakan untuk memecahkan masalah pengambilan
keputusan dalam dunia nyata. Dengan menguraikan ke dalam tiga unsur berikut,
yang pertama mengidentifikasi alternatif misalnya variabel keputusan, yang
kedua mengidentifikasi kendala dari masalah, dan yang ketiga mengidentifikasi
kriteria objektif. Teknik yang banyak digunakan dalam Riset Operasi ialah
Pemrograman Linear. Model
Integer Programming
adalah kasus khusus dari
model Pemrograman Linear di mana variabel keputusan dibatasi menjadi nilai
integer
.
Dalam dunia nyata, salah satu penerapan
integer programming
ialah
penyelesaian teka-teki matematika seperti Sudoku,
Challenger Puzzle
dan
N-Queens Problem
. Dalam karya ilmiah ini, masalah penyelesaian teka-teki Sudoku
dan
Challenger Puzzle
dimodifikasi dari artikel yang berjudul
Teaching Integer
Programming via Sudoku and Other Math Puzzles
yang ditulis oleh Daryl L.
Santos tahun 2007, sedangkan
N-Queens Problem
diformulasikan sendiri.
Tujuan Penelitian
Tujuan dari karya ilmiah ini ialah memformulasikan beberapa masalah
teka-teki matematika yaitu Sudoku,
Challenger Puzzle,
dan
N-Queens Problem
menggunakan
integer programming
dan menyelesaikannya menggunakan LINGO
11.0.
TINJAUAN PUSTAKA
Pada abad ke-18, seorang ahli matematika asal Swiss, Leonhard Euler,
mengembangkan konsep
“Latin squares”
. Dalam konsep ini, angka atau simbol
dalam kotak hanya akan muncul satu kali di setiap baris atau kolom. Jadi, dalam
setiap baris atau kolom tidak ada angka atau simbol yang sama. Kemudian, di
Amerika Serikat terdapat permainan teka-
teki angka yang dinamakan “
Number
Place
”. Saat itu, permainan ini dimuat di
sebuah majalah terbitan Amerika
Serikat,
Dell Magaziness
, di akhir tahun 1970-an. Teka-teki angka yang dimuat
ini merupakan pengembangan dari teka-teki yang dibuat oleh Howard Garnes.
penerbitan di Jepang. Perusahaan tersebut menerbitkan permainan teka-teki angka
di sebuah media cetak khusus teka-teki,
Monthly Nikolist
. Alhasil, teka-teki ini
menjadi terkenal di Jepang. Masyarakat Jepang menamakannya dengan
“Suji wa
doku
shin ni kagiru”
yang kemudian disingkat menjadi Sudoku. Dalam bahasa
Jepang, sudoku diambil dari kata
”su”
yang artinya angka dan
“doku”
berarti
sendiri. Artinya, dalam permainan ini, hanya boleh ada satu angka dalam satu
baris dan kolom (Asal Usul
Puzzle
Sudoku 2013). Teka-teki angka lainnya yang
juga dibahas dalam karya ilmiah ini, adalah
Challenger Puzzle
yang dimodifikasi
dari (Santos 2007).
Pada tahun 1848, Max Bezzel memperkenalkan permainan
Eight Queens
Puzzle
. Franz Nauck mengumumkan solusi pertama pada tahun 1850 serta
mengembangkan teka-teki ini menjadi
N-Queens Problem
. Dalam permainan ini
terdapat
N
ratu pada papan catur berukuran
. Sejak itu banyak
matematikawan, termasuk Carl Friedrich Gauss, mencoba menyelesaikan masalah
Eight Queens Puzzle
dan
N-Queens Problem
(
Eight Queens Puzzle
2009). Pada
karya ilmiah
N-Queens Problem
yang dibahas hanya yang berukuran 8
8 dengan
8 ratu catur yang tidak saling menyerang satu sama lain.
DESKRIPSI DAN FORMULASI MASALAH
Deskripsi Masalah
1.
Sudoku
Sudoku adalah sebuah permainan teka-teki berdasarkan logika dengan
kombinasi penempatan angka. Pada permainan Sudoku pemain diminta untuk
mengisi
kotak, sehingga setiap kotak dapat diisi dengan angka 1 sampai
dengan angka
“n”
itu sendiri. Pada karya ilmiah ini akan dibahas Sudoku yang
berukuran 9×9. Pada permainan ini tiap baris dan tiap kolom diisi angka 1 sampai
dengan 9 dan tidak boleh ada angka yang sama. Pada Gambar 1 diberikan contoh
Sudoku yang belum memiliki solusi.
2 4
6
8
3
5 7 9 2
1 9
7
8
6 9
9
2
1
5
3
Gambar 1 Contoh Sudoku yang belum diselesaikan
3
Grid
beraturan
Grid
acak
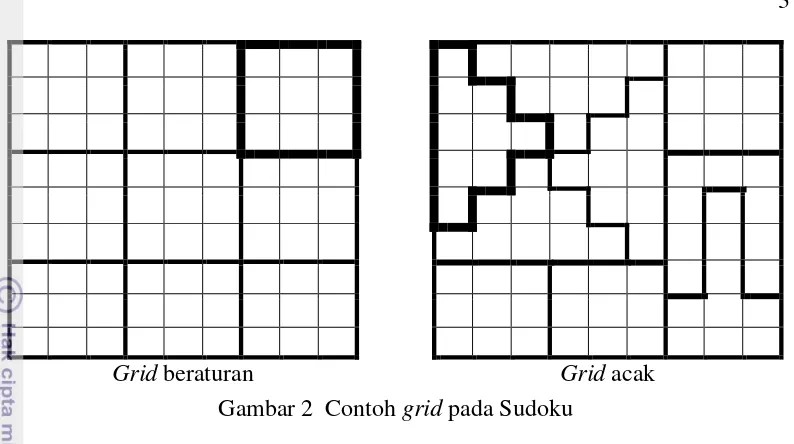
Gambar 2 Contoh
grid
pada Sudoku
Sudoku yang dibahas pada karya ilmiah ini, selain bentuk
grid-
nya ada yang
beraturan maupun acak, juga ditambah
grid
warna tertentu.
Sudoku yang memiliki
solusi adalah Sudoku yang telah berisi angka 1 sampai dengan 9 pada setiap baris,
kolom dan
grid
sehingga tidak ada angka yang sama.
2.
Challenger Puzzle
Challenger Puzzle
adalah salah satu jenis teki matematika. Pada
teka-teki ini disediakan seperangkat sel berukuran
dan jumlah semua angka di
setiap baris, kolom, dan diagonal sudah ditetapkan, serta beberapa sel telah
ditentukan nilai awalnya. Pada karya ilmiah ini akan dibahas
Challenger Puzzle
yang berukuran 4
4 dan 5
5. Aturan
Challenger Puzzle
yaitu sel-sel yang
kosong diisi dengan angka 1 sampai dengan 9 dan angka-angka tersebut boleh
berulang sehingga penjumlahan angka di setiap baris, kolom, dan diagonal sesuai
dengan angka yang sudah ditetapkan.
16
17
1
16
5
15
3
16
6
19
2
16
2
14
6
4
16
2
7
16
16
16
16
16
16
16
16
17
20
18
Gambar 3 Contoh
Challenger Puzzle
yang belum diselesaikan
Challenger Puzzle
yang memiliki solusi adalah
Challenger Puzzle
yang
semua sel nya telah berisi angka dengan penjumlahan yang tepat. Pada Gambar 3
diberikan contoh
Challenger Puzzle
yang belum memiliki solusi.
3.
N-Queens Problem
kolom. Dengan demikian, solusi permainan ini mensyaratkan bahwa tidak ada dua
ratu berbagi baris, kolom, atau diagonal yang sama sehingga tidak satupun dari
mereka bisa memukul dalam satu gerakan. Gambar 4 merupakan contoh
N-Queens Problem
yang belum memiliki solusi.
Gambar 4 Contoh
N-Queens Problem
yang belum diselesaikan
Formulasi Masalah
1.
Sudoku
Dalam karya ilmiah ini, masalah sudoku akan diformulasikan ke dalam
integer programming.
Indeks yang digunakan:
i
= 1, 2, ..., 9 merupakan indeks untuk baris
j
= 1, 2, ..., 9 merupakan indeks untuk kolom
k
= 1, 2, ..., 9 merupakan indeks untuk nilai sel
Variabel keputusan didefinisikan sebagai berikut:
{
Terdapat
729 variabel biner.
Sudoku Tipe 1
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
5
Terdapat
= 81 kendala.
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
Berikut ini akan diberikan contoh gambar Sudoku Tipe 1.
Gambar 5 Contoh Sudoku Tipe 1
Sudoku Tipe 2
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
4.
Setiap kotak yang berwarna sama pada diagonal berisi angka 1 sampai 9
tanpa ada pengulangan.
∑
,
, i+j
=10
5.
Setiap kotak yang berwarna sama di atas dan di bawah diagonal berisi
angka 1 sampai 9 tanpa ada pengulangan.
+
+
+
+
+
+
+
+
= 1,
+
+
+
+
+
+
+
+
= 1,
Berikut ini akan diberikan contoh gambar Sudoku Tipe 2.
Gambar 6 Contoh Sudoku Tipe 2
Sudoku Tipe 3
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
7
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
4.
Kedua diagonal berisi angka 1 sampai dengan 9 tanpa pengulangan.
∑
,
, i+j
=10
∑
,
, i=j
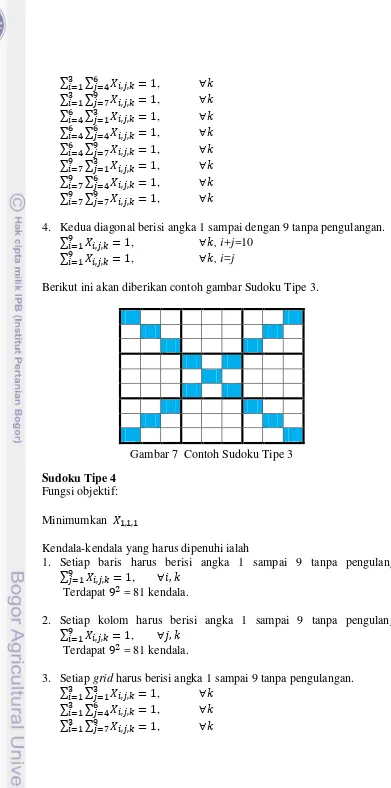
Berikut ini akan diberikan contoh gambar Sudoku Tipe 3.
Gambar 7 Contoh Sudoku Tipe 3
Sudoku Tipe 4
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
4.
Pada kotak yang berwarna sama berisi angka 1 sampai 9 tanpa
pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
Berikut ini akan diberikan contoh gambar Sudoku Tipe 4.
Gambar 8 Contoh Sudoku Tipe 4
Sudoku Tipe 5
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
9
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
4.
Kedua diagonal berisi angka 1 sampai dengan 9 tanpa pengulangan.
∑
,
, i+j
=10
∑
,
, i=j
Berikut ini akan diberikan contoh gambar Sudoku Tipe 5.
Gambar 9 Contoh Sudoku Tipe 5
Sudoku Tipe 6
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
4.
Setiap kotak yang berwarna sama pada diagonal berisi angka 1 sampai 9
tanpa ada pengulangan.
∑
,
, i+j
=10
5.
Setiap kotak yang berwarna sama di atas dan di bawah diagonal berisi
angka 1 sampai 9 tanpa ada pengulangan.
∑
∑
,
∑
∑
,
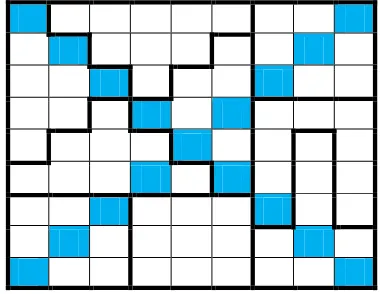
Berikut ini akan diberikan contoh gambar Sudoku Tipe 6.
Gambar 10 Contoh Sudoku Tipe 6
Sudoku Tipe 7
Fungsi objektif:
Minimumkan
Kendala-kendala yang harus dipenuhi ialah
1.
Setiap baris harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
Terdapat
= 81 kendala.
2.
Setiap kolom harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
,
11
3.
Setiap
grid
harus berisi angka 1 sampai 9 tanpa pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
∑
,
4.
Pada kotak yang berwarna sama berisi angka 1 sampai 9 tanpa
pengulangan.
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
∑
∑
,
Berikut ini akan diberikan contoh gambar Sudoku Tipe 7.
Gambar 11 Contoh Sudoku Tipe 7
2.
Challenger Puzzle
Variabel keputusan :
Misalkan :
merupakan angka yang berada pada baris
i
dan kolom
j.
Berikut ini akan diberikan contoh
Challenger Puzzle
untuk Tipe A.
16
16
16
16
16
16
16
16
16
16
Gambar 12 Contoh
Challenger Puzzle
Tipe A
Tipe A
Indeks :
i
= 1, 2, 3, 4 merupakan indeks untuk baris
j
= 1, 2, 3, 4 merupakan indeks untuk kolom
Fungsi objektif
Minimumkan
Kendala :
1.
Jumlah semua angka di setiap kolom adalah 16.
∑
,
j
= 1,2,3,4
2.
Jumlah semua angka di setiap baris adalah 16.
∑
,
i
= 1,2,3,4
3.
Jumlah semua angka pada kedua diagonal sel adalah 16.
∑
,
i
= j
∑
,
i
+
j
= 5
4.
Semua
bernilai bilangan bulat positif dari 1 sampai 9.
{1,2,3,4,5,6,7,8,9},
13
25
25
25
25
25
25
25
25
25
25
25
25
Gambar 13 Contoh
Challenger Puzzle
Tipe B
Tipe B
Indeks :
i
= 1, 2, 3, 4, 5 merupakan indeks untuk baris
j
= 1, 2, 3, 4, 5 merupakan indeks untuk kolom
Fungsi objektif
Minimumkan
Kendala :
1.
Jumlah semua angka di setiap kolom adalah 25.
∑
,
j
= 1,2,3,4,5
2.
Jumlah semua angka di setiap baris adalah 25.
∑
,
i
= 1,2,3,4,5
3.
Jumlah semua angka pada kedua diagonal sel adalah 25.
∑
,
i
= j
∑
,
i
+
j
= 6
4.
Semua
bernilai bilangan bulat positif dari 1 sampai 9.
{1,2,3,4,5,6,7,8,9},
Berikut ini diberikan contoh
Challenger Puzzle
untuk Tipe C.
12
22
17
16
18
24
13
24
12
19
Gambar 14 Contoh
Challenger Puzzle
Tipe C
Tipe C
i
= 1, 2, 3, 4 merupakan indeks untuk baris
Fungsi objektif
Minimumkan
Kendala :
1.
Jumlah angka di setiap kolom mengikuti angka yang telah ditetapkan.
∑
∑
∑
∑
2.
Jumlah angka di setiap baris mengikuti angka yang telah ditetapkan.
∑
∑
∑
∑
3.
Jumlah semua angka pada kedua diagonal sel mengikuti angka yang telah
ditetapkan.
+
+
+
=12
+
+
+
=19
4.
Semua
bernilai bilangan bulat positif dari 1 sampai 9.
{1,2,3,4,5,6,7,8,9},
Berikut ini akan diberikan contoh
Challenger Puzzle
untuk Tipe D.
25
24
29
25
16
21
18
28
20
26
23
29
Gambar 15 Contoh
Challenger Puzzle
Tipe D
Tipe D
i
= 1, 2, 3, 4, 5 merupakan indeks untuk baris
j
= 1, 2, 3, 4, 5 merupakan indeks untuk kolom
Fungsi objektif
15
Kendala :
1.
Jumlah angka di setiap kolom mengikuti angka yang telah ditetapkan.
∑
∑
∑
∑
∑
2.
Jumlah angka di setiap baris mengikuti angka yang telah ditetapkan.
∑
∑
∑
∑
∑
3.
Jumlah semua angka pada kedua diagonal sel mengikuti angka yang telah
ditetapkan.
+
+
+
+
=25
+
+
+
+
=29
4.
Semua
bernilai bilangan bulat positif dari 1 sampai 9.
{1,2,3,4,5,6,7,8,9},
3.
N-Queens Problem
Indeks :
i
= 1, 2, ..., 8 merupakan indeks untuk baris
j
= 1, 2, ..., 8 merupakan indeks untuk kolom
Variabel keputusan :
Misalkan :
merupakan angka yang berada pada baris
i
dan kolom
j.
Fungsi objektif
Minimumkan
Kendala :
1.
Jumlah angka di setiap kolom bernilai 1.
∑
,
j
= 1,2,3,4,...,8
2.
Jumlah angka di setiap baris bernilai 1.
∑
,
i
= 1,2,3,4,...,8
3.
Jumlah angka di setiap sel miring bernilai kurang dari atau sama dengan 1.
∑
,
i
+
j =
4
(
)
∑
,
i
+
j =
5
(
)
∑
,
i
+
j =
6
(
)
∑
,
i
+
j =
7
(
)
∑
,
i
+
j =
8
(
)
∑
,
i + j =
9
(
)
∑
,
i
+
j =
10
(
)
∑
,
i
+
j =
11
(
)
∑
,
i
+
j =
12
(
)
∑
,
i
+
j =
13
(
)
∑
,
i
+
j =
14
(
)
∑
,
i
+
j =
15
(
)
∑
,
j = i
–
6
(
)
∑
,
j = i
–
5
(
)
∑
,
j = i
–
4
(
)
∑
,
j = i
–
3
(
)
∑
,
j = i
–
2
(
)
∑
,
j = i
–
1
(
)
∑
,
i = j
(
)
∑
,
j = i
+ 1
(
)
∑
,
j = i
+ 2
(
)
∑
,
j = i
+ 3
(
)
∑
,
j = i
+ 4
(
)
∑
,
j = i
+ 5
(
)
∑
,
j = i
+ 6
(
)
Gambar 16 Posisi untuk penjumlahan sel miring pada
N-Queens Problem
4.
Semua
bernilai 0 atau 1.
17
HASIL DAN PEMBAHASAN
Pada bagian ini akan dibahas penyelesaian Sudoku,
Challenger Puzzle,
dan
N-Queens Problem
menggunakan
integer programming
dan
software
LINGO
11.0.
Sudoku
Terdapat tujuh macam tipe Sudoku yang berbeda-beda, akan dibahas satu
per satu sesuai dengan tipe nya.
1.
Sudoku Tipe 1
Sudoku tipe ini ialah Sudoku yang paling sering ditemukan, karena
merupakan Sudoku dasar. Sintaks program LINGO 11.0 dan solusinya dapat
dilihat pada Lampiran 1.
4
5
7
6
8
9
4
3
5
7
2
6
8
1
9
2
1
4
7
5
8
2
9
1
3
4
6
7
5
6
7
8
9
5
3
4
6
1
7
8
9
5
3
2
4
5
9
3
1
4
6
5
9
2
3
1
7
4
6
8
1
2
7
3
1
6
4
5
8
2
7
9
3
7
8
3
6
9
2
5
7
8
3
4
6
9
2
5
1
3
8
9
4
6
3
7
8
2
5
1
9
4
6
5
6
9
4
3
2
5
6
9
4
8
1
3
7
9
1
6
3
5
2
9
4
1
6
7
3
5
8
2
Bentuk awal
Solusi
Gambar 17 Sudoku Tipe 1
2.
Sudoku Tipe 2
Sudoku Tipe 2 merupakan Sudoku dengan variasi warna. Pada tipe ini
ditambahkan kendala tidak ada pengulangan pada kotak yang memiliki warna
yang sama. Sintaks program LINGO 11.0 dan solusinya dapat dilihat pada
Lampiran 3.
9
6
2
3
9
4
6
1
2
7
3
8
5
1
5
3
4
6
7
1
8
5
9
3
2
4
6
2
6
4
9
2
5
3
6
8
4
9
1
7
6
9
4
3
7
6
9
1
4
3
8
7
5
2
2
9
1
8
3
5
2
7
9
6
1
8
3
4
3
4
7
2
6
1
3
8
4
7
5
2
6
9
1
7
1
6
3
4
7
2
8
1
9
5
6
3
8
3
4
6
1
9
8
3
5
2
4
6
1
7
9
1
9
3
5
4
2
8
1
6
9
3
7
5
4
2
8
Bentuk awal
Solusi
3.
Sudoku Tipe 3
Sudoku Tipe 3 merupakan Sudoku dengan tambahan kendala tidak ada
pengulangan angka pada kedua diagonal Sudoku. Sintaks program LINGO 11.0
dan solusinya dapat dilihat pada Lampiran 4.
3
5
9
2
7
6
4
3
1
5
9
8
2
7
1
2
8
4
6
7
5
9
3
5
9
3
8
4
6
7
5
9
2
3
8
4
6
1
8
4
8
3
6
5
7
2
9
1
4
6
1
3
5
9
4
6
1
3
7
8
2
1
7
6
3
2
1
7
8
9
4
6
3
5
9
8
5
7
2
1
3
4
6
6
2
3
5
1
7
4
6
2
3
8
5
1
7
9
3
9
2
8
3
7
1
9
4
6
2
5
8
Bentuk awal
Solusi
Gambar 19 Sudoku Tipe 3
4.
Sudoku Tipe 4
Sudoku Tipe 4 merupakan Sudoku dengan variasi warna. Selain itu, tidak
boleh ada pengulangan angka dalam satu
grid
dan pada warna yang sama juga
tidak boleh ada pengulangan angka. Dibutuhkan ketelitian yang lebih dalam
menyelesaikan Sudoku Tipe 4. Sintaks program LINGO 11.0 dan solusinya dapat
dilihat pada Lampiran 5.
3
2
8
7
1
5
3
2
6
8
9
7
1
4
9
8
2
3
9
8
4
7
1
5
6
2
3
3
7
6
1
4
3
2
8
9
5
1
5
2
8
1
7
5
9
4
3
2
6
8
6
8
4
9
2
6
1
5
3
7
6
3
1
9
6
2
3
5
7
8
1
4
9
2
3
9
6
8
2
7
4
5
1
4
5
7
2
4
5
8
1
9
6
3
7
2
1
7
5
8
6
2
1
7
3
5
4
9
8
6
Bentuk awal
Solusi
19
5.
Sudoku Tipe 5
Sudoku Tipe 5 merupakan Sudoku modifikasi dengan
grid
acak dan kendala
tidak boleh ada pengulangan angka pada kedua diagonal Sudoku. Solusi yang
diperoleh melalui LINGO 11.0 dapat dilihat pada Lampiran 6.
4
1
8
3
7
4
9
1
5
8
2
3
6
7
6
7
1
5
9
8
6
4
7
3
1
2
5
9
3
6
9
1
4
2
3
5
6
7
9
8
1
4
9
7
8
6
2
9
7
3
8
4
6
1
2
5
1
6
2
9
3
1
8
6
4
2
5
9
7
3
5
1
3
8
6
7
5
2
1
9
3
4
8
6
6
9
5
7
8
6
1
9
2
5
4
7
3
8
5
4
3
8
9
5
4
7
3
1
8
6
9
2
2
9
7
4
1
3
2
8
9
6
7
5
4
1
Bentuk awal
Solusi
Gambar 21 Sudoku Tipe 5
6.
Sudoku Tipe 6
Sudoku Tipe 6 merupakan Sudoku modifikasi dengan kondisi
grid
acak
dengan kendala tidak ada pengulangan pada kotak yang berwarna sama pada
sudoku serta sebuah diagonal Sudoku. Solusi yang diperoleh melalui LINGO 11.0
dapat dilihat pada Lampiran 7.
8
1
9
7
3
2
8
5
1
6
9
4
7
3
7
6
3
1
5
7
6
2
3
4
1
8
5
9
5
8
3
6
1
5
9
8
7
3
4
6
2
1
3
4
7
9
8
3
1
4
5
7
2
9
6
8
7
2
8
1
5
4
7
6
2
9
8
3
1
5
9
3
8
6
4
9
3
1
8
5
6
2
4
7
5
6
2
1
9
8
5
7
6
2
3
1
9
4
6
3
1
5
8
6
4
3
9
1
7
5
8
2
2
8
5
7
6
1
2
9
4
8
5
7
3
6
Bentuk awal
Solusi
7.
Sudoku Tipe 7
Sudoku Tipe 7 merupakan Sudoku modifikasi dengan kondisi
grid
acak dan
menggunakan variasi warna. Selain itu, ditambahkan kendala tidak ada
pengulangan angka pada kotak yang berwarna sama. Solusi yang diperoleh
melalui LINGO 11.0 dapat dilihat pada Lampiran 8.
2
4
1
8
3
2
4
6
7
1
9
8
5
3
7
3
5
2
9
7
1
3
8
5
6
2
4
9
5
2
9
3
6
8
5
4
2
9
3
1
7
6
3
5
4
2
1
9
3
7
5
8
4
6
2
1
6
8
4
3
5
6
8
1
4
2
7
9
3
5
9
6
1
8
7
5
2
9
6
3
1
4
8
7
7
1
2
3
8
4
7
5
1
6
2
3
9
8
9
3
8
5
4
1
9
2
3
7
8
5
6
4
3
8
4
7
2
3
6
8
9
4
5
7
1
2
[image:30.595.71.482.132.804.2]Bentuk awal
Solusi
Gambar 23 Sudoku Tipe 7
Challenger Puzzle
Pada karya ilmiah ini
Challenger Puzzle
memiliki empat tipe, yaitu Tipe A,
Tipe B, Tipe C, dan Tipe D. Tipe A dan Tipe C berukuran 4×4 sedangkan Tipe B
dan Tipe D berukuran 5×5. Pada Gambar 12, 13, 14, dan 15 terdapat
Challenger
Puzzle
yang belum dan yang sudah memiliki solusi. Solusi yang diperoleh melalui
LINGO 11.0 dapat dilihat pada Lampiran 8, 9, 10, dan 11.
1.
Tipe A
16
16
4
16
4
6
2
4
16
3
16
3
5
2
6
16
4
16
3
4
5
4
16
6
7
16
6
1
7
2
16
16
16
16
16
16
16
16
16
16
16
Bentuk awal
Solusi
21
2.
Tipe B
25
25
2
6
25
1
2
9
7
6
25
3
25
3
9
9
2
2
25
4
25
5
9
4
6
1
25
25
7
4
1
4
9
25
7
25
9
1
2
6
7
25
25
25
25
25
25
25
25
25
25
25
25
25
[image:31.595.108.504.60.734.2]Bentuk awal
Solusi
Gambar 25
Challenger Puzzle
Tipe B
3.
Tipe C
12
12
5
2
22
5
7
8
2
22
4
17
9
3
4
1
17
6
16
6
2
5
3
16
1
6
18
4
1
7
6
18
24
13
24
12
19
24
13
24
12
19
Bentuk awal
Solusi
Gambar 26
Challenger Puzzle
Tipe C
4.
Tipe D
25
25
8
5
24
8
6
3
2
5
24
7
6
29
4
7
3
6
9
29
2
1
25
2
5
9
8
1
25
4
16
1
2
4
3
6
16
8
2
21
3
8
1
7
2
21
18
28
20
26
23
29
18
28
20
26
23
29
Bentuk awal
Solusi
Gambar 27
Challenger Puzzle
Tipe D
N-Queens Problem
1.
Tipe 1
[image:32.595.58.485.18.827.2]
Bentuk awal
Solusi
Gambar 28
N-Queens Problem
Tipe I
2.
Tipe II
Bentuk awal
Solusi
23
3.
Tipe III
[image:33.595.100.510.44.823.2]
Bentuk awal
Solusi
Gambar 30
N-Queens Problem
Tipe III
SIMPULAN
Sudoku,
Challenger Puzzles, dan N-Queens Problem
dapat diformulasikan
menggunakan
integer programming
dan diselesaikan menggunakan LINGO 11.0
DAFTAR PUSTAKA
Asal Usul
Puzzle
Sudoku. 2013. [diunduh 7 Oktober 2013]; Tersedia pada:
http://www.blackits.net/id/art-and-culture/the-origins-of-the-sudoku-puzzle.html
Eight Queens Puzzle
. 2009. [diunduh 9 Oktober 2013]; Tersedia pada:
http://www.reachinformation.com/define/eight%20queens%20puzzle.aspx#s12
Lampiran 1 Sintaks Program LINGO 11.0 Sudoku Tipe 1 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,1,4)=1;X(1,3,5)=1;X(1,4,7)=1;X(1,6,6)=1;X(1,7,8)=1;X(1,9,9)=1;X(2,2,2)=1;X(2,4,1)=1;X(2, 6,4)=1;X(2,8,7)=1;X(2,9,5)=1;X(3,1,6)=1;X(3,3,7)=1;
X(3,4,8)=1;X(3,5,9)=1;X(3,6,5)=1;X(3,7,3)=1;X(3,9,4)=1;X(4,1,5)=1;X(4,2,9)=1;X(4,4,3)=1;X(4, 5,1)=1;X(4,7,4)=1;X(4,8,6)=1;X(5,1,1)=1;X(5,6,2)=1;
X(5,7,7)=1;X(5,9,3)=1;X(6,1,7)=1;X(6,2,8)=1;X(6,3,3)=1;X(6,5,6)=1;X(6,6,9)=1;X(6,7,2)=1;X(6, 8,5)=1;X(7,1,3)=1;X(7,3,8)=1;X(7,7,9)=1;X(7,8,4)=1;
X(7,9,6)=1;X(8,2,5)=1;X(8,3,6)=1;X(8,4,9)=1;X(8,5,4)=1;X(8,8,3)=1;X(9,1,9)=1;X(9,3,1)=1;X(9, 4,6)=1;X(9,6,3)=1;X(9,7,5)=1;X(9,9,2)=1;
Min=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#3:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k )))=1);
@FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#GE#7:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(row(i):@FOR(val(k):@FOR(col(j):@BIN(X(i,j,k))))); end
end
Solusi Sudoku Tipe 1
Global optimal solution found.
Objective value: 0.000000
Objective bound: 0.000000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 0
25
X( 8, 6, 8) 1.000000 0.000000 X( 8, 7, 1) 1.000000 0.000000 X( 8, 8, 3) 1.000000 0.000000 X( 8, 9, 7) 1.000000 0.000000 X( 9, 1, 9) 1.000000 0.000000 X( 9, 2, 4) 1.000000 0.000000 X( 9, 3, 1) 1.000000 0.000000 X( 9, 4, 6) 1.000000 0.000000 X( 9, 5, 7) 1.000000 0.000000 X( 9, 6, 3) 1.000000 0.000000 X( 9, 7, 5) 1.000000 0.000000 X( 9, 8, 8) 1.000000 0.000000 X( 9, 9, 2) 1.000000 0.000000
Lampiran 2 Sintaks Program LINGO 11.0 Sudoku Tipe 2 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,1,9)=1;X(1,3,6)=1;X(1,5,2)=1;X(1,7,3)=1;X(1,9,5)=1;X(2,2,1)=1;X(2,4,5)=1;X(2,6,3)=1;X(2, 8,4)=1;X(2,9,6)=1;
X(3,1,2)=1;X(3,4,6)=1;X(3,6,4)=1;X(3,7,9)=1;X(4,1,6)=1;X(4,2,9)=1;X(4,4,4)=1;X(4,5,3)=1;X(4, 7,7)=1;X(5,2,2)=1;
X(5,4,9)=1;X(5,6,1)=1;X(5,7,8)=1;X(5,8,3)=1;X(6,1,3)=1;X(6,3,4)=1;X(6,4,7)=1;X(6,6,2)=1;X(6, 7,6)=1;X(6,9,1)=1;
X(7,2,7)=1;X(7,5,1)=1;X(7,8,6)=1;X(7,9,3)=1;X(8,1,8)=1;X(8,2,3)=1;X(8,5,4)=1;X(8,6,6)=1;X(8, 7,1)=1;X(8,9,9)=1;
X(9,1,1)=1;X(9,3,9)=1;X(9,4,3)=1;X(9,6,5)=1;X(9,7,4)=1;X(9,8,2)=1;X(9,9,8)=1;
MIN=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#3:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k )))=1);
@FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#GE#7:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):(X(1,9,k)+X(2,8,k)+X(3,7,k)+X(4,6,k)+X(5,5,k)+X(6,4,k)+X(7,3,k)+X(8,2,k)+X(9, 1,k))=1);
@FOR(val(k):(X(5,7,k)+X(6,6,k)+X(7,5,k)+X(8,6,k)+X(9,7,k)+X(8,8,k)+X(7,9,k)+X(6,8,k)+X(7, 7,k))=1);
27
@FOR(row(i):@FOR(val(k):@FOR(col(j):@BIN(X(i,j,k))))); end
Solusi Sudoku Tipe 2 Global optimal solution found.
Objective value: 0.000000 Objective bound: 0.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0
X( 6, 1, 3) 1.000000 0.000000 X( 6, 2, 8) 1.000000 0.000000 X( 6, 3, 4) 1.000000 0.000000 X( 6, 4, 7) 1.000000 0.000000 X( 6, 5, 5) 1.000000 0.000000 X( 6, 6, 2) 1.000000 0.000000 X( 6, 7, 6) 1.000000 0.000000 X( 6, 8, 9) 1.000000 0.000000 X( 6, 9, 1) 1.000000 0.000000 X( 7, 1, 4) 1.000000 0.000000 X( 7, 2, 7) 1.000000 0.000000 X( 7, 3, 2) 1.000000 0.000000 X( 7, 4, 8) 1.000000 0.000000 X( 7, 5, 1) 1.000000 0.000000 X( 7, 6, 9) 1.000000 0.000000 X( 7, 7, 5) 1.000000 0.000000 X( 7, 8, 6) 1.000000 0.000000 X( 7, 9, 3) 1.000000 0.000000 X( 8, 1, 8) 1.000000 0.000000 X( 8, 2, 3) 1.000000 0.000000 X( 8, 3, 5) 1.000000 0.000000 X( 8, 4, 2) 1.000000 0.000000 X( 8, 5, 4) 1.000000 0.000000 X( 8, 6, 6) 1.000000 0.000000 X( 8, 7, 1) 1.000000 0.000000 X( 8, 8, 7) 1.000000 0.000000 X( 8, 9, 9) 1.000000 0.000000 X( 9, 1, 1) 1.000000 0.000000 X( 9, 2, 6) 1.000000 0.000000 X( 9, 3, 9) 1.000000 0.000000 X( 9, 4, 3) 1.000000 0.000000 X( 9, 5, 7) 1.000000 0.000000 X( 9, 6, 5) 1.000000 0.000000 X( 9, 7, 4) 1.000000 0.000000 X( 9, 8, 2) 1.000000 0.000000 X( 9, 9, 8) 1.000000 0.000000
Lampiran 3 Sintaks Program LINGO 11.0 Sudoku Tipe 3 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,3,3)=1;X(1,5,5)=1;X(1,6,9)=1;X(1,8,2)=1;X(1,9,7)=1; X(3,2,5)=1;X(3,3,9)=1;X(3,5,3)=1;X(3,6,8)=1;X(3,7,4)=1; X(3,8,6)=1;X(4,1,8)=1;X(4,9,4)=1;X(5,4,6)=1;X(5,5,1)=1; X(5,6,3)=1;X(6,2,1)=1;X(6,3,7)=1;X(6,7,6)=1;X(6,8,3)=1; X(8,2,6)=1;X(8,3,2)=1;X(8,4,3)=1;X(8,6,5)=1;X(8,7,1)=1; X(8,8,7)=1;X(9,1,3)=1;X(9,4,9)=1;X(9,7,2)=1;X(9,9,8)=1;
Min=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
29
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#3:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k )))=1);
@FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#GE#7:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):(X(1,9,k)+X(2,8,k)+X(3,7,k)+X(4,6,k)+X(5,5,k)+X(6,4,k)+X(7,3,k)+X(8,2,k)+X(9, 1,k))=1);
@FOR(val(k):(X(1,1,k)+X(2,2,k)+X(3,3,k)+X(4,4,k)+X(5,5,k)+X(6,6,k)+X(7,7,k)+X(8,8,k)+X(9, 9,k))=1);
@FOR(row(i):@FOR(val(k):@FOR(col(j):@BIN(X(i,j,k))))); end
Solusi Sudoku Tipe 3
Global optimal solution found.
Objective value: 0.000000 Objective bound: 0.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0
31
Lampiran 4 Sintaks Program LINGO 11.0 Sudoku Tipe 4 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,2,3)=1;X(1,3,2)=1;X(1,5,8)=1;X(1,7,7)=1;X(1,8,1)=1; X(2,1,9)=1;X(2,2,8)=1;X(2,8,2)=1;X(2,9,3)=1;X(3,5,3)=1; X(4,1,1)=1;X(4,3,5)=1;X(4,7,2)=1;X(4,9,8)=1;X(5,5,6)=1; X(6,1,6)=1;X(6,3,3)=1;X(6,7,1)=1;X(6,9,9)=1;X(7,5,2)=1; X(8,1,4)=1;X(8,2,5)=1;X(8,8,7)=1;X(8,9,2)=1;X(9,2,1)=1; X(9,3,7)=1;X(9,5,5)=1;X(9,8,8)=1;X(9,9,6)=1;
Min=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#3:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#3:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k )))=1);
@FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#LE#6#AND#i#GE#4:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#3:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):@SUM(col(j)|j#LE#6#AND#j#GE#4:@SUM(row(i)|i#GE#7:X(i,j,k)))=1); @FOR(val(k):@SUM(col(j)|j#GE#7:@SUM(row(i)|i#GE#7:X(i,j,k)))=1);
@FOR(val(k):(X(1,1,k)+X(1,4,k)+X(1,7,k)+X(4,1,k)+X(4,4,k)+X(4,7,k)+X(7,1,k)+X(7,4,k)+X(7, 7,k))=1);
@FOR(val(k):(X(1,2,k)+X(1,5,k)+X(1,8,k)+X(4,2,k)+X(4,5,k)+X(4,8,k)+X(7,2,k)+X(7,5,k)+X(7, 8,k))=1);
@FOR(val(k):(X(1,3,k)+X(1,6,k)+X(1,9,k)+X(4,3,k)+X(4,6,k)+X(4,9,k)+X(7,3,k)+X(7,6,k)+X(7, 9,k))=1);
@FOR(val(k):(X(2,1,k)+X(2,4,k)+X(2,7,k)+X(5,1,k)+X(5,4,k)+X(5,7,k)+X(8,1,k)+X(8,4,k)+X(8, 7,k))=1);
@FOR(val(k):(X(2,2,k)+X(2,5,k)+X(2,8,k)+X(5,2,k)+X(5,5,k)+X(5,8,k)+X(8,2,k)+X(8,5,k)+X(8, 8,k))=1);
@FOR(val(k):(X(2,3,k)+X(2,6,k)+X(2,9,k)+X(5,3,k)+X(5,6,k)+X(5,9,k)+X(8,3,k)+X(8,6,k)+X(8, 9,k))=1);
@FOR(val(k):(X(3,1,k)+X(3,4,k)+X(3,7,k)+X(6,1,k)+X(6,4,k)+X(6,7,k)+X(9,1,k)+X(9,4,k)+X(9, 7,k))=1);
@FOR(val(k):(X(3,2,k)+X(3,5,k)+X(3,8,k)+X(6,2,k)+X(6,5,k)+X(6,8,k)+X(9,2,k)+X(9,5,k)+X(9, 8,k))=1);
@FOR(val(k):(X(3,3,k)+X(3,6,k)+X(3,9,k)+X(6,3,k)+X(6,6,k)+X(6,9,k)+X(9,3,k)+X(9,6,k)+X(9, 9,k))=1);
Solusi Sudoku Tipe 4
Global optimal solution found.
Objective value: 0.000000 Objective bound: 0.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0
33
X( 6, 6, 8) 1.000000 0.000000 X( 6, 7, 1) 1.000000 0.000000 X( 6, 8, 4) 1.000000 0.000000 X( 6, 9, 9) 1.000000 0.000000 X( 7, 1, 3) 1.000000 0.000000 X( 7, 2, 9) 1.000000 0.000000 X( 7, 3, 6) 1.000000 0.000000 X( 7, 4, 8) 1.000000 0.000000 X( 7, 5, 2) 1.000000 0.000000 X( 7, 6, 7) 1.000000 0.000000 X( 7, 7, 4) 1.000000 0.000000 X( 7, 8, 5) 1.000000 0.000000 X( 7, 9, 1) 1.000000 0.000000 X( 8, 1, 4) 1.000000 0.000000 X( 8, 2, 5) 1.000000 0.000000 X( 8, 3, 8) 1.000000 0.000000 X( 8, 4, 1) 1.000000 0.000000 X( 8, 5, 9) 1.000000 0.000000 X( 8, 6, 6) 1.000000 0.000000 X( 8, 7, 3) 1.000000 0.000000 X( 8, 8, 7) 1.000000 0.000000 X( 8, 9, 2) 1.000000 0.000000 X( 9, 1, 2) 1.000000 0.000000 X( 9, 2, 1) 1.000000 0.000000 X( 9, 3, 7) 1.000000 0.000000 X( 9, 4, 3) 1.000000 0.000000 X( 9, 5, 5) 1.000000 0.000000 X( 9, 6, 4) 1.000000 0.000000 X( 9, 7, 9) 1.000000 0.000000 X( 9, 8, 8) 1.000000 0.000000 X( 9, 9, 6) 1.000000 0.000000
Lampiran 5 Sintaks Program LINGO 11.0 Sudoku Tipe 5 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,1,4)=1;X(1,3,1)=1;X(1,5,8)=1;X(1,7,3)=1;X(1,9,7)=1; X(2,2,6)=1;X(2,4,7)=1;X(2,6,1)=1;X(2,8,5)=1;X(2,9,9)=1; X(3,2,3)=1;X(3,4,6)=1;X(3,6,9)=1;X(3,8,1)=1;X(3,9,4)=1; X(4,1,9)=1;X(4,2,7)=1;X(4,4,8)=1;X(4,6,6)=1;X(4,8,2)=1; X(5,1,1)=1;X(5,3,6)=1;X(5,5,2)=1;X(5,7,9)=1;X(5,9,3)=1; X(6,2,5)=1;X(6,4,1)=1;X(6,6,3)=1;X(6,7,8)=1;X(6,9,6)=1; X(7,1,6)=1;X(7,3,9)=1;X(7,5,5)=1;X(7,7,7)=1;X(7,9,8)=1; X(8,1,5)=1;X(8,2,4)=1;X(8,4,3)=1;X(8,6,8)=1;X(8,8,9)=1; X(9,2,2)=1;X(9,4,9)=1;X(9,6,7)=1;X(9,8,4)=1;X(9,9,1)=1;
MIN=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
@FOR(val(k):(X(1,2,k)+X(1,3,k)+X(1,4,k)+X(1,5,k)+X(1,6,k)+X(2,3,k)+X(2,4,k)+X(2,5,k)+X(3, 4,k))=1);
@FOR(val(k):(X(1,7,k)+X(1,8,k)+X(1,9,k)+X(2,7,k)+X(2,8,k)+X(2,9,k)+X(3,7,k)+X(3,8,k)+X(3, 9,k))=1);
@FOR(val(k):(X(4,3,k)+X(5,2,k)+X(5,3,k)+X(5,4,k)+X(6,1,k)+X(6,2,k)+X(6,3,k)+X(6,4,k)+X(6, 5,k))=1);
@FOR(val(k):(X(2,6,k)+X(3,5,k)+X(3,6,k)+X(4,4,k)+X(4,5,k)+X(4,6,k)+X(5,5,k)+X(5,6,k)+X(6, 6,k))=1);
@FOR(val(k):(X(4,7,k)+X(4,8,k)+X(4,9,k)+X(5,7,k)+X(5,9,k)+X(6,7,k)+X(6,9,k)+X(7,7,k)+X(7, 9,k))=1);
@FOR(val(k):(X(7,1,k)+X(7,2,k)+X(7,3,k)+X(8,1,k)+X(8,2,k)+X(8,3,k)+X(9,1,k)+X(9,2,k)+X(9, 3,k))=1);
@FOR(val(k):(X(7,4,k)+X(7,5,k)+X(7,6,k)+X(8,4,k)+X(8,5,k)+X(8,6,k)+X(9,4,k)+X(9,5,k)+X(9, 6,k))=1);
@FOR(val(k):(X(5,8,k)+X(6,8,k)+X(7,8,k)+X(8,7,k)+X(8,8,k)+X(8,9,k)+X(9,7,k)+X(9,8,k)+X(9, 9,k))=1);
@FOR(val(k):(X(1,1,k)+X(1,4,k)+X(1,7,k)+X(4,1,k)+X(4,4,k)+X(4,7,k)+X(7,1,k)+X(7,4,k)+X(7, 7,k))=1);
@FOR(val(k):(X(1,2,k)+X(1,5,k)+X(1,8,k)+X(4,2,k)+X(4,5,k)+X(4,8,k)+X(7,2,k)+X(7,5,k)+X(7, 8,k))=1);
@FOR(val(k):(X(1,3,k)+X(1,6,k)+X(1,9,k)+X(4,3,k)+X(4,6,k)+X(4,9,k)+X(7,3,k)+X(7,6,k)+X(7, 9,k))=1);
@FOR(val(k):(X(2,1,k)+X(2,4,k)+X(2,7,k)+X(5,1,k)+X(5,4,k)+X(5,7,k)+X(8,1,k)+X(8,4,k)+X(8, 7,k))=1);
@FOR(val(k):(X(2,2,k)+X(2,5,k)+X(2,8,k)+X(5,2,k)+X(5,5,k)+X(5,8,k)+X(8,2,k)+X(8,5,k)+X(8, 8,k))=1);
@FOR(val(k):(X(2,3,k)+X(2,6,k)+X(2,9,k)+X(5,3,k)+X(5,6,k)+X(5,9,k)+X(8,3,k)+X(8,6,k)+X(8, 9,k))=1);
@FOR(val(k):(X(3,1,k)+X(3,4,k)+X(3,7,k)+X(6,1,k)+X(6,4,k)+X(6,7,k)+X(9,1,k)+X(9,4,k)+X(9, 7,k))=1);
@FOR(val(k):(X(3,2,k)+X(3,5,k)+X(3,8,k)+X(6,2,k)+X(6,5,k)+X(6,8,k)+X(9,2,k)+X(9,5,k)+X(9, 8,k))=1);
@FOR(val(k):(X(3,3,k)+X(3,6,k)+X(3,9,k)+X(6,3,k)+X(6,6,k)+X(6,9,k)+X(9,3,k)+X(9,6,k)+X(9, 9,k))=1);
@FOR(val(k):(X(1,9,k)+X(2,8,k)+X(3,7,k)+X(4,6,k)+X(5,5,k)+X(6,4,k)+X(7,3,k)+X(8,2,k)+X(9, 1,k))=1);
@FOR(val(k):(X(1,1,k)+X(2,2,k)+X(3,3,k)+X(4,4,k)+X(5,5,k)+X(6,6,k)+X(7,7,k)+X(8,8,k)+X(9, 9,k))=1);
@FOR(row(i):@FOR(val(k):@FOR(col(j):@BIN(X(i,j,k))))); end
Solusi Sudoku Tipe 5
Global optimal solution found.
Objective value: 0.000000 Objective bound: 0.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0
35
X( 8, 2, 4) 1.000000 0.000000 X( 8, 3, 7) 1.000000 0.000000 X( 8, 4, 3) 1.000000 0.000000 X( 8, 5, 1) 1.000000 0.000000 X( 8, 6, 8) 1.000000 0.000000 X( 8, 7, 6) 1.000000 0.000000 X( 8, 8, 9) 1.000000 0.000000 X( 8, 9, 2) 1.000000 0.000000 X( 9, 1, 3) 1.000000 0.000000 X( 9, 2, 2) 1.000000 0.000000 X( 9, 3, 8) 1.000000 0.000000 X( 9, 4, 9) 1.000000 0.000000 X( 9, 5, 6) 1.000000 0.000000 X( 9, 6, 7) 1.000000 0.000000 X( 9, 7, 5) 1.000000 0.000000 X( 9, 8, 4) 1.000000 0.000000 X( 9, 9, 1) 1.000000 0.000000
Lampiran 6 Sintaks Program LINGO 11.0 Sudoku Tipe 6 dan solusinya
model:sets: row/1..9/; col/1..9/; val/1..9/;
LINK(row,col,val):X; endsets
X(1,2,8)=1;X(1,4,1)=1;X(1,6,9)=1;X(1,8,7)=1;X(1,9,3)=1; X(2,1,7)=1;X(2,2,6)=1;X(2,4,3)=1;X(2,6,1)=1;X(2,8,5)=1; X(3,1,5)=1;X(3,3,8)=1;X(3,5,3)=1;X(3,7,6)=1;X(3,9,1)=1; X(4,1,3)=1;X(4,3,4)=1;X(4,5,7)=1;X(4,7,9)=1;X(4,9,8)=1; X(5,2,7)=1;X(5,4,2)=1;X(5,6,8)=1;X(5,8,1)=1;X(5,9,5)=1; X(6,1,9)=1;X(6,2,3)=1;X(6,4,8)=1;X(6,6,6)=1;X(6,8,4)=1; X(7,2,5)=1;X(7,4,6)=1;X(7,5,2)=1;X(7,7,1)=1;X(7,8,9)=1; X(8,1,6)=1;X(8,3,3)=1;X(8,5,1)=1;X(8,7,5)=1;X(8,8,8)=1; X(9,2,2)=1;X(9,5,8)=1;X(9,6,5)=1;X(9,7,7)=1;X(9,9,6)=1;
MIN=X(1,1,1);
@FOR(row(i):@FOR(val(k):@SUM(col(j):X(i,j,k))=1)); @FOR(col(j):@FOR(val(k):@SUM(row(i):X(i,j,k))=1)); @FOR(col(j):@FOR(row(i):@SUM(val(k):X(i,j,k))=1));
@FOR(val(k):(X(1,1,k)+X(2,1,k)+X(2,2,k)+X(3,1,k)+X(3,2,k)+X(3,3,k)+X(4,1,k)+X(4,2,k)+X(5, 1,k))=1);
@FOR(val(k):(X(1,2,k)+X(1,3,k)+X(1,4,k)+X(1,5,k)+X(1,6,k)+X(2,3,k)+X(2,4,k)+X(2,5,k)+X(3, 4,k))=1);
@FOR(val(k):(X(1,7,k)+X(1,8,k)+X(1,9,k)+X(2,7,k)+X(2,8,k)+X(2,9,k)+X(3,7,k)+X(3,8,k)+X(3, 9,k))=1);
@FOR(val(k):(X(4,3,k)+X(5,2,k)+X(5,3,k)+X(5,4,k)+X(6,1,k)+X(6,2,k)+X(6,3,k)+X(6,4,k)+X(6, 5,k))=1);
@FOR(val(k):(X(2,6,k)+X(3,5,k)+X(3,6,k)+X(4,4,k)+X(4,5,k)+X(4,6,k)+X(5,5,k)+X(5,6,k)+X(6, 6,k))=1);
@FOR(val(k):(X(4,7,k)+X(4,8,k)+X(4,9,k)+X(5,7,k)+X(5,9,k)+X(6,7,k)+X(6,9,k)+X(7,7,k)+X(7, 9,k))=1);
@FOR(val(k):(X(7,1,k)+X(7,2,k)+X(7,3,k)+X(8,1,k)+X(8,2,k)+X(8,3,k)+X(9,1,k)+X(9,2,k)+X(9, 3,k))=1);
37
@FOR(val(k):(X(5,8,k)+X(6,8,k)+X(7,8,k)+X(8,7,k)+X(8,8,k)+X(8,9,k)+X(9,7,k)+X(9,8,k)+X(9, 9,k))=1); @FOR(val(k):(X(1,9,k)+X(2,8,k)+X(3,7,k)+X(4,6,k)+X(5,5,k)+X(6,4,k)+X(7,3,k)+X(8,2,k)+X(9, 1,k))=1); @FOR(val(k):(X(2,2,k)+X(2,3,k)+X(2,4,k)+X(3,2,k)+X(3,3,k)+X(3,4,k)+X(4,2,k)+X(4,3,k)+X(4, 4,k))=1); @FOR(val(k):(X(6,6,k)+X(6,7,k)+X(6,8,k