APLIKASI DIAGONALISASI MATRIKS DALAM PERSILANGAN DIHIBRID KACANG KAPRI (pisum sativum)
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh :
Mega Hylda Carolina Simanungkalit NIM: 143114013
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
APLIKASI DIAGONALISASI MATRIKS DALAM PERSILANGAN DIHIBRID KACANG KAPRI (pisum sativum)
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Oleh :
Mega Hylda Carolina Simanungkalit NIM: 143114013
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
APLICATION MATRIX IN THE DISTRIBUTION OF DIHYBRID NUTS OF KAPRI
Final Paper
Presented as Partial Fulfilment of the
Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program
Written by:
Mega Hylda Carolina Simanungkalit Student ID: 143114013
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS
FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN MOTTO
“Jangan Protes pada Proses” -Merry Riana-
“Keberutungan milik orang yang berani” -Mega Hylda-
vi
HALAMAN PERSEMBAHAN
Karya ini saya persembahkan untuk Ibuku Tercinta
Lamriwati Pasaribu
Kepada abangku Leo Mulia Simanungkalit, serta adikku Khaswa Giovani Simanungkalit
Dosen pembimbingku yang selalu sabar dan setia membantu selama proses penulisan ini hingga akhir
Teman-teman dan keluarga Matematika Universitas Sanata Dharma yang telah menemani, membantu, menolong, memotivasi, dan memberi semangat selama proses
ix
APLIKASI DIAGONALISASI DALAM PERSILANGAN DIHIBRID KACANG KAPRI (pisum sativum)
Oleh:
Mega Hylda Carolina Simanungkalit 143114013
ABSTRAK
Seiring berkembangnya ilmu pengetahuan, banyak permasalahan di luar bidang matematika yang tidak dapat diselesaikan secara langsung. Salah satu cara yang dapat dilakukan adalah membawa permasalahan tersebut menjadi sebuah model matematika agar dapat diselesaikan dengan mudah. Sebagai contoh, dalam ilmu genetika terdapat persilangan antar jenis tumbuhan supaya memperoleh keturunan yang bersifat unggul. Salah satu penerapan ilmu matematika yang berhubungan dengan genetika adalah Aljabar Linear dengan menggunakan konsep diagonalisasi matriks. Hal ini bertujuan untuk mengetahui sifat pewarisan genotipe ke-n dalam jangka waktu yang panjang pada kasus persilangan tumbuhan kacang kapri dengan genotipe BBkk dan bbKK. Permasalahan tersebut dapat diselesaikan dengan analisis diagonalisasi matriks dengan menggunakan persamaan 𝐴𝑛 = 𝑃𝐷𝑛𝑃−1 berdasarkan peluang dari genotip induknya. Pada kasus persilangan dihibrid kacang kapri, dilakukan persilangan sifat setengah unggul pada bijinya dengan semua kemungkinan keturunan yang ada. Genotipe BBkk (bulat hijau) dan bbKK (keriput kuning) pada kacang kapri.
x ABSTRACT
As the development of science, a lot of problems outside the realm of mathematics that can not be resolved directly. One way to do is to bring these problems into a mathematical model that can be solved easily. For example, in genetics there are crosses between species in order to obtain offspring that are superior. One application of mathematics relating to genetics is Linear Algebra using the concept of matrix diagonalization. It aims to determine the nature of the n-th genotype inheritance in the long term in the case of crossing pea plants with genotype BBKK and BBKK. Those problems can be solved by matrix diagonalization analysis using the equation
An= PDnP−1based on the opportunities of the parent genotype. In the case of pea dihybrid cross, carried crosses half superior properties in the seeds with all the possible offspring there. Genotype BBKK (round green) and BBKK (wrinkled yellow) on nuts of kapri.
xi
KATA PENGANTAR
Puji syukur dipanjatkan ke hadirat Tuhan Yang Maha Esa, yang selalu melimpahkan curahan berkat, kasih dan penyertaan-Nya sehingga penulis dapat menyelesaikan tugas akhir ini dengan baik.
Tugas akhir dengan judul “Implementasi Matriks dalam Persilangan Dihibrid Kacang Kapri (pisum sativum)” yang telah diselesaikan penulis merupakan salah satu syarat untuk memperoleh gelar sarjana Sains pada program studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma. Dalam menyelesaikan tugas akhir ini, penulis tidak lepas dari bantuan, dukungan, serta bimbingan dari orang-orang di sekitar penulis. Oleh karena itu, melalui tulisan ini dengan segala kerendahan hati dan rasa hormat, penulis ingin menyampaikan ucapan terima kasih kepada:
1. Bapak Sudi Mungkasi Ph.D. selaku Dekan Fakultas Sains dan Teknologi, Universitas Sanata Dharma.
2. Bapak Hartono, Ph.D. selaku Ketua Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma sekaligus Dosen Pembimbing yang selalu sabar dan mau membimbing penulis sehingga dapat menyelesaikan tugas akhir ini dengan baik.
3. Romo Prof. Dr. Frans Susilo, SJ. selaku Dosen Pembimbing Akademik
4. Romo/Bapak/Ibu dosen Program Studi Matematika Universitas Sanata Dharma, yang telah membimbing dan membagikan ilmunya kepada penulis selama perkuliahan.
5. Ibu saya tercinta Lamriwati Pasaribu yang selalu setia memberikan dukungan secara moril maupun materiil, perhatian, kasih sayang, nasihat serta penguatan yang diberikan kepada penulis.
xiii DAFTAR ISI
halaman
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... Error! Bookmark not defined. HALAMAN PENGESAHAN ... Error! Bookmark not defined. HALAMAN MOTTO ... iv
HALAMAN PERSEMBAHAN ... vi
PERNYATAAN KEASLIAN KARYA ... Error! Bookmark not defined. LEMBAR PERNYATAAN ... Error! Bookmark not defined. ABSTRAK ... ix
ABSTRACT ... x
KATA PENGANTAR ... xi
DAFTAR ISI ... xiii
DAFTAR TABEL ... xv
BAB I PENDAHULUAN ... 1
A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 7 C. Tujuan Penulisan ... 7 D. Manfaat Penulisan ... 7 E. Batasan Masalah... 7 F. Metode Penulisan ... 8 G. Sistematika Penulisan ... 8
BAB II NILAI EIGEN DAN VEKTOR EIGEN ... 11
A. Nilai Eigen dan Vektor Eigen ... 11
xiv
BAB III ... 11
A. Genetika ... 11
B. Penggunaan Matriks Persilangan Dihibrid Kacang Kapri (pisum sativum).... 33
1. Genotipe BBkk (bulat hijau) ... 33
2. Genotipe bbKK (keriput kuning) ... 56
BAB IV KESIMPULAN DAN SARAN ... 767
A. Kesimpulan ... 767
B. Saran ... 767
xv DAFTAR TABEL halaman Tabel 3.1 ... 31 Tabel 3.2 ... 32 Tabel 3.3 ... 34 Tabel 3.4 ... 34 Tabel 3.5 ... 35 Tabel 3.6 ... 35 Tabel 3.7 ... 37 Tabel 3.8 ... 56 Tabel 3.9 ... 57 Tabel 3.10 ... 57 Tabel 3.11 ... 58 Tabel 3.12 ... 62
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Matematika adalah ilmu mengenai logika, besaran, struktur, pergerakan, susunan, serta konsep-konsepnya yang berhubungan antara satu dengan yang lainnya. Matematika dibagi menjadi tiga bagian besar yaitu aljabar, analisis dan geometri. Banyak sekali penerapan ilmu matematika dalam kehidupan sehari-hari, contohnya dalam biologi genetika. Salah satu cabang ilmu matematika yang berhubungan dengan ilmu genetika adalah Aljabar Linear.
Aljabar Linear erat sekali hubungannya dengan matriks. Matriks merupakan salah satu metode yang sangat ampuh dalam menyelesaikan persamaan matematika. Matriks terdiri dari entri-entri berupa bilangan real atau kompleks. Entri-entri dari sebuah matriks disebut elemen.
Pada umumnya 𝑎𝑖𝑗 akan menyatakan entri matriks 𝐴 yang berada pada baris 𝑖 dan kolom 𝑗. Jika A adalah matriks 𝑚𝑥𝑛, maka
Dalam tugas akhir ini akan dibahas tentang persilangan genetika pada persilangan dihibrid dan sifat mendasar pada matriks dianggap telah diketahui. Secara etimologi kata ‘genetika’ berasal dari kata ‘genos’ dalam bahasa Latin, yang berarti asal muasal kejadian. Genetika ialah ilmu yang mempelajari seluk beluk informasi hayati dari generasi ke generasi. Genetika juga merupakan ilmu pewarisan sifat pada makhluk hidup.
Dalam genetika terdapat beberapa sifat pewarisan dengan menggunakan persilangan. Persilangan monohibrid adalah persilangan dengan satu sifat beda. Dalam hal ini, maksudnya adalah pada persilangan ini kita hanya memperhatikan satu sifat pada makhluk hidup saja, misalnya warna pada tumbuhan (merah, putih, hijau) atau bentuk pada tumbuhan (bulat, lonjong). Persilangan dihibrid adalah persilangan dengan dua sifat beda. Dalam hal ini, maksudnya adalah pada persilangan ini terdapat dua sifat beda pada makhluk hidup yang diperhatikan, misalnya warna pada tumbuhan (merah, putih, hijau) dan bentuk pada tumbuhan (bulat, lonjong).
Anggota dari pasangan gen yang memiliki pengaruh berlawanan disebut alel. Alel dominan pada suatu makhluk hidup menyatakan sifat yang kuat pada makhluk hidup tersebut dan disimbolkan dengan huruf besar, sedangkan alel resesif menyatakan sifat yang lemah pada suatu makhluk hidup dan disimbolkan dengan huruf kecil. Sebagai contoh, dapat diambil tumbuhan kacang polong yang memiliki variasi bentuk pada bijinya. Jika B menentukan bentuk bulat pada biji, K menentukan warna kuning pada biji, maka B, K merupakan alel dominan. Jika b menentukan bentuk keriput pada biji, k menentukan warna hijau pada biji, maka b, k adalah alel resesif. Maka B, b, K, k merupakan alel pada persilangan dihibrid. Hasil persilangan antara dua individu yang mempunyai sifat yang berbeda adalah hibrid.
Pada pewarisan sifat terdapat beberapa istilah yaitu; genotipe, homozigot, heterozigot dan gamet. Genotipe adalah susunan genetik dari sifat keturunan yang tidak tampak oleh mata dan tidak berubah karena faktor lingkungan pada suatu makhluk hidup, misalnya pada biji tumbuhan dengan genotipe BB (biji bulat) . Homozigot adalah individu yang genotipnya terdiri dari alel yang sama, misalnya biji tumbuhan yang memiliki genotipe BB (biji bulat). Heterozigot adalah individu yang genotipnya terdiri dari alel yang berbeda, misalnya biji tumbuhan yang memiliki genotipe Bb (biji bulat) . Gamet adalah sel reproduksi pada suatu makhluk hidup atau sering juga disebut sel kelamin pada makhluk hidup. Lebih jelasnya akan dibahas pada bab selanjutnya mengenai genetika.
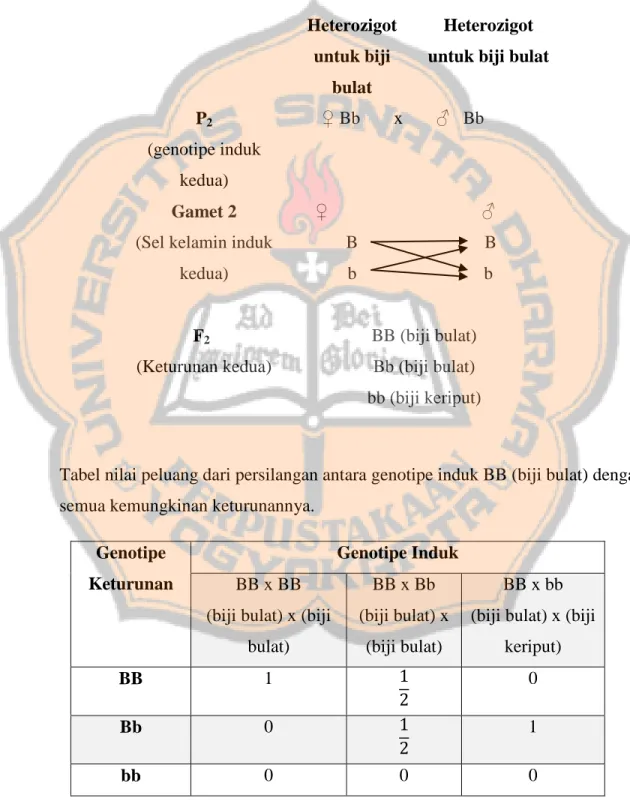
Dalam ilmu genetika khususnya pewarisan sifat, dapat ditemukan adanya variasi sifat yang diturunkan. Contoh kasus persilangan monohibrid dilakukan melalui pengamatan pada biji tumbuhan dengan menyilangkan tumbuhan biji bulat dengan biji keriput:
Homozigot untuk biji bulat Homozigot untuk biji keriput P1 (genotipe induk pertama) ♀BB x ♂bb Gamet 1
(Sel kelamin induk pertama) ♀ B ♂ b F1 (Keturunan pertama) Bb (biji bulat)
Persilangan monohibrid selanjutnya dilakukan melalui pengamatan pada biji tumbuhan dengan menyilangkan tumbuhan biji bulat dengan biji bulat yang merupakan hasil dari keturunan pertama pada persilangan di atas
Heterozigot untuk biji
bulat
Heterozigot untuk biji bulat
P2
(genotipe induk kedua)
♀ Bb x ♂ Bb
Gamet 2
(Sel kelamin induk kedua) ♀ B b ♂ B b F2 (Keturunan kedua) BB (biji bulat) Bb (biji bulat) bb (biji keriput)
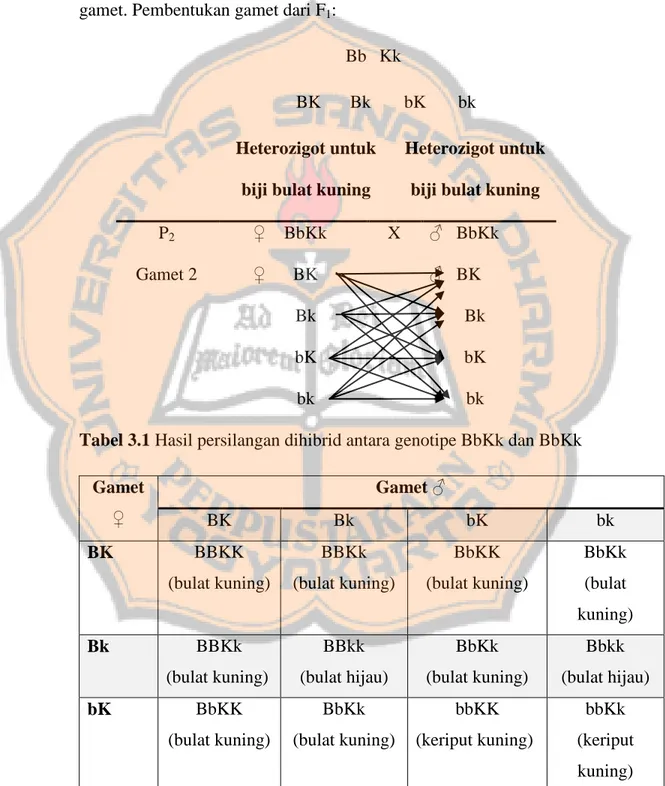
Tabel nilai peluang dari persilangan antara genotipe induk BB (biji bulat) dengan semua kemungkinan keturunannya.
Genotipe Keturunan
Genotipe Induk
BB x BB (biji bulat) x (biji
bulat)
BB x Bb (biji bulat) x
(biji bulat)
BB x bb (biji bulat) x (biji
keriput) BB 1 1 2 0 Bb 0 1 2 1 bb 0 0 0
Untuk persilangan BB (biji bulat) x BB (biji bulat) diperoleh nilai peluang 1 pada genotipe keturunan BB (biji bulat) diperoleh dengan cara:
Gamet B
B BB (biji bulat)
P(BB) =𝑛(𝐵𝐵)𝑛(𝑆) =11 = 1
Jadi, nilai peluang persilangan antara genotipe BB dan BB adalah sepenuhnya menghasilkan genotipe keturunan BB dengan nilai peluangnya adalah 1. Hal yang sama dapat dilakukan juga pada persilangan BB dan Bb serta BB dan bb. Nilai peluang yang telah didapat akan dibentuk ke dalam matriks dan akan dicari diagonalisasi dari matriks tersebut. Jika menghitung generasi ke-n, dibutuhkan aplikasi pada aljabar linear yaitu dengan menggunakan nilai eigen, vektor eigen serta diagonalisasi matriks untuk mengetahui pewarisan generasi selanjutnya.
Pada tugas akhir ini akan dibahas persilangan dihibrid pada kacang kapri karena proses persilangan mudah untuk dilakukan dan terdapat secara jelas sifat-sifat yang akan diwariskan. Dalam hal ini, akan diamati persilangan dengan variasi yang berbeda tersebut. Setelah mendapatkan hasil persilangan dihibrid, maka akan dicari peluang dari setiap hasil persilangan. Entri-entri dari matriks yang akan dibuat adalah nilai peluang dari setiap hasil persilangan yang telah dilakukan. Terdapat dua kasus persilangan pada kacang kapri yang akan dibahas. Kasus yang pertama adalah kacang kapri genotipe BBkk (bulat hijau) disilangkan dengan semua genotipe keturunannya. Sedangkan kasus yang kedua adalah kacang kapri genotipe bbKK (keriput kuning) disilangkan dengan semua genotipe keturunannya
Dari hasil matriks yang entri-entrinya berisi nilai peluang dari setiap persilangan akan dilanjutkan dengan mencari diagonalisasi matriks tersebut. Matriks 𝑛 𝑥 𝑛 dapat didiagonalkan jika hanya jika matriks tersebut mempunyai 𝑛 vektor eigen yang bebas linear. Diagonalisasi suatu matriks dilakukan dengan menentukan nilai eigen dan vektor eigen dari matriks yang sudah didapatkan nilai peluangnya.
Andaikan 𝐴 matriks persegi berordo 𝑛𝑥𝑛, vektor taknol 𝒙 di dalam 𝑅𝑛 dikatakan vektor eigen 𝐴, dan 𝜆 merupakan suatu skalar, jika
𝐴𝒙 = 𝜆𝒙
𝜆 disebut sebagai nilai eigen dari 𝐴 dan 𝒙 disebut sebagai vektor eigen yang berkaitan dengan nilai eigen 𝜆. Setelah nilai eigen dan vektor eigennya diselidiki, maka dapat dicari diagonalisasi matriksnya. Diagonalisasi matriks dilakukan untuk menghitung matriks yang pangkatnya besar, seperti persilangan pada tumbuhan. Misalkan 𝐴 matriks berukuran 𝑛 𝑥 𝑛 yang dapat didiagonalkan, artinya matriks 𝐴 dapat ditulis dalam bentuk
𝐴 = 𝑃𝐷𝑃−1
dengan 𝐷 merupakan matriks diagonal yang berisi nilai eigen dan 𝑃 matriks yang kolomnya berisi vektor eigen matriks 𝐴. Kemudian untuk mengitung 𝐴𝑛, cukup menghitung nilai
𝐴𝑛= 𝑃𝐷𝑛𝑃−1
Hal ini bertujuan untuk meramalkan suatu hasil persilangan 𝑛 generasi selanjutnya sehingga dapat ditentukan hasil persilangan yang sesuai dengan keinginan. Untuk jangka waktu (𝑡) yang sangat panjang yaitu ketika waktu (𝑡) menuju tak hingga, dapat diketahui distribusi suatu populasi dari kacang kapri dengan persilangan dihibrid yang dilakukan.
B. Rumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, maka rumusan masalah yang akan dibahas adalah:
1. Bagaimana menerapkan matriks dalam persilangan dihibrid kacang kapri? 2. Bagaimana mengetahui persamaan eksplisit untuk menentukan pewarisan
genotipe generasi ke-n dalam persilangan dihibrid kacang kapri?
C. Tujuan Penulisan
Berdasarkan rumusan masalah di atas, tujuan dari penulisan makalah ini adalah sebagai berikut:
1. Mendapatkan penerapan matriks untuk persilangan dihibrid kacang kapri. 2. Mengetahui persamaan eksplisit untuk menentukan pewarisan genotipe
generasi ke-n dalam persilangan dihibrid kacang kapri.
D. Manfaat Penulisan
Manfaat dari penulisan makalah ini adalah sebagai berikut:
1. Memperluas wawasan pembaca tentang metode matriks dalam menganalisa persilangan dihibrid kacang kapri.
2. Menambah pengetahuan pembaca tentang penerapan matriks dalam menentukan pewarisan genotipe persilangan dihibrid kacang kapri.
E. Batasan Masalah
Dalam makalah ini, penulis hanya membahas tentang penggunaan matriks dalam persilangan dihibrid pada kacang kapri dengan mencari nilai eigen dan vektor eigennya serta limitnya untuk jangka waktu yang panjang. Teori-teori berkaitan dengan aljabar linear seperti, sistem persamaan linear, determinan,
basis, ruang vektor, invers, dimensi, kebebasan linear, teori peluang dan limit dianggap sudah diketahui. Pada tugas akhir, akan dibahas mengenai nilai eigen, vektor eigen serta diagonalisasi matriks. Adapun matriks dalam tugas akhir ini diasumsikan dapat didiagonalkan.
F. Metode Penulisan
Metode penulisan dalam makalah ini adalah metode studi pustaka dengan membaca dan mempelajari buku-buku atau jurnal-jurnal yang berkaitan dengan ilmu matematika serta biologi sehingga dapat menggunakan teori matriks untuk diimplementasikan pada ilmu biologi khususnya persilangan dihibrid pada kacang kapri.
G. Sistematika Penulisan
Sistematika penulisan makalah ini adalah sebagai berikut: BAB I PENDAHULUAN
A. Latar Belakang Masalah B. Rumusan Masalah C. Tujuan Penulisan D. Manfaat Penulisan E. Batasan Masalah F. Metode Penulisan G. Sistematika Penulisan
BAB II NILAI EIGEN DAN VEKTOR EIGEN A. Nilai Eigen dan Vektor Eigen
B. Diagonalisasi Matriks
BAB III APLIKASI MATRIKS DALAM PERSILANGAN DIHIBRID KACANG KAPRI
A. Genetika
B. Penggunaan Model Matriks dalam Persilangan Dihibrid 1. Genetika BBkk (bulat hijau)
2. Genetika bbKK (keriput kuning)
BAB IV KESIMPULAN A. Kesimpulan B. Saran
BAB II
NILAI EIGEN DAN VEKTOR EIGEN
Dalam bab ini, akan dibahas tentang nilai eigen, vektor eigen dan diagonalisasi matriks. Teori yang terdapat pada bab ini akan digunakan pada bab selanjutnya dalam perhitungan untuk mengetahui persamaan eksplisit pewarisan genotipe keturunan generasi ke-n pada kacang kapri.
A. Nilai Eigen dan Vektor Eigen
Kata “vektor eigen” adalah gabungan bahasa Jerman dan Inggris. Dalam bahasa Jerman “eigen” diartikan sebagai “sebenarnya” atau “karakteristik”. Oleh karena itu nilai eigen dapat juga dinamakan nilai sebenarnya atau nilai karakteristik.
Definisi 2.1.1 (Anton,2014) Misalkan 𝐴 adalah matriks berukuran 𝑛 𝑥 𝑛, maka
vektor tak nol 𝒙 di 𝑅𝑛 disebut vektor eigen dari 𝐴, jika 𝐴𝒙 adalah kelipatan skalar dari 𝒙
𝐴𝒙 = 𝜆𝒙 (1)
untuk suatu skalar 𝜆. Skalar 𝜆 disebut nilai eigen dari 𝐴 dan 𝒙 dikatakan sebuah vektor eigen yang bersesuaian dengan 𝜆.
Contoh 2.1.2:
Diketahui matriks 𝐴 berukuran 2 x 2
dengan nilai eigen yang bersesuaian adalah 𝜆 = 3 dan vektor 𝒙 = (1,2) merupakan vektor eigen, karena
𝐴𝒙 = �38 −1� �0 12� = �36� = 3 �12� = 3𝒙 = 𝜆𝒙 Catatan :
1. Jika 𝒙 = 𝟎, persamaan 𝐴𝒙 = 𝜆𝒙 berlaku untuk semua bilangan real 𝜆. 2. Jika 𝒙 merupakan vektor eigen yang bersesuaian dengan nilai eigen 𝜆, 𝑠𝒙,
dengan 𝑠 merupakan bilangan real tak nol, juga merupakan vektor eigen, karena
𝐴(𝑠𝒙) = 𝑠𝐴𝒙 = 𝑠λ𝐱 = λ(𝑠𝒙)
Persamaan Karakteristik Teorema 2.1.3
Bilangan real 𝜆 merupakan nilai eigen dari matriks 𝐴 jika dan hanya jika 𝜆 memenuhi persamaan karakteristik
|𝐴 − 𝜆𝐼|= 𝟎 (2)
Bukti
Misalkan 𝐴 matriks berukuran 𝑛 𝑥 𝑛. Berdasarkan definisi, 𝜆 adalah nilai eigen dari matriks 𝐴 dengan vektor tak nol 𝒙 merupakan vektor eigennya
jika dan hanya jika
𝐴𝒙 = 𝜆𝒙 = 𝜆𝐼𝒙 (3)
jika dan hanya jika
Supaya λ menjadi nilai eigen, maka harus ada penyelesaian yang tidak nol dari persamaan (𝐴 − 𝜆𝐼)𝒙 = 𝟎. Persamaan ini akan mempunyai penyelesaian nontrivial (taknol) jika dan hanya jika
𝑑𝑒𝑡(𝐴 − 𝜆𝐼)= 0
Persamaan 𝑑𝑒𝑡(𝐴 − 𝜆𝐼)= 0 dengan 𝜆 sebagai variabel disebut persamaan karakteristik dari matriks 𝐴. Akar-akar atau skalar-skalar yang memenuhi persamaan ini adalah nilai-nilai eigen (nilai-nilai karakteristik) dari matriks 𝐴. Det (𝐴 − 𝜆𝐼) = 𝑓(𝜆) berupa polinom dalam 𝜆 yang dinamakan polinom karakteristik.
Matriks 𝐴 − 𝜆𝐼 dapat dijabarkan sebagai berikut
⎣ ⎢ ⎢ ⎢ ⎡𝑎11𝑎− 𝜆 𝑎12 𝑎13 … 𝑎1𝑛 21 𝑎22− 𝜆 𝑎23 … 𝑎2𝑛 𝑎31 𝑎32 𝑎33− 𝜆 … 𝑎3𝑛 ⋮ ⋮ ⋮ ⋮ ⋮ 𝑎𝑛1 𝑎𝑛2 𝑎𝑛3 … 𝑎𝑛𝑛− 𝜆⎦ ⎥ ⎥ ⎥ ⎤
Dari pemahaman definisi di atas, jelas bahwa jika 𝐴 adalah matriks 𝑛𝑥𝑛, maka persamaan karakteristik dari matriks 𝐴 mempunyai derajat 𝑛 dengan bentuk
𝑑𝑒𝑡(𝐴 − 𝜆𝐼)=𝑓(𝜆)= 𝑎0+ 𝑎1𝜆1+ 𝑎2𝜆2+ ⋯ + 𝑎𝑛−1𝜆𝑛−1+ 𝑎𝑛𝜆𝑛 = 0
Dengan 𝑎0+ 𝑎1𝜆1+ 𝑎2𝜆2+ ⋯ + 𝑎𝑛−1𝜆𝑛−1+ 𝑎𝑛𝜆𝑛 merupakan persamaan karakteristik yang mempunyai paling banyak n penyelesaian yang berbeda, sehingga suatu matriks 𝑛𝑥𝑛 mempunyai paling banyak n nilai eigen yang berbeda.
Contoh 2.1.4:
𝐴 = �4 −12 1 � Penyelesaian:
𝐴 − 𝜆𝐼 = �4 −12 1 � − �𝜆 00 𝜆� = �4 − 𝜆2 1 − 𝜆�−1 Dengan menggunakan persamaan karakteristik
|𝐴 − 𝜆𝐼|=(4 − 𝜆)(1 − 𝜆)+ 2 = 0
�𝜆2− 5𝜆 + 6� = 0
dengan kata lain
(𝜆 − 2)(𝜆 − 3) = 0
Maka nilai-nilai eigen dari A harus memenuhi persamaan (𝜆 − 2)(𝜆 − 3) = 0. Oleh karena itu, nilai eigennya adalah 𝜆1 = 2, 𝜆2 = 3. Untuk mencari vektor eigen yang bersesuaian, substitusikan setiap 𝜆 pada matriks 𝐴 − 𝜆𝐼.
• Untuk 𝜆1= 2
𝐴𝒙 = 𝜆𝒙
�4 −12 1 � �𝑥𝑥12�= 2�𝑥𝑥12�
4𝑥1 − 𝑥2 = 2𝑥1 ⟺ 4𝑥1− 2𝑥1 = 𝑥2 ⟺ 2𝑥1 = 𝑥2 Maka vektor eigen �𝑥𝑥1
2�=� 1 2�. • Untuk 𝜆2= 3 𝐴𝒙 = 𝜆𝒙 �4 −12 1 � �𝑥𝑥1 2�= 3� 𝑥1 𝑥2�
4𝑥1 − 𝑥2 = 3𝑥2 ⟺ 4𝑥1 = 4𝑥2 ⟺ 𝑥1 = 𝑥2 Maka vektor eigen �𝑥𝑥1
2�=�11�.
B. Diagonalisasi Matriks
Diagonalisasi matriks berguna untuk mempermudah menghitung matriks 𝐴𝑘 dengan 𝐴 adalah matriks persegi dan 𝑘 adalah bilangan asli yang cukup besar. Apabila tidak didiagonalisasikan kita harus mengalikan entri-entri matriks tersebut satu per satu. Apabila matriks tersebut telah diubah ke dalam matriks diagonal maka hanya tinggal menghitung pangkat dari entri tak nol matriks diagonalnya.
Definisi 2.2.1 (Anton, 2014) Sebuah matriks persegi 𝐴 dikatakan dapat
didiagonalisasi jika terdapat sebuah matriks 𝑃 yang dapat dibalik sedemikian rupa sehingga 𝑃−1𝐴𝑃 adalah sebuah matriks diagonal. Matriks 𝑃 dikatakan mendiagonalisasi 𝐴.
Terorema 2.2.2 (Anton, 2014) Jika 𝐴 adalah suatu matriks 𝑛𝑥𝑛, maka
pernyataan berikut ekivalen: a. 𝐴 dapat didiagonalkan
b. 𝐴 mempunyai 𝑛 vektor eigen yang bebas linear Bukti:
(a)→(b) : karena 𝐴 dapat didiagonalkan, maka ada suatu matriks yang dapat dibalik
sedemikian sehingga 𝑃−1𝐴𝑃 diagonal untuk suatu matriks invertibel 𝑃 dan matriks diagonal 𝐷. Katakanlah 𝑃−1𝐴𝑃 = 𝐷 , dimana
𝐷 = � 𝜆1 0 … 0 0 𝜆2 … 0 0 0 ⋱ 0 0 0 … 𝜆𝑛 � (6)
Dari rumus 𝑃−1𝐴𝑃 = 𝐷 kita dapatkan bahwa 𝐴𝑃 = 𝑃𝐷yaitu: 𝐴𝑃 = 𝐴[𝒙𝟏 𝒙𝟐 ⋯ 𝒙𝒏]
= [𝐴𝒙𝟏 𝐴𝒙𝟐 ⋯ 𝐴𝒙𝒏]
dan
𝑃𝐷 = [𝜆1𝒙𝟏 𝜆2𝒙2 ⋯ 𝜆𝑛𝒙𝒏]. (7) Jika kita menganggap 𝒙𝟏, 𝒙2, … , 𝒙𝒏 vektor-vektor kolom dari 𝑃 dimana 𝑃 bersifat invertibel, maka kolom-kolom dari 𝐴𝑃 berturut-turut adalah 𝐴𝒙𝟏, 𝐴𝒙𝟐, … ,𝐴𝒙𝒏. Karena 𝐴𝑃 = 𝑃𝐷 maka berlaku
𝐴𝒙𝒋 = 𝜆𝑗𝒙𝒋
dengan 𝜆𝑗 adalah nilai eigen, untuk 𝑗 = 1,2, … , 𝑛 Ini berarti bahwa 𝒙𝒋 merupakan
vektor eigen yang bersesuaian dengan 𝜆𝑗. Karena 𝑃 adalah matriks tak singular maka vektor-vektor kolom dari 𝑃 bebas linear. Jadi 𝑃 mempunyai 𝑛 vektor eigen yang bebas linear.
(b)→(a) : Misalkan 𝐴 matriks berukuran 𝑛𝑥𝑛. Asumsikan 𝐴 mempunyai 𝑛 vektor eigen yang bebas linear yaitu 𝒙𝟏, 𝒙2, … , 𝒙𝒏. Vektor-vektor eigen tersebut dapat ditulis sebagai kolom dari matriks berukuran 𝑛𝑥𝑛, yaitu
Matriks tersebut tak singular karena mempunyai 𝑛 vektor kolom di ℝ𝑛 yang bebas linear. Maka
𝐴𝑃 = 𝐴[𝒙𝟏 𝒙𝟐 … 𝒙𝒏] = [𝐴𝒙𝟏 𝐴𝒙𝟐 … 𝐴𝒙𝒏] dengan demikian
𝐴𝑃 = [𝜆𝟏𝒙𝟏 𝜆2𝒙2 … 𝜆𝑛𝒙𝒏] (8)
karena 𝐴𝒙𝑖 = 𝜆𝑖𝒙𝑖, dengan 𝜆𝑖 merupakan nilai eigen yang bersesuaian dengan vektor eigen 𝒙𝑖. Dalam hal ini, mungkin terjadi bahwa beberapa vektor eigen yang berbeda memiliki nilai eigen yang sama.
Misalkan 𝐷 matrks diagonal yang berisi nilai eigen 𝜆𝑖 yang bersesuaian dengan 𝒙𝑖, dapat ditulis 𝑃𝐷 = [𝒙𝟏 𝒙𝟐 … 𝒙𝒏] � 𝜆1 0 … 0 0 𝜆2 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … 𝜆𝑛 � = [𝜆𝟏𝒙𝟏 𝜆2𝒙𝟐 … 𝜆𝑛𝒙𝒏]
Maka dapat disimpulkan bahwa
𝐴𝑃 = 𝑃𝐷
Karena 𝑃 mempunyai invers, persamaan tersebut dapat dikalikan dengan 𝑃−1 sehingga diperoleh
𝑃−1𝐴𝑃 = 𝑃−1𝑃𝐷
Karena vektor-vektor kolom dari 𝑃 bebas linear maka 𝑃 dapat dibalik sehingga 𝐴 dapat didiagonalkan.
Adapun prosedur dalam mendiagonalkan suatu matriks adalah sebagai berikut (Anton, 2014):
1. Cari n vektor eigen yang bebas linear dari 𝐴 katakanlah 𝒙𝟏,𝒙𝟐, … , 𝒙𝑛
2. Bentuk matriks 𝑃 yang mempunyai 𝒙𝟏,𝒙𝟐, … , 𝒙𝑛 sebagai vektor-vektor kolomnya.
3. Selanjutnya matriks 𝑃−1𝐴𝑃 akan menjadi matriks diagonal dengan 𝜆1,𝜆2, … , 𝜆𝑛 berturut-turut sebagai entri diagonalnya, dengan 𝜆𝑖, adalah nilai eigen yang bersesuaian dengan 𝜆𝑖, untuk 𝑖 = 1,2, … , 𝑛.
Teorema 2.2.3 (Vektor eigen yang berkaitan dengan nilai eigen)
Misalkan 𝒙1 dan 𝒙2 adalah dua vektor eigen dari matriks 𝐴 yang berkaitan dengan nilai eigen 𝜆1 dan 𝜆2. Jika 𝜆1≠ 𝜆2 maka {𝒙1, 𝒙2} bebas linear. (Wono Setya B, 1995 : 283)
Bukti :
Karena 𝒙𝟏 dan 𝒙𝟐 merupakan vektor eigen dengan nilai eigen masing masing 𝜆1 dan 𝜆2 maka
𝐴𝒙𝟏= 𝜆1𝒙𝟏 dan 𝐴𝒙𝟐= 𝜆2𝒙𝟐 (10)
Akan ditunjukkan kedua vektor eigen bebas linear, dicari bilangan 𝑠1 dan 𝑠2 yang memenuhi
𝑠1𝒙𝟏+ 𝑠2𝒙𝟐= 𝟎 (11) Kalikan persamaan 𝑠1𝒙1+ 𝑠2𝒙2 = 𝟎 dengan matriks 𝐴 dan diperoleh
𝐴(𝑠1𝒙𝟏+ 𝑠2𝒙𝟐) = 𝟎 𝑠1𝐴𝒙𝟏+ 𝑠2𝐴𝒙𝟐= 𝟎
Kemudian dengan menggunakan persamaan 𝐴𝒙𝟏= 𝜆1𝒙𝟏dan 𝐴𝒙𝟐 = 𝜆2𝒙𝟐, diperoleh
𝑠1𝜆1𝒙𝟏+ 𝑠2𝜆2𝒙𝟐= 𝟎 (12) Misalkan 𝜆1≠ 0 kemudian kalikan 𝜆1 dengan persamaan 𝑠1𝒙𝟏+ 𝑠2𝒙𝟐= 𝟎 lalu kurangkan dengan persamaan 𝑠1𝐴𝒙𝟏+ 𝑠2𝐴𝒙𝟐= 𝟎 sehingga
𝜆1(𝑠1𝒙𝟏+ 𝑠2𝒙𝟐)= 0 𝑠1𝜆1𝒙1+ 𝑠2𝜆1𝒙2= 0 (𝑠1𝜆1𝒙1+ 𝑠2𝜆1𝒙2) −(𝑠1𝜆1𝒙1+ 𝑠2𝜆2𝒙2)= 0 𝑠1𝜆1𝒙1− 𝑠1𝜆1𝒙1+ 𝑠2𝜆1𝒙2− 𝑠2𝜆2𝒙2= 0 𝑠2𝜆1𝒙2− 𝑠2𝜆2𝒙2= 0 𝑠2(𝜆1− 𝜆2)𝒙2= 0
Karena (𝜆1− 𝜆2)𝒙𝟐 ≠ 𝟎 maka 𝑠2= 0. Kemudian substitusikan nilai 𝑠2 ke persamaan 𝑠1𝒙𝟏+ 𝑠2𝒙𝟐= 𝟎, dan diperoleh 𝑠1𝒙𝟏= 𝟎. Karena 𝒙𝟏≠ 𝟎 maka 𝑠1 = 0. Dengan demikian kedua vektor eigen bebas linear. ∎
Teorema 2.2.4 (Matriks 𝑛 × 𝑛 yang mempunyai 𝑛 buah nilai eigen)
Jika matriks 𝐴 berukuran 𝑛 × 𝑛 mempunyai 𝑛 buah nilai eigen yang berbeda, maka matriks 𝐴 dapat didiagonalkan. (Wono Setya B, 1995 : 284)
Pembuktian Teorema 2.2.4 menggunakan induksi matematis. Pembuktian dengan induksi matematis :
1. Langkah awal : teorema tersebut bernilai benar untuk 𝑛 = 2, karena
matriks 𝐴 berukuran 2 × 2 mempunyai dua buah vektor eigen 𝒙1 dan 𝒙2 yang bersesuaian dengan nilai-nilai eigen yang berbeda 𝜆1 dan 𝜆2 maka berdasarkan Teorema 2.2.3 𝒙1 dan 𝒙2 bebas linear. Sehingga menurut Teorema 2.2.2 matriks 𝐴 dapat didiagonalkan.
2. Langkah induksi : misalkan teorema tersebut benar untuk 𝑛 = 𝑘, yaitu
matriks 𝐴 berukuran 𝑘 × 𝑘 mempunyai 𝑘 buah vektor eigen yakni 𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘 yang bersesuaian dengan nilai-nilai eigen yang berbeda
𝜆1, 𝜆2, 𝜆3, … , 𝜆𝑘. Karena 𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘 bebas linear. Sehingga menurut Teorema 2.2.2 matriks 𝐴 dapat didiagonalkan.
Akan dibuktikan bahwa teorema juga berlaku untuk 𝑛 = 𝑘 + 1
Misalkan 𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘+1 adalah vektor eigen dari matriks 𝐴 berukuran
(𝑘 + 1)× (𝑘 + 1) yang bersesuaian dengan nilai-nilai eigen yang berbeda 𝜆1, 𝜆2, 𝜆3, … , 𝜆𝑘+1. Akan dibuktikan bahwa {𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘+1} adalah himpunan bebas linear.
Diasumsikan {𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘+1} tidak bebas linear. Dengan demikian, skalar 𝑠1, 𝑠2, 𝑠3, … , 𝑠𝑘+1 tidak semuanya bernilai nol, sehingga
𝑠1𝒙1+ 𝑠2𝒙2+ 𝑠3𝒙3+ ⋯ + 𝑠𝑘+1𝒙𝑘+1= 𝟎 (13) Karena 𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘+1 adalah vektor eigen yang bersesuaian dengan masing-masing nilai eigen 𝜆1, 𝜆2, 𝜆3, … , 𝜆𝑘+1 maka
𝐴𝒙1 = 𝜆1𝒙1, 𝐴𝒙2 = 𝜆2𝑥, 𝐴𝒙3 = 𝜆3𝒙3, … , 𝐴𝒙𝑘+1 = 𝜆𝑘+1𝒙𝑘+1 (14) Kalikan persamaan (13) dengan matriks 𝐴
𝐴(𝑠1𝒙1+ 𝑠2𝒙2+ 𝑠3𝒙3+ ⋯ + 𝑠𝑘+1𝒙𝑘+1) = 𝟎 𝑠1𝐴𝒙1+ 𝑠2𝐴𝒙2+ 𝑠3𝐴𝒙3+ ⋯ + 𝑠𝑘+1𝐴𝒙𝑘+1= 𝟎 Dengan menggunakan persamaan (14) diperoleh
𝑠1𝜆1𝒙1+ 𝑠2𝜆2𝒙2+ 𝑠3𝜆3𝒙3+ ⋯ + 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1= 𝟎 (15) Misalkan 𝜆𝑘+1≠ 0 kemudian kalikan 𝜆𝑘+1 dengan persamaan (13)
𝜆𝑘+1(𝑠1𝒙1+ 𝑠2𝒙2+ 𝑠3𝒙3+ ⋯ + 𝑠𝑘+1𝒙𝑘+1) = 𝟎
𝑠1𝜆𝑘+1𝒙1+ 𝑠2𝜆𝑘+1𝒙2+ 𝑠3𝜆𝑘+1𝒙3+ ⋯ + 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1= 𝟎
Persamaan (15) dikurangkan dengan persamaan yang di atas sehingga diperoleh (𝑠1𝜆1𝒙1+ 𝑠2𝜆2𝒙2+ 𝑠3𝜆3𝒙3+ ⋯ + 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1)− (𝑠1𝜆𝑘+1𝒙1+ 𝑠2𝜆𝑘+1𝒙2+ 𝑠3𝜆𝑘+1𝒙3+ ⋯ + 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1) = 𝟎 𝑠1𝜆1𝒙1− 𝑠1𝜆𝑘+1𝒙1+ 𝑠2𝜆2𝒙2− 𝑠2𝜆𝑘+1𝒙2+ 𝑠3𝜆3𝒙3− 𝑠3𝜆𝑘+1𝒙3+ ⋯ + 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1− 𝑠𝑘+1𝜆𝑘+1𝒙𝑘+1= 𝟎 𝑠1(𝜆1− 𝜆𝑘+1)𝒙1+ 𝑠2(𝜆2− 𝜆𝑘+1)𝒙2+ 𝑠3(𝜆3− 𝜆𝑘+1)𝒙3+ ⋯ + 𝑠𝑘(𝜆𝑘− 𝜆𝑘+1)𝒙𝑘= 𝟎
Karena {𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘} merupakan himpunan bebas linear sehingga persamaan ini menjadi
𝑠1(𝜆1− 𝜆𝑘+1)= 𝑠2(𝜆2− 𝜆𝑘+1)= 𝑠3(𝜆3− 𝜆𝑘+1)= ⋯ = 𝑠𝑘(𝜆𝑘− 𝜆𝑘+1)= 0 Dan karena 𝜆1, 𝜆2, 𝜆3, … , 𝜆𝑘+1 berbeda, maka diperoleh
𝑠1 = 𝑠2= 𝑠3= ⋯ = 𝑠𝑘 = 0 (16)
Subsitusikan nilai-nilai di atas ke persamaan (13) dan diperoleh 𝑠𝑘+1𝒙𝑘+1= 0
Karena vektor Eigen 𝒙𝑘+1 tak nol, maka
𝑠𝑘+1= 0 (17)
Persamaan (16) dan (17) bertentangan dengan pernyataan bahwa 𝑠1, 𝑠2, 𝑠3, … , 𝑠𝑘+1 tidak semuanya bernilai nol, sehingga muncul kontradiksi. Jadi terbukti bahwa {𝒙1, 𝒙2, 𝒙3, … , 𝒙𝑘+1} bebas linear. Sehingga menurut Teorema 2.2.2 matriks 𝐴 dapat didiagonalkan.
Maka terbukti bahwa Teorema 2.2.4 benar untuk matriks 𝐴 berukuran 𝑛 × 𝑛 yang mempunyai 𝑛 buah nilai eigen yang berbeda maka 𝐴 dapat didiagonalkan.∎ Namun apabila suatu matriks hanya memiliki 𝑘 < 𝑛 buah nilai eigen belum tentu matriks tersebut tidak dapat didiagonalkan.
Contoh 2.2.5:
Diberikan matriks 𝐴 berikut
𝐴 = �0 0 −21 2 1 1 0 3 �
Akan dicari suatu matriks 𝑃 yang mendiagonalkan matriks 𝐴 tersebut. Jawab :
Diperoleh persamaan karakteristiknya adalah
(𝜆 − 1)(𝜆 − 2)2=0
Vektor eigen yang bersesuaian adalah:
ketika 𝜆 = 2 ⟶ 𝒙1 =�−10 1 �, 𝒙2 = � 0 1 0� ketika 𝜆 = 1 ⟶ 𝒙3 =�−21 1 �
Selanjutnya dibentuk matriks 𝑃 = �
−1 0 −2
0 1 1
1 0 1 �
Menurut Teorema 2.2.3 telah ditunjukan bahwa ketiga vektor eigen tersebut bebas linear, maka dapat langsung dicari matriks diagonal yang terbentuk.
𝐷 = 𝑃−1𝐴𝑃 𝑃 = (𝒙1 𝒙2 𝒙3) 𝑃 = �−1 0 −20 1 1 1 0 1 � Hitung 𝑃−1. 𝐾𝑜𝑓(𝑃) = ⎝ ⎜ ⎜ ⎛ �1 10 1� − �0 11 1� �0 11 0� − �0 −20 1 � �−1 −21 1 � − �−1 01 0� �0 −21 1 � − �−1 −20 1 � �−1 00 1� ⎠ ⎟ ⎟ ⎞ 𝐾𝑜𝑓(𝑃) = �1 1 −10 1 0 2 1 −1�
𝐴𝑑𝑗𝑜𝑖𝑛 (𝑃) = � 11 01 21 −1 0 −1� 𝐷𝑒𝑡 (𝑃) = �−1 0 −20 1 1 1 0 1 � = −1 �1 10 1� − 0 − 2 �0 11 0� = −1 − 0 + 2 = 1 𝑃−1= 1� 1 0 21 1 1 −1 0 −1� 𝑃−1=� 1 0 21 1 1 −1 0 −1� sehingga 𝐷 = 𝑃−1𝐴𝑃 = � 11 01 21 −1 0 −1� � 0 0 −2 1 2 1 1 0 3 � � −1 0 −2 0 1 1 1 0 1 � = �2 0 00 2 0 0 0 1�
Terdapat beragam permasalahan di dalam ilmu matematika terapan yang membutuhkan perhitungan pangkat tinggi dari sebuah matriks persegi. Akan ditunjukkan bahwa diagonalisasi matriks dapat digunakan untuk menyederhanakan perhitungan pangkat tinggi tersebut untuk matriks-matriks yang dapat didiagonalisasi.
Untuk dapat menghitung 𝐴𝑛 secara lebih mudah, maka harus diketahui bahwa 𝐴
kolomnya berisi vektor eigen dari matriks 𝐴 dan matriks diagonal 𝐷 yang berisi nilai eigen sedemikian sehingga
𝐴 = 𝑃𝐷𝑃−1 Dengan melakukan pengkuadratan pada kedua ruas:
𝐴2= �𝑃𝐷𝑃−1�2
𝐴2 = (𝑃𝐷𝑃−1)(𝑃𝐷𝑃−1) 𝐴2 = 𝑃(𝐷𝑃−1𝑃)𝐷𝑃−1
Proses tersebut dapat diulang pada pangkat yang lebih tinggi, sehingga secara umum diperoleh
BAB III
APLIKASI DIAGONALISASI MATRIKS DALAM PERSILANGAN DIHIBRID
KACANG KAPRI
Dalam bab ini, akan dibahas tentang analisis pewarisan sifat genetika lebih khususnya pada persilangan dihibrid. Dengan bantuan ilmu di bidang matematika dapat diterapkan teori teori tentang matriks, peluang, diagonalisasi matrik untuk mengetahui distribusi populasi pada keturunan ke-n, dengan cara mengaplikasikan teori-teori matriks dalam genetika.
A. Genetika
Genetika erat hubungannya dengan pewarisan sifat, faktor keturunan, variasi keturunan, evolusi, dan perkembangan. Setiap individu memiliki gen yang merupakan kesatuan terkecil di dalam sel yang berperan menentukan sifat keturunan. Terdapat banyak sifat pada tanaman, binatang dan mikroba yang diatur oleh suatu gen. Pada tumbuhan, masing-masing induk akan mewariskan sifat kepada keturunannya. Pewarisan yang dapat dikenali dari orang tua kepada keturunannya secara genetik disebut hereditas.
Gen sendiri terdapat di dalam kromosom. Kromosom merupakan struktur di dalam inti sel yang terdiri dari satu molekul DNA dan berbagai protein yang membentuk informasi genetik. Kromosom secara garis besar terbagi menjadi dua bagian yaitu autosom dan gonosom. Autosom adalah kromosom yang tidak menentukan jenis kelamin. Sedangkan gonosom adalah kromosom yang menentukan jenis kelamin individu.
Gen merupakan faktor turunan tersimpan di dalam kromosom, yaitu di dalam manik-manik yang disebut kromomer atau nukleosom dari kromosom. Gen sebagai suatu zat yang berukuran sangat kecil yang mengandung satuan informasi genetik yang mengatur sifat-sifat menurun tertentu dan memenuhi lokus suatu kromosom. Setiap kromosom mengandung banyak gen. Gen terdiri dari DNA yang diselaputi dan diikat oleh protein. Jadi, secara kimia dapat disebut bahwa material yang menyimpan informasi genetik itu adalah DNA.
Dalam ilmu biologi sering terjadi adanya hasil-hasil persilangan yang terkadang tidak diinginkan. Dalam ilmu genetika khususnya pewarisan sifat pada manusia, dapat ditemukan adanya variasi sifat yang diturunkan. Variasi sifatnya seperti, struktur rambut, bentuk hidung, golongan darah, warna kulit, ukuran tubuh dan lain sebagainya. Pada tumbuhan terdapat variasi seperti batang suatu tanaman ada yang tinggi dan ada yang rendah, bunga suatu tanaman memiliki variasi warna, ada yang warna merah dan ada yang berwarna putih.
Pada kenyataannya sifat keturunan tidak hanya dapat dilihat oleh mata, sebab tidak cukup hanya membedakan suatu batang tanaman yang tinggi dari yang rendah saja, melainkan masih perlu diperhatikan variasi yang ada pada batang tanaman tersebut. Timbulnya suatu variasi persilangan dalam sifat keturunan tertentu disebabkan oleh pengaruh gen yang terdapat pada suatu makhluk hidup.
Anggota dari pasangan gen yang memiliki pengaruh berlawanan disebut alel. Alel dominan pada suatu makhluk hidup menyatakan sifat yang kuat pada makhluk hidup tersebut dan disimbolkan dengan huruf besar, sedangkan alel resesif menyatakan sifat yang lemah pada suatu makhluk hidup dan disimbolkan dengan huruf kecil. Sebagai contoh pada tumbuhan kacang polong yang memiliki variasi bentuk pada bijinya. Jika B menentukan bentuk bulat pada biji, K menentukan warna kuning pada biji, maka B, K merupakan alel dominan. Jika b menentukan bentuk keriput pada biji, k menetukan warna hijau pada biji, maka b,
k adalah alel resesif. Maka B, b, K, k merupakan alel pada persilangan dihibrid. Hasil persilangan antara dua individu yang mempunyai sifat yang berbeda adalah hibrid.
Sifat keturunan yang dapat kita lihat serta amati berdasarkan warna, bentuk, ukuran disebut dengan fenotip seperti warna tumbuhan, tinggi tumbuhan. Sedangkan sifat keturunan yang tidak tampak oleh mata dan tidak berubah karena faktor lingkungan pada suatu makhluk hidup disebut genotip. Contoh genotip pada persilangan kacang polong adalah BK (bulat kuning), bk (hijau keriput).
Individu yang genotipnya terdiri dari alel yang sama disebut homozigot (misalnya BBKK adalah homozigot dominan yang menyatakan sifat yang kuat pada suatu tanaman yaitu bulat kuning, sedangkan bbkk menunjukkan homozigot resesif ( sifat lemah) pada suatu tanaman yaitu hijau keriput ), sedangkan individu yang genotipnya terdiri dari alel yang berbeda disebut heterozigot (misalnya BbKk yaitu terdapat alel dominan dan alel resesif). Gamet adalah sel reproduksi pada suatu makhluk hidup atau sering juga disebut sel kelamin pada makhluk hidup. Terdapat beberapa istilah yang dipakai dalam persilangan antara lain:
P1 = pasangan induk pertama dari persilangan biji P2 = pasangan induk kedua dari suatu makhluk hidup F1 = keturunan pertama pada makhluk hidup
F2 = keturunan kedua dari suatu makhluk hidup ♂ = tanda jenis kelamin jantan
BBKK = alel dominan homozigot bbkk = alel resesif homozigot BbKk = alel heterozigot
B = gen untuk bentuk bulat pada biji b = gen untuk bentuk keriput pada biji K = gen untuk warna kuning pada biji k = gen untuk warna hijau pada biji
Anggota dari pasangan gen yang memiliki pengaruh berlawanan disebut alel. Misalnya B menentukan bentuk bulat pada biji, K menentukan warna kuning pada biji, b menentukan bentuk keriput pada biji, dan k menentukan warna hijau pada biji. Maka B, b, K, k merupakan alel pada persilangan dihibrid.
Pada kasus pertama akan disilangkan tumbuhan kapri yang memiliki sifat yang tidak seutuhnya unggul (sifat unggulnya adalah bentuk biji yang bulat sedangkan sifat yang tidak unggulnya adalah biji berwarna hijau dengan genotip BBkk) dengan semua kemungkinan yang ada.
Pada kasus kedua akan disilangkan tumbuhan kapri yang memiliki sifat yang tidak seutuhnya unggul (sifat unggulnya adalah biji berwarna kuning sedangkan sifat yang tidak unggulnya adalah bentuk biji yang keriput dengan genotip bbKK) dengan semua kemungkinan yang ada.
1. Kacang kapri (pisum sativum)
Kapri atau kacang kapri (pisum sativum) adalah sejenis tumbuhan sayur yang mudah dijumpai di pasar-pasar tradisional Indonesia. Kapri termasuk dalam golongan sayur buah, artinya buahnya yang dimakan sebagai sayur dan
tidak digolongkan sebagai buah-buahan, seperti juga tomat dan cabai. Tipe buah ini adalah polong, dipanen ketika masih muda dan bijinya belum berkembang penuh, sehingga berbentuk pipih dan lunak. Berikut adalah sifat kacang kapri yang dipelajari oleh Mendel (Strickberger, 1976):
a. biji bulat dan berkerut b. keping biji kuning dan hijau c. warna bunga putih dan ungu d. polong yang penuh dan mengerut e. polong kekuningan dan hijau
f. polong dekat poros batang dan di ujung g. tanaman tinggi dan pendek
2. Persilangan Monohibrid
Persilangan Monohibrid adalah persilangan antara dua individu dengan satu sifat beda. Contoh persilangan monohibrid yang dilakukan pengamatan pada biji tumbuhan dengan menyilangkan tumbuhan biji bulat dengan biji keriput : Homozigot untuk biji bulat Homozigot untuk biji keriput P1
(genotipe induk pertama)
♀BB x ♂ bb
Gamet 1
(Sel kelamin induk pertma)
♀ B ♂ b
F1
(Keturunan pertama)
Bb (biji bulat)
Dibawah ini terdapat persilangan monohibrid pada biji tumbuhan dengan menyilangkan tumbuhan biji bulat dengan biji bulat hasil dari keturunan pertama pada persilangan
Heterozigot
untuk biji bulat
Heterozigot untuk biji bulat P2
(genotipe induk kedua)
♀Bb x ♂ Bb
Gamet 2 (Sel kelamin induk
kedua) ♀ B, b ♂ B, b F2 (Keturunan kedua) BB (biji bulat) Bb (biji bulat) Bb (biji bulat) bb (biji keriput)
Hasil persilangan yang diperoleh adalah tiga genotipe biji bulat yaitu BB, Bb, Bb dan satu genotipe biji keriput yaitu bb.
3. Persilangan Dihibrid
Persilangan dihibrid adalah persilangan antara dua individu dengan dua sifat beda. Berikut adalah persilangan kacang kapri dihibrid berbiji bulat kuning dan berbiji keriput hijau yang dilakukan Mendel:
Homozigot untuk biji bulat kuning
Homozigot untuk biji keriput hijau
P1 ♀ BBKK X ♂ bbkk
Gamet 1 ♀ BK ♂ bk
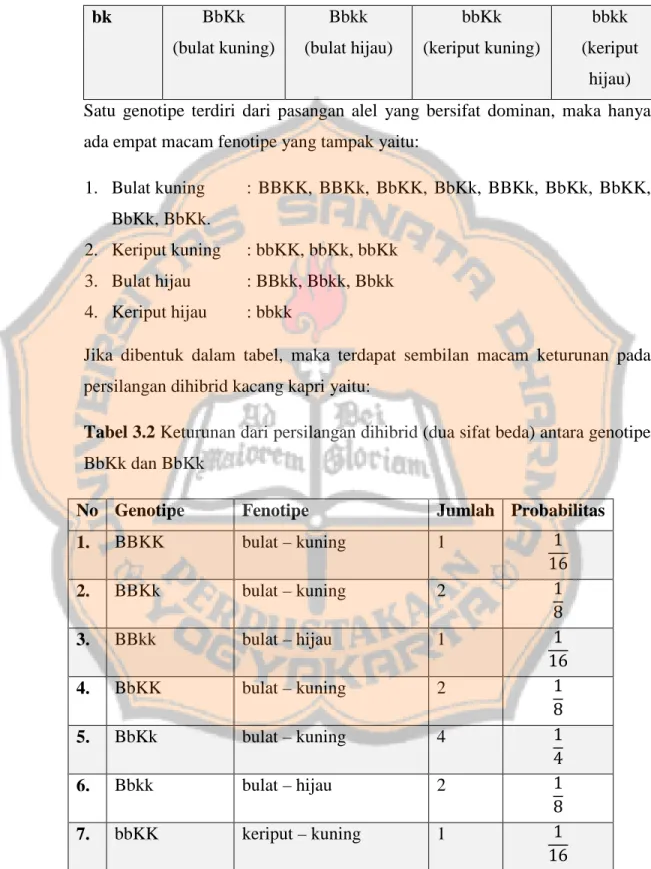
Hasil persilangan untuk keturunan pertama adalah bulat kuning karena B bersifat dominan terhadap b dan K bersifat dominan terhadap k. Hasil dari persilangan F1 antara BbKk dan BbKk akan menghasilkan empat macam gamet. Pembentukan gamet dari F1:
Bb Kk
BK Bk bK bk
Heterozigot untuk biji bulat kuning
Heterozigot untuk biji bulat kuning
P2 ♀ BbKk X ♂ BbKk Gamet 2 ♀ BK ♂ BK
Bk Bk
bK bK
bk bk
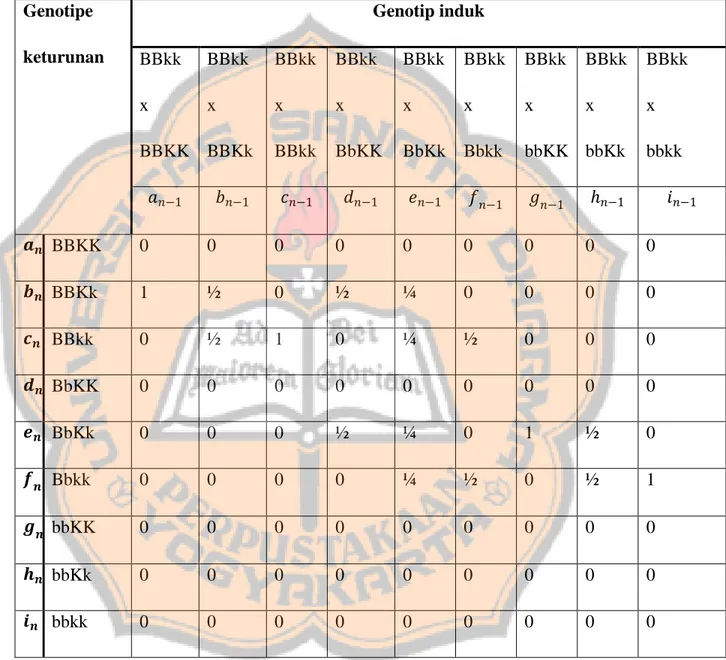
Tabel 3.1 Hasil persilangan dihibrid antara genotipe BbKk dan BbKk Gamet ♀ Gamet ♂ BK Bk bK bk BK BBKK (bulat kuning) BBKk (bulat kuning) BbKK (bulat kuning) BbKk (bulat kuning) Bk BBKk (bulat kuning) BBkk (bulat hijau) BbKk (bulat kuning) Bbkk (bulat hijau) bK BbKK (bulat kuning) BbKk (bulat kuning) bbKK (keriput kuning) bbKk (keriput kuning)
bk BbKk (bulat kuning) Bbkk (bulat hijau) bbKk (keriput kuning) bbkk (keriput hijau) Satu genotipe terdiri dari pasangan alel yang bersifat dominan, maka hanya ada empat macam fenotipe yang tampak yaitu:
1. Bulat kuning : BBKK, BBKk, BbKK, BbKk, BBKk, BbKk, BbKK, BbKk, BbKk.
2. Keriput kuning : bbKK, bbKk, bbKk 3. Bulat hijau : BBkk, Bbkk, Bbkk 4. Keriput hijau : bbkk
Jika dibentuk dalam tabel, maka terdapat sembilan macam keturunan pada persilangan dihibrid kacang kapri yaitu:
Tabel 3.2 Keturunan dari persilangan dihibrid (dua sifat beda) antara genotipe
BbKk dan BbKk
No Genotipe Fenotipe Jumlah Probabilitas
1. BBKK bulat – kuning 1 1 16 2. BBKk bulat – kuning 2 1 8 3. BBkk bulat – hijau 1 1 16 4. BbKK bulat – kuning 2 1 8 5. BbKk bulat – kuning 4 1 4 6. Bbkk bulat – hijau 2 1 8 7. bbKK keriput – kuning 1 1 16
8. bbKk keriput – kuning 2 1 8
9. bbkk keriput – hijau 1 1
16
B. Penggunaan Matriks Pada Persilangan Dihibrid Kacang Kapri (pisum sativum)
Matriks dapat memudahkan kita dalam memprediksi hasil dari suatu persilangan dan sifat yang akan muncul. Dengan metode perhitungan matriks, perhitungan akan lebih mudah untuk dimengerti. Misalkan pada populasi tanaman kapri yang memiliki genotipe BBkk dan bbKK. Pada tugas akhir ini akan dibahas dua kasus genotipe pada kacang kapri yaitu genotipe yang tidak seutuhnya unggul BBkk dan bbKK. Alel Bk menggambarkan tumbuhan dengan biji bulat dan warna hijau dengan sifat unggulnya pada bentuk bulatnya sementara alel bK adalah tumbuhan dengan biji keriput dan warna kuning dengan sifat unggulnya pada warnanya.
Pada akhirnya akan diketahui sifat generasi ke-n pada tanaman kapri yang telah disilangkan antara genotipe yang tidak seutuhnya unggul dengan berbagai macam kemungkinan keturunan yang ada. Dari hasil tersebut dapat dilihat apakah tumbuhan kapri yang genotipenya tidak seutuhnya unggul akan tetap menghasilkan genotipe yang seutuhnya tidak unggul atau malah menghasilkan genotipe unggul seluruhnya.
1. Genotipe BBkk (bulat hijau)
Adapun nilai peluang dari setiap keturunan diperoleh dengan cara :
a) Persilangan antara BBkk dan BBKK menghasilkan keturunan dengan genotipe BBKk dengan nilai peluangnya adalah 1. Adapun nilai
peluang yang diperoleh dari kemungkinan genotipe yang disilangkan adalah:
P (induk) : BBkk (Bulat Hijau) x BBKK (Bulat Kuning) Gamet : Bk dan BK
Tabel 3.3 Persilangan BBkk dan BBKK
Gamet BK
Bk BBKk (Bulat Kuning)
P(BBKk) =n(BBKk)n(S) =11 = 1
yang dapat dilihat pada baris kedua kolom pertama tabel 3.7.
b) Persilangan antara BBkk dan BBKk memperoleh nilai peluang 1
2 pada
keturunan bergenotipe BBKk dan 1
2pada keturunan bergenotipe BBkk.
Adapun nilai peluang yang diperoleh dari kemungkinan genotipe yang disilangkan adalah:
P (induk) : BBkk (Bulat Hijau) x BBKk (Bulat Kuning) Gamet : Bk dan BK, Bk
Tabel 3.4 Persilangan BBkk dan BBKk
Gamet BK Bk Bk BBKk (Bulat Kuning) BBkk (Bulat Kuning) P(BBKk) =n(BBKk)n(S) = 12 P(BBkk) =n(BBkk)n(S) = 12
yang dapat dilihat pada baris kedua dan ketiga pada kolom kedua tabel 3.7.
c) Persilangan antara BBkk dan BBkk memperoleh nilai peluang 1 yang sepenuhnya memeliki keturunan bergenotipe BBkk. Adapun nilai peluang yang diperoleh dari kemungkinan genotipe yang disilangkan adalah:
P (induk) : BBkk (Bulat Hijau) x BBkk (Bulat Hijau) Gamet : Bk dan Bk
Tabel 3.5 Persilangan BBkk dan BBkk
Gamet Bk
Bk BBkk (Bulat Hijau)
P(BBKK) = n(BBkk)n(S) =11 = 1
yang dapat dilihat pada baris dan kolom ketiga tabel 3.7.
d) Persilangan antara BBkk dan BbKK memperoleh nilai peluang 1
2
dengan keturunan yang memiliki genotipe BBKk dan 1
2 pada keturunan
dengan genotipe BbKk Adapun nilai peluang yang diperoleh dari kemungkinan genotipe yang disilangkan adalah:
P (induk) : BBkk (Bulat Hijau) x BbKK (Bulat Kuning) Gamet : Bk dan BK
Tabel 3.6 Persilangan BBkk dan BbKK
Gamet BK bK
Bk BBKk
(Bulat Kuning)
BbKk
P(BBKK)=n(BBKkn(S) )=12
P(BBKK) =n(BbKk)n(S) =12
yang dapat dilihat pada baris kedua dan kelima pada kolom keempat tabel 3.7.
Untuk selanjutnya dilakukan cara yang sama untuk mendapatkan setiap nilai peluang setiap keturunan.
Suatu individu mewarisi suatu gen dari tiap pasangan gen induknya untuk membentuk pasangan gennya sendiri. Sehingga, jika persilangan induk BBkk dan BBKK maka kecenderungan bahwa keturunannya akan mewarisi gen BK atau gen Bk dari induk tersebut. Dalam kondisi lain, jika persilangan induk BBkk dan BBKk maka kecenderungan bahwa keturunannya akan mewarisi genotipe BBKk atau genotipe BBkk sama besarnya. Adapun gen yang diwarisi adalah gen Bk dan BK. Sedangkan, persilangan induk BBkk dan BBkk maka kecenderungan bahwa keturunannya akan mewarisi gen Bk sepenuhnya. Begitu juga dengan pewarisan gen yang lainnya dilakukan dengan hal yang sama.
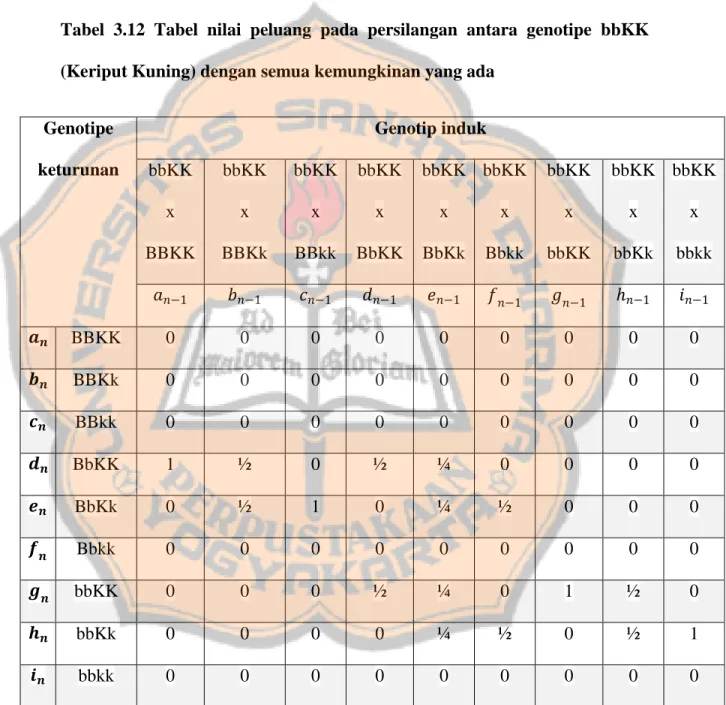
Tabel 3.7 Tabel nilai peluang pada persilangan antara genotipe BBkk (Bulat Hijau) dengan semua kemungkinan yang ada
Genotipe keturunan Genotip induk BBkk x BBKK BBkk x BBKk BBkk x BBkk BBkk x BbKK BBkk x BbKk BBkk x Bbkk BBkk x bbKK BBkk x bbKk BBkk x bbkk 𝑎𝑛−1 𝑏𝑛−1 𝑐𝑛−1 𝑑𝑛−1 𝑒𝑛−1 𝑓𝑛−1 𝑔𝑛−1 ℎ𝑛−1 𝑖𝑛−1 𝒂𝒏 BBKK 0 0 0 0 0 0 0 0 0 𝒃𝒏 BBKk 1 ½ 0 ½ ¼ 0 0 0 0 𝒄𝒏 BBkk 0 ½ 1 0 ¼ ½ 0 0 0 𝒅𝒏 BbKK 0 0 0 0 0 0 0 0 0 𝒆𝒏 BbKk 0 0 0 ½ ¼ 0 1 ½ 0 𝒇𝒏 Bbkk 0 0 0 0 ¼ ½ 0 ½ 1 𝒈𝒏 bbKK 0 0 0 0 0 0 0 0 0 𝒉𝒏 bbKk 0 0 0 0 0 0 0 0 0 𝒊𝒏 bbkk 0 0 0 0 0 0 0 0 0
Berdasarkan Tabel 3.7, pasangan induk BBkk x BBKK menghasilkan genotipe keturunan BBKk. Pasangan induk BBkk x BBKk menghasilkan genotipe keturunan BBKk dan BBkk. Pasangan induk BBkk x BBkk
menghasilkan genotipe keturunan BBkk. Pasangan induk BBkk x BbKK menghasilkan genotipe keturunan BBKk dan BbKk. Pasangan induk BBkk x BbKk menghasilkan genotipe keturunan BBKk, BbKk, Bbkk. Pasangan induk BBkk x bbKK menghasilkan genotipe keturunan BbKk. Pasangan induk BBkk x bbKk menghasilkan genotipe keturunan BbKk dan Bbkk. Pasangan induk BBkk x bbkk menghasilkan genotipe keturunan bbkk.
Distribusi dari kesembilan genotipe yang mungkin pada kacang kapri tersebut setelah sejumlah generasi dapat dibuat :
Untuk 𝑛 = 0,1,2, …
𝑎𝑛= peluang dari tumbuhan dengan genotipe BBKK pada generasi ke-n 𝑏𝑛= peluang dari tumbuhan dengan genotipe BBKk pada generasi ke-n 𝑐𝑛= peluang dari tumbuhan dengan genotipe BBkk pada generasi ke-n 𝑑𝑛= peluang dari tumbuhan dengan genotipe BbKK pada generasi ke-n 𝑒𝑛= peluang dari tumbuhan dengan genotipe BbKk pada generasi ke-n 𝑓𝑛= peluang dari tumbuhan dengan genotipe Bbkk pada generasi ke-n 𝑔𝑛= peluang dari tumbuhan dengan genotipe bbKK pada generasi ke-n ℎ𝑛= peluang dari tumbuhan dengan genotipe bbKk pada generasi ke-n 𝑖𝑛= peluang dari tumbuhan dengan genotipe bbkk pada generasi ke-n
Sehingga ketika 𝑛 = 0 maka, 𝑎0, 𝑏0, 𝑐0, 𝑑0, 𝑒0, 𝑓0, 𝑔0, ℎ0 dan 𝑖0 menentukan distribusi awal dari setiap genotipe itu. Dengan demikian untuk setiap penjumlahan berlaku hukum probabilitas
Dari hasil Tabel 3.7, genotipe-genotipe keturunan pada persilangan BBkk dengan semua keturunan ditentukan dengan menggunakan persamaan diantaranya 𝑎𝑛 menyatakan genotipe keturunan BBKK, 𝑏𝑛 menyatakan genotipe keturunan BBKk, 𝑐𝑛 menyatakan genotipe keturunan BBkk,𝑑𝑛 menyatakan genotipe keturunan BbKK, 𝑒𝑛 menyatakan genotipe keturunan BbKk, 𝑓𝑛 menyatakan genotipe keturunan Bbkk, 𝑔𝑛 menyatakan genotipe keturunan bbKK, ℎ𝑛 menyatakan genotipe keturunan bbKk, 𝑖𝑛 menyatakan genotipe keturunan bbkk. Sedangkan 𝑎𝑛−1, 𝑐𝑛−1, 𝑑𝑛−1, 𝑒𝑛−1, 𝑓𝑛−1, 𝑔𝑛−1, ℎ𝑛−1, 𝑖𝑛−1 menyatakan persilangan genotipe induk antara genotipe BBkk dengan semua kemungkinan keturunan yang ada.
Berdasarkan Tabel 3.7, dapat ditentukan distribusi genotipe untuk setiap generasi dari distribusi genotipe pada generasi sebelumnya yang berasal dari nilai peluang setiap genotipe dengan beberapa persamaan berikut:
𝑎𝑛 = 0
diperoleh dari nilai peluang genotipe keturunan BBKK, dimana nilai peluang dari setiap hasil persilangan adalah 0.
𝑏𝑛= 𝑎𝑛−1+12𝑏𝑛−1+12𝑑𝑛−1+12𝑒𝑛−1
diperoleh dari nilai peluang genotipe keturunan BBKk dengan beberapa hasil nilai peluang dari persilangan. Diantaranya adalah persilangan antara genotipe BBkk dan BBKK menghasilkan nilai peluang 1, persilangan antara genotipe BBkk dengan BBKk, BbKK, BbKk menghasilkan nilai peluang 12.
𝑐𝑛 =12𝑏𝑛−1+ 𝑐𝑛−1+12𝑓𝑛−1
diperoleh dari nilai peluang genotipe keturunan BBkk dengan beberapa hasil nilai peluang dari persilangan. Diantaranya adalah persilangan antara genotipe BBkk dengan BBKk, Bbkk menghasilkan nilai peluang 12, sedangkan
persilangan antara genotipe BBkk dengan BBkk menghasilkan nilai peluang 1.
𝑑𝑛= 0
diperoleh dari nilai peluang genotipe keturunan BbKK, dimana nilai peluang dari setiap hasil persilangan adalah 0.
𝑒𝑛 =12𝑑𝑛−1+41𝑒𝑛−1+ 𝑔𝑛−1+12ℎ𝑛−1
diperoleh dari nilai peluang genotipe keturunan BbKk dengan beberapa hasil nilai peluang dari persilangan. Diantaranya adalah persilangan antara genotipe BBkk dengan BbKK, bbKk menghasilkan nilai peluang 1
2, persilangan antara genotipe BBkk dengan BbKk menghasilkan nilai peluang 14 dan persilangan antara genotipe BBkk dengan bbKK menghasilkan nilai peluang 1.
𝑓𝑛 =14𝑒𝑛−1+21𝑓𝑛−1+12ℎ𝑛−1+ 𝑖𝑛−1
diperoleh dari nilai peluang genotipe keturunan Bbkk dengan beberapa hasil nilai peluang dari persilangan. Diantaranya adalah persilangan antara genotipe BBkk dengan BbKk menghasilkan nilai peluang 14, persilangan antara genotipe BBkk dengan Bbkk, bbKk menghasilkan nilai peluang 1
2 dan persilangan antara genotipe BBkk dengan bbkk menghasilkan nilai peluang 1. 𝑔𝑛 = 0
diperoleh dari nilai peluang genotipe keturunan bbKK, dimana nilai peluang dari setiap hasil persilangan adalah 0.
ℎ𝑛 = 0
diperoleh dari nilai peluang genotipe keturunan bbKk, dimana nilai peluang dari setiap hasil persilangan adalah 0.
𝑖𝑛 = 0
diperoleh dari nilai peluang genotipe keturunan bbkk, dimana nilai peluang dari setiap hasil persilangan adalah 0.
Persamaan-persamaan berikut dapat ditulis dalam notasi matriks sebagai
𝒙(𝑛)= 𝐴𝒙(𝑛−1) 𝑛 = 0,1,2, …
𝒙(𝑛) menyatakan distribusi keturunan untuk generasi ke-n dan 𝒙(𝑛−1)menyatakan distribusi generasi sebelumnya atau genotipe induk dimana
𝒙(𝑛)= ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑎𝑏𝑛𝑛 𝑐𝑛 𝑑𝑛 𝑒𝑛 𝑓𝑛 𝑔𝑛 ℎ𝑛 𝑖𝑛⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ , 𝒙(𝑛−1)= ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑎𝑏𝑛−1𝑛−1 𝑐𝑛−1 𝑑𝑛−1 𝑒𝑛−1 𝑓𝑛−1 𝑔𝑛−1 ℎ𝑛−1 𝑖𝑛−1⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Berdasarkan nilai peluang yang ada, maka terbentuklah matriks 𝐴 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡0 0 0 0 0 0 0 0 0 1 12 0 12 14 0 0 0 0 0 12 1 0 14 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 4 0 1 1 2 0 0 0 0 0 14 12 0 12 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dari persamaan 𝒙(𝑛)= 𝐴𝒙(𝑛−1) dapat diperoleh • untuk n = 1 𝒙(1)= 𝐴𝒙(0) • untuk n = 2 𝒙(2)= 𝐴𝒙(2−1) = 𝐴𝒙(1) = 𝐴𝐴𝒙(0)= 𝐴2𝒙(0), dengan 𝒙(1)= 𝐴𝒙(0) • untuk n = 3 𝒙(3)= 𝐴𝒙(3−1) = 𝐴𝒙(2) = 𝐴𝐴𝐴𝒙(0) = 𝐴3𝒙(0), dengan 𝒙(2)= 𝐴𝐴𝒙(0) ⋮
Secara umum dapat ditulis, 𝒙(𝑛) = 𝐴𝑛𝒙(0), 𝑛 = 1,2,3, …
Sebagai konsekuensi, kita dapat menentukan persamaan eksplisit untuk 𝐴𝑛. Dapat digunakan persamaan 𝒙(𝑛) = 𝐴𝑛𝒙(0) untuk memperoleh sebuah persamaan eksplisit untuk 𝒙(𝑛). Untuk menentukan persamaan eksplisit 𝐴𝑛, kita harus mendiagonalisasikan A. Dalam hal ini, kita menentukan sebuah matriks dapat dibalik P dan sebuah matriks diagonal D sedemikian sehigga
𝐴 = 𝑃𝐷𝑃−1
Dengan diagonalisasi semacam ini, maka diperoleh
𝐴𝑛= 𝑃𝐷𝑛𝑃−1 untuk 𝑛 = 1,2, … dimana 𝐷𝑛= ⎣ ⎢ ⎢ ⎢ ⎡𝜆0 𝜆1 0 0 ⋯ 0 2 0 ⋯ 0 0 0 𝜆3 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 𝜆𝑘⎦ ⎥ ⎥ ⎥ ⎤𝑛 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡𝜆1𝑛 0 0 ⋯ 0 0 𝜆2𝑛 0 ⋯ 0 0 0 𝜆3𝑛 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 𝜆𝑘𝑛⎦ ⎥ ⎥ ⎥ ⎥ ⎤
Setelah mendapatkan nilai peluang dari setiap kemungkinan, langkah selanjutnya adalah menyelesaikan persamaan karakteristik dari setiap matriks yang dihasilkan dengan menggunakan rumus det(λI – A) = 0 agar mendapatkan nilai eigen dan vektor eigen yang bersesuaian
𝑑𝑒𝑡(𝜆𝐼 − 𝐴) = 0 𝑑𝑒𝑡 ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝜆0 𝜆1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 𝜆3 0 0 0 0 0 0 0 0 0 𝜆4 0 0 0 0 0 0 0 0 0 𝜆5 0 0 0 0 0 0 0 0 0 𝜆6 0 0 0 0 0 0 0 0 0 𝜆7 0 0 0 0 0 0 0 0 0 𝜆8 0 0 0 0 0 0 0 0 0 𝜆9⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ − ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡0 0 0 0 0 0 0 0 0 1 1 2 0 1 2 1 4 0 0 0 0 0 1 2 1 0 1 4 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 14 0 1 12 0 0 0 0 0 14 12 0 12 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0
Nilai eigen yang diperoleh adalah 𝜆1= 1,𝜆2= 𝜆3 =12,𝜆4=14 ,𝜆5= 𝜆6 = 𝜆7=
𝜆8 = 𝜆9= 0 • Untuk 𝜆1= 1 (𝜆𝐼 − 𝐴)𝒙 = 𝟎 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡1 0 0 0 0 0 0 0 0 1 12 0 12 14 0 0 0 0 0 12 0 0 14 12 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 12 34 0 1 12 0 0 0 0 0 14 12 0 12 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑥𝑥12 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡00 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dengan menggunakan program Maple 17, maka diperoleh vektor eigen yang bersesuaian sebagai berikut :
𝒙𝟏= ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 0 1 0 0 0 0 0 0⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ • Untuk 𝜆2= 𝜆3 =12 (𝜆𝐼 − 𝐴)𝒙 = 𝟎 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡1 2 0 0 0 0 0 0 0 0 1 0 0 12 14 0 0 0 0 0 12 −12 0 14 12 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 12 14 0 1 12 0 0 0 0 0 14 0 0 12 1 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 12⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑥𝑥12 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡00 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dengan menggunakan program Maple 17, maka diperoleh vektor eigen yang bersesuaian sebagai berikut :
𝒙𝟐 = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 1 −1 0 0 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ dan 𝒙𝟑= ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 0 −1 0 0 1 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
• Untuk 𝜆4=14 (𝜆𝐼 − 𝐴)𝒙 = 𝟎 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡14 0 0 0 0 0 0 0 0 1 −14 0 12 14 0 0 0 0 0 12 −34 0 14 12 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 12 0 0 1 12 0 0 0 0 0 14 −14 0 12 1 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 14⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑥𝑥12 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡00 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dengan menggunakan program Maple 17, maka diperoleh vektor eigen yang bersesuaian sebagai berikut :
𝒙𝟒= ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 −1 1 0 1 −1 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
• Untuk 𝜆5=𝜆6= 𝜆7= 𝜆8= 𝜆9= 0 (𝜆𝐼 − 𝐴)𝒙 = 𝟎 ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡0 0 0 0 0 0 0 0 0 1 −12 0 12 14 0 0 0 0 0 12 −1 0 14 12 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 12 −14 0 1 12 0 0 0 0 0 14 −12 0 12 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡𝑥𝑥12 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡00 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dengan menggunakan program Maple 17, maka diperoleh vektor eigen yang bersesuaian sebagai berikut :
𝒙𝟓 = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 −2 1 0 0 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ , 𝒙𝟔 = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 0 0 1 −2 1 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ , 𝒙𝟕= ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 0 1 0 0 −2 0 0 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ 𝒙𝟖 = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 1 0 0 −2 0 0 1 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ , 𝒙𝟗= ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 𝑥1 𝑥2 𝑥3 𝑥4 𝑥5 𝑥6 𝑥7 𝑥8 𝑥9⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 0 2 −1 0 −4 2 1 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞
maka diperoleh matriks 𝑃 yang kolom-kolomnya berisi vektor-vektor eigen yang bersesuaian dengan nilai eigennya
𝑃 = [𝒙𝟏 𝒙𝟐 𝒙𝟑 𝒙𝟒 𝒙𝟓 𝒙𝟔 𝒙𝟕 𝒙𝟖 𝒙𝟗], 𝑃 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡00 01 00 −1 −20 1 00 00 10 02 1 −1 −1 1 1 0 1 0 −1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 −2 0 −2 −4 0 0 1 −1 0 1 −2 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 ⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ , 𝑃−1= ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡1 1 1 1 1 1 1 1 12 1 0 2 1 0 2 1 0 0 0 0 1 1 1 2 2 2 0 0 0 2 1 0 4 2 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ,
dengan 𝑃−1 adalah invers dari vektor-vektor eigen yang bersesuaian.
𝐷 = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡1 0 0 0 0 0 0 0 00 1 2 0 0 0 0 0 0 0 0 0 12 0 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0⎦⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ,