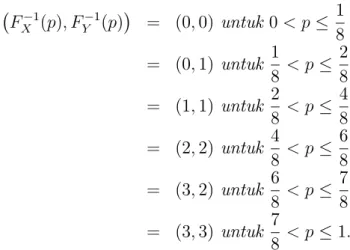Teori Comonotonic
Pada bab ini konsep teori comonotonic akan dipaparkan dari awal dan berakhir pada konsep teori ini untuk jumlah dari peubah - peubah acak1. Setelah
itu untuk membantu pemahaman akan diberikan sebuah contoh yang sangat berkaitan dengan kepentingan tugas akhir ini pada bab selanjutnya.
3.1
Pengurutan Variabel Acak
Sebelum membahas masalah pengurutan variabel acak, perlu ditekankan bah-wa variabel acak yang digunakan di buku ini adalah variabel acak yang memi-liki mean yang terbatas. Konsep yang digunakan untuk mengurutkan variabel acak adalah konsep urutan stop loss dan convex. Untuk suatu variabel acak X berlaku
lim
x!1x(1 FX(x)) = limx! 1xFX(x) = 0
dengan
FX(x) = PrfX xg
1Semua de…nisi (kecuali de…nisi 21), teorema, bukti, dan penjelasan di bab ini dikutip
dari paper [1] The Concept of Comonotonicity in Actuarial Science and Finance : Theory karangan J. Dhaene dkk.
De…nisi 21 dikutip dari paper [7] Upper and Lower Bound for Sums of Random Variables karangan R. Kaas dkk.
dan E[X] = 0 Z 1 FX(x)dx + 1 Z 0 (1 FX(x)) dx: (3.1)
Persamaan terakhir dapat kita dapatkan dengan cara sebagai berikut
E[X] = 1 Z 1 xf (x)dx = 0 Z 1 xf (x)dx 1 Z 0 x [ f (x)] dx E[X] = 0 Z 1 xdFX(x) 1 Z 0 xd (1 FX(x)) :
Dengan integral parsial kita akan dapatkan
E[X] = xFX(x)j 0 1 0 Z 1 FX(x)dx x(1 FX(x))j10 + 1 Z 0 (1 FX(x)) dx E[X] = 0 Z 1 FX(x)dx + 1 Z 0 (1 FX(x)) dx
yang sesuai dengan persamaan (3.1). Persamaan ini akan kita modi…kasi men-jadi E[(X 0)+] = 1 Z 0 (1 FX(x)) dx dengan (X d)+ = maxfX d; 0g = 8 < : X d 0 ; X > d ; X d :
De…nisi 18 Stop Loss Premium dide…nisikan sebagai
E (X d)+ =
1
Z
d
[1 FX(x)] dx ; 1 < d < 1: (3.2)
De…nisi 19 Misalkan X dan Y adalah dua buah peubah acak. Kita katakan X melebihi Y dalam urutan stop loss, dinotasikan dengan X sl Y, jika dan
hanya jika X memiliki stop loss premium yang lebih rendah dari Y
Berikutnya kita akan membuktikan bahwa untuk suatu keadaan yang sesuai dengan de…nisi di atas, kita akan mendapatkan
E[X] E[Y ]:
Untuk membuktikan pernyataan di atas kita akan memisalkan bahwa d adalah suatu bilangan yang kecil. Dengan pemisalan ini kita dapat mengklaim kebe-naran pernyataan di atas untuk semua nilai d yang lebih besar.
Misalkan d < 0 maka E (X d)+ = 1 Z d [1 FX(x)] dx = 0 Z d [1 FX(x)] dx + 1 Z 0 [1 FX(x)] dx d + E (X d)+ = 0 Z d FX(x)dx + 1 Z 0 [1 FX(x)] dx lim d! 1d+E (X d)+ = limd! 1 0 Z d FX(x)dx+ lim d! 1 1 Z 0 [1 FX(x)] dx = E[X]:
Dengan demikian untuk d ! 1, de…nisi (19) membawa kita kepada hasil yang menunjukkan bahwa
E[X] E[Y ]:
De…nisi 20 Misalkan X dan Y adalah dua buah peubah acak. Kita katakan X melebihi Y dalam urutan convex, dinotasikan dengan X cxY, jika dan hanya
E[X] = E[Y ] dan
E (X d)+ E (Y d)+ ; 1 < d < 1:
De…nisi 21 Misalkan X dan Y adalah dua buah peubah acak. Kita katakan X melebihi Y dalam urutan convex, dinotasikan dengan X cxY, jika dan hanya
E[f (X)] E[f (Y )] untuk semua fungsi convex f.
Proposisi 22 Jika X cxY maka V ar[x] V ar[Y ]:
Bukti.
V ar[X] = E[X2] E[X]2
Oleh karena E[X] = E[Y ] maka kita cukup membuktikan bahwa E[X2] E[Y2]: Perhatikan bahwa f (X) = X2 adalah fungsi convex. Dengan demikian
berlaku E[f (X)] = E[X2] E[f (Y )] = E[Y2]: Jadi jelas terbukti bahwa V ar[X] V ar[Y ]:
3.2
Invers Fungsi Distribusi
Pada bahasan mengenai teori peluang invers fungsi distribusi kumulatif tidak dijelaskan karena fungsi distribusi kumulatif bisa saja merupakan suatu fungsi yang tidak turun sehingga dapat terjadi kemungkinan terdapatnya beberapa titik yang mempunyai nilai fungsi yang sama. Akan tetapi pada bahasan ini akan dijelaskan de…nisi invers fungsi distribusi yang "biasa" dipakai, yaitu dengan memakai sifat fungsi distribusi kumulatif yang tidak turun dan kontinu kanan. Invers fungsi distribusi kumulatif FX(x) = PrfX xg dide…nisikan
sebagai suatu fungsi tak turun yang kontinu kiri
FX1(p) = inffx 2 R j FX(x) p ; p2 [0; 1]g: (3.3)
Adapun sifat yang perlu diperhatikan adalah untuk setiap x 2 R dan p 2 [0; 1] berlaku
FX1(p) x, FX(x) p:
Akan tetapi pada pembahasan di buku ini kita tidak akan mende…nisikan invers fungsi distribusi seperti pada pengertian di atas. Untuk itu akan dide…nisikan suatu bentuk yang lain, yaitu
FX1+(p) = supfx 2 R j FX(x) p ; p2 [0; 1]g (3.4)
Dengan kedua bentuk di atas kita akan mendapatkan bahwa untuk setiap p 2 [0; 1], pilihan yang tepat untuk invers FX di titik p ada pada interval
tutup
FX1(p); FX1+(p) dengan ketentuan bahwa
sup ? = 1 inf ? = 1
FX1(0) = 1 FX1+(0) =1:
Hal yang patut menjadi catatan adalah invers FX di titik p tidaklah harus
FX1(p)atau FX1+(p) akan tetapi merupakan salah satu bagian dari selang tut-up yang dibentuk oleh keduanya. Selain itu FX1(p) dan FX1+(p) mempunyai nilai …nite di selang (0; 1) : Untuk seterusnya kita akan memakai ketentuan bahwa p 2 (0; 1) :
Oleh karena invers FX di titik p berada pada suatu selang maka kita akan
mende…nisikan invers untuk FX di titik p seperti berikut
FX1( )(p) = FX1(p) + (1 )FX1+(p) ; p2 (0; 1) 2 [0; 1] : (3.5) Secara otomatis FX1( )(p) adalah suatu fungsi yang tak turun. Sifat yang dapat ditarik dari de…nisi ini adalah
FX1(p) FX1( )(p) FX1+(p) ; p2 (0; 1) : Apabila gra…k dari FX ditinjau maka ketiga nilai FX1(p); F
1( )
X (p);dan F 1+
X (p)
hanya akan berbeda pada saat ketiganya berada pada suatu segmen horizon-tal dengan nilai p yang sama. Sekarang misalkan bahwa terdapat d dimana 0 < FX(d) < 1. Dengan demikian nilai dari FX1(FX(d)) dan FX1+(FX(d))
berhingga dan FX1(FX(d)) d FX1+(FX(d)): Jadi untuk suatu d 2 [0; 1]
, d dapat dituliskan menjadi
d = dFX1(FX(d)) + (1 d)FX1+(FX(d)) = F 1( d)
Hasil ini mengakibatkan untuk suatu peubah acak X dan untuk suatu d dimana 0 < FX(d) < 1; terdapat d 2 [0; 1] sedemikian sehingga F
1( d)
X (FX(d)) = d:
Pada teorema berikut ini akan dijelaskan hubungan antara invers fungsi distribusi dari peubah acak X dan fungsi monoton g(X).
Teorema 23 Misalkan X dan g(X) adalah suatu peubah acak bernilai real dan misalkan 0 <p <1.
1. Jika g adalah fungsi yang tidak turun dan kontinu kiri maka
Fg(X)1 (p) = g(FX1(p)): (3.6)
2. Jika g adalah fungsi yang tidak turun dan kontinu kanan maka
Fg(X)1+(p) = g(FX1+(p)): (3.7)
3. Jika g adalah fungsi yang tidak naik dan kontinu kiri maka
Fg(X)1+(p) = g(FX1(1 p)): (3.8)
4. Jika g adalah fungsi yang tidak naik dan kontinu kanan maka
Fg(X)1 (p) = g(FX1+(1 p)): (3.9)
Bukti. Akan dibuktikan untuk masing-masing kriteria.
1. Misalkan g adalah fungsi yang tidak turun dan kontinu kiri. Pernyataan di bawah ini saling ekuivalen.
Fg(X)1 (p) x, inffg(z) 2 R j Fg(X)(g(z)) pg x
Fg(X)1 (p) x, inffg(z) 2 R j Prfg(X) g(z)g pg x
Fg(X)1 (p) x, inffz 2 R j PrfX zg pg supfy j g(y) xg Fg(X)1 (p) x, FX1(p) supfy j g(y) xg
2. Misalkan g adalah fungsi yang tidak turun dan kontinu kanan. Pernya-taan di bawah ini saling ekuivalen.
Fg(X)1+(p) x, supfg(z) 2 R j Fg(X)(g(z)) pg x
Fg(X)1+(p) x, supfg(z) 2 R j Prfg(X) g(z)g pg x
Fg(X)1+(p) x, supfz 2 R j PrfX zg pg inffy j g(y) xg Fg(X)1+(p) x, FX1+(p) inffy j g(y) xg
Fg(X)1+(p) x, g(FX1+(p)) x
3. Misalkan g adalah fungsi yang tidak naik dan kontinu kiri. Pernyataan di bawah ini saling ekuivalen.
Fg(X)1+(p) x, supfg(z) 2 R j Fg(X)(g(z)) pg x
Fg(X)1+(p) x, supfg(z) 2 R j Prfg(X) g(z)g pg x
Fg(X)1+(p) x, inffz 2 R j PrfX zg 1 pg supfy j g(y) xg Fg(X)1+(p) x, FX1(1 p) supfy j g(y) xg
Fg(X)1+(p) x, g(FX1(1 p)) x
4. Misalkan g adalah fungsi yang tidak naik dan kontinu kanan. Pernyataan di bawah ini saling ekuivalen.
Fg(X)1 (p) x, inffg(z) 2 R j Fg(X)(g(z)) pg x
Fg(X)1 (p) x, inffg(z) 2 R j Prfg(X) g(z)g pg x
Fg(X)1 (p) x, supfz 2 R j PrfX zg 1 pg inffy j g(y) xg Fg(X)1 (p) x, FX1+(1 p) inffy j g(y) xg
Fg(X)1 (p) x, g(FX1+(1 p)) x
Oleh karena peubah acak X; FX1(U ); FX1( )(U ); dan FX1+(U ) berasal dari fungsi distribusi yang sama maka dapat dikatakan bahwa
3.3
Teori Comonotonic untuk Himpunan
Teori comonotonic akan dijelaskan pertama kali untuk suatu himpunan dari n-vektor di Rn:Sebuah n-vektor (x
1; :::; xn)akan dinotasikan dengan x. Untuk
dua buah n-vektor x dan y, notasi x y akan digunakan untuk menjelaskan urutan perkomponen atau dengan kata lain xi yi 8i = 1; 2; :::; n:
De…nisi 24 Himpunan A Rn dikatakan comonotonic jika untuk setiap x
dan y di A berlaku salah satu dari x y atau y x: Untuk suatu himpunan A Rn notasi A
i;j akan digunakan untuk
menje-laskan proyeksi himpunan A pada bidang (i,j). Ai;j dide…nisikan sebagai
Ai;j =f(xi; xj)j x 2 Ag:
Lemma 25 Himpunan A Rn dikatakan comonotonic jika dan hanya jika
Ai;j comonotonic untuk setiap i 6= j di f1; 2; :::; ng:
Bukti. Akan dibuktikan bahwa jika Ai;j comonotonic untuk setiap i 6= j di
f1; 2; :::; ng maka himpunan A Rn dikatakan comonotonic.
Jika Ai;j comonotonic untuk setiap i 6= j di f1; 2; :::; ng maka dapat
diben-tuk kumpulan vektor dalam suatu himpunan A dimana undiben-tuk setiap vektor x dan y di dalam A berlaku x y atau y x:Dengan demikian, sesuai de…nisi di atas, A adalah suatu himpunan yang comonotonic.
Akan dibuktikan jika himpunan A Rn comonotonic maka A
i;j
comono-tonic untuk setiap i 6= j di f1; 2; :::; ng:
Jika himpunan A Rncomonotonic maka A
i;j =f(xi; xj)j x Ag adalah
himpunan-himpunan yang comonotonic karena setiap elemen dari Ai;j adalah
bagian dari elemen A.
Dari kedua hasil di atas dapat ditarik kesimpulan bahwa himpunan A Rn dikatakan comonotonic jika dan hanya jika Ai;jcomonotonic untuk setiap i 6= j
3.4
Teori Comonotonic untuk Vektor Acak
Suatu himpunan A Rn dikatakan support dari X jika PrfX 2 Ag = 1. De…nisi berikut ini akan terkait dengan support dari suatu vektor acak. De…nisi 26 Suatu vektor acak X dikatakan comonotonic jika X mempunyai support yang comonotonic.
Teorema 27 Suatu vektor acak X dikatakan comonotonic jika dan hanya jika salah satu pernyataan ekuivalen ini berlaku.
1. Vektor acak X mempunyai support yang comonotonic. 2. Untuk setiap x = (x1; :::; xn) berlaku
FX(x) = minfFX1(x1); :::; FXn(xn)g:
3. Untuk suatu peubah acak uniform (0,1) U berlaku X = Fd X11(U ); :::; FXn1(U ) :
4. Terdapat suatu peubah acak Z dan sebuah fungsi yang tidak turun fi
(i = 1; 2; :::; n)sehingga
X= (fd 1(Z); :::; fn(Z)) :
Bukti. Asumsikan kita mempunyai vektor acak X dengan support comono-tonic B.
(1) ) (2) Misalkan x 2 Rn dan de…nisikan Aj =fx 2 B j yj xjg:
Karena sifat comonotonic pada himpunan B (vektor-vektor pada B telah teru-rut) maka terdapat i sedemikian sehingga Ai =\nj=1Aj: Dengan demikian
FX(x) = PrfX 2 \nj=1Ajg = PrfX 2 Aig = FXi(xi) = minfFX1(x1); :::; FXn(xn)g:
Persamaan di atas timbul karena sifat dari Ai Aj 8j = 1; 2; :::; n sehingga
FXi(xi) FXj(xj) 8j = 1; 2; :::; n:
(2) ) (3) Asumsikan bahwa FX(x) = minfFX1(x1); :::; FXn(xn)g 8x = (x1; :::; xn) : PrfFX1 1(U ) x1; :::; F 1 Xn(U ) xng = PrfU FX1(x1); :::; U FXn(xn)g PrfFX1 1(U ) x1; :::; F 1 Xn(U ) xng = PrfU minfFX1(x1); :::; FXn(xn)gg PrfFX1 1(U ) x1; :::; F 1 Xn(U ) xng = minfFX1(x1); :::; FXn(xn)g: Apabila kita bandingkan dengan
FX(x) = minfFX1(x1); :::; FXn(xn)g maka dapat ditarik kesimpulan bahwa
X = Fd X1
1(U ); :::; F 1 Xn(U ) :
(3) ) (4) Dengan jelas kita telah mendapatkan salah satu fungsi yang tidak turun yaitu FX11(x) dimana peubah acaknya adalah U yaitu peubah acak uniform (0,1).
(4) ) (1) Asumsikan bahwa terdapat suatu peubah acak Z dengan support B dan sebuah fungsi yang tidak turun fi (i = 1; 2; :::; n)sehingga
X = (fd 1(Z); :::; fn(Z)) :
Himpunan keluaran dari X yang mungkin adalah f(f1(z); :::; fn(z)) j z 2 Bg
dimana sudah pasti himpunan ini bersifat comonotonic. Dengan demikian X juga bersifat comonotonic.
Dengan menggunakan cara yang serupa dengan pembuktian teorema di atas maka dapat dihasilkan
X = Fd 1( 1)
X1 (U ); :::; F 1( n) Xn (U ) : Hal ini dikarenakan
PrfF 1( 1)
X1 (U ) x1; :::; F 1( n)
sehingga PrfF 1( 1) X1 (U ) x1; :::; F 1( n) Xn (U ) xng = minfFX1(x1); :::; FXn(xn)g dengan i 2 [0; 1].
Jika U U nif orm (0; 1)maka 1 U U nif orm (0; 1). Hal ini mengaki-batkan
X = Fd X1
1(1 U ); :::; F 1
Xn(1 U ) : Untuk selanjutnya notasi Xc = (Xc
1; :::; Xnc) akan digunakan untuk
menje-laskan vektor acak comonotonic dari vektor acak X: Dari teorema di atas telah dibuktikan bahwa himpunan keluaran / ouput dari Xc adalah
f FX11(p); :::; F 1
Xn(p) j 0 < p < 1g:
Himpunan di atas belum tentu terhubung dalam suatu kurva. Hal ini dikare-nakan oleh sifat fungsi FXi(xi) yang tidak turun. Andaikan FXi(xi) adalah suatu fungsi yang monoton naik maka himpunan di atas terhubung dalam satu kurva. Untuk melihat bentuk keterhubungan dari himpunan ini maka akan dide…nisikan suatu himpunan kurva terhubung dari Xc sebagai berikut
f FX11( )(p); :::; F 1( )
Xn (p) j 0 < p < 1; 0 1g: Untuk lebih jelasnya akan diberikan contoh sebagai berikut
Contoh 28 Sebagai contoh, hanya akan diberikan contoh dengan distribusi yang diskrit. Misalkan X U nif ormf0; 1; 2; 3g sedangkan Y Binomial(3;12): Jika X dan Y bersifat saling bebas maka support dari (X,Y) adalah
f(x; y) j x 2 f0; 1; 2; 3g; y 2 f0; 1; 2; 3gg: Support dari vektor acak (Xc; Yc) adalah
f FX1(p); F 1
dengan FX1(p); FY1(p) = (0; 0) untuk 0 < p 1 8 = (0; 1) untuk 1 8 < p 2 8 = (1; 1) untuk 2 8 < p 4 8 = (2; 2) untuk 4 8 < p 6 8 = (3; 2) untuk 6 8 < p 7 8 = (3; 3) untuk 7 8 < p 1:
Himpunan kurva terhubung dari (Xc; Yc) dapat dibuat dengan menghubungkan
keenam titik di atas seperti pada gambar berikut.
3.5
Jumlah Peubah Acak Comonotonic
Dalam subbab ini notasi Sc akan dipakai untuk menjelaskan jumlah dari kom-ponen vektor acak comonotonic Xc = (Xc
1; :::; Xnc):Dengan demikian
Sc = X1c+ ::: + Xnc:
Teorema 29 invers fungsi distribusi FSc1( ) dari jumlah peubah acak co-monotonic Sc diberikan oleh
FSc1( )(p) = n X i=1 FX1( ) i (p); 0 < p < 1; 0 1:
Bukti. Misalkan X = (X1; :::; Xn) dan vektor comonotonic-nya adalah X c
= (X1c; :::; Xnc):Dengan melihat hasil dari teorema sebelumnya maka didapatkan
Sc = X1c+ ::: + Xnc = g(U )d dengan g(u) = n X i=1 FX1 i(u); o < u < 1:
Jelas bahwa g adalah suatu fungsi yang tidak turun dan kontinu kiri. Dengan memanfaatkan hasil dari persamaan (3.6) didapatkan
FSc1(p) = Fg(U )1 (p) = g(FU1(p)) = g(p); 0 < p < 1: Dengan demikian FSc1(p) = g(p) = n X i=1 FX1 i(p); 0 < p < 1: Di lain pihak juga berlaku
Sc = X1c + ::: + Xnc = h(U )d dengan g(u) = n X i=1 FX1+ i (u); 0 < u < 1:
Jelas bahwa g adalah suatu fungsi yang tidak turun dan kontinu kanan. De-ngan memanfaatkan hasil dari persamaan (3.7) didapatkan
FSc1+(p) = Fh(U )1+(p) = h(FU1+(p)) = h(p); 0 < p < 1: Dengan demikian FSc1+(p) = h(p) = n X i=1 FX1+ i (p); 0 < p < 1: Dari kedua hasil di atas didapatkan
FSc1( )(p) = FSc1(p) + (1 )FSc1+(p) = n X i=1 FX1 i(p) + (1 ) n X i=1 FX1+ i (p) = n X i=1 FX1 i(p) + (1 )F 1+ Xi (p) = n X i=1 FX1( ) i (p); 0 < p < 1; 0 1: Berikut ini adalah sifat-sifat dari jumlah peubah acak comonotonic Sc:
1. Oleh karena Sc =Pn i=1
FX1( )
i (p)maka berlaku untuk suatu U U nif orm (0; 1) Sc d= n X i=1 FX1( ) i (U ): 2. Himpunan kurva terhubung dari Sc diberikan oleh
fFSc1( )(p) j 0 < p < 1; 0 1g atau ( n X i=1 FX1( ) i (p)j 0 < p < 1; 0 1 ) :
3. Untuk masing-masing nilai peluang p = f0; 1g berlaku FSc1(0) = n X i=1 FX1 i(0) = 1 FSc1+(0) = n X i=1 FX1+ i (0) FSc1(1) = n X i=1 FX1 i(1) FSc1+(1) = n X i=1 FX1+ i (1) = +1:
4. Apabila diberikan suatu invers fungsi distribusi FXi1; fungsi distribusi kumulatif dari Sc dapat ditentukan dengan
FSc(x) = supfp 2 (0; 1) j FSc(x) pg = supfp 2 (0; 1) j FSc1(p) xg = sup ( p2 (0; 1) j n X i=1 FX1 i(p) x ) : Perhatikan bahwa untuk sebarang peubah acak X berlaku
FX selalu naik , FX1 kontinu di (0,1)
dan
FX kontinu , FX1 selalu naik di (0,1).
Dengan memakai fakta ini akan didapat bahwa
FSc selalu naik dan kontinu di FSc1+(0); FSc1(1) apabila FXi selalu naik dan kontinu. Bukti. Pernyataan FXi selalu naik , F 1 Xi kontinu di (0,1) mengakibatkan FXi selalu naik , n X i=1 FX1 i kontinu di (0,1)
atau
FXi selalu naik , F 1
Sc kontinu di (0,1). Dengan kata lain didapatkan hasil bahwa
FXi selalu naik , FSc selalu naik di F 1+
Sc (0); FSc1(1) : Di lain sisi didapatkan bahwa pernyataan
FXi kontinu , F 1 Xi selalu naik di (0,1) mengakibatkan FXi kontinu , n X i=1 FX1 i selalu naik di (0,1) atau FXi kontinu , F 1 Sc selalu naik di (0,1). Dengan kata lain didapatkan hasil bahwa
FXi kontinu , FSc kontinu di F 1+
Sc (0); FSc1(1) : Dari kedua hasil ini didapatkan pernyataan bahwa
FSc selalu naik dan kontinu di F 1+
Sc (0); FSc1(1) apabila FXi selalu naik dan kontinu.
Pernyataan di atas juga mengakibatkan untuk suatu x dimana FSc1+(0) < x < FSc1(1); berlaku n X i=1 FX1 i(FSc(x)) = x:
Teorema 30 Stop Loss Premium dari jumlah komponen comonotonic Sc dari
suatu vektor acak (Xc
1; :::; Xnc) diberikan oleh E (Sc d)+ = n X i=1 E (Xi di)+ ; FSc1+(0) < d < FSc1(1) (3.10) dengan di = F 1( d) Xi (FSc(d)); (i = 1; 2; :::; n); d2 [0; 1] :
Bukti. Misalkan d 2 FSc1+(0); FSc1(1 ). Dengan demikian 0 < FSc(d) < 1: Selanjutnya akan dibuktikan terlebih dahulu bahwa support terhubung dari Xc hanya memiliki satu titik potong dengan bidang fx j x1+ ::: + xn= dg:
Misalkan terdapat dua titik potong antara support terhubung dari Xc de-ngan bidang fx j x1+ ::: + xn = dg yaitu y dan z: Oleh karena y dan z adalah
anggota dari support terhubung dari Xc maka berlaku salah satu dari y z atau y z: Misalkan berlaku y z: Dengan demikian
8i = 1; 2; :::; n berlaku yi zi atau n X i=1 yi n X i=1 zi:
Akan tetapi hal ini jelas melanggar fakta bahwa y dan z adalah anggota dari bidang fx j x1 + ::: + xn = dg dimana seharusnya berlaku
n X i=1 yi = n X i=1 zi:
Hal yang serupa berlaku untuk kasus y z dan kasus dimana terdapat lebih dari dua titik potong antara support terhubung dari Xc dengan bidang fx j x1 + ::: + xn = dg: Selanjutnya didapat bahwa d adalah titik potong tunggal
antara support terhubung dari Xc dengan bidang fx j x1+ ::: + xn = dg:Hal
ini dikarenakan untuk 0 < FSc(d) < 1 terdapat d 2 [0; 1] dimana d = F 1( d)
Sc (FSc(d)): Dengan kata lain d adalah anggota dari support terhubung dari Xc: Di lain sisi berlaku
n X i=1 di = d dengan di = F 1( d) Xi (FSc(d)); (i = 1; 2; :::; n); d2 [0; 1] :
Hal ini mengatakan bahwa d adalah anggota dari bidang fx j x1+:::+xn = dg:
Jadi d adalah satu-satunya titik potong antara support terhubung dari Xc dengan bidang fx j x1+ ::: + xn= dg:
Sekarang misalkan xc adalah anggota dari support terhubung dari Xc:
De-ngan demikian berlaku
(xc1+ ::: + xcn d)+ = (xc1 d1)++ ::: + (xcn dn)+: Selanjutnya E (Sc d)+ = E (X1c + ::: + Xnc d)+ = E (X1c d1)++ ::: + (X c n dn)+ = n X i=1 E h FX1 i(U ) di + i = n X i=1 E (Xi di)+ :
Proposisi 31 Jika d FSc1+(0) maka E[(Sc d)+] = n P i=1 E[Xi] d: Bukti. Pernyataan d FSc1+(0) berarti d supfx R j FSc(x) 0g: Dengan kata lain
FSc(d) = 0g: Jadi Sc > d: Dengan demikian E[(Sc d)+] = n X i=1 E[(Xi di)+] E[(Sc d)+] = n X i=1 E[Xi di] E[(Sc d)+] = n X i=1 E[Xi] d:
Proposisi 32 Jika d FSc1(1) maka E[(Sc d)+] = 0:
Bukti. Pernyataan
d FSc1(1) berarti
d inffx R j FSc(x) 1g: Dengan kata lain
FSc(d) = 1: Jadi
Sc d: Dengan demikian jelas bahwa
E[(Sc d)+] = 0:
Ekspresi dari stop loss premium dapat dibentuk dalam persamaan lain yaitu jika FSc1+(0) < d < FSc1(1) maka
E[(Sc d)+] = E[ Xi F 1( d) Xi (FSc(d)) +] = E[ Xi FXi1(FSc(d)) +] F 1( d) Xi (FSc(d)) F 1 Xi(FSc(d)) (1 FSc(d)) : Bukti. E[ Xi F 1( d) Xi (FSc(d)) + ] = 1 Z FXi1( d)(FSc(d)) [1 FXi(x)] dx E[ Xi F 1( d) Xi (FSc(d)) +] = 1 Z F 1 Xi(FSc(d)) [1 FXi(x)] dx FXi1( d)(FSc(d)) Z FXi1(FSc(d)) [1 FXi(x)] dx
Oleh karena F 1( d)
Xi (FSc(d))dan F 1
Xi(FSc(d))mempunyai nilai yang sama pada fungsi FXi(x), yaitu FSc(d) maka
FXi1( d)(FSc(d)) Z FXi1(FSc(d)) [1 FXi(x)] dx = h F 1( d) Xi (FSc(d)) F 1 Xi(FSc(d)) i (1 FSc(d)) : Jadi E[ Xi F 1( d) Xi (FSc(d)) +] = 1 Z FXi1(FSc(d)) [1 FXi(x)] dx FXi1( d)(FSc(d)) Z FXi1(FSc(d)) [1 FXi(x)] dx E[ Xi F 1( d) Xi (FSc(d)) +] = E[ Xi F 1 Xi(FSc(d)) +] h F 1( d) Xi (FSc(d)) F 1 Xi(FSc(d)) i (1 FSc(d)) : Dalam kasus FXi adalah suatu fungsi yang monoton naik maka
F 1( d) Xi (FSc(d)) = F 1 Xi(FSc(d)) sehingga E[ Xi F 1( d) Xi (FSc(d)) + ] = E[ Xi FXi1(FSc(d)) +]:
3.6
Batas Atas Comonotonic untuk Jumlah Peubah
Acak
Pada subbab ini akan dijelaskan batas atas dari jumlah peubah acak S = X1+:::+Xndimana fungsi distribusi marginal dari X1; :::; Xndiberikan. Batas
atas akan ditentukan dalam urutan (aturan convex ). Oleh karena itu batas atas ini akan disebut sebagai batas atas convex untuk S = X1+ ::: + Xn:
Teorema 33 Untuk suatu vektor acak (X1; :::; Xn) berlaku
X1+ ::: + Xn cx X1c+ ::: + X c n:
Bukti. Oleh karena
E [(X1+ ::: + Xn)] = E [(X1c+ ::: + X c n)]
maka hanya perlu dibuktikan bahwa
E (X1+ ::: + Xn d)+ E (X1c+ ::: + X c
n d)+
untuk semua d dimana d 2 FSc1+(0); FSc1(1) : Sebelumnya perlu diketahui dahulu bahwa untuk setiap (x1; :::; xn)dan (d1; :::; dn) dimana d1+ ::: + dn = d
berlaku
(x1 d1) + ::: + (xn dn) (x1 d1)++ ::: + (xn dn)+:
Dengan demikian
((x1 d1) + ::: + (xn dn))+ ((x1 d1)++ ::: + (xn dn)+)+
((x1 d1) + ::: + (xn dn))+ (x1 d1)++ ::: + (xn dn)+:
Dengan memakai sifat ini maka didapatkan
E ((X1 d1) + ::: + (Xn dn))+ E [(X1 d1)++ ::: + (Xn dn)+] E (X1+ ::: + Xn d)+ n X i=1 E [(Xi di)+]
sehingga terbukti bahwa
E (X1+ ::: + Xn d)+ E (X1c+ ::: + X c
n d)+ :
Jadi terbukti sudah bahwa X1+ ::: + Xn cxX1c + ::: + Xnc:
Hasil inilah yang menunjukkan batas atas convex untuk S = X1+ ::: + Xn
dan oleh karena Xic bersifat comonotonic 8i = 1; 2; :::; n maka sudah pasti
berlaku
Untuk lebih jelasnya akan diberikan contoh dengan peubah acak yang berdis-tribusi lognormal. Untuk selanjutnya contoh ini akan sangat membantu pema-haman pada bagian aplikasi teori comonotonic untuk pencarian batas atas harga opsi asia.
Contoh 34 Contoh untuk variabel lognormal.
Misalkan kita mempunyai vektor acak ( 1X1; :::; nXn) dimana i 6= 0
8i = 1; 2; :::; n. Misalkan pula Xi LN ( i; 2i) atau dengan kata lain ln(Xi)
N ( i; 2
i): Dengan demikian berlaku
E[Xi] = exp( i+ 1 2 2 i) V ar[Xi] = exp(2 i+ 2 i) e 2 i 1 :
Sekarang akan dicari terlebih dahulu invers fungsi distribusi dari F iXi(x) = p:
Perhatikan bahwa persamaan di atas sama dengan Prf iXi xg = p: Apabila i > 0 Prf iXi xg = Pr Xi x i = p: Berdasarkan sifat dari peubah acak lognormal maka
PrfXi x ig = ln(x i) i i ! = p sehingga 1 (p) = ln( x i) i i atau iexp i+ i 1(p) = x: (3.11) Apabila i < 0 Prf iXi xg = Pr Xi x i = p:
Dengan demikian 1 Pr Xi x i = p atau Pr Xi x i = 1 p: Dari persamaan di atas bisa didapatkan
ln(x i) i i ! = 1 p atau ln(x i) i i = 1(1 p) = 1(p): Akhirnya didapatkan iexp i i 1(p) = x: (3.12)
Dari kedua hasil pada persamaan (3.11) dan (3.12) didapatkan F 1 iXi(p) = x = iexp i+ sign( i) i 1(p) (3.13) dimana 0 < p < 1 sign( i) = 8 < : 1 1 bila i > 0 bila i < 0 : Stop loss premium untuk variabel Xi ditentukan oleh
E[(Xi di)+] = exp( i+ 1 2 2 i) (di;1) di (di;2) dimana di;1= i + 2 i ln(di) i di;2= di;1 i = i ln(di) i sedangkan E[(di Xi)+] = E[(Xi di)+] E [Xi] + di = exp( i+1 2 2 i) ( di;1) + di ( di;2) :
Sekarang akan dicari E[ i(Xi di)+] untuk tiap kondisi i: Apabila i > 0 E[ i(Xi di)+] = iE[(Xi di)+] (3.14) = iexp( i+ 1 2 2 i) (di;1) idi (di;2) : Apabila i < 0 E[ i(Xi di)+] = iE[(di Xi)+] (3.15) = iexp( i+ 1 2 2 i) ( di;1) idi ( di;2) :
Jadi dari hasil pada persamaan (3.14) dan (3.15) didapatkan E[ i(Xi di)+] = iexp( i+
1 2
2
i) (sign( i)di;1) idi (sign( i)di;2) :
(3.16) Beralih kepada kasus jumlah peubah acak lognormal, sekarang de…nisikan
S = n X i=1 iXi dan Sc = n X i=1 F 1 iXi(U ): Sesuai dengan convex order maka berlaku
S cx Sc:
Oleh karena FSc1(FSc(x)) = x dan dengan bantuan persamaan (3.13) maka berlaku juga n X i=1 F 1 iXi(FSc(x)) = x n X i=1 iexp i+ sign( i) i 1((FSc(x))) = x dengan FSc1+(0) < x < FSc1(1):
Sekarang akan dicari E[(Sc d) +] dimana FSc1+(0) < d < FSc1(1) E[(Sc d)+] = n X i=1 E[( iXi F i1Xi(FSc(d)))+] = n X i=1 E[ i(Xi exp i+ sign( i) i 1(FSc(d)) )+]: Dengan menggunakan hasil pada persamaan (3.16) didapatkan
E[(Sc d)+] = n X i=1 iexp( i+ 1 2 2 i) (sign( i)di;1) (3.17) n X i=1
iexp i + sign( i) i 1(FSc(d)) (sign( i)di;2) dengan di;1 = i + 2 i ln(exp [ i+ sign( i) i 1(FSc(d))]) i = i+ 2 i i sign( i) i 1(FSc(d)) i = i sign( i) 1(FSc(d)) sehingga
sign( i)di;1 = sign( i) i 1(FSc(d)) (3.18) dan di;2 = i ln(exp [ i+ sign( i) i 1(FSc(d))]) i = i i sign( i) i 1(F Sc(d))) i = sign( i) 1(FSc(d))) sehingga sign( i)di;2 = 1(FSc(d))): Berikutnya (sign( i)di;2) = 1(FSc(d))) = 1(1 FSc(d))) = 1 FSc(d): (3.19)
Dengan kata lain, persamaan (3.18) dan (3.19) membuat persamaan (3.17) menjadi E[(Sc d)+] = n X i=1 iexp( i+ 1 2 2 i) sign( i) i 1(FSc(d)) d [1 FSc(d)] : (3.20)
3.7
Batas Bawah Comonotonic untuk Jumlah
Peubah Acak
Pada subbab sebelumnya telah dijelaskan mengenai batas atas convex untuk S = X1 + ::: + Xn: Penjelasan pada subbab ini akan memperlengkap batas
convex untuk S = X1 + ::: + Xn yaitu dengan menambahkan konsep batas
bawah convex untuk S = X1+:::+Xn:Idenya berasal dari ekspektasi bersyarat
dari suatu variabel acak yang selalu lebih kecil secara urutan (aturan convex ) daripada variabel acaknya sendiri.
Teorema 35 Untuk suatu vektor acak X dan suatu variabel acak berlaku
n X i=1 E [Xi j ] cx n X i=1 Xi:
Bukti. Dari sifat suatu fungsi convex kita mendapatkan bahwa untuk suatu fungsi convex v berlaku
E [v (X1+ ::: + Xn)] = E [E [v (X1+ ::: + Xn)j ]]
E [v (E [X1+ ::: + Xnj ])] :
Di lain hal kita dapatkan bahwa
E [v (E [X1+ ::: + Xnj ])] = E [v (E [X1 j ] + ::: + E [X1 j ])] :
sehingga
Dari hasil ini telah dibuktikan pernyataan di atas adalah benar. Misalkan S = X1+ ::: + Xn dan de…nisikan
Sl = E [S j ] = E [X1 + ::: + Xnj ] = n X i=1 E [Xi j ] :
Dengan demikian dari teorema di atas didapatkan Sl cx S:
Variabel Sl inilah yang akan menjadi batas bawah convex untuk S = X
1 +
::: + Xn: Seperti pada batas atas convex, akan ditunjukkan bahwa
V ar Sl V ar [S] :
Dengan memanfaatkan sifat dari fungsi convex dan karena f (X) = X2 adalah suatu fungsi convex maka
E (E [S j ])2 E E S2 j = E S2 : Dengan demikian terlihat jelas bahwa
V ar Sl = V ar [E [S j ]]
= E (E [S j ])2 E [E [Sj ]]2 = E (E [S j ])2 E [S]2