PENYELESAIAN MASALAH PRODUKSI DAN DISTRIBUSI ZERO INVENTORY MUHAMAD ROFI HIDAYAT

MUHAMAD ROFI HIDAYAT

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2012

ABSTRAK

MUHAMAD ROFI HIDAYAT. Penyelesaian Masalah Produksi dan Distribusi Zero Inventory. Dibimbing oleh FARIDA HANUM dan PRAPTO TRI SUPRIYO.

Pada karya ilmiah ini dibahas masalah produksi dan distribusi zero inventory. Diasumsikan bahwa fasilitas produksi mempunyai tingkat produksi yang terbatas dan terdapat waktu tempuh antarlokasi pelanggan. Pelanggan mempunyai urutan yang tetap dalam menerima pengiriman. Setiap pelanggan mengajukan jumlah permintaan dan time window untuk menerima pengiriman. Produk mempunyai umur yang terbatas. Umur produk dimulai segera setelah pesanan diproduksi. Karena pabrik mempunyai fasilitas produksi yang terbatas dan hanya terdapat sebuah truk untuk mengirimkan barang, maka mungkin tidak semua pelanggan menerima pengiriman dalam time window yang diajukan oleh pelanggan. Permasalahannya ialah memilih pelanggan mana yang mendapatkan pengiriman sehingga jumlah permintaan yang dipenuhi adalah maksimum tanpa melanggar kendala umur produk dan time window pelanggan. Metode heuristik digunakan untuk mencari jadwal produksi dan distribusi yang fisibel. Namun solusi yang dihasilkan metode heuristik belum dipastikan optimal, maka solusi yang ditemukan menggunakan metode heuristik dijadikan batas bawah dari solusi (jadwal) optimal. Selanjutnya digunakan metode pencabangan dan pembatasan menggunakan search tree untuk menentukan jadwal produksi dan distribusi yang optimal.

Kata kunci: zero inventory, time window, heuristik, metode pencabangan dan pembatasan, search tree.

ABSTRACT

MUHAMAD ROFI HIDAYAT. Solution of a Zero-Inventory Production and Distribution Problem. Under supervision of FARIDA HANUM and PRAPTO TRI SUPRIYO.

In this paper, a zero-inventory production and distribution problem is discussed. It is assumed that production facilities have limited production rate and there are traveling times between locations. Furthermore, each customer has a fixed sequence in recieving deliveries and requests a certain delivery quantity as well as a time window for receiving the delivery. Moreover, the products have limited lifespan, which starts as soon as the production of customer’s order is completed. Since the production facilities have limited resources and there is only one truck to deliver all the deliveries, then not all of the customers can receive the deliveries within their specified time windows. The problem is to choose customers to receive the deliveries, which maximize the total demand satisfied, without violating the constrains on product lifespan and the delivery time window. A heuristic method can be used to seek the feasible production and distribution solution. However, a heuristic solution can not be verified as an optimal solution, but nevertheless, it can be considered as a lower bound of the optimal solution. Furthermore, a branch and bound procedure using search tree is used to find the optimal production and distribution solution.

PENYELESAIAN MASALAH PRODUKSI DAN

DISTRIBUSI ZERO INVENTORY

MUHAMAD ROFI HIDAYAT

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2012

Judul Skripsi

: Penyelesaian Masalah Produksi dan Distribusi

Zero Inventory

Nama

: Muhamad Rofi Hidayat

NIM

: G54070082

Menyetujui,

Pembimbing I

Dra. Farida Hanum, M.Si.

NIP: 19651019 199103 2 002

Pembimbing II

Drs. Prapto Tri Supriyo, M.Kom.

NIP: 19630715 199002 1 002

Mengetahui,

Ketua Departemen

Dr. Berlian Setiawaty, MS.

NIP: 19650505 198903 2 004

Tanggal Lulus:

KATA PENGANTAR

Alhamdulillahirobbil’alamin. Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Selawat serta salam semoga senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman. Penyusunan karya ilmiah ini tidak lepas dari bantuan beberapa pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Keluarga tercinta, Mamah dan Papah, terima kasih atas doa, didikan, kasih sayang, nasihat-nasihat, dan motivasinya kepada penulis; untuk Rian dan Rosa, kakak dan adik tercinta atas doa dan dukungannya,

2. Dra. Farida Hanum, M.Si. selaku dosen pembimbing I, terima kasih atas waktu, ilmu, motivasi, doa serta kesabarannya dalam membimbing penulis,

3. Drs. Prapto Tri Supriyo, M.Kom. selaku dosen pembimbing II, terima kasih atas waktu, ilmu, motivasi, doa serta kesabarannya dalam membimbing penulis,

4. Dr. Ir. Amril Aman, M.Sc. selaku dosen penguji, terimakasih atas waktu, ilmu, motivasi, doa serta kesabarannya,

5. semua dosen Departemen Matematika, terima kasih atas semua ilmu, saran dan doanya, 6. staf Departemen Matematika: Bapak Yono, Mas Hery, Bapak Deni, Ibu Ade, Bapak Epul,

Bapak Bono dan Ibu Susi atas semangat dan doanya;

7. keluarga besar Alm. H. Aspuri serta keluarga besar Alm. M. Rebo, terima kasih atas motivasi dan doanya,

8. Aprilia Ramadhina, terimakasih atas kasih sayang, motivasi, doa dan kesabarannya,

9. teman-teman satu bimbingan : Ali, Cita, Ayum, Rizky Abe, terima kasih atas motivasi dan doanya,

10.sahabat-sahabatku : Fajar, Denda, Mutia melon, Ayung, Sri, Rachma, Rizky abe, Dian tile, Pandi, Della, Tyas, terima kasih untuk tawa yang kalian bagi,

11.penghuni Wisma Byru : Mas Reza, Mas Agus, Mbambit, Dika, Sony, Bakhtiar, Riza, Iin, Hakim, Damas, Fadly, Teguh, Abay, Mas Ahmad, Engkong Lingga, Mumu, Bagus, Pepeng dan lain-lain. Terima kasih atas semua motivasi dan tawa yang kalian bagi,

12.sahabat-sahabatku di Cilegon : Tedy, Toni, Empho, Bahri, Yasser, Cahya, Reza, Faisyal, Fahmi, terima kasih untuk semuanya,

13.kakak kelas angkatan 41, 42, dan 43 yang tidak bisa penulis sebutkan satu per satu,

14.teman-teman angkatan 44 : Mutia melon, Sri, Rachma, Ayung, Della, Tyas, Fajar, Pandi, Dian tile, Rizky abe, Denda, Imam, Ima, Lili, Yanti, Dora, Lingga, Iam, Ririh, Sari, Lugina, Ruhiyat, Wahyu, Pepi, Wenti, Tita, Nadiroh, Anis, Yuyun, Nurul N, Nurul A, Istiti, Devi, Deva, Cita, Tanti, Selvi, Fani R, Fani kodok, Ayum, Yuli, Ipul, Puying, Endro, Na’im, Indin, Aqil, Lilis, Tendy, Ikhsan, Yogi, Olih, Arina, Resha, Nurus, Atik, Masay, Siska, Nunuy, Lukman, Eka, Aswin, Ali, Aje, Vianey, Gan gan, Christoper, Fikri. Terima kasih atas bantuan, dukungan, nasihat dan doanya,

15.adik kelas angkatan 45, 46 dan 47 yang yang tidak bisa penulis sebutkan satu per satu, 16.teman-teman Tim Basket Matematika dan Tim Basket FMIPA.

Semoga tulisan ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya dalam bidang matematika.

Bogor, Mei 2012

RIWAYAT HIDUP

Penulis dilahirkan di Serang pada 22 Juni 1989 yang merupakan anak kedua dari tiga bersaudara dari pasangan Bapak Buchari Muslim dan Ibu Romlah.

Penulis menempuh pendidikan formal di SD YPWKS V Cilegon dan lulus pada tahun 2001. Tahun 2004 penulis lulus dari SMP Negeri 2 Cilegon. Tahun 2007 penulis lulus dari SMA Negeri 1 Cilegon dan pada tahun yang sama penulis diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur SPMB.

Selama mengikuti perkuliahan, penulis mengikuti beberapa kegiatan kepanitiaan yang diselenggarakan oleh Gugus Mahasiswa Matematika (GUMATIKA) IPB pada rentang waktu 2008-2010, antara lain panitia try out Ujian Tengah Semester dan Ujian Akhir Semester Pengantar Matematika dan Kalkulus I untuk Mahasiswa Tingkat Persiapan Bersama, panitia Welcome Ceremony Mathematics (WCM) angkatan 45 dan angkatan 46. Pada tahun 2009 penulis juga menjadi asisten dosen untuk beberapa mata kuliah, di antaranya Kalkulus II pada tahun 2009 dan Analisis Numerik pada tahun 2010.

DAFTAR ISI

Halaman

DAFTAR TABEL ...viii

DAFTAR GAMBAR ...viii

DAFTAR LAMPIRAN ... ix

I PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan... 1

II LANDASAN TEORI ... 1

2.1 Fungsi Linear dan Pertaksamaan Linear ... 1

2.2 Pemrograman Linear ... 2

2.3 Pemrograman Integer ... 2

2.4 Graf ... 2

2.5 Traveling Salesman Problem ... 5

2.6 Metode Pencabangan dan Pembatasan ... 5

III PEMBAHASAN ... 6

3.1 Deskripsi Masalah ... 6

3.2 Metode Heuristik ... 9

IV PENYELESAIAN MASALAH PRODUKSI DAN DISTRIBUSI ZERO INVENTORY ... 11

4.1 Proses Pencabangan ... 14

4.2 Proses Pembatasan ... 14

4.3 Contoh Penggunaan Proses Pencabangan dan Pembatasan ... 16

V SIMPULAN DAN SARAN ... 19

5.1 Simpulan ... 19

5.2 Saran ... 19

DAFTAR PUSTAKA ... 20

DAFTAR TABEL

Halaman

1 Contoh pesanan dan time window pelanggan ... 7

2 Waktu pengiriman (dalam satuan waktu) ... 7

3 Tabel kefisibelan jadwal dengan setiap kemungkinan pasangan pelanggan ... 11

4 Pesanan dan time window pelanggan ... 16

5 Waktu pengiriman (dalam satuan waktu) ... 16

6 Tabel kefisibelan jadwal dengan setiap kemungkinan pasangan pelanggan ... 17

7 Tabel jadwal fisibel setelah dilakukan beberapa iterasi ... 17

DAFTAR GAMBAR

Halaman 1 Graf G



V E,



. ... 2 2 Digraf . ... 3 3 Graf G₁



V E,



. ... 3 4 Digraf G₂ ( , ).V A ... 3

5 Contoh graf tak terhubung dan graf terhubung. ... 4

6 Graf C3=(V,E). ... 4

7 Contoh tree. ... 4

8 Contoh rooted tree. ... 4

9 Ilustrasi Contoh 10. ... 8

10 Bagan produksi dan distribusi jadwal fisibel



 0, 2,3,5 . ... 8

11 Bagan produksi dan distribusi jadwal



 0,1, 2,3,5 . ... 11

12 Search tree dengan semua kemungkinan jadwal dengan n5. ... 12

13 Bagan produksi dan distribusi jadwal



₅\{4} 0,1, 2,3,5 setelah distribusi ditunda 1 satuan waktu. ... 13

14 Bagan produksi dan distribusi jadwal



₅\{4} 0,1, 2,3,5 setelah distribusi ditunda 2 satuan waktu. ... 13

15 Skema penyelesaian masalah produksi dan distribusi zero inventory. ... 15

16 Bagan jadwal produksi dan distribusi dari barisan parsial



_[7]\ [4],[7] .





... 17

17 Search tree untuk pencarian jadwal optimal. ... 18

18 Bagan produksi dan distribusi jadwal



₇\{2,5, 6} 0,1,3, 4, 7 . ... 19

19 Search tree yang memuat semua kemungkinan jadwal dengan n=7. ... 36

20 Search tree (lanjutan 1). ... 47

21 Search tree (lanjutan 2). ... 48



,



DAFTAR LAMPIRAN

Halaman

1 Syntax Program LINGO 8.0 untuk menyelesaikan Massalah Knapsack pada Contoh 1 .. 22

2 Detail penghitungan Contoh 10 ... 22

3 Penghitungan Contoh 11 ... 23 4 Pembuktian Proposisi 1... 24 5 Penghitungan Contoh 12 ... 25 6 Pembuktian Proposisi 2... 25 7 Penghitungan Contoh 13 ... 27 8 Penghitungan Contoh 14 ... 34 9 Penghitungan Contoh 15 ... 34 10 Pembuktian Proposisi 3... 35

Dalam dunia bisnis terdapat beberapa macam jenis bisnis yang dijalankan, salah satunya adalah proses bisnis make-to-order. Pada proses ini produksi terjadi setelah pesanan dari pelanggan diterima. Namun ketika produksi dan fasilitas yang terlibat dalam proses produksi tersebut mempunyai kapasitas yang terbatas, terutama ketika produk mempunyai umur (lifespan) yang terbatas, proses bisnis ini menjadi suatu masalah yang menarik. Contoh masalah seperti ini adalah misalkan produsen memproduksi bahan perekat yang dipakai untuk panel kayu lapis. Bahan perekat tersebut mempunyai umur efektif 7 hari, setelah itu kekuatan perekat akan menurun tajam.

Pelanggan biasanya memesan kepada produsen dan menentukan time window yang diinginkan untuk menerima pengiriman. Kendala time window sangatlah penting karena produk yang dipesan (misalnya bahan perekat) adalah bahan baku yang digunakan pelanggan untuk digunakan dalam proses produksi pabrik pelanggan, maka waktu pengiriman dari produsen ke pelanggan harus memenuhi time window yang diinginkan pelanggan.

Apabila waktu pengiriman dinilai takfisibel, artinya waktu pengiriman tidak memenuhi time window, maka negosiasi dengan pelanggan harus dilakukan, baik untuk membatalkan pengiriman ataupun untuk

window).

Masalah time window menjadi perhatian utama, selain itu diasumsikan bahwa tidak ada pesanan khusus (misalnya modifikasi dari produk) yang diperbolehkan, truk mempunyai kapasitas yang cukup untuk membawa semua pesanan bersama-sama kepada pelanggan, dan pesanan pelanggan sementara disimpan di pabrik sampai dimuat ke truk. Dalam kasus ini, tidak ada persediaan rutin produk yang disimpan di dalam pabrik untuk masa mendatang (kasus zero-inventory) karena produk mempunyai umur yang terbatas serta untuk menghindari tambahan biaya yang besar dalam proses pembuangan limbah yang ramah lingkungan.

Sumber utama karya ilmiah ini ialah artikel berjudul A zero-inventory production and distribution problem with a fixed customer sequence yang ditulis oleh Ronald Armstrong, Su Gao, dan Lei Lei pada tahun 2008.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah menentukan pelanggan mana yang mendapat pengiriman agar memenuhi kendala umur produk, serta memenuhi time window pelanggan menggunakan metode search tree untuk menentukan jadwal produksi serta distribusi optimal sehingga total permintaan maksimum.

II LANDASAN TEORI

Untuk memahami masalah zero-inventory dan penyelesaiannya dengan menggunakan metode heuristik diperlukan pengertian beberapa konsep berikut.

2.1 Fungsi Linear dan Pertaksamaan Linear

Fungsi linear dan pertaksamaan linear merupakan salah satu konsep dasar yang harus dipahami untuk mempermudah dalam pembahasan pemrograman linear.

Definisi 1 (Fungsi Linear)

Suatu fungsi f x x( ,_{1 2},...,xn) dalam variabel-variabel x x₁, ₂,...,xn adalah suatu

fungsi linear jika dan hanya jika untuk suatu

himpunan konstanta c c₁, ₂,...,cn, fungsi f dapat ditulis sebagai :

1 2 1 1 2 2

( , ,..., n) ... n n.

f x x x c x c x  c x

(Winston 2004)

Sebagai contoh, f x x( ,_{1 2})5x₁7x₂

merupakan fungsi linear, sementara

2 2

1 2 1 2

( , ) 2 5

f x x  x  x bukan fungsi linear. Definisi 2 (Pertaksamaan Linear)

Untuk sembarang fungsi linear

1 2

( , ,..., n)

f x x x dan sembarang bilangan b, pertaksamaan f x x( ,_{1 2},...,xn)b dan 1 2 ( , ,..., n) f x x x b adalah pertaksamaan linear. (Winston 2004)

2.2 Pemrograman Linear

Pemrograman linear (PL) adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut :

a) Tujuan masalah ialah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan disebut fungsi objektif. b) Nilai variabel keputusan harus memenuhi

suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel.

(Winston 2004)

2.3 Pemrograman Integer

Pemrograman integer (integer programming/IP) adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa bilangan bulat, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa bilangan bulat, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser 1972)

Definisi 3 (Masalah Knapsack)

Masalah knapsack adalah IP yang mempunyai sebuah kendala. Berikut adalah masalah knapsack dengan setiap variabel bernilai 1 atau 0. 1 1 2 2 1 1 2 2 max ... terhadap ... 0 atau 1 ( 1, 2,..., ) n n n n i z c x c x c x a x a x a x b x i n          

Nilai ci adalah benefit bila i terpilih, b adalah

jumlah sumber daya yang tersedia, dan ai

adalah jumlah sumber daya yang dipakai oleh i. Bila xi bernilai 1, artinya xi dipilih. Bila xi

tidak dipilih maka xibernilai 0.

(Winston 2004)

Contoh 1

Misalkan PT Alam Jaya Permai Finance mempertimbangkan 2 penanaman modal. Penanaman modal 1 akan memberikan hasil bersih sebesar $3,000 dan penanaman modal 2 akan memberikan hasil bersih sebesar $2,000. Setiap penanaman modal membutuhkan suatu arus kas tertentu, yaitu Rp 1.000,00 untuk penanaman modal 1, dan Rp 2.000,00 untuk penanaman modal 2. Perusahaan tersebut memiliki sebanyak Rp 10.000,00 untuk

menanam modal. Maka masalah tersebut dapat diformulasikan sebagai masalah knapsack dengan penjelasan sebagai berikut. Misalkan

1, jika penanaman modal dilakukan 0, jika selainnya

i xi 

 

Masalah knapsack dapat dituliskan sebagai

1 2 1 2 max 3 2 terhadap 2 10 i 0 atau 1 ( 1, 2) z x x x x x i      

Setelah digunakan LINGO 8.0 (dapat dilihat pada Lampiran 1) ditemukan solusi yaitu z = 5 dengan rincian x1 = 1 dan x2 = 1 yang berarti

penanaman modal 1 dan modal 2 keduanya dilakukan sehingga perusahaan mendapatkan hasil bersih sebesar Rp 5.000,00.

2.4 Graf

Beberapa konsep graf yang digunakan dalam karya ilmiah ini adalah sebagai berikut.

Definisi 4 (Graf)

Suatu graf G adalah pasangan terurut



V E,



, dengan V himpunan takkosong dan hingga dan E adalah himpunan pasangan tak terurut yang menghubungkan elemen-elemen

V dan dinotasikan dengan G( , ).V E

Elemen dari V dinamakan simpul (node/vertex), dan elemen E dinamakan sisi (edge), dinotasikan sebagai {i, j}, yaitu sisi yang menghubungkan simpul i dengan simpul

j

,

dengan

i j

,



V

.

(Foulds 1992)

Contoh 2

G:

Gambar 1 Graf G



V E,



.

Graf G



V E,



pada Gambar 1 mempunyai himpunan simpul V



v v v v₁, ₂, ,_{3 4}



dan mempunyai himpunan sisi E





v v₁, ₂



,



v v1, 3

 

, v v2, 4



,



v v3, 4





.

v2

v1 v4

Definisi 5 (Digraf)

Digraf atau graf berarah (directed graph) adalah pasangan terurut ( , ),V A dengan V

adalah himpunan takkosong dan terbatas dari simpul-simpul dan A adalah himpunan pasangan terurut elemen-elemen berbeda di

.

V _{Elemen dari} A biasa disebut sisi berarah dan dituliskan sebagai

 

i j, dengan

i j

,



V

.

(Foulds 1992)

Contoh 3

D:

Gambar 2 Digraf . Digraf D



V A,



pada Gambar 2 ialah digraf dengan himpunan simpul V



v v v v₁, ₂, ₃, ₄



dan himpunan sisi berarah A





v v₁, ₂



,



v v2, 3

 

, v v2, 4



,



v v3, 1

 

, v v3, 4





.

Definisi 6 (Underlying Graph)

Underlying graph dari digraf D adalah graf yang diperoleh dari digraf D dengan mengganti semua sisi berarah

 

u v, atau

 

v u, dengan sisi (edge) uv.

(Chartrand & Oellermann 1993)

Contoh 4

1

G :

Gambar 3 Graf G₁



V E,



.

Graf G1 merupakan underlying graph dari

digraf D pada Contoh 3. Definisi 7 (Asimetrik)

Suatu digraf D dikatakan asimetrik jika setiap pasang simpulnya dihubungkan oleh paling banyak satu sisi berarah.

(Chartrand & Oellermann 1993)

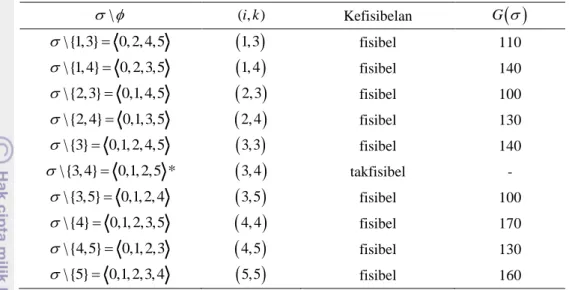
Contoh 5

2

D :

Gambar 4 Digraf G₂( , ).V A

Digraf D2 merupakan digraf tidak asimetrik

dan digraf D pada Contoh 3 merupakan digraf asimetrik karena hanya ada sebuah sisi berarah yang menghubungkan antarsimpul pada digraf D.

Definisi 8 (Walk)

Suatu walk pada graf G



V E,



adalah suatu barisan simpul dan sisi dari G dengan bentuk v₁,



v v₁, ₂



,v₂,



v v₂, ₃

 

,..., v_n1,v_n



,

,

n

v atau ditulis v v₁, ₂,...,v_n . Walk tersebut menghubungkan simpul v₁ dengan v_n. Suatu walk v v₁, ₂,...,v_n dikatakan tertutup jika

1 n

v v .

(Foulds 1992)

Contoh walk pada graf G₁ pada Contoh 4 ialah v v v v v v₁, ₂, , ,_{3 1 2}, ₄ .

Definisi 9 (Cycle)

Cycle merupakan walk v v₁, ₂,...,v_n dengan 3

n , v₁v_n dan semua simpul berbeda. (Chartrand & Oellermann 1993)

Definisi 10 (Graf Terhubung)

Graf C



V E,



disebut terhubung (connected) jika untuk setiap pasang simpul

i

v dan v_j dalam himpunan V terdapat path dari v_i kev_j.

(Foulds 1992)

Ilustrasi untuk graf terhubung dan graf tak terhubung diberikan dalam Contoh 6.

Graf C₁ adalah contoh graf yang tidak terhubung karena tidak terdapat path dari v₁

ke v₄, sedangkan graf C₂ adalah graf yang terhubung.



,



D V A v1 v4 v2 v3 v1 v4 v3 v2 v1 v3 v2

Contoh 6

1

C :

2

C :

Gambar 5 Contoh graf tak terhubung dan graf terhubung.

Definisi 11 (Incidence dan Adjacent) Misalkan diberikan graf G



V E,



, dengan e

 

u v, E, ,u vV, maka u dan

v dikatakan adjacent di G _dan eincidence dengan u dan v.

(Chartrand & Oellermann 1993)

Contoh 7

3:

C

Gambar 6 Graf C3=(V,E).

Dari Gambar 6 diketahui bahwa simpul v1 dan

v3 adjacent di C3, sedangkan simpul v1 dan v2

tidak adjacent di C₃. Sisi e1 incidence

dengan simpul v1 dan v3 sedangkan e1 sisi

tidak incidence dengan v2.

Definisi 12 (Tree)

Tree adalah graf yang terhubung yang tidak mempunyai cycle.

(Chartrand & Oellermann 1993)

Contoh 8 T:

Gambar 7 Contoh tree.

Definisi 13 (Rooted Tree/Tree Berakar) Suatu tree berarah (directed tree) adalah suatu digraf asimetrik sedemikian sehingga underlying graphnya adalah suatu tree.

Suatu tree berarah T dikatakan rooted tree jika terdapat simpul r dari T, yang dinamakan root (akar), sehingga untuk setiap simpul v dari T terdapat pathr-v di T.

(Chartrand & Oellermann 1993)

Contoh 9 T1:

Gambar 8 Contoh rooted tree.

Simpul v1 pada rooted treeT1 merupakan root

dari tree T1. Jika T suatu rooted tree, maka

biasanya root digambarkan pada bagian atas dari rooted tree T dan disebut dengan level 0. Simpul-simpul yang adjacent dengan root diletakkan satu level di bawahnya, yaitu level 1 dan seterusnya.

Definisi 14 (Height/Tinggi)

Suatu rooted tree T memiliki height (tinggi) h jika terdapat bilangan bulat terbesar h sedemikian sehingga terdapat simpul pada level h.

(Chartrand & Oellermann 1993)

Height dari rooted treeT1 adalah 2.

Definisi 15 (Child dan Parent/Anak dan Orang tua)

Jika simpul vTadjacent dengan simpul u dan u terletak di level di bawah v maka u dikatakan child (anak) dari v dan v disebut parent (orang tua) dari u.

(Chartrand & Oellermann 1993)

Simpul v3 merupakan child dari v1 dan v1

merupakan parent dari v3 di rooted tree T1

pada Contoh 9.

Definisi 16 (Leaf/Daun)

Simpul yang tidak mempunyai child (anak) disebut daun (leaf).

(Chartrand & Oellermann 1993)

Simpul v2, v4, dan v5 di rooted tree T1 pada

Contoh 9 merupakan daun. v2 v4 v1 v3 v3 v2 v4 v1 v3 v2 v4 v1 _e 1 e2 e3 v3 v5 v1 v4 v2 v4 v5 v1 v3 v2

Definisi 17 (Balanced Tree/Tree Seimbang) Suatu rooted tree T dengan tinggi h dikatakan seimbang (balanced) jika setiap daun dari T berada pada level h atau h-1.

(Chartrand & Oellermann 1993)

Rooted tree T1 pada Contoh 9 adalah sebuah

tree yang seimbang.

2.5 Traveling Salesman Problem

Traveling Salesman Problem (TSP) adalah suatu permasalahan di mana seorang salesman akan mengunjungi seluruh kota yang ada dan diharuskan kembali ke kota awal pada akhir perjalanannya. Dalam perkembangannya TSP memiliki beberapa variasi, antara lain: Traveling Salesman Problem with Time Window (TSPTW) yang merupakan TSP dengan tambahan waktu pelayanan di setiap kota dan m-Traveling Salesman Problem (m -TSP) yang menggunakan sejumlah salesman untuk mengunjungi seluruh kota.

(Hoffman & Padberg 2009)

Traveling Salesman Problem with Time Window

Traveling Salesman Problem with Time Window merupakan pengembangan dari TSP. Pada TSPTW rute yang ditempuh memiliki tambahan kendala waktu pelayanan (time window) untuk setiap konsumen.

Time window pada setiap konsumen dapat berbeda satu sama lain, tetapi memiliki karakteristik yang sama, yaitu berupa selang waktu. Time window [ , ]a bi i menunjukkan

selang waktu pelayanan pada konsumen ,i dengan a_i sebagai batas awal dan b_i sebagai batas akhir. Misalkan terdapat n kota yang akan dikunjungi, dan T_i adalah waktu pelayanan pada kota ke-i, maka untuk setiap i haruslah berlaku: ; 1, 2,..., i i i a  T b  i n (1) , ; , 1, 2,..., i i j j T 



T i j n (2) , i j i j   

Pada pertaksamaan (1), waktu pelayanan T_i

berada di antara batas awal a_i dan batas akhir

i

b dari time window. Kendaraan harus melayani pelanggan tidak kurang dari waktu

i

a dan tidak lebih dari waktu bi, sedangkan pada pertaksamaan (2), dipastikan waktu pelayanan di kota j (T_j) lebih besar atau sama dengan waktu tempuh antara kota i dan

kota j (



_{i j,} ) ditambah waktu pelayanan di kota i ( ).Ti

(Sutapa et al. 2003) 2.6 Metode Pencabangan dan Pembatasan

Metode pencabangan dan pembatasan dapat digunakan untuk menyelesaikan masalah optimisasi diskret dengan cara memecah himpunan solusi fisibel menjadi subhimpunan-subhimpunan yang lebih kecil secara berturutan sehingga menghasilkan subproblem-subproblem, menghitung batas nilai fungsi objektif dari setiap subproblem dan menggunakannya untuk membuang subproblem tertentu untuk pertimbangan selanjutnya. Batas-batas nilai fungsi objektif diperoleh dengan cara mengganti suatu himpunan masalah terhadap suatu himpunan kendala dengan himpunan kendala yang lebih longgar (relax), sehingga nilai dari solusi yang terakhir lebih baik dari solusi sebelumnya. Prosedur berakhir ketika setiap subproblem menghasilkan solusi fisibel atau ketika setiap subproblem menunjukkan solusi yang tidak lebih baik dari yang sudah didapatkan. Solusi terbaik yang ditemukan selama prosedur adalah global optimum.

Untuk sembarang masalah Q, dinotasikan v(Q) sebagai nilai (atau solusi optimal) dari Q. Unsur penting dari metode pencabangan dan pembatasan untuk masalah pengoptimuman diskret Q dalam bentuk





min f x( ) |xS adalah sebagai berikut: (i) relaksasi dari masalah Q, yaitu masalah

R yang berbentuk min



g x( ) |xT



dengan ST dan untuk setiap , ,

x yS f x( ) f y( ) berimplikasi ( ) ( );

g x g y

(ii) adanya aturan pencabangan: yaitu aturan untuk memecah himpunan fisibel Si dari

subproblem Qi ke dalam subhimpunan

1, i S ..., S_iq, dengan 1 ; q ij i j S S

(iii) Suatu prosedur batas bawah, yaitu prosedur untuk menemukan (atau yang mendekati dari bawah) v(Ri) untuk

masalah relaksasi Ri dari setiap

subproblem Qi;

(iv) aturan pemilihan subproblem, yaitu aturan untuk memilih subproblem selanjutnya untuk diproses;

(v) prosedur batas atas, yaitu heuristik untuk menemukan solusi fisibel terhadap masalah Q;

(vi) suatu prosedur uji, yaitu prosedur untuk memberi nilai variabel atau menghilangkan subproblem.

(Balas & Toth 1985)

Jika masalah pengoptimuman dalam bentuk max



f x( ) |xS



, maka poin (i), (iii), dan (v) adalah sebagai berikut:

(i) relaksasi dari masalah Q, yaitu masalah R yang berbentuk max



g x( ) |xT



dengan ST dan untuk setiap , ,

x yS f x( ) f y( ) berimplikasi ( ) ( );

g x g y

(iii) suatu prosedur batas atas, yaitu prosedur untuk menemukan (atau yang mendekati dari atas) v(Ri) untuk masalah relaksasi

Ri dari setiap subproblem Qi;

(v) prosedur batas bawah, yaitu heuristik untuk menemukan solusi fisibel terhadap masalah Q.

III PEMBAHASAN

3.1 Deskripsi Masalah

Masalah yang dibahas pada karya ilmiah ini adalah masalah produksi dan distribusi zero-inventory dengan sebuah truk pengangkut dan urutan pelanggan yang tetap. Fasilitas produksi mempunyai tingkat produksi yang terbatas, dan truk pengirim mempunyai waktu tempuh yang harus diperhitungkan antarlokasi pelanggan. Setiap pelanggan memesan sejumlah permintaan pada setiap time window yang pelanggan tentukan untuk menerima pengiriman. Umur dari produk dimulai segera setelah pesanan pelanggan selesai diproduksi, yang mengakibatkan produk kadaluarsa dalam waktu tertentu. Karena fasilitas produksi dan truk pengirim adalah sumber daya yang terbatas, maka ada kemungkinan tidak semua pelanggan mendapatkan pengiriman yang sesuai dengan time windownya. Jika suatu pelanggan terpilih menjadi pelanggan yang menerima pengiriman, maka kapanpun truk pengirim sampai di lokasi pelanggan sebelum batas awal time window akan terdapat waktu tunggu dan kapanpun truk pengirim sampai setelah batas akhir time window, maka pengiriman terlambat sehingga pengiriman ditolak.

Masalah ini merupakan permasalahan umum yang dihadapi dalam proses pendistribusian barang. Misalkan,

0,1,..., , ,...,

S i j n melambangkan urutan dari n pelanggan, dengan pelanggan i0 menyatakan pabrik. Urutan pelanggan S dikatakan tetap bermakna bahwa untuk sembarang pasangan pelanggan i dan j,

, ,

i jS dengan i j, jika kedua pelanggan i dan j tersebut termasuk pelanggan yang menerima pengiriman barang, maka pelanggan i harus menerima pengiriman sebelum pelanggan j. Diasumsikan produk memiliki umur yang terbatas, dinotasikan

sebagai B, dengan B0. Umur dari pesanan pelanggan i, untuk setiap i,dimulai segera setelah pesanan pelanggan i selesai diproduksi, dan akan berkurang selama pelanggan i menunggu produksi pesanan pelanggan j. Fasilitas pabrik memiliki tingkat produksi (r) yang terbatas, 0  r , sehingga dibutuhkan sebanyak d r/ satuan waktu untuk memproduksi sejumlah pesanan sebanyak d (dengan d r/ 0 bisa berupa bilangan positif apa saja, tidak harus bilangan bulat), dan truk pengirim barang memiliki waktu pengiriman yang diperhitungkan antara pelanggan i dan pelanggan j (dinotasikan sebagai



_{i j,} ) dengan



_{i j,} 0, 0i, jn. Setiap pelanggan j, jS, memiliki permintaan pesanan sebanyak d_j dan time window[ ,a b_{j j}].

Permasalahannya ialah memilih suatu subhimpunan dari himpunan pelanggan S, yaitu S, untuk menerima pengiriman sehingga jumlah total permintaan pelanggan yang dipenuhi adalah maksimum sementara kendala time window pelanggan, kapasitas pabrik dan waktu tempuh truk pengirim serta umur produk semuanya terpenuhi. Permasalahan tersebut dinotasikan sebagai masalah P.

Dalam permasalahan produksi dan pendistribusian zero-inventory dengan n pelanggan didefinisikan





 [0],[1],...,[ ],...,[ ] |[0]i k 0, 1 [ ] i n, 1 i k k, n merupakan barisan parsial sembarang dari S yang mempertahankan urutan di S, dan mendefinisikan jadwal produksi dan distribusi. Jadi  merupakan solusi dari masalah P. Notasi [i]

menyatakan pelanggan ke-i dalam  berikut pesanannya.

 T_[0] = waktu saat truk bermuatan meninggalkan pabrik dengan

[0] _{[ ]i} [ ]i /

T d r

 





(3)  a_{[ ]i} = waktu awal penerimaan pada time

window pelanggan [i]

 b_{[ ]i} = waktu akhir penerimaan pada time window pelanggan [i]

 T_{[ ]i} = waktu saat pelanggan [i] menerima pesanan dengan





[ ]i max [ ]i, [ 1]i [ 1],[ ]i i ,

T  a T_ 



_

(4)  w_{[ ]i} = waktu tunggu pada pelanggan [i]

dengan





[ ]i max 0, [ ]i [ 1]i [ 1],[ ]i i , (5)

w  a _T _ 



_ _

 _{[ ]i} = waktu keterlambatan pengiriman pelanggan [i] dengan





[ ]i max 0,T[ ]i b[ ]i ,

   (6)

 l_{[ ]i} = keterlambatan umur produk pelanggan [i], artinya lama waktu produk sudah kadaluarsa sebelum sampai di pelanggan [i], dengan   [ ] [ ] [ ] ,1 max 0, (7) h i i h h i d l T B r          _{  }  _ _  _    _{  } 



 Pada (7), _{   } ,1 h / h  h id r



mendefinisikan titik waktu di mana umur dari pesanan pelanggan [i] dimulai, sehingga

[ ] [ ] ,1 h h h i d B r     



mendefinisikan titik waktu ketika produk untuk pelanggan [i] kadaluarsa. Ilustrasi untuk besaran yang didefinisikan dapat dilihat pada Contoh 10 dengan data pelanggan, pesanan pelanggan dan time window diberikan pada Tabel 1 serta data waktu pengiriman antarlokasi pelanggan diberikan pada Tabel 2.

Tabel 1 Contoh pesanan dan time window pelanggan Pelanggan (j)

1 2 3 4 5

Pesanan pelanggan (d_j) 30 40 60 30 40 Waktu awal penerimaan (a_j) 19 26 31 32 36 Waktu akhir penerimaan (b_j) 24 32 36 35 37

Tabel 2 Waktu pengiriman (dalam satuan waktu) Waktu pengiriman



_{i j,} ( , )i j 1 2 3 4 5 0 4 5 3 4 3 1 6 4 5 4 2 3 6 2 3 4 5 4 3 Contoh 10 Misalkan



 0,1, 2,3, 4,5 , r10 dan 22.

B Pabrik memproduksi semua pesanan pelanggan. Seluruh pesanan pelanggan selesai diproduksi pada waktu

0 _i i/ T d r   



3 5 1 2 4 d d d d d r r r r r      30 40 60 30 40 10 10 10 10 10      20.

Truk meninggalkan pabrik setelah semua pesanan pelanggan selesai diproduksi, yaitu waktu ke 20. Umur pesanan pelanggan, misalkan pelanggan ke-2, dimulai segera setelah pesanan pelanggan ke-2 selesai diproduksi, yaitu pada waktu ke-7.

Misalkan ingin diketahui waktu kadaluarsa produk pesanan pelanggan 2.

2 1 2 1 / h h d d d r B B r r     _  _  



30 40 +22 10 10   _  _   29

Jadi waktu produk pesanan pelanggan ke-2 kadaluarsa ialah pada waktu ke-29. Selanjutnya akan dicari waktu pelayanan

( ),Ti waktu tunggu (wi), waktu

keterlambatan pengiriman (i), dan keterlambatan umur produk ( ),li untuk setiap

i 1 24 T  w10  1 0 l10 2 30 T  w2 0  2 0 l21 3 33 T  w30  3 0 l3 0 4 37 T  w4 0  4 2 l4 0 5 40 T  w50  5 3 l5 0

Proses penghitungan dapat dilihat pada Lampiran 2. Dari hasil penghitungan dapat diketahui antara lain bahwa pelanggan ke 1 menerima pesanan pada waktu ke 24, pelanggan 2 menerima pesanan pada waktu ke 30, dan seterusnya, tidak ada waktu tunggu disetiap pelanggan, namun produk mengalami keterlambatan pengiriman ke pelanggan ke 4 sebanyak 2 satuan waktu dan ke pelanggan ke 5 sebanyak 3 satuan waktu, produk kadaluarsa sebanyak 1 satuan waktu sebelum sampai ke pelanggan. Diagram waktu produksi dan distribusi dapat dilihat pada Gambar 9.

Gambar 9 Ilustrasi Contoh 10. Pada Contoh 10, produk kadaluarsa

sebelum sampai ke tempat pelanggan. Dalam kasus seperti ini, jadwal produksi distribusi dikatakan tidak fisibel. Selanjutnya akan dibahas mengenai kefisibelan



, seperti dalam teorema berikut.

Definisi 18 (Kefisibelan )

Suatu jadwal  dikatakan fisibel (berarti  _{ialah solusi fisibel dari masalah} P) jika  memiliki  _{[ ]i} 0 dan l_{[ ]i} 0, untuk setiap

[ ]i 



.

(Armstrong et al. 2008) Jika terdapat [ ]i 



, yang menyebabkan

[ ]i 0

  atau l_{[ ]i} 0, maka  bukan solusi fisibel. Pelanggan [i] dikatakan pelanggan yang fisibel jika  _{[ ]i} 0 dan l_{[ ]i} 0.

Dari Definisi 18, jadwal fisibel adalah jadwal yang memenuhi time window setiap pesanan pelanggan tanpa menyebabkan pengiriman ke salah satu pelanggan terlambat dan juga tidak menyebabkan produk kadaluarsa sebelum sampai di tempat pelanggan.

Contoh 11

Berdasarkan Contoh 10,



 0,1, 2,3, 4,5 memiliki   ₅ 3 0, maka menurut Definisi 18,



adalah jadwal yang takfisibel. Adapun contoh jadwal yang fisibel dengan data seperti pada Contoh 10 ialah



 0, 2,3,5 (penghitungan dapat dilihat di Lampiran 3) yang bagannya diperlihatkan pada Gambar 10 berikut.

Gambar 10 Bagan produksi dan distribusi jadwal fisibel



 0, 2,3,5 .

= pelanggan ke-i =time window = keterlambatan umur produk

i B=22 4 3 7 1 2 4 5 37 33 1 24 2 29 3 13 16 produksi distribusi 5 40 20 3 30 waktu

= pelanggan ke-i = time window = waktu tunggu

distribusi 31 36 4 2 26 produksi 19 29 10 3 14 5 2 3 5 i waktu

Saat urutan pelanggan S tetap, masalah P menjadi non-trivial. Pada kasus khusus dengan time window yang sepenuhnya relax, waktu tempuh di asumsikan instan, dan misalkan ₁ 2,3,..., j j n d d  



sehingga

pelanggan 1 selalu menerima pengiriman. Kemudian setelah pesanan pelanggan 1 diproduksi, pesanan pelanggan 1 hanya mempunyai B unit waktu untuk memilih pesanan lain untuk diproduksi sebelum kadaluarsa. Misalkan Xj 1 jika pelanggan j dipilih untuk menerima pesanan dan Xj0 jika selainnya,  j S\{1}. Maka P menjadi:

\{1} \{1} Max terhadap , {0,1}, \ {1} j j j S j j j S j G d X d X r B X j S        





atau masalah knapsack biner. Masalah knapsack biner dikenal sebagai masalah NP-hard maka masalah P menjadi kompleks.

(Armstrong et al. 2008) 3.2 Metode Heuristik

Dalam penyelesaian masalah produksi dan distribusi zero inventory diperlukan algoritme heuristik untuk menentukan batas bawah total permintaan yang dipenuhi dengan tetap memperhatikan kefisibelan . _{Pada bagian ini} akan dibahas metode heuristik yang menentukan batas bawah dari total permintaan yang dipenuhi pada jadwal fisibel. Sebelum membahas heuristik batas bawah diberikan definisi berikut.

Definisi 19 (Solusi optimal)

Misalkan G

 



adalah total permintaan yang diperoleh dari jadwal fisibel , dengan

 

_{[ ]i} [ ]i. G d 



 



(8) Masalah P dikatakan terselesaikan jika terdapat jadwal fisibel yang optimal * sehingga

 

* * max{ ( ) | untuk setiap jadwal fisibel } (9) G G  G    (Armstrong et al. 2008) Definisi 20 (Potensi dari pelanggan [i])

Untuk setiap barisan parsial



 [0],[1], ...,[ ],...,[ ] |1i k  k n , dengan [ ]i 



, potensi dari pelanggan [i] didefinisikan sebagai

[ ]i [ ]i [ ]i

p T a (10) yang menunjukkan seberapa banyak waktu pengiriman ke pelanggan [i] yang bisa dikurangi tanpa menyebabkan waktu tunggu di [i].

(Armstrong et al. 2008) Misalkan  merupakan barisan parsial yang berisi pelanggan [ ]h [ ]i [ ]j dengan

[ ]j 0

  dan p_{[ ]i} 0. Di sini [ ]h [ ]i berarti pelanggan [h] dilayani sebelum pelanggan [i]. Proposisi 1 Misalkan diberikan sembarang barisan parsial  yang memuat pelanggan [ ],h [ ],i [ ]j dengan [ ]h [ ]i [ ],j  _{[ ]j} 0. Jika p_{[ ]i}  _{[ ]j} , maka penghapusan pelanggan [h] dari  tidak akan mengubah ketakfisibelan dari [j].

(Armstrong et al. 2008) Bukti Proposisi 1 dapat dilihat di Lampiran 4.

Contoh 12

Berdasarkan Contoh 10, barisan parsial 0,1, 2,3, 4,5



 merupakan jadwal yang takfisibel karena  ₅ 3. Misalkan i3,

5.

j Dari persamaan (10), diperoleh

3 3 3 33 31 2.

p  T a    Jadi p₃ ₅. Misalkan h1. Penghapusan pelanggan 1 dari  menghasilkan



 0, 2,3, 4,5 , dengan 0 17 T   2 0 2 26 T   3 0 3 31 T   4 0 4 35 T   5 1 5 38 T 

(penghitungan lengkap dapat dilihat di Lampiran 5). Karena   ₅ 1 0, maka dari Definisi 18,



 0, 2,3, 4,5 merupakan jadwal yang takfisibel. Ini berarti, setelah

1

h dihapus, j5 tetap takfisibel.

Proposisi 1 bermakna misalkan terdapat pelanggan [ ],h [ ],i [ ]j dengan [ ]h [ ]i [ ].j

Jika terdapat keterlambatan pengiriman ke pelanggan [ ]j (yang menyebabkan pelanggan [ ]j menjadi takfisibel) dan waktu yang dapat dikurangi dari pelanggan [ ]i lebih besar dari waktu keterlambatan pelanggan [ ],j maka

penghapusan pelanggan [ ]h dari jadwal tidak akan mengubah ketakfisibelan pelanggan [ ].j

Proposisi 1 juga bermakna bahwa tidaklah efisien menghapus pelanggan [ ]h untuk ditukar kefisibelannya dengan pelanggan [ ]j

jika terdapat pelanggan [ ]i di antara pelanggan [ ]h dan [ ]j di dalam  dengan

[ ] [ ]

0p_i   _j.

Misalkan * adalah barisan parsial (jadwal) optimal untuk P. Didefinisikan

* S\ *,

   (11) yaitu himpunan dari pelanggan yang dihapus dari S saat didapatkan solusi optimal



*. Misalkan G* adalah jumlah permintaan optimal yang didapat dari *. Metode heuristik yang digunakan dalam karya ilmiah ini mencari * (bukan



*) dan diakhiri dengan batas bawah (dinotasikan dengan G0). Setiap iterasi dimulai dengan barisan parsial  yang diberikan dan pada awalnya dimisalkan  S. Selama proses iterasi, algoritme heuristik batas bawah mencari pesanan (i*,k*), dengan 1 i* k*n,

*, * ,

i k 



dan *i k* diperbolehkan, untuk dihapus secara permanen dari  sehingga nilai

 

, _i 0,_i 0 i i l G  _ d      



menjadi lebih baik dengan ( \ { *, *}) max{ ( \ { , }) | , , }. (12) G i k G i k i k i k       

Setelah pesanan (i*,k*) dihapus dari , barisan parsial yang berkurang





' \ *, * ,i k







menjadi input barisan parsial berikutnya. Pencarian berlanjut sampai

 menjadi fisibel.

(Armstrong et al. 2008) Saat n besar (misalnya 50), penghitungan menyeluruh dari semua kemungkinan pasangan (i,k) di setiap iterasi untuk mengidentifikasikan (i*,k*) bisa menjadi tidak efisien. Untuk menyelesaikan permasalahan dengan n yang besar, proposisi berikut dapat digunakan untuk mempercepat pencarian (i*,k*).

Proposisi 2 Untuk setiap  yang diberikan yang mengandung [ '],i [ ],i [ ],v dan [ ],z

dengan i'  i v z,  _{[ ]z} 0, dan

[ ]v [ ]z,

p   jika | * | 2



 dan [ ]z *, maka





* [ '],[ ] .i i





(Armstrong et al. 2008) Bukti Proposisi 2 dapat dilihat di Lampiran 6.

Proposisi 2 berimplikasi bahwa jika * 2,



 dan misalkan pelanggan [ ]z ialah pelanggan yang mengalami keterlambatan pengiriman dan pelanggan [ ]v adalah pelanggan terdekat yang memesan sebelum pelanggan [ ],z dengan p_{[ ]v}  _{[ ]z} , maka

* { *, *},i k

  dengan i*k*, yang mungkin hanya salah satu dari pasangan berikut:

{( , ) |1i k  i v v,  k z}, (13a) {( , ) |i k v  i k n}. (13b) (Armstrong et al. 2008) Contoh 13

Berikut akan diberikan contoh penggunaan metode heuristik terhadap 5 pelanggan,

0,1, 2, 3, 4, 5 ,



 dengan data permintaan serta time window pelanggan mengikuti Tabel 1 dan data waktu pengiriman antarlokasi pelanggan mengikuti Tabel 2 serta B22 dan r10.

Berdasarkan penghitungan yang telah dilakukan sebelumnya, jadwal  

0,1, 2,3, 4,5 merupakan jadwal yang takfisibel karena   ₅ 3 0 (dapat dilihat di Contoh 10). Diketahui p₃ ₅. Disini v3 dan z5, dan n5. Berdasarkan pada (13a) dan (13b), pasangan (i,k) yang mungkin ialah pasangan yang memenuhi pertaksamaan 1 i 3,3 k 5 atau 3  i k 5. Berikut akan ditampilkan tabel kemungkinan pelangggan yang dihapus dari jadwal berdasarkan (13a) dan (13b).

Tabel 3 Tabel kefisibelan jadwal dengan setiap kemungkinan pasangan pelanggan yang dihapus dari jadwal dan nilai G

 



untuk setiap jadwal fisibel

\   ( , )i k Kefisibelan G

 



\{1,3} 0, 2, 4,5





 

1,3 fisibel 110 \{1, 4} 0, 2,3,5





 

1, 4 fisibel 140 \{2,3} 0,1, 4,5





 

2,3 fisibel 100 \{2, 4} 0,1,3,5





 

2, 4 fisibel 130 \{3} 0,1, 2, 4,5





 

3,3 fisibel 140 \{3, 4} 0,1, 2,5 *





 

3, 4 takfisibel - \{3,5} 0,1, 2, 4





 

3,5 fisibel 100 \{4} 0,1, 2,3,5





 

4, 4 fisibel 170 \{4,5} 0,1, 2,3





 

4,5 fisibel 130 \{5} 0,1, 2,3, 4





 

5,5 fisibel 160 Jadwal



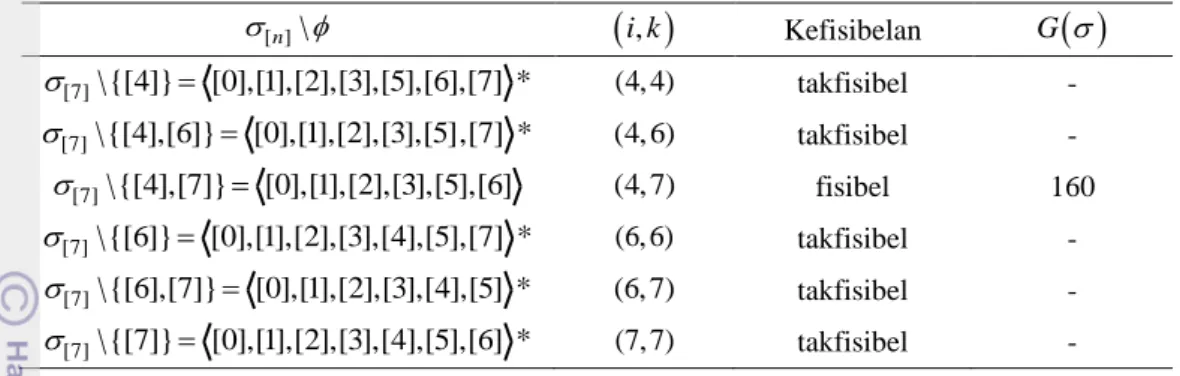
\{3, 4} 0,1, 2,5 * merupakan jadwal yang takfisibel, maka \ {3, 4} menjadi input barisan parsial berikutnya dan pencarian berlanjut sampai barisan parsial

\{3, 4,5} 0,1, 2



 ditemukan, dengan nilai

 

70.

G





Berdasarkan persamaan (12), diperoleh batas bawah dari total permintaan yang fisibel ialah G0 170 (penghitungan lengkap dapat dilihat di Lampiran 7). Berikut diberikan gambar bagan produksi dan distribusi jadwal

0,1, 2,3,5



 dengan G( ) 170.

Gambar 11 Bagan produksi dan distribusi jadwal



 0,1, 2,3,5 .

IV PENYELESAIAN MASALAH PRODUKSI DAN DISTRIBUSI

ZERO INVENTORY

Metode heuristik digunakan hanya untuk

mencari batas bawah. Jadwal fisibel yang ditemukan menggunakan metode heuristik tidak terjamin keoptimalannya, maka jumlah permintaan dari jadwal yang ditemukan menggunakan metode heuristik dijadikan batas bawah untuk mencari jadwal yang optimal. Pencarian jadwal yang akan dibahas dalam karya ilmiah ini menggunakan proses pencarian pencabangan dan pembatasan menggunakan search tree. Untuk setiap barisan pelanggan S yang diberikan,

didefinisikan search tree sebagai berikut. Misalkan simpul

i

menyatakan pelanggan ,i dengan 1 i n, dan simpul 0 menyatakan pabrik. Bersumber dari setiap simpul i, dengan 0 i n, terdapat tepat n1 cabang yang berbeda yang mengarah ke simpul j, dengan j i 1,i2,...,n1, dan .n Artinya, dari simpul 0, terdapat n cabang yang keluar mengarah ke simpul 1, 2,...,n pada level 1. Dari simpul 1 pada level 1 pada tree, terdapat

= pelanggan ke-i = time window = waktu tunggu

i produksi distribusi 1 2 3 7 3 5 13 17 1 21 2 27 3 30 5 36 31 waktu

1

n cabang yang keluar mengarah ke simpul 2,3,...,n pada level 2, sementara dari simpul

1

n



pada level 1 hanya mempunyai 1 cabang keluar yang mengarah ke simpul n di level 2. Tree yang dihasilkan merupakan tree yang tidak seimbang, memiliki

n



1

level dan

memiliki





0,1,.., ! ! ! k n n k n k  _



total simpul. Gambar 12 menunjukkan contoh search tree dengan semua kemungkinan jadwal dengan

5.

n

Gambar 12 Search tree dengan semua kemungkinan jadwal dengan n5. Dapat dilihat, sembarang barisan parsial

sepanjang cabang dari simpul 0 ke sembarang simpul i dalam tree tersebut mendefinisikan suatu jadwal .

Misalkan



_{[ ]k}  [0],[1],...,[ ],[ ] |1 [ ]i k  k n

 ialah barisan parsial fisibel yang menunjukkan urutan dari root (pabrik) ke simpul (pelanggan) pada level k sepanjang cabang. Beberapa definisi di bawah ini digunakan untuk menentukan parameter yang terkait dengan



_{[ ]k}.

Definisi 21 (Keterlambatan waktu pengiriman simpul [i]) Keterlambatan waktu pengiriman simpul

[ ] [ ]i 



_k , ialah [ ] [ ] [ ] [ ] T i i i i s b T w (14) yang menyatakan penundaan maksimum dalam waktu pengiriman ke simpul [i] tanpa membuat pengiriman terlambat.

(Armstrong et al. 2008)

Definisi 22 (Keterlambatan waktu pengiriman jadwal



_{[ ]k} ) Keterlambatan pengiriman pada barisan parsial



_{[ ]k} , ialah

[ ]k min{[ ]| [ ] [ ]}

T T

i k

s_  s  i  (15) yang menyatakan penundaan maksimum pada waktu pengiriman dalam barisan parsial



_{[ ]k}.

(Armstrong et al. 2008) Contoh 14

Jadwal



₅\{4} 0,1, 2,3,5 adalah jadwal fisibel dengan 1 3 T s  s₃T 6 2 5 T s  s₅T 1 5\{4} 1 T s_ 

(proses penghitungan dapat dilihat di Lampiran 8). s₁T 3 berarti penundaan maksimum waktu pengiriman ke simpul 1 adalah 3 satuan waktu dan

5\{4} 1

T

s_  berarti setiap simpul di dalam



₅\ {4} dapat ditunda sebanyak 1 satuan waktu tanpa mengubah kefisibelan



₅\{4}. Bagan produksi-distribusi diberikan pada Gambar 13 berikut.

Gambar 13 Bagan produksi dan distribusi jadwal



₅\{4} 0,1, 2,3,5 setelah distribusi ditunda 1 satuan waktu.

Definisi 23 (Keterlambatan lifespan dari simpul [i])

Keterlambatan lifespan dari simpul [ ],i

dengan [ ]i 



_{[ ]k} , dinotasikan sebagai s_{[ ]}Li, dengan [ ] [ [ ] _1,.., [ ]/ ] L i i _{h i} h s B T d r    



(16) mendefisinisikan penundaan maksimum waktu pengiriman ke simpul [ ]i tanpa membuat produk kadaluarsa.

(Armstrong et al. 2008) Definisi 24 (Keterlambatan lifespan dari

jadwal



_{[ ]k} ) Misalkan

[ ]k

L

s_ adalah keterlambatan lifespan dari barisan parsial



_{[ ]k}, dengan

[ ]k min{[ ]| [ ] [ ]} L L i k s_  s  i  (17) [ ]k L

s_ mendefinisikan penundaan maksimum pada waktu pengiriman pada barisan parsial

[ ]k



tanpa melanggar kendala lifespan di setiap simpul.

(Armstrong et al. 2008) Contoh 15

Berdasarkan Contoh 13 didapatkan barisan parsial  yang fisibel yaitu

5\{4} 0,1, 2,3,5



 dengan 1 4 L s  s₃L 4 2 2 L s  s₅L 3 5\{4} 2 L s_ 

(proses perhitungan dapat dilihat di Lampiran 9). s₁L 4 berarti penundaan maksimum waktu pengiriman ke simpul 1 adalah 4 satuan waktu dan

5\{4} 2

L

s_  berarti setiap simpul dalam



₅\{4} dapat ditunda sebanyak 2 satuan waktu tanpa membuat produk kadaluarsa di setiap simpul pada ₅\ {4}. Bagan produksi dan distribusi diberikan pada Gambar 14 berikut.

Gambar 14 Bagan produksi dan distribusi jadwal



₅\{4} 0,1, 2,3,5 setelah distribusi ditunda 2 satuan waktu.

= pelanggan ke-i = time window = penundaan pengiriman

i produksi distribusi 1 2 3 31 28 22 5 5 3 2 1 3 7 13 17 36 waktu 18

= pelanggan ke-i = time window = penundaan pengiriman

i produksi 1 2 3 5 19 23 29 32 37 distribusi 5 3 2 1 3 7 13 17 waktu

Penyelesaian masalah produksi dan distribusi zero inventory adalah sebagai berikut. Analisis yang akan dibahas memperkenalkan skema pencabangan yang menjamin pencarian cabang hanya untuk jadwal yang fisibel dan skema pembatasan yang mem-fathom solusi fisibel yang lebih kecil dari batas bawah.

4.1 Proses Pencabangan

Dalam bahasan sebelumnya _{[ ]k} ialah barisan parsial fisibel yang menunjukkan urutan dari root (pabrik) ke simpul (pelanggan) pada level k sepanjang cabang. Misalkan



_{[ ]k} dipadankan dengan [k] pada level k pada search tree, dan misalkan [ ]k i, 1 i n. Ketika pencarian sampai pada simpul [k], dengan [ ]k i, barisan parsial

[ ]k



dan parameter [ ]k T s_ dan [ ]k L s_ dapat diketahui.

Bersumber dari simpul [ ]k i, terdapat tepat n i cabang ke simpul i1,..., ,..., .j n Misalkan simpul j, dengan i j n, adalah salah satu kandidat simpul yang berpadanan pada level k1. Jika dilakukan pencabangan dari simpul i ke simpul j, maka barisan parsial pada simpul j [k 1], yaitu



_[k1], dibentuk dengan menambahkan simpul j ke ujung



_{[ ]k}, dituliskan _[k1] _{[ ]k} || j .

(Armstrong et al. 2008) Pada



_[k1], truk pengangkut harus menunggu di pabrik sampai pesanan pelanggan j selesai diproduksi, dan waktu kedatangan truk ke pelanggan pertama di

[k 1]



 ditunda selama



dj/ .r Jika waktu

pengiriman pada simpul pertama pada



_{[ ]k} ditunda selama  satuan waktu, dengan

[ ] [ ] min{ , }, k k T L s_ s_



 maka setidaknya

pengiriman ke satu simpul di



_{[ ]k} menjadi takfisibel sehingga membuat barisan parsial

[ ]k



menjadi takfisibel. Jadi aturan pencabangan dari simpul [ ]k i ke simpul j untuk setiap barisan parsial



_{[ ]k} ialah sebagai berikut:

jika salah satu kondisi di bawah ini dilanggar: [ ] [ ] min{ , }, k k T L j d r s_ s_ atau (18) [k 1] j j T _ T b (19) maka pencabangan tidak dilakukan.

(Armstrong et al. 2008) 4.2 Proses Pembatasan

Misalkan



_{[ ]k} ialah sembarang barisan parsial pada level k, 1 k n, pada search tree. Jumlah maksimum permintaan yang dapat dipenuhi oleh sembarang cabang yang memuat



_{[ ]k} sebagai barisan parsial ialah tidak lebih dari

[ ] [ ] , k k h h d g



dengan [ ]k { |j 

  [ ]k  j n} adalah himpunan dari kandidat pesanan yang ditambahkan ke dalam

[ ]k



untuk membentuk jadwal akhir. Nilai

[ ]k

g_ dapat ditentukan dengan menyelesaikan

masalah knapsack 0 – 1 berikut:

[ ] [ ] [ ] [ ] [ ] [ ] Max terhadap .min{ , } {0,1}, k k k k k k j j j T L j j j j g d X d X r s s X j  _   _            





dengan Xj = 1 jika pelanggan j dipilih sebagai

kandidat pelanggan yang menerima pengiriman dan Xj = 0 jika selainnya.

(Armstrong et al. 2008) Proposisi 3 Misalkan G0 adalah batas bawah dari G*. Untuk sembarang simpul [k] di level k pada search tree, 1 k n, yang berpadanan dengan barisan parsial



_{[ ]k}, jika

[ ] [ ] 0 , k k h h  d g G    



maka semua

simpul keturunan dari simpul [k] harus di-fathom.

(Armstrong et al. 2008) Bukti Proposisi 3 dapat dilihat di Lampiran 10. Proposisi 3 berfungsi untuk mendapatkan kandidat pelanggan yang akan masuk ke dalam jadwal akhir. Setelah kandidat pelanggan didapatkan, nilai G( ) dari  yang didapatkan diperiksa apakah lebih besar dari batas bawah atau tidak. Jika lebih besar, maka jadwal yang optimal telah ditemukan, jika tidak maka pencarian kandidat pelanggan dilakukan sampai diperoleh jadwal  optimal.

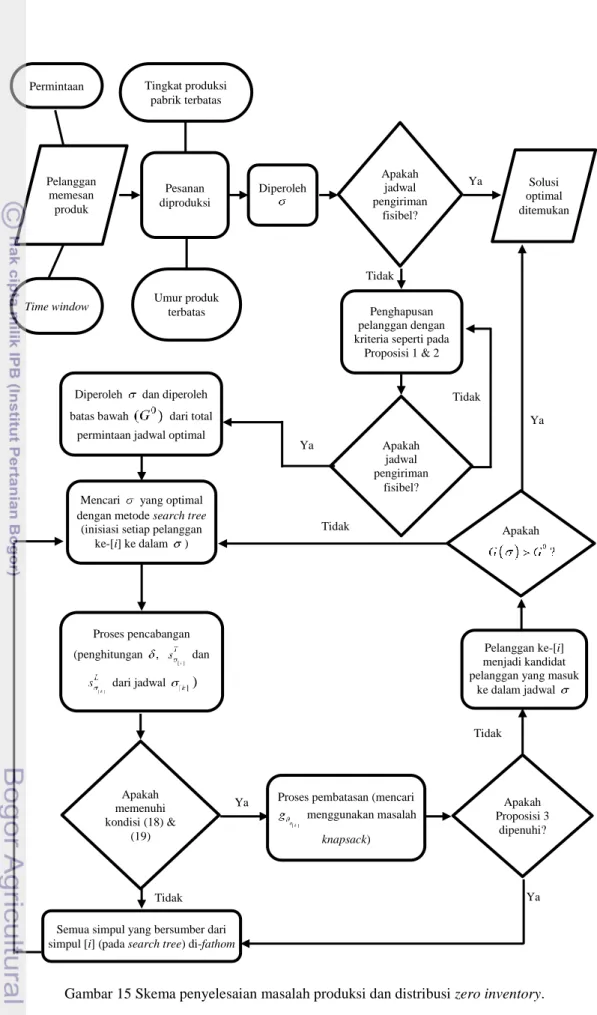
Dalam Gambar 16 diberikan skema keseluruhan penyelesaian masalah produksi dan distribusi zero inventory dalam bentuk diagram alir.

Gambar 15 Skema penyelesaian masalah produksi dan distribusi zero inventory.

Pelanggan ke-[i]

menjadi kandidat pelanggan yang masuk

ke dalam jadwal Apakah Proses pencabangan (penghitungan dan dari jadwal ) Tingkat produksi pabrik terbatas Umur produk terbatas Permintaan Pelanggan memesan produk Time window Pesanan diproduksi Apakah jadwal pengiriman fisibel? Penghapusan pelanggan dengan kriteria seperti pada

Proposisi 1 & 2

Ya Solusi

optimal ditemukan

Tidak

Diperoleh _{dan diperoleh}

batas bawah dari total

permintaan jadwal optimal

Mencari yang optimal

dengan metode search tree

(inisiasi setiap pelanggan

ke-[i] ke dalam )

Proses pembatasan (mencari menggunakan masalah

knapsack)

Semua simpul yang bersumber dari

simpul [i] (pada search tree) di-fathom

Apakah jadwal pengiriman fisibel? Tidak Apakah memenuhi kondisi (18) & (19) Ya Apakah Proposisi 3 dipenuhi? Ya Ya Tidak Tidak Diperoleh Tidak Ya