BAB II
AKAR-AKAR PERSAMAAN
2.1 PENDAHULUAN
Salah satu masalah yang sering terjadi pada bidang ilmiah adalah masalah untuk mencari akar-akar persamaan berbentuk :
f(x) = 0
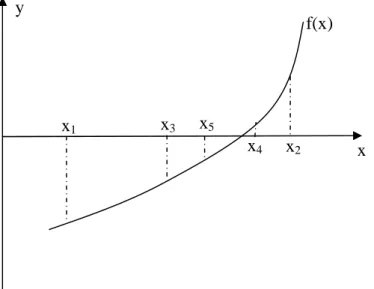
Fungsi f di sini adalah fungsi atau persamaan tak linear. Nilai x = x0 yang memenuhi f(x) =
0 disebut akar persamaan atau fungsi tersebut. Sehingga
x0 di sini menggambarkan fungsi tersebut memotong sumbu x di x = x0.Persamaan atau fungsi f dapat berbentuk sebagai berikut: (a) Persamaan aljabar atau polinomial
f(x) = pn(x) = anxn + an-1xn-1 + … + a1x + a0 dengan an ¹ 0, n ³ 2
(b) Persamaan transenden
Yaitu persamaan yang mengandung fungsi antara lain trigonometri, logaritma, atau eksponen
Contoh: (i) ex + cos(x) = 0 (ii) ln(x) + log(x2) = 0
(c) persamaan campuran
Contoh: (i) x3 sin(x) + x = 0 (ii) x2 + log(x) = 0
Untuk polinomial derajat dua, persamaan dapat diselesaikan dengan rumus akar persamaan kuadrat. Misalkan bentuk persamaan kuadrat adalah:
ax2 + bx + c = 0
dapat dicari akar-akarnya secara analitis dengan rumus berikut.
x12 =
Untuk polinomial derajat tiga atau empat, rumus-rumus yang ada sangat kompleks dan jarang digunakan. Sedangkan untuk menyelesaikan polinomial dengan derajat yang lebih tinggi atau persamaan tak linear selain polinomial, tidak ada rumus yang dapat digunakan untuk menyelesaikannya. Metode Numerik memberikan cara-cara untuk menyelesaikan bentuk tersebut.
2.2 METODE SETENGAH INTERVAL
Metode setengah interval merupakan metode yang paling sederhana. Langkah-langkah yang dilakukan pada penyelesaian persamaan dengan metode setengah interval adalah :
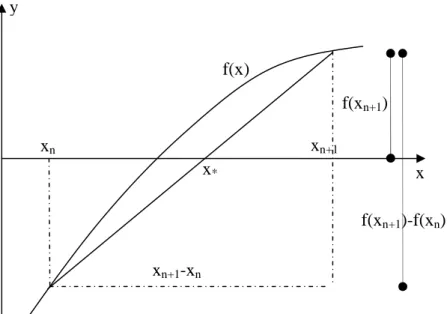
1. Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu apabila 0.
2. Estimasi pertama dari akar xt dihitung dengan
3. Buat evaluasi berikut untuk menentukan di dalam sub interval maka akar persamaan berada :
a. Jika 0. akar persamaan berada pada sub interval pertama, kemudian tetapkan .
y
x f(x)
b. Jika 0. akar persamaan berada pada sub interval kedua, kemudian tetapkan , dan lanjutkan pada langkah ke 4.
c. Jika 0. akar persamaan adalah dan hitungan selesai. 4. Hitung perkiraan baru dari akar dengan, .
5. Apabila perkiraan baru sudah cukup kecil, maka hitungan selesai, dan xt adalah akar
persamaan yang dicari, jika belum kembali ke langkah 3.
Contoh :
Hitung salah satu akar dari persamaan pangkat tiga berikut ini,
3 3 0
Penyelesaian.
Dihitung nilai f(x) pada interval antara dua titik, misalnya x=1 dan x=2. Untuk x=1, 1 1 1 31 3 4
x=2, 2 2 2 32 3 3
Karena 1 dan 2 berbeda tanda maka fungsi memotong sumbu x paling tidak satu kali. 1,5 1,5 1,5 1,5 31,5 3 0,01831 y x f(x) x1 x2 x3 x4 x5
Hasil hitungan metode setengah interval Iterasi x1 X2 X3 f(x1) f(x2) f(x3) 1 1 2 1,5 -4,0 3,0 -1,875 2 1,5 2 1,75 -1,875 3,0 0,17187 3 1,5 1,75 1,625 -1,875 0,17187 -0,94335 4 1,625 1,75 1,6875 -0,94335 0,17187 0,40942 5 1,6875 1,75 1,71875 -0,40942 0,17187 -0,12478 6 1,71875 1,75 1,73437 -0,124478 0,17187 -0,02198 7 1,71875 1,73437 1,72656 -0,12478 0,17187 -0,02198
2.3 METODE INTERPOLASI LINIER
Metode interpolasi linier, dikenal juga dengan metode false position yang didasarkan pada interpolasi antara dua nilai dari fungsi yang mempunyai tanda berlawanan. Dengan metode ini suatu fungsi dapat lebih cepat diperoleh daripada metode setengah interval.
Contoh 2.
Hitung salah satu akar dari persamaan 3 3 0. Penyelesaian.
Langkah pertama adalah menghitung nilai f(x) pada interval antara dua titik sedemikian sehingga nilai f(x) pada kedua titik berlawanan tanda.
x=1, 1 1 1 31 3 4 x=2, 2 2 2 32 3 3 Dengan menggunakan persamaan diatas :
2 3 4 2 1 1,571423
1,57142 1,57142 1,57142 31,57142 3 1,36449
Karena bertanda negatif maka akar terletak antara x=1,57142 dan x=2. 2 3— 1,36449 2 1,57142 1,705403
1,70540 1,70540 1,70540 31,70540 3 0,24784
Prosedur perhitungan seperti diatas dilanjutkan sampai akhirnya didapat nilai $ 0
Iterasi x1 X2 X3 f(x1) f(x2) f(x3) 1 1,0 2,0 1,57142 -4,0 3,0 -1,36449 y x f(x) xn xn+1 f(xn+1) f(xn+1)-f(xn) x* xn+1-xn
2 1,57142 2,0 1,70540 -1,36449 3,0 -0,24784 3 1,70540 2,0 1,72788 -0,24784 3,0 -0,03936 4 1,72788 2,0 1,73140 -0,03936 3,0 -0,00615 5 1,73140 2,0 1,73194
2.4 METODE NEWTON-RAPHSON
Metode ini paling banyak digunakan dalam mencari akar-akar dari suatu persamaan. Turunan pertama pada % adalah ekivalen dengan kemiringan.
&% '()()*( atau % % '( '+( f(x) A B 0 f(xi) f(xi)-0 xi xi+1 f(x) Garis singgung di A
Contoh 3.
Selesaikan soal pada contoh 1 dengan metode Newton-Raphson. Penyelesaian.
3 3 0
Turunan pertama dari persamaan tersebut adalah : & 3 2 3
Dengan menggunakan persamaan % % ''+(
(
Pada awal hitungan ditentukan nilai % sembarang, misalnya 1;
1 1 1 31 3 4
&
1 31 21 3 2
1 42 3
Langkah berikutnya ditetapkan 3,
3 3 3 33 3 24
&
3 33 23 3 30
3 2430 2,2
Hitungan dilanjutkan dengan prosedur yang sama dan hasilnya diberikan dalam Tabel.
Jumlah iterasi xi xi+1 f(xi) f(xi+1)
1 1,0 3,0 -4,0 24,0 2 3,0 2,2 24,0 5,888 3 2,2 1,83 5,888 0,987387 4 1,83 1,73778 0,987387 0,05442 5 1,73778 1,73207 0,05442 0,0001816 2.5 METODE SECANT
Kesulitan metode Newton-Raphson adalah diperlukannya turunan pertama dari f(x). Kadang sulit untuk mendiferensialkan persamaan yang akan diselesaikan. Untuk itu didekati bentuk diferensial didekati dengan nilai perkiraan berdasarkan diferensial beda hingga.
&% % %)
% %)
% % %% %) % %)
Contoh 4.
Selesaikan soal pada contoh 1 dengan metode Secant. Penyelesaian.
Iterasi 1 :
Diambil dua nilai awal x=1 dan x=2
Untuk x=1, 1 1 1 31 3 4 x=2, 2 2 2 32 3 3 Dengan menggunakan persamaan diatas,
2 32 1 3 4 1,57142 Iterasi 2 : 2 2 3 1,57142 1,57142 1,36449 , 1,57142 1,364491,57142 21,36449 3 1,70540
Hitungan dilanjutkan dengan prosedur yang sama dan hasilnya diberikan dalam Tabel.
Jumlah x1 x2 x3 f(x1) f(x2) f(x3) f(x) A B 0 f(xi) f(xi)-0 xi xi+1 f(x) Garis singgung di A f(xi-1)
iterasi 1 1,0 2,0 1,57142 -4,0 -3,0 -1,36449 2 2,0 1,57142 1,70540 -3,0 -1,36449 -0,24784 3 1,57142 1,70540 1,73513 -1,36449 -0,24784 0,02920 4 1,70540 1,73513 1,73199 -0,24784 0,02920 -0,000575 5 1,73513 1,73199 1,73205 2.6 Metode Iterasi
Dalam metode ini digunakan suatu persamaan untuk memperkirakan nilai akar persamaan. Persamaan tersebut dikembangkan dari fungsi 0, yaitu
-Transformasi ini dapat dilakukan dengan manipulasi aljabar atau menambahkan parameter x pada kedua sisi dari persamaan aslinya. Sebagai contoh;
3 3 0 .)
Dengan memberikan nilai perkiraan awal xi , maka dapat dihitung perkiraan baru xi+1
dengan rumus iteratif;
% -%
Besar kesalahan dihitung dengan rumus; /0 1% %
% 1 100%
Contoh 5
Hitung akar dari persamaan 3 3 0 dengan metode iterasi. Penyelesaian.
Dapat ditulis; 3 3 3 3 3
% % 3% 3 3
Apabila ditentukan perkiraan awal x1=2, didapat;
% 3% 3 3 2 3 2 3 3 1,70998 Besar kesalahan : /0 1 1 100% 1 1,70998 2 1,70998 1 100% 16,9607%
Hitungan dilanjutkan dengan prosedur yang sama dan hasil seperti pada Tabel
1 2,00000 2 1,70998 16,9607 3 1,73313 1,3362 4 1,73199 0,0658 5 1,73205 0,0034 6 1,73205 0,0002
Persamaan 3 3 0 dapat juga diubah dalam bentuk;
.)
%
(.()
Untuk perkiraan awal x1=2, didapat;
3 3 2 2 3 3 3 Besar kesalahan : /0 1 1 100% 1 3 2 3 1 100% 33,3333%
Hitungan dilanjutkan dengan prosedur yang sama dan hasil seperti pada Tabel
Iterasi 45 67% 1 2,00000 2 3,00000 33,3333 3 11,0000 72,7273 4 483,000 97,7226 5 37637290 99,9987
Gambar 4. Prosedur Metode Newton-Raphson secara grafis