PERANAN PERSYARATAN KARUSH-KUHN-TUCKER DALAM MENYELESAIAN PEMROGRAMAN KUADRATIS SKRIPSI AMALIA

SKRIPSI

AMALIA

050803033

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

2009

PERANAN PERSYARATAN KARUSH-KUHN-TUCKER DALAM MENYELESAIAN PEMROGRAMAN KUADRATIS

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

AMALIA 050803033

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2009

PERSETUJUAN

Judul : PERANAN PERSYARATAN KARUSH KUHN

QQQQQQQQQQQQQQQQQ.gTUCKER DALAM MENYELESAIKAN

QQQQQQQQQQQQQQQQQ .PEMROGRAMAN KUADRATIK

Katagori : SKRIPSI

Nama : AMALIA

Nomor Induk Mahasiswa : 050803033

Program Studi : PROGRAM (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

qqqqqqqqqqqqqqqqqqqqqqqqqqALAM (FMIPA) UNIVERSITAS SUMATERA

qqqqqqqqqqqqqqqqqqqqqqqqqkUTARA Diluluskan di

Medan, Desember 2009 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. H. Haludin Panjaitan Drs. Marwan Harahap, M.Eng

NIP. 194603091979021001 NIP. 194612251974031001

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Dr. Saib Suwilo, M.Sc NIP. 196401091988031004

PERNYATAAN

PERANAN PERSYARATAN KARUSH KUHN TUCKER DALAM MENYELESAIAN PEMROGRAMAN KUADRATIS

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Desember 2009

AMALIA 050803033

PENGHARGAAN

Puji dan syukur penulis ucapkan kehadirat Allah SWT karena atas berkah dan rahmat-Nya kepada penulis hingga dapat menyelesaikan skripsi ini.

Pada kesempatan ini penulis mengucapkan banyak terima kasih kepada : 1. Bapak Drs. Marwan Harahap, M.Eng dan Bapak Drs. H. Haludin Panjaitan,

selaku pembimbing pada penyelesaian skripsi ini yang telah memberikan bimbingan, pengarahan serta pemeriksaan terhadap skripsi ini sehingga dapat selesai dengan baik.

2. Bapak Dr. Saib Suwilo, M.Sc dan Drs. Henry Rani Sitepu, M.Si, selaku Ketua dan Sekretaris Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

3. Bapak Prof. DR. Eddy Marlianto, M.Sc, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, seluruh Staf Pengajar jurusan Matematika yang telah mendidik penulis selama mengikuti perkuliahan. 4. Ayahanda dan Ibunda tercinta, abang dan kakak, serta seluruh keluarga yang telah

memberikan semangat dan dukungan yang tak ternilai harganya.

5. Rekan-rekan mahasiswa Matematika stambuk 2005, khususnya Depi, Feby, Nenna, Rima, Sundari, Yuni, Andika, Radhi, Santri, dan masih banyak lagi yang tidak mungkin disebutkan satu persatu, terima kasih atas bantuannya.

ABSTRAK

Salah satu bentuk khusus dari permasalahan pemrograman nonlinier adalah masalah pemrograman kuadratik. Dimana pemrograman kuadratik ini memiliki fungsi tujuan yang berbentuk kuadratik dan fungsi kendala berbentuk linier. Dalam penelitian ini dirancang sebuah penyelesaian permasalahan pemrograman kuadratik dengan menggunakan persyaratan Karush Khun Tucker. Syarat yang harus dipenuhi untuk optimum adalah bahwa turunan parsial pertama dari fungsi tujuan terhadap semua variabel dan pengali lagrange bernilai nol. (λ_ig_i(x)=0)

ABSTRACT

One particular form of nonlinear programming is a quadratic programming problem. This quadratic programming where the objective function which has a quadratic form and the constraint function is a linear. In this research we proposed a quadratic programming problem solving using Karush Khun Tucker requirements. The condition that must be met for the optimum is that the first partial derivative of the objective function of all variables and Lagrange multiplier is zero. (λ_ig_i(x)=0).

DAFTAR ISI Halaman Persetujuan ii Pernyataan iii Penghargaan iv Abstrak v Abstract vi

Daftar Isi vii

Daftar Tabel viii

Daftar Gambar ix Bab 1 Pendahuluan 1.1 Latar Belakang 1 1.2 Perumusan Masalah 2 1.3 Tinjauan Pustaka 3 1.4 Tujuan Penelitian 5 1.5 Kontribusi Penelitian 6 1.6 Metode Penelitian 6

Bab 2 Landasan Teori

2.1 Pemrograman Nonlinier 7

2.1.1 Pemrograman Nonlinier Tak Berkendala 7

2.1.2 Pemrograman Nonlinier Berkendala 8

2.2 Permasalahan Pemrograman Kuadratis 12

2.2.1 Pemilihan Portofolio dengan Sekuritas Beresiko 12 2.2.2 Masalah Transportasi dengan Diskon Volume pada 14 Biaya Pengiriman Barang

2.3 Konveksitas Fungsi 16

2.6.1 Fungsi Konveks atau Konkaf Satu Variabel 17

2.6.2 Fungsi Konveks dan Konkaf untuk Beberapa Variabel 17

2.4 Matriks Hessian 19

2.5 Matriks Definite Positif 22

2.6 Persyaratan Karush Khun Tucker 24

2.7 Masalah Komplementaritas 27

Bab 3 Pembahasan

3.1 Pemrograman Kuadratis Tak Berkendala 29

3.2 Pemrograman Kuadratis Berkendala modifikasi simpleks 30

3.3 Pemrograman Kuadratis Karush Kuhn Tucker 37

Bab 4 Penutup

4.1 Kesimpulan 41

4.2 Saran 42

DAFTAR TABEL

Halaman

Table 1.1 Uji Konveksitas untuk Fungsi Dua Variabel 19

DAFTAR GAMBAR

Halaman

Gambar 1.1 Bentu Himpunan Konveks dan bukan Konveks 16

Gambar 1.2 Plot dari f(x₁,x₂)=x₁3+x₂3 +2₁2+4x₂2+6 21

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Pesatnya perkembangan ilmu pengetahuan dan teknologi membuat matematika menjadi sangat penting artinya. Oleh karena itu dapat dikatakan bahwa perkembangan ilmu pengetahuan dan teknologi tersebut tidak lepas dari peranan matematika. Hampir dapat dipastikan bahwa setiap bagian dari ilmu dan teknologi baik dalam unsur kajian umum ilmu murni maupun terapannya memerlukan peranan matematika sebagai ilmu bantunya.

Salah satu bagian dari matematika terapan adalah program linear (linear

programming) yang merupakan suatu model dari penelitian operasional (operation

research) yang digunakan untuk memecahkan masalah optimasi. Dalam masalah

optimasi ini kita diminta untuk menentukan nilai optimum (nilai maksimumatau nilai minimum) dari suatu fungsi matematik. Namun dalam pemograman linier semua fungsi yang terlibat (fungsi tujuan dan fungsi kendala) adalah linier. Meskipun pada dasarnya diaplikasikan pada banyak masalah praktis, asumsi ini sering kali tidak sesuai. Pada kenyataannya, banyak ahli ekonomi menemukan drajat nonlinearitas yang merupakan suatu aturan dan bukan merupakan suatu perkecualian dalam berbagai masalah. Oleh sebab itu, sering kali memang perlu untuk segera mengarahkan pada masalah pemrograman nonlinier, sehingga kita memfokuskan perhatian pada area yang penting ini.

Terdapat banyak jenis masalah pemrograman nonlinier, tergantung pada karakteristik fungsi tujuan dan fungsi kendala. Salah satunya adalah pemograman kuadratis yang merupakan bentuk khusus dari pemrograman nonlinier. Dimana masalah pemrograman kuadaratis ini memiliki kendala linier, tetapi fungsi tujuan

berbentuk kuadratis. Oleh karena itu, satu-satunya perbedaan antara pemrograman ini dengan pemrograman linier terletak di fungsi tujuannya yang melibatkan pangkat dua dari variabel atau perkalian dari dua variabel.

Beberapa metode telah dikembangkan untuk menyelesaikan kasus pemrograman kuadratis dengan asumsi tambahan fungsi tujuan merupakan fungsi konkaf. Salah satu metode untuk menyelesaikan masalah pemrograman kuadratis adalah dengan persyaratan Karush-Kuhn-Tucker. Metode ini sangat efektif untuk permasalahan optimasi nonlinier dengan kendala pertidaksamaan.

1.2 Perumusan Masalah

Dengan pendekatan persyaratan Karush-Kuhn-Tucker dapat diperoleh optimasi dari pemrograman kuadratis. Dalam hal ini kondisi yang perlu diperhatikan adalah mengikuti syarat cukup agar mendapatkan nilai-nilai variabel yang optimal untuk mencapai hasil yang diinginkan.

1.3 Tinjauan Pustaka

1. Pemrograman Kuadratis

Pemrograman kuadratis adalah masalah optimasi dimana memaksimumkan atau meminimumkan fungsi tujuan yang berbentuk kuadratis dengan fungsi kendalanya berbentuk persamaan atau pertidaksamaan linier.

Bentuk fungsi kuadratis dengan variabel x=

(

x₁,x₂,...,x_n

)

adalah :

( )

k j n k n j kj n j j jx q x x c x f

∑

∑∑

= = = + = 1 1 1 2 1

Dengan menggunakan notasi matriks maka persamaan diatas dapat disederhanakan menjadi

f

( )

x cx xTQx

2 1

+ =

Dengan kendala Ax≤b dan x≥0

Dimana: nxn

Q∈ℜ = matriks simetris (nxn) yang dikenal juga dengan matriks Hessian

mxn

A∈ℜ = matriks kendala

n

x∈ℜ = vektor kolom dari variabel keputusan n

c∈ℜ = vector baris dari fungsi tujuan

m

b∈ℜ = vector kolom dari kendala bagian kanan

T = transposisi matriks

Adanya faktor 2 1

pada fungsi tujuan merupakan konstanta qij (elemen dari

Q) dimana q_ij =q_ji. Maka setelah melakukan perkalian matriks dan vektor maka

fungsi tujuannya dinyatakan dalam q_ij, c_j(elemen c) dan untuk tiap suku dengan j

i= dalam penjumlahan ganda x_ix_j = x2_j sehingga -

2 1

ij

q merupakan koefisien dari

2 j

x . Ketika i≠ j maka −

(

q_ijx_ix_j +q_ijx_jx_i

)

2 1

, sehingga −q_ij adalah koefisien total

untuk perkalian xi dan xj.

Ketika fungsi objektif f (x) adalah cembung sempurna (konkaf) untuk semua

daerah layak diperoleh titik yang merupakan minimum lokal dan juga global. Maka dalam kondisi seperti ini menjamin bahwa Q adalah definite positif.

2. Kondisi Karush-Kuhn-Tucker

Pada tahun 1951 Kuhn Tucker mengemukakan suatu teknik optimisasi yang dapat digunakan untuk pencarian titik optimum dari suatu fungsi yang berkendala. Metode Karush Kuhn Tucker ini dapat dipergunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa memandang sifat dari fungsi tersebut apakah linier atau nonlinier. Jadi metode Kuhn Tucker ini bersifat teknik yang umum dalam

pencarian titik optimum dari setiap fungsi. Metode Karush Kuhn Tucker dapat digunakan untuk memecahkan persoalan baik yang nonlinier maupun yang linier.

Jika kita menghadapi masalah optimasi dalam bentuk :

Maksimumkan / minimumkan : Z = f

( )

X dengan X ={x₁,x₂,...,x_n}t

Dengan kendala : g_i

( )

X ≤/≥0 dengan i= 1,2,3,…,m X ≥0

m≤n (jumlah kendala lebih kecil dari variabel)

Pertama tuliskan kembali persyaratan-persyaratan yang tak negative seperti 0 ,..., 0 , 0 ₂ 1 ≤ − ≤ − ≤

−x x x_n , sehingga himpunan kendalanya adalah m+n persyaratan

ketidaksamaan yang masing-masing dengan tanda lebih kecil dari pada atau sama dengan. Kemudian tambahkan variabel-variabel kurang 2

2 2 2 2 1, n ,..., n m n x x x _{+ + +}

berturut-turut pada ruas kiri dari kendala-kendala tadi, yang dengan demikian merubah tiap-tiap ketidaksamaan menjadi suatu kesamaan. Variabel-variabel kendur (slack

variables) yang ditambahkan disini berbentuk suku-suku kuadrat untuk menjamin

bahwa mereka tak negatif. Kemudian bentuk fungsi Lagrange :

( )

[

( )

]

[

2

]

1 1 1 2 i n i n m m i m i i n i i g X x x x X f L ₊ + + = = + + − − − − ≡

∑

λ

∑

λ

Untuk λ₁,λ₂,...,λ_m+n adalah pengali-pengali Lagrange. Terakhir selesaikan sistem persamaan 0 = ∂ ∂ j x L

₍

₎

m n j=1,2,...,2 + 0 = ∂ ∂ i L λ

(

i=1,2,...,m+n

)

0 ≥ i λ

(

i=1,2,...,m+n

)

Persamaan-persamaan diatas membentuk persyaratan Karush-Kuhn-Tucker untuk maksimasi ataupun minimasi program liner dan nonlinier.

3. Kondisi Optimal dalam Pemrograman Kuadratis

Prosedur menggunakan Kondisi Karush-Kuhn-Tucker untuk memecahkan suatu masalah optimasi dalam pemrograman kuadratis dengan kendala berupa suatu pertidaksamaan, secara essensial melibatkan langkah-langkah yang sama seperti halnya dalam menggunakan teorema Lagrange untuk memecahkan masalah optimasi dengan kedala berupa persamaan, yaitu pertamabentuklah suatu ”Lagrangean” L.[3]

Jadi dalam hal ini dibentuk suatu fungsi

( )

x y x Qx cx y

(

Ax b

)

L = T + + −

2 1 ,

Dimana y adalah baris vektor dimensi m. Maka kondisi Karush-Kuhn-Tucker untuk

lokal minimum memenuhi 0 ≥ ∂ ∂ j x L , j=1,2,...,n c+xTQ+ yA≥0 0 ≥ ∂ ∂ i y L , i=1,2,...,m Ax−b≤0 0 = ∂ ∂ j j x L x , j=1,2,...,n xT

(

cT +Qx+ATy

)

=0

( )

x =0 g y_{i i} , i=1,2,...,m y

(

Ax−b

)

=0 0 ≥ j x , j=1,2,...,n x≥0 0 ≥ i y , i=1,2,...,m y≥0 Dimana n

y∈ℜ = surplus variabel nonnegatif

m

v∈ℜ = slack variabel nonnegatif.

1.4 Tujuan Penelitian

Adapun tujuan penulisan ini adalah menguraikan cara dan persyaratan Karush-Kuhn-Tucker untuk mendapatkan nilai optimum (nilai maksimum atau nilai minimum) dari pemrograman kuadratis.

1.5 Kontribusi Penelitian

Selain untuk tambahan literatur dan pengetahuan pembaca mengenai metode yang dapat digunakan dalam menentukan nilai optimum dari pemograman kuadratis, dalam bidang ekonomi penelitian ini juga bermanfaat untuk membantu memformulasikan pemrograman kuadratis dalam pemilihan portofolio dan sekuritasnya yang beresiko.

1.6 Metode Penelitian

Metode penelitian dalam tulisan ini adalah :

1. Membuat formulasi model pemrograman kuadratis dalam bentuk persyaratan Karush-Kuhn-Tucker

2. Fungsi tujuan yang telah dimodifikasi menjadi

( )

x f

( )

X g

( )

X L _i m i

∑

= + = 1 1

,λ λ ; harus sesuai pada titik tersebut

3. Menghitung titik-titik kritis dan menguji nilai untuk fungsi objektif pada setiap titik-titik kritis tersebut yang membuat nilai fungsi objektif menjadi optimum. 4. Mencari semua solusi

( )

x,λ dalam himpunan persamaan berikut

( )

, =0 ∂ ∂ _λ x x L j ; j=1,2,...,n Dimana

( )

, ≥0 ∂ ∂ _λ λ x L i ; λ≥0

( )

, =0 ∂ ∂ _λ λ λ L x i i ; i=1,2,...,l

5. Diperoleh titik-titik kritis yang merupakan solusi optimal dari pemrograman kuadratis.

BAB 2

LANDASAN TEORI

2.1 Pemrograman Nonlinier

Pemrograman nonlinier merupakan pemrograman dengan fungsi tujuannya saja atau bersama dengan fungsi kendala berbentuk nonlinier yaitu pangkat dari variabelnya lebih dari satu. Salah satu bentuk umun masalah pemrograman nonlinier adalah untuk menentukan x=

(

x₁,x₂,...,x_n

)

sehingga mencapai tujuan untuk:

Maksimumkan / Minimumkan : f

( )

x

Dengan kendala : g_m

( )

x ≥0 dan 0

≥ x

Dengan f

( )

x dan g_m

( )

x merupakan fungsi yang diketahui dengan n variabel

keputusan.

Terdapat banyak jenis masalah pemrograman nonlinier dalam berbagai bentuk. Hal ini tergantung pada karakteristik fungsi tujuan dan kendalanya. Pemrograman nonlinier dapat mempunyai kendala ataupun tidak mempunyai kendala.

2.1.1 Pemrograman Nonlinier Tak Berkendala

Pemrograman nonlinier tak berkendala merupakan masalah optimasi yang tidak memiliki batasan-batasan, sehingga untuk x=

(

x1,x2,...,xn

)

mempunyai fungsi tujuan adalah

Maksimumkan / Minimumkan : f

( )

x

Syarat perlu dan cukup agar suatu penyelesaian x = x* merupakan penyelesaian optimal saat f(x) merupakan fungsi yang dapat diturunkan adalah

0 = ∂ ∂ j x f Pada x = x* , untuk j=1,2,...,n

Dimana f

( )

x merupakan fungsi konkaf, kondisi ini juga mencukupi, sehingga

mencari solusi untuk x* tereduksi menjadi penyelesaian dari sistem n persamaan

yang diperoleh dengan n turunan parsial sama dengan nol.

Ketika variabel xj memiliki kendala nonnegativitas atau xj ≥0, kondisi yang diperlukan dan mungkin cukup akan berubah menjadi

⎩ ⎨ ⎧ = ≤ ∂ ∂ 0 0 j x f pada pada , , * * x x x x = = jika jika 0 0 * * > = j j x x Untuk setiap .j

Setelah titik kritis yang memenuhi kondisi diketahui, masing-masing titik digolongkan sebagai maksimum atau minimum lokal jika fungsi tersebut bersifat konveks ataupun konkaf disekitar titik tersebut. Maksimum dan minimum global akan ditemukan dengan membandingkan minimum lokal dan maksimum lokal dan kemudian menguji nilai dari fungsi tersebut dengan sebagian variabel mendekati −∞ atau +∞. Jika fungsi diketahui konveks maupun konkaf, maka titik kritisnya pastilah merupakan minimum global maupun mkasimum globalnya.

2.1.2 Pemrograman Nonlinier Berkendala

Pemrograman nonlinier berkendala merupakan masalah optimasi yang memiliki batasan-batasan, sehingga untuk x=

(

x1,x2,...,xn

)

, maka bentuk standard untuk program-program tak linier yang mengandung hanya kendala-kendala kesamaan (equality) adalah Maksimumkan / Minimumkan : f

( )

x Dengan kendala : g₁

( )

x =0 …………

( )

x =0 g_m

Disini m≤n (jumlah kendala lebih kecil daripada variabel) , jika terjadi bahwa m > n, maka biasanya tidak dapat diselesaikan. Pada program minimasi dapat

diubah ke dalam bentuk program maksimasi dengan mengalikan fungsi objektif -1. Suatu metode yang dapat dipakai untuk menyelesaikan masalah optimasi ini adalah metode pengali Lagrange. Metode pengali Lagrange dipilih karena prinsip kerjanya sederhana dan mudah dimengerti. Metode ini dimulai dengan pembentukan fungsi Lagrangian yang didefinisikan sebagai:

(

X

)

f

( )

X g

( )

X L m j m j

∑

= + = 1 ,λ λ Teorema:

Syarat perlu bagi sebuah fungsi f(X) dengan kendala gi(X)=0, dengan j=1,2,...,m agar mempunyai minimum relatif pada titik X* adalah derivasi parsial pertama dari

fungsi Lagrangenya yang didefinisikan sebagai L=L

(

x₁,x₂,...,x_n,λ₁,λ₂,...,λ_m

)

terhadap setiap argumennya mempunyai nilai nol. Teorema:

Syarat harus bagi sebuah fungsi f(X) agar mempunyai minimum (atau maximum)

relatif pada titik X* adalah jika fungsi kuadrat, Q, yang didefinisikan sebagai

j i n i n j i j

x

x

x

x

L

Q

∂

∂

∂

∂

∂

=

∑ ∑

=1 =1 2

dievaluasi pada X = X* harus definit positif (atau negatif) untuk setiap nilai dX yang

memenuhi semua kendala.

Syarat perlu agar i j

n i n j i j x x x x L Q ∂ ∂ ∂ ∂ ∂ =

∑∑

=1 =1 2

menjadi definit positif (atau negatif) untuk setiap variasi nilai dX adalah setiap akar dari polinomial, z_i, yang didapat dari

(

)

(

)

(

)

0 0 0 0 0 0 0 0 0 3 2 1 2 23 22 21 1 13 12 11 2 1 3 2 1 2 22 12 2 23 22 21 1 21 11 1 13 12 11 K K M K M M M K M M M K K K K K K M K M M M K O M M K K K K mn m m m n n m m nn n n n n n n n g g g g g g g g g g g g gn g g z L L L L g g g L L z L L g g g L L L z L − − − Dengan

(

)

j i ij x x X L L ∂ ∂ ∂ = 2 *,λ dan

( )

j i ij x X g g ∂ ∂ = *

Pengali Lagrange mempunyai arti secara fisik yang menarik. Misalkan terdapat permasalahan optimasi dengan satu kendala sebagai berikut:

Maksimumkan / Minimumkan : f

( )

x

Dengan kendala : g

( )

x =b

Fungsi Lagrange-nya adalah

(

X

)

f

( )

X

(

b g

( )

X

)

L ,λ = +λ −

Syarat perlu untuk penyelesaian diatas adalah : 0 = ∂ ∂ i x L untuk i=1,2,...,n dan 0 = ∂ ∂ λ L

Persamaan diatas menghasilkan : 0 = ∂ ∂ − ∂ ∂ i i x g x f _λ untuk i=1,2,...,n

( )

=0 −g X b atau b=g

Maka : 0 = ∂ ∂ ∂ − ∂ ∂ ∂ i i i i x x g x x f _λ untuk i=1,2,...,n atau 0 1 1 = ∂ ∂ ∂ − ∂ ∂ ∂

_∑

∑

− − i n i i i n i i x x g x x f _λ atau n _i i i i n i i x x g x x f _∂ ∂ ∂ = ∂ ∂ ∂

∑

∑

− −1 1 λ atau 43 42 1 43 42 1 dg i n i i df i n i i x x g x x f _∂ ∂ ∂ = ∂ ∂ ∂

_∑

∑

− −1 1 λ

Menghasilkan hasil yang final yaitu : df =λdb atau df =λ*db

Dari Persamaan ini dapat ditarik kesimpulan bahwa: pada penyelesaian optimum, perubahan fungsi tujuan f, berbanding lurus dengan perubahan kendala b

dengan faktor sebesar pengali Lagrange λ.

Bentuk standard dari program-program tak linier yang mengandung hanya kendala-kendala ketidaksamaan adalah :

Maksimumkan / Minimumkan : f

( )

x

Dengan kendala : g_i

( )

x ≤0 untuk i=1,2,...,n 0

≥ x

Kunci dari penanganan permasalahan di atas adalah merubah kendala pertidaksamaan menjadi persamaan dengan menambah variabel slack. Masalah

pemrograman ini ditandai dengan adanya kendala-kendala yang sama sepenuhnya dengan pemrograman linier. Semua fungsi kendala g_i

( )

x adalah linier, tetapi fungsi

tujuan f

( )

x berbentuk nonlinier. Masalah ini dipertimbangkan secara sederhana

dengan hanya memiliki satu fungsi nonlinier yang diperhitungkan, bersama dengan daerah layak dari pemrograman linier. Sejumlah algoritma khusus yang didasari atas perluasan metode simpleks telah dikembangkan untuk memperhitungkan fungsi tujuan yang nonlinier.

2.2 Permasalahan Pemrograman Kuadratis

Masalah pemrograman kuadratis memiliki fungsi tujuan yang berbentuk kuadratis yang melibatkan 2

j

x dan x_ix_j

(

_i≠ j

)

dan memiliki kendala berbentuk linier.

Pemrograman kuadratis sangat penting karena dapat diterapkan pada berbagai masalah yang ada. Beberapa contoh kasus yang merupakan masalah dari pemrograman kuadratis ini adalah :

2.2.1 Pemilihan Portofolio dengan Sekuritas Beresiko

Saat ini para manjer professional dari portofolio besar biasa menggunakan model komputer berbasis pemrograman nonlinier untuk memandu pekerjaan mereka. Oleh karena itu inverstor harus memperhatikan baik ekspetasi pendapatan maupun resiko investasi, pemrograman nonlinier digunakan untuk menentukan portofolio yang pada asumsi tertentu dapat menghasilkan keseimbangan optimal antara kedua factor tersebut. Pendekatan ini sebagian besar merupakan hasil riset yang dilakukan oleh Harry Markowitz dan William Sharpe, pemenang hadiah nobel tahun 1990 dalam bidang ekonomi karena hasil risetnya tersebut.

Model pemrograman nonlinier untuk masalah ii dapat dirumuskan sebagai berikut. Misalkan terdapat n senis saham/sekuritas yang sedang dipertimbangkan

untuk masuk dalam portofolio, dan variabel keputusan x_j

(

j=1,2,...,n

)

adalah share

dari saham j yang masuk dalam portofolio. μ_i dan σ_jj adalah (estimasi) rata-rata

dan varians masing-masing untuk pendapatan setiap share dari saham j, dengan σ_jj

sebagai ukuran resiko dari saham ini. Untuk i=1,2,...,n

(

i≠ j

)

, adalah σ_ij kovariansi

dari pendapatan setiap share antara saham i dan saham j. Oleh karena itu sulit

mengestimasi seluruh nilai σij, langsung dari σii dan σjj. Kemudian, nilai ekspetasi

( )

x

R dan variansi V

( )

x dari total pendapatan keseluruhan portofolio adalah

( )

j n j jx x R

∑

= = 1 μ Dan

( )

n _j i i n j ijx x x V

∑∑

= = = 1 1 σ

Dengan V

( )

x mengukur resiko yang terasosiasi dengan portofolio. Salah satu

cara untuk mempertimbangkan keseimbangan antara dua faktor adalah dengan menggunakan V

( )

x sebagai fungsi tujuan untuk diminimalkan dan menggunakan

kendala yang memastikan R

( )

x tidak lebih kecil dari ekspetasi pendapatan minimum

yang dapat diterima. Model pemrograman nonlinier yang lengkap adalah

Minimumkan

( )

n _j i i n j ijx x x V

∑∑

= = = 1 1 σ Dengan kendala x_j L n j j ≥

∑

=1 μ B x p _j n j j ≥

∑

=1 0 ≥ j x untuk j=1,2,...,n

dengan L adalah ekspetasi pendapatan minimum yang dapat diterima, P_j adalah

harga tiap share dari saham j dan B adalah jumlah uang yang dianggarkan untuk

portofolio.

Untuk memilih nilai L yang sesuai agar tercapai keseimbangan terbaok antara

( )

x

R dan V

( )

x relatif sulit. Jadi daripada berhenti dengan satu pilihan nilai L, pendekatan pemrograman nonlinier parametric biasa digunakan untuk membangkitkan solusi optimal sebagai fungsi L pada kisaran nilai L yang lebar. Langkah selanjutnya

adalah mengevaluasi R

( )

x dan V

( )

x untuk solusi optimal tersebut dan memilih solusi

yang memberikan keseimbangan antara dua nilai itu. Prosedur ini sering disebut pembangkitan solusi pada batas efisien dari grafik dua dimensi titik-titik

( ) ( )

, }

{R x V x untuk nilai x yang layak. Alasannya adalah titik {R

( ) ( )

x ,V x} yang

optimal untuk x (pada beberapa nilai L) pasti terletak pada batas daerah layak setiap nilai optimal x disebut efisien karena tidak ada solusi layak lain yang

sekurang-kurangnya memiliki satu nilai ukuran yang sama R atau V dan lebih baik pada

2.2.2 Masalah Transportasi dengan Diskon Volume pada Biaya Pengiriman Barang

Jenis aplikasi dari masalah transportasi dengan volume pada biaya pengiriman barang adalah menentukan rencana yang optimal untuk mengirimkan barang dari berbagai sumber ke berbagai tempat tujuan pengiriman, dengan kendala sumber dan permintaan, dengan tujuan untuk meminimalkan total biaya pengiriman. Kita asumsikan biaya pengiriman per unit dari sumber tertentu ke tujuan pengiriman adalah tetap, tanpa memperhatikan jumlah pengiriman. Pada kenyataannya, biaya ini mungkin tidak tetap. Diskon volume kadang tersedia untuk pengiriman dalam jumlah yang besar sehingga biaya marginal pengiriman satu atau lebih unit mungkin akan mengikuti pola bila jumlah pengiriman besar maka biaya marginal juga akan semakin besar begitu juga sebaliknya.

Dengan demikian hasilnya adalah biaya yang terjadi dari pengiriman x unit

diberikan dalam bentuk fungsi nonlinier C

( )

x , yang merupakan fungsi poongan linier

sama dengan biaya marginal.. konsekuensinya, jika setiap kombinasi dari sumber dan tujuan memiliki fungsi biaya pengiriman yang sama maka biaya pengiriman x_ij unit

dari sumber i=1=(1,2,...,m) ke tujuan j=1=(1,2,...,n) dinyatakan dengan funsi nonlinier )Cij(xij sehingga keseluruhan fungsi tujuan diminimalkan adalah

( )

_∑∑

= = = m i n j ij ij x C x f 1 1 ) (

Meskipun dengan funsi tujuan yang nonlinier, kendala dari permasalahan ini adalah kendala linier khusus yang sesuai dengan model permasalahan tranportasi.

Dari contoh-contoh kasus diatas maka dapat kita tuliskan bentuk standard dari pemrograman kuadratis yaitu

Minimumkan :

( )

i j n i n j ij n j j jx q x x c x f

∑

∑∑

= = = + = 1 1 1 2 1

Dengan menggunakan notasi matriks maka persamaan diatas dapat disederhanakan menjadi Minimumkan : f

( )

x cx xTQx 2 1 + =

Dengan kendala: Ax≤b dan x≥0

Dimana: nxn

Q∈ℜ = matriks simetris (nxn) yang dikenal juga dengan matriks Hessian

mxn

A∈ℜ = matriks kendala

n

x∈ℜ = vektor kolom dari variabel keputusan n

c∈ℜ = vector baris dari fungsi tujuan

m

b∈ℜ = vector kolom dari kendala bagian kanan

T = transposisi matriks

Adanya faktor 2 1

pada fungsi tujuan merupakan konstanta qij (elemen dari

Q) dimana q_ij =q_ji. Maka setelah melakukan perkalian matriks dan vektor maka

fungsi tujuannya dinyatakan dalam qij, cj(elemen c) dan untuk tiap suku dengan

j

i= dalam penjumlahan ganda x_ix_j = x2_j sehingga -

2 1

ij

q merupakan koefisien dari

2 j

x . Ketika i≠ j maka −

(

q_ijx_ix_j +q_ijx_jx_i

)

2 1

, sehingga −qij adalah koefisien total untuk perkalian x_i dan x_j.

Beberapa algoritma telah dikembangkan untuk khasus pemrograman kuadratis dengan funsi tujuan merupakan fungsi konkaf. Satu cara untuk membuktikan bahwa fungsi tujuan merupakan fungsi konkaf adalah dengan membuktikan kondisi yang sepadan dengan xTQx≥0. Untuk semua x yaitu Q merupakan matriks definite positif. Penyelesaian dari masalah pemrograman kuadratis ini dapat dilakukan dengan pendekatan kondisi persyaratan Karush Kuhn Tucker kemudian dinyatakan ulang dalam bentuk yang mirip dengan program linier, sehingga mempermudah mencari solusi optimalnya.

2.3 Konveksitas Fungsi

Konsep konveksitas sering digunakan dalam bidang penelitian operasianal, terutama dalam ruang lingkup pemrograman nonlinier. Konsep fungsi konveks berhubungan langsung dengan himpunan konveks. Jadi, jika f

(

x₁,x₂,...,x_n

)

adalah

fungsi konveks maka kumpulan titik-titik yang terletak diatas atau pada grafik

(

x x xn

)

f ₁, ₂,..., membentuk himpunan konveks. Hal yang sama, kumpulan titik yang

terletak di bawah atau pada grafik fungsi konkaf adalah himpunan konveks.

Himpunan konveks mempunyai sifat penting yaitu untuk beberapa himpunan konveks, kumpulan titik yang berada dalam semua himpunan (irisan dari himpunan konveks) juga merupakan himpunan konveks. Dengan demikian, kumpulan titik yang terletak di atas atau pada fungsi konveks dan di bawah atau pada fungsi konkaf adalah merupakan himpunan konveks juga. Jadi, himpunan konveks dapat dilihat secara intuitif sebagai kumpulan titik dengan batas atas fungsi konveks dan batas bawah fungsi konkaf.

Sebuah himpuan vektor berdimensi-m adalah konveks jika untuk dua vektor

yang termasuk dalam himpunan ini berlaku bahwa penggal garis (line segment) antara

kedua vektor juga termasuk dalam himpunan ini.

Gambar 1.1 Bentuk Himpunan Konveks dan Bukan Konveks

Q P R S Penggal garis antara P dan Q C C

2.3.1 Fungsi Konveks atau Konkaf Satu Variabel Definisi :

Fungsi satu variabel f

( )

x disebut fungsi konveks jika setiap pasangan nilai x,

katakanlah x′ dan x′′

(

x′<x′′

)

, f

[

λx′′+(1−λ)x′

]

≤λf(x′′)+(1−λ)f(x′) untuk semua

nilai λ yang memenuhi 0<λ <1. Fungsi tersebut merupakan fungsi konveks ketat jika ≤ dapat diganti < dan merupakan fungsi konkaf (fungsi konkaf ketat) jika pernyataan ≤ diganti dengan ≥ (atau dengan >).

( )

x

f bersifat konveks jika untuk setiap pasang titik pada grafik f

( )

x , segmen

garis yang menghubungkan kedua titik ini terletak pada ataupun diatas grafik f

( )

x

dan begitu juga sebaliknya untuk fungsi konkaf. Tepatnya jika memeiliki turunan kedua, maka f

( )

x bersifat konveks jika dan hanya jika d2f

( )

x /dx2 >0 untuk setiap

nilai x yang mungkin.

Uji konveksitas untuk fungsi satu variabel :

Pertimbangkan fungsi satu variabel f

( )

x yang memeiliki turunan kedua untuk

setiap nilai x yang mungkin. Dengan demikian, fungsi f

( )

x dapat bersifat:

1. Konveks jika dan hanya jika

( )

₂ 0 2 ≥ dx x f d

untuk setiap nilai x yang mungkin.

2. Konveks ketat jika dan hanya jika

( )

₂ 0 2 > dx x f d

untuk setiap nilai x yang mungkin.

3. Konkaf jika dan hanya jika ₂

( )

0 2 ≤ dx x f d

untuk setiap nilai x yang mungkin.

4. Konkaf ketat jika dan hanya jika

( )

₂ 0 2 < dx x f d

untuk setiap nilai x yang mungkin.

2.3.2 Fungsi Konveks dan Konkaf untuk Beberapa Variabel

Konsep fungsi konveks dan konkaf dari satu variabel dapat digeneralisasikan untuk fungsi dengan lebih dari satu variabel. Dengan demikian, saat f

( )

x digantikan

dengan fungsi f

(

x₁,x₂,...,x_n

)

definisi masih diterapkan apabila x digantikan oleh

(

x ,x ,...,x

)

. Hal yang sama, penafsiran geometri yang berhubungan juga berlaku

setelah generalisasi konsep titik dan segmen garis. Jadi, sama dengan nilai

( )

x,y

tertentu ditafsirkan sebagai sebuah titik dalam ruang dua dimensi. Setiap kemungkinan nilai dari

(

x1,x2,...,xn

)

dapat diartikan sebagai titik dalam ruang

−

m dimensi (ruang Euclide).

Misalakan m=n+1, titik pada grafik f

(

x₁,x₂,...,x_n

)

menjadi nilai yang

mungkin dari titik

[

x₁,x₂,...,x_n, f

(

x₁,x₂,...,x_n

)

]

. Kemudian,

(

x₁,x₂,...,x_n,x_n+1

)

dikatakan terletak di atas, tepat, atau di bawah grafik f

(

x₁,x₂,...,x_n

)

tergantung pada

nilai xn+1 yang lebih besar, sama dengan atau lebih kecil daripada

(

)

n m x x x f ₁, ₂,..., . Definisi :

Segmen garis yang menghubungkan kedua titik

(

x1′,x′2,...,xm′

)

dan

(

x1′′,x2′′,...,xm′′

)

merupakan penjumlahan titik-titik

(

x1,x2,...,xm

)

= [λx1′′+(1−λ)x1′,λx2′′+(1−λ)x′2,...,λxm′′ +(1−λ)x′m]

dengan 0≤λ≤1. Jadi segmen garis dalam ruang m−dimensi merupakan generalisasi

langsung dari segmen garis dalam ruang dua dimensi. Definisi :

(

x x xn

)

f ₁, ₂,..., merupakan fungsi konveks jika untuk setiap pasang titik pada grafik

(

x x xn

)

f ₁, ₂,..., , segmen garis yang menghubungkan kedua titik tersebut seluruhnya

terletak di atas atau tepat pada grafik fungsi f

(

x₁,x₂,...,x_n

)

. Fungsi tersebut

merupakan fungsi konveks ketat jika segmen garis tersebut seluruhnya terletak diatas grafik kecuali pada kedua titik akhirnya. Begitu juga sebaliknya untuk fungsi konkaf dan fungsi konkaf ketat.

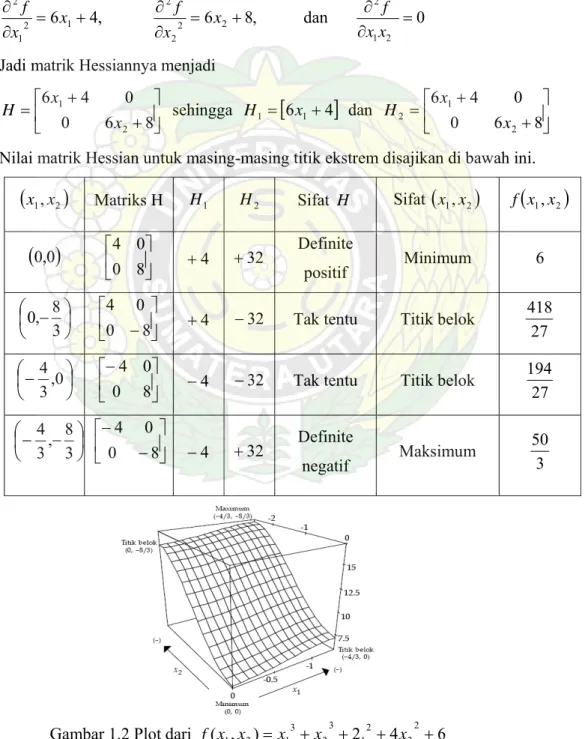
Turunan parsial kedua dapat digunakan untuk menguji fungsi banyak variabel konveks atau tidak, meskipun dengan cara yang lebih kompleks. Misalnya, jika terdapat dua variabel dan semua turunan parsial ada di semua tempat, uji konveksitas menilai tiga kuantitas memenuhi pertidaksamaan yang sesuai untuk semua nilai

Tabel 1.1 Uji Konveksitas untuk Fungsi Dua Variabel

Kuantitas Konveks Konveks Ketat Konkaf Kankaf Ketat ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ₂ 2 2 1 2 1 2 2 2 2 1 2 2 1 2 1 2 _{( , ) ( , ) ( , )} dx dx x x f d dx x x f d dx x x f d 2 1 2 1 2 _{( , )} dx x x f d 2 2 2 1 2 _{( , )} dx x x f d 0 ≥ 0 ≥ 0 ≥ 0 > 0 > 0 > 0 ≥ 0 ≤ 0 ≤ 0 > 0 < 0 <

(

x x xn

)

f ₁, ₂,..., adalah konveks jika dan hanya jika matriks Hessian

nya n

n× − positif definite untuk semua nilai

(

x₁,x₂,...,x_n

)

yang mungkin. Uji

konveksitas selalu diperlukan sebagai sifat umum fungsi. Akan tetapi, beberapa fungsi nonkonveks memenuhi syarat konveksitas pada interval tertentu dari variabel. Dengan demikian, penting untuk membicarakan fungsi yang menjadi konveks pada daerah tertentu.

2.4 Matriks Hessian

Matrik Hessian adalah matrik yang setiap elemennya dibentuk dari turunan

parsial kedua dari suatu fungsi. Milsalkan f(x) fungsi dengan n variabel yang memiliki

turunan parsial kedua dan turunan-turunannya kontinu, Matriks Hessian dari f(x)

ditulis H adalah ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ 2 2 2 2 1 2 2 2 2 2 2 1 2 2 1 2 2 1 2 2 1 2 n n n n n x f x x f x x f x x f x f x x f x x f x x f x f H L L O L L L L

Matrik Hessian dapat digunakan untuk melakukan uji turuanan kedua fungsi

lebih dari satu variabel, yaitu untuk mengidentifikasi optimum relatif dari nilai fungsi tersebut. Penggolongan titik stasioner fungsi dua variabel dengan menggunakan Matriks Hessian misalkan f(x)= F(x1,...,xn) adalah fungsi bernilai real

dimana semua turunan parsialnya kontinu. Misalkan x₀ adalah titik stasioner dari F

dan kita definisikan H = H(x₀) dengan persamaan

) (x₀ F H j iy x

ij = dimana H(xt) adalah Hessian dari F pada x0

Titik stasioner dapat digolongkan sebagai berikut :

1. x₀ adalah suatu minimum relatif dari F jika H (x ) ₀ definite positif

2. x0 adalah suatu maksimum relatif dari F jika H (x ) 0 definite negatif 3. x0 adalah suatu titik pelana dari F jika H (x ) 0 indefinite

Teorema 2.2 :

Misalkan nilai eigen dari matriks Hnxn adalah λ1, λ2 , λ3, …, λn yang didefinisikan oleh

0

=

−H

I

λ dengan I adalah matriks identitas ukuran nxn. Maka :

(i) H adalah definite negatif jika dan hanya jika nilai eigen dari matriks H yaitu λ1, λ2 ,

λ3, …, λn kesemuanya bertanda negatif.

(ii) H adalah definite positif jika dan hanya jika nilai eigen dari matriks H yaitu λ1, λ2 ,

λ3, …, λn kesemuanya bertanda positif.

(iii) H adalah Semi definite negatif jika dan hanya jika nilai eigen dari matriks H yaitu

λi ≤ 0, i = 1, 2, 3, …, n

(iv) H adalah Semi definite positif jika dan hanya jika nilai eigen dari matriks H yaitu

λi ≥ 0, i = 1, 2, 3, …, n Contoh : 6 4 2 ) , ( 2 ₂2 1 3 2 3 1 2 1 x =x +x + x + x + x f

(

3 4

)

0 4 3 1 1 1 2 1 1 = + = + = ∂ ∂ x x x x x f

(

3 8

)

0 8 3 2 _{2 2 2} 2 2 = + = + = ∂ ∂ x x x x x f

Persamaan di atas dipenuhi oleh titik-titik(0, 0); (0, –8/3); (–4/3, 0); dan (–4/3, –8/3) Untuk mengetahui titik yang mana yang maximum dan yang mana yang minimum, harus diselidiki matrik Hessiannya. Derivasi kedua dari f adalah:

, 4 6 1 2 1 2 + = ∂ ∂ x x f , 8 6 2 2 2 2 + = ∂ ∂ x x f dan 0 2 1 2 = ∂ ∂ x x f

Jadi matrik Hessiannya menjadi

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + = 8 6 0 0 4 6 2 1 x x H sehingga H₁=

[

6x₁+4

]

dan _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + = 8 6 0 0 4 6 2 1 2 x x H

Nilai matrik Hessian untuk masing-masing titik ekstrem disajikan di bawah ini.

(

x1,x2

)

Matriks H H1 H2 Sifat H Sifat

(

x1,x2

)

f

(

x1,x2

)

( )

0,0 _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 8 0 0 4 4 + +32 Definite positif Minimum 6 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − 3 8 , 0 _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ −8 0 0 4 4

+ −32 Tak tentu Titik belok

27 418 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− ,0 3 4 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡− 8 0 0 4 4

− −32 Tak tentu Titik belok

27 194 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− −} 3 8 , 3 4 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − 8 0 0 4 4 − +32 Definite negatif Maksimum 3 50

Gambar 1.2 Plot dari ( , ) 2 4 22 6 2 1 3 2 3 1 2 1 x =x +x + + x + x f

2.5 Matriks Definite Positif

Bentuk kuadrat pada

(

x₁,x₂,...,x_n

)

adalah ekspresi yang dapat kita tulis

sebagai

[

]

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ n n x x x A x x x M 2 1 2

1, ,..., . . . Dengan A adalah matriks simetrik nxn. Jadi misalkan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = n x x x X M 2 1

maka bentuk ini dapat ditulis sebagai XtAX

Definisi

Bentuk kuadrat XtAX disebut definite positif jika XtAX > 0 untuk semua x ≠ 0,

sedangkan matriks simetrik A kita sebut matriks definit positif jika XtAX adalah

bentuk kuadrat definit positif. Contoh :

Dipunyai matriks simetrik berikut :

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − = 2 1 0 1 2 1 0 1 2 a

Untuk mengkaji apakah matriks A bersifat definte positif, maka:

[

x1 x2 x3

]

AX Xt = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − 2 1 0 1 2 1 0 1 2 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 3 2 1 x x x =

[

x₁ x₂ x₃

]

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ + − − + − − 3 2 3 2 2 2 1 2 2 2 x x x x x x x ) x 2 x ( x ) x x 2 x ( x ) x x 2 ( x_{1 1}− ₂ + ₂ − ₁+ ₂ − ₃ + ₃ − ₂ + ₃ = 2 3 3 2 3 2 2 2 2 1 2 1 2 1 x x x x 2 x x x x 2 2x − − + x − − + x = 2 3 3 2 2 2 2 1 2 1 2x x 2 2x x 2 2x − + x − + x =

= 2 3 2 3 3 2 2 2 2 2 2 1 2 1 2 1 (x 2x x x ) (x 2x x x ) x x + − + + − + + 2 3 2 3 2 2 2 1 2 1 (x x ) (x x ) x x + − + − + =

Dari sini dapat disimpulkan bahwa matrik A bersifat definit positif karena memenuhi: 0 ) ( ) ( 2 3 2 3 2 2 2 1 2 1 + x −x + x −x +x > x kecuali jika x₁ = x₂ = x₃ =0

Sebaliknya matrik A dan bentuk kuadrat XtAXdisebut :

1. Definite negatif jika XtAX< 0 , untuk semua x ≠ 0 .

2. Semidefinite positif jika XtAX _{≥0 , untuk semua x.}

3. Semidefinite negatif jika XtAX≤0 , untuk semua x.

4. Indefinite bila tidak termasuk golongan diatas.

Himpunan syarat perlu dan syarat cukup untuk bentuk-bentuk definit positif dan negatif. yaitu :

1. Syarat perlu dan syarat cukup untuk bentuk definite positif.

Suatu himpunan syarat perlu dan syarat cukup bentuk XtAX sebagai definite

positif adalah 0 11 > h , 0 22 21 12 11 _> h h h h , 0 33 32 31 23 22 21 13 12 11 > h h h h h h h h h , . . . , A >0

Jika n minor dari A adalah positif, maka XtAX adalah definite positif.

DanXtAXhanya definite positif, jika minor-minor ini positif.

2. Syarat perlu dan syarat cukup untuk bentuk definite negatif

Suatu himpunan syarat perlu dan syarat cukup bentuk XtAX _{menjadi definite}

negatif atau setaranya untuk Xt(−A)X sebagai definite positif adalah

0 11 < h , 0 22 21 12 11 _> h h h h , 0 33 32 31 23 22 21 13 12 11 < h h h h h h h h h , . . . , (−1)n A >0 Dimana a_ijadalah elemen-elemen dari A (bukan –A)

2.6 Persyaratan Karush Khun Tucker

Pada tahun 1951 Kuhn Tucker mengemukakan suatu teknik optimisasi yang dapat digunakan untuk pencarian titik optimum dari suatu fungsi yang berkendala. Metode Karush Kuhn Tucker ini dapat dipergunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa memandang sifat dari fungsi tersebut apakah linier atau nonlinier. Jadi metode Kuhn Tucker ini bersifat teknik yang umum dalam pencarian titik optimum dari setiap fungsi. Metode Karush Kuhn Tucker dapat digunakan untuk memecahkan persoalan baik yang nonlinier maupun yang linier.

Jika kita menghadapi masalah optimasi dalam bentuk :

Maksimumkan / minimumkan : Z = f

( )

X dengan X ={x₁,x₂,...,x_n}t

Dengan kendala : g_i

( )

X ≤/≥0 dengan i= 1,2,3,…,m X ≥0

m≤n (jumlah kendala lebih kecil dari variabel)

Pertama tuliskan kembali persyaratan-persyaratan yang tak negative seperti 0 ,..., 0 , 0 ₂ 1 ≤ − ≤ − ≤

−x x xn , sehingga himpunan kendalanya adalah m+n persyaratan ketidaksamaan yang masing-masing dengan tanda lebih kecil dari pada atau sama dengan. Kemudian tambahkan variabel-variabel kurang 2

2 2 2 2 1, n ,..., n m n x x x _{+ + +}

berturut-turut pada ruas kiri dari kendala-kendala tadi, yang dengan demikian merubah tiap-tiap ketidaksamaan menjadi suatu kesamaan. Variabel-variabel kendur (slack

variables) yang ditambahkan disini berbentuk suku-suku kuadrat untuk menjamin

bahwa mereka tak negatif. Kemudian bentuk fungsi Lagrange :

( )

[

( )

]

[

2

]

1 1 1 2 i n i n m m i m i i n i i g X x x x X f L ₊ + + = = + + − − − − ≡

∑

λ

∑

λ

Untuk λ1,λ2,...,λm+n adalah pengali-pengali Lagrange. Terakhir selesaikan sistem persamaan

0 = ∂ ∂ i x L

₍

₎

m n i=1,2,...,2 + 0 = ∂ ∂ i L λ

(

i=1,2,...,m+n

)

0 ≥ i λ

(

i=1,2,...,m+n

)

Untuk fungsi konveks, syarat perlu dan cukup untuk mencapai titik minimum dapat dicari menggunakan syarat Karush Kuhn Tucker. Tetapi untuk fungsi nonkonvek, syarat Karush Kuhn Tucker merupakan syarat perlu saja, tetapi belum cukup untuk mencapai optimal. Jadi untuk masalah jenis konveks, syarat Karush Kuhn Tucker menjadi syarat perlu dan cukup untuk sebuah minimum/maksimum global.

Teorema 1 (Frederick S. Hillier dan Gerald J. Lieberman, 1994)

Misalkan f(x,y) merupakan fungsi 2 variabel. f(x,y) merupakan fungsi konveks jika

dan hanya jika dipenuhi ketiga syarat berikut : (i) 2 2 2 2 1 2 1 2 2 2 2 1 2 2 1 2 1 2 _{( , ) ( , )} . ) , ( ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = dx dx x x f d dx x x f d dx x x f d (ii) ( ₂, ) 0 1 2 1 2 ≥ dx x x f d (iii) ( ₂, ) 0 2 2 1 2 ≥ dx x x f d

Teorema 2 (Frederick S. Hillier dan Gerald J. Lieberman, 1994)

Suatu fungsi 2 variabel f(x,y) merupakan fungsi konkaf jika tidak memenuhi paling

tidak satu dari ketiga syarat pada teorema 1, atau dengan kata lain –f(x,y) merupakan

fungsi konveks.

Teorema 3 (Frederick S. Hillier dan Gerald J. Lieberman, 1994)

Untuk permasalahan dengan asumsi f(x) konkaf dan gj(x) konveks, maka syarat perlu dan cukup keoptimalannya berdasarkan teorema berikut. Misalkan

) ( ),..., ( ), ( ), (x g1 x g2 x g x

) ,..., , ( _{1 2} * n x x x

x = ′ ′ ′ merupakan penyelesaian optimal untuk masalah program nonlinier

apabila terdapat sejumlah λ_i untuk i=1,2,...,m sehingga semua syarat terpenuhi :

(i) 0 1 = ∂ ∂ + ∂ ∂

_∑

= i j m j i i x g x f _λ i=1,2,...,n (ii) 0λ_jg_j = j=1,2,...,m (iii) gj ≤0 j=1,2,...,m (iv) λ_j ≥0 j=1,2,...,m

Syarat Karush Kuhn Tucker untuk program nonlinier berkendala : Teorema

Diasumsikan )f(x),g1(x),g2(x),...,gm(x merupkan fungsi yang dapat diturukan maka * ( ₁, ₂,..., )

n

x x x

x = ′ ′ ′ menjadi solusi optimal untuk permasalahan pemrograman

nonlinier hanya jika terdapat sejumlah m bilangan μ1,μ2,...,μm sehingga semua syarat kondisi Karush Kuhn Tucker berikut ini terpenuhi :

(i) 0 1 ≤ ∂ ∂ − ∂ ∂

_∑

= j m i i j x g x f λ pada * x x= untuk j=1,2,...,n (ii) 0 1 = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂

_∑

= j m i i j j x g x f x λ pada x=x* untuk j=1,2,...,n (iii) 0( *)_{− ≤} i i x b g untuk j=1,2,...,m (iv)

[

( *)₋

]

₌0 i i i g x b λ untuk j=1,2,...,m (v) * _≥0 j x untuk j=1,2,...,m (vi) 0λ_j ≥ untuk j=1,2,...,m

Dapat dilihat darik kondisi (ii) dan (iv) memerlukan hasil perkalian dua kuantitas sama dengn nol. Oleh karena itu, tiap kondisi ini menyatakan bahwa setidaknya salah satu dari kuantitas itu harus sama dengan nol. Akibatnya, kondisi (iv) dapat digabung dengan kondisi (iii) untuk menyatakan mereka dalam bentuk lain sebagai berikut.: 0 ) ( * _{− =} i i x b

Demikian pula kondisi (ii) dapat digabung dengan kondisi (i) menjadi : 0 1 = ∂ ∂ − ∂ ∂

_∑

= j i m i i j x g x f _λ (atau 0≤ jika * ₌0 j x ) untuk j=1,2,...,m

Ketika m=0 (tidak ada kendala yang berbentuk fungsi), jumlahan berbilai 0 dan fungsi gabungan (i,ii) menjadi kondisi yang ada. Oleh karena itu, untuk m>0, tiap suku dalam jumlahan mengubah kondisi untuk m=0 dengan memasukkan pengaruh dari kendala berbentuk fungsi yang bersangkutan.

Dalam kondisi diatas, μi setara dengan variabel dual dalam pemrogramana linier dan memiliki interpretasi ekonomi yang juga dapat diperbandingkan. Akan tetapi, μ_i juga ada dalam penurunan matematika seperti dalam faktor pengali Lagrange. Pada kondisi (iii) dan (v) hanya melakukan penegasan kelayakan dari solusi. Kondisi yang lainnya menghilangkan sebagian besar solusi layak lainnya menjadi kandidat yang mungkin untuk menjadi solusi optimal.

Corollary

Diasumsikan bahwa f

( )

x merupakan fungsi konkaf dan g₁(x),g₂(x),...,g_m(x)

merupakan fungsi konveks (misalakan saja masalah ini merupakan masalah pemrograman konveks), dengan semua fungsi ini memenuhi kondisi biasa. Lalu

) ,..., , ( * 2 * 1 * * n x x x

x = adalah solusi optimal jika dan hanya jika semua kondisi teorema

terpenuhi.

2.7 Masalah Komplementaritas

Saat kita berhadapan dengan pemrograman kuadratis, maka kita harus mengetahui terlebih dahulu bagaimana menyelesaikan permasalahan pemrograman nonlinier tertentu dapat direduksi menjadi memecahkan masalah komplementaritas. Dengan variabel w1,w2,...,wp dan z1,z2,...,zp , masalah komplementaritas bertujuan menemukan solusi layak untuk kendala

) (z F

Yang juga memenuhi kendala komplementaritas

0

= z wT

Disini, w dan z adalah vektor kolom. F adalah fungsi bernilai vektor yang diketahui, dan T menandakan transpose matriks. Masalah ini tidak memiliki fungsi tujuan, sehingga secara teknis bukanlah murni masalah pemrograman nonlinier. Hal ini disebut masalah komplementaritas karena hubungan komplementernya.

0

=

w atau z_i =0 (atau kedua-duanya) untuk i=1,2,...,p

Suatu kasus khusus yang penting yaitu masalh komplementaritas linier dengan Mz

q z F( )= +

Dengan q merupakan vektor kolom yang diketahui dan M adalah matriks pxpyang

diketahui. Algoritma yang efisien telah dikembangkan untuk pemecahan masalah ini dengan asumsi tertentu tentang sifat matriks M. satu jenis algoritma menggunakan pemutaran (pivoting) dari satu solusi BF (Basic Feasible) kesolusi BF selanjutnya,

seperti metode simpleks dalam pemrograman linier.

Masalah komplementaritas ini memiliki aplikasi dalam teori permainan, masalah keseimbangan ekonomi, dan masalah keseimbangan teknik sebagai tambahan sebagai aplikasi dari pemrograman nonlinier.

BAB 3

PEMBAHASAN

Dalam masalah optimasi terdapat dua bentuk optimasi yaitu, optimasi fungsi tak bersyarat dan optimasi fungsi bersyarat. Kita sudah mengenal beberapa cara untuk menyelesaikan bentuk yang pertama seperti uji turunan pertama, uji turunan kedua, untuk fungsi satu variabel, serta uji parsial kedua untuk fungsi dua variabel, semuanya telah diuraikan pada bab sebelumya. Sedangkan untuk jenis yang kedua merupakan jenis yang paling banyak kita jumpai dalam kehidupan nyata. Banyak aplikasi dari pemodelan matematika dalam optimasi fungsi yang mensyaratkan beberapa kondisi atau syarat untuk diperoleh suatu solusi optimal. Syarat ini yang mengoptimumkan fungsi tujuan. Persoalan dengan model tersebut dinamakan optimasi bersyarat. Bentuk umum dari optimasi fungsi dengan kendala adalah tentukan nilai dari variabel keputusan (nilai ekstrim) x=

(

x₁,x₂,...,x_n

)

yang memaksimumkan (meminimumkan)

fungsi dari permasalahan:

Maksimumkan / minimumkan : Z = f

( )

X

Dengan kendala : g₁

( )

X (≤/ ≥ )b₁

. . .

g_i

( )

X (≤/≥ )b_i dengan i= 1,2,3,…,m

Dimana f(X) merupakan fungsi tujuan (objective function), dan g_i

( )

X (≤ ,= ,≥ )b_i

merupakan fungsi kendala.

3.1 Pemrograman Kuadratis Tak Berkendala

Contoh : Maksimalkan

( )

_{24 2} 2 x x x f = − − Dengan kendala x≥0

4 2 0 -2 -4 25 20 15 10 5 0 x y x y 24 - x^2 - 2*x

Gambar 1.3 Contoh yang mengambarkan solusi optimal dapat terletak pada titik dengan nilai turunan negatif, bukan nol, karena titik tersebut terletak pada batas kendala nonnegativitas.

Solusi optimal untuk suatu masalah dengan satu variabel terletak pada x=0 meskipun turunannya bernilai negatif. Oleh karena itu setiap permasalahan yang memiliki fungsi konkaf untuk dimaksimalkan pada kendala nonnegativitas, mempunyai turunan yang kurang dari satu atau sama dengan nol untuk x=0 adalah kondisi yang diperlukan dan cukup untuk x=0 menjadi optimal.

3.2 Pemrograman Kuadratis Berkendala Modifikasi Simpleks

Contoh : Maksimalkan : 2 2 2 1 2 1 2 1 2 1, ) 15 30 4 2 4 (x x x x xx x x f = + + − − Dengan kendala : x₁+2x₂ ≤30 0 1≥ x 0 2 ≥ x Penyelesaian :

Dalam kasus ini diperoleh

[

15 30

]

= c _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 2 1 x x x _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − = 8 4 4 4 Q

Maksimum global karena f

( )

x adalah

konkaf dan =−2≤0 ∂ ∂ x f pada x=0 Jadi, x=0 adalah optimal.

[

1 2

]

= A b=

[ ]

30 Catat bahwa : = Qx xT

[

x₁ x₂

]

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − 8 4 4 4 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 2 1 x x = [

(

4x₁−4x₁

)

(

−4x₁+8x₂

)

] _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 2 1 x x = 2 21 2 1 2 1 2 1 4 4 8 4x − xx − x x + x = 2 21 22 2 1 12 2 1 21 2 1 11x q xx q xx q x q − − + Mengalikan dengan 2 1 − mengghasilkan 2 2 2 1 2 1 4 4 2 2 1 x x x x Qx xT =− + − −

Yang merupakan bagian nonlinier dari fungsi tujuan untuk contoh ini. Oleh karena 4

11 =

q dan q₂₂ =8 ini menggambarkan bahwa q_jj 2 1

− merupakan koefisien dari 2 j

x

dalam fungsi tujuan. Fakta bahwa q12 =q21 =−4 menggambarkan bahwa baik −qij maupun −qji adalah koefisien total untuk perkalian xi dan xj.

Kondisi KKT untuk Pemrograman Kuadratis

Untuk konkritnya, kita mulai dengan membentuk kondisi Karush Kuhn Tucker adalah sebagai berikut : 1. )(j=1 . 15+4x₂−4x₁−μ₁ ≤0 2. )(j=1 . 0x_j(15+4x₂ −4x₁−μ₁)= 1. (j=2). 030+4x₁−8x₂ −2μ₁≤ 2. (j=2). x₂(30+4x₁−8x₂−2μ₁)=0 3. x₁+2x₂ −30≤0 4. μ1(x1+2x2−30)=0 5. 0x₁≥ , x₂ ≥0 6. 0μ₁ ≥

Untuk mulai menyatakan ulang kondisi ini di dalam bentuk yang lebih tepat, kita memindahkan konstanta dalam kondisi 1(j=1),1(j=2), dan 3 ke sisi sebelah kanan dan lalu menambahkan slack variabel nonnegatif yang dilambangkan dengan

1 2 1,y ,v

y untuk mengubah pertidaksamaan menjadi persamaan.

1. (j=1). −4x₁+4x₂ −μ₁+y₁=−15 1. )(j=2 . −4x₁−8x₂ −2μ₁+y₂ =−30

3. x₁+2x₂+v₁ =30

Perhatikan bahwa kondisi 2(j=1)sekarang dapat dinyatakan ulang secara sederhana, yaitu memerlukan syarat x1 =0atau y1 =0, yaitu

2(j=1).x₁y₁ =0

Dengan cara yang sama, kondisi 2(j=2) dan 4 dapat digantikan dengan 2(j=2). x₂y₂ =0

4. μ₁v₁ =0

Untuk setiap dari tiga pasang variabel ini (x₁.y₁),(x₂.y₂),(μ₁,v₁) dua variabel

tersebut disebut variabel komplementer,karena hanya satu dari dua variabel ini yang dapat bernilai selain nol. Bentuk baru kondisi 2(j=1),2(j=2),dan 4 ini dapat digabung menjadi satu kendala yaitu :

1 1y

x + x₂y₂ + μ₁v₁ = 0

Yang disebut kendala komplementaritas.

Setelah mengalikan dengan -1 persamaan untuk kondisi 1(j=1) dan 1(j=2) untuk mendapat ruas kanan nonnegatif, kita sekarang memiliki bentuk yang diinginkan untuk keseleruhan kondisi seperti yang ditunjukkan sebagai berikut.

15 4 4x₁− x₂ +μ₁−y₁ = 30 2 8 4 1+ 2 + 1− 2 = − x x μ y 30 2 2 1 1+ x +v = x 0 1 ≥ x , x₂ ≥0, μ₁≥0, y₁ ≥0, y₂ ≥0, v₁≥0 1 1y x + x₂y₂ + μ₁v₁ = 0

Bentuk ini cukup baik karena, kecuali untuk kendala komplementaritas, kondisi ini adalah kendala pemrograman linier .

Untuk setiap masalah pemrograman kuadratis, kondisi Karush Kuhn Tucker-nya dapat direduksi menjadi bentuk inidengan haTucker-nya mengandung kendala pemrograman linier ditambah satu kendala komplentaritas. Dalam notasi matriks dapat dituliskan bentuk umumnya adalah

T T c y u A Qx+ − = b v Ax+ = 0 ≥ x , u ≥0, y≥0, v≥0 0 = +u v y xT T

Dengan element vektor u adalah u_i dari bagian sebelumnnya dan elemen-elemen vektor kolom y dan v adalah slack variabel. Oleh karena fungsi tujuan

masalah asli diasumsikan konkaf dan fungsi kendalanya linier sehingga konveks maka corollary teorema pada kondisi Karush Kuhn Tucker dapat digunakan. Oleh karena itu, x optimal jika dan hanya jika y, danu v memiliki nilai sehingga semua empat

vektor memenuhi kondisi di atas. Masalah asli tereduksi menjadi masalah untuk mencari solusi layak untuk kendala ini.

Metode Modifikasi Simpleks

Metode modifikasi simpleks memanfaatkan kata kunci bahwa, dengan perkecualian pada kendala komplementer bentuk kondisi Karush Kuhn Tucker yang telah diperoleh tidak lebih daripada kendala pemrogramn linier. Lebih jauh lagi, kendala komplementer menyatakan secara sederhana dan tidak langsung bahwa tidak mungkin bagi pasangan variabel komplementer untuk keduanya menjadi variabel basis (satu-satunya variabel >0) saat solusi BF menjadi pertimbangan. Oleh karena itu, masalah ini menjadi masalah pencarian solusi BF awal pada tiap masalah pemrograman linier yang memeiliki kendala ini, dengan kendala tambahan ini atas identitas dari variabel basis.