MODEL ANTRIAN DENGAN KEDATANGAN BERDISTRIBUSI
POISSON DAN WAKTU PELAYANAN BERDISTRIBUSI ERLANG
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun Oleh :
Nama : Marcelina Novi Agustiarini
NIM : 103114005
PROGRAM STUDI MATEMATIKA
JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
v
HALAMAN PERSEMBAHAN:
Kupersembahkan skripsi ini kepada:
Tuhan Yesus dan Bunda Maria yang telah memberkati saya sehingga dapat menyelesaikan skripsi ini
Ibu dan ayah yang selalu memberikan doa dan dukungan sehingga skripsi ini dapat selesai
Ibu Lusi yang selalu membimbing dan membantu saya dengan penuh kesabaran
Sahabat-sahabat dan semua orang yang selalu mendukung dan menyayangi saya
vii
ABSTRAK
viii
ABSTRACT
ix
KATA PENGANTAR
Puji syukur kepada Tuhan Yang Maha Esa atas rahmat yang telah dilimpahkan sehingga skripsi ini dapat terselesaikan.
Skripsi ini penulis ajukan kepada yang terhormat panitia penguji Skripsi untuk melengkapi syarat untuk menempuh gelar sarjana pada Prodi Matematika Universitas Sanata Dharma Yogyakarta.
Dalam penyusunannya penulis membutuhkan bantuan dari berbagai pihak. Oleh karena itu, pada kesempatan ini dengan segala kerendahan hati penulis ingin menyampaikan ucapan terima kasih kepada:
1. Bapak dan Ibu Agus Yulianto atas segala doa dan motivasi yang diberikan. 2. Ibu Lusia Krismiati Budiasih, M.Si, selaku dosen pembimbing yang dengan penuh kesabaran telah membimbing dan membantu saya selama penyusunan skripsi ini.
3. Bapak Ir. Ig. Aris Dwiatmoko, M. Sc dan Ibu Ch. Enny Murwaningtyas, S. Si, M. Si selaku dosen penguji yang membantu perbaikan skripsi ini. 4. Bapak dan Ibu Dosen yang telah memberikan ilmu kepada penulis selama
penulis kuliah di Universitas Sanata Dharma ini.
5. Segenap karyawan sekretariat FST, lab. GM, dan Perpustakaan Paingan atas pelayanan yang telah diberikan kepada penulis.
6. Sahabat-sahabat dalam perjalanan kuliah: Arga, Ayu, Yosi, Agnes, Roy, Marsel, Leni, Pandu, Tika, Ratri, Sari, Astri, dan Dini.
7. Semua mahasiswa Prodi Matematika atas semua pelajaran yang begitu berharga.
8. Serta bantuan dari semua pihak yang tidak dapat disebutkan satu persatu.
x
berharap semoga skripsi ini dapat memberikan manfaat dan berguna bagi semua pihak.
Yogyakarta, 25 Juli 2014 Penulis,
xi
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
PERNYATAAN KEASLIAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN PUBLIKASI ... vi
ABSTRAK ... vii
ABSTRACT ... viii
KATA PENGANTAR ... ix-x DAFTAR ISI ... xi-xii BAB I PENDAHULUAN A. Latar Belakang Masalah... 1
B. Rumusan Masalah ... 3
C. Batasan Masalah ... 4
D. Tujuan Penulisan ... 5
E. Metode Penulisan ... 5
F. Manfaat Penulisan... 5
G. Sistematika Penulisan ... 5
xii
B. Nilai Harapan ... 15
C. Variansi ... 18
D. Fungsi Pembangkit Momen ... 19
E. Distribusi Poisson ... 21
F. Distribusi Gamma ... 23
G. Distribusi Eksponensial ... 32
H. Distribusi Erlang ... 34
I. Uji Sampel Tunggal Kolmogorov-Smirnov ... 41
BAB IIIMODEL-MODEL ANTRIAN A. Unsur-unsur Dasar Antrian ... 45
B. Peran Distribusi Poisson ... 53
C. Peran Distribusi Erlang ... 60
D. Model Antrian dengan Pelayan Tunggal ... 62
E. Model Antrian dengan Pelayan Ganda ... 88
F. Model Biaya ... 99
BAB IVMODELANTRIAN BEBERAPA FASE PADA RSUD GUNUNG JATI CIREBON ... 108
BAB VPENUTUP A. Kesimpulan ... 121
B. Saran ... 123
DAFTAR PUSTAKA ... 124
1
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Pada kehidupan sehari-hari sering ditemukan istilah antrian. Antrian merupakan proses saling menunggu giliran untuk menerima pelayanan. Contoh antrian adalah antrian dalam pengambilan kartu ujian untuk para mahasiswa, antrian pembayaran uang kuliah, antrian pengambilan karcis parkir, dll. Dalam antrian, yang mengantri tidak hanya orang tetapi juga bisa berupa barang. Misalnya: antrian bahan mentah yang akan diproses dan dijadikan bahan produksi, antrian komoditi ekspor di pelabuhan, antrian mobil yang akan diperbaiki dalam sebuah bengkel, dll. Berikut adalah contoh nyata sebuah antrian orang (gambar kiri) dan antrian barang (gambar kanan).
2
pelanggan tiba di satu sarana pelayanan kemudian bergabung dalam sebuah antrian. Pelayan memilih pelanggan dari antrian untuk memulai pelayanan. Setelah selesainya pelayanan, pelayanan akan memilih pelanggan yang baru dan diulangi kembali proses tersebut dari awal.
Antrian dapat terjadi karena kebutuhan akan pelayanan melebihi kapasitas yang disediakan. Kedatangan pelanggan tidak diketahui sebelumnya. Jika diketahui maka pengoperasian sarana tersebut dapat dijadwalkan sehingga keharusan untuk menunggu tidak ada atau dengan kata lain tidak ada antrian. Rata-rata lamanya waktu menunggu dalam sebuah antrian sangat tergantung pada rata-rata tingkat kecepatan pelayanan.
Antrian yang terlalu lama dan sangat panjang tentu akan sangat merugikan bagi pelanggan maupun pelayan dalam antrian tersebut. Apabila jumlah pelayan ditambah tentu akan menambah biaya yang lebih besar dari sebelumnya. Tetapi, apabila jumlah pelayan tidak ditambah maka antrian dapat terjadi dalam waktu yang lama yang akhirnya dapat menyebabkan pelayananan menjadi tertunda dan tidak optimal. Dampak yang lebih buruk dari antrian yang terlalu panjang dan lama adalah hilangnya pelanggan.
3
itu, kedatangan pelanggan dapat dipelajari karakteristiknya. Karakteristik-karakteristik dalam sebuah antrian dapat terwakilkan dengan adanya distribusi. Pada tulisan ini, distribusi kedatangan dapat diwakilkan dengan distribusi Poisson.
Selain itu, waktu pelayanan dalam sebuah antrian juga dapat dipelajari karakteristiknya. Waktu pelayanan juga dapat terwakilkan dengan suatu distribusi seperti waktu antar kedatangan. Distribusi Erlang akan dipergunakan dalam tulisan ini untuk menyatakan waktu pelayanannya. Dengan demikian, distribusi Poisson dan distribusi Erlang dapat dipergunakan untuk menganilisa sebuah antrian.
Dalam tulisan ini akan dipelajari karakteristik kinerja sebuah sistem antrian. Ukuran kinerja sistem dalam sebuah sistem meliputi rata-rata jumlah pelanggan dalam sistem, rata-rata-rata-rata jumlah pelanggan menunggu dalam antrian, rata-rata waktu yang dihabiskan seorang pelanggan dalam sistem, dan rata-rata yang dihabiskan pelanggan seorang pelanggan menunggu dalam antrian.
Ukuran kinerja dalam sistem dapat dipergunakan untuk menghitung biaya optimal pada sebuah antrian. Biaya optimal berkaitan dengan laju pelayanan optimum. Secara umum model biaya berusaha menyeimbangkan biaya menunggu dan biaya kenaikan tingkat pelayanan.
B. RUMUSAN MASALAH
4
2. Bagaimana distribusi Poisson dapat dipergunakan dalam sebuah antrian?
3. Bagaimana distribusi Erlang dapat dipergunakan dalam sebuah antrian?
4. Bagaimana ukuran kinerja sistem pada model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang?
5. Bagaimana mengoptimumkan biaya pada model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang?
C. BATASAN MASALAH
1. Model antrian yang dibahas adalah model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang.
2. Model antrian yang dibahas adalah: a. ( ⁄ ⁄ ) ( ⁄ ) b. ( ⁄ ⁄ ) ( ⁄ )
3. Waktu pelayanan pada masing-masing tahap adalah sama dan berdistribusi eksponensial.
5
D. TUJUAN PENULISAN
Penulisan ini bertujuan untuk membahas dasar-dasar sebuah antrian, peran distribusi Poisson dan Erlang dalam sebuah antrian serta mencari ukuran-ukuran kinerja sistem pada model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang.
E. METODE PENULISAN
Metode penulisan yang dipergunakan adalah metode studi pustaka, sehingga di dalam skripsi ini tidak ditemukan hal-hal yang baru. Jenis-jenis sumber pustaka yang digunakan penulis tercantum dalam daftar pustaka.
F. MANFAAT PENULISAN
Manfaat yang diharapkan dari penulisan ini adalah memberikan wawasan pengetahuan tentang model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang.
G. SISTEMATIKA PENULISAN
BAB I PENDAHULUAN
6 C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Manfaat Penulisan G. Sistematika Penulisan
BAB II DISTRIBUSI PEUBAH ACAK DAN UJI SAMPEL TUNGGAL KOLMOGOROV-SMIRNOV
A. Peubah Acak B. Nilai Harapan C. Variansi
D. Fungsi Pembangkit Momen E. Distribusi Poisson
F. Distribusi Gamma G. Distribusi Eksponensial H. Distribusi Erlang
I. Uji Sampel Tunggal Kolmogorov-Smirnov
BAB III MODEL-MODEL ANTRIAN A. Unsur-unsur Dasar Antrian B. Peran Distribusi Poisson C. Peran Distribusi Erlang
7
E. Model Antrian dengan Pelayan Ganda F. Model Biaya
BAB IV MODELANTRIAN BEBERAPA FASE PADA RSUD GUNUNG JATI CIREBON
Contoh kasus penerapan model antrian dengan waktu antar kedatangan berdistribusi Poisson dan waktu pelayanan berdistribusi Erlang.
8
BAB II
DISTRIBUSI PEUBAH ACAK DAN UJI SAMPEL TUNGGAL
KOLMOGOROV-SMIRNOV
A. PEUBAH ACAK (VARIABEL RANDOM)
Definisi 2.1 Percobaan
Percobaan adalah suatu proses di mana pengamatan sengaja dibuat untuk memperoleh hasil.
Definisi 2.2 Ruang Sampel
Ruang sampel adalah himpunan semua kemungkinan hasil suatu percobaan. Ruang sampel biasanya dilambangkan dengan huruf S.
Contoh 2.1:
Ruang sampel S bagi percobaan pelemparan sekeping uang logam sebanyak 2 kali dapat ditulis sebagai: S = {AA, AG, GA, GG}, dengan G dan A masing-masing menyatakan “sisi gambar” dan “sisi angka”.
Definisi 2.3 Probabilitas
9
Definisi 2.4 Peubah Acak
Peubah acak adalah fungsi yang nilainya berupa bilangan real yang ditentukan oleh setiap unsur dalam ruang sampel.
Peubah acak dituliskan menggunakan huruf kapital dan nilainya dinotasikan dengan suatu huruf kecil. Misalkan menyatakan suatu peubah acak, nilai dari dinyatakan dengan .
Contoh 2.2:
Perhatikan Contoh 2.1, misalkan peubah acak menyatakan banyaknya sisi angka yang muncul, maka peubah acak dapat dituliskan sebagai berikut:
banyaknya sisi angka yang muncul pada pelemparan sekeping uang logam sebanyak 2 kali.
Maka nilai numerik 0, 1, atau 2 dapat diberikan pada setiap titik sampel. Bilangan-bilangan 0, 1, atau 2 merupakan besaran acak yang nilainya ditentukan oleh hasil percobaan.
Definisi 2.5 Peubah Acak Diskrit
Sebuah peubah acak dikatakan dsikrit jika himpunan nilainya adalah berhingga atau tak berhingga terbilang.
10
Contoh 2.3:
Misalkan dalam pelemparan sekeping uang logam sebanyak 2 kali dan merupakan banyaknya sisi angka yang muncul, maka semua kemungkinan nilai dan peluangnya dapat dicantumkan pada tabel berikut ini:
Tabel 2.1 Peubah acak diskrit beserta semua kemungkinan nilai dan peluang
0 1 2
( )
Definisi 2.6 Fungsi Probabilitas Diskrit
Fungsi ( ) adalah suatu fungsi probabilitas suatu peubah acak diskrit untuk setiap hasil yang mungkin jika:
1. ( ) 2. ∑ ( ) 3. ( ) ( )
Definisi 2.7 Peubah Acak Kontinu
Jika nilai peubah acak adalah sebuah interval atau kumpulan dari interval-interval, maka disebut peubah acak kontinu.
11
percobaan, biasanya dituliskan menggunakan notasi seperti: atau atau atau atau atau .
Probabilitasnya dinyatakan dengan ( ) ( ) ( ) ( ).
Contoh 2.4:
Sebuah peubah acak kontinu yang mengambil nilai antara dan mempunyai fungsi probabilitas ( ) .
Akan dicari ( ).
( ) ⁄ dan ( ) ⁄ , maka
( ) . ⁄ ⁄ /( )
Definisi 2.8 Fungsi Probabilitas Kontinu
Fungsi probalitas peubah acak kontinu, dikenal dengan nama fungsi densitas probabilitas (Probability Density Function / PDF ), untuk setiap hasil x yang mungkin jika:
1. ( )
2. ∫ ( )
3. ( ) ∫ ( )
12
Fungsi ( ) adalah fungsi probabilitas bersama peubah acak diskrit X
dan Y jika:
1. ( ) untuk setiap ( ) 2. ∑ ∑ ( )
3. ( ) ( )
Untuk setiap A di bidang xy, ,( ) - ∑ ∑ ( )
Contoh 2.5:
Dua buah kelereng diambil dari sebuah kantong yang berisi 3 kelereng biru, 2 kelereng merah, dan 3 kelereng hijau. Misalkan merupakan banyaknya kelereng yang berwarna hijau yang terambil dan merupakan banyaknya kelereng merah yang terambil. Nilai ( ) yang mungkin adalah (0,0), (0,1), (1,0), (1,1), (0,2), dan (2,0). Sebagai contoh ( ) memperlihatkan bahwa probabilitas kelereng merah dan hijau yang terambil. Banyaknya semua kemungkinan hasil dari pengambilan 2 kelereng adalah ( ) . Banyaknya kemungkinan hasil pengambilan 1 kelereng merah dari 2 kelereng merah dan 1 kelereng hijau dari 3 kelereng hijau ( )( ) . Maka ( )
. Perhitungan probabilitas
bersama yang lain dapat dituliskan dalam tabel berikut:
13
( ) total
baris
0 1 2
0
1
0
2
0 0
total kolom
1
Definisi 2.10 Fungsi Probabilitas Bersama Kontinu
Fungsi ( )adalah fungsi probabilitas bersama peubah acak kontinu dan jika:
(1.) ( ) , untuk setiap ( ) (2.) ∫ ∫ ( )
(3.) ,( ) - ∫ ∫ ( )
Untuk setiap A di bidang xy.
Definisi 2.11 Fungsi Distribusi Kumulatif Peubah Acak Diskrit
Fungsi distribusi kumulatif dari ditulis dengan ( ).
14
Definisi 2.12 Fungsi Distribusi Kumulatif Peubah acak Kontinu
Fungsi distribusi kumulatif dari ditulis dengan ( ).
( )dari peubah acak kontinu dengan fungsi probabilitas kontinu ( )
adalah: ( ) ( ) ∫ ( ) , untuk .
Definisi 2.13 Fungsi Probabilitas Kontinu
Misalkan ( ) adalah fungsi distribusi untuk peubah acak kontinu , maka ( )dapatditentukan oleh:
( ) ( ) ( )
jika turunannya ada.
Definisi 2.14 Dua Peubah Acak yang Bebas
Peubah acak dan dikatakan saling bebas jika dan hanya jika ( ) ( ) ( )
untuk semua kemungkinan nilai-nilai dan , dengan ( ) merupakan fungsi probabilitas dari peubah acak dan ( ) merupakan fungsi probabilitas dari peubah acak dan ( ) merupakan fungsi probabilitas bersama dari peubah acak dan .
15
Perhatikan Contoh 2.5, maka dapat diperlihatkan bahwa peubah acak dan tidak saling bebas. Dari Tabel 2.2 terlihat bahwa ( )
Maka dapat disimpulkan peubah acak dan tidak saling bebas.
B. NILAI HARAPAN (MEAN / RATA-RATA)
Definisi 2.15 Nilai Harapan Peubah Acak Diskrit
Jika adalah suatu peubah acak, yakni * +, dengan fungsi probabilitas ( ), maka nilai harapan adalah:
( ) ∑
( )
Definisi 2.16 Nilai Harapan Peubah Acak Kontinu
16
( ) ∫ ( )
Teorema 2.1 Nilai Harapan dari Jumlahan Dua atau Lebih Peubah
Acak
Jika dan merupakan suatu peubah acak, maka nilai harapan dari jumlah peubah acak tersebut adalah:
( ) ( ) ( )
Bukti:
Menurut Definisi 2.15, maka diperoleh persamaan, yaitu:
)
Teorema 2.2 Nilai Harapan dari Selisih Dua atau Lebih Peubah Acak
Jika dan merupakan suatu peubah acak, maka nilai harapan dari selisih peubah acak tersebut adalah:
( ) ( ) ( )
17
Menurut Definisi 2.15, maka diperoleh persamaan, yaitu:
)
Teorema 2.3 Nilai Harapan dari Peubah Acak yang Saling Bebas
18
C. VARIANSI
Definisi 2.17 Variansi Peubah Acak Diskrit
Jika adalah suatu peubah acak, * + , dengan fungsi probabilitas ( ) dan nilai harapan , maka variansi adalah:
∑( ) ( )
Definisi 2.18 Variansi Peubah Acak Kontinu
Jika adalah suatu peubah acak dengan fungsi probabilitas ( ) dan nilai harapan , maka variansi adalah:
∫ ( ) ( )
19
Teorema 2.4 Variansi Peubah Acak
Jika adalah suatu peubah acak, maka variansi adalah: ( )
Bukti:
Untuk peubah acak diskrit:
Menurut Definisi 2.15, persamaan (2.1) menjadi:
2
Untuk peubah acak kontinu:
20
2 2
2 2
2
) (
) (
X E
dx x f x
D. FUNGSI PEMBANGKIT MOMEN
Definisi 2.19 Momen ke-
Momen ke- dari peubah acak adalah ( ) dan dinotasikan .
Definisi 2.20 Fungsi Pembangkit Momen
Fungsi pembangkit momen ( ) untuk peubah acak adalah ( ) ( ).
Definisi 2.21 Fungsi Pembangkit Momen Bersama
Fungsi pembangkit momen bersama dari * + jika ada adalah
( ) . ∑ /
Teorema 2.5 Fungsi Pembangkit Momen dari Jumlahan Peubah Acak
21 Bukti:
Karena adalah peubah acak yang saling bebas maka menurut Teorema 2.3 dan Definisi 2.20 menjadi:
E. DISTRIBUSI POISSON
Distribusi Poisson adalah salah satu distribusi peubah acak diskrit yang digunakan untuk menghitung jumlah kejadian khusus selama jangka waktu tertentu. Misalnya: jumlah dering telepon dalam kurun waktu 1 jam.
Definisi 2.22 Distribusi Poisson
Distribusi probabilitas bagi peubah acak Poisson , yang menyatakan banyaknya hasil percobaan yang terjadi selama suatu selang waktu atau daerah tertentu didefinisikan sebagai berikut:
( ) ( ) untuk 1 2
dengan merupakan rata-rata banyaknya hasil percobaan yang terjadi selama selang waktu atau dalam daerah yang dinyatakan.
Teorema 2.6 Nilai Harapan Distribusi Poisson
22
( )
Bukti:
Misalkan . Dari Definisi 2.15 dan Definisi 2.22, maka diperoleh persamaan, yaitu:
Teorema 2.7 Variansi Distribusi Poisson
Variansi dari peubah acak diskrit ( ) adalah: ( )
Bukti:
Dari Definisi 2.15 dan Definisi 2.22, maka diperoleh persamaan, yaitu:
23 persamaan (2.3) menjadi:
F. DISTRIBUSI GAMMA
Distribusi Gamma mendapat namanya dari fungsi Gamma yang sudah dikenal luas, dan dipelajari dalam banyak bidang matematika. Distribusi Gamma merupakan salah satu distribusi kontinu yang juga merupakan suatu keluarga distribusi. Beberapa distribusi merupakan distribusi khusus dari distribusi Gamma, seperti distribusi Eksponensial dan distribusi Erlang.
Definisi 2.23 Fungsi Gamma
Fungsi Gamma didefinisikan sebagai berikut:
24
Definisi 2.24 Fungsi Probabilitas Kontinu Distribusi Gamma
Fungsi densitas probabilitas dari distribusi Gamma, yaitu:
( ) { ( ) ( )
dengan parameter dan .
Teorema 2.8 Sifat-sifat Distribusi Gamma
Di bawah ini terdapat beberapa sifat penting dari distribusi Gamma, yaitu: (1). ( ) ( ) ( ) untuk setiap bilangan bulat positif dengan
(2). ( )
(3). ( ) ( ) untuk setiap bilangan bulat positif
Bukti:
(1). Menggunakan Definisi 2.23 dengan teknik pengintegralan kalkulus
∫ ∫ di mana ,
( ) ( ) , , dan
25 (2.4) menurut Definisi 2.23 menjadi:
)
26
(3). Menurut persamaan (2.4) dan Definisi 2.23 diperoleh persamaan:
)
Berdasarkan Teorema 2.8(1), Teorema 2.8(2), dan persamaan (2.5) maka diperoleh persamaan baru, yaitu:
27
Dari Teorema 2.8(3) diperoleh bahwa ( ) ( ) , maka Definisi 2.24 dapat dituliskan ulang menjadi:
Definisi 2.25 Fungsi Probabilitas Kontinu Distribusi Gamma
Fungsi densitas probabilitas dari distribusi Gamma, yaitu:
( ) {( )
dengan parameter dan .
Teorema 2.9 Nilai Harapan Distribusi Gamma
Nilai harapan dari peubah acak kontinu ( ) adalah
( )
Bukti:
Menurut Definisi 2.16, maka diperoleh persamaan, yaitu:
( ) ∫ ( )
(2.6)
Misalkan maka maka persamaan (2.6) menjadi:
du e u k
u X
E k u
k
1
0
) ( )! 1 ( ) ( ) (
(2.7)
28
Menurut Teorema 2.8(3), maka persamaan (2.8) menjadi:
Teorema 2.10 Momen ke-n distribusi Gamma
Momen ke-n dari peubah acak kontinu ( ) adalah
( ) ( ) ( )
Bukti:
Menurut Definisi 2.16 dan Definisi 2.19 diperoleh persamaan, yaitu:
29
Menurut Definisi 2.23, maka persamaan (2.10) menjadi:
)
Teorema 2.11 Fungsi Pembangkit Momen Distribusi Gamma
Fungsi pembangkit momen dari peubah acak kontinu ( ) adalah
( )
. /
Bukti:
Berdasarkan Definisi 2.16 dan Definisi 2.20, maka diperoleh persamaan:
30
31
Teorema 2.12 Variansi Distribusi Gamma
Variansi dari peubah acak kontinu ( ) adalah
Bukti:
Menggunakan Teorema 2.10 diperoleh persamaan:
32
Menurut Teorema 2.8(1) dan Teorema 2.8(3), maka persamaan (2.14) menjadi:
2
Dari Teorema 2.4 persamaan (2.15) menjadi:
2
G. DISTRIBUSI EKSPONENSIAL
33
antar rusaknya suatu mesin, selang waktu antar kedatangan pelanggan ke suatu bank, dan sebagainya.
Definisi 2.26 Fungsi Probabilitas Kontinu Distribusi Eksponensial
Distribusi Eksponensial mempunyai fungsi densitas probabilitas sebagai berikut:
( ) {
dengan parameter adalah sebuah bilangan real, konstanta positif.
Teorema 2.13 Nilai Harapan Distribusi Eksponensial
Nilai harapan dari peubah acak kontinu ( ) adalah
( )
Bukti:
Dari Definisi 2.25 dan 2.26 diperoleh bahwa . Dari Teorema 2.9 juga diperoleh bahwa: ( ) , sehingga nilai harapan dari peubah acak kontinu ( ) adalah:
1 ) (
k
X E
34
Fungsi pembangkit momen dari peubah acak kontinu ( ) adalah
( )
. /
Bukti:
Dari Definisi 2.25 dan 2.26 diperoleh bahwa . Dari Teorema 2.11 juga diperoleh bahwa: ( )
. / , sehingga fungsi pembangkit
momen dari peubah acak kontinu ( ) adalah:
) 1 (
1 ) 1 (
1 )
(
t t t
m
k
H. DISTRIBUSI ERLANG
35
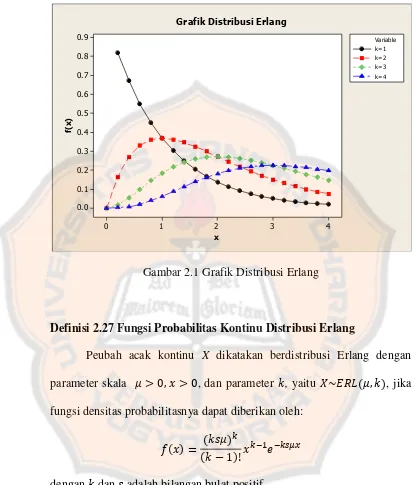
Gambar 2.1 Grafik Distribusi Erlang
Definisi 2.27 Fungsi Probabilitas Kontinu Distribusi Erlang
Peubah acak kontinu X dikatakan berdistribusi Erlang dengan parameter skala , dan parameter , yaitu ( ), jika fungsi densitas probabilitasnya dapat diberikan oleh:
( ) ( ) ( )
dengan dan adalah bilangan bulat positif.
Teorema 2.15 Nilai Harapan Distribusi Erlang
Nilai harapan dari peubah acak kontinu ( ) adalah
( )
4 3
2 1
0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0
x
f(
x
)
k =1 k =2 k =3 k =4 Variable
36 Bukti:
Dari Definisi 2.25 dan 2.27 diperoleh bahwa . Dari Teorema 2.9 juga diperoleh bahwa:
( )
Sehingga nilai harapan dari peubah acak kontinu ( ) adalah:
s
ks k X
E( ) 1
Teorema 2.16 Momen ke-n distribusi Erlang
Momen ke-n dari peubah acak kontinu ( ) adalah
( ) ( ) ( ) ( )
Bukti:
Dari Definisi 2.25 dan 2.27 diperoleh bahwa . Dari Teorema 2.10 juga diperoleh bahwa:
( ) ( ) ( )
Sehingga momen ke-n dari peubah acak kontinu ( ) adalah:
) ( )! 1 ( ) (
1 )
( k n
k ks X
E n n
37
Teorema 2.17 Momen ke-2 distribusi Erlang
Momen ke-2 dari peubah acak kontinu ( ) adalah
( )
Bukti:
Dari Teorema 2.16 jika n = 2, maka persamaannya menjadi:
Teorema 2.18 Fungsi Pembangkit Momen Distribusi Erlang
Fungsi pembangkit momen dari peubah acak kontinu ( ) adalah
( )
38 Bukti:
Dari Definisi 2.25 dan 2.27 diperoleh bahwa . Dari Teorema 2.11 juga diperoleh bahwa: ( )
. / , sehingga fungsi pembangkit
momen dari peubah acak kontinu ( ) adalah:
k X
ks t t
m
1
1 )
(
Teorema 2.19 Variansi Distribusi Erlang
Variansi dari peubah acak kontinu ( ) adalah
( )
Bukti:
Dari Definisi 2.25 dan 2.27 diperoleh bahwa . Dari Teorema 2.12 juga diperoleh bahwa:
Sehingga variansi dari peubah acak kontinu ( ) adalah:
2 2
ks k
39
Teorema 2.20
Jika terdapat peubah acak dan mempunyai distribusi eksponensial dengan nilai harapan , maka mengikuti
distribusi Erlang dengan parameter .
Bukti:
Diberikan dan maka akan dibuktikan berdistribusi Erlang. Misalkan peubah acak yang berdistribusi eksponensial dengan nilai harapan yang sama, yakni:
) ( ... ) ( )
(X1 E X2 E Xk
E
atau
1 1 ... 1 1
2 1
k
(2.16)
Karena berdistribusi eksponensial dengan nilai harapan yang sama, maka menurut Teorema 2.14 fungsi pembangkit momennya adalah
( )
. /
40 pembangkit momen distribusi Gamma pada Teorema 2.11.
Dari Definisi 2.25 dan 2.27 diperoleh bahwa , maka persamaan (2.17) menjadi:
k pembangkit momen distribusi Erlang pada Teorema 2.18.
41
I. Uji Sampel Tunggal Kolmogorov-Smirnov
Uji sampel Kolmogorov-Smirnov adalah suatu uji goodness of fit
(keserasian). Artinya, yang diperhatikan adalah tingkat kesesuian antara distribusi dari serangkaian sampel (skor yang diobservasi) dengan suatu distribusi teoritis tertentu. Uji ini diperkenalkan pada tahun 1933 oleh matematikawan Rusia A. N. Kolmogorov. Uji ini menetapkan apakah secara logis nilai-nilai sampel dapat dianggap berasal dari suatu populasi dengan distribusi teoritis tertentu.
Dalam uji ini, pengujian dilakukan pada dua buah fungsi distribusi kumulatif, yaitu fungsi distribusi kumulatif yang dihipotesiskan dan fungsi distribusi kumulatif yang diamati. Misalkan dengan mengambil sebuah sampel acak dari suatu fungsi distribusi ( ) yang belum diketahui. Akan dipastikan apakah dapat disimpulkan bahwa ( ) ( ) untuk semua , dengan ( ) adalah fungsi distribusi kumulatif yang dihipotesiskan.
Dimisalkan juga ( )adalah fungsi sebaran kumulatif dari suatu sampel acak yang diamati dengan N pengamatan. Dengan adalah
sembarang nilai yang mungkin,
N k XSN , k adalah jumlah pengamatan
42
deviasi maksimum, dinyatakan dengan D = maksimum F0
X SN
X .Perlu diperhatikan bahwa signifikasi suatu nilai D tertentu
D adalahbergantung pada jumlah pengamatan (N). Untuk maka ditolak dan diterima sedangkan jika maka diterima dan ditolak.
Langkah-langkah penghitungan uji sampel tunggal Kolmogorov-Smirnov adalah:
1. Tentukan hipotesis terlebih dahulu.
Dapat disesuaikan dengan kasus yang diamati, yaitu sebagai berikut: ( ) ( )
( ) ( )
2. Tetapkan tingkat signifikasi yang digunakan.
3. Hitung ( ) dan ( ) dari nilai-nilai data yang diamati. 4. Hitung | ( ) ( )| dari setiap nilai yang diamati. 5. Carilah
6. Carilah
7. Jika maka ditolak dan diterima sedangkan maka diterima dan ditolak.
Untuk memudahkan penghitungan, uji sampel Kolmogorov-Smirnov dapat dilakukan dengan SPSS. Contohnya dapat dilihat dalam Contoh 2.8 berikut ini:
43
Di bawah terdapat data suatu sampel acak. Apakah datanya berdistribusi Poisson?
Tabel 2.3 Data Suatu Sampel Acak
Data
1 4 1 1 3 5 2
2 2 2 2 2 3
Uji hipotesis:
1. H0 : data berdistribusi Poissson
H1 :data tidak berdistribusi Poisson
2. Tingkat signifikasi ( ) 3. Daerah penolakan :
Asymp. Sig. (2-tailed)< maka H0 ditolak
Asymp.Sig. (2-tailed)> maka H1 ditolak
Tabel 2.4 Hasil SPSS
One-Sample Kolmogorov-Smirnov Test
Data
N 13
Poisson Parametera,,b Mean 2.3077 Most Extreme
Differences
Absolute .099
44
Negative -.099
Kolmogorov-Smirnov Z .359
Asymp. Sig. (2-tailed) 1.000
a. Test distribution is Poisson. b. Calculated from data.
4. Dari hasil uji One-Sample Kolmogorov-Smirnov Test di atas tampak bahwa nilai Asymp. Sig. (2-tailed) adalah 1.
Asymp. Sig. (2-tailed) = 1 = 0,05
Jadi, Asymp. Sig. (2-tailed)> . Dengan demikian berarti H0 diterima dan
45
BAB III
MODEL-MODEL ANTRIAN
A. UNSUR-UNSUR DASAR MODEL ANTRIAN
Antrian merupakan proses saling menunggu giliran untuk menerima pelayanan. Dalam proses antrian biasanya pelanggan tiba di satu sarana pelayanan kemudian bergabung dalam sebuah antrian. Pelayan memilih pelanggan dari antrian untuk memulai pelayanan. Setelah selesainya pelayanan, pelayan akan memilih pelanggan yang baru dan diulangi kembali proses tersebut dari awal.
Dalam antrian terdapat beberapa unsur-unsur dasar, diantaranya sebagai berikut:
1. Distribusi Kedatangan
Pada sistem antrian, distribusi kedatangan merupakan faktor penting yang berpengaruh besar terhadap kelancaran pelayanan. Dalam distribusi kedatangan memuat waktu antar kedatangan yang berarti waktu antara kedatangan dua pelanggan yang berurutan.
Waktu antar kedatangan diringkas dalam bentuk distribusi probabilitas, yang umumnya disebut distribusi kedatangan. Kedatangan pelanggan untuk masuk dalam sistem antrian terbagi menjadi dua, yaitu:
46
Kedatangan secara individu merupakan situasi di mana pelanggan datang secara individu (sendiri). Contoh dari situasi ini adalah seorang nasabah bank yang datang ke bank untuk melakukan transaksi.
b. Kedatangan secara berkelompok
Kedatangan secara berkelompok merupakan situasi di mana para pelanggan datang secara berkelompok. Contoh dari situasi ini adalah sekelompok orang yang datang bersama-sama ke sebuah restoran.
Distribusi kedatangan biasanya dinyatakan pada suatu distribusi probabilitas tertentu yang sudah banyak dikenal, seperti distribusi Poisson, distribusi Eksponensial ataupun distribusi Erlang.
2. Distribusi waktu pelayanan
Distribusi waktu pelayanan berkaitan dengan waktu yang dibutuhkan pelayan untuk melayani pelanggan dari awal mula datang sampai pelayanan selesai dilakukan. Pelayanan kepada pelanggan terbagi menjadi dua cara, yaitu:
a. Pelayanan secara individual
47
yang dilakukan oleh seorang tukang cukur kepada seorang pelanggannya.
b. Pelayanan secara kelompok
Pelayanan secara kelompok adalah pelayanan di mana pelayan melayani pelanggan secara berkelompok. Contoh dari pelayanan ini adalah pelayanan kepada beberapa pelanggan restoran yang datang secara bersamaan dan berada dalam satu meja yang sama.
Dalam distribusi pelayanan diperlukan pola pelayanan yang dikenal dengan waktu pelayanan. Waktu pelayanan merupakan waktu yang dibutuhkan seorang pelayan untuk melayani satu pelanggan. Waktu pelayanan ini dapat bersifat deterministik, atau berupa variabel acak yang distribusi probabilitasnya dianggap telah diketahui seperti distribusi Poisson, distribusi Eksponensial ataupun distribusi Erlang.
3. Rancangan sarana pelayanan
48
pelayanan yang tersusun secara seri, di mana para pelanggan harus melaluinya sebelum pelayanan dinyatakan lengkap.
Ada empat model struktur antrian dasar yang umum terjadi dalam seluruh sistem antrian, yaitu:
a. Satu barisan dan satu fase pelayanan
Satu barisan berarti hanya ada satu jalur untuk memasuki sistem pelayanan. Sedangkan satu fase pelayanan menunjukkan bahwa hanya ada satu pelayanan. Setelah menerima pelayanan, pelanggan keluar dari sistem. Contoh untuk model ini adalah seorang pelanggan tukang cukur yang mengantri di seorang tukang cukur, seorang yang mengantri di sebuah bilik ATM, dll.
Gambar 3.1 Model antrian dengan satu barisan dan satu fase pelayanan Keterangan: S = pelayan (server)
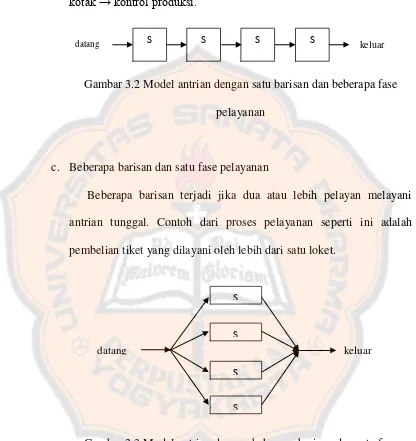
b. Satu barisan dan beberapa fase pelayanan
Beberapa fase pelayanan menunjukkan ada dua atau lebih pelayanan yang dilaksanakan secara berurutan. Contoh untuk model ini adalah proses pengisian teh botol dalam pabrik yang harus melalui beberapa tahap, yaitu pengisian botol → penyegelan → pencetakan
Datang Keluar
49
kode produksi dan tanggal kadaluarsa → penempatan botol dalam
kotak → kontrol produksi.
Gambar 3.2 Model antrian dengan satu barisan dan beberapa fase pelayanan
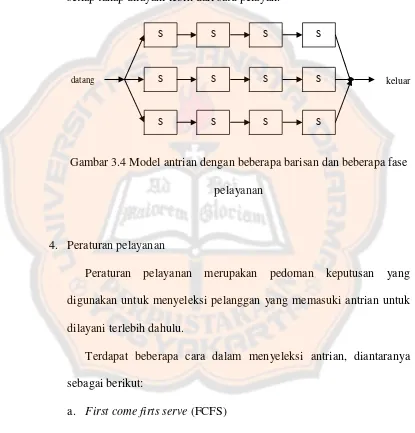
c. Beberapa barisan dan satu fase pelayanan
Beberapa barisan terjadi jika dua atau lebih pelayan melayani antrian tunggal. Contoh dari proses pelayanan seperti ini adalah pembelian tiket yang dilayani oleh lebih dari satu loket.
Gambar 3.3 Model antrian dengan beberapa barisan dan satu fase pelayanan
d. Beberapa barisan dan beberapa fase pelayanan
Bebrapa barisan dan beberapa fase pelayanan berarti setiap sistem mempunyai beberapa pelayan pada setiap tahap, sehingga lebih dari
keluar datang
S
S S S
S S S S
keluar
50
satu pelanggan dapat dilayani pada suatu waktu. Contoh dari proses pelayanan seperti ini adalah pelayanan kepada pasien di rumah sakit dari pendaftaran, diagnosa, penyembuhan sampai pembayaran dimana setiap tahap dilayani lebih dari satu pelayan.
Gambar 3.4 Model antrian dengan beberapa barisan dan beberapa fase pelayanan
4. Peraturan pelayanan
Peraturan pelayanan merupakan pedoman keputusan yang digunakan untuk menyeleksi pelanggan yang memasuki antrian untuk dilayani terlebih dahulu.
Terdapat beberapa cara dalam menyeleksi antrian, diantaranya sebagai berikut:
a. First come firts serve (FCFS)
First come firts serve merupakan salah satu peraturan pelayanan yang berarti pelanggan yang datang pertama dilayani pertama, misalnya seseorang yang mengantri untuk membeli karcis di loket gedung bioskop.
S S S S
datang S S S S keluar
51 b. Last come first serve (LCFS)
Last come first serve adalah peraturan pelayanan yang mempunyai arti pelanggan yang datang terakhir akan dilayani pertama. Contoh dari peraturan pelayanan ini adalah bongkar pasang barang di dalam truk dimana barang yang dikeluarkan dari truk terlebih dahulu adalah barang yang dimasukkan ke dalam truk terakhir.
c. Service in random order (SIRO)
Service in random order adalah peraturan pelayanan yang mempunyai arti bahwa pelayanannya dilakukan secara acak, misalnya pengambilan kertas undian. Dalam pengambilan kertas undian, pelayan bebas memilih secara acak.
d. Priority
Priority merupakan peraturan pelayanan yang berarti
pelayanannya didasarkan pada prioritas tertentu, misalnya pelayanan kepada pasien yang kondisinya kritis.
5. Ukuran antrian
Ukuran antrian adalah panjang antrian yang dapat dilayani. Ada dua macam ukuran antrian, yaitu:
a. Antrian terbatas
52
memenuhi kapsitas (ukuran), pelanggan yang baru tiba tidak dapat masuk ke dalam antrian. Misalnya, antrian mobil yang akan dicuci ditempat pencucian hanya terbatas. Hal ini dikarenakan ruang untuk mobil di tempat pencucian mobil tersebut terbatas.
b. Antrian tidak terbatas
Pelanggan yang diijinkan memasuki antrian tidak terbatas jumlahnya. Misalnya: pelanggan yang datang di tempat pengisian bensin jumlahnya tidak dibatasi berapapun boleh mengantri untuk membeli.
6. Sumber pemanggilan
Sumber pemanggilan berkaitan dengan sifat sumber yang meminta pelayanan. Sumber pemanggilan terdiri dari dua faktor, yaitu:
a. Terbatas
Dalam sumber pemanggilan terbatas memiliki arti bahwa pelanggan yang akan memperoleh pelayanan sifat sumbernya terbatas. Misalnya, pada sistem antrian pembayaran sks hanya terbatas untuk mahasiswa.
b. Tidak terbatas
53 7. Perilaku manusia
Model-model antrian yang mewakili situasi di mana manusia mengambil peran sebagai pelanggan atau pelayan harus dirancang untuk memperhitungkan pengaruh dari perilaku yang dilakukan manusia. Pelayan yang berupa manusia dapat mempercepat layu pelayanan ketuka jalur antrian memanjang. Sedangkan pelanggan yang berupa manusia juga dapat berpindah dari satu jalur antrian ke jalur lainnya dengan harapan dapat mengurangi waktu menunggu. Masih terdapat ciri-ciri perilaku manusia lainnya dalam situasi antrian sehari-hari.
Dalam situasi antrian biasanya terdapat dua asumsi yang sering dipergunakan, yaitu:
a. Pelanggan antri secara berurutan
b. Kecepatan pelayanan yang dilakukan pelayan dianggap sama untuk setiap pelanggan
B. PERAN DISTRIBUSI POISSON
54
pelanggan dapat dipelajari karakteristiknya. Karakteristik-karakteristik kedatangan pelanggan dalam sebuah antrian adalah sebagai berikut:
a. Dalam sebuah antrian, banyaknya kedatangan yang tiba pada interval tertentu tidak mempengaruhi banyaknya kedatangan pada interval yang lainnya.
Misalnya banyaknya kedatangan yang tiba antara pukul 18.00-18.10 tidak mempengaruhi banyaknya kedatangan yang tiba antara 18.15-18.25.
b. Probabilitas ada satu kedatangan yang tiba selama waktu lebih kecil dibanding probabilitas ada satu kedatangan yang tiba selama waktu .
Misalnya probabilitas ada satu kedatangan selama 30 menit kurang dari probabilitas ada satu kedatangan yang tiba selama 45 menit. c. Dalam sebuah antrian, kedatangan dalam selang waktu yang singkat
terkadang ada terkadang tidak ada kedatangan. Oleh karena itu, kedatangan pelanggan lebih dari satu dalam selang waktu yang singkat dapat diabaikan.
Misalnya dalam selang waktu 1 menit terkadang ada kedatangan terkadang tidak ada kedatangan, jika ada hanya 1 orang saja maka kedatangan lebih dari satu pelanggan diabaikan.
55
karakteristik tersebut juga mirip dengan karakteristik-karakteristik yang dimiliki oleh distribusi Poisson. Karakteristik-karakteristik dari distribusi Poisson adalah sebagai berikut:
a. Banyaknya hasil percobaan yang terjadi dalam suatu selang waktu tertentu tidak bergantung pada banyaknya hasil percobaan yang terjadi pada selang waktu yang terpisah.
b. Probabilitas terjadinya satu hasil percobaan selama selang waktu yang sangat singkat sebanding dengan panjang selang waktu tersebut. c. Probabilitas bahwa lebih dari satu hasil percobaan dalam selang waktu
yang singkat dapat diabaikan.
Karena karakteristik-karakteristik dalam sebuah antrian dapat terwakilkan oleh distribusi Poisson maka model antrian dalam tulisan ini kedatangan dalam antrian mengikuti proses Poisson. Kedatangan mengikuti proses Poisson artinya banyaknya pelanggan yang datang untuk memperoleh pelayanan sampai pada waktu tertentu mengikuti distribusi Poisson.
56
kedatangan setelah kedatangan ke- . Panjang selang ini dinamakan waktu antar kedatangan.
Definisi 3.1 Proses Poisson
* ( ) + adalah suatu proses Poisson dengan laju jika memenuhi: 1. ( )
2. Untuk setiap , ( ) (s) adalah suatu peubah acak Poisson dengan rata-rata ( )
3. Banyaknya kedatangan dalam interval ( - saling bebas dengan banyaknya kedatangan yang terjadi sampai waktu atau untuk dan , nilai ( ) ( ) saling bebas dengan nilai ( ) dimana
57
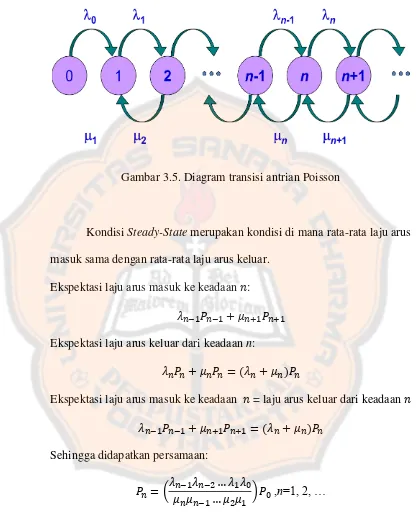
Gambar 3.5. Diagram transisi antrian Poisson
Kondisi Steady-State merupakan kondisi di mana rata-rata laju arus masuk sama dengan rata-rata laju arus keluar.
Ekspektasi laju arus masuk ke keadaan :
Ekspektasi laju arus keluar dari keadaan n:
( )
Ekspektasi laju arus masuk ke keadaan = laju arus keluar dari keadaan
( )
Sehingga didapatkan persamaan:
(
* n 1 2
58
Definisi 3.2
Probabilitas ada kedatangan selama waktu didefinisikan sebagai:
* + * ( ) + ( )
dengan merupakan rata-rata kedatangan.
Contoh 3.1:
Panggilan telepon mengikuti suatu proses Poisson dengan laju 20 / jam. Tentukan peluang bahwa 15 panggilan telepon terjadi pada satu jam pertama.
Penyelesaian:
Yang dimaksud adalah * ( ) +. Karena panggilan telepon mengikuti proses Poisson maka peluang tersebut berdasarkan Definisi 3.2 dapat dituliskan sebagai berikut:
* ( ) + ( )
Contoh 3.2:
59 Penyelesaian:
Yang diminta adalah * ( ) ( ) ( ) +.Karena banyaknya kedatangan pada proses Poisson memiliki sifat saling bebas, maka * ( ) ( ) + * ( ) +, sehingga:
* ( ) ( ) ( ) + * ( ) + * ( ) +
Mengingat ( ) berdistribusi Poisson dengan laju 20 / jam, maka: * ( ) ( ) ( ) +
( )
( )
Teorema 3.1 Waktu Antar Kedatangan
Waktu-waktu antar kedatangan dari suatu proses Poisson adalah saling bebas, semuanya berdistribusi eksponensial dengan parameter .
Bukti:
Misalkan kedatangan-kedatangan terjadi di waktu-waktu . Misalkan merupakan waktu antara dibukanya sistem hingga kedatangan pertama atau ditulis dengan , sehingga
menunjukkan waktu antara kedatangan ke- hingga
. Sehingga barisan * + dengan merupakan barisan dari waktu antar kedatangan. Akan ditunjukkan berdistribusi eksponensial.
60
* + * ( ) + dengan ( ) adalah banyaknya kedatangan sampai waktu , sehinggamenurut Definisi 3.2 :
* + * ( ) +
Maka fungsi distribusi kumulatif dari adalah:
0 untuk t 1
Karena menurut Definisi 2.11 fungsi probabilitas ( ) adalah turunan dari fungsi distribusi kumulatif ( ), maka fungsi probabilitas dari dapat diperoleh dengan cara berikut ini:
0 untuk t
)
Jadi, berdistribusi eksponensial dengan parameter sehingga dapat disimpulkan waktu antar kedatangan berdistribusi eksponensial.
C. PERAN DISTRIBUSI ERLANG
61
kedua datang, dan seterusnya. Rentang dari sampai pembeli pertama muncul dapat dikatakan sebagai waktu menunggu pembeli pertama. Lama menunggu sampai pembeli kedua datang dapat ditentukan dengan +( ). Secara rekursif dapat dicari waktu menunggu sampai pada pembeli ke- dengan cara berikut ini:
+( ) ( ) ( )
Jika merupakan waktu antar kedatangan pembeli dan pembeli ke- , maka waktu tunggu sampai pembeli ke- dapat dituliskan dengan cara berikut ini:
Definisi 3.3 Waktu Tunggu
Waktu tunggu sampai kedatangan ke- dengan laju kedatangan adalah
Karena dengan berdistribusi eksponensial dengan parameter maka menurut Teorema 2.20 berdistribusi Erlang.
Fungsi densitas probabilitas dari distribusi Erlang menurut Definisi 2.27 adalah:
( ) ( ) ( )
62
D. MODEL ANTRIAN DENGAN PELAYAN TUNGGAL
1. Notasi Kendall-Lee
Notasi yang sesuai untuk meringkaskan karakteristik dari antrian dibakukan dalam suatu notasi yaitu notasi Kendall-Lee. Notasi tersebut dibakukakn dalam format berikut ini:
( ⁄ ⁄ ) ( ⁄ ⁄ )
Keterangan:
a = distribusi kedatangan
b = distribusi waktu pelayanan
c = jumlah pelayan paralel ( )
d = peraturan pelayanan
e = jumlah maksimum yang diijinkan dalam sistem (dalam antrian + dalam pelayanan)
f = ukuran sumber pemanggilan
Notasi yang disimbolkan a dan b dapat diganti dengan kode berikut ini:
i. M Markov atau kedatangan berdistribusi Poisson
ii. bila waktu pelayanan berdistribusi Erlang dengan parameter iii. MMarkov atau waktu pelayanan berdistribusi eksponensial
63
akan terjadi proses antrian. Secara intuitif, semakin lama seorang pelanggan menunggu semakin kecil presentase waktu sarana tersebut tidak dipergunakan, dan sebaliknya. Tetapi, apabila jumlah pelayan ditambah untuk mengurangi waktu pelangga maka biaya untuk yang harus dikeluarkan untuk menggaji pelayan juga bertambah, dan sebaliknya. Karena hal tersebut perlu adanya beberapa karakteristik yang mengukur kinerja sistem. Kinerja menurut KBBI adalah kemampuan kerja. Pada tulisan ini yang dimaksudkan kinerja adalah ukuran kemampuan sistem. Di bawah ini merupakan ukuran-ukuran kinerja pada antrian, yaitu:
Ls = rata-rata banyaknya pelanggan dalam sistem Lq = rata-rata banyaknya pelanggan dalam antrian Ws = rata-rata waktu menunggu dalam sistem Wq = rata-rata waktu menungggu dalam antrian
2. Model antrian dengan waktu pelayanan berdistribusi eksponensial
64
maksimum yang diijinkan dalam sistem adalah tak hingga. Begitu pula dengan sumber yang menghasilkan para pelanggan yang datang memiliki kapasitas tak hingga.
Ukuran-ukuran dasar dari kinerja dengan model antrian ( ⁄ ⁄ ) adalah:
(3.1)
( )
(3.2)
( )
(3.3)
(3.4)
Penurunan mengenai ukuran-ukuran kinerja pada model antrian ( ⁄ ⁄ ) ( ⁄ ) dapat dilihat pada buku Operations Research
an Introduction (Hamdy A. Taha, 2007:573).
Contoh 3.3:
65
tidak dapat menangani lebih dari satu mobil setiap saat. Bagaimana analisis ukuran-ukuran kinerjanya?
Penyelesaian:
Mobil-mobil tiba sesuai distribusi Poisson dengan rata-rata 4 mobil / jam itu berarti laju kedatangannya (λ) adalah 4 mobil / jam. Karena waktu untuk membersihkan mobil konstan untuk semua mobil mengikuti distribusi eksponensial dengan rata-rata 10 menit / mobil maka:
laju pelayanannya() menit mobil
mobil jam
Model ini merupakan model antrian ( ⁄ ⁄ ) ( ⁄ ).
Permasalahan di sini adalah menentukan ukuran-ukuran kinerjanya. Ukuran-ukuran kinerja meliputi , , , dan .
a) Penentuan rata-rata banyaknya mobil dalam antrian ( ) menggunakan persamaan (3.1), yaitu:
. /
mobil / jam
Jadi, rata-rata banyaknya mobil dalam antrian ( ) adalah 1,33 mobil / jam atau dalam 3 jam terdapat 4 mobil yang mengantri.
66
( ) ( ) jam 20 menit
Jadi, rata-rata waktu menunggu dalam antrian ( ) adalah 20 menit.
c) Penentuan rata-rata waktu menunggu dalam sistem ( ) menggunakan persamaan (3.3), yaitu:
( ) ( ) jam 30 menit
Jadi, rata-rata waktu menunggu dalam sistem ( ) adalah 30 menit.
d) Penentuan rata-rata banyaknya mobil dalam sistem ( ) menggunakan persmaan (3.4), yaitu:
mobil
Jadi, rata-rata banyaknya mobil dalam sistem ( ) adalah 2 mobil / jam.
3. Model antrian dengan waktu pelayanan berdistribusi Erlang
67
pada model antrian berdistribusi eksponensial banyaknya fase hanya satu sedangkan pada model antrian berdistribusi Erlang banyaknya fase dalam model antrian jumlahnya dapat berhingga dan tak berhingga.Tetapi,model antrian berdistribusi Erlang tidak memberikan ekspresi analitis yang dapat ditelusuri untuk probabilitas . Sebaliknya, hasil-hasil dari model ini hanya memberikan ukuran-ukuran dasar dari kinerja.
Pada bagian ini akan diperlihatkan ukuran-ukuran dasar dari kinerja seperti Ls, Lq, Ws, dan Wq secara umum.
Sistem adalah pengamatan yang dilakukan selama waktu . Misalkan banyaknya pelanggan yang datang pada waktu adalah . Jumlah pelanggan keseluruhan yang datang selama waktu didefinisikan sebagai berikut ini:
∑
Sedangkan pelanggan keseluruhan yang selesai pelayanan dan pergi pada waktu adalah . Jumlah banyaknya pelanggan yang selesai pelayanan kemudian pergi selama waktu didefinisikan sebagai berikut ini:
∑
68
Kondisi antrian biasanya diasumsikan untuk setiap dan setelah waktu banyaknya pelanggan yang telah dilayani .
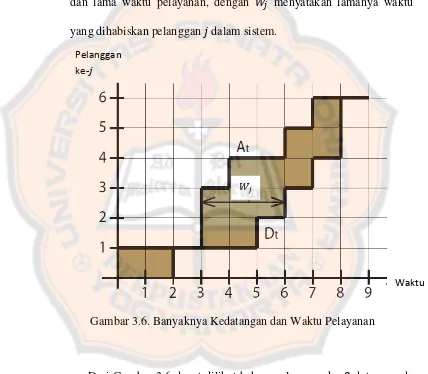
Gambar 3.6 berikut mengilustrasikan waktu kedatangan pelanggan dan lama waktu pelayanan, dengan menyatakan lamanya waktu yang dihabiskan pelanggan dalam sistem.
Gambar 3.6. Banyaknya Kedatangan dan Waktu Pelayanan
Dari Gambar 3.6 dapat dilihat bahwa pelanggan ke- datang pada dan selesai pelayanan pada sehingga lama waktu pelayanan .
Langkah pertama adalah menghitung bagian yang diarsir secara horizontal (waktu keseluruhan) dan vertikal (banyaknya pelanggan keseluruhan).
Pelanggan
69
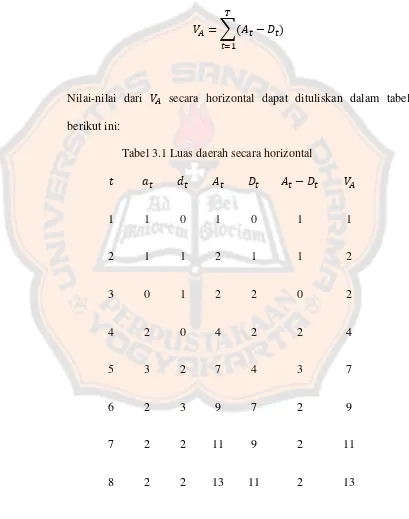
Secara horizontal nilai bagian yang diarsir ( )dapat didefinisikan sebagai berikut:
∑( )
Nilai-nilai dari secara horizontal dapat dituliskan dalam tabel berikut ini:
Tabel 3.1 Luas daerah secara horizontal
1 1 0 1 0 1 1
2 1 1 2 1 1 2
3 0 1 2 2 0 2
4 2 0 4 2 2 4
5 3 2 7 4 3 7
6 2 3 9 7 2 9
7 2 2 11 9 2 11
8 2 2 13 11 2 13
70
Rata-rata banyaknya pelanggan dalam sistem ( ) juga dapat didefinisikan sebagai berikut:
T L V
T V
T L L
s A
A T
t t
s
1(3.6)
Selanjutnya adalah menghitung secara vertikal. Jumlah banyaknya pelanggan adalah . Nilai bagian yang diarsir ( )dapat didefinisikan sebagai berikut:
∑
Nilai-nilai dari secara vertikal dapat dituliskan dalam tabel berikut ini:
Tabel 3.2 Luas daerah secara vertikal
71
2 2 4
3 3 7
4 3 10
5 2 12
6 1 13
Rata-rata lama menunggu dalam sistem ( ) adalah
C W V
C V
C W W
s A
A C
j j
s
1(3.7)
Rata-rata kedatangan didefinisikan sebagai banyaknya pelanggan selama waktu dan dituliskan sebagai berikut:
(3.8)
72 s s
s s
s s
s s
A A
W L
W T C L
T C W L
C W T L
V V
(3.9)
Misalkan merupakan lama waktu pelanggan untuk menunggu dalam antrian dan merupakan lama waktu menunggu dalam sistem, maka didapatkan sebuah persamaan:
(3.10)
dimana merupakan lama waktu pelayanan. , , dan merupakan peubah acak.
Jika merupakan rata-rata waktu menungggu dalam antrian maka dapat dituliskan menjadi:
( ) (3.11)
dan jika merupakan rata-rata waktu menunggu dalam sistem maka dapat dituliskan juga menjadi:
73
Dari persamaan persamaan (3.10), (3.11), (3.12), dan Teorema 2.1 dapat dituliskan sebuah persamaan, yaitu:
) (
) ( ) (
) (
) (
S E W W
S E T E
S T E T E
q s
q q s
(3.13)
Misalkan merupakan suatu peubah acak yang berdistribusi eksponensial atau Erlang, maka persamaan (3.13) akan menjadi:
s W
Ws q 1
(3.14)
Karena banyaknya tahap hanya satu ( ) maka persamaan (3.14) menjadi:
1 q
s W
W
(3.15)
Misalkan merupakan rata-rata banyaknya pelanggan yang menunggu dalam antrian dan merupakan rata-rata banyaknya pelanggan yang menunggu dalam sistem, maka didapatkan sebuah persamaan:
74
dimana merupakan rata-rata banyaknya pelanggan yang sedangg dilayani. , , dan merupakan peubah acak.
Rata-rata banyaknya pelanggan yang sedang dilayani ( )dapat didefiniskan sebaga berikut:
( ) (3.17)
Dari persamaan (3.9), persamaan (3.13), persamaan (3.16), dan persamaan (3.17) didapatkan sebuah persamaan baru, yaitu:
q
Little’s Formula.
Teorema 3.2 Rumus Pollaczek-Khintchine
75
( ) ( )
dengan λ merupakan rata-rata kedatangan pelanggan di sebuah sarana
pelayanan dan merupakan , dengan merupakan rata-rata waktu
pelayanan. Bukti:
Waktu pelayanan seorang pelanggan harus menunggu untuk dilayani dapat dituliskan dengan cara berikut ini:
Jika dituliskan dengan simbol maka persamaan di atas menjadi:
( ) ( ) (3.19)
dengan merupakan lama waktu pelayanan kepada pelanggan.
76
Dengan menggunakan persamaan (3.15) dan persamaan (3.20), maka diperoleh:
Probabilitas pelayan sibuk saat pelanggan datang sama dengan tingkat kesibukan pelayan. Oleh karena itu, jika dituliskan dengan simbol maka akan menjadi:
r(pelayan sibuk) (3.22)
Dengan menggunakan persamaan (3.9) maka didapatkan persamaan:
77
Bila persamaan (3.21) disubstitsikan ke persamaan (3.23), maka persamaannya menjadi:
) (S E
(3.24)
Dengan demikian tingkat kesibukan pelayan dapat ditentukan dengan persamaan (3.24).
Dari persamaan (3.9), persamaan (3.22) dan persamaan (3.24) maka persamaan (3.19) menjadi suatu persamaan baru, yaitu:
78
Gambar 3.7. Waktu Pelayanan
Misalkan merupakan waktu menunggu (dalam antrian) untuk pelanggan . merupakan banyaknya pelanggan dalam antrian dan merupakan sisa waktu pelayanan oleh pelanggan .
Gambar 3.7 akan membantu memahami konsep sisa waktu pelayanan. Gambar tersebut menunjukkan sisa waktu dalam antrian. ( ) merupakan sisa waktu pada saat . adalah waktu pelayanan dari pelanggan . Jika pada waktu di mana sistem sedang kosong maka didefinisikan ( ) sebagai banyaknya pelanggan yang telah dilayani dan keluar dari sistem pada waktu .
Rata-rata sisa waktu pada interval , - adalah rata-rata nilai pada sumbu dalam interval. Luas wilayah kurva dibagi dengan diberikan oleh:
) ( ) ( 2 1
2 1 1 ) ( 1
) (
1 2 )
(
1 2 0
t M
S
t t M
S t
dt t R t
t M
i i t
M
i i t
79
) ( lim ) ( lim 2 1 ) ( 1 lim
) (
1 2
0 M t
S
t t
t M t
dt t R t t
t M
i i
t
(3.26)
Selanjutnya diasumsikan bahwa sistem adalah periodik maka rata-rata waktu dapat digantikan dengan rata-rata dari limit yang bersangkutan dan definisinya adalah:
Rata-rata sisa waktu = ( ) ,
-Jika rata-rata waktu adalah rata-rata jarak yang ditetapkan, maka:
( ) ∫ ( ) (3.27)
Karena sistem adalah lossless (tidak ada pelanggan yang pergi) maka jika banyaknya pelanggan tidak selalu bertambah, banyaknya antrian cenderung sama dengan limitnya. Dapat dikatakan tingkat kepergian harus sama dengan rata-rata kedatangan sehingga dapat didefinisikan sebagai berikut:
( ) (3.28)
80
Dari persamaan (3.25), menggunakan persamaan (3.29) diperoleh:
)
Teorema 3.3 Ukuran-Ukuran Kinerja dengan Waktu Pelayanan
Berdistribusi Erlang dengan Pelayan Tunggal
Jika merupakan rata-rata laju kedatangan, merupakan rata-rata laju pelayanan, dan merupakan banyaknya fase maka ukuran-ukuran kinerja dengan waktu pelayanan distribusi Erlang adalah sebagai berikut:
1. Rata-rata waktu menungggu dalam antrian ( ) adalah: ( )
( )
81
( ) ( )
3. Rata-rata waktu menungggu dalam sistem ( ) adalah: ( ) ( )
( )
4. Rata-rata banyaknya pelanggan dalam sistem ( ) adalah: ( ) ( )
( )
Bukti:
1. Berdasarkan Teorema 3.2 dan Teorema 2.17, maka didapatkan persamaan:
82
2. Berdasarkan persamaan (3.9), Teorema 3.2 dan Teorema 2.17, maka didapatkan persamaan:
didapatkan persamaan:83
k k k W Ls s
2 2 ) 1 (
2 2 ) 1 (
2
Contoh 3.4:
Perhatikan Contoh 3.3. Sarana pelayanannya tidak dapat menangani lebih dari satu mobil setiap saat ini berarti fasenya hanya 1 ( ). Pada bagian ini Contoh 3.1 akan dikerjakan ulang dengan waktu pelayanan menggunakan distribusi Erlang, sehingga model antrian menjadi ( ⁄ ⁄ ) ( ⁄ ).
a) Penentuan rata-rata banyaknya mobil dalam antrian ( ) menggunakan Teorema 3.3(2), yaitu:
( ) ( )
( ) ( )
mobil / jam
Jadi, rata-rata banyaknya mobil dalam antrian ( ) adalah 1,33 mobil / jam atau dalam 3 jam terdapat 4 mobil yang mengantri.
b) Penentuan rata-rata waktu menunggu dalam antrian ( ) menggunakan Teorema 3.3(1), yaitu:
( ) ( )
( )
( ) jam 20 menit
84
c) Penentuan rata-rata waktu menunggu dalam sistem ( ) menggunakan Teorema 3.3(3), yaitu:
( ) ( ) ( )
( ) ( ) ( )
jam 30 menit
Jadi, rata-rata waktu menunggu dalam sistem ( ) adalah 30 menit.
d) Penentuan rata-rata banyaknya mobil dalam sistem ( ) menggunakan Teorema 3.3(4), yaitu:
( ) ( ) ( )
( ) ( ) ( )
mobil / jam
Jadi, rata-rata banyaknya mobil dalam sistem ( ) adalah 2 mobil / jam.
Pada saat fasenya satu maka antrian dengan distribusi Erlang hasilnya akan sama dengan distribusi eksponensial.
Contoh 3.5:
85
atau bebas terhadap tahapan lainnya. Kerusakan mesin mengikuti proses Poisson dengan rata-rata terjadi 3 kerusakan per jam. Apabila hanya ada 1 tenaga mekanis dalam bengkel, berapa rata-rata waktu menganggur dari mesin yang rusak untuk diperbaiki?
Penyelesaian:
Karena mesin bubut memerlukan 4 tahapan dalam perbaikan mesin, maka banyak fasenya adalah 4 atau dan model antriannya menjadi ( ⁄ ⁄ ) ( ⁄ ). Waktu yang diperlukan untuk melaksanakan setiap tahapan adalah 10 menit. Berati laju pelayanannya () adalah :
laju pelayanannya() tahapan menit
tahapan jam
Sedangkan dalam 1 jam terjadi 3 kerusakan mesin. Itu berarti laju kerusakan mesin adalah:
( ) kerusakanjam
Rata-rata waktu menanggur dari mesin yang rusak dapat diperoleh dengan mencari rata-rata waktu mengantri mesin bubut dalam sistem ( ).
86
Rata-rata waktu mengantri mesin bubut dalam sistem ( ) menggunakan persamaan (3.21) adalah:
( ) ( ) ( )
( ) ( ) ( )
jam 47 5 menit
Jadi, rata-rata waktu menganggur dari mesin yang rusak untuk diperbaiki adalah 47,5 menit.
Contoh 3.6:
Seorang penjahit memerlukan 1 hari penuh untuk menjahit 1 stel pakaian. Kedatangan pelanggan mengikuti distribusi Poisson dengan rata-rata kedatangan sebanyak 1 orang setiap 2 hari. Secara rata-rata berapa lama seorang langganan diharapkan menunggu untuk dilayani dalam antrian?
Penyelesaian:
Penjahit memerlukan 1 hari penuh untuk menjahit 1 stel pakaian. Banyaknya tahapan dalam menjahit jumlahnya tidak tentu sehingga fase yang diperlukan penjahit dalam menjahit 1 stel pakaian diasumsikan 1 dan model antriannya menjadi( ⁄ ⁄ ) ( ⁄ ).