*Correspondence address. Department of Management, The Hong Kong Polytechnic University, Kowloon, Hong Kong.
Parallel machine scheduling with batch delivery costs
Guoqing Wang
!,",
*
, T.C. Edwin Cheng
#
!Department of Business Administration, Jinan University, Guangzhou, People's Republic of China "Department of Management, The Hong Kong Polytechnic University, Kowloon, Hong Kong
#Ozce of the Vice President (Research and Postgraduate Studies), The Hong Kong Polytechnic University, Kowloon, Hong Kong
Received 12 May 1998; accepted 8 July 1999
Abstract
We consider a scheduling problem in whichnindependent and simultaneously available jobs are to be processed on
mparallel machines. The jobs are delivered in batches and the delivery date of a batch is equal to the completion time of the last job in the batch. The delivery cost depends on the number of deliveries. The objective is to minimize the sum of the total#ow time and delivery cost. We"rst show that the problem is NP-complete in the ordinary sense even when
m"2, and NP-complete in the strong sense whenmis arbitrary. Then we develop a dynamic programming algorithm to solve the problem. The algorithm is pseudopolynomial whenmis constant and the number of batches has a"xed upper bound. Finally, we identify two polynomially solvable cases by introducing their corresponding solution methods. ( 2000 Elsevier Science B.V. All rights reserved.
Keywords: Parallel machine scheduling; Batch delivery cost
1. Introduction
Batch scheduling, as combinations of sequencing and partitioning, has attracted much attention of researchers in recent years. Most of the results in batch scheduling area fall into the following three categories: (i) item availability family schedu-ling problems, (ii) batch availability scheduschedu-ling problems, and (iii) batch processing scheduling problems. The interested reader is referred to the recent reviews by Webster and Baker [1], Liaee and Emmons [2], and Cheng et al. [3]
In this paper, we study a problem which falls into a di!erent category of batch scheduling problems,
namely batch delivery problems. Batch delivery problems were"rst introduced by Cheng and Kahl-bacher [4]. In [4], they studied single machine batch delivery scheduling to minimize the sum of the total weighted earliness and delivery costs. The earliness of a job is de"ned as the di!erence be-tween its delivery date and completion time. They showed that the problem is NP-complete in the ordinary sense, and the equal weight case is poly-nomially solvable. Cheng and Gordon [5] pro-vided a dynamic programming algorithm to solve the general problem. The algorithm is pseudo-polynomial when the number of batches has a"xed upper bound. They also provided a polynomial algorithm to solve the common processing time case. Cheng et al. [6] further showed that this problem can be formulated as a classical parallel machine scheduling problem, thus the complexity
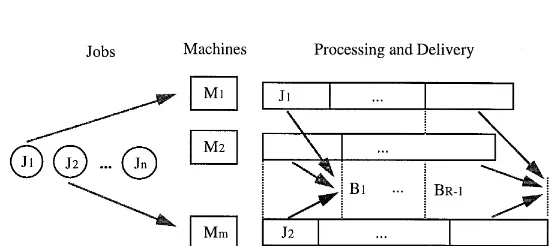
Fig. 1. Problem descriptions. results and algorithms for the corresponding
paral-lel machine scheduling problem can be easily ex-tended to the problem. Cheng et al. [7] studied the single machine batch delivery problem to minimize the sum of the total weighted earliness and mean batch delivery time.
Hermann and Lee [8] considered a single ma-chine batch delivery problem where all jobs have a common due date and the objective is to minim-ize the sum of the earliness and tardiness penalties and delivery costs of the tardy jobs. They provided a pseudopolynomial dynamic programming algo-rithm to solve the problem. Chen [9] showed that, when the common due date is a decision variable, the problem can be solved polynomially. Yuan [10] showed that the single machine batch delivery problem to minimize the sum of the total weighted earliness and tardiness and delivery costs of the tardy jobs is NP-complete in the strong sense.
While all prior batch delivery scheduling re-search focuses on the single machine environment, we study a parallel machine batch delivery schedul-ing problem in this paper. The problem can be formally stated as follows (see Fig. 1). There are nindependent nonpreemptive jobs to be sequenced for processing onmparallel identical machines, and partitioned into several batches for delivery. All jobs are available for processing at time zero. All jobs in a batch are delivered to the customer to-gether. The batch delivery date is equal to the completion time of the last job in a batch. Thus the
#ow time of a job is equal to the batch delivery date on which it is delivered. The delivery cost is a non-decreasing function of the number of batch
delive-ries. The objective is to sequence and partition the jobs to minimize the sum of the total#ow time and delivery cost.
Batch delivery is characteristic of many practical systems in which jobs are transported and ultimate-ly delivered in containers such as boxes or carts. For such systems, an important performance cri-terion is to minimize the work-in-process (WIP) inventories which are related to the total#ow time. As there are always some costs associated with each delivery, we obtain a situation which can be modelled as the above batch delivery problem.
The rest of the paper is organized as follows. In Section 2, we introduce the notation to be used. In Section 3, we show that the problem under study is NP-complete and provide a dynamic programming algorithm to solve the problem optimally. In Sec-tion 4, we identify some polynomially solvable cases. Finally, we present our conclusions in the last section.
2. Notation
In this section, we introduce the notation to be used in the paper:
n : number of jobs; m : number of machines; J"MJ
1,2,J
nN : job set to be processed; p
B
Adopting the three-"eld notation introduced by Graham et al. [11], we denote our problem as Pm/bd/(+F
i#a(R)).
3. NP-completeness and dynamic programming
In this section, we consider the complexity issues of the problem. First, it is interesting to note that, when the delivery cost is negligible, Pm/bd/(+F
i#a(R)) simply reduces to the classical
parallel machine scheduling problem Pm//+C i. It is
well known that Pm//+C
i is solved by the
general-ized shortest processing time (SPT) rule: schedule the jobs in the order of nondecreasing processing times, and assign each job to the earliest available machine [12].
Next, we give a simple proof for the NP-com-pleteness for the problem under study. Assume that the batch delivery cost is so large that all jobs must be delivered in one batch. i.e. R"1. Then Pm/bd/(+F
i#a(R)) is equivalent to the classical
parallel machine scheduling problem Pm//C .!9. Since Pm//C
.!9 has been shown to be NP-com-plete in the ordinary sense when m is "xed, and NP-complete in the strong sense whenmis arbit-rary [13], we have the following theorem.
Theorem 1. Even whenR"1, Pm/bd/(+F
i#a(R)) isNP-complete in the ordinary sense whenmisxxed and m*2, and NP-complete in the strong sense whenmis arbitrary.
The following lemma establishes several proper-ties for an optimal schedule for the problem.
Lemma 1. There exists an optimal schedule
nH"SB
1,2,B
RTforPm/bd, R);/(+Fi#a(R)) in which
(i) there is no idle time before each job;
(ii) all jobs assigned to the same machine are sched-uled in the SPT order;
(iii) B
lcontains all jobs whichxnish processing in the time interval(D
l~1,Dl],l"1,2,R. Proof. (i) Trivial.
(ii) Assume that jobsJ
iandJjare assigned to the
same machine andJ
j followsJi immediately such
thatp
delivered in the same batch or not.
(iii) Let us number all jobs in the order of their completion time innH. Assume that the batches are numbered in accordance with the numbers of their last jobs. It is clear that, without loss of generality, we can assumeD
1(2(DR. Let Jj be the "rst
job inB
R. If there are any jobs betweenJj andJn
(the last job in B
R) which are assigned to other
batches, then there must be at least one batch, say B
l, such that Cj)Dl(DR. Let n@be a schedule
obtained by simply assigningJ
jtoBl. It is obvious
thatG(nH)*G(n@), a contradiction. Following the same argument with the jobs in batchB
R~1and so
on, we can show that there exists an optimal sched-ule in which all batches consist of a number of jobs which"nish processing contiguously. Since all jobs which processing atD
l,l"1,2,R, can all be as-signed to B
l in any optimal schedule, we have
shown thatB
l contains all jobs which "nish
pro-cessing in the time interval (D
l~1,Dl]. h
Based on Lemma 1, we can develop a dynamic programming algorithm to solve the problem. Let
; be an upper bound for the number of batch
deliveries, and P"+ni/1p
i. The algorithm is
for-mally described as follows. Algorithm PMBD-1:
(a) Renumber the jobs in the SPT order, i.e. p
imum total#ow time if we have scheduled jobs J
of the jobs assigned to machine u is
(d) Initial conditions: For each t
k"0,2,P,
Lemma 2. Algorithm PMBD-1 solves the problem
Pm/bd, R);/+(F
i#a(R))inO(nm;2Pm`U~1)time.
Proof. Due to Lemma 1, there exists an optimal schedule with jobs assigned to each machine in the SPT order, and each job in assigned to the "rst batch after the completion of the job. If J
j is
as-signed to machine u, then C
j"tu, and if minimum assignment by de"nition, we have
justi-"ed the validity of the recursive relations. So the algorithm PMBD-1 solves the problem Pm/bd,R);/(+F
i#a(R)).
The time complexity of the algorithm can be established as follows. Since only m!1 of the values t
1,2,t
m are independent, the number of
di!erent states of the recursive relations is at most
nPm`U~1forR"1,2,;. For each state, the right-hand side of Eq. (1) can be calculated in O(m;)
time. Thus, the overall computational complexity of Algorithm PMBD-1 isO(nm;2Pm`U~1). h
Lemma 2 implies that the problem Pm/bd,
R);/(+F
i#a(R)) is not strongly NP-complete
for any constant m and ;. But it is not clear
whether Pm/bd,R);/(+F
i#a(R)) is strongly
NP-complete or pseudopolynomically solvable for a constantmand an arbitrary;.
4. Polynomially solvable cases
In this section, we "rst consider a special case where the job assignment is predetermined. It is evident that the problem reduces to an optimal batching problem in this case. This special case characterizes the practical scenario where each ma-chine is dedicated to a special group of jobs. Ac-cording to Lemma 1, we can provide a backward dynamic programming algorithm to solve the opti-mal batching problem as follows.
Algorithm PMBD-2:
(a) Schedule the jobs on each machine in the SPT order, and then renumber all the jobs in ac-cordance with the job completion times. (b) De"neH
R(j,l) as the minimum total
comple-tion time of the jobsJ
j,2,Jn when they are assigned to the delivery batchesB
l,2,BR.
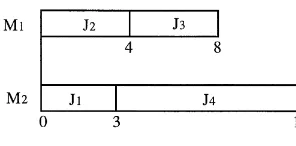
Fig. 2. Example 1.
Now we present a numerical example for the special case to demonstrate the optimality of the algorithm.
Example 1. Consider the instance with J"
MJ
1,2,J4N, m"2, and a(R)"7R. Assume that J
1 and J4 are assigned on M1,J2 and J3 are
assigned onM
3, and all jobs are sequenced in the
SPT order on each machine (as shown in Fig. 2). Now using algorithm PMBD-2 to solve the in-stance, we have the following results:
WhenR"1, we have
H
1(4, 1)"H1(5, 2)#C4"12,
H
1(3, 1)"H1(5, 2)#2C4"24,
H
1(2, 1)"H1(5, 2)#3C4"36,
H
1(1, 1)"H1(5, 2)#4C4"48,
and so
G(nH1)"7R#H
1(1, 1)"55.
WhenR"2, we have
H
2(4, 2)"H2(5, 3)#C4"12,
H
2(3, 2)"H2(5, 3)#2C4"24,
H
2(2, 2)"H2(5, 3)#3C4"36,
H
2(1, 1)"minMH2(4, 2)#3C3,
H
2(3, 2)#2C2,H2(2, 2)#C3N"32,
and so
G(nH2)"7R#H
1(1, 1)"46.
WhenR"3, we have
H
3(4, 3)"H3(5, 4)#C4"12,
H
3(3, 3)"H3(5, 4)#2C4"24,
H
3(2, 2)"minMH3(4, 3)#2C3,
H
2(3, 3)#C2N"28,
H
3(1, 1)"H3(2, 2)#C1"31.
Thus
G(nH3)"7R#H3(1, 1)"52.
WhenR"4, we have
H
4(4, 4)"H4(5, 5)#C4"12,
H
4(3, 3)"H4(4, 4)#C3"20,
H
4(2, 2)"H4(3, 3)#C4"24,
H4(1, 1)"H4(2, 2)#C1"27,
and so
G(nH4)"7R#H
4(1, 1)"55.
Hence, we obtained an optimal schedule nH"
SB
1,B2TwithB1"MJ1,J2NandB2"MJ3,J4N.
We now consider the special case with identical processing times, Pm/bd,p
i"p/(+Fi#a(R)). Let n
0"vn/mw, g"n0m!n. Letnu be the number of
jobs processed on machineuunder a speci"c sched-ule. Then we have the following lemma.
Lemma 3. There exists an optimal schedule for
Pm/bd,p
i"p/(+Fi#a(R)) in which n0!1)
n
u)n0,u"1,2,m.
Proof. Suppose there exists an optimal schedule nHin which the condition is not satis"ed. Accord-ing to Lemma 1, we can assume that there is no inserted idle time innH. Then there must be a pair of machinesuandvsuch thatn
u*nv#2 and the
last job on machineuis also the last job of the last batch delivery. It is clear that moving the last job on machineuto the last position on machinevwill not increase the total penalty. Repeating this pro-cess, we can obtain a desired optimal schedule. h
Let pH
R"SB1,2,B
RT be an optimal schedule
with R batch deliveries for the problem Pm/bd, p
i"p/(+Fi#a(R)). LetbMl"bl/m, l"1,2,R!1. We have
Lemma 4. There exists an optimal schedule with Rbatch deliveries forPm/bd, p
Proof. According to Lemma 1, we can assume that innH
Rthere is no inserted idle time andBl contains
all jobs which"nish processing in the time interval (D
Now assume thatnHR satis"ed Lemmas 3 and 4. LetbMl"vb
l/mw. We have
Lemma 5. There exists an optimal schedule with Rbatch deliveries forPm/bd,p
i"p/(+Fi#a(R))in which DbMk!bMlD)1 for any pair of k andl, where k"1,2,R, l"1,2,R.
Proof. We"rst show that changing the sequence of B
l,l"1,2,R!1, will not cause any increase in the total penalty. It is not di$cult to see that the sequencing of batch deliveriesB
l,l"1,2,R!1, is equivalent to the classical single machine total weighted#ow time scheduling problem, denoted as 1//+w
lCl, with wl"bMlm and pl"bMlp. It is well
known that the total weighted #ow time is mini-mized by sequencing the jobs in the weighted shor-test processing time (WSPT) order [14]. Since p
1/w1"2"pR~1/wR~1"p/m, Bi, l"1,2,R !1, can be sequenced in an arbitrary order.
Now, we can prove the lemma by showing
DbMl~1!bMlD)1, l"2,2,R. (5)
Then we can easily obtain the desired results. Now, assume that there are some batches such thatbMl"1. Note thatb
l may be less thanmin this
case. Since it is trivial whenbMl~1"1 (orbMl`1"1), we suppose bMl~1'1 (or bMl`1'1). From (6) (or (7)), we can easily show thatbMl~1)2 or (bMl`1)2), and thus (5) holds again.
This completes the proof. h
Based on these results, we can easily construct an optimal schedule with R batch deliveries nH
ciated total penalty can be calculated as
G(nH
Now, we can construct a simple algorithm to solve the problem as follows.
Algorithm PMBD-3:
It is clear that Algorithm PMBD-3 solves the prob-lem Pm/bd,p
i"p/(+Fi#a(R)) in O(n/m) time. It
should be pointed out that, the algorithm, although e$cient, is not actually polynomial when each batch delivery has an equal delivery costc, i.e.a(R)"cR.
The following numerical example demonstrates the optimality of the algorithm.
Example 2. Consider the instance with J"MJ
1,
2,J7N, m"2,a(R)"7R, pi"p"2,i"1,2, 7.
From Lemma 3, we know that there exists an optimal schedule in which all jobs are sequenced as shown in Fig. 3. It is clear thatn
0"4,g"1. Using
algorithm PMBD-3 to solve the instance, we have the following results.
WhenR"1, we havebM
0"4 and h"0, and so
Fig. 3. Example 2.
WhenR"2, we havebM
0"2 andh"0, and so
G(nH2)"7R#20p"54.
WhenR"3, we havebM0"2 andh"2, and so G(nH3)"7R#18p"57.
WhenR"4, we havebM0"1 andh"0, and so
G(nH4)"7R#16p"60.
Now we can obtain an optimal schedule nH"SB
1,B2T with B1"MJ1,J2,J3,J4,N and
B
2"MJ5,J6,J7N.
5. Conclusions
In this paper, we have studied the parallel ma-chine scheduling with batch delivery costs. We have shown that the problem to minimize the sum of the total#ow time and delivery cost is NP-complete in the strong sense. We have then provided a dynamic programming algorithm to solve the problem. The algorithm is pseudopolynomial when the number of machines is constant and the number of batches has a "xed upper bound. We also have provided two polynomial time algorithms to solve the special cases where the job assignment is given or the job processing times are equal.
There are a number of issues which are of interest for further research. First, it is interesting to investi-gate the open problem posed in the paper, i.e. whether it is pseudopolynomially solvable or strong-ly NP-complete when the number of machines is constant and the number of batches is arbitrary. It is also interesting to investigate polynomial time algo-rithms for the special case where the job processing times are equal and the batch delivery cost function is linear. Another interesting issue is to develop e!ective heuristics to solve the general problem, and it is evident that a viable strategy is to combine the
list scheduling procedure for the classical parallel machine scheduling problems [15] with the optimal batching algorithm proposed in this paper.
Acknowledgements
This research was supported in part by The Hong Kong Polytechnic University under grant number 350/239.
References
[1] S. Webster, K.R. Baker, Scheduling groups of jobs on a single machine, Operations Research 43 (1995) 692}703. [2] M.M. Liaee, H. Emmons, Scheduling families of jobs with setup times, International Journal of Production Econ-omics 51 (1997) 165}176.
[3] T.C.E. Cheng, J.N.D. Gupta, G. Wang, A review of# ow-shop scheduling research with setup times, Production and Operations Management (1999), to appear.
[4] T.C.E. Cheng, H.G. Kahlbacher, Scheduling with delivery and earliness penalties, Asia-Paci"c Journal of Opera-tional Research 10 (1993) 145}152.
[5] T.C.E. Cheng, V.S. Gordon, Batch delivery scheduling on a single machine, Journal of the Operational Research Society 45 (1994) 1211}1215.
[6] T.C.E. Cheng, V.S. Gordon, M.Y. Kovalyov, Single ma-chine scheduling with batch delivery, European Journal of Operational Research 94 (1996) 277}283.
[7] T.C.E. Cheng, M.Y. Kovalyov, B.M.T. Lin, Single machine scheduling to minimize batch delivery and job earliness penalties, SIAM Journal on Optimization 7 (1997) 547}559.
[8] J.W. Hermann, C.-Y. Lee, On scheduling to minimize earliness}tardiness and batch delivery costs with a com-mon due date, European Journal of Operational Research 70 (1993) 272}288.
[9] Z.-L. Chen, Scheduling and common due date assignment with earliness}tardiness penalties and batch delivery costs, European Journal of Operational Research 93 (1996) 49}60.
[10] J. Yuan, A note on the complexity of single-machine sched-uling with a common due date, earliness}tardiness, and batch delivery costs, European Journal of Operational Research 94 (1996) 203}205.
[11] R.L. Graham, E.L. Lawler, J.K. Lenstra, A.H.G. Rinnooy Kan, Optimization and approximation in deterministic sequencing and scheduling: A survey, Annals of Discrete Mathematics 5 (1979) 287}326.
[12] R.W. Conway, W.L. Maxwell, L.W. Miller, Theory of Scheduling, Addison-Wesley, Reading, MA, 1966. [13] M.R. Garey, D.S. Johnson, Computers and Intractability:
A Guide to the Theory of NP-completeness, Freeman, New York, 1979.