Analisis Matematika Analisis Grafik dan

(1)

Nama : Maria Fransisca Tanggal : 23 Februari 2017

NPM : 1506728743 Paraf Asisten :

Kelompok : 1

Topik Pemicu : Insulasi Kalor

(Konduksi Panas Dua-Dimensi (keadaan tunak)) I. Outline

1. Analisis Matematika

2. Analisis Grafik dan Faktor Bentuk 3. Metode Analisis Numerik

4. Iterasi Gauss-Seidel II. Pembahasan

Secara umum, aliran kalor untuk benda 2 dimensi dalam keadaan tunak dan tanpa adanya reaksi pembentukkan panas berlaku persamaan Laplace

∂2T ∂ x2+

∂2T ∂ y2=0

di mana konduktivitas panas konstan. Persamaan ini merupakan fungsi kuadrat yang menyatakan 2 koordinat x dan y. Sehingga, aliran kalor di titik x dan y dapat diukur menggunakan persamaan Fourier

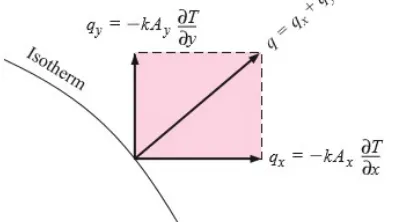
qx=−kAx∂ T ∂ x

qy=−kAy ∂T ∂ y

Penjumlahan kedua persamaan di atas (qx + qy) menghasilkan total aliran kalor yang terarah yang akan tegak lurus dengan garis T konstan, seperti pada gambar 1.

Gambar 1. Sketsa Aliran Kalor dalam Dua Dimensi (Sumber: J.P Holman, 2010)

(2)

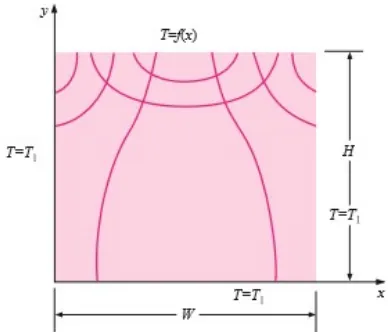
Gambar 2. Isotermis dan garis aliran kalor in papan persegi panjang (Sumber: J.P. Holman, 2010)

Berdasarkan gambar di atas, tiga sisi pelat dijaga pada temperatur T1, dan sisi atas memiliki distribusi temperatur tertentu. Distribusi ini dapat bernilai konstan atau kompleks, contohnya distribusi sinus.

Solusi persamaan diferensial berdasarkan gambar, dapat diasumsikan

T=XY dimana X=X(x)

Y=Y(y)

Distribusi temperatur berbentuk sinus, dan kondisi batas

T=T1 Pada Y=X=W=0

T=Tmsin

(

πx

W

)

+T1 Pada y=H

Setelah melalui serangkaian penurunan rumus yang panjang (sumber: Buku Perpindahan Kalor oleh Holman), gambar diatas dapat dicari nilai aliran panasnya dengan menggunakan penurunan sejumlah rumus yang

menghasilkan rumus akhir sinh(¿nπy/W) sinh(¿nπy_¿/W) T−T1

T2−T1= 2 π

∑

n=1

∞

(−1)n+1

+1

n sin

(3)

2. Analisis Grafik dan Faktor Bentuk

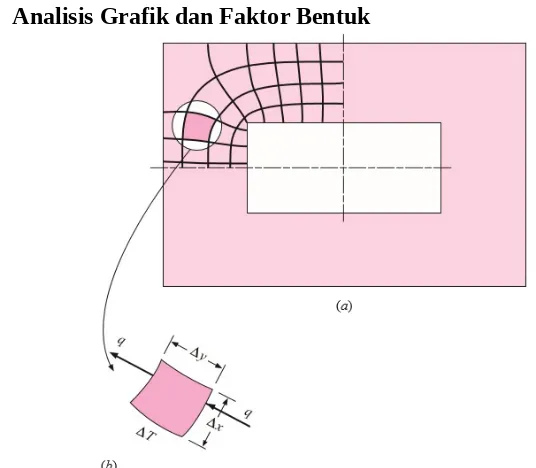
Gambar 3. Sketsa menunjukkan elemen yang digunakan untuk analisis dua dimensi persegi kurvilinear

(Sumber: J.P. Holman, 2010)

Pada Gambar 3, temperatur pada permukaan dalam dijaga pada suhu T1 dan permukaan luar dijaga pada suhu T2. Untuk menghitung perpindahan panas, sketsa isotermis dan jalur aliran kalor telah dipaparkan diatas untuk membantu perhitungan ini (Gambar 2.b). Digunakan persamaan Fourier

q=−k ∆ x(1)∆ T ∆ y

Aliran kalor akan memiliki nilai yang sama di setiap bagian dari jalur aliran kalor, dan total nilai aliran kalor ini merupakan penjumlahan aliran kalor di setiap jalur. Jika pada sketsa dibuat sedemikian rupa sehingga ∆x≅∆y, maka aliran kalor akan sebanding dengan ∆T yang bersebrangan dengan elemen. Pada kasus ini, aliran kalor bernilai konstan, maka besar ∆T akan sama di setiap lajur aliran kalor yang sama. Oleh karena itu,

∆ T=∆ Toverall N

N merupakan besar kenaikan suhu antara permukaan dalam dengan permukaan luar.

q=M

N k ∆ Toverall= M

N k(T2−T1)

M diatas merupakan jumlah jalur aliran kalor. Rasio antara M/N

(4)

q=kS ∆ Toverall

Dalam sistem dua dimensi, kita dapat menetapkan faktor bentuk konduksi S seperti persamaan dibawah. Nilai dari S berbeda dan bergantung pada bentuk dan dimensi elemen. Untuk mencari nilai S secara lengkapnya, persamaan dapat dilihat di Tabel 3.1 (Buku Perpindahan Kalor oleh Holman).

Dari persamaan yang tertera di tabel, ditemukan cosh−1 _{atau invers}

cosinus hiperbolik yang dirumuskan

¿x ±

√

x2−1 ¿ cosh−1_x=_ln

¿ )

Untuk dinding tiga dimensi, faktor bentuk yang terpisah digunakan dalam menghitung aliran kalor pada bidang sisi dan sudut. Jika semua dimensi dalam lebih besar dari seperlima tebal dinding, maka

S_dinding=A L

S_sisi=0,54D

S_sudut=0,15L

Kunci dari metode ini adalah ketelitian dan keterampilan dalam menggambarkan bujur-sangkar kurvilinear. Namun, metode ini tidak banyak bermanfaat dalam menyelesaikan soal-soal sederhana.

3. Metode Analisis Numerik

Selain kedua pendeketan yang diatas, terdapat juga

(5)

Gambar 4.Sketsa yang menunjukkan nomenklatur yang digunakan dalam analisis numerik konduksi kalor dua dimensi

(Sumber: J.P. Holman, 2010)

Titik-titik node yang terlihat di gambar 4, lokasi m menunjukkan tambahan pada arah x, dan lokasi n tambahan pada arah y. Kita ingin menentukan suhu pada setiap titik node di dalam benda itu dengan menggunakan persamaan awal sebagai kondisi yang menentukan. Jika ∆x=∆y, maka didapat persamaan sebagai berikut

T_m₊_1,_n+T_m₋_1,_n+T_m,n₊₁+T_{m , n}₋₁−4T_{m , n}=0

Dalam hal ini kondisi konduktivitas termal tetap, sehingga aliran kalor dapat dinyatakan dalam diferensial suhu. Persamaan dengan sederhana menunjukkan bahwa aliran kalor netto pada setiap node ialah nol pada keadaan tunak. Pada hakekatnya, dalam pendekatan numerik beda-berhingga distribusi suhu yang kontinu digantikan dengan sejumlah batangan penghantar kalor khayalan yang bersambungan pada setiap titik node, dan tidak mempunyai pembangkitan kalor. Kita juga dapat menyusun jalan beda-berhingga yang memperhitungkan pembangkitan kalor. Kita hanya tinggal menambahkan suku q_k ke dalam persamaan umum sehingga

T_m₊_1,_n+T_m₋_1,_n+T_m,n₊₁+T_{m , n}₋₁+q(∆ x)

2

k −4Tm ,n=0

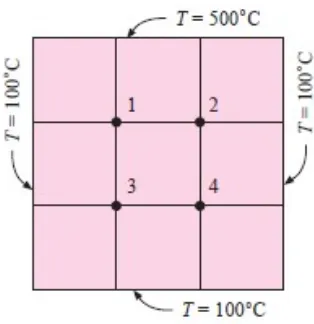
Untuk menggunakan metode numerik, Persamaan awal harus ditulis untuk setiap node di dalam bahan itu, dan sistem penamaan yang dihasilkan lalu diselesaikan untuk rnendapatkan suhu pada setiap node. Contoh yang paling sederhana ialah seperti pada Gambar 5 di bawah:

(6)

100+500+T2+T3−4T1=0

T1+500+100+T4−4T2=0

100+T1+T4+100−4T3=0

T3+T2+100+100−4T4=0

Penyelesaian persamaan di atas akan menghasilkan T1=T2=250°C T3=T4=150° C

Jika suhu ditentukan, maka perhitungan aliran kalor menjadi q=

_∑

k ∆ x∆ T

∆ y

∆T dapat ditentukan pada batas-batas pada soal, yaitu dihitung dari muka yang 500ºC atau pada ketuga muka yang 100ºC. Jika kita menggunakan kisi yang cukup halus, kedua nilai yang didapat mesti sangat mendekati sama satu sama lain. Dalam prakteknya, biasanya paling baik digunakan rata-rata dan kedua nilai itu untuk perhitungan. Jika benda padat berada dalam kondisi batas konveksi,seperti pada gambar 5,

suhu pada permukaan harus dihitung dengan cara yang berbeda dari metode di atas. Persamaan umumnya jika Δx = Δy adalah

Tm, n

(

h ∆ x k +2

)

−

h ∆ x k T ∞−

1

2

(

2Tm−1,n+Tm , n+1+Tm ,n−1

)

=0

(7)

Saat jumlah titik node sangat besar, teknik ini menghasilkan solusi yang lebih efisien untuk menyelesaikan persamaan node daripada digunakannya inversi matriks langsung. Pada persamaan sebelumnya, kita dapat suhu Ti dan suhu-suhu node Tj di sebelahnya sebagai

Ti=

qi=

∑

j ❑

( Tj Rij)

∑

j ❑

( 1 Rij)

Iterasi Gauss-Seidel memanfaatkan persamaan-persamaan beda seperti dalam persamaan sebelumnya, menurut prosedur sebagai berikut :

 Mula-mula suatu perangkat awal untuk nilai Ti diandaikan.  Kemudian dengan persamaan 6 dihitung nilai-nilai baru untuk

suhu node Ti, dengan menggunakan nilai Tj yang terbaru.  Proses ini diulangi terus-menerus sehingga perbedaan antara

dua perhitungan cukup kecil

III. Sumber Rujukan

Holman, J.P. 2010. Heat Transfer : Tenth Edition. New York: McGraw-Hill Companies, Inc.

Incropera, Frank. 2007. Fundamentals of Mass and Heat Transfer 6th Edition. Massachusetts : John Wiley & Sons, Inc

Yunus, Asyari. Buku Pengantar Perpindahan Panas dan Massa untuk Teknik Mesin Universitas Darma Persada. [ONLINE] Tersedia di