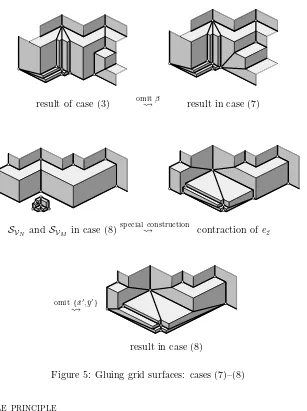
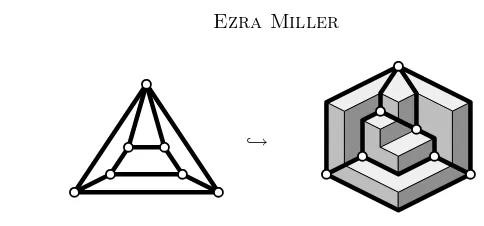
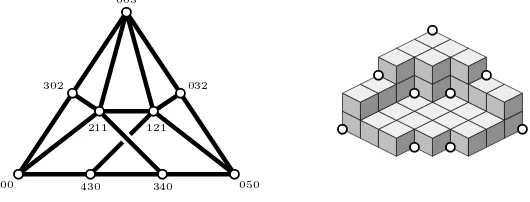
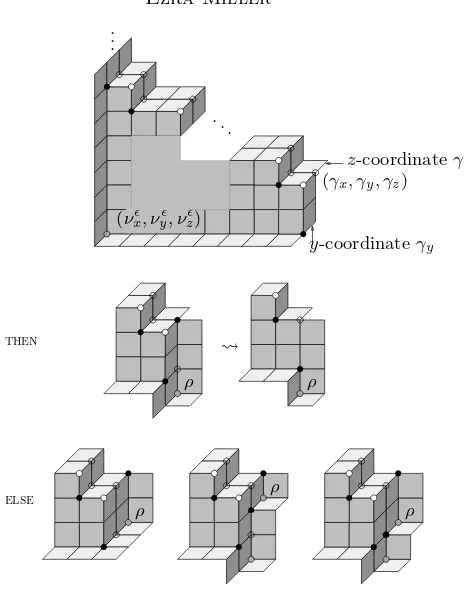
Documenta Mathematica
of an extended map, see page 48thematischen Gebieten und wird in traditioneller Weise referiert. Documenta Mathematicaerscheint am World Wide Web unter:
http://www.mathematik.uni-bielefeld.de/documenta
Artikel k¨onnen als TEX-Dateien per E-Mail bei einem der Herausgeber ein-gereicht werden. Hinweise f¨ur die Vorbereitung der Artikel k¨onnen unter der obigen WWW-Adresse gefunden werden.
Documenta Mathematicapublishes research manuscripts out of all mathe-matical fields and is refereed in the traditional manner.
Documenta Mathematicais published on the World Wide Web under: http://www.mathematik.uni-bielefeld.de/documenta
Manuscripts should be submitted as TEX -files by e-mail to one of the editors. Hints for manuscript preparation can be found under the above WWW-address.
Gesch¨aftsf¨uhrende Herausgeber / Managing Editors: Alfred K. Louis, Saarbr¨ucken [email protected]
Ulf Rehmann (techn.), Bielefeld [email protected] Peter Schneider, M¨unster [email protected] Herausgeber / Editors:
Don Blasius, Los Angeles [email protected] Joachim Cuntz, Heidelberg [email protected] Bernold Fiedler, Berlin (FU) [email protected]
Friedrich G¨otze, Bielefeld [email protected] Wolfgang Hackbusch, Leipzig (MPI) [email protected]
Ursula Hamenst¨adt, Bonn [email protected] Max Karoubi, Paris [email protected] Rainer Kreß, G¨ottingen [email protected] Stephen Lichtenbaum, Providence Stephen [email protected] Alexander S. Merkurjev, Los Angeles [email protected]
Anil Nerode, Ithaca [email protected]
Thomas Peternell, Bayreuth [email protected] Wolfgang Soergel, Freiburg [email protected] G¨unter M. Ziegler, Berlin (TU) [email protected]
ISSN 1431-0635 (Print), ISSN 1431-0643 (Internet)
SPARC Leading Edge
Documenta Mathematicais a Leading Edge Partner of SPARC, the Scholarly Publishing and Academic Resource Coalition of the As-sociation of Research Libraries (ARL), Washington DC, USA.
Documenta Mathematica
Band 7, 2002
Kengo Matsumoto
C∗-Algebras Associated
with Presentations of Subshifts 1–30
Gordon Heier
Effective Freeness of Adjoint Line Bundles 31–42
Ezra Miller
Planar Graphs as Minimal Resolutions of
Trivariate Monomial Ideals 43–90
J. Brodzki, R. Plymen
Complex Structure on the Smooth Dual of GL(n) 91–112
Victor Reiner
Equivariant Fiber Polytopes 113–132
Shoji Yokura
On the Uniqueness Problem
of Bivariant Chern Classes 133–142
B. Mirzaii, W. van der Kallen
Homology Stability for Unitary Groups 143–166
Raymond Brummelhuis, Heinz Siedentop, and Edgardo Stockmeyer The Ground State Energy
of Relativistic One-Electron Atoms
According to Jansen and Heß 167–182
Frans Oort and Thomas Zink Families of p-Divisible Groups
with Constant Newton Polygon 183–201
Paul Balmer, Stefan Gille, Ivan Panin and Charles Walter The Gersten Conjecture for Witt Groups
in the Equicharacteristic Case 203–217
Martin Olbrich
L2-Invariants of Locally Symmetric Spaces 219–237
Cornelia Busch
The Farrell Cohomology ofSP(p−1,Z) 239–254
Guihua Gong
On the Classification
of Simple Inductive Limit C∗-Algebras, I:
The Reduction Theorem 255–461
Winfried Bruns and Joseph Gubeladze
Rost Projectors and Steenrod Operations 481–493
Tam´as Hausel and Bernd Sturmfels
Toric Hyperk¨ahler Varieties 495–534
Bernhard Keller and Amnon Neeman The Connection Between May’s Axioms for a Triangulated Tensor Product and Happel’s Description
of the Derived Category of the Quiver D4 535–560
Anthony D. Blaom
Reconstruction Phases for
Hamiltonian Systems on Cotangent Bundles 561–604
Marc A. Rieffel
Group C∗-Algebras as Compact
Quantum Metric Spaces 605–651
Georg Schumacher
Asymptotics of Complete K¨ahler-Einstein Metrics – Negativity of the
C∗
-Algebras Associated
with Presentations of Subshifts
Kengo Matsumoto
Received: May 28, 2001 Revised: March 4, 2002
Communicated by Joachim Cuntz
Abstract. Aλ-graph system is a labeled Bratteli diagram with an up-ward shift except the top vertices. We construct a continuous graph in the sense of V. Deaconu from a λ-graph system. It yields a Renault’s groupoid C∗-algebra by following Deaconu’s construction. The class of
theseC∗-algebras generalize the class ofC∗-algebras associated with
sub-shifts and hence the class of Cuntz-Krieger algebras. They are unital, nuclear, uniqueC∗-algebras subject to operator relations encoded in the structure of theλ-graph systems among generating partial isometries and projections. If theλ-graph systems are irreducible (resp. aperiodic), they are simple (resp. simple and purely infinite). K-theory formulae of these
C∗-algebras are presented so that we know an example of a simple and
purely infinite C∗-algebra in the class of these C∗-algebras that is not
stably isomorphic to any Cuntz-Krieger algebra.
2000 Mathematics Subject Classification: Primary 46L35, Secondary 37B10.
Keywords and Phrases: C∗-algebras, subshifts, groupoids, Cuntz-Krieger
algebras
1. Introduction
In [CK], J. Cuntz-W. Krieger have presented a class ofC∗-algebras associated
to finite square matrices with entries in {0,1}. The C∗-algebras are simple
σ((xn)n∈Z) = (xn+1)n∈Z,(xn)n∈Z ∈ Σ
Z. For a closed σ-invariant subset Λ
of ΣZ, the topological dynamical system Λ with σ is called a subshift. The
topological Markov shifts form a class of subshifts. In [Ma], the author has generalized the class of Cuntz-Krieger algebras to a class ofC∗-algebras
associ-ated with subshifts. He has formulassoci-ated several topological conjugacy invariants for subshifts by using the K-theory for theseC∗-algebras ([Ma5]). He has also
introduced presentations of subshifts, that are named symbolic matrix system andλ-graph system ([Ma5]). They are generalized notions of symbolic matrix andλ-graph (= labeled graph) for sofic subshifts respectively.
We henceforth denote byZ+andNthe set of all nonnegative integers and the
set of all positive integers respectively. A symbolic matrix system (M, I) over a finite set Σ consists of two sequences of rectangular matrices (Ml,l+1, Il,l+1), l∈
Z+. The matrices Ml,l+1 have their entries in the formal sums of Σ and the
matricesIl,l+1 have their entries in{0,1}. They satisfy the following relations
(1.1) Il,l+1Ml+1,l+2=Ml,l+1Il+1,l+2, l∈Z+.
It is assumed for Il,l+1 that forithere existsj such that the (i, j)-component
Il,l+1(i, j) = 1 and that forjthere uniquely existsisuch thatIl,l+1(i, j) = 1. A
λ-graph systemL= (V, E, λ, ι) consists of a vertex set V =V0∪V1∪V2∪ · · ·,
an edge set E = E0,1∪E1,2∪E2,3∪ · · ·, a labeling map λ : E → Σ and a
surjective map ιl,l+1 : Vl+1 → Vl for each l ∈Z+. It naturally arises from a
symbolic matrix system. For a symbolic matrix system (M, I), a labeled edge from a vertex vli ∈Vl to a vertex vl+1j ∈Vl+1 is given by a symbol appearing
in the (i, j)-component Ml,l+1(i, j) of the matrix Ml,l+1. The matrix Il,l+1
defines a surjection ιl,l+1 from Vl+1 to Vl for each l ∈ Z+. The symbolic
matrix systems and the λ-graph systems are the same objects. They give rise to subshifts by looking the set of all label sequences appearing in the labeled Bratteli diagram (V, E, λ). A canonical method to construct a symbolic matrix system and a λ-graph system from an arbitrary subshift has been introduced in [Ma5]. The obtained symbolic matrix system and the λ-graph system are said to be canonical for the subshift. For a symbolic matrix system (M, I), let
Al,l+1be the nonnegative rectangular matrix obtained from Ml,l+1 by setting
all the symbols equal to 1 for each l ∈Z+. The resulting pair (A, I) satisfies
the following relations from (1.1)
(1.2) Il,l+1Al+1,l+2=Al,l+1Il+1,l+2, l∈Z+.
We call (A, I) the nonnegative matrix system for (M, I).
In the present paper, we introduce C∗-algebras fromλ-graph systems. If a λ
-graph system is the canonicalλ-graph system for a subshift Λ, theC∗-algebra
coincides with theC∗-algebraOΛassociated with the subshift. Hence the class
C -Algebras Associatedwith Presentations of Subshifts 3
then define theC∗-algebraOL associated withL as the Renault’sC∗-algebra
of a groupoid constructed from the continuous graph. For an edge e∈El,l+1,
we denote bys(e)∈Vlandt(e)∈Vl+1its source vertex and its terminal vertex
respectively. Let Λl be the set of all words of lengthl of symbols appearing in
the labeled Bratteli diagram of L.We put Λ∗ =∪∞
l=0Λl where Λ0 denotes the
empty word. Let {vl1, . . . ,vlm(l)} be the vertex set Vl. We denote by Γ−l (vli)
the set of all words in Λl presented by paths starting at a vertex of V 0 and
terminating at the vertexvli.Lis said to be left-resolving if there are no distinct edges with the same label and the same terminal vertex. L is said to be predecessor-separated if Γ−l (vli) 6= Γl−(vlj) for distinct i, j and for all l ∈ N.
Assume that L is left-resolving and satisfies condition (I), a mild condition generalizing Cuntz-Krieger’s condition (I). We then prove:
Theorem A (Theorem 3.6 and Theorem 4.3). Suppose that aλ-graph sys-temLsatisfies condition (I). Then theC∗-algebraO
L is the universal concrete
unique C∗-algebra generated by partial isometries S
α, α ∈ Σ and projections
IfLis predecessor-separated, the following relations:
hold for i = 1,2, . . . , m(l), where Sµ = Sµ1· · ·Sµk for µ = (µ1, . . . , µk), µ1, . . . , µk ∈ Σ. In this case, OL is generated by only the
partial isometriesSα, α∈Σ.
IfLcomes from a finite directed graphG, the algebraOLbecomes the
Cuntz-Krieger algebra OAG associated to its adjacency matrix AG with entries in {0,1}.
We generalize irreducibility and aperiodicity for finite directed graphs to λ -graph systems. Then simplicity arguments of the Cuntz algebras in [C], the Cuntz-Krieger algebras in [CK] and theC∗-algebras associated with subshifts
in [Ma] are generalized to ourC∗-algebrasO
L so that we have
Theorem B (Theorem 4.7 and Proposition 4.9). If L satisfies condi-tion (I) and is irreducible, the C∗-algebra O
L is simple. In particular if L is
aperiodic,OL is simple and purely infinite.
There exists an actionαLof the torus groupT={z∈C| |z|= 1}on the
alge-bra OL that is called the gauge action. It satisfies αLz(Sα) = zSα, α ∈ Σ
for z ∈ T. The fixed point subalgebra OLαL of OL under αL is an
AF-algebra FL, that is stably isomorphic to the crossed product OL⋊αL T. Let (A, I) = (Al,l+1, Il,l+1)l∈Z+ be the nonnegative matrix system for the symbolic matrix system corresponding to the λ-graph system L. In [Ma5], its dimen-sion group (∆(A,I),∆+(A,I), δ(A,I)),its Bowen-Franks groupsBFi(A, I), i= 0,1
and its K-groups Ki(A, I), i= 0,1 have been formulated. They are related to
topological conjugacy invariants of subshifts. The following K-theory formu-lae are generalizations of the K-theory formuformu-lae for the Cuntz-Krieger alge-bras and the C∗-algebras associated with subshifts ([Ma2],[Ma4],[Ma5],[Ma6],
cf.[C2],[C3],[CK]).
Theorem C (Proposition 5.3, Theorem 5.5 and Theorem 5.9).
(K0(FL), K0(FL)+,αcL∗)∼= (∆(A,I),∆+(A,I), δ(A,I)),
Ki(OL)∼=Ki(A, I), i= 0,1,
Exti+1(OL)∼=BFi(A, I), i= 0,1
whereαcL denotes the dual action of the gauge action αL onOL.
We know that the C∗-algebra O
L is nuclear and satisfies the Universal
Coef-ficient Theorem (UCT) in the sense of Rosenberg and Schochet (Proposition 5.7)([RS], cf. [Bro2]). Hence, if L is aperiodic,OL is a unital, separable,
nu-clear, purely infinite, simple C∗-algebra satisfying the UCT, that lives in a
classifiable class by K-theory of E. Kirchberg [Kir] and N. C. Phillips [Ph]. By Rørdam’s result [Rø;Proposition 6.7], one sees that OL is isomorphic to the
C∗-algebra of an inductive limit of a sequenceB
1→B2→B3→ · · · of simple
Cuntz-Krieger algebras (Corollary 5.8).
We finally present an example of a λ-graph system for which the associated
C∗-algebra is not stably isomorphic to any Cuntz-Krieger algebraOAand any
Cuntz-algebraOn forn= 2,3, . . . ,∞. The example is aλ-graph systemL(S)
C -Algebras Associatedwith Presentations of Subshifts 5
Theorem D (Theorem 7.7). TheC∗-algebraOL(S) is unital, simple, purely
infinite, nuclear and generated by five partial isometries with mutually orthog-onal ranges. Its K-groups are
K0(OL(S)) = 0, K1(OL(S)) =Z.
In [Ma7], among other things, relationships between ideals of OL and sub λ
-graph systems ofLare studied so that the class ofC∗-algebras associated with
λ-graph systems is closed under quotients by its ideals.
Acknowledgments: The author would like to thank Yasuo Watatani for his suggestions on groupoidC∗-algebras andC∗-algebras of HilbertC∗-bimodules.
The author also would like to thank the referee for his valuable suggestions and comments for the presentation of this paper.
2. Continuous graphs constructed from λ-graph systems
We will construct Deaconu’s continuous graphs from λ-graph systems. They yield Renault’s r-discrete groupoidC∗-algebras by Deaconu ([De],[De2],[De3]).
Following V. Deaconu in [De3], by a continuous graph we mean a closed subset E ofV ×Σ× V where V is a compact metric space and Σ is a finite set. If in particularV is zero-dimensional, that is, the set of all clopen sets form a basis of the open sets, we sayE to be zero-dimensional or Stonean.
Let L= (V, E, λ, ι) be aλ-graph system over Σ with vertex set V =∪l∈Z+Vl and edge setE=∪l∈Z+El,l+1that is labeled with symbols in Σ byλ:E→Σ, and that is supplied with surjective maps ι(= ιl,l+1) :Vl+1 → Vl for l ∈Z+.
Here the vertex sets Vl, l∈Z+ are finite disjoint sets. Also El,l+1, l∈Z+ are
finite disjoint sets. An edgeein El,l+1 has its source vertexs(e) in Vland its
terminal vertext(e) inVl+1respectively. Every vertex inV has a successor and
every vertex in Vl forl ∈ Nhas a predecessor. It is then required that there
exists an edge in El,l+1 with labelα and its terminal isv ∈Vl+1 if and only
if there exists an edge inEl−1,l with labelαand its terminal is ι(v)∈Vl. For
u∈Vl−1 andv∈Vl+1,we put
Eι(u, v) ={e∈El,l+1 |t(e) =v, ι(s(e)) =u},
Eι(u, v) ={e∈El−1,l |s(e) =u, t(e) =ι(v)}.
Then there exists a bijective correspondence betweenEι(u, v) andE
ι(u, v) that
preserves labels for each pair of vertices u, v. We call this property the local property of L. Let ΩL be the projective limit of the system ιl,l+1 : Vl+1 →
Vl, l∈Z+,that is defined by
ΩL={(vl)l∈Z+ ∈
Y
l∈Z+
Vl |ιl,l+1(vl+1) =vl, l∈Z+}.
We endow ΩL with the projective limit topology so that it is a compact
the set of all triplets (u, α, v)∈ΩL×Σ×ΩL such that for eachl ∈Z+, there
existsel,l+1∈El,l+1 satisfying
ul=s(el,l+1), vl+1=t(el,l+1) and α=λ(el,l+1)
whereu= (ul)
l∈Z+, v= (v
l)
l∈Z+∈ΩL.
Proposition 2.1. The setEL⊂ΩL×Σ×ΩLis a zero-dimensional continuous
graph.
Proof. It suffices to show thatEL is closed. For (u, β, v)∈ΩL×Σ×ΩL with
(u, β, v) 6∈ EL, one finds l ∈ N such that there does not exist any edge e in
El,l+1 withs(e) =ul, t(e) =vl+1 andλ(e) =β. Put
Uul ={(wi)i∈Z+∈ΩL|wl=ul}, Uvl+1 ={(wi)i∈Z+∈ΩL|wl+1=vl+1}.
They are open sets in ΩL. Hence Uul× {β} ×Uvl+1 is an open neighborhood of (u, β, v) that does not intersect withEL so thatEL is closed. ¤
We denote by{vl1, . . . ,vlm(l)} the vertex setVl.Put forα∈Σ, i= 1, . . . , m(1)
Ui1(α) ={(u, α, v)∈EL|v1=v1i wherev= (vl)l∈Z+∈ΩL}.
ThenU1
i(α) is a clopen set inEL such that
∪α∈Σ∪m(1)i=1 U 1
i(α) =EL, Ui1(α)∩Uj1(β) =∅ if (i, α)6= (j, β).
Put t(u, α, v) = v for (u, α, v) ∈ EL. Suppose that L is left-resolving. It is
easy to see that if U1
i(α) 6= ∅, the restriction of t to Ui1(α) is a
homeomor-phism onto Uv1 i ={(v
l)
l∈Z+ ∈ΩL | v
1 =v1
i}. Hence t : EL → ΩL is a local
homeomorphism.
Following Deaconu [De3], we consider the setXL of all one-sided paths ofEL:
XL={(αi, ui)∞i=1∈ ∞ Y
i=1
(Σ×ΩL)|(ui, αi+1, ui+1)∈EL for alli∈N
and (u0, α1, u1)∈EL for someu0∈ΩL}.
The set XL has the relative topology from the infinite product topology of
Σ×ΩL. It is a zero-dimensional compact Hausdorff space. The shift map
σ: (αi, ui)i=1∞ ∈XL →(αi+1, ui+1)∞i=1∈XL is continuous. Forv= (vl)l∈Z+∈ ΩL and α ∈ Σ, the local property of L ensures that if there exists e0,1 ∈
E0,1 satisfying v1 = t(e0,1), α = λ(e0,1), there exist el,l+1 ∈ El,l+1 and u =
(ul)
l∈Z+ ∈ΩL satisfying u
l =s(e
l,l+1), vl+1 =t(el,l+1), α =λ(el,l+1) for each
l∈Z+.Hence ifLis left-resolving, for anyx= (αi, vi)∞i=1∈XL, there uniquely
exists v0∈ΩL such that (v0, α1, v1)∈EL. Denote byv(x)0 the unique vertex
C -Algebras Associatedwith Presentations of Subshifts 7
Lemma 2.2. For aλ-graph system L, consider the following conditions
(i) Lis left-resolving.
(ii) EL is left-resolving, that is, for (u, α, v),(u′, α, v′)∈EL,the condition
v=v′ impliesu=u′.
(iii) σis a local homeomorphism onXL.
Then we have
(i)⇔(ii)⇒(iii).
Proof. The implications (i)⇔(ii) are direct. We will see that (ii)⇒(iii). Sup-pose thatLis left-resolving. Let{γ1, . . . , γm}= Σ be the list of the alphabet.
Put
XL(k) ={(αi, vi)∞i=1∈XL|α1=γk}
that is a clopen set of XL. Since the familyXL(k), k = 1, . . . , m is a disjoint
covering ofXL and the restriction ofσto each of themσ|XL(k):XL(k)→XL is a homeomorphism, the continuous surjectionσis a local homeomorphism on
XL. ¤
Remark. We will remark that a continuous graph coming from a left-resolving, predecessor-separatedλ-graph system is characterized as in the following way. LetE ⊂ V ×Σ× Vbe a continuous graph. Following [KM], we define thel-past context ofv∈ V as follows:
Γ−l (v) ={(α1, . . . , αl)∈Σl | ∃v0, v1, . . . , vl−1∈ V;
(vi−1, αi, vi)∈ E, i= 1,2, . . . , l−1,(vl−1, αl, v)∈ E}.
We sayE to be predecessor-separated if for two verticesu, v ∈ V, there exists
l ∈ N such that Γ−l (u) 6= Γ−l (v). The following proposition can be directly proved by using an idea of [KM]. Its result will not be used in our further discussions so that we omit its proof.
Proposition 2.3. Let E ⊂ V ×Σ× V be a zero-dimensional continuous graph such thatEis left-resolving, predecessor-separated. If the mapt:E → Vdefined byt(u, α, v) =vis a surjective open map, there exists aλ-graph systemLE over
Σ and a homeomorphismΦ from V onto ΩLE such that the map Φ×id×Φ:
V ×Σ× V →ΩLE ×Σ×ΩLE satisfies(Φ×id×Φ)(E) =ELE.
3. The C∗-algebraO L.
In what follows we assume L to be left-resolving. Following V. Deaconu [De2],[De3],[De4], one may construct a locally compact r-discrete groupoid from a local homeomorphismσonXL as in the following way (cf. [An],[Re]). Set
GL={(x, n, y)∈XL×Z×XL | ∃k, l≥0; σk(x) =σl(y), n=k−l}.
The range map and the domain map are defined by
The multiplication and the inverse operation are defined by
(x, n, y)(y, m, z) = (x, n+m, z), (x, n, y)−1= (y,−n, x).
The unit spaceG0
L is defined to be the spaceXL={(x,0, x)∈GL| x∈XL}.
A basis of the open sets forGL is given by
Z(U, V, k, l) ={(x, k−l,(σl|V)−1◦(σk(x))∈GL |x∈U}
where U, V are open sets ofXL, and k, l∈Nare such that σk|U andσl|V are
homeomorphisms with the same open range. Hence we see
Z(U, V, k, l) ={(x, k−l, y)∈GL |x∈U, y∈V, σk(x) =σl(y)}.
The groupoid C∗-algebra C∗(G
L) for the groupoid GL is defined as in the
following way ([Re], cf. [An],[De2],[De3],[De4]). Let Cc(GL) be the set of all
continuous functions onGL with compact support that has a natural product
structure of∗-algebra given by
(f∗g)(s) = X
t∈GL,
r(t)=r(s)
f(t)g(t−1s) = X
t1,t2∈GL,
s=t1t2
f(t1)g(t2),
f∗(s) =f(s−1), f, g∈C
c(GL), s∈GL.
Let C0(G0L) be the C∗-algebra of all continuous functions onG0L that vanish
at infinity. The algebraCc(GL) is aC0(G0L)-module, endowed with aC0(G0L
)-valued inner product by
(ξf)(x, n, y) =ξ(x, n, y)f(y), ξ∈Cc(GL), f ∈C0(GL0), (x, n, y)∈GL,
< ξ, η >(y) = X
x,n (x,n,y)∈GL
ξ(x, n, y)η(x, n, y), ξ, η∈Cc(GL), y∈XL.
Let us denote by l2(G
L) the completion of the inner productC0(G0L)-module
Cc(GL). It is a Hilbert C∗-right module over the commutative C∗-algebra
C0(G0L). We denote by B(l2(GL)) the C∗-algebra of all bounded adjointable
C0(G0L)-module maps on l2(GL). Let π be the ∗-homomorphism of Cc(GL)
into B(l2(G
L)) defined by π(f)ξ=f ∗ξ for f, ξ ∈Cc(GL). Then the closure
ofπ(Cc(GL)) in B(l2(GL)) is called the (reduced)C∗-algebra of the groupoid
GL, that we denote byC∗(GL).
Definition. The C∗-algebraO
L associated with λ-graph system L is defined
to be theC∗-algebraC∗(G
L)of the groupoid GL.
We will study the algebraic structure of the C∗-algebra OL. Recall that Λk
denotes the set of all words of Σk that appear inL. Forx= (α
n, un)∞n=1∈XL,
C -Algebras Associatedwith Presentations of Subshifts 9
is written as v(x)n = (v(x)ln)l∈Z+ ∈ ΩL = lim←−Vl. Now L is left-resolving so that there uniquely exists v(x)0 ∈ΩL satisfying (v(x)0, α1, u1) ∈EL. Set for
µ= (µ1, . . . , µk)∈Λk,
U(µ) ={(x, k, y)∈GL|σk(x) =y, λ(x)1=µ1, . . . , λ(x)k =µk}
and forvli∈Vl,
U(vli) ={(x,0, x)∈GL |v(x)l0=vli}
wherev(x)0= (v(x)l0)l∈Z+∈ΩL.They are clopen sets ofGL. We set
Sµ =π(χU(µ)), Eli=π(χU(vl
i)) in π(Cc(GL))
where χF ∈ Cc(GL) denotes the characteristic function of a clopen set F on
the spaceGL.Then it is straightforward to see the following lemmas.
Lemma 3.1.
(i) Sµ is a partial isometry satisfying Sµ = Sµ1· · ·Sµk, where µ = (µ1, . . . , µk)∈Λk.
(ii) Pµ∈ΛkSµSµ∗= 1 fork∈N.We in particular have
(3.1) X
α∈Σ
SαSα∗ = 1.
(iii) El
i is a projection such that
(3.2)
m(l) X
i=1
Eil= 1, Eil= m(l+1)
X
j=1
Il,l+1(i, j)Ejl+1,
where Il,l+1 is the matrix defined in Theorem A in Section 1,
corre-sponding to the mapιl,l+1:Vl+1→Vl.
Take µ= (µ1, . . . , µk)∈Λk, ν = (ν1, . . . , νk′)∈Λk ′
and vli ∈Vl withk, k′≤l
such that there exist paths ξ, η in L satisfyingλ(ξ) =µ, λ(η) = ν andt(ξ) =
t(η) =vli.We set
U(µ,vli, ν) ={(x, k−k′, y)∈GL|σk(x) =σk ′
(y), v(x)lk=v(y)lk′ =vli,
λ(x)1=µ1, . . . , λ(x)k =µk, λ(y)1=ν1, . . . , λ(y)k′ =νk′ }.
The setsU(µ,vli, ν), µ∈Λk, ν
∈Λk′
, i= 1, . . . , m(l) are clopen sets and gener-ate the topology ofGL.
Lemma 3.2.
SµEilSν∗=π(χU(µ,vl
i,ν))∈π(Cc(GL)).
Hence theC∗-algebraO
L is generated bySα, α∈ΣandEli, i= 1, . . . , m(l), l∈
Z+.
The generatorsSα, Eilsatisfy the following operator relations, that are
Lemma 3.3.
SαSα∗Eli=EilSαSα∗,
(3.3)
S∗αEilSα= m(l+1)X
j=1
Al,l+1(i, α, j)El+1j ,
(3.4)
forα∈Σ, i= 1,2, . . . , m(l), l∈Z+,whereAl,l+1(i, α, j)is defined in Theorem
A in Section 1.
The four operator relations (3.1),(3.2),(3.3),(3.4) are called the relations (L). LetAl, l∈Z+be theC∗-subalgebra ofOLgenerated by the projectionsEil, i=
1, . . . , m(l), that is,
Al=CE1l⊕ · · · ⊕CEm(l)l .
The projections Sα∗Sα, α ∈ Σ and Sµ∗Sµ, µ ∈ Λk, k ≤ l belong to Al, l ∈ N
by (3.4) and the first relation of (3.2). Let AL be the C∗-subalgebra of OL
generated by all the projections El
i, i = 1, . . . , m(l), l ∈ Z+. By the second
relation of (3.2), the algebraAlis naturally embedded inAl+1 so thatALis a
commutative AF-algebra. We note that there exists an isomorphism between Al and C(Vl) for eachl ∈Z+ that is compatible with the embeddings Al ֒→
Al+1andIl,l+1t (=ι∗l,l+1) :C(Vl)֒→C(Vl+1).Hence there exists an isomorphism
betweenAL andC(ΩL). Letk, l be natural numbers withk≤l. We set
DL=TheC∗-subalgebra ofOL generated bySµaSµ∗, µ∈Λ∗, a∈ AL.
Fl
k =TheC∗-subalgebra ofOL generated bySµaSν∗, µ, ν∈Λk, a∈ Al.
Fk∞=TheC∗-subalgebra ofOL generated bySµaSν∗, µ, ν∈Λk, a∈ AL.
FL=TheC∗-subalgebra ofOL generated bySµaSν∗, µ, ν∈Λ∗,
|µ|=|ν|, a∈ AL.
The algebraDL is isomorphic to C(XL). It is obvious that the algebra Fkl is
finite dimensional and there exists an embeddingιl,l+1 :Fkl ֒→ F l+1
k through
the preceding embeddingAl ֒→ Al+1. Define a homomorphismc : (x, n, y)∈
GL→n∈Z.We denote byFL the subgroupoidc−1(0) ofGL. LetC∗(FL) be
its groupoidC∗-algebra. It is also immediate that the algebraFLis isomorphic
toC∗(FL). By (3.1),(3.3),(3.4), the relations:
Eil= X
α∈Σ m(l+1)
X
j=1
Al,l+1(i, α, j)SαEjl+1Sα∗, i= 1,2, . . . , m(l)
hold. They yield
SµEilSν∗= X
α∈Σ m(l+1)
X
j=1
Al,l+1(i, α, j)SµαEjl+1S∗να forµ, ν ∈Λk,
that give rise to an embedding Fl
k ֒→ Fk+1l+1. It induces an embedding ofFk∞
intoF∞
C -Algebras Associatedwith Presentations of Subshifts 11
Proposition 3.4. (i) F∞
k is an AF-algebra defined by the inductive limit of the embeddings
ιl,l+1:Fkl ֒→ F l+1 k , l∈N.
(ii) FL is an AF-algebra defined by the inductive limit of the embeddings
λk,k+1:Fk∞֒→ Fk+1∞ , k∈Z+.
be the expectation from OL onto the fixed point subalgebraOLαL under αL
defined by
By the relations (3.6), each element X∈ PL is expressed as a finite sum
X = X
Then the following lemma is routine.
Lemma 3.5. The fixed point subalgebra OLαL of OL under αL is the
AF-algebra FL.
We can now prove a universal property ofOL.
Theorem 3.6. The C∗-algebraO
L is the universal C∗-algebra subject to the
relations(L).
Proof. Let O[L] be the universal C∗-algebra generated by partial isometries
op-the similarly defined subalgebras of O[L] to Fkl,FL respectively. The algebra
F[k][l] as well asF l
k is a finite dimensional algebra. Since sµelis∗ν6= 0 if and only
ifSµEliSν∗ = 06 ,the correspondence sµelis∗ν →SµEilSν∗,|µ|=|ν|=k≤l yields
an isomorphism fromF[k][l] to Fl
k. It induces an isomorphism fromF[L] to FL.
By the universality, for z ∈C,|z| = 1 the correspondence sα →zsα, α ∈Σ,
el
i → eli, i = 1, . . . , m(l), l ∈ Z+ gives rise to an action of the torus group
T on O[L], which we denote by α[L]. Let E[L] be the expectation from O[L]
onto the fixed point subalgebra O[L]α[L] under α[L] similarly defined to (3.5).
The algebra O[L]α[L] is nothing but the algebra F[L]. By the universality of
O[L], the correspondence sα → Sα, α ∈ Σ, eli → Eil, i = 1, . . . , m(l), l ∈ Z+
extends to a surjective homomorphism from O[L] to OL, which we denote by
πL. The restriction ofπLtoF[L] is the preceding isomorphism. As we see that
EL◦πL=πL◦E[L] andE[L] is faithful, we conclude thatπL is isomorphic by
a similar argument to [CK; 2.12. Proposition]. ¤
4. Uniqueness and simplicity
We will prove thatOLis the uniqueC∗-algebra subject to the operator relations
(L) under a mild condition onL,called (I). The condition (I) is a generalization of condition (I) for a finite square matrix with entries in{0,1}defined by Cuntz-Krieger in [CK] and condition (I) for a subshift defined in [Ma4]. A related condition for a HilbertC∗-bimodule has been introduced by
Kajiwara-Pinzari-Watatani in [KPW]. For an infinite directed graph, such a condition is defined by Kumjian-Pask-Raeburn-Renault in [KPRR]. For a vertexvli∈Vl, let Γ+(vli)
be the set of all label sequences in Lstarting atvli. That is,
Γ+(vli) ={(α1, α2, . . . ,)∈ΣN | ∃en,n+1∈En,n+1 forn=l, l+ 1, . . .; vli=s(el,l+1), t(en,n+1) =s(en+1,n+2), λ(en,n+1) =αn−l+1}.
Definition. Aλ-graph systemLsatisfies condition (I) if for eachvli∈V,the
setΓ+(vl
i)contains at least two distinct sequences.
Forvli∈VlsetFil={x∈XL |v(x)l0=vli} wherev(x)0= (v(x)l0)l∈Z+∈ΩL= lim
←−Vl is the uniqueι-orbit forx∈XL such that (v(x)0, λ(x)1, v(x)1)∈EL as
in the preceding section. By a similar discussion to [Ma4; Section 5] (cf.[CK; 2.6.Lemma]), we know that ifLsatisfies (I), forl, k∈Nwithl≥k, there exists
yl
i∈Filfor each i= 1,2, . . . , m(l) such that
σm(yl
i)6=yjl for all 1≤i, j≤m(l), 1≤m≤k.
By the same manner as the proof of [Ma4;Lemma 5.3], we obtain
Lemma 4.1. Suppose that L satisfies condition (I). Then for l, k ∈ N with l≥k, there exists a projectionql
k ∈ DL such that
(i) ql
ka6= 0for all nonzeroa∈ Al,
(ii) ql
kφmL(qkl) = 0for all m= 1,2, . . . , k,whereφmL(X) = P
C -Algebras Associatedwith Presentations of Subshifts 13
(i) The correspondence: X ∈ Fl
k −→ QlkXQlk ∈ QlkFklQlk extends to an
We then prove the uniqueness of the algebraOL subject to the relations (L).
Theorem 4.3. Suppose that L satisfies condition (I). Let Sbα, α ∈ Σ and
from the AF-algebraFLonto the AF-algebraFbL.By Theorem 3.6, the algebra
OL has a universal property subject to the relations (L) so that there exists
a surjective homomorphism ˆπ from OL onto ObL satisfying ˆπ(Sα) = Sbα and
ˆ
π(El
i) =Ebil.The restriction of ˆπto FL is the preceding isomorphism onto FbL.
NowLsatisfies (I). LetQlkbe the sequence of projections as in Lemma 4.2. We
putQbl
By a similar argument to [CK;2.9.Proposition], it follows that the map X ∈
Put
Γ−1(x) ={γ∈Σ|(v−1, γ, v(x)0)∈ELfor some v−1∈ΩL}.
We define the creation operatorsSeβ, β∈Σ onHL by
e
Sβex= ½e
βx ifβ ∈Γ−1(x),
0 ifβ 6∈Γ−1(x).
Proposition 4.4. Suppose that Lsatisfies condition (I). If Lis predecessor-separated, OL is isomorphic to the C∗-algebraC∗(Seβ, β ∈Σ)generated by the
partial isometries Seβ, β∈Σon the Hilbert space HL.
Proof. Suppose thatL is predecessor-separated. Define a sequence of projec-tionsEel
i, i= 1, . . . , m(l), l∈N and Eei0, i= 1, . . . , m(0) by using the formulae
(1.7) from the partial isometries Seβ, β ∈ Σ. It is straightforward to see that e
El
i, i = 1, . . . , m(l), l ∈ Z+ are nonzero. The partial isometries Seβ and the
projectionsEel
i satisfy the relations (L). ¤
Let Λ be a subshift andLΛits canonical λ-graph system, that is left-resolving and predecessor-separated. It is easy to see that Λ satisfies condition (I) in the sense of [Ma4] if and only if LΛ satisfies condition (I).
Corollary 4.5(cf.[Ma],[CaM]). The C∗-algebra OLΛ associated with
λ-graph system LΛ is canonically isomorphic to the C∗-algebra O
Λ associated
with subshift Λ.
We next refer simplicity and purely infiniteness of the algebraOL. We introduce
the notions of irreducibility and aperiodicity forλ-graph system
Definition.
(i) Aλ-graph systemL is said to be irreducible if for a vertex v∈Vl and
x= (x1, x2, . . .)∈ ΩL = lim
←−Vl, there exists a path in L starting atv
and terminating atxl+N for someN ∈N.
(ii) Aλ-graph system Lis said to be aperiodic if for a vertex v ∈Vl there
exists an N ∈ N such that there exist paths in L starting at v and terminating at all the vertices ofVl+N.
Aperiodicity automatically implies irreducibility. Define a positive operatorλL
onAL by
λL(X) = X
α∈Σ
Sα∗XSα for X ∈ AL.
We say thatλLisirreducibleif there exists no non-trivial ideal ofAL invariant
under λL, andλL isaperiodic if for a projectionEil ∈ Al there exists N ∈ N
such thatλN
C -Algebras Associatedwith Presentations of Subshifts 15
Lemma 4.6.
(i) Aλ-graph system Lis irreducible if and only ifλL is irreducible.
(ii) Aλ-graph system Lis aperiodic if and only ifλL is aperiodic.
We thus obtain
Theorem 4.7. Suppose that a λ-graph system L satisfies condition (I). If L
is irreducible,OL is simple.
Proof. Suppose that there exists a nonzero idealI ofOL. AsLsatisfies
condi-tion (I), by uniqueness of the algebra OL,I must contain a projection Eil for
some l, i. HenceI ∩ AL is a nonzero ideal ofAL that is invariant under λL.
This leads toI=AL so thatOL is simple. ¤
The above theorem is a generalization of [CK; 2.14.Theorem] and [Ma;Theorem 6.3]. We next see that OL is purely infinite (and simple) if L is aperiodic.
Assume that the subshift presented byλ-graph systemLis not a single point. Note that ifLis aperiodic, it satisfies condition (I). By [Bra;Corollary 3.5], the following lemma is straightforward.
Lemma 4.8. Aλ-graph systemLis aperiodic if and only if the AF-algebraFL
is simple.
As in the proof of [C3;1.6 Proposition], we conclude
Proposition 4.9 (cf.[C;1.13 Theorem]). If a λ-graph system L is aperi-odic,OL is simple and purely infinite.
5. K-Theory
The K-groups for the C∗-algebras associated with subshifts have been
com-puted in [Ma2] by using an analogous idea to the Cuntz’s paper [C3]. The dis-cussion given in [Ma2] well works for our algebrasOL associated withλ-graph
systems. Let (A, I) be the nonnegative matrix system of the symbolic matrix system for L. We first study theK0-group for the AF-algebraFL. We denote
by Λk(vl
i) the set of words of length k that terminate at the vertex vli. Let
Fkl,i be theC∗-subalgebra ofFkl generated by the elementsSµEilSν∗, µ, ν∈Λk.
It is isomorphic to the full matrix algebraMnl
i(k)(C) of sizen
l
i(k) wherenli(k)
denotes the number of the set Λk(vl
i), so that one sees
Fl k ∼=Mnl
1(k)(C)⊕ · · · ⊕Mn l
m(l)(k)(C). The map Φl
k : [SµEilSµ∗]∈K0(Fkl)→[Eil]∈K0(Al) fori= 1,2, . . . , m(l), µ∈
Λk(vl
i) yields an isomorphism between K0(Fkl) and K0(Al) = Zm(l) = Pm(l)
i=1 Z[Eil].The isomorphisms Φlk, l∈Ninduce an isomorphismΦk = lim−→ l
Φl k
from K0(Fk∞) = lim−→ ιl,l+1∗
K0(Fkl) ontoK0(AL) = lim−→ ιl,l+1∗
The latter group is denoted by ZIt, that is isomorphic to the abelian group
matrix system (A, I) defined in [Ma5]. The dimension group for a nonnegative square finite matrix has been introduced by W. Krieger in [Kr] and [Kr2]. It is realized as theK0-group for the canonical AF-algebra inside the Cuntz-Krieger
algebra associated with the matrix ([C2],[C3]). If aλ-graph systemLis arising from the finite directed graph associated with the matrix, the C∗-algebrasOL
andFLcoincide with the Cuntz-Krieger algebra and the canonical AF-algebra
respectively (cf. Section 7). Hence in this case, K0(FL) coincides with the
Krieger’s dimension group for the matrix.
Let p0 : T → OL be the constant function whose value everywhere is the
C -Algebras Associatedwith Presentations of Subshifts 17
4.6] and [Ma2;Corollary 4.7], the automorphism β−1 : K
0(FL) → K0(FL)
corresponds to the shift σon lim
−→{ZIt, λ(A,I)}.That is, ifx= (x1, x2, . . .) is a
sequence representing an element of lim
−→{ZIt, λ(A,I)},thenβ
−1xis represented
by σ(x) = (x2, x3, . . .). As the dimension automorphism δ(A,I) of ∆(A,I) is
defined to be the shift of the inductive limit lim
−→{ZIt, λ(A,I)}([Ma5]), we obtain
Proposition 5.3. (K0(FL), K0(FL)+,αcL∗)∼= (∆(A,I),∆+(A,I), δ(A,I)).
We will next present the K-theory formulae forOL. AsK1(OL⋊αLT) = 0,the Pimsner-Voiculescu’s six term exact sequence of the K-theory for the crossed product (OL⋊αLT)⋊cαL Z[PV] says the following lemma:
Therefore we have the K-theory formulae for OL by a similar argument to
Proposition 5.6. The C∗-algebra OL is nuclear and satisfies the Universal
Coefficient Theorem in the sense of Rosenberg and Schochet [RS] (also [Bro2]).
Hence, for an aperiodicλ-graph system L, OL is a unital, separable, nuclear,
purely infinite, simpleC∗-algebra satisfying the UCT so that it lives in a
classi-fiable class of nuclearC∗-algebras by Kirchberg [Kir] and Phillips [Ph]. As the
K-groupsK0(OL), K1(OL) are countable abelian groups withK1(OL) torsion
free by Theorem 5.5, Rørdam’s result [Rø;Proposition 6.7] says the following: Corollary 5.7. For an aperiodic λ-graph system L, the C∗-algebra O
L is
isomorphic to the C∗-algebra of an inductive limit of a sequenceB
1→B2 →
B3→ · · · of simple Cuntz-Krieger algebras.
Set the Ext-groups
Ext1(OL) = Ext(OL), Ext0(OL) = Ext(OL⊗C0(R)).
As the UCT holds for our algebras as in the lemma below, it is now easy to compute the Ext-groups by using Theorem 5.5.
Lemma 5.8([RS],[Bro2]). There exist short exact sequences
0−→Ext1Z(K0(OL),Z)−→Ext1(OL)−→HomZ(K1(OL),Z)−→0,
0−→Ext1Z(K1(OL),Z)−→Ext0(OL)−→HomZ(K0(OL),Z)−→0
that split unnaturally.
We denote byZI the abelian group defined by the projective limit lim←− l {
Il,l+1:
Zm(l+1) → Zm(l)}. The sequence A
l,l+1, l ∈ Z+ naturally acts on ZI as an
endomorphism that we denote byA. The identity onZI is denoted byI. Then
the cokernel and the kernel of the endomorphismI−A onZI are the
Bowen-Franks groups BF0(A, I) and BF1(A, I) for (A, I) respectively ([Ma5]). By [Ma5;Theorem 9.6], there exists a short exact sequence
0−→Ext1Z(K0(A, I),Z)−→BF0(A, I)−→HomZ(K1(A, I),Z)−→0
that splits unnaturally. And also
BF1(A, I)∼= HomZ(K0(A, I),Z).
As in the proof of [Ma5;Lemma 9.7], we see that Ext1Z(ZIt,Z) = 0 so that Ext1Z(Ker(id−λ(A,I)) inZIt,Z) = 0.This means that Ext1Z(K1(A, I)),Z) = 0. Theorem 5.5 says thatKi(A, I)∼=Ki(OL) so that we conclude by Lemma 5.8,
Theorem 5.9.
(i) Ext(OL) = Ext1(OL)∼=BF0(A, I) =ZI/(I−A)ZI,
(ii) Ext0(OL)∼=BF1(A, I) = Ker(I−A)in ZI.
C -Algebras Associatedwith Presentations of Subshifts 19
6. Realizations as endomorphism crossed products and Hilbert C∗-bimodule algebras
Following Deaconu’s discussions in [De2],[De3],[De4], we will realize the algebra OLas an endomorphism crossed productFL×βLN.Recall that the algebraFL is isomorphic to theC∗-algebraC∗(F
L) of the groupoidFL. The groupoidFL
is written as
{(x, y)∈XL×XL|σk(x) =σk(y) for somek∈Z+}.
Put
βL(f)(x, y) =
1
p
p(σ(x))p(σ(y))f(σ(x), σ(y)), f ∈Cc(FL), x, y∈XL
wherep(x) is the number of the pathszsuch thatσ(z) =x,and for (x, n, y)∈
GL
v(x, n, y) =
( √ 1
p(σ(x)), ifn= 1 and y=σ(x),
0 otherwise.
RegardingC∗(FL) as a subalgebra ofC∗(GL), one sees thatvis a nonunitary
isometry satisfying βL(f) = vf v∗ ([De2],[De3],[De4]). Then βL is a proper
corner endomorphism ofC∗(F
L) such thatC∗(GL) is isomorphic to the crossed
productC∗(F
L)×βLN(cf.[Rø2]). We will write the isometryvin terms of the generators Sα, Eil. For l ∈ N, i = 1, . . . , m(l), we denote by nli the number
of the edges e in El−1,l such that t(e) = vli. As L is left-resolving, it is the
number of the symbols α∈Σ such that S∗
αSαEil 6= 0. It follows that nliEil = P
α∈ΣSα∗SαEil. Note that ifIl,l+1(i, j) = 1,thennli=n l+1
j . Then one obtains
(6.1) v=
m(l) X
i=1
1
p
nl i
X
α∈Σ
SαEil
where the right-hand side does not depend on the choice of l ∈ N. We can immediately see that OL is generated by the C∗-algebra FL and the above
isometryv,that satisfies
(6.2) v∗v= 1, vFLv∗⊂ FL, v∗FLv⊂ FL.
The universality (Theorem 3.6) of the algebraOLcorresponds to the
universal-ity of the crossed productC∗(F
L)×βLN.It needs however a slightly complicated argument to directly determine the operator relations (L) by using (6.1) and (6.2), as it is possible. There are some merits to realizeOL asFL×βLN.One is the fact that its purely infiniteness is immediately deduced from Rørdam’s result [Rø2;Theorem 3.1] under the condition thatFLis simple. The other one
is K-theory formulae. Rørdam also in [Rø2; Corollary 2.2] showed that (i) K0(FL×βLN)∼=K0(FL)/(id−βL∗)K0(FL).
(cf.Paschke [Pa], Deaconu [De3]). These are precisely the formulae of Lemma 5.4 with Lemma 5.2.
In [De3; Section 3], Deaconu showed that the groupoidC∗-algebras of continu-ous graphs are realized asC∗-algebras constructed from HilbertC∗-bimodules defined in [Pi] (see also [Kat]). A special case of continuous graphs was studied in Kajiwara-Watatani [KW]. We identify the algebraC(ΩL) of all continuous
functions on ΩL with the commutative C∗-algebra AL. Let XAL be the set
C(EL) of all continuous functions onEL, that is identified withP⊕α∈ΣCSαAL,
becauseLis left-resolving. We endowXAL with a HilbertC
∗-bimodule
struc-ture overAL defined by
(Sαa)·b=Sα·ab, < Sαa, Sβb >AL=a
∗S∗ αSβb,
φL(b)Sαa=bSαa=Sα·Sα∗bSαa
for a, b ∈ AL, α, β ∈ Σ. A special case of this construction of the Hilbert
C∗-bimodules is seen in the proof of [PWY;Theorem 4.2] for theC∗-algebras
associated with subshifts. The above mentioned Deaconu’s result says the following proposition:
Proposition 6.1. The C∗-algebra constructed from the Hilbert C∗-bimodule
(φL, XAL) overAL is isomorphic to theC
∗-algebraO L.
7. Examples
In this section, we give two kinds of examples of λ-graph systems and study their associated C∗-algebras. The first ones appear as presentations of sofic
shifts. The second one is defined by a Shannon graph with countable infinite vertices.
Presentations of sofic shifts come from labeled graphs with finite vertices that are calledλ-graphs (cf. [Fi],[Kr4],[Kr5],[LM],[We],. . . ). Let G= (V, E) be a finite directed graph with finite vertex set V and finite edge set E. Let G = (G, λ) be a labeled graph over Σ defined byGand a labeling mapλ:E→Σ.
Suppose that it is left-resolving and predecessor-separated. Let AG be the
adjacency matrix of G, that is defined by
AG(e, f) =
½ 1 ift(e) =s(e),
0 otherwise
for e, f ∈ E. The matrix AG defines a shift of finite type by regarding its
edges as its alphabet. Since the matrixAG is of entries in{0,1}, we have the
Cuntz-Krieger algebraOAG defined byAG ([CK] cf.[KPPR],[Rø]). By putting
C -Algebras Associatedwith Presentations of Subshifts 21
Proposition 7.1. The C∗-algebra OLG is isomorphic to the Cuntz-Krieger
algebra OAG.
Proof. Let V = {v1, . . . , vm} be the vertex set of G. Let Sα, α ∈ Σ be the
canonical generating partial isometries ofOLG. We denote by E1, E2, . . . , Em
the set of all minimal projections of Al = ALG, l ∈ N corresponding to the
vertices v1, . . . , vm.As the labeled graph G is predecessor-separated, they are
written in terms of Sα, α ∈ Σ as in (1.7). Note that in the algebra OLG,
SαEi 6= 0 if and only if there exists an edge e ∈ E satisfying λ(e) =α and
t(e) =vi.As Gis left-resolving, the correspondence
e∈E←→(λ(e), t(e))∈ {(α, vi)∈Σ×V |SαEi6= 0}
is bijective. For e∈E, putse=Sλ(e)Et(e)∈ OLG, whereEvi denotesEi. As
Et(e) =s∗ese for e ∈ E and Sα =P e∈E, λ(e)=α
se for α ∈ Σ, the algebra OLG is
generated by the partial isometriesse, e∈E. It is immediate to see that the
following relations hold:
X
e∈E
ses∗e= 1, s∗ese= X
f∈E
AG(e, f)sfs∗f.
This means that the C∗-algebra generated by s
e, e∈E is the Cuntz-Krieger
algebra OAG defined by the matrixAG. ¤
If, in particular, a labeled graph G = (G, λ) has different labels for different edges, it defines a shift of finite type. In this case, one may identify the edge set E with the alphabet Σ. LetLG be theλ-graph systemLG as in the above one. LetSα, α∈Σ be the generating partial isometries of OLG. It is obvious that the relations (1.4),(1.5) and (1.6) give rise to the following relations:
Sα∗Sα= X
β∈E
AG(α, β)SβSβ∗, α∈Σ.
Remark. While completing this paper, Toke M. Carlsen let the author know his preprint [Ca], where he shows that the C∗-algebra associated with sofic shifts are isomorphic to the Cuntz-Krieger algebras of their left Krieger cover graphs. His result is a special case of the above proposition.
We will next present a λ-graph system for which the associated C∗-algebra
is not stably isomorphic to any Cuntz-Krieger algebra and any Cuntz alge-bra. There is a method introduced in [KM] to constructλ-graph systems from Shannon graphs. By a Shannon graph we mean here a left-resolving labeled directed graph with countable vertices and finite labels.
Let us consider a Shannon graph defined as follows: Let V = {v1, v2, . . . ,}
edges labeledβ are fromv1 tov2 and fromv2n tov2n+2 forn= 1,2, . . . .The
edges labeled γ are self-loops at vn for n = 2,3, . . . . The edge labeled δ is a
self-loop at v1. The edges labeled ǫ are from v1 to vn for n = 1,2, . . . . The
resulting labeled graph is left-resolving and hence it is a Shannon graph. We denote it by S. We will construct a λ-graph systemL(S) from the Shannon graphS by a method introduced in [KM] as in the following way. For a vertex
v ∈ V and for l ∈ N, let Γ−l (v) be the set of all label sequences of length l
terminating atv.Define an equivalence relationv≈(l)v′ for verticesv, v′∈V
by Γ−l (v) = Γ−l (v′). For l = 0, define v ≈
(l) v′ for all v, v′ ∈ V. The vertex
set Vl is then defined by the set of ≈(l)-equivalence classes of V. We denote
byVl={vl1, . . . ,vlm(l)}.The verticesv l
i, i= 1, . . . , m(l) ofVl may be identified
with {Γ−l (v) :v∈V}. We define a mapιl,l+1 :Vl+1 →Vl byιl,l+1(vl+1j ) =vli
ifvl+1j ⊂vli.We define an edge labeledω∈Σ fromvli tovl+1j if there exists an edge labeledωin S from a vertex invl
i to a vertex invl+1j . Then the resulting
labeled graph with vertex setsVl, labeled edges fromVltoVl+1 and surjective
mapsιl,l+1:Vl+1→Vlforl∈Z+defines aλ-graph system over Σ ([KM]). We
denote it byL(S).
The vertex setsVl, l∈Z+ are written as in the following way:
V0:v01={vn |n= 1,2, . . .}.
V1:v11={v1},v12={v2n |n= 1,2, . . .},v13={v2n+1 |n= 1,2, . . .}.
V2:v21={v1},v22={v2},v23={v2n | n= 2,3, . . .}, v24={v2n+1 |n= 1,2, . . .}.
V3:v31={v1},v32={v2},v33={v4},v34={v2n |n= 3,4, . . .}, v35={v2n+1 |n= 1,2, . . .}.
V4:v41={v1},v42={v2},v43={v4},v44={v6},v54={v2n |n= 4,5, . . .}, v46={v3},v47={v2n+1 |n= 2,3, . . .}.
V5:v51={v1},v52={v2},v53={v4},v54={v6},v55={v8}, v56={v2n |n= 5,6, . . .},v57={v3},v58={v5}, v59={v2n+1 |n= 3,4, . . .}.
V6:v61={v1},v26={v2},v63={v4},v64={v6},v65={v8},v66={v10}, v67={v2n |n= 6,7, . . .},v68={v3},v69={v5},v610={v7}, v611={v2n+1 |n= 4,5, . . .}.
V7:v71={v1},v27={v2},v73={v4},v74={v6},v75={v8},v76={v10}, v77={v12},v78={v2n |n= 7,8, . . .},v79={v3},v710={v5},v711={v7}, v712={v9},v713={v2n+1 |n= 5,6, . . .}.
C -Algebras Associatedwith Presentations of Subshifts 23
Lemma 7.2. The λ-graph system L(S)is aperiodic.
Proof. Take and fix an arbitrary vertexvli∈Vl, letkbe the minimum number
such thatvk∈vli.There exists a path of lengthkinL(S) that starts atvliand
ends atvl+k1 ={v1} ∈Vl+k whose label is (α, α, . . . , α). There exist edges from vl+k1 tovl+k+1j for allj= 1,2, . . . , m(l+ 1) whose labels areǫ. This means that
L(S) is aperiodic. ¤
Therefore the associated C∗-algebra O
L(S)is simple and purely infinite.
Let us compute its K-groups. We first present the matrices At
Proof. It suffices to show the surjectivity of the induced map
z= [zi]2l+1i=1 ∈Z2l+1/(Atl,l+1−Il,l+1t )Z2l−1−→(ϕl(z), ψl(z), ξl(z))∈Z3.
For (m, n, k)∈Z⊕Z⊕Z,putz= [zi]2l+1i=1 where
zi=
0 fori= 1,2, . . . ,2l−3,2l, m fori= 2l−2,
n fori= 2l−1, k fori= 2l+ 1.
Then we see that ϕl(z) =m, ψl(z) =n, ξl(z) =k. ¤
We denote by ρl+1 the above isomorphism from Z2l+1/(Al,l+1t −Il,l+1t )Z2l−1
onto Z3. Let L be the matrix −
1 1 0 −1 0 1 −1 0 1
. Since the following diagram is
commutative:
Z2l−1/(At
l−1,l−Ilt−1,l)Z2l−3 It
l,l+1
−−−−→ Z2l+1/(At
l,l+1−Il,l+1t )Z2l−1 ρl
y ρl+1
y
Z3 −−−−→L Z3,
we obtain
Proposition 7.5. K0(OL(S))∼= 0.
Proof. AsL3= 0, by Theorem 5.5, it follows that
K0(OL(S)) = lim−→{Z2l+1/(Atl,l+1−Il,l+1t )Z2l−1,I¯l+1,l+2t }= lim−→{Z3, L} ∼= 0.
¤
Concerning the groupK1(OL(S)), one sees
Proposition 7.6. K1(OL(S))∼=Z.
Proof. Forl≥5, putx(l) = [xi]2li=1−1∈Z2l−1where
x1= 1, x2=−1, x3=−2,
xi=−1 for i= 4,6,8, . . . ,2l−4,2l−3,2l−1,
xi= 0 for i= 5,7,9, . . . ,2l−5,2l−2.
It is easy to see that
Ker(Atl,l+1−Il,l+1t ) =Zx(l), Il,l+1t x(l) =x(l+ 1).
Hence we obtainK1(OL(S))∼=Zby Theorem 5.5. ¤
C -Algebras Associatedwith Presentations of Subshifts 27
Theorem 7.7. TheC∗-algebraOL(S)is unital, simple, purely infinite, nuclear
and generated by five partial isometries with mutually orthogonal ranges. Its K-groups are
K0(OL(S))∼= 0, K1(OL(S))∼=Z.
As theK1-group of a Cuntz-Krieger algebra is the torsion-free part of itsK0
-group, the algebraOL(S)lives outside the Cuntz-Krieger algebras (cf.[Ma3]). Remark. M. Tomforde in [T] considered C∗-algebras associated to labeled graphs as a generalization of Cuntz-Krieger algebras (cf.[T2]). He deals with labeled directed graphs with (generally) infinite vertices. If the labeled graphs have finite vertices, the resulting graphs are ones in the first examples of this section. In this case, hisC∗-algebras coincide with ourC∗-algebras. The referee
informed to the author that his algebras in general are not ours of λ-graph systems.
References
[An] C. Anantharaman-Delaroche,Purely infiniteC∗-algebras arising from dynamical systems, Bull. Soc. Math. France125(2)(1997), 199–225. [Bl] B. Blackadar,K-Theory for operator algebras, Springer-Verlag, Berlin,
Heidelberg and New York, 1986.
[Bra] O. Bratteli,Inductive limits of finite-dimensionalC∗-algebras, Trans.
Amer. Math. Soc.171(1972), 195–234.
[Bro] L. G. Brown, Stable isomorphism of hereditary subalgebras of C∗
-algebras, Pacific. J. Math. 71(1977), 335–348.
[Bro2] L. G. Brown,The universal coefficient theorem for Ext and quasidiag-onality, Operator Algebras and Group Representation, Pitman Press
17(1983), 60–64.
[Ca] T. M. Carlsen, On C∗-algebras associated with sofic shifts, preprint
2000.
[CaM] T. M. Carlsen and K. Matsumoto,Some remarks on the C∗-algebras
associated with subshifts, preprint 2001.
[C] J. Cuntz, Simple C∗-algebras generated by isometries, Commun.
Math. Phys. 57(1977), 173–185.
[C2] J. Cuntz,K-Theory for certain C∗-algebras, Ann. Math.113(1981),
181–197.
[C3] J. Cuntz, A class of C∗-algebras and topological Markov chains II:
reducible chains and the Ext-functor for C∗-algebras, Invent. Math. 63(1980), 25–40.
[CK] J. Cuntz and W. Krieger, A class of C∗-algebras and topological
Markov chains, Invent. Math.56(1980), 251–268.
[De] V. Deaconu,Groupoids associated with endomorphisms, Trans. Amer. Math. Soc. 347(1995), 1779–1786.
[De3] V. Deaconu, Generalized solenoids andC∗-algebras, Pacific J. Math.
190(1999), 247–260.
[De4] V. Deaconu,Continuous graphs and C∗-algebras, Operator Theoret-ical Methods (Timi¸c soara, 1998) Theta Found., Bucharest (2000), 137–149.
[EL] R. Excel and M. Laca, Cuntz-Krieger algebras for infinite matrices, J. reine. angew. Math.512(1999), 119–172.
[Fi] R. Fischer, Sofic systems and graphs, Monats. f¨ur Math. 80 (1975), 179–186.
[H] D. Huang,Flow equivalence of reducible shifts of finite type and Cuntz-Krieger algebras, J. reine angew. Math.462(1995), 185–217. [KPW] T. Kajiwara, C. Pinzari and Y. Watatani,Ideal structure and
simplic-ity of the C∗-algebras generated by Hilbert modules, J. Funct. Anal. 159(1998), 295–322.
[KPW2] T. Kajiwara, C. Pinzari and Y. Watatani, Hilbert C∗-bimodules and
countably generated Cuntz-Krieger algebras, J. Operator Theory 45
(2001), 3–18.
[KW] T. Kajiwara and Y. Watatani, Hilbert C∗-bimodules and continuous
Cuntz-Krieger algebras considered by Deaconu, J. Math. Soc. Japan
54(2002), 35–60.
[Kat] Y. Katayama,Generalized Cuntz algebrasOM
N, RIMS kokyuroku858
(1994), 87–90.
[Kir] E. Kirchberg, The classification of purely infinite C∗-algebras using
Kasparov’s theory, preprint,1994.
[Kit] B. P. Kitchens, Symbolic dynamics, Springer-Verlag, Berlin, Heidel-berg and New York, 1998.
[Kr] W. Krieger, On dimension functions and topological Markov chains, Invent. Math.56(1980), 239–250.
[Kr2] W. Krieger, On dimension for a class of homeomorphism groups, Math. Ann252(1980), 87–95.
[Kr3] W. Krieger,On sofic systems I, Israel J. Math.48(1984), 305–330. [Kr4] W. Krieger,On sofic systems II, Israel J. Math60 (1987), 167–176. [KM] W. Krieger and K. Matsumoto, Shannon graphs, subshifts and
lambda-graph systems, to appear in J. Math. Soc. Japan.
[KPR] A. Kumjian, D. Pask and I. Raeburn, Cuntz-Krieger algebras of di-rected graphs, Pacific J. Math.184(1998), 161–174.
[KPRR] A. Kumjian, D. Pask, I. Raeburn and J. Renault, Graphs, groupoids and Cuntz-Krieger algebras, J. Funct. Anal.144(1997), 505–541. [LM] D. Lind and B. Marcus, An introduction to symbolic dynamics and
coding, Cambridge University Press., 1995.
[Ma] K. Matsumoto,OnC∗-algebras associated with subshifts, Internat. J. Math. 8(1997), 357–374.
C -Algebras Associatedwith Presentations of Subshifts 29
[Ma3] K. Matsumoto, A simple C∗-algebra arising from a certain subshift, J. Operator Theory42(1999), 351-370.
[Ma4] K. Matsumoto,Dimension groups for subshifts and simplicity of the associated C∗-algebras, J. Math. Soc. Japan 51(1999), 679-698. [Ma5] K. Matsumoto,Presentations of subshifts and their topological
conju-gacy invariants, Doc. Math.4(1999), 285-340.
[Ma6] K. Matsumoto,Bowen-Franks groups for subshifts and Ext-groups for C∗-algebras, K-Theory23(2001), 67–104.
[Ma7] K. Matsumoto,C∗-algebras associated with presentations of subshifts II. Ideal structure and lambda-graph subsystems, preprint, 2001. [Pas] W. Paschke, The crossed product of a C∗-algebra by an
endomor-phism, Proc. Amer. Math. Soc. 80(1980), 113–118.
[Ph] N. C. Phillips,A classification theorem for nuclear purely infinite sim-ple C∗-algebras, Doc. Math.5(2000), 49–114.
[Pi] M. V. Pimsner, A class of C∗-algebras, generalizing both
Cuntz-Krieger algebras and crossed product byZ, in Free Probability Theory, Fields Institute Communications12(1996), 189–212.
[PV] M. Pimsner and D. Voiculescu, Exact sequences for K-groups and Ext-groups of certain cross-products C∗-algebras, J. Operator Theory 4(1980), 93–118.
[PWY] C. Pinzari, Y. Watatani and K. Yonetani, KMS states, entropy and the variational principle in full C∗-dynamical systems, Commun.
Math. Phys. 213(2000), 331–381.
[Pu] I. Putnam, C∗-algebras from Smale spaces, Canad. J. Math. 48
(1996), 175–195.
[Re] J. N. Renault,A groupoid approach to C∗-algebras, Lecture Notes in
Math. Springer793(1980).
[Ri] M. Rieffel,C∗-algebras associated with irrational rotations, Pacific J.
Math. 93(1981), 415–429.
[Rø] M. Rørdam, Classification of Cuntz-Krieger algebras,, K-Theory 9
(1995), 31–58.
[Rø2] M. Rørdam, Classification of certain infinite simple C∗-algebras,, J.
Funct. Anal.131(1995), 415–458.
[Ro] J. Rosenberg, Appendix to O. Bratteli’s paper “Crossed products of UHF algebras ”, Duke Math. J.46(1979), 25–26.
[RS] J. Rosenberg and C. Schochet, The K¨unneth theorem and the uni-versal coefficient theorem for Kasparov’s generalized K-functor, Duke Math. J.55 (1987), 431–474.
[T] M. Tomforde,C∗-algebras of labeled graphs, preprint.
[T2] M. Tomforde, A unified approach to Exel-Laca algebras and C∗ -algebras associated to directed graphs, preprint.
[We] B. Weiss,Subshifts of finite type and sofic systems, Monats. Math.77
Kengo Matsumoto
Department of Mathematical Science Yokohama City University
Sato 22-2, Kanazawa-ku, Yokohama 236-0027, Japan
Effective Freeness of Adjoint Line Bundles
Gordon Heier
Received: March 19, 2002
Communicated by Thomas Peternell
Abstract. This note shows how two existing approaches to provid-ing effective (quadratic) bounds for the freeness of adjoint line bundles can be linked to establish a new effective bound which approximately differs from the linear bound conjectured by Fujita only by a factor of the cube root of the dimension of the underlying manifold. As an application, a new effective statement for pluricanonical embeddings is derived.
2000 Mathematics Subject Classification: 14C20, 14F17, 14B05. Keywords and Phrases: adjoint linear system – vanishing theorem – Fujita conjecture.
1 Introduction and statement of the Main Theorem
Let L be an ample line bundle over a compact complex projective manifold
X of complex dimensionn. LetKX be the canonical line bundle of X. The
following conjecture is due to Fujita [Fuj87].
Conjecture 1.1 (Fujita). The adjoint line bundle KX+mL is base point
free (i.e. spanned by global holomorphic sections) for m ≥n+ 1. It is very ample form≥n+ 2.
The standard example of the hyperplane line bundle onX =Pnshows that the
Ein and Lazarsfeld [EL93] (see also [Fuj93]), and n = 4 is due to Kawamata [Kaw97]. In arbitrary dimension n, the state-of-the-art is that KX +mL is
base point free for any integermthat is no less than a number roughly of order
n2 (see below for exact statements).
To the author’s knowledge, [Dem00] constitutes the most recent survey on the subject under discussion. It contains an extensive list of references (see also the references at the end of this article) and, furthermore, introduces the reader to various other effective results in algebraic geometry.
The above-mentioned bound in the case of arbitrary dimensionncan be derived from each of the following two theorems, due to Angehrn and Siu [AS95] (see also [Siu96]) and Helmke [Hel97], [Hel99], respectively. Although the proofs of these two theorems adhere to the same inductive approach, the key ideas at their cores are of a different nature. In Proposition 3.5, we will show how to use the techniques in question seamlessly in a back-to-back manner. This insight, together with the numerical considerations in Section 2, will lead to the improved bound asserted in the Main Theorem and proved in Section 3. First, let us state the bound given by [AS95].
Theorem 1.2([AS95]). The line bundleKX+mLis base point free form≥ 1
2n(n+ 1) + 1.
Secondly, we state Helmke’s result. Due to the nature of his technique, the assumptions of his theorem are formulated in a slightly different way. We quote the result in the way it is presented in [Hel97], because the slight improvement achieved in [Hel99] is not relevant for our purposes.
Theorem 1.3 ([Hel97]). Assume thatL has the additional properties that
Ln> nn
and for allx∈X:
Ld.Z
≥mx(Z)·nd
for all subvarieties Z ⊂X with x ∈ Z, d = dimZ ≤n−1 and multiplicity mx(Z)≤
¡n−1 d−1 ¢
atx. ThenKX+Lis base point free.
Ifn≥3, it is clear that we need to set
m0:= max{n· d sµn
−1
d−1
¶
:d∈Nand 1≤d≤n}
to determine the minimal bound m0 deducible from Theorem 1.3 such that
KX+mLis base point free for any integerm≥m0. Since
d
sµn
−1
d−1
¶
≥ √d1 3
n1−1 d
according to our Lemma 2.3, we find that the m0 which one can derive from
Theorem 1.3 is essentially also of the order n2.
We conclude this section with the statement of our Main Theorem, which asserts that the boundm0 can be chosen to be a number of the ordern
4 3. Theorem1.4(Main Theorem). The line bundleKX+mLis base point free
for any integerm with
In order to understand precisely the nature of the numerical conditions in the assumptions of Theorem 1.3, we prove some auxiliary estimates in this section. We begin with the following lemma.
Lemma 2.1. For allx∈]0,1[ : 1<³1−1x´
1−x x
< e.
Proof. It is obvious that 1 is a strict lower bound of the given expression, so it remains to show that
Taking log on both sides of the inequality, we see that we are done if we can show that
g(x) := x−1
x log(1−x)<1
on the open unit interval. However, for this it suffices to prove that limx→0+g(x) = 1 andg′(x)<0. The former is easily verified using L’Hˆopital’s rule, while the latter follows readily from a simple computation.
In the proof of the subsequent Lemma 2.3, we will employ Lemma 2.1 in the form of the following corollary.
The preceding considerations allow us to estimate the binomial coefficients from Theorem 1.3 in the form of the following lemma.
Lemma 2.3. Let 1≤d≤n−1. Then
Proof. In [Ahl78], page 206, Stirling’s formula is stated as
Γ(x) =√2π xx−12e−xe
for anyx≥1. Thus, for the proof of the desired estimate from above, Stirling’s formula enables us to proceed as follows.
µ
Resorting to Corollary 2.2, we eventually conclude:
µn
The desired estimate from below is proved analogously:
Using Corollary 2.2 again, we obtain:
µn
−1
d−1
¶1 d
≥ d
r
1 3n
n d =
1 d √
3
n1−1 d
d .
3 Proof of the Main Theorem
The following theorem states the improved effective freeness bound which we shall prove at the end of this section.
Theorem3.1(Main Theorem). The line bundleKX+mLis base point free
for any integerm with
m≥(e+1 2)n
4 3 +1
2n 2 3 + 1,
wheree≈2.718 is Euler’s number.
First of all, let us recall how a result of this type can be proved by means of multiplier ideal sheaves.
Let x∈X be an arbitrary but fixed point. The key idea of both [AS95] and [Hel97] is to find an integer m0 (as small as possible) and a singular metric h
of the line bundlem0Lwith the following two properties:
1. Lethbe given locally bye−ϕ. Then the curvature currenti∂∂ϕ¯ dominates
a positive definite smooth (1,1)-form onX in the sense of currents. 2. Let themultiplier ideal sheafofhbe defined stalk-wise by (χ∈X):
(Ih)χ:={f ∈ OX,χ:|f|2e−ϕ is locally integrable atχ}.
Then, in a neighborhood ofx, the zero set of Ih, which we denote by
V(Ih), is just the pointx. (This is the key property we are looking for.
Note that the support ofV(Ih) is just the set of points where h is not
locally integrable.) The first property implies that
Hq(X,Ih(KX+m0L)) = (0) (q≥1),
due to the vanishing theorem of Nadel [Nad89], [Nad90]. (In the special case when the singular metric is algebraic geometrically defined, Nadel’s vanish-ing theorem is the same as the theorem of Kawamata and Viehweg [Kaw82], [Vie82].) With this information and the second property, it is easy to obtain an element of Γ(X, KX+m0L) which does not vanish atx. Namely, consider
the short exact sequence