DIKTAT
PENGANTAR STOKHASTIK
Oleh
Drs. Yerizon, M. Si
Dra. Minora Longgom Nasution
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI PADANG
KATA PENGANTAR
Puji syukur penulis panjatkan kehadirat Allah SWT, yang telah memberikan rahmat dan karunia-Nya, sehingga penulis dapat menyelesaikan diktat “Pengantar Stokhastik” ini.
Diktat ini penulis susun dengan maksud agar mahasiswa pengikut mata kuliah Pengantar Stokhastik dapat lebih mudah mempelajari dan memahami materi mata kuliah ini. Karena materi Pengantar Stokhastik agak sulit dipahami dibandingkan dengan materi matematika lainnya. Untuk itu diktat ini disusun sedemikian rupa sehingga lebih mudah dipahami. Disamping manfaat bagi mahasiswa, diharapkan diktat ini juga bermanfaat bagi dosen yang mengajarkan mata kuliah ini.
Penulis menyadari, bahwa diktat ini masih jauh dari sempurna, untuk itu penulis sangat mengharapkan kritik dan saran dari semua pihak, demi kesempurnaan diktat ini pada edisi-edisi berikutnya. Pada kesempatan ini penulis juga mengucapkan terima kasih banyak kepada semua pihak yang telah membantu dalam penyusunan diktat ini.
Akhirnya penulis mengharapkan agar diktat ini dapat bermanfaat sebagai mana mestinya.
Padang, Oktober 2003
DAFTAR ISI
Halaman
KATA PENGANTAR i
DAFTAR ISI ii
BAB 1 PENDAHULUAN 1
1.1 Peluang 1
1.2 Distribusi Peluang Diskret Khusus 8
1.3 Beberapa Distribusi Peluang Kontinu 21
BAB 2 RANTAI MARKOV WAKTU DISKRIT 26
2.1 Pengantar 26
2.2 Matriks Peluang Transisi 29
2.3 Beberapa Model Rantai Markov 33
2.4 Analisis Langkah Pertama Sederhana 36
2.5 Beberapa Rantai Markov Khusus 40
BAB 3 PRILAKU JANGKA PANJANG RANTAI MARKOV 46
3.1 Matriks Peluang Transisi Reguler 46
3.2 Klasifikasi State 49
3.3 Teorema Limit Dasar dari Rantai Markov 54
BAB 4 RANTAI MARKOV WAKTU KONTINU 57
4.1 Pengantar 57
4.2 Proses Kelahiran Murni 58
4.3 Proses Kematian Murni 61
4.4 Proses Kelahiran dan Kematian 63
BAB 5 MODEL ANTRIAN 68
5.1 Proses Antrian 68
5.2 Model Antrian Pelayan Tunggal 68
5.3 Model Antrian Pelayan Majemuk 72
5.4 Antrian dengan Populasi Hingga 75
1.2 Distribusi Peluang Diskret Khusus
Banyak peubah acak yang dihasilkan dalam percobaan statistika mempunyai sifat yang sama dan pada dasarnya dapat dinyatakan dengan distribusi peluang yang sama. Misalnya semua peubah acak yang menyatakan banyaknya sukses dalam n usaha bebas dalam suatu percobaan. Jika peluang sukses tidak berubah pada tiap n usaha, mempunyai ciri umum yang sama dan karenanya dapat dinyatakan dengan rumus tunggal.
Orang harus hati-hati memilih distribusi peluang yang tepat menggambarkan pengamatan yang dihasilkan oleh percobaan. Dalam bagian ini akan dibahas beberapa distribusi peluang diskret. Tapi sebelumnya akan disajikan kembali beberapa definisi dan teorema yang berkaitan dengan distribusi peluang diskret.
Bukti:
2 = E(x - )2
= E(x2 - 2x + 2)
= E(x2) - 2E(x) + 2 (karena E(x) = ) = E(x2) - 22 + 2
= E(x2) - 2 Distribusi Seragam(Uniform)
Distribusi peluang diskret yang paling sederhana adalah yang peubah acaknya memperoleh semua harganya dengan peluang sama. Distribusi peluang semacam ini disebut distribusi seragam atau uniform.
Definisi 1.2.1
Fungsi f(x) adalah suatu fungsi peluang atau distribusi peluang suatu peubah acak diskret X jika memenuhi,
a. f(x) 0
b.
x x f( ) 1 c. P(X = x) = f(x)
Definisi 1.2.2
Misalkan X suatu peubah acak diskret dengan distribusi peluang f(x), maka nilai harapan X adalah E(x) =
x x xf( ).
Teorema 1.2.1
Variansi peubah acak X adalah 2
Notasi f(x;k) telah dipakai sebagai pengganti f(x) untuk menunjukkan bahwa distribusi seragam tersebut bergantung pada parameter k.
Bukti :
Untuk membuktikan teorema 1.2.2 dilakukan sebagai berikut : Menurut definisi 1.2.2 di atas, maka diperoleh,
Dari teorema 1.2.1, diperoleh,
kemudian tentukan rata-rata dan variansinya.Jawab
Ruang sampel dari masalah di atas adalah S = {1, 2, 3, 4, 5, 6}. Jadi peluang yang muncul tiap mata dadu adalah 1/6, hal ini merupakan distribusi uniform sehingga peluangnya f(x; 6) = 1/6, untuk x = 1, 2, 3, 4, 5, dan 6.
Berdasarkan teorema 1.2.2 di atas maka diperoleh
= 3,5
Definisi 1.2.3
Misalkan peubah acak X mempunyai distribusi uniform diskret. Maka distribusi peluangnya diberikan dengan
f(x ; k) =
k 1
. untuk x = x1, x2, x3, …xk.
dimana xi xj dengan i j.
Teorema 1.2.2
Rataan dan variansi distribusi uniform diskret f(x ; k) adalah
Distribusi Bernoulli
Peubah acak bernoulli hanya mempunyai dua nilai yaitu 0 dan 1 dalam satu kali percobaan. Nilai 0 dan 1 ini biasanya dikaitkan dengan “gagal” dan “sukses”. Dan peluang sukses dinyatakan dengan p dan gagal dengan 1 - p. Untuk lebih jelasnya perhatikan definisi berikut.
Distribusi bernoulli biasa juga dilambangkan dengan X ~ Bernoulli(p). Rataan dan variansi dari distribusi Bernoulli dinyatakan dengan teorema berikut.
Bukti :
Dari definisi 1.2.2 dan 1.2.4, diperoleh
p) ; xf(x E(x)
1
0 x
=
1
0
x -1 x
q xp x
= 0.p0q1-0 + 1p1q1-1 = p Dari teorema 1.2.1 diperoleh,
E(xi - )2
2
E(x2) – [E(x)]2
Dari hasil E(x) = p, sekarang akan dicari E(x2) sebagai berikut E(x ) x f(x ;p)
1
0 x
2
2
=
1
0
x -1 x 2
q p x x
= 02.p0q1-0 + 12 p1q1-1 = p Jadi E(x - )2
i
2
E(x2) – [E(x)]2 = p – p2 = p(1-p) = pq. Contoh
Sebuah mata uang dilempar satu kali, dicatat bahwa hasilnya yang muncul muka “M” dan belakang “B”. Tentukan peluang muncul muka, rata-rata dan variansinya
Jawab
Ruang sampel dari masalah di atas adalah S = {M, B} dan misalkan kejadian muncul muka adalah A = {M}, dan Belakang adalah C = {B}.
Definisi 1.2.4
Suatu peubah acak X dikatakan mengikuti distribusi Bernoulli dengan parameter p jika hanya mempunyai dua kemungkinan nilai yaitu 0 dan 1 dan distribusi peluangnya didefinisikan dengan
f(x; p) = px(1-p)1-x = px(q)1-x , untuk x = 0, 1
Teorema 1.2.3
Distribusi Bernoulli f(x; p) mempunyai rata-rata dan variansi = p dan 2
Sehingga peluang muncul muka adalah P(M) = n(s) n(A)
=
2 1
, dalam hal ini sesuai dengan distribusi bernoulli yaitu f(x; p) = px(1-p)1-x, untuk x = 0, 1.
Karena p = 0,5 dan dari definisi 1.2.4, f(x; p) = (0,5)x(0,5)1-x, untuk x = 0, 1. Setelah dilakukan pelemparan ternyata mata uang muncul adalah muka, berarti x = 1 atau berhasil. Akibatnya f(x; p) = (0,5)1(0,5)1-1 = 0,5.
Berdasarkan teorema 1.2.3, diperoleh = p = 0,5 dan 2
= 0,5.0,5 = 0,25
Distribusi Binomial
Suatu peubah acak Binomial dapat dipandang sebagai jumlah n peubah acak Bernoulli, yakni banyaknya yang berhasil dalam n usaha Bernoulli.
Suatu percobaan Binomial memenuhi persyaratan berikut : a. percobaan terdiri atas n usaha yang berulang.
b. Tiap usaha memberikan hasil yang dapat ditentukan sukses atau gagal.
c. Peluang sukses, dinyatakan dengan p, tidak berubah dari usaha yang satu ke yang berikutnya.
d. Tiap usaha, bebas dengan usaha yang lainnya.
Distribusi bernoulli biasa juga dilambangkan dengan X ~ B(n,p). Rataan dan variansi dari distribusi Binomial dinyatakan dengan teorema berikut.
Bukti
Berdasarkan definisi 1.2.2, diperoleh = E(x) =
n
1 x
x -n x(1 p)
p x n
x =
n
1 x
x -n x
p) 1 ( p x)! -(n x!
n!
x
Definisi 1.2.5
Banyaknya sukses X dalan n usaha suatu percobaan binomial disebut suatu peubah acak binomial.
Definisi 1.2.6
Bila suatu usaha binomial dapat menghasilkan sukses dengan peluang p dan gagal dengan peluang q = 1 – p, maka distribuasi peluang acak binomial X, yaitu banyaknya sukses dalam n usaha bebas adalah
b(x;n,p) = pxqn-x x
n
, x = 0, 1, 2, …., n.
Teorema 1.2.4
=
E(x) = np. Selanjutnya akan dibuktikan 2= npq sebagai berikut : Sekarang akan dicari E(x2) = E[x(x -1)] + E(x)
Untuk mendapatkan E(x2) terlebih dahulu kita cari E[x(x -1)] sebagai berikut : E[x(x-1)] =
1. Sebuah tes benar-salah terdiri dari 10 pertanyaan. Berapa peluang untuk memperoleh 8 jawaban yang benar?. Tentukan rata-rata dan variansinya.
Jawab
p(delapan jawaban adalah benar) = b(8;10,1/2) =
=
10
2 1 ! 2 !. 8
.9.8! 10
= 45
10
2 1
Maka diperoleh
= np = 4.0,2 = 0,8 dan 2
= npq = 4.0,2.0,8 = 0,64.
2. Sebuah pesawat dengan 4 mesin dapat terbang jika sekurang-kurangnya 2 mesinnya bekerja. Berapa peluang pesawat itu dapat terbang dengan baik jika mesin-mesinya beroperasi secara independen dan tiap-tiap kerusakannya (mesin tidak berfungsi) mempunyai peluang q.
Jawab
Missal p = 1- q = peluang mesin yang tidak rusak, q peluang pesawat itu dapat terbang jika sekurang-kurangnya 2 mesin bekerja.
b(x;4 , q) =
1-q xq4-x x4
, x = 0, 1, 2, 3, 4
P(terbang baik) =
4 0q q -1 4 4
+
3 1q q -1 3 4
+
2 2q q -1 2 4
= 1 - 4q + 6q2 – 4q3 + q4 + 4(1 – 3q + 3q2 – q3) + 6(1- 2q + q2) q2
= 1 - 4q + 6q2 – 4q3 + q4 + 4 – 12q + 12q2 - 4q3 + 6q2 - 12q3 + 6q4
= 1 - 4q3 + 3q4
Teorema 1.2.5
Jika X mempunyai distribusi binomial dengan parameter n dan p dan Y =
n X
maka E(y) = p dan
n ) p 1 ( p 2
y
Distribusi Multinomial
Distribusi multinomial merupakan perluasan dari distribusi binomial.
Contoh
Bila dua dadu dilantunkan enam kali, berapakah peluang mendapat jumlah 7 atau 11 muncul dua kali, sepasang bilangan yang sama satu kali, dan pasangan lainnya tiga kali. Jawab
Misalkan kejadian berikut menyatakan E1 : jumlah 7 atau 11
E2 : pasangan bilangan yang sama muncul
E3 : baik pasangan yang sama maupun jumlah 7 atau 11
tidak muncul.
Ruang sampel dari soal di atas adalah S = {(1,1),(1,2),…,(6,6)} Maka peluang p1 = P(E1) = 8/36 = 2/9
p2 = P(E2) = 6/36 = 1/6
p3 = P(E3) = 22/36 = 11/18
dengan menggunakan distribusi Multinomial x1 = 2, x2 = 1, dan x3 = 3, maka diperoleh
peluangnya, yaitu
f(2,1,3; 2/9,1/6,11/18, 6) =
3 , 1 , 2
6
2 3
18 11 6 1 9 2
=
! 3 ! 1 ! 2
!
6 2 3
18 11 6 1 9 2
= 0,1127.
Distribusi Hipergeometrik
Misalkan suatu contoh berukuran n diambil secara acak (tanpa pengembalian) dari sebuah kantong yang berisi N buah benda yang mengandung k yang sukses dan N – k yang gagal.
Definisi 1.2.7
Bila suatu usaha tertentu dapat menghasilkan k macam hasil E1, E2, E3,….,Ek dengan
peluang p1, p2, p3,….,pk, maka distribusi peluang acak X1, X2, X3,….,Xk, yang
menyatakan terjadinya E1, E2, E3,….,Ek dalam n usaha bebas ialah
f(x1, x2 ,…., xk; p1, p2, p3,.,pk, n) =
k 2 1,x ,....,x
x n
k 2
1 x
k x
2 x
1 ,p ,....,p
p
dengan
k
1 i
x i
= n dan
k
1 i
p i
Contoh
Suatu kantor mempunyai 10 orang pekerja yang terdiri dari 3 orang pria dan 7 orang wanita. Manajer memilih empat diantara mereka secara random untuk mengikuti kursus singkat guna peningkatan kualitas.
a) Berapa peluang akan terpilihnya jumlah yang sama antara p dan w. b) Berapa peluang wanita lebih banyak dari pria
Jawab
a) Dari soal diketahui bahwa N = banyak pekerja dikantor, akan dipilih empat dari sepuluh untuk mengikuti kursus, jadi n = 4, karena ada 3 pria maka k = 3. karena yang akan dipilih harus 2 pria dan 2 wanita maka disini jelas p = 2 dan w = 2
b) Disini jelas bahwa kemungkinan wanita 4 atau 3.
Sehingga P(wanita > pria) =
Distribusi peluang peubah acak hipergeometrik X, yaitu banyaknya sukses dalam sampel acak ukuran n yang diambil dari N benda yang mengandung k bernama sukses dan N – k bernama gagal adalah
Teorema 1.2.6
Rataan dan variansi distribusi hipergeometrik h(x;N,n,k) adalah
Distribusi Poisson
Percobaan yang menghasilkan peubah acak X yang bernilai numerik, yaitu banyaknya sukses selama selang waktu tertentu atau dalam daerah tertentu, disebut percobaan Poisson. Panjang selang waktu tersebut dapat berupa menit, jam, hari dan sebagainya. Misalnya X menyatakan banyaknya hubungan telepon sejam yang diterima suatu kantor.
Suatu percobaan Poisson memiliki sifat sebagai berikut.
1. banyaknya sukses terjadi dalam suatu selang waktu atau daerah tertentu tidak terpengaruh oleh (bebas dari) apa yang terjadi pada selang waktu atau daerah lain yang terpilih.
2. peluang terjadinya suatu sukses (tunggal) dalam selang waktu yang amat pendek atau dalam daerah yang kecil sebanding dengan panjang selang waktu atau besarnya daerah dan tidak bergantung pada banyaknya sukses yang terjadi di luar selang waktu atau daerah tersebut.
3. peluang terjadinya lebih dari satu sukses dalam selang waktu yang pendek atau daerah yang sempit tersebut dapat diabaikan.
Distribusi peluang suatu peubah acak Poisson X disebut distribusi Poisson dan dinyatakan dengan p(x,μ) atau X ~ POI(λ), karena nilainya hanya bergantung pada μ, yaitu rata-rata banyaknya sukses yang terjadi dalam selang waktu atau daerah tertentu.
Bukti :
E(x) =
0 x
x
-x! e
x
=
1 x
x
-x! e
x
=
1 x
x
-1)! -x(x
e
x
=
1 x
1 -x
-1)! -(x e
=
1 x
1 -x
-1)! -(x e
Definisi 1.2.9
Banyaknya sukses X dalam suatu percobaan Poisson disebut suatu peubah acak Poisson.
Definisi 1.2.10
Distribusi peluang peubah acak Poisson X, yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu, diberikan oleh
... 2, 1, 0, x , ! )
;
(
x e x
p
x
dan menyatakan rata-rata banyaknya sukses yang terjadi dalam selang waktu atau daerah tertentu tersebut dan e = 2, 71828…
Teorema 1.2.7
Karena
1 x
1 -x
-1)! -(x e
= 1 maka E(x) = . Kemudian variansi distribusi Poisson diperoleh dengan mula-mula mencari
E[x(x-1)] =
0 xx
-x! e 1)
-x(x
=
2 xx
-x! e 1)
-x(x
=
2 xx
-2)! -1)(x -x(x
e 1)
-x(x
=
2 x2 2 -x
-2)! -(x e
= 2
2 x
2 -x
-2)! -(x e
Karena
1 x
2 -x
-2)! -(x e
= 1, maka E[x(x-1)] = 2. Maka E(x2) = E[x(x-1)] + E(x) = 2+ . Jadi var(x) = E(x2) – [E(x)]2 = 2+ - 2=
Contoh
1. Rata-rata terjadinya kecelakaan di persimpang jalan adalah tiga kali dalam satu minggu. Berapakah peluang terjadi kecelakaan tepat lima kali dalam satu minggu. Tentukan rata-rata dan variansinya
Jawab
Dari soal diketahui = 3 dan x = 5. Untuk itu , x 0,1,2,... !
) ;
(
x e x
p
x
Sehingga P(3) = ! 5
3 e-3 5
= 0,1008. Karena rata-rata = maka = 3. dan variansi 2 =
sehingga 2 = 3
2. Misalkan diketahui bahwa jumlah kendaraan pada persimpangan tertentu dalam interval (0, t) mengikuti distribusi poison X(t) dan rata-rata adalah 3t (t dalam satuan menit).
a) Tentukan peluang akan lewat paling sedikit 2 kendaraan dalam interval (0, t). b) Misalkan kejadian A paling sedikit 4 kendaraan lewat selama menit pertama
dan kejadian B paling banyak 2 kendaraan lewat selama menit kedua. Tentukan peluang terjadinya A dan B.
c) Tentukan rata-rata dan variansinya Jawab
a) Poisson(3t) = , !
) 3 ( )
3 (
3
x t e t p
x t
Peluang untuk jumlah kendaraan yang lewat paling banyak 2, merupakan komplemen dari
1
0 3
! 3
x
x t
x t e
= e-3t + 3t e-3t, sehingga
P(jumlah kendaraan lewat 2) = 1 – (e-3t
+ 3t e-3t).
b). P(A) =
k x
x t
x t e
4 3
! 3
, untuk t = 1 maka P(A) =
k x
x x e
4 3
! 3
P(B) =
2
0 3
! 3
x
x t
x t e
, untuk t = 1 maka P(B) =
2
0 3
! 3
x
x x e
,
P(A) P(B) = {1-
3
0 3
! 3
x
x x e
}
2
0 3
! 3
x
x x e
,
= (0,3856413)(0,4177639) = 0,161107 = 0,16
c). Karena rata-rata = maka = 3t dan variansi 2 = maka 2
= 3t.
Distribusi Binomial Negatif
Misalkan suatu percobaan yang berbagai sifatnya sama dengan percobaan binomial, kecuali di sini usaha diulangi sampai terjadi sejumlah sukses tertentu. Ingin diketahui peluang bahwa sukses ke k terjadi pada usaha ke x. Percobaan semacam ini disebut percobaan binomial negatif.
Distribusi peluang peubah binomial negatif akan dinyatakan dengan b*(x;k,p) atau X ~ NB(p,r), karena nilainya tergantung pada banyaknya sukses yang diinginkan dan peluang sukses dalam usaha tertentu.
Definisi 1.2.11
Banyaknya usaha X untuk menghasilkan k sukses dalam suatu percobaan binomial negatif disebut peubah binomial negatif.
Definisi 1.2.12
Bila usaha yang saling bebas dilakukan berulang kali menghasilkan sukses dengan peluang p sedangkan gagal dengan peluang q = 1 – p, maka distribusi peluang peubah acak X, diberikan oleh
b*(x; k, p) = pkqx-k 1
-k
1 -x
Contoh
1. Misalkan seseorang melantunkan tiga uang logam sekaligus. Tentukan probabilitis ia akan mendapat semuanya muka atau semuanya belakang yang kedua kalinya terjadi pada lantunan kelima.
Jawab
Dengan menggunakan distribusi binomial negatif untuk x = 5, k = 2 dan p = ¼ diperoleh b*(5; 2,1/4) =
3 2
4 3 4 1 1
4
= 4 5
5
4 3
=
256 27
2. Suatu kejadian yang saling bebas akan berhasil dengan peluang 0,4 dan gagal dengan peluang 0,6. Berapakah peluang terjadi 2 berhasil dari 5 usaha.
Jawab
Dengan menggunakan distribusi binomial negatif untuk x = 5, k = 3 dan p = 0,4 diperoleh b*(5; 3,0,4) =
0,4 2 0,6 32 4
= 6
0,4 2 0,6 3Distribusi Geometrik
Misalkan suatu kejadian E yang saling bebas mempunyai peluang p yang tidak berubah pada setiap usaha tertentu. Misalkan X banyaknya usaha yang diperlukan agar E terjadi sekali, maka X berdistribusi geometri.
Distribusi geometri biasa juga dilambangkan dengan X ~ GEO(p). Rataan dan variansinya adalah seperti teorema berikut.
Contoh
Dalam suatu proses produksi diketahui bahwa rata-rata 1 di antara 100 butir hasil produksi, cacat. Berapa peluang memeriksa 5 butir dan baru menemukan yang cacat pada yang kelima?. Tentukan rata-rata dan variansinya.
Definisi 1.2.13
Distribusi geometric yaitu bila usaha yang saling bebas dan dilakukan berulang kali menghasilkan sukses dengan peluang p dan gagal dengan peluang q = 1 – p, maka distribusi peluang peubah acak X, yaitu banyaknya usaha yang berakhir pada sukses yang pertama, diberikan oleh
g(x; p) = p qx-1 x = 1, 2, 3, …
Teorema 1.2.8
Rata-rata dan variansi distribusi Geometri g(x; p) adalah =
p
1 dan 2
= 2
Jawab
Gunakan distribusi goemetri dan dari soal diperoleh x = 5 dan p = 0,01, maka g(5; 0,01) = (0,01)(0,99)4 = 0,0096.
Karena rata-rata = p
1 maka = 0,01
1
= 100
Dan variansi 2
= 2
p
q maka 2
= 2
(0,01) 0,99
=
99 100
Latihan 1.2
1. Dari 5 kunci pada suatu rantai kunci, misalkan tepat satu yang membuka suatu gembok, tetapi tidak diketahui yang mana. Misalkan X banyak kunci yang dicobakan dalam usaha membuka gembok, dengan pemisalan bahwa kunci dicoba secara acak tanpa pengembalian. Hitunglah fungsi peluangnya X serta tentukan nilai rata-rata dan variansinya.
2. Lampu hijau pada suatu persimpangan, nyala selama 15 detik, kuning 5 detik, dan merah 55 detik. Misalkan bahwa keadaan lalu-lintas mengakibatkan variasi acak dalam waktu tiba di persimpangan, sehingga “mendapat lampu hijau” merupakan kejadian yang berpeluang disebut “berhasil” dan kita tiba pada setiap saat dalam siklus lampu dengan peluang yang sama. Cari distribusi X yang menyatakan bahwa banyaknya yang berhasil dalam suatu usaha perjalanan ke persimpangan itu, kemudian tentukan rata-rata dan variansinya.
3. Seorang pemain basket, melakukan tembakan sebanyak 10 kali dan peluang untuk masuk 0,3 tiap-tiap tembakan. Berapa peluang untuk memenangkan 6 kali tembakan.
4. Jika peluang menang dari kuda pacuan yang kita pilih = 0,2 dan x adalah nomor pilihan yang terdiri dari 20 pilihan.
a. berapa peluang jika nomor 4 yang terpilihan
b. Berapa peluang paling banyak 4 nomor yang terpilih c. Hitunglah rata-rata dan variansinya
5. Menurut teori genetika, persilangan tertentu sejenis marmut akan menghasilkan keturunan berwarna merah, hitam dan putih dalam perbandingan 8 : 4 : 4. Carilah peluang bahwa lima dari 8 turunan akan berwarna merah, dua hitam dan satu putih. 6. Seorang tukang ketik rata-rata melakukan dua kesalahan per halaman. Berapakah
1.3 Beberapa Distribusi Peluang Kontinu
Pada bagian ini akan dibahas akan dibahas beberapa distribusi peluang kontinu. Tapi sebelumnya akan disajikan kembali beberapa definisi dan teorema yang berkaitan dengan distribusi peluang kontinu.
Distribusi Normal
Distribusi normal merupakan distribusi kontinu yang terpenting dalam seluruh bidang statistika. Distribusi ini sering pula disebut distribusi Gauss.
Selanjutnya akan dibuktikan bahwa parameter dan 2 adalah betul rataan dan variansi distribusi normal sebagai berikut:
Terlebih dahulu akan ditunjukkan rataan yaitu dengan menggunakan definisi di atas, tulislah
E(X) =
2 -x 2 1
-e 2
1 x
dx =
2 -x 2 1
-e x 2
1
dx.
Definisi 1.3.1
Fungsi f(x) adalah fungsi padat peluang peubah acak kontinu X, yang didefinisikan di atas himpunan semua bilangan real R, bila
1. f(x) 0 untuk semua x R. 2.
1 dx f(x)
3. P(a < x < b) =
b
a
dx f(x)
Definisi 1.3.2
Misalkan X suatu peubah acak kontinu dengan distribusi peluang f(x), maka Nilai harapan (rata-rata) X adalah E(x) =
dx f(x)
x .
Definisi 1.3.3
Fungsi padat peubah acak normal X, dengan rataan dan variansi 2
, adalah F(x) = n(x; ,) =
2
) -x ( 2 1
-e 2
1
, untuk (- < x < ), dengan = 3,14159….. dan e = 2,71828….
Definisi 1.3.4
Dengan menganti Z =
dari sini kita lihat satu persatu agar mudah mengintegralnya.
Untuk
Berdasarkan definisi di atas maka diperolah
ze merupakan fungsi ganjil. Jadi E(x) = .
Sekarang akan dibuktikan variansi 2
=
merupakan distribusi normal baku dengan parameter = 0 dan
2
= 1 dan dengan menggunakan definisi di atas maka diperoleh
Jadi terbukti bahwa parameter dari distribusi normal adalah dan 2
.
Distribusi Eksponensial
Distribusi eksponensial biasa dinotasikan dengan X ~ EXP(λ), dan mempunyai fungsi padat peluang seperti definisi berikut.
Bukti.
Rataan dapat dihitung dengan cara berikut
Definisi 1.3.5
Fungsi padat peluang distribusi eksponensial diberikan oleh
Teorema 1.3.1
Variansi dapat dihitung dengan cara berikut
2
0
λx 2
2 x λe dxE[X]
=
2 1
Distribusi Gamma
Distribusi gamma biasa dinotasikan dengan X ~ GAM(λ,k), dan mempunyai fungsi padat peluang seperti definisi berikut.
Dengan menggunakan integral parsial maka diperoleh,
0
2 0
1| ( 1) ( 1) ( 1)
)
(k e xxk k e xxk dx k k dan
0
1 )
1
( e xdx
Bukti.
Rataan dapat dihitung dengan cara berikut
0
λx 1 k k
dx Γ(k)
e x λ x ] [X
E =
0
λx k 1 k
dx 1) Γ(k
e x λ k
=
k
Variansi dapat dihitung dengan cara berikut 2 E[X2]E[X]2 =
2
k
Perlu dicatat bahwa GAM(λ,1) = EXP(λ). Definisi 1.3.6
Fungsi padat peluang distribusi eksponensial diberikan oleh
Γ(k)
e x
λ
) (
λx 1 k k
x
f , untuk x ≥ 0
dimana
0
1 )
(k e xxk dx
Teorema 1.3.2
Rata-rata dan variansi distribusi eksponensial adalah =
k
dan 2
= 2 λ
Latihan 1.3
1. Misalkan X adalah berapa kali sisi gambar muncul bila sekeping uang logam setimbang dilemparkan 40 kali. Hitunglah peluang bahwa X = 20. Gunakan hampiran normal dan kemudian bandingkan dengan nilai peluang pastinya.
2. Untuk menentukan keefektifan suatu diit tertentu dalam menurunkan kadar kolesterol di dalam darah, 100 orang menjalani diit ini. Setelah berdiit selama beberapa lama yang dianggap cukup, kadar kolesterol mereka diukur. Ahli gizi yang melakukan percobaan ini telah memutuskan untuk menyarankan diit ini bila sedikitnya 65 persen dari orang-orang tersebut menunjukkan penurunan kadar kolesterol setelah menjalani diit tersebut. Berapa peluang bahwa ahli gizi itu akan merekomendasikan diit tersebut bila sesungguhnya diit tersebut tidak berpengaruh pada kadar kolesterol di dalam darah.
3. Suatu ujian sering dianggap baik (dalam arti memberikan perpencaran skor nilai bagi yang menempuhnya) jika skor ujian yang dihasilkannya dapat dihampiri oleh suatu fungsi kepekatan normal.dosen sering menggunakan nilai skor ujian untuk menduga parameter normal dan 2, dan kemudian menetapkan nilai A bagi mereka yang memperoleh nilai lebih besar daripada + , B bagi mereka yang nilainya antara dan + , C bagi mereka yang nilainya antara - dan , D bagi mereka yang nilainya antara - 2 dan - , dan E bagi mereka yang nilainya dibawah - 2. Hitunglah berapa persen peluang masing-masing mahasiswa yang mendapat niali A, B, C, D, dan E.
4. Buktikan
2 -x 2 1
-e 2
1
dx = 1
5. Buktikan jika X N(x;,), maka
BAB 1
PENDAHULUAN
1.1Peluang
Pengertian pokok dalam teori peluang adalah eksperimen yang hasilnya (outcome) tidak dapat ditentukan sebelumnya. Eksperimen merupakan suatu percobaan yang dapat diulang dengan kondisi yang sama, sedangkan hasilnya belum tentu sama. Ruang sampel suatu eksperimen adalah himpunan semua hasil eksperimen yang mungkin. Suatu event atau kejadian adalah himpunan bagian dari ruang sampel.
Ada beberapa aturan yang berlaku dalam teori peluang, seperti dalam teorema berikut.
Bukti.
(i). Karena AAc = S dan A∩Bc = Ǿ, maka kita punya 1 = P{S} = P{ AAc} = P{A} + P{Ac}
(ii). Karena kejadian A – B dan A∩B saling lepas dan (A – B) A∩B = A maka P{A} = P{(A – B) A∩B}= P{A – B} + P{A∩B}.
(iii). Jika AB, maka B dapat dikomposisikan dalam kejadian saling lepas A dan B – A. Maka P{B} = P{A (B – A)} = P{A} + {B – A} P{A}
(iv). Kejadian A B dapat dikomposisikan dalam kejadian saling lepas A - B dan B. Maka P{A B} = P{(A – B) B} = P{A - B} + P{B}= P{A}- P{A∩B} + P{B}. Karena P{A - B} = P{A}- P{A∩B}.
Definisi 1.1.1
Misalkan A adalah sebarang kejadian dalam ruang sampel S Peluang dari kejadian A adalah P{A} yang memenuhi tiga aksioma berikut.
(i). 0 ≤ P{A} ≤ 1. (ii). P{S} = 1
(iii). Untuk sebarang barisan kejadian-kejadian A1, A2, ... yang saling lepas,
1 1
} {
n n
n
n P A
A
P
Teorema 1.1.1
Misalkan A dan B adalah sebarang kejadian. Maka (i). P{Ac} = 1 – P{A}
Dari teorema di atas maka diperoleh akibat berikut.
Peluang terjadinya suatu kejadian B bila diketahui bahwa kejadian A telah terjadi disebut peluang bersyarat dan dinyatakan dengan P(B | A). Lambang P(B | A) biasanya dibaca “peluang B terjadi bila diketahui A” atau “peluang B, bila A diketahui dan didefinisikan sebagai berikut.
Jika P{AB}P{A}P{B} atau ekivalen dengan P{A|B}P{A} maka kejadian A dan B dikatakan mutually independent atau independent. Dari teorema di atas dapat dikatakan bahwa peluang A dan B terjadi serentak sama dengan peluang A terjadi dikalikan dengan peuang terjadinya B bila A telah terjadi.
Secara umum dapat ditulis.
Definisi berikut memberikan pengertian tentang partisi dari suatu ruang sampel. Akibat 1.1.1
Untuk sebarang kejadian A, B dan C maka
P{A B C} = P{A} + P{B}+ P{C}- P{A∩B}- P{B∩C} - P{A∩C} + P{A∩B∩C}
Definisi 1.1.2
Untuk sebarang kejadian A dan B dalam ruang sampel S, peluang bersyarat dari kejadian A, jika diberikan B didefinisikan dengan
0 } { , } {
} {
} |
{ P B
B P
B A P B A
P atau P{AB}P{A|B}P{B}
Akibat 1.1.2
Untuk sebarang kejadian A1, A2, …, An berlaku
} ... |
{ }... |
{ } | { } { } ...
{A1 A2 An P A1 P A2 A1 P A3 A1 A2 P An A1 A2 An
P
Definisi 1.1.3
Kejadian A1, A2, …, An adalah partisi dari ruang sampel S. Jika kejadian Ai adalah
saling lepas dan gabungannya S yaitu jika j i untuk
j i A
A dan A1A2...An S
Teorema berikut dikenal sebagai formula peluang total.
Bukti.
Jelas bahwa P{A|Bi}P{Bi} = P{A ∩ Bj} dan (A ∩ Bi)(A ∩ Bj) = A ∩( Bi ∩ Bj)= Ǿ untuk
sebarang i ≠ j. Kita punya
n i
i i P B
B A P 1
} { } |
{ =
n i
i
B A P 1
}
{ = P{AB1AB2...ABn} = )}
... (
{A B1 B2 Bn
P = P{A}. Teorema di atas valid jika kejadian B1, B2, ..., Bn
berbentuk sebuah partisi. Karena A (B1 B2 … Bn}= S
Teorema berikut dikenal sebagai teorema Bayes.
Bukti.
Dengan menggunakan peluang bersyarat dalam definisi 1.1.2 kita punya
} {
} {
} | {
A P
A B P A B
P i i
selanjutnya dengan menggunakan formula peluang total untuk penyebut dari sisi kanan maka terbukti teorema di atas.
Contoh.
1. Sebuah perusahaan memproduksi produk yang sama dengan menggunakan tiga mesin yang berbeda, katakan B1, B2 dan B3 yang masing-masing dengan kapasitas produksi
60%, 30%, dan 10%. Persentase produksi yang cacat tiap mesin adalah 6%, 3%, dan 5%.
a. Hitunglah peluang, bahwa produk diambil secara acak adalah cacat.
b. Hitunglah peluang bersyarat, bahwa produk cacat yang diambil secara acak berasal dari mesin B1, B2 dan B3
Teorema 1.1.2 (Formula Peluang Total)
Misalkan A, B1, B2, ..., Bn menunjukkan kejadian sehingga Bj ∩ Bj = Ǿ untuk sebarang i
≠ j dan A (B1 B2 … Bn. Maka
n i
i i P B
B A P A
P
1
} { } | { }
{ di mana P{Bi} > 0. (i = 1, 2, …, n)
Teorema 1.1.3 (Teorema Bayes)
Misalkan A, B1, B2, ..., Bn menunjukkan kejadian sehingga Bj ∩ Bj = Ǿ untuk sebarang i
≠ j dan A (B1 B2 … Bn. Maka
n
i i i
i i i
B P B A P
B P B A P A B P
1
} { } | {
} { } | { } | {
Jawab.
a. Misalkan A adalah kejadian bahwa produk yang diambil secara acak adalah cacat. Maka dengan menggunakan formula peluang total kita punya
b. Dengan menggunakan formula Bayes diperoleh
}
2. Pada suatu perguruan tinggi, 40 % laki-laki dan 1 % wanita tingginya lebih dari 6 kaki. Selanjutnya 60 % mahasiswa adalah wanita. Jika seorang mahasiswa dipilih secara acak dan tingginya lebih dari 6 kaki, maka berapa peluang yang terpilih tersebut adalah wanita?.
Jawab.
Misalkan W = {mahasiswa yang tingginya lebih dari 6 kaki} dan P(W|A) adalah peluang bersyarat bahwa seorang mahasiswa adalah wanita jika diberikan mahasiswa yang tingginya lebih dari 6 kaki. Dengan menggunakan teorema Bayes diperoleh
)
Harapan Matematika
.
Sekarang pandanglah fungsi g(x) dari peubah acak X, yaitu tiap nilai g(x) dapat ditentukan bila diketahui nilai X. Misalnya bila X bernilai 2 maka g(X) bernilai g(2). Khususnya bila X peubah acak diskret dengan distribusi peluang f(x), x = -1, 0, 1, 2 dan g(X) = X2, maka
P[g(X) = 0] = P(X = 0) = f(0)
P[g(X) = 1] = P(X = -1) + P(X = 1) = f(-1) + f(1) P[g(X) = 4] = P(X = 2) = f(2)
Dengan menggunakan definisi 1.1.4 maka diperoleh
) (
)] ( ) ( [ ) ( )]
( [
x g
x g X g P x g X
g E
= 0.P[g(X) = 0] + 1.P[g(X) = 1] + 4.P[g(X) = 4] = 0.f(0) + 1.[f(-1) + f(1)] + 4.f(2)
=
x
x f x g( ) ( )
Hasil ini diperluas secara umum seperti teorema berikut.
Contoh.
Misalkan X suatu peubah acak dengan distribusi peluang sebagai berikut.
x 0 1 2 3
f(x) 1/3 1/2 0 1/6
Hitunglah nilai harapan dari Y = (X – 1)2
. Definisi 1.1.4
Misalkan X adalah suatu peubah acak dengan distribusi peluang f(x). Maka nilai harapan X atau harapan matematik X adalah
x
x xf X
E( ) ( ) bila X diskret
xf x dx
X
E( ) ( ) bila X kontinu
Teorema 1.1.4
Misalkan X suatu peubah acak dengan distribusi peluang f(x). Nilai harapan fungsi g(x) adalah
x
x f x g X
E( ) ( ) ( ) bila X diskret
g x f x dx
X
Jawab.
Penggunaan teorema 1.1.4 diperoleh
3
0 2
2] ( 1) ( )
) 1 [(
x
x f x X
E
= (-1)2f(0) + (0)2f(1) + (1)2f(2) + (2)2f(3) = (1)(1/3) + (0)(1/2) + (1)(0) + (4)(1/6) = 1.
Sekarang pengertian harapan matematik dapat diperluas dengan dua peubah acak X dan Y dengan distribusi peluang f(x,y).
Contoh.
Hitunglah E(Y/X) untuk fungsi padat
lainnya untuk x
0
1 y 0 2, x 0 , 4
) 3 1 ( ) , (
2
y x y x f
Jawab.
Dengan menggunakan definisi 1.1.5 diperoleh dxdy
y y Y
X
E 1
0 2
0
2
4 ) 3 1 ( )
(
= y y dy 1
0
3
2 ) 3 (
=
8 5
Latihan 1.1
1. Buktikan P(A – B) = P(A) – P(A∩B)
2. Buktikan P{A B C} = P{A} + P{B}+ P{C}- P{A∩B}- P{B∩C} - P{A∩C}+ P{A∩B∩C}
3. Buktikan P(Ǿ) = 0. Definisi 1.1.5
Bila X dan Y peubah acak dengan distribusi peluang gabungan f(x,y) maka nilai harapan fungsi g(X,Y) adalah
x y
y x f y x g Y
X g
E[ ( , )] ( , ) ( , ) bila X dan Y diskret
dxdy y x f y x g Y
X g
4. Buktikan peluang bersyarat memenuhi aksioma dalam definisi 1.1.1.
5. Misalkan Z adalah peubah acak diskrit yang mempunyai kemungkinan nilai 0, 1, 2, 3 dan fungsi massa peluang
p(0) = ¼ p(2) = 1/8
p(1) = ½ p(3) = 1/8
a. Tentukan rata-rata E[Z] b. Hitung variansi Var[Z]
6. Tentukan mean dan variansi dari peubah acak dengan fungsi padat peluang
nya untukxlain
x untuk x
x untuk x
x f
, 0
2 1
, 2
1 0
, )
BAB 2
RANTAI MARKOV WAKTU DISKRIT
2.1. Pengantar
Sejak abad yang lalu disadari akan manfaat dari model yang menggunakan peluang dibanding model yang deterministik (tertentu). Banyak phenomena fisika dan ilmu lainnya sekarang dipelajari adalah phenomena yang acak. Bahkan dalam phenomena sosial, teknik dan managemen pun diselidiki phenomena yang acak. Secara statistika hal menunjukkan bahwa kebutuhan akan peubah acak yang tergantung pada waktu (time) atau ruang (ruang) sangat terasa. Proses stokhastik (Stochastic Processes) adalah himpunan peubah acak yang merupakan fungsi dari waktu atau sering juga disebut proses acak.
Contoh dari proses stokhastik adalah sebagai berikut.
1. Misalkan Xn menyatakan hasil lemparan ke-n dari sebuah dadu. Maka {Xn , n > 1}
merupakan himpunan peubah acak, sehingga membentuk proses stokhastik.
2. Misalkan X(t) menyatakan banyaknya pengunjung yang masuk toko swalayan selama suatu periode waktu tertentu (0,t). Maka {X(t), t T} merupakan sebuah proses stokhastik.
Dari contoh 1, ruang statenya adalah {1, 2, 3, 4, 5, 6}.Untuk contoh 2, setiap harga t akan menghasilkan suatu peubah acak X(t) dan mempunyai ruang statenya sendiri. Misalnya ingin dicari ruang state X(2), yaitu banyaknya pengunjung selama 2 jam. Maka ruang statenya adalah {0, 1, 2, …}. Begitu juga untuk X(3) dan seterusnya.
Salah satu proses stokhastik yang penting adalah proses (rantai) Markov yang didefinisikan sebagai berikut.
Artinya peluang terjadinya kejadian pada hari ini hanya bergantung pada kejadian hari kemarin, kejadian besok hanya bergantung pada hari ini dan seterusnya.
Proses stokhastik dispesifikasikan ke dalam empat kelompok yaitu
1. waktu diskrit dan ruang state diskrit, seperti dalam pelemparan sebuah dadu. 2. waktu diskrit dan ruang state kontinu, curah hujan setiap hari.
Definisi 2.1.2
Sebuah proses stokastik {Xn, n = 0, 1, 2, …} disebut proses (rantai) Markov waktu
diskrit jika
P{Xn+1= j | X0 = i0, …, Xn-1= in-1, Xn = i} = P{Xn+1= j | Xn = i}
untuk setiap waktu n dan setiap state i0, i1, …, in-1, i, j.
Definisi 2.1.1
Himpunan harga-harga yang mungkin untuk suatu peubah acak Xn dari suatu proses
3. waktu kontinu dan ruang state diskrit, banyak pasien yang datang ke rumah sakit. 4. waktu kontinu dan ruang state kontinu, temperatur suatu daerah pada suatu interval waktu
Kita akan membicarakan rantai Markov yang mempunyai peluang transisi stationer
(stationary transition probabilities), yaitu peluang transisi yang bebas dari waktu n, sehingga Pijn,n1 Pij dan memeuhi
0
ij
P untuk i, j = 0, 1, 2, …
0 1
j ij
P untuk i = 0, 1, 2, …
Contoh
1. Seorang pegawai pergi bekerja setiap hari dengan kereta api atau bus. Dia tidak pernah naik kereta api dua hari berturut-turut. Tapi jika hari ini naik bus maka hari berikutnya dia bisa naik bus lagi atau kereta api. Ini merupakan rantai Markov, karena pilihan untuk esok hanya bergantung pada pilihan hari ini. Ruang state dari proses ini adalah {t (kereta api), b (bus)}. Maka matriks peluang transisinya adalah
2 / 1 2 / 1
1 0
b t
b t
2. Tiga orang anak A, B dan C sedang berlatih main bola. A selalu menendang bola ke B dan B selalu menendang bola ke C, tapi C menendang bola kepada yang disukainya, bisa ke A atau ke B. Misalkan Xn menunjukkan anak ke-n yang menendang bola. Ini
merupakan rantai Markov, karena pilihan anak menendang hanya bergantung pada yang terakhir memegang bola. Ruang state dari proses ini adalah {A, B, C}. Maka matriks peluang transisinya adalah
Definisi 2.1.3.
Peluang transisi satu langkah (one-step transition probability) didefinisikan sebagai }
|
{ 1
1
, P X j X i
Pijnn n n
Definisi 2.1.4 .
Matriks peluang transisi satu langkah dari rantai Markov didefinisikan sebagai
. . . . . . .
. . .
. . . . . . .
. . .
. . .
3 2 1 0
13 12 11 10
03 02 01 00
i i i i ij
P P P P
P P P P
P P P P
0 2 / 1 2 / 1
1 0 0
0 1 0
C B A
C B A
Bukti.
Misalkan P{X0 i0}i0. } ,...,
,
{X0 i0 X1 i0 Xn in
P
= P{X0 i0,X1i0,...,Xn1in1}.P{Xn in|X0 i0,X1i0,...,Xn1in1} = P{X0 i0,X1i0,...,Xn1in1}.P{Xn in|Xn1in1}
= P{X0 i0,X1i0,...,Xn1in1}. Pin1,in
Dengan cara induksi kita akan peroleh =
n n n
n i i i
i i i i
i P P P
P i X
P 0 0 , , , ,
1 1 2 2 1 0
0 ... ,
} ,
{
= i Pi i Pi i Pin in Pin ,in 1 1
, 2 2
, 1 1 , 0
0 ... ,
Contoh.
1. Misalkan seorang pejudi mempunyai modal awal M dolar. Tiap kali main dia pasang $1. peluang dia menang p dan kalah 1-p = q. Modal penjudi tersebut dapat mencapai 0 (habis) dan akan tetap sama dengan 0 untuk seterusnya. Tentukan fungsi peluang transisi dari proses tersebut.
Jawab.
Misalkan Xn , n ≥ 0 menyatakan banyaknya modal penjudi pada waktu n. Maka diperoleh
lainnya j , 0
1 -i j , q
1 i j , p Pi,j
2. Misalkan {Xn} adalah rantai Markov dengan ruang state {0, 1, 2} mempunyai matriks
peluang transisi Teorema 2.1.1
Jika P{X0 i0}i0 maka
n i n i i i i i i n
n i P P P
X i X i X
P{ 0 0, 1 1,..., } 0 0,1 1,2... 1, .
Definisi 2.1.5
Suatu state i dikatakan state menyerap (absorbing state) jika Pii = 1 atau Pij = 0
2 1 0
1 , 0 8 , 0 1 , 0
0 1 , 0 9 , 0
7 , 0 2 , 0 1 , 0
2 1 0 P
dan distribusi awal π0 = P{X0 = 0} = 0,3, π1 = P{X0 = 1} = 0,4, π2 = P{X0 = 2} = 0,3.
Tentukanlah P{X0 = 0, X1 = 1, X2 = 2}.
Jawab.
P{X0 = 0, X1 = 1, X2 = 2} =
0P
0,1P
1,2 = (0,3)(0,2)(0) = 0.Latihan 2.1
1. Seorang mahasiswa mempunyai kebiasaan belajar sebagai berikut. Jika dia belajar pada suatu malam, dia 70 % pasti tidak belajar pada malam berikutnya. Jika peluang dia tidak belajar dua malam berturut-turut, maka tentukanlah matriks peluang transisi dari proses tersebut.
2. Misalkan {Xn} adalah rantai Markov dengan ruang state {0, 1, 2} mempunyai matriks
peluang transisi
2 1 0
2 , 0 1 , 0 7 , 0
1 , 0 1 , 0 8 , 0
5 , 0 3 , 0 2 , 0
2 1 0 P
dan distribusi awal π0 = P{X0 = 0} = 0,4, π1 = P{X0 = 1} = 0,5, π2 = P{X0 = 2} = 0,1.
Tentukanlah P{X0 = 0, X1 = 1, X2 = 2}, P{X0 = 1, X1 = 0, X2 = 2}, P{X0 = 2, X1 = 1, X2
= 2}, P{X0 = 1, X1 = 1, X2 = 0}.
3. Misalkan pesan biner 0 dan 1 dikirim melalui chanel yang terdiri dari beberapa stage, dimana pengiriman melalui setiap stage mempunyai peluang kesalahan yang tetap yaitu sebesar α. Misalkan X0 = 0 adalah sinyal yang dikirim dan Xn adalah sinyal yang
diterima di stage ke-n. Asumsikan { Xn } adalah rantai Markov dengan peluang-peluang
transisi P00 = P11 = 1 - dan P01 = P10 = dimana 0 < < 1.
a. Tentukan peluang bahwa tidak terjadi kesalahan sampai stage ke-n = 2. b. Tentukan peluang bahwa sebuah sinyal yang benar diterima di stage 2.
Petunjuk: P{ X0 = 0, X1 = 0, X2 = 0} + P{ X0 = 0, X1 = 1, X2 = 0}
2.2. Matriks Peluang Transisi
Teorema 2.2.1
Peluang transisi n-langkah dari Rantai Markov memenuhi
0 k
1) (n kj ik (n)
ij P P
P (*)
dimana kita definisikan
j i , 0
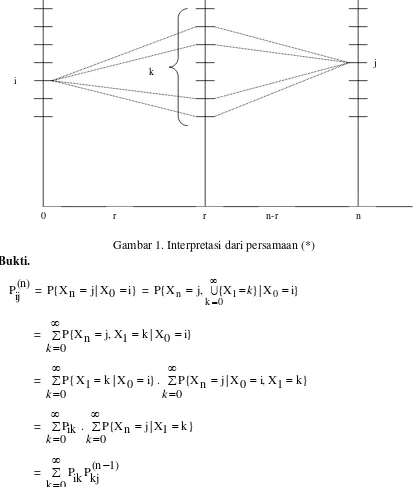
Persamaan (*) disebut persamaan Chapman-Kolmogorov dan diinterpretasikan seperti gambar berikut..
Bukti.
Pij(n) = P{Xn j |X0 i} = P{X j, {X } |X0 i} 0
k 1
n
k
=
0
i} 0 X | k 1 X j, n P{X k
=
0
i} 0 X | k 1 X P{ k
.
0
k} 1 X i, 0 X | j n P{X k
=
0ik P k
.
0
k} 1 X | j n P{X k
=
0 k
1) (n kj P ik P
Dari teori matriks kita mengenali bahwa relasi (*) adalah formula untuk perkalian matriks, sehingga P(n) = PxP(n-1) . Dengan iterasi formula ini maka diperoleh
P(n) = PxPxPx...xP = Pn,
Dengan kata lain Pij(n) adalah elemen dari matriks Pn. Jadi
0 r r n-r n
i k
j
Contoh.
Misalkan {Xn} adalah rantai Markov dengan ruang state {0, 1, 2} mempunyai matriks
peluang transisi
a. Tentukanlah matriks peluang transisi dua langkah P2. b. Tentukan P{X3 1 |X10}
c. Tentukan P{X3 1 |X0 0}
Jawab.
a. Untuk menentukan P2 ada dua cara yang bisa dilakukan yaitu dengan menggunakan teorema 2.2 dan dengan mengalikan matriks P dengan dirinya sendiri.
Cara I. Dengan cara yang sama diperoleh
c. P{X3 1 |X0 0} = P01(3)
=
2 0
2 k1 P 0k P k
= 00P P01(2) + 01P P11(2) + 02P P21(2) = (0,1)(0,13) + (0,2)(0,14) + (0,7)(0,17) = 0,16
Latihan 2.2
1. Misalkan matriks peluang transisi dari suatu rantai Markov adalah
2 / 1 2 / 1
0 1 P
Tentukanlah P21(3), P11(3).
2. Sebuah partikel bergerak diantara state 0, 1, 2 menurut proses Markov yang mempunyai matriks peluang transisi
0 0,5 0,5
0,5 0 0,5
0,5 0,5 0
2 1 0
2 1 0 P
Misalkan Xn menunjukkan posisi partikel pada gerakan ke-n. Hitunglah
0} 0 X | 0 n
P{X untuk n = 0, 1, 2, 3, 4.
3. Misalkan pesan biner 0 dan 1 dikirim melalui chanel yang terdiri dari beberapa stage, dimana pengiriman melalui setiap stage mempunyai peluang kesalahan yang tetap yaitu sebesar α. Misalkan X0 = 0 adalah sinyal yang dikirim dan Xn adalah sinyal yang
diterima di stage ke-n. Asumsikan { Xn } adalah rantai Markov dengan peluang-peluang
transisi P00 = P11 = 1 - dan P01 = P10 = dimana 0 < < 1. Tentukan
0} 0 X | 0 5
P{X , peluang transmisi yang benar melalui stage.
4. Misalkan Xn menunjukkan kualitas barang ke-n yang diproduksi oleh suatu sistem
produksi dengan Xn = 0 berarti “Bagus” dan Xn = 1 berarti “Cacat”. Anggap Xn adalah
rantai Markov dengan matriks peluang transisi
0,88 0,12
0,01 0,99
1 0
1 0 P
β β
-1
α
-1
α 1
0
1 0 P
Maka Zn = (Xn-1, Xn) adalah rantai Markov yang mempunyai empat state yaitu (0,0),
(0,1), (1,0) dan (1,1). Tentukan matriks peluang transisinya.
2.3. Beberapa Model Rantai Markov
2.3.1. Model Inventory
Misalkan sebuah barang harus tersedia agar dapat memenuhi permintaan. Asumsikan penambahan barang dilakukan pada akhir periode ke-n = 0, 1, 2, …. Misalkan δn
menyatakan total permintaan komoditi selama periode n, adalah peubah acak yang mempunyai fungsi distribusi bebas dari periode waktu,
k a k} n
P{δ untuk k = 0, 1, 2, …..
dimana ak ≥ 0 dan 1
0
k k
a
. Banyak stok diperiksa setiap akhir periode. Kebijakan
penambahan stok ditentukan oleh dua bilangan non-negatif s dan S > s dengan interpretasi sebagai berikut. Jika pada akhir periode jumlah stok tidak lebih besar dari s maka stok harus ditambah sehingga mencapai S. Jika stok lebih dari s maka tidak ada penambahan stok. Misalkan Xn menyatakan banyaknya stok pada akhir periode n. Maka state yang
mungkin untuk proses {Xn} adalah
S, S-1, …, +1, 0, -1, -2, …. Menurut aturan kebijakan inventory, diperoleh
s S
n X jika 1 n
δ
S
n X s jika n
δ
n X n X
Maka fungsi peluang transisinya dapat didefinisikan sebagai berikut. ij
P
= P{Xn1 j |Xn i}=
s S
i jika j} -S 1 n P{δ
i s jika } j -i 1 n P{δ
Contoh.
Dalam penyediaan spare part, dengan permintaan yang mungkin 0, 1, 2 dalam sebarang periode dan
0,5 0} n
P{δ P{δn 1}0,4 P{δn 2}0,1
Misalkan s = 0 dan S = 2. Maka ruang state dari proses {Xn} adalah {2, 1, 0, -1}. State -1
P10 = P{Xn10 |Xn 1}
= P{δn 1}0,4
Jika Xn = 1 dan Xn+1 = 0 maka berarti terdapat satu
permintaan, sehingga δn 1
P11 = P{Xn11 |Xn 1}
= P{δn 0}0,5
Jika Xn = 1 dan Xn+1 = 1 maka berarti tidak ada
permintaan, sehingga δn 0
Dengan cara yang sama maka diperoleh matriks peluang transisinya yaitu,
5 , 0 4 , 0 1 , 0 0
0 5 , 0 4 , 0 1 , 0
5 , 0 4 , 0 1 , 0 0
5 , 0 4 , 0 1 , 0 0
2 1 0 1
2 1 0 1 P
2.3.2. Rantai Ehrenfest
Misalkan tersedia dua kotak dan d buah bola dengan nomor 1, 2, ..., d. Pada awalnya sebuah bola berada di dalam kotak pertama, sedangkan sisanya berada di kotak kedua. Tersedia undian dengan nomor 1, 2, ..., d. Kemudian diambil selembar undian secara acak (undian dikembalikan sebelum pengambilan berikutnya). Bola dengan nomor yang sama dengan nomor undian yang terambil dipindahkan dari kotaknya dimasukkan ke kotak lain. Proses ini dilakukan tak hingga kali. Tentukan fungsi peluang transisi dari proses ini. Jawab.
Misalkan Xn menyatakan banyaknya bola pada kotak pertama setelah pengambilan (trial)
ke-n. Maka { Xn } adalah rantai Markov dengan ruang keadaan (state) S = {0, 1, 2, …, d}
Karena ada i bola pada kotak I, maka undian juga ada k. Maka peluang untuk mengambil bola dari kotak I adalah i/d dan bola ini dipindahkan ke kotak II. Maka
P{ Xn+1 = i-1 | Xn = i } = Pi,(i-1) =
d i
Kotak I Kotak II Undian
i bola pada waktu n
Dengan cara yang sama diperoleh
P{ Xn+1 = i+1 | Xn = i } = Pi,(i+1) =
d i -d
P{ Xn+1 = j | Xn = i } = Pi,j = 0 untuk j i + 1 dan j i - 1
Maka fungsi peluang transisinya adalah
lainnya j 0,
1 i j , i)/d (d
1 -i j , i/d j
i,
P
Untuk d = 3 maka matriks peluang transisinya adalah
0 1 0 0
3 / 1 0 3 / 2 0
0 3 / 2 0 3 / 1
0 0 1 0 P
Latihan 2.3
1. Misalkan model inventory suku cadang yang diperbaiki 0, 1, dan 2 diminta dalam sebarang periode dengan
P{ δn = 0} = 0,4 P{ δn = 1} = 0,3 P{ δn = 2} = 0,3
dan misalkan s = 0 dan S = 3. Tentukan matriks peluang transisi untuk rantai Markov {Xn} dimana Xn didefinisikan sebagai jumlah barang yang tersedia pada akhir period
eke-n.
2. Sebuah kotak A dan B memuat N bola. Sebuah bola diambil secara acak diantara N bola yang ada. Kemudian kotak dipilih secara acak (A terpilih dengan peluang p dan B terpilih dengan peluang q) dan bola yang terambil ditempatkan ke dalam kotak ini. State dari tiap pengambilan dinyatakan sebagai banyaknya bola di kotak A. Tentukanlah matriks peluang transisi dari rantai Markov ini.
3. Sebuah kotak A dan B memuat N bola. Misalkan pada waktu t terdapat tepat k bola di A. Pada waktu t+1 sebuah kotak dipilih secara acak dalam proporsi isinya (yaitu A terpilih dengan peluang k/N dan B terpilih dengan peluang (N-k)/N). Kemudian bola dipilih dari A dengan peluang p atau dari B dengan peluang q dan ditempatkan ke dalam kotak yang terpilih sebelumnya. Tentukanlah matriks peluang transisi dari rantai Markov ini.
4. Misalkan model inventory yang direview secara periodik dan δn adalah total permintaan
dalam periode n dan Xn adalah jumlah barang di akhir periode n. Sebuah kebijakan (s,
a. Anggap s = 1, S = 4 dan X0 = S = 4. Jika δ1 = 2, δ2 = 3, δ3 = 4, δ4 = 0, δ5 = 2, δ6 = 1
δ7 = 2, δ8 = 2, berapa tingkat stok Xn di akhir periode n = 1, 2, …, 8.
b. Anggap δn , δn , … adalah peubah acak independen dimana P{ δn = 0} = 0,1,
P{ δn = 1} = 0,3, P{ δn = 2} = 0,3, P{ δn = 3} = 0,2, dan P{ δn = 4} = 0,1. Maka X0 ,
X1 , …. adalah rantai Markov. Tentukan P41 dan P04.
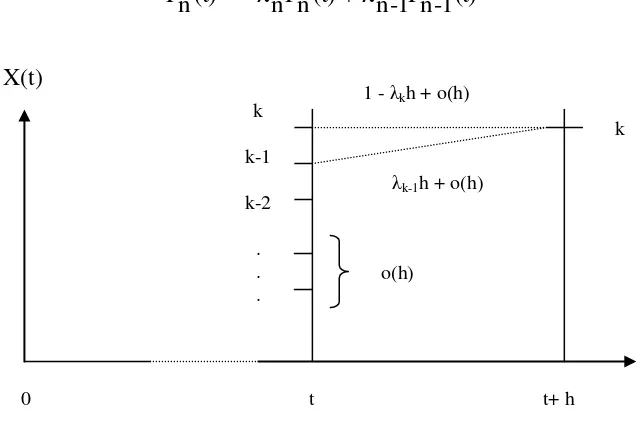
2.4. Analisis Langkah Pertama Sederhana
Misalkan {Xn} adalah rantai Markov dengan matriks peluang transisi
1 0 0
γ β α
0 0 1
2 1 0
2 1 0 P
dimana > 0, β > 0, γ > 0 dan α + β + γ = 1. Jika proses mulai di state 1 maka proses akan terserap di state 0 atau state 2. Sekarang timbul dua pertanyaan berapa lama waktu dibutuhkan dan berapa rata-rata banyaknya langkah dibutuhkan sehingga proses terserap. Kedua pertanyaan tersebut dengan mudah dapat dijawab dengan menggunakan analisis langkah pertama sebagai berikut.
Misalkan
T = min { n ≥ 0 | Xn = 0 atau Xn = 2 }
adalah waktu yang dibutuhkan proses sampai terserap. Selanjutnya misalkan u adalah peluang proses sampai ke state menyerap dan v adalah rata-rata banyaknya langkah dibutuhkan sampai proses ke state menyerap, jika dimulai di state 1 (X0 = 1) , sehingga
u = P{XT 0 |X0 1}. v = E{T |X0 1}
Untuk menentukan u dan v digunakan analisis langkah pertama Ada 3 kemungkinan untuk X1 yaitu X1 = 0, X1 = 2 dan X1 = 1.
Kemungkinan I, X1 = 0
Maka diperoleh T = 1, sehingga P{XT 0 |X0 1} = P{X10 |X0 1} = dan jika X0 = 0 maka P{XT 0 |X0 0} = P{X1 0 |X0 0} = 1.
Kemungkinan II, X1 = 2.
Maka diperoleh T = 1, sehingga P{XT 2 |X0 1} = P{X12 |X0 1} = γ dan 2}
1 X | 0 T
P{X = P{X10 |X12} = 0. Kemungkinan III, X1 = 1.
Maka
u = P{XT0 |X01}
=
2 0 k
1} 0 X | k 1 X 0, T P{X
=
2 0 k
1} 0 X | k 1 }P{X k 1 X 1, 0 X | 0 T P{X
=
2 0 k
1} 0 X | k 1 }P{X k 1 X | 0 T P{X
= P{XT 0 |X10}.P{X10 |X0 1} + P{XT 0 |X11}.P{X11 |X0 1} + P{XT 0 |X1 2}.P{X12 |X0 1}
= 1() + u(β) + 0(γ) Sehingga diperoleh
β
-1
α
u atau
γ α
α
u
Selanjutnya rata-rata waktu yang dibutuhkan sampai proses terserap adalah v = E{T |X0 1}
=
2
0 k
1} 0 X | k 1 X E{T, 1
=
2
0 k
1} 0 X | k 1 }P{X k 1 X 1, 0 X | E{T 1
=
2 1 1 0
0
k E{T |X k }P{X k |X 1} 1
= 1 + E{T |X10}.P{X1 0 |X0 1} + E{T |X11}.P{X11 |X0 1} + E{T |X12}.P{X12 |X0 1}
= 1 + (0)() + (v)(β) + (0)(γ) Sehingga diperoleh
β
-1
1
v
1 0 0 0
23 22 21 20
13 12 11 10
0 0 0 1
3 2 1 0
3 2 1 0 P
P P P P
P P P P
Penyerapan terjadi di state 0 dan 3 dan state 1 dan 2 adalah “transient”. Misalkan
T = min{ n ≥ 0 | Xn = 0 atau Xn = 3 }
ui = P{XT 0 |X0 i} untuk i = 1,2
vi = E{T |X0 i} untuk i = 1,2
Maka u0 = 1, u3 = 0 dan v0 = v3 = 0. Ada dua kemungkinan untuk keadaan awal yaitu
X0 = 1 dan X0 = 2.
Misalkan X0 = 1.
Maka dengan menggunakan analisis langkah pertama diperoleh u1 = P{XT0 |X01}
=
3 0 k
1} 0 X | k 1 X 0, T P{X
=
3 0 k
1} 0 X | k 1 }P{X k 1 X 1, 0 X | 0 T P{X
=
3 0 k
1} 0 X | k 1 }P{X k 1 X | 0 T P{X
= P{XT 0 |X10}.P{X10 |X0 1} + P{XT 0 |X11}.P{X11 |X0 1} + P{XT 0 |X1 2}.P{X12 |X0 1} + P{XT 0 |X13}.P{X13 |X0 1}
= (u0)P10 + (u1)P11 + (u2)P12 + (u3)P13
Dengan cara yang sama jika X0 = 2 maka diperoleh
u2 = (u0)P20 + (u1)P21 + (u2)P22 + (u3)P23
Secara umum kita punya
nj j ij
i
u
P
u
0
untuk i = 0, 1, 2, …, n
Contoh.
Seekor tikus dimasukkan ke dalam “Maze” berikut
0 1 7 makanan (ruang 7) sebelum kena setrum (ruang 8) jika tikus dilepas di ruang i.
Jawab.
Misalkan Xn adalah ruangan yang ditempati tikus pada langkah ke-n. Matriks peluang
transisinya adalah
dilepaskan di ruang i. Maka diperoleh persamaan
5